Estabilização de órbitas periódicas instáveis utilizando controle por modos deslizantes com compensação adaptativa

(1)

ESTABILIZAÇ ÃO DE ÓRBITAS PERI ÓDICAS INST ÁVEIS UTILIZANDO CONTROLE POR MODOS DESLIZANTES COM COMPENSAÇ ÃO

ADAPTATIVA

Geraldo Francisco de Souza Rebou¸cas

Disserta¸cão de Mestrado apresentada ao Programa de Pós-gradua¸cão em Engenharia Mecânica, da Universidade Federal do Rio Grande do Norte, como parte dos requisitos necessários à obten¸cão do t´ıtulo de Mestre em Engenharia Mecânica.

Orientador: Wallace Moreira Bessa

(2)

(3)

Rebou¸cas, Geraldo Francisco de Souza

Estabiliza¸cão de órbitas periódicas instáveis utilizando controle por modos deslizantes com compensa¸cão adaptativa/Geraldo Francisco de Souza Rebou¸cas. – Natal: UFRN/PPGEM, 2014.

XV, 79 p.: il.; 29,7cm.

Orientador: Wallace Moreira Bessa

Disserta¸c˜ao (mestrado) – UFRN/PPGEM/Programa de Engenharia Mecˆanica, 2014.

Referˆencias Bibliogr´aficas: p. 74 – 78.

(4)

`

(5)

Agradecimentos

Aos meus amigos e colegas do curso de Engenharia Mecânica da UFRN e também aos meus professores, tanto da gradua¸cão como da pós-gradua¸cão, com seus desafios que me instigaram a estudar cada vez mais.

Aos meus amigos da Rep´ublica do Jambeiro, tanto os antigos como os novos moradores. Os Engs. Kletson Vieira, Thallys Belo, Francisco Jonas, Marcel Abreu e Samuelson Nascimento, bem como a Amauri Morais. Obrigado pelas brincadeiras, gargalhadas e pelo apoio durante minha jornada na UFRN.

Ao M.Sc. João Deodato, com seu apoio alvoro¸cado mas sempre bem-humorado em vários momentos que vivi dentro desta institui¸cão, estando sempre aberto a conversar e sugerir caminhos para o prosseguimento das pesquisas que culminaram na elabora¸cão deste trabalho.

Ao mestrando Andr´e Lopes e aos doutorandos Marcelo Tanaka e Josiane Fer-nandes, sempre dispostos a trocar ideias, tirar d´uvidas e ajudar.

Ao meu orientador Prof. DSc. Wallace Moreira Bessa, que me propôs um tema tão interessante, por seus conselhos e conversas elucidativas sobre os mais variados assuntos, acadêmicos ou não.

(6)

Resumo da Disserta¸cão apresentada à UFRN como parte dos requisitos necessários para a obten¸cão do grau de Mestre em Ciências (M.Sc.)

ESTABILIZAÇ ÃO DE ÓRBITAS PERI ÓDICAS INST ÁVEIS UTILIZANDO CONTROLE POR MODOS DESLIZANTES COM COMPENSAÇ ÃO

ADAPTATIVA

Janeiro/2014

Orientador: Wallace Moreira Bessa Programa: Engenharia Mecˆanica

(7)

Abstract of Dissertation presented to UFRN as a partial fulfillment of the requirements for the degree of Master of Science (M.Sc.)

STABILIZATION OF UNSTABLE PERIODIC ORBITS USING SLIDING MODE CONTROL WITH ADAPTIVE COMPENSATION

January/2014

Advisor: Wallace Moreira Bessa Department: Mechanical Engineering

(8)

Sum´

ario

Lista de Figuras x

Lista de Tabelas xii

Lista de S´ımbolos xiii

Lista de Abreviaturas xv

1 Introdu¸c˜ao 1

1.1 Organiza¸c˜ao do Trabalho . . . 2

2 Sistemas Ca´oticos 4 2.1 Oscilador de Duffing . . . 5

2.2 Bifurca¸c˜oes . . . 8

2.3 Se¸c˜ao de Poincar´e . . . 11

2.4 Orbitas peri´odicas inst´aveis . . . 13´

3 T´opicos de Controle N˜ao Linear 17 3.1 Estabilidade . . . 17

3.1.1 Teoria de Estabilidade de Lyapunov . . . 18

3.2 Controle por Modos Deslizantes . . . 21

3.2.1 Aplica¸c˜ao com fun¸c˜ao sinal . . . 27

3.2.2 Aplica¸cão com fun¸cão de satura¸cão . . . 31

3.3 Controle de Sistemas Ca´oticos . . . 31

3.3.1 Aplica¸cão: Órbita Periódica Instável . . . 34

4 Compensa¸cão Adaptativa 37 4.1 Aplica¸cão: Órbita Periódica Instável . . . 41

5 Estabiliza¸cão de Órbitas Periódicas Instáveis 44 5.1 Dependência paramétrica . . . 45

5.2 Controle de Caos . . . 49

(9)

5.2.2 Aplica¸c˜ao: Varia¸c˜ao de ±10% . . . 50

5.2.5 Aplica¸cão: Órbita genérica . . . 54

5.3 Estimativa do desempenho . . . 56

5.3.1 Aplica¸c˜ao: Varia¸c˜ao de +7% . . . 57

5.4 Estabiliza¸c˜ao de OPIs de periodicidade elevada . . . 57

6 Conclusões 62 A Leis adaptativas integrais 64 A.1 Aplica¸cão: Órbita genérica . . . 67

(10)

Lista de Figuras

2.1 Reprodu¸c˜ao do gr´afico obtido por Lorenz, (GLEICK, 1987) . . . 5

2.2 Desenho esquem´atico do pˆendulo for¸cado . . . 6

2.3 Configura¸c˜oes poss´ıveis para |a2|= 0,2 e|a3|= 1,19 . . . 7

2.4 Desenho esquem´atico da viga de Moon . . . 7

2.5 Diagrama de bifurca¸c˜ao para o mapa log´ıstico . . . 9

2.6 Diagrama de bifurca¸c˜ao para o estadox1 . . . 10

2.7 Amplia¸c˜oes da Figura 2.6 . . . 11

2.8 Aplica¸cão das ideias de Poincaré à fun¸cão senoidal . . . 12

2.9 Aplica¸c˜ao das ideias de Poincar´e a um problema mais complexo . . . 12

2.10 Se¸c˜oes de Poincar´e para o oscilador de Duffing da Eq. 2.3, ambas desprezando os primeiros 30% instantes iniciais . . . 13

2.11 Amplia¸c˜oes sucessivas da Figura 2.9 . . . 13

2.12 Rela¸cão entre OPIs e a Se¸cão de Poincaré . . . 15

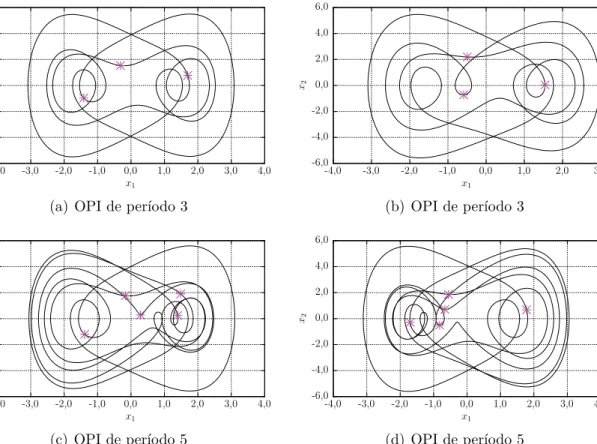
2.13 OPIs de per´ıodo 3 e 5 . . . 16

3.1 Visualiza¸cão gráfica de uma fun¸cão de energia e sua derivada . . . 20

3.2 Representa¸cão esquemática das fases de aproxima¸cão e deslizamento no plano de fase do erro . . . 23

3.3 Representa¸cão gráfica do comportamento da fun¸cão sinal, sgn(s) . . . 25

3.4 Modos deslizantes com fun¸c˜ao sinal . . . 29

3.5 Representa¸cão gráfica do comportamento da fun¸cão de satura¸cão, sat(s) 30 3.6 Representa¸cão gráfica da superf´ıcie de deslizamento com a fun¸cão de satura¸cão . . . 30

3.7 Modos deslizantes com fun¸c˜ao de satura¸c˜ao . . . 32

3.8 Compara¸cão entre a OPI e a órbita genérica . . . 34

3.9 Modos deslizantes com fun¸cão de satura¸cão e OPI como referência . . 35

4.1 Modos deslizantes com compensa¸c˜ao adaptativa . . . 42

5.1 Resposta temporal . . . 45

5.2 Se¸c˜oes de Poincar´e para diferentes valores de a3 . . . 46

(11)

5.4 Compara¸c˜ao entre as OPIs de per´ıodo 3 . . . 48

5.5 Compara¸c˜ao entre as OPIs de per´ıodo 5 . . . 48

5.6 Modos deslizantes suavizados . . . 50

5.7 Modos deslizantes suavizados e compensa¸c˜ao adaptativa . . . 51

5.8 Varia¸c˜ao de ±10%: Modos deslizantes e compensa¸c˜ao adaptativa . . . 52

5.11 Estabiliza¸cão de uma órbita genérica . . . 55

5.12 Desempenho do CMD+CA em fun¸cão da varia¸cão paramétrica . . . . 58

5.13 Varia¸c˜ao de +7%: Modos deslizantes e compensa¸c˜ao adaptativa . . . 59

5.14 OPI de per´ıodo 3, varia¸c˜ao de +10% . . . 60

5.15 OPI de per´ıodo 5, varia¸c˜ao de +10% . . . 61

A.1 Modos deslizantes com compensa¸c˜ao adaptativa . . . 68

A.2 Comportamento dos coeficientes we,i . . . 69

A.3 Modos deslizantes com compensa¸c˜ao adaptativa normalizada . . . 70

A.4 Compensa¸c˜ao adaptativa normalizada: comportamento dos coefici-entes we,i. . . 71

A.5 Modos deslizantes com compensa¸c˜ao adaptativa, we unit´ario . . . 72

(12)

Lista de Tabelas

3.1 Resultados obtidos pelo controlador por modos deslizantes . . . 31

3.2 Controlador por modos deslizantes, OPI e ´orbita gen´erica . . . 34

4.1 Controlador adaptativo por modos deslizantes . . . 43

5.1 Compara¸c˜ao entre o CMD e o CMD+CA . . . 50

5.2 Desempenho do controlador por modos deslizantes com compensa¸c˜ao adaptativa . . . 56

5.3 Desempenho do controlador por modos deslizantes com compensa¸c˜ao adaptativa para OPIs . . . 57

5.4 An´alise das estimativas . . . 57

(13)

Lista de S´ımbolos

ai i-´esima constante, p. 6

ω Frequˆencia de oscila¸c˜ao, p. 6

t Tempo, p. 6

x Vetor de estado, p. 8

xi i-ésima variável de estado do sistema, ou i-ésima componente do vetor de estado, p. 8

y Sa´ıda de interesse de determinado sistema, p. 8

T Per´ıodo de oscila¸c˜ao, p. 11

Pi i-ésimo ponto da se¸cão de Poincaré, p. 14

j Periodicidade de determinada OPI, p. 14

r1 Distância entre dois pontos na se¸cão de Poincaré, p. 14

V(·) Candidata a fun¸c˜ao de Lyapunov, p. 20

x(n) _n_{-ésima derivada de} _x _{em rela¸cão ao tempo, p. 21} f(t,x) Fun¸cão que representa a dinâmica do sistema, p. 21

b(t,x) Ganho do esfor¸co de controle, p. 21

u(t,x) Esfor¸co de controle, p. 21

fe(t,x) Estimativa para a fun¸c˜aof(t,x), p. 21

F(t,x) Fun¸c˜ao delimitadora, p. 21

bm Ganho m´ınimo do esfor¸co de controle, p. 21

bM Ganho m´aximo do esfor¸co de controle, p. 21

(14)

ei i-´esima componente do erro, p. 22

xi,d i-´esima vari´avel de estado desejada, p. 22 e Vetor de erro, p. 22

xd Vetor de estado desejado, p. 22

s Vari´avel de deslizamento, p. 22

λ Taxa de convergˆencia do erro, p. 22 c Vetor de coeficientes, p. 23

η Taxa de convergˆencia para a superf´ıcie de deslizamento, p. 24

ue Estimativa do esfor¸co de controleu(t,x), p. 24

K ganho da fun¸cão sinal e da fun¸cão de satura¸cão, p. 25

EQM Erro quadr´atico m´edio, p. 26

p Quantidade de itera¸c˜oes, p. 26

φ Espessura da regi˜ao limite, p. 29

d(t,x) Perturba¸cões, distúrbios externos e dinâmica não modelada, p. 37

δ Valor limite das perturba¸c˜oes e dist´urbios, p. 37

de(t) Termo de compensa¸c˜ao adaptativa, p. 39 we Vetor de coeficientes de Fourier, p. 40

θ₍_t₎ _{Vetor de fun¸c˜oes senoidais, p. 40}

σ Diferen¸ca percentual param´etrica, p. 44

(15)

Lista de Abreviaturas

EDO Equa¸cão Diferencial Ordinária, p. 5 OPI Orbita Periódica Instável, p. 14´

CMD Controle/Controlador por Modos Deslizantes, p. 21 EQM Erro Quadr´atico M´edio, p. 26

(16)

Cap´ıtulo 1

Introdu¸

c˜

ao

Desde a segunda metade do século passado f´ısicos, biólogos, matemáticos, enge-nheiros, economistas dentre outros desenvolveram uma nova abordagem para a com-plexidade existente na natureza, o Caos. Com ele passamos a perceber organiza¸cão e padrões onde antes só havia aleatoriedade, imprevisibilidade e irregularidade.

O comportamento caótico tem sido amplamente observado na natureza, tanto em fenômenos f´ısicos e qu´ımicos quanto em sistemas biológicos. O caos também está presente em diversas aplica¸cões de engenharia, sejam elas mecânicas ou elétricas, podendo ser encontrado em simples osciladores mecânicos e nos mais avan¸cados sistemas de comunica¸cão. No que concerne aos sistemas mecânicos, comumente os efeitos das não-linearidades sobre o comportamento dinâmico do sistema são de caráter indesejável.

Recentemente tem-se verificado que existem situa¸cões nas quais a riqueza da dinâmica não-linear torna-se atraente. O comportamento caótico, por exemplo, possui uma grande sensibilidade às condi¸cões iniciais e ao valor dos parâmetros, o que implica no fato de que mudan¸cas significativas no comportamento de um sistema caótico podem ser atingidas mediante pequenas varia¸cões paramétricas. Deste modo, esta caracter´ıstica pode ser extremamente favorável quando se tem por objetivo dar maior flexibilidade ao sistema dinâmico controlado.

A infinidade de órbitas periódicas instáveis, OPIs que estão associadas a uma resposta caótica, nos permite, através de pequenas corre¸cões em um único parâmetro de controle, conseguir que um sistema caótico se adeque às mais variadas condi¸cões, e se comporte de modo inteiramente distinto, conforme a situa¸cão desejada (OTT

et al., 1990).

(17)

apenas seu diagrama de bifurca¸cão, mas também como se comportam suas se¸cões de Poincaré e suas órbitas periódicas instáveis. Vale ressaltar a importância deste estudo uma vez que na prática conseguimos obter apenas valores aproximados para os parâmetros do modelo, que podem alterar seu comportamento mesmo estando próximos aos valores reais do sistema f´ısico.

O controle por modos deslizantes, desenvolvido na extinta União Soviética com os trabalhos de EMELYANOV e KOSTYLEVA (1964), FILIPPOV (1964), ITKIS (1976), UTKIN (1977) dentre outros, tem como objetivo dividir a tarefa de controle em um conjunto de sub tarefas mais simples (SLOTINE e LI, 1991), sendo ampla-mente utilizado no controle de diversos sistemas não lineares, e aplicado também a sistemas caóticos, devido às suas caracter´ısticas de tolerância em rela¸cão a distúrbios e incertezas de modelagem, conforme mostrado em ABLAY (2009), DADRASet al.

(2009) e SALARIEH e ALASTY (2009), não oferecidas pelos métodos clássicos de controle de caos, (FUH e TUNG, 1996).

No entanto esta estratégia pode resultar em oscila¸cões de alta frequência no esfor¸co de controle, fato indesejado a sistemas mecânicos. Para contornar este pro-blema podemos suavizar o esfor¸co de controle. No entanto, essa solu¸cão implica no surgimento de uma região de erro residual.

Com o objetivo de reduzir o erro residual podemos adotar estratégias de com-pensa¸cão adaptativa, conforme observado em BARI Ć et al. (2005), que utilizam redes neurais do tipo perceptron de múltiplas camadas, e HUANG e KUO (2001) que utilizam séries de Fourier para a aproxima¸cão do termo compensador. Além de BESSA et al. (2013), BESSA et al. (2012), BESSA et al. (2009) e LAYEGHI

et al. (2008), que utilizam lógica difusa como fun¸cão aproximadora para controlar sistemas caóticos.

Neste trabalho analisaremos como o esfor¸co de controle, necessário para estabi-lizar uma OPI, se comporta frente a diferentes n´ıveis de varia¸cão paramétrica. Para tanto, utilizaremos o controle por modos deslizantes com compensa¸cão adaptativa cujas fun¸cões de base compõem uma série de Fourier. Para o desenvolvimento do controlador utilizaremos inicialmente órbitas genéricas, passando em seguida a utili-zar como referência OPIs pertencentes ao modelo nominal, finalizando com a adi¸cão do termo de compensa¸cão adaptativa para reduzir o erro residual.

1.1 Organiza¸

c˜

ao do Trabalho

Visando facilitar o entendimento deste trabalho decidimos divid´ı-lo em 5 cap´ıtulos. Este primeiro cap´ıtulo contempla uma introdu¸c˜ao sobre o tema de estudo, apresen-tando nossa motiva¸c˜ao inicial, bem como os objetivos que esperamos alcan¸car.

(18)

oscilador de Duffing, falando de sua história, aplica¸cão em diversos campos da en-genharia e interpreta¸cão f´ısica. Em seguida conceituamos algumas das principais ferramentas para análise de sistemas caóticos, como o diagrama de bifurca¸cão e a se¸cão de Poincaré, aplicando-as ao oscilador de Duffing. Tratamos também da iden-tifica¸cão de órbitas periódicas instáveis, que, conforme veremos adiante, têm papel fundamental no controle de caos.

Iniciamos o Cap´ıtulo 3 com a defini¸cão de estabilidade, e uma rápida introdu¸cão sobre a teoria de estabilidade de Lyapunov. Em seguida desenvolvemos um contro-lador por modos deslizantes, inicialmente utilizando a fun¸cão sinal e posteriormente a fun¸cão de satura¸cão. Em ambos os casos controlamos o oscilador de Duffing numa órbita genérica. Em seguida apresentamos uma breve revisão sobre as estratégias clássicas para controle de sistemas caóticos, que se baseiam na utiliza¸cão de órbitas periódicas instáveis, devido a pequena quantidade de energia necessária para es-tabilizá-las. Utilizando modos deslizantes para controlar uma OPI de per´ıodo 1, pudemos notar a diminui¸cão no esfor¸co de controle em rela¸cão a órbita genérica.

No Cap´ıtulo 4, apresentamos a estratégia de compensa¸cão adaptativa para di-minuir o erro residual apresentado pela utiliza¸cão da fun¸cão de satura¸cão no con-trolador por modos deslizantes. Como fun¸cão aproximadora utilizamos uma série de Fourier truncada em 3 termos, cujos coeficientes, os termos que multiplicam as fun¸cões trigonométricas, são ajustados utilizando uma lei de adapta¸cão deduzida com base na teoria de Lyapunov.

Para avaliar o desempenho do termo de compensa¸cão e de sua lei adaptativa, controlamos novamente a OPI de per´ıodo 1 do cap´ıtulo anterior, comparando o desempenho de ambos os controladores não apenas graficamente, mas também com o erro quadrático médio obtido em cada caso.

No come¸co do Cap´ıtulo 5 estudamos a sensibilidade paramétrica do oscilador de Duffing, com foco sobre o parâmetro que multiplica o termo cúbico. Analisamos como se comportam sua resposta temporal, sua se¸cão de Poincaré e as OPIs que fazem parte de cada configura¸cão.

Em seguida utilizamos o controlador por modos deslizantes com compensa¸cão adaptativa desenvolvido no Cap´ıtulo 4 para estabilizar uma OPI de per´ıodo 1 sub-metida a diferentes n´ıveis de varia¸cão paramétrica. Com isso, pudemos derivar rela¸cões entre os coeficientes de performance do controlador utilizado e a varia¸cão paramétrica sobre o sistema. Conclu´ımos este cap´ıtulo com a estabiliza¸cão de OPIs de periodicidade elevada.

No Cap´ıtulo 6 apresentamos nossas considera¸cões finais, conclusões obtidas, e sugestões para trabalhos futuros.

(19)

Cap´ıtulo 2

Sistemas Ca´

oticos

Com o surgimento da ciência moderna em meados do século XVI, a humanidade come¸cou a procurar a explica¸cão para os fenômenos presentes na natureza, bus-cando entendê-la por completo. Inicialmente estudou-se o movimento dos corpos, avan¸cando em seguida com o estudo dos fluidos, ondas, eletricidade etc. (GLEICK, 1987).

Na literatura existem vários trabalhos que se propõem a desvendar os fenômenos da natureza utilizando vários modelos matemáticos que levam em considera¸cão várias caracter´ısticas diferentes. Após um estudo teórico sobre cada modelo, prosse-gue-se com a realiza¸cão de experimentos para comprovar a teoria. E nesse ponto sempre existem divergências. Normalmente considera-se que tal fato se deve a al-guns fatores desprezados no modelo teórico, tais como resistência do ar, ru´ıdo, atrito, dentre outros.

Algumas justificativas para se desprezar as não linearidades são a busca de um melhor entendimento do sistema através de sua simplifica¸cão, ou que os termos não lineares podem ser aproximados linearmente, ou até que eles são desprez´ıveis.

Na mecânica dos fluidos e sistemas mecânicos os termos não lineares tendem a ser os termos que queremos deixar de fora quando buscamos compreender estes conceitos de uma maneira mais simples. Sem o atrito, por exemplo, a equa¸cão do movimento representa uma condi¸cão singular, como o deslizar de um disco de hóquei no gelo. O atrito altera a velocidade e sofre altera¸cões por causa da velocidade, o que cria um comportamento de grande riqueza, não observado em sistemas lineares. Em meados do século XX, com o surgimento dos primeiros computadores, cientis-tas e engenheiros come¸caram a utilizar tais máquinas para simular o comportamento de sistemas reais e assim as simula¸cões passaram a ser um novo tipo de experimento. Em suas simula¸cões, o meteorologista e matemático americano Edward Lorenz1_,

visando diminuir o tempo de processamento computacional de seu experimento

1

(20)

numérico, resolveu simplificar um modelo de equa¸cões (diferenciais parciais) con-vectivas2 _{em três equa¸cões diferenciais ordinárias, EDOs, preservando, no entanto,}

suas caracter´ısticas não lineares. Com isso ele obteve alguns resultados estranhos para várias repeti¸cões da mesma simula¸cão, (LORENZ, 1963).

Buscando aumentar a dura¸cão de seu experimento computacional, Lorenz uti-lizou dados obtidos no decorrer de uma simula¸cão anterior. Na verdade ele arre-dondou dados impressos pelo computador pois pensava que pequenas altera¸cões nas condi¸cões iniciais do seu sistema de EDOs não lineares seriam irrelevantes, tal como acontece para sistemas lineares. No entanto observou-se o contrário, um gráfico com os dois experimentos, como o da Figura 2.1, mostrou que ao invés de tenderem a se aproximar, as curvas se afastaram, de modo que após algumas itera¸cões os gráficos são completamente distintos.

Figura 2.1: Reprodu¸cão do gráfico obtido por Lorenz, (GLEICK, 1987) Era o Efeito Borboleta: para pequenas varia¸cões nas condi¸cões meteorológicas qualquer previsão perde o valor rapidamente. Os erros e as incertezas se multipli-cam, formando um efeito de cascata ascendente através de uma cadeia de aspectos turbulentos, que vão de tormentas a redemoinhos continentais. O Efeito Borboleta ganhou assim um nome técnico: dependência sens´ıvel às condi¸cões iniciais.

2.1 Oscilador de Duffing

A equa¸cão de Duffing é uma EDO não linear de segunda ordem que, conforme pode ser observado em BRENNAN e KOVACIC (2011), descreve o comportamento qualitativo e quantitativo de vários sistemas f´ısicos como circuitos elétricos, vigas, rotores, placas, fibras ópticas, cascas e alguns sistemas biológicos. Possui este nome em homenagem ao Engenheiro Mecânico alemão Georg Duffing (1861–1944) que foi um dos pioneiros na análise de sistemas não lineares, tratando do comportamento de sistemas cuja rigidez não obedece a lei de Hooke. Em seu trabalho, Duffing analisou inicialmente a dinâmica de um pêndulo livre prosseguindo com a análise do caso for¸cado, conforme mostrado na Figura 2.2.

2

(21)

ωt M sen

m

θ

m g

l

Figura 2.2: Desenho esquem´atico do pˆendulo for¸cado

ml2d2θ

dt2 +mglsenθ =Msenωt

Para chegar a sua famosa equa¸c˜ao, Duffing utilizou s´eries de Taylor3_{, uma}

ferra-menta comumente utilizada para lineariza¸cão de sistemas não lineares. No entanto, ao linearizar o termo senθ em torno de 0 rad, Duffing foi além e, em vez de consi-derar apenas o primeiro termo da série, que é a prática tradicional, ele considerou também o termo cúbico, gerando assim um polinômio não linear.

ml2d 2_θ

dt2 +mgl

θ− θ

3

6

=Msenωt (2.1)

Apesar de continuar com um sistema não linear, Duffing passou de uma equa¸cão diferencial transcendental para uma equa¸cão diferencial algébrica, o que auxiliou na obten¸cão dos pontos de equil´ıbrio para o caso de oscila¸cões livres. Utilizando esta abordagem ele obteve uma melhor descri¸cão matemática do comportamento real do sistema.

Neste trabalho analisaremos a forma geral desta equa¸c˜ao, que adiciona amorte-cimento viscoso linear ao sistema estudado originalmente por Duffing. Com isso, chegamos a seguinte equa¸c˜ao:

¨

θ+a1θ˙+a2θ+a3θ3 =a4sen(ωt) (2.2) onde as constantes a1, a2, a3 e a4 representam, respectivamente, os coeficientes de amortecimento, rigidez linear, rigidez c´ubica e a amplitude do for¸camento senoidal. Do ponto de vista mecˆanico, podemos entender o termoa2θ+a3θ3_{como uma mola}

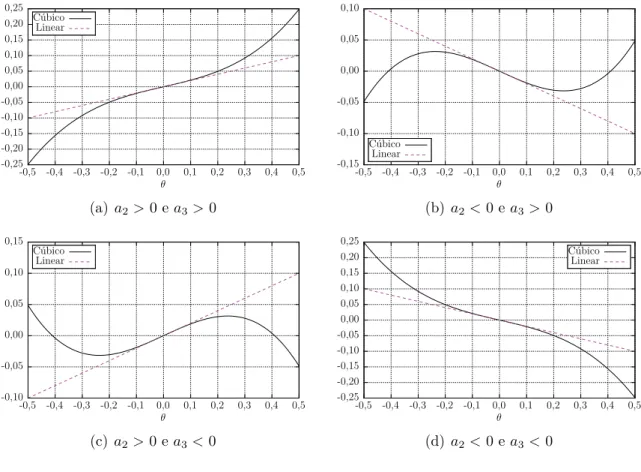
que apresenta rigidez n˜ao linear com o parˆametroa2dominando o comportamento do sistema para pequenos deslocamentos e o termoa3 definindo o comportamento para grandes deslocamentos, conforme pode ser percebido na Figura 2.3, onde podemos

3

(22)

perceber que o comportamento reala2θ+a3θ3 _{se aproxima do comportamento linear} a2θ em torno da origem.

-0,25 -0,20 -0,15 -0,10 -0,05 0,00 0,05 0,10 0,15 0,20 0,25

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

θ

C´ubico Linear

(a) a2>0 ea3>0

-0,15 -0,10 -0,05 0,00 0,05 0,10

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

θ

C´ubico Linear

(b) a2<0 ea3>0

-0,10 -0,05 0,00 0,05 0,10 0,15

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

θ

C´ubico Linear

(c) a2>0 ea3<0

-0,25 -0,20 -0,15 -0,10 -0,05 0,00 0,05 0,10 0,15 0,20 0,25

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

θ

C´ubico Linear

(d) a2<0 ea3<0

Figura 2.3: Configura¸c˜oes poss´ıveis para |a2|= 0,2 e |a3|= 1,19

Na Figura 2.3(a), temos uma mola não linear de rigidez positiva, enquanto que na Figura 2.3(d) temos uma mola de rigidez negativa. Já nas Figuras 2.3(b) e 2.3(c) temos o comportamento de duplo po¸co, nesse caso o sistema possui três pontos de equil´ıbrio, sendo um deles instável. Observando a Eq. 2.1 do pêndulo, por exemplo, podemos perceber que este sistema apresenta comportamento de duplo po¸co, cor-respondendo a Figura 2.3(c). O caso em que a2 < 0 e a3 > 0 corresponde a viga de MOON e HOLMES (1979), mostrada na Figura 2.4, que se trata de uma viga elástica sujeita a flambagem devido a for¸cas de corpo magnéticas.

viga

Imãs ω

F cos t

(23)

Fazendoθ=x1 e ˙θ =x2, em que: x= [x1 x2]T _{e definindo a sa´ıda de interesse} do sistema como: y = x1, podemos reescrever a Eq. 2.2 em vari´aveis de estado, chegando a:

˙

x1 =x2

˙

x2 =−a1x2−a2x1−a3x3₁+a4sen(ωt) (2.3)

y =x1

Após esta breve discussão sobre o oscilador de Duffing, com sua história, for-mula¸cão matemática e caracter´ısticas f´ısicas, daremos continuidade a este cap´ıtulo com a análise de suas caracter´ısticas não lineares básicas, que estão presentes na mai-oria destes sistemas, bem como suas outras caracter´ısticas, que fazem deste sistema um sistema caótico.

2.2 Bifurca¸

c˜

oes

Muito antes de descobrirmos o fenômeno da dependência sens´ıvel às condi¸cões iniciais já sab´ıamos que o comportamento qualitativo de um sistema depende dos valores de seus parâmetros. Um sistema linear massa mola amortecedor de segunda ordem por exemplo, pode apresentar oscila¸cões subamortecidas, criticamente amor-tecidas, sobreamortecidas ou até instáveis, dependendo do valor de cada parâmetro. O mesmo ocorre para os sistemas não lineares, que podem apresentar comporta-mento de sela, nó ou centro, que por sua vez podem ser estáveis, instáveis ou dege-nerados (WIGGINS, 1990).

Toda mudan¸ca qualitativa no comportamento do sistema em fun¸cão de seus parâmetros recebe o nome de bifurca¸cão. A literatura está repleta de sistemas que apresentam bifurca¸cões dos mais variados tipos. Um sistema clássico que apresenta bifurca¸cões é omapa log´ıstico, proposto por MAY (1976), que consiste num sistema discreto que pode ser aplicado em sistemas biológicos, econômicos e sociais:

xi+1 =axi(1−xi) (2.4)

Aplicando a Eq. 2.4 à análise do crescimento populacional podemos interpretarxi como a quantidade de habitantes em determinado intervalo de tempoie o parâmetro

a como a taxa de crescimento populacional. Al´em disso, percebemos que o termo 1−xi mant´em o crescimento dentro de certos limites, pois quandoxi aumenta 1−xi diminui.

(24)

Fi-gura 2.5. Nela, percebemos que os diferentes valores dea definem o comportamento qualitativo para o mapa log´ıstico, que pode tender a um valor constante, oscilar entre 2, 4 ou mais valores ou n˜ao convergir para nenhum valor em especial.

0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

1,0 1,5 2,0 2,5 3,0 3,5 4,0

xi

a

Figura 2.5: Diagrama de bifurca¸c˜ao para o mapa log´ıstico

Verifica-se, por exemplo, que variando o parâmetro a de 2,9 para 3,1 percebe-se uma mudan¸ca no comportamento da popula¸cão, passando de um valor fixo para um estado de alternância populacional e tal mudan¸ca representa umabifurca¸cão no sistema. Varia¸cões adicionais do parâmetro provocam mudan¸cas extremas no com-portamento, tais como quase-periodicidade e caos. Com a descoberta da dinâmica caótica, as pesquisas se concentraram em descobrir como a natureza de um sistema muda drasticamente.

Geralmente, para sistemas for¸cados, como é o caso do oscilador de Duffing, ana-lisamos a influência da amplitude do for¸camento na resposta do sistema, como em SHARMA et al.(2012), SIEWE e HEGAZY (2011) e MATSUMOTO et al. (1984). No entanto, podemos utilizar o diagrama de bifurca¸cão para estudar a influência de qualquer parâmetro de determinado sistema, como em DOS SANTOS e SAVI (2009) e MACHADOet al.(2003), onde, além da amplitude do for¸camento, se estu-dam outros parâmetros importantes, como por exemplo a frequência do for¸camento senoidal.

Na prática de engenharia, a modelagem se configura como uma das maiores fontes de erro, que pode surgir quando desprezamos parcelas importantes da dinâmica do sistema (dinâmica não modelada) ou durante a determina¸cão de seus parâmetros. Da´ı a necessidade de analisarmos a influência de cada parâmetro para a resposta desejada.

(25)

0,05, a2 =−0,2, a3 = 1,19,a4 = 6,6 e ω = 1,0, obtemos a seguinte equa¸c˜ao: ˙

x1 =x2

˙

x2 =−0,05x2+ 0,2x1 −1,19x3

1+ 6,6 sen(t)

(2.5)

Ainda em rela¸cão a importância do termo cúbico, salientamos que, caso des-prezássemos sua influência, ou sejaa3 = 0, obter´ıamos um sistema instável4_{. O que}

n˜ao acontece devido a presen¸ca deste termo.

Para simular o comportamento deste sistema implementamos o m´etodo de Runge-Kutta5 _{de quarta ordem utilizando a linguagem de programa¸c˜ao C++, com}

atua-liza¸c˜ao dos estadosxi do sistema a cada 2π×10−3 unidades de tempo.

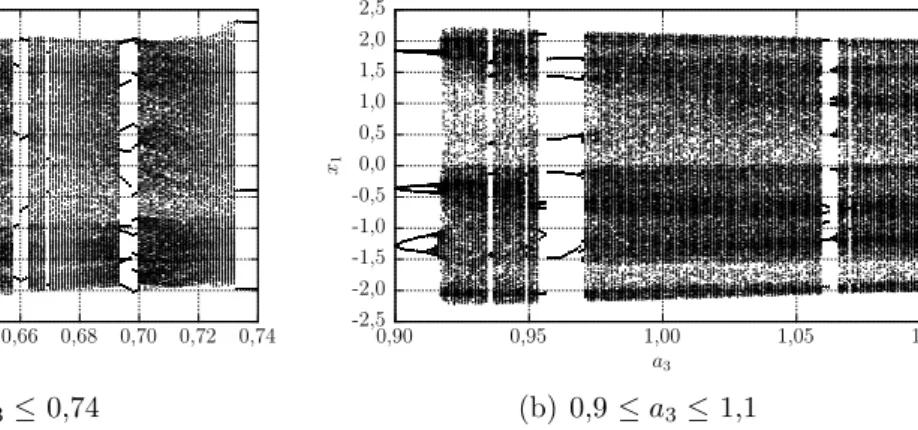
Conforme mencionado anteriormente, nossa sa´ıda de interesse ´e a vari´avel de estado x1 e por isso, analisaremos seu comportamento quando a3 varia entre 0,4 e 1,4; conforme mostrado na Figura 2.6.

Neste pequeno intervalo podemos notar alguns aspectos importantes. Inicial-mente temos uma varia¸cão na periodicidade do sistema, que come¸ca com per´ıodo 1 para a3 = 0,4, sofrendo bifurca¸cão antes que a3 seja 0,5, passando a apresentar per´ıodo 2. Quandoa3 ≈0,58, ocorre nova bifurca¸cão e o sistema passa a apresentar per´ıodo 4, conforme Figura 2.7(a).

-2,5 -2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5

0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4

x1

a3

Figura 2.6: Diagrama de bifurca¸c˜ao para o estado x1

No entanto este comportamento n˜ao permanece por muito tempo. Antes que

a3 seja 0,6 temos o in´ıcio do comportamento caótico, que por sua vez dá lugar ao comportamento periódico em alguns trechos, como por exemplo,a3 = 0,66 e pouco antes de a3 = 0,7, conforme mostrado na Figura 2.7(a). Tais trechos de compor-tamento periódico em meio ao comporcompor-tamento caótico recebem o nome de janelas periódicas. De forma similar o comportamento caótico em meio ao comportamento periódico pode ser chamado de janela caótica.

4

As ra´ızes da equa¸cão caracter´ıstica da solu¸cão homogênea da EDO linear resultante seriam:

ρ1=−0,473 (est´avel) eρ2= +0,423 (inst´avel). 5

(26)

Situa¸cões semelhantes ocorrem na Figura 2.7(b), onde o comportamento caótico volta a ocorrer. Tal análise mostra a importância cr´ıtica do parâmetro a3 para o sistema, uma vez que diferen¸cas m´ınimas separam o comportamento periódico do caótico.

-2,5 -2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5

0,56 0,58 0,60 0,62 0,64 0,66 0,68 0,70 0,72 0,74

x1

a3

(a) 0,56≤a3≤0,74

-2,5 -2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5

0,90 0,95 1,00 1,05 1,10

x1

a3

(b) 0,9≤a3≤1,1

Figura 2.7: Amplia¸c˜oes da Figura 2.6

2.3 Se¸

c˜

ao de Poincar´

e

Durante a análise do comportamento de um sistema, a investiga¸cão sobre sua pe-riodicidade é uma questão fundamental. Sabendo disso, Henri Poincaré6_{, enquanto}

estudava o problema dos trˆes corpos7_{, teve a ideia de reduzir a dimens˜ao do mesmo,}

analisando apenas informa¸c˜oes em instantes de tempo pr´e-determinados.

Tomemos como exemplo uma EDO de segunda ordem ¨x = f(t, x). Na época de Poincaré, uma das ferramentas mais utilizadas para análise de um sistema deste tipo era o plano de fase que, dependendo de f(t, x), pode ter uma forma bastante complexa. Para driblar este problema, ele propôs a análise do que acontece apenas em intervalos de tempo pré-fixados, gerando um mapa discreto do sistema.

Por exemplo, suponha que a solu¸cão para a EDO do parágrafo anterior seja dada por x= sent. Se em vez de analisarmos todo o seu comportamento ao longo do tempo, analisarmos apenas o que acontece em cada instante ti = iT, onde i = 0,1,2, . . . e T = 2π, obteremos gráficos mais simples sem perder informa¸cões sobre a periodicidade do sistema, uma vez que os pontos em destaque na Figura 2.8(a) dão uma ideia sobre o comportamento oscilatório da solu¸cão, sem que seja preciso visualizar sua solu¸cão completa. Tal ideia aparece novamente na Figura 2.8(b) onde conseguimos descobrir que além de periódica a solu¸cão possui per´ıodo 1, uma vez

6

F´ısico-matem´atico francˆes (1854–1912)

7

Problema proposto para analisar a estabilidade do sistema solar, estudando inicialmente a ´

(27)

que os pontos se sobrepõem. De posse da se¸cão de Poincaré, um gráfico mais simples que o plano de fase, podemos verificar facilmente a periodicidade do sistema.

-1,0 -0,8 -0,6 -0,4 -0,2 0,0 0,2 0,4 0,6 0,8 1,0

0,0 5,0 10,0 15,0 20,0

x

t

(a) Resposta temporal

-1,0 -0,5 0,0 0,5 1,0

˙

x

(b) ´Orbita no plano de fase

Figura 2.8: Aplica¸cão das ideias de Poincaré à fun¸cão senoidal

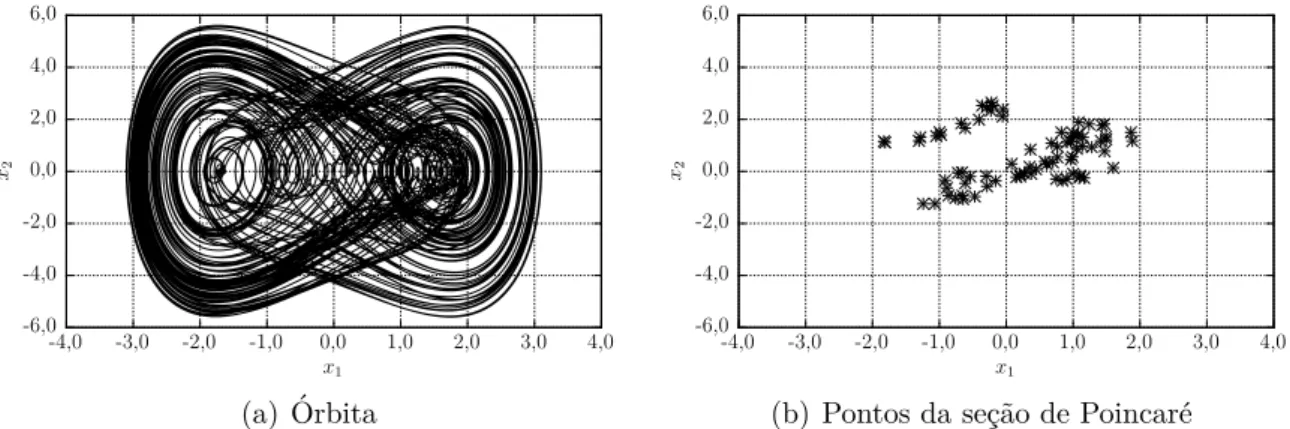
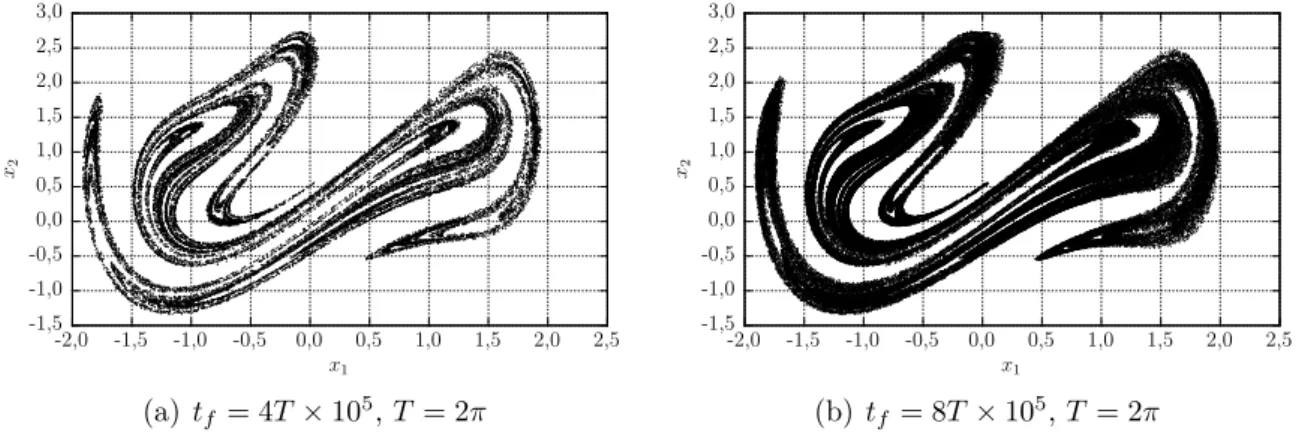
Dada a simplicidade do exemplo anterior, podemos até duvidar da eficiência da técnica proposta por Poincaré. No entanto, para sistemas que não possuem peri-odicidade definida, como os sistemas caóticos, a se¸cão de Poincaré é de extrema importância. Observe, por exemplo, a Figura 2.9 que mostra o comportamento do oscilador de Duffing dado pela Eq. 2.3 em suas primeiras 500 unidades de tempo. Nesse curto espa¸co de tempo podemos notar sua complexidade, conforme apresen-tado no plano de fase da Figura 2.9(a). Analisando sua Se¸cão de Poincaré, perce-bemos a forma¸cão de um aglomerado de pontos numa região central do plano de fase. Estendendo nossa análise a intervalos de tempo cada vez maiores, conforme mostrado na Figura 2.10, percebemos o desenvolvimento de um padrão neste aglo-merado de pontos, que passa a apresentar uma forma definida e invariante no tempo.

-6,0 -4,0 -2,0 0,0 2,0 4,0 6,0

-4,0 -3,0 -2,0 -1,0 0,0 1,0 2,0 3,0 4,0

x2

x1

(a) ´Orbita

-6,0 -4,0 -2,0 0,0 2,0 4,0 6,0

-4,0 -3,0 -2,0 -1,0 0,0 1,0 2,0 3,0 4,0

x2

x1

(b) Pontos da se¸c˜ao de Poincar´e

(28)

seu car´ater atrativo. Devido a esta propriedade importante podemos nos referir a cada uma das Figuras 2.10 como o atrator8 _{do oscilador de Duffing. Geralmente os}

atratores dos sistemas caóticos possuem dimensão fractal, sendo então denominados

atratores estranhos.

Outra caracter´ıstica importante dos sistemas caóticos é que suas trajetórias não se interceptam, apenas se localizam muito próximas uma das outras. Na Figura 2.9 temos a impressão de que alguns trechos da órbita se sobrepõem, no entanto isso não acontece, como pode ser comprovado na Figura 2.11.

-1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5 3,0

-2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5

x2

x1

(a) tf = 4T×105,T = 2π

-1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5 3,0

-2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5

x2

x1

(b) tf = 8T×105, T = 2π Figura 2.10: Se¸c˜oes de Poincar´e para o oscilador de Duffing da Eq. 2.3, ambas desprezando os primeiros 30% instantes iniciais

0,0 0,5 1,0 1,5 2,0

2,0 2,2 2,4 2,6 2,8 3,0

x2

x1

(a) Amplia¸c˜ao de uma parte da Figura 2.9

1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 1,45 1,50

2,60 2,62 2,64 2,66 2,68 2,70 2,72 2,74 2,76 2,78 2,80

x2

x1

(b) Amplia¸c˜ao de uma parte da Figura 2.11(a)

Figura 2.11: Amplia¸c˜oes sucessivas da Figura 2.9

2.4 Orbitas peri´

´

odicas inst´

aveis

Dado um sistema periódico, se tomarmos pontos defasados de intervalos de tempo iguais obteremos uma quantidade de pontos igual ao per´ıodo do sistema, conforme mostrado na Figura 2.8 e discutido na Se¸cão 2.3. Já o regime caótico não possui

8

(29)

periodicidade definida e nesses casos utilizamos a se¸cão de Poincaré para observar a dispersão dos pontos obtidos em intervalos de tempo iguais ao per´ıodo de excita¸cão. Com isso obtemos uma infinidade de pontos que se acumulam dentro de uma região do plano de área finita.

Por não possuir periodicidade definida, um sistema caótico oscila entre as vizi-nhan¸cas de vários pontos de equil´ıbrio com os mais variados per´ıodos, retornando, em alguns casos, após algumas itera¸cões. As órbitas periódicas instáveis, OPIs, surgem durante a passagem do sistema por essas vizinhan¸cas, são órbitas que não possuem estabilidade para tornar o comportamento periódico, apenas aparecem du-rante alguns instantes dando lugar a outra órbita de periodicidade distinta.

Atualmente existem diversos métodos para identifica¸cão de OPIs. Por exemplo, FUH (2009) utiliza o algoritmo de Nelder-Mead, tratando o problema de deteçcão de órbitas como um problema de otimiza¸cão, enquanto que DEANE e MARSH (2006) desenvolveram um método espec´ıfico para deteçcão de OPIs em sistemas for¸cados.

Além disso, PINGEL et al. (2001), com base no trabalho de DAVIDCHACK e LAI (1999), que identifica OPIs para sistemas discretos, desenvolveram um método similar para sistemas cont´ınuos baseado na se¸cão de Poincaré. Neste trabalho, utili-zaremos ométodo dos pontos recorrentes próximos, proposto por AUERBACHet al.

(1987), uma técnica simples e pioneira na extra¸cão de OPIs, que também se utiliza do conhecimento da se¸cão de Poincaré.

Para identificar uma órbita de per´ıodoj, o método dos pontos recorrentes próxi-mos calcula a distância euclidiana entre dois pontos da se¸cão de Poincaré defasados dej itera¸cões. Se esta distância for menor que um certo valorr1 então este conjunto

de pontos corresponde a uma OPI de per´ıodoj.

||Pi−Pi+j|| ≤r1 (2.6)

Na Eq. 2.6 o parˆametroj representa o valor do per´ıodo procurado, o parˆametroi

varia de 1 até o número de pontos da se¸cão de Poincaré menos o per´ıodo, Np−j,r1

representa a distância entre dois pontos ePi é oi-ésimo ponto da se¸cão de Poincaré. Os estadosxdo sistema entre os pontosPi ePi+j que satisfazem a desigualdade 2.6 formam uma órbitaj-periódica.

Para exemplificar o funcionamento do método dos pontos recorrentes próximos, obtivemos duas OPIs de per´ıodo 1 para o oscilador de Duffing com valor nominal do parâmetroa3, exibidas na Figura 2.12. Os pontos destacados em cada uma das órbitas das Figuras 2.12(a) e 2.12(b) são os pontos Pi e Pi+1 da se¸cão de

(30)

Como, dadas as dimensões da figura, a distância entrePi ePi+1 é pequena, vide

Figura 2.12(c), temos a impressão de que existe apenas um ponto em cada órbita, quando na verdade temos dois pontos a uma pequena distânciar1.

Como n˜ao temos como estimar um valor m´ınimo parar1 de modo que todo par

de pontos abaixo desta distância formem uma OPI, decidimos utilizar a desigual-dade 2.6 para calcular as distâncias entre todos os pontos da se¸cão de Poincaré, tomados de 2 a 2, ordenando cada par de maneira crescente, obtendo as menores distâncias para as órbitas desejadas. Tivemos algumas dificuldades para encon-trar órbitas com periodicidade maior do que 1, pois quando buscávamos órbitas de per´ıodo 2, por exemplo, encontrávamos uma OPI de per´ıodo 1 que se repetia por 2 per´ıodos. -5,0 -4,0 -3,0 -2,0 -1,0 0,0 1,0 2,0 3,0 4,0 5,0

-2,5 -2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5 3,0

x2

x1

(a) OPI de per´ıodo 1

-5,0 -4,0 -3,0 -2,0 -1,0 0,0 1,0 2,0 3,0 4,0 5,0

-3,0 -2,5 -2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5

x2

x1

(b) Outra OPI de per´ıodo 1, com ´orbita espelhada em rela¸c˜ao a Figura 2.12(a)

0,55 0,56 0,57 0,58 0,59 0,60 0,61 0,62 0,63 0,64 0,65

-1,200 -1,195 -1,190 -1,185 -1,180

x2

x1

(c) Detalhe da Figura 2.12(a)

-1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5 3,0

-2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0

x2

x1

Fig. 2.12(a) Fig. 2.12(b)

(d) OPIs na Se¸c˜ao de Poincar´e

Figura 2.12: Rela¸cão entre OPIs e a Se¸cão de Poincaré

(31)

-6,0 -4,0 -2,0 0,0 2,0 4,0 6,0

-4,0 -3,0 -2,0 -1,0 0,0 1,0 2,0 3,0 4,0

x2

x1

(a) OPI de per´ıodo 3

-6,0 -4,0 -2,0 0,0 2,0 4,0 6,0

-4,0 -3,0 -2,0 -1,0 0,0 1,0 2,0 3,0

x2

x1

(b) OPI de per´ıodo 3

-6,0 -4,0 -2,0 0,0 2,0 4,0 6,0

-4,0 -3,0 -2,0 -1,0 0,0 1,0 2,0 3,0 4,0

x2

x1

(c) OPI de per´ıodo 5

-6,0 -4,0 -2,0 0,0 2,0 4,0 6,0

-4,0 -3,0 -2,0 -1,0 0,0 1,0 2,0 3,0 4,0

x2

x1

(d) OPI de per´ıodo 5

(32)

Cap´ıtulo 3

T´

opicos de Controle N˜

ao Linear

Podemos definir o controle não linear como o ramo da teoria de controle que lida tanto com sistemas não lineares como variantes no tempo. Enquanto o projeto de um controlador linear para um sistema como o oscilador de Duffing se baseia numa versão linearizada deste sistema, válida apenas na vizinhan¸ca de um ponto de opera¸cão estipulado, um controlador não linear apresenta como vantagem uma maior faixa operacional.

Do ponto de vista prático, podemos ressaltar que, como na natureza, o compor-tamento linear é uma raridade, a obten¸cão de sensores e atuadores lineares se torna mais dif´ıcil e custosa. Da´ı o alto custo dos componentes de um sistema de controle linear, que demanda sensores e atuadores de elevada qualidade, devido a necessidade de apresentar comportamento linear em toda sua faixa de opera¸cão, enquanto que um sistema de controle não linear pode utilizar componentes de menor qualidade e baixo custo, sem comprometer seu desempenho.

Outro ponto fraco da abordagem linear está na dificuldade de lineariza¸cão de algumas não linearidades não diferenciáveis como por exemplo o atrito de Coulomb, zona morta e histerese. Todos estes fatores contribuem para o desenvolvimento e aplica¸cão de técnicas de controle não linear, que além de considerarem mais detalhes do comportamento do sistema, abrangem uma maior faixa de opera¸cão e utilizam equipamentos de menor custo.

3.1 Estabilidade

(33)

a afirma¸c˜ao anterior como:

Defini¸cão 3.1. Estabilidade: O sistema ˙x = f(t,x) é dito estável se, para cada

ǫ >0 finito, existe δ=δ(ǫ)>0 tamb´em finito, tal que:

||x(0)||< δ ⇒ ||x(t)||< ǫ, ∀t≥0 (3.1) Al´em disso, de maneira mais restrita podemos definir:

Defini¸cão 3.2. Estabilidade assintótica: O sistema ˙x = f(t,x) é dito assintotica-mente estável se for estável e existirem δ e x¯ finitos tais que:

||x(0)||< δ ⇒ lim

t→∞x(t) = ¯x (3.2)

em que ¯x é conhecido como o ponto de equil´ıbrio do sistema. Percebe-se que a diferen¸ca entre ambas as defini¸cões está no fato de que a Defini¸cão 3.2 exige que o sistema convirja para um estado de equil´ıbrio enquanto que pela Defini¸cão 3.1 o estado do sistema pode oscilar indefinidamente numa vizinhan¸ca qualquer de raioǫ. Um caso particular de estabilidade assintótica ocorre quando a convergência de um sistema para o ponto de equil´ıbrio é limitada por uma fun¸cão exponencial. Defini¸cão 3.3. Estabilidade exponencial: O sistema ˙x=f(t,x) possui estabilidade exponencial se existirem constantesc, k e λ estritamente positivas tal que:

||x(t)|| ≤k||x(t0)||e−λ(t−t0)

,∀||x(t0)||< c (3.3) Perceba que quando t → ∞ o estado do sistema x(t) tende a origem, que ´e o ponto de equil´ıbrio deste sistema.

3.1.1 Teoria de Estabilidade de Lyapunov

No final do século XIX, o f´ısico e matemático russo Aleksandr M. Lyapunov (1857–1918) desenvolveu os alicerces de uma teoria para análise de estabilidade que se destaca por não necessitar da solu¸cão do sistema, utilizando como base conceitos f´ısicos de energia, facilitando bastante o seu entendimento intuitivo.

Em seu trabalho, Lyapunov desenvolveu dois métodos de investiga¸cão, o método indireto, que se baseia na análise do sistema linearizado. E o método direto, que se baseia na existência de fun¸cões com caracter´ısticas espec´ıficas.

(34)

equil´ıbrio para a origem, ou seja, ¯x=0. Assim, sempre que mencionarmos a origem estaremos nos referindo ao ponto de equil´ıbrio do sistema.

Conforme mencionado anteriormente, uma das principais caracter´ısticas da te-oria de Lyapunov é a sua correla¸cão com a energia f´ısica de um sistema. Para entendermos melhor essa rela¸cão, tomemos como exemplo um sistema linear com-posto por massa, mola e amortecedor sob oscila¸cão livre, dado por:

mx¨+cx˙ +kx= 0 (3.4)

A energia total deste sistema é dada pela soma de suas energias cinética e po-tencial, sendo uma fun¸cão de sua posi¸cão e velocidade, ou seja:

E(x,x˙) = 1 2(mx˙

2₊_kx2₎ _(3.5)

cuja derivada temporal ´e dada por: ˙

E(x,x˙) = mx˙x¨+kxx˙ = ˙x(mx¨+kx)

=−cx˙2 (3.6)

Assim, na ausência do amortecedor (c = 0) teremos um comportamento osci-latório, em que a energia total será constante ao longo do tempo, pois ˙E = 0. Já no caso amortecido ocorrerá dissipa¸cão de energia que, partindo de um valor inicial positivo, diminuirá ao longo do tempo, tendendo a zero, pois ˙E ≤0. Percebe-se que, para qualquer estado inicial deste sistema, seu estado tenderá sempre a um compor-tamento estacionário, o que corresponde perfeitamente ao exposto na Defini¸cão 3.1, uma vez que dado||x(0)||< δ, sempre teremos ǫ > 0 tal que ||x(t)||< ǫ para todo

t≥0.

A Teoria de Estabilidade de Lyapunov, como é conhecida, mostra que além da fun¸cão de energia, existem outras fun¸cões que podem ser utilizadas para investigar a estabilidade de um sistema. Para que o sistema seja considerado estável, no entanto, tais fun¸cões devem apresentar algumas caracter´ısticas presentes na fun¸cão de energia.

Percebe-se que comom, k >0 e tanto a posi¸cão como a velocidade estão elevadas ao quadrado, a energia será sempre positiva, anulando-se apenas quandox= ˙x= 0, que é a origem do plano de fase. Matematicamente, uma fun¸cão que apresenta tais caracter´ısticas é dita positiva definida.

Defini¸cão 3.4. Uma fun¸cão positiva definida é uma fun¸cão V(x) tal que V(0) = 0

(35)

Já outras fun¸cões, que se anulam em outros pontos além da origem, são definidas como:

Defini¸cão 3.5. Uma fun¸cão positiva semidefinida é uma fun¸cãoV(x)tal queV(0) = 0 e V(x)≥0 para todo x6= 0.

De forma similar podemos dizer que uma fun¸c˜ao V(x) ´e negativa definida ou

negativa semidefinida se−V(x) ´e positiva definida ou positiva semidefinida, respec-tivamente.

Conforme mencionamos anteriormente, a fun¸cão de energia do sistema massa mola amortecedor possui derivada temporal menor ou igual a zero, sendo considerada uma fun¸cãonegativa semidefinida. Com isso, podemos descreve-la como uma fun¸cão positiva definida cuja derivada temporal é uma fun¸cão negativa semidefinida. Sendo este o conjunto de caracter´ısticas que nos permite dizer que um sistema é estável.

Em suma, para que um sistema seja estável é suficiente que exista uma fun¸cão

V(x) positiva definida tal que sua derivada temporal ˙V(x) seja negativa semidefi-nida. Caso a fun¸c˜aoV(x) satisfa¸ca ambos os requisitos ela recebe o nome defun¸c˜ao de Lyapunov.

No entanto, se ˙V for negativa definida, o sistema irá convergir para a origem, ou seja, garante-se sua estabilidade assintótica. Infelizmente existem casos em que não conseguimos obter fun¸cões que atendam perfeitamente a esses requisitos, como por exemplo o sistema massa mola amortecedor da Eq. 3.4, cujo comportamento de sua fun¸cõesE(x,x˙) e ˙E(x,x˙) pode ser observado na Figura 3.1, onde temos uma fun¸cão positiva definida na Figura 3.1(a), cuja derivada temporal mostrada na Figura 3.1(b) se anula sobre todo o eixox, sendo portanto negativa semidefinida.

-10 -5

0 5

10 ˙

x

-10 -5

0 5

10

x

0 40 80 120

E

(a) Candidata a fun¸c˜ao de Lyapunov

-10 -5

0 5

10 ˙

x

-10 -5

0 5

10

x

-100 -80 -60 -40 -20 0

˙

E

(b) Derivada temporal deE

(36)

Para obter tal resultado matematicamente, temos duas alternativas: o teorema da invariˆancia de LaSalle1 _{que se aplica a sistemas autˆonomos e o lema de Barbalat}2

para sistemas não autônomos. O lema de Barbalat será brevemente discutido no Apêndice A com o intuito de demonstrar a estabilidade da lei adaptativa integral. Entretanto, para uma discussão detalhada sobre ambos consulte KHALIL (2002).

3.2 Controle por Modos Deslizantes

O controle por modos deslizantes, CMD, nasceu na extinta União Soviética, originando-se com os trabalhos de FILIPPOV (1964) sobre equa¸cões diferenciais com descontinuidades e EMELYANOV e KOSTYLEVA (1964), ITKIS (1976) e UTKIN (1977) sobre controladores com estrutura variável. O sucesso desta estratégia de controle se baseia na escolha apropriada da superf´ıcie de deslizamento, que é para onde devemos levar o sistema. Uma vez que o sistema convirja para este lugar geométrico, suas caracter´ısticas farão com que o erro tenda a zero, deslizando sobre esta superf´ıcie.

Considere um sistema de n-´esima ordem, dado por:

x(n) =f(t,x) +b(t,x)u(t,x) (3.7) tendo como sa´ıda de interesse a vari´avel x. Reescrevendo-o na forma de vari´aveis de estado, chegamos a:

     

    

˙

xi =xi+1, para i de 1 at´e n−1 ˙

xn=f(t,x) +b(t,x)u(t,x)

y=x1

(3.8)

Na prática, apesar de f e b serem desconhecidas, frequentemente temos uma no¸cão do comportamento de ambas. Por exemplo, apesar de não sabermos precisa-mente o valor do coeficiente de amortecimento em determinado sistema, podemos estimar uma faixa de valores onde este se encontra. Assim, podemos supor que o ganho do controladorb se encontra num determinado intervalo entre dois extremos e que a fun¸cão f é limitada por uma fun¸cão dex, ou seja:

|fe(t,x)−f(t,x)| ≤F(t,x) 0< bm ≤b(t,x)≤bM

(3.9)

em quefeé uma estimativa para a fun¸cãof,F é a fun¸cão delimitadora ebmebM são

1

Joseph P. LaSalle, matem´atico americano (1916–1983)

2

(37)

constantes que representam o ganho m´ınimo e máximo, respectivamente. O ganho estimado pode ser dado pela média geométrica entre o ganho máximo e m´ınimo:

be =

q

bmbM (3.10)

Al´em disso:

0≤β−₁

≤ be

b ≤

s bM

bm

(3.11)

Podemos tamb´em definir o erro entre a sa´ıda obtida x1 e a sa´ıda desejada x1,d, como:

e1 =x1−x1,d ou, na forma vetorial:

e=x−xd

Uma das principais caracter´ısticas do controle por modos deslizantes é a trans-forma¸cão o problema de rastreamento do vetor de estado variante no tempoxd(t) de ordem n, em um problema mais simples de estabiliza¸cão de primeira ordem. Com isso, em vez de rastrearmos xd devemos estabilizar uma grandeza escalar s num determinado valor (no caso s = 0). Definindo s de maneira adequada poderemos obter o resultado esperado de forma mais simples. Como, por exemplo:

s=

d

dt +λ

n−₁

e1 (3.12)

onde λ > 0. Percebe-se que a defini¸c˜ao de s como dada pela Eq. 3.12 assegura um

comportamento dinâmico estável para o erro e1, uma vez que o polinômio carac-ter´ıstico resultante é um polinômio de Hurwitz3_{, cuja defini¸cão é dada por:}

Defini¸cão 3.6. Um polinômio de Hurwitz possui todos os seus coeficientes reais e positivos e todas as suas ra´ızes têm parte real negativa. Ou seja, um polinômioP(x)

tal que:

P(x) =anxn+an−1xn −₁

+. . .+a1x+a0, com ai >0 para i de 0 at´e n e

P(x) = (x+z1)(x+z2). . .(x+zn−₁)(x+z_n), com Re(z_i)<0 parai de 1 at´en

Igualando a Eq. 3.12 a zero, obtemos uma EDO de ordemn−1 linear homogˆenea, cuja solu¸c˜ao (no caso e1) tende a zero de acordo com a constante λ. Assim, nosso

3

(38)

objetivo passa a ser o de manter a quantidade s= 0. Perceba que a Eq. 3.12 pode ser reescrita como: s=cT_{e, em que:}

ci =

(n−1)! (i−1)!(n−i)!λ

n−_i

(3.13)

s˜ao coeficientes que fazem de sum polinˆomio de Hurwitz. Por exemplo, escrevendo a Eq. 3.12 para um sistema de segunda ordem,n = 2, obtemos:

s= ˙e1+λe1 = 0 ⇒e2 =−λe1

cujo lugar geométrico está representado na Figura 3.2 pela linha diagonal tracejada. Supondo as condi¸cões iniciais x(t = 0) iguais aos valores desejados xd, a Eq. 3.12 garante a convergência do erro e1 para zero num intervalo de tempo finito. Nesse caso dizemos que as variáveis de estado do sistema deslizam sobresaté chegar a zero. Por conta disso, o lugar geométrico em que s = 0 recebe o nome de superf´ıcie (ou plano) de deslizamento. Por outro lado, caso as condi¸cões iniciais sejam diferentes dos valores de referência, teremos inicialmente uma fase de aproxima¸cão, precedendo a fase de deslizamento. Ambas as fases podem ser vistas na Figura 3.2.

e₁ e₂

s = 0 −λ

deslizamento

e(t = 0)

aproximação

Figura 3.2: Representa¸cão esquemática das fases de aproxima¸cão e deslizamento no plano de fase do erro

Visando dotar a superf´ıcie de deslizamento s com propriedades atrativas, isto é, para fazer com que a dinâmica do erro seja atra´ıda para a superf´ıcie de deslizamento e, ao chegar a este lugar geométrico, se mantenha nele devemos utilizar a teoria de estabilidade de Lyapunov, descrita na subse¸cão 3.1.1.

Define-se então uma fun¸cão positiva definida, candidata a fun¸cão de Lyapunov:

V(s) = 1 2s

2 _(3.14)

cuja derivada temporal seja negativa definida, ou seja:

dV

dt ≤0⇒

1 2

d dts

(39)

Para garantir esse ´ultimo quesito, SLOTINE e LI (1991) definiram a condi¸c˜ao de deslizamento, dada por:

1 2

d dts

2 _{≤ −}_η_|_s_| _(3.16)

onde η é uma constante estritamente positiva. Vale ressaltar que, apesar do nome, a condi¸cão de deslizamento se faz importante durante a fase de aproxima¸cão, pois ela garante que a fase de deslizamento ocorrerá. Outro fato importante sobre a Eq. 3.16 é que ela garante a convergência do erroepara a superf´ıciesnum intervalo de tempo finito. Integrando a Eq. 3.16 entre t = 0 e o instante em que o erro e chega à superf´ıcie s, ts, temos:

1 2

d dts

2 ₌_sds

dt ≤ −η|s| Z s(t=ts)

s(t=0) s

|s|ds≤ −η

Z ts

0 dt

|s(t=ts)| − |s(t = 0)| ≤ −η(ts−0) Lembrando que s(t=ts) = 0, temos:

ts ≤

|s(t= 0)|

η (3.17)

Observando a Eq. 3.17, podemos perceber que o parâmetro η dita a taxa com a qual o sistema converge para a superf´ıcie de deslizamento, uma vez que quanto maior o valor de η, menor será o tempo para que o erro chegue atés= 0.

Dando continuidade ao desenvolvimento do controlador por modos deslizantes, sabemos que para mantermos o valor desnulo é necessário também que sua varia¸cão em rela¸cão ao tempo também seja nula. Assim, derivando a Eq. 3.12 em rela¸cão ao tempo, temos:

˙

s = ˙en+qTe ˙

s= ˙xn−x˙n,d+qTe em que:

q1 = 0

qi =ci−1, para i de 2 at´en

Inserindo a Eq. 3.8, temos: ˙

s=f +bu−x˙n,d+qTe (3.18) Como na pr´atica desconhecemos o comportamento exato de f e b, a melhor estimativa poss´ıvelue deu para que tenhamos ˙s= 0 ´e dada por:

ue = 1

be

(40)

Para satisfazermos a condi¸c˜ao de deslizamento, dada pela Eq. 3.16, adicionamos um termo descont´ınuo a ue na superf´ıcie de deslizamento e assim:

u=ue−Ksgn(s) (3.20)

em que a fun¸cão sgn(s) é chamada de fun¸cão sinal. Seu comportamento, que pode ser observado na Figura 3.3, é dado por:

sgn(s) =

          

+1 , ses >0 0 , se s= 0 −1 , ses <0

(3.21)

s

−1

sgn(s)

1

Figura 3.3: Representa¸cão gráfica do comportamento da fun¸cão sinal, sgn(s) A importância da utiliza¸cão da fun¸cão sinal para o controle por modos deslizantes reside no fato de que, conforme a Eq. 3.20, o ganhoK atua sobre o sistema apenas enquanto o erro e se encontra fora da superf´ıcie de deslizamento, possuindo papel fundamental na fase de aproxima¸cão. Quando o sistema converge, s = 0, o esfor¸co de controleu se torna igual aue, dado pela Eq. 3.19. Nota-se também que a parcela da atua¸cão devido a sgn(s) possui sinal oposto ao de s, uma vez que a fun¸cão sinal está multiplicada por−1.

Justificada a importância da fun¸cão sgn(s) devemos definir um valor m´ınimo para o ganhoK =K(x) de modo a garantir a condi¸cão de deslizamento dada pela Eq. 3.16. De fato, inserindo as Eqs. 3.20 e 3.19 na condi¸cão de deslizamento, temos:

1 2

d dts

2 ₌_s_s_˙₌_s_f ₊ b

be

(−fe+ ˙xn,d−qTe)−bKsgn(s)−x˙n,d+qTe

ss˙=s

f − b

be

fe+

b be

−1

( ˙xn,d−qTe)−bKsgn(s)

Sabendo quef =fe+ (f −fe), temos: 1

2

d dts

2 ₌_s_f

e+ (f−fe)−

b be

fe+

b be

−1

( ˙xn,d−qTe)−bKsgn(s)

=s

(f−fe) +

b be

−1

( ˙xn,d−qTe−fe)−bKsgn(s)

(41)

Da Eq. 3.13 temos que: beue = ˙xn,d−qTe−fe. Assim, lembrando que|f−fe| ≤F e definindo o ganho K como:

K ≥b−₁

e β(η+F) +β(β−1)|fe+qTe−x˙n,d| (3.22) conseguimos satisfazer a condi¸c˜ao de deslizamento, dada pela Eq. 3.16, o que asse-gura a natureza atrativa da superf´ıcie de deslizamento s e garante erro e1 nulo em intervalo de tempo finito.

Para avaliar o desempenho obtido por cada um dos controladores utilizados neste trabalho utilizaremos o Erro Quadrático Médio, EQM ou EQM, para quantificar o erro apresentado por cada configura¸cão do controlador.

Na estat´ıstica, mais precisamente no estudo das técnicas de estima¸cão, o erro quadrático médio representa a média ponderada do quadrado da diferen¸ca entre o valor real e o valor estimado, ou seja, para um processo comp itera¸cões, temos:

EQM =

1

p

X

i=1

(x(1i)−x (i) 1,d)2 =

1

p

X

i=1

(e(1i))2 (3.23)

no qual o ´ındiceientre parênteses indica a itera¸cão. Para mensurar a magnitude do esfor¸co de controle, calcularemos sua norma L2, que, para uma fun¸cão f(t), pode

ser definida como:

kf(t)k2 = v u u u t

tf

Z

0

|f(τ)|2_dτ _(3.24)

em que tf ´e o tempo final da simula¸c˜ao.

Como tanto o EQM como a norma L2 dependem da frequˆencia de atualiza¸c˜ao

das variáveis de estado e do intervalo de simula¸cão, é necessário que mantenhamos estes valores constantes nos próximos exemplos para que possamos compará-los sob as mesmas condi¸cões.

Por isso, decidimos arbitrar o intervalo de simula¸c˜ao de 0 a 80 unidades de tempo, com taxa de atualiza¸c˜ao do estadoxdo sistema a cada 2π×10−₃

(42)

3.2.1 Aplica¸

c˜

ao com fun¸

c˜

ao sinal

Para ilustrar o funcionamento do controlador por modos deslizantes, podemos aplicá-lo ao oscilador de Duffing, mostrado na Se¸cão 2.1 e dado pela Eq. 2.5. Com isso, obtemos a equa¸cão para o oscilador de Duffing controlado, dada por:

˙

x1 =x2

˙

x2 =−0,05x2+ 0,2x1−1,19x31+ 6,6 sen(t) +u(t)

(3.25)

Utilizamos novamente o método de Runge-Kutta de quarta ordem para com-putar a solu¸cão numérica da Eq. 3.25, com atualiza¸cão das variáveis de estado xi a cada 2π ×10−₃

unidades de tempo e o dobro disso para o esfor¸co de controle

u(t). O sinal de referência é dado pelo estado x1,d da órbita genérica mostrada na Fig. 3.4(a) e definido pela Eq. 3.26. Admitimos que o sistema parte do repouso, ou seja,x(t = 0) = 0.

x1,d(t) = 2,5 sen(1,843t+ 0,644)−0,5 ˙

x1,d=x2,d(t) = 4,6075 cos(1,843t+ 0,644)

(3.26)

Comparando as Equa¸c˜oes 3.8 e 3.25, conclu´ımos quef(t,x) =−0,05x2+ 0,2x1− 1,19x3

1+6,6 sen(t) e que o ganho do controlador ´eb= 1. Para demonstrar a robustez

do controlador proposto adotaremos uma diferen¸ca fixa σ de +10% sobre o valor nominal do parˆametroa3, de modo que a′

3 =a3(1 +σ) = 1,309.

Para garantirmos o comportamento est´avel do erro e1 no plano de deslizamento da Eq. 3.12, utilizamosλ= 2. Com isso podemos definir a superf´ıcie de deslizamento

s, como:

s= ˙e1+λe1 =e2+ 2e1 (3.27)

eqT_e _{como 2}_e2_.

A diferen¸ca F entre f e fe pode ser calculada como:

F ≥ |fe−f|

=| −a1x2−a2x1−a′

3x31+a4sen(ωt) +a1x2+a2x1+a3x31 −a4sen(ωt)|

=|(a3 −a ′ 3)x31|

Para uma varia¸c˜ao gen´erica σ, onde |σ|<1, temos:

a′

(43)

assim:

F ≥ |[a3−a3(1±σ)]x3₁| =| ±σa3x3₁|

=|σa3x3₁|

Como nesta aplica¸c˜ao σ = 0,1 ea3 = 1,19, temos queF ≥0,119|x3

1|. Definindo η igual a 5, podemos expressar o ganhoK da fun¸c˜ao sinal como:

K ≥η+F = 5 + 0,119|x3₁| (3.28) Com isso, o esfor¸co de controle u(t) para o oscilador de Duffing ser´a definido como:

u= ˙x2,d+ 0,05x2−0,2x1+ 1,19x31−6,6 sen(t)−

−2e2−(5,0 + 0,119|x3₁|) sgn(s) (3.29) Os resultados obtidos podem ser visualizados na Figura 3.4. Analisando o plano de fase do erro, mostrado na Figura 3.4(c), podemos notar a fase de aproxima¸cão, dada por uma curva que se inicia próximo ao ponto (−1,0; −4,0) e termina próximo ao ponto (−1,0; 2,0), chegando à fase de deslizamento. Da´ı em diante percebemos que a superf´ıcie de deslizamento não permanece nula ao longo do tempot, conforme mostrado na Figura 3.4(d), mas apresenta oscila¸cões que, apesar da pequena am-plitude possuem alta frequência. Estas mesmas oscila¸cões podem ser observadas no esfor¸co de controle u(t), mostrado em detalhes na Figura 3.4(f) e na sa´ıda obtida pelo sistema, mostrada na Figura 3.4(b).

Estas oscila¸cões de alta frequência, apresentadas tanto pelo esfor¸co de controle quanto pela superf´ıcie de deslizamento, são conhecidas na literatura comochattering, que se caracteriza como um fenômeno indesejado aos sistemas mecânicos, devido não apenas a extrema atividade do esfor¸co de controle, mas também pela possibilidade de excitar dinâmicas não modeladas (desprezadas durante a modelagem) no sistema. A raiz deste fenômeno está na descontinuidade da fun¸cão sgn(s) em torno da origem, que provoca varia¸cões bruscas no esfor¸co de controle, se manifestando na superf´ıcie de deslizamento e consequentemente no erro obtido.

Para solucionar este problema, devemos buscar uma forma de suavizar a descon-tinuidade, o que pode ser obtido pela substitui¸cão da fun¸cão sinal por uma fun¸cão de satura¸cão sat(s), dada por:

sat(s) =

 



sgn(s) , se |s| ≥1