Curso de Especialização em Matemática para Professores do Ensino Básico
MATEMÁTICA FINANCEIRA PARA O ENSINO BÁSICO
Gleison Silva Vilefort Costa
Gleison Silva Vilefort Costa
MATEMÁTICA FINANCEIRA PARA O ENSINO BÁSICO
Trabalho apresentado ao Curso de Especialização em Matemática para Professores do Ensino Básico da Universidade Federal de Minas Gerais.
Orientador: Prof. Dr. Luiz Gustavo Farah
LISTA DE FIGURAS
LISTA DE TABELAS
SUMÁRIO
INTRODUÇÃO ... 5
1 JUROS ... 6
1.1 Juros Simples ... 6
1.1.1 Fórmula de Juros Simples ... 6
1.1.2 Fórmulas derivadas... 7
1.1.3 Montante (M) ... 9
1.1.4 Exemplos ... 11
1.2 Juros Compostos ... 12
1.2.1 Demonstração da Fórmula ... 12
1.3 Taxas de Juros – Classificação ... 15
1.3.1 Taxa nominal ... 15
1.3.2 Taxa efetiva ... 15
1.3.3 Taxas equivalentes ... 16
1.3.4 Taxa real ... 19
2 RENDAS CERTAS ... 22
2.1 Classificação de rendas ... 22
2.1.1 Renda Imediata postecipadas – Sem entrada ou imediata ... 22
2.1.2 Renda Antecipada – Com entrada ... 25
2.1.3 Renda diferida – Com carência ... 28
3 SISTEMAS DE AMORTIZAÇÃO ... 31
3.1 Sistema francês de amortização (Price) ... 31
3.2 Sistema de Amortização Constante (SAC) ... 34
3.3 Análise comparativa das tabelas Price e SAC ... 37
CONCLUSÃO ... 38
1. INTRODUÇÃO
A matemática financeira é essencial para os alunos que estão no Ensino Básico e iniciando uma vida profissional. O conhecimento se faz necessário, para que os jovens se protejam, dos juros abusivos, quando na aquisição de um bem ou mesmo na aplicação do seu dinheiro.
É um grande problema para os educadores, na transferência do aprendizado. A apatia, o desinteresse e a indisciplina por parte dos alunos, são resultados de uma aparente contradição que existe entre a origem e desenvolvimento dos conteúdos matemáticos e a forma como eles são aplicados pela escola.
Gostaria de com este modesto trabalho, contribuir nas decisões dos alunos, no que diz respeito a: pagamentos, recebimentos, empréstimos, financiamentos e etc.
A economia encontra-se estabilizada, a oferta do crédito é grande e as pessoas estão se endividando cada vez mais.
Os juros simples, compostos, descontos, capitalizações e amortizações de dívidas pelo Sistema Francês de Amortização (PRICE) e o Sistema de Amortização Constante (SAC), agregam conteúdos interessantes.
1. JUROS
Podemos definir juros como rendimento de uma aplicação financeira, valor referente ao atraso no pagamento de uma prestação ou a quantia paga pelo empréstimo de um capital. Podemos destacar duas modalidades:
Juros Simples; Juros Compostos.
1.1 Juros Simples
O regime de juros será simples quando o percentual de juros incidir apenas sobre o capital inicial. Sobre os juros gerados a cada período não incidirão novos juros.
Os juros são diretamente proporcional ao valor do capital emprestado, dentro de um período unitário de tempo, dia, mês e ano também diretamente proporcionais ao período que o mesmo ficar emprestado.
Em matemática financeira é comum representar a taxa de juro que incide sobre o capital inicial pela letra (i), com o símbolo % que lê-se “por cento”. Ele significa dividir o número por 100.
Exemplo: se a porcentagem é 1% a razão centesimal é 1/100 e o número decimal é igual a 0,01, nesse caso a taxa i = 1% então i = 1/100 = 0,01.
1.1.1 Fórmula de Juros Simples
A expressão matemática utilizada para o cálculo das situações envolvendo juros simples é a seguinte :
J = C . i . n (a)
(J) em letra maiúscula o cálculo dos juros produzidos (C) em letra maiúscula o capital inicial
(i) em letra minúscula taxa percentual
1.1.2 Fórmulas derivadas
Como a fórmula envolve quatro variáveis, basta conhecer três delas para gerar a variável desconhecida.
- Para calcular o capital isolamos a incógnita C
C = J (b)
i . n
- Para obter o período n, temos
n = J (c)
C . i
- Para calcular a taxa i, temos
i = J (d)
C . n
Exemplos:
1- Calcular os Juros Simples obtidos pela aplicação do capital R$5.400,00 à taxa de 8% ao mês, durante 8 meses.
J = ?
C = 5.400,00 i = 8 = 0,08 100
J = C . i . n
J = 5.400,00 x 0,08 x 8
J = 3.456,00
Os juros obtidos é de R$3.456,00
2- Calcular o capital inicial, que a Juros Simples de 20% ao ano, produziu em um período de 9 anos um montante no valor de R$6.300,00.
C = ?
J = 6.300,00 i = 20 i = 0,2 100
N = 9
j = C . i . n
C = J . i . n
C = 6.300,00 . 0,2 . 9
C = 6.300,00 . 1,8
C = R$3.500,00
3- Qual o tempo necessário para que um capital no valor de R$ 900,00, emprestado a uma taxa de Juros Simples de 4% ao mês, gere uma renda total de R$288,00 de juros no período.
n = ? C = 900,00
I = 4 = 0,04 100
J = 288,00
J = C . i . n
n = J . C . i
n = 288,00 . 900,00 . 0,04
n = 288,00 . 36
n = 8 meses .
C = J (b) i . n
4- A que taxa de Juros Simples mensal devemos emprestar a quantia de R$7.500,00, para que em 12 meses, obtenhamos um valor total de R$450,00 de Juros?
i = ?
C = 7.500,00 n = 12
J = 450,00
J = C . i . n
i = J . C . n
i = 450,00 . 7.500,00 . 12
i = 450,00 . = 0,005 90.000
i = 0,5% .
1.1.3 Montante (M)
Montante (M) é a soma do capital com os juros produzidos em um determinado período.
M = C + J
(e)
É possível calcular os juros ou o capital que compõem um montante, quando se conhece, além do Montante, apenas o tempo e a taxa.
Para obtermos os juros produzidos vamos precisar substituir a equação (b) na equação (e),
Equação (b) C = J i . n
Equação (e) M = C + J
Substituindo = M = J + J i . n 1
M = J + J. i. n i . n
M = J (1+ i.n)
i . n
Isolando a incógnita J, obtemos,
J = M.i.n Juros produzidos (f) 1+ i . n
Para obtermos o capital, substituímos (a) na equação (e)
Equação (e) M = C + J
M = C + J M = C + C . i. n M = C (1 + i . n)
C = M Capital obtido (g) 1+ i . n
.1.4 Exemplos
1- Um capital ficou emprestado à taxa de Juros Simples de 5% ao ano durante 8 anos. Qual é o valor dos Juros produzidos, se ao fim desse período o Montante era de R$630,00.
i= 5 = 0,05 100
n = 8
J = ?
J = (M . i . n)
1 + i . n (f)
J = 630,00 . 0,05 . 8 1 + 0,05 . 8
J = 252 = J = R$180,00 juros produzidos 1,4
2- Qual é o capital, que emprestado por 12 meses, à taxa de Juros Simples de 3% ao mês, produz o Montante de R$4.352,00?
M = R$ 4.342,00 i = 3 = 0,03 100
n = ?
C = M (g) (1 + i . n)
C = 4.352,00 . 1 + 0,03 . 12
C = 4.352,00 1,36
O capital emprestado é de: C = R$3.200,00
1.2 Juros Compostos
O regime de juros compostos é o mais comum no sistema financeiro. Os juros gerados a cada período são incorporados ao principal para o cálculo dos juros do período seguinte.
Chamados de capitalização o momento em que os juros são incorporados ao principal.
Importante: a taxa i tem que ser expressa na mesma medida de tempo de n, ou seja, taxa de juros ao mês para n meses.
Para calcularmos apenas os juros basta diminuir o capital inicial do montante ao final do período: J = M – Co
1.2.1 Demonstração da Fórmula
Seja (M) o Montante ao fim de n períodos de capitalização composta, Co o
capital inicial e (i) a taxa de juros em cada período.
1º mês: M1 = Co (1 + i) => M1 = Co (1 + i)1
2º mês: M2 = M1 (1 + i) => M2 = Co (1 + i)2
3º mês: M3 = M2 (1 + i) => M3 = Co (1 + i)3
e assim por diante.
Ao fim de n períodos, o Montante Mn será dado pela fórmula:
Mn = Co (1 + i)n
(h)
Isolando Co na equação anterior, obtemos a fórmula que fornece o capital
inicial, em função do Montante Mn, da taxa i e do tempo n.
Co = Mn
Exemplos de Juros Compostos
1) Calcular o montante produzido pelo capital de R$15.600,00, aplicado a juros compostos de 5% ao mês, durante 6 meses.
Resolução: M6 = ?
C0 = 15.600,00
i = 5 = 0,05 100
n = 6
Aplicando a Fórmula: Mn = C0 (1 + i) n
M6 = 15.600 (1 + 0,05) 6
M6 = 15.600 . (1,05) 6
M6 = 15.600 . 1.3401
Assim o valor do montante produzido é de: M6 = 20.905,49
2) Calcular o capital inicial necessário para que, a juros compostos de 6% ao mês, produza o montante de R$15.600,00, durante 9 meses.
Resolução: M9 = 15.600,00
C0 = ?
i = 6 = 0,06 100
n = 9
Aplicando a Fórmula: Mn = C0 (1 + i) n
C0 = Mn .
( 1 + i ) n C0 = 15.600 .
( 1 + 0,06 )9 C0 = 15.600 .
( 1,06 )9
C0 = 15.600 .O
1,69
3- Quantos meses foram necessários para que um capital inicial de R$8.000,00, a Juros Compostos de 5% ao mês, produza um montante de R$21.226,38?
Mn = Co (1 + i)n
Mn = 21.226,38
C0 = 8.000,00
i = 5 . = 0,05 100
n =?
21.226,38 = 8.000,00 . (1 + 0,05)n 21.226,38 = (1 + 0,05)n
8.000,00
Log 2,65329770514 = n Log (1 + 0,05)
n = Log 2,65329770514 Log (1 + 0,05)
n= 20
Assim foram necessários 20 meses.
4- A que taxa de juros ao mês um capital inicial de R$5.000,00 produziu um montante de R$7.969,24037265 durante o período de 8 meses?
Mn = Co (1 + i)n
C0 = 5.000,00
Mn = 7.969,24037265
n = 8 i = ?
7.969,24 = (1 + i)8 5.000,00
1,59384807453 = (1 + i)8
(1,59384807453)1/8 = [ (1 + i)8]1/8 1 + i = 1,06
1.3 Taxas de Juros
Um dos elementos principais em matemática financeira são as taxas de juros que correspondem a taxa de renumeração do capital no determinado tempo. As taxas de juros podem ser classificadas de várias maneiras. Veremos abaixo algumas delas:
1.3.1 Taxa nominal
A taxa nominal de juros é usada para demonstrar os efeitos da inflação no período analisado, tendo por base os fundos financeiros.
Sendo a taxa nominal de 24% ao ano (a.a.) e visto que a capitalização é mensal, qual será a taxa de juros ao mês?
Como um ano tem 12 meses basta dividir pela taxa 24% A taxa mensal será de 2%
Estas duas taxas são proporcionais, pois utilizando meses como unidade de tempo, temos a seguinte proporção:
24 = 2 12 1
Observe uma coisa interessante: os 2% capitalizados mensalmente após um ano, tem que ser maior que 24%. Caso contrário não há capitalização.
É comum os bancos, em geral, utilizarem desta forma para atrair seus clientes. Oferecem em destaque uma taxa anual, mas embutem no contrato uma capitalização mensal. Esta taxa anual não contém os juros mensais, por isto dá-se o nome de taxa nominal.
1.3.2 Taxa efetiva
É denominada taxa efetiva a taxa de juros quando o período referente coincide com o período de capitalização.
Exemplo: vamos supor uma aplicação de 100.000,00 a juros de 2% ao mês, no período de 1 ano.
Utilizaremos a seguinte fórmula para o cálculo do montante composto:
Mn = Co (1 + i)n
M = ?
C = 100.000,00 i = 0,02
n = 12
M = 100.000,00 . (1 + 0,02)12 M = 100.000,00 . 1.2682418 M = 126.824,18
J = M – C
J = 126.824,18 – 100.000,00 J = 26.824,18
R$26.824,18 x 100 = 26,82 R$100.000,00
Então a taxa efetiva será de aproximadamente: 26,82%
1.3.3 Taxas equivalentes
Duas taxas são equivalentes quando, aplicadas sobre um mesmo capital, referindo a períodos de capitalização diferentes, produzem o mesmo montante.
Situação concreta
Evolução na linha do tempo de R$100,00 na data zero, as taxas de 10% ao mês e 21% ao bimestre.
x 1,10 x 1,10 x 1,10 x 1,10
100,00 110,00 121,00 133,10 146,41
100,00 121,00 146,41
x 1,21 x 1,21
No mesmo tempo, 10% ao mês e 21% ao bimestre, produzem o mesmo montante.
Taxas equivalentes podem ser aplicadas ao mesmo capital (C), durante o mesmo intervalo de tempo e produzir mesmo montante.
Seja o capital (C) aplicado por um ano a uma taxa anual (ia), o montante (Ma)
ao final do período (n) de um ano será igual a Ma = C (1 + ia).
Consideremos agora, o mesmo capital (C) aplicado por 12 meses a uma taxa mensal (im ), o montante (Mm) ao final do período 12 meses será igual a
Mm= C (1+ im)12
Pela definição, para determinar a taxa equivalente anual devemos ter: Mm = Ma
Portanto, C . (1+ ia ) = C . (1 + im )12
Dai concluímos que: 1+ ia = ( 1+ im )12
ia = taxa anual
im = taxa mensal
1) Exemplo
Qual a taxa anual de juros equivalente a 2% ao mês? Temos que:
im = 2% = 2/100 = 0,02
1 + ia = (1 + im)12
Para determinar a taxa anual resolvemos:
1+ ia = (1,02)12
1+ ia = 1,2682
ia = 1,2682 – 1
ia = 0,2682
ia = 26,82%
2) Exemplo
Qual a taxa mensal de juros equivalente a 24% anual? 1 + ia = (1 + im)12
(1 + ia)1/12 = [(1 + im)n] 1/12
(1 + ia)1/12 = 1 + im
ia = 24 =0,24
100
Para determinar a taxa mensal resolvemos:
im = (1 + 0,24)1/12 - 1
im = 0,01808758248
im = 0,018 . 100 = 1,81
1.3.4 Taxa real
É muito importante observarmos a taxa real de juros. Ela é o ganho real de um investimento em um período, pois ela contém a taxa efetiva e a taxa de inflação (perda do valor do dinheiro) no período de capitalização.
Em tempos de inflação alta a não observância dessa taxa fez com que muitas pessoas perdessem as suas economias, as taxas de juros para investimentos eram altas e gastavam os rendimentos dos juros. Quando retiravam o montante do dinheiro aplicado, elas percebiam a perda considerável do seu valor devido à taxa de inflação.
Vamos conhecer aqui a relação entre as taxas de juros nominal e real. Para isto vamos supor que um determinado capital (C) é aplicado por um período de tempo unitário (n) a uma certa taxa nominal (i). O montante (M) ao final do período será dado por M = C (1 + i ). Consideramos agora que durante o mesmo período, a taxa de inflação (desvalorização da moeda) foi igual a (J). O capital (C) corrigido por esta mesma taxa de inflação acarretaria um ̅ , ao final do período dado por ̅ = C (1 + J).
A taxa real de juros, indicada por (r), será aquela que aplicada ao montante ̅, produzirá o montante M. Podemos então escrever que M = ̅ (1 + r).
Substituindo M e ̅ vem que:
C (1 + i) = C (1 + J) . (1 + r)
Daí então vem que:
(1 + i) = (1 + J) . (1 + r), em que:
i = Taxa de juros nominal J = Taxa de inflação r = Taxa real de juros
Fórmula da taxa Real de Juros: r = (1 + i) – 1 (1 + J)
Um aspecto interessante sobre a taxa real de juros é que ela pode ser inclusive negativa no caso J > i.
Exemplo:
Pedro deposita em uma conta poupança uma certa quantia em dinheiro a juros de 6% ao ano, com uma inflação estimada em 7,8% ao ano. Calcular a taxa real do investimento.
Taxa real = 1 + taxa nominal – 1 1 + taxa de inflação
r = Taxa real de juros J = Taxa de inflação i = Taxa de juros nominal
J = 7,8 = 0,078 100
i = 6 = 0,06 100
0,02 x 100 = 2%
r = ?
(1 + i) = (1 + J) . (1 + r)
(1 + 0,06) = (1 + 0,078) . (1 + r)
1,06 = 1 + r 1,078
r = 0,983302411874 - 1 r = - 0,01669758 x 100 r = -1,7%
Veja o exemplo a seguir com taxa real positiva:
Numa operação financeira com taxas pré-fixadas, um banco empresta R$120.000,00 para ser pago em uma única parcela após um ano no valor R$150.000,00, sendo a inflação no período de empréstimo igual a 10%. Pede-se calcular as taxas nominal e real deste empréstimo.
Teremos que a taxa nominal será igual a:
i = 150.000,00 – 120.000,00 => 30.000,00 = 0,25 120.000,00 120.000,00
Portanto i = 25% ( taxa nominal )
Como a taxa de inflação no período é igual J =10%
Substituindo na fórmula da taxa de juros real,
(1 + i) = (1 + r) . (1 + J)
(1 + 0,25) = (1 + r) . (1 + 0,10)
1,25 = (1 + r) . 1,10
1 + r = 1,25 => r = 1,1364 – 1 1,10
2 RENDAS CERTAS
Uma renda é denominada certa quando todos os seus elementos: número de parcelas, período, valores das parcelas e vencimentos podem ser pré-fixados. Caso contrário, ela é dita renda aleatória.
Se todas as parcelas que constituem a renda são iguais, ela é denominada constante (série uniforme), caso contrário ela é dita variável.
2.1 Classificação de rendas
A renda pode ser classificada em:
a) Renda imediata ou postecipada – sem entrada b) Rendas antecipadas – com entrada
c) Rendas diferidas – com carência
2.1.1 Renda Imediata postecipada – Sem entrada ou imediata
Na amortização postecipada, imediata ou sem entrada, a primeira prestação ou pagamento se dá no fim do primeiro período, ou seja, na época 1. Vamos analisar a Figura 1 a seguir, que representa uma renda postecipada de n = 4 termos ou prestações.
Para facilitar a notação representamos (1 + i ) pela letra (u).
Podemos estabelecer nesse período uma equivalência de capitais entre o valor da dívida D e o somatório das prestações (P).
Du4 = Pu3 + Pu2 +Pu + P S 4
Colocando P em evidência
Du4 = P (u3 + u2 +u + 1) S4
Observe que a expressão entre parênteses é a soma dos 4 primeiros termos de uma progressão geométrica de razão u4.
S = u3 + u2 + u + 1
u.S = u (u3 + u2 +u + 1) u.S = u4 + u3 +u2 + u
Vamos subtrair
u.S – S
Colocando S em evidência
S (u – 1) = u4-1
S = u4– 1 => D = P.S . u4 - 1 u – 1 u - 1
Exemplo:
Sr. José do Carmo deposita em um banco, no fim de cada mês, durante 5 meses, a quantia de R$1.000,00. Calcule o montante da renda acumulada, imediatamente após o último depósito, sabendo que o banco está pagando juros de 20% ao mês.
Vamos esquematizar o nosso exemplo:
1000 1000 1000 1000 1000
0 1 2 3 4 5
M = Pu4 + Pu3 + Pu2 +Pu + P
Colocando P em evidência.
M = P (u4 + u3 + u2 +u + 1) S
S = u4 + u3 + u2 +u + 1
u.S = u5 + u4 + u3 +u2 + u
Vamos subtrair
uS – S
Colocando S em evidência
S (u – 1) = u5-1
S = u5– 1
u – 1
Fórmula:
D = P. u5– 1 u = 1 + i u - 1
Resolvendo o exercício:
D = ?
P = 1.000,00
i = 0.2
n = 5
D = 1000 . (1 + 0.2)5 - 1 D=R$7.441,60 ( 1 + 0.2) - 1
2.1.2 Renda Antecipada – Com entrada
Nas rendas antecipadas, ou com entrada, o pagamento da primeira prestação se dá na data atual, ou seja, no momento da constituição da dívida. Denotaremos esse momento de período 0.
Vamos supor agora que o fluxo de caixa fosse antecipado, ou seja, com os pagamentos periódicos realizados no início dos períodos como mostra a Figura 2.
u = (1 + i)
Como a dívida deverá ser liquidada no fim do quarto período, podemos estabelecer, nesse período, uma equivalência de capitais entre o valor da dívida D e o somatório das prestações P.
Ou seja:
Du4 = Pu4 + Pu3 + Pu2 + Pu S5
Colocando P em evidência.
Du4 = P (u4 + u3 + u2 +u) S
S= u4 + u3 + u2 +u
Vamos dividir ambos lados por u
S = u4 + u3 + u2 + u u u
S = u3 +u2 + u + 1
u
Vamos subtrair S – S
u
Colocando primeiro S em evidência
S 1 – u => S (1 – u) u u
S (1 – u) = 1 – u4 u
S = u. (1 – u4)
(1 - u )
S = (– u5 + u)
(-u + 1)
Então, onde n = 5
D = P. ( un + u) (- u + 1)
Exemplo:
0 1 2 3 4
S5
u5 u4 u3 u2 u
S = u5 + u4 + u3 + u2 +u ÷ u ambos os lados
S = u5 + u4 + u3 + u2 +u
u u
S u – u6 = 1 – u5 => S = u (1 - u5) => S = u – u6 1 – u 1 – u 1 - u
Concluímos que:
D = P. S => D = P . (u – u6) (1 – u ) Onde:
D = ?
P = 1.000,00 u = (1 + i) i = 0,02 n = 6
D = 1000 . (1 + 0.02) – (1 + 0.02)6 D = R$5.308,12 1 - (1 + 0, 02)
2.1.3 Renda diferida – Com carência
Quando os primeiros pagamentos forem exigidos a partir de um outro período que não seja o primeiro, neste caso existirá um intervalo de tempo em que não ocorre o pagamento. Esse intervalo de tempo é chamado de carência.
A figura 3 representa essa situação, para o caso de n = 4 prestações e um intervalo de n = 2 períodos.
Du6 = Pu3 + Pu2 + Pu + P
OBS: Devemos tomar cuidado pra não confundir o prazo de carência com a data do primeiro pagamento. Por exemplo, se o primeiro pagamento for efetuado 6 meses após a compra, com pagamentos mensais, a carência será de 5 meses, pois o que nos serve como comparação é o modelo básico e, nele, o primeiro pagamento seria efetuado 1 mês após a compra e a carência será igual a 5 meses que é a diferença entre 6 e 1.
Exemplo:
Uma compra foi efetuada em 4 parcelas de R$500,00, com o primeiro pagamento feito há 3 meses da compra, sob taxa de 20% ao mês. Qual o valor à vista, na data da compra?
500 500 500 500
0 1 2 3 4 5 6
VP = 500 + 500 + 500 + 500 (1.2)3 (1.2)4 (1.2)5 (1.2)6
Trazendo os pagamentos para a data focal zero, temos:
D = P + P + P + P
u3 u4 u5 u6 S
6
D = P ( 1 + 1 + 1 + 1 )
u3 u4 u5 u6
S = 1 + 1 + 1 + 1
u3 u4 u5 u6
uS = 1 + 1 + 1 + 1
u2 u3 u4 u5
uS – S =
S (u – 1) = 1 - 1 => S (u – 1) = u6 - u2 u2 u6 u8
S = u6 – u2 => S = u6 - u2
u8 (u - 1) u9– u8
D = P. u6 – u2 => u9– u8
(1.2)6 - (1.2)2
D = 500,00 . (1.2)9 - (1.2)8
3 SISTEMAS DE AMORTIZAÇÃO
Classificaremos os dois mais usados sistemas de amortização, sendo eles: a) Sistema francês de amortização (PRICE)
b) Sistema de Amortização Constante (SAC)
3.1 Sistema francês de amortização (PRICE)
Pelo sistema Francês, o devedor se compromete a amortizar o empréstimo com prestações constantes, periódicas e postecipado . Como essas prestações são constantes, à medida que vão sendo pagas, a dívida diminui e os juros tornam-se menores, enquanto as cotas de amortização tornam-se automaticamente maiores.
É fundamental lembrarmos também que, em qualquer sistema de amortização, uma prestação é constituída de duas parcelas, ou seja:
Prestação = Juro + Amortização
Cada prestação fixa do sistema Francês é calculada pela fórmula que já estudamos anteriormente para amortizações de séries uniformes.
Neste sistema, de prestação constante, teremos sempre juros decrescentes e amortização crescente.
Denominamos planilha de um financiamento a uma tabela onde cada linha representa um dos meses do financiamento e as colunas representam as parcelas de juro, amortização, saldo devedor e prestação, no caso das planilhas do sistema Francês, devemos calcular inicialmente a prestação usando uma fórmula e, em seguida, o valor do juro calculado sobre o saldo devedor da parcela anterior.
Exemplo:
Preencha a planilha do financiamento de R$240.000,00 pelo Sistema Francês de Amortização com 12 prestações mensais, com taxa de 3% ao mês na aquisição de um apartamento.
0 1 2 3 ……….……….. n
P P P P P P P P P P P P
Trazendo todas as prestações para a data focal zero, temos:
D = P + P + P +...+ P . u1 u 2 u 3 u n
onde u = i +1 Portanto
D = P. 1 + 1 + 1 + ...+ 1 . u 1 u 2 u 3 u n
Temos agora que determinar a soma da progressão geométrica entre parêntese que chamaremos ( S )
S = 1 + 1 + 1 + ... + 1 . multiplicamos os dois lados por u u 1 u2 u 3 u n
uS = 1 + 1 + 1 +... + 1 . u u 2 u (n-1)
fazendo uS - S, temos
S (u– 1) = 1 – 1 . un S = un - 1
un .(u – 1)
lembrando que u = 1+ i
S = un - 1 un . i
portanto o valor de D é dado por:
D = P . S
Esta é a fórmula para cálculo das prestações do sistema (PRICE):
P = D . (un . i)
(un -1)
Agora que conhecemos a fórmula podemos calcular as prestações, no exemplo em questão lembrando que u = (1 + i) e n = 12.
a) Cálculo da Prestação P = D . ( un . i ) .
(un– 1) D = R$240.000,00 i = 3 = 0,03 100
n = 12 u = (1 + i) P = ?
P= 240.000,00 (1 + 0,03)12 . 0,03 (1 + 0,03)12 - 1
P = 24.110,90
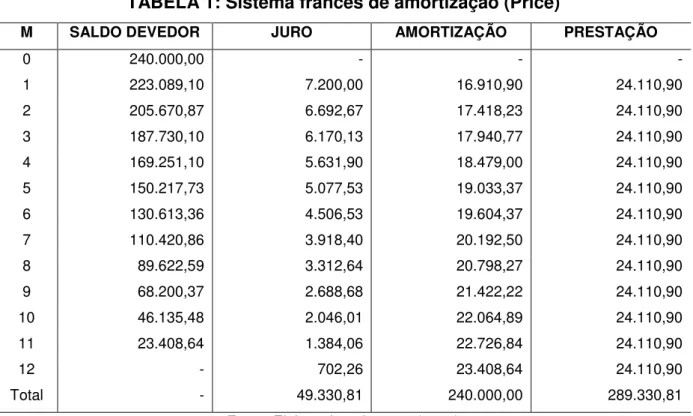
TABELA 1: Sistema francês de amortização (Price)
M SALDO DEVEDOR JURO AMORTIZAÇÃO PRESTAÇÃO
0 240.000,00 - - -
1 223.089,10 7.200,00 16.910,90 24.110,90
2 205.670,87 6.692,67 17.418,23 24.110,90
3 187.730,10 6.170,13 17.940,77 24.110,90
4 169.251,10 5.631,90 18.479,00 24.110,90
5 150.217,73 5.077,53 19.033,37 24.110,90
6 130.613,36 4.506,53 19.604,37 24.110,90
7 110.420,86 3.918,40 20.192,50 24.110,90
8 89.622,59 3.312,64 20.798,27 24.110,90
9 68.200,37 2.688,68 21.422,22 24.110,90
10 46.135,48 2.046,01 22.064,89 24.110,90
11 23.408,64 1.384,06 22.726,84 24.110,90
12 - 702,26 23.408,64 24.110,90
Total - 49.330,81 240.000,00 289.330,81
3.2 Sistema de Amortização Constante (SAC)
Esse é o sistema mais usado atualmente para financiamentos da casa própria.
Principais características são:
1. As parcelas de amortização são constantes; 2. O valor das prestações são decrescentes.
Para a construção da planilha do Sistema de Amortização constante (SAC), é necessário conhecer o valor a ser amortizado (A) em cada etapa. Para isso, vamos Dividir o valor total da dívida (D), pelo número de períodos (n).
A = D n
O valor (Pk) de cada prestação no período k, é composto de duas parcelas, os
juros indicados por (Jk),calculados sobre o saldo devedor do período anterior,
somados a quota de amortização (A). Pk = A + ( Jk-1 . i )
Neste exemplo vamos construir uma planilha do ( SAC ).
Leandro contraiu um empréstimo de R$ 10.000,00 pelo Sistema de Amortização Constante (SAC), a juros de 10% ao mês, a serem pagos em 5 parcelas. Qual o valor de amortização e de cada prestação?
Resolução: Sejam D0, D1, D2, D3, D4 ,D5, os saldos devedores nos períodos 0,
1, 2, 3,4, 5, respectivamente e (Jk) os juros do período (n). Temos então:
Vamos calcular primeiro o Valor da amortização (A) do (SAC): A = D
n D= 10.000,00
n= 5
A = 10.000,00 5
1ª Prestação; P1= A + ( D . i )
P1= 2.000,00 + ( 10.000,00. 0,10 )
P1= R$3.000,00
2ª Prestação; P2= (D – A) . i + A
P2= ( 10.000,00 - 2.000,00 ) . 0,10 + 2.000,00
P2= R$ 2.800,00
3ª Prestação;
P3= ( D - A .2) . i + A
P3= ( 10.000,00 - 2.000,00 . 2 ) . 0,10 + 2.000,00
P3= R$ 2.600,00
4ª Prestação;
P4= ( D - A . 3 ) . i + A
P4= ( 10.000,00 - 2.000,00 . 3 ) . 0,10 + 2.000,00
P4= R$ 2.400,00
5ª Prestação;
P5= ( D – A . 4 ) . i + A
P5= ( 10.000,00 – 2.000,00 . 4 ) . 0,10 + 2.000,00
P5= R$ 2.200,00
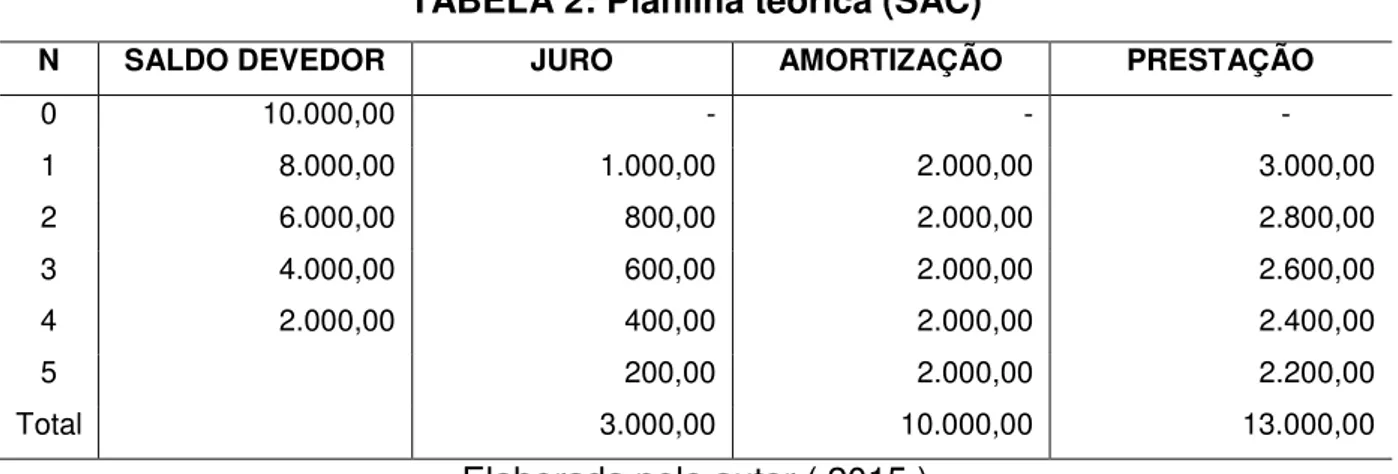
TABELA 2: Planilha teórica (SAC)
N SALDO DEVEDOR JURO AMORTIZAÇÃO PRESTAÇÃO
0 10.000,00 - - -
1 8.000,00 1.000,00 2.000,00 3.000,00
2 6.000,00 800,00 2.000,00 2.800,00
3 4.000,00 600,00 2.000,00 2.600,00
4 2.000,00 400,00 2.000,00 2.400,00
5 200,00 2.000,00 2.200,00
Total 3.000,00 10.000,00 13.000,00
Agora vamos fazer um novo exemplo para o sistema (SAC), com os mesmos valores da tabela (PRICE) feita anteriormente, para a realização de uma análise comparativa.
Exemplo:
O financiamento de R$240.000,00 pelo Sistema de Amortização Constante (SAC), com 12 prestações mensais, com taxa de 3% ao mês na aquisição de um apartamento.
R$240.000,00 ÷ 12 = R$20.000,00 Valor de cada Amortização
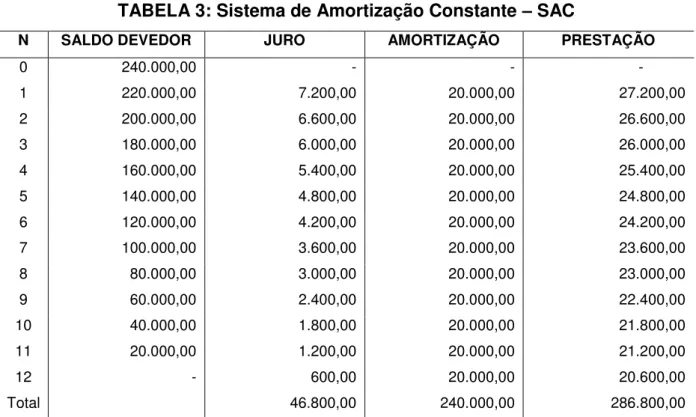
TABELA 3: Sistema de Amortização Constante – SAC
N SALDO DEVEDOR JURO AMORTIZAÇÃO PRESTAÇÃO
0 240.000,00 - - -
1 220.000,00 7.200,00 20.000,00 27.200,00
2 200.000,00 6.600,00 20.000,00 26.600,00
3 180.000,00 6.000,00 20.000,00 26.000,00
4 160.000,00 5.400,00 20.000,00 25.400,00
5 140.000,00 4.800,00 20.000,00 24.800,00
6 120.000,00 4.200,00 20.000,00 24.200,00
7 100.000,00 3.600,00 20.000,00 23.600,00
8 80.000,00 3.000,00 20.000,00 23.000,00
9 60.000,00 2.400,00 20.000,00 22.400,00
10 40.000,00 1.800,00 20.000,00 21.800,00
11 20.000,00 1.200,00 20.000,00 21.200,00
12 - 600,00 20.000,00 20.600,00
Total 46.800,00 240.000,00 286.800,00
Fonte: Elaborada pelo autor (2015)
3.3 Análise comparativa das tabelas (PRICE) e (SAC)
Comparar as tabelas (PRICE) e (SAC) somando as parcelas, ou os juros pagos, pode ser um erro. É possível ver o resultado desse somatório nas tabelas, das páginas 33 e 36, em que o total pago na tabela (SAC) é menor que na (PRICE). Isto não significa poder afirmar que o (SAC) seria melhor devido ao “menor pagamento de juros”.
O Sistema de Amortização Constante possui esta característica pelo simples fato de se destinar um maior volume de dinheiro para os pagamentos iniciais, quando comparado à tabela (PRICE). A única análise possível é que no (SAC) existe o benefício de você quitar a dívida, inicial, de maneira mais rápida, porém, existe a desvantagem de se precisar de mais dinheiro imediatamente para entrar no financiamento.
Dessa forma, podemos afirmar que os dois exemplos apresentados são equivalentes do ponto de vista da matemática financeira. Isso porque o fator preponderante a ser levado em consideração é a taxa de juros, em que ambos os casos é de 3% ao mês. Basta também trazer a série de pagamentos de cada uma delas para o valor presente. Em ambos, o valor é R$ 240.000,00, este é o valor da dívida original.
CONCLUSÃO
Aprendi após o desenvolvimento deste trabalho que a matemática financeira facilita o cálculo e a resolução de muitos problemas.
Entender os complexos métodos utilizados pelo mercado financeiro na obtenção do lucro máximo é uma questão de sobrevivência para todo e qualquer cidadão.
As armadilhas dos cartões de crédito e o crédito consignado na folha de pagamento do trabalhador, pode onerar seu salário por muito tempo, devido a altas taxas de juros.
REFERÊNCIAS
D’AMBRÓSIO, Nicolau e UBIRATAN. Matemática comercial e financeira. 29 ed. São Paulo: Companhia Editora Nacional, 1983.
FARIA, Rogério G. de. Matemática comercial e financeira. 5. ed., São Paulo: Makron Books, 2000.
LIMA, Elon Lages, et al., Temas e problemas. Rio de Janeiro: Coleção do Professor
de Matemática, SBM, 2001.
LISBOA, René José Malta. Normas da ABNT para apresentação de teses, dissertações, monografias e trabalhos acadêmicos: norma NBR 14.724. Belo Horizonte, 2013.
MARZAGÃO, Lineu José. Matemática Financeira.
MINELLE, Roberto Domingues; VIVEIROS, Leonardo Tassinori. Apostila Caixa Econômica Federal.
SÁ, Ilydio Pereira de. Matemática comercial e financeira. 2. ed.