Restauração de sistemas de distribuição de energia elétrica utilizando evolução diferencial com árvore de ancestralidade

(1)

Restaura¸

c˜

ao de Sistemas de Distribui¸

c˜

ao

de Energia El´

etrica Utilizando Evolu¸

c˜

ao

Diferencial com ´

Arvore de

Ancestralidade

Ricardo S´ergio Prado

Texto submetido à banca examinadora designada pelo Colegiado do Programa de Pós-Gradua¸cão em Engenharia Elétrica da Universidade Federal de Minas Gerais

para a obten¸c˜ao do t´ıtulo de Doutor em Engenharia El´etrica

Orientador:

Frederico Gadelha Guimar˜aes

Escola de Engenharia

Departamento de Engenharia El´etrica

(2)

(3)

(4)

Problemas de Restaura¸c˜ao de Sistemas de Distribui¸c˜ao de Energia (SDE), como

restau-ra¸cão de servi¸co, redu¸cão de perdas resistivas e planejamento da expansão do sistema, são normalmente formulados como problemas de otimiza¸cão multiobjetivo com várias res-tri¸cões inerentes ao sistema. Vários Algoritmos Evolucionários (AE) têm sido propostos

na resolu¸c˜ao desses tipos de problemas, mas a grande maioria deles ainda demandam um tempo computacional muito grande quando aplicados em grandes SDE (milhares

de barramentos e chaves). Neste trabalho é apresentada uma nova abordagem para a restaura¸cão de servi¸co em SDE de larga escala utilizando um algoritmo discreto para Evolu¸cão Diferencial baseado em uma Lista de Movimentos com Árvore de

Ancestrali-dade (DE-Tree), no qual a Árvore de Ancestralidade é utilizada para construir a lista de movimentos. A Representa¸cão Nó-Profundidade (RNP) é utilizada para representar

computacionalmente a topologia do sistema elétrico e dois operadores, o Preserve An-cestor Operator (PAO) e oChange Ancestor Operator(CAO), são utilizados na evolu¸cão

da popula¸cão. A abordagem proposta mostra que a Evolu¸cão Diferencial é adequada na resolu¸cão de problemas de otimiza¸cão de SDE preservando o mecanismo de autoadapta-¸cão da muta¸cão diferencial. Resultados apresentados na reconfigura¸cão de SDE sugerem

(5)

Problems in Power Distribution System Restoration (PDSR), such as service resto-ration, power loss reduction, and expansion planning, are usually formulated as

multi-objective and multi-constrained optimization problems. Several Evolutionary Algo-rithms (EAs) have been developed to deal with PDSR problems, but the majority of

EAs still demand high running time when applied to large-scale Distribution Systems (thousands of buses and switches). This work presents a new approach for service resto-ration in large-scale distribution systems that employs a Discrete Differential Evolution

based on List of Movements with ancestor Tree (DE-Tree), in which the Ancestor Tree is used to obtain the list of movements. The Node-Depth Encoding (NDE) is used to

computationally represent the electrical topology of the system and its operators, the Preserve Ancestor Operator (PAO) and the Change Ancestor Operator (CAO), are used to evolve the population. The proposed approach makes Differential Evolution suitable

for treating combinatorial optimization problems related to PDSR preserving the self-adaptive differential mutation mechanism. Results presented on Distribution System

(6)

Ao Prof. Frederico Gadelha Guimar˜aes pela valorosa orienta¸c˜ao prestada no

desen-volvimento deste trabalho, pela amizade e pelos jantares gastronˆomicos.

Ao Prof. Oriane Magela Neto (in memoriam), colega de outrora, pela amizade e

orienta¸c˜ao inicial deste trabalho, sempre atencioso e que sempre nos contagiou, a todos, com seu sorriso (gargalhada) sempre alegre.

Aos professores e funcion´arios do PPGEE da UFMG que, direta ou indiretamente,

contribu´ıram para a realiza¸c˜ao deste trabalho.

Ao Instituto Federal de Minas Gerais - Campus Ouro Preto pelo apoio dispensado

ao longo destes anos de doutoramento.

Aos colegas e amigos S´ılvia, Rodrigo, Betˆania, Lucas e ´Erica, Tatiana, Denise, Alan,

Andr´e, pela amizade e os momentos agrad´aveis que desfrutamos juntos durante esses anos.

(7)

Resumo iii

Agradecimentos v

Lista de Figuras viii

Lista de Tabelas x

S´ımbolos xii

1 Introdu¸c˜ao 1

1.1 Apresenta¸c˜ao . . . 1

1.2 Contexto Hist´orico . . . 2

1.3 Conceitos B´asicos . . . 3

1.3.1 Muta¸c˜ao Diferencial . . . 5

1.3.2 Cruzamento . . . 8

1.3.3 Sele¸c˜ao . . . 9

1.4 Objetivos . . . 11

1.5 Motiva¸c˜ao . . . 12

1.6 Estrutura do Trabalho . . . 13

2 DE Para Otimiza¸cão Combinatória 14 2.1 Indexa¸cão por Posi¸cão Relativa . . . 16

2.2 Transforma¸c˜ao Direta e Reversa. . . 17

2.3 Abordagem por Matriz de Permuta¸c˜ao - AMP . . . 18

2.4 Abordagem por Matriz de Adjacˆencias - AMA . . . 19

2.5 Lista de Movimentos: Abordagem Proposta . . . 19

2.6 Lista de Movimentos Swap . . . 22

2.7 Lista de Movimentos 2-opt. . . 25

2.8 Lista de Movimentos N´o-Profundidade . . . 27

2.8.1 Preserve Ancestor Operator . . . 28

2.8.2 Change Ancestor Operator . . . 30

2.8.3 Estrutura de dados para a lista de movimentos RNP . . . 32

2.9 Resumo . . . 40

3 Restaura¸cão de Sistemas de Distribui¸cão de Energia Elétrica 42 3.1 Sistema de Distribui¸cão de Energia Primária . . . 42

(8)

3.2 O Problema de Restaura¸c˜ao . . . 44

3.3 Formula¸c˜ao Matem´atica . . . 45

3.4 DE Aplicada ao Problema de Restaura¸c˜ao de SDE . . . 49

3.5 DE-Tree: DE com ´Arvore de Ancestralidade Exemplo Ilustrativo . . . 50

3.5.1 Inicializa¸c˜ao da Popula¸c˜ao. . . 50

3.5.2 Muta¸c˜ao Diferencial . . . 55

3.5.3 Cruzamento . . . 63

3.5.4 Busca Local . . . 65

3.5.5 Arvore de Ancestralidade´ . . . 67

3.6 Resumo . . . 70

4 Resultados Experimentais 71 4.1 Testes Realizados . . . 71

4.2 Fun¸c˜ao Objetivo . . . 73

4.3 Resultados. . . 74

4.3.1 Testes Para Falta ´Unica . . . 77

4.3.2 Testes para M´ultiplas Faltas. . . 82

4.3.3 Compara¸c˜ao do DE-Tree com outras Abordagens . . . 86

4.3.4 Simula¸c˜ao do M´etodo de Monte Carlo . . . 87

4.3.5 Rastreamento do N´umero de Opera¸c˜oes de Chaveamento . . . 89

5 Conclus˜oes 91 5.1 Contribui¸c˜oes da Tese . . . 92

5.2 Sugest˜oes para Trabalhos Futuros. . . 93

A Exemplo Ilustrativo 94 A.1 Indexa¸c˜ao por Posi¸c˜ao Relativa - IRP . . . 95

A.2 Transforma¸c˜ao Direta e Reversa - FBT. . . 97

A.3 Matriz de Permuta¸c˜ao - AMP . . . 98

A.4 Matriz de Adjacˆencias - AMA . . . 100

A.5 Lista de Movimentos - LM. . . 102

(9)

1.1 Muta¸c˜ao Diferencial . . . 6

1.2 Distribui¸c˜ao dos vetores diferen¸ca - gera¸c˜ao 1 . . . 7

2.1 Lista de Movimentos Swap: Passo 1 . . . 23

2.7 Heur´ıstica de refinamento 2-opt . . . 25

2.8 Lista de Movimentos 2-opt: Passo 1 . . . 26

2.12 Representa¸c˜ao de um indiv´ıduo por um grafo . . . 27

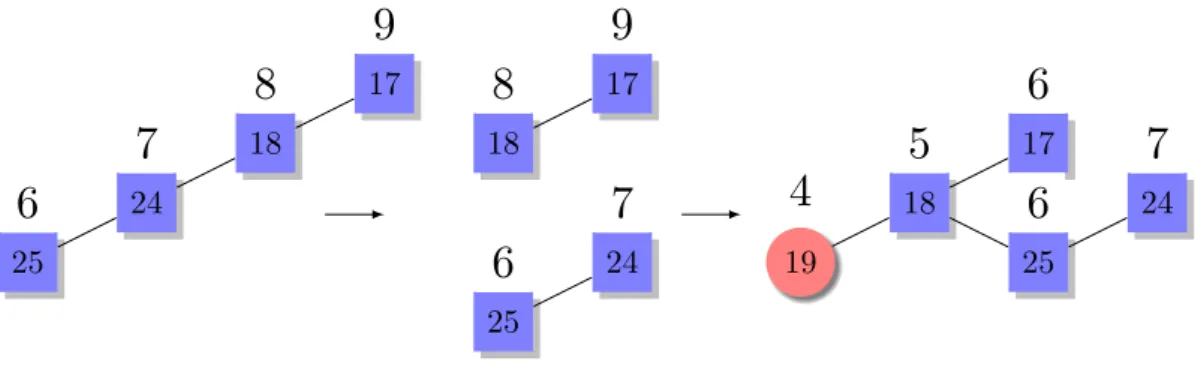
2.13 Poda de uma sub´arvore de T1 e respectivas RNP . . . 29

2.14 Enxerto da sub´arvore podada em T3 . . . 30

2.15 Sub´arvore gerada para r = 16 . . . 30

2.16 ÁrvoreT3 após o enxerto no nó 17 . . . 31

2.17 Indiv´ıduosG0,G1 eG2 aplicados a equa¸c˜ao da muta¸c˜ao diferencial . . . . 33

2.18 Primeiro movimento da lista de Movimentos. . . 34

2.19 Segundo movimento da lista de Movimentos . . . 35

2.20 Aplica¸c˜ao do PAO ao n´o 20. . . 36

2.21 Aplica¸c˜ao do CAO ao n´o 25. . . 37

2.22 Aplica¸c˜ao do PAO ao n´o 25. . . 38

2.23 Aplica¸c˜ao do quarto movimento da lista ao vetor base. . . 39

2.24 Aplica¸c˜ao do quinto movimento da lista ao vetor base. . . 40

2.25 Vetor mutante resultante da muta¸c˜ao diferencial. . . 40

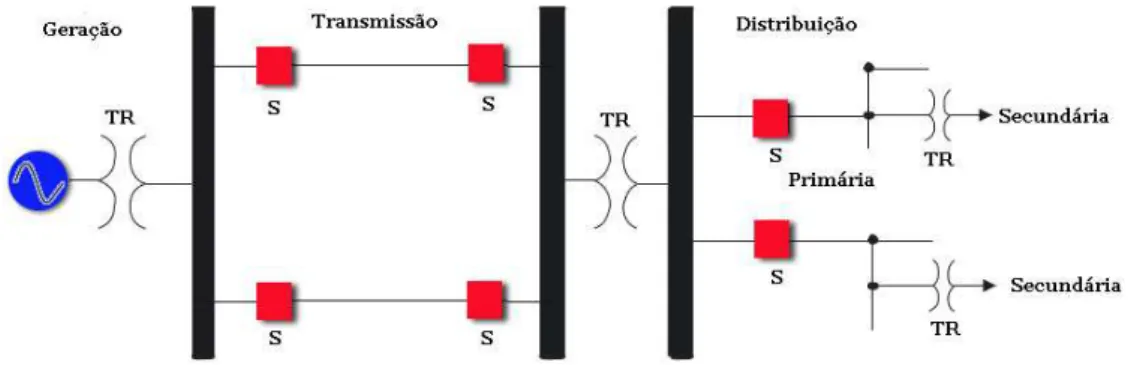
3.1 Sistema el´etrico de potˆencia . . . 43

3.2 Restaura¸c˜ao de servi¸co . . . 44

3.3 Representa¸c˜ao em grafo do SDE da Fig. 3.2 . . . 45

3.4 Indiv´ıduo I0 . . . 51

3.5 Gera¸c˜ao da popula¸c˜ao inicial . . . 53

3.6 Arvore de Ancestralidade da Popula¸c˜ao Inicial´ . . . 55

3.7 Adi¸cão do vetor mutante à árvore de ancestralidade . . . 60

(10)

3.8 Adi¸cão do vetor mutante à árvore de ancestralidade - Estratégia 2 . . . . 64

3.9 Adi¸cão do vetor experimental à árvore de ancestralidade . . . 66

3.10 Adi¸cão do vetor experimental à árvore de ancestralidade . . . 67

3.11 ´Arvore de ancestralidade da popula¸c˜ao final . . . 69

4.1 Alimentador 23 do SDE-SC . . . 72

4.4 Melhor solu¸cão encontrada para a Fun¸cão Agregada para uma única falta no Sistema 1. . . 80

4.5 Melhor solu¸cão encontrada para a Fun¸cão Agregada para uma única falta no Sistema 2. . . 81

4.6 Melhor solu¸cão encontrada para a Fun¸cão Agregada para três faltas si-multâneas no Sistema 1. . . 84

4.7 Melhor solu¸cão encontrada para a Fun¸cão Agregada para três faltas si-multâneas no Sistema 2. . . 85

4.8 Diagrama de caixa da Fun¸c˜ao Objetivo Agregada e Perdas Resistivas. . . 88

4.9 Diagrama de caixa das restri¸c˜oes de Carregamento da Rede e Carrega-mento das Subesta¸c˜oes. . . 88

4.10 Diagrama de caixa para o Número de opera¸cões de chaveamentos e res-tri¸cões de queda de tensão. . . 88

4.11 Opera¸cões de chaveamento a partir da configura¸cão inicial até a melhor solu¸cão na Árvore de Ancestralidade. . . 90

A.1 Rotas TSP aleat´orias para um problema com 10 cidades . . . 94

A.2 Constru¸c˜ao da lista de movimentosMr1r2: Passo 1 . . . 102

A.3 Constru¸c˜ao da lista de movimentosMr1r2: Passo 2 . . . 103

A.4 Aplica¸c˜ao do 1o _{movimento da lista ao vetor base} _{. . . 104}

A.5 Aplica¸c˜ao do 2o movimento da lista ao vetor base . . . 104

A.6 Aplica¸c˜ao do 3o _{movimento da lista ao vetor base} _{. . . 104}

(11)

2.1 Lista de N´os Adjacentes . . . 28

3.1 Lista de N´os Adjacentes . . . 46

3.2 Lista de N´os Adjacentes do SDE . . . 51

4.1 Configur˜ao corrente dos sistemas antes da ocorrˆencia das faltas. . . 76

4.2 Exemplo de Configura¸cões para os sistemas após da ocorrência das faltas. 77 4.3 Resultados para uma única falta no setor 504 . . . 77

4.4 Melhor resultado encontrado para uma ´unica falta no Sistema 1. . . 78

4.5 Melhor resultado encontrado para uma ´unica falta no Sistema 2. . . 78

4.6 Resultdos obtidos para 3 faltas simultˆaneas ocorridas nos setores 504, 182 e 486. . . 82

4.7 Melhor reusltado encontrado para cada objetivo/restri¸c˜ao para 3 Faltas simultˆaneas ocorridas no Sistema 1.. . . 82

4.8 Melhor reusltado encontrado para cada objetivo/restri¸c˜ao para 3 Faltas simultˆaneas ocorridas no Sistema 2.. . . 82

4.9 Valores M´edios obtidos com os algoritmos DE-Tree, AEMT e MEAN-DE 86 4.10 Valores M´edios obtidos com os algoritmos DE-Tree e MEAN-DE . . . 87

(12)

AE Algoritmos Evolucion´arios

AG Algoritmo Gen´etico

AMA Abordagem por Matriz de Adjacˆencias

AMP Abordagem por Matriz de Permuta¸c˜ao

CE Computa¸c˜ao Evolutiva

DE-Tree Evolu¸c˜ao Diferencial com ´Arvore de Ancestralidade

DE Evolu¸c˜ao Diferencial

EE Estrat´egias Evolucion´arias

FBT Transforma¸c˜ao Direta e Reversa(do inglˆes: Forward/Backward Transformation)

IRP Indexa¸cão por Posi¸cão Relativa (do inglês: Indexing by Relative Position)

MPF Ordena¸c˜ao de n´os pelo Modelo Pai-Filho

NA Chaves seccionadoras normalmente abertas

NF Chaves seccionadoras normalmente fechadas

PE Programa¸c˜ao Evolutiva

PG Programa¸c˜ao Gen´etica

PSO Otimiza¸c˜ao por Enxame de Part´ıculas (do inglˆes: Particle Swarm Optimization)

RNP Representa¸c˜ao N´o-Profundidade

RS Restaura¸c˜ao de Servi¸co

SDE Sistema de Distribui¸c˜ao de Energia

TSP Problema do Caixeiro Viajante (do inglˆes: Traveling Salesman Problem)

(13)

x Vari´avel real que representa cada parˆametro do sistema.

X Vetor de vari´aveis reais representando uma solu¸c˜ao.

X Região de dom´ınio, espa¸co dos parâmetros ou espa¸co de busca de otimiza¸cão.

f(.) Fun¸c˜ao objetivo.

bL,j Limite inferior de cada parˆametro do sistema.

bU,j Limite superior de cada parˆametro do sistema.

Np N´umero de indiv´ıduos da popula¸c˜ao.

Vg,i Vetor mutanteida gera¸c˜ao g

Xg,r0 Vetor base da equa¸cão da muta¸cão diferencial da gera¸cão g

Xg,r1 Vetor 1 da equa¸cão da muta¸cão diferencial da gera¸cãog

Xg,r2 Vetor 2 da equa¸cão da muta¸cão diferencial da gera¸cãog

F Fator de multiplica¸cão escalar da equa¸cão da muta¸cão diferencial

Ug,i Vetor experimental da gera¸c˜aog

Cr Probabilidade de cruzamento

N Estrutura de vizinhan¸ca

P Matriz de Permuta¸c˜ao

PF Matriz de Permuta¸c˜ao ponderada pelo escalarF

G Grafo representando uma estrutura em ´arvores.

(14)

Introdu¸

c˜

ao

1.1 Apresenta¸

c˜

ao

Para lidar com certos problemas nas áreas da engenharia e da computa¸cão, que pelos mé-todos tradicionais são considerados intratáveis ou que demandam um tempo de execu¸cão

computacional elevado, engenheiros e pesquisadores têm buscado na natureza modelos que sirvam de inspira¸cão. Esta inspira¸cão em processos naturais tem possibilitado criar

modelos computacionais com larga aplica¸cão na resolu¸cão de problemas práticos na in-dústria e comércio. Na área de otimiza¸cão de sistemas, muitos processos observados na

natureza têm sido utilizados como modelos na tentativa de solucionar tais problemas. Um olhar mais agu¸cado entre otimiza¸cão de sistemas e evolu¸cão biológica levou ao de-senvolvimento de um paradigma importante nas técnicas de inteligência computacional:

a Computa¸cão Evolutiva (CE), que se utiliza dos princ´ıpios da evolu¸cão dos seres vi-vos, como sele¸cão natural e heran¸ca genética, na resolu¸cão de problemas complexos de

otimiza¸cão. O paradigma da CE data da década de 1950, quando o uso dos princ´ıpios da teoria da evolu¸cão das espécies de Charles Darwin foram utilizados pela primeira vez na resolu¸cão de problemas de engenharia. Na década seguinte, vertentes distintas

dessas t´ecnicas foram desenvolvidas: a Programa¸c˜ao Evolutiva (PE) [Fogel and Fogel 1996] desenvolvida por Lawrence J. Fogel nos Estados Unidos e, quase simultaneamente

na Alemanha, as Estratégias Evolucionárias (EE) apresentadas por I. Rechenberg e H. P. Schwefel [Beyer and Schwefel 2002]. Uma década mais tarde, John Henry Holland

e Ann Arbor apresentam o método Algoritmo Genético (AG) utilizado na solu¸cão de problemas práticos de otimiza¸cão [Das and Suganthan 2011]. Estas três áreas seguem separadamente até que, na década de 1990, são unificadas como dialetos diferentes de

uma mesma tecnologia denominada, então, por Computa¸cão Evolutiva. Também nesta mesma década, seguindo em linhas gerais o mesmo paradigma, surge a Programa¸cão

(15)

Gen´etica (PG), uma nova vertente proposta por J.R. Koza [Koza 1990] e o algoritmo Evolu¸c˜ao Diferencial (DE)1 _[_{Storn and Price 1995}_{], tema em que este trabalho discorre.}

Muitos algoritmos h´ıbridos posteriormente desenvolvidos incorporam muitas das caracter´ısticas e t´ecnicas acima citadas e, consequentemente, s˜ao dif´ıceis de serem

classi-ficados. Assim, todos esses métodos são referidos como Algoritmos Evolucionários (AEs) e esta divisão é meramente histórica. Hoje em dia, as meta-heur´ısticas inspiradas na natureza são constitu´ıdas pelos AEs (compreendendo os AGs, PE, EEs, PG, DE, etc.)

bem como os algoritmos de Otimiza¸c˜ao por Enxame de Part´ıculas (PSO)2[Kennedy and Eberhart 1995], os Sistemas Imunol´ogicos Artificiais [de Castro and Timmis 2002], os

algoritmos de Estima¸c˜ao de Distribui¸c˜ao [Larranaga and Lozano 2002] e muitos outros.

O DE surgiu na d´ecada de 1990 como um AE utilizado na otimiza¸c˜ao de sistemas a

variáveis cont´ınuas e é um algoritmo de otimiza¸cão importante e poderoso em sistemas mono-objetivo [Price et al. 2005,Mezura-Montes and Coello 2006] e em sistemas

multi-objetivo [Xue et al. 2003,Batista et al. 2009]. Atualmente, ele tem sido utilizado com algum sucesso em um grande número de problemas de natureza combinatória [Lichtblau 2002,Onwubolu and Davendra 2009,Price et al. 2005], em que o conjunto de solu¸cões

fact´ıveis é um subconjunto dos números inteiros não-negativos e, portanto, pertencentes a uma classe de problemas do mundo real de natureza estritamente discreta.

1.2 Contexto Hist´

orico

O algoritmo DE surgiu do algoritmo Recozimento Simulado Genético3 desenvolvido por Kenneth Price. Este algoritmo era um algoritmo combinatório baseado em popula¸cão que realizava um “recozimento” dirigido pelo desempenho médio dessa popula¸cão. Logo

após o desenvolvimento desse algoritmo, Price foi contactado por Rainer Storn que es-tava interessado em solucionar o problema de ajuste dos parâmetros do Polinômio de

Tchebychev aplicando o algoritmo de recozimento simulado genético. Após alguns expe-rimentos, Price modificou o algoritmo utilizando variáveis reais ao invés de codifica¸cão

em bit-string e operadores aritméticos ao invés de operadores lógicos. Essas modifica-¸cões transformaram o recozimento genético combinatório em um otimizador a variáveis cont´ınuas. A descoberta do algoritmo DE aconteceu quando Price surgiu com a ideia

de usar as diferen¸cas entre vetores como uma maneira de perturbar e evoluir a popu-la¸cão (método, esse, denominado então por muta¸cão diferencial), um cruzamento por

recombina¸cão discreta e uma sele¸cão em pares. Price e Storn detectaram que a muta¸cão

1

do inglˆesDifferential Evolution 2

do inglˆesParticle Swarm Optimization 3

(16)

diferencial, com recombina¸cão discreta e sele¸cão em pares, não necessitava de um fator de recozimento. Assim, o mecanismo de recozimento foi removido surgindo o algoritmo

DE [Feoktistov 2006].

O primeiro artigo sobre o DE apareceu como um relat´orio t´ecnico escrito por R.

Storn e K. V. Price em 1995 [Storn and Price 1995]. Um ano depois ele participou do First International Contest on Evolutionary Optimization (1st ICEO), realizado em con-junto com o IEEE International Conference On Evolutionary Computation (CEC) em

Nagoya, Japão. O DE terminou o confronto em terceiro lugar e foi considerado o melhor algoritmo evolucionário na resolu¸cão de fun¸cões de testes cont´ınuas (os dois primeiros

lugares foram dados a algoritmos não evolutivos pois, apesar de não serem aplicáveis a vários tipos de problemas, resolviam as fun¸cões testes mais rápido que o DE). Em

1997, Price apresenta o DE no Second International Contest on Evolutionary Optmiza-tion [Price 1997] e acabou sendo um dos melhores entre os algoritmos concorrentes. Dois artigos consecutivos [Price and Storn 1997a] e [Price and Storn 1997b] descrevendo o

al-goritmo em detalhes são, então, publicados. Na competi¸cão de otimiza¸cão de problemas cont´ınuos clássicos de 10 dimensões no CEC de 2005, o DE assegurou a segunda

colo-ca¸c˜ao e uma variante auto-adaptativa do DE, denominada SaDE4 [Qin and Suganthan 2005], assegurou o terceiro lugar, embora tenha tido um desempenho insuficiente em

problemas acima de 30 dimensões. Outras variantes do DE continuaram a assegurar as melhores coloca¸cões nas subsequentes competi¸cões do CEC como as do CEC-2006 em otimiza¸cão de parâmetros reais com restri¸cões (1o _{lugar), CEC-2007 competi¸cão em}

oti-miza¸c˜ao multiobjetivo (2o _{lugar), CEC-2008 competi¸c˜}_{ao em otimiza¸c˜}_{ao global em larga}

escala (3o _{lugar), CEC-2009 competi¸c˜}_{ao em otimiza¸c˜ao multiobjetivo (1}o _{lugar, dado a}

um algoritmo DE baseando no MOEA/D5 para problemas sem restri¸cões) e CEC-2009 competi¸cão em computa¸cão evolucionária em ambientes dinâmicos e incertos (1o _lugar)

[Das and Suganthan 2011].

1.3 Conceitos B´

asicos

Muitas vezes, em engenharia, nos deparamos com o problema de otimiza¸cão que consiste em encontrar a melhor solu¸cão dentro de certas restri¸cões e flexibilidades existentes em

um determinado sistema. O objetivo da otimiza¸cão é, então, encontrar um conjunto de valores dos parâmetros do sistema para o qual o seu desempenho é o melhor sobre estas

restri¸cões. Em um sistema não-linear a variáveis cont´ınuas, a solu¸cão de um problema

4

Self-adaptive Differential Evolution

5

(17)

de otimiza¸c˜ao irrestrito para um sistema mono-objetivo ´e definida como:

x∗_{= arg min}

x f(x) (1.1)

onde:

x∗ _{´e a solu¸c˜ao ´}_{otima. ´}_{E o argumento que minimiza a fun¸c˜}_ao _f₍_x_).

f(.) :X ⊂Rn→Ré a fun¸cão de custo ou fun¸cão objetivo a ser minimizada ou maximizada6_.

X é a região de dom´ınio, espa¸co dos parâmetros ou espa¸co de busca de otimiza¸cão. Ela é definida como:

X =_{x_∈Rn:bL,j ≤xj ≤bU,j;j= 1, . . . , n}

em quebL,je bU,j s˜ao, respectivamente, os limites inferior e superior de cada

parˆametroj do sistema.

´

E importante destacar que solu¸cão ótima pode ser local, se ela for a melhor solu¸cão dentro de uma determinada vizinhan¸ca, ou pode ser global, caso em que é a melhor solu¸cão encontrada para o sistema.

O algoritmo DE, assim como outros AEs, ´e baseado em popula¸c˜oes e, portanto,

utiliza um conjunto de vetoresX de solu¸cões candidatas aleatoriamente geradas dentro da região de dom´ınio_X como popula¸cão inicial. Para um sistema multivariável, a solu¸cão

x, ou indiv´ıduo da popula¸c˜ao, ´e representada por um vetor dado por:

Xi =

xg,i,1, xg,i,2, xg,i,3, . . . , xg,i,n

T

(1.2)

onde o subscritogindica a gera¸c˜ao em que cada indiv´ıduo pertence,i indica o indiv´ıduo

dentro da popula¸cão e o terceiro subscrito indica um dos j parâmetros da solu¸cão.

O objetivo da otimiza¸cão passa, então, a ser o de encontrar o vetor de parâmetros

X∗ _{o qual minimiza a fun¸c˜ao objetivo} _f₍_._{), isto ´e:}

f(X∗₎_{< f}₍_X₎ _∀ _X _{∈ X} _(1.3)

Uma vez criada a popula¸c˜ao inicial, o algoritmo DE realiza o processo de muta¸c˜ao

para evoluir a popula¸cão e gerar novas solu¸cões ótimas. Basicamente, a evolu¸cão diferen-cial proposta por Price e Storn consiste em, através da equa¸cão da muta¸cão diferendiferen-cial,

6

(18)

criar indiv´ıduos mutantes. Os indiv´ıduos mutantes resultantes, por sua vez, passam por um processo de recombina¸c˜ao com os indiv´ıduos da popula¸c˜ao corrente gerando uma

po-pula¸cão de indiv´ıduos experimentais. Estes competem com os indiv´ıduos da popula¸cão corrente por um lugar na próxima gera¸cão [Price et al. 2005]. Cada uma destas etapas

´e apresentada nas Se¸c˜oes de1.3.1a 1.3.3.

1.3.1 Muta¸c˜ao Diferencial

Após gerada a popula¸cão inicial, o algoritmo DE realiza a muta¸cão diferencial como o principal processo de evolu¸cão da popula¸cão. A muta¸cão diferencial consiste em, para

cada indiv´ıduo correnteXg,i da popula¸c˜ao (tamb´em denominadovetor alvo), gerar um

indiv´ıduo mutanteVg,i. Para tanto, trˆes indiv´ıduos distintos entre si e entre o vetor alvo

são escolhidos aleatoriamente dentro da popula¸cão para fazerem parte da equa¸cão da

muta¸c˜ao diferencial (Eq.1.4): o primeiro denominadovetor base (Xg,ro) e os outros dois

vetores diferen¸ca (Xg,r1 e Xg,r2, respectivamente). O vetor mutante ´e obtido da soma

vetorial entre a diferen¸ca entre os vetores diferen¸ca, ponderada pelo escalarF, e o vetor base.

Vg,i = Xg,r0 + F.(Xg,r1 − Xg,r2) (1.4)

onde: Xg,r0 6= Xg,r1 6= Xg,r2 6= Xg,i.

O fator escalarF´e um n´umero real positivo que controla a amplitude da diferen¸ca

vetorial e, consequentemente, o tamanho do passo da muta¸cão no espa¸co de busca e a taxa em que a popula¸cão evolui. O intervalo indicado para o fator escalar éF _∈ (0,1+). Embora não haja um limite superior para F, raramente valores maiores que 1 são

uti-lizados [Price et al. 2005]. Por outro lado, quando F = 1, combina¸cões distintas dos vetores diferen¸ca geram vetores mutantes idênticos, o que reduz o número de vetores

mutantes pela metade [Price et al. 2005]. Normalmente, a escolha do melhor valor é feita por tentativa e erro numa bateria de testes que demandam um tempo considerável. Valores t´ıpicos encontrados na literatura estão entre F= 0,6 e F= 0,9. A Figura 1.1

ilustra como ´e obtido um vetor mutante Vg,i em um sistema bidimensional.

A equa¸cão da muta¸cão diferencial gera vetores mutantes que serão maiores ou

meno-res dependendo da distribui¸cão da popula¸cão corrente no espa¸co de busca do problema. Essa diversidade de vetores afeta tanto o tamanho do passo de convergência como a

sua orienta¸cão para as curvas de n´ıvel da fun¸cão objetivo [Storn and Price 1995]. Esta propriedade do DE é mostrada nas Figuras1.2 à1.47 para as curvas de n´ıvel da fun¸cão

peaks (Equa¸c˜ao 1.5) utilizada como exemplo.

7

(19)

Xg,r0

Xg,r2

Xg,r1

F(Xg,r1 −Xg,r2)

Vg,i =Xg,r0F(Xg,r1−Xg,r2)

X2

X1

Figura 1.1: _Muta¸c˜_{ao Diferencial: a diferen¸ca ponderada,} _F₍_X_g,r₁₋_X_g,r₂_{), ´e} adici-onada ao vetor base, Xg,r0, para produzir o vetor mutante,Vg,i. (Figura reproduzida

de: [Price et al. 2005] p´ag. 39).

f(x1, x2) = 3(1−x1)2.exp

x2₁+ (x2+ 1)2

−10

x1

5 −x31−x52

. exp

x2₁+x2₂

−13.exp

(x1+ 1)2+x22

(1.5)

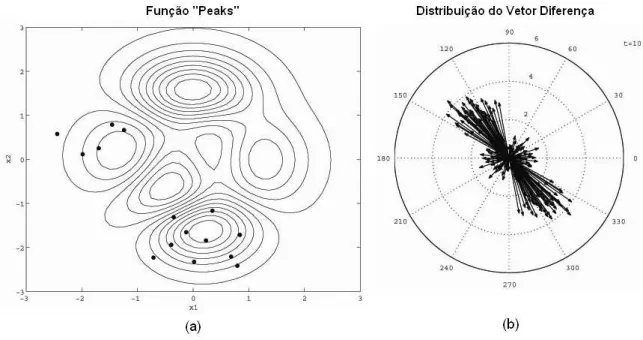
A Figura 1.2(a) mostra a distribui¸cão da popula¸cão nas curvas de n´ıvel da fun¸cão peakspara a gera¸cão 1 e, na Figura1.2(b), são tra¸cados, em um diagrama polar, todas as

combina¸cões poss´ıveis que podem ser obtidas para os vetores diferen¸ca dessa popula¸cão. Observa-se que, inicialmente, os tamanhos dos vetores diferen¸ca são grandes devido a

distribui¸cão, ainda aleatória, da popula¸cão e estão uniformemente distribu´ıdos em todas as dire¸cões.

`

A medida que a popula¸c˜ao evolui e converge para as bacias de atra¸c˜ao, observa-se

que todas as combina¸cões poss´ıveis dos vetores diferen¸ca tendem a ter tamanhos equi-valentes às distâncias existentes entre essas bacias de atra¸cão e, também, direcionam-se

para elas. Essa caracter´ıstica inerente ao DE ´e mostrada na Figura1.3para a gera¸c˜ao 10.

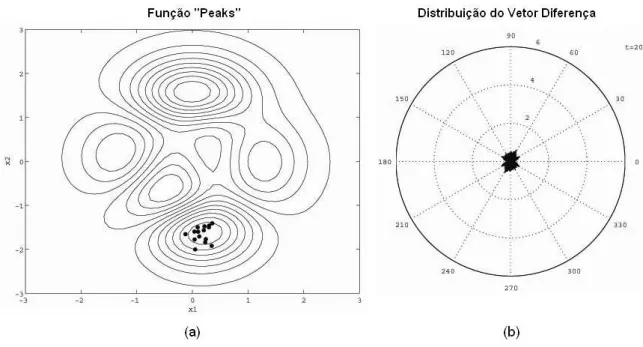
A Figura1.4(a)mostra que, para esse exemplo, após 20 gera¸cões a popula¸cão

(20)

Figura 1.2: _Gera¸c˜_{ao 1: Popula¸c˜}_{ao ainda aleat´}_{oria (a) e vetores diferen¸ca grandes e} uniformemente distribu´ıdos (b).

Figura 1.3: _{Gera¸c˜ao 10: Distribui¸c˜}_{ao da Popula¸c˜}_{ao em torno das bacias de atra¸c˜}_ao (a) e vetores diferen¸ca direcionados para as bacias de atra¸c˜ao (b).

com toda a popula¸c˜ao dentro da bacia de ´otimo global e o tamanho dos vetores diferen¸ca

estarem limitados a esta regi˜ao, o DE inicia uma busca local pelo valor ´otimo.

Essa caracter´ıstica do DE em obter a diferen¸ca entre dois indiv´ıduos da popula¸cão e usá-la para definir as dire¸cões de busca e ajustar o passo da muta¸cão (inicialmente

(21)

Figura 1.4: _{Gera¸c˜ao 20: Popula¸c˜}_{ao atra´ıda para o m´ınimo global (a) e tamanho dos} vetores diferen¸ca e sua distribui¸c˜ao prop´ıcios a uma busca local (b)

1.3.2 Cruzamento

Após a etapa de muta¸cão diferencial, o DE realiza a etapa de cruzamento para gerar os vetores experimentais. Nesta etapa, cada indiv´ıduo alvoXg,ida popula¸cão corrente e seu

vetor mutante correspondenteVg,i se recombinam para produzir um vetor experimental

Ug,i [Price et al. 2005]:

Ug,i=Ug,i,j =

(

Cruzamento(Vg,i,j, Xg,i,j), serand(0,1) ≤ Crou j = jrand

Xg,i,j, c. c.

(1.6) onde:

j: j´esimo _{parˆametro do vetor correspondente,}

Cr: probabilidade de cruzamento,

jrand: parˆametro do vetor mutante escolhido aleatoriamente.

Na sua vers˜ao cl´assica, o algoritmo DE utiliza uma probabilidade de cruzamento

Cr ∈ [0,1]. A probabilidade de cruzamentoCr controla a fra¸c˜ao dos parˆametros do vetor

mutante que serão copiados para a solu¸cão corrente. Um parâmetro do vetor mutante escolhido aleatoriamente, jrand, é copiado para o vetor experimental para garantir que

(22)

Nos AEs, o cruzamento é realizado através da recombina¸cão discreta entre dois vetores pais da mesma popula¸cão para gerar dois vetores filhos. Diferentemente, o DE

realiza a recombina¸cão entre um vetor da popula¸cão corrente (o vetor alvo) e o vetor mutante correspondente para gerar um único filho: o vetor experimental.

1.3.3 Sele¸c˜ao

O método de sele¸cão utilizado no DE é semelhante ao método (µ+λ) utilizado nas EE,

em que, os melhores µ vetores da combina¸cão dos µ pais com os λ filhos compõem a próxima gera¸cão. A diferen¸ca está no fato de que, ao invés de ranquear a popula¸cão

formada por pais e filhos, DE realiza uma competi¸cão entre cada vetor pai com o seu vetor filho correspondente selecionando um deles para a próxima gera¸cão (método de sele¸cão (1 + 1)). Essa técnica de comparar cada vetor experimental (vetor filho) com o

vetor corrente de mesmo ´ındice (vetor pai) garante manter a melhor solu¸cão obtida para o indiv´ıduo daquele ´ındice. Este método de sele¸cão garante a diversidade dos indiv´ıduos

e evita a convergência prematura da popula¸cão, o que é importante no DE, já que a distribui¸cão espacial da popula¸cão influencia diretamente o desempenho do algoritmo

[Storn and Price 1995].

Baseada na fun¸c˜ao objetivo do vetor alvoXg,i e do vetor experimentalUg,i, a sele¸c˜ao

´e realizada da seguinte maneira: se a fun¸c˜ao objetivo do vetor experimental for menor

ou igual à do vetor alvo, o vetor experimental o substitui na próxima gera¸cão; caso contrário, o vetor alvo é preservado e vai para a próxima gera¸cão:

Xg+1,i=

(

Ug,i, sef(Ug,i)≤f(Xg,i)

Xg,i, c. c.

(1.7)

Uma vez que a nova gera¸cão esteja completa, o processo de muta¸cão, recombina-¸cão e sele¸cão é repetido até que um determinado critério de parada estabelecido seja

alcan¸cado. O Algoritmo 1 apresenta o pseudocódigo do algoritmo DE na sua forma clássica. Esta versão clássica do algoritmo DE é também referida na literatura como

DE/ rand/1/bin8_{. Modifica¸c˜}_{oes na etapa de muta¸c˜ao e na escolha do tipo de}

cruza-mento podem gerar varia¸cões interessantes no algoritmo DE. Além da escolha aleatória para o vetor base, apresentada na sua versão clássica, outras duas versões são

apresen-tadas em [Price et al. 2005]. Estas vers˜oes s˜ao a best e a target-to-best. Na primeira,

8

(23)

o vetor base é o indiv´ıduo com a melhor fun¸cão objetivo da popula¸cão corrente. Na segunda o vetor base é uma recombina¸cão direta entre o vetor alvo e o melhor indiv´ıduo

da popula¸c˜ao corrente conforme mostrado na Equa¸c˜ao 1.8:

Xg,r0 = Xg,i + λ.(Xg,best − Xg,i). (1.8)

Algorithm 1Pseudocódigo DE Clássico. Listagem reproduzida de [Price et al. 2005] pág. 42

Input: Np // N´umero de indiv´ıduos da popula¸c˜ao

Input: D // dimens˜ao do problema

Input: F // fator escalar da equa¸cão da muta¸cão diferencial // Gera¸cão da popula¸cão de vetores experimentais

repeat

for(i= 0;i < N p;i+ +) do repeat

Xr0 =f loor(rand(0,1)×N p);

until (r0 == i);

repeat

until ((r1 == r0)OR(r1 == i));

repeat

until ((r2 == r1)OR(r2 == r0)OR(r2 == i));

jrand=f loor(D×rand(0,1));

// Cria vetores experimentais

for(j= 0;j <D;j+ +) do

if (rand(0,1)_{≤ C}r)OR(j == jrand) then

Uj,i = Xj,r0 + F×(Xj,r1 − Xj,r2)

else

Uj,i = Xj,i;

// Sele¸cão da próxima gera¸cão

for(i= 0;i < N p;i+ +) do if f(Ui)≤f(Xi)then

Xi=Ui;

until(crit´erio-de-parada n˜ao encontrado);

De maneira a não aumentar o número de parâmetros iniciais, o fator de multiplica-¸cão escalar λna Equa¸cão 1.8é escolhido ser o mesmo fator de multiplica¸cão escalarF

(24)

DE/best/1/bin _⇒ Vg,i = Xg,best + F.(Xg,r1 − Xg,r2)

DE/target₋to₋best/1/bin _⇒ Vg,i = Xg.i + F.(Xg,best − Xg,i) + F.(Xg,r1 − Xg,r2).

Outra modifica¸cão na equa¸cão da muta¸cão diferencial sugerida por Price e Storn

está no número de vetores diferen¸ca que participam da muta¸cão. Os autores sugerem, além de 1 vetor diferen¸ca conforme apresentado na versão clássica, 2 ou até 3 vetores

diferen¸ca na equa¸c˜ao da muta¸c˜ao diferencial como mostrado abaixo:

DE/rand/2/bin _⇒ Vg,i = Xg,r0 + F.(Xg,r1 − Xg,r2) + F.(Xg,r3 − Xg,r4)

DE/rand/3/bin _⇒ Vg,i = Xg,r0 + F.(Xg,r1 − Xg,r2) + F.(Xg,r3 − Xg,r4) +

F.(Xg,r5 − Xg,r6)

Outras versões para o DE podem ser obtidas combinando estas varia¸cões na equa¸cão da muta¸cão diferencial com outros tipos de cruzamentos. Utilizando-se, por exemplo, uma recombina¸cão exponencial apresentada em [Storn and Price 1995] com a versão

clássica do DE, obtém-se a versãoDE/rand/1/exp.

1.4 Objetivos

Em linhas gerais, o principal objetivo desta tese ´e desenvolver uma meta-heur´ıstica para

o algoritmo DE no dom´ınio das variáveis discretas. Esta meta-heur´ıstica deve preservar, de uma maneira análoga, o interessante mecanismo de busca observado na evolu¸cão diferencial no dom´ınio das variáveis cont´ınuas. Para tanto, os operadores aritméticos da

equa¸cão da muta¸cão diferencial no dom´ınio das variáveis cont´ınuas são redefinidos para o dom´ınio das variáveis discretas, tornando a muta¸cão diferencial mais significativa e

genérica no contexto dos problemas de natureza combinatória. Os objetivos espec´ıficos podem ser divididos em três partes principais:

• Elabora¸cão de uma revisão das principais abordagens apresentadas na literatura para o algoritmo DE aplicados em problemas combinatórios, enumerando suas vantagens e desvantagens.

(25)

1.5 Motiva¸

c˜

ao

No âmbito dos problemas de otimiza¸cão combinatória, devido à sua importância tanto no mundo cient´ıfico bem como no mundo industrial, novas adapta¸cões têm sido propostas na literatura para o algoritmo DE com o intuito de observar aquelas caracter´ısticas

obti-das no dom´ınio obti-das variáveis cont´ınuas. Recentemente, várias adapta¸cões do algoritmo DE aplicado a problemas de natureza combinatória têm sido apresentadas na literatura.

Diversas dessas abordagens consistem simplesmente em aplicar a equa¸cão da muta¸cão diferencial definida no dom´ınio das variáveis cont´ınuas diretamente em problemas de natureza combinatória. Todavia, em problemas de natureza combinatória, a diferen¸ca

vetorial no espa¸co das variáveis cont´ınuas não tem uma correspondência clara no espa¸co das variáveis discretas. Isto deve-se ao fato de que, diferen¸cas de números inteiros que

são meramente rótulos e não representam nenhuma quantidade numérica, não geram solu¸cões viáveis e nem representam dire¸cões significativas no espa¸co das variáveis

discre-tas. Exemplos dessas abordagens são a Indexa¸cão Por Posi¸cão Relativa (IRP)9 [Price et al. 2005] e a Transforma¸cão Direta e Reversa (FBT)10[Onwubolu and Davendra 2009] aplicadas em alguns problemas combinatórios com permuta¸cão. Outras abordagens

em-pregam esquemas mais sofisticados redefinindo ou conceituando o que seria a diferen¸ca vetorial no dom´ınio das vari´aveis discretas. Exemplos dessas abordagens s˜ao a

Aborda-gem Por Matriz de Permuta¸cão e a Abordagem Por Matriz de Adjacências apresentadas em [Price et al. 2005]. Tais abordagens são em geral aplicáveis especificamente a uma

classe de problemas combinat´orios.

Isto posto, uma abordagem para a evolu¸cão diferencial onde os operadores aritmé-ticos da muta¸cão diferencial são definidos especificamente para problemas combinatórios

mostra-se interessante. Estes operadores especiais no contexto das variáveis discretas, mas análogos àqueles aplicados às variáveis cont´ınuas, devem ser definidos de modo a

preservar as caracter´ısticas que tornaram o DE um otimizador importante no dom´ınio das variáveis cont´ınuas. Isso permitiria sua aplica¸cão direta em problemas combinatórios

sem a necessidade de rotinas especiais de repara¸cão das solu¸cões não triviais ou fora do espa¸co de busca do problema.

9

do inglˆesIndexing by Relative Position 10

(26)

1.6 Estrutura do Trabalho

Os t´opicos apresentados neste trabalho est˜ao organizados conforme mostrado a seguir:

Cap´ıtulo 2 - DE Para Otimiza¸cão Combinatória: Discorre-se acerca dos prin-cipais trabalhos relacionados à evolu¸cão diferencial no dom´ınio das variáveis discretas.

Nele, apresenta-se um estudo cr´ıtico detalhado considerando as abordagens mais citadas na literatura, a saber, Indexa¸cão por Posi¸cão Relativa, Transforma¸cão Direta e Reversa,

Matriz de Permuta¸cão e Matriz de Adjacências. Ao final do cap´ıtulo a abordagem por Lista de Movimentos é proposta e as poss´ıveis defini¸cões para esta lista são apresentadas

para algumas estruturas de dados comumente utilizadas na representa¸c˜ao de solu¸c˜oes de problemas discretos.

Cap´ıtulo 3 - Restaura¸cão de Sistemas de Distribui¸cão de Energia El´ e-trica: Apresenta-se o problema de Restaura¸cão de sistemas de distribui¸cão de energia elétrica com contingências devido a faltas no setor primário da rede. Com o objetivo

de reconfigurar o sistema elétrico, propõe-se uma versão do algoritmo DE com lista de movimentos, o algoritmo DE-Tree. Para esta versão do algoritmo, desenvolveu-se uma

estrutura de dados, denominada de Árvore de Ancestralidade, que possibilita armaze-nar a sequência das manobras de chaves necessária para reconfigurar o sistema, além de guardar as informa¸cões acerca dos movimentos que serão utilizados na equa¸cão da

muta¸c˜ao diferencial.

Cap´ıtulo 4 - Resultados Experimentais: Descrevem-se os resultados das

simu-la¸cões realizadas em um sistema de distribui¸cão de energia elétrica real de grande porte, com o intuito de averiguar o desempenho do algoritmo proposto. Testes são realizados

para o caso de contingências devido a uma única falta e três faltas simultâneas no sistema elétrico.

(27)

DE Para Otimiza¸

c˜

ao

Combinat´

oria

Do ponto de vista prático, um problema de otimiza¸cão consiste em encontrar a melhor configura¸cão de um dado sistema de modo que ele opere de forma rápida e eficiente em

um tempo reduzido. Teoricamente, consiste em determinar os valores extremos de uma fun¸cão, isto é, o máximo ou m´ınimo valor que uma fun¸cão pode assumir em um dado

intervalo. Neste cenário, a otimiza¸cão pode ser dividida em duas categorias: aquela onde as solu¸cões são codificadas como variáveis reais e aquela onde as solu¸cões são codificadas

como variáveis discretas. Nesta última, encontra-se a classe de problemas designados como Problemas de Otimiza¸cão Combinatória. Problemas de otimiza¸cão combinatória ocorrem em áreas tão diversas como as de projetos de sistemas de distribui¸cão de

ener-gia, roteamento de ve´ıculos, aloca¸cão de pessoas ou máquinas a tarefas, empacotamento de caixas em contêineres, sequenciamento de genes e DNA, dentre outras. Tais

proble-mas e suas variantes podem ser enquadrados e tratados em uma das seguintes classes de problemas te´oricos de natureza combinat´oria: Problema do Caixeiro Viajante, Problema

de Roteamento de Ve´ıculos, Problema de Empacotamento, Problema de Programa¸c˜ao de Tarefas, Problema da Mochila, etc. Para tanto, para cada tipo de problema conside-rado, o espa¸co de busca deve ser bem definido. Na classe de problemas combinat´orios,

os espa¸cos de busca são representados por um conjunto finito de solu¸cões cujos parˆ a-metros podem ser do tipo arranjo, grupamento, ordena¸cões, permuta¸cões ou mesmo por

uma estrutura em grafo e, portanto, necessitam ser tratados de uma maneira especial, diferente daquelas utilizadas em problemas estritamente de natureza cont´ınua.

Muitos algoritmos têm sido propostos na área da otimiza¸cão para solucionar pro-blemas de natureza estritamente combinatória. Estes algoritmos são classificados como Exatos ou Aproximados. Os algoritmos exatos garantem encontrar, para um número

(28)

finito de instâncias, uma solu¸cão ótima. Entretanto, o tempo computacional necessário gasto para encontrar tal solu¸cão ótima pode ser exponencial no pior caso, o que é

impra-ticável em problemas reais. Assim, os algoritmos aproximados, apesar de não garantirem encontrar a solu¸cão ótima mas sim uma boa solu¸cão em um tempo computacional menor,

tˆem sido objeto de pesquisa nos ´ultimos anos.

Dos m´etodos aproximados podem-se destacar os Algoritmos Construtivos e os Al-goritmos de Busca Local. Os algoritmos construtivos consistem em inserir componentes

em uma solu¸cão, inicialmente vazia, de forma incremental até que uma solu¸cão com-pleta seja obtida. Eles são tipicamente os métodos aproximados mais rápidos apesar de

muitas vezes retornarem solu¸cões de qualidade inferior quando comparados aos algorit-mos de busca local. Já os algoritmos de busca local partem de uma solu¸cão inicial e

iterativamente substituem a solu¸c˜ao atual por uma solu¸c˜ao melhor em uma dada Estru-tura de Vizinhan¸ca apropriadamente predefinida. Esta estrutura de vizinhan¸ca pode ser formalmente definida como [Blum and Roli 2003]:

Defini¸cão 2.1. Seja_X o espa¸co de busca de um problema ex uma solu¸cão deste problema. Uma estrutura de vizinhan¸ca é uma fun¸cão_N(x)_{⊆ X} que

associa à cada solu¸cãox∈ X uma solu¸cãox’∈ N(x). N(x) denota o conjunto de solu¸cões x’que pode ser obtido dex.

A transi¸cão de uma solu¸cão x para uma solu¸cão vizinha x’ é designada como um movimento. Os movimentos poss´ıveis em uma estrutura de vizinhan¸ca estão relacionados

com a estrutura de dados utilizada na representa¸c˜ao do problema. Para uma solu¸c˜ao representada por um vetor os movimentos poss´ıveis seriam, por exemplo, uma troca de seus elementos. Esta troca de elementos do vetor podeira gerar um vetor vizinho com

caracter´ısticas melhores que a do original e, assim, o substituiria no conjunto de solu¸c˜oes. Em uma estrutura em grafos, um movimento para gerar uma estrutura de vizinhan¸ca

seria a adi¸c˜ao ou remo¸c˜ao de arestas e, assim, para cada tipo de problema uma estrutura de vizinhan¸ca tem que ser definida.

A partir da defini¸cão de estrutura de vizinhan¸ca é poss´ıvel definir o conceito de solu¸cões que localmente são m´ınimas para uma dada estrutura de vizinhan¸ca:

Defini¸cão 2.2. Uma solu¸cão _bx é localmente m´ınima (ou m´ınimo local) em

(29)

Dentro da classe dos algoritmos aproximados est˜ao as meta-heur´ısticas, uma classe de algoritmos que combina as heur´ısticas b´asicas com procedimentos avan¸cados visando

melhorar a eficiência e eficácia na explora¸cão do espa¸co de busca do problema. Dentro das meta-heur´ısticas estão inclu´ıdos, dentre outros, os algoritmos Colônia de Formigas,

Busca Local Iterativa,Recozimento Simulado,Busca Tabu e os Algoritmos Evolutivos.

A meta-heur´ıstica DE, uma classe dos AE, devido ao seu grande sucesso na otimi-za¸cão de problemas no espa¸co das variáveis cont´ınuas tem recebido adapta¸cões no seu

mecanismo de muta¸cão diferencial para atender a otimiza¸cão de problemas estritamente de natureza combinatória. Este cap´ıtulo apresenta e discute algumas destas abordagens

propostas na literatura especializada e, ao final, apresenta uma nova abordagem deno-minada porLista de Movimentos, que visa preservar o interessante mecanismo de busca

do DE no dom´ınio das vari´aveis discretas.

2.1 Indexa¸

c˜

ao por Posi¸

c˜

ao Relativa

Em [Lichtblau 2002] é apresentada uma versão discreta para a evolu¸cão diferencial apli-cada em alguns problemas de otimiza¸cão combinatória baseados em permuta¸cão usando

a abordagem denominada Indexa¸cão Por Posi¸cão Relativa (IRP1). Nesta abordagem, os indiv´ıduos da popula¸cão são representados por vetores cujos parâmetros são arrays

de números inteiros. O princ´ıpio básico é transformar cada parâmetro dos vetores no dom´ınio dos inteiros para o dom´ınio dos reais no intervalo [0,1]. Para tanto, os vetores são normalizados dividindo-se cada parâmetro pelo maior dentre eles. Após esta

nor-maliza¸cão (conversão dos parâmetros inteiros em números reais), a equa¸cão da muta¸cão diferencial (Eq. 1.4) é aplicada diretamente como no caso do dom´ınio cont´ınuo. A

con-versão de volta para o dom´ınio dos inteiros é obtida usando-se uma indexa¸cão baseada na posi¸cão relativa de cada elemento dentro do vetor. Os elementos no vetor são

orde-nados de acordo com seus valores. Assim, o menor número real obtido é relacionado ao menor valor inteiro, o próximo menor valor real ao próximo menor valor inteiro e assim sucessivamente, até todos os elementos no vetor serem convertidos para o dom´ınio dos

números inteiros novamente. Um exemplo ilustrativo desta abordagem para o Problema do Caixeiro Viajante (TSP2_{), formulado no Apêndice}_A_{, é apresentado no Apêndice}_A.1_.

Essa abordagem sempre resultará em solu¸cões válidas, desde que os valores conver-tidos para o dom´ınio dos números reais não sejam idênticos. Se isso ocorrer, o vetor

mutante resultante ter´a valores inteiros idˆenticos e, portanto, ele deve ser reparado ou

1

do inglˆesIndexing by Relative Position 2

(30)

descartado. No exemplo apresentado no Apêndice A.1 é fácil observar que esta abor-dagem tão somente embaralha os parâmetros do vetor e uma muta¸cão idêntica àquela

obtida na muta¸cão diferencial não é obtida. Além disso, esta abordagem só é aplicável tão somente em problemas combinatórios com permuta¸cão e, mesmo assim, ela não é

capaz de identificar a gera¸cão de permuta¸cões idênticas [Price et al. 2005].

2.2 Transforma¸

c˜

ao Direta e Reversa

A Transforma¸c˜ao Direta e Reversa (FBT3) apresentada em [Onwubolu and Davendra 2009], tamb´em referida como Abordagem de Onwubolu, utiliza o mesmo princ´ıpio de

Lichtblau no que diz respeito a transformar os parâmetros de números inteiros dos vetores em números reais, aplicar a equa¸cão de muta¸cão diferencial e retorná-los para

o dom´ınio dos inteiros. A diferen¸ca está na forma como isso é feito. Nesta abordagem, uma “transforma¸cão direta” é utilizada para transformar os elementos inteiros do vetor para o dom´ınio das variáveis cont´ınuas. Isso é feito utilizando a expressão:

xpf_i = ₋1 + xi(1 +α) (2.1)

onde:

xi é o iesimo´ parâmetro do vetor 9sobrescritopf denota a representa¸cão dos

elementos do vetor em ponto-flutuante).

α´e um n´umero POSITIVO muito pequeno.

Uma vez que os elementos dos vetores estão no dom´ınio dos números reais, a equa¸cão da muta¸cão diferencial é aplicada. Em seguida, a opera¸cão inversa (“transforma¸cão

reversa”) que converte os valores reais de volta para o dom´ınio dos inteiros (Eq. 2.2) ´e aplicada em cada elemento do vetor mutante para obter sua representa¸c˜ao discreta.

xi = round

(1 + xpf_i )(2−α)

, (2.2)

onde a fun¸c˜ao round arredonda seu argumento para o inteiro mais pr´oximo.

Essa abordagem geralmente gera solu¸cões inválidas, ora devido à gera¸cão de solu¸cões

fora do espa¸co de busca, ora devido à gera¸cão de solu¸cões com valores repetidos e, portanto, necessitam de um mecanismo de reparo adequado. [Price et al. 2005] relatam que, apesar dos bons resultados de trabalhos apresentados por Onwubolu usando esta

abordagem, há motivos para acreditar que os sucessos obtidos são consequência direta

3

(31)

dos mecanismos de reparos adotados e da prudência na escolha das heur´ısticas utilizadas. O ApêndiceA.2apresenta um exemplo ilustrativo da aplica¸cão dessa abordagem no TSP.

2.3 Abordagem por Matriz de Permuta¸

c˜

ao - AMP

Essa abordagem, apresentada por Price e Storn em [Price et al. 2005], faz uma analogia entre a diferen¸ca vetorial no dom´ınio dos números reais e a matriz de permuta¸cão na análise combinatória. Assim no dom´ınio dos números reais a diferen¸ca entre dois vetores

resulta em um vetor, no campo da análise combinatória, duas permuta¸cões poderiam definir um mapeamento que também é uma permuta¸cão. Este mapeamento é

repre-sentado por uma matriz de Permuta¸cão. Seguindo essa analogia, a muta¸cão diferencial equivaleria, nos problemas combinatórios com permuta¸cão, à matriz de permuta¸cão (ou

Permuta¸c˜ao Diferencial).

SejamPuma matriz de permuta¸c˜ao que mapeia a permuta¸c˜ao dos elementos de um

dado vetor em outro e, xg,r1 e xg,r2, os dois vetores da equa¸c˜ao da muta¸c˜ao diferencial

aleatoriamente escolhidos da popula¸c˜ao. A matriz de permuta¸c˜ao P que mapeia xg,r2

emxg,r1 satisfaz a rela¸c˜ao:

xg,r1 = Pxg,r2 (2.3)

Pode-se dizer, portanto, que a matriz de permuta¸c˜aoP“leva”xg,r2 `axg,r1. No contexto

da evolu¸cão diferencial, esta matriz é considerada a “diferen¸ca” obtida de duas solu¸cões

candidatas. A equa¸cão análoga à equa¸cão da muta¸cão diferencial (Eq 1.4) é, então, escrita como:

vg,i=PF.x_g,r0 (2.4)

onde PF é a matriz de permuta¸cão modificada pelo parâmetro escalar F, significando aqui, uma probabilidade de se utilizar uma parcela da permuta¸cão representada pela matriz de permuta¸cão originalP. Portanto, esta abordagem aplica algumas permuta¸cões

ao vetor base aleatoriamente selecionadas do conjunto de permuta¸c˜oes da matrizP.

Segundo [Price et al. 2005], esta abordagem tende a estagnar a explora¸c˜ao do espa¸co

de busca,uma vez que os movimentos derivados de permuta¸cões são raramente produti-vos. Além disso, esse método não é capaz de identificar se duas solu¸cões são equivalentes.

(32)

2.4 Abordagem por Matriz de Adjacˆ

encias - AMA

Storn [Price et al. 2005,Onwubolu and Davendra 2009], propôs a Abordagem por Matriz de Adjacências (AMA), em que os vetores solu¸cões da equa¸cão da muta¸cão diferencial são codificados em matrizes de adjacências. Como na AMP, esta abordagem também

estabelece uma analogia do que seria a diferen¸ca vetorial na análise combinatória. Aqui, entretanto, a diferen¸ca vetorial é a “diferen¸ca” entre a representa¸cão dos dois vetores

xg,r1e xg,r2 pelas suas respectivas matrizes de adjacˆencias.

Sejam xg,r0, xg,r1e xg,r2 as matrizes de adjacˆencias dos vetores da equa¸c˜ao da

mu-ta¸cão diferencial. Assim, usando aritmética Módulo 24 e uma vez que as opera¸cões de adi¸cão e subtra¸cão nesta aritmética são idênticas, a equa¸cão da muta¸cão diferencial é dada por:

vg,i = xg,r0 ⊕ F.(xg,r1 ⊕ xg,r2) (2.5)

onde: o operador ⊕indica a opera¸c˜ao l´ogica XOR.

Essa abordagem é restrita a problemas combinatórios com permuta¸cão. Porém,

rotinas especiais de reparo devem ser aplicadas às solu¸cões obtidas pois há casos em que a diferen¸ca entre duas solu¸cões (duas matrizes de adjacências) nem sempre gera uma

solu¸cão que é uma matriz de adjacências. Além disso, solu¸cões idênticas mas com seus parâmetros simplesmente “rotacionados” dentro do vetor geram matrizes de adjacências

idênticas. Consequentemente, a matriz diferen¸ca entre estas solu¸cões será sempre zero [Price et al. 2005]. Na ocorrência desses casos, a solu¸cão obtida deverá ser reparada ou descartada. No ApêndiceA.4 um exemplo, também para o TSP, é apresentado.

2.5 Lista de Movimentos: Abordagem Proposta

Ao longo das se¸cões deste cap´ıtulo apresentaram-se as principais abordagens encontradas na literatura para a utiliza¸cão do DE no dom´ınio das variáveis discretas. Essas

abor-dagens podem ser classificadas em dois principais grupos: um grupo onde a equa¸cão da muta¸cão diferencial no dom´ınio das variáveis cont´ınuas é aplicada diretamente em problemas combinatórios, caso das abordagens IRP e FBT, e o outro em que a

equa-¸cão da muta¸cão diferencial é redefinida para a classe de problemas combinatórios, como ocorre para a AMP e AMA. No primeiro grupo há necessidade de reparos nas

solu-¸cões geradas, ora devido a solu¸cões repetidas, ora devido a solu¸cões fora do espa¸co de busca do problema. Isto se deve ao fato de que os operadores aritméticos da equa¸cão da

4

(33)

muta¸cão diferencial, operadores estes definidos para o dom´ınio das variáveis cont´ınuas, não são definidos no espa¸co das variáveis discretas. Já no segundo grupo as

aborda-gens não são abrangentes e estão restritas a problemas combinatórios com permuta¸cão e, mesmo assim, em alguns casos necessitam de algum mecanismo de reparo para as

solu¸c˜oes geradas.

Embora as técnicas apresentadas sejam importantes no contexto da otimiza¸cão dis-creta, as limita¸cões apresentadas comprometem o seu uso em um grande número de

problemas de natureza combinat´oria.

Com o objetivo de contornar tais problemas, esta se¸c˜ao apresenta uma nova

abor-dagem para a evolu¸cão diferencial, denominada Lista de Movimentos, que busca ser genérica no âmbito dos problemas de natureza combinatória. A flexibilidade existente

nesta abordagem deve-se ao fato de que os movimentos definidos na lista de movimentos s˜ao espec´ıficos para cada tipo de problema combinat´orio. Assim, os movimentos da lista

ora são representados por vetores dearrays, ora por matrizes ou por uma outra estrutura de dados mais apropriada a cada tipo de problema tratado. Além disso, nenhum meca-nismo de reparo ou rotina auxiliar se faz necessária para reparar solu¸cões encontradas e

a autoadapta¸cão da DE, observada no dom´ınio das variáveis cont´ınuas, é preservada no espa¸co de variáveis discretas.

De modo a conceber uma meta-heur´ıstica para o método de otimiza¸cão do algoritmo DE aplicado a problemas de natureza combinatória, a diferen¸ca entre dois vetores no

espa¸co das variáveis cont´ınuas deve ser redefinida para o espa¸co das variáveis discretas, uma vez que o operador diferen¸ca não é definido neste dom´ınio. Assim, a diferen¸ca veto-rial entre as duas solu¸cões candidatas da equa¸cão da muta¸cão diferencial é representada

por uma Lista de Movimentos e definida como:

Defini¸cão2.3. Operador Subtra¸cão: A opera¸cão de subtra¸cão entre duas solu¸cões candidatas origina uma lista de movimentos. A lista de movimentos

resultante, Mij, é a lista contendo uma sequência de movimentos válidos

mk, tal que, a aplica¸cão destes movimentos à solu¸cãoxj ∈ X leva à solu¸cão

xi ∈ X.

Sejamxg,r1 exg,r2 duas solu¸c˜oes candidatas de um problema combinat´orio qualquer,

escolhidas aleatoriamente da popula¸cão corrente, para realizar a “diferen¸ca vetorial” da equa¸cão da muta¸cão diferencial. Com base na Defini¸cão 2.3, a lista de movimentos

obtida ´e dada por:

(34)

onde⊖é um operador de subtra¸cão binário especial que retorna a lista de movimentos

Mr1r2 que representa o “caminho” ou a “distância” entre a solu¸cãoxg,r2 e a solu¸cãoxg,r1.

Esta lista, de algum modo, captura a diferen¸ca entre estas duas solu¸c˜oes.

A multiplica¸c˜ao da lista de movimentos por um escalar deve ser tamb´em definida:

Defini¸cão 2.4. Operador Multiplica¸cão por Escalar: A multiplica¸cão

da lista de movimentos, Mij, por um escalar λ ∈ [0,1], retorna a lista M

′

ij

com os primeiros _⌈λ _{× |}Mij|⌉ movimentos deMij , onde|Mij|´e o tamanho

da lista.

Como o escalarλ∈[0,1], esta multiplica¸c˜ao prioriza, ou considera, t˜ao somente os 100λ%primeiros movimentos da lista.

Aplicando a Defini¸cão2.4 à Equa¸cão 2.6, com o escalar λsubstitu´ıdo pelo fator de

multiplica¸cão escalar Fda evolu¸cão diferencial, a multiplica¸cão por escalar no dom´ınio discreto pode ser escrita como:

M′

r1r2 =F ⊗Mr1r2 (2.7)

onde ⊗ é um operador de multiplica¸cão binário especial no dom´ınio das variáveis dis-cretas.

Finalmente, a aplica¸cão de uma lista de movimentos a uma dada solu¸cão é definida pela opera¸cão de adi¸cão:

Defini¸cão 2.5. Operador Adi¸cão: A opera¸cão de adi¸cão é a aplica¸cão da

sequˆencia de movimentos da lista M′

ij à solu¸cão xk e a soma resultante é a

nova solu¸c˜aox′

k.

Seja o vetor solu¸c˜aoxg,r0, escolhido aleatoriamente na popula¸c˜ao corrente, o vetor

base da equa¸cão da muta¸cão diferencial. O vetor mutante, resultante da adi¸cão do vetor base à lista de movimentos dada pela Equa¸cão 2.7, é dado por:

vg,i = xg,r0⊕M_r′1r2 (2.8)

(35)

Com as defini¸cões acima, pode-se escrever a equa¸cão da muta¸cão diferencial que determina o vetor mutante como:

vg,i = xg,r0⊕F⊗(xg,r1⊖xg,r2)

vg,i = xg,r0⊕F⊗Mr1r2

vg,i = xg,r0⊕Mr′1r2

(2.9)

que é a abordagem discreta proposta para a equa¸cão da muta¸cão diferencial (Eq.1.4).

A defini¸cão para a lista de movimentos é genérica e a estrutura de dados utilizada para representá-la depende da estrutura de dados utilizada para representar as solu¸cões

do problema. Desta forma, as defini¸c˜oes acima podem ser aplicadas a qualquer tipo de problema combinat´orio. Para tanto, a estrutura de dados da Lista de Movimentos deve

ser bem definida e espec´ıfica para o tipo de problema combinat´orio em quest˜ao.

A abordagem por Lista de Movimentos proposta para evolu¸c˜ao diferencial discreta

tem como pilar a Defini¸cão 2.3que define como uma lista de movimentos é constru´ıda. Segundo esta defini¸cão, a lista de movimentos deve conter uma sequência de movimentos válidos, tal que, a aplica¸cão destes movimentos a uma solu¸cão xj leva a uma outra

solu¸c˜ao xi pertencente ao espa¸co de solu¸c˜oesX. Portanto, para cada tipo de problema

combinatório, baseado na defini¸cão da estrutura de dados utilizada na representa¸cão

das solu¸cões do problema, é definida a estrutura de dados que melhor represente a lista de movimentos. As se¸cões 2.6a 2.8 apresentam algumas estruturas de dados utilizadas na representa¸cão das solu¸cões de alguns problemas de otimiza¸cão combinatória e as

representa¸c˜oes poss´ıveis para as listas de movimentos.

2.6 Lista de Movimentos

Swap

Problemas combinatórios com permuta¸cão podem ter suas solu¸cões representadas por

uma estrutura de dados do tipoarray. Quando representados desta forma, uma poss´ıvel representa¸c˜ao da estrutura de dados da lista de movimentos seria uma lista de pares

de ´ındices (i,j) dos elementos do array indicando quais elementos da solu¸cão sofreram um movimento de troca de posi¸cão (movimento de swap). Sejam, por exemplo, duas solu¸cões candidatas de um problema combinatório com permuta¸cão representadas pelos

(36)

Xg,r1 =

h

A B C D E F G H i

(2.10)

Xg,r2 =

h

E D A F H B C G

i

A lista de movimentos Mij =MXr2,Xr1 contendo os movimentos necess´arios para levar

a solu¸cão Xg,r2 à solu¸cão Xg,r1 é escrita anotando-se os pares de ´ındices dos elementos

da solu¸cãoXg,r2 que devem ser trocados de modo a se obter a solu¸cãoXg,r1. As Figuras 2.1à 2.6ilustram tal procedimento.

xg,r1 =

A B C D E F G H

xg,r2 =

E D A F H B C G

xg,r2 =

A D E F H B C G

E A

Figura 2.1: _Passo1: _{Troca dos elementos de ´ındice 0 e 2 para obter o primeiro} movimento da lista: MXr2,Xr1 = [(0,2)].

xg,r1 =

A B C D E F G H

xg,r2 =

A D E F H B C G

xg,r2 =

A B E F H D C G

D B

Figura 2.2: _Passo2: _{Troca dos elementos de ´ındice 1 e 5 para obter o segundo} movimento da lista: MXr₂,Xr₁ = [(0,2) (1,5)].

xg,r1 =

A B C D E F G H

xg,r2 =

A B E F H D C G

xg,r2 =

A B C F H D E G

E C

(37)

xg,r1 =

A B C D E F G H

xg,r2 =

A B C F H D E G

xg,r2 =

A B C D H F E G

F D

Figura 2.4: _Passo4: _{Troca dos elementos de ´ındice 3 e 5 para obter o quarto} movi-mento da lista: MXr2,Xr1 = [(0,2) (1,5) (2,6) (3,5)].

xg,r1 =

A B C D E F G H

xg,r2 =

A B C D H F E G

xg,r2 =

A B C D E F H G

H E

Figura 2.5: _Passo5: _{Troca dos elementos de ´ındice 4 e 6 para obter o quinto} movi-mento da lista: MXr₂,Xr₁ = [(0,2) (1,5) (2,6) (3,5) (4,6)].

xg,r1 =

A B C D E F G H

xg,r2 =

A B C D E F H G

xg,r2 =

A B C D E F G H

H G

Figura 2.6: _Passo6: _{Troca dos elementos de ´ındice 6 e 7 para obter o ´}_ultimo movi-mento da lista: MXr₂,Xr₁ = [(0,2) (1,5) (2,6) (3,5) (4,6) (6,7)].

A Lista de Movimentos final obtida com estes movimentos ´e dada por:

MXr2,Xr1 = [(0,2) (1,5) (2,6) (3,5) (4,6) (6,7)]. (2.11)

Os movimentos deMXr2,Xr1 aplicados à solu¸cãoXg,r2 geram a solu¸cãoXg,r1, assim,

(38)

2.7 Lista de Movimentos 2-opt

Em alguns problemas combinatórios com permuta¸cão, como por exemplo o caso do TSP, trocar elementos (os vértices representando as cidades) de posi¸cão dentro doarray (movimentos de swap) não geram solu¸cões muito úteis. Solu¸cões melhores são geradas

quando trocas de arestas (percursos) são realizadas. Este tipo de troca é utilizado em métodos de busca local e é conhecido como heur´ıstica de refinamento k-opt. Nesta

opera¸cão, k arcos (ou percursos) em uma configura¸cão são removidos e substitu´ıdos por outros novos k arcos resultando em uma nova configura¸cão. A Figura 2.7 ilustra o caso de um refinamento 2-opt em que 2 arcos de uma configura¸cão são removidos e

substitu´ıdos por 2 outros gerando uma nova configura¸c˜ao.

A nova configura¸c˜ao obtida com o refinamento 2-opt mostrada na Figura 2.7 ´e

equivalente a inverter o percurso entre as duas inser¸cões realizadas. Na forma de um array, as duas configura¸cões são escritas conforme a Eq.2.12.

1 2

4 3

1 2

4 3

Figura 2.7: _{Heur´ıstica de refinamento 2-opt: Os arcos tracejados s˜ao substitu´ıdos por} retas gerando uma nova configura¸c˜ao.

XAntes =

h

1 2 3 4 i

(2.12)

XDepois =

h

1 3 2 4 i

Uma representa¸cão em lista de movimentos baseada neste princ´ıpio pode ser obtida através de uma lista de duplas de ´ındices indicando as posi¸cões dos elementos do array

onde as inser¸cões foram realizadas e as inversões de percursos que devem ser feitas. As Figuras2.8à2.11ilustram os procedimentos necessários para se obter uma representa¸cão

para lista de movimentos com inser¸c˜oes 2-opt realizadas na solu¸c˜aoXg,r2 de modo a obter

(39)

xg,r1 =

A B C D E F G H

xg,r2 =

F H B C G

xg,r2 =

F H B C G

E D A

A D E

Figura 2.8: _Passo1: _{inverter os elementos entre as inser¸c˜}_{oes feitas nos ´ındices 0 e 2} para obter o primeiro movimento da lista: MXr2,Xr1 = [(0,2)].

xg,r1 =

A B C D E F G H

xg,r2 =

A C G

xg,r2 =

A C G

D E F H B

B H F E D

Figura 2.9: _Passo2: _{inverter os elementos entre as inser¸c˜}_{oes feitas nos ´ındices 1 e 5} para obter o segundo movimento da lista: MXr₂,Xr₁ = [(0,2) (1,5)].

xg,r1 =

A B C D E F G H

xg,r2 =

A B G

xg,r2 =

A B G

H F E D C

C D E F H

Figura 2.10: _Passo3: _{inverter os elementos entre as inser¸c˜oes feitas nos ´ındices 2 e 6} para obter o terceiro movimento da lista: MXr₂,Xr₁ = [(0,2) (1,5) (2,6)].

xg,r1 =

A B C D E F G H

xg,r2 =

A B C D E F

xg,r2 =

A B C D E F

H G

G H

Figura 2.11: _Passo4: _{inverter os elementos entre as inser¸c˜oes feitas nos ´ındices 6 e 7} para obter o ´ultimo movimento da lista: MXr2,Xr1 = [(0,2) (1,5) (2,6) (6,7)].

A lista de movimentos final obtida com estes movimentos ´e dada pela Equa¸c˜ao2.13

abaixo:

(40)

2.8 Lista de Movimentos N´

o-Profundidade

Uma estrutura de dados eficiente para representar problemas combinatórios cujas solu-¸cões são grafos do tipo árvore é a Representa¸cão Nó-Profundidade (RNP) apresentada

em [Delbem et al. 2004,dos Santos 2009,Santos et al. 2010,Mansour et al. 2010]. Nesta representa¸cão, a codifica¸cão é realizada como uma lista contendo os nós da árvore e suas

respectivas profundidades em rela¸cão à raiz. A lista é formada por tuplas (n, p), onden

´e o n´o e psua profundidade.

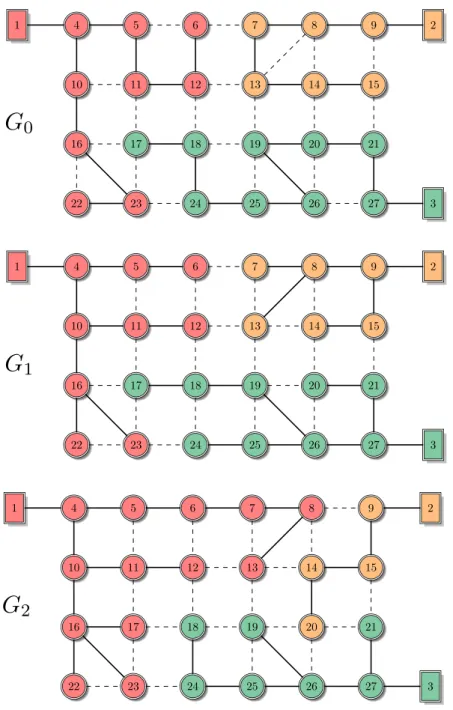
Seja, por exemplo, um problema combinatório qualquer cujos indiv´ıduos são repre-sentados por um grafoG1 como o da Figura 2.12. No grafo é identificado uma floresta

com três árvores T1, T2 e T3 cujas ra´ızes são respectivamente os nós 1, 2 e 3.

1 4 5 6 7 8 9 2

10 11 12 13 14 15

16 17 18 19 20 21

22 23 24 25 26 27 3

G

1

Figura 2.12: _{Representa¸c˜}_{ao de um indiv´ıduo por um grafo (figura reproduzida de} [dos Santos 2009] p´ag. 56).

As três árvores são, então, representadas, usando a RNP, por meio de uma matriz

indicando os nós e suas profundidades a partir da raiz conforme mostrado na Equa-¸cão 2.14. A ordem dos nós é obtida através de uma busca em profundidade realizada

em cada ´arvore [dos Santos 2009].

T1 = "

prof. no´

# =

"

0 1 2 3 2 3 4 3 4 4

1 4 5 6 10 11 12 16 22 23 #

T2 = "

prof.

no´ #

= "

0 1 2 3 3 2 3

2 9 8 7 13 15 14 #

T3 = "

prof. no´

# =

"

0 1 2 3 2 3 4 5 3 4

3 27 21 20 26 19 18 17 25 24 #

(2.14)

(41)

poda de uma subárvore a partir de um nó p de uma árvore e enxerta a subárvore em um nóede outra árvore da floresta;ii)e oChange Ancestor Operator (CAO) que, além

dos nós de poda e enxerto, determina um novo nó raizr para a subárvore, o qual passa a ser o nó de enxerto. O nó de enxerto deve ser um nó válido pertencente à lista de

adjacência de nós do grafoG. A Tabela2.1apresenta a lista de adjacência de nós para o grafo da Figura2.12. Uma vez obtida as RNPs das árvores de uma floresta de um grafo, novas florestas podem ser obtidas diretamente da RNP com a aplica¸cão dos operadores

PAO e CAO. A seguir, é apresentada a utiliza¸cão destes dois operadores para gera¸cão de novos indiv´ıduos.

N´o N´os Adjacentes

1 4

2 9

3 27

4 1 5 10

5 4 6 11

6 5 7 12

7 6 8 13

8 7 9 13 14

9 2 8 15

10 4 11 16