Canelamento das Foras de Vnulo em Anel
Condutor Carregado om nq Cargas por Meio de uma
Carga Q de Sinal Contrario Posiionada no Centro
Canellationofonstraintforesinthehargedondutorringwithnq hargesbyahargeQwithoppositesignplaedon
theenter
Norberto Helil Pasqua
ePaulo DanielEmmel y
Departamento deFsia,UniversidadeFederaldeS~aoCarlos
UFSCar(UniversidadeFederaldeS~aoCarlos)-Brasil
C.P.676,13565-905, S~aoCarlos, SP,Brasil
Reebidoem04/01/2001. Aeitoem12/03/2001
OproblemapropostoeodeumanelondutorderaioRarregadoomnargasq,emquesedeseja
anularas foras de vnulo que nele atuam. A solu~ao e oloar no entro doanel determinada
argaQdesinalontrario,demodoqueasomadasforaseletriassobreadaargadoaneldevido
a arga entral eas outras argas doanel sejanula. Busa-se, portanto, umafun~aoQ(nq) que
forneaovalordaargaentralemfun~aodenq. Oresultadomostra-nosqueQ(nq)eproporional
anln(n)qparan2.
Theproposed problemistoalulate theharge tobeplaedintheenterofaring,inwhihwe
distribute n harges equal to q, so that the onstraint fore beome null. The solution for this
problem is to plaea hargeQ of oppositesign inthe enter of the ring,so the sum of eletri
foresineahhargeinthering,duetotheentralhargeandtheotherharges,beomenull. We
searhfor afuntionQ(nq) thatgivesthevalue ofQintermsofnq. Theresultis that Q(nq) is
proportionaltonln(n)qforn2.
I Introdu~ao
ConsideremosumanelondutorderaioR ,ujoo
te-nha umdi^ametrotal que qualquerquantidade de
ar-gas (n > 2) seja distribudalinearmente em toda sua
extens~ao. Tomando-se nq argas id^entias entre si e
abandonando-asaleatoriamentenesseanel,
aomovimentodessasateenontraremposi~oesemque
n~aoexperimentemnenhumaforaresultante.
O movimento observado da i-esimaarga | ate o
estabeleimento doequilbrioeletrostatio|edevido
aforarepulsivadeCoulomb[1℄entreestaeasdemais.
Estaforatemaforma
F
i =
q
i
4
0 n
X
j 0
q
j
r 2
ij ^r
ij
; (1)
onder
ij =j r
i r
j
j eadist^aniaentre duasargas,
0
e onstante de permissividade eletriae no somatorio
n~aoseonsideraj =i.
Apesar da forarepulsiva,as argas permaneer~ao
no anel devido a presena de foras de vnulo, que
tambem s~ao de origem eletria. Consequentemente,
quantomaiorn,maiordeveraseraintensidadedetais
foras paraqueosistema permaneaem equilbrio. O
aumulodeargasnoanelgeratens~oesquepodem ser
anuladas, oloando-se determinadaarga puntiforme
Q de sinal oposto a q posiionadano entro do anel.
Anularessasforasdevnuloeequivalenteaobteruma
foraresultantenula,F
res
=0,sobreadaargado
sis-tema,istoe,sobreasnqargasdoanelesobreaarga
entral Q.
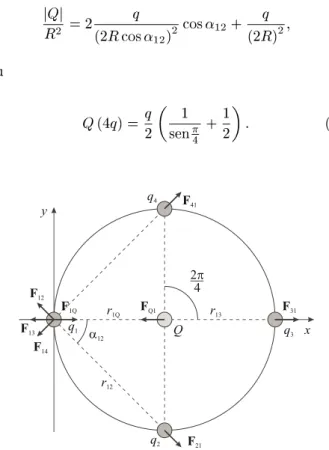
Paraoalulode Q(nq),onsiderou-seumsistema
artesiano(videFiguras1,2e3) omorigem emuma
arga q
1 , P
q1
(0;0), de modoque o eixo-y tangenieo
aneleoeixo-xpassepeloseuentro,ondeesta
posiio-nadaaargaentral,P
Q
=(R ;0). Dadaasimetriado
anel eo mesmo valor dasn argas, o ^angulo formado
pelosraiosdeduasargasonseutivasserade2=n.Ja
adist^aniaemmodulodeq
1
ateaj-esimaargaq
j
pro-jetadasobre oeixo-xpodeseresritaomod(q
1 ;q
j )=
jr
1j
j= 2Ros
1j ,
1j =
1 2
n (j 1)
2
o^angulo
e-mail:(pasquaoug167460)polvo.ufsar.br
formado entre r
1j
e o eixo-x, om j = 2;3;:::;n.
Observe-seque, poronstru~ao,
1j
enontra-seno
in-tervalo
2 ;
2
, n~ao variando, portanto, o sinal de
os
1j
, que sera sempre positivo. A onstru~ao do
sistema dessa forma apresenta a vantagem da
simpli-a~ao do alulo, uma vez que, dada a simetria da
distribui~ao,aomponentedaforaresultanteparalela
aoeixo-yserasemprenula,eaomponenteparalelaao
eixo-xtomadasobreaargaq
1
,teraaforma
F
1x =jF
1Q j
n
X
j=2 jF
1j jos
1j
=0; (2)
II Desenvolvimento
Consideremos primeiramenten=2,ouseja,duas
ar-gas q sobre o anel. Proura-se por um determinado
valor de Q(2q) tal que F
res
= 0. No equilbrio, as
duasargasq
1 eq
2
enontram-sediametralmente
opos-tas(
12
=0). Dopontodevistadeq
1
,ouseja,apartir
deq
1
,obtem-se
F
1x =jF
1Q j jF
12 j=0;
ou
jq
1 jjQj
r 2
1Q =
q
1 q
2
r 2
12 :
Sendoj r
1Q
j=R ,jr
12
j=2R ,eq
1 =q
2
=q,tem-seque
Q(2q)= q
4
: (3)
Note-sequeQ(2q)n~aodependedoraiodoanel.
Ob-viamente,istodeve-seaofatodeQestarposiionadaa
meiadist^aniaentreq
1 eq
2 .
Tomemos,agora,tr^esargasqsobreoaneleusando
omorefer^eniaaFigura1,alulemosovalordeQ(3q)
demaneiraquearesultantenadire~ao^xsejanula,
F
1x =jF
1Q j jF
12 jos
12 jF
13 jos
13 =0:
Como jF
12 j = jF
13 j, q
1 = q
2
= q, jr
1Q
j = R e
jr
12 j = jr
13
j = 2Ros
12
, sendo
12 =
13 =
6 ,
segueque
jQj
R 2
=2 q
2R sen
3
2 sen
3 ;
poisos
2
=sen. Aqui,paran=3,novamente
Q n~ao depende de R omo era de se esperar.
Final-mente,
Q(3q)= q
2sen
3
: (4)
Paraquatroargasqsobre oanel,aomponentex
daforaresultantetemaseguinteforma
F
1x =jF
1Q j jF
12 jos
12 jF
13 j jF
14 jos
14 =0:
ApartirdaFigura2,observa-seque,
jQj
R 2
=2 q
(2Ros
12 )
2 os
12 +
q
(2R ) 2
;
ou
Q(4q)= q
2
1
sen
4 +
1
2
: (5)
Figura2. Quatroargasdistribudassobreoanel
ondutor.
Aindaeinsuienteonumerodeargasparaquese
possaabstrair eobteruma fun~ao. Sigamos emfrente
aresentandomaisargasaoanel.
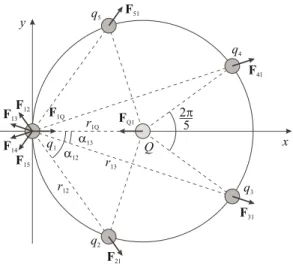
on-Figura3. Cinoargasdistribudassobreoanelondutor.
Ent~ao,
F
1x =j F
1Q j jF
12 jos
12 jF
13 jos
13
jF
14 jos
14 jF
15 jos
15 =0;
ou
jQj
R 2
=2 q
(2Ros
12 )
2 os
12 +2
q
(2Ros
13 )
2 os
13 :
Portanto,
Q(5q)= q
2
1
sen
5 +
1
sen
5 2
: (6)
Seguindoomesmoraionioparaalgunsoutros
va-lores de n e organizando os dados omo feito abaixo,
veria-sequehauma rela~aoentre onumero de
ar-gaseonumerodeparelasaseremsomadas,bemomo
avaria~aodovalordoargumentodeseno:
Duasargasq) Q(2q)= q
2
1
2sen(
2 )
Tr^esargasq) Q(3q)= q
2
1
sen(
3 )
Quatroargasq)Q(4q)= q
2
1
sen(
4 )
+ 1
2sen(
4 2)
Cino argasq ) Q(5q)= q
2
1
sen(
5 )
+ 1
sen(
5 2)
Seisargasq) Q(6q)= q
2
1
sen(
6 )
+ 1
sen(
6 2)
+ 1
2sen(
6 3)
Sete argasq) Q(7q)= q
2
1
sen(
7 )
+ 1
sen(
7 2)
+ 1
sen(
7 3)
Oitoargasq) Q(8q)= q
2
1
sen(
8 )
+ 1
sen(
8 2)
+ 1
sen(
8 3)
+ 1
2sen(
8 4)
d
Pode-senotaraexist^eniadedoispadr~oes,umpara
numeropardeargasqe,outroparanumerompar.
E
possvelent~aogeneralizar,demodoaenontrarovalor
deQ(nq)para qualquern>2:
Q(nq)= q
2
n 1
2
X
1
sen
n i
; paranmpar (7) e,
Q(nq)= q
2
2
4 1
2 +
n 2
2
X
i=1 1
sen
n i
3
5
; para n par: (8)
Alimita~aoparaousodaseriedizrespeitoa
Para n muito grande | uja ordem de grandeza
su-pere apreis~aodamaquina|oalulotorna-sealem
delento,impreiso. Ograndenumerodetermos
soma-dostornaoerroabsolutomaiorqueovalordasparelas
adiionadas,prejudiandoaobten~aodovalordaarga
entral. Uma solu~aoparaeste problemaefraionara
soma demodoalimitarapropaga~aodoerro.
A Figura 4 abaixo mostra omo evolui o valor da
argaentralemrela~aoaargadistribudasobreoanel
ondutor numintervalo den =2a10 argas(neste e
nos demais graos aarga q foi tomada igual a
uni-dade). Estegraoinformaqueovalordaargaentral
resemaisrapidamente queaargadoanel.
Figura4. Evolu~aodaserienointervalon=2:::10.
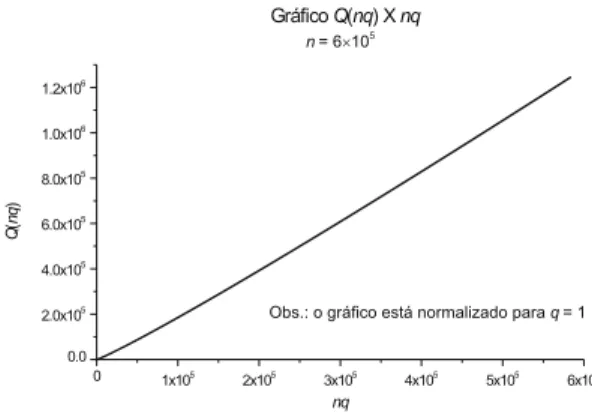
Como se omporta Q(nq) para valoresgrandes de
n? A Figura 5 apresenta valores de Q(nq) no
inter-valo den=2a10 6
. Pode-seobservarque,onformen
rese,aurvapareetenderaumareta. Pergunta-se:
seraQ(nq)linearomnqquando nformuitogrande?
E, existeuma express~aomatematiaquedesreveesse
resimento equeseja,aomesmotempo,maispratia
queasseriesenontradasaima? Arespostaaambasas
perguntasesim. Orestante destetrabalhoedediado
abusadessa express~aomatematiaeasuaanalise.
Arealidadefsiaimp~oeque,paraadete~aode
ar-gas eletriasemum objeto,n sejasuperior a10 6
. Em
eletr^ometrostpios(omoumKeithleymodelo617),o
intervalodeopera~aoenontra-seentre10 13
e10 8
A.
Sendo a arga eletriaelementar deum eletron ou de
umprotonequivalentea1;60210 19
C,veria-seque
taiseletr^ometrosdetetamquantidadesdeargasentre
10 6
e 10 11
unidades. Tal intervalo sera usado na
ob-Figura5. Evolu~aodaserienointervalon=2:::10 6
.
Pode-seonsideraraEq.(7) eaEq.(8) omosendo
equivalentes,poisno intervalo itado aimae
omple-tamenteindiferentenserparoumpar. Alemdisso,na
Eq.(7) observa-se que o fator 1=2 sotem import^ania
quando n 10, de modo que se pode despreza-lo.
Istopermitetrabalharomumauniaexpress~aoparan
grande. Ent~ao,tomandoaseriempar,Q(nq)
sr
,tem-se
Q(nq)
sr =
q
2
n 1
2
X
i=1 1
sin
n i
: (9)
Como a Eq.(9) n~ao depende do raio do anel, este
pode ser onsiderado de um tamanho tal que a
dis-tribui~ao de argas seja ontnua. Neste aso e fail
transformar a seriempar em uma integral, usando a
deni~aodesomadeRiemann[2℄paraparti~aoregular
lim
x!0 X
k f(w
k )x=
Z
b
a
f(x)dx:
Assim,fazendo naEq.(9)
n i=x,
n
=xetomando
olimitedex!0,enontra-se
Q(nq)= n
q
2
2
2n
Z
n
sxdx;paran2:
Aposalgumamanipula~aoalgebriaobtem-se a
se-guinte fun~aodenominadaobtida, Q(nq)
ob ,
Q(nq)
ob =
nq
2 ln
(
os
2n
1+os
n
1+sin
2n
sin
n
)
: (10)
Comparando-seosgraosdasequa~oes(9)e(10),
veria-seque,paravaloresgrandesden,essaspareem
posiionar-separalelamente(Figuras6e7).
Epossvel
melhoraristo,visandoaonverg^eniadasduasurvas,
atravesde uma adequada altera~ao dos limites de
in-tegra~ao. Tomaram-se, para tanto, intervalos de
inte-gra~ao de tamanho onstante evariou-se a origem do
dife-foionseguidaatravesdoseguinteintervalo: x
i =
9
16 e
x
f =
2 15
16n
,demodoaobter-seafun~aomelhorada,
Q(nq)
me ,
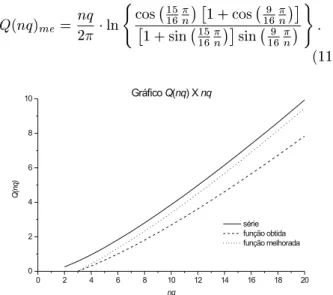
Q(nq)
me =
nq
2 ln
(
os 15
16
n
1+os 9
16
n
1+sin 15
16
n
sin 9
16
n
)
:
(11)
Figura6. Compara~aodaserieomasfun~oesobtidae
me-lhorada no intervalo n = 2:::20. A legenda india que a
urvaserie refere-seaEq.(9),fun~aoobtida omEq.(10)e
fun~aomelhoradaemEq.(11).
Figura7. Graoomparativodaserieomasfun~oes
obtidaemelhoradanointervalon=900a1000 argas.
n fun~ao melhorada/serie
10 1
0;87557
10 2
0;99338
10 4
0:99977
10 8
0;99990
Tabela2-Afun~aomelhoradaonverge
as-sintotiamenteparaaserie.
Pode-senotarqueafun~aomelhoradaestadebom
aordoomaserie. Talonord^ania,estudadaparan
variando, em ordem, de 10 1
a 10 8
, deu-se
assintotia-mente onformeobservado naTabela2. Aquie
enon-tradaumaoutralimita~aoparaoalulodeQatraves
da serie. A quantidade maxima de argas permitida,
ou onumero inteiromaximopossvelde seoperarem
linguagem Fortran 90 (for Windows) 1
deveser menor
ouiguala10 9
.
Devido a onverg^enia da fun~ao melhorada e
possvelextrapolaroslimitesimpostosaousodaserie.
Paravaloresdenomsentidofsio,istoe,valores
om-preendidosentre10 6
e10 11
argaselementares,afun~ao
representaumaboaferramentaparaoalulodaarga
entral.
Pode-seobterumafun~aoparaoalulodeQmais
ompata, a medida em que se onsidera somente o
termo dominante da Eq.(11). No intervalo entre 10 6
e 10 11
argas elementares os argumentos de senos,
de osenos e de logaritmos neperianos s~ao
suiente-mentepequenosparapoderemserexpandidosemserie
de Taylor 2
ate termos de segunda ordem. Assim, a
fun~ao aproximada, Q(nq)
ap
, pode ser esrita
aproxi-madamenteomo
Q(nq)
ap
= nq
2
lnn+ln
32
9
15
32 +O
1
n
:
Como 32
9
1e a onstante subtrativa pouo afeta o
alulo para o intervalo de n onsiderado, pode-se
-nalmente esrever,
Q(nq)
ap =
q
2
nln( n): (12)
Deve-se observar, entretanto, que o termo dominante
daserie,Eq.(12)apresentamaiorimpreis~aoqueaEq.
(11)oumesmoqueaEq.(10). Noaso,omomostrado
na Tabela 3, no intervalo de interesse, a impreis~aoe
eradeuma parteemem.
n fun~ao aproximada /serie
10 1
0;94879
10 2
0;97345
10 4
0;98654
10 8
0;99323
Tabela 3 - A fun~ao aproximada onverge
de forma mais lenta para a serie, quando
omparadaomafun~aomelhorada.
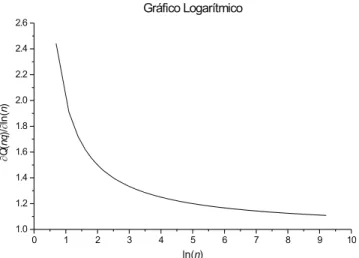
EmboraQn~aosejalinearomnq,onformeEq.(12),
tem-se que ln(Q) torna-se linear om ln(n) para n
muitogrande. Istoeveriadoatravesdaderivada
lo-gartmiadeQ
lim
n!1
ln[Q(nq)
ap ℄
ln(n)
= lim
n!1
1+ 1
ln(n)
=1;
1
NoFortran90,oomandoINTEGER(4)permite-nosoperaromnumerosinteirosnointervalode 2:147:483:648a2:147:483:647.
2
os( )
=1
2
+O 4
,sin()
= O 3
eln( 1)
=
2
+O 3
emostradonaFigura8atravesdeumgraode ln(Q)
ln(n)
versus ln(n).
Figura8.Ovalordeln[Q(nq)me℄tendealinearizar-seom
ln(n)quandon2.
III Conlus~ao
A fun~ao melhorada esta de bom aordo om a serie
e, portanto, onstituium modode seobterovalor da
argaentral deformamais rapida. Comestafun~ao,
epossvelextrapolarovalordaserieemregi~oesondeo
usodaserieeimpratiavelpormeiosnumerios.
Den-tro darealidade fsia, istoe, omn entre 10 6
e10 11
,
pode-se usar a fun~ao aproximada (ou o termo
domi-nante daserie),istoe,
Q(nq)
ap =
q
2
nln( n);
oqualapresentaimpreis~aodeumaparteememnesse
intervalo.
Caberessaltarqueapropostainiialdesteestudofoi
soluionarumproblemaessenialmenteteorio.
Perma-neeemaberto,portanto,oestudodeasos
experimen-taisquevenhamaseutilizardoaquiexposto.
Refer^enias
1. Reitz, J. R., Milford, F. J., Christy, R. W.
Fundamentos da Teoria do Eletromagnetismo.
7 a
edi~ao,RiodeJaneiro,Campus,1982.
2. Swokowski, E.W. Calulo om Geometria
Analtia. 2 a
edi~ao, S~ao Paulo, Makron Books,