Estudo teórico das espécies heterobimetálicas laGa, ceGa, euGa e ybGa em fase gasosa .

EuGa E YbGa EM FASE GASOSA

Maion Pierre Lourenço

ESTUDO TEÓRICO DAS ESPÉCIES

HETEROBIMETÁLICAS LaGa, CeGa, EuGa E YbGa

EM FASE GASOSA

Dissertação apresentada ao Departamento de

Químia do Instituto de Ciênias Exatas da

Universidade Federalde MinasGerais omo

re-quisitoparialparaaobtenção dograude

Mes-tre emQuímia

−

Físio-Químia.

BeloHorizonte

- AoprofessorAmaryCesarpelaorientação,onheimentoompartilhado,disussões

e,além de tudo, pelaamizade.

- SouompletamentegratoaoprofessorRiardoJoséAlvespeloapoioeompreensão.

- Ao meu pai Pedro Donizete Aladim Lourenço e irmão Bruno Jeferson Lourenço,

peloarinho, apoioe inentivo.

- AosamigosdodepartamentodequímiadaUFMG:Jarbas,Freddy,Daniel,Prisila,

Luan, Maros pela amizade,ompanheirismo e disussões sobre iênia e assuntos

ans.

- Atodos osmeusamigosefamiliaresqueonviveram omigonessetempode estudo

e queompartilharamomigo algumasexperiênias.

- Agradeço a todos que de algum modo ontribuíram para o desenvolvimento desse

trabalho.

- AoCNPq pela bolsade mestrado.

∗

∗

Opresente trabalho foi realizadoom apoio doCNPq, ConselhoNaional deDesenvolvimento

LISTA DE FIGURAS . . . v

LISTA DE TABELAS. . . vi

LISTA DE ACRÔNIMOS . . . xii

RESUMO . . . xiii

ABSTRACT . . . xiv

1 Introdução 1 2 Base teória 4 2.1 Métodos Teórios de Cálulo de Estruturas Eletrnias . . . 4

2.1.1 A aproximação de Born

−

Oppenheimer . . . 4

2.1.2 MétodoHartree-Fok . . . 6

2.2 Métodos de Correlação Eletrnia . . . 10

2.2.1 Métodode Interação de Congurações CI. . . 11

2.2.2 MétodoMultionguraional SCF . . . 11

2.2.3 MétodoMulti-referênial MRCI . . . 12

2.2.4 MétodoNEVPT2 . . . 13

2.3 Métodos Relativístios . . . 14

2.3.1 Equação Quântia Relativístia emQuatroComponentes . . . 14

2.3.2 OHamiltonianoRelativístioMulti-eletrnio . . . 16

2.3.3 A Equação de Pauli. . . 19

2.3.4 Pseudopotenial . . . 21

2.3.5 PseudopotenialRelativístio . . . 24

2.4 Cálulodas Propriedades Espetrosópias eElétrias Moleulares . . . . 26

2.4.1 Propriedades Espetrosópias . . . 26

Ce, Eu, Yb) 30

3.1 Detalhes Computaionais. . . 30

3.2 Resultados . . . 33

3.2.1 Resultados LaGa . . . 33

3.2.2 Resultados CeGa . . . 34

3.2.3 Resultados EuGa . . . 39

3.2.4 Resultados YbGa . . . 44

3.3 Disussão . . . 47

4 CálulosCorrelaionadosdasEspéiesHeterobimetáliasLnGa(Ln=La, Ce, Eu, Yb) 53 4.1 Detalhes Computaionais. . . 53

4.2 Resultados . . . 54

4.2.1 Resultados LaGa . . . 54

4.2.2 Resultados CeGa . . . 58

4.2.3 Resultados EuGa . . . 63

4.2.4 Resultados YbGa . . . 68

4.3 Comparaçãoom Resultados ExperimentaisÚteis . . . 72

4.4 Disussão . . . 74

5 Correções RelativístiasMassa-veloidade e Darwin nasEspéies Hete-robimetálias LnGa(Ln=La, Ce, Eu, Yb) 79 5.1 Detalhes Computaionais. . . 79

5.2 Resultados . . . 80

5.3 Disussão . . . 81

6 Conlusões e Perspetivas 87 A Uso de Simetria 88 A.1 Usode Simetria . . . 88

A.1.1 Notação Referente a Simetria C

2

v

Utilizada para Construir o Es-paço de Orbitais . . . 90

B Função de Onda Multionguraional 92

2.1 Desenhoilustrandoaspropriedadesespetrosópias: energiadeexitação

T

e

para os estados S

n

(n=0, 1, 2), distânia internulear de equilíbrio R

0

, energiade dissoiaçãode equilíbrioD

e

eaenergiade dissoiaçãoorrigida para aenergia doponto zero D

0

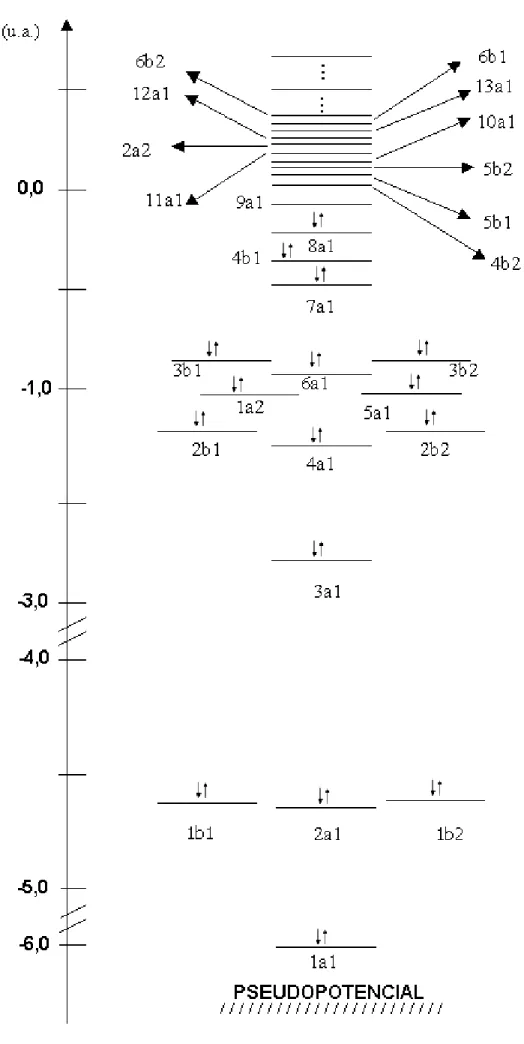
. . . 28

3.1 Diagrama semiquantitativo dos orbitais moleulares da espéie LaGa

ob-tido porálulo RHFdo estado X

1

_A1

. . . 35

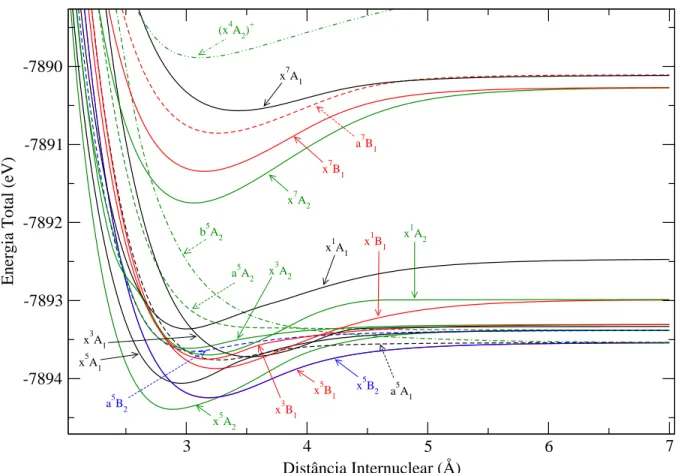
3.2 Curvas de Energia Potenial para o estado fundamental e alguns estados

exitadosda espéie LaGa. CáluloHartree-Fok. . . 37

3.3 Diagrama semiquantitativo dos orbitais moleulares da espéie CeGa

ob-tido porálulo RHFdo estado X

1

_A

1

. . . 38

3.4 Curvas de Energia Potenial para o estado fundamental e alguns estados

exitadosda espéie CeGa. CáluloHartree-Fok. . . 41

3.5 Diagrama semiquantitativo dos orbitais moleulares da espéie EuGa

ob-tido porálulo RHFdo estado X

1

_A1

. . . 42

3.6 Curvas de Energia Potenial para o estado fundamental e alguns estados

exitadosda espéie EuGa. CáluloHartree-Fok. . . 43

3.7 Diagrama semiquantitativo dos orbitais moleulares da espéie YbGa

ob-tido porálulo RHFdo estado X

1

_A1

. . . 49

3.8 Curvas de Energia Potenial para o estado fundamental e alguns estados

exitadosda espéie YbGa. CáluloHartree-Fok. . . 50

4.1 Curvas de Energia Potenial para o estado fundamental e alguns estados

exitadosda espéie LaGa. CáluloMCSCF . . . 56

4.2 Curvas de Energia Potenial para o estado fundamental e alguns estados

exitadosda espéie LaGa. CáluloNEVPT2 . . . 59

4.3 Curvas de Energia Potenial para o estado fundamental e alguns estados

exitadosda espéie CeGa. CáluloNEVPT2 .. . . 63

4.5 Curvas de Energia Potenial para o estado fundamental e alguns estados

exitadosda espéie EuGa. CáluloMCSCF. . . 65

4.6 Curvas de Energia Potenial para o estado fundamental e alguns estados

exitadosda espéie EuGa. CáluloNEVPT2 . . . 67

4.7 Curvas de Energia Potenial para o estado fundamental e alguns estados

exitadosda espéie YbGa. CáluloMCSCF. . . 70

4.8 Curvas de Energia Potenial para o estado fundamental e alguns estados

exitadosda espéie YbGa. CáluloNEVPT2 . . . 72

5.1 CurvasdeEnergiaPotenialparaoestadofundamentaleostrêsprimeiros

estadosexitadosdaespéieLaGaobtidasporálulosMCSCFsemeom

orreçõesrelativístias. . . 81

5.2 CurvasdeEnergiaPotenialparaoestadofundamentaleostrêsprimeiros

estadosexitadosdaespéieCeGaobtidasporálulosMCSCFsemeom

orreçõesrelativístias. . . 82

5.3 CurvasdeEnergiaPotenialparaoestadofundamentaleostrêsprimeiros

estadosexitadosdaespéieEuGaobtidasporálulosMCSCF semeom

orreçõesrelativístias. . . 83

5.4 CurvasdeEnergiaPotenialparaoestadofundamentaleostrêsprimeiros

estadosexitadosdaespéieYbGaobtidasporálulosMCSCFsemeom

3.1 Funçães de bases atmias primitivase ontraídas e pseudopoteniais. Q

éo número de elétrons noaroço. . . 31

3.2 Espaço de orbitais inativos (parêntese) e ativos (olhete) e o número de

elétrons no espaço ativo dos estados eletrnios das espéies LnGa(Ln=

La,Ce, Eu, Yb)utilizadosnos álulosHartree-Fok. Estadode referênia

X

5

_A2

, onguração:

(7

a1

)

2

₍₈

_a1

₎

1

₍₉

_a1

₎

1

₍₃

_b1

₎

2

₍₄

_b1

₎

1

₍₃

_b2

₎

2

₍₄

_b2

₎

1

₍₁

_a2

₎

2

. . . 32

3.3 Número atmioeonguração eletrnia dos lantanídeos. . . 33

3.4 Conguração eletrnia dos elementos La, Ce, Eu , Yb e Ga esrita na

formadasimetria C

∞

v

e C

2

v

. . . 33 3.5 Conguraçãoeletrniaeaenergiade exitaçãoT

e

(eV)em3,0Å(om

re-laçãoaoestadofundamental)paraosestadosobtidosporálulos

Hartree-Fok da espéie LaGa. . . 36

3.6 Estados eletrnios, espaço ativo CAS, energia de exitação T

e

(eV), dis-tânia interatmia de equilíbrio R

0

(Å), energia de dissoiação D

e

(eV), momento de diplo elétrio

µ

z

(D) e a polarizabilidade isotrópia

α

¯

(Å

3

)

paradiferentes onguraçõeseletrniasobtidasporálulosHartree-Fok

daespéie LaGa. . . 39

3.7 Conguraçãoeletrniaeaenergiade exitaçãoT

e

(eV)em3,0Å(om re-laçãoaoestadofundamental)paraosestadosobtidosporálulos

Hartree-Fok da espéie CeGa. . . 40

3.8 Estados eletrnios, espaço ativo CAS, energia de exitação Te (eV),

dis-tânia interatmia de equilíbrio R

0

(Å), energia de dissoiação D

e

(eV), momento de dipolo elétrio

µ

z

(D) e a polarizabilidade isotrópia

α

¯

(Å

3

)

paradiferentes onguraçõeseletrniasobtidasporálulosHartree-Fok

laçãoaoestadofundamental)paraosestadosobtidosporálulos

Hartree-Fok da espéie EuGa. . . 45

3.10 Estados eletrnios, espaço ativo CAS, energia de exitação T

e

(eV), dis-tânia interatmia de equilíbrio R

0

(Å), energia de dissoiação D

e

(eV), momento de dipolo elétrio

µ

z

(D) e a polarizabilidade isotrópia

α

¯

(Å

3

)

paradiferentes onguraçõeseletrniasobtidasporálulosHartree-Fok

daespéie EuGa. . . 46

3.11 Conguraçãoeletrniaeaenergiade exitaçãoT

e

(eV)em3,0Å(om re-laçãoaoestadofundamental)paraosestadosobtidosporálulos

Hartree-Fok da espéie YbGa. . . 48

3.12 Estados eletrnios, espaço ativo CAS, energia de exitação T

e

(eV), dis-tânia interatmia de equilíbrio R

0

(Å), energia de dissoiação D

e

(eV), momento de diplo elétrio

µ

z

(D) e a polarizabilidade isotrópia

α

¯

(Å

3

)

para diferentes ongurações eletrnias obtidasporáluloHartree-Fok

daespéie YbGa. . . 51

3.13 Energiade exitação

T

e

(eV), distâniainteratmiade equilíbrio

R

0

(Å), energiadedissoiação

D

e

(eV),momentodediploelétrio

µ

z

(D)ea polari-zabilidadeisotrópia

α

¯

(Å

3

)paraostrêsprimeirosestadoseletrnios

obti-dosporálulosHartree-FokdasespéiesheterobimetáliasLnGa(Ln=La,

Ce, Eu, Yb). . . 52

4.1 Espaço de orbitaisinativos (parêntese) e ativos(olhete), númerode

elé-trons(NE)noespaçoativodosestadoseletrniosdasespéiesLnGa(Ln=La,

Ce,Eu,Yb)utilizadosnosálulosMCSCFeNEVPT2. Estadode

referên-iaX

5

_A2

, onguração:

(7

a1

)

2

₍₈

_a1

₎

1

₍₉

_a1

₎

1

₍₃

_b1

₎

2

₍₄

_b1

₎

1

₍₃

_b2

₎

2

₍₄

_b2

₎

1

₍₁

_a2

₎

2

. 55

4.2 Estado eletrnio, espaço ativo CAS, energia de exitação eletrnia T

e

(eV)em 3,0Å om relaçãoaoestado fundamental,distâniainteratmia

de equilíbrio R

0

(Å), energia de dissoiação D

e

(eV), momento de dipolo elétrio

µ

z

(D) e a polarizabilidadeisotrópia

α

¯

(Å

3

) para diferentes

on-guraçõeseletrnias obtidas porálulos MCSCF da espéie LaGa. . . 57

4.3 Estados eletrnios, espaço ativo CAS, energiade exitação eletrnia T

e

(eV)em 3,0Å om relaçãoaoestado fundamental,distâniainteratmia

de equilíbrio R

0

(Å), energia de dissoiação D

e

(eV), momento de dipolo elétrio

µ

z

(D) e a polarizabilidadeisotrópia

α

¯

(Å

3

on-4.4 Estados eletrnios, espaço ativo CAS, energiade exitação eletrnia T

e

(eV)em 3,0Å om relaçãoaoestado fundamental,distâniainteratmia

de equilíbrio R

0

(Å), energia de dissoiação D

e

(eV), momento de dipolo elétrio

µ

z

(D) e a polarizabilidadeisotrópia

α

¯

(Å

3

) para diferentes

on-guraçõeseletrnias obtidas porálulos MCSCF da espéie CeGa. . . . 62

4.5 Estados eletrnios, espaço ativo CAS, energiade exitação eletrnia T

e

(eV) em 3,0Å om relação aoestado fundamental,distâniainteratmia

de equilíbrio R

0

(Å), energia de dissoiação D

e

(eV), momento de dipolo elétrio

µ

z

(D),polarizabilidadeisotrópia

α

¯

(Å

3

) para diferentes

ongu-raçõeseletrnias obtidasporálulos NEVPT2 daespéie CeGa. . . 64

4.6 Estados eletrnios, espaço ativo CAS, energiade exitação eletrnia T

e

(eV)em 3,0Å om relaçãoaoestado fundamental,distâniainteratmia

de equilíbrio R

0

(Å), energia de dissoiação D

e

(eV), momento de dipolo elétrio

µ

z

(D) e a polarizabilidadeisotrópia

α

¯

(Å

3

) para diferentes

on-guraçõeseletrnias obtidas porálulos MCSCF da espéie EuGa.. . . 66

4.7 Estados eletrnios, espaço ativo, energia de exitação eletrnia T

e

(eV) em 3,0 Å om relação ao estado fundamental, distânia interatmia de

equilíbrioR

0

(Å), energia de dissoiaçãoD

e

(eV),momentode dipolo elé-trio

µ

z

(D)ea polarizabilidadeisotrópia

α

¯

(Å

3

)para diferentes

ongu-raçõeseletrnias obtidasporálulos NEVPT2 daespéie EuGa. . . 68

4.8 Estados eletrnios, espaço ativo CAS, energiade exitação eletrnia T

e

(eV) em 3,0 Å om relação ao estado fundamental, distânia

interat-mia de equilíbrio T

e

(Å), energia de dissoiação D

e

(eV), momento de dipoloelétrio

µ

z

(D) e polarizabilidade isotrópia

α

¯

(Å

3

) para diferentes

ongurações eletrnias obtidaspor álulosMCSCF daespéie YbGa.. 71

4.9 Estados eletrnios, espaço ativo CAS, energiade exitação eletrnia T

e

(eV)em 3,0Å om relaçãoaoestado fundamental,distâniainteratmia

de equilíbrio R

0

(Å), energia de dissoiação D

e

(eV), momento de dipolo eleétrio

µ

z

(D)e apolarizabilidadeisotrópia

α

¯

(Å

3

) paradiferentes

on-guraçõeseletrnias obtidas porálulos NEVPT2 da espéie YbGa. . . 73

4.10 Energiade dissoiaçãoorrigidapara a energiado pontozero D

o

(eV) ea onstante vibraionalharmnia

ω

e

(m

−

1

) e não harmnia

ω

e

x

e

(m

−

1

)

para os três primeiros estados eletrnios obtidos por álulos NEVPT2

energiadedissoiação

D

e

(eV),momentodediploelétrio

µ

z

(D)ea polari-zabilidadeisotrópia

α

¯

(Å

3

)paraostrêsprimeirosestadoseletrnios

obti-dosporálulosHartree-FokdasespéiesheterobimetáliasLnGa(Ln=La,

Ce, Eu, Yb). . . 77

4.12 Energiade exitação

T

e

(eV), distâniainteratmiade equilíbrio

R0

(Å), energia de dissoiação

D

e

(eV), momento de diplo elétrio

µ

z

(D) e a po-larizabilidadeisotrópia

α

¯

(Å

3

) para os três primeiros estados eletrnios obtidosporálulosMCSCFdas espéiesheterobimetáliasLnGa(Ln=La, Ce, Eu, Yb). . . 78

4.13 Energiade exitação

T

e

(eV), distâniainteratmiade equilíbrio

R0

(Å), energiade dissoiação

D

e

(eV), momentode diplo elétrio

µ

z

(D), polari-zabilidade isotrópia

α

¯

(Å

3

) para ostrês primeirosestados eletrnios ob-tidos por álulos NEVPT2 das espéies heterobimetálias LnGa(Ln=La, Ce, Eu, Yb). . . 78

5.1 Estado eletrnio, autovalor do operador Darwin (eV), autovalordo ope-rador massa-veloidade MV (eV), valor da Energia Total Corrigida ETC (eV)eoperentual daontribuiçãomassa-veloidadeeDarwin%MVDem 3,0Å. . . 85

5.2 Estado eletrnio, energia de exitação eletrnia T

e

(eV) em 3,0Å om relaçãoaoestadofundamental,distâniainteratmiadeequilíbrioR

0

(Å), energia de dissoiação D

e

(eV) para diferentes ongurações eletrnias obtidas por álulo MCSCF das espéies LnGa. Os efeitos relativístios (orreçãode massa-velidadeeDarwin)sãoomparadosomosresultados dos álulosnão relativístios. . . 86

A.1 Tabelade multipliaçãodo grupo C

2

v

. . . 89

A.2 Tabelade arateres dogrupoC

2

v

. . . 89

A.3 Tabelado produtodireto do grupo C

2

v

. . . 89

A.4 Orbitaisformados porsimetria do grupo C

2

v

. Relação entre a ombinção dos orbitaisatmios OA e ostipos de simetriado grupo C

∞

v

eC

2

v

. . . 90

B.2 Estados eletrnios e o espaço de orbitais moleulares dos quintetos da

espéie LaGa om a respetiva função de onda multionguraional om

asduas onguraçõeseletrnias de maior peso. . . 94

B.3 Estados eletrnios e o espaço de orbitais moleulares dos heptetos da

espéie LaGa om a respetiva função de onda multionguraional om

asduas onguraçõeseletrnias de maior peso. . . 95

B.4 Estadoseletrnios e o espaço de orbitais moleularesdos simpletose

tri-pletosdaespéie CeGa oma respetivafunção de onda

multiongurai-onal om asduas onguraçõeseletrnias de maiorpeso. . . 96

B.5 Estados eletrnios e o espaço de orbitais moleulares dos quintetos da

espéie CeGa om a respetiva função de onda multionguraional om

asduas onguraçõeseletrnias de maior peso. . . 97

B.6 Estados eletrnios e o espaço de orbitais moleulares dos heptetos da

espéie CeGa om a respetiva função de onda multionguraional om

asduas onguraçõeseletrnias de maior peso. . . 98

B.7 Estadoseletrnios e o espaço de orbitais moleularesdos simpletose

tri-pletosdaespéie EuGaom arespetivafunçãode onda

multiongurai-onal om asduas onguraçõeseletrnias de maiorpeso. . . 99

B.8 Estados eletrnios e o espaço de orbitais moleulares dos quintetos da

espéie EuGa om a respetiva função de onda multionguraional om

asduas onguraçõeseletrnias de maior peso. . . 100

B.9 Estados eletrnios e o espaço de orbitais moleulares dos heptetos da

espéie EuGa om a respetiva função de onda multionguraional om

asduas onguraçõeseletrnias de maior peso. . . 101

B.10 Estadoseletrnios e o espaço de orbitais moleularesdos simpletose

tri-pletos da espéie YbGa om a respetiva função de onda

multiongura-ionalom as duas ongurações eletrnias de maior peso. . . 102

B.11 Estados eletrnios e o espaço de orbitais moleulares dos quintetos da

espéie YbGa om a respetiva função de onda multionguraional om

asduas onguraçõeseletrnias de maior peso. . . 103

B.12 Estados eletrnios e o espaço de orbitais moleulares dos heptetos da

espéie YbGa om a respetiva função de onda multionguraional om

ROHF Hartree-Fok restritode amadaaberta 2

MCSCF Cálulo multionguraionalde altaonsistênia 2

NEVPT2 Teoria de perturbação de n elétronsde valênia 2

RHF Hartree-Fok restrito 8

CI Interaçãode ongurações 10

CC Coupled-loster 11

QED Eletrodinâmiaquântia 17

DHF Dira-Hartree-Fok 18

ECP Pseudopotenial efetivo 21

RECP Pseudopotenial relativístio 24

Essa dissertação trata da eluidação da estrutura eletrnia das espéies

heterobi-metalias LnGa(Ln=La, Ce, Eu, Yb) neutras e em fase gasosa usando pseudopotenial

relativístios. Oslantanídeossãode grandeinteresseemdiferentes áreasdaquímia: em

químia de oordenação, em químia de organometálios e, também, em atálise. Há

uma espetativa que as espéies LnGa(Ln=La, Ce, Eu, Yb) ativem a ligação C-H do

metano om resultados melhores que aqueles apresentados pelos elementos lantanídios

individuais.

Esse trabalho foi inspirado pelos resultados da síntese dos omplexos ontendo um

entro heterobimetálio, onde um metal é um lantanídeo e o outro é um metal de

tran-sição. Iniialmente, os álulos foram feitos utilizando o método ROHF e MCSCF. O

método NEVPT2 foi usado om o objetivo de melhorar a desrição do efeito da

orre-lação eletrnia dos sistemas sobre investigação. As urvas de energia potenial foram

obtidas, assim omo as propriedades espetrosópias e elétrias moleulares, pelos três

métodos teórios.

Os efeitos relativístiossão preponderantes para os elementos pesados, então, om o

objetivo de investigar esses efeitos nas espéies heterobimetálias LnGa, os operadores

massa-veloidadeeDarwin foraminluídospelométodoMCSCF. Aurvadeenergia

po-tenialeaspropriedadesespetrosópiasforamobtidaseomparadasom osresultados

Theurrentdissertationdealswiththeeluidationofeletronistrutureofgasphase

neutralheterobimetallispeiesLnGa(Ln=La,Ce,Eu,Yb)usingrelativistieetiveore

potentials. Lanthanides are of a great interest in dierent areas of hemistry:

oorde-nation hemistry, organometallihemistryand atalysis. Anexpetationis that Ln-Ga

speies may nd atalysis apliation as hydroarbons CH bond ativation with

perfor-mane expeted better than the individual lanthanideelements.

This work was inspired by results from reent synthesis of omplexes ontaining a

heterobimetali enter, where one metal is a lanthanide and the other is a transition

metal. Initially,alulationswere performedatROHF andMCSCF levelsfor theground

state anda fewexited states. The NEVPT2 orrelated methodwasperformedwiththe

purpose of inreasing the amount of dynami orrelation inluded in the system under

investigation. Potentialenergy surfaes were obtained as wellas some spetrosopi and

eletrimoleularproperties fromthese three omputationalmethods.

The relativisti eets are important in dealing with heavy elements. In order to

investigatethiseetsintheheterobimetallispeiesLnGa,themass-veloityandDarwin

operator were individually alulated at MCSCF method. The potential surfaes and

the spetrosopi properties were then obtained and ompared with the non-relativisti

Introdução

Os lantanídeos são de grande interesse em diferentes áreas da químia. Eles podem ser

estudados na químia de oodenação, na químia de ompostos organometálios, 1

em

atálise para investigar a ativação da ligação C

−

H do metano. 13

Sistemas

moleula-res ontendo lantanídeos têm sido alvo de estudo na químia teória onde aplia-se e

desenvolve-se métodos teórios e algorítimosomputaionais para resolver,

aproximada-mente, as equações da meânia quântia para diferentes sistemas. 2,4 6

Estes métodos

teórios podem ser utilizados para se investigar a estrutura eletrnia de átomos e

mo-léulas, 5

propriedades físias e químias 6

de lantanídeos. Além disso, os metais pesados

(a partir do 4

0

períododa tabela periódia) sofrem efeitos relativístios preponderantes

devido a grande arga nulear que atua, eletrostatiamente, sobre os elétrons mais

in-ternos. O tratamento teório orreto destes efeitos é desrito pela equação de Dira 79

(umaequaçãoquântiarelativistiamenteorreta). Aapliaçãodaequaçãode Dirapara

sistemasmultieletrnioseodesenvolvimentode métodos aproximativos(teorias)e

algo-rítimosomputaionaispararesolvê-lageraumnovoampodaquímiateóriaonheido

omo químia quântia relativístia. 9,10

Pouo se sabe sobre as ligações químias envolvendo lantanídeos e outros metais de

transição, porém existe na literatura informações onsolidadas de ligaçes, simples ou

multiplas, entre metais de transição. Ligações metálias em omplexos de terras raras

são pouo onheidasdevido aofatode osorbitais4f seenontraremno interiordoíone

serem protegidos oublindados 11

pelos orbitais 5se 5p.

O primeiro omplexo heterobimetálio sintetizado apresentando uma ligação entre

lantanídeo e um metal de transição foi [(C

4

H

8

O)(

η

5

₋

C

5

H

5

)

2

Lu-Ru(CO)

2

(

η

5

₋

C

5

H

5

)℄. 12

Nesseomposto,aligaçãoLu-Ruéovalenteepolarizada. Areaçãoentre[(

η

5

-C

5

Me

5

)Al℄

4

e [(

η

5

-C

5

Me

5

)

2

Ln℄(Ln=Eu, Yb), em ondiçõesespeías, produz ristaisde omposição

[(

η

5

-C

5

Me

5

)

2

Ln(II)-Al(I)(

η

5

mostramque a interação entre [(

η

5

-C

5

Me

5

)

2

Ln℄(Ln=Eu, Yb) om [(

η

5

-C

5

Me

5

)Al℄ é

pre-dominantemente eletrostátia om uma transferênia de arga mínima ou ontribuição

ovalente. 13

EstudosteóriosmostraramqueosorbitaisHOMOdoligante[(

η

5

-C

5

Me

5

)Al℄

tem umpar de elétronsisolado queage omouma basede Lewis. 11

A oordenação desse

fragmento [(

η

5

-C

5

Me

5

)Al℄ om um omplexo de lantanídeo pode resultar em um

om-plexo om o entro heterobimetálio omposto de um átomo de alumínio e um átomo

lantanídeo. 13

CompostosontendoligaçõesdotipoLn-Ga,[(

η

5

-C

5

Me

5

)

2

Eu(II)-

{

Ga(I)(

η

5

-C

5

Me

5

)

}

2

℄ e[(

η

5

-C

5

Me

5

)

2

(THF)Yb(II)-Ga(I)(

η

5

-C

5

Me

5

)℄,foramsintetizados pelareaçãoentre [(

η

5

-C

5

Me

5

)Ga℄emetaloenosdivalentesdeeurópio[(

η

5

-C

5

Me

5

)

2

Eu℄eitérbio[(

η

5

-C

5

Me

5

)

2

Yb

(THF)

1

−

n

℄ 14

em ondições espeías. Este trabalho demonstrou pela primeria vez a

oordenação de [(

η

5

-C

5

Me

5

)Ga℄ om metais lantanídeos e a primeira ligação

gálio(I)-lantanídeo(II). Os omplexos ontendo entros heterobimetálios Ln-Ga e Ln-Al são

análogos, porém, om o Al, somente omplexos de omposição [(

η

5

-C

5

Me

5

)

2

Ln-Al(

η

5

-C

5

Me

5

)℄(Ln=Eu, Yb) foram obtidos sendo que ligantes adiionaissão oordenados om

omplexos de Ga. Os sítios de oordenação adiionais dos omplexos de Ln-Ga podem

ser um resultado domaior volume atmio do Gae, onseqüentemente, maior distânia

de ligação Ln-Ga.

A ligação Nd-Ga foi investigadaom a síntese doomplexo heterobimetálio [Nd(L

′

)

(N

′′

)(

µ

-I)℄

2

[L

′

=Bu

t

NCH

2

CH

2

{C(NCSiMe

3

CHNBu

t

)};N

′′

=N(SiMe

3

)

2

℄. 15

Esseestudo

apre-sentouaprimeiraligaçãoNd-Gaeaestruturadeumomplexoqueéestáveltantoem

solu-çãoquantoemestadosólido,emontrasteomo[(

η

5

-C

5

Me

5

)

2

Ln-Al(

η

5

-C

5

Me

5

)℄(Ln=Eu,

Yb)que imediatamentedissoiaemsolução. 15

A ligaçãoNd-Ga envolve transferêniade

argade um entromais polarizávelGa(I)para oentroNd(III) gerando umaligaçãode

aráter ovalente, istofaz daligação Nd-Ga uma ligação relativamenteforte.

Tendo omo motivação os resultados experimentais dos omplexos ontendo entros

heterobimetálios, álulos

ab initio

Hartree-Fok restrito de amada aberta (ROHF) 16

e álulos orrelaionados: multionguraional (MCSCF) 10,16

e NEVPT2 1719

foram

utilizadospara eluidarasonguraçõeseletrniasdas espéies heterobimetáliasLnGa

(Ln=La,Ce, Eu, Yb). Foram investigados asongurações eletrnias de menorenergia

das espéies heterobimetálias neutras e isoladas e de vários estados exitados. Foram

obtidas as urvas de energia potenial referentes a ada estado eletrnio estudado e

suas respetivas propriedades espetrosópias: energia de exitação, distânia

harmniasenãoharmniaseaenergiadedissoiaçãoorrigidaparaaenergiadoponto

zeroparaostrês primeirosestadoseletrniosdasespéiesheterobimetáliasobtidospelo

métodoNEVPT2. As propriedadeselétrias,momento de dipoloea polarizabilidade

fo-ram tambémaluladas. Finalmenteas ontribuições dos efeitos relativístios,orreção

massa-veloidade e o efeito Darwin, foram detalhados. Todos os álulos foram feitos

utilizandopseudopotenialrelativístio. 20,21

Os objetivosdesse trabalhoforam: eluidaras estruturas eletrniasdas espéies

he-terobimetáliasLnGa(Ln=La, Ce, Eu, Yb)neutraseemfasegasosa utilizandoométodo

Hartree-Fok,ométodomultionguraionaleNEVPT2; alularaspropriedades

espe-trosópias eelétriasmoleulares pelos diferentes métodos teórios;investigaros efeitos

das orreções relativístiasmassa-veloidadee Darwin nesses sistemas.

AjustiativaemestudarapossíveloordenaçãodoLa([Xe℄5d

1

6s

2

)edoYb([Xe℄4f

14

6s

2

)

ao Ga ([Ar℄3d

10

4s

2

4p

1

) foi o fato de eles serem os elementos extremos da série dos

lan-tanídeos sendo que o La não tem orbital f disponível e o Yb tem orbital f totalmente

preenhido. O interesse noCe ([Xe℄4f

1

5d

1

6s

2

) foi o fato de eleser o primeirolantanídeo

dasérieomorbitalf. AmotivaçãoemestudaraligaçãoEu

−

Gafoiofatode oGapoder doar um elétronpara preenher o orbital f do Eu([Xe℄4f

7

6s

2

/[Xe℄4f

6

5d

1

6s

2

) e assim

for-marumaligaçãoovalente. AlternativamenteoGatambémpoderiareeberdoiselétrons

doEu para estabilizar asua onguraçãoeletrnia semi-preenhida 4s

2

4p

1

Base teória

2.1 Métodos Teórios de Cálulo de Estruturas

Eletr-nias

2.1.1 A aproximação de Born

−

Oppenheimer

OHamiltonianomoleularé desritoda seguinte forma

ˆ

H

mol

=

N

e

X

i

=1

T

i

+

NA

X

A

=1

T

A

+

N

e

X

i

=1

NA

X

A

=1

V

iA

+

N

e

X

i

=1

N

e

X

j>i

V

ij

+

NA

X

A

=1

NB

X

B>A

V

AB

,

(2.1)

o primeiro termo é a energia inétia dos N

e

elétrons, o segundo é a energia inétia dos N

N

núleos atmio, o tereiro é o potenial de atração dos N

e

elétrons om os N

N

núleos, o quarto é o potenial de repulsão do(s) elétron(s) i om o(s) elétron(s) j, o

quinto é o termo de repulsão do(s) núleo(s) A e B. V é o potenial Coulombiano. O

Hamiltonianomoleularatua sobre afunção de onda

ˆ

H

mol

Φ(

~r

i

, ~

R

A

) =

E

mol

Φ(

~r

i

, ~

R

A

)

,

(2.2)

em que

~r

i

representa a oordenada dos N

e

elétronse

R

~

i

a oordenada dos N

A

núleos. Sabe-se que os elétrons movimentam-se numa veloidade muito mais elevada que

os núleos em um sistema sistema moleular. A aproximação de Born

−

Oppenheimer onsiste em separar as oordenadas que representam o movimento eletrnio das que

representam o movimento nulear do Hamiltoniano

H

ˆ

mol

. Para isso, assume-se que a veloidadedos elétronsé muito maior quea veloidade dos núleos. Assim, onsidera-se

de repusão núleo-núleo é parametrizado. Com essa aproximaçãoa equação 2.2torna

(

H

_ele

₊

H

_nucl

_)Φ

_elet

_Φ

_nucl

_{= (}

_E

_ele

₊

_E

_nucl

_)Φ

_elet

_Φ

_nucl

_,

(2.3)

onde

Φ

elet

= Φ

elet

(

~r

i

;

R

~

A

)

,

Φ

nucl

= Φ

elet

(

R

~

A

)

,

(2.4)

são as funções de onda que desrevem o movimento dos elétrons e dos núleos,

res-petivamente.

Φ

elet

depende expliitamente das oordenadas eletrnias mas depende parametriamentedas oordenadas nuleares

16

assim omo a energia

E

elet

=

E

elet

(

R

~

A

)

.

(2.5)

OHamiltonianoeletrnio é

ˆ

H

elet

=

N

e

X

i

=1

T

i

+

N

e

X

i

=1

NA

X

A

=1

V

iA

+

N

e

X

i

=1

N

e

X

j>i

V

ij

.

(2.6)

A energia totalpara um núleo xodeve também inluira repulsãonulear

E

tot

=

E

elet

+

NA

X

A

=1

NB

X

B

=1

V

AB

.

(2.7)

Resolvendooproblemaeletrnioépossívelresolveromovimentonulear,paraisso,omo

os elétronsse movem muito mais rápido queos núleos, é razoável aproximara equação

2.6 para representar as oordenadas eletrnias pelo valor esperado da parte eletrnia

do Hamiltoniano 2.6. Então, obtem-se o Hamiltoniano nulear para o movimento dos

núleos no ampodos elétronsé

H

_nucl

₌

N

A

X

A

=1

T

A

+

D

N

e

X

i

=1

T

i

+

N

e

X

i

=1

N

A

X

A

=1

V

iA

+

N

e

X

i

=1

N

e

X

j>i

V

ij

E

+

N

A

X

A

=1

N

B

X

B>A

V

AB

=

NA

X

A

=1

T

A

+

E

ele

(

R

~

A

) +

NA

X

A

=1

NB

X

B>A

V

AB

=

N

A

X

A

=1

AenergiatotalE

tot

(

R

A

)

provêumpotenialparaomovimentonulear. AfunçãoE

tot

(

R

A

)

onstituiaurva de energiapotenial. Essa função é obtidaresolvendo aequção de

Sh-roedingereletrnia paradiferentes geometriasmoleulares obtendo,emada geometria,

o auto-valor. Os autovalores eas distânias internuleares são oloadas num gráo de

modoa obter aurva de energia potenial.

Finalmente, a soluçãoda equação de Shroedingernulear

H

_nucl

_Φ

_nucl

₌

_E

_Φ

_nucl

(2.9)

desreve a vibração,rotação e translação damoléula.

2.1.2 Método Hartree-Fok

Para sistemas atmiosontendomais de um elétrone sistemasmoleulares

multieletr-nios, a equação de Shroedingernão tem solução exata e, diversos estudos foramfeitos

para seobter soluçõesaproximadas desta equação. 10,16

O Hamiltonianoeletrnio, em unidades atmias (u.a.), para um sistema

multiele-trnio é:

H

_elet

₌

₋

N

X

i

=1

▽

2

r

2

+

N

X

i

=1

M

X

A

=1

Z

A

r

iA

+

N

X

i

=1

N

X

j>i

1

r

ij

.

(2.10)

A equção de Shroedinger, para um sistema multieletrnio,independete dotempoé

H

_elet

_Φ

_elet

₌

_E

_elet

_Φ

_elet

_.

(2.11)

Φ

elet

éaautofunçãoqueéasoluçãoexata daequçãode Shroedinger, Eéoseu autovalor (energia) exato. Como não existe solução exata para sistemas multieletrnios, iremos

onsiderarumsistemadepartíulasindependentes. Ohamiltonianototalparaumsistema

de N elétrons éigual a soma dos hamiltonianos

h

(

i

)

de um elétron

H

₌

N

X

i

=1

h

(

i

)

.

(2.12)

ˆ

h

(

i

)

ψ

j

(

x

i

) =

ǫ

j

ψ

j

(

x

i

)

,

(2.13)

onde

ǫ

j

é a energia orbital,

ψ

(

x

) é um spin-orbital que é representado pelo produto do orbital espaial

φ

(

r

) e da função de spin

α

(

ω

) ou

β

(

ω

) (dependendo das orientações

do spin),

r

e

ω

são as ooredenadas espaiais e de spin, respetivamente, estas duas

oordenadas são esritas emfunção de

x

,

x

=(

r

,

ω

).

A solução da equação integro-diferenial para um sistema de N partíulas

indepen-dentes será igual ao produto das funções de onda de um elétron(orbital). Este método

é onheido omo aproximação orbital. Este onsiste em esrever a função de onda de

N elétrons exata

Φ

elet

omo uma função de onda aproximada

Ψ

HF

. Esta função tem a

forma

Ψ

HF

=

ψ

i

(

x

1

)

ψ

j

(

x

2

)

...ψ

N

(

x

k

)

,

(2.14)

Ψ

HF

é autofunção de

H

H

_Ψ

HF

₌

_E

_Ψ

HF

_,

(2.15)

onde autovalorE éa soma das energias orbitais

E

=

ǫ

i

+

ǫ

j

+

. . .

+

ǫ

k

.

(2.16)

O modelo de partíulas independentes não desreve orretamente a natureza da

dis-tribuição eletrnia e seus estados pois não onsidera a repulsão entre os elétrons. Pelo

prinípiodaexlusãode Pauli, 16

afunçãode ondaquedesreveum ertoestadoquântio

tem queserantissimétria. Nesse asoamelhorfunção deonda quedesreve umsistema

de N elétrons é afunção de ondaesrita na formade um determinantede Slater 16

Ψ

0

=















ψ

i

(

x

1

)

ψ

j

(

x

1)

. . . ψ

k

(

x

1)

ψ

i

(

x

2

)

ψ

j

(

x

2)

. . . ψ

k

(

x

2)

.

.

.

.

.

. .

.

. .

.

.

ψ

i

(

x

N

)

ψ

j

(

x

N)

. . . ψ

k

(

x

N)















.

E0

=

d

x

Ψ

∗

0

H

Ψ

∗

0

R

d

x

Ψ

∗

0

Ψ

∗

0

,

(2.17)

esrevendo essas integrais nanotação de Dira temos:

E

0

=

h

Ψ

0

|

H

|

Ψ

0

i

h

Ψ

0

|

Ψ

0

i

.

(2.18)

Apliando-se a função de onda na forma de um determinante de Slater, maninpulando

adequadamente, obtem-seaexpressãoparaaenergiatotaleletrnia emfunçãodos

spin-orbitais.

E0

=

N

X

i

=1

h

ψ

i

(

x

1

)

|

H

(1)

core

|

ψ

i

(

x

1)

i

+

N

X

i

N

X

j>i

[

h

ψ

i

(

x

1)

ψ

j

(

x

2)

r

−

1

12

ψ

i

(

x

1)

ψ

j

(

x

2)

i

−h

ψ

i

(

x

1)

ψ

j

(

x

2)

r

−

1

12

ψ

i

(

x

2)

ψ

j

(

x

1)

i

]

.

(2.19)

Eliminandoafunçãodespindospin-orbital,onsiderandoqueosspins

α

'se

β

'spodem

ser representados pelomesmooribitalespaial,obtem-seaexpressão paraaenergiatotal

eletrnia dependente apenas da parte radial

φ

(

r

)

. Essa aproximção é onheida omo

Hartree-Fok restrito (RHF) 10,16

e é ideal para estudar sistemas de amada fehada. A

expressão para aenergia total eletrnia, nestaaproximção, é

E

HF

= 2

N

2

X

i

=1

H

_ii

core

+

N

2

X

i

=1

N

2

X

j

=1

(2

J

ij

−

K

ij

)

,

(2.20)

onde

H

_ii

core

=

h

φ

i

(1)

|

H

(1)

core

|

φ

i

(1)

i ≡ h

φ

(1)

| −

1

2

▽

2

₋

X

α

z

α

r

1

α

|

φ

(1)

i

e

J

ij

=

h

φ

i

(1)

φ

j

(2)

|

1

r12

|

φ

i

(1)

φ

j

(2)

i

, K

ij

=

h

φ

i

(1)

φ

j

(2)

|

1

r12

|

φ

j

(1)

φ

i

(2)

i

,

H

core

omoutroelétrondesritopor

φ

j

. OmétodoHFéusadoparaobterosorbitais,iniiando om uma função base, que minimizaa integralvariaionalHF.

Utilizandoo métodovariaionalpara minimizara energia

E0

,obtem-se uma equação

de alto valor onde o operador é não linear. Esta equação é onheida omo equação de

Hartree-Fok (HF). A soluçãodesta equaçãogera os orbitais

φ

i

's ótimos quereproduz a energia total eletrnia mínima. Estes orbitais otimizados são usados para onstruir a

função de onda

Ψ

0

. A equação de HF é

ˆ

F φ

i

(1) =

ǫ

i

φ

i

(1)

,

(2.21)

onde

F

ˆ

é o operador de Fok e

φ

i

(1)

é o o orbital espaial do elétron 1,

φ

i

(1)

≡

φ

i

(

r

1)

. A equação de HFé uma equação integro-diferenial,o operador

F

ˆ

têm a seguinte forma

ˆ

F

(1) = ˆ

H

(1)

core

+

N/

2

X

j

=1

[2 ˆ

J

j

(1)

−

K

ˆ

j

(1)]

,

(2.22)

ˆ

J

eo operadorde Coulomb

ˆ

J

j

(1)

f

(1) =

f

(1)

Z

|

φ

j

(2)

|

2

1

r12

dv2

(2.23)

e

K

ˆ

é ooperador de troa

ˆ

K

j

(1)

f

(1) =

φ

j

(1)

Z

_φ

∗

j

(2)

f

(2)

r12

dv

2

.

(2.24)

Com as devidas operações 16

pode-se obter aexpressão para a energiaorbital

ǫ

i

= ˆ

H

ii

core

+

N/

2

X

j

=1

(2

J

ij

−

K

ij

)

,

(2.25)

e, onsequentemente, aexpressão para a energiade HFtotal

E

HF

= 2

n/

2

X

i

=1

ǫ

i

−

N/

2

X

i

=1

N/

2

X

j

=1

(2

J

ij

−

K

ij

) +

V

N N

,

(2.26)

onde o últimotermo é aoordenada nulear que étratada omo um parâmetro.

Aoexpandir osorbitais

φ

i

'sem uma base

φ

i

=

b

X

s

=1

algébrio. Anovaequaçãodeorrentedessaexpansãoéonheidaomoaequaçãode

HF-Roothan: 10,16

b

X

s

=1

C

si

(

F

rs

−

ǫ S

rs

) = 0

, r

= 1

,

2

,

3

, . . . , b,

(2.28)

F

rs

=

h

χ

r|

F

|

χ

si

, S

rs

=

h

χ

r|

χ

si

,

(2.29)

det

(

F

rs

−

ǫS

rs

) = 0

.

(2.30)

onde2.28 éaequação seulareaequação 2.30éa ondiçãopara asoluçãonão trivialda

equação seular.

A equação de HF-Roothaan é resolvida por um proesso iterativo. Iniialmente, é

dada afunção espaial

φ

i

expandida emuma base

χ

s

. Esse onjuntoiniialde orbitaisé usado para obtero operador de Fok 2.22. Os elementosde matriz (2.29) são alulados

e,emseguida,aequaçãoseular (2.30)éresolvidapara gerarum onjuntoiniialde

ǫ

i

's; esses

ǫ

i

'ssãousadospararesolver2.28paraum ertoonjuntodeoeientes C

si

's. Esses oeientes são utilizados para gerar um novo onjunto de orbitais

φ

i

's que são usados para alular um novo operador

F

ˆ

e assim o proesso se repete. O proesso se repete

até que o valor dos oeientes C

si

's obtidos por uma iteração seja o mesmo, ou o mais próximopossível,do valordos oeientes obtidos poruma iteração anterior.

2.2 Métodos de Correlação Eletrnia

O método de Hartree-Fok trata a repulsão entre os elétrons omo uma média, isso

implia que um elétron não irá sentir a repulsão dos outros elétrons, que ompõem o

sistema atmio ou moleular, individualmente. 10,16

Isso pode ser visto pelas integrais

J e K. Devido a essa limitação, surgem os métodos pós-Hartree-Fok. Métodos teórios

diferentes foram propostos para orrigir as deiênias deorrentes do método

Hartree-Fok; esses métodos são onheidos omo métodos de orrelação eletrnia. 10,16

Os métodos orrelaionados que mantém o prinípio variaional são: 10,16

interação

de ongurações(do inglêsConguration Interation CI), oampode altaonsistênia

eateoriadofunionaldensidade(doinglêsdensityfuntionaltheory DFT).Umaoutra

lasse de métodos, porém, não variaionais, são os métodos perturbativos. 10,16

Esses

métodos são onheidos omo teoria de perturbação de muitos orpos (do inglês many

bodyperturbationtheory). Dentreelesumemespeialfoiutilizadoemnossoestudo,este

é onheido omo teoria de perturbação de valênia de n-elétrons (do inglês n-eletron

valene state perturbation theory NEVPT2). 1719

Outro método que não é variaional

é o método oupled-loster 10,16

CC. A seguir, brevemente, serão tratados os métodos

CI, MCSCF e NEVPT2. 1719

2.2.1 Método de Interação de Congurações CI

O método CI onsiste em ombinar as ongurações eletrnias de modo a obter uma

funçãode ondaomdiversaspossibilidadesde interações. 10,16

Afunçãode ondaé

expan-dida omo uma ombinaçãolinear de determinantes

Φ

i

om os oeienest da expansão determinados para se obter o mínimo de energia. Os orbitais moleulares usados para

onstruir os determinantes de Slater exitados são obtidos pela função de onda HF. A

função de ondaCI

Ψ

CI

éesrita omo

Ψ

CI

=

a0

Φ

HF

+

X

S

a

S

Φ

S

+

X

D

a

D

Φ

D

+

X

T

a

T

Φ

T

+

. . .

=

X

i

a

i

Φ

i

.

(2.31)

Essaexpansãoontémsomasponderadasnosrespetivosoeientesdedeterminantes

que são formados por exitações eletrnias simples (S) duplas (D), triplas (T), et. É

obtidoovaloresperadodoHamilonianoeletrnioomafunçãodeonda

Ψ

CI

,emseguida, é introduzido os multipliadores de Lagrange para se obter o funional que minimiza

a energia variaional. O proedimento variaional onsiste em derivadar a função de

Lagrange em função dos oeientes a

i

's. Através do método variaional é obtido uma equação seular, que é um sistema de equações lineares representado por uma matriz

ujo a diagonalização gera os autovalores e os autovetores do problema. O primeiro

autovalororrespondeaoestadofundamentaleosegundo orrespondeaoprimeiroestado

exitado e assim suessivamente. OmétodoCI explora aorrelação eletrnia dinâmia

por apresentarapenas uma únia onguração eletrniaomo referênia.

2.2.2 Método Multionguraional SCF

terminantes de Slater serem reotimizados faz om que esse método desreva om maior

eiênia a orrelação estátiado quea orrelação dinâmia. Aoonsiderar apenas uma

onguração, o métodoMCSCF oinide om ométodoHartree-Fok.

Um dos problemas do método MCSCF é seleionar quaissão as ongurações de

re-ferênia neessária para obter as propriedades de interesse. Um modo de seleionar as

ongurações eletrnias é onheido omo espaço ativo ompleto (do inglês omplete

ative spae CAS). 10

Neste método as ongurações são obtidas partiionando os

orbi-taismoleulares em um espaço ativo e um espaço inativo. Osorbitais inativostem 2ou

0 elétrons, ou seja, são duplamente oupados ou vazios. Os orbitais moleulares ativos

podem ter oupaçõessimples, duplas ou zero, e estas diversas possibilidades de

ongu-rações são exploradas para se obter a interação de ongurações. Para representar este

métodoCAS utilizamosumanotaçãoomum [n,m℄-CASSCF,onde nindiaonúmerode

elétrons distribuídosem todos osm possíveis orbitaismoleulares.

Um modode ontrolar a quantidade de ongurações no métodoCAS é restringir o

espaço CAS, este método é onheido omo RASSCF (do inglês restrited ative spae

self-onsistent eld). 22

Neste método os orbitais moleulares são distribuídos em três

regiões,RAS1,RAS2,RAS3,adaumatendorestriçõesnonúmerode oupações

(exita-ções) permitidas. OespaçoRAS1 pode fazerexitações simplesouduplas para oRAS3.

ORAS2ésimilaraoCAS,elepodefazerqualquer tipodeexitaçõesinternas,alémdisso,

elepode fazer exitações simplesou duplaspara o RAS3.

2.2.3 Método Multi-referênial MRCI

O método CI onsidera apenas a formação das diferentes ongurações eletrnias

(di-ferentes determinantes de Slater) a partir de exitações eletrnias provenientes de um

únio determinante. 10

Isso signia ter omo referênia, paratais exitações eletrnias,

apenas a função de onda Hartree-Fok.

Uma função de onda MCSCF, om pouas ongurações, pode ser usada omo

refe-rêniaparageraroutrasonguraçõeseletrnias. Essasnovasonguraçõessãosomadas

(expandidas)juntamenteomasonguraçõesbase(quesão referênias)eapenasosseus

oeientes são otimizados. Nesse aso,os orbitaisdosdeterminantes formadospelas

vá-rias referênias não são reotimizados, ou seja, a expansão multi-referenial explora uma

orrelação dinâmia, equivalente ao CI. Porém, omo essa expansão é feita om

om muitas ongurações. O método MRCI, assim omo o método MCSCF, desreve

melhor aorrelação estátiado que aorrelação dinâmia.

Essemétodoéonheidoomointeraçãodeonguraçõesdemuitasreferênias,MRCI

(do inglês Multi-referene Conguration Interation). A função de onda MRCI numa

largaesala(muitasonguraçõesnoMCSCF) pode gerarfunçõesde ondaauradas,que

éequivalentea função de ondamultionguraionalenvolvendo muitas ongurações. O

métodoMRCI é um métodoque exigeum altousto omputaional.

2.2.4 Método NEVPT2

OmétodoNEVPT2 18,19

faz uso dométodomultionguraional 10,16

(orrelaçãoestátia)

e dométodo de perturbação de segunda ordem MP2 10,16

(orrelaçãodinâmia)para

elu-idar aonguraçãoeletrnia de sistemasmultieletrnioseexplorar aorrelaçãotanto

estátia quanto dinâmia om eiênia e menor usto omputaional, uma vez que o

método multionguraional pode gerar um alto usto omputaionalquando se deseja

um erto resultado dependente de um númeromuito grandede ongurações.

Para efetuar álulos NEVPT2 são utilizados pouas ongurações eletrnias que

são geradas noespaço ativo (CAS) e tratadaspelométodoMCSCF, as outras

possibili-dades de ongurações são geradas pelas ongurações otimizadas (função de onda om

osdevidos orbitaiseoeientes otimizados)que são tratadasporteoriade perturbação.

Embora o método perturbativo envolva orrelação dinâmia, o fato de as ongurações

eletrniasseremgeradaspormuitasreferênias (muitasongurações)peloqualos

orbi-taisque ompõemos determinantes de Slater são otimizados,o tratamentoperturbativo

é feito e o resultado é de melhor qualidade do que o método perturbativo baseado em

uma únia referênia. O híbrido de orrelação estátia mais dinâmia, que é a idéia do

métodoNEVPT2, émelhorqueométodomultionguraionalompouasongurações

eletrnias.

O objetivo do métodoNEVPT2 é apresentar uma teoria de perturbação baseada na

função de onda CAS-CI de ordem zero em que a interação entre os elétrons no espaço

ativo é onsiderada também em um outro espaço om as devidas propriedades. 10,16

A

funçãode ondaCAS-CI éesritaomoum produto antisimetrizadodeelétronsde aroço

(n

c

)e de valênia(n

v

),

|

Ψ

0

_m

i

=

|

Φ

c

Ψ

v

m

i

,

(2.32)

ˆ

P

_CAS

H

ˆ

_P

ˆ

_CAS

_|

_Ψ

0

onde

P

ˆ

CAS

é oprojetordo espaçoCAS-CI.

A função de onda perturbada terá a forma

|

Φ

−

k

l

Ψ

v

µ

+

k

i

, onde

Φ

−

k

l

é um produto de orbitais om n

c

−

k elétrons inativos (de aroço ou virtual) e

Ψ

v

+

k

µ

é a função de onda multionguraional de valênia om n

v

+

k elétrons. O número k representa o número de elétrons promovidos do espaço inativo para o espaço ativo: de ordem -2

≤

k

≤

2. É requerido que

|

Φ

−

k

l

Ψ

v

µ

+

k

i

não interaja via os elétronsativosom uma função de onda de outroespaçoquetem amesmaordemde perturbação,então étiradoovaloresperadodo

operador Hamiltoniano

H

ˆ

na ondição,

h

Φ

−

k

l

Ψ

v

+

k

µ

|

H

ˆ

|

Φ

−

k

l

Ψ

v

+

k

v

i

= 0

, para µ

6

=

v

(2.34)

A função de onda

|

Φ

−

k

l

Ψ

v

µ

+

k

i

pode ser esrita omo uma ombinação de determinantes om apartede aroçoiguala

Φ

−

k

l

etodasaspossíveisdistribuiçãode n

v

+

kelétronsno espaço ativo,os determinantes surgemdo espaçoCAS-CI om n

v

+

k elétrons.

2.3 Métodos Relativístios

2.3.1 Equação Quântia Relativístia em Quatro Componentes

Quando um orpo marosópio possui uma veloidade próxima à veloidade da luz, a

meânia Newtoniana não é mais apliada a esse fenmeno. Nessas ondições o orpo

tem que ser desrito por equações que sejam invariantes om relação as transformadas

de Lorentz 23

e, om isso, um novo onjunto de equações dinâmias é formulado: essa

nova teoria é onheida omo a teoria da relatividade espeial. 23

O mesmo fenmeno é

observadoquandoumorpomirosópiosemoveaumaveloidadepróximaàveloidade

da luz, para isso a equação de Shroedinger, que desreve partíulas mirosópias, não

é mais apliada,euma nova teoria tem queser formulada,peloquala equação quântia

seja relativistiamenteorreta. Daí surge a meânia quântia relativístia. 710

AequaçãoquântiarelativistiamenteorretaéonheidaomoaequaçãodeDira. 7,8

Essa equação é uma equação relativistiamenteorreta e é invariante às transformações

de Lorentz.

Partindoda dinâmiarelativístia,temos aenergia total ralativístia

E

=

±

c

q

p

2

ondeéaveloidadedaluznováuo,

p

x

, p

y

e p

z

são osomponentedomomentolineare m

0

éa massade repouso. Emmeânia quântia essaequação éreesrita introduzindo o

operadorHamiltonianoH=i

~

∂

∂t

paraaenergiatotalEe,usandoasregrasdequantizações annias, os operadores p

ξ

=

−

i

~

∂

∂ξ

(

ξ

=

x, y, z

) para as omponentes artesianas do

momento linear. Podemos esrever a igualdade de operadores

i

~

∂

∂t

=

±

c

s

−

~

2

∂

2

∂

2

x

+

∂

2

∂

2

y

+

∂

2

∂

2

z

+

m

0

c

2

.

(2.36)

Asdiuldadesinerentesàpresençadaraízquadradadasomadosquadradosdos

ope-radoresdifereniaismomentolinear tornaaequação 2.36 desinteressante paraapliações

prátias. Para eliminaressa raíz, Dira 7

propósum métodoque linearizaaequação 2.36

pela onstrução de um produto notável para a soma do termos quadrátios que formam

o argumento daraiz quadrada esrita nolado direito dessa equação.

Alinearizaçãodoargumentodoladodireitodaraíz quadradapresentenoladodireito

da equação 2.35 pode ser realizada, om a preservação da simetria entre os termos p

x

, p

y

, p

z

em

0

c

2

,se a igualdade

p

2

_x

+

p

2

_y

+

p

2

_z

+

m

2

₀

c

2

=

α

x

p

x

+

α

y

p

y

+

α

z

p

z

+

βm0c

2

2

,

(2.37)

for satisfeita para um onjunto de oeientes

α

x

,

α

y

,

α

z

e

β

. Se osoeientes tiverem as propriedades.

[

α

x

, α

y

]

+

=

α

x

α

y

+

α

y

α

x

= 0 [

α

x

, β

]

+

=

α

x

β

+

βα

y

= 0

[

α

y

, α

z

]

+

=

α

y

α

z

+

α

z

α

y

= 0 [

α

y

, β

]

+

=

α

y

β

+

βα

y

= 0

(2.38)

[

α

z

, α

x

]

+

=

α

z

α

x

+

α

x

α

z

= 0 [

α

z

, β

]

+

=

α

z

β

+

βα

z

= 0

e

α

_x

2

=

α

2

_y

=

α

_z

2

=

β

2

= 1

.

(2.39)

Substituindoaequação 2.37(na formade operadores) notermodentro daraiz quadrada

da equação 2.36 e ainda apliando a igualdade de operadores resultante sobre a função

de onda

Ψ(

r, t

)

temos aequação de Dira 7,8

dependente dotempo

−

i

~

_cα

_{· ▽}

₊

_βm

₀

_c

2

₊

_V

₍

_r

₎

Ψ(

r, t

) =

i

~

∂

e, se o potenialV for independente dotempo, temos a equação de Diraindependente

dotempo 8

−

i

~

_cα

_{· ▽}

₊

_βm

₀

_c

2

₊

_V

₍

_r

₎

Ψ(

r

) =

E

Ψ(

r

)

.

(2.41)

Ambas equações(dependentee independentedotempo)são própriasparauma partíula

de spin 1/2. A função de onda relativístia

Ψ(

r, t

)

é uma função de onda em quatro

ompontentes epode ser esritada seguinte maneira

Ψ(

r, t

) =

Ψ

L

(

r, t

)

Ψ

S

(

r, t

)

onde

Ψ

L

(

r, t

) =

Ψ

Lα

(

r, t

)

Ψ

Lβ

(

r, t

)

,

Ψ

S

(

r, t

) =

Ψ

Sα

(

r, t

)

Ψ

Sβ

(

r, t

)

.

(2.42)

Os índies L e S são provenientes do inglês large e small, respetivamente. Essa

notação referenia a omponente eletrnia (omponente grande large) da função de

onda ea omponenteque desreve a partepositrnia(omponentepequena small)da

funação de onda relativístia. 810

A álgebra denida pelas relações 2.39 e 2.38 não é satisfeita por nenhum onjunto

de números omplexos em geral. Uma solução pode se enontrada, entretanto, para

α

x

,

α

y

,

α

z

e

β

formando um onjunto de quatro matrizesquadradas, de dimensão 4

×

4, linearmenteindependentes

α

x

=

0

σ

x

σ

x

0

!

, α

y

=

0

σ

y

σ

y

0

!

, α

z

=

0

σ

z

σ

z

0

!

, β

=

I

0

0

−

I

!

,

(2.43)

onde I é uma matriz unidade e asmatrizes

σ

's são as matrizesde Pauli 810

σ

x

=

0 1

1 0

!

, σ

y

=

0

−

i

i

0

!

, σ

z

=

1

0

0

−

1

!

.

(2.44)

Com esse proedimento a linearizaçãodo Hamiltonianoésatisfeita. As matrizes

α

's e

β

são onheidas omo as matrizesde Dira. 810

2.3.2 O Hamiltoniano Relativístio Multi-eletrnio

para desrever o sistema multieletrnio ou moleular relativístio. O Hamiltonianode

Dira paraum sistemamulti-eletrnio 24 é

ˆ

H

=

n

X

i

=1

ˆ

h

i

_D

+

n

X

i>j

1

r

ij

=

n

X

i

=1

(

c

α

ˆ

i

·

p

ˆ

i

+

βmc

2

+

V

(

r

i

)) +

n

X

i>j

1

r

ij

,

(2.45)

onde o primeirotermo é a energia inétia do elétron i, V

(

r

i

)

é potenialde atração do elétroniom onúleoeoúltimotermoéopotenialde atraçãoelétron-elétron. Esse

Ha-miltonianoéonheidoomooHamiltonianoDira-Coulomb, 24

ˆ

H

DC

. EsseHamiltoniano nãoéinvarianteomrelaçãoastransformadasdeLorentz,devidoaofatodopotenialnão

estarrepresentado porumaformarelativistiamenteorreta. Parasanar esserestrição, é

neessárioreorreraumoutrateoria,onheidaomeletrodinâmiaquântia (Quantum

Eletrodynamis" QED) 10,24

.

O operadorde Coulomb mostraadependênia dainteração eletrostátiaapenas om

a distânia, não om o tempo. Isso não éorreto quando a relatividadeé onsiderada, 10

impliaqueainteraçãode repulsãoentreduaspartíulasoorreminstantaneamente. Isso

viola um dos prinípios fundamentais da relatividade que é nada pode se mover mais

rápidamente que a veloidade da luz. A interação relativístia requer uma desrição,

eletrdinâmiaquântia, que envolve troa de fótons entre duas partíulas de arga. Os

fótons viajam na veloidade da luz e arregam a informação equivalente ao operador

de interação lássio, Coulomb. Para atender a eletrodinâmia quântia, é neessário

expandir o termo de atração/repulsão em ordem da onstante de estrutura na,

α

≈

1

c

. Retendo termos que ontribuem até a ordem

1

c

2

, gera o operador de Coulomb mais o termo de interação de Breit

10,24

ˆ

g

ij

B

=

1

r

ij

−

1

r

ij

α

i

·

α

j

+

(

α

i

×

r

ij

)(

α

j

×

r

ij

)

r

2

ij

,

(2.46)

otermoforadoparênteseéooperadorCoulombiano,oprimeirotermodentrodoparêntese

é o operador de Gaunt e o tereiro é o operador de Breit.

α

's são as matrizes de Dira