Análise sísmica usando transformada de Curvelet

’

Universidade Federal do Rio Grande do Norte Centro de Ciˆencias Exatas e da Terra

Departamento de F´ısica Te´orica e Experimental Programa de P´os-Gradua¸c˜ao em F´ısica

TESE DE DOUTORADO

AN ´

ALISE S´ISMICA USANDO TRANSFORMADA

CURVELET

Michelli Silva de Oliveira

Orientador: Prof. Dr. Liacir dos Santos Lucena

Dedico este trabalho

Agradecimentos

A Deus acima de tudo.

Ao meu orientador, Professor Doutor Liacir dos Santos Lucena, por permitir trabalhar ao seu lado, pelo apoio e incentivo no desenvolvimento deste trabalho.

Ao Professor Doutor Gilberto Corso e ao Professor Doutor Edcarlos Alves pelas con-tribui¸c˜oes dadas a esta tese.

Ao Professor e amigo Marcos Vin´ıcius por estar sempre disposto a ajudar.

Ao Conselho nacional de desenvolvimento Cient´ıfico e Tecnol´ogico CNPq pelo suporte financeiro concedido.

Ao meu marido Vladimi, companheiro e melhor amigo, por fazer parte de mais uma etapa da minha vida, sempre me confortando com seu carinho, amor e paciˆencia.

`

A minha filha Ana Beatriz, agrade¸co por vocˆe ter existido durante o desenvolvimento deste trabalho, vocˆe foi minha fonte de inspira¸c˜ao. Obrigada por estar sempre animada e sorrindo para mim mesmo com toda a minha ausˆencia.

`

A minha m˜ae Neuza, irm˜a M´arcia e minha madrinha Maria Diamantina pelo incen-tivo, mesmo `a distˆancia nunca deixaram de estar presentes, sempre me confortando com palavras encorajadoras fortalecendo meus momentos mais dif´ıceis.

A todos meus amigos, em especial minhas amigas Cl´audia Cruz e Nivˆania que muito me fortaleceram.

Resumo

A explora¸c˜ao petrol´ıfera ´e uma das atividades mais complexas e de dif´ıcil execu¸c˜ao na ind´ustria do petr´oleo e tamb´em ´e umas de suas tarefas mais importantes. Devido aos elevados custos dos m´etodos diretos usados para localiza¸c˜ao e avalia¸c˜ao das jazidas de petr´oleo, tais como a perfura¸c˜ao de po¸cos explorat´orios para a medi¸c˜ao de propriedades

in situ, m´etodos indiretos s˜ao utilizados com esta finalidade. O principal destes m´etodos ´e o da sondagem s´ısmica. Neste processo de explora¸c˜ao, ondas s´ısmicas geradas por explos˜oes ou por vibradores, propagam-se no subsolo e ap´os serem espalhadas pelas het-erogeneidades das estruturas geol´ogicas retornam `a superf´ıcie onde s˜ao coletadas para constru¸c˜ao dos sismogramas ou imagens s´ısmicas. No entanto, os sismogramas contˆem, al´em das informa¸c˜oes sobre as estruturas do subsolo, uma grande quantidade de ru´ıdo, sendo o principal deles o chamado ru´ıdo de rolamento superficial (”ground roll”ou on-das de Rayleigh). A atenua¸c˜ao desses ru´ıdos ´e essencial para uma boa interpreta¸c˜ao dos dados e sinais s´ısmicos. A an´alise dos sismogramas pode ser feita utilizando-se diversos tipos de transformadas espectrais que levam o sinal s´ısmico para o espa¸co das frequˆencias (Transformada de Fourier) ou para o espa¸co tempo-frequˆencia (Transformada Wavelet), onde costuma ser mais simples atenuar ou remover os ru´ıdos de uma forma cir´urgica. Isto permite que, ao levar o sinal s´ısmico de volta ao espa¸co original, o sinal represente apenas as informa¸c˜oes sobre as estruturas geol´ogicas de interesse. Por outro lado, a transformada

superficiais ou ao longo de curvas. A an´alisecurvelet mapeia o espa¸co das frequˆencias em diferentes escalas e em setores angulares, de modo que se pode identificar as regi˜oes deste espa¸co dominadas pelo ru´ıdo presente no sinal. Remover os coeficientes referentes a essas regi˜oes ´e remover o ru´ıdo do sinal. Assim, nesta tese implementamos e aplicamos a an´alise

curvelet para remover o ru´ıdo de rolamento superficial dos sinais s´ısmicos. Testamos este m´etodo tanto para um sismograma sint´etico quanto para um sismograma real e obtivemos uma ´otima atenua¸c˜ao do ru´ıdo em ambos os casos.

Abstract

Sum´

ario

Agradecimentos ii

Resumo iv

Abstract vi

Introdu¸c˜ao 1

1 A Prospec¸c˜ao de Petr´oleo e a Explora¸c˜ao S´ısmica 5

1.1 A Sondagem S´ısmica e as Ondas S´ısmicas . . . 7

1.1.1 Ondas de Corpo ou Ondas de Volume . . . 9

1.1.2 Ondas de Superf´ıcie . . . 10

1.1.3 Velocidade de Propaga¸c˜ao das Ondas S´ısmicas . . . 12

1.2 M´etodos S´ısmicos e a Sondagem S´ısmica . . . 13

1.3 Aquisi¸c˜ao de Dados S´ısmicos . . . 15

1.4 O Ruido de Rolamento Superficial ou Ruido Ground Roll . . . 17

1.5 T´ecnicas de Filtragem . . . 18

2 Sinais Temporais e Transformadas 20 2.1 Introdu¸c˜ao . . . 20

2.2 A An´alise de Fourier . . . 21

2.3 A Transformada de Fourier-Gabor . . . 24

2.4 A Transformada em Ondaletas . . . 27

2.4.1 Transformada Cont´ınua em Ondaletas . . . 28

3 A An´alise Curvelet 34

3.1 Introdu¸c˜ao . . . 34

3.2 Defini¸c˜ao da Transformada Curvelet . . . 36

3.3 Propriedades da Transformada Curvelet. . . 40

3.3.1 Tight frame . . . 40

3.3.2 Parˆametro de escala parab´olico . . . 40

3.3.3 Comportamento oscilat´orio . . . 41

3.3.4 Momentos nulos . . . 41

3.4 Transformada CurveletDiscreta . . . 42

3.4.1 Defini¸c˜ao . . . 42

3.4.2 Coroniza¸c˜ao discreta . . . 42

3.5 As fun¸c˜oes curvelets. . . 45

4 Remo¸c˜ao de Ru´ıdo S´ısmico usando An´alise Curvelet 47 4.1 Introdu¸c˜ao . . . 47

4.2 An´alise Curvelete a decomposi¸c˜ao do sinal . . . 49

4.3 Identifica¸c˜ao e remo¸c˜ao do ru´ıdo . . . 51

4.4 Reconstru¸c˜ao do sinal . . . 53

4.5 Procedimento para remo¸c˜ao de ru´ıdo de rolamento superficial . . . 53

5 An´alise de dados reais usando transformada curvelet 67 5.1 Introdu¸c˜ao . . . 67

5.2 O dado s´ısmico real versus dado sint´etico . . . 68

5.3 A extra¸c˜ao do ru´ıdo de rolamento superficial do dado s´ısmico real . . . 70

5.4 Supress˜ao do ru´ıdo de rolamento superficial: an´alise em ondaletas versus an´alise curvelet . . . 83

6 Conclus˜oes e Perspectivas 86

Lista de Figuras

1.1 Esquema descritivo da propaga¸c˜ao de uma onda prim´aria ou lon-gitudinal. Figura reproduzida/adaptada da p´agina de internet http://www.tjhsst.edu/_∼jlafever/wanimate/Wave Properties2.html [2]. . . 9 1.2 Esquema descritivo da propaga¸c˜ao de uma onda secund´aria ou de

cisalhamento. Figura reproduzida/adaptada da p´agina de internet http://www.tjhsst.edu/_∼jlafever/wanimate/Wave P roperties2.html[2]. . . 10 1.3 Esquema descritivo da propaga¸c˜ao de uma onda de

Rayleigh ou onda R. Figura reproduzida/adaptada da p´agina de internet http://www.tjhsst.edu/_∼jlafever/wanimate/Wave P roperties2.html[2]. . . 11

1.4 Esquema descritivo da propaga¸c˜ao de uma onda

de Love ou onda L. Figura reproduzida/adaptada da p´agina de internet http://www.tjhsst.edu/_∼jlafever/wanimate/Wave P roperties2.html[2]. . . 12 1.5 Distribui¸c˜ao de velocidades comumente encontradas na prospec¸c˜ao de

petr´oleo. Figura reproduzida de THOMAS[1]. . . 13 1.6 Esquema da aquisi¸c˜ao de dados s´ısmicos terrestres e mar´ıtimos. Figura

reproduzida de OLIVEIRA[3]. . . 15 1.7 Representa¸c˜ao da forma¸c˜ao de um tra¸co s´ısmico pelas reflex˜oes de um

pulso pelas camadas sedimentares do subsolo. Figura reproduzida de OLIVEIRA[3]. . . 16 1.8 Exemplo de sismograma captado por um conjunto de geofones durante uma

2.1 a) Exemplo de (a) um sinal temporal estacion´ario e sua representa¸c˜ao no espa¸co das frequˆencias obtida pela an´alise de Fourier do sinal; (b) um sinal temporal n˜ao estacion´ario e sua representa¸c˜ao no espa¸co das frequˆencias obtida pela an´alise de Fourier. Figura adaptada da p´agina de internet http://astro.if.ufrgs.br/med/imagens/fourier.htm [9]. . . 23 2.2 Representa¸c˜ao simb´olica da caixa de Heisemberg no plano

tempo-frequˆencia. A energia do “´atomo” de Gabor est´a distribu´ıda nesta caixa centrada em (u, ξ) e com larguras σt no tempo e σω na frequˆencia. Figura

reproduzida de LEITE[15]. . . 26 2.3 Representa¸c˜ao de uma fam´ılia de ondaletas cont´ınuas (figura (a)) e de seu

espectro de Fourier (figura (b)). Figura reproduzida de MALLAT[16]. . . . 29 2.4 Esquema ilustrativo da divis˜ao do espa¸co tempo-frequˆencia (a) para a

transformada de Fourier-Gabor; e (b) para a transformada em ondaletas. . 31 3.1 Decomposi¸c˜ao di´adica do espa¸co de frequˆencia. Na figura (a) temos

esta decomposi¸c˜ao em termos da janela radial; na figura (b) temos esta decomposi¸c˜ao em termo das janelas radial e angular; j´a na figura (c) temos que a ´area sombreada ´e a fatia do espa¸co de Fourier onde as

curvelets tem seu suporte definido. Figura adaptada da p´agina de internet http://www.math.washington.edu/ hart/uwss.pdf [29]. . . 38 3.2 Decomposi¸c˜ao di´adica do espa¸co de frequˆencia da transformada curvelet

discreta. A regi˜ao sombreada representa uma fatia t´ıpica deste espa¸co localizada pela janela ˜Uj,l. . . 44

4.2 Distribui¸c˜ao de padr˜oes para conjuntos de zonas angulares selecionados na escala 2. Na parte superior da figura temos os ˆangulos selecionados nessa escala e na parte inferior temos a reconstru¸c˜ao parcial do sinal para esses ˆangulos nessa escala. . . 56 4.3 Distribui¸c˜ao de energia para os diferentes ˆangulos da escala 2. . . 57 4.4 Conjunto de ˆangulos da escala 2 cujos coeficientes foram selecionados para

a reconstru¸c˜ao de parte do sinal indicado na figura 4.1.b. . . 58 4.5 Distribui¸c˜ao de padr˜oes para conjuntos de zonas angulares selecionados na

escala 3. . . 59 4.6 Distribui¸c˜ao de energia para os diferentes ˆangulos da escala 3. . . 60 4.7 Conjunto de ˆangulos da escala 3 cujos coeficientes foram selecionados para

a reconstru¸c˜ao de parte do sinal indicado na figura 4.1.b. . . 60 4.8 Distribui¸c˜ao de padr˜oes para conjuntos de zonas angulares selecionados na

escala 4. . . 61 4.9 Distribui¸c˜ao de energia para os diferentes ˆangulos da escala 4. . . 62 4.10 Conjunto de ˆangulos da escala 4 cujos coeficientes foram selecionados para

a reconstru¸c˜ao de parte do sinal indicado na figura 4.1.b. . . 63 4.11 Distribui¸c˜ao de padr˜oes para conjuntos de zonas angulares selecionados na

escala 5. . . 64 4.12 Distribui¸c˜ao de energia para os diferentes ˆangulos da escala 5. . . 65 4.13 Conjunto de ˆangulos da escala 5 cujos coeficientes foram selecionados para

a reconstru¸c˜ao de parte do sinal indicado na figura 4.1.b. . . 66 5.1 Figura comparativa entre sismogramas. Na figura (a) temos um exemplo

de sismograma sint´etico; e na figura (b) temos um exemplo de sismograma real. Nos dois sinais, o ru´ıdo de rolamento superficial aparece com uma estrutura triangular macrosc´opica. . . 69 5.2 Figura contendo: (a) o dado original real a ser analisado; (b) o dado

5.3 Distribui¸c˜ao de padr˜oes para conjuntos de zonas angulares selecionados na escala 2. Na parte superior da figura temos os ˆangulos selecionados nessa escala e na parte inferior temos a reconstru¸c˜ao parcial do sinal para esses ˆangulos nessa escala. . . 72 5.4 Distribui¸c˜ao de energia para os diferentes ˆangulos da escala 2. . . 73 5.5 Conjunto de ˆangulos da escala 2 (marcados em vermelho) cujos coeficientes

foram selecionados para a reconstru¸c˜ao do sinal s´ısmico real. . . 74 5.6 Distribui¸c˜ao de padr˜oes para conjuntos de zonas angulares selecionados na

escala 3. Na parte superior da figura temos os ˆangulos selecionados nessa escala e na parte inferior temos a reconstru¸c˜ao parcial do sinal para esses ˆangulos nessa escala. . . 75 5.7 Distribui¸c˜ao de energia para os diferentes ˆangulos da escala 3. . . 76 5.8 Conjunto de ˆangulos da escala 3 (marcados em vermelho) cujos coeficientes

foram selecionados para a reconstru¸c˜ao do sinal s´ısmico real. . . 77 5.9 Distribui¸c˜ao de padr˜oes para conjuntos de zonas angulares selecionados na

escala 4. Na parte superior da figura temos os ˆangulos selecionados (mar-cados em vermelho) nessa escala e na parte inferior temos a reconstru¸c˜ao parcial do sinal para os ˆangulos correspondentes nessa escala. . . 78 5.10 Distribui¸c˜ao de energia para os diferentes ˆangulos da escala 4. . . 79 5.11 Conjunto de ˆangulos da escala 4 (marcados em vermelho) cujos coeficientes

foram selecionados para a reconstru¸c˜ao do sinal s´ısmico real. . . 80 5.12 Distribui¸c˜ao de padr˜oes para conjuntos de zonas angulares selecionados na

escala 5. Na parte superior da figura temos os ˆangulos selecionados (mar-cados em vermelho) nessa escala e na parte inferior temos a reconstru¸c˜ao parcial do sinal para os ˆangulos correspondentes nessa escala. . . 81 5.13 Distribui¸c˜ao de energia para os diferentes ˆangulos da escala 5. . . 82 5.14 Conjunto de ˆangulos da escala 5 (marcados em vermelho) cujos coeficientes

Lista de Tabelas

5.1 Balan¸co de energia (em porcentagem) para as escalas 2 _≤ j _≤ 5. O GR representa a energia do ru´ıdo de rolamento superficial; e RW a energia das ondas refletidas. . . 80 5.2 Distribui¸c˜ao de energia (em porcentagem) para as escalas 1 _≤ j _≤ 5. O

Introdu¸c˜

ao

A explora¸c˜ao petrol´ıfera ´e uma das tarefas mais complicadas e de dif´ıcil execu¸c˜ao na ind´ustria do petr´oleo e tamb´em ´e umas das tarefas mais importantes desta ind´ustria.

A tarefa de localizar jazidas de petr´oleo e de avaliar o seu potencial de produ¸c˜ao re-presenta um intrigante e complicado problema na ´area de Ciˆencia e Tecnologia, pois as jazidas e reservat´orios naturais de petr´oleo e g´as natural s˜ao encontrados em estruturas geol´ogicas que constituem sistemas de alta complexidade, com heterogeneidades em to-das as escalas e com uma enorme variedade em suas caracter´ısticas b´asicas, tais como permeabilidade e porosidade.

As dificuldades na localiza¸c˜ao das jazidas s˜ao aumentadas tamb´em pelo elevado n´ıvel de incerteza advindo da quantidade reduzida de informa¸c˜oes sobre o subsolo e suas estru-turas geol´ogicas.

A alternativa para a busca por jazidas de petr´oleo, diante da impossibilidade de per-fura¸c˜ao de um grande n´umero de po¸cos explorat´orios, ´e o uso de m´etodos indiretos.

O principal m´etodo indireto ´e o da explora¸c˜ao s´ısmica. Este m´etodo consiste em gerar ondas s´ısmica que se propaguem no subsolo. Essas ondas s˜ao geradas por explos˜oes para o caso de pesquisa continental e por canh˜oes de ar comprimido para a explora¸c˜ao no mar e, em se propagando no subsolo, experimentam os fenˆomenos de espalhamento, refra¸c˜ao, difra¸c˜ao, reflex˜ao e outros, pelas diversas camadas e estruturas geol´ogicas do subsolo. Uma parte destas ondas retorna `a superf´ıcie trazendo informa¸c˜oes sobre as camadas e estruturas geol´ogicas do interior da Terra.

Na verdade, o problema de descobrir as propriedades f´ısicas e as estruturas geol´ogicas do subsolo atrav´es dos sinais s´ısmicos captados na superf´ıcie por geofones ou hidrofones ´e chamado de espalhamento inverso. Este problema ´e de dif´ıcil solu¸c˜ao e pertence a uma classe de problemas denominada problemas mal postos. Estes problemas aparecem em diversas ´areas da ciˆencia, mas ´e ainda mais complicado de se resolver no caso da prospec¸c˜ao s´ısmica, pois o volume da regi˜ao espalhadora das ondas s´ısmicas, no caso o subsolo, ´e muito grande, h´a falta de conhecimento sobre as velocidades de propaga¸c˜ao das ondas s´ısmicas nas diferentes estruturas e regi˜oes do subolo e tamb´em devido ao acentuado grau de desordem do subsolo.

Apesar da enorme dificuldade em se interpretar adequadamente as imagens obtidas para o subsolo a partir de dados s´ısmicos, essas s˜ao as mais importantes fontes de in-forma¸c˜ao sobre grandes volumes de subsuperf´ıcie e permitem, se bem interpretadas, a delimita¸c˜ao apropriada dos reservat´orios e jazidas de petr´oleo. Na verdade, as imagens s´ısmicas s˜ao o meio mais difundido e preciso para guiar a interpola¸c˜ao e a extrapola¸c˜ao de dados colhidos em po¸cos explorat´orios. Essas imagens, se bem interpretadas, fornecem as informa¸c˜oes mais confi´aveis sobre grandes quantidades de subestruturas da crosta ter-restre.

geralmente existem nas transi¸c˜oes entre camadas geol´ogicas e, a partir destes dados, s˜ao constru´ıdas as imagens das camadas e estruturas geol´ogicas. No entanto, os dados s´ısmicos ou sismogramas cont´em, al´em das informa¸c˜oes sobre as estruturas do subsolo, uma grande quantidade de ru´ıdo e a atenua¸c˜ao desses ru´ıdos ´e essencial para uma boa interpreta¸c˜ao desses dados. A an´alise dos sismogramas pode ser feita utilizando-se diversos tipos de transformadas espectrais. Nesta tese de doutorado vamos descrever e/ou estudar os prin-cipais tipos de an´alise que podem ser utilizados no estudo de sinais s´ısmicos para remover os ru´ıdos e recuperar as informa¸c˜oes sobre as estruturas do subsolo, bem como entender as limita¸c˜oes desses m´etodos de an´alise e implementar o m´etodo de an´alise curvelet para a remo¸c˜ao de ru´ıdos em sismogramas de explora¸c˜ao s´ısmica.

Assim, para descrevermos os trabalhos realizados no decorrer de nosso doutoramento, esta tese de doutorado foi estruturada em cinco cap´ıtulos principais e um cap´ıtulo de conclus˜ao.

No primeiro cap´ıtulo vamos falar um pouco sobre a prospec¸c˜ao de petr´oleo e en-tender como funciona o m´etodo de sondagem s´ısmica, como s˜ao geradas e captadas as ondas s´ısmicas que permitem a forma¸c˜ao dos sismogramas e entender como o m´etodo de sondagem s´ısmica ´e utilizado para o estudo das propriedades geol´ogicas do subsolo e para a busca de jazidas de petr´oleo.

No cap´ıtulo 2 desta tese, vamos estudar e descrever as principais transformadas es-pectrais utilizadas para se estudar sinais temporais e/ou atenuar ru´ıdos presentes nesses sinais, desde a transformada de Fourier at´e a transformada wavelet (transformada em ondaletas). Tamb´em vamos perceber as limita¸c˜oes dessas transformadas e a necessidade de um outro tipo de transformada para se estudar/analisar sinais s´ısmicos.

No cap´ıtulo 3 vamos definir e estudar a transformada curvelet e entender esta an´alise e suas propriedades.

J´a no cap´ıtulo 5, descrevemos o procedimento e os resultados da an´alise curvelet

aplicada a sinais s´ısmicos e discutiremos os resultados obtidos em compara¸c˜ao com os resultados de outros m´etodos de an´alise.

Cap´ıtulo 1

A Prospec¸c˜

ao de Petr´

oleo e a

Explora¸c˜

ao S´ısmica

A atual sociedade humana ´e extremamente dependente dos combust´ıveis fosse´ıs, como o petr´oleo e o g´as natural, com isto a ind´ustria do petr´oleo ´e uma das mais importantes e significativas do mercado mundial. Das tarefas realizadas, a explora¸c˜ao petrol´ıfera ´e uma das mais complicadas e de dif´ıcil execu¸c˜ao e tamb´em ´e umas das mais importantes desta ind´ustria.

Localizar jazidas de petr´oleo sob a crosta terrestre, quer seja em terras continentais ou em terreno submarino, e avaliar seu potencial de produ¸c˜ao, representa um intrigante e complicado problema na ´area de Ciˆencia e Tecnologia, pois esses reservat´orios naturais s˜ao encontrados em estruturas geol´ogicas que constituem sistemas de alta complexidade. As dificuldades na localiza¸c˜ao das jazidas de petr´oleo s˜ao enormes e s˜ao aumentadas, ainda mais, pelo elevado n´ıvel de incerteza advindo da quantidade reduzida de informa¸c˜oes sobre o subsolo e suas estruturas geol´ogicas.

jazidas de petr´oleo ´e bem pequeno e o volume de subsolo do qual se tem dados coletados diretamente, comparado ao volume total do campo petrol´ıfero, corresponde a uma fra¸c˜ao praticamente desprez´ıvel ( 10−12_).

A perfura¸c˜ao de po¸cos explorat´orios ´e utilizada para confirmar a existˆencia de uma jazida de petr´oleo em uma regi˜ao, onde os m´etodos indiretos indicaram uma grande probabilidade de existˆencia de ´oleo. Assim, a pesquisa com po¸co explorat´orio ir´a confirmar a existˆencia dessa jazida e avaliar seu potencial de produ¸c˜ao de petr´oleo.

Os m´etodos indiretos s˜ao, diante da impossibilidade de perfura¸c˜ao de um grande n´umero de po¸cos explorat´orios, a melhor alternativa para a busca por jazidas de petr´oleo. Estes m´etodos indiretos tem custos bastante moderados e, mesmo sujeitos a inter-preta¸c˜oes e visualiza¸c˜oes, fornecem informa¸c˜oes detalhadas do subsolo e de suas estruturas geol´ogicas.

O principal m´etodo indireto usado no estudo das estruturas geol´ogicas do subsolo ter-restre e na prospec¸c˜ao de petr´oleo ´e aexplora¸c˜ao s´ısmica ousondagem s´ısmica. Este m´etodo consiste em gerar ondas s´ısmicas que se propaguem no subsolo. Estas ondas s˜ao geradas por explos˜oes para o caso de pesquisa continental e por canh˜oes de ar comprimido para a explora¸c˜ao no mar e, em se propagando no subsolo, experimentam os fenˆomenos de espalhamento, refra¸c˜ao, difra¸c˜ao, reflex˜ao e outros, pelas diversas camadas e estruturas geol´ogicas do subsolo. Uma parte dessas ondas retorna `a superf´ıcie trazendo informa¸c˜oes sobre as camadas e estruturas geol´ogicas do interior da Terra.

Vale ressaltar que o m´etodo de sondagem s´ısmica tamb´em ´e bastante utilizado no estudo das estruturas geol´ogicas das placas tectˆonicas para estudar regi˜oes onde ocorreram abalos s´ısmicos e, por exemplo, calcular a probabilidade de novos abalos. Embora, o foco do estudo da sondagem s´ısmica, nesta tese, seja a prospec¸c˜ao de petr´oleo, os m´etodos e ferramentas aqui estudados e desenvolvidos tamb´em podem ser aplicados em estudos sismol´ogicos.

Nas se¸c˜oes deste primeiro cap´ıtulo vamos estudar e entender como funciona o m´etodo de sondagem s´ısmica e como este m´etodo ´e utilizado para o estudo das propriedades geol´ogicas do subsolo e para a busca de jazidas de petr´oleo. Com este entendimento inicial sobre sondagem s´ısmica, estaremos aptos a, nos pr´oximos cap´ıtulos, estudar as principais ferramentas matem´aticas utilizadas na an´alise e interpreta¸c˜ao dos dados obtidos nas sondagens s´ısmicas.

Devemos ainda ressaltar que este ´e um cap´ıtulo b´asico que trata da descri¸c˜ao geral da prospec¸c˜ao de petr´oleo e da sondagem s´ısmica usada para localizar e delimitar jazidas de petr´oleo e g´as natural, portanto as descri¸c˜oes apresentadas aqui s˜ao de conhecimento geral da engenharia de petr´oleo. A principal referˆencia utilizada na constru¸c˜ao deste cap´ıtulo foi o livro do THOMAS[1]. Outras referˆencias que se fizerem necess´arias ser˜ao citadas no decorrer do cap´ıtulo.

1.1

A Sondagem S´ısmica e as Ondas S´ısmicas

A sondagem s´ısmica ou explora¸c˜ao s´ısmica ´e um m´etodo indireto de explora¸c˜ao do subsolo terrestre que faz uso de aparelhos e t´ecnicas especiais para estudar e carac-terizar o subsolo. Este m´etodo tem sido comumente utilizado pelo fato de ser capaz de cobrir grandes ´areas e, ao mesmo tempo, ser economicamente vi´avel, permitindo assim, uma observa¸c˜ao cautelosa e barata do subsolo terrestre, sendo largamente empregado na localiza¸c˜ao de jazidas de petr´oleo e g´as natural e tamb´em no estudo e detec¸c˜ao de falhas geol´ogicas.

mecˆanica que transportam energia de deforma¸c˜ao el´astica no meio em que foram geradas. A velocidade de propaga¸c˜ao destas ondas depende das propriedades el´asticas e da densi-dade do meio em que elas se propagam. ´E a sua reflex˜ao e refra¸c˜ao entre as camadas do subsolo que nos permite inferir as propriedades do subsolo e de suas camadas e estud´a-las. Para entendermos as ondas s´ısmicas e seu efeito sobre o solo e subsolo devemos lem-brar que quando se aplica uma for¸ca sobre a superf´ıcie de um corpo, pode-se modificar sua forma e/ou seu volume. A elasticidade ´e a propriedade de um corpo resistir a essa deforma¸c˜ao e de retornar `a sua forma e/ou volume iniciais depois que a for¸ca causadora da deforma¸c˜ao cessa.

A teoria da elasticidade estuda as rela¸c˜oes entre as for¸cas e as mudan¸cas na forma e volume dos corpos, com base nos conceitos de tens˜ao (stress) e deforma¸c˜ao (strain). Segundo a lei de Hooke, para pequenas deforma¸c˜oes, as que ocorrem em rochas podem ser consideradas como perfeitamente el´asticas e como as ondas s´ısmicas geradas na explora¸c˜ao s´ısmica e prospec¸c˜ao de petr´oleo s˜ao causadoras de pequenas deforma¸c˜oes (da ordem de 10−6_{% a 10}−3_{%), as estudadas na sondagem s´ısmica podem ser consideradas deforma¸c˜oes} el´asticas.

A tens˜ao sobre uma superf´ıcie ´e definida como a for¸ca por unidade de ´area na superf´ıcie. Quando esta tens˜ao ´e perpendicular `a ´area em que atua, esta tens˜ao ´e denominadatens˜ao normal. E quando ela ´e tangencial `a ´area em que atua, ´e denominadatens˜ao cisalhante outens˜ao de cisalhamento. As tens˜oes que atuam em um corpo ou superf´ıcie podem causar sua deforma¸c˜ao.

A deforma¸c˜ao (ou strain) de um corpo ´e a mudan¸ca na forma e/ou volume de um corpo quando este est´a sujeito a a¸c˜ao de uma tens˜ao. A deforma¸c˜ao normal, ou seja, a deforma¸c˜ao de um corpo devido `a uma tens˜ao normal modifica o volume do corpo, mas n˜ao modifica a forma do corpo. J´a a deforma¸c˜ao cisalhante modifica a forma mas n˜ao modifica o volume do corpo.

1.1.1

Ondas de Corpo ou Ondas de Volume

Asondas de corpoouondas de volumes˜ao as que se propagam atrav´es do interior da Terra. Elas apresentam dire¸c˜oes radiais a partir do ponto onde foram geradas com desvios devidos `as varia¸c˜oes de densidade do meio.

As ondas de volume s˜ao respons´aveis pelos primeiros tremores sentidos durante um terremoto e podem ser classificadas em dois tipos: as ondas prim´arias (ondas P); e as ondas secund´arias (ondas S).

Asondas prim´ariasouondas Pouondas compressionaiss˜ao ondas longitudinais, ou seja, s˜ao ondas nas quais o deslocamento e a vibra¸c˜ao das part´ıculas do meio ocorre na mesma dire¸c˜ao da propaga¸c˜ao da energia da onda. As ondas longitudinais s˜ao mais velozes que as ondas S e, por isto, s˜ao os primeiros eventos a serem detectados ap´os um abalo s´ısmico. Na figura 1.1 ´e mostrado um esquema descritivo da propaga¸c˜ao de uma onda longitudinal ou prim´aria, onde podemos ver que o deslocamento das part´ıculas do meio ocorre na dire¸c˜ao de propaga¸c˜ao da onda.

Asondas secund´ariasouondas Souondas de cisalhamentos˜ao ondas transver-sais, ou seja, s˜ao ondas de volume nas quais o movimento das part´ıculas do meio ocorre na dire¸c˜ao transversal `a dire¸c˜ao de propaga¸c˜ao da onda. As ondas S se propagam apenas em corpos s´olidos, pois os fluidos n˜ao suportam for¸cas de cisalhamento. Sua velocidade ´e, em um dado meio, menor que a velocidade das ondas P, mas sua amplitude ´e v´arias vezes maior. Na figura 1.2 ´e mostrado um esquema descritivo da propaga¸c˜ao de uma onda de cisalhamento ou secund´aria, onde podemos ver que o deslocamento das part´ıculas do meio ocorre na dire¸c˜ao perpendicular `a propaga¸c˜ao da onda.

Figura 1.2: Esquema descritivo da propaga¸c˜ao de uma onda secund´aria ou de cisalhamento. Figura reproduzida/adaptada da p´agina de internet http://www.tjhsst.edu/_∼jlafever/wanimate/Wave Properties2.html [2].

1.1.2

Ondas de Superf´ıcie

Existem dois tipos de ondas de superf´ıcie: as ondas de Rayleigh e as ondas de Love.

As ondas de Rayleigh ou ondas R s˜ao o resultado da superposi¸c˜ao de ondas P e S. A existˆencia destas ondas foi prevista por Lord Rayleigh em 1985 e s˜ao ondas que provocam vibra¸c˜oes no sentido contr´ario `a propaga¸c˜ao da onda, causando um movimento de rolamento (como uma ´orbita el´ıptica) em sentido contr´ario ao movimento da onda. Esta onda tamb´em ´e denominada onda de rolamento superficial e sua amplitude diminui rapidamente com a profundidade.

A figura 1.3 mostra um esquema descritivo para uma onda R. Observe que a onda se propaga em uma dire¸c˜ao e o movimento dos elementos de volume do meio descrevem um rolamento cuja intensidade diminui rapidamente com a profundidade.

Figura 1.3: Esquema descritivo da propaga¸c˜ao de uma onda de Rayleigh ou onda R. Figura reproduzida/adaptada da p´agina de internet http://www.tjhsst.edu/_∼jlafever/wanimate/Wave Properties2.html [2].

Como veremos, ainda nesse cap´ıtulo, o principal tipo de ru´ıdo presente nos sinais s´ısmicos obtidos em sondagens s´ısmicas e chamado de ru´ıdo de rolamento superficial, ´e devido a ondas do tipo Rayleigh.

e sua energia ´e obrigada a permanecer nas camadas superiores da Terra devido ao fato de ocorrer por reflex˜ao interna total. Essas ondas s˜ao o resultado da superposi¸c˜ao de duas ondas S, s˜ao ligeiramente mais r´apidas que as ondas de Rayleigh e s˜ao muito destrutivas. Na figura 1.4 ´e mostrado um esquema descritivo da propaga¸c˜ao de uma onda Love. Observe que os elementos de volume do meio de propaga¸c˜ao sofrem um cisalhamento no plano horizontal cuja intensidade diminui com a profundidade.

Figura 1.4: Esquema descritivo da propaga¸c˜ao de uma onda de Love ou onda L. Figura reproduzida/adaptada da p´agina de internet http://www.tjhsst.edu/_∼jlafever/wanimate/Wave Properties2.html [2].

1.1.3

Velocidade de Propaga¸c˜

ao das Ondas S´ısmicas

A velocidade de propaga¸c˜ao das ondas s´ısmicas ´e fun¸c˜ao da densidade e das constantes el´asticas do meio. Consequentemente, depende da constitui¸c˜ao mineral´ogica da rocha, do grau de cimenta¸c˜ao, dos est´agios de compacta¸c˜ao, da porosidade, do conte´udo e da satura¸c˜ao de fluidos, al´em de depender da temperatura e da presen¸ca de microfraturas na rocha.

no geral, usada para caracterizar uma determinada rocha, ou seja, as velocidades calcu-ladas ou estimadas para as ondas s´ısmicas numa regi˜ao do subsolo podem determinar a composi¸c˜ao das rochas daquela subsuperf´ıcie.

Na figura 1.5 ilustramos a distribui¸c˜ao de velocidades comumente encontradas na prospec¸c˜ao de petr´oleo. Como o m´etodo da sondagem s´ısmica permite o c´alculo destas velocidades, pode-se estimar os parˆametros das rochas a partir do conhecimento das ve-locidades.

Figura 1.5: Distribui¸c˜ao de velocidades comumente encontradas na prospec¸c˜ao de petr´oleo. Figura reproduzida de THOMAS[1].

1.2

M´

etodos S´ısmicos e a Sondagem S´ısmica

terrestre e retornam `a superf´ıcie.

H´a dois principais m´etodos s´ısmicos: o m´etodo s´ısmico de refra¸c˜ao, que registra so-mente as ondas refratadas com ˆangulo cr´ıtico e que tem grande aplica¸c˜ao na ´area de sismologia e, no entanto, tem aplica¸c˜ao restrita na ´area de prospec¸c˜ao de petr´oleo; e o m´etodo s´ısmico de reflex˜ao que registra as ondas refletidas pelas descontinuidades do interior do subsolo e ´e largamente utilizado na ´area de prospec¸c˜ao de petr´oleo.

Destes m´etodos vamos estudar apenas o segundo, discutindo o estritamente necess´ario para um melhor entendimento dos cap´ıtulos seguintes e do trabalho original desta tese.

Para o levantamento s´ısmico de uma ´area do subsolo come¸ca-se com a gera¸c˜ao de ondas s´ısmicas artificiais na superf´ıcie terrestre, onde se faz uso de dinamite ou de vibradores com queda de peso, ou no mar, onde se faz uso de canh˜oes de ar comprimido. As ondas s´ısmicas assim geradas tem um pulso caracter´ıstico conhecido como assinatura da fonte e s˜ao captadas ap´os se refletirem e/ou refratarem em cada uma das descontinuidades e camadas do interior do subsolo por onde viajam.

Os receptores utilizados para captar e registrar as reflex˜oes s˜ao, basicamente, de dois tipos: os eletromagn´eticos (geofones) que s˜ao utilizados para registros em terra; e os de press˜ao (hidrofones) usados para levantamentos em ´aguas oceˆanicas.

Os geofones s˜ao compostos por uma bobina suspensa dentro de um campo magn´etico gerado por um potente im˜a acondicionado por um inv´olucro imperm´eavel. O geofone ´e firmemente cravado na superf´ıcie da Terra e quando uma onda s´ısmica o atinge, o movimento relativo entre a bobina e o im˜a gera uma corrente el´etrica induzida que ´e proporcional `a v´arios fatores, inclusive `a amplitude da onda incidente.

Os hidrofones utilizam-se de cristais piezoel´etricos que geram uma corrente el´etrica proporcional `a varia¸c˜ao da press˜ao produzida pelas ondas s´ısmicas na ´agua.

1.3

Aquisi¸c˜

ao de Dados S´ısmicos

Utilizando-se uma fonte artificial de ondas s´ısmicas, como dinamite para os casos em terra e ar comprimido para os casos em mar, s˜ao produzidas ondas que ir˜ao se propagar no interior da crosta terrestre.

Para todos os fins pr´aticos, a propaga¸c˜ao das ondas s´ısmicas ´e regida pelas mesmas leis da ´otica geom´etrica. Assim, quando uma frente de onda incide sobre uma interface separando duas rochas com velocidades e densidades diferentes, parte da energia da onda ´e refletida e retorna `a superf´ıcie e parte ´e refratada para o meio inferior e continua sua propaga¸c˜ao.

A quantidade de energia que ´e refletida depende do contraste de impedˆancia das rochas. ´

E poss´ıvel simular a resposta s´ısmica de um pacote sedimentar ou tra¸co s´ısmico (tamb´em chamado de sismograma sint´etico) a partir do conhecimento de velocidades e densidades das rochas que o comp˜oe e da assinatura da fonte.

Usando um conjunto de geofones (ou hidrofones) convenientemente distribu´ıdos e orde-nados, como esquematizados na figura 1.6, pode-se captar as ondas refletidas nas diversas camadas e descontinuidades do subsolo.

Figura 1.6: Esquema da aquisi¸c˜ao de dados s´ısmicos terrestres e mar´ıtimos. Figura re-produzida de OLIVEIRA[3].

forma do pulso incidente. Os geofones ou hidrofones registram as superposi¸c˜oes das am-plitudes s´ısmicas ou reflex˜oes individuais que variam de valores negativos a positivos e s˜ao armazenados em um tra¸co s´ısmico. Cada tra¸co s´ısmico ´e apresentado como uma s´erie temporal de amplitudes que tem sua ´area positiva preenchida.

Na figura 1.7[1] est´a ilustrada a forma¸c˜ao de um sismograma atrav´es das reflex˜oes de um pulso pelas camadas sedimentares do subsolo.

Figura 1.7: Representa¸c˜ao da forma¸c˜ao de um tra¸co s´ısmico pelas reflex˜oes de um pulso pelas camadas sedimentares do subsolo. Figura reproduzida de OLIVEIRA[3].

Na figura 1.7.A tem-se a representa¸c˜ao das camadas sedimentares do subsolo. Em 1.7.B vˆe-se as inomogeneidades ou impedˆancias ac´usticas dessas camadas sedimentares. Em 1.7.C temos o pulso incidente e a reflectividade das diversas camadas. Na figura 1.7.D temos as reflex˜oes individuais de cada uma das camadas sedimentares, e finalmente, em 1.7.E tem-se o tra¸co s´ısmico final registrado em apenas um geofone.

1.4

O Ruido de Rolamento Superficial ou Ruido

Ground Roll

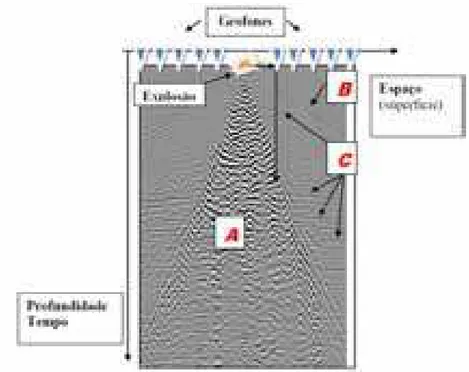
Os registros obtidos por um conjunto de geofones ou hidrofones das reflex˜oes da onda nas camadas de subsuperf´ıcies formam um sismograma. Na figura 1.8[3] ´e mostrado um sismograma constru´ıdo a partir dos dados de um conjunto de geofones durante uma sondagem s´ısmica.

Figura 1.8: Exemplo de sismograma captado por um conjunto de geofones durante uma sondagem s´ısmica. Figura reproduzida de OLIVEIRA[3].

Estes sinais indesejados que aparecem nos sismogramas s˜ao chamados de ru´ıdos. O principal sinal indesejado nos sismogramas de sondagem s´ısmica s˜ao sinais coerentes de-vidos a ondas de superf´ıcie, do tipo das ondas de Rayleigh, que contribuem com cerca de dois ter¸cos de toda a energia s´ısmica captada pelo geofone durante essas sondagens[5]. Esses sinais indesejados s˜ao chamados de ru´ıdo de rolamento superficial ou ru´ıdo

ground roll.

O ru´ıdo de rolamento superficial est´a sempre presente nos sismogramas de sondagem s´ısmica e, no exemplo da figura 1.8, ele aparece geometricamente com a forma de um cone central marcado porA. A forma de cone para o registro do ru´ıdo de rolamento superficial vem do posicionamento dos geofones em rela¸c˜ao ao ponto de tiro (ponto de energia onde s˜ao geradas as ondas s´ısmicas para o levantamento s´ısmico).

As principais caracter´ısticas do ru´ıdo de rolamento superficial s˜ao: grandes amplitudes, maiores que as do sinal refletido nas camadas do subsolo; baixa velocidade; e concentra¸c˜ao de energia em frequˆencias baixas[5].

Por serem ondas do tipo Rayleigh, as ondas do ru´ıdo de rolamento superficial se limitam a uma propaga¸c˜ao pr´oxima `a superf´ıcie da Terra sem transmitir energia para o seu interior. E, ent˜ao, as amplitudes que constituem oground rolln˜ao contˆem informa¸c˜oes relacionadas com as interfaces de reflex˜oes e ir˜ao se sobrepor `as amplitudes (menores) que foram refletidas pelas estruturas geol´ogicas do interior da terra.

1.5

T´

ecnicas de Filtragem

O ru´ıdo de rolamento superficial e outros sinais indesejados precisam ser removidos do sismograma para que se possa estudar as estruturas presentes e, com isto, estudar as estruturas do interior da terra.

ser aplicados ou no dom´ınio da frequˆencia ou no dom´ınio do tempo. Os filtros passa-alta e passa banda, por exemplo, s˜ao aplicados no dom´ınio da frequˆencia e s˜ao incapazes de separar as grandes amplitudes do ru´ıdo de rolamento superficial das amplitudes das reflex˜oes. Isto ocorre porque, para uma mesma banda de frequˆencia, as amplitudes do ru´ıdo e do sinal de interesse se sobrep˜oe fortemente[5]. Por isto, usando-se este tipo de filtragem, frequˆencias baixas presentes nas reflex˜oes s˜ao perdidas.

Por outro lado, os filtros baseados na transformada f ₋ k s˜ao bastante utilizados para remover os ru´ıdos de rolamento superficial[7], por´em estas transformadas tˆem a desvantagem de gerar distor¸c˜oes nos sinais das reflex˜oes devido ao fato das amplitudes do

ground roll serem bem maiores que as amplitudes das reflex˜oes.

Cap´ıtulo 2

Sinais Temporais e Transformadas

2.1

Introdu¸c˜

ao

Toda grandeza f´ısica pode ser representada por uma fun¸c˜ao f(t) que d´a o seu compor-tamento com o tempo. A princ´ıpio, conhecendo-se a fun¸c˜ao que representa uma grandeza f´ısica, conhecemos o comportamento desta grandeza em qualquer tempo e nos referimos a esta fun¸c˜ao como sendo osinal temporalda grandeza f´ısica. Entretanto, o sinal tempo-ral n˜ao fornece toda a informa¸c˜ao que precisamos para estudar e analisar a grandeza f´ısica. Em muitos casos ´e necess´ario realizar uma transforma¸c˜ao matem´atica sobre a fun¸c˜ao para que esta possa ser analisada em um dom´ınio diferente do dom´ınio temporal e, desta forma, possamos obter outras informa¸c˜oes relevantes e importantes sobre a grandeza f´ısica.

As transforma¸c˜oes mais utilizadas para se analisar sinais temporais s˜ao as chamadas transformadas espectrais, que levam o sinal temporal para o espa¸co das frequˆencias e permitem recuperar as frequˆencias presentes no sinal temporal.

Por outro lado, os sinais temporais obtidos no mundo real a partir do estudo de alguma grandeza f´ısica de interesse est˜ao sempre contaminados. Por exemplo, em um sismograma coletado para se estudar a estrutura interna de uma ´area da crosta terrestre h´a v´arios outros sinais misturados que atrapalham o estudo do sismograma por n˜ao pertencerem ao fenˆomeno de interesse. Chamamos estes sinais esp´urios ou indesejados de ru´ıdos.

recuperar o sinal desejado. Estes procedimentos de atenua¸c˜ao de ru´ıdos s˜ao conhecidos como filtragem [8].

Assim, procedimentos matem´aticos tˆem sido propostos para atenuar estes sinais que n˜ao pertencem ao fenˆomeno observado e que n˜ao s˜ao de interesse do pesquisador.

As transformadas espectrais est˜ao entre os filtros mais utilizados para remo¸c˜ao de ru´ıdos na explora¸c˜ao do petr´oleo. Nestes casos, ´e feita uma transformada sobre o sinal levando-o para o espa¸co das frequˆencias e as frequˆencias dos sinais indesejados s˜ao aten-uadas ou removidas e, ao se realizar a transformada inversa para levar o sinal de volta ao espa¸co temporal, o sinal desejado deve, em teoria, estar livre dos ru´ıdos.

Neste cap´ıtulo vamos estudar brevemente as principais transformadas espectrais uti-lizadas para se estudar sinais temporais e/ou atenuar ru´ıdos presentes nesses sinais, bem como perceber as limita¸c˜oes destas transformadas.

2.2

A An´

alise de Fourier

Em 1807, o f´ısico e matem´atico francˆes Jean-Baptiste Joseph Fourier desenvolveu um m´etodo de an´alise de fun¸c˜oes peri´odicas em s´eries trigonom´etricas convergentes que pas-saram a se chamar S´eries de Fourier.

Levando-se em considera¸c˜ao que senos e cossenos s˜ao fun¸c˜oes peri´odicas, ele propˆos que qualquer fun¸c˜ao peri´odica pode ser decomposta em termos destas fun¸c˜oes base num som´at´orio infinito. Assim, uma fun¸c˜ao f(t) peri´odica pode ser escrita em termos de fun¸c˜oes senoidais (senos e cossenos) como:

f(t) = a0+

∞

∑

n=1

[

ancos

(

nπt L

)

+bnsen

(

nπt L

)]

(2.1) onde os coeficientes da expans˜ao,an ebn, s˜ao determinado a partir da rela¸c˜ao de

ortogo-nalidade das fun¸c˜oes base da expans˜ao (senos e cossenos) e s˜ao dados por:

an=

1 L ∫ L −L f(t) cos ( nπt L )

bn = 1 L ∫ L −L f(t)sen ( nπt L )

dt, n = 1,2,3, . . . (2.3) Com o sinal, f(t), escrito como uma s´erie de Fourier na forma da equa¸c˜ao (2.1), podemos analis´a-lo mais facilmente no dom´ınio temporal e, tamb´em, transform´a-lo para outros dom´ınios para obter e estudar informa¸c˜oes que n˜ao est˜ao dispon´ıveis neste dom´ınio. Usando a Transformada de Fourier (TF), que ´e uma transformada integral que leva uma fun¸c˜ao peri´odica em suas componentes no dom´ınio das frequˆencias, podemos trans-formar o sinal temporal em uma fun¸c˜ao que est´a representada no dom´ınio das frequˆencias a partir da integral:

ˆ

f(ω) =F[f](ω) =

∫ ∞

−∞

f(t)e−iωtdt (2.4) Por outro lado, conhecendo-se o espectro f(ω) de um sinal temporal, ´e poss´ıvel obter este sinal utilizando a transformada inversa de Fourier, dada por:

f(t) = f[F](t) = 1 2π

∫ ∞

−∞

ˆ

f(ω)eiωtdt (2.5) Diz-se ent˜ao que f(t) e ˆf(ω) formam um par de transformadas, indicando isto por f(t) _↔ fˆ(ω). Ou seja, de um sinal temporal podemos obter o sinal no espa¸co das frequˆencias e vice-versa.

O fato das fun¸c˜oes de base da s´erie de Fourier ou, equivalentemente, da integral da transformada de Fourier (equa¸c˜ao (2.4)), se estender de menos a mais infinito, torna esta transformada adequada para se estudar um sinal estacion´ario. Assim, no estudo de sinais estacion´arios, utilizar um filtro do tipo Fourier ´e uma boa escolha para decompor o sinal do dom´ınio do tempo em sinais harmˆonicos simples para o dom´ınio das frequˆencias. Neste novo dom´ınio pode-se analisar o sinal e atenuar as frequˆencias dos sinais indesejados e, em tese, ao voltar ao dom´ınio temporal pela transformada de Fourier inversa, recupera-se o sinal sem a presen¸ca de ru´ıdos e sinais indesejados.

no espa¸co das frequˆencias. J´a na figura 2.1.b temos a fun¸c˜ao f(t) = cos(ν0) dentro de uma caixa limitada no intervalo [₋b/2, b/2] e sua respectiva representa¸c˜ao no espa¸co das frequˆencias, o que j´a nos mostra a limita¸c˜ao da an´alise de Fourier para analisar sinais n˜ao-estacion´arios.

Figura 2.1: a) Exemplo de (a) um sinal temporal estacion´ario e sua representa¸c˜ao no espa¸co das frequˆencias obtida pela an´alise de Fourier do sinal; (b) um sinal temporal n˜ao estacion´ario e sua representa¸c˜ao no espa¸co das frequˆencias obtida pela an´alise de Fourier. Figura adaptada da p´agina de internet http://astro.if.ufrgs.br/med/imagens/fourier.htm [9].

Apesar de ser extremamente ´util e importante no estudo de sinais estacion´arios, a transformada de Fourier n˜ao pode “visualizar” ou recuperar uma informa¸c˜ao localizada em um tempo espec´ıfico. Ou seja, a transformada de Fourier ´e ineficaz para fornecer a localiza¸c˜ao de um evento no sinal, tal como mudan¸ca de frequˆencia, descontinuidades, singularidades e fenˆomenos transientes em geral.

algum trecho extremamente ru´ıdoso ou que contenha pontos anˆomalos, o processamento de todo o sinal ficar´a comprometido. E, no caso dos sinais s´ısmicos da prospec¸c˜ao de petr´oleo, as partes mais importante dos sinais costumam ser os eventos pontuais ou sin-gularidades presentes no sinal temporal.

Como ferramentas de an´alise alternativas `a Tranformada de Fourier no estudo de sinais n˜ao-estacion´arios ou que contenham descontinuidades pontuais, surgiram outras transfor-madas espectrais que visam incorporar `a an´alise de um sinal a possibilidade de localizar um evento no sinal ao mesmo tempo que leva o sinal temporal do espa¸co dos tempos para o espa¸co das frequˆencias. Vamos estudar brevemente algumas destas transformadas nas se¸c˜oes seguintes deste cap´ıtulo.

2.3

A Transformada de Fourier-Gabor

Para cobrir a deficiˆencia da Transformada de Fourier em estudar sinais n˜ao esta-cion´arios e interessado em representar sinais n˜ao-estaesta-cion´arios em problemas de comu-nica¸c˜ao usando fun¸c˜oes de base oscilat´orias no plano tempo-frequˆencia, o f´ısico Dennis Gabor[11] desenvolveu um m´etodo que divide o sinal temporal original em partes e realiza uma an´alise de Fourier em cada parte em separado.

Este m´etodo ´e denominado Transformada Fourier-Gabor ou Transformada de Fourier Janelada (em inglˆes Short Time Fourier Transform).

A transformada de Fourier Janelada usa uma fun¸c˜ao auxiliar no integrando da trans-formada de Fourier que divide o sinal temporal em partes, atrav´es de janelas de formato gaussiano, e faz a transformada de Fourier em cada parte do sinal, permitindo obter informa¸c˜oes sobre quais frequˆencias ocorrem em cada parte do sinal.

Matematicamente temos que a transformada de Fourier-Gabor relaciona o sinal tem-poralf(t) com a fun¸c˜ao de an´alisegu,ξ(t), conhecida como´atomo de Gabor, pela equa¸c˜ao:

f(u, ξ) =

∫ ∞

−∞

f(t)g_u,ξ∗ (t)dt (2.6)

gu,ξ(t) =g(t−u)eiξt. (2.7)

Desta forma, a transfomada de Fourier-Gabor ´e dada por:

ˆ

f(u, ξ) =

∫ ∞

−∞

f(t)g(t₋u)e−iξtdt (2.8) Sendo assim, a transformada de Fourier janelada est´a definida no dom´ınio tempo frequˆencia (ω, t). E a energia de gu,ξ ´e concentrada na vizinhan¸ca de u em um intervalo

de tamanhoσt e sua transfomada de Fourier ´e uma transla¸c˜ao porξ:

ˆ

gu,ξ(ω) = ˆg(ω−ξ)e−iu(ω−ξ) . (2.9)

A transformada inversa de Fourier Gabor ´e dada por:

f(t) = 1 2π ∫ ∞ −∞ ∫ ∞ −∞ ˆ

f(u, ξ)g(ξ₋t)eiξu_{dudξ . (2.10)}

A fun¸c˜ao gu,ξ(t), da transformada de Fourier-Gabor, ´e delimitada por uma regi˜ao

e, tamb´em por isto, conhecida como uma fun¸c˜ao janelada. A energia de gu,ξ(t) est´a

concentrada na vizinhan¸ca de u em um intervalo de tamanho σt. E a energia de ˆgu,ξ(t) ´e

localizada na frequˆenciaξ em um intervalo de tamanho σω.

No plano tempo-frequˆencia (t, ω), o espalhamento da energia do “´atomo”gu,ξ ´e

repre-sentado simbolicamente pela “caixa de Heisemberg”, como ilustrado na figura 2.2. Esta “caixa” est´a centrada em (u, ξ) e tem largura σt no tempo e σω na frequˆencia.

A janela usada na transformada de Fourier janelada ´e de tamanho fixo. Isto torna invi´avel a an´alise simultˆanea das componentes de altas frequˆencias e de baixas frequˆencias do sinal, pois h´a um limite, advindo do Princ´ıpio da Incerteza de Heisemberg, para a localiza¸c˜ao tempo-frequˆencia do sinal. A variˆancia temporalσte a variˆancia na frequˆencia

σω do sinal temporal f(t) satisfazem a equa¸c˜ao:

σtσω ≥

1

4π (2.11)

Sendo assim, uma “boa” localiza¸c˜ao na frequˆencia (σω pequeno) implica em n˜ao se

Figura 2.2: Representa¸c˜ao simb´olica da caixa de Heisemberg no plano tempo-frequˆencia. A energia do “´atomo” de Gabor est´a distribu´ıda nesta caixa centrada em (u, ξ) e com largurasσt no tempo e σω na frequˆencia. Figura reproduzida de LEITE[15].

tempo-frequˆencia est´a representada geometricamente pela dimens˜ao do retˆanguloσt×σω.

Do princ´ıpio da incerteza temos que a ´area desse retˆangulo mostrado na figura 2.2, ´e

≥1/4π.

Na transformada de Fourier janelada, uma vez escolhida uma janela do dom´ınio do tempo, esta mesma janela tem de ser usada em todas as frequˆencias. Assim, ´e poss´ıvel se analisar sinais que apresentam componentes de frequˆencias altas ou sinais que apresentam componentes de frequˆencias baixa, mas n˜ao sinais que apresentam ambas componentes, como os sinais geof´ısicos.

2.4

A Transformada em Ondaletas

A Transformada Wavelet ou Transformada em Ondaletas tamb´em surgiu da limita¸c˜ao da an´alise de Fourier em localizar um evento em um sinal temporal e da limita¸c˜ao da transformada de Fourier-Gabor em estudar sinais compostos, simultaneamente, por bandas de altas e de baixas frequˆencias.

Devido `a esta limita¸c˜ao da transformada de Fourier janelada em analisar sinais n˜ao estacion´arios e compostos, simultaneamente, por bandas de altas e de baixas frequˆencias, Grossmann e Morlet [10] usaram fun¸c˜oes de an´alise na base com parˆametros vari´aveisσ e τ relacionados com frequˆencia e tempo, respectivamente, e que ajustavam `as janelas de an´alise do sinal, contornando a limita¸c˜ao da an´alise de Fourier-Gabor. Assim, as fun¸c˜oes de an´alise s˜ao ajustadas pelos parˆametrosσ eτ dependendo da frequˆencia que se deseja analisar, ou seja, para estudar as estruturas de sinaisf(t) em tamanhos diferentes, ´e necess´ario usar uma decomposi¸c˜ao em tempo-frequˆencia com suportes diferentes no tempo.

A transformada em ondaletas ´e uma t´ecnica recente com enorme aplicabilidade no estudo de fun¸c˜oes n˜ao-estacion´arias e de sinais com transientes ou singularidades, como ´e o caso de sinais geof´ısicos[16]. A enorme utilidade das ondaletas est´a na possibilidade de atuarem como fun¸c˜oes de base na decomposi¸c˜ao de sinais temporais (fun¸c˜oes f(t) _∈ L2_{(IR)) de forma mais eficiente que as bases senoidais do m´etodo de Fourier e que as} janelas do m´etodo Fourier-Gabor.

2.4.1

Transformada Cont´ınua em Ondaletas

A Transformada Cont´ınua em Ondaletas ´e uma transforma¸c˜ao matem´atica que decomp˜oe um sinal temporal f(t) _∈ L2_{(IR) em fun¸c˜oes de base denominadas ondaletas} ou wavelets. Esta transformada gera um novo sinal fψ(σ, τ) ∈ L2(IR) que ´e dependente

dos parˆametros σ e τ que s˜ao, respectivamente, o parˆametro de dilata¸c˜ao/contra¸c˜ao e o parˆametro de transla¸c˜ao. Comparando a transformada cont´ınua em ondaletas com a transformada de Fourier janelada, como veremos a seguir, percebe-se que o parˆametroτ ´e similar ao parˆametro de localiza¸c˜ao da transformada de Fourier janelada. J´a o parˆametro σ n˜ao existe na transformada de Fourier janelada.

A decomposi¸c˜ao da fun¸c˜ao f(t) em termos das ondaletas, pode ser representada pela equa¸c˜ao:

fψ(σ, τ) =

∫ +∞

−∞

f(t)ψ_σ,τ∗ (t)dt (2.12)

onde a fun¸c˜aoψ∗

σ,τ(t) ´e conseguida por dilata¸c˜oes (parˆametroσ) e transla¸c˜oes (parˆametro

τ) de uma fun¸c˜ao principal ou fun¸c˜ao prot´otipo, conhecida por ondaleta m˜ae (ou wavelet m˜ae), e dada por:

ψ_σ,τ∗ (t) = √1

|σ_|ψ

(

t₋τ σ

)

(2.13)

ondeσ, τ _∈IR, σ _̸= 0; e o termo √1

|σ_| corresponde a um fator de normaliza¸c˜ao da energia para cada ondaleta, que faz com que cada ondaleta tenha a mesma energia da ondaleta principal.

A dependˆencia da ondaleta com os dois parˆametros, σ e τ, ´e o que torna esta trans-formada uma ferramenta eficiente para analisar sinais n˜ao-estacion´arios e localizar sin-gularidades e transientes, pois ´e poss´ıvel analisar a fun¸c˜ao em um amplo conjunto de localiza¸c˜oes temporais e com rela¸c˜ao a um grande conjunto de frequˆencias.

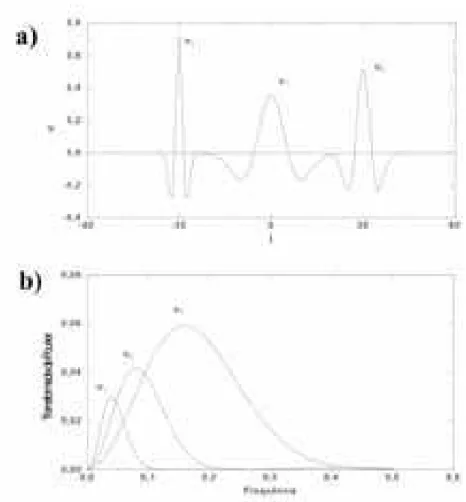
Na figura 2.3.a ilustramos uma fam´ılia de ondaletas cont´ınuas para diferentes valores dos parˆametrosσeτ. J´a na figura 2.3.b ilustramos o espectro de Fourier destas ondaletas. A ondaleta escolhida ´e a segunda derivada da gaussiana, tamb´em conhecida como

Figura 2.3: Representa¸c˜ao de uma fam´ılia de ondaletas cont´ınuas (figura (a)) e de seu espectro de Fourier (figura (b)). Figura reproduzida de MALLAT[16].

para gerar a fam´ılia de ondaletas ´eψ1, que est´a localizada emτ0 = 0 para uma determinada escala σ0, ou seja, ψ1 =ψσ0,τ0=0. Observa-se na figura 2.3.a que quando aψ1 ´e contra´ıda emσ0 _→ σ0

2 e transladada para a direita, τ0 →+τ, ´e gerada a ondaletaψ2, caracterizada por ψ2 = ψσ0/2,τ. J´a a ondaleta ψ3 ´e gerada pela contra¸c˜ao σ0 →

σ0

4 e pela transla¸c˜ao τ0 _{→ −}τ, assim ψ3 =ψσ0/4,−τ.

A transformada em ondaletas, assim como a transformada de Fourier, ´e invers´ıvel. A recupera¸c˜ao do sinal original ´e poss´ıvel pela transformada em ondaletas inversa, cuja express˜ao matem´atica ´e:

f(t) =f_ψ−1(σ, τ) = 1 cψ

∫ +∞

−∞

∫ +∞

−∞

fψ(σ, τ)

1

√

|σ_|ψ

(

t₋τ σ

)

dτdσ

σ2 (2.14) onde o termo Cψ depende da ondaleta dada e, matematicamente, ´e escrito na forma:

Cψ =

∫ +∞

−∞

|ψ(ω)ˆ _|2

|ω_| dω <∞ (2.15) onde o termo _|ψ(ω)ˆ _| ´e a transformada de Fourier da fun¸c˜ao ψ(t).

A equa¸c˜ao 2.15 ´e definida como a condi¸c˜ao de admissibilidade da fun¸c˜aoψ(t), que tem de satisfazˆe-la para que a fun¸c˜ao f(t) possa ser reconstru´ıda sem perda de informa¸c˜ao.

A equa¸c˜ao 2.15 exige, ainda, que ˆψ(0) = 0 ou ∫+∞

−∞ ψ(t)dt = 0, de forma que ψ(t)

muda seu sinal, ao menos, uma vez ao longo de seu dom´ınio e que se anula para t_{→ ∞}. Esta propriedade garante queψ(t) tem car´ater ondulat´orio.

Por outro lado, levando-se em considera¸c˜ao a localiza¸c˜ao da energia da fun¸c˜ao ψ, temos que essa est´a localizada numa regi˜ao do plano (τ, ω) e, portanto, no plano (τ, σ), uma vez queσ _∼1/ω. Isto significa que as amplitudes de ψ s˜ao apreci´aveis apenas nesta regi˜ao. Desta forma, a equa¸c˜ao 2.12 mede as flutua¸c˜oes do sinalf na vizinhan¸ca deτ, cujo tamanho ´e proporcional `a escala σ. Se a ondaleta ´e mais localizada, ou seja, sua energia est´a concentrada em uma pequena regi˜ao do espa¸co, ela fornece uma melhor representa¸c˜ao da fun¸c˜ao no plano tempo-frequˆencia, mas a forma da ondaleta permanece inalterada sob dilata¸c˜ao e transla¸c˜ao (como pode ser visto na figura 2.3).

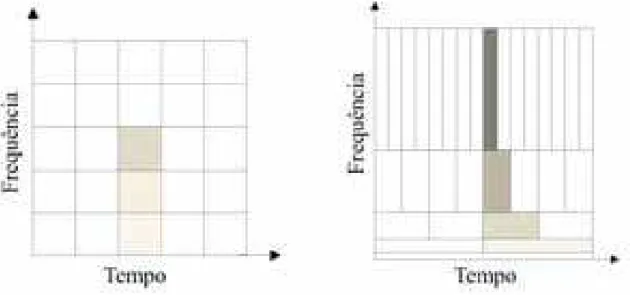
eventos localizados do sinal temporal quando estudado no dom´ınio tempo-frequˆencia. Na figura 2.4.b podemos observar, tamb´em, o esquema da discretiza¸c˜ao do dom´ınio tempo-escala para as ondaletas.

Figura 2.4: Esquema ilustrativo da divis˜ao do espa¸co tempo-frequˆencia (a) para a trans-formada de Fourier-Gabor; e (b) para a transtrans-formada em ondaletas.

Figura reproduzida de MALLAT[16].

2.4.2

Transformada Discreta em Ondaletas

Vimos, at´e agora, que a transformada cont´ınua em ondaletas analisa sinais temporais a partir de sua representa¸c˜ao em termos de fun¸c˜oes de base dadas pela equa¸c˜ao 2.13, onde os parˆametrosσeτ controlam a largura e a localiza¸c˜ao das fun¸c˜oes de an´alise que formam a base.

Com os parˆametrosσ eτ, a transformada cont´ınua em ondaletas ´e uma representa¸c˜ao redundante dos sinais temporais. A diminui¸c˜ao da redundˆancia aumenta a eficiˆencia dos algoritmos de an´alise e uma discretiza¸c˜ao dos parˆametros σ e τ ´e suficiente para passar de uma representa¸c˜ao redundante a uma representa¸c˜ao em uma base ortonormal.

ser escolhido de modo que as ondaletas ψ(t₋kτ0) cubram todo o eixo temporal. Deve-se perceber tamb´em, que a discretiza¸c˜ao de τ deve estar relacionada `a discretiza¸c˜ao de σ=σ₀j, portanto, uma escolha conveniente para τ ´e da forma τ =kσ₀jτ0.

Uma classe particular de ondaletas discretas s˜ao as ondaletas com os seguintes valores num´ericos para os parˆametros de transla¸c˜ao e contra¸c˜ao da ondaleta τ0 = 1 eσ0 = 2, de forma que, temos σ _→ 2j _{e τ → 2}j_{k, com (j, k) ∈ Z×Z. Esta nota¸c˜ao conduz a uma}

estrutura em escalas (´ındice j) e transla¸c˜oes (´ındice k) chamada di´adica, que assemelha-se a uma nota¸c˜ao musical, em que as potˆencias de 2 est˜ao relacionadas com intervalos (oitavas) e dura¸c˜ao das notas.

Ent˜ao, uma ondaleta discreta ´e uma fun¸c˜ao ψ(t), tal que a fam´ılia de fun¸c˜oes

ψj,k(t) =

1

√

2jψ

(

t₋k2j

2j

)

(2.16) seja uma base ortonormal para o L2_{(IR) com j e k inteiros.}

Da defini¸c˜ao acima, se ψ ´e uma ondaleta, ent˜ao, ψj,k tamb´em ser´a para qualquer

j, k _∈Z.

Os parˆametros j e k s˜ao quem controlam, respectivamente, as dilata¸c˜oes e as transla¸c˜oes das ondaletas. Ent˜ao, a transformada discreta em ondaletas ser´a da forma

dj,k =

∫ +∞

−∞

f(t)_√1 2jψ

(

t₋k2j

2j

)

dt (2.17)

onde os coeficientes geradosdj,k0 s˜ao chamados de coeficientes de detalhe oucoeficientes

ondaletas.

Algoritmos baseados nesta transformada s˜ao usados para analisar sinais temporais que s˜ao formados por bandas de alta e baixa frequˆencias e que possuem eventos localizados no tempo ou singularidades. Estas singularidades s˜ao bem localizadas no espa¸co tempo-frequˆencia, permitindo verificar quais coeficientes da transformada discreta em ondaletas s˜ao mais importantes na representa¸c˜ao do sinal.

Cap´ıtulo 3

A An´

alise Curvelet

3.1

Introdu¸c˜

ao

No cap´ıtulo anterior come¸camos a estudar sinais temporais e as transformadas uti-lizadas em suas an´alises. Neste cap´ıtulo vamos dar continuidade ao estudo de trans-formadas tempo-frequˆencia estudando um tipo recente de transformada e com in´umeras aplica¸c˜oes em diversas ´areas da ciˆencia e da tecnologia, a transformada curvelet.

Em todo o corpo desta tese manteremos o termo em inglˆes, curvelet, para esta trans-formada pois, por ser uma an´alise recente, ainda n˜ao h´a na literatura uma tradu¸c˜ao adequada para este termo.

Voltando ao estudado no cap´ıtulo anterior, vimos que a an´alise de Fourier pode ser uti-lizada para decompor um sinal peri´odico em termos de senos e cossenos, ou seja, podemos escrever um sinal peri´odico como uma combina¸c˜ao linear de senos e cossenos e descobrir as frequˆencias presentes no sinal temporal. A an´alise de Fourier ´e extremamente ´util no estudo de sinais estacion´arios, mas apresenta s´erias limita¸c˜oes ao analisar sinais que apresentam descontinuidades ou eventos localizados no tempo.

e n˜ao os dois simultaneamente.

Da limita¸c˜ao da an´alise de Fourier em localizar um evento em um sinal temporal e da limita¸c˜ao da transformada de Fourier-Gabor em estudar sinais compostos, simultane-amente, por bandas de altas e de baixas frequˆencias, surgiu a an´alise em ondaletas. Neste tipo de an´alise, o sinal temporal ou fun¸c˜ao a ser estudada ´e representada em termos de pequenas ondas que sejam localizadas no tempo e que permitem ajustar o tamanho das janelas de an´alise do sinal, contornando a limita¸c˜ao da an´alise de Fourier-Gabor. A transformada em ondaletas ´e uma t´ecnica recente com enorme aplicabilidade no estudo de fun¸c˜oes n˜ao-estacion´arias e de sinais com transientes ou singularidades, como ´e o caso de sinais geof´ısicos[16]. No entanto, esta t´ecnica de an´alise tamb´em tem suas limita¸c˜oes. Por exemplo, apesar de representar surpreendentemente bem descontinuidades pontuais em uma dimens˜ao, a an´alise em ondaletas apresenta severas restri¸c˜oes para representar regi˜oes com descontinuidades superficiais em duas dimens˜oes, ou seja, descontinuidades ao longo de curvas, precisando-se de um n´umero muito grande de coeficientes para tais representa¸c˜oes[22] ou mesmo recuperando representa¸c˜oes imprecisas.

Partindo-se desta limita¸c˜ao na an´alise em ondaletas, Cand`es e Donoho[22] propuseram, em 1999, uma nova classe de fun¸c˜oes de base, as curvelets que podem ser utilizadas na remo¸c˜ao de ru´ıdos de sinais e imagens, na compress˜ao de sinais, no reconhecimento de padr˜oes, entre outras aplica¸c˜oes. A an´alise curvelets consiste em representar um sinal/imagem em termos de fun¸c˜oes de base que tenham em seus parˆametros, al´em dos parˆametros relacionados `a frequˆencia e ao tempo, um parˆametro angular, dando um car´ater direcional `a an´alise e permitindo-se identificar e representar singularidades di-recionais.

3.2

Defini¸c˜

ao da Transformada Curvelet

A transformada curvelet ´e uma nova transformada multiescala com um forte car´ater direcional que vem sendo largamente utilizada na representa¸c˜ao de objetos, imagens e sinais que tem descontinuidades ao longo de curvas[22, 23, 24, 25, 26, 27, 28]. Este car´ater direcional das curvelets vem do fato delas estarem localizadas, al´em do dom´ınio espacial e de frequˆencias, em orienta¸c˜ao angular, o que consiste num passo al´em da an´alise em ondaletas[16]. Nesta se¸c˜ao vamos definir a transformada curvelet cont´ınua e estudar suas propriedades.

Vamos considerar que as fun¸c˜oes de basecurveletsest˜ao definidas em duas dimens˜oes, com vari´avel espacialx,ωe comr eθas coordenadas polares no dom´ınio das frequˆencias. Assim, considerando o par de janelasW(r) e V(t) que s˜ao, respectivamente, a “janela radial” e a “janela angular” e que s˜ao, ambas, suaves, n˜ao-negativas e reais, com W tomando argumentos reais e positivos com suporte r no intervalo (1/2,2) e V tomando argumentos reais com suporte emt _∈[₋1,1].

Estas janelas obedecer˜ao `as condi¸c˜oes de admissibilidade:

+∞

∑

j=−∞

W2(2jr) = 1, r_∈(₃

4, 3 2 ) (3.1) +∞ ∑

l=−∞

V2(t₋l) = 1, t_∈(

−12, 1 2

)

(3.2) Para cadaj _≥j0, o que significa dizer que estamos trabalhando com as escalas “finas” das curvelets, introduziremos as janelas de frequˆencia Uj definida no dom´ınio de Fourier

por:

Uj(r, θ) = 2−3j/4W(2−jr)V

(

2⌊j/2⌋_θ

2π

)

(3.3) onde _⌊j/2_⌋ ´e a parte inteira de j/2. Desta forma, o suporte de Uj ´e uma “fatia” polar

definida pelo suporte de W eV, ou seja, ´e uma janela com largura dependente da escala em cada dire¸c˜ao.

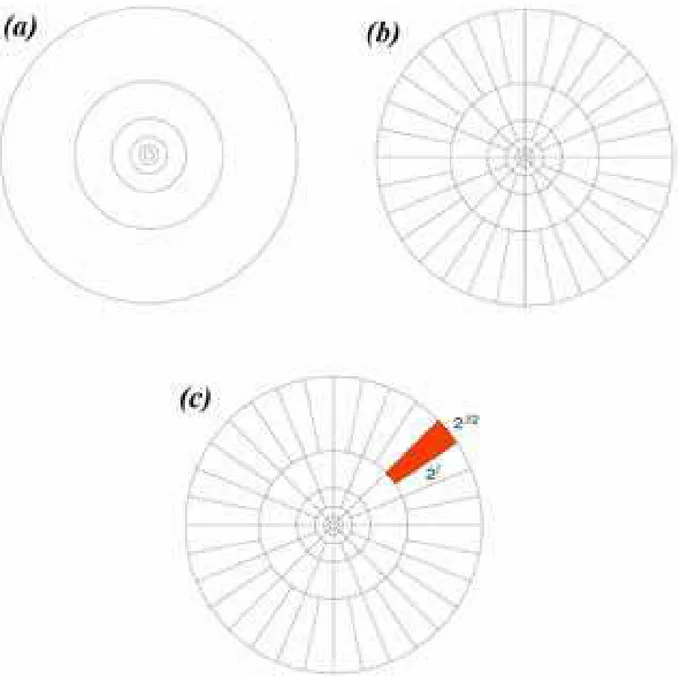
essas janelas em um sinal/imagem a ser estudado, vamos considerar que o espa¸co de frequˆencia, a partir de sua origem, em camada de frequˆencia definidas por 2j _{< W < 2}j+1_, de modo que o espa¸co de frequˆencia fica decomposto em camadas como na figura 3.1.a. J´a a decomposi¸c˜ao do espa¸co de frequˆencia para a constru¸c˜ao da janela angular ´e a segunda decomposi¸c˜ao di´adica e, por isto, feita no espa¸co j´a decomposto na escala radial de modo que temos (W, V) _≤ 2−j/2_{. Esta decomposi¸c˜ao ´e mostrada na figura 3.1.b. Assim, o} suporte das curvelets ´e como uma fatia parab´olica neste espa¸co de frequˆencia sob as decomposi¸c˜oes em escala radial e angular. Na figura 3.1.c a ´area sombreada representa esta fatia parab´olica do espa¸co que ´e dependente de escala em cada dire¸c˜ao, onde as

curveletstem seu suporte definido e onde cada an´alise ser´a feita sobre a imagem/sinal. Para obtermos as curvelets reais que atuam sobre este espa¸co de frequˆencia decom-posto, iremos trabalhar com a vers˜ao sim´etrica da equa¸c˜ao (3.3), ou seja, trabalharemos com:

Uj(r, θ) = Uj(r, θ+π) (3.4)

Para definirmos as fun¸c˜oes curvelets, vamos considerar que temos a fun¸c˜ao ϕ(x), a “curveletm˜ae”, pois todas ascurveletsna escala 2−j _{s˜ao obtidas por rota¸c˜oes e transla¸c˜oes}

deϕj. Assim, as curvelets:

i) apresentam uma sequˆencia igualmente espa¸cada de ˆangulos de rota¸c˜ao θl = 2π ·

2−⌊j/2⌋ _{· l, com l = 0,1, . . . , tal que 0 ≤ θ}

l < 2π. Devemos ressaltar que o

espa¸camento entre ˆangulos consecutivos s˜ao dependentes de escala. ii) e a sequˆencia dos parˆametros de transla¸c˜ao k = (k1, k2)_∈Z2.

Com o estabelecimento dessas nota¸c˜oes, vamos definir as curvelet como fun¸c˜oes de x= (x1, x2) na escala 2−j, com orienta¸c˜ao θl e posi¸c˜ao x(kj,l) =R

−1

θl , por:

ϕj,l,k(x) =ϕj

[

Rθl

(

x₋xj,l_k )] (3.5)

ondeRθ ´e a matriz de rota¸c˜ao de θ em radianos e R−θ1 sua inversa, que tamb´em ´e igual `a

Figura 3.1: Decomposi¸c˜ao di´adica do espa¸co de frequˆencia. Na figura (a) temos esta decomposi¸c˜ao em termos da janela radial; na figura (b) temos esta decomposi¸c˜ao em termo das janelas radial e angular; j´a na figura (c) temos que a ´area sombreada ´e a fatia do espa¸co de Fourier onde as curvelets tem seu suporte definido. Figura adaptada da p´agina de internet http://www.math.washington.edu/ hart/uwss.pdf [29].

Rθ =





cosθ senθ

−senθ cosθ



o que nos d´a:

R−_θ1 =RT_θ =R−θ (3.7)

Ent˜ao, um coeficiente curvelet´e definido como sendo o produto interno entre a fun¸c˜ao f que representa o sinal e a curvelet ϕj,l,k. Ou seja:

c(j, l, k) =_⟨f_|ϕj,l,k⟩=

∫

R2

f(x)ϕj,l,k(x)dx (3.8)

Como a transformada curvelet opera no dom´ınio da frequˆencia, podemos usar o teo-rema de Plancherel e expressar o produto interno da equa¸c˜ao (3.8) como uma integral sobre o plano frequˆencia:

c(j, l, k) = 1 (2π)2

∫

ˆ

f(x)ϕj,l,k(ω)dω =

1 (2π)2

∫

ˆ

f(x)Uj(Rθlω)e

⟨x(j,l),ω_k ⟩_{dω . (3.9)}

Para o caso de escalas mais “grosseiras” (0 _≤ j _≤ j0), podemos introduzir um filtro do tipo passa-baixa, W0, que obedece `a equa¸c˜ao:

|W0(r)_|2 +∑

j≥jo

|W(2−jr)_|2 = 1 (3.10)

E para k1, k2 _∈Z, definimos a curvelet de escala “grossa” como:

ϕj0,k(x) = ϕj0(x−2

−j0_{k) (3.11)}

ˆ

ϕj0(ω) = 2

−j0_{|ω| (3.12)}

Destas equa¸c˜oes percebemos que as curvelets na escala “grossa” s˜ao n˜ao direcionais, ou seja, no maior fator de escala ascurvelets s˜ao sim´etricas.

3.3

Propriedades da Transformada

Curvelet

A transformadacurvelet tem algumas propriedades importantes que devemos ressaltar nesta se¸c˜ao para entendermos melhor a an´alise de sinais utilizando este tipo de transfor-mada.

3.3.1

Tight frame

Um conjunto de fun¸c˜oes ´e chamado de tight framese, mesmo n˜ao sendo um conjunto ortonormal de fun¸c˜oes, funciona da mesma forma que uma base ortonormal e ´e poss´ıvel expandir uma fun¸c˜ao ou sinal em termos deste conjunto de fun¸c˜oes. Ou seja, esse conjunto de fun¸c˜oes chamado de tight frame funciona como um prot´otipo ou arcabou¸co do espa¸co de fun¸c˜oes.

As fun¸c˜oescurveletfuncionam como se fossem uma base ortonormal, na qual ´e poss´ıvel expandir um sinal ou fun¸c˜ao arbitr´ariaf(x1, x2)_∈L2_R2 _{como uma s´erie decurveletsdada} por:

f =∑

j,k,l

⟨f_|ϕj,l,k⟩ϕj,l,k (3.13)

Esta igualdade vale no espa¸co de todas as fun¸c˜oes de quadrado integr´aveis L2 _e, por-tanto, tamb´em ´e v´alida a rela¸c˜ao de Parseval:

∑

j,k,l

|⟨f, ϕj,l,k⟩|2 =||f||2L2_(R)2 (3.14) onde as somas nas equa¸c˜oes (3.13) e (3.14) s˜ao feitas em todas as escalas.

3.3.2

Parˆ

ametro de escala parab´

olico

Dada uma fun¸c˜ao curvelet, ϕi, bem localizada no espa¸co de frequˆencia, isto significa

que a fun¸c˜ao espacial ϕj(x) tem um decaimento r´apido dentro do retˆangulo de 2−j por

2−j/2 _{com o eixo maior apontando na dire¸c˜ao vertical.}