Aproximações semiclássicas nos processos de colisões atômico-moleculares

TESE DE DOUTORAMENTO IFT-T.004/94

Aproximações Semiclássicas nos Processos de Colisões Atômico-Moleculares

Maria Caballero Tijero

Orientador

Prof. Dr. Salomon Sylvain Mizrahi

INSTITUTO DE FÍSICA TEÓRICA

APROXIMAÇÕES SEMICLÁSSICAS NOS PROCESSOS DE COLISÕES

ATÕMICO-MOLECULARES

Maria Caballero Tijero

Orientador: Prof. Salomon S. Mizrahi

Tese de Doutorado

Agradeço ao Prof. Salomon S. Mizrahi a orientação e leitura final deste trabalho.

Ao Prof. Paulo Leal Ferreira, pela acolhida no Instituto de Física Teórica e pelo apoio constante durante minha permanência no mesmo.

Ao Prof. Marcello Damy de Souza Santos que soube me incentivar no estudo da Física Nuclear.

Ao Prof. Gerhard W. Bund, pelos ensinamentos ao longo de meus anos de I.F.T. e pelas valiosas discussões e colaboração nos cálculos computacionais desenvolvidos neste trabalho. Ao Prof. Vicente Pleitez pelo estímulo e colaboração nos momentos de dificuldade e desânimo.

A todos os professores do I.F.T. que com seus ensinamentos e amizade tornaram possível o final deste trabalho.

Aos colegas, impossível citar todos pela limitação do espaço, pela amizade e colaboração, especialmente Felice, Jaime, Orlando, Eduardo, Mauro, Clovis, Dimiter e Claudia cujos conhecimentos e idéias ajudaram na digitação do texto.

Aos funcionários da Secretaria, Recepção , Biblioteca e Sala de Cálculo do I.F.T. por sua amizade e compreensão .

A CAPES, pelo suporte finaceiro no início deste trabalho.

A PUC de São Paulo que mesmo dificultando o término deste trabalho, colaborou com horas-pesquisa para a realização do mesmo.

São comparadas duas alternativas diferentes para descrever um sistema quântico mapeado no espaço de fase: a representação de Weyl-Wigner e a representação dos pacotes de ondas gaussianos. Isto é feito por meio de uma aplicação às colisões moleculares, sendo estas tratadas semiclassicamente. As distribuições que descrevem o sistema nos instantes inicial e final são quânticas, porém a evolução temporal das coordenadas e momenta é clássica. São calculadas as probabilidades de transição da molécula, representada por um oscilador harmônico, de um estado inicial para um estado final após colidir com o átomo represen- tado por uma partícula livre. A expansão do Liouvilliano quântico em série de potências de % permite-nos introduzir correções quânticas para as probabilidades de transição . São estudadas estas correções até a primeira ordem em ft.

Palavras-chaves: Aproximações semiclássicas, Colisões atõmico-moleculares, Função distribuição de Wigner, Estados coerentes, Pacotes de ondas gaussianos.

Two different alternatives for describing a quantum system mapped into the phase space are compared: the Weyl-Wigner representation and the Gaussian Wave-Packet represen- tation. We do that by making an application to molecular collisions which are treated semiclassically. The distributions that describe the system in the initial and final times are quantum-mechanical, but the time-evolution of the coordinates and momenta is clas- sical. We calculate the transition probabilities of the molecule, which is represented by a harmonic oscilator, from an initial state to a final one after colliding with the atom which is represented by a free particle. An expansion of the quantum Liouvillian in powers of h allows us to introduce quantum corrections for the transition probabilities. Those correc- tions are studied up to the first order in h.

1 INTRODUÇÃO 1

2 COLISÕES NO ESPAÇO DE FASE VIA FUNÇÃO DE WIGNER 4 2.1 A FUNÇÃO DISTRIBUIÇÃO DE WIGNER (FDW) 4 2.2 APROXIMAÇÃO CAUSAL (AC) E APROXIMAÇÃO QUASI-CAUSAL

(AQC) 10 2.3 O MÉTODO SQC PARA COLISÕES MOLECULARES 12 2.4 A APROXIMAÇÃO QUASI-CAUSAL (AQC) 14

3 MECÂNICA QUÃNTICA VIA PACOTES GAUSSIANOS 16 3.1 ESTADOS COERENTES. DEFINIÇÕES E PROPRIEDADES 16 3.2 FORMALISMO DOS PACOTES DE ONDAS GAUSSIANOS 20 3.3 APROXIMAÇÃO CAUSAL E APROXIMAÇÃO QUASI-CAUSAL NOS POG 30

4 RESULTADOS E CONCLUSÕES 35 4.1 RESULTADOS 35 4.1.1 RESULTADOS NUMÉRICOS PARA A AC 35 4.1.2 AQC NO FORMALISMO DE WIGNER 36 4.1.3 AQC NO FORMALISMO DOS POG 42 4.2 CONCLUSÕES 51

A Propriedades do Operador de Evolução 53

B Forma Integral da Equação (2.39) 57

C Obtenção das Trajetórias Clássicas 61

E Malha de Pontos no Método SQC 69

F Probabilidades de Transição nas Colisões 72

G Obtenção da Expressão (2.50) 75

H Derivadas em (2.50) e AQC na Terceira Ordem 77

I A Função de Green 80

J Probabilidades de Transição Via Pacotes de Ondas Gaussianos 85

K Forma Covariante do Hamiltoniano 89

L Operador de Evolução Aplicado ao Produto de Funções 91

M Obtenção da Equação (3.90) 93

N Obtenção das Funções e 95

O Primeira Aproximação para Cálculo da AQC nos POG 101

P Segunda Aproximação para AQC nos POG 109

Referências Bibliográficas 110

INTRODUÇÃO

As soluções da equação de Schrõdinger, usando a energia cinética e as interações ele- tromagnéticas de todos os núcleos e dos elétrons das moléculas que colidem, fornecem a descrição exata da dinâmica de um processo de espalhamento molecular. A aproximação de Born-Oppenheimer pode ser usada quando o processo a ser estudado é adiabático e nesse caso, a equação de Schrõdinger para o espalhamento se reduz ao problema do movimento nuclear sobre uma superfície de energia potencial conhecida como uma função de todas as distâncias entre os núcleos. Os cálculos quãnticos estão limitados por problemas referentes à precisão e também pela capacidade do computador e tempo de processamento do mesmo. Até meados dos anos 70 os dados experimentais sobre colisões moleculares eram maior quantidade e mais precisos que os cálculos teóricos existentes para o espalhamento quãntico. Esta disparidade se devia, em parte, ao conhecimento incompleto da energia potencial. Dado que o tratamento clássico simplifica os cálculos, o argumento de que os efeitos quãnticos são desprezíveis, exceto para processos que envolvem átomos de hidrogênio, levou à execução de diversos cálculos [1], supunha-se que a precisão dos resultados clássicos seria maior que a dos cálculos quãnticos, uma vez que neste caso a introdução do número de ondas parciais que correspondem aos estados internos moleculares inicial e final e o alcance do momento angular orbital eram impraticáveis para os computadores da época. E claro que processos que exigem interpretação quãntica não podem ser tratados classicamente, tais como tunelamento e espalhamento em estados classicamente proibidos. Os métodos semiclássicos para o estudo de tais processos são até hoje objeto de pesquisa.

Já em 1959, Wheeler e Ford [2] tinham dado uma importante contribuição para a teoria das colisões atômicas e moleculares mostrando que o espalhamento elástico átomo-átomo poderia ser descrito semiclassicamente. No formalismo semiclássico a descrição do processo de espalhamento é quântica mas os parâmetros dinâmicos que aparecem nas expressões quânticas são calculados usando a Mecânica Clássica. Por meio das amplitudes de proba- bilidade o princípio da superposição da Mecânica Quântica é conservado, portanto é uma combinação da Dinâmica Clássica com a Quântica. Fenômenos quânticos como ressonâncias no espalhamento elástico podem ser descritos com precisão nesta teoria fazendo uma con- tinuação analítica da Mecânica Clássica, incluindo os processos classicamente proibidos tais como o tunelamento.

O sucesso obtido no tratamento semiclássico das colisões elásticas, leva-nos a tentar um estudo similar para descrever colisões mais complexas, tais como a colisão de um átomo e uma molécula diatômica, onde podem aparecer processos inelásticos e reativos. Muitos métodos semiclássicos tem sido desenvolvidos [3]. Sem dúvida o método mais conhecido para descrever a dinâmica das colisões é o das trajetórias clássicas. Neste método as moléculas que colidem obedecem às equações de movimento de Hamilton. A técnica das trajetórias clássicas classificadas por meio dos estados inicial e final é conhecida como MÉTODO QUASTCLÁSSICO (QC) [1]. 0 valor deste método consiste na simplicidade com que pode ser aplicado e na considerável diminuição do tempo de computação, se comparado com o método exato da Mecânica Quântica (QM) [4]. Devido ã natureza clássica das trajetórias, o método QC não consegue descrever os processos clássicamente proibidos que resultam do tunelamento quântico, por este motivo é interessante encontrar técnicas que resolvam este problema mas que conservem o que ele tem de conveniente.

cálculo das probabilidades de transição para colisões colineares átomo-diátomo não reati- vas há discrepâncias entre os resultados obtidos pelo método SQC e QM, os quais iremos investigar.

Neste trabalho mostramos que o formalismo de Lee e Scully corresponde ao termo de ordem zero da expansão do Liouvilliano quântico escrito na representação de Weyl- Wigner, podendo ser obtidos termos de correção de ordem mais elevada. Chamaremos ao termo de ordem zero APROXIMAÇÃO CAUSAL (AC) e ao termo de primeira ordem de APROXIMAÇÃO QUASI-CAUSAL (AQC). Os assuntos relativos ao método SQC e aproximações causai e quasi-causal serão tratados no capítulo 2.

Como a distribuição de Wigner é uma função que pode assumir valores negativos, muitos autores [9, 10] propuseram métodos para suavizar esta distribuição com o intuito de transformá-la numa genuina função distribuição de probabilidade (ou seja não negativa), já que a função distribuição de Wigner é usada com sucesso em muitos campos da Física [9]. Os resultados obtidos com a função não negativa coincidem com os resultados experimentais para sistemas lineares. Para potenciais não lineares porém, os resultados obtidos divergem fortemente dos experimentais. Também, em termos de aproximações semiclássicas, não é clara a interpretação desta distribuição suavizada [11].

Neste trabalho usamos outra alternativa para mapear o espaço de fase, são os estados coerentes ou pacotes de ondas gaussianos [12]. Neste formalismo é também possível obter uma expansão perturbativa que corresponde à aproximação quasi-causal (AQC) para a função de Green, assim como uma expressão para as probabilidades de transição [13].

COLISÕES NO ESPAÇO DE FASE VIA FUNÇÃO

DE WIGNER

2.1 A FUNÇÃO DISTRIBUIÇÃO DE WIGNER (FDW)

A representação da Mecânica Quântica no espaço de fase usando a ordenação de Weyl e a distribuição de Wigner permite que sistemas quânticos sejam analisados em termos quasi-clássicos. Devido ao princípio das incertezas a representação da Mecânica Quântica no espaço de fase é problemática e nada trivial. Como a posição e o momento de uma partícula quântica não podem ser simultaneamente bem definidos, não é possível definir uma genuina distribuição de probabilidade no espaço de fase para esta partícula, porém, a função distribuição de Wigner (FDW) tem sido usada no estudo dos sistemas quânticos com êxito sendo não apenas uma ferramenta de cálculo, mas também permitindo estabelecer no limite > 0 conexões entre a Mecânica Clássica e a Mecânica Quântica. Iremos desenvolver o formalismo considerando, por simplicidade, o sistema de uma só partícula, sem spin e unidimensional. A transição para sistemas tridimensionais e a inclusão do spin pode ser feita sem mudanças conceituais.

Esta forma alternativa de expressar a Mecânica Quântica [14] baseia-se no seguinte princípio: se a cada operador A corresponde uma função de fase a{p,q),é possível descrever um sistema quântico mapeado neste espaço de fase.

A correspondência entre os operadores e as funções de fase é feita via transformada de

Weyl [7, 14, 15]. Da Mecânica Quântica temos^ que se P e Q representam os operadores momento linear e posição respectivamente de uma partícula, sucis relações de comutação são

[P,P] = [Q,Q] = 0, [Q,P] = ih. (2.1)

Os autovetores de P e Q, jp) e |ç) respectivamente, são definidos pelas equações de autovalores

P\p) = pIp), Q\q) = q\q), (2.2)

com as relações de completeza e ortonormalização das bases de autovetores dadas, respec- tivamente, por

/oo roo

dp |p)(p| = 1, / dq |ç)(ç| = 1, (2.3) -OO j—OO

e

(p|p'> = 6{p - p), {q\q') = S{q - q'). (2.4)

0 produto escalar entre vetores dos espaços de Hilbert (mudança de base) é

{q\p) = (27r;i)-'/2e^«P. (2.5)

Usando a relação de completeza (2.3) e fazendo a mudança de variáveis

q' = Q- q" = q + (2.6)

p' = p- -u, p" = p -f -u, (2.7)

obtém-se para um operador genérico A sua representação integral, /OO roo

dp dq a{p,q)A(p,q). (2.8) -OO »/—oo

A função a(p, q) é chamada transformada de Weyl do operador A e é dada por roo 1 1

Por sua vez o operador A(p, q) é dado por

roo ■ 1 I

A(p, q) = dv + -v){q - -v\. (2.10) Outras expressões alternativas para a transformada de Weyl a{p,q) e o operador A(p, ç) são [14, 15]

“(P. l) = - ||A|ç + |), (2.11)

/OO : \L \L

-)(p +-|. (2.12) A expressão (2.8) mostra que se for conhecida a transformada de Weyl de um operador A este pode ser calculado. Vice-versa, por meio das equações (2.9) ou (2.11), dado o operador A pode ser obtida a correspondente transformada de Weyl.

A função de fase a(p, q) não é a quantidade clássica correspondente ao operador quântico A, porém pode ser utilizada para se obter a função clássica correspondente a este operador tomando-se o limite lim%^Qa{jp^q) = ad{p,q).

O operador A(p, ç) desempenha um papel importante na obtenção da função a(p, ç). Usando algumas propriedades deste operador (veja [14] e [15]) e após alguns cálculos algébricos, obtém-se a transformada de Weyl c(p, q) correspondente ao produto de dois operadores AB = C

c(p, q)

a(°) ^ dq õp dp Õq

(2.13)

onde a(p, q) e b(p, q) são as transformadas de Weyl correspondentes aos operadores A e B respectivamente. ^ '

A partir da expressão (2.13) pode ser obtida a transformada de Weyl do comutador de dois operadores C = [A, B] = AB — BA e do anticomutador D = {A, 5} = AB -1- BA, as expressões destas transformadas são respectivamente

c(p, q) = 2i sin

d{p, q) = 2 COS

2 \ dp dp dq ) a{p,q)h(p, q). (2.15) Expandindo em série de potências as funções do seno e do cosseno observa-se que as transformadas de Weyl de comutadores e anticomutadores são expansões em potências de ^ e que o termo de ordem mais baixa da transformada de Weyl de um comutador é exatamente o parêntese de Poisson do produto das transformadas de Weyl dos operadores multiplicado por ih. A função clássica que corresponde a c{p,q) em (2.14) é

limH^oc{p,q) = ^ {aciÍP,q),KiÍP,q)} ih

Um sistema quântico num estado puro pode ser representado pelo operador estatístico

P(i) = |V’(i)){'/’(i)l, (2.16)

e da expressão (2.11) a sua transformada de Weyl é o operador densidade, no espoço de fase,

P{P^ 9,0 = Tr[P{t)A{p, ç)]. (2.17)

A função de Wigner obtida é o produto de p{p^q,t) por (27T^) Assim, a partir da expressão (2.11) obtém-se a função de Wigner

roo ■ 1 1

W^(P, 9, t) = (27t/í)"^ dv - -v\t)^*{q -|- -v; t), (2.18)

ou usando a equação (2.9)

/OO 1 ^ 1

du -I- -ií; 1)%/; {p - -u; t), (2.19) • OO Z L

onde V’ é a transformada de Fourier da função

A função de Wigner é uma distribuição , já que se \'4’{t)) é normalizada^ W{p,q,t) é também normalizada,

/OO roo

dp dq W{p,q,t) = 1, (2.20) ■OO J — OO

e também possui a propriedade de poder ser usada no cálculo do valor médio de um ob- servável no espaço de fase A{t) = (t/>(í)|i4|^(í)), por”*

/oo roo

dp / dqW{p,q,t)a{p,q) = ã(<),

-OO */—OO (2.21)

sendo a{p,q) a transformada de Weyl do operador A anteriormente definida [15].

A FDW é real mas não pode ser considerada uma densidade de probabilidade no espaço de fase, mesmo que forneça as distribuições de probabilidade marginal para a posição e o momentum: dpW(p,q,t) =| ip(q) p> 0 e dqW(p,q,t) =| ip(p) |^> 0, pois ela não é sempre definida positiva. Também não pode tomar a forma de função delta de Dirac S(p — pt)S(q — qf) [9, 14, 15], devido ao princípio de incerteza.

A evolução temporal da FDW é obtida a partir da equação de von Neumann ou equação de Liouville quântica satisfeita pelo operador densidade

^P{t) = -'-[H,P(t)], (2.22)

onde H representa o Hamiltoniano do sistema.

Se h{p, q) representa a transformada de Weyl do operador H, usando a expressão (2.14), pode ser obtida a transformada de Weyl do comutador na equação (2.22), assim, a trans- formada de Weyl da equação de von Neumann será

^ 2 . jW(p,g,t) =-sm

n (dw Q(w)

2 dq dp dp dq Definindo o operador Liouvilliano quântico

h{p,q)W{p,q,t). (2.23)

g(P,9) - ^ sm 1^- Qq h{p^q), (2.24)

a equação (2.23) escreve-se

—iy(p,9,t) = -iCQ{p,q)W{p,q,t). (2.25)

Quando h{jp,q) não depende explicitamente do tempo, e consequentemente C{p,q), a solução formal da equação (2.25) é dada por

onde W{p,q,to) representa a FDW no instante inicial Íq.

O limite clássico de uma quantidade física é obtido calculando o limite para h tendendo a zero da transformada de Weyl do operador correspondente. Quando se trata da FDW este limite nem sempre leva a uma função clássica, pois em Mecânica Quântica existem situações sem análogo clássico. Quando a FDW é o pacote de ondas de incerteza mínima o limite para h tendendo a zero deve ser tomado de forma específica para se obter o limite clássico [14, 15].

Na expressão (2.26) observamos que a dependência em ti de W{p,q,t) provém de duas fontes: da função W{p,q,to) e do operador Liouvilliano definido em (2.24). Isto é impor- tante para se entender o cálculo do limite para h tendendo a zero de W{p,q,t) [16]:

Definindo o operador®

« QW 5(2) ^(1) ^(2) g<- Qi- dq dp dp dq dq dp dp dq ’

vamos introduzir um parâmetro adimensional a no Liouvilliano quântico, escrevemos®

= a)- A expressão (2.26) será escrita usando o parâmetro a como

(2.28)

(2.29) A expansão em série de potências do Liouvilliano quântico é

4“^ = ah

ah ^ (ah\^ \

T ^ “ \~2 ) 3! (^) (2.30)

Quando h{p,q) independe de h tem-se h{p,q) = hd{p,q) = h{p, q). Portanto tomando em (2.30) o limite para a —0 obtém-se

lirn£Íj"^ = ih{p,q) A= liin£(j(p,9) = Cq. (2.31) of—+u h-^0

Na expressão (2.31) o operador Cq é clássico^. Substituindo este resultado em (2.29) obtém- se para a FDW

W(°)(p,ç,í) = e-‘(‘-‘“)''“W(p,9,to). (2.32) ®Os índices 1 e 2 em (2.27) desempenham o papel de h e w em (2.24) respectivamente.

A equação (2.25) no limite para a —0 ficará dh

dt dq dp dp dq = = -iCoW^°l (2.33)

Em (2.33),|/í, representa o parêntese de Poisson das funções h{p,q) e W^'^\p,q,t). Os ingredientes quânticos desta equação estão contidos em W^^^\p,q,t).

A introdução do parâmetro a permite tratar de forma independente os limites h 0 na FDW e na dinâmica da evolução .

2.2 APROXIMAÇÃO CAUSAL (AC) E APROXIMAÇÃO QUASI- CAUSAL (AQC)

Entendemos por causalidade [17] que para um ponto do espaço de fase no instante inicial (po,Ço) a distribuição P(p, ç, Íq) = ^{p — Po)^{q — 9o) determina a evolução desta distribuição para tempos posteriores, conservando-se a estrutura de função delta P(p, ç, t) = 8{p — p(t))8{q — q{t)). Ou seja , se T{p,q,t) satisfaz a equação de Liouville clássica (2.33) então p{t) e q{t) são soluções das equações de Hamilton p{t) = —e q{t) = |^. Como a causalidade determina as trajetórias (p{t),q{t)), é interessante introduzir a aproximação em que é subètituido CQ{p,q) por £o(p,ç) já que Cq{p^q) por apresentar derivadas terceiras, quintas etc. (vide equação (2.30)) possui termos não causais. T{p,q,t) não permanece constante ao longo da trajetória, as funções delta no espaço de fase adquirem uma largura na posição e no momentum [17].

No Apêndice A mostramos que o operador de evolução temporal possui a propriedade [18]

90, to) = W^^\p{to - 0, q{to -t)), (2.34) onde o argumento da função W{po,qo,to) representa po = p{to) e ço = q{to) ou seja o momentum e a posição iniciais e a distribuição W{p{to — í), q{to — t)) indica que a evolução da mesma é clássica porém reversa no tempo já que das equações (2.32) e (2.34) tem-se

Vale subentender que W^°\p,q,t) conserva ingredientes quânticos que provém da FDW inicial W{p,q,to) = W{po,qo,to).

Esta aproximação constitui o que chamamos de aproximação causai (AC), já que a evolução dos pontos é obtida das equações de Hamilton e a equação cuja solução é dada por (2.34) é a (2.33). Portanto para se obter a aproximação causai, o limite para h 0 deve ser considerado somente no operador Cq \ assim o uso do parâmetro a evita que sejam confundidos os termos em h provenientes de W{p,q,to) com os de Cq \ Esta aproximação AC é a mesma adotada na referência [5].

Podem ser obtidas aproximações de ordem mais alta, porém iremos nos dedicar ao estudo da aproximação em primeira ordem. Escrevendo o operador em (2.30) como®

f (I)"" , (2.36) a expansão em série de potências de {ahy é escrita como

OO

4“’ = E(«S)"”'C2n, (2.37) onde®

n=sO

An = A<’>(p,9)

22"(2n + 1)! Substituindo (2.37) em (2.25) temos

(a.,) \ 2n+l

(2.38)

Q OO

-tv(“)(p, 9,Í) + i£ü»'<"'(p, í, í) = -■ E (“»)'" q, t), (2.39) n=l

e a sua forma integral é (ver Apêndice B)

f C2nW'^°‘\p,q,t'). (2.40) n=l -^‘0

A aproximação quasi-causal (AQC) é a solução de (2.40) para n = 1 e é definida por

«'ÃcÍP,«. <) = e-“^<‘-'"IW'(p, 5, i„) - i (aS)= l‘ dt'e-‘^>‘-’'<C2W{p,,, i'). (2.41) ®0 índice 1 em A12 corresponde à função h^^\p,q) e o índice 2 à função que aparecerá à direita do operador quando este seja aplicado à mesma.

^Observamos que em (2.38) para n = 0 obtemos Co dado por (2.31).

O operador de evolução temporal fornece W{p,q,t') = e

Impondo a = 0 na expressão (2.41) obtém-se a aproximação causai, e o único operador de evolução temporal garante a causalidade da evolução . Quando for necessário estudar o limite clássico da função W^q, dever-se-á primeiro fazer a = 0 e depois tomar o limite ^ 0, em (2.41).

2.3 O MÉTODO SQC PARA COLISÕES MOLECULARES

Este método [5] é em princípio o método das trajetórias clássicas ou quasi-clássico (QC) [1, 21], mas os estados inicial e final do sistema são descritos pela distribuição de Wigner, a qual incorpora características quânticas inexistentes no método QC. A distribuição ini- cial, representando o estado inicial do sistema, é propagada no tempo usando o método das trajetórias clássicas (Ver Apêndice C) e a distribuição final pode ser usada para cal- cular probabilidades de transição pois conterá informação sobre o estado final do sistema. Uma das vantagens do método SQC é que seu uso permite calcular processos de transição clássicamente proibidos.

Para a reação A + BC(m) —»■ A + BC{n), os números quânticos m e n referem-se ao estado inicial e final do oscilador. No método SQC a molécula BC{n) é descrita por

(-1)”

Wnn{q2,P2) = exp - I + _eL Ln I 2^ Í2 +

/3^h^ (2.42) que é a função distribuição de Wigner para o oscilador harmônico [15] obtida a partir de (2.18), Ç2 e p2 representam as coordenadas e momenta do oscilador e ^ = (pív/h)^, sendo p a massa^^ e a; a frequência de oscilação da molécula. No {X„},n = 0,1,2..., L„ representa o polinômio de Laguerre de ordem n. Como a energia do oscilador é E = ^

pode-se escrever também a equação (2.42) como

/4E'

(2.43)

As coordenadas e momenta de translação para a partícula livre^^ são representados por çi e pi, o valor inicial para é tomado arbitráriamente grande de forma que a interação átomo-molécula diatômica seja desprezível a grandes distâncias de separação , o valor inicial de pi é determinado pela energia total da colisão

A descrição inicial do sistema é feita pelas coordenadas p\ e q\ no instante inicial e a FDW, equação (2.42), é calculada para cada um dos N pontos tomados de uma malha construída no plano (ç2jP2)- O número de pontos N é finito e tal que uma vez obtido o valor ideal, os resultados fiquem invariantes mesmo que N seja aumentado. A densidade e o tamanho da malha devem ser mínimos dependendo da precisão desejada no cálculo. (Ver Apêndice E).

A probabilidade de transição do oscilador harmônico do estado inicial m para o estado final n, (ver Apêndice F) é dada pela expressão

/oo roo

dpo / dqoWmÍPo,qo)e'^‘^^^~^°''Wn{po,qo)- (2.44) -oo J-oo

constante p no Apêndice D expressão (D.25) é representada por M, p2 e Ç2 por Py ey respectivamente e k = pu)^ nesta mesma expressão .

^^Na expressão (D.25), pi e qi são representados por px e x respectivamente e a massa m representa a massa da partícula livre.

Esta expressão é exata, pois Cq é o Liouvilliano quântico completo do sistema, po , qo representam as coordenadas e momentos no instante inicial to do oscilador harmônico.

2.4 A APROXIMAÇÃO QUASI-CAUSAL (AQC)

Considerando a equação (2.41) com a = 1, obtém-se na AQC^^

“’n(p(í)5 9(0) = q) -f- ifi^ f dt'e'^°^*~*'^C2Wn{p, q, t'). (2.45) Jto

A probabilidade de transição do oscilador do estado m para o estado n será dada, após substituir (2.45) em (2.44), por

Uoo roo

dpo / d9oiüm(po,9o)iün(p(0>9(0) -OO OO

+ih'^ í dpo í dqoWm{po,qo) í dt'C2Wn{p{t' - to), q{t' - to)) . (2.46) J — OO J — OO Jto

A primeira parcela no lado direito de (2.46) corresponde à expressão usada no método SQC [5] e a segunda parcela é a correção referente à AQC.

Sendo (ver (2.38))

£2 = h{p,q)

Q(h) Q{w)

dqi dpi Wi'd^l\ J’ logo para^®

(2.47)

Kp, t)=P- + l^ + \k<ll + (2.48) Zttí\ ZTTI2 z

obtém-se

C2Wm{p{t' - to), q{t' - ío)) = i —'j e'^‘’<‘'~‘°^uj„(po, 9o), 24 \(jPlzeTO OP2zero)

(2.49) ^‘‘Sendo a FDW real a expressão conjugada complexa de (2.41) fornece (2.45).

PueTo e Pizero {çizero c q2zero) são OS momcnta (coordcnadas) da partícula e do oscilador respectivamente no instante inicial. Substituindo (2.49) em (2.46) e usando a propriedade distributiva e‘^*[/(po, 9o)fl'(po, 9o)] = e'^‘/(Po, 9o)e‘^°‘fif(po, 9o), após alguma álgebra (Ver Apêndice G) obtém-se

Pm^n = 27T^ lim lim \f dpo í dqoWmÍPo,qo)wn{p{t),q{t)) _{f-*ooto->-oo (J-oo J-OO} h^a^Vo

X 24

/oo roo

dpo / dqoWm{po,qo) • OO oo

^iCo{t—to).

dp? _2zero ■^n(P2zero, q^zero^

(2.50)

No apêndice H obtemos a expressão das derivadas que aparecem no segundo termo de (2.50) para os diferentes números quânticos do oscilador, dadas por^®

^iCo(t-to).

dp? _2zero ~‘^n(P2zeroi q2zero) — dp? _2zero = {2fhujm2)^ P2{t) ( 3

dy^ + hívm -Plit) to-^t

dy^ , (2.51)

No Apêndice G é dada a expressão da AQC para uma ordem mais alta.

MECÂNICA QUÂNTICA VIA PACOTES

GAUSSIANOS

3.1 ESTADOS COERENTES. DEFINIÇÕES E PROPRIEDADES

Em 1926 Schrõdinger [23] foi pioneiro em considerar os estados coerentes do oscilador harmônico (OH) no estudo de mecânica ondulátoria. Posteriormente, outros autores [24, 25, 26] usaram-nos em diferentes áreas da física. Estados coerentes aqui [27] são definidos como autoestados (|a)) do operador de destruição do oscilador harmônico unidimensional (OHU).

a|a) = a|a), (3.1)

como o operador a não é hermitiano os autovalores q são complexos.

Usando a propriedade de completeza da base ortonormalizada dos autovetores do OHU, \ípn) = OS estados \a) podem ser escritos como

OO

l«) = Z]cn(a)|n), (3.2) n=0

onde [15] Cn(a;) = (nja) = (a"/-\/nT)exp( —|ap/2).

^Os operadores de criação e destruição e a do oscilador harmônico podem ser escritos em função dos operadores P e Q por meio das expressões a — 7^(“o^ + (*7“o)P) e at _ ;^(ao<3 - (i/ao)P), (a^ é o adjunto de a).

A probabilidade de obter, depois de uma medida, o autovalor da energia do OHU (n + l/2)h(j} é dada por

V„(a) = |(n|a)|^ = |c„|' = (3.3) nl

que é uma distribuição de Poisson.

Entre as propriedades mais importantes dos estados coerentes citamos: (para estas demostrações ver [15, 26])

• A não ortogonalidade. Para os estados coerentes, |a) e \^) temos

{a\^) = (3.4)

Como |(a|/3)p = exp{—\a — /3p) para ja — /3| —oo os estados coerentes tornam-se ortogonais. Fazendo em (3.4) a — ^ vemos que |a) é normalizado à unidade.

• A completeza. Os estados coerentes formam um conjunto supercompleto^ portanto^

i / .i^ala){a| = 1, (3.5) 7T J

é a relação de fechamento da base.

• Os estados coerentes correspondem ao estado fundamental do OHU deslocado. 0 operador deslocamento'*

D(a) =

= e 2 e aa^ ^—Q*a (3.6)

é unitário e quando aplicado ao estado fundamental do OHU fornece

D(a)|0) = |a). (3.7) ^Que os estados coerentes formam um conjunto supercompleto significa que não são iinearmente inde- pendentes [26].

^Sendo a complexo pode-se escrever a = x + iy = re‘*, tem-se portanto d^a = dxdy = rdrdQ = d{iíea}d{/mo}.

São estados de incerteza mínima. Escrevendo os operadores P e Q em função dos operadores de destruição e criação a e os valores médios no estado |a) são

(a|Q|a) = (Q) = ’(«• +«), (3.8)

(a|P|a) = (P) = iao y-j (a* - a),

e das expressões (3.8) e (3.9) obtém-se

rLrr>=i.

(3.9)

(3.10)

O parâmetro üq é constante e tem dimensões M^T 'i Calculados®, os desvios quadráticos médios

{AQr = (Q^) - {Q?

{APf = (P") - {PY

onde (AQY = k/2aQ e (AP)^ = alh/2 , tem-se a relação de incerteza de Heisenberg

AQAP=~. (3.11)

A expressão (3.11) mostra que os estados coerentes são os estados mais próximos possíveis dos estados clássicos.

Na representação das coordenadas e momenta, respectivamente, respectivamente, os estados coerentes são dados por [15]

(ç|a) = JVe(í)’“”-ã'i', (3.12)

—P^ —~P (p|a) = Me ^ , = ■^y/h/2{at +a) e P = iao\/h/2{a^ - a).

HQ^) = ÍQ)^ + mal e (P2) = (P)2 + alh/2.

onde as constantes de normalização são

M e 2 -i(lap-a^)

Os operadores bosônicos e a satisfazem a relação de comutação [a, a^] = 1, para qualquer função f{a, a^) que pode ser expandida em série de potências destes operadores^, usando as regras de comutação, os mesmos podem ser ordenados de forma que os fiquem à esquerda dos operadores a: ORDEM NORMAL (ON).

/(o, a') = /<™l(a, a') = Yi (3-14) r,s

Outra alternativa é colocar os operadores a à esquerda dos a^: ORDEM ANTINORMAL (OA)

/(a,at) = (3-15) r,s

Estes coeficientes e que aparecem nas formas normal e antinormal respecti- vamente são diferentes e únicos, permitindo fazer uma correspondência biunívoca entre as funções e dos operadores e as funções ordinárias da variável complexa a,

r,a r,s respectivamente,sendo

de forma que conhecidas as funções /(a, a^) dos operadores, podem ser obtidas as funções /(a, a*) e viceversa*.

A utilidade das funções / decorre do fato de que a partir delas pode ser deduzido um método onde as relações de comutação são substituídas por diferenciações de funções complexas, que levam às funções ou a^).

A função a*) é definida como

Tr{\a){a\f{a,a^)} = (a|/(a, a^)|a) = (3.16) prova das propriedades que se seguem é dada nas referências [15, 28].

mas que também pode ser obtida substituindo em /(a, a^) os operadores a por a+d/da* e por a*, e aplicando a expressão obtida sobre a unidade: /(a + â/ôa*, a*) • 1 = a*). Inversamente, para obter o operador a partir de ,basta ordenar previamente todos os a* à esquerda dos a e substituir a* por e a por a.

Para obter as funções a*) a partir de /(a, a^) devemos substituir os operadores a por a e por a* — d/doL e aplicar a expressão sobre a unidade; — dida) • 1 = a*). Por outro lado, ordenando todos os a a esquerda dos a* e substituindo a por a e a* por obtém-se o que equivale a aplicar a relação de “completeza” (3.5) à função a*)

= / —|a){a|/<°'"(a,Q-). (3.17) J 7T

A expressão que relaciona a*) com é [15]

(3.18) 7T J

assim, a partir de pode ser obtida a função

3.2 FORMALISMO DOS PACOTES DE ONDAS GAUSSIANOS

A expresão (3.10) sugere que façamos as definições

(3.19)

e

|a) = \pq). (3.20)

Usando a representação de a e em função de P e Q em (3.19), o operador deslocamento Z)(a), definido em (3.6) será®

D{p,q) = (3.21)

0 plano complexo onde está definido a é o espaço de fase e a base com a qual trabalhamos neste espaço é {[pç)}. Desenvolveremos com estes estados \pq) (que chamaremos daqui por diante de pacotes de ondas Gaussianos (POG)), um formalismo alternativo ao efetuado no Capítulo 2.

Como está sendo feita uma mudança de rótulo dos estados coerentes para os POG, logo todas as propriedades antes descritas para os estados coerentes são válidas para os POG. Os cáculos aqui serão omitidos e podem ser encontrados nas referências [15, 12].

De forma resumida pode-se observar que: 1

. •

W = = £>(?,,)|0>, (3.22) expressão esta equivalente à (3.7).

• A partir das equações (3.4) e (3.19) a não ortogonalidade destes estados torna-se,

(mIpV) = (3.23)

• Para p = p' e q = q' obtém-se {pq\pq) = 1, o que mostra que estes estados são normalizados.

• Como d{rea}d{Ima} = cPa = (lf2h)dpdq a propriedade de fechamento é (de (3.5)) roo roo

^ J-oo J-OO ^

• Fazendo uso do operador deslocamento da Mecânica Quântica

= I,' - ,),

O POG na representação |ç) é dado por

W\pq) = W\D(p, ç)|0) = - ç|0), (3.25) onde

• Analogamente, como e = \p' — p) obtém-se o POG na representação dos momenta

{p'\pq)=e 2)(p'-p|0), (3.26)

sendo

{?' - P|0) = {Trhal) * e

que é o estado fundamental do OHU na representação dos momenta.

• Observando que

e que

- ^)W\p<i)

^{p'\ pq) = -j{p - ^){p'\pq) podem ser obtidas as expressões

QIm) = (I + ~) |p?>. (3.27)

= (l - t|) (3.28)

• Usando a relação de fechamento da representação das coordenadas da Mecânica Quântica obtém-se os elementos diagonais^® para um operador A na representação POG

/OO fOO

dq' f dq"K{p,q-,q\q"){q'\A\q"), (3.29) -OO J —CO

onde o kernel é

^(p,q-,q',q") = (pqlq'}(q"ípq) = l ^

No caso do operador densidade A = P{t) = \ip{t)){x/^{t)\ a expressão (3.29) leva a /oo roo

dq' I dq"K{p,q-,q',q")ip{q')i^*{q"), (3.30)

e a funçãx) p{p, q, t) é sempre não negativa, assim pode ser considerada uma densidade de probabilidade no sentido estrito do termo.

Na representação dos momenta

/OO roo _ _ dp' I dp"K{p,q,;p',p")tp{p')tp*{p"),

-OO j —OO (3.31)

-hl<p"-p)"+(p'-p)>l-i,(p"-p') o kernel é

K{p,q\p',p") = {Trhalyh

e as funções i^(p') e ^(p") são as transformadas de Fourier de ip{q') e V’(ç^0 respectivamente. Podemos agora dar uma interpretação física para o parâmetro oq: como^^

/oo

dpK{p, ç; q', q") = 2i:h,8{q" - q')8{q' - q),

-oo (3.32)

/OO

dpK{p,q-p',p") = 27T^(5(p" - p')í(p' - p), • OO

obtém-se a partir de (3.30) e (3.31) respectivamente 1

1 -

(3.33)

(3.34)

(3.35)

substituindo em (3.34) e (3.35) p{p,q) por {pq\ip){il’\pq) , Por {V’k)(9lV’) ® \‘^{pW por (^|p)(p1i/’) pode-se identificar os limites

dp

onde |g) e |p) são os autoestados dos operadores Q e P. Também de (3.23) tem-se

aí^oo (^)

Ü-0 = ^^P ~ P'^ = ^P^P''^-

Assim, ao percorrer valores de zero até infinito o parâmetro oq permite interpretar os estados \pq) como uma representação generalizada dos momenta e coordenadas, pois nos limites obtém-se as representações \p) e \q) ”sharp”.

Os ordenamentos normal e anti-normal dos operadores a e têm representação corres- pondente que chamaremos, respectivamente, de covariante e contravariante no formalismo de POG [30]. Assim, para um operador A qualquer as expressões (3.16) e (3.17) fornecem respectivamente a forma covariante

Tr{\pq){pq\A} = {pq\A\pq) = A^^{p,q), (3.40) e a forma contravariante

1 /*oo /*oo

dpi dq\pq){pq\A^'^^{p,q).

Zirtl ./—oo • /—oo (3.41)

1 í'^

-oo J —oo

A relação entre a forma covariante A'^^{p,q) e a forma contravariante A^^^{p,q) é obtida a partir da (3.18)

1 r°°

onde

1 /• OO fOO

ÍP,q) = ^ / dp' I dq'\{pq\p'q')\‘^A^^^{p ,q), JàTTft • /—'OO oo

1/ I / /\|2 -ál“o(9-9'P + ^(P-P'P] \{pq\pq)\ -e “0

(3.42)

é obtida de (3.23).

Para obter a forma covariante de um operador f{Q, P), construímos no formalismo POG expressão equivalente à obtida anteriormente para os estados coerentes, assim [12, 15]

/ I r>\ I 4 /• / ^ h, Õ itl Õ tío/n Õ . yr-ir'V\/ \ (P?I/(Q.P)W = /(« + + 2^ã^,p - 7ãí + —Tp^ • ‘ ^

As forméis covariantes dos operadores Q e P são 12

q) = Ípq\Q\pq) = (9 + + .h d h d

2dp 2aldq 1 = q, (3.44)

'P^^ip^q) = (pq\P\pq) = (p - Gi- +

.h d hüQ d

1 =p. (3.45)

2dq 2 dp^

Analogamente, para obter a forma contravariante de um operador (ver 3.41) f{P,Q) = ^SZodpf-oodq\pq){pq\P^^''{p,q), teremos[12, 15]

tCTV/ \ íí , ^ % d .h d hoQ d

para Q temos

Q^^^{p,q)={q-

h d .n d

+ -1 = 9,

2oo dq 2 dp (3.46)

e para P,

(3.47) 2dq 2 dpj

Para produtos de operadores QP ou PQ seguindo esta mesma regra obtém-se, na forma covariante

{pq\QP\pq) = 9 + % d ih d ih d hai d ih

2a§ dq 2 dp 2 dq ' 2 df) ^ *^■'‘2 (3.48)

<w™P«) = (p-Yãí + —ã?, Na forma contravariante temos

^ h d ih d \ ih

q -

h d ih d ih d hai d

2oQdq 2 dp 2 dq 2 dp) ^ 2 ’

(3.49)

(3.50)

(_^ ih d hüQ d \ ( h d ^ ih d\ ^ ih

As duas formas satisfazem as regras de comutação da Mecânica Quântica^^.

Nestes dois exemplos as formas covariante e contravariante são iguais mas isto nem sempre acontece^'*.

0 mesmo processo é usado para funções polinomiais H = ou seja

'ucv u f „ 9 a\h 9\f h d ih

Usando as propriedades dos estados coerentes [15]

(o;|/{a,a^)/i(a,a^)|a) = f°^\a,oT)eyip ^

= (3.53) 'd^ 9-

a--

(3.52)

onde f{a,al)h(a,a^) = VU(a,a^) e definindo o operador diferencial

e o seu complexo conjugado

n I 9 . 9 D = lao-^,

Oo oq op

n* ^ 9 d Oo oq ap temos

9 9-

(3.54)

(3.55)

9a \2J ^ ^ da* V2j

onde flechas indicam a função sobre a qual atuam as derivadas (à esquerda ou à direita), portanto

9^ 9-^ fi - - 9a 9a* ~ 2^^ ' ^^Observamos que

para a forma covariante e,

^ ih d h d ih d hai d , .

j h d ih d ih d hal d , ^ 2al dq^ 2 dp'^ 2 dq 2 dp para a forma contravariante.

Na representação dos pacotes gaussianos teremos para dois operadores quaisquer A{Q, P) eB{Q,P)

{pq\AB\pq) = A'^^{pq)e^^^’B^^{p,q).

e para o comutador dos dois operadores^® tem-se

{pq\[A,B]\pq) = - r*^ B^''{p,q),

onde foram usados os símbolos

r=e^^^* e r = 62^ ^ n* n

(3.56)

(3.57)

Expandindo em série de potências F e F , e reagrupando os termos, a expressão (3.57) pode ser expressa como

{pq\[A, B]\pq) = A^^

+0{h-^) + --- B^^{p,q), (3.58)

portanto no limite ^ 0 obtém-se

lim^(pç|[A,5]|p9) = {Aci,Bci}, (3.59)

onde limti^oA^^{p,q) = A{p,q) = Ad{p,q) e limn^o B^^^^{p,q) = B{p,q) = Bci(p,q). A equação (3.59) representa o parêntese de Poisson para as quantidades clássiccis. Para a forma contravariante do produto de dois operadores A{Q, P) = h{a, a^) e B{Q,P) — f{a,a^) usa-se a propriedade dos estados coerentes [15]

(3.60)

sendo VF(a,a^) = h{a,a^)f{a,a^). No formalismo dos POG esta expressão fornece *CTV

W^^^{p,q) = h^-^^^ip^q) T ' r^{p^q), (3.61) _nn»^ ^CTV

Para o operador densidade P{t) = \xl){t)){ip{t)\ a equação de Liouville na representação dos POG é dada por

i^^{PQ\P(t)\P<l) = {pq\[H,P(t)]\p<l), (3.62)

usando a equação (3.57) pode-se escrevê-la na forma covariante^®

= '^^^{P,q) (t p^^{p,q,t). (3.63)

Definindo o operador Liouvilliano quântico

C°'' = (r - r), (3.64)

obtém-se

9, t) = -íP-^^P^^ÍP, q, t)- (3.65)

Se a função 'HP^{p,q) não depende explicitamente do tempo a solução formal da (3.65) é dada por (ver Apêndice I)

P^''{P, q, i) = q, to). (3.66) Da expressão (3.41) obtém-se o valor médio do operador A(Q, P)

1 roo roo

(A) = (rl)\A\i)) = — I dpi dqp^'^(p,q,t)A’^'^^(p,q). (3.67) ZTTtl J—oo J—oo

Esta expressão é análoga à (2.21) no formalismo de Weyl-Wigner, as ducis apresentam aparência de valor médio clássico.

Pode ser usada a relação de fechamento (3.24) e depois (3.56) obtendo-se 1 roo roo

^ 9^/ dqA^^(p,q) T p'^^ip,q,t), (3.68) _{^7Ttl J—oo J—oo} integrando-se por partes obtém-se

l roo roo fc —

A relação entre os dois formalismos estudados nos capítulos 2 e 3 deste trabalho é obtida a partir da expressão (3.29) fazendo previamente a mudança de variável q' — qw — ^/2, e q" = + H‘2 e escrevendo no formalismo de Weyl-Wigner [Eq.(2.11)]

í E E o,w{pw^qw) — J {qw 2^’

a transformada de Fourier desta expressão fornece o elemento de matriz f l 1 r°° . í

+ |) = ^ ^’’"^aw{Pw,qw). (3.70) definindo o novo kernel

íx -- _e pwí 1 f°° ç ç

9) Pwj qw) ~ 2 J 9) 9w 2»9tü 2 e observando que

K{p,q;qw - I>9«. + ' g-|^[2(9u.-9)^+Ç]+^(p-p«-)^

o que substituido em (3.71) após integração fornece

K{p,q’,Pw,qw) = e 0 .

(3.71)

(3.72)

Assim obtém-se a relação integral cv 1 í°°

(Pi9) — t / ^9«u / ^Pu/7í(p, ç5Pu;, Çu;)a^(pu,, Çu,). (3.73) 7T#l J—oo • /—oo

A partir de (3.41) pode-se obter a transformada de Weyl {q^u — ||A|çu, -|- |), em termos da forma contravariante,

awÍPw,qw) = ^ dpi dqK{p,q;p^,q^)A^'^^{p,q). (3.74) 7T tl J—oo J—oo

As expressões (3.42), (3.73) e (3.74) mostram que conhecida uma destas tres funções

i’’No caso particular do operador densidade, como a transformada de Weyl aw{pw,<lw) = 2Thpw{pw,qw,t), sendo Pw(Pw,qw,i) a função de Wigner dada por (2.18), tem-se de (3.73)

/OO yOO

A^^{p,q), {p,q) ou atu(pu/j9w) é possível encontrar as outras duas.

A^^{p, ç; al) A^^^Íp, q\ al) = 9; -a^)

^w{Pun qw)

3.3 APROXIMAÇÃO CAUSAL E APROXIMAÇÃO QUASI- CAUSAL NOS POG

No Apêndice I mostramos que a forma covariante do operador densidade pode ser escrita como

/OO fOO

dpo / dqow{p, 9, t|po, 9o, to)Pn^(po, 9o, to), (3.75) • OO J^oo

onde t/;(p, 9, í|po, 9o, to) representa a função de Green. Esta função é definifda por

9, t|po, 9o, to) = 9, to|po, 9o, to), (3.76) é a forma covariante do Liouvilliano quântico dada por (3.64) e io(p, 9, í|po, 90, to) satisfaz a condição

lim w{p, q,t\po, 9o, to) = <5(p - po)^(9 - 9o)- (3.77) t—►to

A expansão em série de potências de h, = H^o permite definir o operador

r*', (3.78) e calculando (d/dt)w{p,q,t\po,qo,to) em (3.76) vemos que a equação diferencial satisfeita pela função de Green é

Q

Usando a (3.78) tem-se para esta função {w{p,q,t\po,qo,to) = tn(í|to)) Q 9 °° / \ 1

+ i£„»(i|í„) = J ç í-j . (3.80) Considerando a colisão colinear não reativa descrita no Apêndice D temos a molécula diatômica (alvo) considerada como um oscilador harmônico e o átomo (projétil) tratado como partícula clássica, assim somente o oscilador terá correções quânticas^®. Para os índices (1) e (2) denotando a partícula livre e o oscilador harmônico respectivamente, tem- se

~ (4^) + 4^^) + + ^"4"*^ + • • • • (3.81) Portanto de como Cq = -f tem-se de (3.78)

d dVP^ d dVP^ d d dqi dpi dpi dqi dq2 dp2 dp2 dq2 A solução formal de (3.80) é

(3.82)

w{t\to) = e ‘‘’^^tüo(^o|ío) oo

(3.83) Na colisão estudada^®

w®'' = ^ + ^ + Ihll + + + (3.84) _{2mi 2m2 2 A \m2 a^J}

sendo Vgff = Voe*”®, temos portanto^^, para n > 1

l)n+iycv ^ ^ (3,85) \O,0/

Substituindo (3.85) em (3.83) tem-se n Jto

w{t\to) = e ‘°^^°tüo(tolM

h Jto

oo g-a(9i-92)

n=2

^®Para duas partículas D* = Yll=i D\ sendo Dk = ~ ^°Ver Apêndice K.

^^Para n > 1, _{ao àçy}

k= 1,2.

Esta expressão representa a função de Green para a colisão colinear não reativa.

Para a colisão colinear, a função distribuição do operador densidade, que designaremos daqui por diante por P{p,q,t) na sua forma covariante^^, será dada pela expressão (3.75)

/oo roo

dpo / dqow{t\to)P{po,qo,to), -CO • / —OO

(3.87)

sendo u;(í|to) dada por (3.86).

Multiplicando (3.86) por P{po, qo, to) e integrando em po e ço obtém-se

P{p,q,t) = e-d^-^°'>^°P{p,q,to)

_1_ 2V^ C r Y il^2.£j—e-'^*'-*°)^°P{p,q,to) h Jto '■ J

(3.88)

com

/oo roo roo roo

dpo dqoWo{to\to)P{po,qo,to) = dpo dqo6{p-po)6{q-qo)P{po,qo,to) = P{p,q,to • OO J —OO J — oo J — oo

onde foi usada a propriedade distributiva^^ para oproduto de duas funções f e g quaisquer

e-’(‘-‘')^(/ • g) = .

Também foi usada a evolução , iü(í'|ío) = e~d*'~^°^^w{to\to), que fornece /OO roo .. f . -

dpo / dqow{t'\to)P{po,qo,to) = P{p,q,t') = e“‘^‘°P{p,q,,to). -OO • /—OO

Ao colidir o átomo com a molécula (oscilador harmônico), esta passa de um estado para outro, pois haverá transferência de energia entre o alvo e o projétil, portanto as proba- bilidades de transição de um estado inicial (i) para um estado final (/)^^ são dadcis por (J.23)

1 /• oo roo _ ■, \r

Vi^i = 7^ / dp dqPi{p,q,to)ed^~^°^^Pf{p,q,to),

ZTTll J—oo oo (3.89)

^^Usaremos daqui por diante para a colisão a notação P(p, q, t) para a forma covariante da distribuição correspondente operador densidade e P{p,q,t) para a forma contravariante.

onde Pi{p,q,t) é a forma contravariante da distribuição correspondente ao operador densi- dade no estado inicial, Pf{p,q,to) é a forma covariante da distribuição do mesmo operador no estado final e £ a forma covariante de Liouvilliano dada por (3.81).

Para calcular e'^*~*°^‘"Pf{p,q,to) = Pf{p,q,t) em (3.89) procedemos de forma análoga à seguida para obter(3.88)^®.

Assim obtém-se

% Jta *•

,i{t-t')Co oo (ã2.£}*Y

Im Y, (3.90)

n=2

Substituindo (3.90) em (3.89) tem-se para as probabilidades de transição a expressão

Pi^S = dpi dqPi{p,q,to)ed^ ^°')^Pf{p,q,to) ZTTfl • /—oo */—oo

1 ^OO roo ^ r — dp dqPi(p,q,to) / df ,TZtl J—oo oo Jtn ^ h 2irh

Im Y n=2 n!

(3.91)

A primeira parcela de (3.91) é a AC na representação dos POG para a colisão estudada, na segunda parcela aparecem as correções quânticas e nela está incluida a AQC.

As expressões das funções Pj e P,- que aparecem em (3.91) são obtidas no apêndice N. Na segunda parcela de (3.91) tem-se

1 ha /m - V — _{^ l}

h ^2 \2ao7 ^ £)• " = /m "

ha n—1 1 2aoSv2ao/ nl^

(3.92) n=2

Ainda somando e subtraindo ao segundo membro de (3.92) Im{aD*/2ao) obtém-se

Im

^,è2\2ao7 n! D*" = Im

a ha 1

- 1 D\ i! "2flo[;^V2ao7 (« + !)!

Usamos também a propriedade dos operadores válida para um operador  qualquer (3.93)

/• l - oo / = Y Jo

A" ;S (" + !)!'

(3.94)

Portanto em (3.93) tem-se

= Im—\ -i]d\ h ^2 \2<io/ 2oo Uo

Substituindo (3.95) em (3.91) obtemos^®

'P.W = /^^A(p,9,<o)e'^‘"‘°^^°P/(p,9,to)

• • Im - l] Pf{p,q,to).

(3.95)

(3.96)

Até aqui todas^^ as correções quânticas são ainda conservadas na segunda parcela de (3.96). Nos apêndices O e P mostramos duas aproximações possíveis para a obtenção da AQC. Neste trabalho as duas aproximações foram tratadas e os resultados numéricos encontram- se no capítulo 4.

^®Usaremos o símbolo

é-jyiy-í dpdq

2nh

RESULTADOS E CONCLUSÕES

4.1 RESULTADOS

0 cálculo numérico apresentado neste capítulo foi efetuado com um computador BUR- ROUGHS 6900, os programas foram elaborados em linguagem FORTRAN IV e para re- solver o sistema de equações diferenciais acopladas foi usado o algoritmo “Diíferential Equa- tion Solver-Runge-Kutta-Verner Fifth and Sixth Order Method”.

4.1.1 RESULTADOS NUMÉRICOS PARA A AC

Os resultados numéricos para a AC (aproximação causai), correspondem ao cálculo da primeira parcela de (2.46) e (3.91) respectivamente, para os limites t oo e íq —oo

/oo roo

dpo / dqoWi{po,qo)wf{p{t),q{t)), (4.1) -oo J—oo

e

1 f°o _

^ ^ J-oo J-oo Qo)PíÍP{t)-Q{i))- (4.2) As funções Wi e Wj em (4.1) encontram-se no Apêndice E do capítulo 2 e as funções P, e Pf estão no Apêndice N do capítulo 3.

O método usado no cálculo de (4.1) é o SQC [5] descrito no parágrafo 2.3 e de forma análoga calculamos (4.2). O estado inicial do oscilador (molécula) é dado pelas distribuições Wi{pQ,qo) e Pi{po,qo) respectivamente, que são calculadas nos pontos da malha construída no espaço de fase. As coordenadas e momenta do átomo e da molécula evoluem de acordo com as equações de Hamilton (método das trajetórias clássicas, Apêndice C), as distribuições Wf{p{t),q{t)) e Pf{p{t),q{t)) descrevem o estado final da molécula. Os resul- tados encontram-se na tabela 4.1.

Observações referentes à tabela 4.1:

• As probabilidades de transição são calculadas para a colisão — He com os métodos QM [4], SQC(l) [5], SQC(2) (nossos cálculos) , POG (nossos cálculos).

• Os cálculos POG(a) (POG(b)) correspondem às probabilidades obtidas tomando na função Pi um número menor que (maior ou igual a) cem polinômios.

• Observamos que o cálculo das probabilidades pelo método POG admite correções . • O processo clássicamente proibido (Po—o para 20hwf2) também é obtido no método POG.

• Os valores que aparecem entre parênteses no método QM representam os limites superiores.

• A energia total {Etotai) refere-se à soma da energia inicial da partícula livre mais a energia inicial do oscilador harmônico, cissim, no caso de 8hwf2, se o oscilador estiver inicialmente no estado fundamental ("Po—/), a energia inicial do oscilador é hw(2, e 7tiwf2 para a partícula livre; analogamente para os demais casos.

4.1.2 AQC NO FORMALISMO DE WIGNER

Deve ser calculada a segunda parcela da equação (2.50), ou seja os limites t oo e to —> —oo em

BWmn í

E, total Pi. QM SQC(l) SQC(2) POG(a) POG(b)

) hw

Po->0 (0.892) 0.893 0.894 0.827 Po- 0.108 0.107 0.108 0.158

Po- 0.014

Ptotal 1.000 1.000 1.002 0.999

0.828 0.156 0.014 0.998

12^

Po^o (0.538) 0.520 0.524 Po. 0.394 0.412 0.414 Po- 0.068 0.068 0.068

0-*3 Po- Po-

Ptotal 1.000 1.000 1.006

0.497 0.348 0.029 0.029 0.005 0.001 0.909 16^

Po-^o (0.204) 0.187 0.193 0.227 Po- 0.434 0.422 0.422 0.337 Po- 0.291 0.314 0.316 0.249 Po- 0.071 0.077 0.076 0.122

Po- 0.045

Po. 0.013

Ptotal 1.000 1.000 1.007 0.993

0.228 0.337 0.249 0.122 0.045 0.013 0.994 20Ç

Po-*o (0.060) 0.046 0.048 0.085 Po- 0.218 0.202 0.207 0.212 Po. 0.366 0.351 0.353 0.259 Po- 0.267 0.294 0.293 0.211 Po- 0.089 0.106 0.105 0.129

Po—5 0.063

Ptotal 1.000 0.999 1.006 0.959

0.086 0.212 0.259 0.211 0.129 0.063 0.960

onde

^Po

a expressão entre colchetes é dada por (2.51) e as derivadas encontram-se no Apêndice H, a constante B = Tr{ha)^Vofl2 , po e qo representam as coordenadas do oscilador harmônico (molécula) no instante to e qi e Ç2 as coordenadas do átomo e molécula respectivamente, e t' — to é o argumento destas.

Na Tabela 4.2 estão as probabilidades de transição para a mesma colisão colinear Hg — H2 calculadas pelos métodos QM [4], SQC(l) [5] e SQC(2) (nossos cáculos). Também colocamos o valor da correção obtido usando a equação (4.3), a reação foi tratada da seguinte forma: Para dadas energias iniciais da partícula livre^ e do oscilador^, é calculada a distribuição de Wigner ini(po,9o) em cada um dos pontos da malha construída no espaço de fase, as coordenadas çi(ío), Pi(^o), P2{ío) = Po e 92(^0) = Ço evoluem de acordo com as equações de Hamilton; após “colidir” com o oscilador a partícula livre volta para a mesma região de origem, quando a energia total final fica constante (a precisão do cálculo desejada é fixada previamente) e as coordenadas 9i(<), Pi(^), 92(0 = ?(0 ) Pí(0 = P(0 usadas para calcular as distribuições Wn{p{t),q{t)) que aparecem na expressão (4.3).

Para confecção da Tabela 4.2 a malha do espaço de fase foi construída com 30 x 30 pontos, e feita simétrica em relação à origem que não foi incluída. A precisão do cálculo é descrita no Apêndice E.

De forma análoga foi construida a Tabela 4.3

• Observamos nas Tabelas 4.2 e 4.3 que as correções não tornam os cálculos SQC mais próximos dos resultados obtidos pelo método QM.

• Como as trajetórias não possuem o mesmo número de pontos, ou seja o instante em que a energia total é constante não é o mesmo para todos os pontos da malha, modificamos o programa do computador impondo que todas as trajetórias tenham o mesmo número de intervalos de tempo, os resultados assim obtidos encontram-se na Tabela 4.4. Todos os cálculos desta tabela correspondem à energia total 8hwf2.

^Na Tabela 4.2 corresponde a bhw/2. ^Na Tabela 4.2 corresponde a Zhw/2.

w„

/oo ro. dpo /

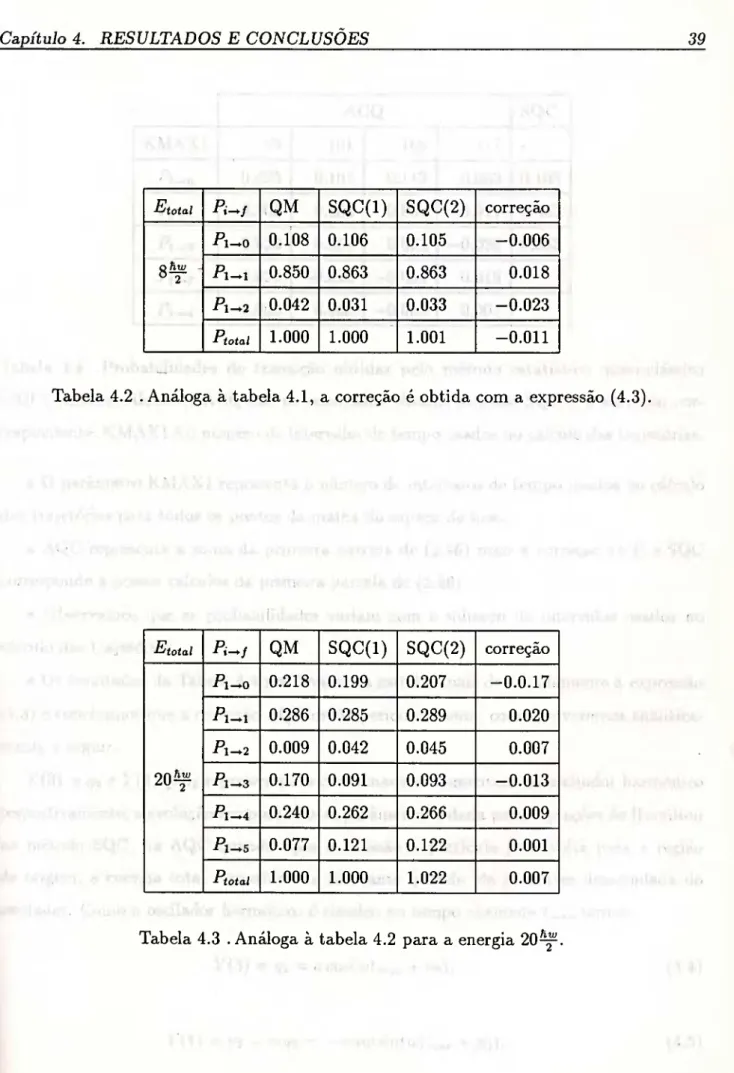
Tabela 4.2 . Análoga à tabela 4.1, a correção é obtida com a expressão (4.3).

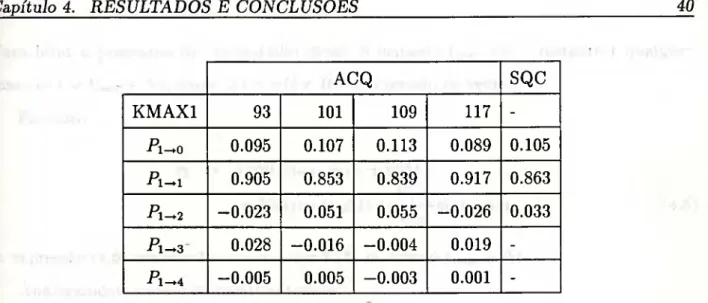
ACQ SQC

KMAXl 93 101 109 117

Pi^o 0.095 0.107 0.113 0.089 0.105 Pi- 0.905 0.853 0.839 0.917 0.863 Pi- -0.023 0.051 0.055 -0.026 0.033 Pi- 0.028 -0.016 -0.004 0.019

Pi- -0.005 0.005 -0.003 0.001

Tabela 4.4 . Probabilidades de transição obtidas pelo método estatístico quasi-clássico (SQC) (nossos cálculos), ACQ são os resultados obtidos somado SQC e a correção cor- respondente, KMAXl é o número de intervalos de tempo usados no cálculo das trajetórias.

• O parâmetro KMAXl representa o número de intervalos de tempo usados no cálculo das trajetórias para todos os pontos da malha do espaço de fase.

• AQC representa a soma da primeira parcela de (2.46) mais a correção (4.3) e SQC corresponde a nossos cálculos da primeira parcela de (2.46).

• Observamos que as probabilidades variam com o número de intervalos usados no cálculo das trajetórias.

• Os resultados da Tabela 4.4 nos levaram a estudar mais detalhadamente a expressão (4.3) e concluímos que a correção AQC oscila periódicamente, como provaremos analitica- mente a seguir.

Y{3) = Ç2 oY(4) = p2 representam a coordenada e momentum do oscilador harmônico respectivamente, a evolução temporal destes parâmetros é dada pelas equações de Hamilton no método SQC, na AQC quando após a colissão a partícula livre volta para a região de origem, a energia total é considerada constante quando ela já estiver desacoplada do oscilador. Como o oscilador harmônico é clássico no tempo chamado tmax tem-se

Y{3) = q2 = acos{wtmax + (l>o), (4.4)

Para levar o programa de computador desde o instante tmax s-té o instante t qualquer, fazemos t = tmax + Aí, sendo Aí = nH e H é o intervalo de tempo.

Portanto

Q2 = a COs{wtmax + <f>0 + wAt)

= Y(3) cos(iüAí) H ^ sin(iüAí). (4-6) mw

A expressão (4.6) representa o novo valor F(3) no tempo tmax + Aí. Analogamente para o momentum tem-se

P2 = —mawsm{wtmax + (f>o + wAt)

= Y{4) cos(tüAí) — mwY{3) sin(iüAí), (4.7)

que é o momentum no tempo í = tmax + Aí.

Em (4.7), para Y{4) = a e —mwY{3) = b, tem-se p2 = acos(u>í) -|- 6sin(ií;í), por conseguinte

P2 = cos^ wt -|- sin^ wt -h 3aò^ cos wt sin^ wt + 3a^b sin wt cos^ wt. (4-8)

Em (2.50) como (ver Apêndice H)

dpi^ f^n{p, q) = Ap% -f Bp2 onde

A = / 2 \ ^ 2 d^w ( 2 \ ^ \hwrn) hwm dy^ \hwm) dy"^ a parcela da correção é

K^(Yvn í°° r°° / \ /■* r /1

27t^—24— J J ^^oWnÍPo-qo) (Apl -f- BP2)

onde í' — ío é o argumento de qi eç2 na integral temporal. Fazendo

a = ^(o — i6), e a* = ^(a ib) ^ íi

— to) —92(í' —ío)l

giwí ^ g-itot

COS wt — , siniüí =

gttoi e"”"*

tem-se

(4.10)

pI = -f -h -f- 3aa*2e-“^‘ (4.11)

com

Apl + Bp2 = /lQ“e“”' + + (3a“a‘ + Ba)e'“* + (3/taa’'' + Ba')e-‘”‘.

(4.12)

Para

Ox = (3AaQ:* -f- B){a -|- a*), 6i = i(3Ao;a* -f B){a — a*) Ü3 = i4(a^ -|- o;*^), 63 = iA{a^ — o:*^),

a expressão (4.12) é dada por

Ap| -|- Bp2 = as cos{3wt) -f 63 sin(3tüí) -|- oi cos(iüí) -|- 61 sin{wt). (4-13)

Como qualquer função periódica pode ser expandida na forma [34] ü ^

t + E[- „ cos{nwt) + bn sin(mi;<)], ^ n=l

(com 0 < wt < tt), portanto, a função em (4.13) é periódica com üq = 02„ = Ò2n = 0 para n = 1,2,... e a2n+i = ^2n-i-i = 0, n = 2,3,.., assim, a parcela da correção (4.9) é periódica. A média temporal desta parcela de correção em um periódo do oscilador harmônico é nula.

4.1.3 AQC NO FORMALISMO DOS POG

com

sin (^) rt S = 1= dre-°

20ft

Para o cálculo da probabilidade Vo^o temos OO

h{p,q,to) = 51 ^n[y{to)] e Po{p2,q2,t) = n=0

e para calcular 'Po->i usamos as funções Pq , I ,y e S da expressão (4.14), e (Apêndice O) (0.43), ou seja

Pi-i ^ y^^A(p,9,ío)A(P2>92,í)

(4.15)

com Pi{p2,q2,t) = y(í)e“5'(‘) e C = cos

Os resultados obtidos estãx) na Tabela 4.5. Esta tabela prova numericamente que, analogamente aos cálculos feitos na seção 4.2 deste capítulo, como a parcela de correção varia com o tempo a média temporal da mesma é nula num período do oscilador, pois oscila periodicamente.

Damos a seguir a prova analítica deste resultado.

Substituindo em (4.14) a função S por uma função F de argumento p^, ou seja S = F{p\), sendo E a energia total do oscilador harmônico

2m2 2

observamos que o argumento ép\ = 2m2E—m\w^portanto , F{p^ pode ser representada por uma função F de argumento Ç2 já que após o desacoplamento da partícula do oscilador harmônico a energia total é constante, ou seja F(j>\) — S = F{q2). Também consideramos P2 = m2V2 = 771292 G F{q2)e~^^'^ = f{q2)i portanto pode-se escrever

P2

sm

Eioial 12^

16^

20^

Pi^j QM SQC(l) POG correção Po-*o (0.538) 0.520 0.497 -0.681 x 10"® Po-i 0.394 0.412 0.348 0.296 x 10"® Po-»o (0.204) 0.187 0.228 -0.604 x IO"* Po-i 0.434 0.422 0.337 0.177 x 10"® Po-o (0.060) 0.046 0.087 0.245 x 10"» Po-i 0.218 0.202 0.212 0.304 x 10"®

Tabela 4.5 .Análoga à tabela 4.1, a correção corresponde à média temporal da segunda parcela de (4.15) num período do oscilador.

Se o período do oscilador é T

tT rT I-T

/ dtm2Ç2[l - /(?2)] = / dtni2q2 ~ / ^^771292/(92)- Jo Jo Jo

A primeira integral em (4.17) resulta em m292lo = »^2[92(T') — 92(0)] = 0 coordenada do oscilador harmônico (clássico) e T é seu período. A segunda

(4.17) é escrita Jq ^<92/(92) = G(92)|o ? com

(4.17) pois 92 é a integral em

como 92(T) = 92(0), então G{q2{T)) = ^(92(6)). Observações referentes à tabela 4.5.

• A reação estudada na tabela 4.5 é a mesma da tabela 4.1.

• QM, SQC e POG referem-se aos métodos das referências [4] e [5] e a primeira parcela da equação (4.14) e (4.15) respectivamente.

• Etotai é a energia da partícula livre mais a energia do oscilador harmônico. • O número de polinômios tomado nas funções P, é 150.

• O número de pontos na malha do espaço de fase é 31.

• A correção corresponde à média temporal, num período do oscilador harmônico para a segunda parcela de (4.14) e (4.15) respectivamente.

A AQC para a aproximação do Apêndice P corresponde ao cálculo das probabilidades Vi^f usando as expressões (P.3) para / = 0 e (P.4) para / = 1 respectivamente, ou seja

Pi-O ^ / ^Í(p,9,Íü)|Fo(p(<),9(<)) - (■‘• '8)

sendo

Fo{t) = ^ /‘dr[e-“í’‘(")-«(")le-"("V2(T)/(p2(r),9(r))], iXCLq */ío

I(p^(r)Mr)) = 1 - (^)

+ ^P2(^)]>

Po e P,- dados pelas expressões do Apêndice N. No caso do cáculo da probabilidade Po^o, tem-se Pq = e~« e Po = e~*' ^n(y)-

Usando estes mesmos símbolos acima definidos

Pi-i ^ / ^fl(P.?,<o)(í>i(p(i),9(<)) - ('‘• 19) onde

^‘(1) = /‘‘í’-le-"t«W-«Wle-»Mp2(T)/'(p2(T),,2(r))], _{noo Jto}

I\P2{r),q2{r)) = J/(r) - 1 -|- C(r),

C(r) = e COS ~ (f 92(r) -f y(r)) [1 - /(p2(r), 92(r))] e Pi = t/e”*' (ver Apêndice N).

O primeiro estudo efetuado foi verificar se a parcela de correção em (4.18) e (4.19) oscilava periodicamente, como acontecia na aproximação drástica do Apêndice 0.

Foram selecionados alguns pontos da malha construída no espaço de fase e observamos que a função

1 - _ap2 2o,

92 (0

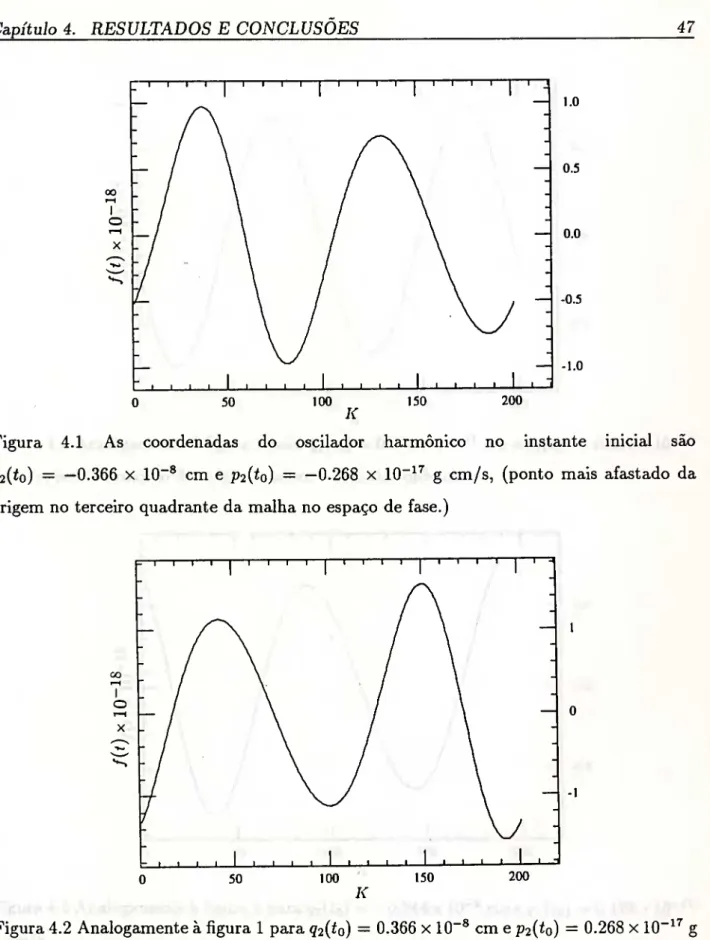
Figura 4.1 As coordenadas do oscilador harmônico no instante inicial são 92(^0) = —0.366 X 10“® cm e ^2(^0) = —0.268 x 10“*^ g cm/s, (ponto mais afastado da origem no terceiro quadrante da malha no espaço de fase.)

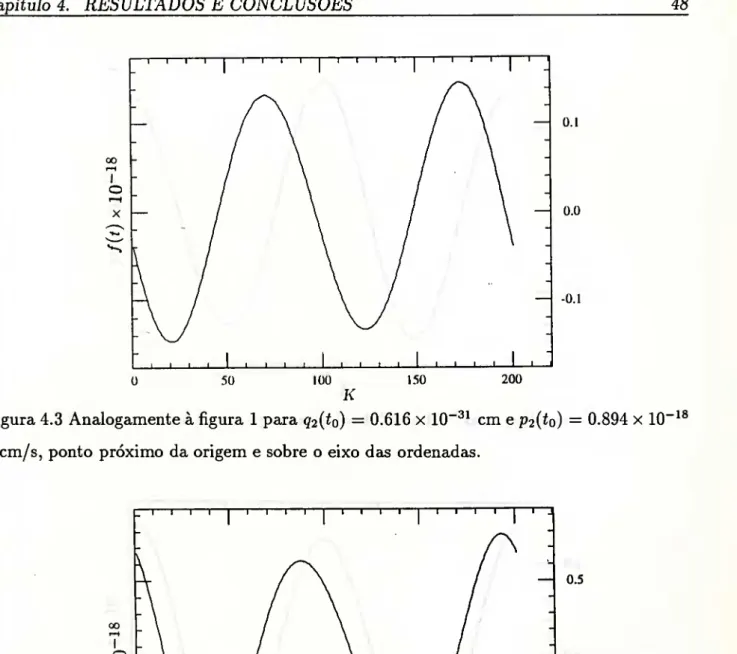
Figura 4.3 Analogamente à figura 1 para 92(^0) = 0.616 x 10 cm e P2(to) = 0.894 x 10 g cm/s, ponto próximo da origem e sobre o eixo das ordenadas.

Figura 4.5 Analogamente à figura 1 para 92(^0) = 0.244 x 10“® cm e ^2(^0) = —0.894 x 10“^* g cm/s.

g cm/s.

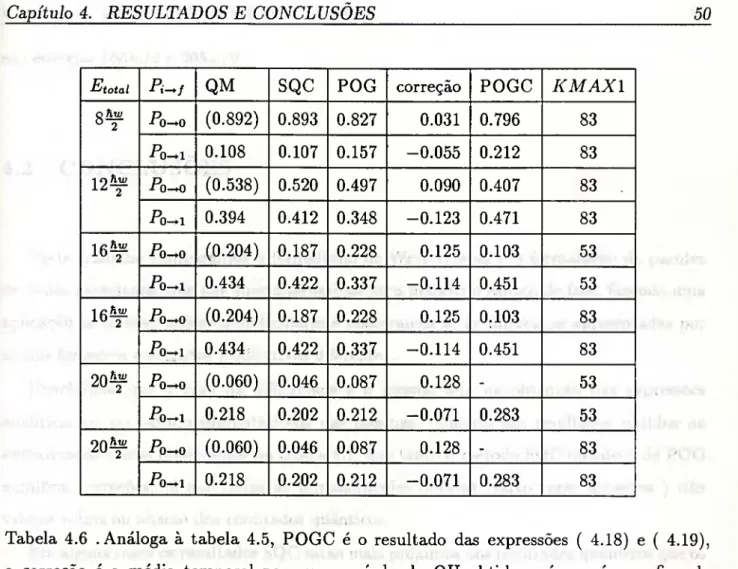
0.894 X 10-^«

Etotal Pi QM SQC POG correção POGC KMAXl 8^ Po->^0 (0.892) 0.893 0.827 0.031 0.796

Po- 0.108 0.107 0.157 -0.055 0.212

83 83 12^ (0.538) 0.520 0.497 0.090 0.407

Po- 0.394 0.412 0.348 -0.123 0.471

83 83 16 hw Pq-*o (0.204) 0.187 0.228 0.125 0.103

Po- 0.434 0.422 0.337 -0.114 0.451

53 53 16^ Po->o (0.204) 0.187 0.228 0.125 0.103

0-+1 0.434 0.422 0.337 -0.114 0.451

83 83 20 hw Po-»0 (0.060) 0.046 0.087 0.128

Po- 0.218 0.202 0.212 -0.071 0.283

53 53 20^ Po-*0 (0.060) 0.046 0.087 0.128

Po- 0.218 0.202 0.212 -0.071 0.283

83 83

Tabela 4.6 .Análoga à tabela 4.5, POGC é o resultado das expressões ( 4.18) e ( 4.19), a correção é a média temporal para um período do OH obtido após o número fixo de intervalos de tempo KMAXl.

Na tabela 4.6 encontram-se os resultados obtidos nos cálculos das probabilidades e respectivas correções, com as expressões (4.18) e (4.19) para as diferentes energias.

Observações referentes à tabela 4.6.

• QM, SQC e POG são os resultados obtidos nas referências [4] e [5] e primeira parcela de (4.18) e (4.19), são os mesmos valores que constam na tabela 4.5.

• A correção foi obtida com a segunda parcela de (4.18) e (4.19) respectivamente. • A energia total (Etotai) é a mesma usada nas tabelas anteriores, ou seja a energia do oscilador harmônico mais a energia da partícula livre.

nas energias 16tíwf2 e 20hwf2.

4.2 CONCLUSÕES

Neste trabalho comparamos o formalismo de Weyl-Wigner e o formalismo de pacotes de ondas gaussianos, que são duas alternativas para mapear o espaço de fase, fazendo uma aplicação às colisões atômico-moleculares e observamos se as diferenças apresentadas por ambos fornecem resultados qualitativos diferentes.

Concluímos que o grau de dificuldade é o mesmo seja na obtenção das expressões analíticas ou no cálculo computacional das mesmas. Quanto aos resultados obtidos na aproximação causai observamos na tabela 4.1, que tanto o método SQC quanto o de POG admitem correções, já que todas as probabilidades obtidas (salvo raras exceções ) dão valores acima ou abaixo dos resultados quânticos.

Em alguns casos os resultados SQC estão mais próximos dos resultados quânticos que os resultados POG mas existem casos em que o comportamento destes resultados é o inverso. A vantagem oferecida por estes métodos semiclássicos é a de exigir nos cálculos com- putacionais um esforço menor que os cálculos quânticos, especialmente para as colisões com energias mais altas.

A correção na AQC proposta para os dois métodos, a partir das expressões (4.3) e segunda parcela de (4.14) respectivamente oscila periodicamente com o tempo, uma média temporal resulta no valor zero para esta correção . Este resultado confirma mais uma vez a analogia entre os dois formalismos SQC e POG.

A segunda correção estudada para os POG, usando a aproximação do Apêndice P, leva a resultados interessantes e não totalmente explorados neste trabalho. Entre estes resultados observamos (ver tabela 4.6)

• Para a energia 20^ a aproximação causai nos POG deu para a probabilidade Po-»i resultado mais próximo do valor quântico que o obtido pelo método SQC, porém, para Po-^o^, que corresponde a um processo clássicamente proibido [5] o valor da correçãx) foi maior que o valor da probabilidade.

• Não foi estudado se o método POG obedece à reversibilidade microscópica com boa aproximação , para isto deveriam ser calculadas as probabilidades Pi_o para as diferentes energias e estes resultados deveriam coincidir com os respectivos valores de Po->i •

• Seria interessante realizar cálculos para aplicar este método dos POG a outras reações diferentes da estudada neste trabalho, por exemplo, poderiam ser estudadas reações do tipo H, - HBr.

• Finalmente, nesta segunda aproximação (Apêndice P) a correção não melhorou os resultados já obtidos com a aproximação causai conforme mostra a tabela 4.6 , porém não sabemos se tomando mais termos na expansão de os resultados obtidos seriam melhores. A expressão analítica para estes novos cálculos foi obtida, porém a dificuldade para efetuar os cálculos numéricos é grande.

Propriedades do Operador de Evolução

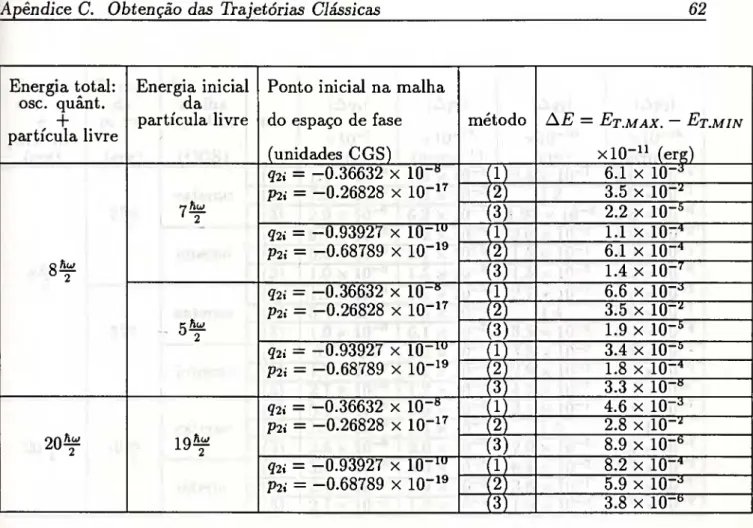
Sendo q{t) e ço as coordenadcis e p{i) e po os momenta do ponto nos instantes t e inicial {t = 0) respectivamente, o operador Liouvilliano Co = i (|“^ — atuando sobre q{t) e p{t) fornece [18] iCoq{t) = ^q{t) = ou seja q{i) = |^ e para o momento iCop{i) = == “§7» ~ equações de Hamilton. Portanto o operador Co pode ser escrito

Para o instante inicial í = 0 e as variáveis ço e po este mesmo operador é dado por Q í dh d dh d \

° \dqodpo dpodqo)'

Expandindo em série de Maclaurin [19] as funções q{t) e p{t) temos oo an

9(<) =12-, n=0

(A.l)

(A.2)

(A.3) J <=0

oo /n = E

n=0 n\

d'" / x' <=0

Por outro lado, da equação de Liouville obtemos para o termo n = 1

= [í^oç(0]t=o = d . .

J f=0

onde ç(0) = qo e analogamente para o momento d

dt p(0 = [*>Cop(í)]t=o = *^oP(0),

(A.4)

(A.5)

(A.6) J t=Q