Probabilistic Broadcasting Protocol In AD HOC Network And Its Advancement: A Review

DOI : 10.5121/ijcses.2010.1201 1

Tasneem Bano

, Jyoti Singhai

1

Department of Computer Science And Engineering, MANIT, Bhopal, India

2

Department of Electronics And Communication Engineering, MANIT, Bhopal, India

ABSTRACT

Broadcasting is a fundamental operation in MANETs where a source node transmits a message that is to be disseminated to all the nodes in the network. Broadcasting is categorized into deterministic and probabilistic schemes. This paper reviews the probabilistic broadcasting protocol because of its adaptability in changing environment. Probabilistic broadcasting is best suited in terms of ad hoc network which is well known for its decentralized network nature. Probability, counter and distance based scheme under probabilistic scheme are discussed in this paper. Besides the basic probability scheme this paper also includes their recent advancements. Rebroadcast is one of the initial task for route discovery in reactive protocols. This review paper identify which protocol gives better performance in terms of reachability, saved rebroadcast and average latency in rebroadcasting a route request message. Simulation results are presented, which shows reachability, saved rebroadcast and average latency of the probabilistic broadcast protocols and their enhancement schemes. The comparative study shows the improvement of enhanced scheme over probabilistic schemes.

KEYWORDS

Probabilistic broadcasting, Probability based scheme, Counter based scheme, Distance based scheme, Reachability, Saved Rebroadcast.

1.

I

2

An optimal broadcast protocol minimizes one or more of the following measures: 1) The maximum time needed for the broadcasted message to reach all nodes;

2) The average time, over all the nodes, needed for the broadcasted message to arrive at each node

The paper is organized as follows Section II briefly describes the probabilistic based protocols. Section III presents analysis and results of probability, counter and distance based scheme and performance metric used in the simulation. Section IV provides an overview of recent advancement in conventional probabilistic scheme and their performance analysis. Section V concludes with the obtained results and their comparative analysis.

2.

RELATED

WORK

Traditional on-demand routing protocol [ 4,5 ] produce a large amount of routing control

traffic by blindly flooding RREQ packets in the entire network during route discovery.

The dissemination of RREQ packets can be quite huge, especially when the network

density is high and the network topology changes frequently. Various broadcasting

protocols have been developed towards mitigating the RREQ floods such as probabilistic

based, counter based and distance based protocol.

Probabilistic based protocol has also been proposed to help control the dissemination of

the routing control packets. Bani Yassein et al. [20, 21] have proposed fixed pair of

adjusted probabilistic broadcasting scheme where the forwarding probability p is adjusted

by the local topology information. Topology information is obtained by proactive

exchange of “HELLO“packets between neighbours to construct a 1-hop neighbour list at

every node. Hanashi, A.M. et al [22] have proposed a probabilistic approach that

dynamically calculates the rebroadcast probability according to the number of neighbour

nodes distributed in the ad hoc network for routing request packets.

The basic idea of the counter based protocol is based on the inverse relation between the

expected additional coverage (EAC) and number of duplicate broadcast packets received

[2,23]. A node is prevented from retransmitting a received broadcast packet when the

EAC of the node’s rebroadcast is low [24]. An adaptive counter based was proposed in

[11] where in the decision to forward the broadcast packet is determined b the function

C(n) where n is the number of neighbours of the forwarding node. Other variants of the

counter based broadcast are color-based [9] and position-based [25].

Distance based protocol makes use of the distance between the source node and the

receiver. In this protocol a node receiving a broadcast message for the first time will

compute the distance to the source node. If this distance is small, the message is dropped

otherwise it is forwarded [2].

3.

PROBABILISTIC

BASED

PROTOCOL

Among the deterministic and probabilistic approaches probabilistic scheme is one of the best ways to reduce rebroadcast. In a probabilistic scheme, nodes rebroadcast the message with a pre determined probability p. the studies in [3, 13] shows that probabilistic broadcast incurs significantly lower overhead as compared to blind flooding. Several probabilistic schemes have been proposed in the past [10, 11]. These include probability-based,counter-based and distance-based [10, 11-14].

Each probability model is represented by the equation:

3

Where P is the probability that a node forwards the broadcast packet and N is the number of nodes in the network. The function f depends on the specific protocol being analyzed.

3.1 Probability-Based Scheme

In the probability based scheme, this is a simple probabilistic approach of probability 1 or 0 for rebroadcasting. A node will broadcast either with probability 1 or with probability 0. That means with probability 1 it behaves like a flooding approach where as with 0 probability it is not broadcasting a single packet.

3.2. Counter-Based Scheme

In the Counter-Based scheme, a node v will only rebroadcast if it receives less than a threshold (T) number of copies of a packet before its RAD expires. Each node keeps track of duplicate packets with a counter; the counter is incremented by 1 for each duplicate packet received before the RAD expires. For a random node v to receive a duplicate packet (and increment its counter) from a random node u, three events must occur:

1) Node u must be a neighbor of node v. 2) Node u must transmit the packet.

3) Node u must transmit the packet before v’s RAD timer expires.

The probability Q that node v increments its counter (i.e. events A, B, and C have all occurred) is equal to P (1U2U3).

3.3 Distance-Based Scheme

In the Distance-Based scheme, a node v will not rebroadcast if it receives its initial packet from a source node s that is within a threshold distance D. Consider an annulus area centered at v, with the radius of the inner circle equal to D and the radius of the outer circle equal to the transmission distance R. (The annulus area is the area outside the circle with radius D and inside the circle with radius R.) If node s is in the annulus area, then v will start a RAD and wait for duplicate packets. During the RAD, if any duplicate packet is received from a node u within a distance of D to v, then v will not rebroadcast. We define the following events to determine the probability of v receiving a duplicate packet from a random node u, such that u is within a distance of D to v, before its RAD expires:

1) Node u is within distance D of node v. 2) Node u transmits the packet.

3) Node u transmits the packet before v’s RAD timer expires

The probability that node v receives this kind of packet is equal to P (1 2 3)

4.

PERFORMANCE

ANALYSIS

OF

PROBABILISTIC

BASED

SCHEME

The performance metrics [2] to be observed are:

4

B. Saved ReBroadcast (SRB): This is a percentage of nodes that have received but not rebroadcast the message and is given by (r - t)/r, where r is the number of hosts receiving the broadcast message, and t is the number of hosts actually transmitted the message.

C. Average Latency: The average time difference between the time the broadcast was initiated to the time the last host finishing its rebroadcast.

All the three schemes are implemented using C++. The simulation results [2] of the probabilistic, counter-based and distance-based schemes are shown in Figure. 1, Figure. 2, and Figure. 3 respectively. Each point in these Figures represents results obtained from a simulation run containing 10,000 broadcast requests. Figure. 1(a) shows the observed RE and SRB associated with the probabilistic scheme. In a small map (which implies a dense host distribution), a small probability P is sufficient to achieve high reachability, while a larger P is needed if the host distribution is sparse. The amount of saving (SRB) decreases, roughly proportionally to (1 - P), as P increases. Also, the performance of broadcasting by flooding can be found at the position where the probability P = 1. Figure. 1(b) shows the broadcast latency at various P values. One of the major problem of probabilistic scheme is how to set the rebroadcast probability Figure. 2 shows the performance of the counter-based scheme. In Figure. 2(a), we see that the reachability RE in fact reaches about the same level as that of the flooding scheme when the counter threshold C >= 3. However, various levels of saving (SRB) can be obtained over the flooding scheme, depending on the density of hosts in a map. For instance, the scheme in higher density maps (e.g., 1 x 1, 3 x 3, or 5 x 5) can offer 27 ~ 67% saving at C = 3, while in lower density maps (e.g., 7 x 7, 9 x 9, or 11 x 11) 8 ~ 20% saving. When C is larger (say

Figure 1. Performance of the probabilistic scheme. (a) Probability P vs. RE (shown in lines) and SRB (shown in bars). (b) P vs. Average Latency.

5

Figure 3. Performance of the Distance-based scheme. (a) Distance threshold D vs. RE (shown in lines) and SRB (shown in bars). (b) Distance threshold D vs. Average latency.

6) and the map is sparse (say 11 x 1 l), the amount of saving decreases sharply. This is because the number of neighbors of a host tends to be small (2.4 neighbors per host in an 11 x 11 map), and thus it is less likely that a host will receive the same broadcast message more than C times. So a threshold C of 3 or 4 is an appropriate choice.

Distance-based scheme [2] incurs a higher broadcast latency than that of the counter-based scheme, as shown in Figure. 2(b) and Figure. 3(b). The reason that the distance-based scheme saves less rebroadcasts than the counter-based scheme is because in the distance-based scheme, a host may have heard a broadcast message so many times but still rebroadcast the message because none of the transmission distances are below a given distance threshold, where the rebroadcast would have been canceled in counter-based scheme.

5.

ADVANCEMENT

IN

CONVENTIONAL

PROBABILISTIC

SCHEME

Various advancement has been done till now, in the above broadcast scheme. Developing new scheme which not only overcome the above limitation but also enhance the performance of conventional scheme with respect to reachability, saved rebroadcast, average latency performance parameter. The three combinational schemes analyzed are as follows:

- Combination of Probabilistic and Counter based scheme. [12] - Combination of Probabilistic and Distance based scheme. [13] - Combination of Counter and Distance based scheme. [14]

All the above stated schemes have been implemented on NS-2[19] simulator and the results are being analyzed on performance parameter such as reachability, saved rebroadcast etc in section III.

5.1 Combination of Probabilistic and Counter based scheme:

6

probability P at each mobile host is dynamically adjusted according to the value of the local packet counter. The value of P changes when the host moves to a different neighborhood. In a sparser area, the rebroadcast probability is set to high value and in denser area, the probability is set to lower value. When compared with the probabilistic approach where P is fixed, this algorithm achieves higher throughput since the total number of rebroadcasts is reduced. On the other hand, the decision of rebroadcast is made immediately after receiving a packet without any delay.

5.1.1 Performance analysis:

In [12] the performance of the broadcasting approach is studied in context with AODV routing protocol. The original AODV protocol uses simple flooding to broadcast routing request. The proposed scheme is implemented on AODV called as dynamic probability AODV [DP-AODV]. In DP-AODV the rebroadcast probability is dynamically set. Whereas in fixed probability AODV [FP-AODV] the rebroadcast probability is fixed. In sparser area, the probability is high and in denser area the probability is low. On the same network topology, the rebroadcast probability P in FP-AODV should be no less than the probability of DP-AODV nodes in sparse area in order to maintain the same level of reachability. As a result, the number of rebroadcasts in DP-AODV is definitely smaller than that of FP-AODV. As shown in Figure. 4, FP-AODV can substantially reduce the number of rebroadcasts in AODV. The saving is around 30%. DP-AODV can further reduce the number by 10%. This indicates that DP-AODV is the most efficient. There is no significant difference among the reachability of the three approaches AODV, DP-AODV, FP-AODV. This indicates that the value of the fixed probability (0.6) in the simulation is a good choice for maintaining high reachability. It also infers that the dynamic probabilistic approach can achieve high throughput without sacrificing reachability. Since rebroadcasts will collide and content channel with each other and the dynamic probabilistic approach incurs the least number of rebroadcasts, it should have the lowest latency.

Figure 4. Comparison of rebroadcast numbers

5.2 Combination of Probabilistic and Distance based scheme

7

information sent periodical by the neighbors. A node sends a broadcast without imposing its choices to its neighbors. In [14], the probabilistic scheme is called simple probabilistic scheme or Mode 1 and further improved modes are proposed and they are as follows:

5.2.1 Density Aware Probabilistic Flooding (Mode 2):

The approach of this mode is the same as of simple probabilistic scheme but the probability p is computed from the local density n (i.e. the number of neighbors). A host will rebroadcast flooding messages with the probability

p = fmode2 (n):

n k n

f

2

mod (1)

Where k is an efficiency parameter to achieve the reachability of the broadcast.

5.2.2 Border Retransmission Based Probabilistic Flooding (Mode 3):

The above stated models have the disadvantage to be locally uniform. Each node in a given area receives a broadcast and determines the probability according to a constant or from the local

density. The probability of sending p with the fmode3 formula:

α

α

µ

µ

+

−

=

M

A

f

(

)

3

mod (2)

With:

• A and : the roof and floor probability levels (with the values 0.0 and 1.0 respectively in this paper),

• : coefficient of convexity,

• M: constant which represents the maximal value of . This value can be evaluated by the

maximal value of the ratio

which corresponds to the case when the distance between src and dest is equal to the transmission radius. Numerically,

-

Where the neighbors of src (Na, number of nodes inside the Za) the neighbors of dest (Nb, number of nodes inside the Zb) and the neighbors of src and dest (Nc, number of nodes inside topology and adjusted by the knowledge of the set of non common neighbors).

5.2.3 Density Aware and Border Node Retransmission Based Probabilistic Flooding (Mode 4):

This mode is a combination of the two previous ones: the probability p is computed from the local topology and adjusted by the knowledge of the set of non common neighbors. Equation (2) is reused but the roof level probability A is evaluated with equation (1):

α

α

µ

µ

Μ

f

4

8

5.2.4 Density Aware and Border Node Retransmission Based Probabilistic Flooding with Neighbor Elimination (Mode 5):

The above mode have a disadvantage: all the reachable nodes would not be contacted in the case of a bad random number. In some situation, a group of neighbors might not rebroadcast the message. Thus resulting in some nodes not being contacted. In the worst cases, a partition of the network can occur even if the missed nodes are reachable. Solution of this problem is presented in [15] it is based on a neighbor elimination scheme: each node checks if all the neighbors have received the broadcast message.

For the modes 3 and 4, each node which forwards the broadcast message includes the list of its neighbors. The receiver can identify which nodes have been covered by checking the neighbor list of the transmitter and comparing with its own neighbor list. In the proposed algorithm for neighbor elimination, each node has a broadcast table BT, where identifiers are recorded for each broadcast already received. This table is extended with an improvement: for each new entry in BT, a list of the neighbors from the neighbor table NT of the receiver is added. The neighbor elimination algorithm is as follows:

Protocol NeighborElimination ()

{

IF messages receives for the first time Get the Broadcast ID bid from the message THEN

Create an entry BTbid in the Broadcast Table. Create a list Lbid with all the IDs in the neighbor table.

END IF

FOR EACH id included in the message DO

IF id is included in Lbid remove id from Lbid END IF

END FOR }

Neighbor Elimination algorithm.

The algorithm is used by the nodes which do not broadcast the message according to probabilistic function of the previous mode (fmode4).

5.2.5 Performance analysis:

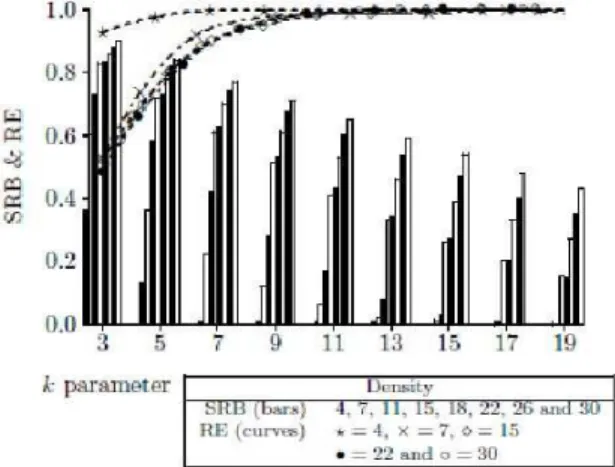
The simulation results of all the 5 modes given [13] shows that the mode 1 scheme is relatively inefficient as shown in Figure. 5, especially in low density (when p<0.7 the number of saved broadcast messages is inverse of the rebroadcast probability). Mode 2 performance is shown in Figure. 6 which is same as the previous mode. The parameter k used in the formula (1) is useful in partial broadcasting.

9

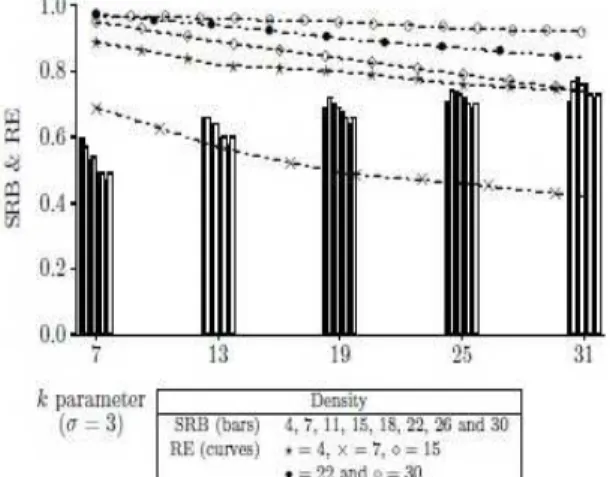
or 2. Figure. 8 presents the performance of mode 4 and it is observed that about 80% of the network can be reached with a saved rebroadcast greater than 0.8 for =3 and hence we conclude that mode 4 is useful in partial broadcasting. Figure. 9 and Figure. 10 present the performance of mode 5 and it is found that the reachability is perfect with whatever value holds.

Figure 5. Simple Probabilistic Flooding (mode 1)

Figure 6. Density aware Probabilistic Flooding (mode 2) parameter k vs. reachability (shown in lines) and saved rebroadcast (shown in bars)

10

Figure 8. Density Aware and border Node Retransmission based Probabilistic Flooding ( mode 4) with =3: parameter k vs. reachability (shown in lines) and saved rebroadcast ( shown in bars).

Figure 9. Density Aware and border Node Retransmission based Probabilistic Flooding with neighbor elimination (mode 5) with =1: parameter k vs. reachability (shown in lines) and saved rebroadcast (shown in bars).

11

5.3 A Combination of Counter and Distance based scheme:

The proposed approach gives nodes closer to the border a higher rebroadcast probability since they create better Expected Additional Coverage (EAC) [2]. Here, a distance threshold is adopted to distinguish between interior and border nodes. Two distinct Random Assessment Delays (RADs) are applied to the border and interior nodes, with the border nodes having shorter RADs than the interior nodes. Most important, the proposed scheme can keep good balance between reachability and rebroadcast efficiency in various network densities.

5.3.1 Algorithm:

The nodes with higher EAC are given a shorter RAD, meaning that they expire earlier to first determine whether to rebroadcast the packets. Conversely, nodes with lower EAC are given a longer RAD, which makes these nodes more likely to be blocked because the rebroadcast packets of short RAD nodes may increase the counters of long RAD nodes.

Tseng et al [18] indicated that border nodes have a higher EAC than interior nodes. Therefore, [14] introduces a distance threshold (Dth) in the counter-based scheme. As shown in Figure. 11, node A denotes the source node, and R denotes the transmission range. The nodes lying within node A's transmission range but outside the range of Dth are called border nodes (e.g. node B and C). The nodes lying within Dth are called interior nodes (e.g. node D and E). The proposed algorithm runs as follows. First, the source node initiates a broadcast request. All of its neighbor nodes increase their counters as soon as they receive the broadcast message. The border nodes initiate an SRAD, and interior nodes initiate an LRAD. The remaining procedure is the same as counter-based scheme. Nodes increase their counters by 1 when hearing a duplicated message during RAD. When the RAD expires, if the nodes' counters exceed the counter threshold (Cth), then the rebroadcast is blocked. Otherwise, the broadcast packets are sent out.

5.3.2 Performance Analysis:

The proposed scheme addresses the distance concept by adding a Dth to distinguish the interior circle from the border annulus. Border nodes, which have higher EAC, determine whether to rebroadcast prior to interior nodes. Nodes with higher EAC values are not suppressed by nodes with lower EAC values thus maintaining a high coverage. The number of rebroadcasts can also be minimized, since the interior nodes may be blocked by border nodes. The simulation results [14] in Figure. 12 shows that when RE reaches 95%, DIS RAD improved the SRB from 23% in the counter-based scheme to 37.5% for the 7x7 map, and from 3.9% in the counter-based scheme to 26% for the 9x9 map. When Dth is set to about 200 meters, and the Cth is set to 3, the proposed scheme can keep good balance between reachability and rebroadcast efficiency in various network densities

12

Figure 11. Example of DIS_RAD

Figure 12. RE and SRB vs. Cth with Dth=200

6.

C

13

R

[1] B. Williams and T. Camp, “Comparison of broadcasting techniques for mobile ad hoc networks”. In Proc. ACM Symposium on Mobile Ad Hoc Networking &Computing (MOBIHOC 2002), pp. 194–205, 2002.

[2] S.-Y. Ni, Y.-C. Tseng, Y.-S. Chen, and J.-P. Sheu, “The broadcast storm problem in a mobile ad hoc network”, Proc.Mobicom_99, 1999.

[3] Y. Sasson, D. Cavin, and A. Schiper, “Probabilistic Broadcast for flooding in wireless mobile ad Hoc networks”, In Proc. IEEE Wireless Communications & Networking Conference (WCNC 2003), pp. 1124–1130, March 2003.

[4] C. E. Perkins, E. M. Belding-Royer, and S. R. Das, "Ad hoc On-Demand Distance Vector (AODV) Routing," IETF Mobile Ad Hoc Networking Working Group INTERNET DRAFT, 19 January 2002.

[5] V. Park and S. Corson, "Temporally-Ordered Routing Algorithm (TORA) Version 1,"

http://www.ietf.org/internet-drafts/draft-ietf-manettora-spec-02.txt, IETF, Work in Progress, July 2001.

[6] M. R. Pearlman, and Z. J. Haas, “Determining the optimal configuration of the zone routing protocol”, IEEE Journal on Selected Areas in Communications, Vol. 17, No. 8, pp. 1395–1414, 1999.

[7] C. Ho, K. Obraczka, G. Tsudik, and K. Viswanath, Flooding for reliable multicast in multihop ad hoc networks, In Proc. ACM DIALM_99, pp. 64–71, 1999.

[8] J. Wu and W. Lou, "Forward-node-set-based broadcast in clustered mobile ad hoc networks," Wireless s Communication andMobile Computing, vol. 3, pp. 155 –173, 2003.

[9] A. Keshavarz-Haddad, V. Ribeiro, and R. Riedi, "Color-Based Broadcasting for Ad Hoc Networks," in Proceeding of the 4thInternational Symposium on Modeling and Optimization in Mobile,Ad Hoc, and Wireless Network (WIOPT' 06). Boston, MA, 2006, pp.1 - 10.

[10] S. Ni, Y. Tseng, Y. Chen, and J. Sheu., "The broadcast storm problem in a mobile ad Hoc networks," in Proceeding of the ACM/IEEE International Conference on Mobile Computing and Networking (MOBICOM),1999, pp. 151-162.

[11] Y.-C. Tseng, S.-Y. Ni, and E.-Y. Shih, "Adaptive approaches to relieving broadcast storms in a wireless multihop ad hoc networks," IEEE Transaction on Computers,, vol. 52, pp. 545- 557, 2003.

[12] Q. Zhang and D. P. Agrawal, "Dynamic Probabilistic Broadcasting in MANETs," Journal of Parallel and DistributedComputing, vol. 65, pp. 220-233, 2005.

[13] J. Cartigny and D. Simplot, "Border node retransmission based probabilistic broadcast protocols in ad hoc networks," Telecommunication Systems,, vol.22, pp. 189-204, 2003.

[14] C Chen, Chin-Kai Hsu and Hsien-Kang Wang, “A distance-aware counter-based broadcast scheme for wireless ad hoc networks”, Military comm. Conference-2005, MILCOM 2005 IEEE 17-20 Oct 2005 pages1052-1058 Vol-2

[15] W. Peng and X.C. Lu, “On the reduction of broadcast redundancy in mobile ad hoc networks,” in Proceedings of the Annual Workshop on Mobile and AdHoc Networking and Computing (MobiHOC 2000), Boston, Massachusetts, USA, Aug. 2000, pp. 129–130.

[16] I. Stojmenovic, M. Seddigh, and J. Zunic, “Dominating sets and neighbor elimination-based broadcasting algorithms in wireless networks,” IEEE Transactions on Parallel and Distributed Systems, vol. 12, no. 12, Dec. 2001.

[17] A. Qayyum, L. Viennot, and A.Laouiti, “Multipoint relaying for flooding broadcast messages in mobile wireless networks,” in Proceedings of the 35th Annual Hawaii International Conference on System Sciences(HICSS’02), Hawaii, 2002.

[18] H. Lim and C. Kim. "Multicast tree construction and flooding in wireless ad hoc networks". In Proceedings of the ACM International Workshop on Modeling, Analysis and Simulation of Wireless and Mobile Systems (MSWIM), 2000

[19] VINT Project. The UCB/LBNL/VINT network simulator-ns (Version

http://www.isi.edu/nsnam/ns).

14 workshop on Performance monitoring, measurement, and evaluation of heterogeneous wireless and wired networks. Terromolinos, Spain, ACM Press, pp. 95-99.

[21] L. M. M. M. Bani-Yassein, M. Ould-Khaoua and S. Papanastasiou. “Performance analysis of adjusted probabilistic broadcasting in mobile ad hoc networks”. International Journal of Wireless Information Networks, March 2006. Springer Netherlands, pages 1–14.

[22] Hanashi A. M, A.Siddique, et al. “Performance evaluation of dynamic probabilistic flooding under different mobility models in MANETs”, Proceedings of the IEEE International Conference on Parallel and Distributed Systems, Vol. 2, Dec.2007, pp. 1-6.

[23] Y.-C. TSENG, S.-Y. NI, Y.-S. CHEN and J.-P. SHEU, “The Broadcast Storm Problem in a Mobile Ad Hoc Network,” Wireless Networks 8, pp. 153–167, 2002

[24] S. al-Humoud, L. M. Mackenzie, M. Ould-Khaoua, and J.Abdulai, "RAD Analysis of Adjusted Counter-Based Broadcast in MANETs," Proc. PGNET’08, 2008.