Classificador máquina de suporte vetorial com análise de Fourier aplicada em dados de EEG e EMG

(1)

Universidade Federal do Rio Grande do Norte

Centro de Ciˆencias Exata e da Terra

Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica

Jhonnata Bezerra de Carvalho

Classificador M´

aquina de Suporte Vetorial

com An´

alise de Fourier

Aplicada em Dados de EEG e EMG

(2)

Jhonnata Bezerra de Carvalho

Classificador M´

aquina de Suporte Vetorial

com An´

alise de Fourier

Aplicada em Dados de EEG e EMG

Trabalho apresentado ao Programa de Pós-Gradua¸cão em Matemática Aplicada e Es-tat´ıstica da Universidade Federal do Rio Grande do Norte, em cumprimento com as exigências legais para obten¸cão do t´ıtulo de Mestre.

´

Area de Concentra¸c˜ao: Probabilidade e Es-tat´ıstica

Orientador:

Prof. Dr. Andr´e Lu´ıs Santos de Pinho

Coorientador:

Prof. Dr. George Freitas von Borries

(3)

Carvalho, Jhonnata Bezerra de.

Classificador máquina de suporte vetorial com análise de Fourier aplicada em dados de EEG e EMG / Jhonnata Bezerra de Carvalho. - Natal, 2016.

xii, 81f: il.

Orientador: Prof. Dr. André Luís Santos de Pinho. Coorientador: Prof. Dr. George Freitas von Borries.

Dissertação (Mestrado) - Universidade Federal do Rio Grande do Norte. Centro de Ciências Exatas e da Terra. Programa de Pós-Graduação em Matemática Aplicada e Estatística.

1. Classificador Binário. 2. Eletroencefalografia. 3. Eletromiografia. 4. Periodograma. 5. Análise de componentes principais. 6. Support vector machine. I. Pinho, André Luís Santos de. II. von Borries, George Freitas. III. Título. RN/UF/CCET CDU 517.445-022.215

Catalogação da Publicação na Fonte

(4)

JHONNATA BEZERRA DE CARVALHO

CLASSIFICADOR M ´

AQUINA DE SUPORTE VETORIAL

COM AN ´

ALISE DE FOURIER

APLICADA EM DADOS DE EEG E EMG

Trabalho apresentado ao Programa de Pós-Gradua¸cão em Matemática Aplicada e Es-tat´ıstica da Universidade Federal do Rio Grande do Norte, em cumprimento com as exigências legais para obten¸cão do t´ıtulo de Mestre.

´

Area de Concentra¸c˜ao: Probabilidade e Es-tat´ıstica

Aprovado em: / /

Banca Examinadora:

Prof. Dr. Andr´e Lu´ıs Santos de Pinho Departamento de Estat´ıstica - UFRN

Orientador

Prof. Dr. George Freitas von Borries Departamento de Estat´ıstica - UNB

Coorientador

Profa_{. Dr}a_{. Carla Almeida Vivacqua}

Departamento de Estat´ıstica - UFRN Examinador Interno

Prof. Dr. Get´ulio Jos´e Amorim do Amaral Departamento de Estat´ıstica - UFPE

Examinador Externo

(5)

Agradecimentos

Ao todo poderoso Deus por ter me dado sa´ude e for¸ca de vontade para chegar at´e

aqui.

Gostaria de agradecer `a CAPES/DS pelo apoio financeiro.

Agrade¸co `a Universidade Federal do Rio Grande do Norte, na qual tenho muito

orgulho de ter sido aluno e com certeza ´e uma das melhores Universidades do pa´ıs.

Gostaria de agradecer imensamente aos meus av´os paternos Osvaldo e Filomena,

por terem me criado e mostrado o caminho para ser a pessoa que sou hoje. Agrade¸co

também à minha avó materna Dona Tereza, mulher muito especial e batalhadora.

Gostaria de agradecer ao meu irm˜ao John Lennon, que infelizmente acabou nos

deixando e foi para os bra¸cos do Pai. Lembro-me de vocˆe meu irm˜ao, todos os dias,

não há um dia sequer que eu não ore por você. Tenho certeza que você está em um

lugar especial perto de Deus.

Agrade¸co `a minha m˜ae Solange, uma mulher batalhadora e guerreira, pelo amor,

incentivo e apoio incondicional. Agrade¸co tamb´em ao meu irm˜ao ca¸cula Jeferson e

meu padrasto Cl´ovis. Agrade¸co ao meu pai Valdir, que tamb´em sempre me apoiou em

seguir em frente e nunca desistir.

Ao meu primo irm˜ao Emerson, por todos os ensinamentos e conselhos.

Agrade¸co aos meus familiares e amigos que sempre acreditaram em mim, em

es-pecial: Gustavo, Alynne, Gilvanete, Marli, Edmilson, Ad´elio, Eric, Ednaldo, Silvana,

Haniel, Otaniel, Enildo, K´atia, Anderson, Amanda, Allan, F´atima, Washington,

Regi-naldo, Wanderley, Rafaela, Dayse, Jairane, Dona L´ucia e Jair.

Agrade¸co imensamente a meu grande amigo Jean, por todas as conversas,

(6)

Ao meu afilhado Victor, por todos os dias felizes e alegres que passamos juntos.

Aos meus compadres Andr´eia e Juca.

Aos meus tios J´o e Vera, por todas as gargalhadas que j´a compartilhamos juntos.

Aos meus primos de cora¸c˜ao Eron, Bruno e Juninho.

Gostaria de agradecer imensamente do fundo do meu cora¸c˜ao `a minha namorada

Inara. N˜ao sei o que seria de mim sem o seu apoio, amizade, paciˆencia, carinho e amor.

Muito obrigado por tudo! Agrade¸co tamb´em `a sua fam´ılia, em especial: Dona Inelda,

Walter e Maria.

Agrade¸co tamb´em aos meus amigos e colegas do PPgMAE: Felipe, Isaac, Evandro,

La´ıs, Mois´es, Wanderson, Daniel (Colombiano), Renato Tigre e F´abio.

Agrade¸co aos professores do Departamento de Estat´ıstica, em especial: Pledson,

Dione, Jeanete, Paulo Roberto, Dami˜ao, Marcelo, Luz Milena, Fernando C´esar e

Moi-s´es.

Agrade¸co ao PET Estat´ıstica, por todos esses anos formando l´ıderes para a

soci-edade. Gostaria de agradecer ao prof. Formiga, um homem generoso, respons´avel e

comprometido com seus deveres. Agrade¸co a todos os ex-petianos e atuais petianos,

em especial: Josen´ılson, Paulo César, Francimário, Kalil, Adré Possati, Sir. Elias e

Joyce.

Agrade¸co ao casal Rumenick e Wilmara, por esses anos de companheirismo e

ami-zade.

Aos meus amigos Fernando Luiz, Marcos e Glauco por todas as raivas no joguinho.

Aos meus grandes amigos Carlos C´esar (Bial) e Jailton. Agrade¸co tamb´em aos meus

colegas de apartamento, Emmanuel Duarte (Man´u) e Everton.

Gostaria de agradecer ao meu orientador o prof. Andr´e Pinho, no qual sua ajuda foi

imprescind´ıvel para a conclus˜ao desse trabalho. Espero que continuemos trabalhando

juntos nessa nova fase da minha vida. Gostaria de agradecer ao meu coorientador o

prof. George, Murilo Coutinho e ao prof. Ricardo por todas as sugest˜oes e ajudas no

desenvolvimento do trabalho.

Por fim, gostaria de agradecer `a banca examinadora, o prof. Get´ulio e a profa_.

Carla, pelas sugest˜oes e cr´ıticas construtivas feitas ao trabalho.

(7)

”E ainda que tivesse o dom

de profecia, e conhecesse todos os

mist´erios e toda a ciˆencia, e ainda

que tivesse toda a f´e, de maneira

tal que transportasse os montes, e

n˜ao tivesse amor, nada seria.”

(8)

Resumo

O classificador M´aquina de Suporte Vetorial, que vem do termo em inglˆes Support

Vector Machine, é utilizado em diversos problemas em várias áreas do conhecimento.

Basicamente o m´etodo utilizado nesse classificador ´e encontrar o hiperplano que

maxi-miza a distˆancia entre os grupos, para aumentar o poder de generaliza¸c˜ao do

classifica-dor. Neste trabalho, são tratados alguns problemas de classifica¸cão binária com dados

obtidos atrav´es da eletroencefalografia (EEG) e eletromiografia (EMG), utilizando a

M´aquina de Suporte Vetorial com algumas t´ecnicas complementares, destacadas a

se-guir como: Análise de Componentes Principais para a identifica¸cão de regiões ativas do

cérebro, o método do periodograma que é obtido através da Análise de Fourier, para

ajudar a discriminar os grupos e a suaviza¸cão por Médias Móveis Simples para a

redu-¸c˜ao dos ru´ıdos existentes nos dados. Foram desenvolvidas duas fun¸c˜oes no sof tware

R, para a realiza¸cão das tarefas de treinamento e classifica¸cão. Além disso, foram

propostos 2 sistemas de pesos e uma medida sumarizadora para auxiliar na decis˜ao do

grupo pertencente. A aplica¸c˜ao dessas t´ecnicas, pesos e a medida sumarizadora no

clas-sificador, mostraram resultados bastantes satisfat´orios, em que os melhores resultados

encontrados foram, uma taxa m´edia de acerto de 95,31% para dados de est´ımulos

visu-ais, 100% de classifica¸c˜ao correta para dados de epilepsia e taxas de acerto de 91,22%

e 96,89% para dados de movimentos de objetos para dois indiv´ıduos.

Palavras-chave: Classificador Bin´ario, Eletroencefalografia, Eletromiografia,

Pe-riodograma, An´alise de Componentes Principais, Suaviza¸c˜ao,Support Vector Machine,

SVM.

(9)

Abstract

The classifier support vector machine is used in several problems in various areas of

knowledge. Basically the method used in this classifier is to find the hyperplane that

maximizes the distance between the groups, to increase the generalization of the

clas-sifier. In this work, we treated some problems of binary classification of data obtained

by electroencephalography (EEG) and electromyography (EMG) using Support Vector

Machine with some complementary techniques, such as: Principal Component Analysis

to identify the active regions of the brain, the periodogram method which is obtained

by Fourier analysis to help discriminate between groups and Simple Moving Average to

eliminate some of the existing noise in the data. It was developed two functions in the

softwareR, for the realization of training tasks and classification. Also, it was proposed

two weights systems and a summarized measure to help on deciding in classification of

groups. The application of these techniques, weights and the summarized measure in

the classifier, showed quite satisfactory results, where the best results were an average

rate of 95.31% to visual stimuli data, 100% of correct classification for epilepsy data

and rates of 91.22% and 96.89% to object motion data for two subjects.

Keywords: Binary Classifier, Electroencephalogram, Electromyography,

Periodo-gram, Principal Component Analysis, Smooth, Support Vector Machine, SVM.

(10)

Sum´

ario

1 Introdu¸c˜ao 1

1.1 Objetivo da disserta¸c˜ao . . . 2

1.2 Contribui¸c˜oes do trabalho . . . 2

1.3 Descri¸c˜ao dos cap´ıtulos . . . 3

2 SVM 4 2.1 SVM com margens r´ıgidas . . . 4

2.2 SVM com margens suaves . . . 10

2.3 SVM e Kernels . . . 15

2.4 Kernels . . . 17

3 Eletroencefalografia e Eletromiografia 20 3.1 Coleta de dados de EEG . . . 20

3.1.1 Dados de Est´ımulos Visuais . . . 21

3.1.2 Dados de Epilepsia . . . 22

3.2 Coleta de dados de EMG . . . 23

3.2.1 Dados de Movimentos com Objetos . . . 23

4 An´alises complementares 25 4.1 Suaviza¸c˜ao . . . 25

4.1.1 M´edias M´oveis Simples . . . 25

4.2 An´alise de Componentes Principais . . . 26

4.2.1 ACP em dados de EEG . . . 27

4.3 An´alise Espectral . . . 30

4.3.1 Fun¸c˜oes peri´odicas . . . 31

(11)

4.3.2 S´eries de Fourier . . . 33

4.3.3 Periodograma . . . 34

4.4 Distribui¸c˜ao Espectral e Transformada de Fourier . . . 36

5 Weighted Fourier Frequencies and SVM 39 5.1 Aplica¸c˜ao do periodograma e a suaviza¸c˜ao . . . 39

5.2 Cria¸c˜ao do classificador . . . 42

5.3 Sistema de pesos . . . 43

5.4 Classifica¸c˜ao . . . 45

5.5 Alguns resultados do WFF-SVM . . . 47

5.6 Alternativa para o sistema de pesos . . . 48

5.7 Decomposi¸c˜ao da soma de quadrados . . . 49

5.8 Proposta dos pesos . . . 49

5.9 Alternativa para a decis˜ao da classifica¸c˜ao . . . 53

6 Aplica¸c˜ao dos resultados propostos 57 6.1 Classifica¸c˜ao de Est´ımulos Visuais . . . 57

6.2 Classifica¸c˜ao de Dados de Epilepsia . . . 62

6.3 Classifica¸c˜ao de Objetos . . . 63

7 Considera¸c˜oes finais 64 7.1 Trabalhos Futuros . . . 66

Referências Bibliográficas 66 A Soma de Quadrados 71 A.1 Demonstra¸cão . . . 71

B Cálculos para a obten¸cão do Lagrangeano 73 B.1 Demostra¸cão . . . 73

B.2 Margens Suaves . . . 74

C Distˆancia de um ponto ao hiperplano 76

(12)

Lista de Figuras

2.1 Dados linearmente separ´aveis com um hiperplano separador. . . 5

2.2 Dados linearmente separ´aveis com 4 hiperplanos separadores diferentes. 6

2.3 Dados linearmente separ´aveis com o hiperplano ´otimo. . . 6

2.4 Ilustra¸c˜oes para 3 situa¸c˜oes citadas; (a) Encontram-se pontos entre as

margens e corretamente classificados; (b) Encontram-se pontos do lado

incorreto, mas entre as margens; (c) Encontram-se pontos do lado

incor-reto e fora das margens. . . 11

2.5 Ilustra¸cões de 3 situa¸cões poss´ıveis, incluindo as variáveis ξi quando os

dados não são linearmente separáveis. . . 12

2.6 Dados linearmente insepar´aveis; (a) visualiza¸c˜ao dos dados; (b)

separa-¸c˜ao dos 2 grupos com o hiperplano separador e os indicadores dos vetores

de suporte. . . 16

2.7 Dados linearmente separ´aveis no espa¸co de caracter´ısticas. . . 18

3.1 Touca com eletrodos em uma pessoa. Fonte: Biosemi Systems. . . 20

3.2 Imagens utilizadas no experimento feito naThe University of Texas - El

Paso - UTEP. . . 21 3.3 Ilustra¸c˜ao dos dados das imagens 1 e 2 para os eletrodos 1 e 2. . . 22

3.4 Sensor de EMG com 2 eletrodos. Fonte: Sapsanis et al.(2013). . . 23

3.5 Figura com as ilustra¸c˜oes dos 6 objetos. Fonte: Sapsanis et al. (2013). . 24

4.1 Ilustra¸c˜ao da aplica¸c˜ao de MMS com s=4. . . 26

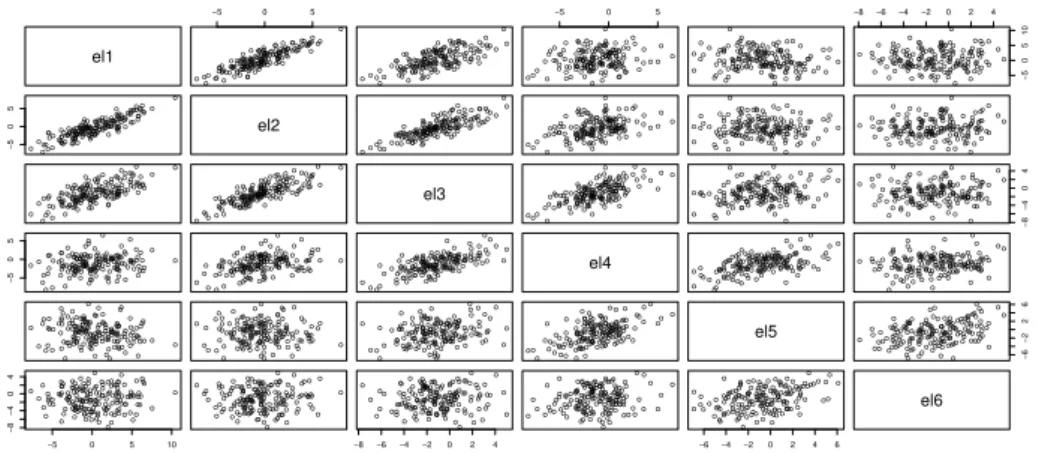
4.2 Gráfico de dispersão para alguns eletrodos de uma repeti¸cão da imagem 1. 27

(13)

4.3 Gráfico da propor¸cão de variância explicada paras os 10 primeiros

com-ponentes principais. . . 28

4.4 Gr´afico de intensidade para os 4 primeiros componentes principais. . . . 29

4.5 S´erie original e Periodograma. . . 36

5.1 Sinais de uma das repeti¸c˜oes das imagens 1 e 3. . . 40

5.2 Periodograma e periodograma suavizado para o eletrodo 72 de uma das repeti¸c˜oes das imagens 1 e 3. . . 41

5.3 Periodogramas e periodogramas suavizados para algumas combina¸c˜oes da imagens 4, 6 e 7, para os eletrodos 33 e 95, para as 4 repeti¸c˜oes. . . 42

5.4 Algumas frequˆencias do periodograma suavizado para o eletrodo 33 para as imagens 4 e 6, com a SVM por frequˆencia. . . 43

5.5 Ilustra¸c˜ao para a aplica¸c˜ao do WFF-SVM. . . 46

5.6 Ilustra¸c˜ao para a aplica¸c˜ao do WFF-SVM com o novo sinal. . . 47

5.7 Ilustra¸c˜ao para o sistema de pesos, em 4 situa¸c˜oes. . . 50

5.8 Ilustra¸c˜ao para o sistema de pesos P2l,k em 6 situa¸c˜oes. . . 52

5.9 Fluxograma para a fase de treinamento do WFF-SVM. . . 55

5.10 Fluxograma para a fase classifica¸c˜ao de uma nova imagem. . . 56

6.1 Gr´aficos de intensidade para as taxas de acerto individuais dos eletrodos para os 3 sistemas de pesos, utilizando o periodograma com e sem a suaviza¸c˜ao por MMS4. . . 59

C.1 Ilustra¸c˜ao geom´etrica de um ponto e uma reta. . . 76

C.2 Alguns segmentos do ponto `a reta. . . 76

C.3 Segmento que possui a menor distˆancia deP a r. . . 77

C.4 Desenho geom´etrico utilizado para a demonstra¸c˜ao. . . 77

(14)

Lista de Tabelas

2.1 Exemplos de algumas fun¸c˜oes Kernel. . . 19

4.1 Correla¸c˜ao de Pearson para os 6 eletrodos. . . 28

5.1 Tabela da taxa de acerto por frequˆencia. . . 44

5.2 Medidas para a utiliza¸cão do WFF-SVM para a classifica¸cão do novo sinal. 47 5.3 Cálculo para os sistemas de pesos (5.2), (5.5) e (5.6) em cada situa¸cão dos dados da Figura 5.7 . . . 52

6.1 Tabela da taxa de acerto para o WFF-SVM com o periodograma e pe-riodograma suavizado com MMS4 para os 3 sistemas de pesos, 2 tipos de decis˜oes e C = 1. . . 58

6.2 Resultados utilizando MMS4 em % para a taxa média de acerto, utili-zando alguns valores do custo (C), número de eletrodos (E) e tipo de decisão. . . 60

6.3 Taxas de acerto em % utilizando a decis˜ao D. . . 61

6.4 Taxas de acerto em % utilizando a decis˜ao DMP. . . 61

6.5 Compara¸c˜oes de resultados para os dados de epilepsia. . . 62

(15)

Siglas

ACI An´alise de Componentes Independentes

ACP An´alise de Componentes Principais

ADL An´alise de Discriminante Linear

AE An´alise Espectral

D Decis˜ao para Todos os Eletrodos

Dl Decis˜ao para o Eletrodol

DMP Decis˜ao M´edia Ponderada para Todos os Eletrodos

DMPl Decis˜ao M´edia Ponderada para o Eletrodo l

EEG Eletroencefalografia

EWR Energia Wavelet Relativa

IVS Indicadores dos Vetores de Suporte

KKT Karush-Kuhn-Tucker

LS-SVM Least Square Support Vector Machine

ME Mixed of Experts

MLPNN Multi-Layer Perceptron Neural Network

MMC M´ınimo M´ultiplo Comum

(16)

MMQ M´etodo de M´ınimos Quadrados

MMS M´edias M´oveis Simples

MMSs M´edias M´oveis Simples com espa¸camentos

P Per´ıodo da Fun¸c˜ao

RN Redes Neurais

SQ Soma de Quadrados

SQErros Soma de Quadrados dos Erros

SQF ator Soma de Quadrados do Fator

SQT otal Soma de Quadrados Total

SVM Supporte Vector Machine

TDW TransformadaWavelet Discreta

WFF-SVM Weighted Fourier Frequencies and SVM

(17)

Cap´ıtulo 1

Introdu¸c˜

ao

A Máquina de Suporte Vetorial é o termo em português para referenciar o

classifica-dorSupport Vector Machine (SVM). Considerando que a grande maioria dos trabalhos

pesquisados utilizarem o termo e a sigla em inglˆes, neste trabalho ser´a adotada a forma

mais citada. A SVM ´e um classificador bin´ario com aprendizagem supervisionada. Isto

significa que para a utiliza¸cão deste método é preciso fornecer exemplos para o seu

treinamento, em que neles est˜ao as respostas corretas para a classifica¸c˜ao, e as classes

s˜ao conhecidas a priori. No aprendizado n˜ao supervisionado o algoritmo tem que

re-conhecer as classes através de padrões existentes com um determinado critério e sem

conhecer as classes. Este tipo de aprendizagem tenta ganhar alguma compreens˜ao do

processo que gerou os dados, e usar os padr˜oes encontrados para formar as classes. O

classificador SVM foi proposto inicialmente por Boser, Guyon e Vapnik (1992), para

o caso dos dados serem linearmente separ´aveis. Desta forma, ´e poss´ıvel separar os

dados através de um hiperplano. Entretanto, existem casos em que os dados não são

linearmente separ´aveis, e a solu¸c˜ao para esse problema foi proposta por Vapnik (1995).

Com isso, a abordagem feita por Boser, Guyon e Vapnik (1992) ficou conhecida como

SVMs com Margens R´ıgidas, e a de Vapnik (1995) como SVMs com Margens Suaves.

Esse classificador ´e muito utilizado em diversos problemas em diversas ´areas do

co-nhecimento, como por exemplo, em Costa, Zeilhofer e Rodrigues (2010) na detec¸c˜ao

de queimadas no Pantanal mato-grossense; em dados de EEG para o reconhecimento

de emo¸c˜oes humanas, em Schaaff e Schultz (2009) e Hosseini, Khalilzadeh e Changiz

(2010); em reconhecimento de n´umeros e letras em Thome (2012). A SVM tamb´em

(18)

1.1 Objetivo da disserta¸c˜ao 2

pode ser aplicada a problemas de regress˜ao como descrito em Smola e Sch¨olkopf (2004)

e ainda em gr´aficos de controle Grasso et al.(2015).

A EEG é um exame que permite captar sinais elétricos emitidos pelo cérebro, já a

EMG capta sinais emitidos pelos musculos. O sinal obtido depende da situa¸c˜ao em que

o indiv´ıduo se encontra e do objetivo do pesquisador. Esses exames s˜ao muito utilizados

para identificar doen¸cas psicol´ogicas (EEG) e musculares (EMG). Em Gomes (2015)

´e descrita a fisiologia do Eletroencefalograma, em que os grandes pioneiros no uso do

EEG foram Richard Caton (1842₋1926), que fez experimentos com esse procedimento em animais e Hans Berger (1873₋1941) que utilizava em seres humanos. Em LAPESE (2005) é relatada a história da EMG, em que Hans Piper é reconhecido como o primeiro

pesquisador a estudar sinais de EMG. Seus trabalhos foram desenvolvidos na Alemanha

durante os anos de 1910 a 1912 utilizando um galvanˆometro sequencial. Posteriormente,

o neurologista Herbert Jasper (1906₋1999) construiu o primeiro eletromi´ografo e criou o eletrodo de agulha unipolar.

O foco do presente trabalho ´e estudar um classificador de sinais (EEG e EMG),

que tem como base a SVM com o uso do periodograma e um sistema de pesos, que foi

proposto por Coutinho (2010).

1.1 Objetivo da disserta¸c˜

ao

O objetivo do trabalho ´e estudar o classificador para sinais proposto por Coutinho

(2010), com o interesse de melhorar da taxa de acerto para o reconhecimento de

es-t´ımulos diferentes. Al´em disso, pretende-se estudar e propor novos sistemas de pesos

que permitam aumentar a taxa de acerto e facilitar o uso do classificador.

1.2 Contribui¸c˜

oes do trabalho

As principais contribui¸cões do trabalho são, a implementa¸cão computacional do

classificador Weighted Fourier Frequencies and SVM proposto por Coutinho (2010)

no sof tware R e o aprimoramento do gr´afico de intensidade para avaliar medidas

(19)

1.3 Descri¸c˜ao dos cap´ıtulos 3

1.3 Descri¸c˜

ao dos cap´ıtulos

No Cap´ıtulo 2 são mostrados os passos para a constru¸cão da fun¸cão objetivo para

encontrar o hiperplano da SVM e alguns conceitos sobre a utiliza¸c˜ao de Kernels. O

Cap´ıtulo 3 introduz uma pequena descri¸c˜ao sobre a coleta de dados de EEG e EMG e

sobre os experimentos que resultaram nos dados utilizados no presente trabalho. No

Cap´ıtulo 4 s˜ao apresentadas algumas an´alises que melhoram o desempenho do

classifica-dor, como a suaviza¸cão por Médias Móveis Simples, Análise de Componentes Principais

com a utiliza¸cão do gráfico de intensidade e a técnica do periodograma. No Cap´ıtulo 5

´e apresentada a metodologia utilizada para a montagem do classificador proposto por

Coutinho (2010). Al´em disso, s˜ao mostrados 2 sistemas de pesos alternativos, uma nova

medida sumarizadora para auxiliar a decis˜ao de um novo est´ımulo e alguns resultados.

No Cap´ıtulo 6 s˜ao avaliados o desempenho e os principais resultados do classificador

em dados reais, comparando-o com outros trabalhos. Finalmente, no Cap´ıtulo 7 est˜ao

as considera¸c˜oes finais e em seguida os Apˆendices A, B e C com algumas

demonstra-¸cões sobre cálculos de alguns resultados da SVM, distância de um ponto à reta e a

(20)

Cap´ıtulo 2

SVM

Neste cap´ıtulo s˜ao apresentados conceitos matem´aticos da SVM com margens

r´ıgi-das e suaves. Além disso, é apresentada uma abordagem não linear para a SVM através

da utiliza¸c˜ao de fun¸c˜oesKernels.

2.1 SVM com margens r´ıgidas

Basicamente, as SVMs com margens r´ıgidas s˜ao usadas para separar dois grupos

1 e 2 que são linearmente separáveis, ou seja, é poss´ıvel encontrar um hiperplano que

separe completamente as duas classes. Um hiperplano ´e um subespa¸co plano afim de

dimensãop₋1 em um espa¸cop₋dimensional (JAMESet al., 2013). Por exemplo, em duas dimensões o hiperplano é um subespa¸co unidimensional, ou seja, uma linha. Em

três dimensões o hiperplano é subespa¸co bidimensional, isto é, um plano. Parap > 3 é

dif´ıcil visualizar o hiperplano, mas a no¸cão de um subespa¸co plano de dimensãop₋1 é a mesma. Segundo James et al. (2013) a defni¸cão matemática do hiperplano é dada

por,

f(x) = w′_hx+bh = 0 (2.1)

em que wh ∈ Rm×1 ´e um vetor coluna de coeficientes do hiperplano, x ∈ Rm×1 ´e

um vetor coluna que representa as vari´aveis e b_h um escalar. Como ilustra¸c˜ao do hiperplano separador, observe a Figura 2.1. Observe que o hiperplano na Figura 2.1

separa o espa¸co gerado pelos pontos em duas partes.

(21)

2.1 SVM com margens r´ıgidas 5

0.1 0.2 0.3 0.4 0.5 0.6 0.7

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

●

● ●

●

● ●

●

● ●

wh'x + bh=0 ●

●

Grupo 1 Grupo 2

Figura 2.1: Dados linearmente separ´aveis com um hiperplano separador.

Considere um conjunto de dados de treinamento representado pelo vetor xi(i =

1,2,_{· · ·} , n) com xi ∈ Rm×1, e a matriz X ∈ Rn×m formada por todas as amostras

de treinamento, em que cada amostra de treinamento possua um r´otulo yi = +1 se

xi ∈ ao grupo 1 e yi = −1 se xi ∈ ao grupo 2. A rotula¸c˜ao dos grupos ´e feita da

seguinte forma,

yi =

  

+1 se w′

hx+bh >0

−1 se w′

hx+bh <0

(2.2)

com isso, pode-se criar uma fun¸cão de decisão g(x) = D(f(x)) para a classifica¸cão em

que, dada uma nova observa¸c˜aox∗ _{∈ ℜ}m×1_,

g(x∗) =D(f(x∗)) =

  

+1 se w′

hx∗+bh >0

−1 se w′

hx∗+bh <0

Note que, na Figura 2.1, est´a representado apenas um poss´ıvel hiperplano e que

se poderia ter infinitos hiperplanos apenas multiplicando wh ou somando em bh uma

constante (Figura 2.2). Uma escolha natural para a determina¸c˜ao do hiperplano seria

o hiperplano de margem m´axima. O procedimento para a obten¸c˜ao desse hiperplano

é feito do seguinte modo, calcula-se a distância de cada observa¸cão de treinamento

para um hiperplano pré-fixado. A menor distância entre o hiperplano e as observa¸cões

(22)

aquele que possui a maior distˆancia m´ınima entre o hiperplano e as observa¸c˜oes (JAMES

et al., 2013). Dessa forma, o crit´erio proposto por Boser, Guyon e Vapnik (1992)

consiste em estimar os coeficientes w que maximizam a distˆancia entre as margens,

no intuito de maximizar o poder de generaliza¸c˜ao do classificador. Na Figura 2.3

pode-se ver o hiperplano de maior margem. As retas pontilhadas s˜ao as margens

que possuem a maior distˆancia entre os dois grupos e os pontos que est˜ao sobre as

margens s˜ao chamados de vetores de suporte. Os c´ırculos utilizados na Figura 2.3 s˜ao

denominados de Indicadores dos Vetores de Suporte (IVS) e estes vetores s˜ao utilizados

para encontrar os coeficientes do hiperplano. A seguir ´e mostrado como encontrar esses

coeficientes.

0.1 0.2 0.3 0.4 0.5 0.6 0.7

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

●

● ●

●

● ●

●

● ●

●

● _●

● ●

●

Grupo 1 Grupo 2

Figura 2.2: Dados linearmente separ´aveis com 4 hiperplanos separadores diferentes.

0.1 0.2 0.3 0.4 0.5 0.6 0.7

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

●

● ●

●

● ●

●

● ●

●

● ● ●

Grupo 1 Grupo 2 IVS

(23)

Note que, no caso dos dados serem linearmente separ´aveis, n˜ao ocorre o caso em

quef(X) = 0, logo, pode-se alterar as condi¸c˜oes de classifica¸c˜ao em (2.2) para,

yi =

  

+1 se w′

hxi+bh ≥a

−1 se w′

hxi+bh ≤ −a

sendoa >0 uma constante, e esses hiperplanos s˜ao denominados margens. Observe que

segundo esse sistema, n˜ao h´a pontos entre os hiperplanosw′

hx+bh = 0 e w′hx+bh±a.

As inequa¸c˜oes podem ser reescritas, dividindo em ambos os lados pora e reajustando

wh e bh. Com isso, obt´em-se,

yi =

  

+1 se w′_x

i+b ≥1

−1 se w′_x

i+b ≤ −1

(2.3)

logo, essas equa¸c˜oes em (2.3) podem ser combinadas para facilitar na manipula¸c˜ao e

cria¸c˜ao da fun¸c˜ao objetivo em (2.5) da seguinte maneira

yi(w′xi+b)≥1 parai= 1,2,· · · , n. (2.4)

Considerando a métrica euclidiana para o cálculo de distâncias, pode-se mostrar

que a distˆancia de qualquer ponto para o hiperplano separador ´e fornecida por,

h(xi) = |

w′_x

i+b|

||w_|| =

|f(xi)|

||w_|| .

Para mais detalhes sobre o cálculo dessa distância ver Apêndice C. Com isso, a distância

entre as margens ´e dada por,

r= 2

||w_||.

Como foi dito anteriormente, para encontrar os coeficientes do hiperplano basta

maximizarrem rela¸c˜ao aw. Note que maximizarr´e equivalente a minimizar a norma

euclidiana dos pesos_||w_||, ou ainda, pode-se encontrar os pesos minimizando _||w_||2 _de

forma equivalente, pois _||w_||2 _{é uma fun¸cão crescente bijetora da norma de} _w _{que é}

mais fácil ser minimizada. Para satisfazer a conven¸cão adotada, as restri¸cões em (2.4)

(24)

margens durante o treinamento. Portanto, o hiperplano ´otimo ´e definido para valores

de w e b que satisfazem (2.4) e para os quais _||w_||2 _{´e m´ınima. Logo, o problema ´e}

resumido em,

min w,b ||

w_||2

2 (2.5)

sob as restri¸c˜oes yi(w′xi+b)≥1 para i= 1,2,· · · , n.

Esse é um problema clássico de otimiza¸cão quadrática convexa, e pode-se utilizar

os multiplicadores de Lagrange para encontrarb e _||w_||sujeito a essas restri¸c˜oes. Para mais detalhes sobre a teoria envolvida sobre a fun¸c˜ao Lagrangeana ver em Santos

(2002). A fun¸c˜ao Lagrangeana primal para esse problema ´e dada por,

Lp =

1 2||w||

2

−

n

X

i=1

αi[yi(w′xi+b)−1] (2.6)

em que cada αi ≥ 0, e eles s˜ao chamados de multiplicadores de Lagrange. A fun¸c˜ao

Lagrangeana em (2.6) deve ser minimizada. Para tanto, osαi’s devem ser maximizados,

e os coeficientesw e b minimizados. Derivando Lp em rela¸c˜ao a w e b obt´em-se,

∂Lp

∂w =w−

n

X

i=1

αiyixi (2.7)

∂Lp

∂b =−

n

X

i=1

αiyi. (2.8)

Igualando as equa¸c˜oes (2.7) e (2.8) a 0 e desenvolvendo os c´alculos, estabelecem-se as

equa¸c˜oes,

w=

n

X

i=1

αiyixi (2.9)

n

X

i=1

αiyi = 0. (2.10)

Substituindo as equa¸cões (2.9) e (2.10) em (2.6), obtém-se a forma dual da fun¸cão

(25)

αi,

LD = n

X

i=1

αi−

1 2

n

X

j=1

n

X

i=1

αiαjyiyjx′ixj,

sob as restri¸c˜oes

  

Pn

i=1αiyi = 0

αi ≥0

. (2.11)

A estratégia da utiliza¸cão da forma dual se tornou padrão para estimar os

parâme-tros da SVM, pois essa nova formula¸cão do problema proporciona vários benef´ıcios,

destacando-se a redu¸c˜ao do problema de alta dimensionalidade dos dados.

Conside-rando que α∗_, _w∗ _e _b∗ _{são a solu¸cão para o problema, esses pontos só serão ótimos se} satisfizerem as condi¸cões complementares do teorema de Karush-Kuhn-Tucker (KKT).

As condi¸c˜oes de KKT aplicadas ao problema s˜ao,

∂Lp

∂w = 0

∂Lp

∂b = 0

yi(w′xi+b) ≥ 1 i= 1,2,· · · , n

αi ≥ 0 ∀i

αi[yi(w′xi+b)−1] = 0 ∀i. (2.12)

Para mais detalhes sobre as condi¸c˜oes de KKT ver Fletcher (1987). Como os vetores de

suporte s˜ao os ´unicos que possuem α∗

i >0, os coeficientes do hiperplano s˜ao calculados

com a express˜ao,

w∗ = X

vetores de suporte

α∗_iyixi. (2.13)

Note que os coeficientes de w s˜ao explicitamente calculados com o treinamento pela

equa¸cão (2.13), porém b não é, embora ele seja implicitamente determinado. Para

encontrar o valor de b basta utilizar a condi¸c˜ao de KKT apresentada em (2.12), com

(26)

2.2 SVM com margens suaves 10

a maior margem, sem que nenhum outro vetor de suporte fique entre as margens,

b∗ = ₋1 2

max {yi=−1}

(w∗′xi) + min

{yi=1}

(w∗′xi)

(2.14)

ou

= ₋1 2

"

max {yi=−1}

(

Nvs

X

j=1

yjαi∗x′jxi) + min

{yi=1}

(

Nvs

X

j=1

yjα∗ix′jxi)

#

em que Nvs ´e o n´umero de vetores de suporte. Outra maneira de calcular o valor de

b∗_{, é utilizando a média aritmética das imagens entre os vetores de suporte,}

b∗ = 1 Nvs

Nvs

X

i=1

1 yi −

Nvs

X

j=1

yjα∗ix′jxi

!

. (2.15)

2.2 SVM com margens suaves

Na maioria dos problemas de classifica¸cão, os dados não são linearmente separáveis

por diversos motivos, como por exemplo: ru´ıdos,outliers, erros de mensura¸c˜ao ou at´e

mesmo que a natureza dos dados n˜ao seja linearmente separ´avel. Entretanto, nessa nova

abordagem é poss´ıvel permitir situa¸cões em que, é poss´ıvel que observa¸cões fiquem entre

as margens e que possa existir erros de classifica¸c˜ao. Desse modo, pode-se encontrar 3

situa¸c˜oes diferentes para o problema,

1. Pontos podem ficar entre e fora das margens e serem classificados corretamente,

ou seja,

0<w′xi+b <1 e yi = +1

ou

0>w′xi+b >−1 e yi = −1

2. Pontos podem ficar entre as margens e serem classificados erroneamente,

0>w′xi+b >−1 e yi = +1

ou

(27)

3. Pontos que estejam fora das margens e classificados erroneamente,

w′xi +b <−1 e yi = +1

ou

w′xi+b >1 e yi = −1.

Essas situa¸c˜oes est˜ao ilustradas na Figura 2.4, (a), (b) e (c), respectivamente.

0.1 0.2 0.3 0.4 0.5 0.6 0.7

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

(a)

● ● ●

●

● ●

●

● ● ● ●

● ●

●

● ●

●

0.1 0.2 0.3 0.4 0.5 0.6 0.7

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

(b)

● ● ●

●

● ●

●

● ● ● ●

● ●

●

● ●

●

0.1 0.2 0.3 0.4 0.5 0.6 0.7

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

(c)

● ● ●

●

● ●

●

● ● ● ●

● ●

●

● ●

●

Grupo 1 Grupo 2 IVS

Figura 2.4: Ilustra¸c˜oes para 3 situa¸c˜oes citadas; (a) Encontram-se pontos entre as margens e corretamente classificados; (b) Encontram-se pontos do lado incorreto, mas entre as margens; (c) Encontram-se pontos do lado incorreto e fora das margens.

A solu¸c˜ao para esse problema foi proposta por Vapnik (1995), em que ´e acrescentado

uma variável folga ξi ≥ 0 para todo i = 1,· · · , n nas restri¸cões (2.3). Com isso, é

poss´ıvel utilizar a SVM linear nas 3 situa¸c˜oes mostradas anteriormente, atrav´es da

vari´avel folga acrescentada nas restri¸c˜oes (2.3) da seguinte maneira,

yi = +1 se w′xi+b≥1−ξi

yi = −1 se w′xi+b ≤ −1 +ξi

essas equa¸c˜oes podem ser combinadas,

(28)

Note que, se 0< ξi ≤1 ent˜ao o ponto est´a entre as margens e classificado

correta-mente; casoξi >1 o ponto est´a fora das margens e houve um erro de classifica¸c˜ao; se

ξi = 0, indica que o ponto est´a fora das margens e classificado corretamente.

Entre-tanto, essa abordagem tem alguns problemas como por exemplo: a n˜ao existˆencia de

restri¸cões para o número de classifica¸cões incorretas. Na Figura 2.5 ilustra uma

situ-a¸cão em que os dados não são linearmente separáveis, e foi considerada a abordagem

proposta por Vapnik (1995) com a adi¸c˜ao das vari´aveis ξi, que ficou conhecida como

SVM com marges suaves.

0.1 0.2 0.3 0.4 0.5 0.6 0.7

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

●

● ●

●

● ●

●

● ●

●

● ξ1

● ξ2

●

ξ3

● ●

●

Grupo 1 Grupo 2 IVS

Figura 2.5: Ilustra¸cões de 3 situa¸cões poss´ıveis, incluindo as variáveis ξi quando os

dados não são linearmente separáveis.

Logicamente, para que o classificador seja bom, ´e interessante que os erros cometidos

sejam os menores poss´ıveis. Em outras palavras, ´e necess´ario minimizar Pn_i₌₁ξi, que

´e um limite para os erros de treinamento. O problema agora ´e maximizar as margens

do hiperplano levando em conta a minimiza¸c˜ao dos erros, e isso ´e feito com o objetivo

de encontrar a margem com o poder de maior generaliza¸c˜ao para se ter uma menor

quantidade de erros de classifica¸c˜ao. Com tudo isso que foi mostrado, tem-se uma nova

fun¸c˜ao objetivo, que ´e expressa da seguinte forma,

min w,b,ξi

||w_||2

2 +C(

n

X

i=1

(29)

sob as restri¸c˜oes yi(w′xi+b)≥1−ξi, ξi ≥0 para i= 1,2,· · · , n.

A constante C é escolhida a priori pelo usuário, e ela estabelece a importância dos

erros no processo de minimiza¸c˜ao da fun¸c˜ao objetivo, para encontrar as margens com

o maior poder de generaliza¸c˜ao, ou seja, diminui a chance do ponto ser classificado

erroneamente. ´E importante notar que, quanto maior o valor de C menor ser˜ao as

margens do hiperplano separador. Caso o problema de classifica¸c˜ao contenha duas

classes linearmente separ´aveis, pode-se usar as equa¸c˜oes (2.17) e (2.16) e basta escolher

C_{−→ ∞}. A fun¸c˜ao Lagrangeana primal para esse novo problema ´e da seguinte forma,

Lp =

1 2||w||

2₊_C(

n

X

i=1

ξi)− n

X

i=1

αi[yi(w′xi+b)−(1−ξi)]− n

X

i=1

λiξi (2.18)

em queαi eλi s˜ao os multiplicadores de Lagrange, e eles devem ser positivos ou iguais

a zero. Derivando (2.18) em rela¸c˜ao a w, b e ξi e igualando a zero cada uma das

derivadas parciais, s˜ao obtidas as seguintes equa¸c˜oes:

w=

n

X

i=1

αiyixi (2.19)

n

X

i=1

αiyi = 0 (2.20)

αi =C−λi (2.21)

substituindo (2.19), (2.20) e (2.21) em (2.18) pode-se obter a fun¸c˜ao dual,

LD = n

X

i=1

αi−

1 2

n

X

j=1

n

X

i=1

αiαjyiyjx′ixj (2.22)

sob as restri¸c˜oes

  

Pn

i=1αiyi = 0

0_≤αi ≤C

.

Para mais detalhes sobre (2.22) ver Apˆendice B. ´E interessante notar que a forma dual

(30)

pela restri¸c˜ao em queαi deve ter um valor menor que a constanteC. Entretanto, para

que a solu¸cão desse novo problema seja ótima, as estimativasα∗_,_w∗ _e_b∗ _{devem atender} às condi¸cões complementares do teorema de KKT, que são,

∂Lp

∂w = 0

∂Lp

∂b = 0 ∂Lp

∂ξi

= 0 i= 1,2,_{· · ·} , n

yi(w′xi+b) ≥ 1−ξi ∀i (2.23)

ξi ≥ 0 ∀i

αi ≥ 0 ∀i

λi ≥ 0 ∀i

αi[yi(w′xi+b)−(1−ξi)] = 0 ∀i (2.24)

λiξi = 0 ∀i (2.25)

e novamente a solu¸c˜ao ´e dada por,

w∗ = X

vetores de suporte

α∗_iyixi.

Mais uma vez ´e importante lembrar que os pontos xi para os quais α∗ > 0, s˜ao

denominados vetores de suporte e que s˜ao fundamentais para calcular o hiperplano

separador. Novamente, para determinar o valor de b, usam-se as equa¸c˜oes (2.24),

(2.25) e (2.23). Combinando as equa¸c˜oes (2.25) e (2.23) resulta em (C ₋αi)ξi = 0.

Com isso,ξi=0 seα < C. Assim, s˜ao tomadas as observa¸c˜oes para as quais 0< αi < C,

e usa-se (2.24) para determinar o valor de b, em que, as equa¸c˜oes s˜ao iguais a (2.14)

e (2.15). Segundo Lorena e Carvalho (2007), nessa abordagem existem 3 tipos de

(31)

2.3 SVM e Kernels 15

(i) αi = 0 =⇒yif(xi)>1 e ξi = 0

(ii) 0< αi < C =⇒yif(xi) = 1 e ξi = 0

(iii) αi =C =⇒yif(xi)<1 e ξi ≥0.

Em (i), os pontos encontram-se fora das margens e corretamente classificados. Em

(ii), os pontos encontram-se sobre as margens do lado correto do hiperplano. Em

(iii), h´a erros, se ξi >1; os pontos s˜ao corretamente classificados entre as margens, se

0< ξi ≤1; ou, pontos sobre as margens, seξi = 0.

Com tudo que foi mostrado at´e agora, pode-se ver que a SVM ´e um classificador

bastante amplo, ou seja, pode ser aplicado em diversos problemas, e que esse

classifica-dor tem algumas das caracter´ısticas importantes, como por exemplo: não é necessário

fazer nenhuma suposi¸cão sobre a distribui¸cão dos dados e o que é levado em conta para

estimar os coeficientes do hiperplano s˜ao os pontos que realmente importam (vetores de

suporte), buscando a maior distˆancia entre os grupos, e com isso, aumentando o poder

de generaliza¸c˜ao do problema. Para mais detalhes sobre tudo que foi exposto at´e o

momento, ver em Steinwart e Christmann (2008), Lorena e Carvalho (2007), Lorena e

Carvalho (2003), Santos (2002), Andreola (2009), Semolini (2002) e Burges (1998).

2.3 SVM e Kernels

Muitas vezes os problemas encontrados na prática não são linearmente separáveis,

e pode acontecer que a abordagem proposta por Vapnik (1995) n˜ao produza resultados

satisfat´orios, n˜ao separando bem as classes envolvidas e produzindo muitos erros de

classifica¸c˜ao, veja um exemplo na Figura 2.6, (a) e (b) respectivamente.

Observe que apesar da utiliza¸c˜ao da SVM com margens suaves a separa¸c˜ao entre os

grupos não é muito satisfatória. Uma medida muito utilizada para verificar a qualidade

do classificador ´e o percentual de acerto, que ser´a chamado de taxa de acerto. Existem

(32)

2.3 SVM e Kernels 16

−2 −1 0 1 2

−2.0 −1.5 −1.0 −0.5 0.0 0.5 1.0 1.5 (a) x1 x2 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●

−2 −1 0 1 2

−2.0 −1.5 −1.0 −0.5 0.0 0.5 1.0 1.5 (b) x1 x2 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● _● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● Grupo 1 Grupo 2 IVS

Figura 2.6: Dados linearmente inseparáveis; (a) visualiza¸cão dos dados; (b) separa¸cão dos 2 grupos com o hiperplano separador e os indicadores dos vetores de suporte.

• após o cálculo do hiperplano ótimo, utilizar os próprios dados de treinamento e classificá-los novamente. Em seguida, basta fazer a razão entre o número de

pontos que foram classificados corretamente com a quantidade total de pontos;

• não utilizar todos os dados dispon´ıveis para o treinamento, apenas uma parte deles, e após o cálculo do hiperplano ótimo, utilizar os dados que não foram

no treinamento para a classifica¸c˜ao, e novamente basta calcular a raz˜ao entre o

n´umero de pontos classificados corretamente (dados que n˜ao foram para o

treina-mento), com o n´umero total de pontos que foram utilizados para a classifica¸c˜ao

(total de pontos dos dados que n˜ao foram para o treinamento).

Para os dados da Figura 2.6 foi utilizado o primeiro modo descrito anteriormente, ou

seja, utilizar todos os dados para o treinamento e depois classificar todos os dados. A

taxa de acerto para esses dados foi de 68,96%; ´e uma taxa que mostra um desempenho

não muito bom da SVM, e isso indica que a técnica não está separando bem os dados.

O que poderia ser feito para tentar aumentar a taxa de acerto? Note que, seria mais

interessante que os grupos fossem separados por uma outra fun¸c˜ao que n˜ao seja o

hi-perplano definido em (2.1), em vez de uma reta, ou ainda que, de alguma maneira fosse

poss´ıvel fazer uma transforma¸c˜ao nos dados, para que eles se tornassem linearmente

separáveis, ou que essa transforma¸cão diminu´ısse o número de erros de treinamento,

(33)

2.4 Kernels 17

problemas, ser´a mostrado um conjunto de transforma¸c˜oes denominadas deKernelsque

poderá resolver problemas quando os dados não são linearmente separáveis, e quando

a SVM de margens suaves n˜ao produzirem resultados satisfat´orios.

2.4 Kernels

As SVMs também lidam com problemas não lineares, ou seja, é poss´ıvel fazer um

mapeamento no espa¸co original dos dados de treinamento, chamando de espa¸co de

en-tradas, para um espa¸co de dimens˜ao maior chamado de espa¸co de caracter´ısticas. Esse

mapeamento pode ser expresso da seguinte forma, seja Φ :X_{−→ ℑ} um mapeamento, em queXdenota o espa¸co de entradas e_ℑo espa¸co de caracter´ısticas. A escolha apro-priada para Φ pode fazer com que os dados de treinamento possam ser linearmente

separáveis. Como ilustra¸cão, foram utilizados os dados da Figura 2.6 que estão no _R2_,

através das variáveis x1 e x2, no qual é poss´ıvel realizar uma transforma¸cão para o R3

com a fun¸c˜ao,

Φ(x) = (x2₁,x1x2,x22).

Com isso, a equa¸c˜ao em (2.1) do hiperplano ´e da forma,

f(x) = w′Φ(x) +b= 0

f(x) = w1x21+w2x1x2+w3x22+b= 0.

Com esse novo espa¸co, pode-se aplicar a SVM linear proposta por Vapnik (1995).

Observe na Figura 2.7, os dados agora s˜ao linearmente separ´aveis, com isso, a taxa de

acerto que antes era de 68,96% agora ´e de 100%.

A ideia dessa metodologia é aplicar uma fun¸cão não linearφnas variáveis que estão

no espa¸co de entradas, tornando uma dimens˜ao maior no espa¸co de caracter´ısticas, e

ap´os isso, utilizar a SVM linear. ´E interessante utilizar a SVM com margens suaves,

pois apesar das transforma¸c˜oes entre os espa¸cos, ainda podem existir dados com algum

(34)

2.4 Kernels 18

● ● ● ● ●

● ●

●

● ●

●

● ● ●

● ●

● ● ●

●

● ●

● ● ●

●

● ●

●

Grupo 1 Grupo 2 IVS

Figura 2.7: Dados linearmente separ´aveis no espa¸co de caracter´ısticas.

de entrada, e computa o produto φ(x′

i)φ(xj) no espa¸co de caracter´ıstica, ou seja,

K(x′_i,xj) =φ(x′i)φ(xj). (2.26)

Como foi mostrado no exemplo anteriormente, o Kernel ´e utilizado para construir

um hiperplano ´otimo no espa¸co de caracter´ıstica. A fun¸c˜ao dual para o problema de

otimiza¸cão com a utiliza¸cão de uma fun¸cãoKernel é dada por,

LD = n

X

i=1

αi−

1 2

n

X

j=1

n

X

i=1

αiαjyiyjK(x′i,xj) (2.27)

sob as restri¸cões em (2.11). Observe que, se φ é a fun¸cão identidade em (2.26), logo

K(x′

i,xj) = x′ixj, dando origem ao Kernel linear, consequentemente, (2.27) torna-se

igual a (2.22).

Segundo Lorena e Carvalho (2003), as fun¸cões Kernels são muito úteis por causa

da simplicidade do seu c´alculo e sua capacidade de representar espa¸cos abstratos.

En-tretanto, para que uma fun¸c˜ao possa ser um Kernel e garanta a convexidade para

a otimiza¸cão, é necessário atender algumas condi¸cões estabelecidas pelo Teorema de

Mercer, ver Cristianini e Shawe-Taylor (2000). Na Tabela 2.1 est˜ao alguns exemplos

dos Kernels mais utilizados (CRISTIANINI; SHAWE-TAYLOR, 2000). Note que o

KernelLinear ´e um caso particular do Polinomial quando k= 0, δ = 1 e d= 1. ´

(35)

2.4 Kernels 19

Tabela 2.1: Exemplos de algumas fun¸c˜oes Kernel. Tipo de Kernel Fun¸c˜ao K(x′

i,xj) correspondente Parˆametros

Polinomial [δ(x′

ixj) +k]d δ, k e d

Gaussiano ou Radial exp_{−σ_||xi−xj||2} σ

Sigmoide tanh [γ(x′

ixj) +λ] γ e λ

ou seja, o problema deixa de ser bin´ario, e se tˆem mais grupos para classificar, algumas

metodologias de como fazer o treinamento e a classifica¸c˜ao em problemas como esses,

s˜ao descritos em Thome (2012).

O software utilizado no presente trabalho para fazer todos os c´alculos de hiperplanos

e gr´aficos, foi o software R 3.1.3 ver R Core Team (2015). Segue abaixo um modelo

b´asico de como utilizar a SVM no R.

Programa¸c~ao em R.

Pacote: kernlab.

Comandos b´asicos para utiliza¸c~ao da SVM:

install.packages("kernlab") # baixar o pacote library("kernlab") # Carregar o pacote

ksvm(x, y, type = "C-svc", kernel = rbfdot(), C = 1) x - dados.

y - r´otulos.

type - indica o tipo da SVM, que por default ´e para classifica¸c~ao

("C-svc").

kernel - Kernel utilizado. Tem como padr~ao o Kernel Gaussiano, e podem

ser utilizados outros tipos de Kernels. Para mais detalhes sobre os ti-pos de Kernel que podem ser utilizados, basta usar o comando ?ksvm.

(36)

Cap´ıtulo 3

Eletroencefalografia e

Eletromiografia

Neste cap´ıtulo ser˜ao introduzidos alguns conceitos t´ecnicos sobre a maneira de como

os dados s˜ao coletados atrav´es da EEG e EMG, juntamente com os experimentos

rea-lizados para a obten¸c˜ao dos dados utirea-lizados no presente trabalho.

3.1 Coleta de dados de EEG

O EEG ´e um exame que permite o estudo do registro das correntes el´etricas

es-pontâneas emitidas pelo cérebro captadas através de receptores chamados de eletrodos

(LAGE, 2013). O EEG pode ser um método não invasivo, ou seja, os eletrodos são

colocados sobre a cabe¸ca do indiv´ıduo, como mostra a Figura 3.1. No m´etodo invasivo,

os eletrodos são colocados dentro do crânio do indiv´ıduo sobre o córtex cerebral.

Figura 3.1: Touca com eletrodos em uma pessoa. Fonte: Biosemi Systems.

(37)

3.1 Coleta de dados de EEG 21

A EEG ´e muito utilizada para identificar doen¸cas psicol´ogicas como a epilepsia,

ou ainda, avalia¸cão do coma, morte encefálica, estresse pós-traumático e até emo¸cões

humanas. Para gerar dados de EEG, ´e preciso realizar algum tipo de est´ımulo no

indiv´ıduo, como por exemplo: imagens emotivas para avaliar as emo¸c˜oes, ou fazer

com que o indiv´ıduo realize atividades no c´erebro como as dire¸c˜oes direita e esquerda,

dependendo do objetivo do pesquisador. Ap´os o est´ımulo, os sinais s˜ao captados pelos

eletrodos e ´e feita uma filtragem para eliminar ru´ıdos. Os sinais s˜ao medidos ao longo

do tempo, mais especificamente em segundos, tornando o dado obtido em uma s´erie

temporal. ´E importante ressaltar que, cada est´ımulo feito geram v´arios sinais, pois

dependem do n´umero de eletrodos, ou seja, cada eletrodo gera um sinal. Existem

v´arios tipos de touca com quantidade de eletrodos diferentes, como noBiosemi Systems

(BIOSEMI, 20–). Nesse sistema existem toucas com 16, 32, 64 e 128 eletrodos dentre

outras quantidades.

3.1.1 Dados de Est´ımulos Visuais

Os dados utilizados no presente trabalho foram os mesmos usados por Coutinho

(2010), os dados foram coletados através de EEG pelo método não invasivo, utilizando

uma touca com 128 eletrodos em um indiv´ıduo. Foram selecionados um conjunto de

10 imagens (ver Figura 3.2) em que cada imagem foi mostrada 4 vezes ao longo de 5

segundos em uma ordem aleat´oria. Ap´os a filtragem dos sinais, cada eletrodo possui um

total de 164 pontos para cada est´ımulo feito. Com isso, um dos objetivos do trabalho

´e classificar corretamente os sinais produzidos pelo experimento.

Figura 3.2: Imagens utilizadas no experimento feito na The University of Texas - El Paso - UTEP.

(38)

3.1 Coleta de dados de EEG 22

palavra “imagem”, denotar´a as imagens da Figura 3.2 em que, a ordem das imagens

por linha ser˜ao os pr´oprios nomes, respectivamente.

Como ilustra¸c˜ao, observe a Figura 3.3, com os sinais da primeira repeti¸c˜ao dos

eletrodos 1 (a) e 2 (b) para as imagens 1 e 2.

(a)

Tempo

0 50 100 150

−15

−10

−5

0

5

10

15

Imagem 1 Imagem 2

(b)

Tempo

0 50 100 150

−15

−10

−5

0

5

10

15

Imagem 1 Imagem 2

Figura 3.3: Ilustra¸c˜ao dos dados das imagens 1 e 2 para os eletrodos 1 e 2.

3.1.2 Dados de Epilepsia

Uma outra aplica¸cão que será realizada são com dados de pacientes com e sem

epi-lepsia. Esses dados est˜ao dispon´ıveis publicamente em EEG (20–) e para mais detalhes

ver Andrzejaket al.(2001). Os objetivos do experimento eram comparar propriedades

dinâmicas de atividade elétrica cerebral, em diferentes regiões de grava¸cão de diferentes

estados cerebrais fisiológicos e patológicos. A base de dados é composta por 5 bancos

(39)

seg-3.2 Coleta de dados de EMG 23

mentos extra´ıdos do EEG em 5 volunt´arios saud´aveis com olhos abertos e fechados

respectivamente. Os bancos C, D e E originaram-se de um arquivo de EEG de

diag-nósticos pré-cirurgicos de pacientes que sofrem de epilepsia. Para a aplica¸cão serão

utilizados apenas os bancos A e E, em que cada banco possui 100 sinais, 1 para cada

eletrodo e cada sinal tem 4097 pontos.

3.2 Coleta de dados de EMG

A EMG é um método de registro dos potenciais elétricos gerados pelas células

musculares (OCARINOet al., 2005). O registro dos sinais s˜ao captador por um sensor

(Figura 3.4) atrav´es de eletrodos, que podem ser agulhas ou receptores superficiais.

Ademais, os dados captados tamb´em formam uma s´erie temporal.

Figura 3.4: Sensor de EMG com 2 eletrodos. Fonte: Sapsanis et al. (2013).

Com o uso da EMG pode-se diagnosticar uma s´erie de doen¸cas, como fadiga

mus-cular ou les˜oes musmus-culares. Fisioterapeus utilizam a EMG para identificar a efic´acia de

tratamentos. A EMG na área de educa¸cão f´ısica é muito utilizada para identificar as

melhores posi¸c˜oes para trabalhar os m´usculos.

3.2.1 Dados de Movimentos com Objetos

Nesse experimento foram utilizados 5 indiv´ıduos saud´aveis (2 homens e 3 mulheres)

com aproximadamente da mesma idade (entre 20 a 22 anos de idade). Cada indiv´ıduo

tinha a tarefa de agarrar diferentes objetos repetitivamente, em que esses objetos foram

essenciais para realizar os movimentos das m˜aos. A velocidade e for¸ca foram

intenci-onalmente e deixou-se cada indiv´ıduo `a vontade para agarrar o objeto. Para captar

(40)

3.2 Coleta de dados de EMG 24

possu´ıa 2 eletrodos que foram colocados em um antebra¸co de cada um dos 5 indiv´ıduos,

em que cada um dos indiv´ıduos realizaram 6 apertos por 30 vezes por 6 segundos em

cada um dos 6 objetos mostrados na Figura 3.5 e cada sinal possui 3000 pontos. Esses

dados est˜ao dispon´ıveis em Lichman (2013) e para mais detalhes ver Sapsanis et al.

(2013).

(41)

Cap´ıtulo 4

An´

alises complementares

Neste cap´ıtulo ser˜ao apresentadas algumas t´ecnicas importantes, que de algum

modo melhoram o desempenho da SVM. Inicialmente ser´a mostrada uma t´ecnica de

su-aviza¸cão, em seguinda uma análise de correla¸cão para alguns eletrodos e um aplica¸cão

da An´alise de Componetes Principais em dados de EEG.

4.1 Suaviza¸c˜

ao

No contexto de Séries Temporais a suaviza¸cão é muito utilizada para eliminar um

pouco dos ru´ıdos e verificar tendência na série. A seguir será definido médias móveis,

ilustrando-se com um exemplo.

4.1.1 M´

edias M´

oveis Simples

As Médias Móveis Simples (MMS) são um tipo de suaviza¸cão bastante simples, e

geralmente uma das mais usadas. Segundo Morettin e Toloi (2006), em MMS ´e feito

um filtro linear. Assim, seja _{Zt, t = 1,· · · , T}, uma s´erie temporal, na qual ´e feita

uma transforma¸c˜ao paraZ∗

t tal que,

Z_t∗ = 1 s

s

X

i=1

Zt+i−1, t = 1,2,· · · , T −s

em que s é o espa¸camento (número de observa¸cões futuras em rela¸cão ao tempo t) e

geralmente deve ser um valor pequeno. Quando essa suaviza¸cão é utilizada, há uma

(42)

4.2 An´alise de Componentes Principais 26

perda des₋1 observa¸cões da série, e essa suaviza¸cão será denotada por MMSs. Observe

na Figura 4.1, o sinal da imagem 1 com e sem a MMS4.

Tempo

0 50 100 150

−10

−5

0

5

10

Imagem 1 Imagem 1 − MMS4

Figura 4.1: Ilustra¸c˜ao da aplica¸c˜ao de MMS com s=4.

Note que, no sinal com MMS4 ´e poss´ıvel perceber que os picos diminu´ıram,

redu-zindo um pouco a oscila¸cão dos pontos e dando uma melhor visão sobre os padrões

do sinal. ´E importante ressaltar que existem outros tipos de suaviza¸c˜ao, como por

exemplo: exponencial, medianas m´oveis etc. Ver Morettin e Toloi (2006).

4.2 An´

alise de Componentes Principais

A An´alise de Componentes Principais (ACP) tem como principal objetivo, explicar

a estrutura de variância e covariância de um vetor aleatório, composto porp variáveis

aleatórias, através de combina¸cões lineares das variáveis originais. Com isso, tenta-se

reduzir o número de variáveis a serem analisadas e interpretar apenas as combina¸cões

lineares, ou seja, as informa¸c˜oes contidas naspvari´aveis originais podem ser

substitu´ı-das por u(u_≤p) componentes principais não correlacionados, para mais detalhes ver Mingoti (2005). A próxima se¸cão será ilustrada com uma aplica¸cão de ACP em dados