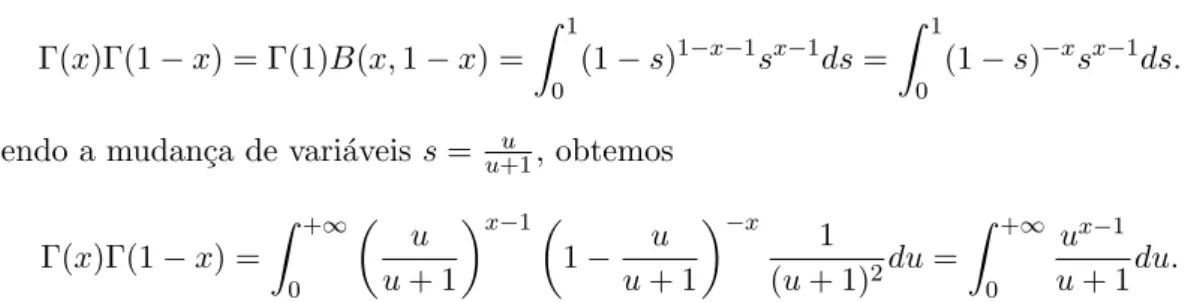Hipótese de Riemann e física

(1)

(2)

José Carlos Valencia Alvites

Orientador:_{Prof. Dr. Paulo Afonso Faria da Veiga}

Dissertação apresentada ao Instituto de Ciências Matemáticas e de Computação - ICMC-USP, como parte dos requisitos para obtenção do título de Mestre em Ciências - Matemática . VERSÃO REVISADA

USP – São Carlos

Março de 2012

Data de Depósito: 26/03/2012

(3)

com os dados fornecidos pelo(a) autor(a)

V152h

Valencia Alvites, José Carlos

Hipótese de Riemann e física / José Carlos Valencia Alvites; orientador Paulo Afonso Faria da Veiga. --São Carlos, 2012.

94 p.

Dissertação (Mestrado - Programa de Pós-Graduação em Matemática) -- Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo, 2012.

1. Função zeta de Riemann. 2. Hipótese de Riemann. 3. Zeros não triviais. 4. Teorema dos Números

(4)

(5)

(6)

Agradecimentos

Meus mais sinceros agradecimentos, sem d´uvida, aos meus pais, Lucy e Rosalio, os amo

por acima de tudo, que sempre acreditaram em mim apesar dos meus defeitos, pelo apoio,

muito obrigado mam´a e pap´a.

A Mary, meu amor, minha companheira, minha melhor amiga, que sempre leva o melhor de mim, que me ensinou a ser uma pessoa melhor, pelo apoio em tempos dif´ıceis, pelas

cr´ıti-cas, para ela com amor e admira¸c˜ao, obrigado bebe.

Ao Professor Paulo, meu orientador, que me apoiou na minha estadia em S˜ao Carlos, pela

orienta¸c˜ao, amizade e por sempre estar disposto a me ajudar no trabalho, este trabalho ´e em

grande parte o produto de suas id´eias e sugest˜oes, professor muito obrigado por seu apoio a

vocˆe e sua fam´ılia que foram muito gentis comigo.

Aos Professores Edgar Vera, que foi meu orientador na gradua¸c˜ao, e Luis Carrillo,

pro-fessores da Facultad de Ciencias Matem´aticas da UNMSM, no Per´u.

Ao ICMC, por me dar a oportunidade.

Aos professores do ICMC pela importante forma¸c˜ao academica.

`

A CAPES, pelo apoio financeiro, sem o qual n˜ao seria poss´ıvel a realiza¸c˜ao deste trabalho,

(7)

(8)

Resumo

Neste trabalho, introduzimos a fun¸c˜ao zeta de Riemann ζ(s), para

s ∈ C_\{1} e apresentamos muito do que ´e conhecido como

justifica-tiva para a hip´otese de Riemann. A importˆancia de ζ(s) para a teoria

anal´ıtica dos n´umeros ´e enfatizada e fornecemos uma prova conhecida

do Teorema dos N´umeros Primos. No final, discutimos a importˆancia de

ζ(s) para alguns modelos f´ısicos de interesse e concluimos descrevendo

(9)

(10)

Abstract

In this work, we introduce the Riemann zeta function ζ(s), s _∈

C_\{1} and present much of what is known to support the Riemann

hypothesis. The importance of ζ(s) to the Analytic number theory is

emphasized and a proof for the Prime Number Theorem is reviewed. In

the end, we report on the importance ofζ(s) to some relevant physical

(11)

(12)

Sum´

ario

1 Introdu¸c˜ao e Motiva¸c˜ao 1

2 Preliminares 5

2.1 Fun¸c˜ao Gama de Euler . . . 5

2.2 A Fun¸c˜ao Zeta de Riemann . . . 13

2.3 Fun¸c˜oes Inteiras de Ordem Um . . . 24

3 A Hip´otese de Riemann 33 3.1 Estabelecendo a Hip´otese de Riemann . . . 33

3.2 Os Zeros n˜ao-triviais de ζ(s) e a Teoria Anal´ıtica dos N´umeros. . . 41

3.3 A Conjetura de Hilbert-P´olya e a Hip´otese de Riemann . . . 55

3.4 Outras Formula¸c˜oes Equivalentes para a Hip´otese de Riemann . . . 55

4 Zeta de Riemann e a F´ısica 63 4.1 Regulariza¸c˜ao Zeta . . . 64

4.2 O Bilhar Circular Aberto . . . 69

4.3 Mecˆanica Estat´ıstica . . . 74

5 Considera¸c˜oes Finais 77

A Informa¸c˜oes Adicionais 79

B Mais Informa¸c˜oes 87

´_{Indice Remissivo} ₉₅

(13)

(14)

Nota¸

c˜

ao

C O conjunto dos n´umeros complexos.

Z O conjunto dos n´umeros inteiros.

N O conjunto dos n´umeros inteiros n˜ao negativos.

R O conjunto dos n´umeros reais.

Γ(s) A fun¸c˜ao Gama de Euler.

ζ(s) A fun¸c˜ao Zeta de Riemann.

ξ(s) A ξ-fun¸c˜ao de Riemann.

S A faixa cr´ıtica.

L A reta cr´ıtica.

Λ(x) A fun¸c˜ao de von Mangoldt.

Ψ(x) A fun¸c˜ao de Chebyshev.

π(x) A fun¸c˜ao de contagem de n´umeros primos.

γE A constante de Euler-Mascheroni.

LQ O conjunto dos n´umeros livres de quadrados.

H(Ω) O conjunto das fun¸c˜oes anal´ıticas em Ω_⊆C.

[_·] A fun¸c˜ao ch˜ao.

Li(x) A fun¸c˜ao integral logar´ıtmica Euleriana.

(15)

(16)

1

Introdu¸

c˜

ao e Motiva¸

c˜

ao

Em 1737, Euler provou que a s´erie (Pdenota o conjunto dos n´umeros primos)

X

p∈P

1

p,

diverge, o que implica na existˆencia de infinitos n´umeros primos. Um outro resultado

impor-tante obtido por Euler ´e apresentado na seguinte f´ormula

Y

p∈P

1₋ 1

ps

₋1

=X

n≥1

1

ns, ∀s∈R, s >1. (1.1)

Euler tamb´em calculou a soma da s´erie infinitaP_n_≥₁_n1s, paras= 2, encontrando o valor

X

n≥1

1

n2 =

π2

6 .

Um m´etodo interessante para calcular o valor deP_n_≥₁_n1s, paraspar esinteiro negativo

´ımpar, é descrito no Apêndice B. A rela¸cão expressa na equa¸cão (1.1) foi o est´ımulo inicial

para que Riemann iniciasse suas pesquisas envolvendo a s´erie infinitaP_n_≥₁ _n1s. Na sua c´elebre

publica¸c˜ao de 1859, entituladaSobre os N´umeros Primos Menores que uma Magnitude Dada

[20], Riemann considerou a fun¸c˜ao

ζ(s) =X n≥1

1

ns. (1.2)

Queζ(s) ´e facilmente estendida para valores descomplexos localizados no semi-plano

com-plexo_{s_∈C:R₍_s₎_>₁_}_{´e uma consequˆencia imediata do fato que}_|_ns_|₌_na_{, onde}_s₌_a₊_ib_;

a, b∈ R, i2 = −1, implicando na convergência absoluta da série no lado direito da equa¸cão

(17)

(1.2), neste dom´ınio. Contudo, neste trabalho, Riemann n˜ao apenas considerou o dom´ınio

acima, mas a extens˜ao de ζ(s) no conjunto C_\{1}.

Para ver queζ(s) pode ser estendida como uma fun¸c˜ao meromorfa em C, com uma ´unica

singularidade descrita por um polo simples em s= 1, n˜ao podemos usar a equa¸c˜ao (1.2). Ao

contrário, nós nos servimos de uma extensão meromorfa da fun¸cão Γ(s) de Euler, que é uma

generaliza¸cão da fun¸cão fatorial. Ao mesmo tempo, com a ajuda desta fun¸cão Γ(s) obtemos

uma rela¸c˜ao funcional compat´ıvel, que concorda com (1.2) em R₍_s₎ _>_{1, dada a seguir [10]}

(Mais adiante no texto, estabeleceremos esta rela¸c˜ao!)

ζ(s) = 2sπs−1sinπs 2

Γ(1−s)ζ(1−s), ∀s∈C_\{1}. (1.3)

A extens˜ao meromorfa da fun¸c˜ao zeta de Riemann,ζ(s) definida em (1.2), com s∈C_{\ {}1},

é o tema central desta disserta¸cão. Esta fun¸cão é o ingrediente principal de um dos mais

complexos e ricos problemas da matem´atica moderna, conhecido como a “A Hip´otese de

Riemann”, o qual se manifesta e afeta um grande número de áreas da Matemática. ´

E f´acil mostrar, considerando o anulamento da fun¸c˜ao sin πs₂ em (1.3), que ζ(s) possui

ra´ızes triviais em s = ₋2,₋4,₋6, . . . A Hip´otese de Riemann conjetura que ζ(s) apresenta

tamb´em zeros n˜ao-triviais nareta cr´ıtica

{s∈C:R₍_s_{) =} 1

2}.

Essa conjetura emergiu do fato que Riemann calculou três zeros, usando o que é hoje con-hecida como a fórmula de Riemann-Seigel [10]. Outros zeros na reta cr´ıtica foram obtidos analiticamente por outros renomados matemáticos (Gram, Backlund, Hutchinson, Titch-marsh, Turing, Lehmer, Meller, Lehman, Rosser, Yohe, Schoenfeld, Brent, van de Lune, te

Riele, Winter, Odlyzko, Wedeniwski, Gourdon e Patrick Demichel), e hoje j´a conhecemos

mais de 1,5 bilhões de zeros aproximados na reta cr´ıtica, obtidos usando métodos numéricos

[27]. Ademais, mostra-se em alguns casos, e há forte indica¸cão nos tratamentos numéricos,

que todos os zeros s˜ao simples, isto ´e, de multiplicidade um.

A Hip´otese de Riemann faz parte da lista dos 23 grandes problemas da Matem´atica

pro-postos por Hilbert no Congresso Internacional de Matem´aticos de Paris, em 1900, sendo

ainda um dos poucos por resolver, juntamente com a Conjetura de Goldbach (Todo n´umero

par maior ou igual a 4 ´e a soma de dois primos.) e o Teorema de Kronecker-Weber

es-tendido para corpos n˜ao-abelianos (No caso abeliano, este teorema estabelece queum corpo

numérico algébrico cujo grupo de Galois sobre Q seja abeliano, é um subcorpo de um corpo ciclotômico, ou seja, um corpo obtido ao adicionar-se uma raiz complexa da unidade aos números racionais.).

Como dissemos acima, na Matemática, a fun¸cão zeta e a Hipótese de Riemann tem

con-sequências em diversas áreas. Um exemplo marcante é a Teoria dos Números, e todos os

dom´ınios que se relacionam com ela (Teoria dos C´odigos, Geometria Alg´ebrica, etc), onde

observamos que ζ(s) nos fornece uma medida da densidade dos n´umeros primos na reta real

(18)

uma “contagem” (estimativa) dos n´umeros primos, obtido original e independentemente por Jacques Hadamard e Charles Jean de la Vall´ee-Poussin. Posteriormente, este teorema foi

demonstrado, sem usar a Teoria Anal´ıtica dos N´umeros, por Atle Selberg e Paul Erd¨os.

Selberg tamb´em obteve uma famosa f´ormula de tra¸co com seu nome [22], que apresenta

uma rela¸cão estreita com os zeros de ζ(s) (O Teorema dos Números Primos será tratado na

se¸c˜ao 3.2). Podemos continuar mencionando tamb´em a Teoria de Operadores (Conjetura de

Hilbert-P´olya), a Teoria das Matrizes Aleat´orias, etc.

A rela¸cão deζ(s) e da Hipótese de Riemann com temas da F´ısica é também muito vasta.

Por exemplo, na Mecânica Clássica, estão associados com o bilhar circular aberto [7], na

Mecânica Estat´ıstica Clássica, temos o Teorema de Lee-Yang sobre os zeros de fun¸cões de

parti¸c˜ao, as quais determinam as quatidades termodinˆamicas de sistemas tais como gases e

cadeias de spins [14], [16] e os fenômenos de transi¸cões de fase (bifurca¸cões) que podem

ocor-rer nos mesmos. Na Mecˆanica Estat´ıstica Quˆantica, os zeros deζ(s) aparecem, por exemplo,

na descri¸cão do sistema de um gás dito Riemannium [18]. As matrizes aleatórias também

são frenquente variáveis na Mecânica Estat´ıstica e seu espectro importante para descrever as

propriedades destes sistemas. Relacionam-se, conforme exposto acima, naturalmente com a

Hip´otese de Riemann. A fun¸c˜aoζ(s) fornece uma ferramenta muita utilizada para a

regular-iza¸c˜ao de operadores, fornecendo um sentido matem´atico para integrais de caminho utilizadas

por Hawking [29]. ζ(s) tamb´em aparece em sistemas dinˆamicos recorrentes na teoria do Caos

Quˆantico (fase de Berry) [4] e a f´ormula de Selberg relaciona-se, por exemplo, com modelos

f´ısicos com espa¸co tempo do tipo Kaluza-Klein [29].

Curiosamente, embora confirmar ou n˜ao a Hip´otese de Riemann seja um dos

proble-mas mais importantes da Matem´atica, entendemos que ´e muito frequente que profissionais e

pesquisadores da Matemática não conhecem seus requisitos m´ınimos. Entendemos também

que essa atitude provém de muitos fatores, até aqueles que fogem do escopo da ciência em si. Contudo, pensamos ser esta uma atitude pouco recomendada aqui.

Neste contexto, decidimos preparar e redigir um texto contendo alguns dos pontos

fun-damentais para que qualquer estudioso da matem´atica, a come¸car por um estudante em vias

de se graduar, possa compreender e estabelecer uma id´eia geral b´asica do problema.

De forma alguma deve o leitor concluir que nos tornamos um expert no assunto, sobretudo

porque, como frisamos acima, trata-se aqui de um assunto n˜ao trivial e extremamente amplo.

Nosso texto, esperamos, poder´a ser considerado uma porta de entrada no tema.

Com este prop´osito, procuramos apresentar um texto relativamente auto-contido, com

muitas das demonstra¸cões básicas e todos os ingredientes necessários ao tema.

Infelizmente, s´o tomamos conhecimento do excelente livro [6] quando este trabalho j´a

estava finalizado. Outras excelentes referˆencias no tema de ζ(s) s˜ao [10], [15], [26] e [9].

Sobre o uso extensivo de resultados genéricos de Análise Complexa temos as referências [8] e

[1].

Para completar nosso trabalho, realizamos uma discuss˜ao breve e pouco aprofundada

(19)

Por fim, vale mencionar que além da solu¸cão de um grande problema em si, a confirma¸cão

da Hipótese de Riemann trará um aprimoramento do número de primos menores que um

número dado x, refinando o resultado atual do Teorema dos Números Primos (ver se¸cão 3.2

do cap´ıtulo 3).

Concluindo, esperamos que o leitor interessado consiga aqui se motivar para aprimorar

seus conhecimentos no tema e, qui¸c´a, poder juntar algum gr˜ao de conhecimento a tudo o que

(20)

2

Preliminares

Neste cap´ıtulo, apresentamos resultados básicos clássicos e algumas defini¸cões a serem

uti-lizados no decorrer do trabalho. Apresentamos algumas provas que, a nosso ver, n˜ao s˜ao

facil-mente encontrados na literatura na forma aqui apresentada ou cujas demonstra¸c˜oes trazem algum argumento t´ecnico que seja relevante em algum ponto subsequente do texto.

No que segue, usamos as seguintes nota¸c˜oes. Dadosa,b∈R, coma < b, denotamos

H(a, b) =_{z_∈C:a <R₍_z₎_{< b}_}_,

e, convencionamos que

H(a,+_∞) =_{z_∈C:a <R₍_z₎_} _e H(_−∞, b) =_{z_∈C:R₍_z₎_{< b}_}_.

Tamb´em, para Ω_⊆ C denotamos por H(Ω) o conjunto das fun¸c˜oes anal´ıticas (holomorfas)

em Ω eB(0;R) ´e o disco em Ccom centro em 0 e raio R > 0. As nota¸c˜oesO,Oǫ,≪ e ≪ǫ

ser˜ao muito usadas no texto e foram definidas no Apˆendice A.

2.1 Fun¸

c˜

ao Gama de Euler

A fun¸cão Gama é a aplica¸cão Γ :H(0,+_∞)_→Cdefinida como

Γ(z) :=

Z _∞

0

e−ttz−1dt. (2.1)

Para ver que a defini¸c˜ao acima faz sentido, observamos que se H(0,+_∞)_∋z=σ+iτ,σ,

τ ∈R, ent˜ao

Z _∞

0

e−ttz−1dt=

Z 1 0

e−ttz−1dt+

Z _∞

1

e−ttz−1dt.

Analisamos as duas integrais do lado direito:

(21)

R1

0 e−ttz−1dt : Claramente

R01e−ttz−1dt

≤R₀1e−ttz−1

dt =R₀1e−t_tσ−1_dt_{. Logo como}_et _> 1, para qualquer t_∈(0,1), ent˜ao e−t<1, assim

e−ttσ−1< tσ−1, _∀t_∈(0,1)_⇒

Z 1 0

e−ttσ−1dt < Z 1

0

tσ−1dt <_∞

⇒ Z 1

0

e−ttz−1dt <∞.

R_∞

1 e−ttz−1dt : An´alogo ao caso anterior,

R1∞e−ttz−1dt

≤ R1∞e−ttσ−1dt. Agora, como

et=P_k_≥₀ t_kk_! ent˜ao t_nn_! _≤et para qualquer t_≥1 e n_∈N. Assim, consideremos n′ _∈N

tal que σ < n′_{, ent˜}_ao _σ₋₍_n′_{+ 1)}_<_{0, logo}

e−ttσ−1 _≤tσ−(n′+1)n′!, _∀t_≥1_⇒

Z _∞

1

e−ttσ−1dt_≤n′! t σ−n′ σ₋n′

! +∞

1 =

n′!

n′₋_σ <∞

⇒ Z _∞

1

e−ttz−1dt

<∞, ∀z∈H(0,+∞).

Portanto, Γ(z) é bem definida. Além disso, pelo método de integra¸cão por partes, é claro

que, para z∈H(0,+∞), temos a recorrˆencia

Γ(z+ 1) =zΓ(z). (2.2)

Ademais, pelo c´alculo direito, Γ(1) = Γ(2) = 1.

Assim, para qualquer n∈N,

Γ(n) = (n₋1)!,

o que tamb´em justifica escrever 0! = 1.

Agora vamos provar que Γ(z) pode ser estendida para uma fun¸c˜ao meromorfa emC. Para

este fim, usamos o seguinte lema.

Lema 2.1 . Seja (cn)∞n=0 uma sequˆencia em C tal que

P

n≥0|cn| converge e S ={−n:n∈

N_{∪ {}0} ecn6= 0}. Então,f(z) =P_n_≥₀ _zc₊n_n converge absolutamente para qualquer z∈C\S e uniformemente em subconjuntos limitados de C_\S. Além disso, f é uma fun¸cão meromorfa em C com polos simples no conjunto S e Res(f,−n) =cn, para qualquer −n∈S.

Demonstra¸c˜ao: Seja A ⊂ C um conjunto limitado. Ent˜ao, existe R > 0 tal que A ⊆

B(0;R). Assim,_|z_|< Rpara qualquerz_∈A. Logo, sen_≥Rtemos_|z+n_{| ≥}n_−|z_{| ≥}n₋R.

Isto implica que| 1

z+n| ≤ n−1R, para|z|< Re n > R. Portanto, se n0> R,

m

X

n=n0

cn

z+n ≤

m

X

n=n0

|cn|

|z+n_| ≤

m

X

n=n0

|cn|

n₋R ≤

1

n0−R

m

X

n=n0

|cn|

!

, _∀m_≥n0.

Da ´ultima desigualdade, temos que a s´erie P_n>R cn

z+n converge absolutamente. Ademais,

como | cn

z+n| ≤ | cn|

(22)

no conjunto A. Isto implica que a s´erie P_n_≥₀ cn

z+n define uma fun¸c˜ao que tem um n´umero

finito de polos simples emS que est˜ao contidos emB(0;R). Portanto, temos que

f(z) =X n≥0

cn

z+n,

é uma fun¸cão meromorfa com polos simples em S. Então, para qualquer −n ∈ S podemos

escrever

f(z) = cn

z+n+

X

−m∈S−{−n}

cm

z+m,

ondeP₋_m_∈_S_−{−_n_} cm

z+m ´e uma fun¸c˜ao anal´ıtica emz=−n. Assim, Res(f,−n) =cn e como

n´e arbitr´ario, temos Res(f,−n) =cn, ∀ −n∈S.

Finalmente, podemos estabelecer o seguinte teorema.

Teorema 2.2 . Γ(z) pode ser estendida a uma fun¸c˜ao meromorfa no plano complexo, com polos simples em 0,−1,−2, .... Al´em disso, vale que

Res(Γ,−n) = (−1) n

n! .

Demonstra¸c˜ao: Para z∈H(0,+∞), temos

Γ(z) =

Z _∞

0

tz−1e−tdt=

Z 1 0

tz−1e−tdt+

Z _∞

1

tz−1e−tdt. (2.3)

A segunda integral do lado direito converge para todoz=x+iy_∈C. De fato,

Z _∞

1

tz−1e−tdt ≤

Z _∞

1

tx−1e−tdt.

Repetindo o argumento acima, lembrando que, para t _≥ 1, n_tn! ≥e−t para qualquer n∈ N,

sejanx∈Ntal que nx> x, ent˜ao x−(nx+ 1)<0 assim temos

Z _∞

1

tx−1e−tdt≤nx!

Z _∞

1

tx−(nx+1)_dt₌_n

x!

lim t→+∞

tx−nx

x−nx − 1

x−nx

= nx!

nx−x

.

Assim temos que, para qualquerz_∈C,R₁∞tz−1_e−t_dt_{converge, ent˜}_{ao esta integral representa}

uma fun¸cão inteira. Por outro lado, como a fun¸cão exponencial é inteira, a sua série de Taylor

converge uniformemente em subconjuntos compactos deCe temos

Z 1 0

tz−1e−tdt =

Z 1 0

tz−1 

X

n≥0

(−1)ntn n!



dt

= X

n≥0

(₋1)n

n!

Z 1 0

tn+z−1dt

= X

n≥0

(₋1)n

n!

1

n+z

(23)

Assim, substituindo em (2.3), obtemos

Γ(z) =X

n≥0

(₋1)n

n!

1

n+z

+

Z _∞

1

tz−1e−tdt, (2.4)

para qualquerz∈H(0,+∞), logo comoP_n_≥₀ (−_n1)_!n <∞, pelo Lema 2.1, o lado direito desta

´

ultima igualdade define uma fun¸c˜ao meromorfa em C com polos simples em 0,₋1,₋2, ... e

Res(Γ,−n) = (−_n1)_!n.

No restante deste trabalho, para evitar confus˜ao e para evitar a introdu¸c˜ao de novas

nota¸cões, vamos continuar denotando por Γ(z) a extensão meromorfa da fun¸cão Γ(z) definida

em (2.1). Agora, ´e claro que, de (2.2) e do Teorema 2.2 , temos o seguinte corol´ario.

Corol´ario 2.3 . Para qualquer z_∈C_\{−1,₋2,₋3, . . ._}

Γ(z+ 1) =zΓ(z).

Como exemplo, vamos verificar a consistência de (2.4) com o corolário último. Seja

z_∈C_{\ {−}1,₋2, . . ._}, ent˜ao de (2.4) temos

Γ(z+ 1) = X

n≥0

(₋1)n

n!

1

n+ 1 +z

+

Z +∞

1

tze−tdt

= X

n≥0

(−1)n+1 (n+ 1)!

− n+ 1

n+ 1 +z

+ (−e−ttz)

+∞

1 +z

Z +∞

1

tz−1e−tdt

= X

n≥0

(−1)n+1 (n+ 1)!

z

n+ 1 +z −1

+1

e +z Z +∞

1

tz−1e−tdt

= z X

n+1=m≥1

(−1)m

m!

1

m+z

− X

n+1=m≥1

(−1)m

m! + 1

e +z Z +∞

1

tz−1e−tdt

= z



X

m≥1

(−1)m

m!

1

m+z + 1 z  ₋  X

m≥1

(−1)m

m! + 1



+1

e +z Z +∞

1

tz−1e−tdt

= zX

m≥0

(−1)m

m!

1

m+z

−X

m≥0

(−1)m

m! + 1

e+z Z +∞

1

tz−1e−tdt

= zX

m≥0

(−1)m

m!

1

m+z

−1_e +1

e +z Z +∞

1

tz−1e−tdt

= z



X

m≥0

(−1)m

m!

1

m+z

+

Z +∞

1

tz−1e−tdt 



= zΓ(z).

Agora, com ajuda da fun¸cão Γ(z) vamos definir a fun¸cão Beta que será de utilidade na

parte de regulariza¸c˜ao Zeta (se¸c˜ao 4.1). Observamos que, para u, v∈H(0,+∞),

Γ(u) =

Z _∞

0

e−ttu−1dt e Γ(v) =

Z _∞

0

(24)

Logo, fazendo a mudan¸cat=x2, temos Γ(u) =

Z _∞

0

e−x2x2(u−1)2xdx= 2

Z _∞

0

e−x2x2u−1dx.

Analogamente,

Γ(v) = 2

Z _∞

0

e−x2x2v−1dx.

Multiplicando as duas igualdades anteriores

Γ(u)Γ(v) = 4

Z _∞

0

e−x2x2u−1dx

Z _∞

0

e−y2y2v−1dy

= 4

Z _∞

0

Z _∞

0

e−(x2+y2)x2u−1y2v−1dxdy.

Considerando a integral dupla e usando coordenadas polares, obtemos

Γ(u)Γ(v) = 4

Z π

2

0

Z _∞

0

e−r2r2(u+v)−1cos2u−1θsin2v−1θdrdθ

=

2

Z _∞

0

e−r2r2(u+v)−1dr

2

Z π

2

0

cos2u−1θsin2v−1θdθ !

=

Z _∞

0

e−r2(r2)((u+v)−1)2rdr

2

Z π

2

0

⇒Γ(u)Γ(v) = Γ(u+v) 2

Z π

2

0

. (2.5)

A integral da ´ultima express˜ao pode ser calculada como segue:

2

Z π

2

0

cos2u−1θsin2v−1θdθ=

Z π

2

0

(cos2θ)u−1(sin2θ)v−1(2 cosθsinθ)dθ

=

Z π

2

0

(1₋sin2θ)u−1(sin2θ)v−1(2 cosθsinθ)dθ,

e, fazendo a mudan¸cas= sin2θ, temos

2

Z π

2

0

cos2u−1θsin2v−1θdθ=

Z 1 0

(1₋s)u−1sv−1ds.

Então, a fun¸cão beta B(v, u) é definida como

B(v, u) :=

Z 1 0

(1₋s)u−1sv−1ds. (2.6)

Logo, de (2.5) temos

Γ(u)Γ(v) = Γ(u+v)B(v, u), (2.7)

(25)

Sejax_∈(0,1). Da equa¸c˜ao acima temos

Γ(x)Γ(1₋x) = Γ(1)B(x,1₋x) =

Z 1 0

(1₋s)1−x−1sx−1ds=

Z 1 0

(1₋s)−xsx−1ds.

Fazendo a mudan¸ca de vari´aveiss= _uu₊₁, obtemos

Γ(x)Γ(1₋x) =

Z +∞

0

u u+ 1

x−1

1₋ u

u+ 1

−x 1

(u+ 1)2du=

Z +∞

0

ux−1 u+ 1du.

Agora, usando este resultado, vamos provar uma rela¸c˜ao que vai ser de muita utilidade, no

que segue, e que nos diz que Γ(z) n˜ao tem zeros. Para este fim, vamos usar o seguinte lema.

Lema 2.4 . Paray _∈(0,1), temos

Z +∞

0

u−y u+ 1du=

π

sinπy.

Demonstra¸c˜ao: Considere o conjunto G =_{z _∈ C:z = 0₆ ,arg(z)_∈ (0,2π)_}, e o ramo do logaritmo seguinte

log(reiθ) = logr+iθ

onde θ _∈ (0,2π). Logo, para z _∈ G seja f(z) := e−ylogz_{. Assim} _f _{´e um ramo da fun¸c˜ao}

exponencialz−y. Agora, considere emC o caminho dado na Fig. 2.1,

Figura 2.1: Caminho γ usado na integral da Eq. (2.8).

onde 0< r <1< R. Assim, temos que seγ :=CR+L2+Cr+L1. Como γ ´e homot´opica a

zero e desde que limz→−1(z+ 1)f_z(₊₁z) =e−πiy, temos que Res

f(z)

z+1,−1

=e−πiy. Assim, pelo

Teorema dos res´ıduos temos _I

γ

f(z)

z+ 1dz = 2πie

(26)

Agora observemos o que acontece com as integraisR_L1 f_z₊₁(z)dz e R_L2 f_z₊₁(z)dz:

Z

L1

f(z)

z+ 1dz=

Z R

r

f(teiα)

teiα_{+ 1}e

iα_dt, _(2.9)

consideremosg: [r, R]_×[0,π₂]_→Rdefinida como

g(t, α) =f(te iα₎

teiα_{+ 1}e

iα₋ t−y

t+ 1

.

´

E claro que g(t,0) = 0, para qualquer t ∈ [r, R]. Como [r, R]×[0,π₂] ´e compacto, ent˜ao

g ´e uniformemente cont´ınua. Assim, para qualquer ε > 0, existe δ0 > 0 de modo que se

(t−t′)2+ (α−α′)2 < δ2₀

⇒g(t, α)−g(t′, α′)< ε R.

Em particular, set′ =te α′ = 0, temos

g(t, α) =_|g(t, α)_|< ε

R, ∀α < δ0

⇒

Z R

r

g(t, α)dt≤ ε(R−r)

R < ε, ∀α < δ0

⇒ Z R

r

f(teiα₎

teiα_{+ 1}e

iα_dt₋Z R r

t−y

t+ 1dt

< ε, _∀α < δ0

⇒ lim α→0+

Z

L1

f(z)

z+ 1dz= limα→0+

Z R

r

f(teiα₎

teiα_{+ 1}e iα_dt₌

Z R

r

t−y

t+ 1dt. (2.10)

Similarmente, como log(z) = log(z) + 2πi, ent˜ao

Z

L2

f(z)

z+ 1dz=

Z r

R

f(te−iα)

te−iα_{+ 1}e−

iα_dt₌Z r

R

f(teiα₎

te−iα_{+ 1}e−

iα_dt₌Z r

R

e−ylog(teiα) te−iα_{+ 1} e−

iα_dt

=

Z r

R

e−y(log(teiα)+2πi) te−iα_{+ 1} e−

iα_dt₌

−e−2πyi Z R

r

e−y(log(teiα)) te−iα_{+ 1} e−

iα_dt

⇒

Z

L2

f(z)

z+ 1dz=−e−

2πyi

Z R

r

iα_dt. _(2.11)

Semelhante ao caso anterior, consideremosh: [r, R]_×[0,π₂]_→R, dada por

h(t, α) =e−

y(log(teiα₎₎

te−iα_{+ 1} e−

iα₋ t−y

t+ 1

.

Ainda, como no caso anterior, h ´e uniformemente cont´ınua e h(t,0) = 0 para qualquer

t_∈[r, R]. Portanto,_∀ε >0,_∃δ1 >0 de modo que

h(t, α)< ε

R, ∀α < δ1 ⇒ Z R

r

(27)

e, pela defini¸c˜ao de limite

lim α→0+

Z

L2

f(z)

z+ 1dz =−e

−2πyi _lim α→0+

Z R

r

iα_dt

!

=−e−2πyi Z R

r

t−y

t+ 1dt. (2.12)

N´os estimamos agora as integrais R_C

R

f(z)

z+1dz e

R

Cr

f(z)

z+1dz:

_zf_{+ 1}(z)

≤ |z|−

y

|z+ 1_| ≤

|z|−y

|1_{− |}z_||

⇒ Z

Cr

f(z)

z+ 1dz

≤ 2πr

1−y

1₋r e

Z

CR

f(z)

z+ 1dz

≤ 2πR

1−y

R₋1

⇒ lim r→0

Z

Cr

f(z)

z+ 1dz = limR→+∞

Z

CR

f(z)

z+ 1dz = 0. (2.13)

Agora, da equa¸c˜ao (2.8), temos

Z

CR

f(z)

z+ 1dz+

Z

L2

f(z)

z+ 1dz+

Z

Cr

f(z)

z+ 1dz+

Z

L1

f(z)

z+ 1dz=

I

γ

f(z)

z+ 1dz= 2πie− iπy

⇒

Z

CR

f(z)

z+ 1dz+

Z

Cr

f(z)

z+ 1dz = 2πie

−iπy₋Z L2

f(z)

z+ 1dz+

Z

L1

f(z)

z+ 1dz

,

ent˜ao, de (2.9), (2.10), (2.11), (2.12) e (2.13) obtemos

lim α→0+

Z

CR

f(z)

z+ 1dz+

Z

Cr

f(z)

z+ 1dz

= 2πie−iπy₋(1₋e−2πyi)

Z R

r

t−y

t+ 1dt.

Logo, pela defini¸c˜ao de limite, para qualquerη >0 existeδ >0 de modo que, se 0< α < δ,

⇒2πie−iπy₋(1₋e−2πyi)

Z R

r

t−y

t+ 1dt−

Z

CR

f(z)

z+ 1dz+

Z

Cr

f(z)

z+ 1dz

< η

2.

Tomando os limitesR_→+_∞ e r_→0, obtemos

2πie−iπy₋(1₋e−2πyi)

Z +∞

0

t−y

t+ 1dt

≤ η

2 < η.

Finalmente, como η >0 ´e arbitr´ario, segue que

Z +∞

0

t−y

t+ 1dt=

2πie−πiy 1−e−2πiy =

π

sin(πy).

Para concluir, conforme foi mencionado antes do Lema 2.4 , que Γ(z) n˜ao possui zeros,

estabelecemos a seguinte proposi¸c˜ao.

Proposi¸c˜ao 2.5 . Para qualquer s∈C_\Z temos

Γ(s)Γ(1₋s) = π

(28)

Demonstra¸c˜ao: Como Γ(x)Γ(1₋x) = R₀+∞u_ux₊₁−1du, para qualquer x _∈ (0,1), ent˜ao pelo lema anterior

Γ(x)Γ(1₋x) = π

sinπ(1₋x) =

π

sin(πx), x∈(0,1).

Al´em disso, como (0,1) tem pontos limite emC_\Z, ent˜ao

Γ(s)Γ(1₋s) = π

sin(πs), ∀s∈C\Z.

Assim, podemos estabelecer agora o teorema que segue.

Teorema 2.6 . A fun¸c˜ao Γ(z) n˜ao tem zeros.

Demonstra¸c˜ao: Pela proposi¸c˜ao anterior, para qualquers∈C_\Z, temos que

Γ(s)Γ(1₋s) = π

sin(πs).

Então Γ(z) não tem zeros em C_\Z, assim os únicos zeros poss´ıveis de Γ(z) só podem estar

em Z. Mas Γ(z) tem polos em 0,−1,−2, . . . e Γ(n) = (n−1)! para qualquer n ∈ N. Em

consequˆencia, Γ(z) n˜ao tem zeros.

2.2 A Fun¸

c˜

ao Zeta de Riemann

Nesta se¸cão, vamos introduzir a fun¸cão zeta de Riemann que é o tema central do nosso

trabalho. Vamos tamb´em fornecer algumas de suas propriedades. Uma delas, o Produto de

Euler dado no Teorema 2.7 , adverte-nos da sua rela¸c˜ao com a teoria dos n´umeros.

A fun¸cão Zeta de Riemann é definida como a fun¸cãoζ :H(1,+_∞)_→Ctal que

ζ(s) :=X n≥1

1

ns. (2.14)

Para ver que esta defini¸cão é boa, é suficiente provar que para qualquer s ∈ H(1,+∞),

P

n≥1 n1s <∞. Mais geralmente, vamos provar que a s´erie que define ζ(s) converge

absolu-tamente emH(1,+_∞). Al´em disso, mostraremos queζ(s)_∈H(H(1,+_∞)).

De fato, primeiro vamos provar que a s´erie que define ζ(s) converge absolutamente em

H(1,+_∞). Seja s=σ+it_∈H(1,+_∞), logo 1< σ. Comons =nσ+it =nσnit =nσeitlogn,

temos que para qualquerm∈N

m

X

n=1

_n1s

=

m

X

n=1

1

nσ.

Agora consideremoss=σ+itfixo em H(1,+∞) e definimos f : [1,+∞) →R, do seguinte

modof(x) = _x1σ. Claramente,f ´e decrescente e cont´ınua. Logo, usando o crit´erio da integral,

para a s´erieP_n_≥₁_n1σ, temos

Z +∞

1

uσdu= lim_b_→₊_∞

Z b

1

uσdu= lim_b_→₊_∞

b1−σ

1₋σ −

1

1₋σ =

1

(29)

Ent˜ao, para qualquers∈H(1,+∞), a somaP_n_≥₁

n1s

´e convergente, logoP_n_≥₁ _n1s converge

absolutamente para todo s_∈H(1,+_∞).

Agora, provaremos que ζ(s) ´e uma fun¸c˜ao anal´ıtica em H(1,+∞). Para isto, basta provar

que a s´erie que defineζ(s) converge uniformemente em subconjuntos compactos deH(1,+_∞).

Para tal, escrevemos ζ(s) = P_n_≥₁gn(s), onde {gn(s) = _n1s}n∈N ⊆ H(H(1,+∞)). Seja

A _⊂ H(1,+_∞), compacto. Como A ´e compacto, existe σ0 > 0 tal que, para qualquer

s=σ+it∈A, temos que 1< σ0≤σ, e ent˜ao

_n1_s

= 1

nσ ≤ 1

nσ0,

para qualquer s_∈A. Como vimos na demonstra¸c˜ao de convergˆencia absoluta, P_n_≥₁_n1σ₀ <

∞. Ent˜ao, pelo teste de WeierstrassP_n_≥₀ _n1s converge uniformemente emAe,

consequente-mente,ζ(s) ´e anal´ıtica emH(1,+_∞).

Vamos agora mostrar o primeiro resultado importante envolvendoζ(s).

Teorema 2.7 (Produto de Euler). Para s=σ+it∈H(1,+∞). Temos

ζ(s) =Y p∈P

1₋ 1

ps

₋1

.

Demonstra¸c˜ao: SejaX∈N, comX≥2, e consideremos a fun¸c˜ao

ζX(s) :=

Y

p∈P

p≤X

1₋ 1

ps

₋1

.

Observemos que, como _p1s

= _p1σ <1, vale

1− 1

ps

₋1

=X

k≥0

1

pks.

Assim, a convergência da série no lado direito é absoluta. Logo, se p1, p2, . . . , pm ∈ P, são

tais que 2 =p1 < p2 < . . . < pm ≤X, ent˜ao

Y

p∈P

p≤X

1₋ 1

ps

₋1

=

 X

k1≥0

1

pk1s₁  

 X

k2≥0

1

pk2s₂  . . .

 X

km≥0

1

pkms

m



= X k1,...,km≥0

1 (pk1₁ . . . pkm

m )s

.

Agora, notemos que a série múltipla acima não tem termos repetidos, pois, se

1 (pk1₁ . . . pkm

m )s

= 1

(pr1₁ . . . prm

m )s ⇒p k1

1 . . . pkmm =pr11 . . . prmm.

Logo, pelo Teorema Fundamental da Aritm´etica, concluimos que k1 =r1, . . . , km =rm.

Al´em disso, para qualquer n_∈N e n_≤X, existemk1, . . . , km ∈N tais que n=pk11 . . . pkmm.

Como esta descomposi¸cão é única temos que

Y

p∈P

p≤X

1₋ 1

ps

₋1

= X

n≤X 1

ns +

′

X

n>X 1

(30)

onde _′ denota a soma de todos os n´umeros naturais maiores que X, de tal forma que seus

divisores primos s˜ao≤X. Agora, concentremo-nos nesta ´ultima soma. Temos

′ X n>X 1 ns ≤ ′ X n>X 1

nσ <

X

n>X 1

nσ.

Novamente, consideremosf : [1,+_∞)_→ R, definida como f(x) = _x1σ. Assim, dado M ∈ N

com M ≥X, consideremos a parti¸c˜ao Q={X < X + 1< . . . < M} de [X, M]. Com isso,

considerando a soma inferiors(f, Q) de f em rela¸c˜ao a Q, podemos escrever

s(f, Q)

| {z }

f(X+1)+f(X+2)+...+f(M)=PM n>Xnσ1

≤

Z M

X

f(u)du=

Z M

X 1

uσdu≤

Z M

X 1

uσdu+ 1 Xσ ⇒ M X n>X 1

nσ ≤

u1−σ

1₋σ

M X + 1 Xσ ⇒ ∞ X n>X 1

nσ ≤

X1−σ σ₋1 +

1

Xσ ≤ 1

Xσ−1 +

X1−σ σ₋1 =

σX1−σ σ₋1

⇒ ′ X n>X 1 ns < σX

1−σ

σ−1 .

Assim, X1−σ → 0, quando X → +∞, pois σ > 1. Isso implica que P′_n>X _n1s → 0, quando

X_→+_∞. Consequentemente,

Y

p∈P

p≤X

1− 1

ps

₋1

= X

n≤X 1

ns +

′

X

n>X 1

ns

e, quandoX _→+_∞, obtemos o resultado desejado

Y

p∈P

1₋ 1

ps

₋1

=X

n≥1

1

ns.

Corolário 2.8 . A fun¸cão ζ(s) não tem zeros no conjunto H(1,+_∞).

Demonstra¸c˜ao: Admitamos que existe s0 =σ0+iτ0 ∈H(1,+∞) tal que ζ(s0) = 0. Logo

para qualquerp∈P, temos

1₋ 1

ps0

₋1

=1 +X j≥1

1

ps0j

≥1₋X j≥1

_p_s0j1

= 1₋X j≥1

1

pσ0j = 1− 1

pσ0 ₋₁

⇒

1₋ 1

ps0

₋1

≥1₋ 1

(31)

Agora, se e10/σ0 < p, ent˜ao _pσ₀1₋₁ < _e101₋₁ < ₁₀1, portanto, _pσ₀1₋₁ ∈(0,1/10). Logo

considere-mos a desigualdade e−2x<1−x, parax∈(0,1/10), que pode ser comprovada graficamente

ou pelo fato seguinte:

Da Desigualdade (2.49), temos que, para qualquer w∈C, com|w| ≤1/2,

e−2|w|2 ≤ |(1−w)ew|.

Em particular, se x∈(0,1/2),

e−2x2 _≤(1₋x)ex,

⇒e−2x2−x_≤1₋x.

Mas,e−2x< e−2x2−x, parax_∈(0,1/2). Em particular parax_∈(0,1/10) tamb´em a desigual-dade ´e cumprida.

Assim, como _pσ01₋₁ ∈(0,1/10) ent˜ao e

−_pσ02−1 _<₁− 1

pσ0₋₁. Logo, substituindo em (2.15),

temos

1₋ 1

ps0

₋1

> e−pσ02−1

⇒ Y

p∈P:p>e10/σ₀

1₋ 1

ps0

₋1

≥e−2

P

p∈P:p>e10/σ0 1

pσ0−1

>0

⇒ Y

p∈P:p>e10/σ₀

1₋ 1

ps0

−1

6

= 0,

o que implica

ζ(s0) =

  Y

p∈P:p≤e10/σ₀

1₋ 1

ps0

₋1

   Y

p∈P:p>e10/σ₀

1₋ 1

ps0

₋1

₆= 0,

que ´e uma contradi¸c˜ao.

Observa¸c˜ao 2.9 . Do Produto de Euler, as duas seguintes observa¸c˜oes surgem:

1. ζ(s) pode ser definida, em alternativa, usando o Produto de Euler.

2. O Produto de Euler mostra a liga¸cão da fun¸cão zeta de Riemann com os números primos.

Agora vamos ver que ζ(s) pode ser estendida para uma fun¸c˜ao meromorfa em C. Para

isso, vamos usar o lema seguinte.

Lema 2.10 . Para s_∈H(1,+_∞), temos

Γ(s)ζ(s) =

Z +∞

0

(32)

Demonstra¸c˜ao: Para qualquers_∈H(1,+_∞), temos

Γ(s) =

Z +∞

0

ts−1e−tdt.

Logo, fazendo a mudan¸ca de vari´avelt=nx, onden∈N, obtemos

Γ(s) =

Z +∞

0

(nx)s−1e−nxndx=ns Z +∞

0

xs−1e−nxdx.

Ent˜ao,

Γ(s) 1

ns =

Z +∞

0

xs−1e−nxdx⇒Γ(s)ζ(s) =X n≥1

Z +∞

0

xs−1e−nxdx

⇒Γ(s)ζ(s) =

Z +∞

0

xs−1 

X

n≥1

e−nx 

dx=

Z +∞

0

xs−1

e−x

1₋e−x

dx=

Z +∞

0

xs−1 ex₋₁dx.

Então, nós estamos prontos para provar que ζ(s) admite uma extensão meromorfa no

plano complexo.

Teorema 2.11 . A fun¸c˜aoζ(s) admite a uma fun¸c˜ao meromorfa emC com polo simples em

s= 1 e com Res(ζ,1) = 1.

Demonstra¸c˜ao: Pelo Lema 2.10 , temos que, paras_∈H(1,+_∞),

Γ(s)ζ(s) =

Z +∞

0

ts−1 et₋₁dt.

Ent˜ao,

Γ(s)ζ(s) =

Z 1 0

ts−1

et₋₁dt+

Z +∞

1

ts−1

et₋₁dt. (2.16)

Vemos que a segunda integral desta ´ultima igualdade converge para qualquers∈C. De fato,

seσ=R₍_s_),

Z +∞

1

ts−1

et₋₁dt

≤

Z +∞

1

t

s−1

et₋₁

dt=

Z +∞

1

tσ−1

et₋₁dt.

Observamos que t_nn_! _≤P_k_≥₁t_kk_! =et₋₁ _∀_n _∈_N _e _t_∈ _[1_,₊_∞_{). Assim, para} _n

s ∈N de tal

forma queσ₋ns<0, como t

ns

ns! ≤e

t₋_{1, temos}

tσ−1

et₋₁ ≤(ns!)t

σ−1−ns _⇒

Z +∞

1

tσ−1

et₋₁dt≤ns!

Z +∞

1

tσ−1−ns_dt₌ ns!

ns−σ

.

Com isso, temos que, para qualquers∈C, a integralR₁+∞_etst₋−1₁dt converge e portanto

repre-senta uma fun¸c˜ao inteira a que denotaremos porϕ(s) =R₁+∞_etst−₋1₁dt. Por outro lado, para a

primeira intregral do lado direito de (2.16), consideremos a fun¸c˜aoh(z) = _ez1₋₁ que tem polo

simples emz= 0. Ademais, Res(h,0) = limz→0_ezz₋₁ = 1, ent˜ao

h(z) = 1

(33)

ondeG´e uma fun¸c˜ao meromorfa emCcom polos de primeira ordem emz= 2kπi, k_∈Z_\{0_}. Portanto,

h(z) = 1

z+ X

n≥0

cnzn, |z|<2π.

Mas, comoB(0; 2π) ´e limitada, ent˜ao existeM >0 que satisfaz |G(z)|< M, ∀z∈B(0; 2π).

Ent˜ao, por estimativas de Cauchy _|G(n)₍₀₎_{| ≤} M n!

(2π)n < M n₂n!, logo |cn| = |G (n)₍₀₎

n! | < M2n.

Finalmente, como P_n_≥₀ M₂n <∞, segue que

P

n≥0|cn|<∞. Logo paras∈H(1,+∞), como

h(z) = 1_z +P_n_≥₀cnzn converge uniformemente em [0,1], temos

Z 1 0

ts−1 et₋₁dt=

Z 1 0

ts−1h(t)dt=

Z 1 0

ts−1  1

t + X

n≥0

cntn

 dt

⇒

Z 1 0

ts−1

et₋₁dt=

Z 1 0

ts−2+X n≥0

cn

Z 1 0

ts−1+ndt= 1

s₋1 +

X

n≥0

cn

s+n. (2.17)

E, substituindo ϕ(s) e (2.17) em (2.16), obtemos

Γ(s)ζ(s) =

Z 1 0

ts−1 et₋₁dt+

Z +∞

1

ts−1 et₋₁dt=

1

s₋1 +

X

n≥0

cn

s+n +ϕ(s), s∈H(1,+∞)

⇒Γ(s)ζ(s) = 1

s−1 +

X

n≥0

cn

s+n +ϕ(s), s∈H(1,+∞). (2.18)

Assim, pelo Lema 2.1 , esta fun¸c˜ao pode ser estendida a uma fun¸c˜ao meromorfa em C com

polo simples em s = 1 e/ou polos simples em s = 0,−1,−2, . . . dependendo se cn 6= 0 ou

cn= 0. Agora, como Γ(s) n˜ao tem zeros ent˜ao _Γ(1_s₎ ∈H(C), logo de (2.18) paras∈H(1,+∞) temos

ζ(s) = Γ(s)ζ(s)

Γ(s) =

1 Γ(s)



 1 s₋1+

X

n≥0

cn

s+n+ϕ(s) 

.

Agora, considerando as extens˜oes meromorfas de Γ(s)ζ(s) e Γ(s), temos que, como Γ(1) =

0! = 1, ent˜ao ζ(s) tem um polo simple em s= 1 e Res(ζ,1) = 1. Al´em disso, visto que Γ(s)

tem polos simples em s= 0,₋1,₋2, . . . ent˜ao a fun¸c˜ao _Γ(1_s₎ tem zeros simples nestes pontos,

assim ζ(s) tem singularidades remov´ıveis em s= 0,₋1,₋2, . . .. Portanto, ζ(s) estende-se a

uma fun¸c˜ao meromorfa em Ccom polo simples ems= 1.

An´alogo ao que foi feito com Γ(s) na se¸c˜ao anterior, no que segue, denotamos porζ(s) a

extens˜ao meromorfa da fun¸c˜aoζ(s) definida em (2.14).

Agora vamos continuar com um resultado que no pr´oximo cap´ıtulo vai nos ajudar a

analisar os zeros reais deζ(s).

Teorema 2.12 . Para qualquer s∈C_{\ {}1}, temos

ζ(s) =πs−12ssinπs 2

(34)

Demonstra¸c˜ao: Consideramos o caminho C dado na Fig. 2.2 abaixo, e, paras_∈ C, fixo,

consideremos a seguinte integral _Z

C

ws−1 ew₋₁dw.

Figura 2.2: Caminho C.

Pelo Teorema de Cauchy, ´e claro que a integral ´e independente de 0 < ε < 2π e da

distância das linhas horizontais em rela¸cão ao eixo real. Por essa razão, faremos o cálculo

desta integral no limite quando ε _→ 0 e quando a distˆancia entre as linhas horizontais

em rela¸c˜ao ao eixo real tende a zero. Assim considerando novamente o ramo do logaritmo log(w) = log_|w_|+iarg(w), arg(w)_∈(0,2π), temos

|ws−1_|= |w|

R₍_s₎₋₁

earg(w)I₍_s₎.

Como arg(w)_∈(0,2π) , ent˜ao existeM >0 de modo que

|ws−1| ≤M|w|R(s)−1_, _(2.19)

para qualquer w _{∈ {}z _∈ C : z ₆= 0,arg(z) _∈ (0,2π)_}. Agora consideremos a aplica¸c˜ao

ψ(w) = _ew1₋₁ que claramente tem um polo simples em w = 0, ent˜ao g(w) = _eww₋₁ tem

uma singularidade remov´ıvel em w = 0. Assim, podemos estender g de modo que g(0) :=

limw→0 _eww₋₁ = 1. Ent˜ao, _g₍1_w₎ = e w₋₁

w , para w 6= 0. Logo, como g1 ´e continua em w = 0,

temos, parawsuficientemente pequeno e |w| 6= 0

1−_g₍1_w₎

≤_g₍₀₎1 − 1

g(w)

≤ 1

2 ⇒

1

2 ≤

e

w₋₁

(35)

⇒ 1 |ew₋₁_| ≤

2

|w|.

Assim, temos que _Z

Cε

1

|ew₋₁_|dw ≤4π,

onde Cε é a por¸cão de circunferência, de raio ε > 0, que faz parte de C. Assim, de (2.19),

obtemos Z Cε

ws−1 ew₋₁dw

≤M εR(s)−1 Z

Cε

1

|ew₋₁_|dw≤4πM ε

R(s)−1

⇒ lim ε→0

Z

Cε

ws−1

ew₋₁dw = 0. (2.20)

Agora, olhemos para as integrais sobre os caminhos horizontais:

Z

L1

ws−1 ew₋₁dw=

Z R

εcosθ

(t+ (εsinθ)i)s−1

et+(εsinθ)i₋₁ dt.

Análogo à demonstra¸cão do Lema 2.4 consideremosg: [ε, R]×[0,π₂]→R, definido como

g(t, θ) =(t+ (εsinθ)i) s−1

et+(εsinθ)i₋₁ −

ts−1 et₋₁

claramente g(t,0) = 0, ∀t ∈ [ε, R]. Como g ´e uniformemente cont´ınua, ent˜ao dado η > 0,

existe δ >0 de modo que

g(t, θ)< η

R, ∀θ < δ ⇒ Z R

εcosθ

g(t, θ)dt_≤ η

R(R−εcosθ)< η

⇒ lim θ→0

Z R

εcosθ

g(t, θ)dt= 0

⇒ lim θ→0

Z

L1

ws−1 ew₋₁dw=

Z R

0

ts−1

et₋₁dt. (2.21)

Agora como log(w) = log(w) + 2πi, ent˜ao temos que

Z

L2

ws−1 ew₋₁dw=

Z εcosθ R

(t−(εsinθ)i)s−1

et−(εsinθ)i₋₁ dt=

Z εcosθ R

elog(t+(εsinθ)i)(s−1) et−(εsinθ)i₋₁ dt =

Z εcosθ R

e(log(t+(εsinθ)i)+2πi)(s−1)

et−(εsinθ)i₋₁ dt=−e

2πi(s−1)

Z R

εcosθ

e(log(t+(εsinθ)i))(s−1) et−(εsinθ)i₋₁ dt.

Assim, pelos mesmos crit´erios usados no caminho L1, temos que

lim θ→0

Z

L2

ws−1

ew₋₁dw=−e

2πi(s−1)Z R 0

ts−1

et₋₁dt. (2.22)

Logo tomando os limitesR _→+_∞,ε_→0,θ_→0 e de (2.20), (2.21), (2.22) temos

Z

C

ws−1 ew₋₁dw =

Z +∞

0

ts−1

et₋₁dt−e

2πi(s−1)

Z +∞

0

ts−1

et₋₁dt= (1−e

2πi(s−1)₎

Z +∞

0

(36)

⇒

Z

C

ws−1

ew₋₁dw =−2ie

πi(s−1)_sin_π₍_s₋₁₎Z +∞ 0

ts−1

et₋₁dt.

Agora, ses_∈H(1,+_∞) pelo Lema 2.10 temos que Γ(s)ζ(s) =R₀+∞_etst−₋1₁dt, ent˜ao

Z

C

ws−1

ew₋₁dw= 2ie

πi(s−1)_sin(_πs_)Γ(_s₎_ζ₍_s₎_, _∀_s_∈_H₍₁_,₊_∞₎_. _(2.23)

Logo, como R_C _ewws₋−1₁dw tem sentido para qualquer s ∈ C, ent˜ao, da igualdade (2.23)

con-siderando continua¸c˜ao anal´ıtica, temos que

Z

C

ws−1

ew₋₁dw= 2ie

πi(s−1)_sin(_πs_)Γ(_s₎_ζ₍_s₎_, _∀_s_∈_C_. _(2.24)

Agora, vamos calcular a mesma integral usando o Teorema de Res´ıduos no caminhoβdescrito

descrito na Fig. 2.3. Seja s _∈ H(_−∞,0) fixo e consideremos a fun¸c˜ao F(w) = _ewws₋−1₁. Pelo

Figura 2.3: Caminho β.

Teorema dos Res´ıduos,

I

β

ws−1

ew₋₁dw= 2πi m

X

n=1

Res(F,2nπi) + m

X

n=1

Res(F,−2nπi)

!

, (2.25)

notemos que 2kπi´e um polo simples deF,_∀k_∈Z, pois limw→2kπ(w−2kπi)[(w−2kπi)F(w)] = 0. Assim, temos que:

• Se k >0,

Res(F,2kπi) =2kπeπ2i

s−1

(37)

• Se ₋k <0,

Res(F,−2kπi) =2kπe32πi

s−1

= (2kπ)s−1e32π(s−1)i.

Ent˜ao, calculando o lado direito de (2.25), obtemos

I

β

ws−1

ew₋₁dw = 2πi m

X

n=1

(2nπ)s−1(eπ2(s−1)i+e32π(s−1)i)

= 2πi

m

X

n=1

2s−1ns−1πs−1eπ(s−1)i(e−π2(s−1)i+e

π

2(s−1)i) =₋2s+1iπseπis e−

π

2(s−1)i+e

π

2(s−1)i 2

! _m X

n=1

1

n1−s =−2s+1iπseπiscosπ

2(s−1)

_Xm

n=1

1

n1−s =−2

s+1_iπs_eπis_sinπ 2s

_Xm

n=1

1

n1−s

⇒

I

β

ws−1

ew₋₁dw=−2

_Xm

n=1

1

n1−s. (2.26)

Agora, observemos que, se w pertence ao lado vertical direito do quadradoβ, ent˜ao

w

s−1

ew₋₁

= |w

s−1_|

ew₋₁ =

elog|w|(R(s)−1)−arg(w)I(s)

|ew₋₁_| =

1

earg(w)I(s)

|w|R(s)−1

|ew₋₁_|

! .

Logo, como arg(w)∈(0,π₄]∪[7₄π,2π) (limitado), ent˜ao existe M >0 tal que

w

s−1

ew₋₁

≤M|w|

R₍_s₎₋₁ |ew₋₁_|.

Al´em disso,

|eR(w)₋₁_|₌_||_ew_{| −}₁_{| ≤ |}_ew₋₁_{| ⇒} 1

|ew₋₁_| ≤ 1

|eR(w)₋₁_|.

Assim, temos

w

s−1

ew₋₁

≤M |w|

R₍_s₎₋₁ |eR₍_w₎

−1_| ≤M

|R₍_w₎_|R(s)−1

|eR₍_w₎ −1_| .

Logo, se denotamos por LV D o lado direito vertical do quadrado, como a parte real de w ´e

fixo deste lado, temos o seguinte

Z

LV D

ws−1 ew₋₁dw

≤M|R(w)|

R(s)−1

|eR(w)₋₁_| ℓ(LV D) =M

|R₍_w₎_|R(s)−1

|eR(w)₋₁_| (2|R(w)|) =

2M|R₍_w₎_|R(s)

|eR(w)₋₁_|

⇒ lim

R(w)→+∞

Z

LV D

ws−1

ew₋₁dw = 0, (2.27)

ondeℓdenota o comprimento. Analogamente, no lado esquerdo verticalLV E temos a mesma

estimativa, ou seja existeM′ _{de modo tal que}

w

s−1

ew₋₁

≤M′|w|

R(s)−1

(38)

⇒ Z

LV E

ws−1 ew₋₁dw

≤ 2M′|R(w)| R(s)

|eR(w)₋₁_|

⇒ lim

R(w)→−∞

Z

LV E

ws−1

ew₋₁dw = 0. (2.28)

Agora, vejamos o que acontece nos lados superior e inferior do quadrado, novamente temos que existeM′′>0 tal que

w

s−1

ew₋₁

≤M′′|w|

R(s)−1

ew₋₁ ≤M′′

|I₍_w₎_|R(s)−1

ew₋₁ .

Por outro lado, como em linhas horizontais limR(w)→+∞_|ew1₋₁_| = 0 e limR(w)→−∞_|ew1₋₁_| = 1,

ent˜ao existe A >0 de modo que

1

|ew₋₁_| ≤A

nos lados superior e inferior de qualquer quadrado. Ent˜ao,

w

s−1

ew₋₁

≤M′′A|I₍_w₎_|R(s)−1

nos lados superior e inferior de β. Logo, comoR₍_s₎_<_{0 e o comprimento para ambos lados}

´e descrito por 2_|I₍_w₎_|_{, se denotamos como} _L_S _e _L_I _{os lados superior e inferior, temos}

Z

LS

ws−1 ew₋₁dw

≤2M′′A_|I₍_w₎_|R(s) _e

Z

LI

ws−1 ew₋₁dw

≤2M′′A_|I₍_w₎_|R(s)

⇒ lim

I(w)→+∞

Z

LS

ws−1

ew₋₁dw=_I₍_wlim₎_→−∞

Z

LI

ws−1

ew₋₁dw = 0. (2.29)

Assim, de (2.29), (2.28) e (2.27), considerando os lados deβ tendendo ao infinito, e de (2.26)

com (2.24), temos

2ieπi(s−1)sin(πs)Γ(s)ζ(s) =

Z

C

ws−1

ew₋₁dw=−2

X

n≥1

1

n1−s

⇒2ieπi(s−1)sin(πs)Γ(s)ζ(s) =₋2s+1iπseπissinπ 2s

ζ(1₋s)

⇒sin(πs)Γ(s)ζ(s) = 2sπssinπ 2s

ζ(1₋s)

⇒2 sinπ

2s

cosπ

2s

Γ(s)ζ(s) = 2sπssinπ 2s

ζ(1₋s)

⇒cosπ 2s

Γ(s)ζ(s) = 2s−1πsζ(1−s), ∀ R₍_s₎_<_{0 e} _s₆_{= 0}_,₋₂_,₋₄_,₋₆_{, . . .}

e como esta ´e uma igualdade entre fun¸c˜oes meromorfas em C

⇒cosπ 2s

Γ(s)ζ(s) = 2s−1πsζ(1−s), ∀s6= 0.

Fazendo a mudan¸caspor 1−s, temos

cosπ

2(1−s)

Γ(1₋s)ζ(1₋s) = 2−sπ1−sζ(s)

⇒ζ(s) = 2sπs−1sinπs 2

Γ(1₋s)ζ(1₋s), _∀s_∈C_{\ {}1_}.

(39)

2.3 Fun¸

c˜

oes Inteiras de Ordem Um

Como vimos na se¸cão anterior, ζ(s) não é uma fun¸cão inteira. Mas, como veremos no

próximo cap´ıtulo, está associada, algebricamente, a uma fun¸cão inteira. Além disso, esta

é uma fun¸cão inteira de ordem um. Portanto, precisamos introduzir esta defini¸cão e

desen-volver algumas propriedades em rela¸c˜ao a seus zeros. Estas propriedades ajudam a relacionar

alguns dos zeros deζ(s) com a teoria anal´ıtica dos n´umeros e encontrar propriedades destes,

por exemplo ζ(s) tem um número infinito enumerável de zeros não reais.

Para uma melhor compreens˜ao desta se¸c˜ao, recomendamos que o leitor fa¸ca uma leitura

prévia do Apêndice A, na se¸cão de Nota¸cão Assintótica.

Defini¸cão 2.13 . Uma fun¸cão inteira f :C_→Cé de ordem um se

|f(z)|=Oǫ(exp(|z|1+ǫ)), para qualquer ǫ >0.

Lema 2.14 . Seja g∈H(C) tal queg(z)6= 0, para qualquer z∈C, que verifica

|g(z)|= exp(O(|z|3/2))

para qualquer z_∈S_j_≥₁∂B(0;Rj), onde limj→+∞Rj = +∞. Ent˜ao,

g(z) = exp(Az+B),

para algumas constantes A, B.

Demonstra¸c˜ao: Comog(z)= 0 para qualquer₆ z, ent˜ao existe h_∈H(C), tal que

g(z) = exp(h(z)). (2.30)

Tamb´em, como |g(z)| = exp(O(|z|3/2_{)), ent˜}_ao _|_h₍_z₎_|₌_O₍_|_z_|3/2_{). Agora, seja} _z _∈_C_{. Logo,}

como limj→+∞Rj = +∞, temos que existej∈N tal quez∈B(0;Rj). Ent˜ao, pela f´ormula

integral de Cauchy, temos

h′′(z) = 1

πi Z

∂B(0;Rj)

h(w) (w−z)3dw

⇒ |h′′(z)_{| ≤} 1

π Z

∂B(0;Rj)

|h(w)_||(w₋z)_|−3dw. (2.31)

Podemos escolher j suficientemente grande tal quez∈B(0;Rj/2). Assim,

|z₋w_{| ≥ |}w_{| − |}z_{| ≥}Rj−

Rj

2 =

Rj

2 . (2.32)

Usando _|h(w)_|=O(_|w_|3/2_{), existe uma constante}_{M >}_{0 tal que}

(40)

Assim, de (2.32) e (2.33) em (2.31), temos

|h′′(z)| ≤16R−_j1/2.

Logo, se j _→ +_∞, temos h′′(z) = 0 e como z ´e qualquer temos que h(z) = Az +B,

para algumas constantes A, B. Finalmente, usando esse fato em (2.30), obtemos g(z) =

exp(Az+B).

Teorema 2.15 (F´ormula de Jensen). Sejam R, ǫ > 0. Admitamos que f ´e anal´ıtica em

B(0;R+ǫ), que f(z) ₆= 0, para R _{≤ |}z_| < R+ǫ e z = 0, e que f tem zeros z1, . . . , zm em

B(0;R) (contando com as multiplicidades respectivas). Ent˜ao,

1 2π

Z 2π

0

log_|f(Reiθ)_|dθ= log_|f(0)_|+ log

Rm

|z1|. . .|zm|

.

Demonstra¸c˜ao: A demonstra¸c˜ao pode ser encontrada em [8].

Corolário 2.16 . Seja f uma fun¸cão inteira com f(0)6= 0. Então,

1 2π

Z 2π

0

log|f(Reiθ)|dθ−log|f(0)|=

Z R

0

n(r)

r dr,

onde n(r) :=_|{z_∈B(0;r) :f(z) = 0_}|.

Demonstra¸cão: Pela Fórmula de Jensen, só temos que provar queR₀Rn(_rr)dr= log_|_z1_|R_...m_|_z

m|

.

Para isso, ordenemos os zeros em rela¸c˜ao a sua magnitude, isto ´e, rj = |zj|, j = 1, . . . , me

r1 ≤r2 ≤. . .≤rm. Por conveniˆencia, seja r0 = 0 erm+1 =R. Assim, temos que

Z R

0

n(r)

r dr= Z r1

r0

n(r)

r dr+ Z r2

r1

n(r)

r dr+· · ·+ Z rm+1

rm

n(r)

r dr

=

Z r1

r0 0

rdr+ Z r2

r1 1

rdr+· · ·+ Z rm+1

rm

m r dr=

m

X

j=1

jlog

rj+1

rj

= m

X

j=1

log

rj+1

rj

j

= log m

Y

j=1

rj+1

rj

j = log

Rm

r1. . . rm

.

Agora passamos a provar uma propriedade importante das fun¸c˜oes inteiras de ordem um,

que será muito útil no próximo cap´ıtulo.

Teorema 2.17 . Seja f uma fun¸c˜ao inteira de ordem um. Ent˜ao, para X >1, temos

(i)

X

f(ρ)=0 |ρ|≥X

(41)

(ii)

X

f(ρ)=0

ρ6=0

|ρ|−1−ǫ <∞,

para qualquer ǫ >0.

(iii) f tem a seguinte representa¸c˜ao:

f(z) =zreAz+B Y

f(ρ)=0

ρ6=0

1− z

ρ

ez/ρ.

Demonstra¸c˜ao:

(i) Se z= 0 é um zero de multiplicidader def, então consideremos g(z) = f_z(zr), que é uma

fun¸cão inteira e verifica g(0) ₆= 0. Além disso, como f é inteira de ordem um, temos

que, para qualquer ǫ >0,

|f(z)_{| ≪}ǫexp|z|ǫ+1. (2.34)

Logo, como limz→∞_|z1|r = 0, ent˜ao existe R >0 tal que

|z_|> R_⇒ 1

|z_|r < ǫ. (2.35)

Assim, de (2.34) e (2.35), temos que

|g(z)_|= |f(z)|

|z_|r ≪ǫexp|z|

1+ǫ_,

o que equivale a dizer que |g(z)| =Oǫ(exp(|z|1+ǫ)). Portanto, g ´e uma fun¸c˜ao inteira

de ordem um. Aplicando agora o Corol´ario 2.16 , temos que

Z R

0

n(r)

r dr=

1 2π

Z 2π

0

log|g(Reiθ)|dθ−log|g(0)|

= 1

2π Z 2π

0

log|g(Reiθ)|dθ− 1

2π Z 2π

0

log|g(0)|dθ= 1 2π

Z 2π

0

log

g(Re

iθ₎

g(0)

dθ

⇒

Z R

0

n(r)

r dr=

1 2π

Z 2π

0

logg(Re iθ₎

g(0)

dθ. (2.36)

Mas, como_|g(Reiθ₎_{| ≪}

log|g(0)|´e uma constante, ent˜ao em (2.36) temos

Z R

0

n(r)

r dr≪ǫ R

1+ǫ _(2.37)

para qualquerǫ >0. Denotemos porSR o n´umero de zeros de f no anelR ≤ |z|<2R.

Assim, temos

SR≤n(2R) = 1

R Z 3R

2R

n(2R)dr_≤ 1 R

Z 3R

2R

n(r)dr_≤3

Z 3R

2R

n(r)