Analiticidade e efeito gráfico da dilatação em funções octoniônicos quaseconformes do tipo F(Z)=Zn

(1)

unesp

UNIVERSIDADE ESTADUAL PAULISTA

Instituto de Biociencias, Letras e Ciencias Exatas

DEPARTAMENTO DE CIENCIAS DE COMPUTACAO E ESTATISTICA

ANALITICIDADE E EFEITO GR ´AFICO DA

DILATAÇ ÃO EM FUNÇ ÕES OCTONI ÔNICAS

QUASECONFORMES DO TIPO F(Z) =Zn

Luiz Fernando Landucci Benzatti

Disserta¸cão de Mestrado Pós-Gradua¸cão em Matemática

Rua Cristov˜ao Colombo, 2265

15054-000 - Sao Jos´e do Rio Preto - SP - Brasil Telefone: (017) 3221-2444

(2)

Analiticidade e Efeito Gr´

afico da Dilata¸c˜

ao em Fun¸c˜

oes Octoniˆ

onicas

Quaseconformes do tipo

f

(

z

) =

z

n

Luiz Fernando L. Benzatti1

Disserta¸cão apresentada ao Instituto de Biociências, Letras e Ciências Exatas da Universidade Estadual Paulista “Júlio de Mesquita Filho”, Campus de São José do Rio Preto, São Paulo, para a obten¸cão do t´ıtulo de Mestre em Matemática.

Orientador: Prof. Dr. Manoel Ferreira Borges Neto

(3)

Benzatti, Luiz Fernando Landucci.

Analiticidade eefeito gráfico da dilata¸cão em fun¸cões octoniônicas quaseconformes do tipof(z) =zn / Luiz Fernando Landucci Benzatti. - São José doRio Preto : [s.n.], 2008.

59f. ; 30 cm.

Orientador: Manoel Ferreira Borges Neto

Disserta¸cão(mestrado) - Universidade Estadual Paulista, Instituto de Biociências, Letras e Ciências Exatas

1. F´ısica matem´atica. 2. Octˆonios. 3. Quasiconformidade. 4.

Hipercomplexos. 5. Fun¸cões octoniônicas - Dilata¸cão. 6. Fun¸cões

hipercomplexas. I. Borges Neto, Manoel Ferreira. II.

Universidade Estadual Paulista, Instituto de Biociˆencias, Letras e

Ciˆencias Exatas. III. T´ıtulo.

(4)

Disserta¸cão apresentada para obten¸cão do t´ıtulo de Mestre em Matemática do Instituto de Biociências, Letras e Ciências Exatas da Universi-dade Estadual Paulista “Júlio de Mesquita Filho”, Campus de São José do Rio Preto.

BANCA EXAMINADORA

Prof. Dr. Manoel Ferreira Borges Neto Prof. Titular

UNESP - S˜ao Jos´e do Rio Preto

Prof. Dr. Masayoshi Tsuchida Prof. Assistente Doutor

UNESP - S˜ao Jos´e do Rio Preto

Prof. Dr. Siovani Felipussi Prof. Assistente Doutor

UFSCAR - Universidade Federal de S˜ao Carlos

(5)

“The mistakes are there, waiting to be made.”

(6)

`

(7)

Agradecimentos

A Deus, pela sa´ude e pelas oportunidades.

Agrade¸co aos meus pais Luiz e Sandra, e ao meu querido irm˜ao Danilo, pelo amor, carinho, e pelo apoio incondicional que sempre me dedicaram.

`

A minha namorada Amanda, agrade¸co o carinho, a compreens˜ao e os conselhos.

Em especial, agrade¸co ao Prof. Dr. Manoel Ferreira Borges Neto, pela amizade, orienta¸cão e paciência na elabora¸cão deste trabalho.

`

(8)

Resumo

Neste trabalho estudamos transforma¸cões quaseconformes no contexto dos octônios, que são hipercomplexos de oito dimensões. Por não preservar a magnitude dos ângulos, mapeamentos

quaseconformes causam uma dilata¸c˜ao linear.

A partir da defini¸cão métrica de quaseconformidade, utilizamos a forma binomial para mostrar que a distância _|f(y) ₋f(x)_| pode ser escrita como um polinômio em r. Com isso, pudemos desenvolver não só um conjunto de fórmulas como também um método computacional simplificado para o cálculo anal´ıtico da dilata¸cão.

Posteriormente, utilizamos ferramentas gráficas para vizualizar as consequências da dilata¸cão.

(9)

Abstract

In this work we study quasiconformal mappings related to octonionic algebra. Since quasicon-formal mappings do not preserve the magnitude of the angles they cause a linear dilatation. We show that it also happens to 8-dimensional hipercomplex.

Based on the metric definition of quasiconformal mapping we show that the distance_|f(y)₋f(x)_| is a polynomial of variable r. Then it´s possible to make not only a set of formulas but also a computacional method to calculate the dilatation.

We also use some graphical tools to visualize the consequences of dilatation.

(10)

SUM ´ARIO SUM ´ARIO

Sum´

ario

1 Introdu¸c˜ao 1

1.1 Breve Hist´oria dos Octˆonios . . . 1

1.2 Nota Hist´orica: Transforma¸c˜ao Quaseconforme . . . 3

1.3 Constru¸c˜ao dos Octˆonios . . . 3

1.4 Octônios: Defini¸cão e Opera¸cões Elementares . . . 6

1.5 Fun¸c˜oes Octoniˆonicas . . . 7

1.6 N˜ao-associatividade dos Octˆonios . . . 8

2 Dilata¸c˜ao 8 2.1 Coordenadas Esf´ericas . . . 9

2.2 Desenvolvimento de f(x) =xn _{. . . .} ₁₀

2.3 Escrevendo _|f(y)₋f(x)_| como um polinˆomio em r . . . 11

2.3.1 Desenvolvendo_|f(y)₋f(x)_| . . . 12

2.3.2 F´ormula parah2k y . . . 15

2.3.3 Substituindoh2k y em F . . . 17

2.3.4 Escrevendo F como um polinˆomio emr . . . 19

2.3.5 Substituindoh2k y em Fi, Fj, ..., Flk . . . 19

2.3.6 Escrevendo Fi, Fj, ..., Flk como polinˆomios em r . . . 23

2.3.7 Resultado: _|f(y)₋f(x)_|= s X Ps(n)rs. . . 25

2.4 Calculando a dilata¸c˜ao . . . 28

2.5 Método computacional para o cálculo da dilata¸cão . . . 35

2.5.1 Introdu¸c˜ao . . . 35

2.5.2 Algoritmo . . . 36

2.5.3 Implementa¸c˜ao computacional do m´etodo . . . 36

2.5.4 Interface . . . 40

2.5.5 Testes . . . 41

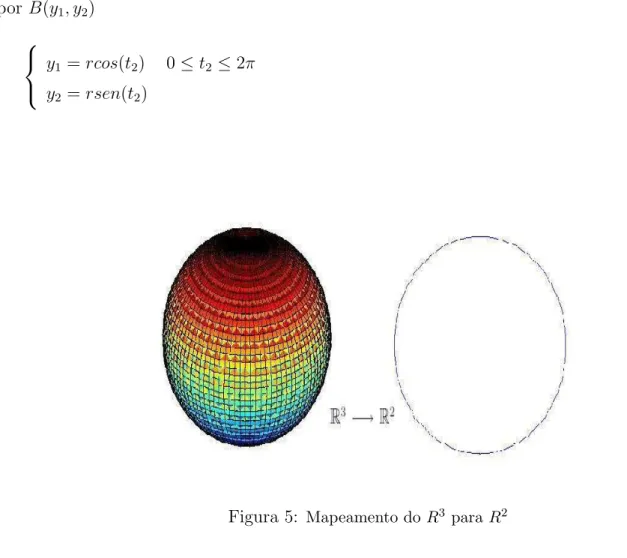
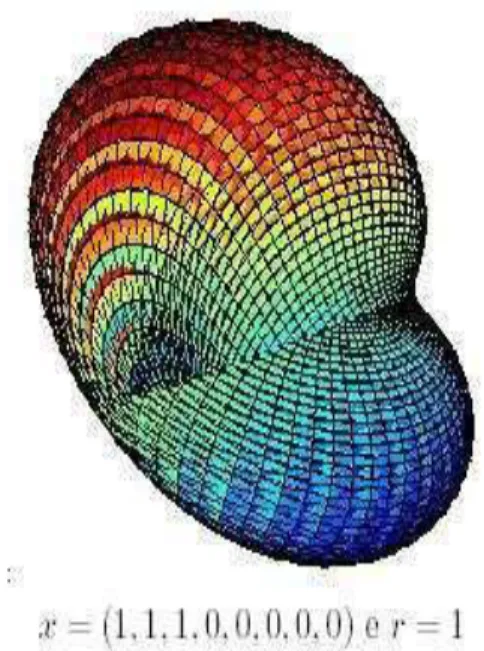
3 An´alise Gr´afica 42 3.1 Mapeamento do R8 _{para o} R3 _{. . . .} ₄₂

3.2 Mapeamento para f(z) =z2 _{. . . .} ₄₅

3.3 Mapeamento para f(z) =z3 _{. . . .} ₄₈

(11)

3.6 Uso da interface para gerar imagem no R3 _{. . . .} ₅₄ 3.7 Desempenho da Interface Gr´afica . . . 57

4 Conclus˜ao 58

(12)

1 INTRODUC¸ ˜AO

1 Introdu¸c˜

ao

Neste trabalho são utilizados dois resultados principais. Em primeiro lugar, a teoria dos octônios, que é, de certo modo, uma extensão não-associativa dos quatérnios. Sua álgebra de divisão nor-mada em 8 dimensões sobre os reais é a mais vasta poss´ıvel que pode ser obtida a partir da constru¸cão de Cayley-Dickson. Em segundo, utilizamos o conceito de fun¸cões quaseconformes, ou seja, fun¸cões que não preservam ângulos. Mais formalmente, uma fun¸cão w = f(z) é quasecon-forme em z0 se não preserva os ângulos entre as curvas através de z0 ez.

Com esses conceitos, desenvolveremos um estudo sobre a dilata¸cão em fun¸cões octoniônicas quase conforme do tipo f(z) =zn_{. A dilata¸cão é uma consequência da transforma¸cão}_{quaseconforme}_. Ao longo deste cap´ıtulo, introduziremos alguns conceitos e defini¸cões necessárias para execu¸cão desse trabalho.

1.1 Breve Hist´

oria dos Octˆ

onios

Muitos matemáticos conhecem a história de como Hamilton descobriu os quatérnios. Em 1835, com 30 anos de idade, ele havia descoberto como tratar números complexos como pares de números reais. Fascinado pela rela¸cão entre complexos e a geometria 2-dimensional, ele tentou por muitos anos descobrir uma álgebra maior, que tivesse o mesmo papel em uma geometria 3-dimensional. Na linguagem moderna, ele estava procurando por uma álgebra de divisão normada 3-dimensional. O problema, claro, era que não existe uma álgebra de divisão normada 3-dimensional. Em outubro de 1843 ele chegou a um resultado importante. Enquanto caminhava com sua esposa em volta do Canal Real, indo para uma reunião na Academia Real Irlandesa, fez sua descoberta histórica.

”Senti o circuito galvˆanico do meu pensamento se fechar; e a fa´ısca que resultou foram as equa¸c˜oes

fundamentais entre i,j e k. Exatamente da maneira que eu sempre as usei.” E em um famoso ato de vandalismo, ele riscou estas equa¸c˜oes em uma pedra da ponte de Brougham:

i2 ₌_j2 ₌_k2 ₌_ijk ₌₋₁

(13)

1.1 Breve História dos Octônios 1 INTRODUÇ ÃO

a morte de Hamilton, por Peter Tait de Edinburgh e Benjamin Peirce de Harvard. Tait escreveu 8 livros sobre quatérnios, enfatizando suas aplica¸cões na f´ısica. Quando Gibbs desenvolveu uma nota¸cão moderna para produto pontual e produto cruzado, Tait condenou isso como uma ”mon-struosidade hermafrodita”. Uma guerra de polêmicas surgiu desde então, tendo os quatérnios como perdedores.

Menos conhecida é a descoberta dos octônios por um colega de faculdade de Hamilton, John T. Graves. Foi o interesse de Graves em álgebra que fez Hamilton come¸car a pensar sobre números complexos e sua expansão. No dia seguinte à descoberta dos quatérnios, Hamilton enviou uma carta de 8 páginas descrevendo os quatérnios para Graves. Graves respondeu ainda em outubro para Hamilton, parabenizando-o por sua descoberta e também complementando: Ainda há algo que me intriga nesse sistema. Eu não tenho ainda uma visão clara da nossa liberdade arbitrária

em criar números imaginários. E então perguntou: Se com sua alquimia você pode criar 3 kg de ouro, por que não continuar?

Em dezembro do mesmo ano, Graves escreveu para Hamilton descrevendo uma nova álgebra 8-dimensional, que ele denominou de ”octavos”. Ele demonstrou que sua nova descoberta era uma álgebra de divisão normada, e usou-a para expressar o produto de duas somas de oito quadrados perfeitos como uma outra soma de oito quadrados perfeitos.

Em janeiro de 1844, Graves escreveu 3 vezes para Hamilton, expandindo sua descoberta. Ele considerou a idéia de uma teoria generalizada, e tentou construir uma álgebra de divisão nor-mada 16-dimensional. Encontrou certas dificuldades e passou a duvidar que isso fosse poss´ıvel. Hamilton se ofereceu para publicar as descobertas de Graves, mas, estando ocupado com suas pesquisas sobre quatérnios, adiou diversas vezes a publica¸cão. Em julho Hamilton escreveu para Graves, mostrando que os octônios eram não-associativos: ”A.BC=AB.C=ABC, se A,B e C são quatérnios. Mas não vale para seus octavos.” De fato, Hamilton criou o termo ”associativo”e os octônios tiveram importante papel em mostrar a importância desse conceito.

Enquanto isso, o jovem Arthur Cayley de Cambridge, vinha pensando nos quatérnios desde que Hamilton anunciou sua existência. Ele parecia procurar rela¸cões entre quatérnios e fun¸cões hiperel´ıpticas. Em mar¸co de 1845, ele publicou um artigo sobre fun¸cões hiperel´ıpticas e adicionou no final um breve comentário sobre octônios. O artigo estava cheio de erros em rela¸cão as fun¸cões el´ıpticas. No entanto, ele foi o primeiro a publicar algum comentário sobre os octônios.

(14)

1.2 Nota Histórica: Transforma¸cão Quaseconforme 1 INTRODUÇ ÃO

Uma razão para os octônios terem, inicialmente, menos destaque que os quatérnios foi a falta de um defensor como Hamilton. Outro motivo, foi a falta de uma aplica¸cão clara na geometria e na f´ısica. Os quatérnios se encaixam perfeitamente no estudo de rota¸cões e momento angular, particularmente no contexto da mecânica quântica. Hoje em dia, tal fenômeno é conhecido como teoria de Clifford. Apesar disso, muitos dizem que Hamilton exagerou na importância atribu´ıda aos quatérnios. Mas sabemos que os quatérnios se encaixam muito bem no nosso entendimento de vários esquemas.

Com os octônios foi diferente. Sua relevância na geometria ficou obscura até 1925, quando Élie Cartan descreveu a ’trialidade’ - a simetria entre vetores ’spinors’ em espa¸cos Euclidianos de 8 dimensões. Sua relevância na f´ısica foi notada em 1934, em um artigo de Jordan, von Neumann e Wigner [2]. No entanto, as tentativas em aplicar a teoria octoniônica à f´ısica obteve pouco sucesso até os anos 80, quando descobriram que octônios explicavam ferramentas interessantes da Teoria das Cordas.

1.2 Nota Hist´

orica: Transforma¸

c˜

ao Quaseconforme

O desenvolvimento moderno dessa teoria teve in´ıcio em meados dos anos 50 e, desde então, vem crescendo enormemente. Parte disso, deve-se ao grande número de aplica¸cões e conexões com outros campos da matemática.

Os trabalhos de Ahlfors tiveram grande impacto em mapeamentosquaseconformes, principalmente na ´area de Espa¸cos de Teichmuller [6].

Por volta de 1920, Grotzsch foi o primeiro a considerar mapeamentos quaseconformes para di-mens˜ao 2, em seus estudos sobre dom´ınios de planos simples [1].

Por´em, os estudos para dimens˜oes maiores, foram desenvolvidos por Lavrentev, com registros de 1938.

O passo mais importante foi dado por Teichm¨uler com mapeamentos quaseconformes em su-perf´ıcies de Riemann [9], levando a uma conex˜ao com diferenciais holomorfas.

1.3 Constru¸c˜

ao dos Octˆ

onios

A maneira elementar de se contruir um octônio é utilizando sua tabela de multiplica¸cão [5]. Os octônios são uma álgebra 8-dimensional com base 1, i, j, k, l, li, lj e lk, e sua multiplica¸cão é dada pela seguinte tabela, que descreve o resultado da multiplica¸cão de um elemento na i-ésima linha por outro na j-ésima coluna.

(15)

1.3 Constru¸cão dos Octônios 1 INTRODUÇ ÃO

Figura 1: Tabela da multiplica¸c˜ao dos octˆonios

interessantes:

• i, j,..., lk s˜ao ra´ızes de -1

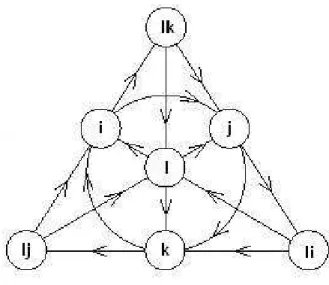
• se ei eej são dois elementos da tabela, comi₆=j, então eiej =₋ejei. Além disso:

• eiej =ek_⇒ei+1ej+1 =ek+1. E tamb´em

• eiej =ek_⇒e2ie2j =e2k

Porém, precisamos de uma maneira mais prática para lembrar o produto dos octônios. Para tanto, apresentamos o Plano Fano.

Plano Fano

Os quatérnios são uma álgebra 4-dimensional com bases 1, i, j e k. Para descrever seu pro-duto, poder´ıamos utilizar a tabela de multiplica¸cão, mas é bem mais fácil notar que:

• 1 ´e a identidade de multiplica¸c˜ao;

(16)

1.3 Constru¸cão dos Octônios 1 INTRODUÇ ÃO

• temos que ij=k, ji=-k e todas as identidades s˜ao obtidas a partir de permuta¸c˜oes c´ıclicas de (i,j,k).

Podemos resumir tais fatos na seguinte figura:

Figura 2: Diagrama da multiplica¸c˜ao dos quat´ernios

Quando multiplicamos dois elementos no sentido horário, obtemos o próximo elemento: por exemplo, ij =k. Mas, quando multiplicamos no sentido anti-horário, obtemos o sinal de menos: ji=₋k. Podemos utilizar o mesmo tipo de figura para multiplicar octônios.

Figura 3: Diagrama da multiplica¸c˜ao dos octˆonios

(17)

1.4 Octônios: Defini¸cão e Opera¸cões Elementares 1 INTRODUÇ ÃO

1.4 Octˆ

onios: Defini¸c˜

ao e Opera¸c˜

oes Elementares

Definimos o conjunto dos octˆonios como

O₌_{_{(x1, x2}_{, x3}_{, x4, x5, x6, x7, x8):} _{x1, x2, x3, x4, x5, x6}_{, x7, x8} _∈ R_}

sendo que, dado x _∈O_{, podemos escrever:}

x=(x1, x2, x3, x4, x5, x6, x7, x8)=x1+ix2+jx3+kx4+lx5+lix6+ljx7 +lkx8

onde i, j, k, l, li, lj, lk s˜ao unidades imagin´arias

i2 ₌_j2 ₌_k2 ₌_l2 _{= (li)}2 _{= (lj)}2 _{= (lk)}2 ₌₋₁

que respeitam a tabela de multiplica¸cão introduzida no tópico anterior[4,5]. A seguir, vamos definir as opera¸cões elementares dos octônios:

Defini¸cão 1. A norma_|x_| de um octônio x=(x1, x2, x3, x4, x5, x6, x7, x8) é o número real

|x_|=px2

1+x22+x23+x24+x25+x26+x27+x28

Defini¸cão 2. O octônio conjugado x dex=(x1, x2, x3, x4, x5, x6, x7, x8) é dado por

x=(x1,−x2,−x3,−x4,−x5,−x6,−x7,−x8)

Defini¸c˜ao 3. Dadox, y_∈O_{, tais que}_x=(x₁_{, x}₂_{, x}₃_{, x}₄_{, x}₅_{, x}₆_{, x}₇_{, x}₈_{) e}_y=(y₁_{, y}₂_{, y}₃_{, y}₄_{, y}₅_{, y}₆_{, y}₇_{, y}₈_),

enunciamos as opera¸c˜oes:

• Adi¸c˜ao:

x+y= (x1+y1, x2+y2, x3+y3, x4+y4, x5+y5, x6+y6, x7+y7, x8+y8) =

(x1+y1)+i(x2+y2)+j(x3+y3)+k(x4+y4)+l(x5+y5)+li(x6+y6)+lj(x7+y7)+lk(x8+y8)

(18)

1.5 Fun¸cões Octoniônicas 1 INTRODUÇ ÃO

xy= (x1y1₋x2y2₋x3y3₋x4y4₋x5y5₋x6y6₋x7y7₋x8y8, x1y2+x2y1+x3y4₋x4y3₋x5y6+x6y5+x7y8+x8y7, x1y3₋x2y4+x3y1+x4y2₋x5y7+x6y8+x7y5₋x8y6, x1y4+x2y3₋x3y2+x4y1₋x5y8₋x6y7+x7y6+x8y5, x1y5+x2y6+x3y7+x4y6+x5y1₋x6y2₋x7y3₋x8y4, x1y6₋x2y5₋x3y8 +x4y7+x5y2+x6y1₋x7y4+x8y3, x1y7+x2y8₋x3y5₋x4y6+x5y3+x6y4+x7y1₋x8y2, x1y8₋x2y7+x3y6₋x4y5+x5y4₋x6y3+x7y2+x8y1)

1.5 Fun¸c˜

oes Octoniˆ

onicas

Sejam D _e D′ _{dom´ınios no espa¸co euclidiano 8-dimensional}R8_, D_⊂O_, D′ _⊂O_{. Uma fun¸c˜ao}

f :D_→D′

é uma fun¸cão octoniônica se f é um mapeamento que faz corresponder a cada x= (x1, x2, x3, x4, x5, x6, x7, x8) _∈ O_um _y₌_f(x),D′ _∈ O_{, ou seja}

f : (x1, x2, x3, x4, x5, x6, x7, x8)_→ (y1, y2, y3, y4, y5, y6, y7, y8)

Sendo f uma fun¸cão octoniônica, podemos decompô-la em parte escalar f1(x) =φ(x) e parte vetorialif2(x) +jf3(x) +kf4(x) +lf5(x) +lif6(x) +ljf7(x) +lkf8(x) =ϕ(x), ou seja

f(x) = f1(x) +if2(x) +jf3(x) +kf4(x) +lf5(x) +lif6(x) +ljf7(x) +lkf8(x) =φ(x) +ϕ(x),

onde fi :R8 _→_R _{s˜ao fun¸c˜oes coordenadas de valores reais para} _i_{= 1,}_2,_3,_4,_5,_6,_7,_8. Consequentemente,

|f(x)_|=pf1(x)2₊_f2(x)2₊_f3(x)2 ₊_f4(x)2₊_f5(x)2₊_f6(x)2₊_f7(x)2₊_f8(x)2_,

(19)

1.6 Não-associatividade dos Octônios 2 DILATAÇ ÃO

1.6 N˜

ao-associatividade dos Octˆ

onios

Sabemos que os octônios são uma álgebra 8-dimensional não-associativa, ou seja, dados a = (y1, y2, y3, y4, y5, y6, y7, y8), b = (x1, x2, x3, x4, x5, x6, x7, x8) e c = (z1, z2, z3, z4, z5, z6, z7, z8), temos que (a.b).c₆=a.(b.c).

No entanto, quando a=b=c, temos que (a.b).c=a.(b.c), conforme mostramos abaixo:

a.b=b.c= (y2

1 −y22−y32−y24−y52−y62−y72−y28, 2y1y2,2y1y3,2y1y4,2y1y5,2y1y6,2y1y7,2y1y8)

(a.b).c = (₋2y1y22−2y1y23−2y1y42−2y1y52−2y1y62−2y1y27−2y1y82+y1(y21−y22−y32−y42−y25−y62−y72−y28, 2y2

1y2+y2(y12−y22−y23−y42−y52−y62−y27−y28), 2y2

1y3+y3(y12−y22−y23−y42−y52−y62−y27−y28), 2y2

1y4+y4(y12−y22−y23−y42−y52−y62−y27−y28), 2y2

1y5+y5(y12−y22−y23−y42−y52−y62−y27−y28), 2y2

1y6+y6(y12−y22−y23−y42−y52−y62−y27−y28), 2y2

1y7+y7(y12−y22−y23−y42−y52−y62−y27−y28), 2y2

1y8+y8(y12−y22−y32−y42−y52−y62−y72−y28)) = a.(b.c)

Esse fato tem grande importância neste trabalho, já que trabalharemos com fun¸cões do tipo f(z) = zn_{, com} _z _∈ _O_.

2 Dilata¸c˜

ao

Já foi dito anteriormente que a dilata¸cão é uma consequência de transforma¸cões quaseconformes. Sabendo que o objetivo principal deste trabalho é o cálculo da dilata¸cão em fun¸cões octoniônicas do tipo f(z) = zn_{, vamos definir transforma¸cão} _{quaseconforme}_.

Defini¸c˜ao M´etrica

Sejam D _e D′ _{dom´ınios no} _{n-espa¸co Euclidiano} _Rn _com _n

≥ 2 e seja f : D _→ D′ _um

homeo-morfismo(cont´ınua, bijetora e preserva topologia). Para x _∈ D _e _{r >} _{0, considere} _{B(x, r) a bola}

fechada (com centro em x) em D_{. Seja}

L(x, r) = max

(20)

2.1 Coordenadas Esféricas 2 DILATAÇ ÃO

H(x, r) = L(x, r)

l(x, r) e H(x) = lim supr→0

H(x, r),

então dizemos que a fun¸cão f équaseconforme se a dilata¸cão H(x) é uniformemente limitada em D_{. Por conveniência, definimos} _f _sendo _K-_{quaseconforme} _{com 1} _≤ _{K <}_∞ _se _f _é

quasecon-forme e H(x)_≤K.

Nos tópicos seguintes, desenvolveremos os ajustes necessários para calcular a dilata¸cão dada na defini¸cão acima.

2.1 Coordenadas Esf´

ericas

Neste tópico explicitamos o processo que nos leva a escrever bolas de oito dimensões, com a fi-nalidade de calcular a distância _|f(y)₋f(x)_|, onde x é o centro da hiperesfera de raio r e y um ponto de sua fronteira.

Considerando as nota¸c˜oes:

cos(ti) = ci e sin(ti) =si,

escrevemos as coordenadas de um ponto na fronteira da hiperesfera como:

               

              

y1 =rc1c2...cn−2cn−1, 0≤tn−1 ≤2π; y2 =rc1c2...cn−2sn−1, −₂1π ≤tn−2 ≤ 1₂π; y3 =rc1c2...sn−2, −1₂π ≤tn−3 ≤ 1₂π; ..., ...;

yj =rc1...cn−jsn−j+1, ...;

..., ...;

yn =rs1, ₋1₂π _≤t1 _≤ 1₂π.

Para n = 3, temos uma esfera noR3 _{definida por:}

   

  

y1 =rc1c2, 0_≤t2 _≤2π; y2 =rc1s2, ₋1₂π_≤t1 _≤ 1₂π; y3 =rs1, 0≤r <∞

(21)

2.2 Desenvolvimento def(x) =xn ₂ _DILATAC_{¸ ˜}_AO                                   

y1 =rc1c2c3c4c5c6c7, 0_≤t7 _≤2π; y2 =rc1c2c3c4c5c6s7, ₋1

2π ≤t6 ≤ 1 2π; y3 =rc1c2c3c4c5s6, ₋1₂π _≤t5 _≤ 1₂π; y4 =rc1c2c3c4s5, ₋1₂π _≤t4 _≤ 1₂π; y5 =rc1c2c3s4, ₋1

2π ≤t3 ≤ 1 2π; y6 =rc1c2s3, ₋1₂π _≤t2 _≤ 1₂π; y7 =rc1s2, ₋1₂π _≤t1 _≤ 1₂π; y8 =rs1, 0_≤r <_∞

2.2 Desenvolvimento de

f

(

x

) =

x

n

Tendo como objetivo calcular a dilata¸cão, através do quociente entre o máximo e o m´ınimo da distância _|f(y)₋f(x)_|, precisamos estudar o desenvolvimento das fun¸cões hipercomplexasf(x) = xn_.

Seja

x=x1+ix2+jx3+kx4+lx5 +lix6+ljx7+lkx8 =x1+hx,

onde hx ´e a parte vetorial dada por

hx =ix2+jx3+kx4+lx5+lix6+ljx7+lkx8

Pelas leis da multiplica¸c˜ao, temos que

h2

x =−x22−x23−x24−x25−x26−x27−x28 ´e um n´umero real.

Para n _∈ N_, _h2

x ´e real e h2n+1x =hxh2nx =h2nx hx imagin´ario da forma h2n

x (ix2+jx3+kx4+lx5+lix6+ljx7+lkx8)=ix2h2nx +jx3h2nx +kx4h2nx +lx5h2nx +lix6h2nx + ljx7h2n

x +lkx8h2nx Assim

h2n+1

x =ix2h2nx +jx3h2nx +kx4h2nx +lx5h2nx +lix6h2nx +ljx7h2nx +lkx8h2nx Ent˜ao, segue-se que

xn_{= (x1}₊_hx)n ₌ n X k=0 µ n k ¶

(22)

2.3 Escrevendo _|f(y)₋f(x)_|como um polinômio em r 2 DILATAÇ ÃO

µ

n 0

¶

xn₁h0x+

µ

n 2

¶

xn₁−2h2x+...+

µ

n 2k

¶

xn₁−2kh2kx +

µ

n 1

¶

xn₁−1h1x+

µ

n 3

¶

xn₁−3h3x+...+

µ

n 2k+ 1

¶

xn₁−(2k+1)h2k+1x =

2k≤n

X k=0 µ n 2k ¶

xn1−2kh2kx +

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

xn1−(2k+1)h2k+1x =

2k≤n

X k=0 µ n 2k ¶

xn−2k 1 h2kx +

| {z }

Re(xn

)

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

xn₁−(2k+1)h2k_x hx

| {z }

I(xn

)

=Re(xn_{) +}_I_(xn₎

2.3 Escrevendo

_|

f

(

y

)

₋

f

(

x

)

_|

como um polinˆ

omio em

r

Neste tópico, desenvolveremos uma idéia central desse trabalho. Vamos mostrar que a expressão |f(y)₋f(x)_|, quandox εO_e_{y ε}O_{são escritos em coordenadas esféricas, é a raiz de um polinômio}

na vari´avel r e de grau 2n da forma

q

P₂(n)r2₊_P(n)

3 r3+...+P (n)

2n r2n (2.1)

Tal resultado já foi demonstrado válido para os quatérnios [3].

Antes de demonstrar que isso é poss´ıvel, devemos discutir sua finalidade. Dada a defini¸cão de dilata¸cão e a distância _|f(y)₋f(x)_| definida como (2.1), segue-se que

H(x) = lim sup r→0

H(x, r) = lim sup r→0

L(x, r)

l(x, r) = lim supr→0

max_|f(y)₋f(x)_| min_|f(y)₋f(x)_| =

= lim sup r→0

maxpP2r2₊_P3r3₊_...₊_P2nr2n

minpP2r2₊_P3r3 ₊_...₊_P2nr2n = lim sup_r_→₀

maxrpP2+P3r+...+P2nr2n−2 minrpP2+P3r+...+P2nr2n−2 =

= max √

P2 min√P2 =

r

maxP2 minP2

(23)

2.3.1 Desenvolvendo _|f(y)₋f(x)_|

Consideremos x = (x1, x2, x3, x4, x5, x6, x7, x8) o centro da bola 8-dimensional de raio r e y = (y1, y2, y3, y4, y5, y6, y7, y8) um ponto de sua fronteira, parametrizado por

                                  

y1 =x1+rcos(t1)cos(t2)cos(t3)cos(t4)cos(t5)cos(t6)cos(t7) y2 =x2+rcos(t1)cos(t2)cos(t3)cos(t4)cos(t5)cos(t6)sen(t7) y3 =x3+rcos(t1)cos(t2)cos(t3)cos(t4)cos(t5)sen(t6)

y4 =x4+rcos(t1)cos(t2)cos(t3)cos(t4)sen(t5) y5 =x5+rcos(t1)cos(t2)cos(t3)sen(t4)

y6 =x6+rcos(t1)cos(t2)sen(t3) y7 =x7+rcos(t1)sen(t2)

y8 =x8+rsen(t1),

com a forma abreviada

                                  

y1 =x1+rc1c2c3c4c5c6c7 y2 =x2+rc1c2c3c4c5c6s7 y3 =x3+rc1c2c3c4c5s6 y4 =x4+rc1c2c3c4s5 y5 =x5+rc1c2c3s4 y6 =x6+rc1c2s3 y7 =x7+rc1s2 y8 =x8+rs1,

e queremos calcular _|f(y)₋f(x)_|para f(z) =zn_. Temos

|f(y)₋f(x)_|=

|Re(yn₎₋_Re(xn_{) +}_I(yn₎₋_I_(xn₎_|₌

¯ ¯ ¯

2k≤n

X k=0 µ n 2k ¶

(yn−2k

(24)

+inh

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

y1n−(2k+1)h2ky

i

y2₋h

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

xn1−(2k+1)h2kx

i

x2o

+jnh

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

y₁n−(2k+1)h2k y

i

y3−

h2k+1_X≤n

k=0

µ

n 2k+ 1

¶

xn₁−(2k+1)h2k x

i

x3

o

+knh

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

y₁n−(2k+1)h2k_y iy4₋h 2k+1≤n

X

k=0

µ

n 2k+ 1

¶

xn₁−(2k+1)h2k_x ix4o

+lnh 2k+1≤n

X

k=0

µ

n 2k+ 1

¶

y₁n−(2k+1)h2k_y iy5₋h 2k+1≤n

X

k=0

µ

n 2k+ 1

¶

+linh 2k+1≤n

X

k=0

µ

n 2k+ 1

¶

y₁n−(2k+1)h2k_y iy6₋h 2k+1≤n

X

k=0

µ

n 2k+ 1

¶

+ljnh

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

y₁n−(2k+1)h2ky

i

y7₋h

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

xn₁−(2k+1)h2kx

i

x7o

+lknh

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

yn₁−(2k+1)h2ky

i

y8₋h

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

xn₁−(2k+1)h2kx

i

x8o¯¯_¯=

¯ ¯ ¯

2k≤n

X k=0 µ n 2k ¶

(y1n−2kh2ky −x n−2k 1 h2kx )

+ih

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

y2y

n−(2k+1)

1 h2ky −x2x

n−(2k+1) 1 h2kx

i

+jh 2k+1≤n

X

k=0

µ

n 2k+ 1

¶

y3yn₁−(2k+1)h2k_y ₋x3xn₁−(2k+1)h2k_x i

+kh

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

y4y₁n−(2k+1)h2k_y ₋x4xn₁−(2k+1)h2k_x i

+lh

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

y5y₁n−(2k+1)h2k_y ₋x5xn₁−(2k+1)h2k_x i

+lih

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

y6y₁n−(2k+1)h2ky −x6x

n−(2k+1) 1 h2kx

i

+ljh

2k+1≤n

X µ _n

2k+ 1

¶

y7yn₁−(2k+1)h2ky −x7x

n−(2k+1) 1 h2kx

(25)

+lkh

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

y8y1n−(2k+1)h2ky −x8x

n−(2k+1) 1 h2kx

i¯ ¯ ¯=

=_|F +iFi+jFj +kFk+lFl+liFli+ljFlj+lkFlk_|=

=qF2₊_F2

i +Fj2+Fk2+Fl2+Fli2+Flj2 +Flk2,

onde

F =¯¯ ¯

2k≤n

X k=0 µ n 2k ¶

(yn−2k

1 h2ky −x n−2k 1 h2kx ),

Fi =

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

(y2yn₁−(2k+1)h2ky −x2x

n−(2k+1) 1 h2kx ),

Fj =

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

(y3yn₁−(2k+1)h2k_y ₋x3xn₁−(2k+1)h2k_x ),

Fk =

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

(y4y₁n−(2k+1)h2k_y ₋x4xn₁−(2k+1)h2k_x ),

Fl =

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

(y5yn1−(2k+1)h2ky −x5x

n−(2k+1) 1 h2kx ),

Fli =

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

(y6yn₁−(2k+1)h2ky −x6x

n−(2k+1) 1 h2kx ),

Flj =

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

(y7yn₁−(2k+1)h2k_y ₋x7xn₁−(2k+1)h2k_x ),

Flk =

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

(y8y

n−(2k+1)

1 h2ky −x8x

n−(2k+1) 1 h2kx ),

(26)

2.3.2 F´ormula para h2k y

Buscamos agora uma f´ormula para o fator h2ky , que aparece em F, Fi, ..., Flk. h2

y =−y22−y23−y24 −y52−y62−y27−y28

Substituindo pela forma parametrizada

h2

y =−[x22+x23 +x24+x52+x26+x27+x28+ 2x2rc1c2c3c4c5c6s7+ 2x3rc1c2c3c4c5s6+ 2x4rc1c2c3c4s5+ 2x5rc1c2c3s4+ 2x6rc1c2s3+ 2x7rc1s2+ 2x8rs1+r2_(c2

1c22c23c24c25c26c27−1)]

e denominando

−c2

1c22c23c24c25c26c27+ 1 =−c2+ 1 =s2

e

Q

=x2c1c2c3c4c5c6s7+x3c1c2c3c4c5s6+x4c1c2c3c4s5+x5c1c2c3s4+x6c1c2s3+x7c1s2+x8s1

Temos

h2

y =h2x−2r

Q

+r2_s2

Como h2k

y = (h2y)k, onde 0≤2k ≤n, ent˜ao h2k

y = (h2x(−2r

Q

+(rs)2₎₎k ₌

µ

k 0

¶

(h2_x)k₍

−2rY+(rs)2)0+

µ

(27)

2.3 Escrevendo _|f(y)₋f(x)_|como um polinômio em r 2 DILATAÇ ÃO + µ k 2 ¶

(h2x) k−2₍

−2rY+(rs)2)2+

... + µ k m ¶

(h2x)k−m(−2r

Y

+(rs)2)m₊ ... + µ k k ¶

(h2_x)k−k₍

−2rY+(rs)2)k_{, (0}

≤m _≤k)

Logo, h2k y = µ k 0 ¶

(h2_x)k₊

µ

k 1

¶

(h2_x)k−1hµ1 0

¶

(₋2rY)1−0(r2s2)0+

µ

1 1

¶

(₋2rY)1−1(r2s2)1i+

µ

k 2

¶

(h2x)

k−2hµ2 0

¶

(₋2rY)2−0(r2s2)0+

µ

2 1

¶

(₋2rY)2−1(r2s2)1 +

µ

2 2

¶

(₋2rY)2−2(r2s2)2i+

...

µ

k m

¶

(h2x)k−m

hµ_m

0

¶

(₋2rY)m−0_(r2_s2₎0₊

µ

m 1

¶

(₋2rY)m−1_(r2_s2₎1₊

µ

2 2

¶

(₋2rY)m−2_(r2_s2₎2₊ ...+

µ

m q

¶

(₋2rY)m−q_(r2_s2₎q₊_...₊

µ

m m

¶

(₋2rY)m−m_(r2_s2₎mi₊

...

µ

k k

¶

(h2x)

k−khµk 0

¶

(₋2rY)k−0(r2s2)0+

µ

k 1

¶

(₋2rY)k−1(r2s2)1+

µ

k 2

¶

(₋2rY)k−2(r2s2)2+...+

µ

k k

¶

(₋2rY)k−k_(r2_s2₎ki_,

Agora podemos separar r de cada termo

h2k y =

hµ_k

0

¶

(h2_x)ki_r0₊

hµ_k

1

¶

(h2_x)k−1

µ

1 0

¶

(₋2Y)1−0(s2)0ir1+

hµ_k

1

¶

(h2x)k−1

µ

1 1

¶

(₋2Y)1−1(s2)1+

µ

k 1

¶

(h2x)k−1

µ

2 0

¶

(₋2Y)2−0(s2)0ir2+

hµ_k

2

¶

(h2x) k−2

µ

2 1

¶

(₋2Y)2−1(s2)1+

µ

k 3

¶

(h2x) k−3

µ

3 0

¶

(28)

hµ_k

2

¶

(h2x) k−2

µ

2 2

¶

(₋2Y)2−2(s2)2+

µ

k 3

¶

(h2x) k−3

µ

3 1

¶

(₋2Y)3−1(s2)1+

µ

k 4

¶

(h2_x)k−4

µ

4 0

¶

(₋2Y)4−0(s2)0ir4+

...+

h

fm+q=irm+q₊ ...+ (s2₎k_r2k_, O elemento genérico dessa sequência, será definido como

fm+q==hµk m

¶µ

m q

¶

(h2_x)k−m₍

−2Y)m−q_(s2₎q₊

µ

k m+ 1

¶µ

m+ 1 q₋1

¶

(h2_x)k−(m+1)₍

−2Y)m−q+2_(s2₎q−1_+...

µ

k m+q

¶µ

m+q 0

¶

(h2_x)k−(m+q)₍

−2Y)m+q(s2)0i, onde 0_≤m+q_≤2k, 0_≤q _≤m_≤k e fm+q= = 0 sem > k.

Por fim, definimos a f´ormula para h2k y

h2k_y = 2k

X

m+q=0

fm+q=rm+q (2.2)

2.3.3 Substituindo h2k

y em F

Nosso objetivo ´e obterF, Fi, ..., Flk como polinˆomios emr. Para tanto, vamos come¸car calculando F. Anteriormente, obtivemos que

F = 2k≤n

X k=0 µ n 2k ¶

(yn−2k

1 h2ky −x n−2k 1 h2kx ) Vamos definir ent˜ao

fn 2k = µ n 2k ¶

(y1n−2kh2ky −x n−2k 1 h2kx )

Substituindo y1 pela forma parametrizada e h2ky pela f´ormula definida

fn ₌

µ

n¶n

(x1+rc)n−2k₍ 2k

X

(29)

µ

n 2k

¶nhµ_n₋_2k

0

¶

xn₁−2k(rc)0 +

µ

n₋2k 1

¶

xn₁−2k−1(rc)1+...+

µ

n₋2k p

¶

xn₁−2k−p(rc)p₊_...₊

µ

n₋2k n₋2k

¶

x0

1(rc)n−2k

i

.

h

fm+q=0r0₊_fm+q=1r1₊_...₊_fm+q=2kr2ki₋_xn−2k 1 h2kx

o

=

Separando em fun¸c˜ao de r

µ

n 2k

¶nhµ_n₋_2k

0

¶

xn−2k

1 c0fm+q=0

i

r0+

hµ_n₋_2k

0

¶

xn−2k

1 c0fm+q=1+

µ

n₋2k 1

¶

xn−2k−1

1 c1fm+q=0

i

r1+

hµ_n₋_2k

0

¶

xn1−2kc0fm+q=2+

µ

n₋2k 1

¶

xn1−2k−1c1fm+q=1+

µ

n₋2k 2

¶

xn1−2k−3c3fm+q=0

i

r2+

+...+

hµ_n₋_2k

0

¶

xn₁−2kc0fm+q=t+...+

µ

n₋2k p

¶

xn₁−2k−pcpfm+q=t−p+...+

µ

n₋2k t

¶

x0₁ctfm+q=0irt+ +...+

hµ_n₋_2k

0

¶

xn−2k

1 c0fm+q=n+...+

µ

n₋2k n₋2k

¶

x0₁cn−2k_fm+q=2ki_rn −

−xn−2k 1 h2kx

o

O primeiro e o ´ultimo termo se anulam. Logo

f_2k(n) =

µ

n 2k

¶hµ_n₋_2k

0

¶

xn−2k

1 c0fm+q=1+

µ

n₋2k 1

¶

xn−2k−1

1 c1fm+q=0

i

r1+

µ

n 2k

¶hµ_n₋_2k

0

¶

xn−2k

1 c0fm+q=2+

µ

n₋2k 1

¶

xn−2k−1

1 c1fm+q=1+

µ

n₋2k 2

¶

xn−2k−2

1 c2fm+q=2

i

r2+

+...+

µ

n 2k

¶hµ_n₋_2k

0

¶

xn−2k

1 c0fm+q=n+...+

µ

n₋2k n₋2k

¶

x0₁cn−2k_fm+q=2ki_rn₊ Para facilitar a visualiza¸c˜ao de fn

2k, definimos

f(2k,t) = µ n 2k ¶h t X p=0 µ

n₋2k p

¶

xn₁−2k−pcp_fm+q=t

−p

i

Portanto

f_2k(n) = n

X

t=1

(30)

2.3.4 Escrevendo F como um polinˆomio em r

Temos que

F = 2k≤n

X

k=0

µ

n 2k

¶

(yn−2k

1 h2ky −xn1−2kh2kx ) Portanto

F = 2k≤n

X

k=0

f_2k(n)= 2k≤n

X

k=0

h_Xn

t=1

f(2k,t)rti₌

=f(0,1)r1₊_f(0,2)r2₊_...₊_f(0,t)rt₊

f(2,1)r1₊_f(2,2)r2₊_...₊_f(2,t)rt₊

+...+

f(2k,1)r1₊_f(2k,2)r2₊_...₊_f(2k,t)rt ₌

= 2k≤n

X

k=0

f(2k,1)r1+ 2k≤n

X

k=0

f(2k,2)r2+...+ 2k≤n

X

k=0

f(2k,t)rt

Por fim, denominamos

ft= 2k≤n

X

k=0 f(2k,t)

e obtemos F como um polinˆomio em r

F = n

X

t=1

ftrt (2.4)

2.3.5 Substituindo h2k

y em Fi, Fj, ..., Flk

Nesse t´opico, vamos escrever Fi como um polinˆomio em r. Seja

Fi =

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

n−(2k+1) 1 h2kx ),

e, separamos f_i2k(n) como

f_i2k(n)=

µ

n 2k+ 1

¶

(y2y1n−(2k+1)h2ky −x2x

(31)

Note que o desenvolvimento de f_i2k(n) ser´a semelhante paraFj, ...Flk. Substituindo y1 pela forma parametrizada, temos

f_i2k(n)=

µ

n 2k+ 1

¶n

y2(x1+rc)n−(2k+1)₍ 2k

X

m+q=0

fm+q=rm+q)₋x2xn₁−(2k+1)h2k_x o

Desenvolvendo (x1+rc)n−(2k+1) _{pela forma binomial}

f_i2k(n)=

µ

n 2k+ 1

¶n

y2hµn−(2k+ 1) 0

¶

xn1−(2k+1)(rc)0+

µ

n₋(2k+ 1) 1

¶

xn1−(2k)(rc)1+...

+

µ

n₋(2k+ 1) p

¶

xn1−(2k+1)−p(rc)p+...+

µ

n₋(2k+ 1) n₋(2k+ 1)

¶

x0)1 (rc)n−(2k+1)

i

.

h

fm+q=0r0+fm+q=1r1+...+fm+q=2kr2ki₋x2xn₁−(2k+1)h2k_x

Substituindo y2 pela forma parametrizada e separando em fun¸c˜ao de r, temos

f_i2k(n) =

µ

n 2k+ 1

¶n

(x2 +rc1c2c3c4c5c6s7)nhµn−(2k+ 1) 0

¶

xn₁−(2k+1)c0fm+q=0ir0+

hµ_n₋_(2k_{+ 1)}

0

¶

xn₁−(2k+1)c0fm+q=1+

µ

n₋(2k+ 1) 1

¶

xn₁−(2k)c1fm+q=0ir1+

+...+

+h t−1

X

p=0

µ

n₋(2k+ 1) p

¶

xn₁−(2k+1)−pcpfm+q=t−(p+1)

i

rt−1+

+h t−1

X

p=0

µ

n₋(2k+ 1) p

¶

xn₁−(2k+1)−pcp_fm+q=t

−p

i

rt₊

+...+

+

µ

n₋(2k+ 1) n₋(2k+ 1)

¶

x0₁cn−(2k+1)_fm+q=2krn−1o

−x2xn₁−(2k+1)h2k_x o

Sabendo que fm+q=0 =¡k₀¢¡0₀¢(h2

x)k−0(−2

Q

)0−0_(s2₎0 ₌_h2k

x , temos

f_i2k(n) =

µ

n 2k+ 1

¶nh x2 1 X p=0 µ

n₋(2k+ 1) p

¶

xn₁−(2k+1)−pcp_fm+q=1

−p+c1c2c3c4c5c6s7x

n−(2k+1) 1 h2kx

i

r1+

+hx2 2

X

p=0

µ

n₋(2k+ 1) p

¶

xn₁−(2k+1)−pcp_fm+q=2

(32)

2.3 Escrevendo _|f(y)₋f(x)_|como um polinômio em r 2 DILATAÇ ÃO c1c2c3c4c5c6s7 1 X p=0 µ

n₋(2k+ 1) p

¶

xn1−(2k+1)−pcpfm+q=2−p

i

r2+

+...+

+hx2 t

X

p=0

µ

n₋(2k+ 1) p

¶

−p+

c1c2c3c4c5c6s7 t−1

X

p=0

µ

n₋(2k+ 1) p

¶

−p−1

i

rt₊_....

+hc1c2c3c4c5c6s7

µ

n₋(2k+ 1) n₋(2k+ 1)

¶

x0₁cn−(2k+1)fm+q=2kirno

Podemos ent˜ao, definir um termo gen´erico de f_i2k(n) como

fi(2k,t) =

µ

n 2k+ 1

¶h x2 t X p=0 µ

n₋(2k+ 1) p

¶

xn₁−(2k+1)−pcpfm+q=t−p+

+hc1c2c3c4c5c6s7 t−1

X

p=0

µ

n₋(2k+ 1) p

¶

xn1−(2k−1)−pcpfm+q=t−p−1

i

Logo

f_i2k(n) = n

X

t=1

fi(2k,t)rt

Os c´alculos da substitui¸c˜ao de h2k

y em Fj, ..., Flk segue de maneira similar a Fi. Desse modo, definimos tamb´em

a) fj(2k,t) =

µ

n 2k+ 1

¶h x3 t X p=0 µ

n₋(2k+ 1) p

¶

−p+

+hc1c2c3c4c5s6 t−1

X

p=0

µ

n₋(2k+ 1) p

¶

xn₁−(2k−1)−pcp_fm+q=t

−p−1

i

⇒f_j2k(n)= n

X

t=1

fj(2k,t)rt _;

b) fk(2k,t) =

µ

n 2k+ 1

¶h

x4 t

Xµ_n₋_(2k_{+ 1)}

p

¶

(33)

+hc1c2c3c4s5 t−1

X

p=0

µ

n₋(2k+ 1) p

¶

xn1−(2k−1)−pcpfm+q=t−p−1

i

⇒f_k2k(n) = n

X

t=1

fk(2k,t)rt _;

c) fl(2k,t) =

µ

n 2k+ 1

¶h x5 t X p=0 µ

n₋(2k+ 1) p

¶

−p+

+hc1c2c3s4 t−1

X

p=0

µ

n₋(2k+ 1) p

¶

−p−1

i

⇒f_l2k(n)= n

X

t=1

fl(2k,t)rt_c) _;

d) fli(2k,t)=

µ

n 2k+ 1

¶h x6 t X p=0 µ

n₋(2k+ 1) p

¶

xn1−(2k+1)−pcpfm+q=t−p+

+hc1c2s3 t−1

X

p=0

µ

n₋(2k+ 1) p

¶

−p−1

i

⇒f_li2k(n) = n

X

t=1

fli(2k,t)rt

e) flj(2k,t) =

µ

n 2k+ 1

¶h x7 t X p=0 µ

n₋(2k+ 1) p

¶

−p+

+hc1s2 t−1

X

p=0

µ

n₋(2k+ 1) p

¶

xn₁−(2k−1)−pcpfm+q=t−p−1

i

⇒f_lj2k(n) = n

X

t=1

(34)

f) flk(2k,t) =

µ

n 2k+ 1

¶h

x8 t

X

p=0

µ

n₋(2k+ 1) p

¶

−p+

+hs1 t−1

X

p=0

µ

n₋(2k+ 1) p

¶

−p−1

i

⇒f_lk2k(n) = n

X

t=1

flk(2k,t)rt _;

2.3.6 Escrevendo Fi, Fj, ..., Flk como polinˆomios em r

Seja

Fi =

2k+1≤n

X

k=0

µ

n 2k+ 1

¶

n−(2k+1) 1 h2kx ), dado

f_i2k(n) = n

X

t=1

fi(2k,t)rt

Temos

Fi =

2k+1≤n

X

k=0

³Xn

t=1

fi(2k,t)rt´₌

=fi(0,1)r1₊_fi(0,2)r2₊_...₊_fi(0,t)rt₊

+fi(2,1)r1₊_fi(2,2)r2₊_...₊_fi(2,t)rt₊

+...+

+fi(2k,1)r1₊_fi(2k,2)_r2₊_...₊_fi(2k,t)_rt₌ 2k+1≤n

X

k=0

fi(2k,1)r1+

2k+1≤n

X

k=0

fi(2k,2)r2+...+

2k+1≤n

X

k=0

fi(2k,t)rt

Definimos ent˜ao

fit =

2k+1≤n

X

(35)

com 1_≤t_≤n.

Por fim, escrevemos Fi em sua forma polinomial

Fi = n

X

t=1

fitrt (2.5)

Analogamente

Fj =

2k+1≤n

X

k=0

³_Xn

t=1

fj(2k,t)rt´=_⇒fjt =

2k+1≤n

X

k=0

fj(2k,t)

=_⇒Fj = n

X

t=1

fjtrt _(2.6)

e ainda:

a) Fk =

2k+1≤n

X

k=0

³Xn

t=1

fk(2k,t)rt´₌

⇒fkt=

2k+1≤n

X

k=0

fk(2k,t)

=_⇒Fk = n

X

t=1

fktrt _; _(2.7)

b) Fl=

2k+1≤n

X

k=0

³_Xn

t=1

fl(2k,t)rt´₌

⇒flt=

2k+1≤n

X

k=0

fl(2k,t)

=_⇒Fl = n

X

t=1

fltrt ; (2.8)

c) Fli =

2k+1≤n

X

k=0

³_Xn

t=1

fli(2k,t)rt´₌

⇒flit =

2k+1≤n

X

k=0

fli(2k,t)

=_⇒Fli = n

X

t=1

flitrt ; (2.9)

d) Flj =

2k+1≤n

X

k=0

³_Xn

t=1

flj(2k,t)rt´=_⇒fljt =

2k+1≤n

X

k=0

(36)

=_⇒Flj = n

X

t=1

fljtrt _; _(2.10)

e) Flk =

2k+1≤n

X

k=0

³_Xn

t=1

flk(2k,t)rt´₌

⇒flkt =

2k+1≤n

X

k=0

flk(2k,t)

=_⇒Flk = n

X

t=1

flktrt (2.11) Por fim, escrevemos toda a parte vetorial Fj, ...Flk como polinˆomios em r.

2.3.7 Resultado: _|f(y)₋f(x)_|=

s X

Ps(n)rs

Vimos at´e aqui que

|f(y)₋f(x)_|=qF2₊_F2

i +Fj2+Fk2+Fl2+Fli2+Flj2 +Flk2, onde,

F = n

X

t=1

ftrt, Fi = n

X

t=1

fitrt, Fj = n

X

t=1

fjtrt, Fk = n X t=1 fktrt Fl = n X t=1

fltrt, Fli = n

X

t=1

flitrt, Flj = n

X

t=1

fljtrt, Flk= n

X

t=1 flktrt

Por isso

F2 ₌³ n

X

t=1 ftrt´

2

= (f1r1+f2r2+...+fnrn)2 =

= n

X

v=1

(fvrv)2+ 2 n X w=1 n X z=1

fwrwfzrz =

p2r2₊_p3_r3₊_....₊_p2nr2n ₌ 2n

X

s=2 psrs

,onde ps fica definido como

ps =         

s−1

X

p=1

fpfs−p, para 2≤s≤n+ 1;

n−p

X

(37)

De maneira an´aloga, temos

Fi = 2n X s=2 pisrs onde, pis =           

s−1

X

p=1

fipfi(s−p), para 2≤s≤n+ 1;

n−p

X

k=0

fi(p+k)fi(n−k), para s =n+p, p >1

e tamb´em:

a) Fj =

2n X s=2 pjsrs onde pjs =           

s−1

X

p=1

fjpfj(s−p), para 2≤s≤n+ 1;

n−p

X

k=0

fj(p+k)fj(n−k), para s=n+p, p > 1

b) Fk =

2n X s=2 pksrs onde pks=           

s−1

X

p=1

fkpfk(s−p), para 2≤s≤n+ 1;

n−p

X

k=0

fk(p+k)fk(n−k), para s=n+p, p >1

c) Fl =

2n X s=2 plsrs onde pls =           

s−1

X

p=1

flpfl(s−p), para 2≤s ≤n+ 1;

n−p

X

k=0

(38)

d) Fli = 2n X s=2 plisrs onde plis =           

s−1

X

p=1

flipfli(s−p), para 2≤s≤n+ 1;

n−p

X

k=0

fli(p+k)fli(n−k), para s=n+p, p >1

e) Flj = 2n X s=2 pljsrs onde pljs=           

s−1

X

p=1

fljpflj(s−p), para 2≤s≤n+ 1; n−p

X

k=0

flj(p+k)flj(n−k), para s =n+p, p >1

f) Flk = 2n X s=2 plksrs onde plks=           

s−1

X

p=1

flkpflk(s−p), para 2≤s≤n+ 1; n−p

X

k=0

flk(p+k)flk(n−k), para s=n+p, p >1

Logo,

F2₊_F2

i +Fj2+Fk2+Fl2+Fli2+Flj2 +Flk2 = 2n

X

s=2

psrs₊ 2n

X

s=2

pisrs₊ 2n

X

s=2

pjsrs₊ 2n

X

s=2

pksrs₊ 2n

X

s=2

plsrs₊ 2n X s=2 plisrs 2n X s=2

pljsrs₊ 2n

X

s=2

plksrs₌

2n

X

s=2

(ps+pis+pjs+pks+pls+plis+pljs+plks)rs ₌ 2n

X

s=2

Ps(n)rs Portanto

|f(y)₋f(x)_|=

v u u t 2n X

(39)

2.4 Calculando a dilata¸cão 2 DILATAÇ ÃO

2.4 Calculando a dilata¸c˜

ao

Exemplo 1: Calculando a dilata¸c˜ao na hiperesfera 8-dimensional causada pela transforma¸c˜ao

quaseconforme f(z) =z2_{, onde} _z _∈_O_.

Seja x = (x1, x2, x3, x4, x5, x6, x7, x8) o centro da hiperesfera 8-dimensional de raio r e y = (y1, y2, y3, y4, y5, y6, y7, y8) um ponto em sua fronteira.

Sabemos que o fator de expans˜ao ser´a P₂(2).

|f(y)₋f(x)_|=

v u u t

2n

X

s=2

Ps(n)rs =

=qF2₊_F2

i +Fj2+Fk2+Fl2 +Fli2+Flj2 +Flk2 Como n = 2, temos

P₂(2) =p2+pi2+pj2+pk2 +pl2+pli2+plj2+plk2

e

p2 =f1f1 =f2

1,pi2 =fi12, pj2 =fj12, pk2 =fk12 , pl2 =f2

l1, pli2 =fli12 , plj2 =flj12 e plk2 =flk12 Por isso

P₂(2) =f2

1 +fi12 +fj12 +fk12 +fl12+ f2

li1+flj12 +flk12 Temos

ft= 2k≤n

X

k=0

f(2k,t)=_⇒f1 =f(0,1)+f(2,1),

fit=

2k+1≤n

X

k=0

fi(2k,t) =_⇒fi1 =fi(0,1),

fjt =

2k+1≤n

X

k=0

fj(2k,t) =_⇒fj1 =fj(0,1),

fkt=

2k+1≤n

X

k=0

(40)

flt=

2k+1≤n

X

k=0

fl(2k,t) =_⇒fl1 =fl(0,1),

flit=

2k+1≤n

X

k=0

fli(2k,t) =_⇒fli1 =fli(0,1),

fljt =

2k+1≤n

X

k=0

flj(2k,t) =_⇒flj1 =flj(0,1),

flkt =

2k+1≤n

X

k=0

flk(2k,t) =_⇒flk1 =flk(0,1),

Dada a f´ormula

f(2k,t) =

µ n 2k ¶h t X p=0 µ

n₋2k p

¶

−p

i

,

calculemos f1 =f(0,1)+f(2,1). Ent˜ao,

f(0,1) = µ 2 0 ¶h 1 X p=0 µ 2 p ¶

x2₁−pcpfm+q=1−p

i

= 2x1c,

e

f(2,1) =

µ 2 2 ¶h 1 X p=0 µ 0 p ¶

x−₁pcp_fm+q=1

−p

i

=₋2Y,

Por isso

f1 = 2x1c₋2Q

Agora, lembramos que

fi(2k,t) =

µ

n 2k+ 1

¶h x2 t X p=0 µ

n₋(2k+ 1) p

¶

−p+

X

p=0

µ

n₋(2k+ 1) p

¶

−p−1

i , por isso, fi(0,1) = µ 2 1 ¶h x2 1 X p=0 µ 1 p ¶

x1₁−pcp_fm+q=1

−p+c1c2c3c4c5c6s7

µ

1 0

¶

x1

1c0fm+q=0

(41)

fi(0,1) = 2(x1c1c2c3c4c5c6s7+x2c)

De maneira an´aloga, encontramos

fj(0,1) = 2(x1c1c2c3c4c5s6+x3c),

fk(0,1) = 2(x1c1c2c3c4s5+x4c),

fl(0,1) = 2(x1c1c2c3s4+x5c),

fli(0,1) = 2(x1c1c2s3+x6c),

flj(0,1) = 2(x1c1s2+x7c)

e

flk(0,1) = 2(x1s1 +x8c)

Como

P₂(2) =f2

1 +fi12 +fj12 +fk12 +fl12+ f2

li1+flj12 +flk12 temos

P₂(2) = [2x1c₋2Q]2_{+ [2(x1c1c2c3c4c5c6s7}₊_x2c)]2_{+ [2(x1}_c1c2c3_c4c5s6₊_x3_c)]2_{+ [2(x1c1c2c3c4s5}₊ x4c)]2 + [2(x1c1c2c3s4+x5c)]2+ [2(x1c1c2s3+x6c)]2+ [2(x1c1s2+x7c)]2+ [2(x1s1+x8c)]2

Agora, lembrando que a dilata¸c˜ao ´e dada por

H(x) =

r

maxP2 minP2,

segue a tabela com a dilata¸c˜ao H(x) para diferentes centros da hiperesfera

x= (x1, x2, x3, x4, x5, x6, x7, x8) M ax(P₂(2)) M in(P₂(2)) H(x) x= (1,1,1,1,1,1,1,1) 32 4 2√2 x= (12,12,12,12,12,12,12,12) 4608 576 2√2

x= (1,0,1,1,0,0,1,0) 16 4 2

(42)

Com o resultado da primeira e segunda linha, vemos que a transla¸cão não causou altera¸cão no valor da dilata¸cão. Com a quarta linha, vemos que a fun¸cãof(z) =z2 _é_conforme _{para os reais.}

Obs: Para encontrar o máximo e o m´ınimo de P₂(2), foi utilizado o software Mathemática 5.2. Os comandos necessários são ”NMaximize”e ”NMinimize”.

Exemplo 2: Calcular a dilata¸c˜ao na hiperesfera 8-dimensional causada pela transforma¸c˜ao

quaseconforme f(z) =z3_{, onde} _z _∈_O_.

Sabemos que

|f(y)₋f(x)_|=

v u u t

6

X

s=2

Ps(3)rs =

=

q

P₂(3)r2₊_P(3) 3 r3+P

(3) 4 r4+P

(3) 5 r5+P

(3) 6 r6

Precisamos encontrar P₂(3). Logo

P₂(3) =p2+pi2+pj2+pk2+pl2+pli2+plj2+plk

e

p2 =f1f1 =f12,pi2 =fi12, pj2 =fj12, pk2 =fk12 ,

pl2 =f2

l1, pli2 =fli12 , plj2 =flj12 e plk2 =flk12 Por isso

P₂(3) =f2

1 +fi12 +fj12 +fk12 +fl12+ f2

li1+flj12 +flk12 Temos

ft= 2k≤n

X

k=0

(43)

fit =

2k+1≤n

X

k=0

fi(2k,t)=_⇒fi1 =fi(0,1)+fi(2,1),

fjt =

2k+1≤n

X

k=0

fj(2k,t) =_⇒fj1 =fj(0,1)+ +fj(2,1),

fkt =

2k+1≤n

X

k=0

fk(2k,t) =_⇒fk1 =fk(0,1)+fk(2,1),

flt=

2k+1≤n

X

k=0

fl(2k,t) =_⇒fl1 =fl(0,1)+fl(2,1),

flit =

2k+1≤n

X

k=0

fli(2k,t)=_⇒fli1 =fli(0,1)+fli(2,1),

fljt =

2k+1≤n

X

k=0

flj(2k,t) =_⇒flj1 =flj(0,1)+flj(2,1),

flkt =

2k+1≤n

X

k=0

flk(2k,t) =_⇒flk1 =flk(0,1)+flk(2,1),

Dada a f´ormula

f(2k,t) =

µ n 2k ¶h t X p=0 µ

n₋2k p

¶

−p

i

,

calculemos f1 =f(0,1)+f(2,1).

f(0,1) = µ 3 0 ¶h 1 X p=0 µ 3 p ¶

x3₁−pcp_fm+q=1

−p

i

=hµ3 0

¶

x3₁c0fm+q=1+

µ

3 1

¶

x2₁c1fm+q=0i= 3x1c

f(2,1) = µ 3 2 ¶h 1 X p=0 µ 1 p ¶

x11−pcpfm+q=1−p

i

= 3hµ1 0

¶

x11c0fm+q=1+

µ

1 1

¶

x01c1fm+q=0

i

=

3hx1

µ 1 1 ¶µ 1 0 ¶

(hx)0(₋2Y)1(s2)0+c

µ

1 0

¶

(h2_x)1i = 3h2_xc₋6x1Y

Portanto

f1 = 3x2

1c+ 3h2xc−6x1

Q

(44)

fi(2k,t) =

µ

n 2k+ 1

¶h x2 t X p=0 µ

n₋(2k+ 1) p

¶

−p+

X

p=0

µ

n₋(2k+ 1) p

¶

xn₁−(2k−1)−pcpfm+q=t−p−1

i , Ent˜ao fi(0,1) = µ 3 1 ¶h x2 1 X p=0 µ 2 p ¶

x2₁−pcp_fm+q=1

−p+c1c2c3c4c5c6s7

µ

2 0

¶

x2₁c0fm+q=0i =

3x2hµ2 0

¶

x21fm+q=1+

µ

2 1

¶

x11c1fm+q=0

i

+x21c1c2c3c4c5c6s7 =

3x2h0 + 2x1ci+x2

1c1c2c3c4c5c6s7

Logo

fi(0,1) = 6x1x2c+ 3x2

1c1c2c3c4c5c6s7 Agora fi(2,1) = µ 3 3 ¶h x2 1 X p=0 µ 0 p ¶

x−₁pcp_fm+q=1

−p+c1c2c3c4c5c6s7 0 X p=0 µ 0 p ¶

x−₁pcp_fm+q=

−p

i

=

=x2hfm+q=1i+c1c2c3c4c5c6s7fm+q=0 =

n

x2hµ1 1

¶µ

1 0

¶

(h2x)0(−2

Y

)1i+c1c2c3c4c5c6s7(h2x)1

o

=₋2x2Y+h2xc1c2c3c4c5c6s7

Por fim

fi1 = (3x2

1+h2x)c1c2c3c4c5c6s7+ 2x2(3x1c−

Y

)

E, de maneira an´aloga, temos

fj1 = (3x2

1+h2x)c1c2c3c4c5s6+ 2x3(3x1c−

Y

),

fk1 = (3x2

1+h2x)c1c2c3c4s5+ 2x4(3x1c−

Y

),

fl1 = (3x2

1+h2x)c1c2c3s4+ 2x5(3x1c−

Y

),

(45)

flj1 = (3x21+h2x)c1s2 + 2x7(3x1c−

Y

)

e

flk1 = (3x2

1+h2x)s1+ 2x8(3x1c−

Y

)

Como

P₂(3) =f2

1 +fi12 +fj12 +fk12 +fl12+ f2

li1+flj12 +flk12 temos

P₂(3) = [3x2

1c+ 3h2xc−6x1

Q

]2_{+ [(3x}2

1+h2x)c1c2c3c4c5c6s7+ 2x2(3x1c−

Y

)]2+

+[(3x2

1+h2x)c1c2c3c4c5s6+ 2x3(3x1c−

Y

)]2+ [(3x21+h2x)c1c2c3c4s5+ 2x4(3x1c−

Y

)]2

+[(3x2

1+h2x)c1c2c3s4+ 2x5(3x1c−

Y

)]2+ [(3x2₁+h2_x)c1c2s3+ 2x6(3x1c−

Y

)]2

+[(3x2

1 +h2x)c1s2+ 2x7(3x1c−

Y

)]2+ [(3x2₁+h2_x)s1+ 2x8(3x1c₋Y)]2 Agora, sabendo que a dilata¸c˜ao ser´a dada por

H(x) =

s

maxP2(3) minP₂(3)

temos

x= (x1, x2, x3, x4, x5, x6, x7, x8) M ax(P2(3)) M in(P (3)

2 ) H(x) x= (1,1,1,1,1,1,1,1) 1,19.107 ₃₃₁₇₇₆ ₆ x= (12,12,12,12,12,12,12,12) 576 16 6

x= (1,0,0,0,0,0,0,0) 9 9 1

x= (0,1,1,1,1,1,1,1) 441 49 3

Exemplo 3:Calcular a dilata¸c˜ao na hiperesfera 8-dimensional causada pela transforma¸c˜ao quasec-onforme f(z) =z4_{, onde} _z _∈_O_.

(46)

2.5 Método computacional para o cálculo da dilata¸cão 2 DILATAÇ ÃO

P2(4) = [4(x31c−3x21

Y

+3x1h2xc−h2x

Y

)]2+

(4(x3

1c1c2c3c4c5c6s7+ 3x21x2c+ (h2xc1c2c3c4c5c6s7−2x2

Y

)x1+x2h2_xc))2+

(4(x3

1c1c2c3c4c5s6+ 3x21x3c+ (h2xc1c2c3c4c5s6−2x3

Y

)x1+x3h2_xc))2+

(4(x3

1c1c2c3c4s5+ 3x21x4c+ (h2xc1c2c3c4s5−2x4

Y

)x1 +x4h2xc))2+

(4(x3

1c1c2c3s4+ 3x21x5c+ (h2xc1c2c3s4−2x5

Y

)x1+x5h2xc))2+

(4(x3

1c1c2s3+ 3x21x6c+ (h2xc1c2s3−2x6

Y

)x1+x6h2_xc))2+

(4(x3

1c1s2+ 3x21x7c+ (h2xc1s2−2x7

Y

)x1+x7h2_xc))2+

(4(x3

1s1+ 3x21x8c+ (h2xs1−2x8

Y

)x1+x8h2xc))2

Agora, sabendo que a dilata¸c˜ao ser´a dada por

H(x) =

s

maxP₂(4) minP₂(4)

temos

x= (x1, x2, x3, x4, x5, x6, x7, x8) M ax(P₂(4)) M in(P₂(4)) H(x) x= (1,1,1,1,1,1,1,1) 8192 576 3.77124 x= (12,12,12,12,12,12,12,12) 1,28.108 _9,_0.106 _3.77124

x= (1,0,0,0,0,0,0,0) 16 16 1

x= (1,1,1,1,0,0,0,0) 1024 64 4

2.5 M´

etodo computacional para o c´

alculo da dilata¸c˜

ao

2.5.1 Introdu¸c˜ao

(47)

2.5 Método computacional para o cálculo da dilata¸cão 2 DILATAÇ ÃO

2.5.2 Algoritmo

Tendo mostrado que o desenvolvimento de _|f(x)₋f(y)_| resulta em um polinômio em r, pode-mos adotar um método mais simples para calcular a dilata¸cão. Sabendo que todos os terpode-mos de |f(x)₋f(y)_| estarão multiplicados por rs_{, com} _s _{= 2,}_{3, ...n, e que, o fator de expansão é dado} pelos termos multiplicados por r2_{, seguiremos o seguinte método para o cálculo da dilata¸cão} _k.

1. Desenvolverf(y) = yn_{, com}_y _{escrito em coordenadas esf´ericas;} 2. Desenvolverf(x) = xn_;

3. Calcular a diferen¸caf(y)₋f(x)

4. Calcular a norma do resultado anterior, ou seja,_|f(y)₋f(x)_|. No entanto, n˜ao extra´ımos a raiz ainda;

5. Expandir o polinˆomio resultante;

6. Dividir o resultado anterior porr2_{, tornando somente o fator de expans˜ao constante(independente} der);

7. Fazerr= 0, eliminando toda parte do polinômio que não influencia na dilata¸cão;

8. Calcular o m´aximo e o m´ınimo do resultado, em fun¸c˜ao de t1, t2, ...t7;

9. Extrair a raiz do m´aximo sobre o m´ınimo.

2.5.3 Implementa¸c˜ao computacional do m´etodo

Para desenvolver o método computacional descrito, foi desenvolvida uma interface em Java, que utiliza o software Mathematica para resolver opera¸cões matemáticas.

Podemos destacar as seguintes vantagens do m´etodo computacional e do uso da interface:

1. A implementa¸cão computacional do método descrito acima é mais simples do que a imple-menta¸cão das fórmulas deduzidas para o cálculo da dilata¸cão;