Uma proposta de um controlador adaptativo por posicionamento de pólos e estrutura variável

(1)

Programa de Pós-Gradua¸cão em Engenharia Elétrica

Uma Proposta de um Controlador Adaptativo por

Posicionamento de P´

olos e Estrutura Vari´

avel

Francisco das Chagas da Silva J´

unior

Orientador: Prof. Dr. Aldayr Dantas de Ara´

ujo

(2)

Uma Proposta de um Controlador Adaptativo por

Posicionamento de P´

olos e Estrutura Vari´

avel

Francisco das Chagas da Silva J´

unior

Disserta¸cão submetida ao Programa de Pós-Gradua¸cão em Engenharia Elétrica da Uni-versidade Federal do Rio Grande do Norte como parte dos requisitos para a obten¸cão do grau de Mestre em Ciências.

Orientador: Prof. Dr. Aldayr Dantas de Ara´ujo

(3)

Ao meu pai - Francisco Chagas `

A minha mãe - Iêda Maria Ao meu irmão - Rodrigo Márcio

(4)

A Deus pelo dom da vida e pela conquista de mais esta vit´oria.

Ao Professor Aldayr Dantas de Araújo, pelo incentivo e pela sua brilhante orienta¸cão acadêmica.

A todos os meus familiares, que puderam me dar for¸ca e tranq¨uilidade para chegar at´e aqui.

Aos amigos Josenalde, Pl´ınio, Maximiliano, Liviane, Marcos, André, Iuri e Rosciano que me ajudaram sempre que precisei nas tarefas do laboratório, necessárias para a cons-tru¸cão deste trabalho.

A todos os professores do DCA e do DEE que me transmitiram seus conhecimentos e experiˆencias profissionais durante este per´ıodo.

A todos os funcion´arios da UFRN, que direta ou indiretamente, colaboraram para a realiza¸c˜ao deste trabalho.

Finalmente, a todos que, de alguma forma, contribu´ıram com este trabalho, mas que aqui n˜ao foram citados.

(5)

Lista de Figuras vi

Lista de Tabelas vii

Resumo viii

Abstract ix

Gloss´ario de Termos x

1 Introdu¸c˜ao 1

1.1 Controle Adaptativo . . . 1

1.1.1 Defini¸c˜ao . . . 1

1.1.2 Controle Adaptativo Direto e Indireto . . . 2

1.1.3 Escalonamento de Ganhos . . . 5

1.1.4 Controle Adaptativo por Modelo de Referˆencia . . . 6

1.1.5 Controle Adaptativo por Posicionamento de P´olos . . . 7

1.2 Sistemas com Estrutura Vari´avel . . . 9

1.3 Controle Adaptativo por Posicionamento de P´olos e Estrutura Vari´avel . . 9

1.4 Estrutura do Trabalho . . . 10

2 Controle Adaptativo por Posicionamento de P´olos 11 2.1 Introdu¸c˜ao . . . 11

2.2 PPC: Parˆametros da Planta Conhecidos . . . 12

2.2.1 Descri¸c˜ao do Problema . . . 13

2.2.2 M´etodo Polinomial . . . 13

(6)

3.3 Controle Equivalente . . . 20

3.4 Solu¸c˜ao de Filippov . . . 21

4 Controle Adaptativo por Posicionamento de Pólos e Estrutura Variável 23 4.1 Introdu¸cão . . . 23

4.2 Descri¸c˜ao do M´etodo . . . 24

4.3 Prova de Estabilidade . . . 25

4.4 C´alculo dos Parˆametros do Controlador . . . 26

5 Aplica¸c˜ao do Controlador 29 5.1 Planta de Primeira Ordem Inst´avel . . . 29

5.1.1 Simula¸c˜oes . . . 29

5.2 Motor de Indu¸c˜ao Trif´asico . . . 32

5.2.1 Modelagem . . . 32

5.2.2 Parˆametros do Motor de Indu¸c˜ao . . . 35

5.2.3 Simula¸c˜oes . . . 36

5.2.4 Sistema de Acionamento . . . 39

5.2.5 Implementa¸c˜ao Pr´atica . . . 40

6 Conclusões e Perspectivas 42 A Modelos Entrada/Sa´ıda 43 A.1 Fun¸cões de Transferência . . . 43

A.2 Polinˆomios Coprimos . . . 43

B Conceitos Sobre Estabilidade 46 B.1 Defini¸c˜ao de Estabilidade . . . 46

B.2 M´etodo Direto de Lyapunov . . . 47

B.2.1 Fun¸c˜oes Definidas Positivas e Negativas . . . 47

B.2.2 Transla¸c˜ao da Origem do Sistema de Coordenadas . . . 48

(7)

(8)

1.1 Esquema de um controlador adaptativo. . . 2

1.2 Diagrama de blocos para controle adaptativo indireto. . . 3

1.3 Diagrama de blocos para controle adaptativo direto. . . 4

1.4 Escalonamento de ganhos. . . 5

1.5 Controle por Modelo de Referˆencia. . . 6

1.6 MRAC Indireto. . . 7

1.7 MRAC Direto. . . 8

2.1 Diagrama de blocos do PPC. . . 15

2.2 Uma realiza¸c˜ao alternativa do PPC. . . 16

3.1 Superf´ıcie de deslizamento em um sistema de estrutura vari´avel. . . 18

3.2 Filtro passa-baixa para obten¸c˜ao deueq. . . 20

3.3 Campo vetorial no modo deslizante (solu¸c˜ao de Filippov) . . . 21

4.1 Diagrama de blocos do VS-APPC para planta de primeira ordem. . . 28

5.1 APPC Indireto utilizando o m´etodo do gradiente. . . 30

5.2 VS-APPC Indireto para sistema de primeira ordem. . . 31

5.3 Comportamento dos parˆametros da planta utilizando leis chaveadas. . . 31

5.4 Diagrama vetorial do motor de indu¸c˜ao (ωs ´e a velocidade s´ıncrona.) . . . . 34

5.5 VS-APPC para o controle de velocidade de um motor de indu¸cão trifásico. 37 5.6 Altera¸cão dos parâmetros da planta. . . 38

5.7 Perturba¸cões no sistema e altera¸cões no sinal de referência do sistema. . . . 38

5.8 Sistema de acionamento. . . 40

5.9 Implementa¸c˜ao pr´atica do VS-APPC. . . 41

(9)

5.1 Parâmetros elétricos do motor . . . 35 5.2 Caracter´ıstica tensão x velocidade do tacogerador . . . 39

(10)

Existem dois métodos principais para a constru¸cão de controladores adaptativos. Um deles é o controle adaptativo por modelo de referência (MRAC) e o outro é o controle adaptativo por posicionamento de pólos (APPC). No MRAC, um modelo de referência é escolhido para gerar a trajetória desejada que o sinal de sa´ıda da planta deve seguir, e ele pode requerer o cancelamento de zeros da planta. Devido a sua flexibilidade em escolher a metodologia de projeto do controlador (realimenta¸cão de estado, projeto de compensador, linear quadrático, etc.) e a lei adaptativa (m´ınimos quadrados, método do gradiente, etc.), o APPC é o tipo mais geral de controle adaptativo. Tradicionalmente, vem sendo desenvolvido em uma abordagem indireta e, como uma vantagem, pode ser aplicado a plantas de fase não-m´ınima, já que não envolve cancelamentos de zeros e pólos. A integra¸cão aos sistemas com estrutura variável permite agregar rapidez no transitório e robustez às varia¸cões paramétricas e perturba¸cões.

O objetivo deste trabalho é desenvolver um controlador adaptativo por posiciona-mento de pólos e estrutura variável (VS-APPC). Portanto, são propostas leis chaveadas em substitui¸cão às leis adaptativas integrais tradicionais. Adicionalmente, são apresen-tadas simula¸cões para uma planta de primeira ordem instável, assim como simula¸cões e resultados práticos da aplica¸cão da técnica proposta a um motor de indu¸cão trifásico.

(11)

There are two main approaches for using in adaptive controllers. One is the so-called model reference adaptive control (MRAC), and the other is the so-so-called adaptive pole placement control (APPC). In MRAC, a reference model is chosen to generate the desired trajectory that the plant output has to follow, and it can require cancellation of the plant zeros. Due to its flexibility in choosing the controller design methodology (state feedback, compensator design, linear quadratic, etc.) and the adaptive law (least squares, gradient, etc.), the APPC is the most general type of adaptive control. Traditionally, it has been developed in an indirect approach and, as an advantage, it may be applied to non-minimum phase plants, because do not involve plant zero-pole cancellations. The integration to variable structure systems allows to aggregate fast transient and robustness to parametric uncertainties and disturbances, as well.

In this work, a variable structure adaptive pole placement control (VS-APPC) is pro-posed. Therefore, new switching laws are proposed, instead of using the traditional inte-gral adaptive laws. Additionally, simulation results for an unstable first order system and simulation and practical results for a three-phase induction motor are shown.

(12)

APPC - Adaptive Pole Placement Control (Controle Adaptativo por Posicionamento de P´olos)

LTI - Linear Time Invariant (Linear e Invariante no Tempo)

MRAC - Model Reference Adaptive Control (Controle Adaptativo por Modelo de Referˆencia)

MRC - Model Reference Control (Controle por Modelo de Referˆencia)

PPC - Pole Placement Control (Controle Adaptativo por Posicionamento de P´olos) SISO - Single Input Single Output (Monovari´avel)

VSC - Variable Structure Control (Controle por Estrutura Vari´avel)

VS-APPC - Variable Structure Adaptive Pole Placement Control (Controle Adapta-tivo por Posicionamento de P´olos e Estrutura Vari´avel)

VS-MRAC - Variable Structure Model Reference Adaptive Control (Controle Adap-tativo por Modelo de Referˆencia e Estrutura Vari´avel)

(13)

Introdu¸c˜

ao

1.1 Controle Adaptativo

A maioria das técnicas para projeto de sistemas de controle são baseadas em um bom entendimento da planta em estudo e seu meio. Entretanto, em muitos casos, a planta a ser controlada é muito complexa e os processos f´ısicos básicos nela presentes não são completamente entendidos, possuindo muitas vezes parâmetros incertos constantes ou variando lentamente. Por exemplo, robôs manipuladores podem carregar objetos grandes com parâmetros inerciais desconhecidos. Sistemas de potência podem ser submetidos a grandes varia¸cões nas condi¸cões de carga. Portanto, as técnicas de projeto de controle precisam ser adicionadas de uma técnica de estima¸cão de parâmetros, visando obter pro-gressivamente um melhor entendimento da planta a ser controlada. É assim intuitivo agregar estima¸cão de parâmetros e controle. Freqüentemente, os dois passos são feitos separadamente. Se a estima¸cão de parâmetros é recursiva, isto é, o modelo da planta é periodicamente atualizado com base em estimativas anteriores e novos dados, estima¸cão e controle podem ser executados concorrentemente [1]. O controle de modelos de plan-tas desconhecidas ou parcialmente conhecidas é objeto de estudo da área de sistemas de controle adaptativo.

1.1.1 Defini¸c˜

ao

A idéia básica em controle adaptativo é estimar os parâmetros desconhecidos da planta (ou equivalentemente, os correspondentes parâmetros do controlador) em tempo real

(14)

✲

✲ ✲

✛

❄

✛

controlador referˆencia

processo sa´ıda ajuste de

parˆametros parˆametros do

controlador

sinal de controle

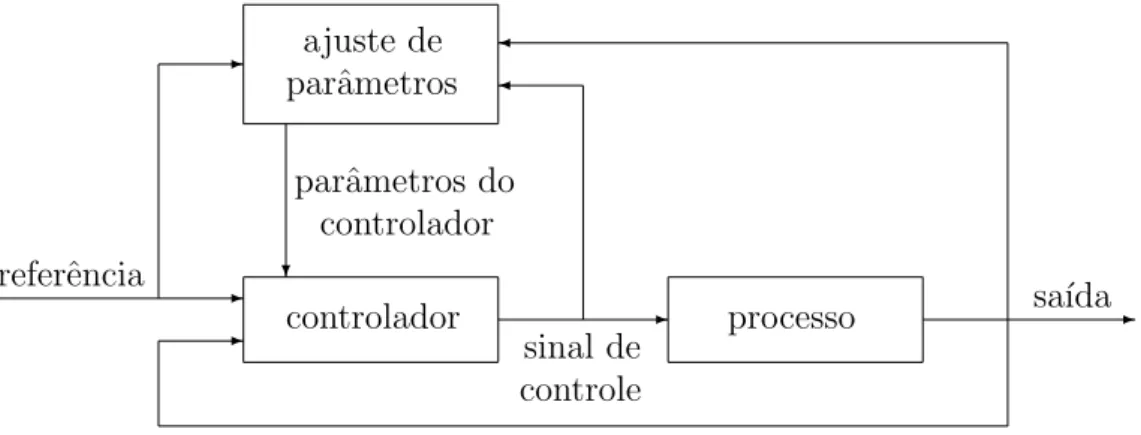
Figura 1.1: Esquema de um controlador adaptativo.

baseado nos sinais medidos do sistema, e usar os parâmetros estimados no cálculo da lei de controle [2], tendo como objetivo alterar o comportamento do sistema de modo a ajustá-lo a circunstâncias novas ou modificadas. Um sistema de controle adaptativo pode ser considerado como um sistema de controle com estima¸cão de parâmetros em tempo real.

Controle adaptativo consiste, portanto, em aplicar alguma técnica de estima¸cão para obter os parâmetros do modelo do processo e de seu meio a partir de medi¸cões de entradas e sa´ıdas e usar este modelo para projetar um controlador [3]. Os parâmetros do controlador são ajustados durante a opera¸cão da planta conforme a quantidade de dados dispon´ıveis. As técnicas de projeto para sistemas adaptativos são estudadas e analisadas em teoria para plantas desconhecidas, mas fixas (isto é, invariantes no tempo). Na prática, elas são aplicadas para plantas desconhecidas e lentamente variantes no tempo.

A estrutura do controlador consiste de uma malha de realimenta¸cão e de um contro-lador com ganhos ajustáveis, conforme mostra a Figura 1.1. A forma como são alterados os ganhos do controlador em resposta a mudan¸cas na planta e perturba¸cões distingue um esquema de controle do outro.

1.1.2 Controle Adaptativo Direto e Indireto

(15)

✁✁ ✁✁✕ ❄ ❄ ✲ ✲ ✲ ✲ ✲ ✛ ✛ θc u

θ(t) Controlador Planta

C(θc)

Estimador de θ∗

r r

C´alculos

θc(t) =F(θ(t))

y P(θ∗

)

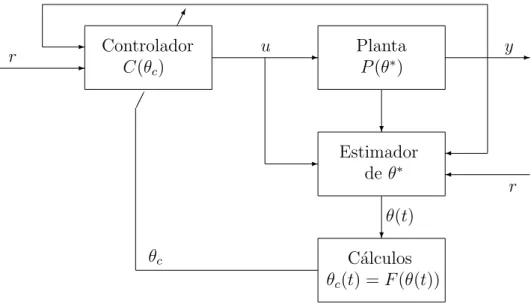
Figura 1.2: Diagrama de blocos para controle adaptativo indireto.

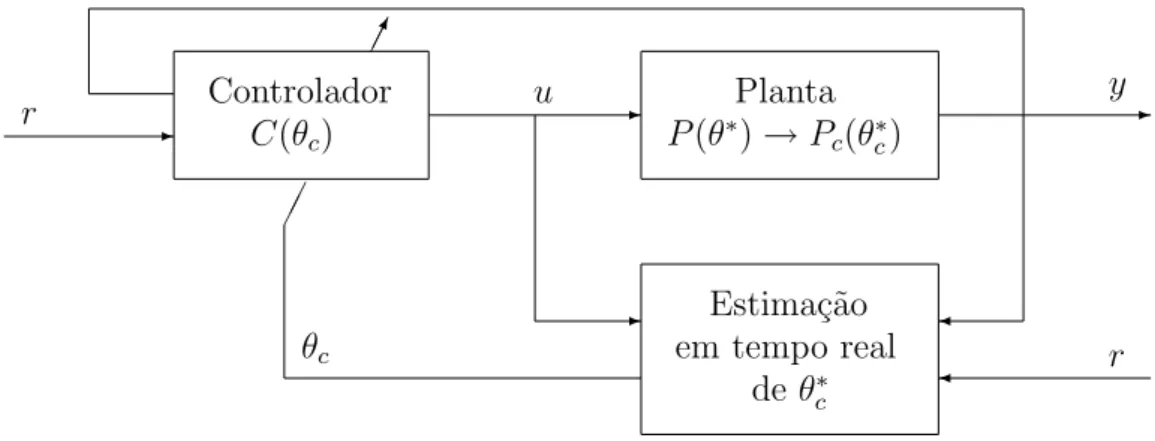
métodos. No primeiro método, conhecido como controle adaptativo direto, o modelo da planta é parametrizado em fun¸cão dos parâmetros do controlador, os quais são es-timados diretamente, sem cálculos intermediários envolvendo estimativas de parâmetros da planta. No segundo método, conhecido como controle adaptativo indireto, os parâmetros da planta são estimados a cada instante e utilizados para o cálculo dos parâmetros do controlador.

No controle adaptativo indireto, o modelo da plantaP(θ∗

) é parametrizado em rela¸cão a um vetor de parâmetros desconhecidos θ∗

. Um estimador em tempo real gera uma estimativaθ(t) deθ∗

a cada instantet, processando a entrada u e a sa´ıday. A estimativa dos parâmetrosθ(t) especifica um modelo estimado caracterizado por ˆP(θ(t)), que é usado para calcular os parâmetros do controlador ou vetor de ganhosθc(t) a cada instantet. Este

modelo, para o projeto do controlador, é tratado como o verdadeiro modelo da planta no instante t. Este princ´ıpio é conhecido como princ´ıpio de equivalência à certeza. As formas da lei de controle C(θc) e da equa¸cão algébrica θc =F(θ) são escolhidas como as

mesmas que seriam usadas para atender os requisitos de desempenho para o modeloP(θ∗

) se θ∗

fosse conhecido. É claro, neste método, que C(θc(t)) é projetada a cada instante t

de modo a satisfazer os requisitos de desempenho do modelo estimado ˆP(θ(t)), que pode ser diferente do modelo da planta desconhecida P(θ∗

). Assim, o principal problema no controle adaptativo indireto ´e escolher a classe de leis de controle C(θc) e a classe de

(16)

✲ ✁✁

✁✁✕

Estima¸c˜ao em tempo real

de θ∗

c

✲ ✲ Controlador

✛

✛ C(θc)

u Planta

P(θ∗

)→Pc(θc∗)

✲ y r

θc r

Figura 1.3: Diagrama de blocos para controle adaptativo direto.

de forma que C(θc(t)) atenda os requisitos de desempenho para o modelo P(θ∗) com

θ∗

desconhecido. A Figura 1.2 mostra o diagrama de blocos para o controle adaptativo indireto.

No controle adaptativo direto, o modelo da planta P(θ∗

) é parametrizado em fun¸cão de um vetor de parâmetros desconhecido θ∗

c do controlador, com o qual C(θ

∗

c) atende

os requisitos de desempenho, para obter o modelo Pc(θ∗c) com exatamente as mesmas

caracter´ısticas entrada/sa´ıda de P(θ∗

).

O estimador de parâmetros em tempo real é projetado baseado emPc(θc∗) ao invés de

P(θ∗

) para prover estimativas diretas θc(t) de θ∗c em cada instante t atrav´es do

proces-samento da entrada u e da sa´ıda y da planta. A estimativa θc(t) ´e ent˜ao usada para

atualizar o vetor de parâmetros do controlador θc sem cálculos intermediários. A escolha

da classe de leis de controle C(θc) e os estimadores de parˆametros que geram θc(t), de

forma que C(θc(t)) atenda os requisitos de desempenho para o modelo P(θ∗) s˜ao os

prin-cipais problemas no controle adaptativo direto. As propriedades do modelo P(θ∗

) são fundamentais na obten¸cão do modelo parametrizado Pc(θ∗c) que é conveniente para a

(17)

✲ ✲ r

✲

u y _✲

✛

Escalonador de ganhos

Controlador

C(θ) Planta

Medi¸c˜oes Auxiliares

✁ ✁ ✁ ✁ ✁

✁ ✁☛

θi

Figura 1.4: Escalonamento de ganhos.

1.1.3 Escalonamento de Ganhos

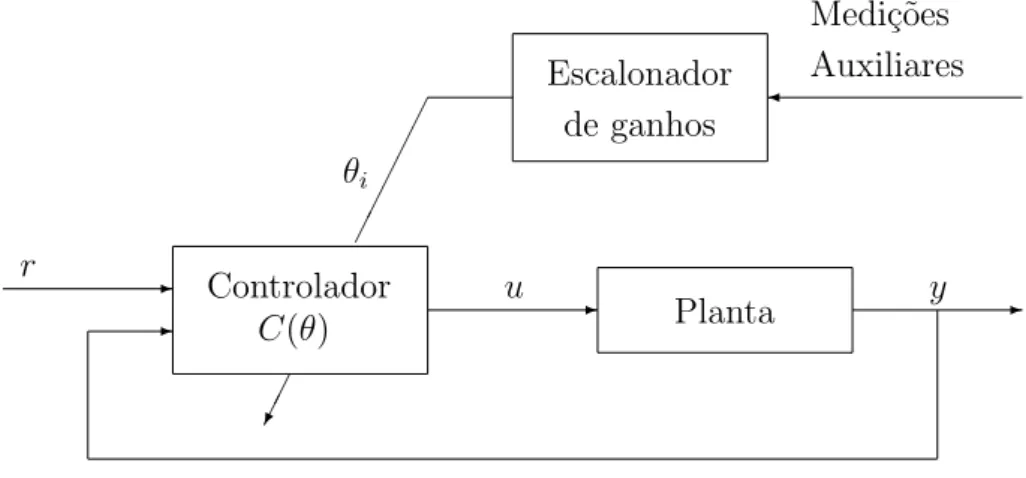
Em alguns sistemas existem variáveis auxiliares que descrevem bem as caracter´ısticas da dinâmica do processo. Se estas variáveis podem ser medidas, elas podem ser usadas para mudar os parâmetros do controlador. Cada conjunto destas variáveis consiste num ponto de opera¸cão do processo.

Vamos considerar um processo onde para cada ponto de opera¸cão i, i = 1,2, ..., N, consistindo das variáveis citadas anteriormente, os parâmetros são conhecidos. Para um dado ponto de opera¸cão i, um controlador por realimenta¸cão com ganhos constantes, dito θi, pode ser projetado para encontrar os requisitos de desempenho para o modelo

linear correspondente. Isto leva a um controlador, ditoC(θ), com um conjunto de ganhos

θ1, θ2, ..., θn cobrindo os N pontos de opera¸cão. Uma vez que um ponto de opera¸cão i é

detectado, os ganhos do controlador podem ser mudados para o valor apropriado de θi,

obtido de um conjunto pré-calculado de ganhos. Esta abordagem é chamada escalona-mento de ganhos e é ilustrada na Figura 1.4.

A vantagem do escalonamento de ganhos é que os ganhos do controlador podem ser mudados tão rapidamente quanto às medidas auxiliares respondem para as mudan¸cas de parâmetros. Mudan¸cas rápidas e freqüentes dos ganhos do controlador, entretanto, podem conduzir à instabilidade. Por isso, existe um limite de acordo com a freqüência e rapidez com que os ganhos do controlador podem ser mudados.

(18)

✲

✲ ✲

✻

✒✑ ✓✏❄

✲ e0

Modelo de Referˆencia

M(s)

r

u

Controlador Planta

C(θ∗

c) G(s)

✲

−

+

y ym

Figura 1.5: Controle por Modelo de Referˆencia.

Apesar de suas limita¸cões, o escalonamento de ganhos é um método popular para lidar com varia¸cões de parâmetros em diversas aplica¸cões, como por exemplo, na avia¸cão.

1.1.4 Controle Adaptativo por Modelo de Referˆ

encia

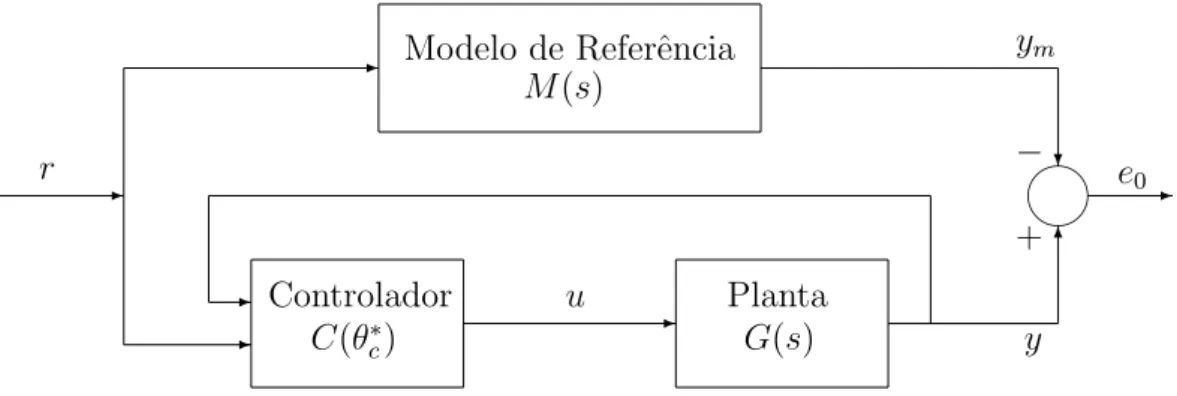
O controle adaptativo por modelo de referência (MRAC) [4] é derivado do problema de acompanhamento de modelo ou problema de controle por modelo de referência (MRC) e é uma das principais abordagens para controle adaptativo. No MRC, um bom en-tendimento da planta e dos requisitos de desempenho, possibilita ao projetista adotar um modelo, conhecido como modelo de referência. Este modelo descreve as caracter´ısticas de entrada/sa´ıda desejadas para a planta em malha fechada. O objetivo do MRC é encontrar a lei de controle por realimenta¸cão que altera a estrutura e a dinâmica da planta de tal forma que as propriedades de entrada/sa´ıda sejam exatamente iguais às do modelo de referência. A desvantagem é que o processo de adapta¸cão ao modelo, em geral, é lento e oscilatório. A estrutura para o esquema MRC para uma planta linear e invariante no tempo é mostrada na Figura 1.5.

A fun¸cão de transferênciaM(s) do modelo de referência é projetada de forma que para um dado sinal de referênciar(t) a sa´ıdaym(t) represente a sa´ıda desejaday(t) que a planta

deve seguir. O controlador por realimenta¸c˜ao C(θ∗

c) ´e projetado de forma que todos os

sinais sejam uniformemente limitados e a fun¸c˜ao de transferˆencia da planta de r para y

seja igual aM(s). Esta condi¸cão garante que para qualquer sinal de referênciar(t), o erro de sa´ıda e0 =y−ym, que representa o desvio da sa´ıda da planta em rela¸cão à trajetória

desejada ym, tenda para zero com o tempo. A condi¸c˜ao de matching para a fun¸c˜ao de

(19)

substituindo-✁✁ ✁✁✕ ❄ ❄ ✲ ✲ ✲ ✲ ✲ ✒✑ ✓✏_e 0 ✻ ❄ ✲ ✛ ✛ θc u

θ(t) Controlador Planta

C(θc)

Estimador de θ∗

r r

C´alculos

θc(t) =F(θ(t))

P(θ∗

) Modelo de Referˆencia

M(s)

−

+

y ym

Figura 1.6: MRAC Indireto.

os pelos zeros de M(s) e tornando os pólos do sistema em malha fechada iguais aos do modelo de referência, através do controlador C(θ∗

c). O cancelamento dos zeros da planta

impõe a restri¸cão da planta ser de fase m´ınima, isto é, ter zeros no semiplano esquerdo. Se qualquer zero da planta estiver no semi-plano direito, seu cancelamento pode facilmente levar a sinais ilimitados, já que com zeros no semi-plano direito, visto que o cancelamento não é perfeito, o sistema pode se tornar instável [4].

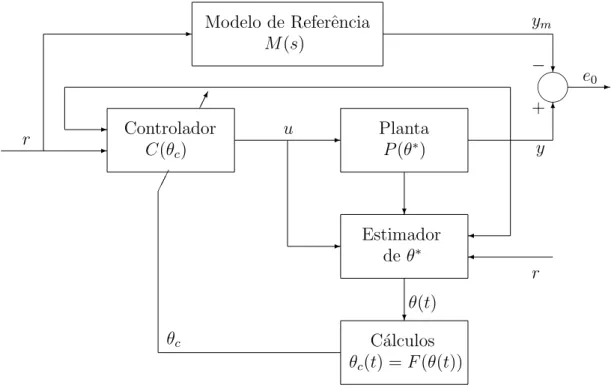
Quandoθ∗

´e desconhecido o esquema MRC da Figura 1.5 n˜ao pode ser implementado, pois θ∗

c não pode ser calculado, sendo assim desconhecido. Uma solu¸cão é substituir θ

∗

c

desconhecido na lei de controle por sua estimativa θc(t) obtida usando o m´etodo direto

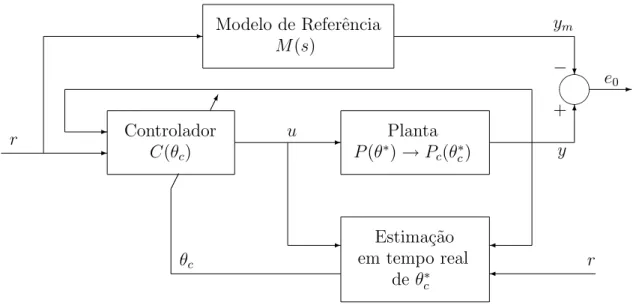
ou indireto. O esquema de controle resultante ´e conhecido como MRAC e pode ser classificado coo MRAC indireto na Figura 1.6 e MRAC direto na Figura 1.7.

1.1.5 Controle Adaptativo por Posicionamento de P´

olos

O controle adaptativo por posicionamento de pólos (APPC) é derivado do controle por posicionamento de pólos (PPC) e problemas de regula¸cão usados no caso de plantas lineares invariantes no tempo (LTI) com parâmetros desconhecidos.

(20)

✲ Estima¸c˜ao em tempo real

deθ∗

c ✁✁ ✁✁✕ ✲ ✲ ✲ ❄ ✻ ✒✑ ✓✏ ✲ ✲ _Controlador ✛ ✛ C(θc)

u Planta

P(θ∗

)→Pc(θc∗)

Modelo de Referˆencia

M(s)

r y ym r − + e0 θc

Figura 1.7: MRAC Direto.

dos pólos de malha fechada. Uma lei de controle por realimenta¸cão é então desenvolvida alocando os pólos de malha fechada nas posi¸cões desejadas.

A estrutura do controlador C(θ∗

c) e o vetor de parˆametros θ

∗

c s˜ao escolhidos de forma

que os pólos da fun¸cão de transferência da planta em malha fechada de r para y sejam iguais aos desejados. O vetor θ∗

c ´e geralmente calculado em fun¸c˜ao de θ

∗

, onde θ∗

é um vetor com os coeficientes da fun¸cão de transferência G(s).

Se θ∗

´e conhecido, ent˜ao θ∗

c ´e calculado e usado na lei de controle. Quando θ

∗

´e desconhecido, θ∗

c é também desconhecido e o PPC não pode ser implementado. Nesse

caso, assim como no caso do MRC, nós podemos usar o princ´ıpio de equivalência à certeza para substituir o vetor desconhecido θ∗

c por sua estimativaθc(t), ou seja, em linhas gerais,

os parâmetros do controlador são calculados das estimativas dos parâmetros da planta como se elas fossem os verdadeiros parâmetros. O esquema resultante é referido como APPC. Se θc(t) é atualizado diretamente usando um estimador de parâmetros em tempo

real, o esquema é referido como um APPC direto. Se θc(t) é calculado em fun¸cão de

θ(t), que ´e uma estimativa para θ∗

(21)

1.2 Sistemas com Estrutura Vari´

avel

A teoria de sistemas com estrutura variável tem sido bastante utilizada no tratamento de problemas de sistemas de controle, principalmente na forma conhecida como controle por modos deslizantes [5-11]. Neste método, as fun¸cões de chaveamento das variáveis de controle devem ser projetadas de modo a restringir a dinâmica do sistema a uma superf´ıcie chamada superf´ıcie deslizante.

Os sistemas com estrutura variável têm como principais caracter´ısticas a rapidez do transitório e robustez a varia¸cões paramétricas e perturba¸cões, dentro de uma faixa de tolerância estipulada no projeto. Em contrapartida, possuem alguns aspectos a considerar, como alto valor do sinal de controle inicial e chaveamento do sinal de controle em alta freqüência, fenômeno chamadochattering.

Esta teoria teve origem no estudo dos controladores à relé e baseia-se no chaveamento das variáveis de controle dentro de um conjunto de fun¸cões das variáveis de estado da planta de acordo com uma dada regra, o que impõe para este método o conhecimento de todas as variáveis de estado do sistema.

1.3 Controle Adaptativo por Posicionamento de P´

olos

e Estrutura Vari´

avel

Conforme foi visto nas Se¸cões 1.1.4 e 1.1.5, as duas principais abordagens do controle adaptativo (MRAC e APPC) utilizam algoritmos de adapta¸cão que, em geral, baseiam-se em uma lei do tipo integral [12]. O sistema resultante apresenta problemas bem conhecidos de estabilidade sob condi¸cões não ideais como, por exemplo, na presen¸ca de distúrbios externos [13,24], e um comportamento transitório inaceitável [14-15].

No caso do APPC, dentro do qual se insere este trabalho, diversos trabalhos têm sido publicados tratando de poss´ıveis solu¸cões para o problema de robustez no que diz respeito a perturba¸cões limitadas [16-17]; dinâmica não-modelada [18-20]; e varia¸cões paramétricas [17].

(22)

controlador, chamado VS-APPC (Controle Adaptativo por Posicionamento de P´olos e Estrutura Vari´avel) [21-23], que substitui as leis integrais do APPC por leis chaveadas.

1.4 Estrutura do Trabalho

(23)

Controle Adaptativo por

Posicionamento de P´

olos

2.1 Introdu¸c˜

ao

A suposi¸cão de que a planta é de fase m´ınima, ou seja, tem zeros no semiplano esquerdo, é bastante restritiva em muitas aplica¸cões. Por exemplo, a aproxima¸cão de atrasos de tempo em processos qu´ımicos e outros processos industriais leva a modelos de planta com zeros no semiplano direito.

Uma classe de esquemas de controle muito popular no caso de parâmetros conhecidos é aquela que muda o posicionamento dos pólos da planta e não envolve cancelamentos de zeros e pólos. Estes esquemas (PPC) são aplicáveis a plantas LTI de fase m´ınima e não m´ınima. A combina¸cão de uma lei de controle por posicionamento de pólos com um estimador de parâmetros ou uma lei adaptativa leva a um APPC e pode ser usado para controlar uma grande variedade de plantas LTI com parâmetros desconhecidos.

O APPC pode ser dividido em duas classes: APPC indireto, onde a lei de controle gera as estimativas dos coeficientes da planta em tempo real, que são usadas então para calcular os parâmetros da lei de controle através da solu¸cão de alguma equa¸cão algébrica; e o APPC direto, onde os parâmetros da lei de controle são gerados diretamente por uma lei adaptativa sem cálculos intermediários que envolvem estimativas dos parâmetros da planta.

O APPC direto ´e restrito a plantas monovari´aveis (SISO) e a uma classe especial

(24)

de plantas onde os parâmetros desejados do controle por aloca¸cão de pólos podem ser expressos na forma de um modelo paramétrico linear ou bilinear [25].

O APPC indireto, por outro lado, é fácil de projetar e é aplicável a uma grande variedade de plantas LTI que não precisam ser de fase m´ınima ou estável. Devido a sua flexibilidade em escolher a metodologia do projeto do controlador (realimenta¸cão de estado, projeto de compensador, linear quadrático, etc.) e lei adaptativa (m´ınimos quadrados, método do gradiente, etc.), o APPC indireto é o tipo mais geral de controle adaptativo. O controle APPC também é conhecido como self-tuning (auto-ajustável). Esta técnica de controle também pode ser aplicada a alguns sistemas não lineares sem qualquer diferen¸ca conceitual [2].

Neste trabalho, é abordado o APPC indireto. O método escolhido para projetar a lei de controle é o método polinomial, que será discutido na Se¸cão 2.2.2.

2.2 PPC: Parˆ

ametros da Planta Conhecidos

Um esquema de controle adaptativo indireto consiste de três partes: a lei adaptativa que provê estimativas em tempo real para os parâmetros da planta; o mapeamento entre os parâmetros da planta e do controlador que é usado para calcular os parâmetros do controlador a partir das estimativas em tempo real dos parâmetros da planta; e a lei de controle.

Diversas leis de controle podem ser desenvolvidas para alcan¸car o objetivo do PPC, como, por exemplo, o método por variáveis de estado, que usa um observador de estados e realimenta¸cão por variáveis de estado, e o controle linear quadrático, que usa uma técnica de otimiza¸cão para projetar o sinal de controle que garante limita¸cão e regula¸cão do sinal de sa´ıda da planta ou erro de rastreamento nulo por minimizar uma certa fun¸cão de custo que reflete o desempenho do sistema em malha fechada [25]. Neste trabalho é abordado o método polinomial.

(25)

2.2.1 Descri¸c˜

ao do Problema

Consideremos uma planta SISO e LTI

y=G(s)u, G(s) = Z(s)

R(s) (2.1)

onde G(s) é estritamente própria (seu grau relativo, ou excesso de pólos, é pelo menos 1) e R(s) é um polinômio mônico (o coeficiente da potência mais alta em sé 1). O objetivo de controle é escolher um sinal de entradaude forma que os pólos de malha fechada sejam os pólos do polinômio mônico Hurwitz (todas as ra´ızes com parte real negativa) A∗

(s). O polinˆomioA∗

(s) é referido como o polinômio caracter´ıstico de malha fechada desejado, e é escolhido baseado nos requisitos de desempenho de malha fechada. Para alcan¸car o objetivo de controle, serão feitas as seguintes suposi¸cões sobre a planta:

S1. R(s) é um polinômio cujo grau n é conhecido.

S2. Z(s) e R(s) s˜ao coprimos e grau(Z)< n.

As suposi¸cões S1 e S2 permitem que Z e R sejam não-Hurwitz em contraste ao caso do MRC onde Z deve ser Hurwitz. Em geral, pela atribui¸cão dos pólos de malha fechada aos pólos deA∗

(s), n´os podemos garantir a estabilidade e convergˆencia da sa´ıda da planta

y para zero sem a utiliza¸cão de uma entrada externa. Nós podemos estender o objetivo do PPC ao incluir o rastreamento, onde y é requerido seguir uma certa classe de sinais de referência r, usando o princ´ıpio do modelo interno como segue: o sinal de referência uniformemente limitado é assumido satisfazer:

Qm(s)r= 0 (2.2)

onde Qm(s) é o modelo interno de r, ou seja, é um polinômio mônico conhecido de grau

q com ra´ızes n˜ao repetidas no eixojω, exceto na origem, e que satisfaz

S3. Qm(s) e Z(s) s˜ao coprimos.

Por exemplo, seyé requerido seguir o sinal de referênciar = 2+sen(2t), entãoQm(s) =

s(s2_{+ 4) e, portanto, de acordo com (S3),}_Z₍_s_{) n˜ao deveria ter}_s_ou_s2_{+ 4 como um fator.}

2.2.2 M´

etodo Polinomial

Vamos considerar a lei de controle

(26)

onde P(s), L(s) e M(s) são polinômios (com L(s) mônico) de grau q +n−1, n−1 e

q+n−1, respectivamente, a serem calculados e Qm(s) satisfaz (2.2) e a suposi¸c˜ao S3.

Aplicando (2.3) `a planta (2.1), n´os obtemos a planta em malha fechada

y= Z(s)M(s)

QmL(s)R(s) +P(s)Z(s)

r (2.4)

cuja equa¸c˜ao caracter´ıstica

QmL(s)R(s) +P(s)Z(s) = 0 (2.5)

tem ordem 2n+q−1. O objetivo agora ´e escolher P eL, tal que

QmL(s)R(s) +P(s)Z(s) =A

∗

(s) (2.6)

seja satisfeita por um polinˆomio Hurwitz mˆonico A∗

(s) de grau 2n+q−1. Devido às suposi¸cões S2 e S3 garantirem que Qm,R,Z são coprimos, existe solu¸cão para queL eP

satisfa¸cam (2.6) e esta solu¸cão é única. A solu¸cão para os coeficientes de L(s), P(s) da equa¸cão (2.6) pode ser obtida pela resolu¸cão da equa¸cão algébrica

Slβl=α

∗

l (2.7)

onde Sl ´e a matriz de Sylvester de QmR e Z de dimens˜ao 2(n+q)×2(n+q)

βl= [lTq, p T_]T_{, α}∗

l = [0, ...,0

| {z }

q

,1, α∗T

]T

lq = [0, ...,0

| {z }

q

,1, lT]T ∈ ℜn+q

l = [ln−2, ln−3, ..., l1, l0]

T

∈ ℜn−1

p= [pn+q−1, pn+q−2, ..., p1, p0]

T

∈ ℜn+q

α∗

= [α∗

2n+q−2, α ∗

2n+q−3, ..., α ∗

1, α

∗

0]

T

∈ ℜ2n+q−1

li,pi e α

∗

i s˜ao os coeficientes de

L(s) =sn−1

+ln−2s

n−2

+...+l1s+l0 =sn−1

+lTαn−2(s)

P(s) = pn+q−1s

n+q−1

+pn+q−2s

n+q−2

+· · ·+p1s+p0 =pTαn+q−1(s)

A∗

(s) = s2n+q−1

+α∗

2n+q−2s

2n+q−2

+· · ·+α∗

1s+α

∗

0 =s2n+q

−1

+α∗T

(27)

✲

✒✑ ✓✏

✲ ✲ ✲

✻

P(s)

Qm(s)L(s)

G(s)

r + u y

−

e

Figura 2.1: Diagrama de blocos do PPC. onde αi(s),[si, si−1, . . . ,1]T.

O fato de Qm, R e Z serem coprimos garante que Sl ´e n˜ao-singular e, portanto, os

coeficientes de L(s) e P(s) podem ser computados da equa¸c˜ao

βl=S

−1

l α

∗

l (2.8)

Usando (2.6), a planta em malha fechada ´e descrita por

y= ZM

A∗ r (2.9)

Similarmente, da equa¸c˜ao da planta em (2.1), da lei de controle em (2.3) e (2.6), obtemos

u= RM

A∗ r (2.10)

Devido r ser um sinal uniformemente limitado e ZM_A∗ e

RM

A∗ serem pr´oprias com p´olos

estáveis,yeusão uniformemente limitados para algum polinômioM(s) de graun+q−1. Por isso, o objetivo do posicionamento de pólos é alcan¸cado pela lei de controle (2.3) sem ter que adicionar restri¸cões emM(s) eQm(s). Quandor = 0, (2.9) e (2.10) implicam que

y e u convergem para zero com taxa de convergˆencia exponencial. Quando r 6= 0 o erro de rastreamento e=r−y´e dado por

e= A

∗

−ZM A∗ r =

LR

A∗ Qmr−

Z

A∗(M −P)r (2.11)

Para erro de rastreamento nulo, (2.11) sugere a escolha de M(s) = P(s) para anular o segundo termo em (2.11). O primeiro termo em (2.11) ´e anulado usando Qmr = 0. Por

isso, o posicionamento de p´olos e o objetivo de rastreamento s˜ao conseguidos pela lei de controle

QmLu=P(r−y) (2.12)

que ´e implementada como mostrado na Figura 2.1 usando n+q−1 integradores para a realiza¸c˜ao do controladorC(s) = P(s)

Qm(s)L(s)

(28)

✲

✒✑ ✓✏

✲ ✲

✒✑ ✓✏

✻

✲

✻

P(s) Λ(s)

Λ(s)−Qm(s)L(s)

Λ(s)

G(s)

r + u y

−

✛

✲

+ +

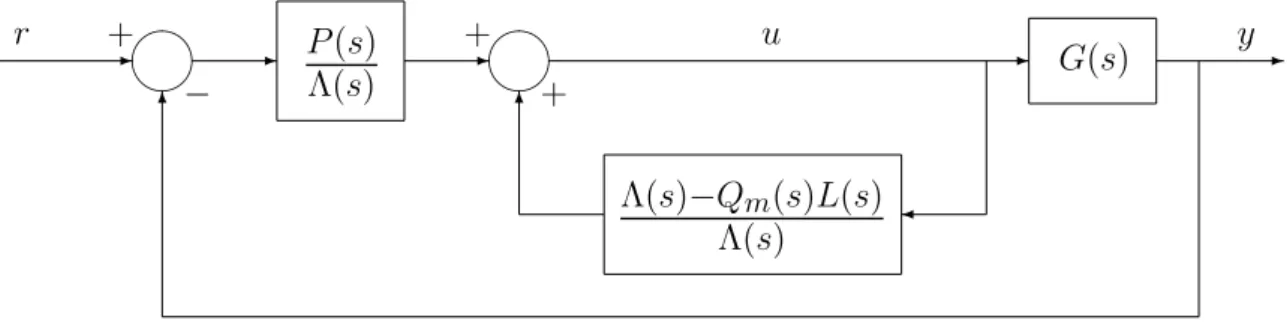
Figura 2.2: Uma realiza¸c˜ao alternativa do PPC.

a realiza¸cão de (2.12) com n+q−1 integradores pode ter uma fun¸cão de transferência, nomeada C(s), com pólos no semi-plano direito. Uma realiza¸cão alternativa de (2.12) é obtida reescrevendo (2.12) como

u= Λ−LQm Λ u−

P

Λ(y−r) (2.13) onde Λ é algum polinômio Hurwitz de grau n+q−1. A lei de controle (2.13) é imple-mentada como mostrada na Figura 2.2 usando 2(n+q−1) integradores para realizar as fun¸cões de transferência estáveis próprias Λ−LQm

Λ e

P

(29)

Sistemas com Estrutura Vari´

avel

3.1 Introdu¸c˜

ao

Conforme foi dito no Cap´ıtulo 1, o VSC tem sua fundamenta¸cão no controle por relés, sendo as fun¸cões de chaveamento das variáveis de controle projetadas de modo a restrin-gir a dinâmica do sistema a uma superf´ıcie chamada superf´ıcie deslizante, e tem como principais caracter´ısticas a rapidez do transitório e robustez a varia¸cões paramétricas e perturba¸cões (dentro de uma faixa de tolerância estipulada no projeto). Esta estratégia de controle tem sido usada com sucesso em manipuladores robóticos, ve´ıculos submarinos, motores elétricos de alta performance e sistemas de potência [2]. O VSC com modos deslizantes é largamente utilizado em pesquisa na área de controle por ser insens´ıvel a varia¸cões paramétricas e perturba¸cões externas [8].

O projeto do controle por modos deslizantes geralmente envolve dois passos principais: primeiro, é feita a sele¸cão de uma superf´ıcie deslizante que induza a uma dinâmica de ordem reduzida estável designada pelo projetista, e, posteriormente, a s´ıntese de uma lei de controle para for¸car as trajetórias do sistema em malha fechada irem e permanecerem na superf´ıcie deslizante.

A maioria das técnicas de projeto para controle por modos deslizantes supõe que todos os estados do sistema são acess´ıveis para a lei de controle. Na prática, nem todos os estados estão fisicamente dispon´ıveis para realimenta¸cão. Neste caso, um controlador por modos deslizantes com realimenta¸cão de estados não pode ser implementado, a menos que um observador seja usado para estimar os estados não-mensuráveis [26], ou os métodos

(30)

✲ ✻ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗◗ ◗ ◗ ◗ ◗ ◗ ◗ ◗

◗_◗_s

x1 x2

s(x)>0 ˙

s(x)<0

s(x)<0 ˙

s(x)>0

❄ ✲ f+₍_x₎

f−

(x)

s(x) = cx1+x2 = 0

r

x(0)

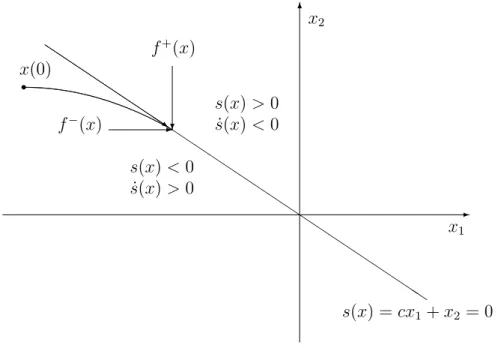
Figura 3.1: Superf´ıcie de deslizamento em um sistema de estrutura vari´avel.

de projeto devem ser modificados de tal forma que somente um subconjunto dos estados seja requerido para implementar a lei de controle.

Este cap´ıtulo tem por objetivo apresentar o desenvolvimento matem´atico do VSC, para um sistema de segunda ordem, que ´e fundamental para o desenvolvimento de um controlador adaptativo com leis chaveadas.

3.2 Descri¸c˜

ao Geral

Consideremos o seguinte sistema de segunda ordem ˙

x1 =x2

˙

x2 =a1x1+a2x2+u

(3.1)

com a1 ea2 conhecidos com incertezas.

Define-se uma superf´ıcie de chaveamentos como

s=x∈R2 |s(x) = cx1+x2 = 0, c >0 (3.2) na qual deseja-se que permane¸cam as vari´aveis de estado x1 e x2 (dinˆamica do sistema),

(31)

Utiliza-se um sinal de controle da forma

u(x) =

 



u+(x), se s(x)>0

u−

(x), se s(x)<0

(3.3)

Sendof(x) uma fun¸c˜ao definida como

f(x) =





x2

a1x1+a2x2+u



 (3.4)

o sistema passa a ser

˙

x=

 



f+(x), se s(x)>0

f−

(x), se s(x)<0 (3.5) Se a condi¸c˜ao ss <˙ 0 ´e satisfeita em uma vizinhan¸ca de s(x) = 0, os campos vetoriais

f+₍_x_{) e} _f−

(x) apontam para s nesta vizinhan¸ca. Portanto, se uma trajetória alcan¸ca s, é for¸cada a deslizar (escorregar ou apresentar um modo deslizante - sliding mode) sobre esta superf´ıcie, ou seja, é definido um modo deslizante em s.

Consideremos o sinal de controle

u=θ1x1+θ2x2 (3.6) com

θ1 =−θ1sgn¯ (sx1), θ1¯ >|a1|

θ2 =−θ¯2sgn(sx2), θ¯2 >|c+a2|

(3.7) onde

sgn(x) =

 



1, se x >0

−1, se x <0

(3.8)

Os valores dos parâmetros ¯θ determinam a rapidez com que a trajetória atinge a superf´ıcie de deslizamento. Pela condi¸cão de deslizamento temos

ss˙ =s(cx˙1+ ˙x2) =s(cx2+a1x1+a2x2+u) (3.9)

Substituindo (3.6) em (3.9), encontramos

ss˙=s[a1x1+ (a2+c)x2+θ1x1+θ2x2] (3.10) Usando (3.7) em (3.10), obtemos

ss˙ =sa1x1+ (a2+c)x2−θ1sgn¯ (sx1)x1−θ2sgn¯ (sx2)x2 ss˙ =a1sx1−θ¯1|sx1|+ (a2+c)sx2 −θ¯2|sx2|

(32)

✲ ✲

u 1 uav

τ s+1

Figura 3.2: Filtro passa-baixa para obten¸c˜ao de ueq.

Então, a condi¸cão de deslizamentoss <˙ 0 é obtida com ¯θ1 >|a1|e ¯θ2 >|c+a2|. Portanto, s torna-se uma superf´ıcie deslizante (Figura 3.1).

Se a1 e a2 s˜ao variantes no tempo e/ou conhecidos com incertezas, a condi¸c˜ao de

deslizamento pode ser satisfeita desde que os parˆametros do vetor ¯θ sejam devidamente dimensionados, ou seja,

¯

θ1 > supt>0|a1(t)|

¯

θ2 > supt>0|c+a2(t)|

(3.12)

Este sistema de controle apresenta dificuldades de implementa¸cão devido à necessi-dade de medi¸cão de todas as variáveis de estado da planta e ao surgimento de sinais de alta frequência (chattering), devido à excessiva atividade de controle decorrente de imperfei¸cões nos mecanismos de chaveamento reais.

3.3 Controle Equivalente

O Controle Equivalente [6] é definido como o controle cont´ınuo que, quando a trajetória está sobre a superf´ıcie deslizante, deveria ser aplicado para manter a trajetória sobre esta superf´ıcie.

No deslizamento, temos para o caso ideal ˙s≡0. Ent˜ao

cx˙1+ ˙x2 = 0

cx2+a1x1+a2x2+u= 0 ueq=−a1x1−(a2+c)x2

Na prática, a obten¸cão de ueq é feita através da filtragem de u (uav) por um filtro

passa-baixa com freqüência de corte suficientemente elevada. Se a freqüência de corte do filtro (1

(33)

✲ ❅ ❅ ❅ ❅ ❅ ❅ ❅ ❅ ❅ ❅ ❅ ❅ ❅ ❅ ❅ ❅ ❅ ❅❅ x1 f−

f+ f∗

s(x) = 0

❄

✲ ❅

❅ ❅❅❘

Figura 3.3: Campo vetorial no modo deslizante (solu¸c˜ao de Filippov)

3.4 Solu¸c˜

ao de Filippov

As equa¸cões diferenciais que surgem em sistemas com estrutura variável apresentam lado direito descont´ınuo (devido à descontinuidade introduzida pelo controle) e, assim, não é poss´ıvel garantir a existência e unicidade de uma solu¸cão para o sistema. Filippov [28] propôs uma defini¸cão que é particularmente adequada para o tipo de equa¸cões diferenciais que surgem em sistemas com estrutura variável. Basicamente, as solu¸cões no sentido de Filippov são absolutamente cont´ınuas como fun¸cões do tempo e, também, cont´ınuas em rela¸cão às condi¸cões iniciais. Isto torna poss´ıvel a extensão do método direto de Lyapunov na análise de estabilidade de sistemas com estrutura variável.

Se ocorre deslizamento em uma dada superf´ıcie s, um campo vetorial f∗

em cada ponto desta superf´ıcie pode ser determinado a partir dos campos vetoriais f+ e f−

dire-cionados conforme a Figura 3.3. Desta maneira é obtido um fecho convexo m´ınimo que é a base do método de Filipov. Uma vez que, o deslizamento ideal ocorre na superf´ıcie de deslizamento, o campo vetorial permanece em um plano tangencial à superf´ıcie. Assim, a equa¸cão para o deslizamento ideal, definida de acordo com Filippov, é dada por

f∗

=αf++ (1−α)f−

(34)

f−

e do gradiente da fun¸c˜ao s(x).

(35)

Controle Adaptativo por

Posicionamento de P´

olos e Estrutura

Vari´

avel

4.1 Introdu¸c˜

ao

Em trabalhos anteriores, foi desenvolvida uma técnica de controle que absorveu as qualidades do VSC, utilizando, ao invés de medi¸cões de todas as variáveis de estado do sistema, apenas medi¸cões de entrada e sa´ıda da planta, a qual foi denominada Controle Adaptativo por Modelo de Referência e Estrutura Variável (VS-MRAC) [11,29-30], tendo em vista que as leis de adapta¸cão integrais do MRAC [31] foram substitu´ıdas por leis chaveadas. Este algoritmo se baseava na abordagem direta do MRAC, sendo assim limi-tada a plantas de fase m´ınima. Com o intuito de simplificar o projeto do controlador, foi proposto um novo controlador, chamado VS-MRAC indireto [32-34], o qual utilizava informa¸cões dos próprios parâmetros nominais da planta para o cálculo da amplitude dos relés, uma vez que tais parâmetros representam grandezas f´ısicas, tais como resistências, capacitâncias, momentos de inércia, etc.

Neste trabalho, é proposto um controlador que agrega as caracter´ısticas do APPC e do VSC, isto é, aplicabilidade a plantas de fase não-m´ınima, transitório rápido e robustez, que é denominado VS-APPC [21-23], onde, assim como no VS-MRAC, as leis adaptativas integrais foram substitu´ıdas por leis chaveadas.

(36)

Neste cap´ıtulo, o objetivo é descrever matematicamente o VS-APPC, onde o chavea-mento é realizado nas leis de adapta¸cão dos parâmetros da planta. As incertezas nos parâmetros da planta podem ser conhecidas mais facilmente, pois representam incertezas de parâmetros f´ısicos. Neste trabalho, será abordado o caso de uma planta de primeira ordem.

4.2 Descri¸c˜

ao do M´

etodo

Consideremos a seguinte planta

y= b

s+au⇒y˙ =−ay+bu (4.1)

onde a e b s˜ao constantes e conhecidas com incertezas. Temos como objetivo estimar a e

b e gerar um sinal de controle u para quey tenda assintoticamente ao sinal de referˆencia

r e para que os p´olos de malha fechada da planta (4.1) sejam alocados nas ra´ızes de

A∗

(s) =s2+α∗

1s+α

∗

0 = 0.

Sejaam >0. Ent˜ao, podemos escrever (4.1) como

˙

y=−amy+ (am−a)y+bu (4.2)

Um modelo para a planta pode ser escrito como ˙ˆ

y=−amyˆ+ (am−ˆa)y+ ˆbu (4.3)

onde â e ˆb são estimativas para a e b, respectivamente [25]. Definimos o erro de estima¸cão e0 como

e0 =y−yˆ (4.4)

e, portanto,

˙

e0 =−ame0+ ˜ay−˜bu (4.5)

com

˜

a= ˆa−a

˜_b_{= ˆ}_b₋_b (4.6) Comoa e b s˜ao constantes, por hip´otese, temos:

˙˜

a = ˙ˆa

˙˜

b =b˙ˆ

(37)

Nos algoritmos convencionais (com leis integrais de estima¸c˜ao) utilizamos ˙ˆ

a=−γ1e0y, γ1 >0

˙ˆ

b=γ2e0u, γ2 >0

(4.8)

onde γ1 e γ2 s˜ao os ganhos adaptativos.

Seja a seguinte candidata a fun¸c˜ao de Lyapunov

V(e0,˜a,˜b) = 1 2 e 2 0+ ˜ a2 γ1

+ ˜b

2 γ2

!

>0 (4.9) ent˜ao,

˙

V(e0,˜a,˜b) =e0e˙0+

˜

aa˙˜ γ1 +

˜

bb˙˜

γ2 (4.10)

Substituindo (4.8) em (4.10) ficamos com ˙

V(e0,a,˜ ˜b) =−ame20 ≤0 (4.11)

que garante [e0,˜a,˜b]T = [0,0,0]T como um ponto de equil´ıbrio est´avel.

As leis de adapta¸cão são do tipo puramente integral (necessidade de ”memória”por parte do mecanismo de adapta¸cão) e podem levar o sistema a apresentar um comporta-mento instável na presen¸ca de distúrbios externos ou dinâmica não modelada da planta [24].

No VS-APPC utiliza-se a mesma estrutura de controle do APPC, porém com um sinal de controle chaveado da mesma forma que o controlador VSC. Portanto, a proposta deste trabalho é substituir as leis integrais de estima¸cão (leis adaptativas) pelas seguintes leis chaveadas para o cálculo de â e ˆb:

ˆ

a=−asgn¯ (e0y), a >¯ |a|

ˆ_b_{= ¯}_bsgn₍_e0u₎_, ¯_{b >}_|_b_| (4.12) As amplitudes dos relés (¯a e ¯b) devem dominar os valores máximos dos parâmetros da planta, para que se possa garantir a estabilidade assintótica, conforme mostra a se¸cão seguinte.

4.3 Prova de Estabilidade

Seja a seguinte candidata a fun¸c˜ao de Lyapunov

V(e0) = 1 2e

2

(38)

ent˜ao,

˙

V(e0) =e0e˙0

=−ame20+ ˜ae0y−˜be0u

=−ame20+ (ˆa−a)e0y−(ˆb−b)e0u

=−ame20+ [−¯asgn(e0y)−a]e0y−[¯bsgn(e0u)−b]e0u

=−ame20−(¯a|e0y|+ae0y)−(¯b|e0u| −be0u)

(4.14)

Desde que ¯a >|a|e ¯b >|b|, ficamos com ˙

V(e0)≤ −ame2₀ <0 (4.15)

o que garantee0 = 0 um ponto de equil´ıbrio globalmente assintoticamente est´avel. Como lim

t→∞|

e0|= 0, n´os temos

|e0˙| ≥c >0,∀t ≥tf >0 (4.16)

Ent˜ao,e0 atinge a superf´ıcie deslizantee0 = 0 em um tempo finitotf. Este procedimento

´e similar a [29].

Com esta técnica de controle, não podemos garantir a convergência das estimativas para os valores corretos dos parâmetros da planta, já que não se trata de adapta¸cão paramétrica e sim de uma lei de controle chaveada. As simula¸cões que são mostradas no cap´ıtulo seguinte mostram uma notável insensibilidade a varia¸cões paramétricas e perturba¸cões.

4.4 C´

alculo dos Parˆ

ametros do Controlador

Conforme mostrado na Se¸c˜ao 2.2.2, a lei de controle

Qm(s)L(s)u=P(s)(r−y) (4.17)

pode ser usada para conseguir o objetivo de controle. Neste trabalho, o controlador será projetado para uma referência constante. Como o polinômioQm(s) é calculado de acordo

(39)

Para uma planta de primeira ordem, temos: L(s) = 1 eP(s) =p1s+p0 e os coeficientes p1 e p0 satisfazem a equa¸c˜ao Diofantina

s(s+a) + (p1s+p0)b =s2 +α∗

1s+α

∗

0 (4.18)

A equa¸cão (4.18) pode ser escrita na forma da equa¸cão algébrica (2.7), ou seja, a matriz de Sylvester de s(s+a) e b é dada por

       

1 0 0 0

a 1 0 0 0 a b 0 0 0 0 b

                0 1 p1 p0         =         0 1 α∗ 1 α∗ 0         (4.19)

cuja solu¸c˜ao ´e

p1 = α∗

1−a

b e p0 = α∗

0

b (4.20)

Como supomos que os parâmetros da planta são conhecidos com incertezas, o princ´ıpio da equivalência à certeza sugere o uso da mesma lei de controle, mas com o polinômio

P(s) = p1s+p0 calculado usando as estimativas dos parˆametros, e, portanto, temos

ˆ

p1 = α∗

1−aˆ

ˆ_b e pˆ0 =

α∗

0

ˆ

b (4.21)

onde ˆp1 e ˆp0 são as estimativas dos parâmetros do controlador que precisam ser geradas em tempo real. No APPC indireto convencional são utilizadas leis adaptativas que são guiadas pelo erro e0. Para isso, podem ser utilizados o método do gradiente, o método dos m´ınimos quadrados, etc. A estima¸cão dos parâmetros pelo método do gradiente é dada por (4.8). Para o VS-APPC serão substitu´ıdas as leis adaptativas por leis chaveadas conforme (4.12).

Uma vez que os parâmetros do controlador podem ser fun¸cões de mais de um parâmetro da planta simultaneamente, o sinal pode ficar indefinido, pois existem dois ou mais sinais chaveados em freqüências elevadas. Além disso, o parâmetro ˆb aparece no denominador das expressões, o que pode causar divisões por zero. Com isso, faz-se necessária a in-trodu¸cão de um valor nominal do parâmetro ˆb, para manter o valor com sinal definido. Reescrevendo as leis chaveadas com a modifica¸cão na expressão de ˆb, temos

ˆ

a=−asgn¯ (e0y),a >¯ |a|

(40)

✲ ✲

✲

b s+a u

✛

❄ ❄

❄

✛ ✛

ˆ

a=−asgn¯ (e0y)

ˆ

b = ¯bsgn(e0u) +bnom

ˆ

p1 = pˆ0 = α∗₀

ˆ

b α∗₁−ˆa

ˆ

b

,

✍✌ ✎☞ (ˆp₁s+ˆp₀)

s

u e

y

ˆ

a ˆb

ˆ

p1 pˆ0

−

+

r

Figura 4.1: Diagrama de blocos do VS-APPC para planta de primeira ordem.

O sinal de controleu é gerado a partir da equa¸cão (4.17) e, portanto, é dado por

˙

u= ˆp0r−pˆ1y˙−pˆ0y (4.23)

(41)

Aplica¸c˜

ao do Controlador

5.1 Planta de Primeira Ordem Inst´

avel

Nesta se¸cão, a estratégia de controle proposta no cap´ıtulo anterior será projetada para uma planta do tipo

G(s) = 1

s−1 =

b

s+a (5.1)

cujo polinˆomio caracter´ıstico escolhido ´e

A∗

(s) = (s+ 1)2 =s2+ 2s+ 1 (5.2) Utilizamos (4.22) para encontrar â e ˆb e, com estes valores, calculamos os parâmetros do controlador, que de acordo com (4.21) e (5.2) são

ˆ

p1 = 2−aˆ

ˆ_b e p0ˆ = 1

ˆ_b (5.3)

O sinal de controle ´e calculado pela equa¸c˜ao (4.23).

5.1.1 Simula¸c˜

oes

Todas as simula¸cões deste trabalho foram feitas com a utiliza¸cão do programa MAT-LAB 6 [35], utilizando como método de integra¸cão o método de Euller.

Para a planta descrita em (5.1), foi utilizado um intervalo de integra¸c˜ao deh= 0,01s. A referˆencia utilizada para a planta (5.1) foi r= 1.

Inicialmente foi feita uma simula¸cão utilizando nas leis adaptativas o método do gra-diente. Foram manipulados os ganhos adaptativos e, para efeito de compara¸cão com a

(42)

Figura 5.1: APPC Indireto utilizando o m´etodo do gradiente.

t´ecnica proposta neste trabalho, escolhemos um resultado obtido quandoγ1 = 1 e γ2 = 1,

que tem uma magnitude do sinal de controle de 0,353. A sa´ıda da planta converge em 6,52s considerando uma tolerˆancia de 2%. A Figura 5.1 mostra o resultado desta simula¸c˜ao.

Na simula¸cão seguinte (Figura 5.2), as leis adaptativas convencionais foram subs-titu´ıdas pelas leis chaveadas propostas em (4.22). Como temos três constantes para serem projetadas, diversos testes foram feitos combinando valores para as mesmas, com o objetivo de conseguir o melhor resultado poss´ıvel em rela¸cão ao tempo de convergência. Após os testes feitos, utlizamos as constantesbnom = 1,5, ¯b= 0,7 e ¯a= 1,1. Observou-se

que a sa´ıda da planta converge em 2,66s considerando também uma tolerância de 2%. Para uma mesma magnitude do sinal de controle (0,353) do caso anterior, o VS-APPC apresentou uma convergência do sinal de sa´ıda da planta bem mais rápida do que o método do gradiente. A Figura 5.3 mostra a evolu¸cão do comportamento dos parâmetros da planta. Podemos observar que o sinal de controle é bem mais suave que no caso do VS-MRAC, devido ao polinômio Qm, que multiplica o sinal de controle u atuando como

(43)

Figura 5.2: VS-APPC Indireto para sistema de primeira ordem.

(44)

5.2 Motor de Indu¸c˜

ao Trif´

asico

Nos dias atuais, os motores de indu¸cão têm cada vez mais tomado o lugar dos motores CC em aplica¸cões de alto desempenho [36]. Em rela¸cão ao motor CC, o motor de indu¸cão apresenta como vantagens robustez, baixo custo, menor frequência de manuten¸cão, e no caso de motores com rotor em gaiola de esquilo, sua principal vantagem é a ausência de contatos deslizantes. No entanto, na máquina CC o controle de velocidade se dá de uma forma bastante simples, já que o torque e o fluxo podem ser impostos à máquina de uma forma desacoplada. Isto fazia com que os motores CC fossem os preferidos em acionamentos de alto desempenho.

Com o surgimento, na década de 70, da teoria de controle vetorial [37], que é baseada na orienta¸cão dada pelo campo do rotor, é que se teve ferramentas teóricas para controlar a velocidade do motor de indu¸cão de forma desacoplada, semelhante ao motor CC [36,38-39], quando o motor é alimentado por fontes de corrente ideais.

Com o avan¸co da eletrônica de potência e do aparecimento de microprocessadores mais rápidos e de menor custo, foi poss´ıvel a implementa¸cão do controle vetorial orientado pelo campo, tornando o motor de indu¸cão mais competitivo em rela¸cão ao motor CC.

Nesta estratégia, um elemento importante de incerteza é o valor da constante de tempo rotórica que varia com as condi¸cões de opera¸cão, mudando o comportamento do sistema, o que impõe o uso de alguma estratégia de controle adaptativo e/ou robusto, que compense poss´ıveis varia¸cões de parâmetros.

5.2.1 Modelagem

A modelagem do motor de indu¸cão já foi bastante discutida em diversos trabalhos [40]. Dessa forma, parte-se do modelo matemático em nota¸cão vetorial [36].

Nesta se¸cão é usada uma técnica vetorial para modelar o motor de indu¸cão. Define-se um sistema de eixos complexos ortogonais,d eq, onde o fluxo do rotor é a referência para o eixo d.

As equa¸cões que descrevem a dinâmica do motor de indu¸cão são:

US =RsiS(t) +Ls

d

dt(iS(t)) +Lm d

dt(iR(t)e

jε

) (5.4)

0 = RriR(t) +Lr

d

dt(iR(t)) +Lm d

dt(iS(t)e

−jε

(45)

Te(t) =

2

3P LmIm

iS(t)

iR(t)ejε

∗

(5.6)

Jdω(t)

dt =Te(t)−Bω(t)−Tl(t) (5.7) dε(t)

dt =ω(t) (5.8)

onde

US - Vetor tens˜ao do estator;

iS eiR - Vetores corrente do estator e corrente do rotor, respectivamente;

Rs e Rr - Resistˆencias por fase do estator e do rotor, respectivamente;

Ls e Lr - Indutˆancias pr´oprias por fase do estator e do rotor, respectivamente;

Lm - Indutˆancia de magnetiza¸c˜ao por fase;

Te - Torque eletromagn´etico no eixo do motor;

Tl - Torque de carga;

J - Momento de in´ercia do rotor;

B - Coeficiente de atrito viscoso da m´aquina;

P - N´umero de pares de p´olos;

ω(t) - Velocidade angular do eixo do motor;

ε - Posi¸c˜ao angular do eixo do motor (ˆangulo entre os eixos da fase 1 do estator e a fase 1 do rotor);

I_m _{- Componente imagin´ario de um n´}_{umero complexo ”}_x_”; [x]∗

- Operador complexo conjugado de um vetor ”x”.

Na prática, o que se busca com a modelagem vetorial é a observa¸cão das correntes do estator de um referencial fixo a um fluxo de referência. Assim, definindo um novo sistema de coordenadas (Figura 5.4) com o eixo de referência direto, dou eixo real (R_e_), coincidindo com o vetor fluxo do rotor (ψR), a componente do vetor fluxo do rotor no

eixo em quadratura, q ou eixo imaginário (I_m_{), é anulada, ou seja,} _ψ_Rq _{= 0.} Baseado na Figura 5.4 e partindo-se da Equa¸cão (5.5), obtemos

0 = Rr

Lr

(ψRd−LmiSe

−jρ

) + d

dt(ψRd) +j

dρ dt −ω

ψRd (5.9)

onde

ψRd - Componente do vetor fluxo do rotor no eixo direto;

(46)

Figura 5.4: Diagrama vetorial do motor de indu¸c˜ao (ωs ´e a velocidade s´ıncrona.)

Observando o diagrama vetorial (Figura 5.4) e com (5.9), as componentes do vetor corrente do estator no eixo direto e em quadratura s˜ao calculadas como

iSd=

1

Lm

ψRd+

Lr

RrLm

dψRd

dt (5.10)

iSq =

Lr

RrLm

dρ

dt −ω(t)

ψRd (5.11)

Pela an´alise do diagrama,

iS(t) = (iSd+jiSq(t))ejρ (5.12)

ψR(t) = ψRd(t)ej(ρ

−_ε)

(5.13) e, o torque da m´aquina (5.6) fica

Te(t) =

2 3P

Lm

Lr

ψRd(t)iSq(t) (5.14)

(47)

quadratura, através de uma rela¸cão linear, até o limite da velocidade nominal do motor. Para obter-se o torque máximo, o fluxo de referência será mantido constante e em seu valor máximo.

5.2.2 Parˆ

ametros do Motor de Indu¸c˜

ao

Foi utilizado um motor de indu¸cão trifásico classe ”B”de 0,25 HP, com 4 pólos, veloci-dade nominal de 1725 rpm (180,64 rad/s), tensões nominais 380 V/220 V para liga¸cão Y e ∆, respectivamente, com freqüência nominal de 60 Hz. As correntes nominais são de 1,26 A em 220 V (liga¸cão ∆) e 0,726 A em 380 V (liga¸cão Y). O rotor é do tipo gaiola de esquilo. O conjugado nominal é de 1,02 N.m.

A obten¸cão dos parâmetros do motor foi através de ensaios de curto-circuito e de circuito aberto [38] e confrontados com os dados fornecidos pelo fabricante. Os resultados obtidos são apresentados na Tabela 5.1.

Rs 29,5012 Ω

Rr 17,8384 Ω

Lm 1,0417 H

Ls 0,0534 + 1,0417 = 1,0951 H

Lr 0,0637 + 1,0417 = 1,1054 H

Tabela 5.1: Parˆametros el´etricos do motor

Também foi fornecido pelo fabricante o momento de inércia do motor, cujo valor é

J = 5×10−4

Kg.m

A obten¸cão da equa¸cão de primeira ordem que representa a planta foi baseada no fato de que, utilizando-se o controle vetorial indireto pelo campo do rotor, com alimenta¸cão dada pelo valor de referência da componente da corrente do estator em quadratura (ir

Sq)

e mantendo-se constante o valor de referˆencia do fluxo do rotor no eixo direto (ψr Rd), a

rela¸cão entre o torque elétrico e a corrente de referência é aproximadamente

Te(t) =KirSq (5.15)

(48)

A entrada da planta (motor) ´e a componente iSq do vetor corrente de estator e a

sa´ıda é a velocidade do rotor ω. Supondo o motor em vazio e sem conjugado de carga, a fun¸cão de transferência da planta é, então, determinada a partir das equa¸cões (5.7) e (5.15) resultando em

ω(s)

iSq(s)

=

K J

s+ B J

=G(s) = b

s+a (5.16)

Para os valores dos parˆametros obtidos [38], o seguinte modelo nominal ´e obtido

G(s) = 3798

s+ 11,3 (5.17)

5.2.3 Simula¸c˜

oes

Para a planta descrita em (5.17), foi um escolhido um polinômio caracter´ıstico que não exigisse um sinal de controle de alta magnitude. Portanto, o polinômio escolhido foi

A∗

(s) = (s+ 12)2 =s2+ 24s+ 144 (5.18) Como a fun¸cão de transferência do motor de indu¸cão também é de primeira ordem, temos os mesmos polinômiosL(s) e P(s) do caso anterior e também o mesmo polinômio Qm(s),

já que aqui o sinal de referência também é constante. Os parâmetros do controlador são

ˆ

p1 = 24−ˆa ˆ

b e p0ˆ =

144

ˆ_b (5.19)

As leis chaveadas utilizadas para o motor de indu¸cão são as mesmas de (4.22) e o sinal de controle é calculado a partir de (4.23).

Para o motor de indu¸cão, foi utilizado um passo de integra¸cão de h = 1ms, ou seja, menor que no caso anterior (h= 10ms). O sinal de referência foi de r= 900 rpm.

Assim como para a planta anterior, foram feitos diversos testes até que se chegasse em três constantes que apresentassem um resultado satisfatório. As constantes utilizadas que mostraram os melhores resultados foram bnom = 3600, ¯b = 3550 e ¯a = 22 (Figura 5.5).

O sinal de sa´ıda da planta e o sinal de referˆencia s˜ao dados em rpm e o sinal de controle

u=iSq ´e dado em mA. Foi verificado que a sa´ıda da planta converge em 0,247s.

(49)

Figura 5.5: VS-APPC para o controle de velocidade de um motor de indu¸c˜ao trif´asico.

a robustez do controlador a este tipo de comportamento. Após o primeiro segundo da simula¸cão, o parâmetro b foi alterado de 3798 para 3700, aos 2s de 3700 para 3900 e aos 3s para 3798 novamente. O parâmetro a foi alterado de 11,3 para 9 aos 3,5s, de 9 para 11,8 aos 4,5s e de 11,8 para 11,3 aos 5,5s. A Figura 5.6 mostra o detalhe da região onde acontecem as mudan¸cas no sinal de controle e no sinal de sa´ıda da planta. Podemos observar que o sinal de controle atua no comportamento do sistema, de tal forma que, apesar das altera¸cões afetarem o sinal de sa´ıda da planta, rapidamente o sinal de sa´ıda volta a seguir a referência.

(50)

Figura 5.6: Altera¸c˜ao dos parˆametros da planta.

(51)

5.2.4 Sistema de Acionamento

O sistema de acionamento, que foi utilizado na implementa¸cão do controlador VS-APPC, é mostrado na Figura 5.8 [41]. Ele é composto por um motor de indu¸cão de 0.25 HP, alimentado por um inversor trifásico VSI/PWM com controle de corrente por janela de histerese. No controle de corrente são usados sensores de efeito Hall para a medi¸cão das correntes de duas fases do motor. Um microcomputador recebe a velocidade do motor, através do sinal de um tacogerador.

A sa´ıda do tacogerador é uma tensão alternada cuja frequência e valor eficaz são proporcionais à velocidade do motor. Essa tensão alternada é atenuada, retificada e filtrada (eliminando os ru´ıdos de medi¸cão) gerando uma tensão cont´ınua proporcional à velocidade do motor. A constante de proporcionalidade do motor é obtida de acordo com a Tabela 5.2. Uma placa de interface A/D transforma esta tensão cont´ınua em um sinal digital para o microcomputador. No microcomputador, um algoritmo de controle, escrito em linguagem ”C”, calcula as correntes de referência e, através de um conversor D/A, estas correntes são fornecidas ao inversor VSI/PWM para a alimenta¸cão do motor.

A placa conversora AD/DA trabalha com tensões de 0 a +10 V e, assim, o sinal de tensão retificado, proporcional à velocidade, é ajustado para esta faixa. As correntes de referência, geradas a partir do algoritmo de controle, são alternadas, de forma que um n´ıvel DC deve ser adicionado para compensar o ciclo negativo das correntes de referência. A interface D/A da placa possui apenas duas sa´ıdas e, então, apenas duas correntes de referência, geradas pelo algoritmo de controle, podem ser enviadas. Como o circuito é trifásico equilibrado, a terceira corrente pode ser obtida pelo valor negativo da soma das outras duas. Assim, projetou-se um circuito para subtrair o n´ıvel DC adicionado às duas correntes de referência geradas pelo controlador, e criar a terceira corrente de referência.

TENS ˜AO (Volts) 0,00 4,30 6,05 7,65 10,07 VELOCIDADE (rpm) 0,00 975,20 1405,00 1820,00 2442,00

(52)

✻

✲ ✲

✲

❅ ❅

❅ ❅❅❘ ✁✁❆❆

r r r

❅❅ ✛ ✛ ✛

Pentium IV 2.8 GHz

v ∝ω

Tacˆometro

Motor de

Inversor

Indu¸c˜ao

ir

S1 irS2

ir S3

iS1 iS2 iS3

Figura 5.8: Sistema de acionamento.

5.2.5 Implementa¸c˜

ao Pr´

atica

Nesta implementa¸c˜ao, foi medido o per´ıodo de amostragem referente ao tempo de processamento do algoritmo de controle e de convers˜oes A/D-D/A, cujo resultado foi

h= 150µs.

(53)

(54)

Conclus˜

oes e Perspectivas

Neste trabalho foi proposto um controlador adaptativo por posicionamento de pólos e estrutura variável, denominado VS-APPC [21-23], que procurou agregar as caracter´ısticas do APPC e do VSC, isto é, aplicabilidade a plantas de fase não-m´ınima, transitório rápido e robustez, através da substitui¸cão das leis adaptativas convencionais por leis chaveadas. Foram feitas duas aplica¸cões: uma para o controle de uma planta instável, através de simula¸cões, e outra para o controle de velocidade de um motor de indu¸cão trifásico, onde foram feitas inicialmente simula¸cões, e posteriormente a implementa¸cão prática. A técnica proposta apresentou transitório bastante rápido em ambas as aplica¸cões.

O controlador VS-APPC indireto apresenta um projeto simples, com o cálculo das amplitudes dos relés estando diretamente relacionado com os parâmetros f´ısicos da planta. A sequência deste trabalho se dará com a posterior generaliza¸cão para plantas de ordem qualquer. A generaliza¸cão segue os mesmos passos do APPC apresentado em [25] e neste trabalho.

(55)

Modelos Entrada/Sa´ıda

A.1 Fun¸c˜

oes de Transferˆ

encia

As fun¸cões de transferência são muito importantes na caracteriza¸cão das propriedades entrada/sa´ıda de sistemas LTI e são usadas largamente na teoria de controle clássica. Vamos considerar um sistema descrito pela equa¸cão diferencial de ordem n

y(n)(t) +an−1y

(n−1)

(t) +· · ·+a0y(t) = bmu(m)(t) +bm−1u

(m−1)

(t) +· · ·+b0u(t) (A.1)

Para obtermos a fun¸cão de transferência do sistema (A.1), nós aplicamos a transfor-mada de Laplace em ambos os lados da equa¸cão e assumimos condi¸cões iniciais nulas. Portanto, comssendo a variável complexa, temos a seguinte fun¸cão de transferência para (A.1)

G(s), Y(s)

U(s) =

bmsm+bm−1s

m−1

+· · ·+b0 sn₊_a

n−1sn

−1+· · ·+_a

0

(A.2) Nós dizemos que G(s) é própria se G(∞) é finita, ou seja, n ≥ m; e estritamente própria seG(∞) = 0, ou seja, n > m.

A equa¸cão caracter´ıstica do sistema (A.1) é definida como a equa¸cão sn₊_a n−1s

n−1

+

· · ·+a0 = 0.

A.2 Polinˆ

omios Coprimos

As propriedades de entrada/sa´ıda dos sistemas apresentados neste trabalho são repre-sentadas por fun¸cões de transferência expressas como a razão de dois polinômios em s

com coeficientes reais, ou seja,