Estrutura a termo da taxa de juros no Brasil e previsibilidade de ciclos econômicos

FUNDAÇÃO GETÚLIO VARGAS

ESCOLA DE ECONOMIA DE SÃO PAULO

PRISCILA FERNANDES RIBEIRO

Estrutura a Termo da Taxa de Juros no Brasil e Previsibilidade

de Ciclos Econômicos

PRISCILA FERNANDES RIBEIRO

Estrutura a Termo da Taxa de Juros no Brasil e Previsibilidade de Ciclos

Econômicos

Dissertação apresentada à Escola de

Economia de São Paulo da Fundação

Getúlio Vargas, como requisito para

obtenção de título de Mestre em

Economia

Orientador: Prof. Dr. Pedro Luiz Valls

Pereira

Ribeiro, Priscila Fernandes.

Estrutura a Termo da Taxa de Juros no Brasil e Previsibilidade de Ciclos econômicos / Priscila Fernandes Ribeiro. - 2010.

90 f.

Orientador: Pedro Luis Valls Pereira.

Dissertação (mestrado) - Escola de Economia de São Paulo.

1. Taxas de juros – Brasil – Modelos econométricos. 2. Ciclos econômicos -- Brasil. 3. Previsão econômica. I.Valls, P. (Pedro). II. Dissertação (mestrado) - Escola de Economia de São Paulo. III. Título.

Priscila Fernandes Ribeiro

Estrutura a Termo da Taxa de Juros no Brasil e Previsibilidade de Ciclos Econômicos

Dissertação apresentada à Escola de Economia de São Paulo da Fundação Getúlio Vargas, como requisito para obtenção de título de Mestre em Economia.

Banca Examinadora:

Prof. Pedro Luiz Valls Pereira (FGV-EESP)

Prof. Luiz Koodi Hotta (IMECC – Unicamp)

Agradecimentos

Ao Professor Pedro Luiz Valls Pereira pelos ensinamentos, incentivos e oportunidades, não somente nesta Dissertação, mas também durante anos de minha vida acadêmica desde os cursos de Estatística Básica na graduação; cuja sabedoria me incentivou nos estudos de Economia e na melhoria contínua desta Dissertação. Obrigada pela paciência inesgotável. A minha Querida Mãe, por todo amor e apoio incondicionais em todos os meus projetos e desafios. As minhas irmãs, por todo incentivo.

Ao Corpo Docente da EESP, pelo compromisso com a excelência acadêmica, e pela vital contribuição para a minha formação.

Aos colegas de turma pelo ambiente de convívio extremamente agradável ao longo do curso de mestrado.

À CAPES pela bolsa de mestrado.

Resumo

O objetivo deste trabalho é caracterizar a Curva de Juros Mensal para o Brasil através de três fatores, comparando dois tipos de métodos de estimação: Através da Representação em Espaço de Estado é possível estimá-lo por dois Métodos: Filtro de Kalman e Mínimos Quadrados em Dois Passos. Os fatores têm sua dinâmica representada por um Modelo Autorregressivo Vetorial, VAR(1), e para o segundo método de estimação, atribui-se uma estrutura para a Variância Condicional. Para a comparação dos métodos empregados, propõe-se uma forma alternativa de compará-los: através de Processos de Markov que possam modelar conjuntamente o Fator de Inclinação da Curva de Juros, obtido pelos métodos empregados neste trabalho, e uma váriavel proxy para Desempenho Econômico,

fornecendo alguma medida de previsão para os Ciclos Econômicos.

Abstract

This work proposes characterize Yield Curve for Brazil by three factors, comparing two types of estimation methods: using State Space model, estimate it by Kalman Filter and Two Steps Least Squares. The factors are the dynamics represented by a Vector Autoregressive model, VAR (1), and the second estimation method is attributed a structure for the conditional variance. To compare the methods used, it is proposed an alternative way of comparison: using Markov processes, an econometric model of the joint dynamic relationship between the slope of yield curve and the economy to predict business cycles.

Lista de Figuras

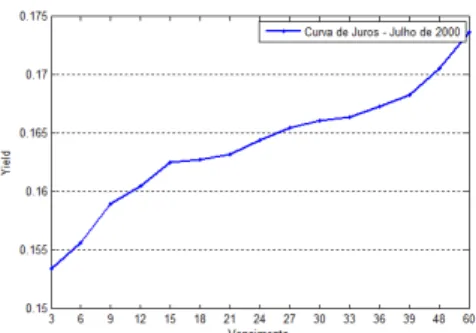
Figura 1: Curva de Juros - Julho de 2000... 14

Figura 2: Curva de Juros - Abril de 2003. ... 15

Figura 3:Curva de Juros - Novembro de 2004 ... 15

Figura 4: Curva de Juros Brasileira - Março de 2000 a Agosto de 2009. ... 26

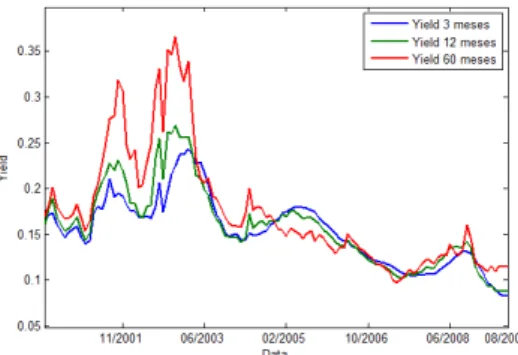
Figura 5: Taxas de Juros de 3, 12 e 60 meses... 27

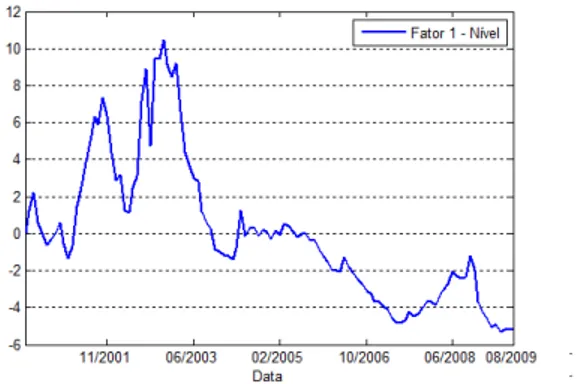
Figura 6: Primeiro Componente Principal – Nível... 28

Figura 7: Segundo Componente Principal – Inclinação ... 29

Figura 8: Terceiro Componente Principal – Curvatura ... 29

Figura 9: Peso de cada Componente Principal na Curva de Juros ... 30

Figura 10: Peso do Fator Nível na Curva de Juros ... 31

Figura 11: Peso do Fator Inclinação na Curva de Juros ... 31

Figura 12: Peso do Fator Curvatura na Curva de Juros... 32

Figura 13: Factor Loadings restritos em Nelson-Siegel (1987)... 32

Figura 14: Fatores estimados por Filtro de Kalman - Fatores Suavizados... 33

Figura 15: Curva de Juros estimada com Fatores Suavizados. ... 33

Figura 16: Peso do Fator Nível na Curva de Juros... 35

Figura 17: Peso do Fator Inclinação na Curva de Juros. ... 35

Figura 18: Peso do Fator Curvatura na Curva de Juros... 36

Figura 19: Fatores estimados por Mínimos Quadrados em Dois Passos... 36

Figura 20: Fatores estimados por Mínimos Quadrados em Dois Passos - com modelo BEKK(1,1) para Variância Condicional... 37

Figura 21: Volatilidades estimadas pelo Modelo BEKK(1,1)... 40

Figura 22: Correlações Condicionais estimadas pelo Modelo BEKK(1,1)... 41

Figura 23: Cronologia Trimestral dos Ciclos de Negócios Brasileiros. ... 47

Figura 24: Variação 12 meses do PIB Brasileiro. ... 65

Figura 25: Probabilidades Filtrada e Suavizada para Ciclos Econômicos utilizando Modelo ... 67

Figura 26: Probabilidades Filtrada e Suavizada para Ciclos Econômicos utilizando Modelo 2. ... 68

Figura 27: Probabilidades Filtrada e Suavizada para Ciclos Econômicos utilizando Modelo 3. ... 70

Figura 28: Probabilidades Filtrada e Suavizada para Ciclos Econômicos utilizando Modelo 4. ... 71

Lista de Tabelas

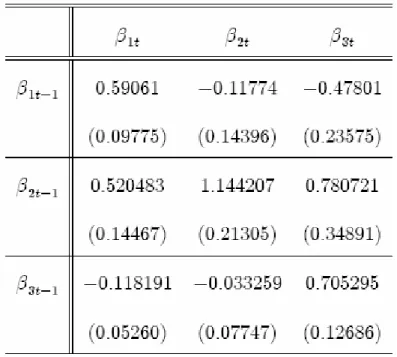
Tabela 1: Parâmetros Estimados do VAR(1) para os Fatores Latentes Suavizados (Erro-Padrão em parênteses) ... 33 Tabela 2: Matriz de Variância entre Fatores Latentes Suavizados... 34 Tabela 3: Matriz de Correlação entre Fatores Latentes Suavizado ... 35 Tabela 4: Parâmetros Estimados do VAR(1) para os Fatores Latentes estimados por

Mínimos Quadrados em 2 Passos (Erro-Padrão em parênteses). ... 37 Tabela 5: Matriz de Variância entre Fatores Latentes estimador por Mínimos Quadrados em Dois Passos... 38 Tabela 6: Matriz de Correlação entre Fatores Latentes estimador por Mínimos Quadrados

em Dois Passos. ... 38 Tabela 7: Parâmetros Estimados do VAR(1) para os Fatores Latentes estimados por

Mínimos Quadrados em 2 Passos com BEKK(1,1) para Variância Condicional (Erro-Padrão em parênteses). ... 39 Tabela 8: Parâmetros Estimados do BEKK(1,1) para os Fatores Latentes (Erro-Padrão em

Súmario

Estrutura a Termo da Taxa de Juros no Brasil: Nelson-Siegel Dinâmico ... 11

Introdução... 11

Modelo de Fatores: Fatos Estilizados... 14

Análise de Componentes Principais ... 16

Modelo Nelson-Siegel Dinâmico ... 19

Representação de um modelo de três fatores... 19

Métodos de Estimação... 23

Estimações e Resultados... 26

Base de Dados ... 26

Análise de Componentes Principais ... 28

Resultados das Estimações ... 31

Conclusão ... 42

Estrutura a Termo e Previsibilidade de Ciclos Econômicos... 43

Introdução... 43

Ciclos Econômicos, Curva de Juros e CODACE... 46

Metodologia... 50

Cadeias de Markov ... 50

Vetor Autorregressivo com Mudanças Markoviana

(

)

Determinação de regimes em um Modelo MS-VAR ... 54

Estimação ... 57

Dados e Resultados... 64

Dados ... 64

Resultados... 65

Conclusão ... 74

Bibliografia... 76

Estrutura a Termo da Taxa de Juros no Brasil: Nelson-Siegel Dinâmico

Introdução

A Estrutura a Termo da Taxa de Juros, também conhecida como yield curve descreve a

relação entre as taxas de juros e o correspondente prazo até a maturidade ou vencimento. Entre outros usos, a curva de juros fornece informação importante na avaliação de ativos financeiros e derivativos, na gestão de riscos financeiros, etc.

Como ferramenta de análise econômica, a curva de juros reflete os preços que os agentes devem pagar para transferir consumo futuro em consumo corrente, os custos de implementar projetos para os investidores e as taxas que o Governo paga para que os títulos de dívida sejam absorvidos pelo mercado1_{. Além disso, como ferramenta macroeconômica,}

a curva de juros reflete as Expectativas dos Agentes em relação ao comportamento das taxas de juros de curto prazo, que é um dos instrumentos de política monetária no combate à inflação e estabilização da atividade econômica2. Para a análise de conjuntura e à produção de previsões macroeconômicas, a Estrutura a Termo da Taxa de Juros pode ser utilizada para obter indicadores antecedentes de inflação e nível de atividade3_.

As aplicações na área de Finanças também são inúmeras. A curva de juros fornece os fatores de desconto necessários para calcular o preço de mercado dos diversos ativos disponíveis. No caso de ativos de renda fixa, os recebimentos futuros relativos aos coupons

1_{Ver detalhes em Macroeconomics in the Global Economy, de Geoffrey Sachs e Felipe}

Larrain, Prentice Hall, 1ª edição, 1993.

2_{Para mais detalhes sobre este tópico, ver Discretion Versus Policy Rules in Practice, de}

John B. Taylor, Carnegie-Rochester Conference Series on Public Policy, 39, 1993; Interest and Prices, de Michael Woodford, Princeton University Press, 2003; e The Econometrics of Financial Markets, de John Campbell, Andrew Lo e Archie McKinley, Princeton University Press, 1996.

3_{Why Does the Yield Curve Predict Output and Inflation?, de Arturo Estrella, The}

e ao valor de face devem ser correspondentes ao valor presente para que o título em questão possa ser devidamente avaliado; no caso de ativos de renda variável, uma das formas propostas para calcular o seu preço justo exige o cálculo do valor presente do fluxo de dividendos e do preço de revenda da ação.

Um dos principais estudos empregados para descrever a Curva de Rendimentos é devido a Litterman e Scheinkman (1991). Neste artigo, os autores partem de uma amostra onde as variáveis são os excessos de retorno de títulos de renda fixa zero-coupon de diversos

vencimentos emitidos pelo Governo Americano. Eles identificaram três fatores principais para explicar o comportamento desses retornos e estes fatores foram identificados como Nível, Inclinação e Curvatura, sendo estes capazes de explicar razoavelmente bem a variabilidade dos dados.

A previsão das taxas de juros também é uma importante ferramenta para avaliar estratégias de longo prazo. Diebold e Li (2006), através da modelagem via componentes exponenciais desenvolvido em Nelson e Siegel (1987), observam que a dinâmica da curva é dada por três fatores associados a Nível, Inclinação e Curvatura conforme Litterman e Scheinkman (1991).

Pelos exemplos citados acima, a Estrutura a Termo da Taxa de Juros vem se tornando um indicador econômico bastante difundido. Há evidência de relação sistemática entre o comportamento da Curva de Juros e Ciclos Econômicos. Em Diebold, Rudebush e Arouba (2006), além da introdução de fatores latentes, os autores adicionam variáveis relacionadas à indicadores da atividade econômica e política monetária e encontram evidências de que essas váriaveis ajudam na explicação do Comportamento da Curva de Juros.

Portanto, esse trabalho se insere no esforço de modelar o comportamento da Estrutura a Termo da Taxa de Juros, de importância inegável em virtude das inúmeras aplicações discutidas acima. O objetivo, portanto, é caracterizar a Curva de Juros Mensal para o Brasil por meio de três fatores, comparando dois tipos de métodos de estimação: Através da Representação em Espaço de Estado do modelo e estimá-lo por Filtro de Kalman e outra, pela mesma representação, mas estimando-o por Mínimos Quadrados em Dois Passos, com e sem estrutura para a Volatilidade para as Taxas de Juros. Os fatores têm sua dinâmica representada por um Modelo Autorregressivo Vetorial de ordem 1, VAR(1).

compará-los: através de Processos de Markov que possam modelar conjuntamente o Fator de Inclinação da Curva de Juros, obtido pelos métodos empregados neste trabalho, e uma váriavel proxy para Desempenho Econômico, fornecendo alguma medida de previsão para

os Ciclos Econômicos, desenvolvida no Capítulo 2.

O modelo a três fatores será estimado neste estudo usando dados de Swap DI-PRÉ

Modelo de Fatores: Fatos Estilizados

A Estrutura a Termo da Taxa de Juros é composta de taxas de curto, médio e longo prazos. Portanto, a curva poderá apresentar diferentes formatos ao longo destas maturidades.

Normalmente, taxas de juros com vencimentos mais longos são maiores que taxas de curto prazo. Este comportamento da curva é chamado de curva normal da taxa de juros e tem este comportamento por refletir um prêmio de risco inflacionário que investidores pedem por títulos de longo prazo.

Quando as taxas de juros se alteram igualmente ao longo da curva, chama-se este comportamente de deslocamento paralelo. Neste caso, a inclinação e curvatura continuam inalteradas, mas o nível se altera.

Uma alteração do formato (ou curvatura) da curva é conhecido como twist e significa que a

taxa de juros de títulos mudaram de forma diferenciada ao longo da curva.

A curva de juros é dita estar invertida, neste caso as taxas de curto prazo são maiores que a de longo prazo quando os investidores claramente têm preferência pelos títulos de longo prazo.

A curva de juros pode variar de formato muito rapidamente em um curto espaço de tempo, como pode-se verificar a seguir.

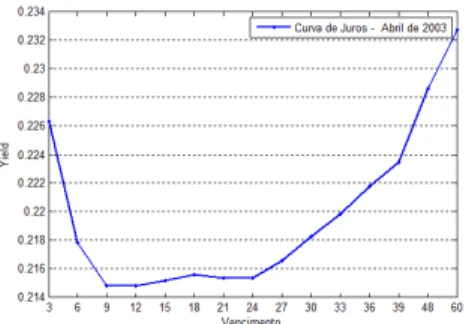
Figura 2: Curva de Juros - Abril de 2003.

Figura 3:Curva de Juros - Novembro de 2004

A Curva de Juros no Brasil é particularmente interessante pois durante o período analisado ela apresenta várias mudanças de inclinação e curvatura, mudando do formato crescente para a curva invertida várias vezes nesse período.

Outro ponto importante é que a curva de juros no Brasil possui alta variabilidade no que se refere à nível da Curva, bem como em Inclinação e Curvatura, com pode ser observado pelas figuras acima.

Análise de Componentes Principais

Conforme Litterman e Scheinkman (1991), uma vez que a Análise de Componentes Principais é capaz de captar variações nas taxas de juros não detectáveis pela análise de duração, ela pode ser utilizada na diversificação de carteiras para redução do risco específico. A duração é capaz de captar somente movimentos paralelos da Curva de Juros. Como será exposto adiante, este deslocamento paralelo será determinado pela Primeira Componente Principal da Curva de Juros.

Em Varga e Valli (2001), é realizado um estudo sobre Análise de Componentes Principais para a Curva de Juros no Brasil, utilizando para isso dados de Swap DI com prazo até 1

ano, no período compreendido entre Janeiro de 1995 a Julho de 1999, com periodicidade diária. Neste trabalho, o três primeiros componentes explicam aproximadamente 94% da variabilidade total da curva, sendo só o primeiro componente responsável por 80% em média, resultado parecido com os encontrados em Litterman e Scheinkman (1991). Com esta análise, o objetivo dos autores é aplicar um procedimento de eliminação de risco conhecido como imunização. Essa técnica se justifica na adição de uma carteira sintética à carteira atual, de forma a eliminar o risco de variações das taxas de juros sobre a carteira original4. Para isso, a variação em valor desta carteira sintética deve ser igual à variação da carteira original. Os autores afirmam que o resultado encontrado com a técnica de Análise de Componentes Principais para o cálculo da carteira sintética é superior à técnica de duração, para o período analisado.

A Análise de Componentes Principais se baseia em uma técnica de diagonalização de matrizes. A partir desta técnica são encontrados autovalores e autovetores.

Suponha que yt yt1, ,yt , sendo variáveis observadas e t 1, . . . ,T . Define-se:

1) zt zt1, ,zt tal que zt yt

1

T t 1 T

yt . Assim, z_t é y_t centrado na

média.

2) k k1, ,kq tal que:

k1 ,z1 1z11 Nz1

k2 ,z2 1z21 Nz2

kT ,zT 1zT1 NzT

Para encontrar o primeiro componente principal, deve-se resolver:

( )

∑

max T _t

t k T Var β β

ϕ k (1)

s.a.

t 1

T t1

2

1 2 1

O vetor 1 11, , 1T é o primeiro componente principal. Uma matriz ZT tal

que suas linhas sejam formadas por t ocorrências dos vetores de zt , então:

) 2 ( 2 1 β β

β Z kt Z Z

T t ′ ′ ′ ′ = ⇒ =

∑

Substituindo na equação (1)

1 max 1

T Z Z

Var zt 1_TZ Z é o estimador da matriz de Variância e Covariância de z_t.

Os demais componentes principais podem ser obtidos repetindo o procedimento de Maximização da equação (1) e acrescentando a restrição de ortogonalidade com os

( )

max 2

1 

  

 

=

=

∑

=

t T

t

v k

T Var

β β

ϕ k

s.a.

j 1 jv

2

v 2 1

, _p 0 para todop v

Denomina-se kt _tT₁ t zt de Escores de Componentes Principais do -ésimo

componente principal.

A restrição de Norma Unitária para os vetores de componentes principais é necessária para

delimitar os valores de 1Var zt 1.

Para a obtenção dos demais componentes principais, acrescentam-se as restrições de ortogonalidade com os componentes já obtidos para garantir que os próximos componentes representem inovações. Assim, para cada componente principal, o valor maximizado encontrado será cada vez menor, permitindo verificar o percetual explicado de cada variável. Esta definição não possui solução única. Ou seja, se v é um componente

principal, v , também será.

Var zt é matriz simétrica não negativa definida. Assim, a1 a são seus

autovalores e 1, , seus respectivos autovetores normalizados, então v v para

todo v _.

Além disso, cada autovalor av é um estimador da variância de yv :

av j 1aj

100

Modelo Nelson-Siegel Dinâmico

Representação de um modelo de três fatores

A abordagem em Nelson-Siegel (1987) descreve a Curva de Juros por meio de pesos exponenciais nos fatores. Nesta abordagem, o modelo proposto é capaz de representar um grande número de vencimentos para as taxas de juros como uma função matemática. Os autores argumentam que estas funções podem ser usadas para obter um modelo parcimonioso, representando os principais fatos estilizados, historicamente observados na Curva de Juros: monotonicidade, convexidade e formato em "Sino", persistência no nível das taxas, maiores volatilidades em maturidades de curto prazo e baixa persistência nos

spreads5.

As funções matemáticas que podem gerar estes fatos estilizados da Curva de Juros estão associadas a soluções de equações diferenciais ou a diferenças. Denota-se o conjunto de

taxas de juros com vencimento em de y . O modelo de Nelson-Siegel que representa a Curva de Juros em um dado instante de tempo é apresentado a seguir, onde 1, 2 , 3

e são parâmetros.

( )

  

 

− − +

   



 ₋

+

= −λτ −λτ −λτ λτ

β λτ

β β

τ e e e

y

Esta representação tem uma interpretação clara e intuitiva: os componentes são de curto, médio e longo prazos. O primeiro componente assume valor constante igual a 1, assim pode ser interpretado como um nível geral que influência igualmente tanto o curto prazo quanto o longo prazo. O segundo componente está associado a 2 e converge a um quando

0 e converge a zero quando , em um dado t. Por isso, usualmente liga-se

este componente a influências das taxas de juros de curto prazo. A taxa de decaimento é determinada pelo parâmetro . O terceiro componente, associado a 3 , converge a zero

quando 0 e quando , mas é côncavo em , para um dado t _{. Por isso, este}

componente está relacionado a taxa de juros de médio prazo, pois o mesmo começa em zero, cresce para maturidades de médio prazo e decai a zero novamente quando se aproxima dos vencimentos de longo prazos, reproduzindo assim um formato de "sino".

Novamente, o parâmetro determina a maturidade de médio prazo, dado que é nesta que o parâmetro atinge o máximo valor.

A representação Nelson-Siegel da Curva de Juros é modificada em Diebold e Li (2006). Os autores mostram que a representação acima pode ser interpretada como um modelo de

fatores latentes e 1t, 2t e 3t são o Nível, Inclinação e Curvatura, que variam ao longo

do tempo e os componentes 1, 1 e , 1 e e podem ser interpretados como os pesos (factor loadings) dos respectivos fatores.

Os motivos para esta representação estão relacionados aos aspectos da curva de juros e sua relação com os fatores que descrevem este comportamento. Uma mudança no fator de

longo prazo, 1t , reproduz a mesma mudança em todas as taxas de juros,

independentemente do vencimento. Diebold e Li (2006) identificam este componente para a Curva de Juros Americana com alta persistência, sendo associado com as Expectativas Inflacionárias dos Agentes Econômicos.

Analogamente, um aumento no fator de curto prazo, 2t , terá efeitos mais

predominantemente nas taxas de curto prazo, afetando a inclinação da curva. Diebold e Li (2006) associam a este fator o comportamento esperado da economia, como, por exemplo, nível esperado da atividade econômica.

Um aumento no fator de médio prazo, 3t , não afetará imediatamente as taxas de juros de

longo prazo, mas terá um efeito maior sobre as taxas de médio prazos, indicando que a curvatura da Curva de Juros irá variar ao longo do tempo e reproduzindo o fato estilizado de formato de " sino " da curva de juros. Diebold e Li (2006) afirmam que nenhuma variável econômica está associada diretamente a curvatura da Curva.

Vale comentar também que os fatores 1t, 2t e 3t recuperados por Diebold e Li

curvatura comumente utilizadas6. Esse resultado é bastante desejável na medida em que a metodologia de Nelson e Siegel não poderia ser considerada adequada se os fatores decorrentes da mesma (que dependem das formas funcionais pré-especificadas para os parâmetros de decaimento) não se assemelhassem aos fatores decorrentes do que os agentes econômicos entendem por medidas de Nível, Inclinação e Curvatura, como exposto em Diebold, Rudebusch e Arouba (2006).

Assim, as taxas de juros, observadas como séries de tempo, podem ser conjuntamente descritas, para as diferentes maturidades, pelo seguinte Modelo de Regressão:

( )

t

y = + + + +

para t 1, . . . ,T _. t, ~ N 0, , onde é uma matriz diagonal. A suposição

anterior implica que variações nas taxas de juros de diferentes maturidades são não correlacionadas.

Neste modelo de regressão, é uma constante para cada maturidade da taxa de juros e pode ser interpretada como efeito fixo na medida que cada constante retrata as características particulares à cada maturidade da taxa de juros, que são observáveis e não observáveis. Além disso, apesar de no Brasil a curva de juros sofrer inúmeros choques no período selecionado, alterando seu comportamento de nível e volatilidade, não é perda de generalidade assumirmos que a constante para toda maturidade, , não varia no tempo, além disso, evitamos ditar uma regra de comportamento para o parâmetro, bem como, em número de parâmetros a serem estimados; 1t, 2t e 3t são os fatores variando no

tempo e j é o peso para o fator j e vencimento .

Na abordagem Nelson-Siegel, os pesos são restritos como exposto em (observacao). Como

explicitado em Diebold e Li (2006), os parâmetros j podem ser considerados constantes

ao longo do tempo. No trabalho de Koopman, Mallee e Van der Wel 2008 , utilizando dados mensais de título zero-coupon do Tesouro Americano disponibilizado por

Fama-Bliss, argumentam que manter o fator de decaimento fixo durante o período estudado

6_{Define-se Nível como sendo a média de todos os}

yields; Inclinação como sendo a

diferença entre os yields de longo prazo e de curto prazo; e Curvatura como sendo igual a

pode ser bastante restritivo, isso porque os fatores de inclinação 2t e de curvatura 3t

dependem apenas . Porém, Diebold e Li (2006) argumentam que o ganho para o ajuste e poder preditivo do modelo é pequeno quando é permitido que o parâmetro de decaimento varie.

Se it é um vetor de variáveis latentes, pode-se mostrar que sua representação pode ser

feita através do Autorregressivo Vetorial VAR , como proposto em Diebold e Li

(2006). A dinâmica de 1t, 2t e 3t , neste caso, pode ser descrita por um modelo

VAR 1 , a saber:

) 6 ( 3 2 1 1 3 1 2 1 1 33 32 31 23 22 21 13 12 11 3 2 1           +                     =           − − − t t t t t t t t t ζ ζ ζ β β β α α α α α α α α α β β β

De acordo com o exposto, esta estrutura, segundo Diebold and Li (2006) já está em Representação de Espaço de Estado. A equação (5) representa a equação de medida ou de

observação e (6) , a equação de transição. De acordo com Koopman 2007 , num trabalho empírico sobre a Curva de Juros Americana, os fatores que descrevem a mesma possuem alta memória. Devido a este fato, o processo proposto pelo autor para os fatores é um Passeio Aleatório:

) 7 ( 3 2 1 1 3 1 2 1 1 3 2 1           +           =           − − − t t t t t t t t t ζ ζ ζ β β β β β β

para t _{1, . . . ,}T _{. As condições iniciais são 1} N 0, , _{diagonal, e 1}

N 0, . não é necessariamente diagonal, ou seja, os erros dos fatores podem ser contemporaneamente correlacionados. Este processo proposto em Koopman (2007) é um caso particular do processo proposto em Diebold e Li (2006). Assim, pode-se testar se o VAR(1) proposto poderá ser reduzido a Passeio Aleatório para os fatores latentes.

Métodos de Estimação

Para estimar a Curva de Juros descrita acima, as abordagens utilizadas serão o Filtro de Kalman e Mínimos Quadrados em Dois Passos, como utilizado por Diebold, Rudebusch e Arouba (2006) e Diebold e Li (2006), respectivamente. Os autores implementaram a estimação simultânea das equações de observação e transição (obs) e (transicao), para o primeiro método e a estimação, em separado, para a equação de observação (obs) obtendo os pesos dos fatores para cada maturidade, e para equação de transição (transicao), para obter a dinâmica entre os fatores que descrevem as taxas de juros. A estimação simultânea de todos os parâmetros em um único passo tem vantagens em termos de inferência estatística. Diebold, Rudebusch e Arouba (2006) esclarecem que a estimação em um único estágio é melhor pois esta consegue levar em conta toda incerteza associada a estimação destes parâmetros de uma única vez. De Pooter (2007), comparando várias classes do Modelo Nelson-Siegel com dados mensais de zero-coupons do Tesouro Americano de Fama-Bliss para o período de Janeiro de 1984 a Dezembro de 2003, encontra que o modelo

a três fatores com parâmetro de decaimento, , constante e estimado em um único estágio por Filtro de Kalman possui Erro Quadrático Médio inferior ao mesmo modelo estimado em dois estágios.

A estimação em um único estágio do modelo dinâmico por Filtro de Kalman resulta nas estimativas de Máxima Verossimilhança Exata dos coeficientes e estimativas suavizadas ótimas dos fatores latentes.

O Filtro de Kalman é um algorítmo utilizado para previsão linear do vetor de estado, neste caso, vetor de variáveis latentes, nas variáveis observadas, as taxas de juros. Sob Normalidade, a Função de Verossimilhança do modelo é obtida através da decomposição do erro de previsão. Uma vez obtida a Função de Verossimilhança, os coeficientes são estimados por métodos numéricos. Após a estimação dos parâmetros, através do algorítmo de Suavizamento é possível recuperar o vetor de estado Suavizado e é possível obter alguma interpretação estrutural para estas estimativas.

A Função de Verossimilhança do sistema depende dos erros de previsão, de suas

respectivas variâncias e do conjunto de parâmetros, , , it, , _{e é dada}

( )

( )

( 1 _{| 1}

1 | 1 | 1 | 1     − − − =

Θ − ′ − −− − =

∑

T

t

F F

L π ς ς

onde t|t 1 yt yt|t 1 é o erro de previsão um passo à frente e

Ft|t 1 E t|t 1 t|t 1 é a variância do erro de previsão .

Para os Mínimos Quadrados em Dois Passos, como descrito acima, as equações de medida são tratadas como um modelo cross-sectional e o Mínimos Quadrados são utilizados para

estimar o parâmetro de decaimento, que é constante ao longo do tempo. Este parâmetro é

determinado minimizando y y 2 _{, para cada vencimento da taxa de juros.}

Num segundo passo, os fatores são tratados como séries temporais e estima-se a dinâmica para o estes como na equação de transição, ou seja, como proposto por Diebold e Li (2006), um VAR(1). Os autores assumem que as variâncias condicionais são constantes ao longo

do tempo, ou seja, t . Assim, fixado o valor de , os fatores latentes podem ser

estimados a cada instante de tempo por Mínimos Quadrados Ordinários. Num segundo passo, os fatores são estimados segundo a dinâmica da equação de estado do modelo. Neste passo, além de replicar os trabalhos de referência, pretende-se estender o modelo de forma a capturar mundanças no comportamento de risco das taxas de juros. Assim, adicionamos à dinâmica citada acima estrutura para a volatidade dos fatores, 1t, 2t e 3t , de acordo

com o modelo Diagonal BEKK (1,1).

Engle e Kroner (1995) propuseram o modelo BEKK, que diferentemente dos modelos VECH para volatilidade, garantem matriz de ariância condicional positiva definida. O modelo proposto é tal que:

(

)

1 1 ′ ′ ′ ∑ + + ′ = ∑ ₋ = − − =

∑

∑

h j i i t i t i g i

t AA A ε ε A B B

onde A _{é matriz tringular inferior e} Ai e Bj são matrizes k k . Neste caso, g 1 e

h 1 . Através de uma parametrização simétrica, t será positiva definida pois AA é

Impõe-se a dinâmica acima para os fatores latentes pois esta captura os riscos intrínsecos à Estrutura a Termo e captura incerteza do nível, inclinação e curvatura, que retrata toda a dinâmica da Curva de Juros, segundo Nelson e Siegel (1987).

A volatilidade no nível corresponde ao componente que é comum às volatilidades, ou incertezas, associadas a todas as taxas de juros da Curva. Na verdade, ela pode ser vista como um modelo implícito da volatilidade do mercado de títulos, que é capturado por Engle, Ng e Rothschild (1988) em termos da variância condicional do excesso de retorno de uma carteira de mercado igualmente ponderada.

A volatilidade associada ao fator de inclinação pode ser associado ao grau de risco dos

spreads das taxas de juros, portanto, as variações nos Prêmios de Risco que os investidores

exigem para adquirir contratos de longo prazo em detrimento aos de curto prazo.

Finalmente, a volatilidade associada ao componente de curvatura capta incertezas associadas ao formato da curva, que pode variar entre convexo, linear e côncavo. Assim, tais variações referem-se à volatilidade das taxas de médio prazo.

Uma forma alternativa para capturar a volatilidade na Estrutura a Termo da Taxa de Juros seria permitir que a volatilidade de cada maturidade fosse incorporada à estimação. No entanto, o resultado seria um modelo M-GARCH de dimensão igual ao número de taxas juros na equação cross-sectional (5).

Estimações e Resultados

Base de Dados

Os dados empregados nesse trabalho são os preços de fechamento mensais das taxas de Swap DI-PRÉ. As maturidades utilizadas foram 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36 , 39, 48 e 60 meses. Os dados foram observados para o período de Março de 2000 a Agosto de 2009. Algumas estatísticas descritivas para os dados de Swap DI-Pré são apresentados na Tabela 14. Na Figura 29, observa-se a Curva de Juros Média e Mediana para o período analisado. A curva de juros média apresenta o comportamento normalmente observado, ou seja, tendência crescente na maturidade. Já a curva de juros mediana apresenta o comportamento flat (sem inclinação), uma indicação de que é esperado, no período

analisado, que as taxas de curto prazo continuem as mesmas. Ou seja, espera-se que a política econômica, em relação à taxa de juros, permaneça a mesma.

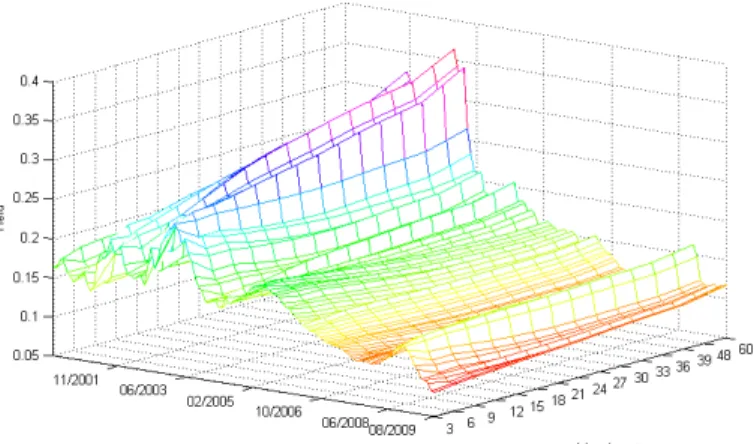
A Curva de Juros para o período estudado contempla vários formatos, com várias mudanças de inclinação e curvatura, assumindo formatos ascendentes e invertidos por várias vezes nesse período, como visto na seção Fatos Estilizados. A Figura 4 abaixo apresenta o

gráfico em três dimensões da curva estudada.

Figura 4: Curva de Juros Brasileira - Março de 2000 a Agosto de 2009.

A Figura 5 abaixo reporta os yields de 3 meses, 1 e 5 anos, para melhor visualização do

Análise de Componentes Principais

Cada componente principal pode ser visto como uma função de pesos das funções da Estrutura a Termo da Taxa de Juros observadas. O primeiro componente principal pode ser observado na Figura 6.

F

Figura 6: Primeiro Componente Principal – Nível

Litterman e Scheinkman (1991) chamaram o Primeiro Componente Principal de Nível porque ele representa variações praticamente constantes ao longo da curva. Estas variações representam os movimentos paralelos da Estrutura a Termo da Taxa de Juros. O percentual explicado pelo primeiro componente é de 92,7%.

Figura 7: Segundo Componente Principal – Inclinação

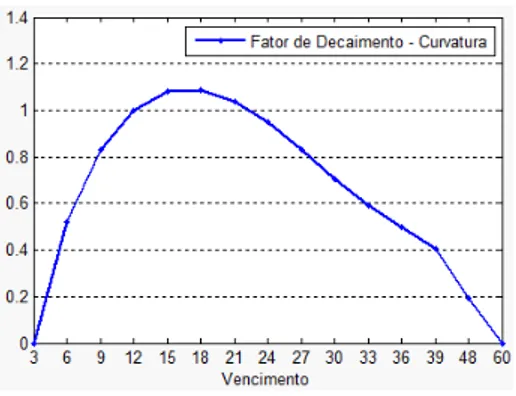
O Terceiro Componente Principal foi denominado Curvatura. Conforme demonstrado por Litterman e Scheinkman (1991), ela está principalmente associada à volatilidade. Esta interpretação é facilmente verificada na Figura 8. Observa-se que o percentual de variação explicado ficou em 1.52%.

Figura 8: Terceiro Componente Principal – Curvatura

Figura 9: Peso de cada Componente Principal na Curva de Juros

F

A interpretação desses pesos é bastante simples: um choque no primeiro fator, Nível, impacta de forma uniforme em todas as taxas de juros da curva, ou seja, deslocamento paralelo da Curva de Juros; um choque no segundo fator, Inclinação, leva a mudanças das taxas de mais curto prazo comparativamente às taxas de longo prazo, ou seja, há mudança de inclinação da Curva de Juros; finalmente, um choque no terceiro fator, Curvatura, leva a deslocamentos diferenciados nas taxas de curto e longo prazos, comparativamente às taxas de médio prazo, ou seja, há uma mudança da curvatura da Curva de Juros.

A validade dos resultados obtidos pela Análise de Componentes Principais depende da hipótese de independência das curvas na Estrutura a Termo. Silveira e Lion (2003) já haviam apontado este problema. Eles sugeriram como alternativa estimar os componentes principais da primeira diferença. De fato, supondo que exista uma forte correlação entre a ETTJ e a ETTJ defasada de um dia, o problema seria eliminado trabalhando com a primeira

diferença da Estrutura a Termo, tal que, yt yt yt 1 . Os resultados encontrados por

Resultados das Estimações

De acordo com a seção Métodos de Estimação para o primeiro método de estimação

empregado aqui, os parâmetros j e os fatores jt foram estimados por Filtro de

Kalman. Foram obtidas também estimativas para as matrizes de variância e covariância

e .

Para a identificação de todos os parâmetros j , os pesos (factor loadings) dos três fatores

nos vencimentos 3 , 12 e 60 meses são restritos a ser 1, 0, 0 , 0, 1, 0 e 0, 0, 1 ,

respectivamente. Assim, o vencimento de 3 meses está diretamente relacionado ao fator de inclinação. Os vencimentos de 12 e 60 meses ligados aos fatores de curvatura e nível, respectivamente. Essa restrição está intimamente relacionada à relevância de cada fator latente na Curva de Juros..

Os pesos estimados pelo Filtro de Kalman são apresentados a seguir:

Figura 10: Peso do Fator Nível na Curva de Juros

Figura 12: Peso do Fator Curvatura na Curva de Juros

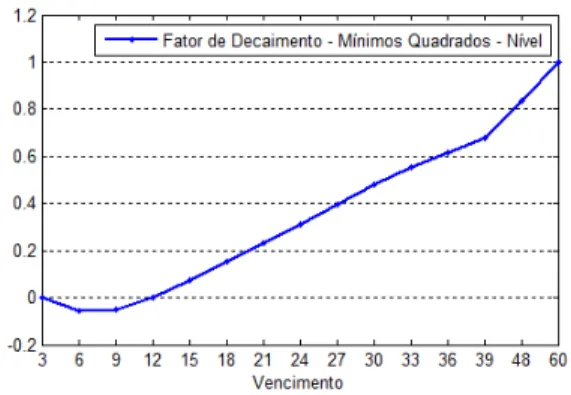
Como mencionado na seção os pesos para o fator de Nível está associado a maturidades

mais longas, 48 e 60 meses. O segundo e terceiro fatores estão associados aos vencimentos de curto e médio prazos, respectivamente. Observando as Figuras acima, as estimativas para os pesos do segundo e terceiro fatores, Inclinação e Curvatura, para o modelo proposto são muito parecidos com os pesos restritos propostos em Nelson-Sielgel (1987), Figura 13.

Figura 13: Factor Loadings restritos em Nelson-Siegel (1987).

Figura 14: Fatores estimados por Filtro de Kalman - Fatores Suavizados.

A Curva Ajustada pelos fatores suavizados é dada a seguir:

Figura 15: Curva de Juros estimada com Fatores Suavizados.

F

A Soma de Quadrados dos Resíduos, resultantes da estimação por Filtro de Kalman é 0.03448.

A análise dos parâmetros do modelo VAR 1 indica alta persistência na dinâmica dos três fatores latentes e há efeitos cruzados aparentemente significantes para a dinâmica dos fatores. O fator 3 influência os fatores 1 e 2. Os resultados são apresentados na Tabela 1.

Os autovalores da matriz de coeficientes do VAR(1) acima são 0. 5493 , 0. 9935 e 0. 8973 . Como um dos autovalores é próximo de um, os componentes do VAR são no mínimo, integrados de primeira ordem e como os outros dois autovalores são menores do que um, isso indica, juntamente com a afirmação anterior, que os componentes são no máximo integrados de ordem 1.

A seguir são apresentadas a Matrizes de Variância e Correlação para os fatores latentes Suavizados.

Tabela 3: Matriz de Correlação entre Fatores Latentes Suavizado

Os três fatores são correlacionados entre si. Vencimentos mais próximos apresentam uma correlação maior comparado a vencimentos mais distantes uns dos outros, sendo este um fato estilizado da Curva de Juros.

Para o segundo método empregado, Mínimos Quadrados em Dois Passos, os pesos estimados no primeiro passo são dados por:

Figura 16: Peso do Fator Nível na Curva de Juros.

Figura 18: Peso do Fator Curvatura na Curva de Juros.

Observando as Figuras acima, as estimativas para os pesos dos três fatores são muito parecidos com os pesos restritos propostos em Nelson-Sielgel (1987), Figura 13.

Os três fatores estimados por Mínimos Quadrados são correlacionados entre si, como apresentado para os fatores estimados por filtro de Kalman. Os fatores estimados são apresentados a seguir.

Figura 19: Fatores estimados por Mínimos Quadrados em Dois Passos.

A Soma de Quadrados dos Resíduos, para esta estimação, é 0.05342. A soma dos quadrados dos resíduos do segundo método é maior do que do primeiro método. Isso indica que o primeiro método, filtro de Kalman, é superior ao segundo método, Mínimos Quadrados em Dois Passos.

para os fatores estimados por filtro de Kalman.

Figura 20: Fatores estimados por Mínimos Quadrados em Dois Passos - com modelo BEKK(1,1) para Variância Condicional.

A análise dos parâmetros do VAR indica alta persistência na dinâmica dos três fatores latentes, tanto por Mínimos Quandrados quanto por Mínimos Quadrados com o modelo BEKK(1,1) para a Variância Condicional, e estas são da mesma magnitude da persistência observada na estimação do Modelo por Filtro de Kalman. As estimativas do VAR(1) para os fatores latentes estimados por Mínimos Quadrados são apresentadas abaixo, na Tabela 4.

Os autovalores da matriz de coeficientes na Tabela 4 são 0. 8206 , 0. 9905 e 0. 9248 . Como um dos autovalores é próximo de um, os componentes do VAR são no mínimo, integrados de primeira ordem e como os outros dois autovalores são menores do que um, isso indica, juntamente com a afirmação anterior, que os componentes são no máximo integrados de ordem 1. A matriz de Variância e de Correlação para os fatores latentes estimados por Mínimos Quadrados em Dois Passos são apresentadas nas Tabelas 5 e 6 a seguir.

Tabela 5: Matriz de Variância entre Fatores Latentes estimador por Mínimos Quadrados em Dois Passos.

Tabela 6: Matriz de Correlação entre Fatores Latentes estimador por Mínimos Quadrados em Dois Passos.

Tabela 7: Parâmetros Estimados do VAR(1) para os Fatores Latentes estimados por Mínimos Quadrados em 2 Passos com BEKK(1,1) para Variância Condicional (Erro-Padrão em parênteses).

Os autovalores da matriz de coeficientes acima são 0. 8002 , 0. 9895 e 0. 9310 . Como um dos autovalores é próximo de um, os componentes do VAR são no mínimo, integrados de primeira ordem e como os outros dois autovalores são menores do que um, isso indica, juntamente com a afirmação anterior, que os componentes são no Máximo Integrados de ordem 1.

A Soma de Quadrados dos Resíduos, para a estimação do Modelo com Estrutura para Variância Condicional é 0. 04792 . Isso indica que em relação a soma de quadrados dos resíduos, este modelo mostra-se superior ao segundo método empregado, Mínimos Quadrados em Dois Passos, porém não é superior a estimação por filtro de Kalman. Assim, a estimação de todos os parâmetros de interesse em um único estágio melhora o ajuste do modelo, indicado pela diminuição da soma de quadrados dos resíduos na estimação por filtro de Kalman. A dinâmica para a Volatilidade Condicional para os Fatores estimados é dada na Tabela 8 a seguir.

t M i 1

m

Ai t i t i Ai j 1

s

Tabela 8: Parâmetros Estimados do BEKK(1,1) para os Fatores Latentes (Erro-Padrão em parênteses)

As Volatilidades estimadas para os Fatores Latentes são dadas na Figura 21 abaixo:

Figura 21: Volatilidades estimadas pelo Modelo BEKK(1,1).

mesmo padrão foi observado para a volatilidade da Curvatura, que captura principalmente incertezas relacionadas ao médio prazo e os rendimentos significativamente aumentaram durante todos os períodos de recessão.

Figura 22: Correlações Condicionais estimadas pelo Modelo BEKK(1,1).

Apresentando variabilidade durante o período de análise, a correlação condicional entre os Fatores Latentes Nível e Curvatura e entre Curvatura e Inclinação, em alguns momentos, superam a correlação condicional entre os Fatores Nível e Inclinação.

Conclusão

Neste trabalho propõe-se a estimação do modelo dinâmico de Nelson-Siegel, como em Diebold e Li (2006). Alguns estudos propõem que este modelo seja estimado em dois passos, porém a estimação dos parâmetros conjuntamente via Filtro de Kalman (Máxima Verossimilhança) é mais eficiente pois evita a estimação do parâmetro de decaimento num primeiro estágio.

Os fatores latentes foram obtidos através do algorítmo de suavizamento do Filtro de Kalman e por Mínimos Quadrados em Dois Passos. Nota-se que estes reproduzem os fatos estilizados citados, como memória e alta variabilidade para taxas com vencimentos mais curtos, porém, a estimação por Filtro de Kalman gerou resultados melhores no que se refere a mínimização da soma de quadrados dos resíduos.

Porém, pretende-se comparar essas estimativas via processos de Cadeias de Markov e Modelos MS-VAR para previsões de ciclos econômicos no Brasil.

Além das estimativas geradas para os fatores nesta seção, utiliza-se também para estimação de ciclos as proxies conhecidas e bastante utilizadas neste tipo de abordagem para Nível,

Estrutura a Termo e Previsibilidade de Ciclos Econômicos

Introdução

Há evidências que a Curva de Juros apresenta um comportamento cíclico e correlacionado com as futuras expansões e recessões econômicas7. Como visto na seção fatos, geralmente a Curva de Juros é positivamente inclinada. Este é o caso observado nos períodos iniciais de expansões econômicas, quando os agentes econômicos esperam um crescimento das taxas de curto prazo. Pelas Teorias de Arbitragem e Preferência de Liquidez, de acordo com Campbell, Lo e Mckinlay (1997) investidores para adquir títulos de longo prazo ao invés de Títulos com vencimento no curto prazo sem risco, exigem um Prêmio de Risco.

Por outro lado, a inclinação da Curva de Juros tende a se tornar horizontal (flat) ou

invertida no final dos períodos de expansão (início de recessão). Uma possível explicação é a existência nestes períodos de Politíca Monetária Restritiva. Outra explicação, pela Teoria das Expectativas, taxas de longo prazo refletem a expectativa dos agentes sobre o futuro das taxas de curto prazo, então a Curva flat ou invertida indicaria que o Mercado espera

uma queda nas taxas de juros reais futuras, dada a probalidade de desempenho econômico mais fraco no futuro.

O interesse sobre o papel das taxas de juros como previsor do nível de atividade econômica notadamente surgiu com o trabalho de Sims (1980). A estimação de um modelo Vetor Autorregressivo com dados americanos, a saber, Nível de Produção Industrial, Índice de Preços no Atacado e estoque de M1, mostrou que o M1 era relevante para a explicar variações do nível de atividade. Porém, ao adicionar a taxa de juros no modelo, M1 tinha seu poder explicativo diminuído e a taxa de juros respondia por 30% da variabilidade daquela variação.

A partir deste trabalho de Sims, muitos outros surgiram para discutir que não somente a taxa de juros era relevante na explicação do nível de atividade, mas também o spread entre

as taxas de juros. Há duas hipóteses sobre as quais o papel do spread pode ser uma variável

7_{Veja, por exemplo, Harvey(1988, 1989); Stock e Watson (1989); Ang, Piazzesi e Wei}

relevante neste contexto. A primeira, Hipótese de Risco de Falência, sobre as expectativas dos agentes acerca da situação econômica no longo prazo, se haverá uma recessão ou expansão da atividade. A segunda, Hipótese de Política Monetária, afirma que o spread é

um bom previsor por conter informações sobre a condução da política monetária.

Existe vasta literatura sobre previsão da Atividade Econômica e Modelos de Escolha Discreta utilizando Estrutura a Termo da Taxa de Juros8. Para esta literatura, modelos de Regressão Linear são utilizados na previsão da taxa de crescimento econômico e os modelos de escolha discreta (Probit e Logit) utilizados para prever a probalidade de recessão econômica, usando basicamente a inclinação da curva. Porém, Ang, Piazzesi e Wei (2006) mostram que a utilização de toda a informação da Curva de Juros pode resultar em estimativas mais precisas do crescimento econômico real. Além disso, as não-linearidades impostas nas fases de transição de um regime para outro, podem capturar mudanças estruturais que podem não ser captadas pelos modelos lineares.

Assim, para comparar os métodos de estimação empregados neste trabalho, sugere-se a estimação de uma relação dinâmica entre o Fator Latente estimado para representar a inclinação da Curva de Juros, a Estrutura a Termo, e uma variável relacionada ao desempenho econômico.

O modelo de comparação resultará, na verdade, em uma estimativa para início e final de recessões, e assim como em outros trabalhos9, terá uma frequência mensal, como mencionado na seção base de dados.

Para a metodologia de comparação, admite-se que o Fator estimado e a variável proxy para

desempenho econômico sigam diferentes processos de Markov, porém mantendo algum tipo de relação. O processo de Markov para o Fator de inclinação estimado para a Curva de Juros representam os ciclos no mercado de títulos, que como mencionado anteriomente, tem relação com os ciclos econômicos, por isso, vem sendo utilizado como um indicador antecedente.

Para fins de comparação com os resultados do modelo, temos as datações oficiais dos ciclos

8_{Harvey (1988,1989), Stock e Watson (1989), Ang, Piazzesi e Wei (2006).}

econômicos no Brasil, fornecidas pelo CODACE.

Portanto, pretende-se identificar o método de estimação mais adequado para descrever o comportamento da Curva de Juros no Brasil, dado a estrutura desenvolvida em Nelson-Siegel (1987) e estendida em Diebold e Li (2006).

Ciclos Econômicos, Curva de Juros e CODACE

O diferencial de juros é frequentemente usado na literatura empírica como um indicador antecedente (Moolman, 2004). Na década de 1990, Estrella e Hardouvelis (1991) foram os primeiros a testar empiricamente o spread como um previsor de ciclos econômicos. O

trabalho mostra que uma inclinação positiva para o spread de taxa de juros implica um

maior crescimento do PIB e que um aumento do spread implica uma redução da

probabilidade de uma recessão quatro trimestres à frente.

Bernard e Gelach (1996) testaram o poder de previsão da Estrutura a Termo nos ciclos econômicos em oito países, usando modelos Probit. Eles concluem que o spread da Curva

de Juros doméstica é estatisticamente significativa para explicar pontos de inflexão das flutuações econômicas e que podem ajudar a fazer previsões futuras de mudanças de estado entre 2 a 5 trimestres.

Estrella e Mishkin (1998) comparam o desempenho de diversas variáveis financeiras, incluindo o spread, o índice de Bolsa entre outros indicadores antecedentes e mostram que

a Estrutura a Termo da Taxa de Juros tem um forte poder de previsão comparativamente aos outros indicadores testados.

Segundo Moolman (2004), a relação entre o ciclo econômicos e a Estrutura a Termo da Taxa de Juros é tal que se a economia estiver em uma fase de crescimento acelerado, de modo que há um consenso geral entre os investidores que a economia está caminhando para uma desaceleração ou recessão no futuro. Portanto, os investidores podem querer se proteger contra recessão e aquisição de ativos financeiros (por exemplo, adquirindo títulos de longo prazo), que irá produzir retornos durante a contração econômica. O aumento da demanda por títulos de longo prazo provoca um aumento no seu preço, o que implica uma redução no rendimento dos títulos de longo prazo. Para financiar estas aquisições, os investidores vendem seus ativos de curto prazo, o que causa um declínio desses preços e, consequentemente,um aumento no rendimento desses ativos. Em outras palavras, se uma recessão é esperada, a longo prazo as taxas de juros irão cair e as taxas de juros de curto prazo subirão. Consequentemente, antes de uma recessão, a inclinação da estrutura a termo se tornará invertida.

Estrutura a Termo com dados diários. Lima e Issler (2002) testaram a Hipótese de Expectativa Racionais para dados mensais. Esses trabalhos concluíram, somente de forma parcial, a favor dessa Hipótese. Porém, Marçal e Valls Pereira (2007), utilizando técnicas de cointegração encontram evidências contrárias a essa hipótese.

O Comitê de Datação de Ciclos Econômicos, CODACE, da Fundação Getúlio Vargas, estabelece uma cronologia de referência para os ciclos econômicos. A metodologia é desenvolvida a partir dos seguintes fatos: cada ponto de máximo local (ponto de pico) do ciclo equivale ao final de um período de expansão, que será seguido, no trimestre seguinte, pelo início de uma recessão; cada ponto de mínimo local (ponto de vale) equivale ao trimestre final de uma recessão, a ser seguido, no trimestre seguinte, pelo início de uma expansão econômica. Os pontos de transição, segundo o relatório do CODACE de Maio de 2009, foram determinados pelo Comitê de acordo com conceitos clássicos de expansão e recessão adaptados às "peculiaridades da economia brasileira".

A figura 23 abaixo representa as datações feitas pelo CODACE no período que compreende o primeiro trimestre de 2000 ao terceiro trimestre de 2009. Segundo as estimativas do Comitê, que utiliza um período maior ao utilizado aqui, 1980 a 2008, o período médio de recessões foi de aproximadamente 6 meses e de expansões 11 meses. A maior fase de expansão durou 21 trimestres entre o terceiro trimestre de 2003 e o terceiro trimestre de 2008, provocando um crescimento acumulado de 30%, medido pelo PIB real trimestral.

Figura 23: Cronologia Trimestral dos Ciclos de Negócios Brasileiros.

consecutivos. A principal variável usada na datação do CODACE foi o Produto Interno Bruto (PIB) trimestral, a preços de mercado, dessazonalizado, calculado pelo IBGE.

Na Figura 23 acima, os períodos considerados como recessões pelo CODACE são, respectivamente, do segundo ao quarto trimestre de 2001; do primeiro ao segundo trimestre de 2003; e a partir do quarto trimestre de 2008. A taxa de crescimento acumulado, de acordo com o IBGE, nestes períodos foram, respectivamente, -1%, -1.7% e -3.6% (este último somente no quarto trimestre de 2008).

O primeiro período considerado como recessão pelo CODACE refere-se ao período entre o segundo e quarto trimestres de 2001. Nesse período, o PIB caiu por três trimestres consecutivos, causado pelos atentados ao World Trade Center e os efeitos do estouro da bolha tecnológica nos Estados Unidos e crise energética no Brasil. A recuperação no fim do ano fez o PIB anual terminar com alta de 1,3%.

O segundo período considerado como recessão pelo CODACE refere-se ao período entre o primeiro e segundo trimestres de 2003. Nesse período a economia brasileira retraiu 1,44% no primeiro trimestre e 0,23% no segundo. Naquele ano, porém, o PIB acabou se recuperando e encerrando com alta de 1,1%. As causas foram, fundamentalmente, a disparada do dólar verificada nos meses anteriores decorrente dos reflexos negativos da forte desaceleração do crescimento da economia mundial sobre a renovação das linhas de crédito para os países emergentes e, particularmente, das expectativas dos agentes econômicos quanto à gestão do endividamento público pelo governo Lula, que tomaria posse em Janeiro de 2003.

O terceiro período considerado como recessão pelo CODACE refere-se ao período entre o quarto trimestre de 2008 e primeiro trimestre de 2009, marcado por intensiva queda do PIB Real brasileiro, com queda total de 3.8%, segundo relatório divulgado em 28 de Dezembro de 2009, sendo, portanto, a maior redução média desde 1980. Para o Comitê, são indicadores do fim da recessão a retomada de expansão por parte da indústria, setor mais afetado pela crise.

Metodologia

Cadeias de Markov

Uma introdução aos conceitos de Cadeias de Markov serão apresentados nesta seção10. O principal resultado desta teoria é que as Cadeias de Markov convergem para uma única distribuição invariante, sendo possível fazer inferência sobre a mesma.

Uma cadeia de Markov é uma série de variáveis aleatórias, X 0 ,X1 ,X2 , . . . , cuja

influência de cada Xi _{,i 0, 1, 2, . . . sobre a distribuição de X}i 1 _{depende somente dos}

valores de Xi _{. Assim, temos que:}

( ) ( )

{

}

(

)

(

)

x x P t

x x x

P + ∈ε = +

onde é algum subconjunto de 0, 1, 2, . . . ,i 1 . Os índices t 0, 1, 2, . . . , são

frequentemente vistos como sucessivos momentos no tempo. O x t _{tem significado}

conhecido como state state das cadeias de Markov, e que neste trabalho possui dimensão

finita.

Uma cadeia de Markov pode ser especificada admitindo uma distribuição marginal para

x 0 - probabilidade inicial dos estados - e uma distribuição condicional para x i 1 _dados

os possíveis valores de (i)

x - a probabilidade de transição de uma estado para outro. Temos

que a probabilidade inicial do estado X como P0 x , e a probabilidade de transição para

o estado x , no momento i 1 , seguir o estado x , no momento i , como Ti x,x . Se

as probabilidades de transição não dependerem do tempo, a cadeia de Markov é dita

estacionária e as probabilidades de transição podem representadas somente por T x,x _.

Utilizando as probabilidades de transição, podemos encontrar a probabilidade de um estado

x ocorrer no momento i 1 , designada por Pi 1 x , a partir das probabilidades

correspondentes no tempo i _{, da seguinte forma:}

Pi 1 x

x

Pi x Ti x,x

(11)

Dadas as probabilidades iniciais P0 , estas determinam o comportamento da cadeia ao

longo do tempo.

As probabilidades no momento i podem também ser consideradas como um vetor linha,

Pi , e as probabilidades de transição no momento i como uma matriz Ti , ou apenas T ,

se a cadeia for estacionária11. Para cadeias estacionárias, Tk

k-ésima potência da matrizT _{refere-se aos k passos das probabilidades de transição, que}

podem ser escritas como Tk x,x _{, resultando, portanto,} Pi P0Ti .

Vetor Autorregressivo com Mudanças Markoviana

(

)

Os Modelos MS-VAR surgem da união de duas ferramentas: VAR introduzido por Sims (1980) e os modelos que utilizam cadeias de Markov para analisar a natureza das mudanças de regime nas séries macroeconômicas, como desenvolvido por Hamilton (1989) sobre ciclos econômicos nos Estados Unidos. Com isso, torna-se possível estimar modelos VAR sujeitos à mudanças de regime.

Na análise de Séries Temporais, a introdução do modelo de Markov-Switching é devido a Hamilton (1988) e Hamilton (1989), este último tendo inspirado as contribuições mais recentes. A classe de modelos MS-VAR fornece uma estrutura conveniente para analisar as representações multivariada com as mudanças de regime. Estes modelos admitem várias estruturas dinâmicas, dependendo do valor da variável de estado, st , que controla o

mecanismo de transição entre os vários estados. Nestes modelos, alguns ou todos os parâmetros podem ser diferentes no que diz respeito ao regime em vigor no instante t .

11_{Uma matriz na qual os elementos são todos não-negativos e o somatório das linhas é igual}

Além disso, os ciclos econômicos são tratados como mudanças de regime comum aos Processos Estocásticos de Séries Temporais Macroeconômicas. Finalmente, o processo MS-VAR condicionado a um processo exógeno está intimamente relacionado a modelos de Espaço de Estado, bem como o conceito de processos duplamente estocásticos introduzido por Tjøstheim (1986).

O Modelo MS-VAR pertence a uma classe mais geral de modelos não-lineares, embora condicional em cada regime o modelo seja linear e apenas um número discreto de regimes seja viável.

Assim, o modelo MS-VAR pode ser escrito, de acordo com Krolzig (2003), como um

processo autorregressivo de Séries Temporais observadas yt y1t,y2t, . . . ,y t T, cujos

parâmetros são incondicionalmente variantes no tempo, mas constantes quando condicionados a uma variável de estado (ou regime) discreta não-observada

st 1, 2, . . . ,m :

( )

( )

(

( )

)

( )

(

( )

)

( )

t s A s y s A s y s B s u

y −µ = 1 ₋1−µ ₋1 +K+ ₋ −µ ₋ + (12)

onde    = = = = = m s s s t m m m t t _{( ,..., ) se}

1 se ) ,..., ( ) ( 1 1 11 1 τ τ µ µ µ µ µ µ

µ , ut é um termo de erro gaussiano

condicionado ao regime st : ut|st NID 0, st . p é a ordem do VAR, m é o

número de regimes não-observados e é a dimensão do vetor de variáveis. Portanto, pode-se denotar este modelo como sendo um MS M VAR p . As funções de transição

nas matrizes dos parâmetros st , A1 st , . . . ,Ap st e st descrevem a

dependência dos parâmetros do VAR em cada regime. A característica importante de um modelo com mudança markoviana é que as realizações não-observadas do regime

st 1, 2, . . . ,m são geradas por um processo estocástico a tempo discreto que pode ser

representado por uma Cadeia de Markov com estados discretos 12, que é definido por suas

12_{A diferença entre os modelos Markovianos e os modelos com limiar Autorregressivo -}

TAR Threshold Autoregressive , STAR Smooth Transition Autoregressive e SETAR Self Exciting Threshold Autoregressive _{- é que nestes modelos a variável}

probabilidades de transição:

(

)

{

}

p _jl

m

l t

t

jl Pr | , 1 1,2,...,

1

1 = = = ∀ ∈

=

∑

=

+ (13)

onde admite-se que a cadeia de Markov é irredutível e ergódica13.

Usualmente, as probabilidades de transição são representadas por um matriz de transição T da seguinte forma:

T

p11 p21 pm1

p12 p22 pm2

p1m p2m pm m

(14)

onde a probabilidade pjl representa a probabilidade de que no instante t 1 a cadeia

mude para o regime l , dado que se encontra no regime j no tempo t.

No modelo descrito pela equação ref: msvar há um salto imediato na média do processo após uma mudança de regime. Freqüentemente, é mais provável assumir que a média se modifica suavemente para um novo nível após a transição de um regime para outro. Nesta

situação, pode-se utilizar um modelo com termo de intercepto, v st , dependendo do

regime. Tem-se, portanto:

( )

( )

( )

( )

t v s A s y A s y B s u

y = + _{1 −1}+K+ ₋ + (15)

Contrariando os modelos VAR lineares e parâmetros invariantes no tempo, a forma média

13_{Existem várias definições para o termo "ergódica". Para alguns autores a propriedade}

finita é que o estado inicial é eventualmente esquecido, para outros é que a média ao longo do tempo converge independentemente do estado inicial. Em geral, estas definições não são equivalentes. Algumas definições excluem cadeias com estados transitórios com