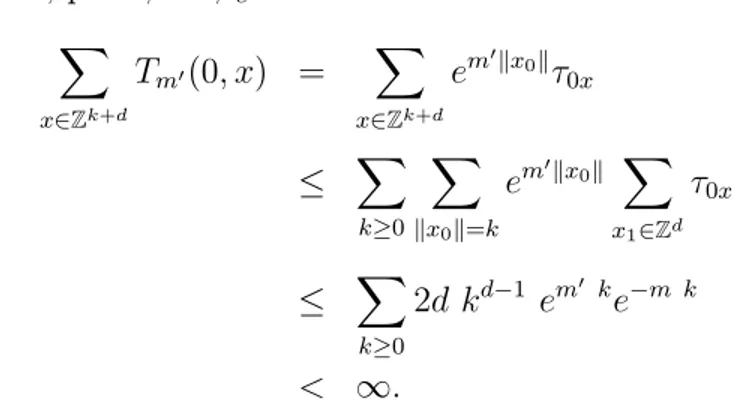Comportamento assintótico das funções de correlação para modelos de spins e percolação de alcance misto

(1)

Comportamento Assintótico das Fun¸cões de Correla¸cão para Modelos de Spins e Percola¸cão

de Alcance Misto

Leandro Martins Cioletti

(2)

Comportamento Assint´

otico das Fun¸

c˜

oes de Correla¸

c˜

ao para

Modelos de Spins e Percola¸

c˜

ao de Alcance Misto

Leandro Martins Cioletti

Orientador: Prof. Gast˜ao de Almeida Braga

(3)

(4)

(5)

Agradecimentos

(6)

Sum´

ario

1 Resumo 5

2 Abstract 6

3 Introdu¸c˜ao 7

4 Modelos de Percola¸c˜ao de alcance misto em Zk+d ₉

4.1 Preliminares . . . 9

4.2 Resultados fundamentais e fase subcr´ıtica . . . 11

4.3 Comportamento assint´otico da conectividade . . . 12

4.3.1 Cotas inferiores . . . 12

4.3.2 Cotas Superiores . . . 14

5 Modelos de Spins com intera¸c˜oesde alcance misto em Zk+d ₂₂ 5.1 Preliminares . . . 22

5.2 Desigualdades de Correla¸c˜ao para sistemas de spins ferromagn´eticos . . . . 23

5.3 Comportamento assintótico Intermediário da correla¸cão spin-spin . . . 27

5.3.1 Cotas inferiores . . . 28

5.3.2 Cotas superiores em altas temperaturas . . . 29

5.3.3 Cotas superiores no regimeχ(β)<∞ . . . 38

6 Apˆendice 45

(7)

1 Resumo

(8)

2 Abstract

(9)

3 Introdu¸

c˜

ao

Nesta tese de doutorado determinamos o comportamento assintótico, em termos de cotas superiores e inferiores no limite de grandes distâncias, de fun¸cões de conectividade e cor-rela¸cão, nos modelos de percola¸cão e spins, respectivamente, em redes hipercúbicas Zk+d

com intera¸c˜oes de alcance misto (exponencial na dire¸c˜ao Zk _{e polinomial de alcance} _R

na dire¸c˜ao Zd_{), na fase subcr´ıtica. Os resultados mais importantes deste trabalho s˜ao os}

Teoremas 2.1, 3.3 e 3.4.

No Cap´ıtulo 2 introduzimos, detalhadamente, emZ0+d _{(sem intera¸c˜ao exponencial e com}

intera¸cão polinomial de alcance infinito) os modelos de percola¸cão de elos independentes em um caso particular de alcance misto. Por meio de cotas inferior e superior, determina-mos o comportamento assintótico da conectividade de dois pontos em fun¸cão da distância entre eles em toda fase subcr´ıtica, sendo esse o conteúdo do Teorema 2.1. Este resultado é uma extensão para Z0+d₍_{d >}_{1) dos resultados de Aizenman e Newman [1] para} _d_{= 1.}

Na prova do teorema nós usamos a desigualdade de Hammersley-Simon-Lieb,veja [2, 3, 4], e a expansão em escalas múltiplas desenvolvidas em [1]. Este cap´ıtulo está baseado na referência [5], onde a prova do Teorema 2.1 foi publicada.

No Cap´ıtulo 3 introduzimos os sistemas de spins ferromagnéticos com intera¸cõesde al-cance misto e estudamos o comportamento da correla¸cão spin-spin. Neste cap´ıtulo são considerados modelos de alcance misto emZk+d_{mais gerais do que os tratados no Cap´ıtulo}

2. A generaliza¸cão é feita em dois sentidos, tanto permitimos o alcanceR tomar qualquer valor emN_∪₊_∞_{, quanto admit´ımos decaimento polinomial com corre¸cões logar´ıtmicas na}

dire¸c˜aoZd _{sendo estes mais gerais que aqueles apresentados no Cap´ıtulo 2. Este cap´ıtulo}

´e baseado no trabalho [6], submetido para publica¸c˜ao.

(10)

Os resultados obtidos no Cap´ıtulo 2 são baseados em desigualdades de correla¸cão [2, 3, 4] e nas técnicas de análise em escalas múltiplas que foram introduzidas por Aizenman e Newman em [1] para modelos de percola¸cão de elos de longo alcance uni-dimensionais. A escolha de introduzir inicialmente os modelos de percola¸cão, e estes com um tipo especial de alcance misto, foi feita com intuito de deixar mais claro como fazer funcionar o método de escalas múltiplas tanto no caso em que as intera¸cões são mistas quanto quando a rede não é mais uni-dimensional. A teoria de perturba¸cão constru´ıda no Cap´ıtulo 3 também pode ser aplicada aos modelos de percola¸cão. A op¸cão por apresentá-la no contexto de sistemas de spins esta relacionada a importância de tais sistemas onde as constantes de acoplamento ou intera¸cão são não-invariantes por transla¸cão. A introdu¸cão do parâmetro

R no Cap´ıtulo 3 trás novidades ao comportamento assintótico das correla¸cões, algo que denotamos por comportamento assintótico intermediário. Este fenômeno é observado quando a distância dos pontos correlacionados é comparado à escalaR da intera¸cão. Nas preliminares dos cap´ıtulos 2 e 3 introduzimos de forma rigorosa os modelos de percola¸cão e de spins, respectivamente. Nas se¸cões que se seguem são discutidos, separadamente em cada um dos cap´ıtulos, os resultados relevantes da teoria e o contexto em que estão inseridos os problemas abordados neste trabalho.

(11)

4 Modelos de Percola¸

c˜

ao de alcance misto em

Z

k+d

4.1 Preliminares

Nesta se¸c˜ao apresentamos os chamados, modelos de percola¸c˜ao de alcance misto emZk+d_.

A defini¸cão geral, de um modelo de percola¸cão de elos envolve basicamente, a defini¸cão de um grafo e uma medida sobre as poss´ıveis configura¸cões (no nosso caso de elos) que podemos obter a partir deste grafo. Neste cap´ıtulo estudamos modelos de percola¸cão cujo o grafo é dado por L_{= (}Zk+d_,B_{), onde cada elemento} _u_∈ Zk+d _{é da forma} _u _{= (}_u₀_{, u}₁_),

com u0 ∈Zk eu1 ∈Zd e o conjunto B ´e formado por determinados pares n˜ao ordenados

(u, v) tais que u, v _∈Zk+d _e _u₆₌_v_{. A especifica¸c˜ao mais precisa de quem ´e o conjunto} B

´e dada mais abaixo.

Os elementos de Zk+d _{s˜ao chamados de} _s´ıtios _ou _v´ertices_{, enquanto que os elementos}

de B _{são chamados de} _elos_{. A especifica¸cão} _{alcance misto}_{, está ligada à medida de}

pro-babilidade que é definida no conjunto de configura¸cões de elos do grafo citado acima. A medida de probabilidade usual para os modelos de percola¸cão de elos independentes é constru´ıda a partir de uma lista de probabilidades, i.e., indicamos individualmente qual a probabilidade de cada elo em B _{estar ”aberto”ou ”fechado”(será definido abaixo).}

Neste cap´ıtulo estaremos interessados em modelos de alcance misto com decaimento po-linomial. De maneira mais precisa, a cada elo b= (u, v)_∈Zk+d_×Zk+d_{, associamos uma}

variável aleatória ωb, independentemente, tomando valores em {0,1} e com distribui¸cão de Bernoulli tal que a probabilidade de ωb = 1 é dada por

puv =puv(β)≡βJuv, (1)

onde β _∈[0,1] e para ε >0, Juv ´e dado por

Juv =           

2

1 +_ku1−v1kd+ε

se u0 =v0 e u1 6=v1;

1 se u1 =v1 e ku0−v0k= 1;

0 caso contr´ario.

(2)

Se ωb = 1 então dizemos que o elo b está aberto, caso contrário dizemos que o elo b está

fechado.

Com a lista de probabilidades dada acima por (1) e (2), a constru¸c˜ao da medida de pro-babilidade segue de forma usual, veja [7]. Tomamos Ω_{≡ {}0,1_}B

(12)

Figura 1: exemplo de configura¸c˜ao em Z1+2_.

seguinte propriedade: existem n0 ∈N, b1, . . . , bn0 ∈B e v1, . . . , vn0 ∈ {0,1} tais que para todo elemento ω _∈C temos ωbi =vi para todo i= 1, . . . , n0.

A seguir daremos algumas defini¸cões básicas que são necessárias para a compreensão deste texto. Diremos que γ é um caminho unindo dois s´ıtios distintos x e y, se γ é um conjunto de elos formado por uma seqüência finita (b1, . . . , bn), com bi = (xi, xi+1) ∈ B

e x1 = x, xn+1 = y. Dada uma configura¸c˜ao ω ∈ Ω e um caminho γ, diremos que

γ esta aberto (na configura¸cão ω) se ωe = 1 para todo bi ∈ γ. Dada uma confi-gura¸cão ω, diremos que dois pontos x, y ∈ Zk+d_{, estão no mesmo} _aglomerado_{, se exite}

um caminho γ aberto ( na configura¸c˜ao ω) unindo estes dois pontos. Diremos que um ponto est´a conectado ao infinito, se o aglomerado deste ponto for infinito. O evento

{ω ∈ Ω : existe um caminho aberto conectando x a y} ser´a denotado por {x ↔ y} e definimos a fun¸c˜ao conectividade entre dois pontos x, y _∈ Zk+d _por _τ_xy _≡ _P₍_{_x _↔ _y_}_).

Para cada subconjunto S _⊂ Zk+d_{, definimos} _τS

xy ≡ P({x ↔ y dentro de S}), que é a probabilidade de x estar conectado a y por um caminho cujo os vértices dos elos deste caminho estão todos contido em S. Também necessitaremos da no¸cão de distância nos grafos que estamos trabalhando. Usaremos a distância induzida pela normaL1 _em _Zk+d_, i.e., kxk ≡ |x1|+. . .+|xk+d|.

Uma grandeza de fundamental importância neste cap´ıtulo será a susceptibilidade que é definida por:

χ(β)≡ X

u∈Zk+d τ0u

e relacionado a ela, estaremos tamb´em interessados em

πc ≡sup{β ∈[0,1] :χ(β)<∞}.

(13)

4.2 Resultados fundamentais e fase subcr´ıtica

Vamos recordar alguns fatos sobre percola¸cão de longo alcance definidos por (1) e (2). Seja θ(β, ε)_≡Pβ,ε(_{0_{↔ ∞}}), a probabilidade da origem estar num aglomerado infinito. Sek+d ≥2 é a dimensão do espa¸co então, por compara¸cão com o modelo de percola¸cão de primeiros vizinhos e para qualquer ε > 0, existe βc = βc(d, ε), tal que θ(β, ε) = 0 se

β < βc eθ(β, ε)>0 se β > βc.

Para k = 0 e d = 1 é conhecido que a existência de βc depende de ε. Se ε > 1, o sistema possui pelo menos um aglomerado infinito com probabilidade positiva indepen-dentemente da escolha do parâmetro β. E portanto dizemos que este sistema não exibe transi¸cão de fase em termos da fun¸cãoθ(β, ε), veja [8]. Já no caso 0_≤ε _≤1, existe umβc como descrito no paragrafo anterior. Assim estes sistemas apresentam transi¸cão de fase com respeito a θ(β, ε), veja [9].

A transi¸c˜ao de fase pode ser medida em termos da susceptibilidade χ(β). Usando a desigualdade de FKG (4), podemos verificar facilmente que πc(d, ε) ≤ βc(d, ε). Para a classe de modelos que estamos trabalhando podemos provar, na verdade que vale a igual-dade. Este importante fato foi demonstrado independentemente por Aizenman e Barsky em [10] e por Menshikov [11].

Nos sistemas que exibem transi¸cão de fase, como os que são estudados aqui, é comum separarmos o espa¸co de parâmetros β em três subconjuntos, o primeiro dado por β < βc, que chamamos de fase subcr´ıtica. Em seguida β = βc que é chamado de ponto cr´ıtico e por último o que compreende os valores maiores queβc, que é chamado de fase supercr´ıtica.

Para os sistemas que abordamos neste trabalho, com k +d _≥ 2, o estudo do compor-tamento assintótico da fun¸cão de conectividade τxy é feito por técnicas completamente distintas em cada uma destas três fases:

1)Na fase supercr´ıtica a fun¸cãoτxy não decai como fun¸cão dos pontosxey, veja [7]. Isto é basicamente justificado pela existência de um único aglomerado infinito quase certamente; 2) Na fase cr´ıtica, i.e., no ponto cr´ıtico, o comportamento assintótico da fun¸cão τxy, pelo menos para dimensões altas, foi obtido viaexpansão em la¸cos, maiores detalhes veja [12].

´

(14)

estudo em dimensões maiores ou iguais a um é feito em [5] para modelos com alcance misto e os resultados são objeto da seguinte se¸cão.

4.3 Comportamento assint´

otico da conectividade

Nesta se¸cão enunciamos o principal resultado deste cap´ıtulo, o Teorema 4.1. Este teorema nos dá informa¸cão sobre o comportamento assintótico da fun¸cão conectividade em modelos de alcance misto em toda a fase subcr´ıtica.

Teorema 4.1. Suponha que β < βc e considere o modelo de percola¸c˜ao de longo alcance

com puv dado por (1) e Juv dado por (2). Ent˜ao existem constantes positivas C1, C2, m1

e m2 que dependem de β tais que

C1 e−m1kx0−y0k

1 +kx1−y1kd+ε ≤

τxy ≤

C2 e−m2kx0−y0k

1 +kx1−y1kd+ε

(3)

para todo x, y ∈Zk+d_.

O teorema acima nos diz, em certo sentido, que a probabilidadepuvdita o comportamento assint´otico da fun¸c˜ao conectividade em toda a fase subcr´ıtica.

A prova deste resultado será dividida em duas partes: 1) primeiro mostramos como obter a cota inferior afirmada em (3). Na verdade este resultado é facilmente obtido pela desigualdade de FKG (4) em toda a fase subcr´ıtica e sua prova será inclu´ıda porque as ideias envolvidas na sua demonstra¸cão serão usadas no Cap´ıtulo 3.

Em seguida apresentamos a prova da cota superior. Para a prova desta cota, precisamos lan¸car mão de outros tipos de desigualdades de correla¸cão. A mais importante delas é a desigualdade de Hammersley-Simon-Lieb, veja [2, 3, 4]. Nesta parte da prova é mostrado como adaptar o argumento de escalas múltiplas introduzido por Aizenman e Newman, para modelos uni-dimensionais, aos modelos de alcance misto em quaisquer dimensões.

4.3.1 Cotas inferiores

Como mencionado anteriormente, a desigualdade de FKG é a principal ferramenta para obten¸cão da cota inferior do Teorema 4.1. No que segue apresentamos todos elementos para que possamos enunciar precisamente esta desigualdade. A prova desta desigualdade pode ser encontrada, por exemplo, em [7]. Em seguida passamos para a demonstra¸cão da cota inferior do Teorema 4.1.

(15)

Considere o espa¸co de probabilidade (Ω,F, P), onde Ω≡ {0,1}B

,F é aσ-álgebra gerada pelos cilindros eP a medida produto obtida à partir das probabilidadespuv sobre os cilin-dros. Usaremos a nota¸cãoIE, para indicar a fun¸cão caracter´ıstica de um conjuntoE ∈ F. Para podermos enunciar de forma precisa o teorema da desigualdade de FKG, vamos pre-cisar introduzir uma ordem parcial no conjunto Ω das configura¸cões. Esta ordem parcial é definida da seguinte maneira: dadosω1, ω2 ∈ Ω, diremos que ω1 ≤ω2, se ω1(b)≤ω2(b)

para todo b ∈ B_{. Diremos que um} _evento _E _{∈ F} _{´e crescente se} _I_E(_ω₎ _≤ _I_E₍_ω′_{) sempre}

queω_≤ω′_{. Por outro lado, diremos que}_E_{´e um evento decrescente se seu complementar,}

Ec_{, é um evento crescente. De maneira mais geral, uma} _{variável aleatória} _f _{: Ω} _→ _R_, num espa¸co mensurável (Ω,F) é dita crescente se f(ω)≤f(ω′_{) sempre que} _ω_≤_ω′_.

Teorema 4.2(Desigualdade de FKG). Sef, g são variáveis aleatórias crescentes tais que

R

f2_{dP <}_∞ _e R

g2_{dP <}_∞_{, ent˜ao}

Z

f dP

Z

g dP _≤

Z

f g dP. (4)

Para a prova desta desigualdade veja [7].

Obs: Uma conseqüência imediata e importante deste resultado é que se A e B são eventos crescentes, então

P(A) P(B)_≤P(A_∩B). (5)

Agora que estamos de posse da desigualdade de FKG, podemos apresentar a prova da cota inferior de (3).

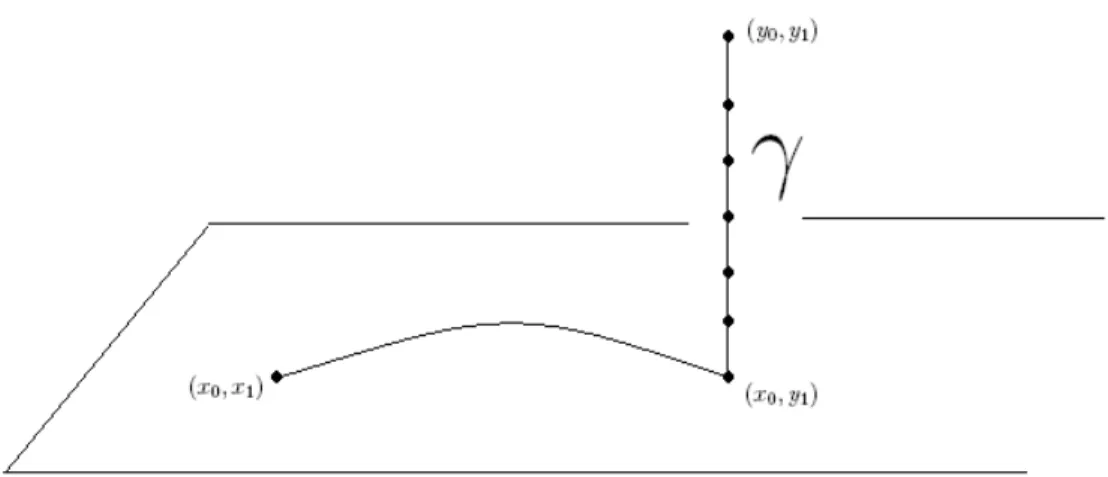
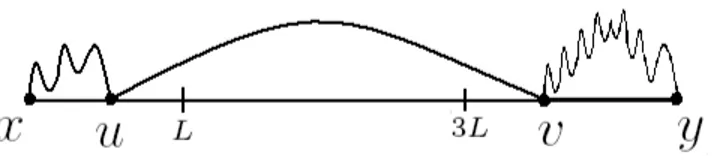
Sejam x, y ∈ Zk+d _{pontos distintos. Considere} _u _≡ ₍_x₀_{, y}₁₎ _∈ Zk+d _e _γ _qualquer

ca-minho de comprimento m´ınimo, de elos de primeiros vizinhos conectando u a y, veja Figura 2.

Considere os eventos A={O elo (x, u) est´a aberto} e B ={γ est´a aberto}.

´

E fato que A∩B ⊂ {x ↔ y} e, já que A e B são eventos crescentes, podemos, após tomar probabilidades destes eventos, usar a desigualdade de FKG para concluir que

P(A) P(B)_≤P(A_∩B)_≤P(_{x_↔y_}) =τxy.

Usando as defini¸c˜oes (1) e (2), podemos calcular explicitamente P(A) e P(B). Donde conclu´ımos que

C1 e−m1kx0−y0k

1 +_kx1−y1kd+ε ≤

τxy, (6)

(16)

Figura 2: sistema uni-dimensional.

4.3.2 Cotas Superiores

Esta é a parte mais delicada da prova do Teorema 4.1. Desenvolveremos esta se¸cão na seguinte sequência: 1) Iniciamos com a introdu¸cão os elementos necessários para a compreensão do enunciado da desigualdade de Van den Berge e Kesten conhecida como desigualdade de BK; 2) e em seguida usamos esta desigualdade para apresentarmos uma prova, simples e curta, da desigualdade de Hammersley-Simon-Lieb. Optamos por provar H-S-L neste trabalho, pelo menos para o modelo de percola¸cão, por que ela é na verdade o pilar para constru¸cão do método de escalas múltiplas, já mencionadas anteriormente, e também da teoria de perturba¸cão que é constru´ıda no cap´ıtulo seguinte para modelos de spins em altas temperaturas.

Desigualdade de BK

Sejam n um inteiro positivo, Γ = {0,1}n_, _G _{o conjunto de todos os subconjuntos de} Γ eP a medida produto em (Γ,_G) determinada por densidades p(i), i.e.,

P = n Y i=1

µi

onde µi({0}) = 1−p(i) e µi({1}) = p(i).

Dados ω∈Γ eS ⊂ {1, . . . , n}, usaremos a nota¸c˜ao

[ω]S ≡ {ω˜ ∈Γ : ˜ωi =ωi ∀i∈S}

para designar o cilindro determinado por ω e S. Para E1, E2 ∈ G, definimos o evento ocorrˆencia disjuntade E1 eE2, denotado porE1◦E2, como

(17)

Para maiores detalhes e prova do teorema enunciado abaixo, veja [7] e referˆencias contidas.

Teorema 4.3 (Desigualdade de BK). Se E1 e E2 s˜ao eventos crescentes em G, ent˜ao

P(E1◦E2)≤P(E1)P(E2). (7)

Observa¸cões: A desigualdade, como enunciada acima pede que o espa¸co amostral Γ seja composto de um número finito de cópias do conjunto _{0,1_}. Portanto não poderia ser diretamente aplicada aos modelos de percola¸cão de alcance misto que estamos tratando neste trabalho. Porém podemos mostrar que é poss´ıvel obter a desigualdade de BK para a medida de probabilidade dos modelos de percola¸cão de elos independentes de alcance misto, se restringirmos os eventos E1 e E2 à uma certa classe de eventos na

σ-álgebra gerada pelos cilindros. Em particular esta desigualdade é verdadeira para os eventos que aparecem na prova da desigualdade de Hammersley-Simon-Lieb, para maiores detalhes veja [7]. Note que a opera¸cão de ocorrência disjunta é uma opera¸cão associativa e, portanto, procedendo uma indu¸cão formal sobre o número de conjuntos, podemos generalizar a desigualdade de BK para qualquer número finito de eventos crescentes. Este fato será usado na prova de H-S-L.

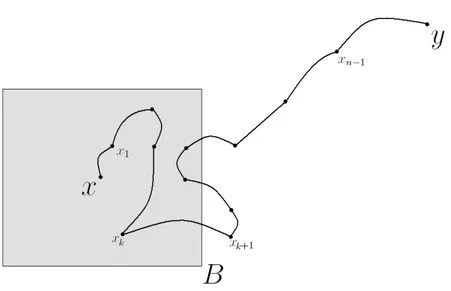
Teorema 4.4(Desigualdade de Hammersley-Simon-Lieb).Dados x, y ∈Zk+d_e_B _⊂Zk+d

tais que x∈B e y∈Bc _ent˜ao

τxy ≤ X

u∈B v∈Bc

τ_xuB puv τvy. (8)

Prova: Dados x, y ∈ Zd_{, considere uma configura¸c˜ao} _ω _{∈ {}_x_↔ _y_}_{. Ent˜ao sabemos que}

existe um caminho aberto em ω conectando x a y. Vamos denotar este caminho por γ e nomear seus elos como segue abaixo:

γ =_{(x, x1),(x1, x2), . . . ,(xn−1, y)}.

Para a configura¸c˜ao ω tomada acima e para o caminho γ, definimos o n´umero

k ≡min{ i ; (xi, xi+1)∈γ, xi ∈B e xi+1 ∈Bc}

que ´e exatamente a primeira sa´ıda do caminhoγ do conjunto separadorB, veja Figura 3. Continuamos o argumento pondo u=xk ev =xk+1. Pela defini¸c˜ao de k temos

ω∈ {x↔u dentro de B} ◦ {(u, v) est´a aberto} ◦ {v ↔y}.

Observe agora que para qualquer ω dado em {x ↔ y} a constru¸cão acima nos permite sempre encontrar u e v, que claramente dependerão de ω de forma que a rela¸cão de pertinência mostrada acima seja verdadeira. Portanto temos

{x_↔y_{} ⊂} [ u∈B v∈Bc

(18)

Figura 3: Os pontos xk e xk+1.

Tomando a probabilidade em (9) e usando a desigualdade de BK, conclu´ımos a prova do teorema.

A seguir desenvolvemos o argumento que prova a cota superior em (3). Primeiro po-demos verificar que a susceptibilidade, χ, pode ser escrita como

χ=X n≥0

X

kx0k=n X x1∈Zd

τ0x.

Aqui usamos apenas a nota¸cãox= (x0, x1)∈Zk+de queτ0xé não negativo para podermos reordenar a soma.

Por hip´otese,χ <∞. Assim, dadoλ ∈(0,1), existe umn0 ∈Ntal que, para todon ≥n0,

temos

X

kx0k=n X x1∈Zd

τox < λ.

Vamos fixar aten¸c˜ao na soma

X x1∈Zd

τox,

para algum valor fixado de kx0k> n0. Neste caso, para cada um dos termos desta soma,

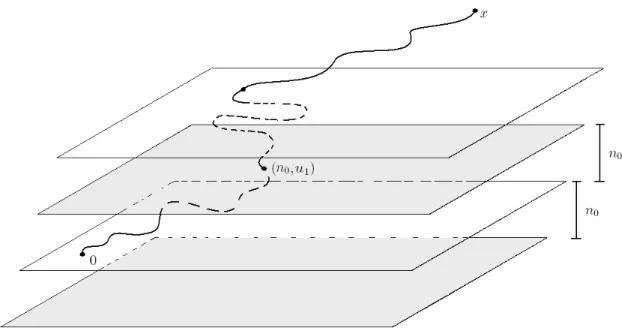
podemos aplicar a desigualdade de Hammersley-Simon-Lieb, comB =_{x_∈Zk+d _:_k_x₀_{k ≤} n0}(veja Figura 4) e obtemos, pela defini¸c˜ao (1) depuv, a seguinte desigualdade

τox ≤

X

kuk=n0

v∈Bc:kv₀−u₀k=1,u₁₌v₁

(19)

Figura 4: cilindro horizontal.

J´a quekv0−u0k= 1 eu1 =v1 temospuv =β em todos os termos da soma acima. Usando a invariˆancia translacional deste modelo e que χ < _∞, podemos afirmar que τox → 0 quando x → ∞ e portanto que existe um ponto v ∈ Zk+d_{, com} _k_v₀_k ₌ _n₀ _{+ 1 tal que a}

desigualdade τvx ≤τvx é válida em todas as parcelas da soma acima. Destas observa¸cões segue que

τ0x ≤β τvx X

kuk=n0

τou

≤βλτvx.

Observe que a desigualdade acima pode ser iterada_⌊kx0k/(n0+ 1)⌋vezes, onde⌊·⌋denota

o menor inteiro maior ou igual ao argumento. Feito isto, obtemos

τox ≤(βλ)⌊kx0k/(n0+1)⌋τv∗_x

para algumv∗ _∈_Zk+d_{. Agora, somando sobre}_x

1 ∈Zdem ambos membros da desigualdade

acima obtemos

X x1∈Zd

τ0x ≤χ(βλ)⌊kx0k/(n0+1)⌋

=χe−mkx0k_,

com e−m _{= (}_βλ₎1/(n0+1)_{. Isto mostra que as parcelas da susceptibilidade decaem}

expo-nencialmente na “dire¸c˜ao temporal”.

(20)

que denotaremos por Tm′(x, y). O papel dos parâmetros bem como sua defini¸cão são

estabelecidos logo abaixo. A introdu¸cão desta nova fun¸cão, pode ser encarada como uma maneira de projetarmos um sistema misto em um sistema de longo alcance. Além disto, esta simples idéia irá nos permitir estender a análise em escalas múltiplas, conhecida an-teriormente para sistemas de longo alcance com decaimento polinomial, para os sistemas de alcance misto.

Seja δ positivo tal que δ < m e defina m′ ₌ _m₋_δ_{. Mostraremos agora uma}

desigual-dade do tipo Hammersley-Simon-Lieb para a fun¸c˜ao conectividesigual-dade modificadaTm′(x, y)≡

em′_k_x0₋_y0_k

τxy, para B dado porB =CL(x)≡ {z ∈Zk+d :kx1−y1k ≤L}.

Para L >1 e y_∈Cc

L(x), temos da desigualdade de Hammersley-Simon-Lieb que

τxy ≤ X

u∈_CL(x)

v∈Cc_L(x)

τxu puv τvy.

Observe que

Tm′(x, y) = em

′_k_x0₋_y0_k

τxy

≤ em′kx0−y0k X u∈_CL(x)

v∈Cc_L(x)

τxu puv τvy

≤ X

u∈_CL(x)

v∈Cc_L(x)

em′kx0−u0kτxu puv em

′_k_y0₋_v0_k

τvy,

onde, na primeira desigualdade usamos Hammersley-Simon-Lieb e na segunda desigual-dade usamos a defini¸cão de puv para concluir que para todas as parcelas não nulas que aparecem no lado direito da desigualdade, temos necessariamente u0 = v0. Da última

desigualdade e da defini¸c˜ao de Tm′, segue imediatamente que

Tm′(x, y)≤

X

u∈_CL(x)

v∈Cc_L(x)

Tm′(x, u) p_uv T_m′(v, y).

Em analogia com a conectividade modificada, introduzimos tamb´em a susceptibilidade modificada

χm′ ≡

X x∈Zk+d

Tm′(0, x).

(21)

χ(β), ´e finita. De fato, paraβ < βc

X x∈Zk+d

Tm′(0, x) =

X x∈Zk+d

em′kx0kτ0x

≤ X

k≥0

X

kx0k=k

em′kx0k X

x1∈Zd τ0x

≤ X

k≥0

2d kd−1 em′ ke−m k

< ∞.

Esta propriedade da susceptibilidade modificada ser´a usada, para provar que a fun¸c˜ao

Tm′(x, y) apresenta decaimento polinomial na dire¸cão Zd em fun¸cão da distância de x₁

a y1 at´e o ponto cr´ıtico. A partir de agora nosso argumento segue de perto as id´eias

introduzidas na se¸c˜ao 3 de [1]. Fixados x, y _∈Zk+d_e _L_{≡ k}_x₁₋_y₁_k_/_{4, j´a mostramos que}

vale a seguinte desigualdade

Tm′(x, y)≤

X

u∈_CL(x)

v∈Cc_L(x)

Tm′(x, u) p_uv T_m′(v, y).

Agora, decompomos a soma em v, do lado direito da desigualdade acima, em dois so-mat´orios e atrav´es das grandezas que definiremos logo abaixo, cotamos cada uma das destas somas separadamente:

X

u∈_CL(x)

v∈Cc_L(x)∩C₃_L(x)

Tm′(x, u)p_uv T_m′(v, y) +

X

u∈_CL(x)

v∈Cc_L(x)∩Cc₃_L(x)

Tm′(x, u)p_uv T_m′(v, y). (10)

A idéia que esta por trás desta decomposi¸cão é agrupar os termos em que u e v estão distantes, no máximo, um múltiplo fixo da escala L e usar a hipótese que χm′ <∞ para

obtermos cotas superiores que ser˜ao dependentes de Tm′ e que v˜ao para zero quando L

vai para infinito. Nos demais termos usamos a finitude de χm′ e as propriedades de p_uv

para as parcelas remanescentes. Nas figuras abaixo representamos graficamente os termos gerais da primeira e segunda parcela, respectivamente, de (10).

(22)

Figura 6: uma representa¸cão gráfica do segundo somatório de (10).

Definindo

T_m′(L)≡sup{T_m′(0, u) :u∈C_Lc(0)} e γ_L ≡

X

u∈_CL(x)

v∈Cc_L(x)

Tm′(x, u) p_uv,

o primeiro termo do lado direito de (10) pode ser cotado por T_m′(L/2)γ_L enquanto o

segundo ´e limitado por

2d+ε ₂_βχ2

m′

1 +_kx1−y1kd+ε

,

o que nos fornece a cota

Tm′(x, y)≤ 2

d+ε ₂_βχ2

m′

1 +_kx1−y1kd+ε

+γLTm′(L/2).

Usando que χm′ <∞, para β < β_c e que P

up0u <∞, podemos afirmar que

X u,v∈Zk+d

Tm′(x, u) p_uv<∞.

Por outro lado, segue da defini¸c˜ao de γL que

γL≤ X u,v∈Zk+d

Tm′(x, u)p_uv I_C

L(x)(u) ICLc(x)(v),

donde conclu´ımos, depois de usar o teorema da convergˆencia dominada de Lebesgue(ver apˆendice), que γL→0 quando L→ ∞.

Para α ∈ (0,2−(d+ε)_{), existe um} _L

0 > 0, tal que γL < α para todo L ≥ L0.

Consi-derando ent˜ao L > L0 seque que

T_m′(L)≤ 2

d+ε ₂_βχ2

m′

1 +_kx1−y1kd+ε

+αT_m′(L/2). (11)

Iterando (11) nvezes, comn sendo o menor inteiro para o qualL2−n_≤_L

0, obtemos para

todoL > L0

T_m′(L)≤

2βχ2

m′Pn_j₌₀−1(α2d+ε)j

1 +kx1−y1kd+ε

+αn_T

(23)

Notando queTm′(x, y)≤T_m′(L), T_m′(L′)≤χ_m′, para qualquer L′ >0 e que

αn ≤2−(d+ε)n = 1 1 +Ld+ε

(1 +Ld+ε₎ 2(d+ε)n ≤

2_·2d+ε 1 +_kx1−y1kd+ε

L

2n

≤ 2(2L0)

d+ε

1 +_kx1−y1kd+ε

,

podemos concluir que, para β < βc eC2 = 2χm′(βχ_m′Pn_j₌₀−1(α2d+ε)j+ (2L₀)d+ε) que

τxy ≤

C2 e−m

′_k_x0₋_y0_k

1 +kx1−y1kd+ε

vale para qualquer m′ ₌ _m₋_δ_{. Finalmente, j´a que} _δ _{pode ser tomado arbitrariamente}

(24)

5 Modelos de Spins com intera¸

c˜

oesde alcance misto

em

Z

k+d

5.1 Preliminares

Nesta se¸c˜ao vamos considerar modelos de Mecˆanica Estat´ıstica do equil´ıbrio com Hamil-tonianos dados por:

HΛ({~σ}) =−

X u,v∈Λ

JuvR ~σu·~σv, (12)

onde u = (u0, u1) ∈ Λ ⊂ Zk+d e ~σu = (σu(1), σu(2), . . . , σu(N)) ∈ Ω ⊂ RN é uma variável aleatória, chamada de spin. Associamos também a esta variável uma distribui¸cão de probabilidade, comumente chamada de distribui¸cãoa priori. Usaremos a nota¸cãodµ(~σu) para nos referir a distribui¸cão a priori no s´ıtio u. As constantes JR

uv, s˜ao chamadas de

constantes de acoplamento ou tamb´em intera¸c˜ao. Neste trabalho estaremos interessados

apenas no caso em que as constantes de acoplamento são não negativas. Neste caso, dizemos que a intera¸cão éferromagnética. Os modelos que denominamosferromagnéticos

de alcance misto s˜ao definidos por intera¸c˜oesda forma:

J_uvR =     

Ku1v1 se u0 =v0 eku1 −v1k< R;

1 se u1 =v1 eku0 −v0k= 1;

0 caso contr´ario.

(13)

Em (13), consideraremos sempre que as constantes Ku1v1 est˜ao bem definidas para todos

u1, v1 ∈ Zd. O parâmetro R que aparece na defini¸cão acima é chamado alcance da

in-tera¸cão. Permitiremos que 1≤R ≤ ∞, embora nosso principal interesse, neste cap´ıtulo, seja em valores finitos do parâmetro R, porém arbitrariamente grandes.

Observa¸cão: Agora as intera¸cões que definem os modelos de alcance misto são mais gerais do que as apresentadas no cap´ıtulo anterior. Além da introdu¸cão do alcance R, agora as itera¸cões, na dire¸cão espacial, i.e., as constantes de acoplamento Ku1v1 não são necessariamente da forma Ku1v1 = 2/(1 +ku1−v1kd+ε).

Dados o Hamiltoniano (12) e o inverso da temperatura β, assumiremos que a medida

a priori, em cada s´ıtiou∈Zk+d_, _dµ₍_~σ_u_{) ´e tal que}

Z

Ω|Λ|

N Y k=1 Y i∈A

(σ_i(k))ai

e|−βHΛ({~σ})|Y i∈Λ

dµ(~σi)<_∞ (14)

(25)

em mecˆanica estat´ıstica

hf(_{~σ_})_iΛ =

Z

Ω|Λ|

f(_{~σ_}) e−βHΛ({~σ})Y i∈Λ

dµ(~σi)

Z

Ω|Λ|

e−βHΛ({~σ})Y i∈Λ

dµ(~σi)

, (15)

assumiremos a existˆencia do limite termodinˆamico

hf(_{~σ_})_{i ≡} lim

|Λ|→∞hf({~σ})iΛ (16)

para fun¸c˜oes cont´ınuas f suportadas em subconjuntos finitos A⊂ Zd_{. Diremos que} _h·i_´e

o estado de Gibbs associado ao Hamiltoniano (12) a temperatura 1/β com condi¸c˜oes de fronteira livre.

5.2 Desigualdades de Correla¸

c˜

ao para sistemas de spins

ferro-magn´

eticos

Neste cap´ıtulo, temos dois objetivos: primeiro apresentamos, para uma grande classe de modelos de spins vetorial tomando valores em RN _{(os valores de} _N _{ser˜ao especificados}

mais tarde) com intera¸cões ferromagnéticas, uma teoria de pertuba¸cão convergente para valores pequenos de β, que nos fornece o comportamento assintótico intermediário da correla¸cãospin-spinh~σx·~σyi, como fun¸cão dekx−yk; Em seguida estendemos os resultados perturbativos, os quais são válidos para pequenos valores deβ, à todos os valores deβpara os quais χ(β), a susceptibilidade do modelo, é finita. Ambos os resultados são baseados em desigualdades de correla¸cão e para modelos escalares (N=1), a condi¸cão χ(β) < ∞

significa que os resultados são válidos até o ponto cr´ıtico, veja [13].

O que estamos denotando por comportamento assintótico intermediário neste texto, é o comportamento da fun¸cão _h~σx·~σyi quando o comprimento kx−yk é comparável comR. Para um sistema em um volume finito Λ eJR _{da forma (13), tudo resume-se a considerar}

kx1 − y1k, a distˆancia entre x e y na dire¸c˜ao Zd, quando kx1 − y1k << R << |Λ|1/d

ou quando R << _kx1 −y1k < |Λ|1/d. Para as medidas a priori dµ(~σ) para os quais s˜ao

válidas as desigualdades de correla¸cão, nosso objetivo é encontrar uma classe de intera¸cões ferromagnéticasJR_{tal que, pelo menos para valores pequenos de}_β_{, a correla¸cão spin-spin} se comporte assintoticamente como a intera¸cão, i.e.

h~σx·~σyiΛ ≈

      

CKx1y1e−mkx0−y0k se kx1−y1k<< R <<|Λ|1/d, (17)

˜

(26)

para algumas constantes C,C˜ e m, uniformemente em Λ. Em particular, esperamos que as cotas acima sejam v´alidas tamb´em quando_|Λ_{| → ∞}e, possivelmente, quandoR _{→ ∞}.

´

E importante ressaltar, que Kx1y1 pode ter um decaimento mais do geral do que polino-mial.

Se R >> _|Λ_|1/d _{então não existe comportamento intermediário já que, neste caso, o} sistema é essencialmente de longo alcance. Dentro do contexto de mecânica estat´ıstica de intera¸cões de longo alcance, a questão se as correla¸cões se comportam como a in-tera¸cão ou não já é uma questão antiga. Para modelos de gases na rede, no regime de baixa atividade, foi provado em [14] que potenciais invariantes por transla¸cão que decaem exponencialmente (polinomialmente) levam ao decaimento das correla¸cões exponencial (polinomial), o mesmo também sendo válido para sistemas de spins clássicos (N=1), em altas temperaturas. Veja [15, 16] para spins limitados e ilimitados, respectivamente. Os efeitos de condi¸cões de contorno e ou campo magnético externo na taxa de decaimento das correla¸cões para modelos escalares N = 1 é estudado em [17] e os resultados sobre a taxa de decaimento das correla¸cões são recuperados, no regime de altas temperaturas, para o caso polinomial. Intera¸cões mistas como as que consideramos neste trabalho, veja (13), foram levadas em conta em [18], no estudo de correla¸cões em modelos de cristais quânticos e a cota superior (17), comR =∞e

Ku1v1 =

2

1 +ku1−v1kd+ε

, com ε >0, (19)

foram obtidas no regime perturbativo, entre outros resultados. Intera¸cões mistas foram também estudadas em [5], onde o método de análise em múltiplas escalas de Aizenanm e Newman [1] foi adaptado para determinar o comportamento assintótico da conectividade até o ponto cr´ıtico, para a percola¸cão de elos independentes d-dimensional. O caso de spins em redes unidimensionais, Z0+1_{, foi considerado em [19], com} _N _{= 1}_{, . . . ,}_{4 e com} K dado por (19), e a cota superior (17) foi obtida na fase desordenada.

(27)

Para R≥1, definimos

kKRk ≡max{sup u1∈Zd

X

{v1∈Zd_:_k_v1₋_u1_k_<R_}

Ku1v1, sup v1∈Zd

X

{u1∈Zd_:_k_u1₋_v1_k_<R_}

Ku1v1},

kJR_{k ≡} ₂_k ₊_k_KR_k _e _k_J_{k ≡} _sup

RkJRk. Quando Ku1v1 ´e invariante por transla¸c˜ao, as quantidades definidas acima se reduzem a normaL1 usual. Vamos assumir por enquanto

apenas que _kJR_k _< _∞ _{e mais tarde nos restringiremos adequadamente à classe de} in-tera¸cões que lidaremos neste trabalho. Vamos assumir também que a medida a priori

dµ(~σu) é uma medida par, i.e.,µé invariante pela aplica¸cãoh(x) = −xque seja da forma

dµ(~σu)≡e−f(k~σuk2) _d~σ

u. (20)

Dado o Hamiltoniano (12) e notando queJuv~σu·~σv ≤Juv(k~σuk2+k~σvk2)/2, uma condi¸cão suficiente para (14) seja válido é que pelo menos uma, das duas condi¸cões abaixo, seja verificada:

F1) f(k)₍₀₎_>_{0 para algum} _k _≥_2;

F2) f(x) = ax+b, a >0 e β satisfazendo βkJR_k_{< a}_.

Sob a hipótese de ferromagnetismo, positividade das correla¸cões é assegurada pela pri-meira desigualdade de Griffiths. As desigualdades de Griffiths I (G-I) e II (G-II), veja [20, 21], são respectivamente dadas por

0≤ hσAiΛ, N ≥1 (21)

e

h~σx·~σyiΛh~σu·~σviΛ ≤ h(~σx·~σy)(~σu ·~σv)iΛ, (22)

para qualquer Λ_⊂Zk+d _{e qualquer conjunto finito} _A _⊂_{Λ, com} _σ_A ₌QN

k=1

Q i∈A(σ

(k)

i )ai. G-II como enunciada acima não se encontra na sua forma mais geral, mas está na forma que a utilizaremos neste trabalho. As condi¸cões na medida a priori e em N para que as desigualdades G-I e G-II sejam válidas são as seguintes:

G1) Se a medida a priori for par então G-I será válida para qualquer N _≥ 1, veja [22] e referências lá citadas;

G2) se a medida a priori for par então G-II será válida para N = 1, veja [22]. A de-sigualdade também é verdadeira para N = 2 para medidas a priori uniformes, veja [23]. Dunlop e Newman [24] mostraram que G-II também é válida paraN = 2 quando a medida a priori considerada é par e da forma

dµ(~σ) =e−f(r)_{dr dθ} _e

Z

R

ebr2

(28)

onde~σ = (rcosθ, rsinθ). Note que se se G2 for satisfeita então G1 também será satisfeita. Para modelos com Hamiltonianos (12), a desigualdade de Simon-Lieb (S-L) [3, 4, 25] para modelos com N = 1,2 afirma que

h~σx·~σyi ≤β X

u∈B v∈Bc

h~σx·~σuiB JuvR h~σv·~σyi, (24)

onde B _⊂Zk+d _e _x_∈_B_, _y_∈ _Bc_{. A desigualdade S-L , na forma acima , foi provada em}

[26] assumindo que a medida a priori satisfaz `as hip´oteses G2 e

SL1) para N = 1 com medida a priori (20), sendo tal que f′′₍_t₎_≥_{0 para} _t_≥_0;

SL2) paraN = 2 com medida a priori (20) ef(t) sendo um polinˆomio cujos os coeficientes de grau maior ou igual a um sejam positivos.

Teorema 5.1. As desigualdades de Griffiths I, II e Simon-Lieb s˜ao satisfeitas pelos

es-tados de Gibbs (16) se: N = 1 e se a medida a priori satisfizer a condi¸c˜ao SL1; N = 2 e

a medida a priori satisfizer SL2 .

A segunda desigualdade de Griffiths implica que os valores esperados são fun¸cões não decrescentes do volume. Portanto se um estado h·i satisfizer as hipóteses do teorema acima, então ele também satisfará a desigualdade de Simon [3]

u∈B v∈Bc

h~σx·~σui JuvR h~σv·~σyi (25)

Al´em do mais, para Hamiltonianos dados por (12), Aizenman e Simon [27] provaram que

SL3) para N = 2,3,4 e medida a priori uniforme na esfera unitária, uma versão um pouco mais forte que (25) também é válida

h~σx·~σyi ≤(β/N) X

u∈B v∈Bc

h~σx·~σui JuvR h~σv·~σyi.

Note que, em particular, a desigualdade de Simon (25) tamb´em ´e satisfeita.

Teorema 5.2. A primeira desigualdade de Griffiths e a desigualdade de Simon s˜ao sa-tisfeitas pelos estados de Gibbs (16) se: as hip´oteses do Teorema 5.1 forem verificadas ;

N = 3,4 com spins uniformemente distribu´ıdos na esfera.

Obs: Considere um sistema de spins cujo Hamiltoniano é dado por (12) e Juv simétrica e não negativa (Juv =Jvu ≥0). Se a medida a priori dµ(~σ) for dada por

(29)

com λ >0 e a ∈ R_{, então as hipóteses do Teorema 5.1 são satisfeitas. Em particular, o}

teorema vale quando dµ(~σ) = e−λ(k~σk2₋₁₎2

d~σ e, tomando o limite λ _{→ ∞}, este resultado também se estende ao modelo de Ising (N = 1) e XY (N = 2) com intera¸cão de longo alcance. Com N = 1 usando o ”truque”de Griffiths [28] que consiste em escrever um modelo de spins S como uma superposi¸cão de modelos de Ising, pode se mostrar que o Teorema 5.1 é satisfeito para spins discretos uniformemente distribu´ıdosσ_{∈ {−}2S,₋2S+ 2, . . . ,0, . . . ,2S−2,2S}. Além do mais, tomando o limite quandon→ ∞sobre os estados

h·in com medida a priori dada por

dµn(~σ) = e−k~σk2n d~σ,

conclu´ımos que o Teorema 5.1 é também satisfeito se os spins são uniformemente dis-tribu´ıdos na bola unitáriak~σk ≤1, com N = 1,2.

5.3 Comportamento assint´

otico Intermedi´

ario da correla¸

c˜

ao

spin-spin

Nesta se¸cão vamos considerar modelos de spinsN-dimensional na rede (k+d)-dimensional e vamos inicialmente mostrar, para valores pequenos deβ, (17) e (18) em termos de cotas inferior e superior, para N = 1,2 e para uma determinada classe de medidas a priori que será especificada mais a frente. Por enquanto, vamos mencionar apenas que nosso resultado para N = 1 cobre o modelo de Ising, com spin discreto em _{−2S,₋2S + 2, . . . ,2S_} uniformemente distribu´ıdo e também com spin cont´ınuo no intervalo [₋S, S]; (17) e (18) em termos de cotas superiores, para N = 3,4 e para spins uniformemente distribu´ıdos na esfera unitária.

Na Subse¸cão 5.3.2, para obter a cotas superiores desenvolvemos uma teoria de pertuba¸cão que não impõe a intera¸cão JR _{a restri¸cão de ser invariante por transla¸cão. Ela deverá} satisfazer a algumas outras hipóteses, veja hipóteses H1-H3 na Se¸cão 5.3.2. Para β não necessariamente pequeno mas tal que χ(β)<_∞, obtemos (17) e (18) em termos de cotas superiores, até a temperatura cr´ıtica, sob as hipóteses H4-H7, veja Subse¸cão 5.3.3, em particular, vamos exigir invariância translacional da intera¸cão JR_.

(30)

5.3.1 Cotas inferiores

Proposi¸c˜ao 5.1. Considere o estado de Gibbs (16) `a temperatura inversa β e suponha

que a medida a priori (20) satisfa¸ca a condi¸c˜ao G2. Ent˜ao, existem constantes positivas

m0, C e C˜, que podem depender de β e JR _{tais que, para todo} _{x, y} _∈_Zk+d

h~σu·~σvi ≥   

CKx1y1e−m0kx0−y0k se kx1−y1k< R,

˜

Ce−mkx−yk _se _k_x

1−y1k ≥R.

Prova: A condi¸cão G2 implica que as desigualdades G-I e G-II são satisfeitas. Vamos supor inicialmente que a variável de spin seja limitada, i.e., _|~σ_{| ≤} S. Fazendo uma expansão em série de Taylor do numerador, usando a hipótese de ferromagnetismo e que

dµ(~σ) ´e par, podemos afirmar que

h~σx·~σy(S2− kσk2z)iΛ ≥0

para qualquer x, y, z _∈Λ. Ent˜ao segue de (22) e da desigualdade acima que

h~σx·~σziΛh~σz·~σyiΛ ≤S2h~σx·~σyiΛ.

Fixados x, y _∈ Λ, tomamos z = (y0, x1) e consideramos primeiro kx1−y1k < R. Seja Γ

um conjunto de elos de primeiros vizinhos formando um caminho retil´ıneo que inicia em (x0, x1) e vai at´e (y0, x1) e sejabo elo com pontos terminaisz ey. Ent˜ao segue, novamente

de (22) e da desigualdade acima, que

h~σx·~σziΓh~σy·~σzib ≤S2h~σx·~σyiΛ.

Já que_h~σx·~σziΓé o valor esperado tomado sobre um sistema uni-dimensional de intera¸cão

de primeiros vizinhos e h~σy ·~σzib envolve integra¸cão sobre as variáveis ~σz e ~σy, é fácil concluir que, para pequenos valores deβ, existem constantes positivasCem0, que podem

depender de β, R, JR _e_S _{tais que}

CKx1y1e−m0kx0−y0k ≤ h~σx·~σyiΛ.

Consequentemente, também vem da monotonicidade que a cota inferior acima continua válida para todos os valores de β para os quais os estados de Gibbs estão bem definidos.

Para o caso _kx1−y1k ≥R, apenas substitua b no argumento acima por Γ1, conjunto dos

elos de primeiros vizinhos formando um segmento retil´ıneo com pontos terminais z ey e assim podemos verificar que

Ce−m0kx0−y0ke−m1kx1−y1k ≤ h~σx·~σyiΛ.

Para o caso de spins ilimitados e kx1−y1k < R, vamos estabelecer a cota inferior pelo

(31)

s´erie de taylor de h~σx ·~σyiΓ, em torno de β = 0, e em seguida usando que dµ(~σ) ´e par

obtemos a seguinte cota inferior

h~σx·~σyiΓ≥

Y

(u,v)∈Γ

βJ_uvR

R

Ω|σ (1)

0 |2dµ(~σ0)

R

ΩeβkJ

R_kk_~_σ0_k2

dµ(~σ0)

!

=CKx1y1e−m0kx0−y0k,

onde C = e−m0 _{´e a raz˜ao entre as integrais acima. Observe que} _m

0 > 0 para qualquer

β >0 por que a raz˜ao entre as integrais ´e sempre menor do que um.

5.3.2 Cotas superiores em altas temperaturas

Vamos come¸car esta se¸cão caracterizando as intera¸cõesJR _{que iremos considerar. Vamos} assumir que JR _{satisfazem às seguintes hipóteses:}

H1) positividade de K: _kJR_k_>₂_k_{, ou equivalentemente,} _k_KR_k_>_0;

H2) limita¸c˜ao local: dados x1, y1 ∈ Zd, existe uma constante positiva C3, que n˜ao

depende de x1 e y1, tais que

Ku1v1 ≤C3Kx1y1 para todo u1, v1 ∈Zd com ku1−x1k ≤1, kv1−y1k ≤1;

H3) hip´otese de convolu¸c˜ao: para todo x1, y1 ∈Zd, existe uma constante positiva C2,

que n˜ao depende dos pontos x1 ey1, tais que

X u1∈Zd

Kx1u1Ku1y1 ≤C2Kx1y1.

Os dois lemas que são apresentados na sequência nos permitem exibir explicitamente um exemplo de uma intera¸cão que satisfaz H1,H2 e H3. Como veremos abaixo, o Lema 1 é um resultado muito mais forte do que precisamos para justificar a hipótese H1. Olhando com cuidado, notamos que este lema prova H1 para os núcleos do tipo (19) em todas as escalas e não somente na escala L = 1 como é pedido em H1. A hipótese H3 para os núcleos da forma (19) é obtida pelo Lema 2. Depois da prova destes dois resultados, mostramos também outras fam´ılias de intera¸cões para as quais são válidas H1 e H3 por simples modifica¸cão dos argumentos que mostraremos agora.

Lema 1. Sejam x, y _∈Zd_{, com} _k_x₋_y_k_{> L/}₂_{, onde} _L _≥₂√_d _{´e dado. e} _K_uv _{dado por}

(19). Ent˜ao, existem constantes C1 =C1(L) e C2 =C2(L) tais que

C1

1 +ku−vkd+ε ≤Kuv ≤

C2

1 +ku−vkd+ε, (26)

(32)

Prova: Suponha inicialmente que L/2 < kx − yk ≤ L. Ent˜ao BL(x) ∩BL(y) 6= ∅

e portanto _ku₋v_k não pode ser maior que duas vezes o comprimento da diagonal do hipercubo para todo u_∈BL(x) ev _∈BL(y). Já que u₆=v então_ku₋v_{k ≥}1 e junto com as observa¸cões acima temos portanto

kx₋y_k

L ≤1≤ ku−vk ≤2

√

dL_≤4√d_kx₋y_k. (27)

Ent˜ao a desigualdade (26) ´e satisfeita com C1 = (4

√

d)−d−ε _e_C

2 = 2Ld+ε.

Agora, se kx−yk > L ent˜ao BL(x)∩BL(y) = ∅ e existe um inteiro n = n(L) tal que

Ln _< _k_x₋_y_{k ≤} _Ln+1_{. Se} _n _{= 1 poderia acontecer de termos} _k_u₋_v_k _{= 1 para algum}

u_∈BL(x) e algum v _∈BL(y). De qualquer forma a cota inferior dada em (27) cont´ınua sendo v´alida se substitu´ımos L por L2_{, nos dando agora a nova constante} _C

2 = 2L2(d+ε).

Para a cota superior, ainda no caso n = 1, basta procedermos como ´e mostrado na desigualdade (28) abaixo:

1

2Lkx−yk ≤ Ln

2 ≤L n

−√dL_{≤ k}u₋v_{k ≤}Ln+1+√dL_≤2Ln+1 _≤2L_kx₋y_k, (28)

onde, para a segunda e quinta desigualdades, usamos a hip´otese L _≥ 2√d e n _≥ 2. A desigualdade (26) segue ent˜ao com C1 = (2L)−d−ε e C2 = (2L)d+ε. Portanto segue que a

desigualdade (26) ´e v´alida em geral com as constantes C1 = 2(2L)−d−ε e C2 = 2L2(d+ε).

Lema 2. Seja Kuv dado por (19). Ent˜ao X

u∈Zd

Kxu Kuy ≤

C3

1 +_kx₋y_kd+ε (29)

para todo x, y ∈Zd_{, com} _C₃ _{= 2}d+2+ε_k_K_k_.

Prova: Seja D=kx−yk. Observe que X

u∈Zd

Kxu Kuy≤

X

ku−xk≤D/2

Kxu Kuy+

X

ku−yk>D/2

Kxu Kuy.

Note que se _ky₋u_{k ≤}D/2 ent˜ao

Kxu ≤

2

1 + (D/2)d+ε ≤

21+d+ε 1 +Dd+ε

PondoC3 = 2d+2+ε, temos

X u∈Zd

Kxu Kuy ≤

C3(2kKk)−1

1 +_kx₋y_kd+ε  

X

ku−yk≤D/2

Kxu+

X

ku−xk>D/2

Kuy  

≤ C3

(33)

Obs: As hipóteses H1 e H2 são, em geral, facilmente verificadas, enquanto H3 requer algumas estimativas. Por exemplo, para Ku1v1 dado por (19) verificamos a validade de H3, com C2 = 2d+2+ǫkKk1, pelo Lema 2. Outro exemplo é

Ku1v1 =

2

(2 +_ku1−v1k)dlnp(2 +ku1−v1k)

, (30)

com p > 1. E neste caso, C2 = 2d+pkKk1.

Agora estamos em condi¸c˜oes de enunciar o principal teorema desta se¸c˜ao

Teorema 5.3. Considere o estado de Gibbs (16) `a temperatura inversaβ e com constantes

de acoplamento JR _{satisfazendo as hip´oteses colocadas acima H1 `a H3. Seja} _S2 _>₀ _tal

que_h~σu·~σvi ≤S2 para todou, v ∈Zk+d. Ent˜ao, sob as hip´oteses do Teorema 5.1, existem

constantes positivas β0, m e C tais que, para todo x, y _∈Zk+d

h~σu·~σvi ≤   

CKx1y1e−mkx0−y0k se kx1−y1k< R, (31)

S2e−2mRkx−yk se kx₁−y₁k ≥R, (32)

sempre que β < β0.

Obs 1: As constantesβ0,meCdependem deβ,R,S2 ekJRke elas ser˜ao explicitamente

determinadas na prova do teorema.

Obs 2: Por hipótese JR _{é simétrica e se} _dµ₍_~σ_{) satisfaz às hipóteses do Teorema 5.1} então as desigualdades G-I, G-II e S-L são válidas. Portanto os modelos de spins menci-onados nas observa¸cões que sucedem o Teorema 5.2, com intera¸cõesdadas por (19) e (30) satisfazem às hipóteses do Teorema 5.3, em particular, _h~σx·~σyi ≤S2. Portanto, segue do Teorema 5.3 que a correla¸cão spin-spin destes modelos decae como (31) e (32), paraβ pe-queno. Junto com as cotas inferiores fornecidas pela Proposi¸cão 5.1 obtemos informa¸cões sobre o comportamento da correla¸cão spin-spin, em termos de cotas inferiores e superio-res. Para sistemas de spins ilimitados satisfazendo as hipóteses do Teorema 5.3, antes de podermos concluir que as cotas (31) e (32) são válidas devemos verificar a existência de uma constante S2 _{tal que} _h_~σ

x·~σyi ≤ S2. Isto normalmente é uma tarefa dif´ıcil. Vamos mencionar apenas que cotas superiores na correla¸cão spin-spin podem ser obtidas sob a hipótese de convexidade(ver apêndice) da fun¸cãof (20) para sistemas ferromagnéticos de longo alcance com Hamiltoniano da forma₋P

i,jJij(σi−σj)2, usando estimativas do tipo ”chessboard”, veja [29].

(34)

1. Primeiro mostramos que h~σx·~σyi decai exponencialmente na “dire¸c˜ao temporal”Zk para β pequeno e _kx0−y0k >0, i.e., se β ´e pequeno existe uma constante positiva

m0 =m0(β) tal que

h~σx·~σyi ≤S2 e−m0kx0−y0k.

Em seguida provamos o decaimento exponencial das correla¸c˜oes na “dire¸c˜ao espacial”Zd_,

i.e., se β é pequeno e sekx1−y1k> R, onde R é o alcance da intera¸cão JR, então,

h~σx·~σyi ≤S2 e−

m₀

R kx1−y1k.

Ambos decaimentos s˜ao obtidos por sucessivas aplica¸c˜oes da desigualdade S-L. Mul-tiplicando ambos os membros das duas desigualdades acima e tomando a raiz qua-drada temos (32) para β pequeno e _kx1−y1k> R:

h~σx·~σyi ≤S2 e−

m₀

2Rkx−yk.

2. A prova de (31) é feita por indu¸cão no número de vezes que aplicamos a desigualdade S-L. Fixadosxeyiremos mostrar, que para cada inteironque, existem fun¸cões não negativas h~σx·~σyi(k), k = 1, . . . , n e R(x,yn) tais que

h~σx·~σyi ≤ n X

k=1

h~σx·~σyi(k)+R(x,yn),

onde, para β pequeno,

R(_xyn) ≤ h~σx·~σyi(n)+R(xyn+1), R(xyn) ≤Cβn

e

h~σx·~σyi(n)≤C βn Kx1y1 e−m0kx0−y0k.

´

E ent˜ao claro como provar (31) a partir das desigualdades acima.

Sob as hipóteses do Teorema 5.1 as desigualdades G-I, G-II e S-L são válidas. Após usar a hipótese _h~σx ·~σui ≤ S2 para todo x, u ∈ Zk+d e a desigualdade de Simon-Lieb com

B =_{x_}, obtemos

h~σx·~σyi ≤βS2

X u∈Zk+d_\{_x_}

J_xuR h~σu·~σyi. (33)

Para z = (z0, z1) ∈Zk+d, defina o hiperplano Hz0 ≡ {u ∈Zk+d : u0 = z0}, que

interpre-taremos como “ hiperplano horizontal na altura z0”. Ent˜ao, observe que, pela defini¸c˜ao

(13) de JR_{, a soma em} _u _{de (33) ´e restrita aos pontos} _u_∈_H

x0 tais que ku1 −x1k< R e

(35)

da base canˆonica deRk_{. Entre estes pontos, seja} _u_{um ponto onde o m´aximo de} _h_~σ_u_·_~σ_y_i

´e atingido. Ent˜ao podemos concluir de (33) que

h~σx·~σyi ≤βS2kJRkh~σu·~σyi. (34)

Pela defini¸c˜ao do ponto u, podemos aplicar sucessivamente a desigualdade acima, pelo menos (kx0−y0k −1) vezes. Este procedimento nos leva `a seguinte desigualdade

h~σx·~σyi ≤(βS2kJRk)kx0−y0kh~σu·~σyi. (35)

Para β < β1 ≡1/(S2kJRk) e m >0 tal que e−m =βS2kJRk, segue de (35) que

h~σx·~σyi ≤S2e−mkx0−y0k, (36)

que ´e a cota superior exponencial (31).

Agora suponha que kx1−y1k ≥R. Pelo mesmo argumento dado acima, podemos aplicar

iterativamente a desigualdade (34), pelo menos⌊kx1−y1k/R⌋ −1 vezes, onde⌊·⌋ denota

o menor inteiro maior ou igual ao argumento. E portanto obter para β < β1

h~σx·~σyi ≤S2e−

mkx₁−y₁k

R .

Multiplicando (36) pela desigualdade acima e tomando a raiz quadrada temos

h~σx·~σyi ≤S2e−

m

2R(kx0−y0k+kx1−y1k),

que ´e a cota (32).

Se u 6= y então (35) nos sugere que a cota superior (36) pode ser melhorada. Mesmo que tivéssemosu=y poder´ıamos ainda tentar melhorar esta cota porque não exploramos ainda o poss´ıvel decaimento na dire¸cão Zd_{. Para terminar a prova do teorema vamos}

assumir, a partir de agora, que kx1 − y1k < R e mostraremos que ainda temos uma

corre¸cão Kx1y1 ao decaimento exponencial (36), como afirmado em (31). A prova será feita usando sucessivas aplica¸cões da desigualdade de Simon-Lieb, junto com uso da cota (36), a hipótese de limita¸cão local H2 e a hipótese de convolu¸cão H3.

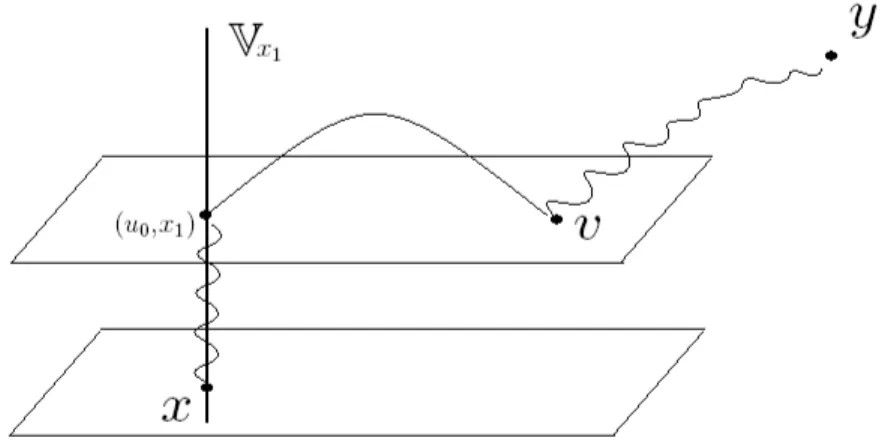
Defina o hiperplano V_z1 _{≡ {}_u _∈ Zk+d _:_u₁ ₌ _z₁_}_{, que interpretamos como o “hiperplano}

vertical de largura z1”, e tome B = Vx1 em (24). Da desigualdade de Simon-Lieb segue que

u∈V_x

1

v∈Vc_x

1

h~σx·~σuiV_x

1 J R

uvh~σv·~σyi. (37)

Segue da defini¸c˜ao de JR

(36)

Figura 7: Representa¸c˜ao em diagrama do lado direito de (37)

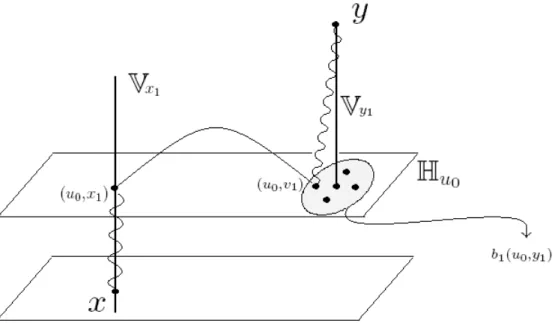
Observe que se x1 6= y1 então (u0, y1), a proje¸cão de y sobre o hiperplano Hu0, é um ponto em Vc

x1 ∩Hu0. Seja b1(u0, y1) ≡ {v ∈ Vcx1 ∩Hu0 : kv1 −y1k = 1} e b∗1(u0, y1) ≡

Vc

x1 ∩ Hu0 −b1(u0, y1). Destas observa¸c˜oes e de (36) com kJRk = 2k (observe que os

valores esperados s˜ao tomados em redes Zk+0_{), temos}

h~σx·~σuiV_x

1 ≤S

2_e−m′_k_x0₋_u0_k

, (38)

onde e−m′

= 2kS2_{β <}_{1, que, quando substitu´ıdo em (37), nos d´a}

h~σx·~σyi ≤βS2 X u∈V_x

1

e−m′kx0−u0k X

v∈Vc x₁∩Hu0

J_uvR_h~σv ·~σyi ≡ h~σx·~σyi(1)+R(1)xy,

onde

h~σx·~σyi(1)≡βS2 X u∈V_x

1

e−m′kx0−u0kX

v∈b1(u0,y1)

J_u1v1R _h~σv ·~σyi

e

R(1)

xy ≡βS2 X u∈V_x

1

e−m′_k_x0₋_u0_kX v∈b∗

1(u0,y1)

JR

u1v1h~σv·~σyi. (39)

Encontraremos agora uma cota superior para _h~σx ·~σyi(1) cuja a dependˆencia em x, y ´e similar a que temos no lado direito de (31). Usando que

kx0−y0k ≤ kx0−v0k+kv0−y0k,

vem de (36) que, para β < β1,

h~σv·~σyi ≤S2e−mky0−v0k ≤S2e−mky0−x0k+mkx0−u0k. (40) Nas parcelas que definem _h~σx·~σyi(1), temos u ∈ Vx1 e v ∈ b1(u0, y1), portanto u1 =x1,

kv1 −y1k ≤1 e segue ent˜ao de H2 que

(37)

Figura 8: Representa¸c˜ao em diagrama de h~σx·~σyi(1)

que, quando substitu´ıdo em _h~σx·~σyi(1), junto com (40) e assumindo que β < β1, nos d´a

h~σx·~σyi(1) ≤(2dβC3S4)Kx1y1e−mky0−x0k X u∈V_x

1

e−m′kukemkuk.

Recordando que e−m ₌ _βS2_k_JR_k _{e que de H1,} _k_JR_k _> ₂_k_{, a soma no lado direito da} desigualdade acima ´e igual a

X u∈Zk

2k

kJR_k kuk

≡C4 <∞,

nos levando a seguinte cota superior

h~σx·~σyi(1)≤(2dβS4C3C4)Kx1y1e−mky0−x0k.

Observe que o lado direito acima nos fornece o comportamento enunciado em (31). Agora vamos mostrar que R(1)xy é uma perturba¸cão de pequena ordem quando analisamos sua dependência com rela¸cão ax, y. Aplicando-se a desigualdade de Simon-Lieb a cadahσvσyi, que aparece na defini¸cão de Rxy(1), juntamente com (38) obtemos a seguinte cota

R(1)

xy ≤β2S4 X u∈V_x

1

e−m′_k_u0₋_x0_kX v∈b∗

1(u0,y1)

JR u1v1

X w∈V_v

1

e−m′_k_v0₋_w0_k X z∈Vc

v₁∩Hw0

JR

w1z1h~σz ·~σyi !

(38)

Fixamos w _∈ V_v1 _{e decompomos a soma acima, em} _z_{, em dois termos, como foi feito}

na lado direito de (39), assim ficamos com

R(1)_xy _{≤ h}~σx·~σyi(2)+Rxy(2),

onde

h~σx·~σyi(2) ≡β2S4 X u∈V_x

1

e−m′kx0−u0k X

v∈b∗

1(u0,y1)

J_u1v1R X

w∈V_v

1

e−m′kv0−w0kX

z∈b1(w0,y1)

J_w1z1R h~σz·~σyi !

e

R(2)_xy _≡β2S4 X

u∈V_x

1

e−m′kx0−u0kX

v∈b∗

1(u0,y1)

J_u1R_v1 X

w∈V_v

1

e−m′kw0−v0k X

z∈b∗

1(w0,y1)

J_w1R_z1_h~σz·~σyi !

.

Em sequˆencia, vamos mostrar que h~σx·~σyi(2) ´e da forma O(β2)Kx1y1exp(−mkx0−y0k) e

que R(2)xy ´e uma pequena perturba¸c˜ao com respeito a esta cota.

Se w _∈ V_v1 _ent˜ao _w₁ ₌ _v₁ _{enquanto se} _z _∈ _b₁₍_w₀_{, y}₁_{) ent˜ao} _k_z₁₋_y₁_{k ≤} _{1. Isto significa}

que, de H2

J_wzR =Kw1z1 ≤C3Kv1y1. Tamb´em, da desigualdade

kx0−y0k ≤ kx0−u0k+ku0 −z0k+kz0 −y0k,

e de (36) temos, para β < β1

(39)

para todo u0, z0 ∈ Zk. Finalmente, observando que v1 = w1 se w ∈ Vv1, temos das observa¸c˜oes acima e da defini¸c˜ao de _h~σx·~σyi(2) que

h~σx·~σyi(2) ≤ (2dβ2S6C3)e−mky0−x0k

X u∈Zk

e−m′kukemkuk

!2 X v∈H_u

0

Kx1v1Kv1y1

≤ (2dC2C3)(βC4)2(S2)3Kx1y1e−mky0−x0k,

onde usamos a hipótese de convolu¸cão H3 na obten¸cão da última desigualdade. Na verdade é importante enfatizar que H3 é o ingrediente chave para estabelecer a cota superior

Kx1y1exp(−mkx0−y0k) durante todo o processo de intera¸c˜ao, que j´a deve estar claro neste

ponto: para mostrar que R(xyn) é uma perturba¸cão de ordem pequena com respeito a esta cota superior , nós aplicamos a desigualdade S-L às correla¸cões que aparecem na defini¸cão deRxy(n) e separamos a soma que vem da aplica¸cão desta desigualdade em duas partes, uma a qual mostraremos, usando a hipótese convolutiva H3, ser O(βn+1₎_K

x1y1exp(−mkx0−

y0k) e outra, o resto, que é apenas uma pequena perturba¸cão com respeito à grandeza

anterior. Portanto o processo iterativo nos d´a a seguinte cota

h~σx·~σyi ≤ n X

i=1

h~σx·~σyi(i)+R(xyn), (41)

onde, para todo n _≥2,

h~σx·~σyi(n) ≤(2dC2C3)n−1(βC4)n(S2)n+1Kx1y1e−mky0−x0k

e

R(_xyn) _≤S2(βS2C4kJRk)n.

Agora, se β < β0 ≡min{_S2_C41_k_JR_k,₂_{d S}2_C2C3C41 }< β1 ent˜ao

∞

X i=2

(2dC2C3)i−1(βC4)i(S2)i+1 <∞

e lim sup n→∞ R

(n)

xy = 0. Para estes valores de β definimos

C(β)≡2dβS4C3C4+

∞

X i=2

(2dC2C3)i−1(βC4)i(S2)i+1

(40)

5.3.3 Cotas superiores no regime χ(β)<∞

Na se¸cão anterior, mostramos sob certas hipóteses (H1-H3) que o decaimento da fun¸cão conectividade é ditado pela taxa de decaimento das constantes de acoplamento se β é suficientemente pequeno. A partir da cotas (31) e (32) do Teorema 5.3 podemos concluir que χ(β), a susceptibilidade, destes modelos é finita no intervalo (0, β0). Naturalmente

surge a questão sobre o comportamento assintótico das conectividades em toda a região para o qualχ(β)<∞. Para dar uma resposta a esta questão, lan¸camos mão dos métodos introduzidos no Cap´ıtulo 1, onde obtivemos o comportamento assintótico das conectivi-dades em todo regime subcr´ıtico.

´

E claro que existem diferen¸cas que saltam aos olhos sobre os modelos de percola¸cão e os modelos de Mecânica Estat´ıstica em que as medidas são definidas a partir por Hamiltoni-anos como em (12). Porém no caso ferromagnético, que é objeto de estudo neste trabalho várias analogias podem ser feitas. A que nos interessa, em particular, é a rela¸cão entre as fun¸cões conectividade e a correla¸cão spin-spin. Esta será explorada de duas maneiras neste trabalho; tanto para adaptar a prova do Teorema 5.3 para os modelos de percola¸cão quanto para adaptar a prova do Teorema 3 para os modelos de mecânica Estat´ıstica defi-nidos por (12). Nesta se¸cão, como ilustra¸cão aos comentários prévios, mostraremos passo a passo como proceder para adaptar as técnicas de escalas múltiplas, introduzidas nos modelos de percola¸cão na prova do Teorema 3, a modelos ferromagnéticos bem gerais. Além disto, mostraremos generaliza¸cões deste método em dois sentidos. Permitiremos tanto que o alcance R da intera¸cão tome valores 1 ≤ R ≤ ∞ e também que os núcleos sejam mais gerais do que (19). Estes por sua vez, deverão satisfazer as hipóteses H4 à H7, listadas logo abaixo. Mencionamos também alguns exemplos de intera¸cõesque satisfazem estas hipóteses.

Outro fato importante a se notar é que, para uma grande classe de modelos de spins escalar (N = 1), a condi¸cão χ(β) < ∞ é equivalente a dizer que β < βc, onde βc é o inverso da temperatura cr´ıtica, veja [13]. Isto é particularmente verdadeiro para modelos de spins escalar mencionados nas observa¸cões que sucedem o Teorema 5.2, com intera¸cões dadas por (19) ou (30).

A partir de agora assumiremos que nossas intera¸c˜oessatisfazem as hip´oteses:

H4) Invariˆancia translacional: existe uma fun¸c˜ao K : R+ _→ R+ _{tal que} _K_x1_y1 ₌ K(_kx1−y1k);

H5) Monotonicidade: K(q)< K(p) se p < q;

(41)

tal que

K

kx1−y1k

2

≤CK˜ (kx1−y1k);

H7) Cota inferior uniforme: existe uma constante positivaν tal que 1

Rν ≤K(R)

para todoR _≥1.

Obs: Observe que as intera¸c˜oes(19) e (30) satisfazem trivialmente H4, H5 e H7. Para H6, pegamos ˜C = 2d+ε _{no caso (19) e para (30) ˜}_C _{= 2}d+p_.

Podemos agora enunciar o principal resultado desta se¸c˜ao

Teorema 5.4. Considere o estado de Gibbs (16) `a temperatura inversaβ e com constantes

de acoplamento JR _{satisfazendo as hip´oteses feitas acima, H4 `a H7. Seja} _S2 _>₀ _{tal que}

h~σu·~σvi ≤S2 para todo u, v ∈Zk+d. Ent˜ao sob as hip´oteses do teorema 5.2 e para β tal

que χ(β)<∞, existem constantes positivas m,m, C˜ e R0 tais que, para todo x, y ∈Zk+d e para todo R > R0

h~σu·~σvi ≤   

CKx1y1e−mkx0−y0k se kx1−y1k< R, (42)

S2e−m˜kx−yk se _kx1−y1k ≥R. (43)

Sob as hipóteses do Teorema 5.2 as desigualdades G-I e Simon são válidas. A prova do teorema acima, será baseada na expansão em escalas múltiplas desenvolvida no cap´ıtulo anterior. A prova será dividida em três partes:

1. como fizemos na prova do Teorema 5.3, primeiro mostraremos que a correla¸c˜ao spin-spin decai exponencialmente na “dire¸c˜ao temporal”x0 ∈ Zk sempre que β for

tal queχ(β)<_∞, i.e., seχ(β)<_∞ent˜ao existem constantes positivasR2 =R2(β)

e m0 =m0(β) tais que

h~σx·~σyi ≤S2e−m0kx0−y0k (44) sempre que kx0−y0k> R2.

Similarmente, também provamos o decaimento exponencial das correla¸cões na “dire¸cão espacial”x1 ∈ Zd para pares de spins suficientemente distantes, i.e., se χ(β) < ∞

ent˜ao existem constantes positivas R3 =R3(β, R) and m1 =m1(β, R)>0 tais que