Duas aplicações da Mecânica Estatística:
Percolação em Grafos Infinitos e Lema Local de
Lovász Algorítmico
Instituto de Ciências Exatas
Departamento de Matemática
Tese de Doutorado
Duas aplicações da Mecânica Estatística:
Percolação em Grafos Infinitos e Lema Local de
Lovász Algorítmico
Rogério Gomes Alves
Orientador: Prof. Dr. Aldo Procacci
Co-orientador: Prof. Dr. Rémy de Paiva Sanchis
Percolação em Grafos Infinitos e Lema Local de
Lovász Algorítmico
Esta tese contém alterações sugeridas pela Comissão Julgadora.
Comissão Julgadora:
• Prof. Dr. Aldo Procacci (Matemática- UFMG)
• Prof. Dr. Bernardo Nunes Borges de Lima (Matemática-UFMG)
• Prof. Dr. Rémy de Paiva Sanchis (Matemática-UFMG)
• Prof. Dr. Roberto Imbuzeiro Oliveira (IMPA)
Agradeço a minha família e amigos pelo apoio até aqui.
Agradeço a todos os professores, funcionários e amigos do departamento de Mate-mática da UFMG que contribuiram de alguma forma com minha vida acadêmica.
Agradeço especialmente os professores Aldo Procacci e Rémy de Paiva Sanchis pela orientação, suporte e ensinamentos durante os anos desse doutorado. Agradeço também aos professores Bernardo N. B. de Lima e Sacha Friedli pela motivação em sempre propor cursos de mecânica estatística, probabilidade e afins no departamento. Por fim, agradeço minha esposa Emely por tornar tudo mais simples e possível durante essa trajetória.
Nesta tese mostramos um critério geral para que grafos infinitos de grau limi-tado tenham uma transição de fase não trivial para o processo de Percolação de elos independentes baseado em uma única desigualdade isoperimétrica, se o grafo possui geodésicas bi-infinitas, ou duas desigualdades isoperimétricas, caso não as tenha. Mos-tramos que nos grafos desta classe, sem geodésicas bi-infinitas, a conectividade finita decai subexponencialmente na região altamente supercrítica, mesmo sepestá arbitra-riamente próximo de 1. Os grafos naquela classe, com geodésicas bi-infinitas, sempre
tem a função de conectividade finita decaindo exponencialmente sepestá próximo de
1 o suficiente.
Estudamos também o Lema Local de Lovász construtivo de Moser e Tardos [59]
e mostramos que há uma relação entre o algoritmo proposto por estes autores e a expansão em polímeros do gás de rede ao identificarmos a noção de ”witness trees” no algoritmo com a noção de árvores de Penrose da expansão. Essa relação nos permite concluir que o algoritmo de Moser-Tardos é eficiente se a expansão em polímeros é convergente.
Palavras-chave: Percolação, transição de fase, função conectividade, expansão em
polímeros, Lema Local de Lovász algorítmico. Abstract
In this work we show a general criterion for bounded degree graphs to exhibit a non-trivial percolation threshold based either on a single isoperimetric inequality if the graph has a biinfinite geodesic, or two isoperimetric inequalities if the graph has not a bi-infinite geodesic. We also study the finite connectivity in graphs satisfying the new general criterion and show that graphs in this class with a bi-infinite geodesic always have finite connectivity functions with exponential decay whenpis sufficiently close 1. On the other hand, we show that there are graphs in the same class with no bi-infinite geodesic for which the finite connectivity decays subexponentially (down to polynomially) in the highly supercritical phase even for p arbitrarily close 1.
We also point out a close connection between the Moser−Tardos algorithmic version of the Lovász local lemma [59] and the cluster expansion of the hard-core lattice gas in statistical mechanics. We show that the notion of witness trees given by Moser and Tardos is essentially coincident with that of Penrose trees in the Cluster expansion scheme of the hard-core gas. Such an identification implies that the Moser−Tardos algorithm is successful in a polynomial time if the cluster expansion converges.
Keywords: Percolation, phase transition, connectivity function, polymer expansion,
algorithmic Lovász Local Lemma.
Introdução 1
1 Percolação em grafos infinitos 5
1.1 Percolação independente em grafos infinitos . . . 5
1.1.1 Percolação de elos independentes . . . 5
1.1.2 O argumento de Peierls . . . 8
1.2 Desigualdades isoperimétricas e transição de fase em percolação . . . . 15
1.2.1 Quais grafos percolam? . . . 15
1.2.2 Uma condição para percolar . . . 21
1.3 Desigualdades isoperimétricas e a conectividade finita de dois pontos . 29
1.3.1 A conectividade finita de dois pontos em grafos gerais . . . 29
1.3.2 Decaimento exponencial/subexponencial da conectividade finita
de dois pontos. . . 31
2 O gás com interação caroço duro e o Lema Local de Lovász algorítmico 37
2.1 O gás de rede com interação caroço duro . . . 37
2.2 A expansão do gás auto-repulsivo com interação caroço duro em um grafo 39
2.3 O Lema Local de Lovász . . . 47
2.4 A conexão com a Mecânica Estatística . . . 51
2.5 O Lema Local de Lovász construtivo . . . 57
2.5.1 A versão algorítmica de Moser-Tardos do Lema Local de Lovász 58
2.6 O Lema Local de Lovász de Moser-Tardos e a Mecânica Estatística. . . . 67
2.6.1 Partições e a Identidade de Penrose . . . 69
2.6.2 Uma variação do esquema de Penrose . . . 71
2.6.3 A conexão entre as árvores de Moser-Tardos e Penrose . . . 78
Os modelos e técnicas da Mecânica Estatística sempre estiveram relacionados a Probabilidade e Combinatória. Embora estas áreas já estejam ligadas à Mecânica Esta-tística quer sejam através de problemas enumerativos tais como o número de caminhos auto-evitantes de um grafo ou pela interseção de alguns ramos, como Percolação em Probabilidade, esta tese é sobre uma conexão mais direta entre essas áreas. A saber, exploraremos as ideias e técnicas de métodos pertubativos da Mecânica Estatística
cha-mados de Cluster Expansion para estudar alguns problemas de Percolação e Método
Probabilístico.
Proposto na década de 50 por Broadbent e Harmmersley [16] como um modelo
probabilístico para a propagação de um fluido em meios porosos, oModelo de Percolação
de elos independentes é formulado sobre um grafo infinitoG(o meio poroso) em que
cada elo (canal de passagem do fluido) deste grafo está independentemente aberto com
probabilidadepou fechado com probabilidade 1−p. Um dos primeiros resultados não
triviais, obtido em [16], é a existência detransição de faseparaZ2. Isto é, existe um valor
crítico do parâmetro p, denotado por pc(G), chamado de ponto crítico tal que acima
deste o fluido percola atingindo infinitos pontos do meio poroso e abaixo do mesmo este comportamento não acontece. Um dos primeiros grafos em que o Modelo de Percolação foi amplamente estudado é a redeZde mais particularmente a rede bidimensionalZ2.
Sabe-se há bastante tempo que o modelo emZdparad≥2 possui uma transição de fase
não trivial, ou seja, temospc(Zd)∈(0,1) sed≥2. O estudo de Percolação em grafos mais
gerais que as redes regulares somente obteve maior atenção da comunidade acadêmica a partir da década de 90. Destacamos aqui o marcante trabalho de Itai Benjamini e
Oded Schramm [10] no qual os autores propuseram interessantes conjecturas que ins
piraram parte dos resultados desta tese.
Embora haja uma representação em polímeros (ou aglomerados) da função de co-nectividade de Percolação emZd, veja Braga, Procacci e Sanchis [14], [15], e do Modelo
de Aglomerado Aleatório∗em alguns grafos mais gerais, veja Procacci e Scoppola [69], os resultados sobre Percolação desta tese não são obtidos por meio da expansão em polímeros. De fato, inspirado nas ideias dessas expansões, mostramos um critério geral para grafos infinitos de grau limitado terem uma transição de fase não trivial para o processo de Percolação de elos independentes baseado em uma única desigualdade isoperimétrica, se o grafo possui geodésicas bi-infinitas, ou duas desigualdades isope-rimétricas, caso o grafo não tenha geodésicas bi-infinitas. Este novo critério extende alguns critérios anteriores de Procacci e Scoppola [68] incorporando, por exemplo, grafos com constante de Cheeger igual a zero (redes regulares) assim como grafos com constante de Cheeger positiva (árvores regulares). Discutimos também a relação
desses resultados com duas conjecturas feitas por Benjamini e Scharamm [10] sobre
transição de fase em grafos gerais. Estudamos também a função de conectividade finita de dois pontos em grafos satisfazendo este novo critério e mostramos que grafos nesta classe, com geodésicas bi-infinitas, sempre tem as funções de conectividade finita decaindo exponencialmente sepestá próximo de 1 o suficiente. Outro resultado é que existem grafos nesta classe, aqueles sem geodésicas bi-infinitas, tais que conectividade
finita decai subexponencialmente na região altamente supercrítica, mesmo se p está
arbitrariamente perto de 1.
O Método Probabilístico desenvolvido por Paul Erdös [13], mais especificamente o Lema Local de Lovász, obtido por Erdös e Lovász [29] em 1975 é uma poderosa técnica não-construtiva amplamente utilizada em diversas áreas como Teoria dos Números, Combinatória e Teoria do Grafos. Fixado um espaço de probabilidade qualquer e uma coleção finita de eventos neste espaço, geralmente eventos que desejamos evitar, o lema nos fornece um critério suficiente para que a probabilidade de nenhum desses eventos ocorrerem seja positiva. Em particular, o lema nos garante a existência de uma
configuração na qual não ocorre os eventos ”indesejáveis”. O Lema Local de Lovász possui uma inesperada ligação com o gás de rede. Essa relação, entre dois assuntos aparentemente distintos, foi elucidada por Scott e Sokal [72] somente em 2005. Neste trabalhos os autores exploraram o fato que a função partição do gás de rede em um grafo
finitoGé simplesmente o polinômio de conjuntos independentes deGpara relacionar
o gás de rede com um resultado de Shearer [74].
Embora o lema nos forneça um poderoso resultado que é a existência de uma configuração com as propriedades desejáveis, em problemas aplicados geralmente além da existência de tais configurações estamos interessados também em encontrá-las. Desta foma um grande esforço para encontrar uma versão construtiva do Lema Local de Lovász foi feito durante a última década do século passado e a primeira década deste século. Tais esforços culminaram em 2010 na versão algorítmica de
Robin A. Moser e Garbor Tardos [59] num contexto mais específico porém de enorme
aplicabilidade. Moser e Tardos mostraram que não apenas existe um algoritmo que encontra tal configuração como também a encontra em tempo polinomial.
Após os trabalhos de Scott e Sokal [72] e Moser e Tardos [59], surge a natural pergunta se essa versão construtiva do Lema Loca de Lovász teria alguma relação com a Mecânica Estatística, mais especificamente o gás de rede. Mostrar que de fato há uma relação entre esses assuntos é o cerne da outra metade desta tese. Demonstramos que há uma ligação muito próxima entre o algoritmo proposto por Moser-Tardos e a expansão em polímeros do gás de rede ao mostrarmos que a noção de ”witness trees” no algoritmo é essencialmente a noção de árvores de Penrose da expansão. Essa identificação nos permite concluir que o algoritmo de Moser-Tardos é eficiente se a expansão em polímeros é convergente.
Essa tese possui uma divisão muito simples: há dois capítulos que podem ser lidos independentemente.
No Capítulo 1 estão os resultados sobre percolação desta tese. Lembramos que
nesta parte não usamos explicitamente a expansão em polímeros. Na Seção 1.1.1
técnica para provarmos a existência de transição de fase. O resto do capítulo é dividido entre os resultados sobre transição de fase, Seção1.2, e sobre a conectividade finita de dois pontos, Seção1.3.
No Capítulo 2 abordamos os resultados sobre o Lema Local de Lovász algoritmo de
Moser-Tardos e o gás de rede. Nas Seções2.1e2.2damos uma pequena introdução ao
gás de rede e a expansão em aglomerados. Na Seção2.3 introduzimos o Lema Local
de Lovász e na Seção2.4 discutimos a relação deste com o gás de rede. Já na Seção
2.5expomos o trabalho de Moser e Tardos. Por fim, na Seção2.6desse capítulo é que mostramos nossos resultados que relacionam o Lema Local de Lovász construtivo com o gás de rede.
1
Percolação em grafos infinitos
1.1 Percolação independente em grafos infinitos
1.1.1 Percolação de elos independentes
Durante todo o texto denotaremos por |X| a cardinalidade, às vezes chamada de
tamanho ou volume, de um conjuntoX. Todos os grafos desta tese, salvo menção em
contrário, serão simples (sem "loops"ou múltiplos elos), não orientados e com conjunto de vértices finito ou (infinito) enumerável.
Considere um grafo G = (V,E) com conjunto de vértices V e conjunto de elos E.
Um caminho emGé um subgrafoS= (VS,ES) em queVS={x1, . . . ,xn}são distintos e
ES={{x1,x2}, . . . ,{xn−1,xn}} ⊆E; o tamanho de um caminhoSé definido por |S| ≡ |ES|.
Dadosx,y∈ V, denotaremos pordG(x,y) ou simplesmented(x,y) a métrica natural de
G dada pelo tamanho do menor caminho entre x e y. Se W ⊂ V, seja GW = (W,EW)
o subgrafo deGinduzido por W em que EW ⊆ Econsiste apenas de elos com pontos
finais emW. Um conjunto de vérticesW ⊂V éconexoemGseGW é conexo. Dizemos
que o conjunto de elosS ⊂ E é conexo se GVS é conexo, em que VS é o conjunto de
vértices deS.
A seguir definimos os conjuntos fronteira deW, a saber, definimos afronteira de elos deWcomo o subconjunto de elos∂eW={e∈E:|e∩W|=1}, afronteira interna de vértice é o subconjunto de vértices∂intv W ={v ∈ W : dG(x,V\W) = 1} e aa fronteira externa de vértice sendo o subconjunto de vétices∂extv W = {v ∈ V\W : dG(x,W) = 1}. Podemos
ver que seG tem grau limitado com ∆(G) ≡ max
v∈V |∂ev| < ∞, então |∂eW| ≤ ∆(G)|∂ int v |e |∂intv | ≤∆(G)|∂eW|. O fecho deWé definido por ¯W =W∪∂extv W.
Daqui em diante neste capítulo o par ordenadoG = (V,E) sempre será um grafo
infinito (o conjunto de vértices V é enumerável), simples, não-orientado, conexo e
de grau limitado com grau máximo ∆(G). O subconjunto AG = {W ⊂ V : |W| <
∞eGW conexo}é o conjunto de todas as componentes conexas e finitas deG. O grafo
cujo o conjunto de vértices é Zd e os elos são os pares ordenados de vértices com
distância euclidiana igual a 1 será denominado simplesmente deZdou redeZd.
Daremos a seguir uma breve introdução ao modelo de percolação de elos indepen-dentes em grafos infinitos tratados neste trabalho. Para uma estudo mais abrangente, embora com maior ênfase emZd, veja por exemplo Grimmett [38] ou Kesten [48].
DadoG= (V,E) ep∈ [0,1], definimos a família de variáveis aleatórias{ωe : e∈ E}
independentes e identicamente distribuidas com distribuição comum de Bernoulli de parâmetrop, isto é, para todoe ∈ E, ωe = 1 (ou dizemos que o elo eestá aberto) com
probabilidade p, ou ωe = 0 (ou dizemos que o elo eestá fechado) com probabilidade
1−p. Uma configuração ωdeGé uma funçãoω : E → {0,1}em que ω(e) = ωe. Seja
ΩG o conjunto de todas as configurações e Pp a medida produto sobre configurações
de elos deG. Juntamente com aσ-álgebraP gerada pelos conjuntos cilíndricos deΩG
temos o espaço de probabilidade (ΩG,P,Pp) domodelo de percolação independente de elos
com parâmetropem G. Dado uma configuraçãoω∈ ΩG, definimos o subconjunto de
elos deEque estão abertos emωporA(ω)={e∈E: ωe=1}e o subconjunto de elos de Eque estão fechados emωporF(ω)={e∈E: ωe=0}.
SejaGN = (VN,EN) um subgrafo finito deGeΩN o conjunto das configurações em
GN. Então dadoω∈ΩN, temos que
Pp(ω)=p|A(ω)|(1−p)|F(ω)|. (1.1)
Dado uma configuraçãoω∈ ΩG, umaglomerado abertoemωé um subgrafo conexo
g = g(ω) = (Vg,Eg) tal que Eg ⊂ A(ω) e ∂eVg ⊂ F(ω). Para tornar a notação menos
vazio deVg. Como estamos interessados em estudar as propriedades de conectividade deA(ω), definiremos a seguir a probabilidade de percolação e a conectividade finita de
dois pontos.
Definição 1.1. Considere o grafoG=(V,E)e dois vértices x,y∈V. Aconectividade finita
de dois pontosφfp(x,y)é definida por
φfp(x,y)=Pp(ω∈ΩG : ∃aglomerado aberto g= g(ω), {x,y} ⊂ g, |Eg|<∞). (1.2)
Aprobabilidade de percolaçãoθp(x)é definida por
θp(x)=Pp(ω∈ΩG : ∃aglomerado aberto g= g(ω), {x} ⊂ g, |Eg|=∞). (1.3)
Já queGé conexo, segue pela desigualdadeFKG (veja, por exemplo, Seção 2.2 de
Grimmett [38]) que o fato deθp(x)>0 não depende do vérticex∈ V. Quando não for
necessário, escreveremos apenasθp. Assim, dizemos que o modelo percolaou quehá
percolação, parap∈[0,1], seθp =θp(x)>0 para algumx∈V.
Note que podemos escrever a probabilidade de percolação em termos de uma função de conectividade. Dado um vérticex∈V, podemos também definir aconectividade finita
de um ponto
φfp(x)=Pp(ω∈ΩG : ∃aglomerado aberto g= g(ω), {x} ⊂ g, |Eg|<∞). (1.4)
Assim,
θp(x)=1−φfp(x). (1.5)
Proposição 1.1. Considere o modelo de percolação independente de elos emG=(V,E). Então
existe um valor crítico pc(G)∈[0,1]do parâmetro definido por
pc=pc(G)= sup
p∈[0,1]{p
: θp(x)=0}, (1.6)
tal queθP >0se p >pc eθP =0se p<pc.
Prova: Como θ0 = 0 e θ1 = 1, é suficiente mostrarmos que θp é uma função
não decrescente em p. Para isto, defina a família de variáveis aleatórias i.i.d. U = {Ue}e∈E, cada uma com distribuição uniforme no intervalo [0,1]. Seja agora o modelo
de percolação definido a partir deU no qual dizemos que um elo estáp-aberto, neste modelo, seUe < p. Note queθp é igual a probabilidade de percolar neste modelo de elosp-abertos. Sendo assim, como neste modelo todo elop-aberto está necessariamente p′-aberto, comp<p′, temos queθ
p ≤θp′.
Isso que estabelece a existência de uma fase abaixo depcem que não há percolação e outra fase acima depcem que há percolação. Se 0< pc(G)<1 então dizemos que há
transição de fase não-trivialou simplesmentetransição de faseno modelo de percolação de elos emG. Dizemos também que o modelo está nafase subcríticasep ∈[0,pc) e nafase
supercríticasep∈(pc,1].
Podemos também definir o modelo de percolação declarando vértices abertos ao invés de elos abertos. Tais modelos são usualmente chamados de percolação de sítios. Vale apena ressaltar que em grafos de grau limitado, transição de fase no modelo de percolação de elos é equivalente a transição de fase no modelo de percolação de sítios. Veja Grimmet e Stacey [40].
1.1.2 O argumento de Peierls
Quando existe transição de fase em um grafoG?
Apresentaremos aqui nesta seção o argumento de Peierls que é a principal técnica para mostrar que determinado grafo possui ponto crítico estritamente menor que 1.
isto é, quepc ∈ (0,1) é uma das primeiras perguntas a serem feitas em um modelo de
percolação em um grafo. Como veremos a seguir, a parte não trivial é mostrar que pc < 1. Vale a pena mencionar os marcantes trabalhos de H. Kesten na rede Z2 como
um dos primeiros nesta questão; em Kesten [46] é mostrado quepc(Z2)≥ 1
2e em Kesten
[47] quepc(Z2)= 1
2.
Embora mostrar quepc <1 seja uma questão com seu próprio interesse, ela se torna
ainda mais relevante se levarmos em conta quepc(G)<1 implica também transição de
fase em vários outros modelos de mecânica estatística emG, como o modelo de Ising,
por exemplo. Veja Häggström [44].
Uma técnica geral para provar quepc < 1 pode ser obtida através do famoso
argu-mento de Peierls, cujo escopo aparece originalmente em Peierls [64], e posteriormente em Griffiths [34] e Dobrushin [26], adaptado ao contexto de percolação em grafos mais gerais que as redes regulares. Podemos ter uma ideia como é o argumento de Peierls analisando o modelo de Ising emZ2. O modelo consiste de variáveis aleatórias
inde-xadas pelos vértices deZ2que representam os spins de elétrons. Estes podem estar em
dois estados: +ou−. A baixa temperatura no modelo de Ising ferromagnético (spins
vizinhos tendem a se alinhar), espera-se que os spins tenham uma configuração similar a um estado de temperatura zero, ou seja, um estado de baixa energia∗. Isto nos leva a uma figura geométrica bastante ilustrativa: os spins com a mesma configuração de um estado de baixa energia formam um infinito oceano, enquanto os spins de configuração diferente do estado de baixa energia ficam presos em ilhas finitas. Veja a figura1.1que
representa o estado + como o estado de baixa energia. As fronteiras dessas regiões
de baixa energia dão uma imagem a que referiremos decontornos. Os contornos, por
sua vez, tem sua energia proporcional ao seu tamanho que é tipicamente pequeno quando estamos à temperatura baixa. Deste modo, o estado de baixa energia pode eventualmente percolar.
Exibiremos a seguir o clássico resultado em que podemos ver como essa ideia pode ser aplicada a percolação.
Figura 1.1: Representação de uma configuração do modelo de Ising em contornos de elos duais em uma caixa finita deZ2com condição de fronteira+[81].
Teorema 1.1. O ponto crítico pc(Zd)satisfaz a seguinte desigualdade se d≥2:
1
2d−1 ≤pc(Z d)≤ 2
3 (1.7)
Prova: A prova da cota inferior é dada mais adiante na proposição 1.3. Para a
cota superior, é suficiente provarmos para d = 2, já que Z2 é um subgrafo de Zd.
Considere então Z2 e seu grafo dualZ2
∗ (o grafo Z2∗ é simplesmente uma translação
deZ2pelo vetor (1/2,1/2)). Acople o modelo de percolação emZ2 com o modelo em
Z2
∗ declarando um eloe∗ de Z2∗ aberto ou fechado se o eloe deZ2, que cruza e∗, está
aberto ou fechado respectivamente. Geometricamente, veja figura 1.2, podemos ver
que se o aglomerado aberto da origem é finito então existe um circuito de elos fechados
ao redor da origem. A demonstração deste fato pode ser encontrada em [48]. Deste
modo é suficiente mostrarmos que a probabilidade de haver um circuito de elos duais fechados é estritamente menor que 1 sepestá suficientemente próximo de 1.
Cada circuito na rede dual formado pornelos fechados tem probabilidade (1−p)n de ocorrer. Faremos agora uma estimativa do número de tais circuitos o suficiente para nossos propósitos. Considere o elo mais a esquerda de um tal circuito que cruza o
eixo-x. Temos no máximonpossibilidades para este elo. Cada um dosn−1 elos restantes
podem ser colocados de no máximo 3 maneiras diferentes. Assim há no máximon3n−1
X
n≥4
n
3[3(1−p)]
n. (1.8)
Note que a série acima é uma função contínua e decrescente empquandop>2/3. Isto nos garante apenas que existep′ < 1 tal que a probabilidade de haver um circuito de
elos duais fechados é estritamente menor que 1 parap>p′.
Considere então o evento Qk em que todos os elos do quadrado de lado 2k+1,
centrado na origem, estão abertos. SejaAko evento em que há um circuito de elos duais
fechados na rede dual que está fora do quadrado de lado 2k+1 centrado na origem.
Analogamente a demonstração acima, temos
Pp(Ak)≤ X n≥8k+4
n
3[3(1−p)]n. (1.9)
Portanto dadop>2/3, sejak0 ∈Ntal quePp( ¯Ak0)>0. ComoQkeAksão independentes, pois dependem de conjuntos de elos disjuntos, ePp(Qk0)>0 , temos que
θp>Pp(Qk0 ∩Ak¯ 0)=Pp(Qk0)Pp( ¯Ak0)>0. (1.10)
Figura 1.2: Um aglomerado aberto da origem deZ2cercado por um circuito fechado no dual [38].
definirmos em grafos mais gerais que a redeZd em ordem de produzir o argumento
de Peierls na demostração do teorema acima.
Definição 1.2. Umconjunto de cortede um grafoG=(V,E)é um conjuntoγ ⊂Etal que
o grafoG\γ ≡(V,E\γ)é desconexo.
DadoG= (V,E), um conjunto de corte finitoγ ⊂ Eé chamado decontornoseG\γtem
exatamente uma componente conexa finita e é minimal com respeito a esta propriedade, ou seja, para qualquer elo e∈ γ o grafo(V,E\(γ\e))não tem componente finita. Dizemos queFG é o
conjunto de todos os contornos de G.
Seγ é um contorno em Gentão denotamos por Gγ = (Iγ,Eγ)a única componente conexa
finita deG\γ. O conjunto Iγ ⊂Vé chamado de o interior de vértices deγe o conjunto Eγ⊂Eé
chamado de interior de elos deγ. O fecho de Gγé o grafoGγ¯ =( ¯Iγ,Eγ)¯ com conjunto de vértices ¯
Iγ=Iγ∪∂extv Iγ e conjunto de elosEγ¯ =Eγ∪γ.
Observação 1. Quando G\γ possui componentes conexas finitas então, de fato, só existirá
apenas uma única tal componte. Com efeito, pela minimalidade na definição de contorno, para qualquer elo e∈γo grafo(V,E\(γ\e))não tem componente finita, logoG\γnão pode ter mais
de uma componente conexa finita.
A definição de contorno acima remonta ao artigo de Rudolf Peierls [64] no estudo do modelo de Ising. Essa noção de contorno em grafos mais gerais que as clássicas redes regulares já tem obtido atenção da comunidade acadêmica. Os contornos da Definição 1.2 foram chamados de "(v,∞)-minimal cutset"em Babson Benjamini [7],
"Peierls contours"em Procacci e Scoppola [68] e "fences"em Procacci e Scoppola [69]. Considere um contornoγ em G = (V,E) e um conjunto finito de vértices X ⊂ V.
Dizemos queγcerca X, denotamos porγ⊙X, seX ⊂Iγ. Dizemos queγsepara X, neste
caso escrevemosγ⊗X, se 0<|X∩Iγ|<|X|.
Denotamos porFGno conjunto de todos os contornos com cardinalidade (ou
tama-nho)n, por FG(X) (FGn(X)) o conjunto dos contornosγ ∈ FG (γ ∈ FGn) que cercamX e,
com um pequeno abuso de notação, parae ∈ E, denotamos porFn
G(e) o conjunto dos
A Proposição1.2abaixo, a qual chamaremos de argumento de Peierls, diz que para haver percolação é suficiente termos uma cota superior exponencial para o número de contornos.
Proposição 1.2. (Argumento de Peierls) Considere o grafoG=(V,E). Se existe uma constante
positiva r e um vértice x∈Vtal que, para todo n∈N,
|FGn(x)| ≤r
n, (1.11)
então
pc(G)≤1− 1
2r. (1.12)
Prova: A demonstração segue facilmente do fato que seg = (Vg,Eg) é um
aglome-rado aberto e finito com{x} ⊂ Vg, então existe um contorno γtal queγ⊙xeγ ⊂ ∂eg,
isto é,γé constituido apenas de elos fechados. Portanto,
φfp(x)≤ X
n≥1
X
γ∈FGn(x)
(1−p)|γ|=X n≥1
[r(1−p)]n<1 (1.13)
sep>1− 21r; logo a igualdade1.5implicapc≤1− 21r.
A seguir veremos a cota inferior para o ponto crítico deGem termos de seu grau
máximo∆(G).
Proposição 1.3. Considere o grafoG=(V,E)com grau máximo∆ = ∆(G). Então
pc(G)≥ 1
∆−1. (1.14)
Prova: Se o vértice x ∈ V está em algum aglomerado aberto e infinito, então para
todo n ∈ N existe um caminho de elos abertos auto-evitante (cada elo é usado no
máximo uma vez) a partir dexde tamanhon. O número de tais caminhos é no máximo
∆(∆−1)n−1e a probabilidade de tal caminho estar aberto épn. Logo temos,
A demonstração termina observando que a expressão (1.15) tende a 0 quando n tende a infinito sep< ∆1−1.
Não é difícil ver que alguns grafos possuem uma cota exponencial para o número de contornos de tamanhon. Por exemplo, o grafoZ2possui a cota|Fn
Z2((0,0))| ≤n3
n−1.
De fato, cada elo de um contorno em Z2 cruza um elo de um circuito na rede dual.
Assim essa cota segue como vimos na demonstração do Teorema 1.1. Para a árvore
bináriaTo com raizo, temos que|FTno(o)|é menor que o número de elos entre os níveis 0 enda árvore (a raiz está no nível 0) e esta quantidade é menor que 2n. Assim ambos
percolam pela Proposição1.2. Há também o exemplo do grafoZque possui infinitos
contornos de tamanho 2 cercando a origem. Deste modo, para todo p < 1, infinitos
desses contornos estão fechados quase certamente e assim θp = 0 sep < 1. Portanto pc(Z)=1.
Nem sempre é imediato mostrar tal cota para o número de contornos de tamanhon
em um grafo. De fato esta tarefa pode ser bem complicada como veremos na próxima
seção. A seguir daremos uma demostração, baseada em Babson-Benjamini [10], de que
grafos com constante de Cheeger positiva possuem uma cota (exponencial) superior
para o número de contornos de tamanhon.
Definição 1.3. A constante de Cheeger do grafoG=(V,E), CG, é definida por
CG = inf
S∈AG
|∂eS|
|S| . (1.16)
Primeiro mostraremos o Lema1.4abaixo que é uma versão do Lema 6 em
Babson-Benjamini [10] e do Lema 2.1 em Timár [80]. Uma melhor cota que a dada pelo Lema
1.4 pode ser encontrada em [48]. Lembre que um multigrafoG é um grafo em que é
permitido ter múltiplos elos, isto é, elos que tem os mesmos vértices finais. Observe que um grafo é um multigrafo. Umpasseioem um grafoGé um sequênciav0,v1, . . . ,vk
de vértices adjacentes do grafo. Se G é um multigrafo, então um passeio será uma
sequência de vértices e elos v0,e1,v1,e2, . . . ,ek,vk em que ei é um elo entre os vértices
vi−1 evi. O passeio será euleriano se ele passa por todo elo exatamente uma vez. Um
se um multigrafo (grafo) finito tem no máximo dois vértices de grau ímpar, então este multigrafo possui um passeio euleriano.
Lema 1.1. Considere o grafoG=(V,E)com grau máximo∆e um vértice v∈V. Então existe
no máximo∆2nsubconjuntos deVde tamanho n que contem v e induzem um subgrafo conexo
deG.
Prova: SejaS⊂Vde cardinalidadenque contémveGSo subgrafo conexo induzido
porS. SejaPSum passeio euleriano deGS, casoGStenha mais de dois vértices de grau ímpar. Considere, ao invés deGS, o multigrafo em que "duplicamos"todos os elos de GS. O passeioPSdetermina o subconjuntoS. Para terminar, basta observar que temos
no máximo∆2npasseios como este.
Proposição 1.4. Se CG > 0, então existe uma constante C > 0 tal que |FGn| ≤ Cn. Em
particular, pc(G)<1.
Prova: Sejaγum contorno ev∈Vum vértice tal queγ⊙ {v}. O número de vértices
na componente conexa finita deγé no máximonC−1
G . Note que o número de contornos
de tamanhonque cercamvé no máximo o número de componentes conexas contendo
vque possuem no máximonC−1
G vértices. Finalizamos ao observar que, pelo Lema1.1,
o número de tais componentes é no máximo∆2nC−G1.
Vale lembrar que em [10] é provado que, de fato,pc(G)≤ 1
1+CG.
1.2 Desigualdades isoperimétricas e transição de fase em
percolação
1.2.1 Quais grafos percolam?
Percolação na redeZd, e suas conexões com a Mecânica Estatística, tem sido
[53] (em Lyons [52] é provado que o ponto crítico de qualquer árvore localmente finitaT é o inverso de seu número de ramificaçãobr(T)†) como também o estudo de percolação no produto cartesiano da árvorer-regular comZd em Grimmett [39]. Entretanto, um
estudo sistemático de percolação em grafos gerais deu-se somente após o fundamental artigo de I. Benjamini e O. Schramm em [10]. Neste trabalho os autores estudaram algu-mas questões sobre percolação e propuseram duas conjecturas (Conjectura 2 e Questão
2 em Benjamini e Schramm [10]), ainda sem solução, sobre quais condições um grafo
deve ter de forma quepc <1.
Conjectura 1.1. (I. Benjamini e O. Schramm) SeG = (V,E) tem dimensão isoperimétrica
maior que1, isto é,
dim(G)≡supnd>0 : inf
S⊂AG
|∂eS|
|S|d−1
d
>0o>1, (1.17)
então pc(G)<1.
Se dim(G) = d, então o tamanho da fronteira de elos |∂eS|é pelo menos de ordem
kd−1
d , para todo subconjunto de vérticesScom|S|= k. E dé o menor número com esta
propriedade. É fácil ver que seG tem constante de Cheeger positiva, isto é, CG > 0,
entãodim(G) = ∞. No entanto, não é imediato quedim(Zd) = d. Podemos encontrar
a demostração deste resultado no Capítulo 6 em Lyons e Peres [55]. É de se esperar,
como no Teorema1.1que, de fato, grafos que não são unidimensionais provavelmente
percolam.
Para a segunda conjectura, lembramos algumas definições. Dado W ⊂ V em um
grafoG, odiâmetrodeW será denotado pordiam(W) = max
x,y∈WdG(x,y) e a bola de raion centrada no vértice xcomo o subconjunto B(x,n) ≡ {v ∈ V : dG(x,v) ≤ n}. Um grafo
G=(V,E) étransitivose e somente se para quaisquerx,y ∈Vexiste um automorfismo que levax em yeG é dito quase-transitivose existe um subconjunto finito V0 ⊂ V tal
que qualquerv ∈ V é levado por algum automorfismo emV0. Dado um conjunto de
geradores S, simétrico (S = S−1), finito para um grupoΓ , o grafo de Cayley é o grafo
G(Γ) = (V,E) com V = Γe {g,h} ∈ Ese e somente se g−1h ∈ S. Dizemos que as bolas
do grafo de CayleyG(Γ) tempelo menos ordem dse existe uma constante k > 0 tal que
|B(id,n)| ≥knd, sendoid ∈ Γo elemento identidade do grupo. O grafo de CayleyG(Γ) temcrescimento polinomialse existemk,d>0 tais que|B(id,n)| ≤k(n+1)de temcrescimento exponencialse|B(id,n)| ≥ Crnpara algum k>0 e r> 1. SejaUqualquer subgrafo finito
de um grafo de CayleyG(Γ) ekG(Γ)\Uk ∈N∪ {∞} o número de componentes conexas
infinitas do complemento deU. O número de fins deG(Γ) é o supremo dos números
kG(Γ)\Uk, dentre todos os subgrafos finitosUdeG(Γ).
Conjectura 1.2. (I. Benjamini e O. Schramm) SejaG =(V,E)um grafo quase-transitivo tal
que existe x∈Vem que|B(x,n)|é pelo menos de ordem n2. Então pc(G)<1.
A Conjectura1.2pode ser vista como um diferente enunciado da Conjectura1.1no
caso de grafos de Cayley de grupos finitamente gerados. Neste caso, de acordo com
[82], o tamanho das bolas em Gcrescem mais do que linearmente se e somente se a
dim(G)>1. A parte fácil desta equivalência pode ser vista na Proposição1.5abaixo.
Proposição 1.5. SejaGum grafo de Cayley de um grupo finitamente gerado com dim(G)=d.
Então|B(x,n)|é pelo menos de ordem nd.
Prova: Provamos por indução em n. Se n = 1, então |B(x,1)| ≥ C com qualquer
C≤ infx∈V|B(x,1)|= |B(x,1)|. Suponha verdadeiro paran−1 ≥ 1. Observe que valem
as seguintes desigualdades
nd−(n−1)d ≤dnd−1 ≤d(2(n−1))d−1. (1.18)
Comodim(G)=d, temos para algumC∗>0,
|B(x,n)| ≥ |B(x,n−1)|+|∂B(x,n−1)|
≥ |B(x,n−1)|+C∗|B(x,n−1)|
d−1
d
≥C(n−1)d+C
∗C
d−1
d (n−1)d−d1
≥Cnd+(C
∗C
d−1
Portanto a afirmação é verdadeira para nse escolhemos C de forma que C∗C
d−1
d ≥
Cd2d−1, ou seja,C≤ Cd∗
dd2d−1
d
.
Há um caso particular em que a Conjectura 1.2 está quase toda resolvida. Se
G é um grafo de Cayley de um grupo finitamente gerado que cresce no máximo
polinomialmente, então ou pc(G) = 1 (grafos que crescem linearmente) ou pc(G) < 1,
veja Lyons e Peres [55] Capítulo 7. Em Lyons [54] é provado que grafos de Cayley de grupos finitamente gerados que crescem exponencialmente tempc< 1. Apesar desses
resultados, a Conjectura1.2 ainda não está totalmente resolvida pois existem grupos com crescimento intermediário, isto é, grupos que crescem superpolinomialmente e
subexponecialmente. Os exemplos destes grupos construidos em Grigorchuk [35]
também tem pc < 1, veja Muchnik e Pak [61]. Todas demonstrações dos resultados
citados acima não usam o argumento de Peierls. A prova em Lyons [54] baseia-se
na existência de uma subárvore com crescimento exponencial (que tem número de
ramificação maior que 1), Muchnik e Pak [61] mostra a existência de um subgrafo,
do grafo de Cayley do grupo de Grigorchuk, isomorfo a Z2. Já o fato que grafos
de Cayley de grupos finitamente gerados que crescem no máximo polinomialmente
possivelmente percolam é baseado no famoso resultado de Gromov [41] que diz que
tais grafos possuem ou um subgrupo de índice finito isomorfo aZ, neste caso o grafo
de Cayley tem dois fins (veja Meier [56]), ou um subgrupo isomorfo aZ2.
Um modo de abordar as Conjecturas1.1 ou1.2 seria usar o argumento de Peierls.
Para isto teríamos de provar que o número de contornos de tamanhondesses grafos
tem uma cota como em (1.11). G. Kozma [51] obtém uma tal cota para a classe de
grafos planares com crescimento polinomial e dimensão isoperimétrica maior que 1.
Demonstrar a cota1.11 é uma questão de intrínseco interesse como pode ser visto em
Babson e Benjamini [7]. Neste artigo os autores introduziram um parâmetroJ= JGdo
grafo que é o menor j ∈ Ntal que qualquer contorno é j-próximo, isto é, o contorno é
conexo no grafoGj = (Vj,Ej),Vj =VeEj ={{x,y} ⊂ V : dG(x,y)≤ j}. Por exemplo,
os elos dos contornos deZ2distam no máximo 2. Assim o grafoZ2temJZ2 =2. Babson
os contornos como em1.11. De fato, a classe de grafos a qual eles mostram que J< ∞ é a classe dos grafos de Cayley de grupos finitamente representados. Depois Procacci e Scoppola [68] provaram queJ < ∞é uma condição suficiente para termos uma cota do tipo (1.11) (e portantopc < 1) em uma maior classe de grafos de grau limitado, a
saber, grafos que possuem um raio geodésico bi-infinito ou tem a constante percolação, definida em (1.23), positiva. O problema é que a condição J < ∞ não engloba todos os grafos que percolam. As árvores d-regulares (d>1), por exemplo, possuem J =∞. Babson e Benjamini conjecturaram em [7] que pelo menos os grafos transitivos com um fim e Constante de Cheeger (1.16) igual a zero possuem J<∞. No entanto, Timár [80]
mostrou que o grafo de Diestel-Leader,DL(2,2), figura1.3, é um exemplo de um grafo
transitivo com um fim que tem Constante de Cheeger igual a zero, percola, mas possui J =∞. Veja o Exemplo1.2.1abaixo.
Exemplo 1.2.1. [O grafo de Diestel-Leader DL(2,2)]
O grafo de Diestel-Leader DL(2,2) foi introduzido por Reinhard Diestel e Imre Leader em 2001 com o intuito de prover um exemplo de uma grafo transitivo que não é quase-isométrico‡a nenhum outro grafo de Cayley. Veja Diestel e Leader [25] para uma introdução ao problema. Embora com esta intenção, apenas alguns anos depois é que Eskin, Fisher e Whyte mostraram em [30] que de fato, tal afirmação é verdadeira.
O grafo de Diestel-Leader DL(2,2) é definido como segue. Sejam T e T′ duas árvores
3-regulares e suponha que elas estão enraizadas no infinito de forma que os níveis de cada uma corresponda aos inteiros. Isso é feito de forma que um vértice de T do nível i tem 2 filhos no nível i+1e um pai no nível i−1; um vértice de T′do nível i tem 2 filhos no nível i−1e um pai no nível
i+1. Geometricamente podemos desenhá-las no plano lado a lado de forma que T está enraizada em cima e T′está enraizada embaixo. Veja a Figura1.3. Denote por hT(v)e hT′(v′)os níveis de
v∈T e v′ ∈ T′, respectivamente. O grafo de Diestel-Leader DL(2,2) é o grafo cujo conjunto de
vértices é dado por{(v,v′) ∈ VT ×VT′ : hT(v) = hT′(v′)}e o conjunto de elos é definido como:
existe um elo entre(v,v′)e(x,x′)se e somente se{v,x}é um elo de T e{v′,x′}é um elo de T′. O
‡Dois espaços métricos (X,d
X) e (Y,dY) são quase-isométricos se existem constantesA ≥ 1 eB ≥ 0
e uma funçãoφ : X → Ytal queA−1d
X(x,y)−A ≤ dY(φ(x), φ(y)) ≤ AdX(x,y)+Ae para todo y ∈ Y
desenho da ”mola” conectando o e o′na Figura1.3serve para visualizarmos os elos: ao movê-la
para cima ou para baixo estamos percorrendo um elo de DL(2,2). Um fato bastante conhecido é que o grafo de Cayley do grupo do acendedor de lâmpada §, com determinado conjunto de geradores, é isomorfo ao grafo de Diestel-Leader DL(2,2). Para mais detalhes sobre DL(2,2) veja [84].
Considere agora os vértices o ∈ VT e o′ ∈ VT′ tais que hT(o) = 0 e hT′(o′) = 0, isto é,
os vértices o e o′ estão no nível zero de suas respectivas árvores. Seja Tn a subárvore de T
formada por todos vértices de T que distam no máximo n de o. Do mesmo modo defina T′
n. Defimos então os tetraedros de tamanho n de DL(2,2)como o subgrafo induzido pelo conjunto
de vérticesTn = {(v,v′) ∈ VDL(2,2) : v ∈ Tn, v′ ∈ T′n}. Veja que a fronteira de ∂eTn deTn é a
união disjunta dos conjuntos Fn = {(v,v′) ∈ VDL
(2,2) : o grau em T de v é1}e F′n = {(v,v′) ∈ VDL(2,2) : o grau em T′de v′é1}. Note também que a distância entre Fn e F′n é n. Portanto a fronteira dos tetraedros produz uma sequência de contornos que podem ficar arbitrariamente separados, assim JDL(2,2) =∞. Note que|Fn|+|F′n|=2n+1e que|Tn|=|VTn| |VT′n|=(2
n+1−1)2.
Assim, esta mesma sequência mostra que a constante de Cheeger de DL(2,2) é zero. Para ver que há transição de fase em DL(2,2), veja o capítulo 7 de [55].
Figura 1.3: O grafo de Diestel Leader DL(2,2) [84].
1.2.2 Uma condição para percolar
Motivado por essas questões definimos abaixo as principais desigualdades isoperi-métricas que aparecem neste trabalho.
Primeiro, definimos uma noção de conectividade chamada de distância em árvore.
Deixemos claro que tal conceito, embora com a palavra "distância"em seu nome, não é uma métrica. Este conceito terá um papel relevante em todo este capítulo, já que este sentido de conectividade será crucial nos resultados deste capítulo.
Definição 1.4. SejaG = (V,E) um grafo e W ∈ AG um conjunto conexo de vértices. Seja
T(GW¯) o conjunto de todas as árvores que são subgrafos deGW¯. Definimos a distância em
árvoredtG(∂eW)da fronteira de elos∂eW de W como
dtG(∂eW)= (V,Emin)∈T(G
¯
W)
∂eW⊂E
|E|. (1.19)
Observação 2. Se W ∈ AGentão dtG(∂eW)é o número de elos da menor (em relação ao número
de elos) árvore que conecta e contém∂eW.
Considere W ∈ AG. Note que se∂intv W é conexa então conectamos a fronteira de elos usando
o menor número de elos possíveis. E no pior dos casos, temos que usar quase todos os vértices de W para conectá-la. Deste modo temos a desigualdade
|∂eW|+|∂intv W| −1≤dt
G(∂eW)≤ |∂eW|+|W| −1 (1.20)
Observação 3. Seγ ∈ FG é um contorno, então Iγ ∈ AG e∂eIγ = γ. Assim, a distância em
árvore dt
G(γ)do contornoγpode ser escrita como
dt
G(γ)= min
(V,E)∈T( ¯Gγ)
γ⊂E
|E|=ℓγ+|γ|, (1.21)
em queℓγé o número de elos de Eγnecessários para conectar∂intv Iγ.
Exemplo 1.2.2. Seja To a árvore binária, com raiz o, e W ⊂ VT
o o conjunto dos vértices que
distam no máximo n de o. Então a distância em árvore dt
G(∂eW)=2
n+2−2, pois temos que usar
Considere agora o grafo Zd (d ≥ 2) e W ⊂ VZd como sendo a bola de raio n. Então a
distância em árvore dt
G(∂eW) é da ordem de |∂eW|, já que quaisquer dois vértices da fronteira
interna de vértices de W distam no máximo2.
Agora definiremos as desigualdades isoperimétricas que terão um papel central em nossos resultados.
Definição 1.5. DadoG=(V,E), seja
RG =R= inf
S∈AG
|∂eS|
dt
G(∂eS)
(1.22)
e
PG =P= inf
S∈AG
|∂eS|
log(diam(S)). (1.23)
Chamamos RGe PG deconstante contornoeconstante percolaçãodeG, respectivamente.
Exemplo 1.2.3. Se To é a árvore binária, com raiz o, e W ⊂ VT
o é o conjunto dos vértices que
distam no máximo n de o, então W é o subconjunto que produz a menor razão na definição das constantes contorno e percolação acima. Logo, pelo Exemplo (1.2.2), RTo >0e PTo >0.
Podemos ver também através do Exemplo (1.2.2) que RZd >0e PZd >0.
A constante percolaçãoPGfoi introduzida em Procacci e Scoppola [68]. Semelhantes
desigualdades já têm sido estudadas em percolação como em Grimmett [36] e [37] e Chayes e Chayes [21].
De acordo com nosso conhecimento, é a primeira vez que vemos a constante con-torno na literatura. Uma quantidade relacionada a constante concon-torno foi introduzida
por Campari e Cassi [20] no estudo do modelo de Ising em grafos gerais. Em [20]
os autores definiram a constanteLG tal que (de acordo com a Definição1.2) qualquer
contorno de tamanhoné conectável com não mais quenLG vértices.
Observação 4. A constante LG definida acima é esencialmente o inverso de RG. Com efeito,
se RG >0, então qualquer contornoγ é conectável (por uma árvore que contémγ) usando no
máximo 1
RG|γ|elos. Assim, lembrando a Observação 3, a constante LG satisfaz a desigualdade
1
RG −1≤LG≤
1
Podemos ver também pela definição que RG ≥
CG
CG+1
. Assim grafos com constante de Cheeger positiva possuem RG >0.
Já a relação da constante contorno RG com o parâmetro de Babson - Benjamini JG pode ser
vista ao notarmos que|Iγ| ≤ JG|γ|. Assim se o grafo satisfaz JG < ∞então, pela desigualdade
(1.20), temos
RG ≥
1 1+JG
>0. (1.24)
Podemos obsevar também que a condição RG > 0 é mais geral que JG < ∞, pois a árvore
d-regular Td (d>1) é um exemplo em que JTd =∞e RTd >0.
Um dos principais resultados deste trabalho é o Teorema 1.2 a seguir. Ele nos dá
um critério para grafos mais gerais percolarem. Esse resultado é de alguma maneira, um passo na direção dos resultados e conjecturas discutidos até aqui.
Antes de enunciamos o Teorema1.2, temos que definir o que chamaremos de
geodé-sica e geodégeodé-sica bi-infinita. Umageodésicaρ= (Vρ,Eρ) emGé um subgrafo infinito de Gtal queVρ ={x0, . . . ,xn, . . .},Eρ ={{x0,x1}, . . . ,{xn−1,xn}, . . .}edG(x0,xn)=npara todo
n∈N. Sejamρeρ′dois raios geodésicos emG, ambos iniciando emx0, com conjunto
de vérticesVρ ={x0,x1, . . . ,xn, . . .}eVρ′ ={x0,y1, . . . ,yn, . . .}respectivamente. SeVρVρ′
são tais quedG(xn,ym) = n+m para qualquer{n,m} ⊂ N, então dizemos que a união
ρ∪ρ′ =(Vρ∪Vρ′,Eρ∪Eρ′) é umageodésica bi-infinitaemG. Ou seja, dados dois vértices
xeyem uma geodésica ou geodésica bi-infinitaρ, o caminho entrexeyemρé o menor
caminho. Essas definições nos levam pensar que grafos sem geodésicas bi-infinitas são
objetos parecidos como cunhas deZ2como o Exemplo1.2.5mais adiante. Resultados
sobre a relação entre geodésicas, geodésicas bi-infinitas e os fins de um grafo podem ser vistos em Watkins [83] e Thomassen e Woess [79]. Em [79], Proposição 5.2, os autores mostraram que grafos quase-transitivos têm sempre uma geodésica bi-infinita.
Teorema 1.2. SejaGum grafo infinito com grau máximo∆e com constante contorno RG, como
definido em (1.22). Suponha que
i) RG >0
Então o ponto crítico deGsatisfaz a desigualdade
pc(G)≤1− 1
2(2e∆2)1/RG (1.25)
O Teorema1.2implica o seguinte corolário.
Corolário 1.2.1. Todo grafo transitivoGque possui RG>0tem pc <1.
O Teorema 1.2 é uma extensão do Teorema 1 em Procacci e Scoppola [68], já que
a condição i) no Teorema 1.2 é mais geral que a finitude do parâmetro de
Babson-Benjamini, como ressaltado na Observação4. Como o Teorema1.2contém uma enorme
classe de grafos que percolam tais como redes regulares com Constante de Cheeger CG = 0, árvores regulares, talvez a condição RG > 0 tenha um papel similar ao da
hipótese dim(G) > 1 na Conjectura 1.1. Em particular, é de interesse a questão de
quandoRG >0 para grafos comdim(G)>1.
Sobre o Corolário 1.2.1, é fato que grafos infinitos quase-transitivos possuem 1, 2 ou infinitos fins. Veja Proposições 6.1 e 6.2 em Mohar [57]. SeG tem 2 fins, entãoG
é essencialmenteZ(veja [56]) e portantopc = 1. SeGtem infinitos fins, entãoCG > 0
e assimpc < 1 pela Proposição 1.4mais o argumento de Peierls ou pela Observação4
mais o Teorema1.2. Resta-nos então a pergunta se grafos quase-transitivos com 1 fim, comRG > 0, tempc <1. Tal questão está relacionada com a cota do tipo (1.11) sobre o
número de contornos de determinado tamanho. Veremos na demostração do teorema
1.2que obtemos é, de fato, uma cota como em (1.11). Como observado em Timar [80],
o grafo de Diestel- LeaderDL(2,2) é um exemplo de um grafo transitivo com um fim
que percola, com constante de CheegerCG = 0, mas que possuem contornos, que são
fronteiras de subgrafos chamados tetraedros, que não são j-próximos para nenhum
j ∈ N. Lembre do Exemplo 1.2.1. Sendo assim, a Questão 3 colocada em Babson e
Benjamini [7] respondida negativamente em Timar [80] pode ser refeita pela questão a seguir.
Questão 1. Existe um grafoGquase-transitivo com1fim e constante de Cheeger CG =0para
Exemplo 1.2.4. Aparentemente, o grafo de Diestel-Leader DL(2,2) tem constante contorno
positiva. Lembre que os tetraedros de DL(2,2) são os subgrafos induzidos porTn = {(v,v′) ∈
VDL(2,2) : v∈ Tn, v′ ∈ T′n}em que a fronteira de∂eTndeTné a união disjunta dos conjuntos Fn= {(v,v′) ∈ VDL
(2,2) : o grau em T de v é1}e F′n = {(v,v′) ∈ VDL(2,2) : o grau em T′ de v′ é1}.
Os tetraedros parecem ser os subgrafos que produzem a pior razão na definição da constante contorno (1.5). Vejamos que os tetraedros tem constante contorno positiva. Fixe (o,x′) ∈ Fn
e (x,0′) ∈ F′
n. Agora considere o menor caminho P em DL(2,2) que conecta (0,x′) e (x,o′). Considere também os caminhos dePTePT′ de Tne Tn′, respectivamente, tal queP=PT× PT′.
Observe que o grafo induzido pelos vértices Tn× PT′∪ PT×T′n∪Fn∪F′né uma árvore minimal
que conecta a fronteira de vértices do tetraedro cuja a cardinalidade do seu conjunto de elos é |ETn|+|ET′
n| = 2(2
n−1). Como |Fn|+|F′
n| = 2n+1, temos que o tetraedro Tn tem constante contorno positiva.
O outro importante resultado deste trabalho, Teorema 1.3, refere-se a classe de
grafos sem geodésicas bi-infinitas a qual o Teorema1.2não se aplica.
Teorema 1.3. Seja Gum grafo infinito com grau máximo ∆, com constantes contorno RG e
percolação PG, como definido em (1.22). Suponha que
i) RG >0
ii) PG >0
Então o ponto crítico deGsatisfaz a desigualdade
pc(G)<1− 1
2(2∆2)1/RGe1/PG. (1.26)
A seguir vemos um exemplo de um grafo G comdim(G) = 1, mas com PG > 0 e
RG>0.
Exemplo 1.2.5. Considere o grafoG=(V,E)em que o conjunto de vérticesVé o subconjunto
deZ2dado porV={(x,y)∈Z2 :x≥0, 0≤y≤log(1+x)}e o conjunto de elosE=EV. Veja
a Figura1.4. Note que os subgrafos finitos e conexos que têm menor fronteira emGem relação
elo na fronteira de W1. Se n > 2então diam(Wn) ≤ 2n e |∂eWn| = ⌊log(1+n)⌋ > 1. Assim
temos que dim(G) =1e que |∂eWn|
log(diam(Wn)) ≥ ⌊log(n+1)⌋/log(2n)> log 4/log 6 >0para todo
n>1. Portanto PG >0. Como a árvore minimal que conecta a fronteira de Wné justamente a
linha que conecta os vértices(n,0)e(n,⌊log(n+1)⌋), segue então que RG >0.
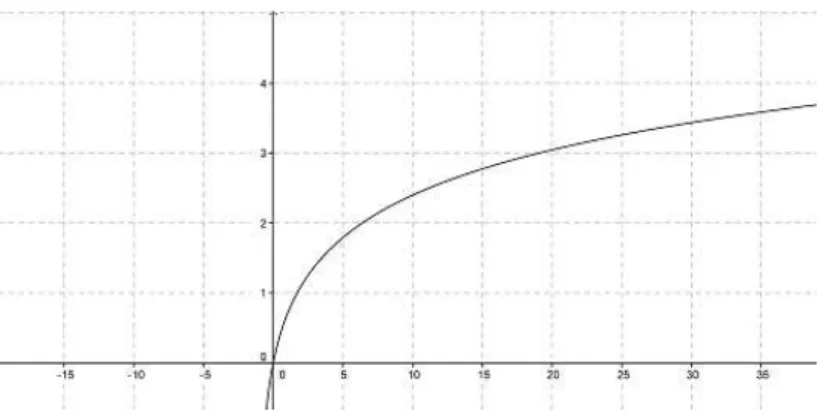
Figura 1.4: O subgrafo deZ2abaixo do gráfico de ln(1+x) e acima do eixo-x.
Observação 5. O Teorema 1.3 pode ser comparado com os resultados obtidos por Campari e
Cassi [20], que podem ser resumidos como
Grafos com dimensão isoperimétrica maior do que1e contornos de tamanho n que são conectáveis com não mais que nLG vértices (LG < ∞) tem uma cota superior
para o número de contornos de tamanho n do tipo Cn, para algum C>0.
A condiçãodim(G) > 1 é muito mais forte que PG > 0. Com efeito, se dim(G) > 1
então existe ǫ > 0, tal que inf
S∈AG
|∂eS|
|S|ǫ > 0. Basta agora notar que isto implica PG > 0 pois log(diam(S))≤ |S|ǫpara todoǫ > 0 e|S|suficientemente grande. De acordo com a discussão da Observação4, a finitude deLGé equivalente aRG >0.
Faremos agora as demostrações dos Teoremas1.2e1.3.
Prova do Teorema1.2: Lembre que seγé um contorno emG=(V,E) ex∈Iγ, então
para qualquer geodésicaρ =(Vρ,Eρ) emGiniciando emxtemos queEρ∩γ ,∅. Então,
para x ∈ V, um contorno γ ∈ Fn
G(x), e uma geodésica ρ iniciando em x, definimos
ex(ρ, γ) como o primeiro elo de Eρ, na ordem natural de ρ, que pertence a γ e, para
rn(x, ρ)={e∈Eρ: ∃γ∈ FGn(x) tal que e=ex(ρ, γ)}. (1.27)
Suponha queGtem uma geodésica bi-infinitaδ. Escolhax, um vértice deδ, e sejam
ρeρ′ duas geodésicas iniciando emxtais queδ= ρ∪ρ′. Então, já queρé geodésica,
temos que|rn(x, ρ)| ≤ supγ∈Fn
Gd
G(x,ex(ρ, γ)) e comoρ∪ρ′ é geodésica bi-infinita comρ
eρ′ iniciando emx, temosd
G(x,ex(ρ, γ))≤dG(ex(ρ′, γ),ex(ρ, γ)) para qualquerγ ∈ FG(x).
Além do mais, see,e′são dois elos quaisquer deγ∈ F
G, então temos quedG(e,e′)≤dtG(γ)
e, por definição,dt
G(γ)≤ |γ|/RG. No fim temos
|rn(x, ρ)| ≤ sup
γ∈FGn(x)
dG(x,ex(ρ, γ))≤ sup
γ∈FGn(x)
dG(ex(ρ′, γ),ex(ρ, γ))
≤ sup γ∈FGn(x)
dt
G(γ)≤
n RG
≤en/RG. (1.28)
Agora observe que
|FGn(x)| ≤
X
e∈rn(x,ρ)
|FGn(e)| ≤ |rn(x, ρ)| sup
e∈E
|FGn(e)|. (1.29)
Nós estimaremos |FGn(e)|, i.e. o número de contornos de cardinalidade fixada n
contendo um elo fixado e. Para cada contorno γ de cardinalidade n tal que e ∈ γ,
defina comoτ(γ) ⊂ Ga árvore com conjunto de elos Eτ(γ) tal que |Eτ(γ)| = dtG(γ). por hipótese RG > 0. Isto implica que, para qualquer contorno γ com cardinalidade n,
|Eτ(γ)| = dtG(γ) ≤ R
−1
G n. Por definição γ ⊂ Eτ(γ), e existem no máximo
R−1
Gn
n
≤ 2R−G1n
maneiras de escolher o conjuntoγemEτ(γ). Então ficamos com
|FGn(e)| ≤
X
τarvore emG
|Eτ|=R−1
Gn,e∈τ
2R−1
Gn. (1.30)
Usando o Lema1.1e queGtem grau máximo∆, temos
|FGn(e)| ≤
h
uniformemente eme∈E. De (1.28) - (1.31) temos
|FGn(x)| ≤ r
n, (1.32)
em que
r=h2e∆2i1/RG (1.33)
Assim, pelo argumento de Peierls1.2, o Teorema1.2está provado.
Prova do Teorema1.3: Escolha agora um vérticex ∈V. Já queGé conexo, infinito
e com grau limitado, existe uma geodésicaρiniciando emx. Sejarn(x, ρ) subconjunto
de elos deρdefinido em (1.27). Comoρé geodésica e, por hipótesePG > 0, nós temos
que para qualquerγ∈ FG, que|γ| ≥PGlog[diam (Iγ)]. Então
|rn(x, ρ)| ≤ sup
γ∈FGn(x)
diam (Iγ)≤en/PG
. (1.34)
Como também RG > 0, nós podemos usar as cotas em (1.30) e (1.31) para concluir
que
|FGn(x)| ≤ r¯
n, (1.35)
em que
¯
r=e1/PGh2∆2i1/RG. (1.36)
1.3 Desigualdades isoperimétricas e a conectividade finita
de dois pontos
1.3.1 A conectividade finita de dois pontos em grafos gerais
A afirmação abaixo é um resultado conhecido em percolação há bastante tempo.
SeGé um grafo com grau máximo∆, então a conectividade finita de dois pontosφfp(x,y) decai (pelo menos) exponencialmente quandodG(x,y)→ ∞,
sepfor suficientemente pequeno.
A prova desta afirmação pode ser encontrada em Grimmett [36] (primeira parte do
Teorema 1.10). O argumento usado é paraZd, mas pode facilmente ser generalizado
para qualquer grafo de grau limitado. Essa afirmação vale para todo o regime subcrítico
em algumas classes de grafos. Podemos ver a prova deste fato para Zd na Seção 5.3
de Aizenman e Newman [1], para grafos quase-transitivos temos o Teorema 3 em
Antunovic e Veselic [6] e para grafos com Constante de Cheeger positiva veja o Teorema 5.3 em Schonmann [71].
Em Procacci e Scoppola [69], Teorema 4.1, os autores obtiveram uma cota superior para a conectividade finita de dois pontos para o modelo de aglomerado aleatório com parâmetrosp ∈ [0,1] eq > 0 em um grafo de grau limitado G, mostrando que a
mesma decai pelo menos exponencialmente paraqfixado epsuficientemente próximo
de zero. Como o processo de percolação independente emGcoincide com o modelo
de grafo aleatório no mesmo grafo, comq=1, o Teorema 4.1 de [69] também implica a afirmação acima. Neste mesmo trabalho, os autores estudaram também propriedades de decaimento da conectividade de dois pontos, no modelo de aglomerado aleatório, com parâmetros q > 0 e p ∈ [0,1] perto de 1. No entanto, eles obtiveram uma cota superior para a conectividade finita da forma,
em queC1 eC2são constantes e fG(x,y) é o número definido abaixo.
Definição 1.6. Dado um grafoG= (V,E), seja x,y ∈ V. Definimos adistância contorno
fG(x,y)por
fG(x,y)= min
γ∈FG γJ
{x,y}
|γ|. (1.38)
Não é difícil ver que existem grafos em que a distância contorno se comporta da seguinte maneira: fG(x,y)/dG(x,y) → 0 quando dG(x,y) → ∞, veja Exemplo 1.3.1
abaixo.
Exemplo 1.3.1. Considere o grafo G do Exemplo 1.2.5, ou seja, G = (V,E) é o grafo cujo
conjunto de vérticesV é o subconjunto de Z2 dado por V = {(x,y) ∈ Z2 : x ≥ 0, 0 ≤ y ≤
ln(1+x)}e o conjunto de elosE= EV. Note que fG((0,0),(n,0)) = |∂eWn|= ⌊ln(1+n)⌋em
que Wn ={(x,y)∈V: x≤n}. Assim fG(x,y)/dG(x,y)→0quando dG(x,y)→ ∞.
Definição 1.7. Dizemos que em um grafo G = (V,E) a conectividade finita de dois pontos
φpf(x,y)decai subexponencialmenteoudecai exponencialmentese
−log(φpf(x,y)) dG(x,y)
→ 0
>0
(1.39)
quando dG(x,y)→ ∞, respectivamente.
Tendo em vista esse fato, os autores em [69] propuseram a seguinte questão.
Questão 2. Há grafos em que a conectividade finita decai subexponencialmente, mesmo quando
p está arbitrariamente próximo de1? Isto é, podemos ter um decaimento da conectividade finita mais lento que o decaimento exponencial?
1.3.2 Decaimento exponencial
/
subexponencial da conectividade finita
de dois pontos
Motivado pelas questões discutidas anteriormente, apresentaremos dois outros te-oremas desta tese.
O primeiro deles, Teorema1.4, nos mostra que o decaimento exponencial da conecti-vidade finita também vale na fase supercrítica, quandopestá suficientemente próximo de 1, se nos restringimos a classe dos grafos que satisfazem a hipótese do Teorema1.2.
Teorema 1.4. SejaG=(V,E)um grafo de grau limitado que satisfaz as hipóteses do teorema
1.2, isto é, possui geodésica bi-infinita e RG > 0. Se r = 2e∆2
1/RG
, p ≥ 4r+4r1 e x,y ∈ V são
vértices que pertencem a uma geodésica bi-infinita, então
φfp(x,y) ≤ 4 3
"r(1 −p) p
#RGdG(x,y)
. (1.40)
Observação 6. O decaimento exponencial da conectividade finita na fase supercrítica foi
pro-vado paraZd por Chayes, Chayes e Newman [22] (veja também [23]) e por Chen, Peres e Pete
[24] para grafos com constante de Cheeger positiva. Não é de nosso conhecimento uma prova desse fato para grafos mais gerais que os mencionados no Teorema1.4.
O segundo teorema, Teorema1.5, diz respeito ao decaimento da conectividade finita em grafos satisfazendo a hipótese do teorema1.3. O Teorema1.5, em particular, nos
dá uma cota inferior como (1.37) respondendo assim, afirmativamente, a Questão 2
levantada em Procacci e Scoppola [69].
Teorema 1.5. SejaG=(V,E)um grafo de grau limitado que satisfaz as hipóteses do Teorema
1.3, isto é, PG > 0e RG > 0. Ser¯ = e1/PG
2
∆21/RG
e p ≥ 14¯+rr¯, então para quaisquer x,y ∈ V
temos que
1 3 h
(1−p)pR−G1
ifG(x,y)
≤ φpf(x,y) ≤ 43 "r(1¯
−p) p
#fG(x,y)
. (1.41)
Observação 7. Note que o grafo Gdo Exemplo 1.3.1 é um exemplo em que a conectividade
φpf((0,0),(n,0))em Gpossui a cota inferior 13(1+n)−α1(p) e a cota superior 43(1+n)−α2(p) com
α1(p)=|ln[(1−p)pR
−1
G]|eα2(p)=|ln[¯r(1−p)p−1]|. Deste modo, o teorema acima nos diz que,
para p grande o suficientelog(φpf(x,y))/dG(x,y)→0, quando dG(x,y)→ ∞.
Terminamos este capítulo com as demonstrações dos Teoremas 1.4 e1.5,
respecti-vamente.
Prova do teorema1.4: Dado um grafoG=(V,E), dizemos que a sequência{VN}N∈N
de subconjuntos finitos de V tende monotonicamente para V, e escrevemos VN ր V,
se para todo N ∈ N, VN é conexo, VN ⊂ VN+1, e ∪N∈NVN = V. Considere o grafo
GN =(VN,EN).
Sejam x,y dois vértices que pertencem a uma geodésica bi-infinita de G. Escolha
uma sequência {VN}N∈N que tende monotonicamente para V e suponha N grande o
suficiente para que{x,y} ∈VN\∂intv VN. Podemos definir agora a conectividade finita de dois pontos, a volume finito como
φfp,N(x,y)=
X
ω∈ΩN:∃gaglomerado aberto
{x,y}⊂Vg, ∂g⊂EN
p|A(ω)|(1−p)|F(ω)|, (1.42)
de modo que
φfp(x,y)=Nlim
→∞φ
f,N
p (x,y), (1.43)
já que os eventos definidos nas probabilidadesφfp,N(x,y) crescem para o evento definido emφfp(x,y).
Portanto, se obtivermos um cota superior paraφfp,N(x,y) uniformemente emNentão obteremos a mesma cota paraφfp(x,y).
Denote
λ≡λ(p)= 1−p p .
φfp,N(x,y)= 1 ZN(p)
X
ω∈ΩN:∃gaglomerado aberto
{x,y}⊂Vg, ∂g⊂EN
λ|F(ω)|, (1.44)
em que
ZN(p)= X ω∈ΩN
λ|F(ω)|=p−|EN|. (1.45)
Uma configuraçãoω∈ΩNé especificada se conhecemos o conjunto de elos fechados. SeC=C(ω) é um conjunto de elos fechados emEN, nós escreveremosC⊙ {x,y}quando existe um contornoγ⊂Ctal queγ⊙{x,y}. Fixada uma configuraçãoω∈Ω, então existe
um único contornoγ contido na fronteira do aglomerado aberto (emω) que contém
{x,y}. Com efeito, a fronteira do aglomerado aberto que contém{x,y}é um conjunto
de corte pela Definição1.2. Se a fronteira não é um contorno, então existe um eloeda fronteira tal queG\(γ\e) ainda tem uma componente conexa finita que é o aglomerado
aberto de{x,y}. Deste modo defina γ como sendo a fronteira do aglomerado menos
esses elos. Suponha agora que exista dois contornosγ eγ′ para o aglomerado aberto
que contém{x,y}. Então existe um elo e ∈ γ′ tal que e < γ. Mas assim o grafo G\γ
contém o eloe, logoG\γ é conexo porqueγ′ é contorno. Isso contradiz o fato de que
γé contorno.
Sendo assim,
ZN(p)= X C⊂EN
λ|C|=p−|EN| (1.46)
e
φfp,N(x,y)= 1 ZN(p)
X
C⊂EN
C⊙{x,y}
λ|C|. (1.47)
Portanto,
φfp,N(x,y)≤ 1 ZN(p)
X
γ∈FGN(x,y)
λ|γ| X
C⊂EN\γ
C∪γ⊙{x,y}
λ|C|≤ X γ∈FG(x,y)
λ|γ|. (1.48)
![Figura 1.1: Representação de uma configuração do modelo de Ising em contornos de elos duais em uma caixa finita de Z 2 com condição de fronteira + [ 81 ].](https://thumb-eu.123doks.com/thumbv2/123dok_br/15133253.13608/18.892.386.558.177.348/figura-representacao-configuracao-modelo-contornos-finita-condicao-fronteira.webp)
![Figura 1.2: Um aglomerado aberto da origem de Z 2 cercado por um circuito fechado no dual [ 38 ].](https://thumb-eu.123doks.com/thumbv2/123dok_br/15133253.13608/19.892.267.672.752.1029/figura-aglomerado-aberto-origem-cercado-circuito-fechado-dual.webp)
![Figura 1.3: O grafo de Diestel Leader DL(2,2) [ 84 ].](https://thumb-eu.123doks.com/thumbv2/123dok_br/15133253.13608/28.892.207.714.733.979/figura-grafo-de-diestel-leader-dl.webp)