Uma estratégia aleatória chamada de MOSES

(1)

Universidade Federal do Rio Grande do Norte

Centro de Ciˆencias Exata e da Terra

Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica

Maria Jucimeire dos Santos

Uma Estrat´

egia Aleat´

oria Chamada de

MOSES

(2)

Maria Jucimeire dos Santos

Uma Estrat´

egia Aleat´

oria Chamada de

MOSES

Disserta¸cão apresentada ao Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica da Universidade Federal do Rio Grande do Norte, em cumprimento com as exigências legais para obten¸cão do t´ıtulo de Mestre.

´

Area de Concentra¸c˜ao: Probabilidade e Estat´ıstica

Orientador:

Prof. Juan Alberto Rojas Cruz

(3)

Catalogação da Publicação na Fonte. UFRN / SISBI / Biblioteca Setorial Centro de Ciências Exatas e da Terra – CCET.

Santos, Maria Jucimeire dos.

Uma estratégia aleatória chamada de MOSES / Maria Jucimeire dos Santos. - Natal, 2013.

73 f. : il.

Orientador: Prof. Dr. Juan Alberto Rojas Cruz.

Dissertação (Mestrado) – Universidade Federal do Rio Grande do Norte. Centro de Ciências Exatas e da Terra. Programa de Pós-Graduação em Matemátca Aplicada e Estatística.

1. Cadeias de Markov – Dissertação. 2. Convergência – Dissertação. 3. Estratégia evolutiva – Dissertação. 4. Grandes desvios – Dissertação. 5. Probabilidade – Estatística – Dissertação. I. Cruz, Juan Alberto Rojas. II. Título.

(4)

(5)

Dedicat´

oria

(6)

Agradecimentos

Primeiramente agrade¸co a Deus que me deu sa´ude e for¸cas para vencer essa batalha. E colocou na minha vida pessoas maravilhosas que contribu´ıram bastante para realiza¸c˜ao deste trabalho.

A minha mãe Maria de Fátima que não tenho nem palavras para descrever o quanto foi importante nessa etapa da minha vida. Caminhou ao meu lado em todos os momentos, a distância e o pouco estudo não foram obstáculos para que ela compreendesse cada fase pela qual estava passando.

Ao meu pai Juarez que sempre acreditou em mim, torceu e fez o que pode para que eu alcan¸casse esse sonho.

Aos meus irm˜aos Jairo e Juciane, pelo amor, dedica¸c˜ao e carinho. Exemplos de apoio uns aos outros.

Ao meu sobrinho Juan Victor que por várias vezes me fez esquecer as minhas preocupa¸cões e entrar no seu mundo mágico, onde tudo é brincadeira.

A minha cunhada Gercileide que desde a gradua¸c˜ao tem colaborado para eu atingir meus objetivos. Sempre pedindo a Deus o meu sucesso.

Ao meu orientador Juan Rojas pela sugest˜ao do tema, por sua paciˆencia, seus ensinamentos e conselhos.

A Antonio um anjo que surgiu na minha vida, sempre se dispôs a me ajudar, a me ouvir. Obrigada pelas sugestões, discussões e ensinamentos.

A Rafael que me ensinou utilizar o software Matlab e contribui na programa¸c˜ao do meu algoritmo.

A Michele que alimentou este sonho e sempre esteve ao meu lado, me apoiando e me guiando.

A Alécia, amiga com a qual tenho uma d´ıvida impagável. Obrigada pelo apoio recebido desde a minha gradua¸cão em Caicó e também pelo impulso para a minha vinda a natal.

(7)

meus objetivos.

As minhas amigas de Caic´o Mariane, Gerlˆania, Denizy e Marluce que sempre contei com elas para compartilhar minhas alegrias, tristezas e dificuldades.

As minhas amigas Ta´ıs, Suzara, Iselda, Gabi, Monara e Carlinha pela aten¸c˜ao, carinho, companheirismo, gargalhadas, momentos de descontra¸c˜ao e todo apoio.

As Mipibuenses pela convivˆencia, em especial a todas que incentivaram e co-laboraram de alguma forma para realiza¸c˜ao deste trabalho.

Aos meus amigos Alcilene, Fabiana, Rafael e Luiz. A amizade de vocˆes me fortalece.

A minha amiga Paulinha pela for¸ca, carinho e amizade. Sempre t˜ao ocupada e mesmo assim encontrava tempo para me ouvir.

A todos os professores do mestrado pelos ensinamentos e conselhos.

Aos meus colegas de mestrado Rafaela, Alex, Aldemir, Ivanildo, Marcio, Jose-mir e Elisângela, companheiros de momentos de angústia, de estudos e reflexões. E a todos os demais colegas do PPGMAE pela for¸ca e carinho.

A Paulinho e Elvis, monitores da escola de ver˜ao, colegas e amigos. Obrigada por me ajudar desde o in´ıcio.

A professora Viviane que esteve presente na pr´e-qualifica¸c˜ao. Obrigada pelos conselhos.

Ao professor André Gustavo que esteve presente na qualifica¸cão. Suas cr´ıticas e sugestões me fortaleceram para a defesa.

A professora Daniele que aceitou o nosso convite para estar presente na defesa de mestrado. Obrigada pelas sugest˜oes.

Em especial agrade¸co a professora Débora que esteve presente em todas as etapas desse trabalho, pré-qualifica¸cão, qualifica¸cão e defesa. Obrigada por todas as cr´ıticas e sugestões. Sua presen¸ca na defesa foi muito importante para mim.

Agrade¸co a todos os funcion´arios do CCET em especial a Liandra, Russinho e a Rafael secret´ario.

A Capes pelo apoio financeiro.

(8)

Resumo

Neste trabalho estudamos uma estratégia aleatória chamada de MOSES, que foi introduzida por Fran¸cois em 1996. Resultados assintóticos desta estratégia; com-portamento das distribui¸cões estacionárias da cadeia associada a estratégia, foram derivados por Fran¸cois, em 1998, da teoria de Freidlin e Wentzell [8]. Detalhamentos destes resultados estão neste trabalho. Por outro lado, notamos que uma aborda-gem alternativa da convergência desta estratégia é poss´ıvel sem fazer uso da teoria de Freidlin e Wentzell, obtendo-se a visita quase certa da estratégia às popula¸cões uniformes que contêm o m´ınimo. Algumas simula¸cões no Matlab são apresentadas neste trabalho.

(9)

Abstract

This paper we study a random strategy called MOSES, which was introduced in 1996 by Fran¸cois. Asymptotic results of this strategy; behavior of the stationary distributions of the chain associated to strategy, were derived by Fran¸cois, in 1998, of the theory of Freidlin and Wentzell [8]. Detailings of these results are in this work. Moreover, we noted that an alternative approach the convergence of this strategy is possible without making use of theory of Freidlin and Wentzell, yielding the visit almost certain of the strategy to uniform populations which contain the minimum. Some simulations in Matlab are presented in this work.

(10)

Sum´

ario

1 Cadeias de Markov 3

1.1 Processos Estoc´asticos . . . 3

1.2 Cadeias de Markov . . . 4

1.2.1 Cadeias de Markov Irredut´ıveis . . . 5

1.2.2 Convergˆencia da Cadeia de Markov . . . 6

1.2.3 Cadeias de Markov N˜ao-Homogˆeneas . . . 8

2 Estrat´egia Aleat´oria MOSES 12 2.1 Algoritmos Evolutivos . . . 12

2.2 Cotas para as Probabilidades de Transi¸c˜ao . . . 15

2.2.1 Dinˆamica da estrat´egia . . . 16

3 Comportamento Assint´otico da estrat´egia MOSES 24 3.1 x-grafo . . . 24

3.2 Princ´ıpio dos Grandes Desvios . . . 29

3.3 Convergˆencia da Estrat´egia MOSES . . . 29

4 Convergência Quase Certa da Estratégia MOSES 39 5 Estratégia MOSES no Matlab: Algumas Simula¸cões 44 5.1 Testes Sobre Tempo Médio da Primeira Visita da estratégia MOSES ao M´ınimo . . . 45

5.2 MOSES Versus Simulated Annealing em Paralelo . . . 48

(11)

SUM ´ARIO 1

Apˆendice 54

Programas . . . 54

Estrat´egia MOSES . . . 54 Simulated Annealing em Paralelo . . . 57

(12)

Introdu¸

c˜

ao

Neste trabalho apresentamos um tipo de estratégia aleatória chamada MOSES (Estratégia Evolutiva Sele¸cão-Muta¸cão) introduzida em 1996, por Fran¸cois [6].

A dinâmica da estratégia emprega muta¸cão e sele¸cão (sem cruzamento). O objetivo de MOSES é encontrar o m´ınimo global de uma fun¸cãof :E →R_{, chamada}

de fun¸cão objetivo, ondeEé um conjunto finito. Uma vizinhan¸ca para cada elemento em E é determinado por um grafo g = (E, A), estas vizinhan¸cas determinam as muta¸cões da estratégia.

Este trabalho ´e baseado no artigo “An evolutionary strategy for global mini-mization and its Markov chain analysis” de Fran¸cois [7].

(13)

Cap´ıtulo 1

Cadeias de Markov

O intuito deste cap´ıtulo é servir como suporte para a leitura deste trabalho. Apresentamos os resultados essenciais da teoria de cadeia de Markov homogênea e não-homogênea, uma vez que a estratégia MOSES possui uma estrutura Markoviana.

1.1 Processos Estoc´

asticos

Defini¸cão 1.1.1. Um Processo Estocástico é uma fam´ılia de variáveis aleatórias definidas sobre o mesmo espa¸co amostral Ω. Se a fam´ılia é enumerável o processo

é denotado por {Xt}_t_∈N. Se a fam´ılia é não-enumerável o processo é denotado por

{Xt}_t_∈[0_,_∞). No primeiro caso, o processo ´e dito um processo a tempo discreto,

enquanto no segundo caso ´e dito a tempo cont´ınuo.

Um processo estocástico pode ser visto como uma fun¸cão de duas variáveis

Xt(w) =X(t, w).

Parat fixo, a fun¸cão é uma variável aleatória e para w fixo temos uma fun¸cão real de t que é chamada de trajetória.

Defini¸c˜ao 1.1.2. O conjunto S de todos os valores assumidos pelo processo ´e cha-mado espa¸co de estados.

(14)

1.2 Cadeias de Markov 4

tempo t. Se o processo no tempo t−1 se encontra no estado i, a probabilidade condicional de no tempot estar no estado j ´e representado por

P(Xt =j|Xt−1 =i),

esta probabilidade ´e chamada de probabilidade de transi¸c˜ao.

1.2 Cadeias de Markov

Um Processo Estoc´astico {Xt}t∈N com espa¸co de estados S = {i1, i2, i3, . . .},

satisfaz `a propriedade de Markov se para todote todos os estados{i1, i2, . . . , it} ∈S temos

P(Xt =it|Xt−1=it−1, Xt−2 =it−2, . . . , X1 =i1) =P (Xt = it|Xt−1=it−1).

Defini¸cão 1.2.1. Um processo a tempo discreto, com espa¸co de estados enumerável, que satisfaz à propriedade de Markov é chamado de cadeia de Markov.

Uma cadeia de Markov é dita homogênea quando as probabilidades de transi¸cão não mudam no tempo, isto é, para todos os estados i, j∈S temos que:

P(Xt+1 =j|Xt =i) =P (X2 =j|X1 =i), ∀t≥1.

A cadeia de Markov é dita não-homogênea se as probabilidades de transi¸cão mudam com o tempo. No caso homogêneo temos

pij =P (Xt =j|Xt−1 =i), ∀ t≥1.

A probabilidade de transi¸c˜ao em n passos pn

ij ´e definida:

pn_ij =P(Xt+n =j|Xt =i), n≥0, i, j ∈S.

Dada uma cadeia de Markov homogˆenea{Xt}t∈N com espa¸co de estados finito

S = {1,2, . . . , n}, existem n2 _{probabilidades de transi¸c˜ao} _p

ij, i = 1,2, . . . , n e

(15)

1.2 Cadeias de Markov 5 P =     

p11 p12 · · · p1n

p21 p22 · · · p2n

... ...

pn1 pn2 · · · pnn

     .

Como veremos adiante, esta matriz não é só uma boa maneira de guardar as informa¸cões das probabilidades de transi¸cão, as suas potências determinam o com-portamento da cadeia. Observe as seguintes propriedades das matrizes de transi¸cão:

(i) Todas as entradas s˜ao n˜ao-negativas, pois representam probabilidades;

(ii) As somas das entradas em cada linha ´e sempre 1.

Uma matriz quadrada que satisfaz as propriedades acima ´e chamada deMatriz Estoc´astica.

1.2.1 Cadeias de Markov Irredut´ıveis

Seja P = (pij)_i,j_∈_S a matriz de transi¸cão de uma cadeia homogênea. As equa¸cões deChapman-Kolmogorovfornecem um método para calcular as proba-bilidades de transi¸cão emn passos. Essas equa¸cões são:

pn_ij+m=

∞

X

k=0

pn_ikpm_kj, ∀ n, m≥0, ∀ i, j∈S.

Se considerarmos P(n) _{como a matriz das probabilidades de transi¸c˜ao em} _n

passospn

ij, ent˜ao a equa¸c˜ao anterior afirma que:

P(n+m) =P(n)·P(m),

onde o ponto representa a multiplica¸c˜ao das matrizes. Assim,

P(n) =P ·P(n−1)= P ·P ·P(n−2)=· · · =Pn

dessa forma, P(n) _{pode ser calculada multiplicando a matriz} _P _{por ela mesma} _n

vezes.

Defini¸c˜ao 1.2.2. O estado j ´e dito ser acess´ıvel a partir do estado i se existe um

n∈N_{, tal que}_pn

(16)

i→j ej →i, ou seja, existe um n1 ∈N tal que pnij1 >0e existe um n2 ∈N tal que

pn2

ji >0. Denotamos por i↔j.

Defini¸c˜ao 1.2.3. Quando todos os estados da cadeia se comunicam dizemos que a cadeia ´eirredut´ıvel.

Defini¸c˜ao 1.2.4. Definimos oper´ıodo de um estado i como sendo

d(i) =mdc{n≥1;pn_ii >0}.

Se d(i) = 1 dizemos que o estado i´e aperi´odico.

Proposi¸c˜ao 1.2.1. Se i↔ j, ent˜ao d(i) =d(j).

Pela Proposi¸cão 1.2.1 podemos concluir que se uma cadeia é irredut´ıvel então todos os estados têm o mesmo per´ıodo. Dessa forma, se um estado tem per´ıodo

d= 1, ou seja, é aperiódico, então todos os outros estados são aperiódicos. Quando isso ocorre dizemos que a cadeia éaperiódica.

1.2.2 Convergˆ

encia da Cadeia de Markov

Defini¸c˜ao 1.2.5. Seja P uma matriz de transi¸c˜ao de uma cadeia de Markov. Se para todo j ∈ S existe lim

n→∞p (n)

ij = πj e

∞

X

j=1

πj = 1, ent˜ao dizemos que a cadeia ´e

erg´odica.

Defini¸cão 1.2.6. Uma distribui¸cão de probabilidade {πj, j∈S} é chamada

distri-bui¸cão estacionária da cadeia de Markov com matriz de transi¸cãoP = (pij)_i,j_∈_S, S =

{1,2,3, . . .}, se

πj =

X

l∈S

πlplj, ∀ j.

Em forma matricial

π =πP =πP2 =πP3=. . .

(17)

Teorema 1.2.2. Seja {Xn} uma cadeia de Markov com espa¸co de estados finito,

irredut´ıvel e aperiódica com matriz de transi¸cãoP = (pij)_i,j_∈_S. Então lim n→∞p

(n)

ij = πj,

onde π= (πj)é a distribui¸cão estacionária.

Observe que o teorema acima garante a existência do comportamento limite da cadeia e também mostra uma forma de encontrar esse limite, bastando para isso encontrar a distribui¸cão estacionária.

Corolário 1.2.3. Toda cadeia de Markov homogênea irredut´ıvel, aperiódica com espa¸co de estados finito possui uma única distribui¸cão estacionária e converge para

ela.

Defini¸c˜ao 1.2.7. Para quaisqueri, j ∈S, a probabilidade de que partindo do estado

i, a primeira visita do processo ao estado j se dˆe no passo n´e dada por,

f_ijn =P(Xn =j, Xn−1 =6 j, ..., X1 6=j|X0 =i).

Defini¸c˜ao 1.2.8. Para os estados i, j fixos, sejaf∗

ij =

∞

X

n=1

f_ij(n). Onde f∗

ij representa

a probabilidade de visitar o estadoj dado que o processo partiu do estadoi. Sei=j,

f∗

ii =

∞

X

n=1

f_ii(n) denota a probabilidade de retornar ao estadoi.

Defini¸c˜ao 1.2.9. O estado j ´e dito ser recorrente se f∗

jj = 1. Se fjj∗ < 1, ent˜ao o

estado j ´e dito transiente.

Defini¸c˜ao 1.2.10. Se f∗

jj= 1, definimos o tempo m´edio de recorrˆencia ao estado j

como µj =

∞

X

n=1

nf_jj(n).

Defini¸c˜ao 1.2.11. Seja j um estado recorrente,

(i) µj =∞ ⇒ j ´e recorrente nulo, (ii) µj <∞ ⇒ j ´e recorrente positivo.

Teorema 1.2.4. Seja P a matriz de transi¸c˜ao de uma cadeia de Markov irredut´ıvel e recorrente positiva. Ent˜ao 1

n

X

k=1

p(_ijk) converge quandon→ ∞e o limite ´e 1

µj

(18)

µj é o tempo médio de recorrência do estado j. O vetor π =

1 µ1 , 1 µ2 , . . . ´e uma

distribui¸c˜ao estacion´aria de P.

Teorema 1.2.5. Para cada cadeia de Markov irredut´ıvel com espa¸co de estados S

existe uma sequˆencia {πj, j ∈S} tal que para cadai e j ∈S lim n→∞ 1 n n X k=1

p(_ijk)

=πj. (1.1)

Teorema 1.2.6. Seja S o espa¸co de estados de uma cadeia de Markov irredut´ıvel. Se S é finito, então a cadeia de Markov possui uma única distribui¸cão estacionária.

A demonstra¸cão do Teorema 1.2.4 pode ser encontrada em Isaacson [11] e as demonstra¸cões dos Teoremas 1.2.5 e 1.2.6 são encontradas em Parzen [13].

1.2.3 Cadeias de Markov N˜

ao-Homogˆ

eneas

Uma Cadeia de Markov Não-Homogênea é descrita por um vetor inicial f(0)

e uma sequência de matrizes de transi¸cão{Pk}∞k=1, onde f(0) é uma distribui¸cão de

probabilidade sobre os estados, isto ´e:

f_i(0)≥0, i= 1,2, ... e

∞

X

i=1

f_i(0) = 1.

Defini¸c˜ao 1.2.12. Sejam P1, P2, ...matrizes de transi¸c˜ao de uma cadeia de Markov

n˜ao-homogˆenea com vetor inicial f(0)_{. Definimos:}

f(k)=f(0)P1·P2·...·Pk e f(m,k)=f(0)Pm+1·...·Pk.

Definimos o j-´esimo elemento de f(k) _por _f(k)

j = P(Xk =j) e definimos o (i, j)-´esimo elemento deP(m,k)₌_P

m+1·Pm+2·...·Pk porPi,j(m,k)=P(Xk = j|Xm=i).

Analogamente para g(k)_{, g}(m,k) _e _g(m,k)

(19)

O objetivo principal da teoria de cadeia de Markov não-homogênea é o com-portamento de f(k) _e _f(m,k) _quando _k _{→ ∞}_{. Pode acontecer que}_f(k) _{convirja para}

o mesmo vetor fixo q, independentemente do vetor inicial f(0) _{utilizado, isto ´e, um}

vetor limite existe e é independente da escolha do vetor inicial. Neste caso, a in-forma¸cão sobre f(k)_{, para} _k _{grande, dá-nos pouca ou nenhuma informa¸cão sobre}

f(0)_{, ou seja, o efeito de} _f(0) _{´e perdido ao longo do tempo. Quando} _f(m,k) _→ _q

quando k → ∞, ∀ m ∈ N_{, independe de} _f(0)_{, este comportamento ´e conhecido}

como convergência com perda de memória e é chamado deergodicidade forte. É poss´ıvel ter também convergência sem perda de memória e perda de memória sem convergência. No último caso o efeito da distribui¸cão inicial é perdido, ou seja, f(k)

e g(k) _{estão em algum sentido próximos, mas não necessariamente existe uma}

con-vergˆencia def(k) _{nem de}_g(k)_{. Esse comportamento ser´a chamado de}_ergodicidade

fraca.

Para efeito de estudar a convergˆencia da cadeia de Markov ´e comum usar a seguinte norma.

Defini¸c˜ao 1.2.13. Se f = (f1, f2, f3, ...)´e um vetor, definimos a norma de f por

kfk=

∞

X

i=1

|fi|.

E se A= (aij) ´e uma matriz quadrada, definimos a norma de Apor

kAk= sup i

∞

X

i=1

|aij|.

Defini¸cão 1.2.14. Uma cadeia de Markov não-homogênea é chamada fracamente ergódica se para todo m

lim

k→∞_f(0)sup_,g(0)

f(m,k)−g(m,k)

= 0

onde f(0) _e _g(0) _{s˜ao vetores iniciais.}

Quando o espa¸co de estados ´e finito o conceito de ergodicidade fraca ´e equiva-lente a: lim n→∞ P

(m,m+n)

ij −P

(m,m+n)

kj

(20)

Outra equivalˆencia para o conceito de ergodicidade fraca ´e:

lim k→∞δ P

(m,k)

= 0, ∀m≥0,

onde δ(Q) = 1−α(Q) e α(Q) ´e o coeficiente erg´odico de Dobrushin definido por

α(Q) = 1−max i,k∈S

X

j∈S

[qij −qkj]+, com [qij −qkj]+= max{0, qij −qkj}. Podemos reescrever o coeficiente erg´odico de Dobrushin como

α(P) = min i,k∈E

X

j∈E

min (Pij, Pkj). Outra desigualdade importante ´e a seguinte:

δ(P Q)≤δ(P)δ(Q).

Defini¸cão 1.2.15. Uma cadeia de Markov não-homogênea é chamada fortemente ergódica se existir um vetor q= (q1, q2, ...), comkqk= 1e qi ≥0, parai= 1,2,3, ...

tal que para todo m

lim k→∞sup_f(0)

f(m,k)−q

= 0,

onde f(0) _{´e um vetor inicial.}

Os dois teoremas a seguir s˜ao resultados fundamentais sobre a ergodicidade forte.

Denotamos por℘a classe das matrizes estocásticasP para as quais existe pelo menos um autovetor à esquerda não negativoψ correspondendo ao autovalor 1 e tal que kψk= 1.

Teorema 1.2.7. Seja{Pn}uma sequˆencia de matrizes de transi¸c˜ao correspondentes

a uma cadeia de Markov não-homogênea fracamente ergódica comPn ∈℘ para todo

n. Se existir uma sequˆencia correspondente de autovetores ψn satisfazendo

X

j

(21)

então a cadeia é fortemente ergódica.

Teorema 1.2.8. Seja{Pn}uma sequˆencia de matrizes de transi¸c˜ao correspondentes

a uma cadeia de Markov n˜ao-homogˆenea com Pn ∈ ℘. Se kPn−Pk → 0 quando

(22)

Cap´ıtulo 2

Estrat´

egia Aleat´

oria MOSES

2.1 Algoritmos Evolutivos

Os algoritmos evolutivos s˜ao processos de pesquisa global que procuram o

m´ınimo global de uma fun¸c˜ao f :E→R_{, onde}_E _{´e finito.}

Em [5] é apresentado um quadro básico para algoritmos evolutivos que é o

seguinte:

1. Inicializa com uma popula¸c˜ao de solu¸c˜oes em E;

2. Avalia cada solu¸c˜ao na popula¸c˜ao;

3. Propõe algumas mudan¸cas aleatórias na popula¸cão;

4. Usa um critério de rejei¸cão para validar cada altera¸cão e avaliar as novas

solu¸c˜oes;

5. Se um critério de parada é satisfeito, retorna a melhor solu¸cão; caso contrário,

vai para etapa 3;

Exemplos desses algoritmos evolutivos s˜ao os algoritmos gen´etico, Simulated

(23)

2.1 Algoritmos Evolutivos 13

formadas por indiv´ıduos, onde cada indiv´ıduo possui representa¸c˜ao bin´aria. O

algo-ritmo pode ser descrito como segue:

Escolhe aleatoriamente uma popula¸c˜ao inicial

Repete:

• Execute sele¸c˜ao;

• Execute cruzamento;

• Execute muta¸c˜ao;

at´e que algum crit´erio de parada seja satisfeito.

Dada uma popula¸cão (b1, b2, . . . , bn) a probabilidade que o indiv´ıduo bi fa¸ca parte da próxima gera¸cão é usualmente definida como:

P(bi´e selecionado) =

f(bi) n

X

j=1

f(bj)

.

A muta¸cão da popula¸cão (b1, b2, . . . , bn) para a popula¸cão

´

b1,b´2, . . . ,b´n

acon-tece com a seguinte probabilidade:

Pbi→ b´i

=pHm(bi,bi)´ (1−pm)l−H(bi,

´

bi)

ondeHbi,b´i

é distância Hamming (número de posi¸cões em que os bits

correspon-dentes são diferentes) entre os caracteres bi e ´bi. Uma referência elementar sobre os algoritmos genéticos pode ser, por exemplo, [14] e [4].

O Algoritmo Simulated Annealing é uma técnica utilizada em problemas de otimiza¸cão combinatória, isto é, min

x f(x), x ∈E, onde f :E →

R_, _E _{finito. O}

termo Annealing ´e associado a um processo utilizado para fundir um metal, onde

este ´e aquecido a uma temperatura elevada e em seguida ´e resfriado lentamente de

(24)

2.1 Algoritmos Evolutivos 14

otimiza¸cão é realizado por n´ıveis em que há a simula¸cão dos n´ıveis de temperatura

no resfriamento. Em cada n´ıvel, dado um pontou∈E, vários pontos na vizinhan¸ca de u são gerados e o correspondente valor de f é calculado. Cada ponto gerado é aceito ou rejeitado de acordo com uma certa probabilidade. Esta probabilidade

de aceita¸c˜ao decresce de acordo com o n´ıvel do processo, ou equivalentemente, de

acordo com a temperatura (veja [9]).

Neste cap´ıtulo, abordamos uma estrat´egia aleat´oria chamada MOSES que pode

ser vista como uma simplifica¸cão do algoritmo genético clássico, uma vez que existe

muta¸cão e sele¸cão; porém não acontece cruzamento, o que evita trabalhar com

representa¸cão binária e simplifica muito o tratamento matemático do mesmo. Esta

estratégia objetiva identificar o m´ınimo global de uma fun¸cãof, chamada de fun¸cão objetivo,f :E→ R_{, onde}_E _{é um conjunto finito, no qual é definida uma estrutura}

de grafog = (E, A), sendoEo conjunto dos v´ertices do grafo eAdenota o conjunto das arestas. Essa estrutura define uma vizinhan¸ca para cada v´ertice emE.

A dinâmica da estratégia MOSES emprega mecanismos de muta¸cão e sele¸cão.

A muta¸cão atua como um passeio aleatório no grafo g e o processo de sele¸cão atua identificando o indiv´ıduo com a menor imagem e também selecionando os indiv´ıduos

a serem mutados para o menor elemento da popula¸c˜ao atual. Os parˆametros

asso-ciados à estratégia MOSES, tais como o tamanho da popula¸cão, probabilidades

de muta¸c˜ao e a geometria do problema (do grafo g = (E, A)) determinam a con-vergˆencia para um m´ınimo global (veja os Teoremas 3.3.5 e 3.3.7). No Cap´ıtulo 4,

obtemos resultados sobre a convergência da estratégia MOSES, estes resultados não

impõe condi¸cões sobre o tamanho da popula¸cão.

No caso da estratégia MOSES o tamanho da popula¸cão é fixo e é igual a um

inteiro n≥2. O parâmetro que controla o número de indiv´ıduos a serem mutados em cada gera¸cão é denotado por pT. Esse parâmetro pode depender da gera¸cão, é tomado no intervalo (0,1) e é visto como probabilidade de muta¸cão.

A estrat´egia MOSES pode ser resumida da seguinte maneira:

(25)

2.2 Cotas para as Probabilidades de Transi¸c˜ao 15

2. Repete

• DadoN um número aleatório com distribui¸cão binomial bin(n, pT).

• Seleciona o indiv´ıduo ´otimo ˆxda popula¸c˜ao.

• Substitui os N primeiros indiv´ıduos pela muta¸c˜ao e os n− N outros indiv´ıduos por ˆx.

• AtualizapT.

A grande caracter´ıstica de MOSES é que a busca é hierárquica. Indiv´ıduos

realizam diferentes graus de pesquisa de acordo com sua posi¸c˜ao na popula¸c˜ao. Aos

indiv´ıduos das primeiras posi¸c˜oes ´e permitido fazer longas caminhadas. Essa

hierar-quia é obtida do número aleatório de descendentes por muta¸cão em cada gera¸cão. A

probabilidade de quek indiv´ıduos sejam mutados ´e dada pela distribui¸c˜ao binomial

bin(n, pT). Dessa forma, para todo 0≤k≤n, temos:

P (N =k) =





n k



pk_T (1−p_T)n−k.

Vários critérios podem ser utilizados para conter a evolu¸cão. Um critério

natu-ral é assumir que o parâmetro de muta¸cãopT diminua para zero. A grande vantagem da estratégia MOSES em rela¸cão ao algoritmo genético é que a análise matemática

do procedimento pode ser descrita em detalhes, devido ao fato que a estrat´egia

MOSES não utiliza cruzamento em sua dinâmica. A constru¸cão da estratégia, e

especificamente, a escolha da distribui¸cão binomial, é motivada pela aplica¸cão do

formalismo do princ´ıpio dos grandes desvios que ser´a abordado posteriormente.

2.2 Cotas para as Probabilidades de Transi¸

c˜

ao

Nesta se¸c˜ao descrevemos formalmente a estrat´egia MOSES e obtemos cotas

(26)

que f é uma fun¸cão injetora arbitrária, definida num conjunto finito qualquer, de-notado por E, f : E → R_{. Além disso, existe um ´}_{unico ponto m´ınimo global e}

é denotado por a∗_{. ´}_{E importante destacar que a hipótese da fun¸cão ser injetora}

não é tão restritiva, pois caso contrário, podemos fazer uma perturba¸cão tornando

a fun¸c˜ao injetora (ver anexo). Por outro lado, no Cap´ıtulo 4, apresentamos uma

nova abordagem para a análise da convergência de MOSES que não precisa desta

hip´otese.

Nota¸cões e defini¸cões: Fixamos um número inteiron≥2 e definimos o conjunto das popula¸cões de tamanhonporX =En_{. Isto é, uma popula¸cão}_x_{é simplesmente} um vetor de tamanho n, com entradas em E. Dizemos que:

x∈X ⇔x= (x1, x2, . . . , xn), xi ∈E, ∀i= 1, . . . , n.

A popula¸cão uniforme (a, . . . , a) com a∈E é identificada pela nota¸cão (a) = (a, . . . , a).

Denotamos ˆx como o m´ınimo de uma popula¸c˜ao: ˆ

x∈ {x1, x2, . . . , xn}, f(ˆx)≤f(xi), ∀ i= 1, . . . , n.

Como foi comentado na introdu¸c˜ao, a vizinhan¸ca N(xi) de cada indiv´ıduo xi esta associada a um grafog = (E, A) conexo e tal que:

1. N(xi) ={yi ∈E/yi6=xi,(xi, yi)∈A}, |N(xi)| ≥2; 2. sim´etrico, isto ´e,

xi ∈N(xj), se e somente se, xj ∈N(xi);

2.2.1 Dinˆ

amica da estrat´

egia

(27)

i) identifica ˆx0

ii) Gera um número aleatórioNda distribui¸cão binomialbin n, PT(1)

, ondePT(t) =

exp (−1/T(t)), com t= 1,2, ...e T(t)→0

iii) X1 = x1 = (y1, y2, . . . , yN,xˆ0,xˆ0, . . . ,xˆ0) onde os yi s˜ao escolhidos em N(xi)∩ (E\ {xˆ0}), i ∈ {1,2, . . . , n}, com probabilidade uniforme.

Etapa 2:

i) identifica ˆx1

ii) Gera um número aleatório N da distribui¸cão binomial bin n, PT(2)

iii) X2 = x2 = (z1, z2, . . . , zN,xˆ1,xˆ1, . . . ,xˆ1) onde zi s˜ao escolhidos em N(yi)∩ (E\ {xˆ1}), i ∈ {1,2, . . . , n}, com probabilidade uniforme.

...

Assim obtemos um conjunto de vetores aleat´orias X0, X1, X2, . . . com espa¸co

de estadosX, onde X é o conjunto de todas as popula¸cões e a distribui¸cão deXt é determinada somente pela distribui¸cão deXt−1. Logo, X0, X1, X2, . . .é uma cadeia

de Markov.

`

A dinˆamica da estrat´egia MOSES tem associada uma cadeia de Markov com

espa¸co de estadosX (o conjunto de todas as popula¸c˜oes). A seguir descrevemos de maneira expl´ıcita as probabilidades de transi¸c˜ao.

Seja q_T₍_t₎ a matriz de transi¸c˜ao no tempot, isto ´e

qT(t)(x, y) =P

X_tT₊₁(t) =y|X_tT(t) =x.

Para efeito de simplificar a nota¸c˜ao escrevemos T =T (t), assim

qT (x, y) =P XtT+1 =y|XtT =x

.

(28)

n´umeros inteiros sucessivos i∈ {1, . . . , n}, definido como

I(x, y) ={1≤i≤n; yi 6= ˆx}. O n´umero de elementos neste subconjunto ´e denotado por

C(x, y) =|I(x, y)|.

A transi¸c˜ao entre xey ´e poss´ıvel se, e somente se, π(x, y)6= 0, onde

π(x, y) = Y i∈I(x,y)

1N(xi)∩(E\{ˆx})(yi)

|N(xi)∩(E\ {xˆ})|

Y

i /∈I(x,y)

1{ˆx}(yi).

Nesse caso, a probabilidade de transi¸cão da popula¸cão xpara y é dada por:

qT (x, y) =P(N =C(x, y))π(x, y).

A quantidade C(x, y) representa o número de indiv´ıduos da popula¸cão y que são diferentes de ˆx. Durante a análise, esta quantidade é vista como um custo de comunica¸cão de uma etapa entre as popula¸cões x e y. Ele expressa a dificuldade para a cadeia XT

t

se deslocar de xpara y em uma única etapa. Observa¸cão 2.2.1. Note que a matriz de transi¸cão qT é irredut´ıvel.

De fato, sejam x, y∈X duas popula¸c˜oes quaisquer, onde

x= (a1, a2, . . . , an) e

y= (b1, b2, . . . , bn),

sendo ai, bi ∈ E, i = 1, . . . , n. Como o grafo g = (E, A) ´e conexo, para todo i ∈

{1, . . . , n}existe um caminho em g = (E, A), ligandoai com bi;

(29)

a2 →a22 →a23 →. . .→ar2 →b2

...

an →a2n →a3n →. . .→ arn →bn.

Dessa forma, podemos construir as seguintes popula¸c˜oes em X:

x= (a1, a2, . . . , an)

x1 = a21, a22, . . . , a2n

x2 = a31, a32, . . . , a3n

...

xr−1= (ar1, ar2, . . . , arn)

y = (b1, b2, . . . , bn)

x→x1→ x2 →. . .→xr−1→ y

Portanto, para duas popula¸c˜oes quaisquer x, y ∈ X existe r ∈ N _{tal que}

qr

T (x, y)> 0.

Além disso, observe que a matriz de transi¸cão qT é aperiódica. De fato, pela Proposi¸cão 1.2.1 é suficiente mostrar que existe um estado aperiódico. Para isto,

considere uma popula¸c˜ao uniforme x = (a, a, . . . , a), note que q1

T(x, x) > 0, (se

N =bin(n, pT) = 0 então todos os indiv´ıduos são mutados para o ponto m´ınimo da popula¸cão) assim o estado xé aperiódico. Portanto, a cadeia é aperiódica.

O fato de que a matriz de transi¸cão qT seja irredut´ıvel e finita garante a existência de uma única distribui¸cão estacionária (Teorema 1.2.6), que permite usar

teoria de Freidlin e Wentzell. Também temos que a matriz qT é ergódica, pois é irredut´ıvel, aperiódica e finita (Corolário 1.2.3).

(30)

qT, a qual é fundamental no estudo assintótico da cadeia associada à estratégia. Proposi¸cão 2.2.1. Seja y uma popula¸cão que é acess´ıvel a partir dexem um único passo, então a probabilidade de transi¸cão satisfaz a seguinte desigualdade:

1

2nπ(x, y)e

−C(x,y)/T _≤_q

T (x, y)≤2nπ(x, y)e−C(x,y)/T.

Demonstra¸c˜ao. ConsidereC(x, y) =k, logo:

P (N =C(x, y)) =P (N =k) =





n k



(pT)k(1−pT)n−k,

onde pT =e(−1/T). Observemos:

i) (1−pT)n ≤





n k



(1−pT)n−k

De fato (1−pT)≤1 ent˜ao (1−pT)n ≤(1−pT)n−k. Sendo assim,

(1−pT)n ≤





n k



(1−p_T)n−k.

ii)   n k 

(1−pT)n−k ≤max

k   n k  .

De fato, como (1−pT)≤1 ent˜ao (1−pT)n−k ≤1. Sendo assim,   n k 

(1−pT)n−k ≤





n k



 ≤max

k   n k  .

iii) max k   n k 

(31)

2.2 Cotas para as Probabilidades de Transi¸c˜ao 21 De fato, max k   n k  ≤ n X k=0   n k 

1k1n−k = (1 + 1)n = 2n.

De i), ii) e iii) conclu´ımos que: (1−pT)n ≤





n k



(1−pT)n−k ≤max

k   n k 

≤2n.

Multiplicando (pT)kπ(x, y) por toda a desigualdade abaixo (1−pT)n ≤





n k



(1−p_T)n−k ≤2n.

Obtemos:

(1−pT)n(pT)kπ(x, y)≤





n k



(1−pT)n−k(pT)kπ(x, y)≤2n(pT)kπ(x, y).

Isto ´e,

(1−pT)n(pT)kπ(x, y)≤P(N =k)π(x, y)≤2n(pT)kπ(x, y). Como k=C(x, y) e pT =e−1/T, ent˜ao

(1−pT)n e−1/T

k

π(x, y)≤qT (x, y)≤2n e−1/T

k

π(x, y).

Como pT ↓0 podemos considerar pT ≤1/2 logo (1−pT)≥ 1/2, (1−pT)n ≥ (1/2)n. Portanto,

1

2nπ(x, y)e

−C(x,y)/T _≤_q

(32)

Corol´ario 2.2.2. lim

T→0−T lnqT (x, y) =C(x, y).

Demonstra¸c˜ao. Aplicando logaritmo na desigualdade da proposi¸c˜ao anterior:

ln

1 2n

+lne−C(Tx,y)

+ln (π(x, y))≤lnqT (x, y)≤ln (2n)+

lne−CT(x,y)

+ln (π(x, y)).

Isto ´e, ln 1 2n

−C(x, y)

T + ln (π(x, y))≤lnqT (x, y)≤ln (2

n₎₋C(x, y)

T + ln (π(x, y)).

Multiplicando−T pela desigualdade anterior, obtemos:

−T ln (2n)−T

−C(x, y)

T

−T ln (π(x, y))

≤ −T lnqT (x, y)

≤ −T ln

1 2n −T

−C(x, y)

T

−T ln (π(x, y)).

Portanto,

−Tln (2n) +C(x, y)−T ln (π(x, y))

≤ −TlnqT(x, y)

≤ −Tln

₁

2n

+C(x, y)−Tln (π(x, y)).

Sendo assim, quando T →0, obtemos:

C(x, y)≤ lim

T→0−TlnqT(x, y)≤C(x, y).

Logo,

lim

(33)

Essas estimativas s˜ao o ponto de partida para desenvolver a an´alise da

es-trat´egia e aplicar o formalismo dos grandes desvios.

(34)

Cap´ıtulo 3

Comportamento Assint´

otico da

estrat´

egia MOSES

Neste cap´ıtulo apresentamos resultados assint´oticos sobre o comportamento

da distribui¸cão estacionária da cadeia de Markov associada à estratégia MOSES.

Esses resultados s˜ao derivados da teoria dos grandes desvios de Freidlin e Wentzell

[8]. Iniciamos o cap´ıtulo apresentando o conceito de x-grafo que ´e necess´ario para descrever a teoria dos grandes desvios.

3.1 x

-grafo

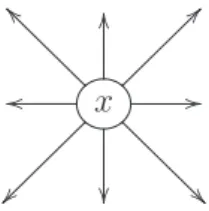
Defini¸cão 3.1.1. Um x-grafo g é um grafo orientado que não contém nenhuma aresta partindo de x e, tal que, para qualquer y 6=x existe um único caminho em g

ligando y a x.

(35)

3.1 x-grafo 25

~~

_!!

// x oo

//

OO

oo

^^

>> ``

Figura 3.1: x-grafo

Denotamos por G(x) o conjunto de todos osx-grafos.

Mostramos a seguir uma defini¸c˜ao mais geral de x-grafo que pode ser encon-trada em Freidlin e Wentzell [8]:

Defini¸cão 3.1.2. Seja L um conjunto finito, cujos elementos são denotados pe-las letras i, j, k, m, n, e etc, e seja W um subconjunto em L. Um grafo orientado constitu´ıdo por arestas m → n(m∈L\W, n ∈L, n 6=m) é chamado W-grafo caso satisfa¸ca as seguintes condi¸cões:

1. Cada ponto m∈L\W ´e um ponto inicial de exatamente uma aresta; 2. N˜ao existem ciclos no grafo.

A condi¸c˜ao 2 pode ser substitu´ıda pela seguinte condi¸c˜ao:

2′_. _{Para qualquer ponto}_m_∈_L_\_W _{existe uma sequˆencia de arestas que levam ele}

para algum ponton∈W.

Denotamos por G(W) o conjunto dos W-grafos. Dado um grafo g e um conjunto de n´umeros pmn associados a cada aresta (m → n) do grafo, definimos

π(g) = Y

(m→n)∈g

pmn.

A seguir apresentamos uma maneira alternativa de descrever a distribui¸c˜ao

(36)

3.1 x-grafo 26 ´

E importante destacar que esta representa¸cão da distribui¸cão estacionária através

de x-grafo é fundamental para estabelecer a teoria dos grandes desvios de Freidlin e Wentzel. Uma referência que trata com detalhes é Catoni [1].

Lema 3.1.1. Considere uma cadeia de Markov com espa¸co de estados L e proba-bilidades de transi¸c˜ao pij. Suponha que cada estado pode ser alcan¸cado a partir de

qualquer outro estado em um n´umero finito de passos.

Então a distribui¸cão estacionária da cadeia é

 

 !

X

i∈L

Qi

"−1

Qi, i∈L

 



, onde

Qi =

X

g∈G{i}

π(g). (3.1)

Demonstra¸cão. Como os números Qi são positivos então é suficiente verificar:

Qi=

X

j∈L

Qjpji, (i∈L). Ou seja,

Qi

X

k6=i

pik=

X

j6=i

Qjpji. (3.2)

Substituindo os números definidos pela Fórmula (3.1) em (3.2), então em ambos

os lados obtemos a soma π(g) sobre todos os grafos g satisfazendo as seguintes condi¸c˜oes:

1. Cada ponto m ∈ L ´e o ponto de partida de exatamente uma aresta m →

n(n6=m, n∈L);

2. No grafo existe exatamente um ciclo fechado e esse ciclo cont´em o pontoi. Exemplo 3.1.1. Considere uma cadeia de Markov com espa¸co de estados{A, B, C}

(37)

3.1 x-grafo 27

P =



   

1 2 0

1 2

1 0 0

0 1 0



   

.

Encontraremos a distribui¸c˜ao estacion´aria usando o lema acima. Primeiro

analisamos todos osA-grafos. Note:

π(gA1) = 1·0, π(gA2) = 1·1, π(gA3) = 0·0.

Logo,

QA= π(gA1) +π(gA2) +π(gA3) = 0 + 1 + 0 = 1.

Analisando todos os B-grafos:

π(gB1) = 0·0, π(gB2) =

1

2·1, π(gB3) = 0·1.

(38)

3.1 x-grafo 28

QB =π(gB1) +π(gB2) +π(gB3) = 0 +

1 2+ 0 =

1 2. Analisando todos os C-grafos:

π(gC1) = 1·

1

2, π(gC2) = 0·0, π(gC3) = 0·

1 2. Logo,

QC =π(gC1) +π(gC2) +π(gC3) =

1

2 + 0 + 0 = 1 2. Pelo lema anterior, a distribui¸cão estacionária da cadeia é

 

 !

X

i∈L

Qi

"−1

Qi, i∈L

 



. Assim,

µ(A) = QA

QA+QB +QC

= 1

1 +1 2 +

1 2

= 1 2,

µ(B) = QB

QA+QB+QC =

1 2

1 +1 2 + 12

= 1 4, e µ(C) = QC

QA+QB +QC =

1 2

(39)

3.2 Princ´ıpio dos Grandes Desvios 29

3.2 Princ´ıpio dos Grandes Desvios

Uma teoria desenvolvida por Freidlin e Wentzell [8] chamada princ´ıpio dos

grandes desvios diz que se as matrizes de transi¸c˜ao (qT)T≥0 associada a uma cadeia

de Markov irredut´ıvel com espa¸co de estados finito X satisfaz: 1

2nπ(x, y)e

−C(x,y)/T _≤_q

T (x, y)≤2nπ(x, y)e−C(x,y)/T, (3.3) ent˜ao

∀ x∈X, lim

T→0−T lnµT (x) =W(x)−Wmin,

onde

W(x) = min g∈G(x)

X

(y→z)∈g

V1(y, z), ∀ x∈X e

V1(x, y) = inf

(_r₋₁

X

k=0

C(xk, xk+1), x0 =x, xk ∈X, xr =y, r≥2

)

.

W(x) é chamado de energia virtual eV1(x, y) custo de comunica¸cão em vários

pas-sos. Além disso, valor m´ınimo deW é denotado porWmineW∗={x, W (x) =Wmin}. Uma consequência do princ´ıpio dos grandes desvios que é útil no estudo da

estrat´egia MOSES (que pode ser encontrado em Suzuki [14]) ´e o lema a seguir.

Lema 3.2.1. Se um subconjunto X− de X satisfaz:

1. Para cada x∈X+ :=X\X−, existe y ∈X− tal que C(x, y) = 0, e

2. Para cada par de x∈X+ e y ∈X−, C(y, x)> 0,

então a distribui¸cão estacionária limite limT→0µT(x) =µ∞(x)> 0, se x∈X−.

3.3 Convergˆ

encia da Estrat´

egia MOSES

Nesta se¸c˜ao descrevemos resultados sobre o comportamento assint´otico da

(40)

3.3 Convergˆencia da Estrat´egia MOSES 30

para o ´otimo global.

Trabalhamos com caminhos em E e também em X, a diferen¸ca entre eles é que os caminhos emE são caminhos no grafog= (E, A) e os caminhos em X =En são as trajetórias da cadeia de Markov.

De acordo com Cerf [2], se um subconjunto U ⊂X satisfaz a condi¸c˜ao

∀x∈X ∃(ˆx)∈U tal que V1(x,(ˆx)) = 0,

ent˜ao a energia virtualW pode ser calculada emU com

V (x, y) = inf

(_r₋₁

X

k=0

C(xk, xk+1), x0 =x, xk ∈/U(1≤k < r), xr =y, r≥2

)

.

Note que o subconjuntoUformado pelas popula¸cões uniformes satisfaz essa condi¸cão. Os resultados a seguir fazem uso desse resultado. Além disso, para as popula¸cões

uniformes (a) e (b) utilizamos a nota¸c˜ao V (a, b) e W (a) em vez de V ((a),(b)) e

W((a)).

Lema 3.3.1. Seja a6=a∗ _onde _a∗ _{´e o ponto m´ınimo de} _f_{. Ent˜ao temos}

V (a, a∗_{) =}_d₍_{a, a}∗₎_.

Onde d(a, a∗₎_{´e a distˆancia no grafo} _g_.

Demonstra¸c˜ao. i) Mostrar que V (a, a∗₎_≥_d₍_{a, a}∗₎_.

De fato, considerex1, x2, ..., xr ∈/U tais que:

a→x1→ x2 →x3 →...→xr →a∗. Definimos:

br =

 



a∗_, _se _a∗ _∈_x

r

(41)

br−1=

 



br, se br ∈xr−1

ar−1, onde ar−1 ∈xr−1 e (ar−1, br)∈A.

br−k =

 



br−k+1, se br−k+1∈xr−k

ar−k, ondear−k ∈xr−k e (ar−k, br−k+1)∈A.

b0 =a.

Sea∗_∈_x

rentãoC(xr, a∗) = 0. Neste caso, da sequência (b0, b1, ..., br) obtemos um caminho (c0, c1, ..., cm) onde ci ∈E e m≤r, da´ı, d(a, a∗)≤m. Como as popula¸cõesxi, i= 1, ..., r não são uniformes então C(xk, xk+1)≥1. Portanto,

C(a, x1) +C(x1, x2) +...+C(xr, a∗)≥1 + 1 +....+ 1 =r≥d(a, a∗). Se a∗ _∈_/ _x

r ent˜ao C(xr, a∗) ≥ 1 e V (a, a∗) ≥ r+ 1. Formamos o caminho (c0, c1, ..., cm) em g a partir da sequˆencia (b0, b1, ..., br), sendo m ≤ r + 1. Portanto,

d(a, a∗)≤m≤r+ 1≤V (a, a∗). ii) Mostrar que V (a, a∗₎_≤_d₍_{a, a}∗₎_.

Considere um caminho em g = (E, A) que realiza d(a, a∗_{) :} _a

0 = a → a1 →

· · · →ar= a∗ e o caminho emX

x0 = (a, a, a,· · · , a)

↓

x1= (a1, a, a,· · · , a)

↓

(42)

xk =

ak,˜bk,˜bk,· · · ,˜bk

↓

· · ·

xr=

a∗,˜br,˜br,· · · ,˜br

↓

xr+1= (a∗, a∗, a∗,· · · , a∗).

Denotamos ˜b1 =ae

∀k = 2,· · · , r, ˜bk =

 



ak−1, se f (ak−1)< f

˜_b_k₋₁ ˜

bk−1, caso contr´ario.

Sendo assim, temos que∀ k= 0,· · · , r−1, C(xk, xk+1) = 1. Logo,

r−1

X

k=0

C(xk, xk+1) +C(xr, xr+1) =r+ 0 =d(a, a∗),

ou seja,

r−1

X

k=0

C(xk, xk+1) =d(a, a∗).

Por defini¸c˜ao de ´ınfimo, temos que:

inf

(_r₋₁

X

k=0

C(xk, xk+1), x0 = (a), xk ∈/U(1≤k < r), xr = (a∗), r ≥2

)

≤d(a, a∗),

isto ´e,

V (a, a∗)≤d(a, a∗).

Portanto, de i) e ii), obtemos:

(43)

Lema 3.3.2. A distribui¸cão estacionária limiteµ∞(x)se concentra nas popula¸cões

uniformes.

Demonstra¸cão. Segue-se diretamente do Lema 3.2.1 onde X− são popula¸cões

uni-formes. De fato, se x = (x1, x2, . . . , xn) e tomando y = (ˆx,x, ...,ˆ xˆ), onde ˆx = arg min

xi f(xi), ent˜ao oC(x, y) = 0.

Lema 3.3.3. Suponha que existe um a∗ _∈_E _{tal que:}

∀a, b∈E, a, b6=a∗, V (a, a∗)< V (a∗, b).

Ent˜ao, para todo a6=a∗_{, W}₍_a∗₎_{< W} ₍_a₎_.

Demonstra¸c˜ao.

Figura 3.2: a-grafo Figura 3.3: a∗_-grafo

Seja a∈E, tal quea6=a∗ _e_g _um_a_{-grafo em}_U_{, tal que:}

W (a) = X

(u→v)∈g

(44)

Como a6=a∗ _e_g _{´e um} _a_{-grafo em} _U _{ent˜ao existe} _b_∈_U _{tal que} _a∗ _→_b_∈_g_.

A partir dessea-grafo podemos construir uma∗_{-grafo, retirando a aresta}_a∗_→

b emg e introduzindo a aresta (a→a∗_{). Denotamos esse}_a∗_{-grafo por} _g′_.

Sendo assim, temos:

W(a∗)≤W (a)−V (a∗, b) +V (a, a∗).

Como V (a, a∗₎_{< V} ₍_a∗_{, b}_{), isto ´e,}_V ₍_{a, a}∗₎₋_V ₍_a∗_{, b}₎_<_{0, ent˜ao}

W (a∗)< W(a).

Teorema 3.3.4.Sejan > n∗. A distribui¸c˜ao estacion´aria da cadeia XtT

concentra-se na popula¸c˜ao uniforme (a∗₎ _quando _T _{vai para zero, onde} _a∗ _{´e o ponto m´ınimo}

de f e n∗ = max

a6=a∗d(a, a

∗₎_.

Demonstra¸c˜ao. Sejam (a) e (b) popula¸c˜oes uniformes, a, b6=a∗_{. Temos}

n > n∗ = max

a6=a∗d(a, a

∗₎_≥_d₍_{a, a}∗₎_.

Comoa6=a∗ _{ent˜ao pelo Lema 3.3.1, temos que}

V (a, a∗) =d(a, a∗).

Logo,

n > d(a, a∗) =V (a, a∗). (3.4) Comoa∗_{´e o m´ınimo global, ent˜ao o caminho do menor custo que existe de (}_a∗₎

(45)

∀b6=a∗_{, V} ₍_a∗_{, b}₎_≥_n. _(3.5)

De (3.4) e (3.5), obtemos:

V (a∗, b)> V (a, a∗).

Sendo assim, pelo Lema 3.3.3

W (a∗)< W(a).

Para estabelecer a convergˆencia em probabilidade da estrat´egia para o ponto

de ótimo global fazemos uso do resultado de Trouvé [15]. Antes disso, é necessário

introduzir um ´ındice geométrico que é utilizado para obter a convergência da

es-tratégia MOSES para a solu¸cão m´ınima. Esse ´ındice geométrico é definido como

d∗ = max

a6=a∗_b_:_f₍min_b₎_<f₍_a₎d(a, b). (3.6) Note que esse ´ındice geométrico só depende da fun¸cão f e do grafo muta¸cão, da´ı o nome de ´ındice geométrico.

(46)

O Teorema a seguir foi estabelecido por Trouv´e [15] para cadeias nas quais as

probabilidades de transi¸c˜ao qT satisfa¸cam

kTe−C(x,y)/T ≤qT (x, y)≤KTe−C(x,y)/T e lim

T→0−TlnkT = limT→0−TlnKT = 0

Teorema 3.3.5 (Trouv´e [15]). Existe uma constanteH1 n˜ao negativa, tal que para

toda sequˆencia decrescente T(t)_t_≥1 convergindo para zero, temos

sup x∈X

P(Xt ∈/W∗|X0=x)→0

quando t→ ∞. Se, e somente se,

∞

X

t=1

e−H1/T(t)₌_∞_.

Em Trouvé, uma descri¸cão expl´ıcita deH1é dada em termos da decomposi¸cão

de X em ciclos. Dessa forma, a defini¸c˜ao de H1 ´e bastante complicada. Mas,

Catoni [1] apresenta uma descri¸c˜ao alternativa de H1 que n´os utilizaremos. Catoni

caracterizaH1 em termos de caminhos de (Xt). Assim, para cada caminho,

(47)

entre xe y em X, defina

H(γxy) = max

0≤k<r{W(xk) +C(xk, xk+1)}

onde o máximo é tomado sobre todos os vértices emγxy. SejaH(x, y) o menor valor poss´ıvel deH(γxy) sobre todos os caminhosγxy dexpara y. A quantidadeH(x, y) é chamada altitude de comunica¸cão entre x e y. Então, seguindo os resultados de Catoni, H1 é dado por

H1 = max

x6=(a∗₎H(x,(a

∗₎₎₋_W₍_x₎_.

Para MOSES, um limite superior de H1 pode ser obtido. Esse limite ´e

H1≤d∗.

A seguir apresentamos esse lema que pode ser encontrado em Fran¸cois [7].

Lema 3.3.6. Temos que H1≤d∗.

A demonstra¸c˜ao pode ser encontrada em Fran¸cois [7]. O resultado a seguir

es-tabelece condi¸cões suficientes para convergência em distribui¸cão da estratégia

MO-SES.

Teorema 3.3.7. Seja n > n∗. Suponha que: ∞

X

t=1

e−d∗/T(t)=∞.

Ent˜ao temos

P(Xt = (a∗)|X0 =x)→1

quando t tende para infinito.

Demonstra¸c˜ao. Pelo Lema 3.3.6 temos

(48)

onde H1 ´e uma constante n˜ao negativa. Sendo assim,

−d∗ ≤ −H1.

Da´ı,

−d∗/T(t)≤ −H1/T(t)⇒e−d∗/T(t)≤e−H1/T(t).

Portanto,

∞

X

t=1

e−d∗/T(t)≤

∞

X

t=1

e−H1/T(t)_. _(3.7)

Por hip´otese,

∞

X

t=1

e−d∗/T(t)=∞. (3.8) Portanto, de (3.7) e (3.8), obtemos

∞

X

t=1

e−H1/T(t)₌_∞_.

Sendo assim, pelo Teorema 3.3.5:

sup x∈X

P(Xt ∈/ W∗|X0 =x)→0,

quandot→ ∞.Portanto, o complementar

P(Xt ∈W∗|X0=x)→1,

quandot→ ∞. Pelo Teorema 3.3.4 temos W∗ ₌_{₍_a∗₎_}_{. Logo,}

P(Xt ∈ {(a∗)} |X0=x)→1,

quandot→ ∞. Isto ´e,

P (Xt = (a∗)|X0= x)→1,

(49)

Cap´ıtulo 4

Convergˆ

encia Quase Certa da

Estrat´

egia MOSES

Neste cap´ıtulo apresentamos uma abordagem alternativa da convergˆencia da

estrat´egia MOSES sem fazer uso da teoria de Freidlin e Wentzell. Para isto,

faze-mos uso de um resultado geral em cadeia de Markov n˜ao-homogˆenea, que pode ser

encontrado em [4] ´e o seguinte:

Teorema 4.0.8. Seja {Xn}n∈N uma cadeia de Markov com espa¸co de estados S.

Suponha que existe um subconjunto n˜ao vazio S∗ _⊂_S_{, um n´}_{umero natural} _n

0∈Ne

uma sequˆencia {δk}k∈N tal que:

min i∈S,j∈S∗P

((k−1)n0,kn0)₍_{i, j}₎_≥_δ

k (4.1)

e

X

k≥1

δk =∞. (4.2)

Então S∗ _{é visitado infinitas vezes com probabilidade um e a cadeia de Markov é}

fracamente erg´odica.

Demonstra¸c˜ao. Seja N = X n≥0

(50)

40

S∗_{. Observe que temos a seguinte rela¸c˜ao:}

(N <∞)⊂ ∪n≥1An,

onde An = (Xm ∈/S∗, m≥n). Assim, para provar que P (N <∞) = 0 ´e sufi-ciente mostrar que P(An) = 0, ∀ n. Considerando B1 = (Xnn0 ∈/ S

∗_), _B 2 =

X₍_n₊₁₎_n₀ ∈/S∗

, . . . , Bk+1= X(n+k)n0 ∈/S∗

, da´ı segue queAn ⊂(B1, B2, . . . , Bk+1),

∀k ∈N_{. Da propriedade da cadeia de Markov, obtemos}

P (B1, B2, . . . , Bk+1)≤P(Bk+1|Bk). . . P(B2|B1).

Vamos provar que

P(B2|B1)≤1−δn+1.

Seja ¯Bk o complementar do conjunto Bk. Assim,

P B¯2|B1

= X i∈S∗

P X(n+1)n0 =i|B1

e

P X(n+1)n0 =i|B1

= 1

P(B1)

X

j /∈S∗

P X(n+1)n0 =i|Xnn0 =j

P(Xnn0 =j).

De (4.1) temosP X(n+1)n0 =i|Xnn0 =j

≥δn+1. Sendo assim

P B¯2|B1

≥δn+1

ou

P(B2|B1)≤1−δn+1.

Por um argumento similar, obtemos:

(51)

41

Segue da inequa¸c˜ao anterior que

P(B1, B2, . . . , Bk+1)≤(1−δn+1) (1−δn+2). . .(1−δn+k).

Note que a desigualdade acima mant´em para todo k ∈ N_{. De (4.2) segue que}

P(An) = 0, portanto P(N <∞) = 0, ou ´e equivalente, P (N =∞) = 1.

Agora, precisamos verificar se a cadeia de Markov ´e fracamente erg´odica.

Ob-serve a seguinte inequa¸c˜ao

α(P) = min i,k∈E

X

j∈E

min (Pij, Pkj)≥min i∈S Pij0 onde j0 ´e qualquer elemento deS. Da hip´otese, segue que:

α P(k−1)n0,kn0_≥_δ

k

assim

δ P(k−1)n0,kn0_≤₍₁₋_δ

k). Da inequa¸c˜aoδ(P Q)≤δ(P)δ(Q) e de (4.2) segue que

lim k→∞δ P

(m,k)

= 0,∀m≥0.

A seguir mostramos que a estrat´egia MOSES visita a popula¸c˜ao uniforme (a∗₎

com probabilidade igual a um, onde a∗ _{´e o ponto de m´ınimo global da fun¸c˜ao.}

´

E necess´ario lembrar que a estrat´egia MOSES objetiva encontrar o m´ınimo

global de uma fun¸cão f : E → R_{, onde} _E _{é um conjunto finito e é assumido que}

existe uma estrutura de grafog = (E, A) emE, a qual determina vizinhan¸casN(e), para cada e ∈ E, e este grafo g é conexo. Inicialmente, é dada uma sequência

pT(t) _t_≥1 que determina as muta¸cões. Em cada etapa da estratégia são formadas

(52)

42

fixo.

Dada a popula¸cão Xt = (et1, et2, . . . , etn) a nova popula¸cão Xt+1é dada por

(bt1, bt2, . . . , btm, x∗, . . . , x∗) onde x∗ = arg min{f(et1), f(et2), . . . , f(etn)} e m ´e

amostrado de uma variável aleatória binomial com parâmetros n e pT, sendo bti ∈

N(eti) com P(bti =x) = _|_N₍1_e_ti)_| onde N(eti) ´e a vizinhan¸ca de eti determinada pelo grafo g.

Teorema 4.0.9. A estrat´egia MOSES visita infinitas vezes com probabilidade 1 a popula¸c˜ao uniforme (a∗₎_{, se}

∞

X

t=1

(pT)D = ∞ e D o diâmetro de g (Diâmetro é a

maior distˆancia entre dois v´ertices quaisquer no grafo g).

Demonstra¸c˜ao. Pelo Teorema 4.0.8 ´e suficiente mostrar que existe uma constantek

tal que

P (Xt+D = (a∗)|Xt =x)> pDT ·k, , ∀t∈N, ∀x∈X.

Seja x = (a1, a2, ..., an) uma popula¸c˜ao qualquer, pela conectividade de g existem

e1, e2, . . . , em ∈Etais quee1 ∈N(a1), ei+1∈N(ei) eem =a∗(a∗´e o ponto m´ınimo global de f em≤D).

Consideremos as sequˆencias de popula¸c˜oes:

x1 = (e1, ax1, . . . , ax1), onde ax1 = arg min{f(a1), f(a2), . . . , f(an)}

x2 = (e2, ax2, . . . , ax2), onde ax2 = arg min{f(e1), f(ax1)}

x3 = (e3, ax3, . . . , ax3), onde ax3 = arg min{f(e2), f(ax2)}

...

xm= (a∗, axm, . . . , axm), onde axm = arg min

f(em−1), f axm−1

xm+1= (a∗, a∗, . . . , a∗)

Dessa forma,

P(Xt+1= x1|Xt =x) =n·PT ·(1−PT)(n−1)· 1

(53)

43

P(Xt+2 =x2|Xt+1=x1) =n·PT ·(1−PT)(n−1)· 1

|N(e1)|

...

P (Xt+m+1 =xm+1|Xt+m =xm) = (1−PT)n. Assim,

P (Xt+D = (a∗, a∗, . . . , a∗)|Xt =x)≥(PT)m·(1−PT)(n−1)·(m)·C onde C n˜ao depende de t. Logo,

P(Xt+D = (a∗, a∗, . . . , a∗)|Xt =x)≥(PT)D ·(1−PT)(n−1)·(D)·C, comopT ↓0,(1−pT)≥ 1₂ ent˜ao

P (Xt+D = (a∗, a∗, . . . , a∗)|Xt =x)≥(PT)D(1/2)(n−1)(D)·C = (PT)D ·k.

Observa¸cões importantes: Com esta abordagem não é necessário supor que a

fun¸c˜ao seja injetora, al´em disso, as escolhas dos sucessores nas vizinhan¸cas podem

ser feitas em toda a vizinhan¸caN(xi) e sem a restri¸c˜aoN(xi)− {x∗}, como tamb´em

(54)

Cap´ıtulo 5

Estrat´

egia MOSES no Matlab:

Algumas Simula¸

c˜

oes

Neste cap´ıtulo apresentamos resultados observados a partir da implementa¸c˜ao

da estrat´egia MOSES no software Matlab. Nele, realizamos alguns testes com o

intuito de estudar o tempo médio em que a estratégia atinge o ponto de ótimo pela

primeira vez (m´ınimo global). Tamb´em comparamos a eficiˆencia do MOSES em

rela¸c˜ao ao Simulated Annealing. As fun¸c˜oes usadas para realizar esses testes foram

as seguintes:

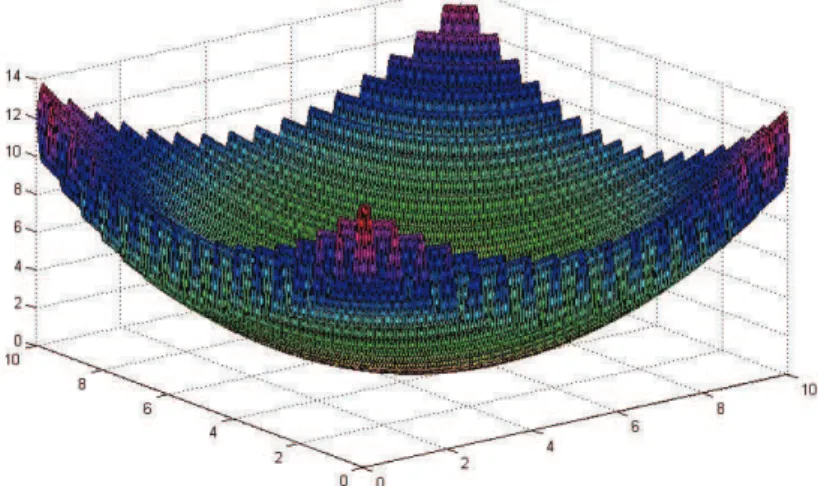
f(x, y) = 0,2 (x−5)2+ (y−5)2

+ 2 sin (10 (x+y−10)) + 2, (5.1)

g(x, y) = 6 +x2−3 cos (2πx) +y2−3 cos (2πy). (5.2) definidas nos intervalos [0,10]2 e [−2,5]2, respectivamente. A primeira fun¸c˜ao teste

f foi utilizada por Fran¸cois [7] e a segunda fun¸c˜ao ´e referenciada a Neto [6].

Gr´aficos, tabelas e figuras s˜ao usados para ilustrar o comportamento da

(55)

5.1 Testes Sobre Tempo M´edio da Primeira Visita da estrat´egia MOSES

ao M´ınimo 45

5.1 Testes Sobre Tempo M´

edio da Primeira

Vi-sita da estrat´

egia MOSES ao M´ınimo

Para verificarmos a eficiência da estratégia MOSES foram realizadas simula¸cões

com as fun¸cões citadas acima. Vale ressaltar que essas fun¸cões apresentam várias

oscila¸c˜oes, o que implica a existˆencia de diversos m´ınimos locais, dificultando a

determina¸c˜ao do m´ınimo global da fun¸c˜ao. Veja as figuras abaixo:

Figura 5.1: Gr´afico da fun¸c˜ao (5.1)

Figura 5.2: Gr´afico da fun¸c˜ao (5.2)

A tabela 5.1 mostra o comportamento do tempo m´edio da primeira visita da

estratégia ao m´ınimo da fun¸cão f quando o tamanho da popula¸cão é n = 500 e

pt = t −1

(56)

ao M´ınimo 46

Ambas as tabelas foram obtidas mediante 50 repeti¸cões da estratégia e a popula¸cão

inicial foi gerada aleatoriamente. As vizinhan¸cas utilizadas na estrat´egia MOSES

s˜ao compostas de 8 v´ertices como ilustra a figura abaixo:

x

__ OO ??

oo //

Figura 5.3: Vizinhan¸ca dex

Tempo médio da primeira visita de MOSES ao m´ınimo, com pt =t(−1/D), n= 500, popula¸cão inicial aleatória

Diˆametro D 5 10 30 35 40 45 55 60 70 80 700 800 1000 Tempo M´edio 1 1 11 44 3 51 29 30 60 13 327 429 491

Tabela 5.1:

Tempo médio da primeira visita de MOSES ao m´ınimo, com pt = _exp(1)1 , n= 500, popula¸cão inicial aleatória

Diˆametro D 5 10 30 35 40 45 55 60 70 80 700 800 1000 Tempo M´edio 1 1 14 44 4 52 30 25 45 10 456 544 760

Tabela 5.2:

Note que o tempo médio associado à primeira tabela é menor do que na segunda

o que talvez pode ser explicado pelo fato da probabilidade utilizada na primeira

tabela ser bem maior do que a utilizada na segunda tabela. De fato, pt = t(−1/D) tende a zero quando t tende ao infinito.

Também estimamos o tempo médio de retorno após fazer pequenas altera¸cões

na dinâmica da estratégia, mais especificamente, não colocamos a restri¸cão de o

indiv´ıduo não poder mutar para o m´ınimo da gera¸cão anterior (essa restri¸cão, como

comenta Fran¸cois, é de caráter técnico que facilita o tratamento matemático da

convergência da estratégia). Com essa altera¸cão da estratégia, não identificamos

diferen¸ca em rela¸c˜ao ao tempo m´edio.

As figuras 5.4 e 5.5 s˜ao obtidas da seguinte maneira: Gera-se 2000 popula¸c˜oes

(57)

ao M´ınimo 47

Figura 5.4:

Figura 5.5:

Nos gráficos anteriores, a estratégia foi processado com o mesmo diâmetro

D= 252, mesma probabilidadept = 1/exp (1) (do número de muta¸cões) e a evolu¸cão foi iniciada em (0,0), porém diferem no tamanho das popula¸cões, sendon= 500 no primeiro gráfico en= 100 no segundo. Observe que, no primeiro caso, o m´ınimo da fun¸cão é encontrado mais rápido do que no segundo caso.

Conclu´ımos esta se¸cão enumerando algumas considera¸cões a respeito das análises

dos testes realizados:

• Notamos que o diˆametro tem efeito direto no tempo m´edio de alcance do

m´ınimo da fun¸cão, porém em qualquer caso o tempo médio é finito que não é

óbvio, dado que a cadeia é homogênea.

(58)

5.2 MOSES Versus Simulated Annealing em Paralelo 48

diâmetro) não foi necessária para a determina¸cão do m´ınimo da fun¸cão, o

que ´e coerente com os resultados obtidos no Cap´ıtulo 4 (Teorema 4.0.9).

Mesmo assim, não conseguimos estabelecer rela¸cões entre todos os parâmetros:

ta-manho da popula¸cão, diâmetro, probabilidade de muta¸cão e o tempo médio. E as

simula¸cões não deram ind´ıcios para essa rela¸cão, pelo menos não percebemos.

5.2 MOSES Versus Simulated Annealing em

Pa-ralelo

Com o intuito de observarmos a eficiência da estratégia aleatória MOSES,

rea-lizamos a implementa¸c˜ao do algoritmo Simulated Annealing em Paralelo no Software

Matlab, para compararmos o desempenho desses dois algoritmos.

Como já foi dito no Cap´ıtulo 2, o Simulated Annealing é um técnica utilizada

para encontrar o m´ınimo global da fun¸c˜aof :S →R_{, sendo}_S_{finito. Neste contexto,}

o processo de otimiza¸cão é realizado por n´ıveis. Em cada n´ıvel é dado um ponto

u ∈ S, v´arios pontos na vizinhan¸ca de u s˜ao gerados e o correspondente valor de

f é calculado. Cada ponto gerado é aceito ou rejeitado de acordo com uma certa probabilidade. Esta probabilidade de aceita¸cão decresce de acordo com o n´ıvel do

processo.

Resultados te´oricos sobre a convergˆencia desse algoritmo podem ser

encontra-dos, por exemplo, no artigo de Cruz e Dorea [3].

Para efeito de compara¸c˜ao da estrat´egia MOSES e o Simulated Annealing

fixamos um tamanho da popula¸cão n para MOSES e realizamosn simula¸cões inde-pendentes no Simulated Annealing, o que nós chamamos de Simulated Annealing em

(59)

5.2 MOSES Versus Simulated Annealing em Paralelo 49

∀i= 1,· · · , n, bi =

 



aim, com a1(aim/ai)

ai, caso contr´ario. onde

at(aim/ai) = min

1,exp

−1

ct

(f(aim)−f(ai))

e ct = [D(f (j)−f(i))]/log (t+ 1) como sugeriram Cruz e Dorea [3]. A vizinhan¸ca utilizada na implementa¸c˜ao dos algoritmos Simulated Annealing em Paralelo e o

MOSES nesta se¸c˜ao, foi a seguinte:

x

OO

oo //

Os testes foram realizados com as fun¸c˜oes f eg apresentadas no in´ıcio deste cap´ıtulo, com probabilidade pt = t(

−1

D) e n = 500. Variamos a popula¸c˜ao inicial para cada teste, com o objetivo de verificar o grau de dificuldade para os algoritmos

encontrarem o m´ınimo. A seguir apresentamos tabelas informando esses resultados.

• Nas tabelas abaixo a popula¸cão inicial é centrada em (0,0) e a fun¸cão teste é

f,pt =t( −1

D) en= 500.

Tempo médio da primeira visita de MOSES ao m´ınimo Diâmetro D 5 10 30 35 40 45 55 60 70 80 Tempo Médio 5 9 61 67 123 155 169 179 244 250

Tempo m´edio da primeira visita