Variantes do método dos gradientes conjugados aplicados a sistemas lineares originados dos métodos de pontos interiores.

(1)

Variantes do M´etodo dos Gradientes Conjugados aplicados a sistemas

lineares originados dos M´etodos de Pontos Interiores

A.F.E. COELHO1, A.R.L. OLIVEIRA1 e M.I. VELAZCO2*

Recebido em 6 abril, 2013 / Aceito em 17 dezembro, 2014

RESUMO.Neste trabalho, comparamos duas vers ões precondicionadas do método dos gradientes conju-gados. Essas vers ões diferem da versão clássica, pois consideram que o sistema linear é um sistema de equações normais. Os sistemas lineares que iremos resolver surgem do cálculo das direções dos métodos de pontos interiores. A determinação desta direção consiste no passo de maior esforço computacional e, quando trabalhamos com sistemas de grande porte, o uso de métodos diretos pode ser inviável. Portanto, uma opção é utilizar métodos iterativos precondicionados. Assim, o desempenho de duas vers ões do método dos gradientes conjugados precondicionado é comparado à versão clássica que já foi utilizada, neste mesmo contexto, em trabalhos anteriores. Resultados numéricos mostram que uma dessas vers ões é competitiva em relação à versão clássica.

Palavras-chave: m´etodos de pontos interiores, m´etodo dos gradientes conjugados precondicionado.

1 INTRODUC¸ ˜AO

Desde a década de 80 os métodos de pontos interiores têm atra´ıdo grande interesse. Estes méto-dos são muito eficientes na solução de problemas de grande porte.

Nestes métodos, a cada iteração, são resolvidos dois sistemas lineares no cálculo das direções por métodos diretos ou iterativos. Os métodos diretos apresentam dificuldades em problemas de grande porte devido ao preenchimento da matriz. Em muitos casos, a melhor solução consiste em usar métodos iterativos. A matriz dos sistemas é simétrica e definida positiva permitindo usar o método dos gradientes conjugados. Devido ao mal-condicionamento da matriz nas iterações finais dos métodos é necessário o uso de precondicionadores. Neste trabalho, utilizamos o pre-condicionador h´ıbrido proposto em [5].

*Autor correspondente: Marta In´es Velazco

(2)

Para que o método dos gradientes conjugados seja aplicado, não é necessário que o sistema linear seja do tipo de equações normais. Entretanto, existem versões deste método que consideram a estrutura de equações normais em sua formulação [10]. Note que os sistemas originados dos métodos de pontos interiores são sistemas de equações normais.

O objetivo deste trabalho consiste em avaliar a eficiência de duas versões de gradientes conju-gados precondicionado (GCP) que consideram sistemas de equaç ões normais. Estas versões são particularizadas para os sistemas oriundos dos métodos de pontos interiores.

1.1 M´etodo de Pontos Interiores Preditor-Corretor

Considere o problema primal e o problema dual de programação linear na forma padrão [12]: minimizar ctx, sujeito a Ax =b,x≥0, problema primal, maximizar bty, sujeito a Aty+z=c,z≥0, problema dual,

ondeAé uma matrizm×nde posto completo,cebsão vetores coluna de dimensões apropriadas, xé o vetorn×1 de variáveis primais,yé o vetorm×1 de variáveis duais ezé o vetorn×1 de variáveis de folga duais.

O método preditor-corretor [12] calcula duas direções a cada iteração para as variáveis(x,y,z) de programação linear. De forma resumida, podemos dizer que essas direções são obtidas apli-cando o método de Newton nas condições de otimalidade:

⎛

⎜ ⎝

Ax−b

Aty+z−c X Z e

⎞

⎟

⎠=0; (x,z)≥0.

Definindorp = b− Ax, rd = c− Aty−z era = −X Z e, desejamos que estes res´ıduos (rp,rd,ra)sejam nulos obtendo assim uma solução ótima.

2 M ÉTODO DOS GRADIENTES CONJUGADOS PARA SOLUÇ ÃO DE SISTEMAS DE EQUAÇ ÕES NORMAIS E M ÉTODOS DE PONTOS INTERIORES

Na solução de sistemas com matrizes simétricas e definida positiva é utilizado o método dos gradientes conjugados. Quando trabalhamos com matrizes mal-condicionadas é necessário o uso de precondicionadores para garantir a convergência do método. Em [10] são apresentadas duas versões do método dos gradientes conjugados precondicionado que consideram a estrutura de equaç ões normais em sua formulação. Nesta seção, as mesmas serão particularizadas para as matrizes originadas dos métodos de pontos interiores.

Dado um sistema linearGx=d, existem duas alternativas para se obter um sistema de equac¸ ˜oes normais:

1. Substituindo a vari´avelxporGtu ter´ıamos o sistemaGGtu=d;

(3)

A primeira versão, Gradientes Conjugados Precondicionado – Normal Error (GCPNE), é cons-tru´ıda precondicionando o sistemaGGtu = d, comx = Gtu. A segunda versão, Gradientes Conjugados Precondicionado – Normal Residual (GCPNR), considera o sistema oGtGx=Gtd.

2.1 M´etodos de Pontos Interiores

O passo mais caro de uma iteração de pontos interiores consiste na solução do sistema linear:

(AD At)d y=rp+A(Drd −Z−1ra), (2.1)

ondeD=Z−1X ´e uma matriz diagonal definida positiva.

Para resolver o sistema (2.1), considere o sistema de equações normaisGGtu=d. Relacionando ambos os sistemas, temos as seguintes identidades: o vetorurepresenta as direçõesd ya serem calculadas, a matrizGrepresenta a matriz AD12 _{de forma que}_GGt ₌ _{AD A}t_{. Finalmente, o}

vetord representa o lado direito do sistema linearrp+A(Drd −Z−1ra).

Desta forma, o m´etodoGCPNEpara resolver o sistema (2.1) pode ser resumido como:

Algoritmo 2.1.GCPNE na variável u – Versão para o Sistema do Método de Pontos Interiores

Calcule r0=d−AD Atu0, z0=M−1r0, p0=z0

Para j=0,1, . . . ,at´e convergir, fac¸a:

wj =D

1 2_At_p_j

αj =

rj,zj

wj, wj

uj+1=uj +αjpj

rj+1=rj −αjAD

1 2_w_j

zj+1=M−1rj+1

βj =

rj+1,zj+1

rj,zj

pj+1=zj+1+βjpj

Fim

Outra forma de resolver o sistema (2.1) é compará-lo com o segundo tipo de equações normais: GtGx = Gtd. Note que a matrizG será substitu´ıda por D12_At _{e mantemos a variável} _x _que

representa o valor ded y. O vetorrp+A(Drd − Z−1ra)do sistema (2.1) é representado por Gtd no sistema GtGx = Gtd. Portanto, é necessário recuperar o vetor d do sistema (2.1). Logo, definindo

˜

(4)

temos:

Gtd = AD12_d

= rp+A(Drd−Z−1ra)

= b−Ax+A(Drd −Z−1ra)

= Ab˜−Ax+A(Drd −Z−1ra)

= AD D−1b˜−AD D−1x+ADrd −AD D−1Z−1ra

= AD(D−1b˜−D−1x+rd−D−1Z−1ra)

= AD12_D12₍_D−1_b˜₋_D−1_x₊_r_d₋_D−1_Z−1_r_a₎

Portanto

d =D12₍_D−1_b˜₋_D−1_x₊_rd₋_D−1_Z−1_ra_),

para o sistema (2.1).

Assim, o m´etodoGCPNRpara resolver o sistema (2.1) pode ser resumido como:

Algoritmo 2.2.GCPNR – Vers˜ao para o Sistema do M´etodo de Pontos Interiores

Calcule r0=d−D12_At_x0,_r0˜ =_AD 1

2_{r0, z0}=_M−1_{r0, p0}˜ =_z0.

Para j =0,1, . . . ,at´e convergir, fac¸a:

wj =D

1 2_At_p_j

αj =

zj,r˜j

wj, wj

xj+1=xj+αjpj

rj+1=rj−αjwj

˜

rj+1=AD

1 2_r_j₊₁

zj+1=M−1r˜j+1

βj =

zj+1,r˜j+1

zj,rj˜

pj+1=zj+1+βjpj

Fim

3 EXPERIMENTOS NUM ´ERICOS

(5)

na linguagemFortran. Os sistemas lineares que surgem ao decorrer do método são resolvidos através de uma abordagem direta por fatoração de Cholesky.

Neste trabalho, foi utilizada a versão PCx-Modificado [9, 5, 11]. Esta versão utiliza uma aborda-gem iterativa na solução dos sistemas lineares. Assim, a opção de múltiplas correç ões é desligada e a fatoração de Cholesky é substitu´ıda pela solução iterativa através do método dos gradientes conjugados precondicionado. O precondicionador utilizado é o Precondicionador H´ıbrido [5] com as modificações propostas em [11]. A partir desta versão modificada, as novas versões dos Gradientes Conjugados para sistemas lineares são testadas e comparadas com a mesma.

Todos os testes foram realizados em um processador Intel Core 2 Duo 2.2GHz com 2Gb de RAM, em ambiente Linux.

Os problemas testes são apresentados na Tabela 1. Estes foram selecionados dentro das classes de problemas onde a decomposição de Cholesky produz uma matriz mais densa que a matriz original [5, 9]. Os problemas foram extra´ıdos das bibliotecas de dom´ınio público: NETLIB [3], STOCHPL [4], MISC [1, 2] e QAPLIB [6]. Na tabela, para cada problema é descrito: o número de linhas, colunas, elementos não nulos após o pré-processamento, a densidade da matriz e biblioteca de origem.

3.1 Resultados Computacionais

A eficiência e robustez dos métodos GCPNR e GCPNE é avaliada a partir da comparação dos mesmos com o método dos gradientes conjugados precondicionado utilizado na versão PCx-modificado. Nas comparações, foram considerado:

• Total de iterações de pontos interiores (descritas entre parênteses);

• Total de iterações dos métodos de gradientes conjugados dada pela soma do número de iterações realizadas para o cálculo de cada uma das duas direções do método de pontos interiores;

• Tempo de processamento.

(6)

Tabela 1: Problemas testes.

Problema Linha Colunas N˜ao Nulos Densidade Biblioteca

scsd8-2c-64 5130 35910 112770 0,0612 STOCHLP

scsd8-2r-432 8650 60550 190210 0,0363 STOCHLP

els19 4350 13186 50882 0,0887 QAP

chr22b 5587 10417 36520 0,0627 QAP

scr15 2234 6210 24060 0,1739 QAP

scr20 5079 15980 61780 0,0761 QAP

rou20 7359 37640 152980 0,0552 QAP

ste36a 27683 131076 512640 0,0141 QAP

ste36b 27683 131076 512640 0,0141 QAP

stocfor3 16675 23541 62960 0,0160 NETLIB

qap12 2794 8856 33528 0,1355 NETLIB

qap15 5698 22275 85470 0,0673 NETLIB

nug12 3192 8856 33528 0,1355 MISC

nug15 6330 22275 85470 0,0673 MISC

pds-10 15648 48780 103725 0,0135 MISC

pds-20 32276 106180 226494 0,006608 MISC

pds-30 49944 158489 333260 0,004210 MISC

pds-40 64265 214385 457538 0,003320 MISC

pds-50 80339 272513 581152 0,002654 MISC

pds-60 96503 332862 709178 0,002207 MISC

pds-70 114944 390005 822526 0,001834 MISC

pds-80 126109 430800 916852 0,001687 MISC

pds-90 142823 475448 1002902 0,001476 MISC

pds-100 156243 514577 1096002 0,001363 MISC

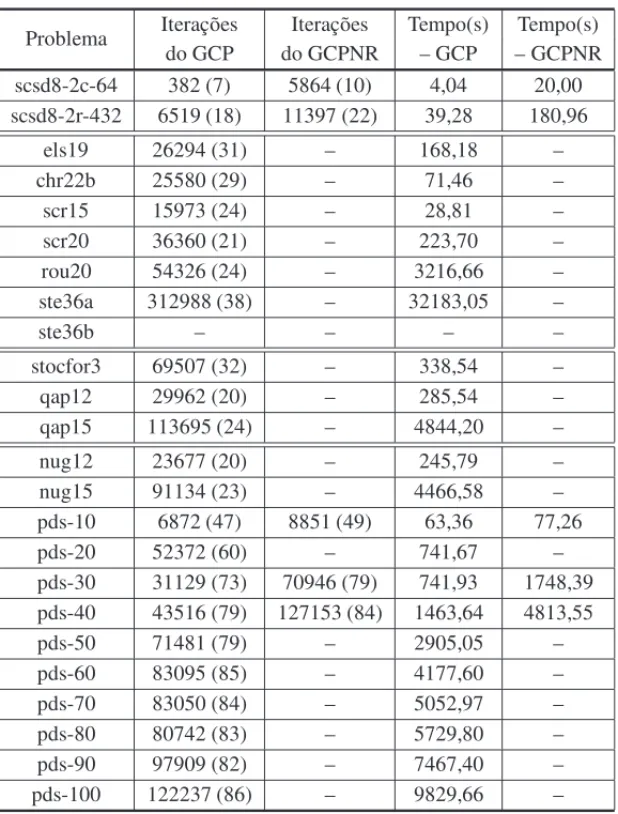
Se somarmos as iterações do método iterativo realizadas nos problemas que convergiram para ambos métodos temos os seguintes resultados: o GCP realizou 88418 iterações e o GCPNR realizou 224211 iterações. O método GCPNR fez mais que o dobro de iterações para resolver os mesmos sistemas e levou quase o triplo do tempo de processamento.

(7)

Tabela 2: Resultados obtidos com os m´etodos GCP e GCPNR.

Problema Iterações Iterações Tempo(s) Tempo(s)

do GCP do GCPNR – GCP – GCPNR

scsd8-2c-64 382 (7) 5864 (10) 4,04 20,00

scsd8-2r-432 6519 (18) 11397 (22) 39,28 180,96

els19 26294 (31) – 168,18 –

chr22b 25580 (29) – 71,46 –

scr15 15973 (24) – 28,81 –

scr20 36360 (21) – 223,70 –

rou20 54326 (24) – 3216,66 –

ste36a 312988 (38) – 32183,05 –

ste36b – – – –

stocfor3 69507 (32) – 338,54 –

qap12 29962 (20) – 285,54 –

qap15 113695 (24) – 4844,20 –

nug12 23677 (20) – 245,79 –

nug15 91134 (23) – 4466,58 –

pds-10 6872 (47) 8851 (49) 63,36 77,26

pds-20 52372 (60) – 741,67 –

pds-30 31129 (73) 70946 (79) 741,93 1748,39

pds-40 43516 (79) 127153 (84) 1463,64 4813,55

pds-50 71481 (79) – 2905,05 –

pds-60 83095 (85) – 4177,60 –

pds-70 83050 (84) – 5052,97 –

pds-80 80742 (83) – 5729,80 –

pds-90 97909 (82) – 7467,40 –

pds-100 122237 (86) – 9829,66 –

(8)

Tabela 3: Resultados obtidos com os m´etodos GCP e GCPNE.

Problema Iterações Iterações Tempo(s) Tempo(s)

do GCP do GCPNE – GCP – GCPNE

scsd8-2c-64 382 (7) 389 (7) 4,04 4,03

scsd8-2r-432 6519 (18) 6914 (18) 39,28 42,26

els19 26294 (31) 26315 (31) 168,18 172,48

chr22b 25580 (29) 25688 (29) 71,46 72,98

scr15 15973 (24) 15886 (24) 28,81 28,99

scr20 36360 (21) 35789 (21) 223,70 254,20

rou20 54326 (24) 54606 (24) 3216,66 3156,59

ste36a 312988 (38) 305066 (38) 32183,05 32256,71

ste36b – 375810 (37) – 41786,72

stocfor3 69507 (32) 69828 (32) 338,54 345,72

qap12 29962 (20) 30519 (20) 285,54 305,59

qap15 113695 (24) 92876 (23) 4844,20 4160,35

nug12 23677 (20) 24111 (20) 245,79 249,23

nug15 91134 (23) – 4466,58 –

pds-10 6872 (47) 6765 (47) 62,94 63,01

pds-20 52372 (60) 53759 (60) 741,67 782,26

pds-30 31769 (74) 31324 (74) 793,66 824,34

pds-40 43516 (79) 43797 (79) 1463,64 1537,23

pds-50 71481 (79) 69471 (79) 2905,05 2959,64

pds-60 83095 (85) 82774 (85) 4177,60 4337,98

pds-70 83050 (84) 77579 (85) 5052,97 4994,45

pds-80 80742 (83) 75626 (83) 5729,80 5658,51

pds-90 97909 (82) 82992 (81) 7467,40 6841,65

pds-100 122237 (86) 126769 (87) 9829,66 10493,45

(–) significa que o m´etodo falhou.

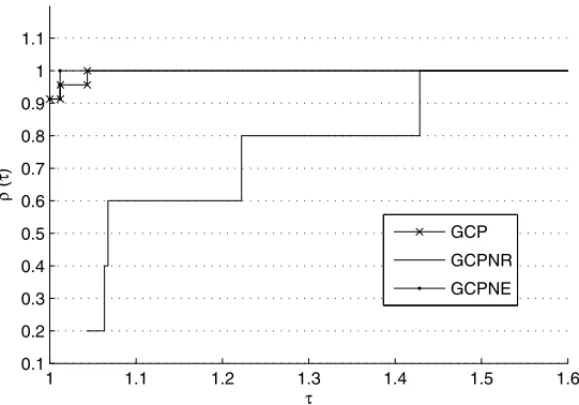
Estes resultados também podem ser observados através do perfil de desempenho [8]. O perfil de desempenho é uma ferramenta para comparar o desempenho desalgoritmos na solução dep problemas. Neste caso, temoss =3 algoritmos e p =24 problemas. Usaremos como medidas de desempenho os seguintes itens: total de iterações de pontos interiores; total de iterações dos métodos dos gradientes conjugados e tempo de processamento.

(9)

1 1.1 1.2 1.3 1.4 1.5 1.6 0.1

0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1

τ

ρ

(

τ

)

GCP

GCPNR

GCPNE

Figura 1: GCP, GCPNR e GCPNE – Perfil de desempenho: Iterac¸˜oes de Pontos Interiores.

1 1.5 2 2.5 3 3.5

0.2 0.4 0.6 0.8 1 1.2

τ

ρ

(

τ

)

GCP

GCPNR

GCPNE

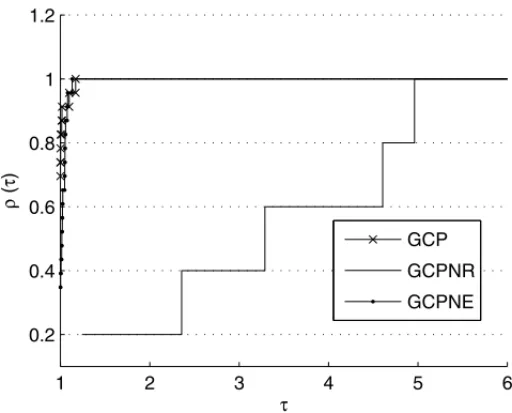
Figura 2: GCP, GCPNR e GCPNE – Perfil de desempenho: Iterac¸˜oes de Gradientes Conjugados.

(10)

1 2 3 4 5 6 0.2

0.4 0.6 0.8 1 1.2

τ

ρ

(

τ

)

GCP GCPNR GCPNE

Figura 3: GCP, GCPNR e GCPNE – Perfil de desempenho: Tempo de Processamento.

4 CONCLUS ˜OES

Neste trabalho, avaliamos a eficiência de diferentes versões do método dos gradientes conjugados precondicionado aplicados aos sistemas lineares oriundos dos métodos de pontos interiores. A principal motivação para testar diferentes versões desses métodos vem da estrutura natural destes sistemas, na forma de equaç ões normais.

Para avaliar a eficiência de cada uma das versões consideramos o total de iterações do método de pontos interiores e do método dos gradientes conjugados e o tempo total de processamento. Os problemas selecionados foram resolvidos utilizando a versão clássica e as duas versões que utilizam a estrutura de equações normais: GCPNE e GCPNR.

A implementação da versão GCPNE no código PCx-modificado é natural visto que a estrutura do método se adequa muito bem aos sistemas encontrados. Os resultados obtidos com essa versão foram muito semelhantes aos da versão clássica. Em poucos casos ocorreram variações no total de iterações do método de pontos interiores. De maneira geral, o tempo e total de iterações do método dos gradientes conjugados também não apresentaram grandes diferenças. Portanto, a versão GCPNE obteve bom desempenho sendo competitiva com a versão GCP.

(11)

AGRADECIMENTOS

Este trabalho contou com o apoio financeiro do Conselho Nacional de Desenvolvimento Cien-t´ıfico e Tecnológico (CNPq) e da Fundação de Amparo a Pesquisa do Estado de São Paulo (FAPESP).

ABSTRACT. This work presents two preconditioned versions of the conjugate gradient method. These versions differ from the classic version; they consider the linear system in

form of normal equations. It will solve linear systems that arise from search directions com-putation in an interior point method. Determining the direction is the step with the largest

computational effort and in large scale problems the use of direct methods might not be

fea-sible. Therefore, one option is to use preconditioned iterative methods to solve the systems. The performances of these two versions of the preconditioned conjugate gradient methods

are compared with the classic version. Numerical result shows that one of these versions is

competitive with the classic one.

Keywords: linear programming, interior point method, conjugate gradient.

REFER ˆENCIAS

[1] Miscellaneous LP models. Hungarian Academy of Sciences OR Lab. Online athttp://www. sztaki.hu/˜meszaros/public_ftp/lptestset/misc.

[2] Mittelmann – LP models. Miscellaneous LP models collect by Hans D. Mittelmann. Online at

http://plato.asu.edu/ftp/lptestset/pds/.

[3] NETLIB collection LP test sets. NETLIB LP repository. Online athttp://www.netlib.org/ lp/data/

[4] Stochastic LP test sets. Hungarian Academy of Sciences OR Lab. Online at http://www. sztaki.hu/˜meszaros/public_ftp/lptestset/stochlp

[5] S. Bocanegra, F.F. Campos & A.R.L. Oliveira. Using a hybrid preconditioner for solving large-scale linear systems arising from interior point methods,Computational Optimization and Applications, 36(1–2) (2007), 149–164.

[6] R.S. Burkard and S. Karisch & F. Rendl. QAPLIB – A Quadratic Assignment Problem Library. European Journal of Operations Research,55(1991), 115–119.

[7] J. Czyzyk, S. Mehrotra, M. Wagner & S.J. Wright. PCx An Interior Point Code for Linear Program-ming.Opt. Methods & Soft.,11-2(1-4) (1999), 397–430.

[8] E.D. Dolan & J.J. Mor´e. Benchmarking optimization software with performance profiles. Mathema-tical Programming,91(2002), 201–213.

(12)

[10] Y. Saad. “Iterative Methods for Sparse Linear Systems”. SIAM Publications, SIAM, Philadelphia, PA, USA, (1997).

[11] M.I. Velazco, A.R.L. Oliveira & F.F. Campos. A note on hybrid preconditions for large scale normal equations arising from interior-point methods.Opt. Methods & Soft.,25(2010), 321–332.