Análise global de sistemas quadráticos e cúbicos com duas circunferências não-concêntricas invariantes

(1)

An´

alise global de sistemas quadr´

aticos e c´

ubicos com

duas circunferˆ

encias n˜

ao-concˆ

entricas invariantes

Alisson de Carvalho Reinol

Orientador: Prof. Dr. Marcelo Messias

(2)

An´

alise global de sistemas quadr´

aticos e c´

ubicos com

duas circunferˆ

encias n˜

ao-concˆ

entricas invariantes

Alisson de Carvalho Reinol Orientador: Prof. Dr. Marcelo Messias

Disserta¸cão submetida ao Pro-grama de Pós-Gradua¸cão em Matemática Aplicada e Computa-cional da Faculdade de Ciências e Tecnologia - FCT/UNESP, Cam-pus de Presidente Prudente, como parte dos requisitos para obten¸cão do T´ıtulo de Mestre em Matemática Aplicada e Computacional.

(3)

FICHA CATALOGRÁFICA

Reinol, Alisson de Carvalho.

R295a Análise global de sistemas quadráticos e cúbicos com duas

circunferências não-concêntricas invariantes / Alisson de Carvalho Reinol. - Presidente Prudente : [s.n], 2014

78 f. : il.

Orientador: Marcelo Messias

Dissertação (mestrado) - Universidade Estadual Paulista, Faculdade de Ciências e Tecnologia

Inclui bibliografia

(4)

(5)

(6)

´

E dif´ıcil agradecer em poucas palavras a todos que, de alguma forma, contribu´ıram para a realiza¸c˜ao deste trabalho. Portanto, desde j´a, gostar´ıa de deixar aqui meus sinceros agradecimentos a todos aqueles que estiveram ao meu lado nas horas serenas e apreensivas e que me ajudaram a vencer mais esta etapa.

Dediquei este trabalho à minha mãe, Concei¸cão, e à minha avó, Lour-des, e gostaria, também, de agradecê-las pela paciência, pelo incentivo, pela for¸ca e pelo carinho. Gostar´ıa de agradecer a toda minha fam´ılia tios, tias, primos, primas, a minha bisavó e, em especial, ao meu tio, José Elias (in memoriam).

Agrade¸co ao meu orientador, professor Marcelo Messias, por acredi-tar em mim e partilhar comigo suas ideias, conhecimentos e experiência. Quero expressar o meu reconhecimento e admira¸cão pela sua competência profissional e minha gratidão pela sua amizade e por fazer parte de várias das minhas conquistas. Agrade¸co, também, ao professor Jaume Llibre, pela oportunidade de estagiar na UAB sob sua orienta¸cão, por me receber de forma tão receptiva e por tudo que me ensinou durante este per´ıodo, o qual foi muito importante para o meu crescimento profissional.

Gostar´ıa de agradecer a todos os meus professores, desde aqueles da educa¸cão básica até os da pós-gradua¸cão, pelos ensinamentos e dedica¸cão, pois gra¸cas a eles cheguei até aqui. Em especial, às professoras Luiza e Vanderloisa, que sempre acreditaram no meu potencial. Aos docentes do Departamento de Matemática e Computa¸cão, minha inspira¸cão. A todos eles minha profunda gratidão e respeito.

Agrade¸co a todos os meus colegas de turma, do ensino básico, gradua¸cão e pós-gradua¸cão, por tornarem a caminhada menos dif´ıcil, compartilhando sonhos, expectativas, risos, ansiedades e angústias pós-provas. Em especial, agrade¸co ao Alex, Bianca, Tha´ısa, por mostrarem que a amizade pode sobre-viver ao tempo, mesmo que sigamos caminhos diferentes; ao Wesley, Kátia, Luis, Eduardo, Renata, La´ıza e todos os meus colegas de gradua¸cão, por

(7)

aprendermos e ensinarmos muito uns aos outros durante aquele per´ıodo; aos irmãos que ganhei no Mestrado, Patr´ıcia, Juliano, Marluce; a todos os colegas da terceira turma do Pós-MAC, principalmente àqueles que tive mais con-tato: Rafael, Daiane, Irineu, Zé, Hemily, Mariane, Luana, Luciene, Gabriella, Mar´ılia; e também aos colegas da primeira, segunda e quarta turma do Pós-MAC, os quais tive o prazer de conviver.

Gostar´ıa de agradecer `a FAPESP pelo apoio financeiro.

Agrade¸co aos funcionários da Se¸cão de Pós-Gradua¸cão e do Escritório de Pesquisa pela aten¸cão e paciência em sanar todas as dúvidas burocráticas, às secretárias da Dire¸cão, em especial, à Vera, por sempre arranjar espa¸co na agenda do meu orientador para uma reunião.

(8)

(Henry Ford)

(9)

Neste trabalho, realizamos o estudo global de sistemas diferenciais polinomiais planares quadráticos e cúbicos com duas circunferências não-concêntricas como curvas algébricas invariantes. Apresentamos todos os poss´ıveis retratos de fase dos campos vetoriais polinomiais associados a tais sistemas no disco de Poincaré. Mostramos que existem 3 classes de equivalência topológica para o caso quadrático e 19 classes de equivalência topológica para o caso cúbico. Como uma consequência deste estudo, provamos que estes sis-temas diferenciais polinomiais não apresentam ciclos limites.

Palavras-chave: Sistemas diferenciais polinomiais, curvas algébricas invari-antes, ciclos limites, compactifica¸cão de Poincaré.

(10)

In this work, we perform a global study of quadratic and cubic planar polynomial differential systems having two nonconcentric circles as invariant algebraic curves. We give all possible global phase portraits on the Poincar´e disk of the polynomial vector fields associated to these systems. We show that there exist 3 topological equivalent classes for quadratic cases and 19 topological equivalent classes for cubic ones. As a consequence, we prove that these polynomial differential systems have no limit cycles.

Keywords: Polynomial differential systems, invariant algebraic curves, limit cycles, Poincar´e compactification.

(11)

Quando estudamos matematicamente fenômenos naturais que envolvem varia¸cões de grandezas f´ısicas com o tempo, somos levados ao estudo da derivada como taxa de varia¸cão e, consequentemente, ao estudo das equa¸cões diferenciais, que são utilizadas na modelagem matemática de fenômenos na-turais relacionados a diversas áreas do conhecimento.

Neste contexto, o estudo de sistemas planares de equa¸c˜oes diferenciais ordin´arias, da forma

˙

x=f(x, y),

˙

y=g(x, y), (1)

onde f eg s˜ao fun¸c˜oes de classeCk_, _k_≥_{1, definidas em um aberto}_U _do_R2_,

é bastante importante, tanto do ponto de vista teórico quanto das aplica¸cões dos métodos matemáticos na modelagem e análise de fenômenos naturais das ciências em geral. Ao sistema (1), está naturalmente associado o campo vetorial X(x, y) = (f(x, y), g(x, y)).

No caso em que as fun¸cões f e g são polinômios nas variáveis x e y, o sistema (1) é chamado de sistema diferencial polinomial de grau d, onde

d= max_{grau(f),grau(g)_}(analogamente, o campo vetorialX´e chamado de

campo vetorial polinomial de grau d). Muitos modelos matemáticos determi-nados por sistemas planares de equa¸cões diferenciais ordinárias encontrados na literatura são polinomiais.

A classifica¸cão topológica de sistemas diferenciais polinomiais lineares no plano é completamente conhecida, podendo ser encontrada em diversos livros como, por exemplo, nos Cap´ıtulos 7 e 9 de [1], no Cap´ıtulo 1 de [14], no Cap´ıtulo 1 de [27] e no Cap´ıtulo 3 de [30]. Porém, a classifica¸cão topológica de sistemas polinomiais planares de grau d _≥ 2 ainda é um problema em aberto dentro da Teoria Qualitativa das Equa¸cões Diferenciais Ordinárias.

Nos últimos anos, o caso quadrático, ou seja, o caso em qued= 2, tem sido intensamente estudado, havendo milhares de artigos publicados sobre o assunto. Mesmo assim, a classica¸cão completa dos sistemas diferenciais

(12)

polinomiais quadráticos ainda é desconhecida. Deste modo, surge o interesse em estudar classes particulares destes sistemas, com propriedades especiais como, por exemplo, a existência de integrais primeiras, invariantes de Dar-boux, curvas algébricas invariantes.

´

E importante notar que a existência de curvas algébricas invariantes influencia bastante o comportamento das solu¸cões de um sistema diferencial polinomial planares. Por exemplo, um sistema quadrático com uma elipse, hipérbole ou duas retas como curvas algébricas invariantes não tem ciclos limites (exceto, talvez, a própria curva) [13], enquanto a existência de uma reta invariante faz com que o sistema tenha no máximo um ciclo limite [5, 6, 12, 28]. Os resultados sobre as consequências advindas da existência de uma hipérbole invariante em um sistema diferencial polinomial quadrático foram apresentadas em [4]; sistemas quadráticos que possuem uma elipse como curva algébrica invariante foram estudados em [7]; com uma parábola invariante em [8] e [32] e com duas retas invariantes em [2].

Este trabalho é parte de um estudo mais amplo sobre o significado da existência de curvas algébricas invariantes em sistemas diferenciais polino-miais. Aqui, consideramos o caso em que tais sistemas são quadráticos ou cúbicos, ou seja, de grau 2 ou 3, respectivamente, e apresentam duas circun-ferências não-concêntricas como curvas algébricas invariantes. Como já era esperado, a existência de tais curvas tem implica¸cões consideráveis no com-portamento global das solu¸cões do sistema e, em particular, na existência ou não de ciclos limites, o que está relacionado ao famoso 16◦ _{Problema de} Hilbert [18, 19].

Esta disserta¸c˜ao est´a estruturada da seguinte maneira:

No Cap´ıtulo 1, apresentamos a compactifica¸cão de Poincaré, técnica que permite o estudo qualitativo global das solu¸cões de campos vetoriais polinomiais, inclusive daquelas ilimitadas, que tendem para o infinito e que não poderiam ser estudadas em regiões compactas do plano.

No Cap´ıtulo 2, falamos a respeito de outra t´ecnica, conhecida como

(13)

tradicional, via lineariza¸c˜ao.

Em seguida, no Cap´ıtulo 3, apresentamos alguns conceitos e resulta-dos da teoria de integrabilidade de Darboux, teoria esta que permite uma liga¸c˜ao entre a integrabilidade de campos vetoriais polinomiais e suas curvas alg´ebricas invariantes.

(14)

Introdu¸c˜ao vii

1 Compactifica¸c˜ao de Poincar´e 1

1.1 Cartas locais . . . 2

1.2 Pontos singulares no infinito . . . 6

1.3 Aplica¸cões da compactifica¸cão de Poincaré . . . 9

1.4 Compactifica¸c˜ao em coordenadas polares . . . 16

1.5 O programa P4 . . . 18

2 Desingulariza¸c˜ao de pontos singulares n˜ao-elementares 20 2.1 Blow-up polar . . . 21

3 Integrabilidade de Darboux 25 3.1 Integrais primeiras e invariantes . . . 26

3.2 Fatores integrantes . . . 33

3.3 Curvas Alg´ebricas Invariantes . . . 34

3.4 Fatores exponenciais . . . 40

3.5 O m´etodo de Darboux . . . 43

4 Sistemas quadráticos e cúbicos com duas circunferências n˜ ao-concêntricas invariantes 52 4.1 Forma normal . . . 57

4.2 Sobre a n˜ao-existˆencia de ciclos limites . . . 59

4.3 Sistemas quadráticos com duas circunfe-rências não-concêntricas invariantes . . . 60

4.4 Sistemas cúbicos com duas circunferências não-concêntricas invariantes . . . 64

Considera¸c˜ao finais 74

(15)

1.1 Proje¸c˜ao central. . . 3

1.2 Cartas locais. . . 4

1.3 Sela-n´o do tipo SN1 e SN2, respectivamente, de p(X) no equador de S2_{. . . .} ₈

1.4 Retrato de fase do sistema (1.5): A origem ´e um ponto de sela. 9 1.5 Retrato de fase do sistema (1.5) no disco de Poincar´e. . . 10

1.6 Retrato de fase do sistema (1.6): A origem ´e um n´o repulsor. . 11

1.7 Retrato de fase do sistema (1.6) no disco de Poincar´e. . . 12

1.8 Retrato de fase do sistema (1.7): A origem é um foco instável. 12 1.9 Retrato de fase do sistema (1.7) no disco de Poincaré. . . 13

1.10 Retrato de fase do sistema (1.8): A origem ´e um centro. . . 14

1.12 Retrato de fase do sistema (1.9) no plano. . . 15

1.14 Mudan¸ca de vari´aveis introduzida pelo sistema (1.10). . . 17

1.15 Painel de controle principal do programa P4. . . 19

2.1 Representa¸c˜ao do que acontece com a origem. . . 21

2.2 Blow-up polar na origem do sistema (2.6). . . 24

2.3 Blow-up polar na origem do sistema (2.9). . . 24

3.1 Gr´afico da fun¸c˜ao H1 e retrato de fase do campo vetorial X, com a=b= 1. . . 30

3.2 Gr´afico da fun¸c˜ao H2 e retrato de fase do campo vetorial Y, com a=b= 1. . . 31

3.3 Gr´afico da fun¸c˜ao H e retrato de fase do campo vetorial X. . . 32

4.1 (i) Transla¸c˜ao, (ii) Homotetia, (iii) Rota¸c˜ao. . . 53

4.2 Poss´ıveis posi¸cões relativas entre as circunferências C1 e C2 dadas em (4.2). . . 54 4.3 Poss´ıveis retratos de fase do sistema (4.3) no disco de Poincaré. 56

(16)

4.4 Blow-up polar do ponto singular R1. . . 63

4.5 Diagrama de bifurca¸c˜ao do sistema (4.6). . . 64 4.6 Retratos de fase do sistema (4.6) no disco de Poincar´e,

rela-cionados com cada regi˜ao descrita na Figura 4.5. . . 65 4.7 Retratos de fase do sistema (4.10) no disco de Poincar´e. A

curva pontilhada representa a circunferˆencia C2, a qual ´e

in-teiramente constitu´ıda por pontos singulares. . . 66 4.8 Retratos de fase no disco de Poincar´e do sistema (4.12) com

apenas pontos singulares elementares. . . 71 4.9 Pontos singulares n˜ao-elementares do sistema (4.12). . . 72 4.10 Retratos de fase no disco de Poincar´e do sistema (4.12) com

pontos singulares n˜ao-elementares (A= 0 e D_̸= 0). . . 72 4.11 Retratos de fase no disco de Poincar´e do sistema (4.12) com

pontos singulares n˜ao-elementares (D= 0 e A_̸= 0). . . 73 4.12 Retratos de fase no disco de Poincar´e do sistema (4.12) com

(17)

1

Compactifica¸

c˜

ao de Poincar´

e

No estudo do retrato de fase de campos vetoriais polinomiais definidos no planoR2_{, constatemente aparecem solu¸c˜oes ilimitadas que tendem para o}

infinito e que, portanto, não podem ser completamente estudadas em regiões compactas do plano. Porém, existem técnicas de compactifica¸cão, como a compactifica¸cão de Poincaré, de Poincaré-Lyapunov e de Bendixson, que nos permitem estudar completamente tais solu¸cões. Neste cap´ıtulo, estudaremos com maior detalhe a compactifica¸cão de Poincaré, que associa a cada ponto do plano R2 _{um ponto da esfera unitária centrada na origem do espa¸co} R3_,

conhecida como esfera de Poincar´e, de tal maneira que o equador da esfera fica associado aos pontos localizados no infinito do R2_{. A compactifica¸c˜ao}

de Poincaré-Lyapunov foi desenvolvida posteriormente à compactifica¸cão de Poincaré e utiliza a mesma ideia, porém, a partir de uma constru¸cão mais abstrata. A vantagem é que, as vezes, ela torna o estudo das singularidades localizadas no infinito mais fácil do que na técnica anterior. Detalhes sobre a compactifica¸cão de Poincaré-Lyapunov e de Bendixson são encontradas no Cap´ıtulo 5 de [16].

Em s´ıntese, a compactifica¸cão de Poincaré consiste em mudan¸cas de variáveis seguidas de uma multiplica¸cão por uma fun¸cão positiva, que trans-forma o campo vetorial no plano R2 _{em um campo vetorial definido no disco}

de Poincar´e, cuja fronteira corresponde ao equador da esfera de Poincar´e (ou seja, aos pontos do R2 _{no infinito).}

Com o advento dos recursos computacionais, o estudo de campos ve-toriais polinomiais no disco de Poincar´e pode ser feito utilizando-se o pro-grama P4 – Planar Polynomial Phase Portraits, desenvolvido em conjunto por pesquisadores da Espanha e da B´elgica e dispon´ıvel gratuitamente no

(18)

endere¸co http://mat.uab.es/_∼artes/p4/p4.htm, da Universidade Autˆonoma de Barcelona. Um tutorial deste programa est´a dispon´ıvel no Cap´ıtulo 9 de [16].

A seguir, faremos a constru¸cão da compactifica¸cão de Poincaré, seguindo o que é feito no Cap´ıtulo 5 de [16], no artigo [20] e no Cap´ıtulo 1 de [29], e apresentaremos algumas aplica¸cões de tal técnica.

1.1 Cartas locais

Consideremos o sistema de equa¸cões diferenciais ordinárias de primeira ordem em duas variáveis reais dado por

˙

x1 =P(x1, x2),

˙

x2 =Q(x1, x2),

(1.1)

onde as fun¸cõesP eQsão polinômios de grau arbitrário nas variáveisx1 ex2.

Ao sistema (1.1) est´a naturalmente associado um campo vetorial polinomial

X(x1, x2) = (P(x1, x2), Q(x1, x2)). Dizemos que o grau de X ´e d, se d =

max_{grau(P),grau(Q)_}.

EmR3_{, consideremos a esfera}S2 ₌_{_y_{= (}_y₁_{, y}₂_{, y}₃₎_∈R3 _:_y2

1+y22+y23 =

1_}, a qual chamaremosesfera de Poincar´e, e oR2_{como sendo o plano contido}

noR3 _{tangente `a esfera}S2 _{no ponto (0}_,₀_,_{1), ou seja,}R2 ₌_{_y_∈R3 _:_y₃ _{= 1}_}_.

Podemos dividir a esfera de Poincar´e emH+ ={y∈S2 :y3 >0} (hemisf´erio

norte), H− = {y ∈ S2 : y3 < 0} (hemisf´erio sul) e S1 = {y ∈ S2 : y3 = 0}

(equador). A proje¸c˜ao do campo vetorial X deR2 _em S2 _{´e obtida usando as}

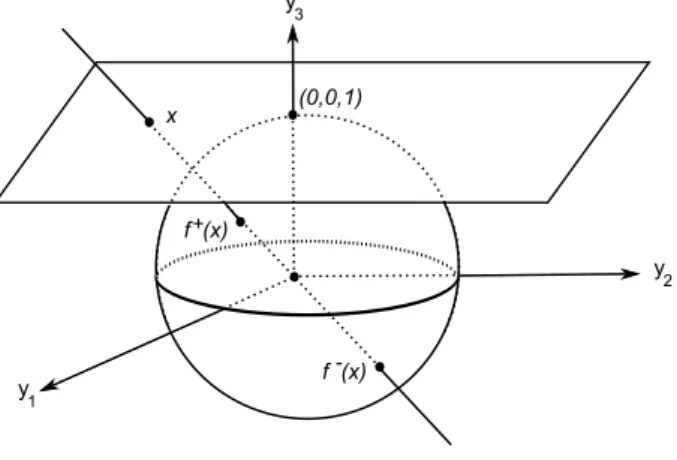
proje¸c˜oes centrais f+ _:_R2 _→_S2 _e_f− _:_R2 _→_S2_{, onde} _f+ _{(respectivamente,}

f−_{) é dada pela interseçcão da reta que passa pelo ponto}_x_{= (}_x

1, x2,1) e pela

origem do R3 _{com o hemisf´erio norte (respectivamente, sul) de} S2_{, conforme}

a Figura 1.1. Obtemos facilmente as express˜oes destas proje¸c˜oes como sendo

f+(x) = 1

∆(x)(x1, x2,1),

f−

(x) =₋ 1

∆(x)(x1, x2,1), onde ∆(x) =√x2

(19)

x

f (x)+

f (x) -(0,0,1)

y

1

y

2

y

3

Figura 1.1: Proje¸c˜ao central.

Deste modo, obtemos um campo vetorial induzido em cada hemisf´erio de S2_{, analiticamente conjugados ao campo vetorial}_X_{, dados por}

¯

X(y) = Df+(x)X(x) se y=f+(x)_∈H+

e

¯

X(y) =Df−

(x)X(x) se y=f−

(x)_∈H−.

Assim, obtemos um campo vetorial polinomial ¯X definido em S2 _\S1_{, ou}

seja, em H+∪H−. Por´em, para estudarmos o comportamento das solu¸c˜oes

ilimitadas de X que tendem para o infinito do R2_{, precisamos estender o}

campo vetorial ¯X para o equadorS1_{, obtendo, assim, um campo vetorial em} S2_.

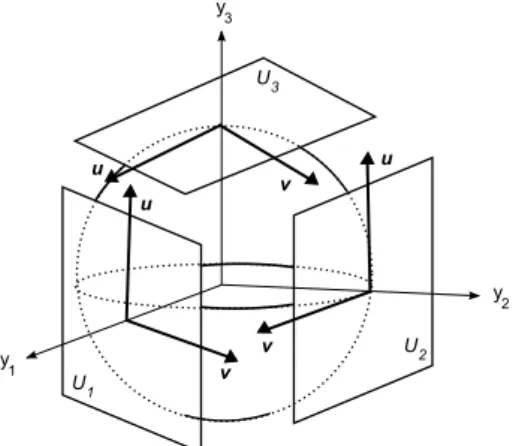
Como ´e usual com superf´ıcies curvas, usaremos cartas para fazer os c´alculos. Para S2 _{usaremos seis cartas locais dadas por} _U_k ₌_{_y _∈S2 _:_y_k _>

0_} e Vk = {y ∈ S2 : yk < 0}, com k = 1,2,3. Sejam φk : Uk → R2 e

ψk:Vk →R2 aplica¸c˜oes definidas por

φk(y) = −ψk(y) =

(

ym

yk

,yn yk

)

com m < n e m, n _̸= k. Denotaremos por z = (u, v) o valor de φk(y) ou

ψk(y) para qualquer k, tal que (u, v) ter´a diferentes significados dependendo

(20)

u v u u v v U₁ U 2 U 3 y 3 y 2 y 1

Figura 1.2: Cartas locais.

A seguir, faremos o c´alculo detalhado para obtermos a express˜ao de

p(X) na carta local U1, onde p(X) ´e o campo vetorial compactificado obtido

a partir de X. Temos que X(x) = (P(x1, x2), Q(x1, x2)). Ent˜ao, ¯X(y) =

Df+₍_x₎_X₍_x_{) com} _y₌_f+₍_x_{) e}

¯

X_|U1 =Dφ1(y) ¯X(y) = Dφ1(y)◦Df

+₍_x₎_X₍_x_{) =}_D₍_φ

1◦f+)(x)X(x).

Como k= 1 e lembrando que m < n,m, n_̸=k e m, n= 1,2,3, ent˜ao

(φ1◦f+)(x) =

(

y2

y1

,y3 y1 ) = ( x2 x1 , 1 x1 )

= (u, v).

Assim, temos que

¯

X_|U₁ =

    ∂u ∂x1 ∂u ∂x2 ∂v ∂x1 ∂v ∂x2    

X(x) =



  

−x2

x2 1 1 x1 − 1 x2 1 0      

P(x1, x2)

Q(x1, x2)





= v2

( −u_vP

( 1 v, u v ) + 1 vQ ( 1 v, u v )

,₋P

( 1 v, u v )) .

Observe que a equa¸cão não está definida para v = 0. Para estendê-la para estes valores, multiplicamos o campo vetorial pelo fator ρ(y) = yd−1

3 ,

onde d ´e o grau de X. Assim,

ρ(y) =yd−1

3 =

(21)

com

∆(x) =

√

x2

1+x22 + 1 =

1

v

√

1 +u2₊_v2_.

Logo,

ρ(y) = 1 ∆(x)d−1 =

1

(1

v

√

1 +u2₊_v2)d−1

=vd−1₍₁₊_u2₊_v2₎(1−d)/2 ₌_vd−1_m₍_z₎_,

onde m(z) = (1 +u2₊_v2₎(1−d)/2_.

Deste modo,

ρ( ¯X_|U1)(z) =v

d+1_m₍_z₎

( −u_vP

( 1 v, u v ) +1 vQ ( 1 v, u v )

,₋P

( 1 v, u v )) .

A express˜ao de p(X) na carta (U1, φ1) ´e dada por

˙

u=vd+1

( −u_vP

( 1 v, u v ) + 1 vQ ( 1 v, u v )) , ˙

v =vd+1

( −P ( 1 v, u v )) , ou seja, ˙

u=vd

( −uP ( 1 v, u v ) +Q ( 1 v, u v )) , ˙

v =₋vd+1_P

( 1 v, u v ) . (1.2)

Analogamente ao que foi feito na cartaU1, obtemos que a express˜ao de

p(X) na carta U2 ´e dada por

˙

u=vd

( P ( u v, 1 v ) −uQ ( u v, 1 v )) , ˙

v =₋vd+1_Q

( u v, 1 v ) , (1.3)

e na carta U3 ´e dada por

˙

u=P(u, v),

˙

v =Q(u, v). (1.4)

Note que a express˜ao de p(X) na carta U3 coincide com a express˜ao de

(22)

k = 1,2,3, s˜ao as mesmas das cartas Uk correspondentes, multiplicadas por

(₋1)d−1_.

Para o estudo completo do campo vetorial X no plano R2_{, incluindo o}

comportamento das solu¸cões em regiões próximas ao infinito, é suficiente tra-balhar com H+∪S1, pois as solu¸cões do campo vetorial emS2 são simétricas

com rela¸cão à origem. Chamaremos a proje¸cão ortogonal deH+∪S1 no disco

unit´ario centrado na origem do R3 _de_{disco de Poincar´e}_.

1.2 Pontos singulares no infinito

Seja ∆ um subconjunto aberto do R2 _e _X _{: ∆}_→ R2 _{o campo vetorial}

polinomial associado ao sistema (1.1). Um ponto x = (x1, x2) ∈ ∆ tal que

X(x) = (0,0) ´e chamado de ponto singular (singularidade, ponto cr´ıtico ou

ponto de equil´ıbrio) de X. O ponto sigular x é dito hiperbólico se os dois autovalores de DX(x) têm parte real diferente de zero e semi-hiperbólico se exatamente um dos autovalores de DX(x) é igual a zero, onde

DX(x) =



  

∂P ∂x1

(x) ∂P

∂x2

(x)

∂Q ∂x1

(x) ∂Q

∂x2

(x)



  

.

Chamamos DX(x) de matriz Jacobiana do campo X (ou do sistema (1.1))

aplicada no ponto x.

Dizemos que umponto singular deX ou p(X) está no infinito quando está localizado no equador (S1_{) da esfera de Poincaré. Note que se} _y _∈S1 _é

um ponto singular no infinito, então ₋y também o será. O comportamento do campo próximo de ₋y é igual ao comportamento do campo próximo de

y multiplicado por (₋1)d−1_{, onde} _d _{´e o grau do campo vetorial estudado.}

Assim, a orienta¸cão continua a mesma quando o grau d do campo vetorial é ´ımpar e é invertida quando o grau é par. Por exemplo, se d é par e y _∈ S1

(23)

Os pontos singulares localizados no equador da esfera de Poincaré es-tarão nas cartas U1, U2, V1 ou V2 e são da forma (u,0), com u ∈ R. Sejam

Pi e Qi os polinˆomios homogˆeneos de grau i, com i = 0,1, ..., d, tais que

P =P0+P1+...+Pd e Q=Q0+Q1+...+Qd s˜ao dados em (1.2) e (1.3).

Como Pi e Qi são polinômios homogêneos de grau i, temos que

Pi

(

1

v, u v

)

= 1

viPi(1, u) e Qi

(

1

v, u v

)

= 1

viQi(1, u).

Assim, a partir da equa¸c˜ao (1.2), temos que (u,0) _∈ S1 _∩₍_U₁ _∪_V₁_{) ´e}

um ponto singular no infinito, se, e somente se,

F(u)_≡Qd(1, u)−uPd(1, u) = 0.

Analogamente, a partir da equa¸c˜ao (1.3), temos que (u,0)_∈S1_∩₍_U₂_∪

V2) ´e um ponto singular no infinito, se, e somente se,

G(u)_≡Pd(u,1)−uQd(u,1) = 0.

Al´em disso, a matriz jacobiana do campo vetorialp(X) no ponto (u,0) ´e dada por





F′₍_u₎ _Q

d−1(1, u)−uPd−1(1, u)

0 ₋Pd(1, u)





se (u,0) pertence aU1∪V1, ou





G′₍_u₎ _P

d−1(u,1)−uQd−1(u,1)

0 ₋Qd(u,1)





se (u,0) pertence aU2∪V2.

Note que, em alguns casos, o equador deS2 _{pode consistir inteiramente}

de pontos singulares. De todos os pontos singulares semi-hiperbólicos e, dentre estes os pontos singulares hiperbólicos, apenas nós e selas podem aparecer no infinito. Temos que, se um dos pontos singulares hiperbólicos ou semi-hiperbólicos no infinito for topologicamente uma sela, então a reta {v = 0_}, ou seja, o equador da esfera S2_{, é necessariamente uma variedade}

(24)

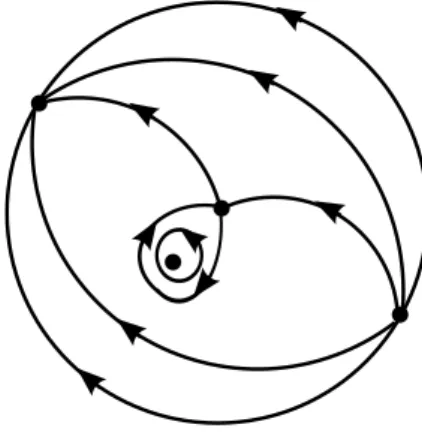
para os pontos singulares semi-hiperbólicos do tipo sela-nó. Além disso, dependendo do seu comportamento, classificamos os pontos singulares do tipo sela-nó em dois tipos: SN1, quando a matriz Jacobiana é da forma





λ _∗

0 0



,

com λ _̸= 0, ouSN2, quando a matriz Jacobiana ´e da forma





0 _∗

0 λ



,

com λ _̸= 0. Os dois casos s˜ao representados na Figura 1.3.

Figura 1.3: Sela-n´o do tipoSN1 eSN2, respectivamente, dep(X) no equador de S2_.

(25)

1.3 Aplica¸

c˜

oes da compactifica¸

c˜

ao de Poincar´

e

Nesta se¸cão, utilizaremos a compactifica¸cão de Poincaré para determi-nar o comportamento global de alguns campos vetoriais polinomiais. Apre-sentamos casos de campos vetoriais lineares, cuja origem é, respectivamente, um ponto de sela, um nó, um foco e um centro, e, por fim, um caso de um campo vetorial não-linear.

Nos exemplos a seguir, os retratos de fase dos campos vetoriais no plano são feitos com o uso do programa Maple (para maiores informa¸cões sobre o uso deste programa no estudo de equa¸cões diferenciais veja [26]) e os retratos de fase dos campos vetoriais no disco de Poincaré são feitos com o aux´ılio do programa P4, o qual abordaremos com mais detalhes na Se¸cão 1.5.

Exemplo 1 Considere o sistema diferencial linear

˙

x=x,

˙

y=₋y. (1.5)

Note que a origem é o único ponto singular do sistema (1.5) e trata-se de um ponto de sela. O retrato de fase no plano do sistema (1.5)é dado pela Figura 1.4.

–1 –0.5 0 0.5 1

y

–1 –0.5 0.5 1

x

(26)

Usando a equa¸c˜ao (1.2), obtemos a express˜ao dep(X) na carta localU1

˙

u=₋2u,

˙

v =₋v.

Assim, há um único ponto singular em U1, a origem, que é um nó atrator.

Como o grau de X é ´ımpar, então a origem de V1 é, também, um nó atrator.

A expressão de p(X) na carta U2 é, usando a equa¸cão (1.3), dada por

˙

u= 2u,

˙

v =v.

Portanto, o único ponto singular em U2 é a origem, donde temos um nó

repulsor. O mesmo ´e verdade para a origem de V2.

Observe que o estudo do sistema (1.5) nas cartas U3 e V3 ´e an´alogo ao

feito no plano.

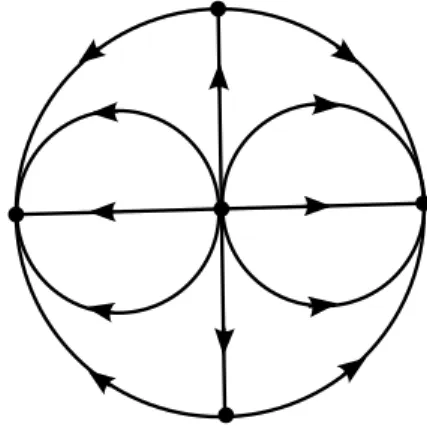
Assim, com base nestes cálculos, podemos desenhar o retrato de fase do sistema (1.5) no disco de Poincaré, que é mostrado na Figura 1.5. Note que as únicas separatrizes do sistema (1.5) são aquelas do ponto de sela e estão contidas nos eixos invariantes x= 0 e y = 0.

Figura 1.5: Retrato de fase do sistema (1.5) no disco de Poincar´e.

˙

x= 2x,

˙

(27)

Apenas a origem é ponto singular do sistema (1.6) e trata-se de um nó re-pulsor. O retrato de fase do sistema (1.6) no plano é dado pela Figura 1.6.

–1 –0.5 0 0.5 1

y

–1 –0.5 0.5 1

x

Figura 1.6: Retrato de fase do sistema (1.6): A origem ´e um n´o repulsor.

A express˜ao de p(X) na carta U1 ´e

˙

u=₋u,

˙

v =₋2v.

Assim, a origem é o único ponto singular em U1 e seu comportamento é de

nó atrator. O mesmo é válido na carta V1.

Na carta local U2, a express˜ao de p(X) ´e dada por

˙

u=u,

˙

v =₋v.

Verifica-se que o único ponto singular em U2 é a origem e ela é um ponto de

sela. O mesmo ocorre na carta V2.

Desta forma, o retrato de fase do sistema (1.6) no disco de Poincar´e ´e dado pela Figura 1.7.

˙

x=x₋y,

˙

(28)

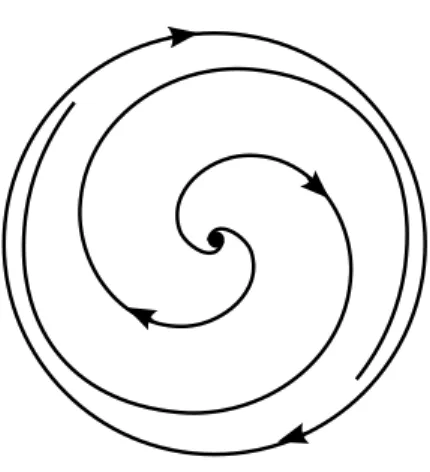
Temos que apenas a origem é ponto singular do sistema (1.7)e ela é um foco instável. O retrato de fase do sistema (1.7) no plano é dado pela Figura 1.8.

–1 –0.5 0 0.5 1

y

–1 –0.5 0.5 1

x

Figura 1.8: Retrato de fase do sistema (1.7): A origem ´e um foco inst´avel.

A express˜ao de p(X) na carta local U1 ´e dada por

˙

u=u2₋_u_{+ 1}_,

˙

v =₋v +uv,

enquanto na carta U2 ´e dada por

˙

u=₋u2₊_u₋₁_,

˙

(29)

Assim, podemos notar que p(X) n˜ao possui pontos singulares nas cartas U1

e U2. O mesmo ´e verdade para as cartas V1 e V2.

Nas cartasU3 e V3, o ´unico ponto singular do sistema (1.7) ´e a origem

e seu comportamento ´e de foco inst´avel, como no plano.

O retrato de fase do sistema (1.7) no disco de Poincar´e pode ser obser-vado na Figura 1.9.

˙

x=y,

˙

y=₋x. (1.8)

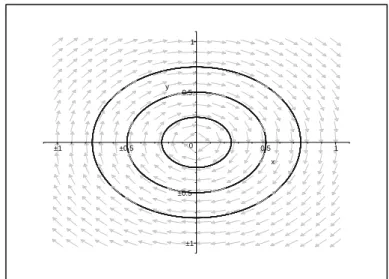
Note que seu ´unico ponto singular ´e a origem e que trata-se de um centro linear, conforme pode ser observado na Figura 1.10.

A express˜ao de p(X) na carta U1 ´e

˙

u=₋u2₋₁_,

˙

v =₋uv,

e na carta U2 ´e dada por

˙

u=u2_{+ 1}_,

˙

v =uv.

Podemos notar que p(X) n˜ao possui pontos singulares nas cartasU1 eU2. O

(30)

–1 –0.5 0 0.5 1

y

–1 –0.5 0.5 1

x

Figura 1.10: Retrato de fase do sistema (1.8): A origem ´e um centro.

Nas cartas U3 eV3, o ´unico ponto singular do distema (1.8)´e a origem

e seu comportamento ´e do tipo centro, como no plano.

O retrato de fase do sistema (1.8) no disco de Poincar´e pode ser obser-vado na Figura 1.11.

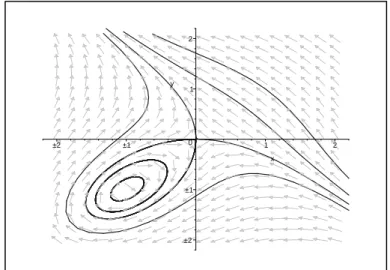
Exemplo 5 Vamos estudar o retrato de fase no disco de Poincar´e do sistema n˜ao-linear

˙

x=₋x₋y2_,

˙

(31)

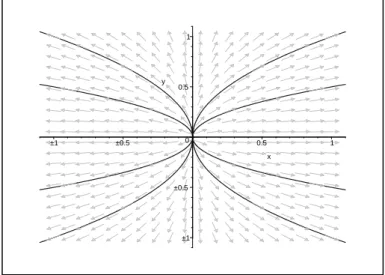
Os pontos (0,0) e (₋1,₋1)s˜ao pontos singulares do sistema (1.9). O ponto

(0,0)é um ponto de sela e o ponto (₋1,₋1) é um centro. As únicas separa-trizes do sistema (1.9) são as do ponto de sela. O retrato de fase do sistema

(1.9) no plano ´e dado pela Figura 1.12.

–2 –1 0 1 2

y

–2 –1 1 2

x

Figura 1.12: Retrato de fase do sistema (1.9) no plano.

Temos que a express˜ao de p(X) na carta U1 ´e dada por

˙

u= 1 + 2uv+u3_,

˙

v =v2₊_u2_v.

Nesta carta, o ponto(₋1,0)é um ponto singular e trata-se de um nó repulsor. Como o grau do sistema (1.9) é par, concluimos que na carta V1, o ponto

diametralmente oposto ao ponto (₋1,0)_∈U1 tamb´em ´e um ponto singular e

trata-se de um n´o atrator.

A express˜ao de p(X) na carta U2 ´e dada por

˙

u=₋1₋2uv₋u3_,

˙

v =₋v2₋_u2_v.

Nesta carta não há pontos singulares. O mesmo é verdade para a carta V2.

(32)

1.4 Compactifica¸

c˜

ao em coordenadas polares

Na Se¸cão 1.1, vimos que a compactifica¸cão de Poincaré consiste, basi-camente, na introdu¸cão das coordenadas (u, v) a partir das fórmulas

(x1, x2) =

(1

v, u v

)

, (x1, x2) =

(u

v,

1

v

)

, (x1, x2) = (u, v),

e da multiplica¸c˜ao do campo vetorial obtido com cada mudan¸ca de vari´avel pelo fator vd−1_.

Este modo mais abstrato de construir um campo vetorial em uma esfera diretamente por meio de cartas é o meio mais prático para cálculos precisos. Porém, também podemos compactificar um campo vetorial polinomial a par-tir do uso de coordenadas polares, como mostraremos nesta se¸cão.

Em geral, esta constru¸cão é prefer´ıvel em casos onde p(X) não tem pontos singulares no infinito, implicando que o conjunto de pontos no in-finito se torna uma órbita fechada. Para estudar o comportamento de p(X) próximo dela, é necessário um estudo global de sua vizinhan¸ca. Porém, essa vizinhan¸ca não está inteiramente contida nas cartas (U1, φ1) ou (U2, φ2).

Inicialmente, consideremos a mudan¸ca de vari´aveis

x1 =

1

ρcosθ, x2 =

1

ρ senθ, (1.10)

(33)

(0,0)

r

2p _q

x y

(0,0)

Figura 1.14: Mudan¸ca de vari´aveis introduzida pelo sistema (1.10).

A ideia geom´etrica desta mudan¸ca de vari´aveis pode ser vista na Figura 1.14.

Observa¸c˜ao 1 Note que se ρ_→0, ent˜ao x_{→ ∞} e y_{→ ∞}.

Derivando cada equa¸c˜ao do sistema (1.10) em rela¸c˜ao a t, obtemos

˙

x1 = −

senθ_·θρ˙ ₋cosθ_·ρ˙

ρ2 ⇔ θρ˙ =

−x˙1ρ2−cosθ·ρ˙

senθ

e

˙

x2 =

cosθ_·θρ˙ ₋ senθ_·ρ˙

ρ2 ⇔ θρ˙ =

˙

x2ρ2+ senθ·ρ˙

cosθ .

Unindo os dois resultados obtidos

−x˙1ρ2−cosθ·ρ˙

senθ =

˙

x2ρ2+ senθ·ρ˙

cosθ ⇔ ρ˙=−ρ

2_{( ˙}_x

1cosθ+ ˙x2 senθ).

(1.11) Com isso, descobrimos a equa¸cão para ˙ρ. Agora vamos descobrir a equa¸cão para ˙θ. Para tal, vamos trabalhar novamente com cada equa¸cão do sistema (1.10) derivada em rela¸cão a t. Assim,

˙

x1 = −

senθ_·θρ˙ ₋cosθ_·ρ˙

ρ2 ⇔ ρ˙ =

−x˙1ρ2− senθ·θρ˙

cosθ

e

˙

x2 =

cosθ_·θρ˙ ₋ senθ_·ρ˙

ρ2 ⇔ ρ˙=

−x˙2ρ2+ cosθ·θρ˙

(34)

Unindo os dois resultados obtidos

−x˙1ρ2− senθ·θρ˙

cosθ =

−x˙2ρ2+ cosθ·θρ˙

senθ ⇔ θ˙=ρ( ˙x2cosθ−x˙1 senθ).

(1.12) Assim, a partir de (1.11) e (1.12), podemos escrever o seguinte sistema

˙

ρ=₋ρ2_{( ˙}_x

1cosθ+ ˙x2 senθ),

˙

θ =ρ( ˙x2cosθ−x˙1 senθ).

(1.13)

Exemplo 6 Considere novamente o sistema diferencial linear do Exemplo 4, ou seja,

˙

x=y,

˙

y=₋x,

e vamos fazer a compactifica¸cão em coordenadas polares deste sistema. Con-siderando a mudan¸ca de variáveis (1.10) e usando a equa¸cão (1.13), obtemos o seguinte sistema

˙

ρ= 0,

˙

θ=₋1. (1.14)

Note que o sistema (1.14)não possui pontos singulares, poisθ˙=₋1e, assim, não há pontos tais que ρ˙ = 0 e θ˙ = 0. Além disso, como ρ˙ = 0 e θ˙ = ₋1, temos que as solu¸cões possuem uma distância radial constante, ou seja, são circunferências centradas na origem, e giram no sentido horário. Isto pode ser observado na Figura 1.11.

1.5 O programa P4

(35)

O programa P4 foi desenvolvido em parceria por pesquisadores da Es-panha e da B´elgica e pode ser baixado gratuitamente no endere¸co http:// mat.uab.es/_∼artes/p4/p4.htm. Ele trabalha em conjunto com o programa

MAPLE ou REDUCE que não vem incluso com o P4 e que deve ser uma aquisi¸cão a parte do usuário.

A Figura 1.15 mostra o painel de controle principal do programa P4. Essa janela é aberta assim que se inicia o programa e sua principal fun¸cão é disponibilizar o local para o usuário introduzir o sistema a ser estudado e alterar alguns de seus parâmetros de funcionamento.

Todos os resultados obtidos analiticamente no Cap´ıtulo 4 deste trabalho foram testados numericamente, utilizando-se o programa P4.

Um tutorial deste programa pode ser encontrado no Cap´ıtulo 9 de [16].

(36)

2

Desingulariza¸

c˜

ao de pontos singulares

n˜

ao-elementares

Seja X um campo vetorial polinomial de classe C∞ _em _R2 _associado

ao sistema de equa¸c˜oes diferenciais ordin´arias

˙

x=P(x, y),

˙

y=Q(x, y). (2.1)

Consideremos, por exemplo, o caso em que P(x, y) = x2 ₋ ₂_xy _e

Q(x, y) = y2₋₂_xy_{. Note que a origem, ou seja, o ponto (0}_,_{0), ´e um ponto}

singular isolado deste sistema. Ao calcular a matriz Jacobiana deste sistema aplicada no ponto (0,0), obtemos a matriz nula. Então, dizemos que este ponto é um ponto singular não-elementar, pois ele não é um ponto singular hiperbólico nem semi-hiperbólico. Neste caso, não é poss´ıvel utilizar, por exemplo, o Teorema de Hartman-Grobmann (este resultado pode ser encon-trado no Cap´ıtulo 6 de [14] e no Cap´ıtulo 1 de [16]), já que este é válido apenas para pontos singulares hiperbólicos. Assim, temos que recorrer a ou-tros métodos para estudar o comportamento do campo próximo a este ponto singular.

Uma técnica poderosa no estudo deste tipo de pontos singulares chama-seblow-up e consiste em mudan¸cas de variáveis que “explodem” (ou “expan-dem”) o ponto singular em uma curva. Em seguida, basta estudarmos o comportamento dos pontos singulares obtidos sobre a curva no novo campo. Caso algum destes pontos singulares ainda seja não-elementar aplicamos no-vamente a técnica e assim sucessino-vamente e de maneira finita até obtermos apenas pontos singulares elementares. A este processo chamamos de blowing-up sucessivo. Para finalizar, aplicamos o processo inverso, conhecido como

(37)

blowing down, e obtemos o retrato de fase do campo na vizinhan¸ca do ponto singular n˜ao-elementar.

Neste cap´ıtulo, estudaremos um tipo deblow-up homogˆeneo conhecido como blow-up polar. Para maiores informa¸c˜oes sobre este e outros tipos de

blow-ups consulte [15] ou o Cap´ıtulo 3 de [16].

2.1 Blow-up polar

Seja X um campo vetorial, conforme definimos anteriormente, associ-ado ao sistema (2.1). Vamos supor que a origem ´e um ponto singular isolassoci-ado do campo X. Consideremos a aplica¸c˜ao

φ:S1_×R_→R2

(θ, ρ)_7−→(ρcosθ, ρ senθ)

Podemos definir um campo vetorial ˆX de classe C∞ _{sobre o cilindro}

S1 _×R _{tal que} _φ_∗_{( ˆ}_X_{) =} _X_{, no sentido que} _Dφ_v_{( ˆ}_X₍_v_{)) =} _X₍_φ₍_v_{)). Este}

campo é chamado de pull back deX por φ e nada mais é do que X escrito em coordenadas polares. A aplica¸cão φé um difeomorfismo e, portanto, uma autêntica mudan¸ca de coordenadas em S1_×₍₀_,_∞_{), exceto em} _{_ρ _{= 0}_}_{, já}

queφleva_{ρ= 0_}no ponto (0,0), de maneira que sua inversaφ−1 _{“explode”}

a origem em um c´ırculo.

Para estudar o retrato de fase de X em uma vizinhan¸ca V da origem, basta estudar o retrato de fase de ˆX na vizinhan¸ca de φ−1₍_V_{) do c´ırculo} S1_{× {}₀_}_.

x y

(0,0)

r

q r

0

-1

r

(38)

Para escrever o campoX em coordenadas polares, consideramos a mu-dan¸ca de vari´aveis

x=ρcosθ, y =ρ senθ. (2.2)

Derivando cada equa¸c˜ao do sistema (2.2) com rela¸c˜ao a t, obtemos ˙

x= ˙ρcosθ₋ senθ_·θρ˙ _⇔ θρ˙ = −x˙ + ˙ρcosθ senθ

e

˙

y = ˙ρ senθ+ cosθ_·θρ˙ _⇔ θρ˙ = y˙−ρ˙ senθ

cosθ .

Unindo os resultados obtidos, ficamos com

−x˙ + ˙ρcosθ

senθ =

˙

y₋ρ˙ senθ

cosθ ⇔ ρ˙ = ˙xcosθ+ ˙y senθ. (2.3)

Agora, vamos descobrir uma equa¸cão para ˙θ. Para isso, vamos proceder analogamente ao que foi feito para ˙ρ, derivando em rela¸cão a t as equa¸cões do sistema (2.2). Assim,

˙

x= ˙ρcosθ₋ senθ_·θρ˙ _⇔ ρ˙ = x˙ + senθ·θρ˙ cosθ

e

˙

y = ˙ρ senθ+ cosθ_·θρ˙ _⇔ ρ˙ = y˙−cosθ·θρ˙

senθ .

Unindo os resultados obtidos, temos

˙

x+ senθ_·θρ˙

cosθ =

˙

y₋cosθ_·θρ˙

senθ ⇔ θ˙=

˙

ycosθ₋x˙ senθ

ρ . (2.4)

De (2.3) e (2.4), obtemos o seguinte sistema

˙

ρ=P cosθ+Q senθ,

˙

θ = Qcosθ−P senθ

ρ ,

(2.5)

onde ˙x=P =P(ρcosθ, ρ senθ) e ˙y=Q=Q(ρcosθ, ρ senθ). Chamamos o campo obtido de ˆX.

Para n˜ao zerarmos o sistema (2.5) ao tomarmos ρ = 0, escolhemos k

o maior inteiro positivo tal que ρk_|_P _e _ρk_|_Q _{e definimos um novo campo}

vetorial ˜X, com

˜

X = Xˆ

(39)

Observe que esta divisão não muda as órbitas de ˆX, muda apenas a parametriza¸cão det. Com isso, observe que o ponto singular (0,0) foi levado para a curva S1_{× {}₀_}_{. Além disso, ao longo de}S1_{× {}₀_} _{os pontos singulares}

são determinados pelas solu¸cões de ˙θ = 0 no sistema associado ao campo ˜X. Vamos ilustrar o uso desta técnica com alguns exemplos.

Exemplo 7 Consideremos o campo vetorialXassociado ao sistema de equa-¸c˜oes diferenciais ordin´arias

˙

x=x2₋₂_xy,

˙

y=y2₋₂_xy. (2.6)

Em coordenadas polares, o sistema (2.6) ´e dado por

˙

ρ=ρ2_(cos3_θ_{+ sen}3_θ₋_{2 cos}2_θ_sen_θ₋_{2 cos}_θ_sen2_θ₎_,

˙

θ = 3ρcosθsenθ( senθ₋cosθ). (2.7)

Note que se tom´assemos ρ = 0 zerar´ıamos o sistema (2.7). Para re-solver isso, escolhemosk= 2, poisρ2_|_P _e_ρ2_|_Q_{, onde}_P ₌_P₍_ρ_cos_{θ, ρ} _sen_θ_{) =}

ρ2_(cos2_θ₋_{2 cos}_θ_sen_θ₎ _e _Q₌_Q₍_ρ_cos_{θ, ρ} _sen_θ_{) =} _ρ2_{( sen}2_θ₋_{2 cos}_θ_sen_θ₎_.

Assim, obtemos o campo vetorial X˜ associado ao sistema

˙

ρ=ρ(cos3θ+ sen3θ₋2 cos2θsenθ₋2 cosθsen2θ),

˙

θ = 3 cosθsenθ( senθ₋cosθ). (2.8)

Em ρ = 0, temos que θ = 0, π/4, π/2, π,5π/4,3π/2 s˜ao solu¸c˜oes do sistema (2.8).

Agora, estudando o campo X˜ localmente em cada um destes pontos singulares, obtemos que todos eles são pontos de sela. Com isso, podemos determinar o comportamento próximo a origem do campo vetorial X. Esse processo é ilustrado pela Figura 2.2.

Exemplo 8 SejaX o campo vetorial associado ao sistema de equa¸c˜oes dife-renciais ordin´arias

˙

x=xy,

˙

y =₋2x2₊_xy₊1

2y

(40)

Blow-up _Blowing-down

Figura 2.2: Blow-up polar na origem do sistema (2.6).

Em coordenadas polares, o sistema (2.9) ´e dado por

˙

ρ=ρ2

(

1 2 sen

3_θ₋_cos2_θ_sen_θ_{+ cos}_θ_sen2_θ

)

,

˙

θ=ρ

(

−2 cos3_θ₋ 1

2cosθsen

2_θ_{+ cos}2_θ_sen_θ

)

.

Neste caso, escolhemos k = 2. Assim, obtemos o campo vetorial X¯

associado ao sistema:

˙

ρ=ρ

(

1 2 sen

3_θ₋_cos2_θ_sen_θ_{+ cos}_θ_sen2_θ

)

,

˙

θ =₋2 cos3_θ₋1

2cosθsen

2_θ_{+ cos}2_θ_sen_θ.

(2.10)

Em ρ= 0, temos que θ =π/2,3π/2 são solu¸cões do sistema (2.10). Estudando o campo X˜ na vizinhan¸ca de cada um destes pontos singu-lares, obtemos que eles apresentam comportamento do tipo nó repulsor (para

θ = π/2) e nó atrator (para θ = 3π/2). Com isso, podemos determinar o comportamento próximo a origem do campo vetorial X. Esse processo é ilustrado pela Figura 2.3.

Blow-up _Blowing-down

(41)

3

Integrabilidade de Darboux

Ao estudarmos o retrato de fase de um campo vetorial, especialmente de dimensão dois, a existência de uma integral primeira simplifica muito este estudo, pois com ela é poss´ıvel determinar a dinâmica global do campo. Porém, não é fácil saber se um campo vetorial possui ou não integral primeira. Neste cap´ıtulo, vamos estudar a existência de integrais primeiras para campos vetoriais polinomiais no plano a partir da teoria de integrabilidade de Darboux, conforme é feito no Cap´ıtulo 2 de [9], no Cap´ıtulo 8 de [16] e no Cap´ıtulo 5 (sobre sistemas Hamiltonianos) de [26]. Este tipo de integra-bilidade é particularmente interessante, pois nos fornece uma liga¸cão entre a integrabilidade do campo e o número de curvas algébricas invariantes que ele possui.

Consideremos o sistema diferencial polinomial complexo no plano (ou simplesmente sistema polinomial) dado por

˙

x=P(x, y),

˙

y=Q(x, y). (3.1)

onde x, y _∈ R _{são as variáveis dependentes, a variável independente} _t _(o

tempo) é um complexo e P e Q são polinômios nas variáveis x e y com coeficientes complexos. Suponhamos que o sistema (3.1) tenha grau d e que os polinômios P e Q sejam relativamente primos no anel dos polinômios complexos nas variáveis x e y. O campo vetorial X associado ao sistema (3.1) é definido por X(x, y) = (P(x, y), Q(x, y)).

Al´em disso, denotaremos por F _{o corpo dos reais} R _{ou complexos} C_,

por sistemaF_-polinomial _{o sistema polinomial (3.1) nas vari´aveis}_x_,_y _{e com}

os coeficientes dos polinˆomiosP eQem F_{e por}F_[_{x, y}_{] o anel dos polinˆomios}

nas vari´aveis x e y e coeficientes em F_.

(42)

3.1 Integrais primeiras e invariantes

Consideremos o campo vetorial X associado ao sistema F_-polinomial

(3.1). Dizemos que X ´e integr´avel em um subconjunto aberto U de F2 _se

existe uma fun¸c˜ao anal´ıtica n˜ao-constante H : U _→F_{, chamada de} _integral

primeira de X em U, tal que H(x(t), y(t)) = c, c constante, para todo t

e para toda solu¸cão ϕ(t) = (x(t), y(t)) de X contida em U, ou seja, H é constante em todas as solu¸cões de X contidas em U.

Note que H ´e uma integral primeira de X em U se, e somente se,

X(H) = _⟨X,_∇H_⟩=P∂H ∂x +Q

∂H ∂y ≡0

em U, onde _∇H ´e o vetor gradiente de H.

Seja U _⊂ F2 _{um conjunto aberto. Dizemos que uma fun¸c˜ao anal´ıtica}

I(x, y, t) :U _×F _→ F _{´e um} _invariante _{do campo vetorial polinomial} _X _em

U se I(x, y, t) = c, c constante, para todos os valores de t para os quais as solu¸c˜oes ϕ(t) = (x(t), y(t)) de X est˜ao definidas e contidas em U, ou seja,

dI dt =P

∂I ∂x +Q

∂I ∂y +

∂I ∂t ≡0.

Se um invariante I é independente de t, então I é uma integral primeira. Seja ϕp(t) = (x(t), y(t)) a solu¸cão de X passando pelo ponto p ∈ F2,

definida em seu intervalo maximal (αp, ωp) tal que ϕp(0) = p. Se ωp = ∞,

definimos o conjunto

ω(p) = _{q_∈F2 _{: existe} _{_t_n_} _com _t_n _{→ ∞}_e _ϕ₍_t_n₎_→_q _quando _n _{→ ∞}}_.

Da mesma maneira, seαp =−∞, definimos o conjunto

α(p) = _{q_∈F2 _{: existe} _{_t_n_} _com _t_n _{→ −∞}_e _ϕ₍_t_n₎_→_q _quando _n_{→ ∞}}_.

Os conjuntosω(p) eα(p) s˜ao chamadosconjunto ω–limite (ou simples-mente ω–limite) e conjunto α–limite (ou α–limite) de p, respectivamente.

(43)

Proposi¸c˜ao 1 Seja U _⊂ F2 _{um aberto e} _X _{o campo vetorial associado ao}

sistema F_-polinomial _(3.1)_{. Se} _H _: _U _→ F _{´e uma integral primeira de} _X

e F : F _→ F _{é uma fun¸cão anal´ıtica, então} _F _◦_H _{é também uma integral}

primeira de X.

Prova. De fato, supondo F =F(x), temos que

X(F _◦H) =_⟨X,_∇(F _◦H)_⟩=P ∂

∂x(F ◦H) +Q ∂

∂y(F ◦H)

=P ( dF dx ∂H ∂x ) +Q ( dF dx ∂H ∂y ) = ( P∂H ∂x ) dF dx + ( Q∂H ∂y ) dF dx ≡0.

Segue an´alogo para F =F(y).

Dizemos que o campo vetorial X ´e Hamiltoniano em U _⊂ F2 _{com um}

grau da liberdade se existe uma fun¸c˜ao anal´ıtica H:U _→F _{tal que}

P = ∂H

∂y e Q=− ∂H

∂x.

Temos que H ´e dita Hamiltoniano de X. Note que, seH ´e Hamiltoniano de

X, ent˜ao H ´e integral primeira deX. De fato,

X(H) =P∂H ∂x +Q

∂H ∂y = ∂H ∂y ∂H ∂x + ( −∂H ∂x ) ∂H ∂y ≡0.

Os campos vetoriais mais simples que possuem integral primeira são os Hamiltonianos. Em geral, a integral primeira de um campo vetorial não-Hamiltoniano é muito dif´ıcil de se detectar. Abaixo trazemos um resultado para campos vetoriais Hamiltonianos definidos em um subconjunto U _⊂R2_.

Proposi¸cão 2 Qualquer ponto singular não-degenerado de um campo veto-rial Hamiltoniano definido em U _⊂R2 _{é uma sela ou um centro.}

Prova. Seja X um campo vetorial definido em um subconjunto U _⊂ R2

(44)

na origem. Temos que a matriz Jacobiana de X no ponto O = (0,0) ´e igual a

DX(O) =



  

∂P ∂x(0,0)

∂P ∂y(0,0) ∂Q

∂x(0,0) ∂Q

∂y(0,0)

    =     

∂2_H

∂x∂y(0,0)

∂2_H

∂y2 (0,0)

−∂

2_H

∂x2(0,0) −

∂2_H

∂y∂x(0,0)

     .

Note que tr(DX(O)) = 0, onde tr(DX(O)) ´e o tra¸co da matrizDX(O), e

det(DX(O)) = ∂

2_H

∂x2 (0,0)

∂2_H

∂y2 (0,0)−

(

∂2_H

∂x∂y(0,0)

)2

´e o determinante da matrizDX(O).

Temos que det(DX(O))_̸= 0, pois, por hipótese, a origem é um ponto singular não-degenerado. Se det(DX(O)) < 0, então a origem é um ponto de sela. Agora, se det(DX(O)) > 0, então a origem é um centro ou um foco fraco. Como H é o Hamiltoniano do campo vetorial X, então H é uma integral primeira de X e, deste modo, H é constante em todas as solu¸cões deX. Se a origem for um foco, então a origem não é um máximo ou m´ınimo local estrito da fun¸cãoH. Suponha que a origem seja um foco estável. Então,

H(x0, y0) = lim

t→∞H(x(x0, y0, t), y(x0, y0, t)) = H(0,0),

para todo (x0, y0) ∈ Vϵ(0,0), onde Vϵ(0,0) ´e um vizinhan¸ca suficientemente

pequena da origem. Como H é, por defini¸cão, anal´ıtica e não-constante, então H(x, y)> H(0,0) (a origem é um m´ınimo local) ou H(x, y)< H(0,0) (a origem é um máximo local), para todo (x, y) _∈ Vϵ(0,0), o que é uma

contradi¸cão. Um argumento similar pode ser usado quando a origem é um foco instável.

Portanto, um ponto singular n˜ao-degenerado de um campo vetorial

Hamiltoniano ´e uma sela ou um centro.

Proposi¸c˜ao 3 Seja X o campo vetorial associado ao sistema (3.1). Ent˜ao

X é Hamiltoniano se, e somente se, div(X)_≡0, onde div(X)é o divergente do campo vetorial X e é dado por div(X) = ∂P

∂x + ∂Q

(45)

Prova. (_⇒) Se X é um campo vetorial Hamiltoniano, então existe uma fun¸cão H tal que P = ∂H

∂y e Q=− ∂H

∂x. Logo, ∂P

∂x = ∂2_H

∂x∂y e ∂Q

∂y =− ∂2_H

∂y∂x.

ComoH´e anal´ıtica, pelo Teorema de Schwarz segue que ∂

2_H

∂x∂y = ∂2_H

∂y∂x.

Logo,

div(X) = ∂P

∂x + ∂Q

∂y = ∂2_H

∂x∂y − ∂2_H

∂y∂x ≡0.

(_⇐) Se div(X)_≡0, definamos

H(x, y) =

∫

P(x, y)dy₋h(x),

ondeh(x) ´e escolhida de tal modo que ∂H

∂x =−Q. DerivandoH com rela¸c˜ao

a x obtemos

∂H ∂x =

∫ _∂P

∂xdy−h

′

(x) = ₋Q _⇒ h′

(x) =

∫ _∂P

∂xdy+Q

⇒ h(x) =

∫ ∫

∂P

∂xdydx+

∫

Qdx.

Como P ´e anal´ıtica, pelo Teorema de Fubini temos que

∫ ∫

∂P

∂xdydx=

∫ ∫

∂P ∂xdxdy.

Logo,

h(x) =

∫ ∫

∂P

∂xdxdy+

∫

Qdx.

Assim,

H(x, y) =

∫

P dy₋

∫ ∫

∂P

∂xdxdy−

∫

Qdx _⇒

⇒ ∂H

∂y =P −

∫ _∂P

∂xdx−

∫ _∂Q

∂ydx=P −

∫ ( ∂P ∂x + ∂Q ∂y )

dx=P.

(46)

Exemplo 9 Seja X o campo vetorial associado ao sistema diferencial linear

˙

x=ax,

˙

y=₋by, (3.2)

com a >0 e b >0 constantes reais.

Considere a fun¸c˜ao H1 :R2 →R dada por

H1(x, y) = xαy

onde α =b/a. Temos que H1 ´e uma integral primeira do campo vetorial X

em R2_{. De fato,}

X(H1) =ax

∂H1

∂x −by ∂H1

∂y =ax(αx

α−1_y₎

−by(xα) = bxαy₋bxαy= 0,

para todo (x, y)_∈R2_.

Assim, H1 ´e constante em todas as solu¸c˜oes de X em R2. Note que a

origem é o único ponto singular do sistema (3.2). Além disso, a origem é ponto de sela da fun¸cão H1 e, consequentemente, do campo vetorial X. O

gr´afico da fun¸c˜ao H1 e o retrato de fase do campo vetorialX podem ser vistos

na Figura 3.1.

–1 –0.5 0 0.5 1

y

–1 –0.5 0.5 1

x

Figura 3.1: Gr´afico da fun¸c˜aoH1 e retrato de fase do campo vetorialX, com

(47)

Agora, seja Y o campo vetorial associado ao sistema diferencial linear

˙

x=ay,

˙

y=₋bx, (3.3)

com a >0 e b >0 constantes reais.

Considere a fun¸c˜ao H2 :R2 →R dada por

H2(x, y) = αx2+y2

onde α = b/a. Temos que H2 ´e uma integral primeira do campo vetorial Y

em R2_{. De fato,}

Y(H2) = ay

∂H2

∂x −bx ∂H2

∂y =ay(2αx)−bx(2y) = 2bxy−2bxy = 0,

Logo, H2 ´e constante em todas as solu¸c˜oes de Y em R2. Note que a

origem é o único ponto singular do sistema (3.3). Além disso, a origem é ponto de m´ınimo local da fun¸cão H2 e, consequentemente, um centro do

campo vetorial Y, pois as curvas de n´ıveis de H2 s˜ao ´orbitas fechadas. O

gr´afico da fun¸c˜ao H2 e o retrato de fase do campo vetorial Y podem ser

vistos na Figura 3.2.

–1 –0.5 0 0.5 1

y

–1 –0.5 0.5 1

x

Figura 3.2: Gr´afico da fun¸c˜aoH2 e retrato de fase do campo vetorialY, com

(48)

Exemplo 10 Seja X o campo vetorial associado ao sistema

˙

x=₋2y,

˙

y= 3x2₋₂_x. (3.4)

Temos que a fun¸c˜ao H :R2 _→R _{dada por}

H(x, y) = ₋x3+x2₋y2

´e uma integral primeira do campo vetorial X em R2_{, pois}

X(H) = ₋2y∂H ∂x + (3x

2

−2x)∂H

∂y =−2y(−3x

2_{+ 2}_x_{) + (3}_x2

−2x)(₋2y) = 0,

Deste modo, H é constante em todas as solu¸cões de X em R2_{. Além}

disso, note que H ´e um Hamiltoniano do campo vetorial X. De fato,

∂H

∂y =−2y e − ∂H

∂x = 3x

2

−2x.

O sistema (3.4) possui dois pontos singulares (0,0) e (2/3,0). Temos que a origem é um ponto de sela e podemos concluir, a partir da Proposi¸cão 2, que o ponto singular (2/3,0)é um centro.

O gr´afico da fun¸c˜ao H e o retrato de fase do campo vetorial X podem ser vistos na Figura 3.3.

–2 –1 0 1 2 y

–2 –1 1 2

x

(49)

3.2 Fatores integrantes

SejaX o campo vetorial associado ao sistema F_{-polinomial (3.1),} _U _⊂ F2 _{um aberto e} _R _:_U _→_F_{uma fun¸c˜ao anal´ıtica n˜ao identicamente nula em}

U. A fun¸c˜ao R ´e umfator integrante do campoX em U se, e somente se,

X(R) = ₋Rdiv(X),

onde div(X) ´e o divergente do campo vetorial X, ou, equivalentemente,

P∂R ∂x +Q

∂R

∂y =−R

(

∂P ∂x +

∂Q ∂y

)

.

A integral primeira H associada ao fator integrante R ´e dada por

H(x, y) =

∫

R(x, y)P(x, y)dy+h(x),

onde h(x) ´e escolhido de modo que ∂H

∂x =−RQ. Note que, X(H) =P∂H

∂x +Q ∂H

∂y =P(−RQ) +Q(RP) = R(−P Q+QP)≡0

e

RP = ∂H

∂y e RQ=− ∂H

∂x. (3.5)

Reciprocamente, dada uma integral primeiraHdo sistema (3.1) sempre podemos encontrar um fator integrante R que satisfa¸ca (3.5).

Exemplo 11 A fun¸c˜ao R : R2 _→ R _{dada por} _R₍_{x, y}_{) = 2}_e2by _{´e um fator}

integrante do sistema

˙

x=₋y₋b(x2₊_y2₎_,

˙

y=x.

De fato,

P∂R ∂x +Q

∂R

∂y = (−y−b(x

2₊_y2_{))0 +}_x₍₄_be2by_{) = 4}_bxe2by_.

(50)

−R ( ∂P ∂x + ∂Q ∂y )

=₋2e2by(₋2bx+ 0) = 4bxe2by.

Logo,

P∂R ∂x +Q

∂R

∂y =−R

( ∂P ∂x + ∂Q ∂y ) .

Proposi¸c˜ao 4 Se o sistema F_-polinomial _(3.1) _{tem dois fatores integrantes}

R1 e R2 em um subconjunto aberto U de F2 e R1/R2 é não-constante, então

a fun¸c˜ao H = R1/R2 ´e uma integral primeira do campo X associado ao

sistema (3.1) no conjuntos aberto U _{\ {}R2 = 0}.

Prova. Como R1 eR2 s˜ao fatores integrantes, ent˜aoX(Ri) =−Ridiv(X),

i= 1,2, por defini¸c˜ao. Ent˜ao,

X(H) = X

(

R1

R2

)

= (X(R1))R2 −R1(X(R2)) (R2)2

= div(X)(−R1R2+R1R2)

(R2)2 ≡

0.

Portanto, H ´e uma integral primeira de X.

De forma an´aloga a fator integrante, dizemos que uma fun¸c˜ao anal´ıtica

V : U _→ R_{, a qual não é identicamente nula em} _U_{, é um} _{fator integrante}

inverso do sistema (4.1) em U se, e somente se, X(V) = V div(X), ou, equivalentemente,

P∂V ∂x +Q

∂V ∂y = ( ∂P ∂x + ∂Q ∂y ) V.

3.3 Curvas Alg´

ebricas Invariantes

Seja f _∈ C_[_{x, y}_], _f _{não constante. A curva algébrica} _f₍_{x, y}_{) = 0 é}

uma curva alg´ebrica invariante (ou, em alguns casos, simplesmente curva invariante) do sistema F_{-polinomial (3.1) se existe} _K _∈C_[_{x, y}_{] tal que}

X(f) =P∂f ∂x +Q

∂f

∂y =Kf.

(51)

Observa¸c˜ao 3 Se o sistema F_-polinomial _(3.1) _{tem grau} _m_{, ent˜ao o grau}

de qualquer cofator K ´e no m´aximo m₋1.

Note que, pela defini¸cão, o campo vetorial X = (P, Q) é tangente à curva algébrica invariante f = 0 e, portanto, f = 0 é formada por órbitas de

X. Ent˜ao, f = 0 ´e invariante pelo fluxo definido porX.

Exemplo 12 Seja X o campo vetorial associado ao sistema diferencial poli-nomial quadr´atico

˙

x=₋y(1 +a2₋_r2_{) + 2}_axy,

˙

y=x(1 +a2₋_r2_{) +}_a₍₋_x2₊_y2₋₁₎_, (3.6)

com a >0 e r >0.

Temos que as curvasf1, f2 :R2 →Rdadas porf1(x, y) =x2+y2−1 = 0

e f2(x, y) = (x−a)2+y2 −r2 = 0, ou seja, f1 ´e a circunferˆencia centrada

na origem com raio 1 e f2 ´e a circunferˆencia centrada no ponto (a,0) com

raior, s˜ao curvas alg´ebricas invariantes do sistema (3.6)com cofatoresK1 =

K2 = 2ya. De fato,

X(f1) = 2x(−y(1 +a2−r2) + 2axy) + 2y(x(1 +a2−r2)

+a(₋x2+y2₋1)) = 2ya(x2+y2₋1) =K1f1

e

X(f2) = 2(x−a)(−y(1 +a2−r2) + 2axy) + 2y(x(1 +a2 −r2)

+a(₋x2+y2₋1)) = 2ya((x₋a)2+y2₋r2) = K2f2.

No Cap´ıtulo 4, analisaremos com mais detalhes a classe de sistemas apresentada no Exemplo 12.

Observa¸cão 4 Na defini¸cão da curva algébrica invariante f = 0, sempre permitimos que esta curva seja complexa, ou seja, f _∈ C_[_{x, y}_]_{, mesmo no}

(52)

Na proposi¸cão seguinte e no decorrer do cap´ıtulo, a conjuga¸cão ¯f sig-nifica conjuga¸cão apenas dos coeficientes do polinômio f.

Proposi¸cão 5 Para um sistema polinomial real (3.1), f = 0 é uma curva algébrica invariante de (3.1) com cofator K se, e somente se, f¯= 0 for uma curva algébrica invariante de (3.1) com cofator K¯.

Prova. Seja f = 0 uma curva alg´ebrica invariante do sistema polinomial real (3.1) com cofator K. Ent˜ao, segue que

X(f) =P∂f ∂x +Q

∂f

∂y =Kf.

Logo,

P∂f ∂x +Q

∂f

∂y =Kf ⇔ P ∂f¯ ∂x +Q

∂f¯

∂y = ¯Kf¯ ⇔ X( ¯f) = ¯Kf ,¯

pois P, Q _∈ R_[_{x, y}_{]. Portanto, ¯}_f _{= 0 ´e uma curva alg´ebrica invariante de}

(3.1) com cofator ¯K.

A rec´ıproca segue de modo an´alogo.

Lema 1 Sejam f, g _∈ C_[_{x, y}_]_{. Assuma que} _f _e _g _{s˜ao relativamente primos}

no anel C_[_{x, y}_]_{. Então,} _{f g} _{= 0}_{é uma curva algébrica invariante do sistema}

polinomial (3.1) com cofatorKf g se, e somente se,f = 0 e g = 0 são curvas algébricas invariantes com cofatores Kf e Kg, respectivamente. Além disso,

Kf g =Kf +Kg.

Prova. (_⇒) Note queX(f g) = (X(f))g+f(X(g)). Sef g = 0 é uma curva algébrica invariante com cofator Kf g, então

X(f g) = Kf gf g ⇒ (X(f))g+f(X(g)) = Kf gf g ⇒ f|X(f) e g|X(g),

pois f e g s˜ao relativamente primos. Logo, existem polinˆomios Kf e Kg

tais que X(f) = Kff e X(g) = Kgg. Portanto, f e g s˜ao curvas alg´ebricas