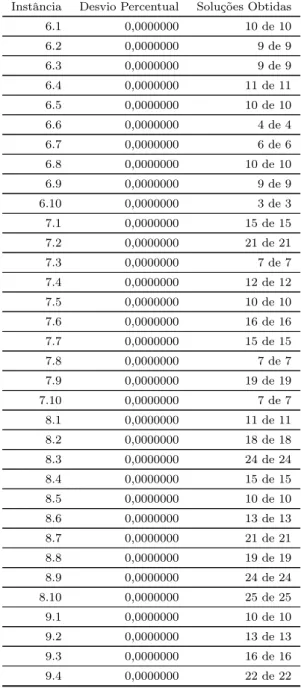
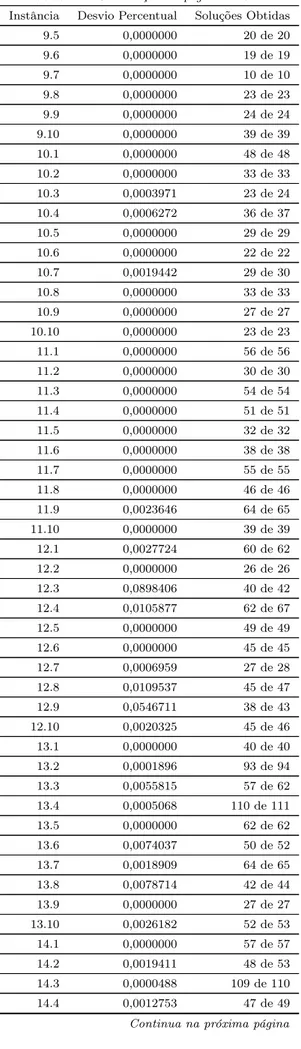
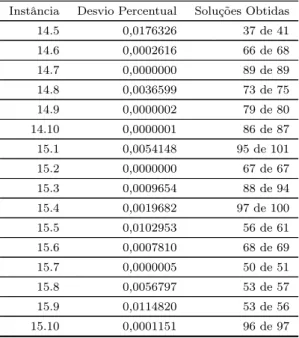
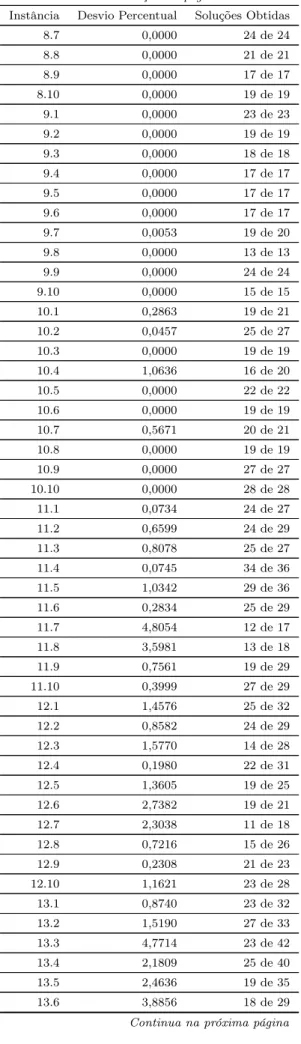
Algoritmos experimentais para o problema biobjetivo da árvore geradora quadrática em adjacência de arestas
Texto
Imagem


Documentos relacionados
A começar pela literatura infantil, passando pelos desenhos animados á televisão e ao cinema, os personagens oferecem imagens que são muito significativas para
Algoritmo de Busca Tabu para o Problema da Árvore Geradora Mínima Generalizado.. Anais do XXVII Encontro Nacional de Engenharia de Produção, Foz do Iguaçu: ABEPRO,
No programa DIRF (Aplicativo disponível no site da Receita Federal) são importadas as informações geradas no sistema de folha como: Nome, CPF, Salário Bruto, Valor da Previdência
(encontrar uma árvore geradora máxima), como você pode usar os algoritmos de Kruskal e Prim (sem alterá-los) para obter uma árvore. • Supondo que todas as arestas de um grafo
O primeiro é o algoritmo de Kruskal que, em cada iteração, escolhe uma aresta segura mais barata possível.. O algoritmo de Kruskal vai aumentando
Elabore um texto de uma lauda, considerando os seguintes elementos: o caráter social do espaço geográfico decorre do fato de que os homens têm fome, sede e frio, necessidades
Após elaborar o texto, em resposta à atividade proposta, verifique se ele contém os seguintes aspectos: a relação entre fixos e fluxos, que elementos você considerou
Os documentos legais de cobrança deverão conter as especificações e as quantidades dos itens fornecidos, de acordo com a solicitação do BRDE formalizada através