Aplicação de técnicas de decomposição em problemas de corte de estoque

Aplicação de técnicas de decomposição em

problemas de corte de estoque

Dissertação de Mestrado Pós-Graduação em Matemática

Instituto de Biociências, Letras e Ciências Exatas Rua Cristóvão Colombo, 2265, 15054-000

Aplicação de técnicas de decomposição em

problemas de corte de estoque

Orientadora:

Prof

. Dr

. Maria do Socorro Nogueira Rangel

Universidade Estadual Paulista “Júlio de Mesquita Filho” Instituto de Biociências, Letras e Ciências Exatas

Campus de São José do Rio Preto

São José do Rio Preto 2013

Thiago Xavier Greccho. – São José do Rio Preto: [s.n.], 2013. 85 f. : il. ; 30 cm.

Orientador: Maria do Socorro Nogueira Rangel

Dissertação (mestrado) - Universidade Estadual Paulista, Instituto de Bio-ciências, Letras e Ciências Exatas

1. Pesquisa operacional. 2. Otimização matemática. 3. Problema de corte de estoque. I. Rangel, Maria do Socorro Nogueira II. Universidade Estadual Paulista, Instituto de Biociências, Letras e Ciências Exatas III. Título.

Aplicação de técnicas de decomposição em

problemas de corte de estoque

Dissertação apresentada para obtenção do título de Mestre em Matemática, área de Análise Aplicada, junto ao Instituto de Biociências, Letras e Ciências Exatas da Universidade Estadual Paulista “Júlio de Mesquita Filho”, Campus de São José do Rio Preto.

Banca Examinadora

Profa_{. Dr}a_{. Maria do Socorro Nogueira Rangel}

Professora Adjunto

UNESP - São José do Rio Preto - SP Orientadora

Profa_{. Dr}a_{. Deisemara Ferreira}

Professora Adjunto UFTM - Uberaba - MG

Prof. Dr. Silvio Alexandre de Araujo Professor Adjunto

UNESP - São José do Rio Preto - SP

A Deus, pelo dom da vida.

Aos meus pais, Claudemir e Iraclides, e à minha irmã Aline, pelo amor, carinho, dedicação e por estarem sempre ao meu lado me apoiando. Não existem palavras para descrever o quão especial eles são em minha vida.

À minha professora orientadora Socorro Rangel, pela orientação e dedicação. Por acreditar nesse trabalho. Obrigado pela compreensão e conselhos, que, com certeza, me ajudaram e continuarão me ajudando no futuro.

Aos professores de pós-graduação: Profo_{. Dr. Sílvio Alexandre de Araújo, Prof}o_.

Dr. Geraldo Nunes Silva, Profo_{. Dr. Cláudio Aguinaldo Buzzi, Prof}o_{. Dr. Adalberto}

Spezamiglio, Profo_{. Dr. Ali Messaoudi pelos ensinamentos, atenção e colaboração. Aos}

professores de graduação, em especial a Profa_{. Dra. Rita de Cássia Pavani Lamas, Prof}o_.

Hermes Antonio Pedroso, Profo_{. Dr. Masayoshi Tsuchida, Prof}o_{. Dr. Alagacone Sri}

Ranga, Profa_{. Dra. Cleonice Fátima Bracciali, Prof}o_{. Dr. Waldemar Donizete Bastos,}

Profo _{Dr. Maurílio Boaventura e a Prof}a _Dra _{Tatiana Miguel Rodrigues, que sempre me}

estimularam a estudar.

A todos os meus colegas do IBILCE (UNESP - Campus de São José do Rio Preto - SP) dos tempos de graduação, em especial aos amigos da matemática: Bárbara, Renato, “Nico” (Douglas), Fernandinho, “Bracinho” (Rafael), Moreno, “Batata” (Vínicius), Tatiana Felix e “Xupeta” (Rodolfo), pela amizade, pelos momentos de estudo e risada principalmente. Também aos amigos de outros cursos ou que não cursamos nenhuma disciplina juntos: “Tanabi” (Fernando), “Farofa” (Bruno), “Cabessa” (Paulo Roberto), “Virso” (Emerson), “Pinda” (Leandro), “Emo” (Luiz), Miguel, Hector e “Se Foda” (Rafael), pela amizade e momentos de distração, principalmente na quadra do IBILCE. Um agradecimento especial ao amigo “Frota” (Rafael) pelo apoio no último ano de graduação do bacharelado, no momento mais difícil em minha vida ele se mostrou um amigo que eu não conhecia.

A todos os amigos de pós-graduação, em especial ao Matheus, Diego, Augusto, Michelli, Gislaine e Aneliza pela amizade, pelos momentos de estudos e conversas, pelas viagens a congressos e eventos do tipo. Ao grupo de otimização do IBILCE, em especial ao Yagor e a Juliana.

obrigado pela dedicação.

A todos os funcionários do IBILCE que, direta ou indiretamente, contribuíram para a realização deste trabalho.

À todas as pessoas que sempre torcem pelo meu sucesso e pela minha felicidade.

mas oportunidades ímpares de superação e evolução. (Maurício Rodrigues de Morais)

Neste trabalho apresentamos métodos de decomposição para problemas de otimização inteira que auxiliam no processo de geração de colunas aplicado ao problema de corte de estoque bidimensional. É feita uma revisão de literatura sobre problemas considerando o corte simultâneo de objetos (ciclos da serra). Visando a aceleração do método de ge-ração de colunas, propomos uma técnica de decomposição para o problema de corte de estoque com minimização de ciclos da serra que incorpora informações duais associadas às restrições de ciclos da serra no subproblema pricing.

In this paper we present decomposition methods for integer optimization problems that will help the column generation process applied to the two-dimensional cutting stock problem. It’s made a literature review about problems considering the simultaneous cutting of objects (cycles saw). Seeking an acceleration in the generation column method, the propose a decomposition technique for the cutting stock problem with minimization saw cycles which incorporates dual information associated to saw cycles restrictions in the pricing subproblem.

Keywords: Two-dimensional cutting stock problems. Saw cycles. Decomposition

1 Problema de corte de estoque bidimensional. . . p. 34

2 Padrão de corte unidimensional. . . p. 35

3 Padrão de corte bidimensional. . . p. 36

4 Padrão de corte homogêneo maximal bidimensional. . . p. 37

5 Corte simultâneo de objetos . . . p. 45

6 Padrão de corte na indústria têxtil . . . p. 51

1 Introdução p. 13

2 Geração de coluna em otimização linear inteira p. 15 2.1 Princípio de decomposição de Dantzig-Wolfe . . . p. 15

2.2 O método de geração de colunas . . . p. 18

2.3 Um exemplo ilustrativo . . . p. 20

3 O problema de corte de estoque p. 31 3.1 O problema de corte de estoque unidimensional . . . p. 31

3.2 O problema de corte de estoque bidimensional . . . p. 33

3.3 Geração de colunas aplicado ao PCE . . . p. 38

3.4 Aplicações do PCE . . . p. 40

3.5 Extensões do PCE . . . p. 41

4 O problema de ciclos da serra p. 44 4.1 Modelos matemáticos para o problema de ciclos da serra . . . p. 46

4.2 Aplicação do PCE-C indústria têxtil . . . p. 50

4.3 Aplicação do PCE-C na indústria de metal . . . p. 53

5 Solução do problema de ciclos da serra via geração de colunas p. 58 5.1 Técnica de decomposição para o PCE

unidimensional com redução de padrões . . . p. 58

5.2 Técnica de decomposição para o PCE

Anexo A Tipologias de classificação p. 70 A.0.1 Tipologia de Dyckhoff . . . p. 70

A.0.2 Tipologia de Wäscher, HauBner e Schumann . . . p. 74

Capítulo 1

Introdução

A competitividade industrial tem estimulado o crescimento de estudos sobre como melhorar o processo de produção, de forma a aumentar a produção e a reduzir cus-tos. Pequenas melhorias podem trazer ganhos significativos e representar uma vantagem importante na competição entre indústrias do mesmo setor. No processo de produção de diversas indústrias, como por exemplo, móveis, metais, papel, têxtil, entre outras, é necessário cortar peças maiores (objetos) em estoque (geralmente padronizadas) em peças menores (itens) para satisfazer uma demanda pré-estabelecida. O problema de encontrar a melhor maneira de fazer isso dá origem ao problema de corte de estoque. Muitos pro-blemas desse tipo têm por intuito minimizar os custos de produção.

Em nosso trabalho, esses custos serão baseados no número de objetos utilizados no atendimento da demanda e na produtividade da máquina de corte. Esses dois objetivos, além de concorrem para redução do custo de produção, também contribuem com o conceito atual de sustentabilidade, uma vez que a redução da matéria-prima utilizada significa a diminuição no uso dos recursos naturais do nosso planeta. Este fato é bem evidente na indústria moveleira. Aumentar a produtividade da máquina de corte contribui com esse conceito em termos da redução de energia gasta pela máquina. A produtividade da máquina de corte está diretamente ligada ao corte simultâneo de objetos. Para melhor compreensão deste trabalho, é interessante que o leitor tenha conhecimento em álgebra linear ([7] e [32]), e programação inteira ([1],[44], [9] e [59]).

Nossa pesquisa está estruturada da seguinte forma: No Capítulo 2, apresentamos o princípio de decomposição de Dantzig-Wolfe aplicado ao problema de otimização linear inteira, que servirá de base para a aplicação do método de geração de colunas, também exposto no mesmo capítulo. Ainda no Capítulo 2, apresentamos um exemplo numérico para exemplificar a teoria discutida.

No Capítulo 3, definimos o problema de corte de estoque, apresentamos modelos matemáticos para esses problemas e definições que servem de alicerce para os modelos. Discutimos o método de geração de colunas aplicado aos problemas de corte de estoque e, por fim, faremos uma breve revisão bibliográfica sobre alguns trabalhos que tratam do problema de corte de estoque.

No Capítulo 4, discutimos o conceito de ciclos da serra. Apresentamos algumas for-mulações matemáticas para o problema de corte de estoque que aborda a redução de ciclos da serra. Analisamos alguns trabalhos que apresentam problemas diretamente ligados ao o número de preparo da máquina de corte.

No Capítulo 5, apresentamos a abordagem proposta em [56] para resolver um problema de corte de estoque unidimensional com objetivo de redução do número de padrões de corte. Apresentamos um método baseado nesse para resolver o problema de corte de estoque bidimensional que visa minimizar o número de ciclos da serra e objetos cortados.

Capítulo 2

Geração de coluna em otimização

linear inteira

De modo geral, os métodos de decomposição são utilizados para resolver um problema através da resolução de uma sequência de problemas de menor dimensão. Tais métodos de decomposição são aplicados não só para resolver problemas com grandes dimensões (os quais não seriam resolvidos facilmente por outros métodos), mas também podemos utilizar esses métodos para desenvolver algoritmos heurísticos [6].

Neste capítulo apresentaremos um método de decomposição para problemas de pro-gramação linear inteira, desenvolvido por Dantzig e Wolfe [14] no início da década de 1960. Com o uso desta técnica podemos aplicar um procedimento de geração de colunas que foi desenvolvido por Gilmore e Gomory [27, 28, 29], que será discutido na seção 2.2 e que servirá de base para o desenvolvimento do nosso trabalho.

2.1

Princípio de decomposição de

Dantzig-Wolfe

Consideremos o problema de programação linear inteira na forma padrão:

ZP I = min cx (2.1)

s.a

Ax=b (2.2)

em que A, uma matriz m×n, c um vetor n×1, b um vetor m×1, são conhecidos e a variável de decisão x é um vetorn×1inteiro.

Podemos particionar a matriz A e o vetor b como:

A=

A1

A2

e b=

b1

b2

,

em que A1 é uma matriz m1 ×n, A2 é uma matriz m2×n, b1 é um vetor m1 ×1 e b2 é um vetor m2×1, comm1+m2 =m.

O conjunto de restrições (2.2) pode ser reescrito como (2.4) - (2.5).

A1x=b1 (2.4)

A2x=b2 (2.5)

Definindo o conjunto X ={x ∈ _Zn _{: A}

2x = b2} =∅. Assim, o problema de progra-mação linear inteiro (P I)pode ser escrito como (2.6) - (2.9).

ZP I−P1 = min cx (2.6)

s.a

A1x=b1 (2.7)

x∈X (2.8)

x≥0, inteiro. (2.9)

As restrições (2.7) serão chamadas de restrições gerais e as restrições (2.8) que geral-mente têm uma estrutura especial, serão chamadas de restrições especiais ou de acopla-mento [18]. O princípio de decomposição de Dantzig-Wolfe [14] trabalha com essas res-trições separadamente. O conjunto de resres-trições gerais definirá o problema principal, que é chamado deproblema mestre. Por conseguinte, o conjunto de restrições especiais definirá um subproblema. Os dois problemas serão resolvidos alternadamente, sempre trocando informações entre eles, conforme descrito na seção 2.2.

Consideremos quev1, v2, . . . , vp são os ppontos extremos deX er1, r2, . . . , rp são os q

raios extremos de X. Como o conjunto X é um conjunto convexo, então qualquer ponto

combinação não negativa dos raios extremos de X, ou seja,

X =

x∈Zn+:x=

p

i=1

viλi+ q

j=1

rjµj, p

i=1

λi = 1, λi ∈ {0,1},∀i, µj ∈Z+,∀j

(2.10)

Se substituirmos X definido de acordo com (2.10) em (2.6) - (2.9), obtemos uma nova formulação para o problema (PI), dada por (2.11) - (2.15).

ZP M1 = min

p

i=1

(cvi)λi+ q

j=1

(crj)µj (2.11)

s.a

p

i=1

(A1vi)λi+ q

j=1

(A1rj)µj =b1, (2.12)

p

i=1

λi = 1, (2.13)

λi ∈ {0,1}, i= 1, . . . , p, (2.14)

µj ∈Z+, j = 1, . . . , q. (2.15) As variáveis de decisão do problema reformulado são as variáveis λi e µj. A restrição

(2.13) é chamada de restrição de convexidade e a nova formulação (2.11) - (2.15) é o problema mestre. A formulação do problema mestre (PM1) é equivalente à formulação do problema original (PI), no sentido em que qualquer solução factível em termos das variáveis do problema mestre pode ser transcrita numa solução factível para o problema original.

Para simplificar, doravante vamos considerar X como sendo fechado, isto é, não

pos-suindo raios extremos.. Assim, o problema mestre (PM1) é dado por (2.16) - (2.19).

ZP M = min p

i=1

(cvi)λi (2.16)

s.a

p

i=1

(A1vi)λi =b1, (2.17)

p

i=1

λi = 1, (2.18)

Apesar do problema (PM) ser em geral um problema mais simples que o original (PI), justamente por possuir um número menor de restrições (m1 + 1restrições, apenas as de acoplamento (2.17) e a de convexidade (2.18)), algumas dificuldades são encontradas para resolver o problema (PM), como por exemplo, o fato das variáveis de decisão λi serem

binárias e o elevado número de pontos extremos, principalmente quando se trata de um problema de grande porte. O alto número de pontos extremos torna inviável a enumeração explícita de todos os pontos extremos, para determinar a solução ótima do problema. Para contornar essas dificuldades podemos fazer a relaxação linear das variáveis λi, isto é, as

variáveis λi podem assumir valores reais entre 0 e 1, dando origem ao problema (PM)

relaxado que será formado pelas expressões (2.16) - (2.18) e (2.20), e em seguida resolver o problema (PM) relaxado utilizando o método de geração de colunas.

0≤λi ≤1, i= 1, . . . , p. (2.20)

Para resolver o problema (PM) relaxado utilizando geração de colunas, considere-mos inicialmente o problema mestre com um subconjunto restrito de variáveis, que é de-nominado problema mestre restrito (PMR). Em cada iteração, o problema será resolvido levando em conta apenas às variáveis do (PMR) produzindo uma solução ótima apenas com as mesmas variáveis. Entretanto, para a solução do problema original é necessário considerar todas as variáveis e colunas possíveis. Assim, é preciso analisar também todos os pontos extremos do conjunto X que não fazem parte do (PMR). Caso existam pontos

extremos atrativos, as variáveis e colunas associadas a esses pontos, devem ser incluídas ao (PMR) e o problema ser novamente otimizado. Esse processo é repetido até que não haja mais colunas atrativas para serem incluídas ao (PMR).

2.2

O método de geração de colunas

cBB−1 = Π = (π1, π2, . . . , πm1, σ) = (π, σ). (2.21)

Em (2.21), cB é o vetor que representa o custo das variáveis que pertence à base. O

custo reduzido de uma variável não-básica é dado porˆcj =cj−cBB−1Aj₁. As colunas que

correspondem aos pontosx∈X tem a forma (2.22).

A1v

1

(2.22)

Para uma variável x ∈ X não-básica associada a uma coluna do tipo (2.22), a

ex-pressão do custo reduzido é dado por (2.23) [9].

cj −cBB

−1_Aj

1 = cv−(π1, π2, . . . , πm1)∗A1v−σ =

= cv−π∗A1v−σ= (2.23)

= (c−πA1)v−σ.

Analisaremos se algum ponto do conjunto X é atrativo para ser incluído noproblema

mestre restrito. Caso haja mais que um, selecionaremos o ponto que tem o custo reduzido mais atrativo. Essa seleção é feita em relação à solução ótima atual do problema mestre restrito. A seleção de um ponto extremo pode ser feita resolvendo (2.24) - (2.26).

min (c−πA1)v−σ (2.24)

s.a

v ∈X, (2.25)

v ≥0, inteiro. (2.26)

O problema (2.24) - (2.26) é denominado subproblema pricing. A solução ótima do subproblema pricing corresponde a um ponto extremo do conjunto X. Se osubproblema

pricing apresentar uma solução ótima menor do que zero (< 0), existe uma variável atrativa e a coluna associada a essa variável é adicionada ao problema mestre restrito, sendo candidata a entrar na base. Caso contrário, quando o subproblema pricing apre-sentar uma solução ótima maior ou igual à zero (≥ 0), nenhum ponto do conjunto X é

que o método de geração de colunas foi aplicado ao problema mestre relaxado. Métodos heurísticos são utilizados para encontrar uma solução inteira para o problema (PM). Na seção 3.3, discutiremos alguns trabalhos da literatura que apresentam métodos heurísticos para obter uma solução inteira para os problemas de corte de estoque, que também serão apresentados e discutidos no capítulo 3, como, por exemplo, [27], [28], [45] e [57] .

2.3

Um exemplo ilustrativo

Nesta seção iremos apresentar um exemplo numérico da aplicação do método de ge-ração de coluna aplicado a um problema de programação linear inteira.

Exemplo 2.3.1. Considere o problema de programação linear contínua:

min x1 + x2 + x3

s.a

x1 + x2 = 2,

x1 + x3 = 1,

x1, x2, x3 ∈ Z+.

(2.27)

Para aplicarmos o princípio de decomposição de Dantzig-Wolfe, tomemos o conjunto

X da forma (2.28).

X =x= (x1, x2, x3)∈Z3+ :x1+x3 = 1 e x1, x2, x3 ≥0. (2.28) Desse modo temos c= (1 1 1)o vetor que representa os custos de cada variável, A1 =

(1 1 0) a matriz que representa a restrição geral, A2 = (1 0 1) a matriz que representa a restrição de acoplamento., b1 = 2 e b2 = 1.

Sejam vi, i= 1, . . . , p os vértices de X e rj, j = 1, . . . , q os raios extremos de X.

vi = ⎛ ⎜ ⎜ ⎝ vi 1 vi 2 vi 3 ⎞ ⎟ ⎟

⎠ i= 1, . . . , p e rj = ⎛ ⎜ ⎜ ⎝

rj₁ rj₂ rj₃

⎞ ⎟ ⎟

Assim, o problema mestre para o problema (2.27) é dado pelas expressões (2.29) -(2.33).

min

p

i=1

(v₁i +v₂i +v₃i)λi + q

j=1

(rj₁+r₂j +r₃j)µj (2.29)

s.a

p

i=1

(vi₁+v₂i)λi+ q

j=1

(r₁j+r₂j)µj = 2, (2.30) p

i=1

λi = 1, (2.31)

λi ∈ {0,1}, i= 1, . . . , p, (2.32)

µj ∈Z+, j = 1, . . . , q. (2.33)

A relaxação para o problema mestre (2.29) - (2.33) é obtida substituindo as restrições (2.32) e (2.33) pelas expressões (2.34) e (2.35), respectivamente.

λi ≥0, i= 1, . . . , p. (2.34)

µj ≥0, j = 1, . . . , q. (2.35)

Considerando que nenhuma solução básica factível é conhecida para o problema mestre, portanto, utilizaremos o método simplex das duas fases com geração de colunas para en-contrar uma solução básica factível inicial. Para mais detalhes sobre esse método ver [1].

FASE I

ξ= min g1+g2 (2.36)

s.a

p

i=1

(vi₁+v₂i)λi+

1

j=1

(r₁j+rj₂)µj + g1 = 2, (2.37)

p

i=1

λi + g2 = 1, (2.38)

λi ≥0, i= 1, . . . , p, (2.39)

µj ≥0, j = 1, . . . , q, (2.40)

g1, g2 ≥0. (2.41)

Desse modo, para a seguir com o método simplex da duas fases. O problema mestre artificial restrito inicial (PM-1) é formado pelas expressões (2.42) - (2.45).

ξ = min g1 +g2 (2.42)

s.a

g1 = 2, (2.43)

g2 = 1, (2.44)

g1, g2 ≥0. (2.45)

FASE I - Iteração 1

Na primeira iteração, a matriz básica factível inicial B é formada pelas colunas

re-lativas às variáveis g1 e g2, nesse caso B = I2. O custo básico cB, relacionado com as

variáveis que estão na base, é dado por cB = (1 1)T. As variáveis xN que não pertencem

à base têm custo zero. E o vetor de recursos b é dado por b = (2 1)T_{. Desse modo, uma}

solução básica para o problema(PM-1) é dado por(2.46) com solução corrente ξ dado por

(2.47).

xB =B

−1_b=

2 1

ξ= 3. (2.47)

A variável dualπ = (π1 π2)referente às restrições(2.43)e(2.44)é dada pela expressão (2.48).

π= (π1 π2) =cTBB

−1 _=cT

BI2 = (1 1). (2.48)

O cálculo dos custos cN das variáveis não básicas é dado por (2.49).

cN = ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩

ci−π Ai = 0−(1 1)

vi

1 +vi2

1

=−vi

1 −v2i −1 com iassociado a λi,

cj −π Aj = 0−(1 1)

rj₁+r₂j

0

=−ri

1−ri2 com j associado a µj.

(2.49)

Desse modo, após os cálculos realizados, o subproblema pricing (SP-1) relativo ao problema (PM-1) é dado por (2.50) - (2.52).

γ = min −v1−v2−1 (2.50)

s.a

v1+v3 = 1, (2.51)

v1, v2, v3 ≥0. (2.52)

Para v1 = 1 e v2 = v3 = 0 as restrições do problema (SP-1) são satisfeitas, logo

v1 = (1 0 0)T _{é um vértice de X. Esse vértice fornece γ = −1 < 0. Como γ < 0 se}

a coluna (2.53) associada à variável λi entrasse na base do problema (PM-1) o valor da

função objetivoξ melhoraria.

1 + 0

Entretanto, note que se v2 −→+∞ então γ −→ −∞, isto é, v2 é ilimitado superior-mente. Passaremos, assim, a determinar o raio extremo associado. Para isso, é necessário escrever o todas as coordenadas do vértice v1 _{em relação a sua segunda coordenada v}

2 da seguinte forma: ⎛ ⎜ ⎜ ⎝ v1 v2 v3 ⎞ ⎟ ⎟ ⎠ = ⎛ ⎜ ⎜ ⎝ 1 0 0 ⎞ ⎟ ⎟ ⎠ + ⎛ ⎜ ⎜ ⎝

0v2

1v2

0v2

⎞ ⎟ ⎟

⎠. (2.54)

Logo, r1 = (0 1 0)T _{é um raio extremo de X, associado a variávelµ1. Calculemos em}

(2.55) o custo reduzido da variável µ1.

cµ1 = 0−π r

1 _{= 0−π}

r1 1+r12

0

= −(1 1)

0 + 1 0

= −1 <0. (2.55)

Comocµ1 <0então a variávelµ1 é candidata a entrar na base com a coluna associada

Aµ1 = (1 0)

T_{. Para decidir que variável sai da base do problema (PM-1) calcularemos em}

(2.56)à direção simplex y e em (2.57) o tamanho do passo ǫ, que vai decidir que variável

sai da base.

y=B−1_A

µ1 =I2

1 0 = 1 0 . (2.56)

ǫ = min

xBi

yi

:yi ≥0

=

xB1

y1 = 2 1

= 2. (2.57)

Assim, a variável g1 sai da base. Nessa iteração foi gerada a coluna Aµ1 = (1 0)

T _que

ξ = min g1+g2 (2.58)

s.a

µ1+g1 = 2, (2.59)

g2 = 1, (2.60)

µ1, g1, g2 ≥0. (2.61)

FASE I - Iteração 2

A matriz básica factível B para o problema (PM-2) é formada pelas colunas relativas

as variáveisµ1 eg2, que nesse caso também é a matriz identidade I2. O vetor custo básico

cB é dado por cB = (0 1)T. Dessa forma temos a solução básica para o problema (PM-2)

dada por(2.62), com solução corrente ξ dado por (2.63).

xB=

2 1

e xN = 0 (2.62)

ξ= 1. (2.63)

Nessas condições temos os seguintes valores:

π= (π1 π2) = (0 1). (2.64)

cN = ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩

ci−π Ai = 0−(0 1)

vi

1+v2i

1

=−1 com i associado a λi,

cj−π Aj = 0−(0 1)

r₁j+rj₂

0

= 0 com j associado a µj.

O subproblema pricing (SP-2) relativo ao problema (PM-2) é dado pelas expressões (2.66) - (2.68).

γ = min −1 (2.66)

s.a

v1+v3 = 1, (2.67)

v1, v2, v3 ≥0. (2.68)

Para v1 = 1 e v2 =v3 = 0 temos que as restrições do problema (SP-2) são satisfeitas, e como já mencionado na iteração anterior v1 = (1 0 0)T _{é vértice de X associado a}

variável λi. Como v1 e v3 são limitadas ev2 não altera o valor da função objetivo γ, isto é, v1 é vértice ótimo de X para a função objetivo γ atual. Logo, a coluna Aλ1 = (1 1)

T

associada a variávelλ1 é candidata a entrar na base.

Os cálculos que decidem a possível variável que sai da base procedem da seguinte maneira:

y=B−₁

Aλ1 =I2

1 1 = 1 1 . (2.69)

ǫ = min

xB1

y1

, xB2

y2 = 2 1, 1 1 = 1

1 = 1. (2.70)

Dessa forma a variável g2 sai da base. A coluna Aλ1 = (1 1)

T _{é gerada para o}

ξ= min g1+g2 (2.71)

s.a

λ1+µ1+g1 = 2, (2.72)

λ1+ g2 = 1, (2.73)

λ1, µ1, g1, g2 ≥0. (2.74)

FASE I - Iteração 3

Nessa iteração a matriz básica inicial factível B, dada por (2.75), para o problema

(PM-3) é formada pelas colunas relativas as variáveis µ1 e λ1, isto é, na base não existem mais variáveis artificiais.

B =

1 1 0 1

. (2.75)

O vetor custo básico cB é dado por cB = (0 0)T. Assim a solução básica para o

problema (PM-3) é dada por (2.76), com solução correnteξ dado por (2.77).

xB=

1 1

e xN = 0 (2.76)

ξ= 0. (2.77)

Nessas condições temos os seguintes valores:

cN = ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩

ci−π Ai = 0−(0 0)

vi

1+v2i

1

= 0 com i associado a λi,

cj−π Aj = 0−(0 0)

r₁j+rj₂

0

= 0 com j associado a µj.

(2.79)

O subproblema pricing (SP-3) relativo ao problema (PM-3) é dado por (2.80) - (2.82).

γ = min 0 (2.80)

s.a

v1+v3 = 1, (2.81)

v1, v2, v3 ≥0. (2.82)

Como γ = 0 para o problema (SP-3), logo a base atual está associada ao valor ótimo do problema artificial (2.36) - (2.41). E como a base não possui variáveis artificiais então a base atual é uma base factível para o problema mestre original relaxado (2.29) - (2.31), (2.34) e (2.35).

FASE II

Nesta fase iremos trabalhar diretamente com o problema mestre original relaxado (2.29) - (2.31), (2.34) e (2.35).

FASE II - Iteração 1

De acordo com a FASE I do método simplex das duas fases com geração de colunas, uma matriz básica inicial factível B, para o problema mestre original relaxado é formada pelas colunas associadas as variáveis µ1 e λ1 e é dado por (2.75). O custo básico cB é

c r1 = (1 1 1) ⎛ ⎜ ⎜ ⎝

0 1 0

⎞ ⎟ ⎟

⎠= 1. (2.83)

c v1 = (1 1 1) ⎛ ⎜ ⎜ ⎝

1 0 0

⎞ ⎟ ⎟

⎠= 1. (2.84)

Assim, o problema mestre restrito (PMO-1) relativo ao problema mestre original re-laxado (2.29) - (2.31), (2.34) e (2.35) é dado por (2.85) - (2.88).

Z = min λ1+µ1 (2.85)

s.a

λ1+µ1 = 2, (2.86)

λ1 = 1, (2.87)

λ1, µ1 ≥0. (2.88)

A solução básica para o (PMO-1) é dada por (2.89) e a solução corrente por (2.90).

xB=

1 1

e xN = 0 (2.89)

Z = 2. (2.90)

O valor dual é dado por (2.91) e os custos relativos por (2.96).

cN = ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩

ci−π Ai = (1 1 1) ⎛ ⎜ ⎜ ⎝ vi 1

v₂i vi

3

⎞ ⎟ ⎟

⎠−(1 0)

vi

1+vi2

1

=vi

3 com iassociado a λi,

cj−π Aj = (1 1 1) ⎛ ⎜ ⎜ ⎝

r₁j r₂j r₃j

⎞ ⎟ ⎟

⎠−(1 0)

rj₁+rj₂

1

=rj₃ com j associado a µj.

(2.92)

Dessa forma o subproblema pricing (SPO-1) é dado por (2.93) - (2.95).

γ = min v3 (2.93)

s.a

v1+v3 = 1, (2.94)

v1, v2, v3 ≥0. (2.95)

O valor ótimo para o problema (SPO-1) é γ = 0≥0 qualquer que seja o ponto ótimo para o problema. Assim sendo, a solução do problema mestre restrito (PMO-1) (2.85) -(2.88) também é ótima para o problema mestre relaxado (2.29) - (2.31), isto é, a solução ótima do problema mestre relaxado é µ1 = 1 associado ao raio extremo r1 = (0 1 0)T e

λ1 associado ao vértice v1 = (1 0 0)T. Em termos das variáveis originais:

⎛ ⎜ ⎜ ⎝ x1 x2 x3 ⎞ ⎟ ⎟

⎠ = µ1r1 + λ1v1 = 1

⎛ ⎜ ⎜ ⎝ 0 1 0 ⎞ ⎟ ⎟ ⎠ + 1

⎛ ⎜ ⎜ ⎝ 1 0 0 ⎞ ⎟ ⎟ ⎠ = ⎛ ⎜ ⎜ ⎝ 1 1 0 ⎞ ⎟ ⎟

⎠. (2.96)

O valor ótimo é Z∗

Capítulo 3

O problema de corte de estoque

O procedimento de geração de colunas para o problema de corte de estoque foi pi-oneiramente estudado nos trabalhos de Gilmore e Gomory em 1961 e 1962, [27] e [28] respectivamente. Nesses trabalhos os autores formularam o problema de corte de estoque unidimensional, propuseram para esta formulação uma relaxação linear e utilizaram o pro-cedimento de geração de colunas para resolver o problema relaxado, obtendo uma solução aproximada para o problema original.

Neste capítulo, definimos o problema de corte de estoque, fazemos algumas definições necessárias para a formulação desses problemas e apresentamos alguns modelos matemáti-cos para o problema de corte de estoque. Na seção 3.3 faremos uma adaptação do método de geração de colunas apresentado na seção 2.2, para o problema de corte de estoque. E por fim, nas seções 3.4 e 3.5 discutimos alguns trabalhos envolvendo estes problemas.

3.1

O problema de corte de estoque unidimensional

Esse trabalho permaneceu desconhecido por muitos anos pelos pesquisadores ocidentais, em virtude dos entraves político-ideológicos ocorridos durante a Guerra Fria. Somente nos anos 1960 o trabalho foi publicado em inglês na revista Management Science.

O problema de corte de estoque unidimensional pode ser definido da seguinte maneira [46]: considere disponível em estoque um número K, suficientemente grande, de objetos

(bobinas, barras, etc.) de comprimento L e um conjunto de m itens, cada item tendo demanda conhecida bi, e de comprimento li, em que li ≤ L, i = 1, . . . , m. O problema

consiste em como cortar os objetos de forma a atender a demanda usando o menor número possível de objetos.

Para apresentar o modelo matemático atribuído a Kantorovich [8, 10], definimos o seguinte conjunto de variáveis aij como sendo o número de vezes que o item i é cortado

no objeto j, i = 1, . . . , m e j = 1, . . . , K. E as variáveis λj, que recebem valor 1, se o

objeto j é cortado e zero, caso contrário. Assim, temos a formulação (3.1) - (3.5).

ZKan = min K

j=1

λj (3.1)

s.a

K

j=1

aij ≥bi, i= 1, . . . , m, (3.2) m

i=1

liaij ≤Lλj, j = 1, . . . , K, (3.3)

λj ∈ {0,1}, j = 1, . . . , K, (3.4)

aij ∈Z+, i= 1, . . . , m, j = 1, . . . , K. (3.5) A função objetivo (3.1) minimiza o número total de objetos cortados. O conjunto de restrições (3.2) garante que a demanda dos itens será atendida, permitindo o excesso de produção. O conjunto de restrições (3.3) garante que se um objeto j é usado (λj = 1),

então as restrições físicas do objeto devem ser respeitadas. As restrições (3.4) e (3.5) definem os domínios das variáveis.

modelou o problema de encontrar um padrão de corte factível como um problema de determinar um caminho em um grafo acíclico e orientadoG(V, S), comL+ 1vértices. A distância entre um vértice e outro, representa uma unidade de comprimento do objeto. O conjunto S representa os arcos do grafo G(V, S)e é definido por (3.6).

S =

(s, t); 0 ≤s < t≤L e t−s=li para algumi≤m

(3.6)

A expressão (3.6) destaca que existe uma arco entre o vértice s e ot se, e somente se, s−t=li para algumi, i= 1, . . . , m. As perdas serão representadas por arcos adicionais

entre os vértices(u, u+ 1), u= 0,1, . . . , L−1. Assim, o problema de encontrar um padrão de corte factível pode ser formulado como determinar um caminho entre os vértices 0 e

L no grafo G(V, S). Definimos a variável zst, s < t como sendo o número de itens de

comprimento(t−s)cortados do objeto. Dessa forma, o modelo matemático apresentado em [8, 10] é dado pelas expressões (3.7) - (3.10).

ZV C = min f (3.7)

s.a

(s,t)∈S

zst −

(t,u)∈S

ztu= ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩

−f, se t= 0; 0, se t = 1,2, . . . , L−1;

f, se t=L.

, (3.8)

(h,h+li)∈S

zh,h+li =bi, i= 1, . . . , m, (3.9)

zst ∈Z+, ∀(s, t)∈S. (3.10)

A função objetivo (3.7) visa minimizar o fluxo da rede, que pode ser vista como a quantidade de objetos cortados [34]. O conjunto de restrições (3.8) representa as restrições de conservação do fluxo de um grafo. As restrições (3.9) garantem que a demanda é atendida.

3.2

O problema de corte de estoque bidimensional

con-junto de peças menores de tamanhos variados e muitas vezes não padronizadas (chamadas de itens), de acordo com algum critério de otimização, como por exemplo, minimizar o número total de objetos cortados, minimizar o desperdício de material, maximizar lucros, minimizar o número de ciclos da serra (este último item será melhor detalhado no capítulo 4), etc. Alguns fatores importantes podem ser considerados nos parâmetros e restrições desses problemas, como por exemplo, capacidade da máquina de corte (limitada ou não), quantidade de objetos em estoque (limitada ou não), tempo de produção, entre outros.

Na literatura, podemos encontrar uma grande diversidade de problemas de corte de estoque. Para facilitar a comunicação entre os pesquisadores, foram propostas duas tipolo-gias para classificar esses problemas, conforme algumas características descritas a seguir. A primeira tipologia é a de Dyckhoff [20], em que o autor apresenta uma classificação para os problemas de corte de estoque fundamentados sobre suas principais característi-cas: dimensionalidade, tipo de alocação, variedades de objetos e variedades de itens. A segunda proposta é a tipologia de Wäscher et al [?], na qual os autores propõem uma tipologia baseada em [20], mas que abrange uma maior quantidade de problemas (para mais detalhes sobre as tipologias ver anexo A).

Deste ponto em diante, iremos trabalhar com o PCE em que duas dimensões são relevantes para o processo de corte. Neste caso, definimos o PCE bidimensional da seguinte maneira. Considere que existam em estoque um número suficientemente grande de objetos (placas de madeira, chapas de aço, etc.), de comprimento L e largura W, e um conjunto

de itens de comprimento li e largura wi, cada um com demanda conhecida bi, para i = 1, . . . , m. O problema consiste em determinar como cortar os objetos de forma a atender

a demanda, de acordo com algum critério de otimização. A figura 1 mostra um exemplo de problema de corte de estoque bidimensional com vários objetos em estoque e vários itens com demanda pré-espeficada.

Mais algumas definições são necessárias para dar suporte ao estudo do problema de corte de estoque.

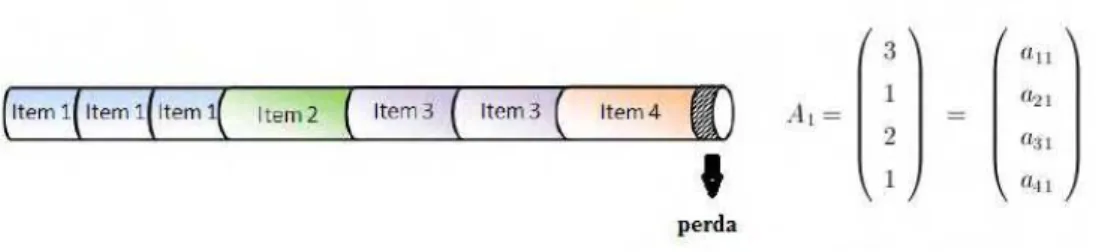
Definição 3.1. [2] Padrão de corte é a maneira de como os itens estão dispostos em um objeto. Associamos a um padrão de corte um vetor m-dimensional Aj, que contabiliza

os itens incluídos no padrão de corte j, definido por (3.11).

AT_j = (a1j, a2j, . . . , amj). (3.11)

Em(3.11), aij, i= 1, . . . , m, representa o número de vezes que o itemi aparece no padrão

de corte j.

Padrões de corte que tem mesmo vetor associado são chamados de equivalentes. Um vetor AT

j = (a1j, a2j, . . . , amj) representa um padrão de corte se, e somente se, satisfaz

as restrições físicas do objeto (3.12). No caso unidimensional as restrições físicas são equivalentes às restrições do problema da mochila (3.12) - (3.13).

l1a1j +l2a2j +. . .+lmamj, (3.12)

a1j, a2j, . . . , amj ∈Z+. (3.13) No caso bidimensional, as restrições físicas são mais complicadas de serem explicitadas, pois as características das máquinas de corte e os tipos de corte são relevantes para a modelagem matemática. Para mais detalhes ver, por exemplo, [23], [39], [25], [64] e [65], entre outros. As figuras 2 e 3 apresentam exemplos de um padrão de corte unidimensional e um bidimensional, respectivamente.

Figura 3: Padrão de corte bidimensional.

Na prática é muito difícil conseguirmos um padrão de corte que utilize a área total do objeto. Nas figuras 2 e 3, as partes hachuradas nos padrões de corte, cujas dimensões não foram pré-definidas, não serão aproveitadas no processo de produção. Essas partes são chamadas perda. No caso unidimensional a perda de uma padrão de corte j é dada por (3.14) e no caso bidimensional por (3.15).

Pj =L− m

i=1

liaij (3.14)

Pj =LW − m

i=1

(liwi)aij (3.15)

Definição 3.2. Padrão de corte homogêneo é o padrão de corte que possui apenas um tipo de item, isto é, o vetor m-dimensional (3.16) que representa esse padrão tem apenas

uma coordenada não nula.

AT_j = (0, . . . , aij, . . . ,0). (3.16)

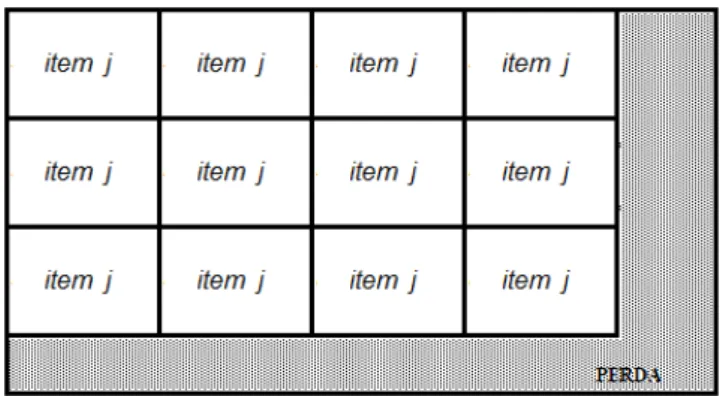
Quando um padrão de corte homogêneo apresenta o maior número possível do item, o padrão é denominado padrão de corte homogêneo maximal.

aij = ⎧ ⎨ ⎩

L lj

·W wj

, se i=j,

0, caso contrário. (3.17)

A figura 4 ilustra um padrão de corte homogêneo maximal no caso bidimensional.

Figura 4: Padrão de corte homogêneo maximal bidimensional.

Uma formulação importante para o PCE, em que todos n padrões de corte factíveis

são conhecidosà priori, foi apresentada em [27], [28] e [29] e é dada por (3.18) - (3.20). A variável de decisão xj representa o número de objetos cortados de acordo com o padrão

de corte j, j = 1, . . . , n.

PCE com padrões de corte conhecidos

ZGG = min n

j=1

cjxj (3.18)

s.a

n

j=1

aijxj ≥bi, i= 1, . . . , m, (3.19)

xj ∈Z+, j = 1, . . . , n. (3.20)

A função objetivo (3.18) visa minimizar o custo total dos objetos cortados. Caso

cj = 1, para todo j = 1, . . . , n, então o problema passa a ser a um problema de redução

a técnica de decomposição de Dantzig-Wolfe ao modelo atribuído à Kantorovich (3.1) -(3.5).

3.3

Geração de colunas aplicado ao PCE

A solução do PCE inteiro, na formulação (3.18) - (3.20), esbarra em duas dificuldades computacionais: o elevado número de padrões de corte (variável xj) que pode existir;

e a existência das restrições de integrabilidade (3.20). A primeira dificuldade pode ser contornada com a relaxação das restrições de integrabilidade (3.20) sobre as variáveisxj,

j = 1, . . . , n, isto é, as restrições (3.20) são substituídas por xj ∈ R+. Já a segunda

dificuldade pode ser contornada com a utilização do procedimento de geração de colunas (seção 2.1).

Considere a relaxação linear do problema (3.18) (3.20) escrita na forma (3.21) -(3.23), em quen é muito maior que m (n≫m).

Relaxação do PCE com padrões de corte conhecidos

ZGG−RL = min n

j=1

cjxj (3.21)

s.a

n

j=1

Ajxj ≥b, (3.22)

xj ≥0, j = 1, . . . , n. (3.23)

O problema mestre restrito (PMR) inicial é formulado, considerando m padrões de

ZP M R = min m

j=1

cjxj (3.24)

s.a

m

j=1

Ajxj ≥bi, i= 1, . . . , m, (3.25)

xj ≥0, j = 1, . . . , m. (3.26)

Note que a matriz associada ao (PMR) inicial é uma matriz diagonal inversível da forma (3.27). Lembre-se que li ≤L ewi ≤W.

[A1. . . Am] =

⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣

a11 0 . . . 0

0 a22 . . . 0 ... ... ... ...

0 0 . . . amm ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ . (3.27)

O subproblema a ser resolvido a cada iteração do procedimento de geração de colunas para verificar se existe um padrão de corte diferente dos que pertencem ao (PMR) e que melhore a solução atual é dado pelas expressões (3.28) - (3.29).

ZSU BP = min (cj −πTAj) (3.28)

s.a.

Aj é um padrão de corte factível. (3.29)

O problema (3.28) - (3.29) é o subproblema pricing para o problema de corte de es-toque. Vale ressaltar que paraAj ser um padrão de corte é necessário e suficiente satisfazer

as condições físicas do objeto. Dado o fato do procedimento de geração de colunas ser apli-cado ao PCE relaxado (3.21) - (3.23), na maioria das vezes obtemos soluções fracionárias, que por vez, não são ótimas para o problema original (inteiro). Assim, a partir da solução do PCE relaxado são utilizados alguns métodos heurísticos para encontrar uma solução inteira para o problema original (3.18) - (3.20).

Quando o PCE permite produção em excesso, Gilmore e Gomory [27, 28, 29] propõem utilizar a solução inteira aproximada, obtida tomando o teto da solução ótima fracionária do PCE relaxado, isto é, sendox∗

∈_Rm

tomemos xi = ⌈x∗i⌉, i = 1, . . . , m, como solução inteira aproximada. Poldi e Arenales

[45, 46] propõem uma heurística para obter uma solução inteira aproximada para o PCE original, quando a demanda deve ser atendida exatamente. A heurística inicia-se tomando como solução inteira aproximada x, com x= (⌊x∗

1⌋,⌊x

∗

2⌋, . . . ,⌊x

∗

n⌋). Se esta solução não

for factível para (3.18) - (3.20), isto é,

n

j=1

aijxj < bi, para algum i, i = 1, . . . , m, então

devemos resolver o problema residual (P-Res) , formado pelas expressões (3.30)-(3.32).

ZP−Res = min n

j=1

xj (3.30)

s.a

n

j=1

aijxj =ri, i= 1, . . . , m, (3.31)

xj ∈Z+, j = 1, . . . , n. (3.32) Na restrição (3.31), ri =bi−

n

j=1

aijxj, i = 1, . . . , m, é a demanda que não foi

aten-dida porx. Note que (P-Res) apresentam as restrições de integrabilidade (3.32). Assim,

devemos resolver o (P-Res) relaxado, obtendo uma solução ótima para o mesmo e caso a solução ótima para o (P-Res) seja fracionária, devemos aplicar a heurística residual nova-mente, e assim, por diante, até obtermos uma solução inteira que satisfaça as restrições de demanda do PCE original.

3.4

Aplicações do PCE

Devido à importância econômica do PCE, surgiram e continuam surgindo importantes pesquisas explorando outros aspectos do problema e que vão além das suas dificuldades básicas de resolução. Pesquisadores de todo o mundo comprovaram em seus trabalhos a vasta aplicabilidade destes problemas em diversas áreas da indústria e o interesse em otimizar vários critérios diferentes, que podem representar, na prática, uma melhora sig-nificativa no processo de produção.

Dentre os trabalhos da literatura sobre PCE aplicados à industria de papel, podemos destacar os de Morabito [37] e Poltroniereet al. [47]. Em [37], é feita uma revisão dos PCE encontrados na literatura da época em que se discutem modelos de otimização, adaptados do modelo de Gilmore e Gomory (3.18) - (3.20) no caso unidimensional para aplicá-los em uma indústria de papel e papelão. Ainda em [37] são apresentos estudos reais para os PCE bidimensionais nas indústrias de móveis. Os autores de [47] apresentam uma formulação para um problema lot-sizing com corte de estoque acoplado, aplicado a uma indústria de papel e propõem heurísticas para resolver este problema.

Existem muitos trabalhos de PCE no contexto de indústrias de móveis. Para este trabalho, destacamos os trabalhos de Morabito e Arenales [40] e de Figueiredo e Rangel [25]. Em [40] é analisado o comportamento de um modelo baseado em (3.18) - (3.20), em uma fábrica de móveis com produção em grande escala em que são priorizados os padrões de corte que facilitam o processo de corte. Por fim, é discutido otrade-off entre padrões de corte que melhora o processo de corte e padrões de corte que geram menos desperdício de matéria prima. Em [25] é proposta uma heurística para gerar um conjunto de padrões de corte de uma fábrica de móveis, dando prioridade também aos padrões de corte que melhoram a produtividade do equipamento de corte.

No contexto dos PCE aplicados às metalúrgicas, podemos ressaltar o trabalho de Chu e Antonio [13]. Nele, é abordado um problema em relação ao caso unidimensional aplicado a uma pequena fábrica de peças de metais em que os objetos não são de comprimento padronizado, pois as sobras de um objeto cortado retornam para o estoque como um novo objeto. O problema permite o corte simultâneo de objetos e visa não apenas minimizar o desperdício de material, como também otimizar o tempo de corte.

Tratando do PCE aplicado à indústria têxtil podemos destacar os trabalhos de De-graeve e Vandebroek [16] e DeDe-graeveet al. [17]. Em ambos os trabalhos, o PCE consiste em encontrar boas combinações de padrões de corte e altura da pilha associada ao tecido, visando minimizar o excesso de produção e o custo de setup.

3.5

Extensões do PCE

problemas, isto é, existem outras possibilidades para o critério de otimização e restrições do problema, dependendo tanto do interesse industrial quanto das características das indústrias no qual os PCE serão aplicados. Nesta subseção iremos realizar uma breve discussão dos PCE na literatura, conforme seus critéros de otimização.

Para o PCE na qual a função objetivo é a minimização do número de padrões de corte, podemos destacar alguns trabalhos. Haessler [31] propõe uma modelagem matemática não-linear para o PCE unidimensional. É apresentado um método heurístico sequencial para resolver o problema, penalizando as trocas de padrões de corte para reduzir o número de padrões de corte na solução. Esse método heurístico fornece bons resultados, pois reduz o número de padrões de corte sem aumentar muito o número de objetos cortados. O trabalho [31] serviu como base para muitos outros trabalhos da literatura (e.g [41], [53] e [63]). Em [41] é apresentada uma linearização para o modelo de [31], tornando possível a utilização do procedimento de geração de colunas para a resolução do problema.

Vanderbeck [56] propõe um modelo matemático, obtido aplicando o procedimento de decomposição deDantzig-Wolfe (seção 2.1) ao modelo (3.1) - (3.5). O autor apresenta um método de geração de colunas para resolver o problema representado pelo modelo obtido, em que os valores duais associados às restrições de demanda e desetup são utilizados no subproblema pricing que gera colunas para o problema mestre. Foerster e Wäscher [26] desenvolvem uma heurística de redução de padrões de corte para o caso unidimensional, em que a partir de uma solução inicial para o problema, a ideia é obter padrões de corte através de combinações dos padrões de corte originais do problema, de maneira que a soma das frequências dos padrões obtidos seja a mesma da soma das frequências dos padrões de corte originais, mantendo assim a mesma quantidade de objetos na nova solução. Diegel et al. [19], a fim de reduzir o número de padrões de corte na solução, analisam os custos e a viabilidade de aumentar a frequência de um padrão de corte pouco utilizado na solução.

serão apresentados e discutidos na seção 4.1. Os trabalhos [16] e [17] serão discutidos na seção 4.2 e o trabalho [13] na seção 4.3.

Capítulo 4

O problema de ciclos da serra

No processo de corte de algumas indústrias, como por exemplo, de móveis (e.g. [52] e [36]) e têxtil (e.g. [16] e [17]), um critério tão importante quanto à minimização do número de objetos cortados é a maximização da produtividade dos equipamentos de corte. Tal produtividade está relacionada, entre outros fatores, com o tipo e número de padrões de corte distintos e ao número de objetos que podem ser cortados simultaneamente. Uma vez que, cortar apenas um objeto e cortar mais de um objeto simultaneamete gera o mesmo gasto de tempo no processo de corte. Aumentar a produtividade do equipamento de corte pode trazer benefícios, como por exemplo, a economia de energia elétrica, a redução do tempo de uso da máquina de corte e a redução do custo operacional da máquina. Neste trabalho estamos interessados em analisar o PCE considerando a produtividade da máquina de corte.

Considere um conjunto de objetos com a mesma espessura. A capacidade da máquina de corte (cap) é o número máximo de objetos que a máquina pode cortar simultaneamente,

de acordo com um padrão de corte. O valor decappode ser calculado por (4.1), em termos

da altura da serra, alt, e da espessura dos objetos, esp.

cap=

alt esp

. (4.1)

Considerando que o tempo necessário para concluir um ciclo da serra não varia com o número de objetos cortados simultaneamente, o tempo utilizado para cortar apenas um objeto é o mesmo para cortar até um número cap de objetos. Desta forma, cortar

um conjunto de objetos simultaneamente diminui o tempo de utilização da máquina e, portanto, aumenta a produtividade do processo de corte. Em uma máquina de corte com capacidadecap, o número de ciclos da serrayj, necessário para cortarxj objetos de acordo

com o padrão de corte j é dado por (4.2).

yj =

xj

cap

!

. (4.2)

A figura 5 ilustra o corte simultâneo de objetos no contexto de uma fábrica de móveis, onde a máquina tem a capacidade de cortar 6 objetos simultaneamente (cap= 6).

Figura 5: Corte simultâneo de objetos, adaptado de [52].

Definição 4.2. Ciclo completo é quando a capacidade da máquina em um determinado ciclo da serra é utilizada em sua totalidade. Caso contrário, é dito ciclo incompleto [48].

4.1

Modelos matemáticos para o problema de ciclos da

serra

Yanasse [60] apresenta um modelo matemático para o problema de redução do número de ciclos da serra (4.3) - (4.6), baseado no modelo PCE (3.18) - (3.20) discutido na seção 3.2.

PCE com redução do número de ciclos da serra (formulação 1)

ZP CE−C = min n

j=1

yj (4.3)

s.a

n

j=1

aijxj ≥bi, i= 1, . . . , m, (4.4)

yj =

xj

cap

!

, j = 1, . . . , n, (4.5)

xj, yj ∈Z+, j = 1, . . . , n. (4.6)

A função objetivo (4.3) visa minimizar o número de ciclos da serra. O conjunto de restrições (4.4) garante que a demanda de todos os itens é atendida, sendo permitido o excesso de produção. O conjunto de restrições (4.5) é definido similarmente à (4.2). As restrições (4.6) representam o domínio das variáveis. Podemos reescrever o modelo para redução de ciclos (PCE-C) como (4.7) - (4.10).

PCE com redução do número de ciclos da serra (formulação 2)

ZP CE−C = min n

j=1

yj (4.7)

s.a

n

j=1

aijxj ≥bi, i= 1, . . . , m, (4.8)

yj ≥

xj

Ainda em [60] o autor demonstra que o valor ótimo da função objetivo do modelo (4.7) - (4.10) é o mesmo da função objetivo do modelo (4.11) - (4.13).

PCE com redução do número de ciclos da serra (formulação 3)

ZP CE−C2 = min

n

j=1

yj (4.11)

s.a

n

j=1

aijyj ≥

bi

cap

!

, i= 1, . . . , m, (4.12)

yj ∈Z+, j = 1, . . . , n. (4.13)

Além da redução de ciclos da serra, podemos também usar como critério de otimização o número de objetos cortados. Nesse caso, substituiremos a função objetivo do modelo (4.7) pela função objetivo (4.14) e obteremos o modelo redução-ciclos-objetos (PCE-CO).

PCE com redução dos números de ciclos da serra e de objetos (PCE-CO)

ZP CE−CO = min n

j=1

xj+ n

j=1

yj = min n

j=1

"

xj +yj # . (4.14) s.a n j=1

aijxj ≥bi, i= 1, . . . , m, (4.8)

yj ≥

xj

cap, j = 1, . . . , n, (4.9) xj, yj ∈Z+, j = 1, . . . , n. (4.10)

de soluções não-dominadas.

No modelo (PCE-CO), se os valores de xj, j = 1, . . . , n são menores ou iguais a cap,

então as variáveisyj, j = 1, . . . , n, são binárias. E neste caso o modelo reduz-se ao PCE

que visa minimizar o número de padrões de corte [60]. Em problemas de redução-ciclos-objetos ligados ao processo de produção de algumas indústrias, quando a diversidade de padrões de corte utilizados no processo de corte é reduzida, então a frequência de alguns padrões de corte pode aumentar. O aumento da frequência pode aumentar o número de ciclos completos. Assim, uma maneira de tentar reduzir o número de ciclos da serra é diminuir o número de padrões de corte distintos, mas redução de padrões de corte não significa necessariamente em redução de ciclos da serra [51].

Na literatura podemos encontrar outras formulações para o problema de redução de ciclos da serra. Mosquera e Rangel [43] propõem um modelo focado no PCE bidimensional na indústria moveleira, que é semelhante ao modelo (PCE-CO) e é considerado que a quantidade de objetos cortados de acordo com um padrão de corte j, é um múltiplo de cap, isto é, são permitidos apenas ciclos completos. O modelo proposto, denominado

modelo de multiplicidade (PCE-CO-MM), é definido por (4.15) - (4.18).

Modelo de multipilicade para redução de ciclos e objetos (PCE-CO-MM)

ZP CE−CO−M M = min n

j=1

"

xj +yj #

(4.15)

s.a

n

j=1

aijxj ≥bi, i= 1, . . . , m, (4.16)

xj =cap yj, j = 1, . . . , n, (4.17)

xj, yj ∈Z+, j = 1, . . . , n. (4.18)

Ranck Jr. [48], observa que o modelo (PCE-CO-MM) não permite a utilização de ciclos com capacidade incompleta. Propõe então o modelo (PCE-CO-RJ) (4.19) - (4.21) que permite que 1,2, ..., cap objetos sejam cortados simultaneamente em um ciclo e as

demandas são atendidas sem excesso de produção. A variável de decisão yαj representa o

Modelo para redução de ciclos da serra de Ranck Jr. [48]

ZP CE−CO−RJ = min n

j=1

cap−₁

α=0

yαj (4.19)

s.a

n

j=1

cap−1

α=0

aijyαj $

cap−α% =bi, i= 1, . . . , m, (4.20)

yαj ∈Z+, j = 1, . . . , n, α= 0,1, . . . , cap−1. (4.21)

Toscanoet. al [52] propõem uma formulação para o problema utilizando a frequência do padrão de corte para controlar os ciclos da serra. Se um padrão de corte j é usado,

ou seja, xj > 0, então a sua frequência deve ser maior ou igual à frequência mínima,

fmin =β cap, em queβé um parâmetro pré-definido que representa um percentual mínimo

de uso da capacidade da máquina de corte em cada ciclo da serra.

São definidos os conjuntos N1 e N2 que são, respectivamente, o conjunto de padrões de corte gerados para o PCE (3.18) - (3.20) e o conjunto de padrões de corte gerados para o problema de corte de estoque reformulado (PCER1) relaxado, descrito por (4.24) -(4.29). Uma solução factível xj obtida para o (PCE-R1) relaxado é analisada. Se existem

padrões com frequência abaixo de fmin, isto é, xj < fmin. Então o padrão de corte j é

incluído no subconjuntoN3 e são adicionadas as restrições (4.22). Mbig é um valor muito

grande e δj uma variável binária definida por (4.23).

fminδj ≤xj ≤Mbigδj, j ∈N3. (4.22)

δj =

1, se o padrão de corte j é usado

0, caso contrário. (4.23)

Com a adição das restrições de frequência mínima (4.22), pode haver uso “excessivo” de objetos. Para evitar essa situação um parâmetro de tolerância, T OL, é definido para

Após as definições anteriores, o problema (PCE-R1) pode ser formulado pelas ex-pressões (4.24) - (4.29).

Modelo para redução de ciclos da serra com frequência mínima

ZP CE−R1 = min

j∈N1∪N2

xj (4.24)

s.a

j∈N1∪N2

aijxj ≥bi, i= 1, . . . , m, (4.25)

fminδj ≤xj ≤Mbigδj, j ∈N3, (4.26)

j∈N1∪N2

xj ≤T OL, (4.27)

xj ∈Z+, j ∈N1∪N2, (4.28)

δj ∈ {0,1}, j ∈N3. (4.29)

Para resolver (4.24) - (4.29) é aplicado um procedimento de geração de colunas baseada na metodologia descrita na seção 2.2. As restrições (4.28) são relaxadas para xj ∈ R,

j ∈ N1 ∪N2, dando origem a um problema inteiro misto. O subproblema de geração de colunas é resolvido usando apenas os valores duais associados às restrições de demanda (4.25). Apenas uma coluna é gerada por iteração. No capítulo 5 discutiremos uma proposta para resolver o problema PCE considerando a redução dos ciclos da serra.

4.2

Aplicação do PCE-C indústria têxtil

da máquina desde que satisfaça a demanda com pouco ou nenhum excesso.

Outra característica do problema é que todo item tem o mesmo comprimento l. Em cada item estão dispostas todas as partes que formam uma peça de roupa, por exemplo, mangas, bolsos, frente, costa, etc. A figura 6 representa um padrão de corte com as peças da roupa representada em cada item. A capacidade da faca de corte caplimita o número

de camadas de tecido que podem ser cortados simultaneamente. O número de itens em um padrão de corte é limitado pelo comprimento da mesa de corte L. Assim, o número máximo de itens em um padrão de corte é dado por (4.30).

Figura 6: Padrão de corte na indústria têxtil , adaptado de [16].

H =

L l

. (4.30)

Tomandoaij, xj e λj como variáveis, em queλj é definida como em (4.23). Definindo

Modelo para corte simultâneo de objetos de Degraeve et al. [16] e [17]

ZDEG = min C n

j=1

λj+ m i=1 n j=1

aijxj (4.31)

s.a

n

j=1

aijxj ≥bi, i= 1, . . . , m, (4.32) n

j=1

l aij ≤L λj, j = 1, . . . , n, (4.33)

xj ≤cap λj, j = 1, . . . , n, (4.34)

aij, xj ∈Z+, i= 1, . . . , m, j = 1, . . . , n, (4.35)

λj ∈ {0,1}, j = 1, . . . , n. (4.36)

A função objetivo (4.31) visa minimizar o custo de preparos da máquina de corte e o número de objetos cortados (camada de tecidos), isto é, minimiza setup e o excesso de produção. O conjunto de restrições de demanda (4.32) são não-lineares, pois as variáveis

aij exj aparecem como um produto. As restrições da mochila (4.33) garante que o número

de itens em um padrão de corte não exceda o tamanho da mesa de corte. Essas restrições permitem que os objetos tenham tamanhos flexíveis, isto é, em um padrão de corte o número de itens (todos com mesmo comprimento) pode variar. O conjunto de restrições (4.34) garante que o número de objetos cortados de acordo com um mesmo padrão de corte, quando usado, não exceda a capacidade da máquina de corte. As restrições (4.35) e (4.36) são as restrições de domínio das variáveis.

O modelo (4.31) - (4.36) é não-linear e pode ser linearizado se os padrões de corte forem gerados antecipadamente. Vale ressaltar que, esta estratégia é viável apenas se a capacidade da mesa de corteH não é muito grande, pois, para m itens distintos, existem

H

k=1

mk padrões de corte factíveis. Porém nem sempre é possível gerar todos os padrões

de corte, em [16] e [17] são apresentadas três propostas para a linearização do modelo.

Segundo os autores de [16] e [17] o modelo (4.31) - (4.36) é explicitamente focado na indústria têxtil de alta costura com baixa demanda. Esse fato pode tornar o modelo inviável para representar problemas com alta demanda. Por exemplo, se é demandado um número muito alto de apenas um tipo de item, o problema não produzirá solução factível.

Para esse caso o limitante superior para o número de itens é dado por

H

i=1

demandab1 do único item tem que satisfazer a expressão (4.37), para o modelo poder ser usado.

b1 ≤

H

i=1

i cap (4.37)

Desse modo, o modelo não pode representar um modelo de ciclos da serra de uma forma geral, uma vez que o conjunto de restrições (4.34) não permite que um padrão de corte quando usado possa ser cortado em um número maior que a capacidade da máquina de corte cap, isto é, o modelo permite que apenas um ciclo possa ser cortado para cada

padrão de corte.

4.3

Aplicação do PCE-C na indústria de metal

O trabalho de Chu e Antonio [13] apresenta um modelo matemático para um PCE unidimensional real que permite o corte simultâneo de objetos, proveniente de uma fábrica especializada em corte de barras de metal com varias formas (quadrado, redondo, triangu-lar, etc.). O modelo matemático leva em consideração algumas características exclusivas dessa fábrica. Uma característica muito relevante dessa fábrica é que quando um objeto não é totalmente utilizado, é possível que a parte restante possa ser reutilizada no futuro, se seu comprimento for superior a um limite pré-determinado r. Nesse caso, a parte

re-utilizável torna-se um novo objeto. Segundo os autores, embora o material rere-utilizável não seja uma perda de matéria-prima, essa situação deve ser evitada por algumas razões. A primeira delas é o alto custo de transporte dos objetos reutilizáveis, uma vez que esses objetos têm de ser deslocados a partir da máquina de corte para a área onde são armazena-dos para cortes futuros. A segunda razão é que os comprimentos armazena-dos objetos reutilizáveis não são padronizados de modo que eles são guardados em uma área específica da fábrica que tem capacidade limitada de armazenamento. E em terceiro lugar, porque não se sabe quando os objetos reutilizáveis serão realmente utilizados, gerando, assim, imobilização de capital. Desse modo, é necessário atribuir um custo de penalidade C, dado por (4.38),

C =C(W) =

W, se W < r, C1+C2W, caso contrário.

(4.38)

Em (4.38) o parâmetro C1 representa o custo de transporte do objeto reutilizável. O parâmetroC2 representa o custo de imobilização de capital, proporcional ao comprimento do objeto.

Outra característica do problema está relacionada com a tolerância dos itens, rigorosa ou normal. Um item com tolerância rigorosa deve ser entregue com boa qualidade (sem deformação geométrica e com composição química uniforme). Para garantir isso, devem ser feitos “ajustes” nas duas extremidades do objeto (exceto nos objetos reutilizados), pois podem existir defeitos de qualidade. Desse modo para alocar um item na extremidade de um objeto com tolerância rigorosa, um comprimento h deve ser cortado antes que o item desejado seja cortado do objeto, isto é, qualquer item com tolerância rigorosa deve ser separado por um comprimentoh a partir das extremidades do objeto do qual ele será

cortado. Por outro lado, um item com tolerância normal pode ser colocado em qualquer extremidade de um objeto. Portanto, dois itens com mesmo comprimento - mas com tolerância diferente - são considerados itens de tipos diferentes. A tolerância dos itens do tipoi é dado por τi e definida pela expressão (4.39).

τi =

1, se o item do tipo i tem tolerância rigorosa,

0, caso contrário. (4.39)

Uma vez que no processo de corte mais do que um objeto do mesmo tipo pode ser cortado simultaneamente, chamamos de pacote o conjunto de objetos cortados simultane-amente e de tamanho do pacote o número de objetos no pacote. O custo de um corte em um pacote k de tamanho de xk é dado por p(xk). O custo de cortar um pacote grande

em uma só vez sempre é menor do que separar os objetos do pacote em dois pacotes menores e depois cortá-los. Definindo η como o custo de preparar um pacote k, dk o

número de cortes necessários para cortar um pacote e µk, dado por (4.40), como o custo

de preparação e de corte de um pacote de tamanhoxk e que requerdk cortes.

A figura 7 ilustra um pacote de tamanho quatro, cuja tolerância dos objetos é rigorosa, que tem material reutilizável e que são necessários quatro cortes para cortar um pacote de acordo com um determinado padrão de corte.

Figura 7: Pacote, adaptado de [13].

Sejam N o número de objetos distintos e b0 o vetor N-dimensional em que aj-ésima entrada representa o número de objetos do tipo j em estoque. Sejam ωk = ω(Wk, Ak),

ϕk = ϕ(Wk, Ak) e dk = d(Wk, Ak), respectivamente, a perda de matéria-prima (que não

constitui um objeto reutilizável), o comprimento da parte reutilizável e o número de cortes necessário, quando um subconjuntoAkde itens é alocado sobre um objeto de comprimento

Wk no pacote k. E tomando ρk =ρ(W, A), dado por (4.41), como custo total incorrido

pela perda de matéria-prima e a parte reutilizável, quando subconjunto Ak de itens é

alocado sobre um objeto de comprimento Wk no pacote k. Em [13] é explicado como

obter os valores deωk, ϕk edk

ρk =ρ(Wk, Ak)≡ω(Wk, Ak) +C(ϕ(Wk, Ak)) =ωk+C(ϕk). (4.41)

Sejam M o número de pacotes e eN um vetor com N-ésima entrada igual a 1 e as

demais igual a zero. Para cada pacote k associamos um vetor N-dimensional λk em que

Modelo para corte simultâneo de objetos de Chu e Antonio [13]

ZCHU = min M

k=1

(xkρk+µk) (4.42)

s.a

M

k=1

Akxk=b, (4.43)

M

k=1

λkxk≤b0, (4.44)

eT_Nλk = 1, k = 1, . . . , M, (4.45)

λk ∈ {0,1}N, k = 1, . . . , M, (4.46)

xk ∈Z+, k = 1, . . . , M, (4.47)

Ak ∈Zn+ k = 1, . . . , M. (4.48)

A função objetivo (4.42) visa minimizar no primeiro termo os custos incorridos pela perda de material e dos materiais reutilizáveis, enquanto o segundo termo minimiza os custos de corte. O conjunto de restrições (4.43) assegura que todos os itens demandados são alocados, mas não permite o excesso de produção. As restrições (4.44) garantem que nenhum objeto é usado mais do que o disponível em estoque, isto é, o tamanho do pacote de objetos do tipo k é limitado pelo número de objetos do tipo k em estoque.

Os conjuntos de restrições (4.43) e (4.44) são compostos por restrições não-lineares, o que torna o modelo matemático não-linear. O conjunto de restrição (4.45) garante que exatamente um tipo de objeto é usado em cada pacote. As restrições (4.46), (4.47) e (4.48) são as restrições de domínio das variáveis.

Nesse modelo, um padrão de corte equivalente a um pacote especificado k é dado por

(λk, Ak), porque a partir de um λk pode-se deduzir o tipo de objeto. Assim, um padrão

de corte é um pacote para o qual o tamanho não é especificado. Em uma abordagem de programação linear, para resolver a não-linearidade do problema, todos os padrões de corte factíveis seriam identificado antecipadamente. Desse modo, a variável de decisão

xk que representa o tamanho do pacote (número de vezes que cada padrão de corte deve

Capítulo 5

Solução do problema de ciclos da

serra via geração de colunas

Neste capítulo apresentaremos a abordagem proposta por Vanderbeck [55, 56] para o PCE unidimensional que considera o problema de minimização do número de padrões de corte (PCE-P) e que usa a informação dual relativa às restrições de frequência do padrão de corte no subproblema pricing. Adaptamos esta abordagem para o PCE bidimensional que considera a minimização de ciclos da serra e do número de objetos (PCE-CO) de forma a incorporar no subproblema pricing as informações duais associadas às restrições que controlam o número de ciclos da serra.

5.1

Técnica de decomposição para o PCE

unidimensional com redução de padrões

O modelo proposto em Vanderbeck [56] para o PCE-P consideraK um limite superior para o número de objetos necessário para atender a demanda de itens. As variáveis de decisão aij representam o número de vezes que o item i é incluído no padrão de corte j,

xj representa o número de objetos cortados de acordo com o padrão j e a variável binária

λj indica se o padrão de corte j é usado (λj = 1) ou (λj = 0). O modelo não-linear inteiro