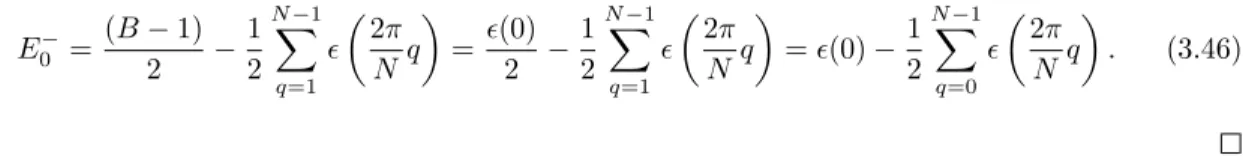Técnicas de diagonilização exata de modelos quânticos unidimensionais: a transformação de Jordan-Wigner e o Ansatz de Bethe

(1)

CURSO DE MESTRADO EM MATEM ´ATICA

T´

ecnicas de Diagonaliza¸c˜

ao Exata de Modelos Quˆ

anticos

Unidimensionais: A Transforma¸c˜

ao de Jordan-Wigner e o

Ansatz de Bethe

Fl´

avio Luis Noronha dos Santos

(2)

(3)

Fl´

avio Luis Noronha dos Santos

Orientador:

Prof. Raphael Campos Drumond

T´

ecnicas de Diagonaliza¸c˜

ao Exata de

Modelos Quˆ

anticos Unidimensionais: A

Transforma¸c˜

ao de Jordan-Wigner e o

Ansatz de Bethe

Disserta¸c˜ao submetida `a banca

examina-dora, designada pelo Programa de

Pós-Gradua¸cão em Matemática da UFMG,

como requisito parcial para a obten¸c˜ao do

t´ıtulo de mestre em Matem´atica.

(4)

(5)

Primeiramente agrade¸co meu orientador, prof. Raphael Campos Drumond, pelas inúmeras horas investidas em me ajudar neste trabalho. Foi ele quem me ajudou desde as dúvidas mais triviais até as mais dif´ıceis demonstra¸cões que precisei fazer. Sou grato também a todos os professores que tive durante minha vida acadêmica, os quais me transmitiram o conhecimento básico para eu chegar até aqui. Agrade¸co a equipe do PICME, programa que investiu em mim desde o in´ıcio da minha gradua¸cão, e ao CNPq e CAPES pelas bolsas de estudo. Agrade¸co meus familiares, especialmente minha mãe, Ione Cordeiro, por todo apoio e suporte que têm me fornecido para que eu possa me dedicar aos estudos. Agrade¸co ainda os colegas e amigos, os quais sempre me encorajaram com os estudos e oram a Deus em meu favor. Por fim, agrade¸co a Deus pela oportunidade e privilégio que temos em estudar, conhecer e compreender a beleza do Universo criado por Ele.

(6)

e sua natureza divina, tˆ

em sido vistos

cla-ramente, sendo compreendidos por meio das

coisas criadas...

(Paulo aos Colossenses, cap.2, versos 2 e 3)

(7)

Neste trabalho são estudados os modelos XY e de Heisenberg em uma dimensão, os quais são utilizados para a descri¸cão de fenômenos f´ısicos, como o magnetismo de materiais. O Hamiltoniano do modelo XY é completamente diagonalizado e foi poss´ıvel obter algumas propriedades termo-dinâmicas de um sistema descrito pelo modelo, tais como energia livre e magnetiza¸cão. Observa-se neste sistema a presen¸ca de uma transi¸cão de fase com a varia¸cão do campo magnético na dire¸cão

z. Para o modelo de Heisenberg foi exposto um procedimento que permite diagonalizar completa-mente o Hamiltoniano. Verifica-se uma interessante semelhan¸ca entre a maioria dos autovalores do Hamiltoniano de Heisenberg com autovalores do Hamiltoniano XY no limite termodinˆamico.

(8)

In the present work the XY and Heisenberg models in one dimension are studied. They are useful to describe certain physical phenomena, such as the magnetic properties of materials. The Hamil-tonian of the XY model is completely diagonalized and it was possible to get some thermodynamic properties of a system described by the model, such as free energy and magnetization. We ob-serve here in this system the presence of a phase transition when changing the magnetic field in the z-direction. For the Heisenberg model, it is described in this work a procedure that allows one to completely diagonalize the Hamiltonian. There is an interesting similarity between most of the eigenvalues of the Heisenberg Hamiltonian and the eigenvalues of the XY Hamiltonian in the thermodynamic limit.

(9)

1 Introdu¸c˜ao 1

2 Preliminares 3

2.1 Estrutura Matemática da Mecânica Quântica . . . 3

2.2 Axiomas da Mecˆanica Quˆantica . . . 8

2.3 Cadeias de Spin . . . 11

2.4 Mecˆanica Estat´ıstica . . . 12

2.5 Transforma¸c˜ao de Jordan-Wigner (TJW) . . . 14

2.6 Propriedades dos Operadores Fermiˆonicos . . . 15

2.7 Diagonaliza¸cão de Formas Quadráticas de Operadores Fermiônicos . . . 18

3 O Modelo XY 23 3.1 Diagonaliza¸c˜ao Exata . . . 24

3.1.1 N´umero Par de Quasipart´ıculas . . . 26

3.1.2 N´umero ´Impar de Quasipart´ıculas . . . 29

3.1.3 N´ıveis de Energia . . . 33

3.2 Propriedades Termodinˆamicas do Modelo . . . 35

4 O Modelo de Heisenberg 43 4.1 Diagonaliza¸c˜ao . . . 44

4.1.1 Subespa¸cos com r=0 e r=1 . . . 44

4.1.2 Subespa¸co com r=2 . . . 45

4.1.3 Subespa¸co com r Qualquer . . . 54

4.2 Propriedades F´ısicas do Modelo . . . 55

4.3 Autoenergias no Modelo de Heisenberg e no Modelo XY . . . 57

5 Conclus˜ao 60

A Ortogonalidade das Solu¸c˜oes no Modelo de Heisenberg 62

(10)

Introdu¸c˜

ao

Com a formula¸cão da mecânica quântica, o conhecimento da matéria condensada alcan¸cou um enorme progresso. Uma das descobertas que merece destaque foi a observa¸cão de Dirac e Heisenberg de que as leis da mecânica quântica explicam o fenômeno do ferromagnetismo. A for¸ca de Coulomb entre os elétrons e o princ´ıpio de exclusão de Pauli dão origem a uma intera¸cão efetiva entre os spins de elétrons dos átomos do material quando as fun¸cões de onda de seus orbitais se sobrepõem. Tal intera¸cão é descrita por termos do tipoJα

ijSiαSjα, α=x, y, z, ondeSαi eSαj s˜ao os operadores de spin nos s´ıtiosiej de uma cadeia comN part´ıculas eJα

ijé uma constante de acoplamento dos spins destes s´ıtios. Se Jijα ≤0 ∀i, j, α, os autoestados mais prováveis (menos energéticos) de tais intera¸cões tendem a ser estados em que os spins se encontram alinhados, o que pode caracterizar um material ferromagnético.

Muitos outros fenômenos envolvendo matéria condensada tem sido estudados ao longo de décadas e uma das principais dificuldades é encontrar Hamiltonianos que descrevem com boa aproxima¸cão as intera¸cões nestes materiais e diagonalizar estes Hamiltonianos, encontrando assim as autofun¸cões, as autoenergias e, consequentemente, as propriedades termodinâmicas do material, bem como poss´ıveis transi¸cões de fase. O problema está no fato de que, em geral, o Hamiltoni-ano exato de um sistema quântico é extremamente dif´ıcil de se tratar e envolve intera¸cões entre part´ıculas em três dimensões. Uma das abordagens poss´ıveis é reduzir o problema para o caso unidimensional e realizar aproxima¸cões neste Hamiltoniano até que se possa diagonalizá-lo. Uma vez encontrados resultados e propriedades para este caso mais simples, tenta-se estendê-los para dimensões maiores, ou obter algum método generalizado para dimensões maiores para encontrar aproximadamente as autofun¸cões e autoenergias do Hamiltoniano. Geralmente, o tipo inicial uti-lizado para um sistema magnético é uma cadeia unidimensional com intera¸cões entre vizinhos. Muitos dos estudos magnéticos se iniciam com um Hamiltoniano do tipo:

H = N

X

i=1

(αSixSxi+1+βS

y iS

y i+1+γS

z

iSzi+1). (1.1)

O Hamiltoniano (1.1) é, na verdade, uma idealiza¸cão de um sistema real, porém, já é considera-velmente dif´ıcil tratá-lo. Este modelo aproximado, no entanto, poderá ser útil para obter alguma estrutura ou caráter geral de sistemas de muitos corpos.

(11)

Diversos casos especiais do Hamiltoniano (1.1) tem sido estudados em detalhes. O modelo de Ising, por exemplo, é obtido tomandoα=β = 0 e foi estudado por Ising [10] e Onsager [11]. O modelo XY, dado porγ = 0, foi estudado inicialmente por Lieb, Schultz e Mattis [7]. O modelo de Heisenberg, estudado por Bethe [9] e Hulthén [14], é definido por α=β = γ. Muitos outros também fizeram contribui¸cões para estes modelos.

Neste trabalho, a fim de diagonalizar alguns Hamiltonianos de modelos magnéticos, é realizada uma revisão em mecânica quântica no cap´ıtulo 2, bem como são expostos o conceito de trans-forma¸cão de Jordan-Wigner, as propriedades dos operadores fermiônicos e a diagonaliza¸cão de formas quadráticas de operadores fermiônicos.

No cap´ıtulo 3 aborda-se o modelo XY na presen¸ca de um campo magnético transverso. Foi rea-lizada a diagonaliza¸cão exata deste modelo e foram obtidas as energias dos autoestados e algumas propriedades termodinâmicas como energia livre e magnetiza¸cão.

O cap´ıtulo 4 mostra um procedimento que permite encontrar todos os autoestados e autoe-nergias do sistema descrito pelo modelo de Heisenberg. Verifica-se que, dependendo dos números quânticos relacionados com os autoestados, os autoestados podem ser interpretados como estados de mágnons espalhados ou estados de mágnons ligados. Verifica-se ainda que, no limite termo-dinâmico, as excita¸cões dos estados espalhados possuem o mesmo valor que algumas excita¸cões de um caso particular do modelo XY num campo magnético transverso. A ortogonalidade das solu¸cões no modelo de Heisenberg é deixada para ser verificada no apêndice A.

(12)

Preliminares

Neste cap´ıtulo estão expostas defini¸cões da estrutura matemática necessária para desenvolver esta disserta¸cão, bem como uma revisão em mecânica quântica e mecânica estat´ıstica e alguns resultados fundamentais relacionados com a transforma¸cão de Jordan-Wigner, as propriedades dos operadores fermiônicos e a diagonaliza¸cão de formas quadráticas de operadores fermiônicos.

O conteúdo das se¸cões 2.1, 2.2 e 2.3 podem ser encontrados nas referências [1], [2] e [3]. Para saber mais sobre mecânica estat´ıstica, assunto da se¸cão 2.4, veja [4]. Informa¸cões sobre a trans-forma¸cão de Jordan-Wigner, descrita na se¸cão 2.5, podem ser encontradas em [5]. Por fim, o conteúdo das se¸cões 2.6 e 2.7, que tratam de operadores fermiônicos, pode ser encontrado em [6].

2.1 Estrutura Matem´

atica da Mecˆ

anica Quˆ

antica

A fim de descrever sistemas quânticos, é necessário utilizar espa¸cos vetoriais complexos como estrutura para tais sistemas. As defini¸cões e resultados desenvolvidos aqui se aplicam a espa¸cos vetoriais de dimensão finita. Alguns deles podem ser generalizados para dimensão infinita, mas não é nosso interesse aqui.

Um espa¸co de Hilbert H ´e um espa¸co vetorial complexo, completo, que possui um produto internoh·,·i, satisfazendo:

hψ, αϕ+βηi=αhψ, ϕi+βhψ, ηi,

hψ, ϕi=hϕ, ψi∗, (2.1)

hψ, ψi ≥0 e se hψ, ψi= 0 ent˜aoψ= 0,

para todoψ, ϕ, η∈ Heα, β∈C_{, e sendo}_h_{ϕ, ψ}_i∗ _{o complexo conjugado de}_h_{ϕ, ψ}_i_.

Um conjunto{ϕj|j= 1,2, ...m} de elementos deH´e dito ortonormal se satisfaz

hϕi, ϕji=δij, i, j= 1,2, ...m,

onde δij = 1 se i = j e δij = 0 caso contr´ario. Um conjunto ortonormal {ϕj|j = 1,2, ...n} de

(13)

elementos deH´e chamado de base ortonormal de Hse, para qualquer ψ∈ H, vale

ψ= n

X

j=1

hϕj, ψiϕj.

´

E poss´ıvel mostrar que todo espa¸co de Hilbert possui uma base. Além disso, duas bases ortonor-mais quaisquer para o mesmo espa¸co possuem a mesma cardinalidade, i.e., o mesmo número de elementos. Dizemos que este número é a dimensão do espa¸co. Como já foi dito, neste trabalho iremos nos restringir ao caso em que a dimensão deHé finita.

SeP´e um subconjunto do espa¸co de HilbertH, definimos seu complemento ortogonal P⊥ :={ϕ∈ H|hϕ, ψi= 0 para todoψ∈P}.

Dados um subespa¸coK deHeψ∈ H, existem ´unicosϕeη tais que

ψ=ϕ+η, ϕ∈ K eη ∈ K⊥.

Uma aplica¸c˜ao linearP:H → H´e chamada projetor ortogonal se satisfaz:

P2=P,

hPψ, ϕi=hψ,Pϕi, ∀ψ, ϕ∈ H.

Exemplo 2.1. Seja {ϕj|j= 1,2, ..., m} um conjunto ortonormal emH. Ent˜ao o operador

Pψ= m

X

j=1

hϕj, ψiϕj, ∀ψ∈ H,

é o projetor ortogonal sobre o espa¸coSpan({ϕj|j = 1,2, ..., m}), que é o espa¸co de todas as poss´ıveis combina¸cões lineares dosϕj.

Seja H um espa¸co de Hilbert. Um funcional linear ´e uma fun¸c˜ao A : H → C _{que satisfaz}

A(αψ+βϕ) =αA(ψ) +βA(ϕ), ∀α, β∈C_{, ψ, ϕ}_{∈ H}_{. O espa¸co dual de}_H_{, denotado por}_H∗_{, ´e o}

espa¸co de todos os funcionais lineares que atuam emH.

Nota¸cão 2.1. Dirac propôs uma nota¸cão para lidar com vetores e funcionais lineares. Segundo sua nota¸cão, para especificar um elementoψ∈ Hutilizamos o s´ımbolo “ket”|ψi, e para o funcional

hϕ,·i ∈ H∗_{utilizamos o s´ımbolo “bra”} _h_ϕ_|_{, em que}_H∗_{´e o espa¸co dual de}_H_{. Dessa maneira temos}

as seguintes equivalˆencias entre nota¸c˜oes:

hϕ, ψi=hϕ|ψi=hϕ||ψi.

Esta nota¸cão é bastante conveniente para realizar cálculos extensos com operadores em espa¸cos de Hilbert.

Exemplo 2.2. Seja ϕ∈ H. Definimos o operadorQ:=|ϕihϕ|de forma que

(14)

Nesta nota¸c˜ao o projetor do exemplo anterior ´e escrito como

P= m

X

j=1

|ϕjihϕj|,

de forma que

P_|ψi= m

X

j=1

|ϕjihϕj|ψi= m

X

j=1

hϕj|ψi|ϕji, ∀|ψi ∈ H.

Defini¸c˜ao 2.1. Dados |ψi ∈ Hehϕ| um funcional linear, definimos as opera¸c˜oes:

|ψi† :=hψ|, (2.2)

hϕ|†:=|ϕi. (2.3)

Defini¸cão 2.2. (Aplica¸cão adjunta) Dada uma aplica¸cão linear A : H → K, definimos a adjunta deA (ou a conjugada Hermitiana de A, se A for uma matriz) sendo a aplica¸cão linear

A†:K → H que satisfaz

hϕ,Aψi=hA†ϕ, ψi, ∀ψ∈ He∀ϕ∈ K. (2.4) Seguem ent˜ao as propriedades:

(αA+βB)†₌_α∗_A†₊_β∗_B†_,

(AB)†=B†A†,B:H → K,A:K → L,

(A†)† =A, (2.5)

kAA†_k=kA_k2=kA†_k2,

(A|ψi)† =hψ|A†.

Defini¸c˜ao 2.3. Dizemos que um operador linearA:H → H´e autoadjunto (ou Hermitiano, se A

for uma matriz) seA=A†, e dizemos que é semidefinido positivo sehψ|A|ψi ≥0 para qualquer ψ∈ H. Dizemos que um operador U : H → H é unitário se possuir um operador inverso tal que

U−1=U†.

Defini¸c˜ao 2.4. Dado o operador linear A :H → He uma base ortonormal {|ϕii, i= 1,· · ·, m}

para o espa¸coH, o tra¸co deA ´e definido por

Tr(A) = m

X

i=1

hϕi|A|ϕii.

´

E poss´ıvel mostrar que o valor do tra¸co de um operador independe da base escolhida.

Considere agora uma curva em um espa¸co de HilbertH,

|ψi:R_{→ H}

t7→ |ψ(t)i,

possuindo o valor inicial|ψ0iemt0. Podemos definir a derivada

d|ψi

dt := lim∆t→0

|ψ(t+ ∆t)i − |ψ(t)i

(15)

onde o limite ´e tomado usando a topologia induzida pelo produto interno. SeHtem dimens˜aon,

|ψ(t)ipode ser escrito como uma soma dos elementos de uma base{|ψ1i, ...,|ψni}deH, de forma que

|ψ(t)i= n

X

k=1

zk(t)|ψki,

podendo ser representado por [ψ(t)]∈Cn_,

[ψ(t)] =



  

z1(t)

.. .

zn(t)



  

,

em quezi :R→C, i= 1,2, ..., n.

A seguir, temos a demonstra¸cão de um teorema que será utilizado na se¸cão 3.2, na qual extrai-remos propriedades termodinâmicas do modelo XY.

Teorema 2.1. Seja A(α) um operador autoadjunto que depende de certo parˆametro α ∈ R_{, e}

|ψ(α)i um autovetor unit´ario com autovalor correspondente v(α). Suponha que A(α), |ψ(α)i e

v(α)são diferenciáveis. Então:

d

dαhψ(α)|A(α)|ψ(α)i=hψ(α)| dA(α)

dα |ψ(α)i. (2.6)

Demonstra¸c˜ao. E f´´ acil ver que

hψ(α)|A(α)|ψ(α)i=v(α).

A fim de derivar a express˜ao acima, utilizaremos a propriedade

d

dαhϕ(α)|η(α)i=

dhϕ(α)|

dα |η(α)i+hϕ(α)| d|η(α)i

dα ,

ondehϕ(α)|e|η(α)isão diferenciáveis. Temos então:

dv(α)

dα =

dhψ(α)|

dα A(α)|ψ(α)i+hψ(α)|A(α)

d|ψ(α)i

dα +hψ(α)| dA(α)

dα |ψ(α)i

=v(α)

_d

hψ(α)|

dα |ψ(α)i+hψ(α)|

d|ψ(α)i

dα

+hψ(α)|dA(α)

dα |ψ(α)i

=v(α) d

dα(hψ(α)|ψ(α)i) +hψ(α)| dA(α)

dα |ψ(α)i

=v(α) d

dα(1) +hψ(α)| dA(α)

dα |ψ(α)i

=hψ(α)|dA_dα(α)|ψ(α)i.

Defini¸c˜ao 2.5. (Produto tensorial) Dados dois espa¸cos de Hilbert H1 e H2, podemos definir

seu produto tensorial

(16)

Definimos ainda o produto tensorial entre os elementos deH1 eH2 de maneira que

⊗:H1× H2→H1⊗ H2

(|ϕ1i,|ϕ2i)7→|ϕ1i ⊗ |ϕ2i, em que

|ϕ1i ⊗ |ϕ2i(f) =f(|ϕ1i,|ϕ2i).

Se um vetor|ϕ12i ∈ H1⊗ H2 puder ser escrito na forma |ϕ12i=|ϕ1i ⊗ |ϕ2i, ent˜ao dizemos que

|ϕ12ié um vetor produto. Quer dizer, os vetores produto são a imagem da aplica¸cão acima definida.

Aqui, temos a seguinte equivalencia das nota¸c˜oes:|ϕ1⊗ϕ2i=|ϕ1i ⊗ |ϕ2i=ϕ1⊗ϕ2.

Se {|ψ1i,|ψ2i, ...,|ψmi} e {|ϕ1i,|ϕ2i, ...,|ϕni} s˜ao bases ortonormais de H1 e H2,

respectiva-mente, ent˜ao{|ψii ⊗ |ϕji|i= 1, ..., m;j= 1, ..., n}´e uma base paraH1⊗ H2. Assim,

dim(H1⊗ H2)= dim(H1)·dim(H2). ComoH1eH2s˜ao espa¸cos de Hilbert, a aplica¸c˜ao definida por

hψk⊗ϕl, ψi⊗ϕji:=hψk|ψii · hϕl|ϕji, (2.7)

estendida por linearidade para cada elemento deH1⊗ H2define um produto interno neste espa¸co.

Ent˜ao a base{|ψii ⊗ |ϕji|i= 1, ..., m;j= 1, ..., n}´e ortonormal.

Denotaremos porB(H1,H2) o conjunto de todas as aplica¸c˜oes linearesC:H1→ H2, enquanto

B(H1) ser´a o conjunto de todos os operadores linearesD:H1→ H1. ´E poss´ıvel mostrar que tais

conjuntos s˜ao espa¸cos de Hilbert. Dados dois operadores A ∈ B(H1) e B ∈ B(H2) definimos o

produto tensorialA_⊗Bem termos dos vetores produto

(A⊗B)(|ϕi ⊗ |ψi) := (A|ϕi)⊗(B|ψi), (2.8)

de onde temosA⊗B= (A⊗1₎₍1_⊗_B_).

´

E fácil ver que a aplica¸cão (A)⊗(B)7→(A⊗B), estendida por linearidade para todo elemento deB(H1)⊗ B(H2), é um isomorfismo entreB(H1)⊗ B(H2) eB(H1⊗ H2). De fato, temos a

Proposi¸cão 2.1. SeH1 eH2 são espa¸cos de Hilbert, então

B(H1)⊗ B(H2)≃ B(H1⊗ H2). (2.9)

Demonstra¸c˜ao. Sejam {|ϕii},{|ψji}bases ortonormais paraH1eH2, respectivamente. Definimos

os operadores linearesEb

a ∈ B(H1), Fcd∈ B(H2), eGb,da,c ∈ B(H1⊗ H2) em termos dos elementos

dessas bases, de forma que

Eab(|ϕii) =δa,i|ϕbi,

Fcd(|ψji) =δc,j|ψdi,

Gb,da,c(|ϕii ⊗ |ψji) =δa,iδc,j|ϕbi ⊗ |ψdi. Os operadoresEb

a,Fcd eGb,da,c formam bases para os espa¸cosB(H1),B(H2) eB(H1⊗ H2),

respec-tivamente. Definimos a aplica¸c˜ao

(17)

2.2 Axiomas da Mecˆ

anica Quˆ

antica

Em um sistema f´ısico que evolui no tempo temos diversas variáveis dinâmicas que o caracterizam, tais como energia, posi¸cão, velocidade, etc. Na mecânica quântica é necessário representar o estado de um “sistema quântico” por um objeto matemático e as variáveis dinâmicas em termos de outros objetos matemáticos a fim de podermos resolver, matematicamente, problemas relacionados a elas. Isso tudo é feito utilizando alguns axiomas da mecânica quântica, dos quais falaremos agora.

Axioma 2.1. (Estados Quˆanticos) Dado um sistema quˆantico, existe um espa¸co de Hilbert H

tal que cada estado deste sistema pode ser representado por algum operadorρ∈ B(H), em que ρé um “operador densidade”, isto é, é autoadjunto, semidefinido positivo e possui tra¸co unitário.

Comoρ´e autoadjunto, ele possui um conjunto de autovetores ortonormais {|ψ1i, ...,|ψni} que forma uma base paraH, e pode ser escrito como

ρ= n

X

j=1

pj|ψjihψj|, (2.10)

em quepj ≥0 paraj= 1, ..., n, uma vez que ele ´e semidefinido positivo. Por ele ter tra¸co unit´ario, precisamos ter

n

X

j=1

pj= 1. (2.11)

Se o estado de um sistema quˆantico puder ser representado por um operador densidade da forma

ρ = |ψihψ|, dizemos que o sistema quântico se encontra num “estado puro”. Para simplificar, dizemos que tal estado puro pode também ser representado pelo vetor |ψi. Observe que, para qualquerα∈R_{, e}iα_|_ψ_i_{também representa tal estado puro, uma vez que tal vetor também gera o}

mesmo operadorρ. Se o estado do sistema n˜ao ´e puro, dizemos que ele se encontra em um “estado misto”.

Axioma 2.2. (Observáveis)Dado um sistema quântico cujos estados puros podem ser represen-tados num espa¸co de HilbertH, se A é um operador linear autoadjunto sobre o Espa¸co de Hilbert

H, dizemos que A é um “observável” sobre H. Para cada variável dinâmica, que é um conceito f´ısico, existe um observável correspondente sobre o espa¸co de HilbertH, de forma que os poss´ıveis valores da variável dinâmica são os autovalores deste observável.

Exemplo 2.3. Considere um sistema quântico cujos estados puros são vetores em H. Existe um operadorH, o qual chamamos de “Hamiltoniano” do sistema, que descreve a energia do sistema quântico. Os poss´ıveis valores que a energia do sistema pode assumir são os autovalores do Hamil-toniano.

Axioma 2.3. (Probabilidade e Valor Médio) Sejamρ∈ B(H)o operador densidade de um sistema quântico e A um observável sobre H. Pelo Teorema Espectral, sabemos que o observável pode ser escrito na forma

A= n

X

j=1

(18)

em que os vetores |aji formam uma base de autovetores ortonormais de A com autovalores aj,

j = 1, ..., n. Assim, ao realizar a medi¸cão da variável dinâmica correspondente ao operador A, a probabilidade do sistema se encontrar num estado representado por|aiié

pai :=hai|ρ|aii, i= 1, ..., n. (2.13)

Assim, o valor esperado, ou valor médio, do observávelAno estadoρé dado por

hAiρ:= n

X

j=1

aj·paj. (2.14a)

O valor esperado pode ser reescrito na forma:

hA_iρ= n

X

j=1

ajhaj|ρ|aji= n

X

j=1

haj|ρA|aji= Tr (ρA), (2.14b)

em que Tr ´e o tra¸co do operador.

Se o sistema quˆantico se encontra num estado puro |ψi, sua matriz densidade ´e dada por

ρ=|ψihψ|e, consequentemente, a express˜ao para o valor esperado do observ´avelAsobre o sistema se simplifica, ficando:

hAi|ψi:=hAiρ=hψ|A|ψi. (2.15) Se ρ é um operador densidade, temos de (2.13) que pai ≥ 0, i = 1, ..., n. Como A é um operador autoadjunto, todos os autovaloresaj são números reais. Assim, de (2.14a) vemos que o valor médio é sempre um número real. Sabemos que os valores assumidos pelas variáveis dinâmicas são reais e, consequentemente, é obvio que o valor médio de seu observável correspondente, para um determinado estadoρ, também deve ser real. Vimos que tal valor médio será sempre real mas, para isso, foi essencial afirmarmos que os observáveis são operadores autoadjuntos.

Defini¸cão 2.6. Considere um sistema quântico cujos estados puros são representados por vetores emH. Se o sistema se encontra no estado|ψi, dizemos que |ψié a “fun¸cão de onda” do sistema quântico. Hé chamado de “espa¸co das fun¸cões de onda” do sistema.

Axioma 2.4. Considere um sistema quˆantico que evolui no tempo, de forma que em cada momento

t a fun¸cão de onda que caracteriza o sistema é |ψ(t)i. A equa¸cão fundamental que descreve a evolu¸cão temporalt7→ |ψ(t)ié chamada “equa¸cão de Schrödinger”, e é dada por

i~d|ψi

dt =H|ψi, |ψ(t0)i=|ψ0i, (2.16)

ondeh= 6,626×10−34_J.s_{´e a constante de Planck,}_~₌_h/₂_π_,_|_ψ

0i´e a fun¸c˜ao de onda inicial do

sistema eH´e o Hamiltoniano do sistema.

No caso de estados mistos em que ρ(t)´e a matriz densidade, temos

dρ dt =−

i

~[H, ρ], ρ(t0) =ρ0, (2.17)

(19)

Se na descri¸cão de SchrödingerAé um observável que independe do tempo enquanto o operador densidade ρ evolui com t, na descri¸cão de Heisenberg podemos interpretar o sistema como se o operador densidade permanecesse constante e o observável variasse com o tempo. Temos:

Tr(ρ(t)A0) = Tr(ρ0A(t)), (2.18)

em que

dA

dt =i[H, A], A(t0) =A0. (2.19)

A equa¸cão de Schrödinger para um estado puro |ψisujeito a um Hamiltoniano independente do tempo possui solu¸cão da forma

|ψ(t)i=U(t)|ψ(0)i, ondeU(t) = exp(−itH/~₎_{, t}_∈R_. _(2.20)

Dado um sistema quˆantico e um Hamiltoniano H que o descreve, utilizamos as seguintes no-menclaturas:

1. Um “autoestado” do sistema é um estado do sistema quântico que corresponde a um autovetor do Hamiltoniano, e seu autovalor correspondente é denominado “autoenergia” do sistema.

2. Se dois ou mais autoestados do Hamiltoniano possuem a mesma energia, dizemos que tais estados são “degenerados”. Assim, a “degenerescência” de um valor de energia do Hamil-toniano é a dimensão do subespa¸co de H que contém todos os autovetores de H com tal autovalor.

3. O autovetor do Hamiltoniano com o menor autovalor é associado ao “estado fundamental” do sistema, e é o estado de menor energia acess´ıvel ao sistema quântico.

4. Cada autovetor do Hamiltoniano que n˜ao corresponde ao estado fundamental corresponde a um “estado excitado” do sistema.

Axioma 2.5. Suponha que, num sistema de N componentes, Hj seja o espa¸co de Hilbert das

fun¸cões de onda do j-ésimo componente. Assim, as fun¸cões de onda do sistema total pertencem a NN

j=1Hj. Os observáveis do sistema global que dizem respeito apenas à k-ésima componente

s˜ao da forma 1_{⊗ · · · ⊗}1_⊗_A_⊗1_{⊗ · · · ⊗}1_{, onde} _A _{∈ B}₍_H

k). Se todos os componentes forem

“mutuamente independentes” e cadai-´esimo componente for descrito pelo operador densidadeρi,

ent˜ao o operador densidade do sistema ser´aNN

i=1ρi, e teremos:

* _N

O

j=1

Aj

+

⊗iρi = Tr





N

O

i=1

ρi N

O

j=1

Aj



=

N

Y

j=1

Tr(ρjAj) = N

Y

j=1

hAjiρj. (2.21)

Proposi¸c˜ao 2.2. Seja H12 =H1⊗ H2. Dada uma matriz densidade ρ12 sobre H12, existe uma

´

unica matriz densidadeρ1 sobre H1 tal que

Tr (ρ1A1) = Tr (ρ12A1⊗12), ∀A1∈ B(H₁), (2.22)

(20)

Chamamos ρ1 de “matriz densidade reduzida” de ρ12, e chamamos de “tra¸co parcial” de ρ12

sobreH2 à opera¸cãoρ127→ρ1, que é denotada por

ρ1= TrH2ρ12.

Demonstra¸c˜ao. Sejam {|ϕ1i, ...,|ϕmi}e{|ψ1i, ...,|ψni}bases ortonormais deH1eH2,

respectiva-mente, eρ12 uma matriz densidade sobreH12. Definimos o operadorρ1por:

(ρ1)ij =hϕi|ρ1|ϕji= n

X

k=1

(hϕi| ⊗ hψk|)ρ12 (|ϕji ⊗ |ψki). (2.23)

Tomando operadores A1 = |ϕpihϕq|, é poss´ıvel ver que a rela¸cão (2.22) é satisfeita. Utilizando a linearidade do tra¸co, conclu´ımos que esta rela¸cão será satisfeita para qualquer operador linear. Suponha agora que existe uma outra matriz densidadeρa que satisfaz a equa¸cão (2.22). Temos:

Tr[(ρ1−ρa)A1] = 0, ∀A1∈ B(H₁).

Tomando operadores A1 = |ϕpihϕq| e substituindo na rela¸c˜ao acima, para p, q = 1, ..., m, temos

ρ1−ρa= 0, de onde conclu´ımos que a matriz densidadeρ1que satisfaz a equa¸cão (2.22) é única.

2.3 Cadeias de Spin

Neste trabalho discutiremos cadeias unidimensionais dos denominados spins-1₂. O “spin” é um momento angular intr´ınseco às part´ıculas fundamentais, por não poder ser atribu´ıdo a uma rota¸cão da part´ıcula, sendo descrito por um espa¸co de Hilbert de dimensão finita. Para uma part´ıcula com spin-1₂ o espa¸co é bidimensional e o momento angular ao longo de uma dada dire¸cão espacial é descrito pelos denominados “operadores de Pauli”.

Defini¸c˜ao 2.7. Dada uma base ortonormal {|1i,|0i} para o espa¸co de HilbertC2_{, de um sistema}

de spin 1₂, definimos os operadores de Pauli como sendo:

σx=|1ih0|+|0ih1|,

σy=−i|1ih0|+i |0ih1|, (2.24a)

σz=|1ih1| − |0ih0|,

cujas representa¸c˜oes matriciais correspondem `as “matrizes de Pauli”:

σx= 0 1 1 0

!

, σy= 0 −i

i 0

!

, σz= 1 0

0 −1

!

. (2.24b)

Os vetores |1i e |0i, que são autovetores do operador σz_{, são identificados com os estados} quânticos em que a componentez do spin de uma part´ıcula se encontra para cima e para baixo, respectivamente.

Defini¸c˜ao 2.8. Definimos operadores de “abaixamento” e “levantamento” σ− _e _σ+_,

respectiva-mente, por:

σ− _:=σx−iσy

2 , σ

+_:=σx+iσy

(21)

Eles possuem tais nomes porque satisfazem:

σ−|0i= 0, σ−|1i=|0i, σ+|0i=|1i, σ+|1i= 0. (2.26)

Lema 2.1. O operador de Pauliσz _{e os operadores abaixamento e levantamento,}_σ− _e_σ+_,

satis-fazem:

exp(±iπσ−_σ+_{) =}_σz_. _(2.27)

Demonstra¸c˜ao.

exp(±iπσ−σ+) =1₊(±iπσ −_σ+₎

1! +

(±iπσ−_σ+₎2

2! +

(±iπσ−_σ+₎3

3! +· · · = (|0ih0|+|1ih1|) +(±iπ(|0ih0|))

1! +

(±iπ(|0ih0|))2

2! +

(±iπ(|0ih0|))3

3! +· · · = (|1ih1|) + (|0ih0|) + (|0ih0|)(±iπ)

1! + (|0ih0|) (±iπ)2

2! + (|0ih0|) (±iπ)3

3! +· · · = (|1ih1|) + (|0ih0|)

1 +(±iπ) 1! +

(±iπ)2

2! + (±iπ)3

3! +· · ·

= (|1ih1|) + (|0ih0|)e±iπ = (|1ih1|)−(|0ih0|) =σz.

Defini¸c˜ao 2.9. Suponha que temos um sistema deN spins-1₂. O espa¸co de Hilbert que o descreve ´e(C2₎⊗N_{, isomorfo a}_H₌_C2N

, o qual ser´a utilizado para nossa descri¸c˜ao. Definimos σx j, σ

y j, σjz,

os operadores de Pauli atuando sobre oj-´esimo s´ıtio, por

σαj :=1⊗ · · · ⊗1⊗σα⊗1⊗ · · · ⊗1, α=x, y, z. (2.28)

Definimos ainda os operadores de abaixamento e levantamentoσ−_j eσ_j+, respectivamente, atuando noj-´esimo s´ıtio da cadeia de spin, por:

σ−_j :=σ x j −iσ

y j

2 , σ

+

j :=

σx j +iσ

y j

2 . (2.29)

Podemos, então, obter as seguintes rela¸cões, as quais serão úteis futuramente:

σjx=σj++σj−, (2.30)

σyj =

σ+j −σj−

i , (2.31)

σz j = (2σ

+

j σj−−1), (2.32)

σjz= exp(±iπσj−σ

+

j). (2.33)

2.4 Mecˆ

anica Estat´ıstica

(22)

Os “estados de Gibbs” são bastante utilizados em mecânica estat´ıstica e descrevem o estado de sistemas em equil´ıbrio térmico a uma temperaturaT. Eles são definidos pelas matrizes densidade

ρβ:=

e−βH

Z , (2.34)

ondeβ =_k1

BT, sendokB= 1,381×10

−23_J/C _{a constante de Boltzmann,}_H _{´e o Hamiltoniano do}

sistema eZ é a “fun¸cão de parti¸cão”, definida por

Z:= Tre−βH = X

|ψi∈AV(H)

e−βE(|ψi), (2.35)

em que a soma acima percorre o conjuntoAV(H), uma base ortonormal de autovetores do Hamil-tonianoH, eE(|ψi) ´e a autoenergia correspondente ao autovetor|ψi.

´

E interessante notar que os estados de Gibbs não variam com o tempo pois o comutador na equa¸cão (2.17) será nulo para tais estados.

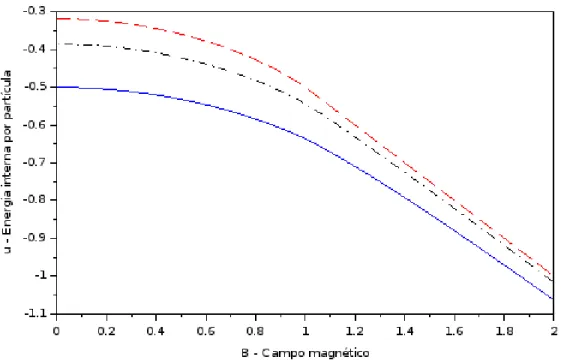
Defini¸c˜ao 2.10. Considere um sistema deN part´ıculas a uma temperaturaT sendo descrito pelo operador densidadeρβ. Definimos a “energia interna” do sistema por

U =hHiρβ, (2.36)

e a energia interna por part´ıcula por

u=U/N. (2.37)

Em sistemas f´ısicos reais, nos quais se deseja medir o valor esperado de algum observável, sabe-se queN, o número de part´ıculas envolvidas, é finito. Entretanto, este número costuma ser muito grande, da ordem de 1023 _{part´ıculas. Este n´}_{umero é tão grande que o sistema se comporta}

aproximadamente como se houvesse infinitas part´ıculas ali. Assim, é uma excelente aproxima¸cão tomar o limite de diversas fun¸cões com N tendendo ao infinito, o que costuma simplificar os cálculos. Chamamos este limite de “limite termodinâmico”.

Defini¸cão 2.11. Dada a fun¸cão de parti¸cão Z de um sistema quântico, a “energia livre” por part´ıcula no limite termodinâmico é definida por:

F=−1_β lim N→∞

1

N lnZ. (2.38)

Da termodinˆamica, temos as rela¸c˜oes:

F=u−T s, (2.39)

s=−∂_∂TF, (2.40)

em ques´e uma fun¸c˜ao denominada “entropia” por part´ıcula.

Defini¸cão 2.12. Dado um sistema quântico num estado de Gibbsρβ, definimos a “magnetiza¸cão”

por part´ıculamz na dire¸c˜ao z por

mz:= h

Mziρβ

(23)

em que

Mz:=

µ0

2 N

X

j=1

σzj, (2.42)

ondeµ0´e uma constante que tem unidade J/T (Joule/Tesla). Para simplifica¸c˜ao, faremos µ0= 1.

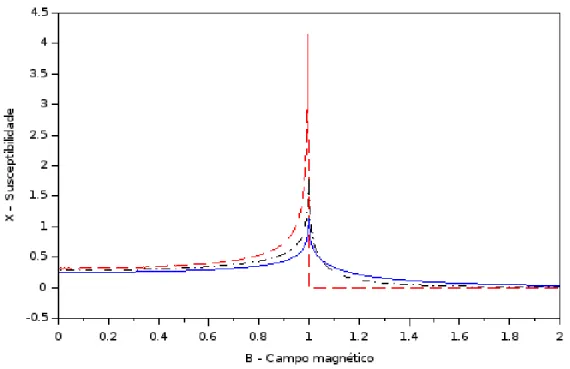
Se o sistema estiver submetido a um campo magnético B, a “susceptibilidade magnética” χ é definida por

χ:= ∂mz

∂B . (2.43)

Mais adiante, na se¸cão 3.2, iremos calcular o valor esperado da magnetiza¸cão de um sistema quântico à temperatura T descrito pelo modelo XY ferromagnético. Demonstramos a seguir um resultado que será utilizado naquela ocasião para calcular o valor esperado de um observável sobre um sistema em equil´ıbrio térmico a uma temperaturaT.

Proposi¸cão 2.3. Seja AV(H) uma base de autoestados do HamiltonianoH de um sistema quântico e seja A um observável sobre este sistema. Então, o valor esperado desse observável para este sistema, se ele se encontra à temperatura T, é dado por:

hAiρβ =

X

|ψi∈AV(H)

hAi|ψi

e−βhHi|ψi

Z .

Demonstra¸c˜ao.

hAiρβ = Tr (Aρβ) = Tr

Ae−

βH

Z

= Tr A

P

|ψi∈AV(H)e−βE(|ψi)|ψihψ|

Z

!

= X

|ψi∈AV(H)

hψ|A|ψie−

βE(|ψi)

Z

= X

|ψi∈AV(H)

hAi|ψi

e−βhHi|ψi

Z .

2.5 Transforma¸c˜

ao de Jordan-Wigner (TJW)

Nesta se¸c˜ao iremos descrever a “transforma¸c˜ao de Jordan-Wigner”, a qual permite mapear N

operadores de spin emN “operadores fermiônicos”. Esses operadores fermiônicos possuem uma álgebra conveniente, como veremos na próxima se¸cão.

Defini¸c˜ao 2.13. Um conjunto de operadoresa1, ..., aN atuando em um espa¸co de HilbertH´e dito

fermiônico se eles satisfazem as rela¸cões abaixo, que chamaremos de RAC (rela¸cões de antico-muta¸cão canônicas):

{aj, ak}= 0,

{aj, a†k}=δjk1,

(2.44)

(24)

Definimos, agora, a transforma¸c˜ao de Jordan-Wigner, que ser´a importante para diagonalizar o Hamiltoniano do modelo XY.

Defini¸c˜ao 2.14. (Transforma¸c˜ao de Jordan-Wigner)Sejamσx j, σ

y

j, σzj os operadores de Pauli

atuando sobre oj-´esimo spin-1₂, de um total de N. Ent˜ao definimos os operadores

aj := exp



−iπ X

l<j

σ_l−σ_l+



σ+_j, (2.45)

a†j :=σ−j exp



+iπ X

l<j

σ_l−σ+_l



. (2.46)

A defini¸cão que fizemos para os operadores acima é chamada de transforma¸cão de Jordan-Wigner.

Utilizando a equa¸c˜ao (2.33) podemos, alternativamente, escrever:

aj= j−1 Y

l=1

σzl

!

σj+, a†j= j−1 Y

l=1

σzl

!

σj−. (2.47)

´

E poss´ıvel ver que os operadoresaj satisfazem as RAC, sendo então operadores fermiônicos. A transforma¸cão de Jordan-Wigner pode também ser invertida para descrevermos os operadores de Pauli em termos dos operadores fermiônicosa1, a2, ..., an. Isso será feito no cap´ıtulo 3.

2.6 Propriedades dos Operadores Fermiˆ

onicos

Sejam a1, a2, ..., aN operadores atuando no espa¸co de Hilbert H satisfazendo as RAC. A seguir vamos obter algumas informa¸cões da estrutura deHe dos operadoresaj decorrentes das rela¸cões de anticomuta¸cão, seguindo referência [6].

Proposi¸cão 2.4. Sea1, a2, ..., aN são operadores fermiônicos, então:

1. Os operadores a†_jaj s˜ao operadores semidefinidos positivos, com autovalores 0 e 1.

2. Se |ψié um autoestado normalizado de a†jaj com autovalor 1, então aj|ψié um autoestado

normalizado de a†jaj com autovalor 0. Se |ψi ´e um autoestado normalizado de a†jaj com

autovalor 0, ent˜aoaj|ψi= 0.

3. Se |ψié um autoestado normalizado de a†jaj com autovalor 0, então a†j|ψié um autoestado

normalizado de a†jaj com autovalor 1. Se |ψi ´e um autoestado normalizado de a†jaj com

autovalor 1, ent˜aoa†_j|ψi= 0. Demonstra¸c˜ao.

1. Dado|ψiqualquer, temos

(25)

Note que, pelas RAC, (a†jaj)2=a†jaj. Seja |ϕium autovetor dea†jaj com autovalor corres-pondenteξ. Logo,

(a†jaj)2|ϕi=ξ2|ϕi= (a†jaj)|ϕi=ξ|ϕi ⇒ξ2=ξ, de onde conclu´ımos queξ= 0 ouξ= 1.

2. Seja|ψium autovetor unit´ario dea†_jaj com autovalor 1. Logo,

||aj|ψi||2= (aj|ψi)†(aj|ψi) =hψ|a†jaj|ψi=hψ|ψi= 1,

de onde conclu´ımos que aj|ψi é unitário. Utilizando as RAC, é poss´ıvel ver queajaj = 0, logo (a†_jaj)aj|ψi= 0. Semelhantemente, se|ψifor autovetor unitário dea†jaj com autovalor correspondente 0, então

||aj|ψi||2= (aj|ψi)†(aj|ψi) =hψ|a†jaj|ψi=hψ|0|ψi= 0.

3. Considerando que|ψi´e um autovetor unit´ario com autovalor 0, e utilizando as RAC, temos

||a†_j|ψi||2=hψ|aja†j|ψi=−hψ|a†jaj|ψi+hψ|ψi= 0 +hψ|ψi= 1,

de onde vemos quea†j|ψi´e unit´ario. Utilizando novamente as RAC, temos

||a†j|ψi||2= (a†j|ψi)†(a†j|ψi) =hψ|aja†j|ψi=−hψ|a†jaj|ψi+hψ|ψi=−1 + 1 = 0.

Dizemos que a†_j atua como um “operador cria¸c˜ao” para a†_jaj, enquanto aj atua como um “operador destrui¸c˜ao” para a†jaj.

Os operadoresa†jaj s˜ao autoadjuntos e comutam uns com os outros. Consequentemente, existe um vetor|ψi, autovetor simultˆaneo de todos osa†_jaj. Para cadaj, temosa†jaj|ψi=αj|ψi,em que

αj = 0 ouαj = 1. Aplicando sobre|ψisimultaneamente todos os operadores destrui¸c˜aoajpara os quaisαj= 1, chegamos a um estado|vacital que a†jaj|vaci= 0 para todoj.

Teorema 2.2.Para os operadores fermiˆonicosa1, a2, ..., aN e o vetor|vacidescritos acima, temos:

1. Existe um conjunto de2N _{estados ortonormais que s˜}_{ao simultaneamente autoestados de todos}

osa†_jaj.

2. SejaW o subespa¸co de Hgerado por estes2N _{autoestados. Os operadores}_a

j ea†j deixamW

invariante.

3. Seja W⊥ _{o complemento ortogonal de}_W _em_H_{. Ent˜}_ao _a_j _e _a†

j deixam W⊥ invariante.

As-sim, as restri¸c˜oes destes operadores a W⊥ _{tamb´em satisafzem as rela¸c˜}_{oes de anticomuta¸c˜}_ao

canˆonicas e, consequentemente, tamb´em podemos identificar um subespa¸co de W⊥ _de

(26)

Demonstra¸c˜ao.

1. Para cada vetorφ= (φ1, ..., φN), em queφj= 0 ou 1, definimos o estado

|φi= (a†₁)φ1_...₍_a†

N)φN|vaci.

Fazendo todas as combina¸c˜oes poss´ıveis para os valores dosφj, chegamos ao conjundo dese-jado de 2N _{vetores ortonormais.}

2. Os vetores definidos acima formam a base deW. Basta verificar queaj ea†j levam elementos da base em elementos da base ou no vetor 0. Suponha que φj = 0. Logo,aj|φi= 0 ∈ W. Agora suponha queφj = 1. Sejaφ′ o vetor proveniente de trocar aj-´esima coordenada deφ por 0. Sejasj_φ:=Pj−1

k=1φk. Ent˜ao,

aj|φi=aj(a†1)φ1...(a†N)φN|vaci =(−1)sjφ(a†

1)φ1...(a†j−1)

φj−1_a_j(_a†

j)...(a†N) φN

|vaci

=(−1)sjφ(a†

1)φ1...(aj†−1)φj−1(1−a†jaj)...(a†N)φN|vaci =(−1)sjφ(a†

1)φ1...(a†j−1)φj−1(a†j)0...(a†N)φN|vaci

−(−1)sjφ(a†

1)φ1...(a†j−1)

φj−1₍_a†

jaj)...(a†N) φN

|vaci

=(−1)sjφ|φ′i+ 0 =(−1)sjφ|φ′i ∈ W.

Por racioc´ıcio equivalente, ´e poss´ıvel ver que osa†j mapeiam os elementos da base deW nela mesma ou no vetor 0.

3. Sejam |ϕi ∈ W⊥ _e _|_ψ_{i ∈ W} _{quaisquer. Para verificar que} _a

j mapeia W⊥ nele mesmo, precisamos que o produto interno deaj|ϕicom|ψiseja nulo. De fato,

hψ|aj|ϕi= (a†j|ψi)†|ϕi.

Como o vetor (a†_j|ψi) pertence aW, temos que o produto acima ´e igual a zero, demostrando queaj mapeiaW⊥ nele mesmo. Com o mesmo racioc´ıcio ´e poss´ıvel mostrar que a†j mapeia

W⊥ _{nele mesmo.}

No processo acima nós conseguimos “quebrar” Hcomo uma soma direta de um númerodde subespa¸cos ortogonais W1,W2, ...,Wd, cada um de dimensão 2N. Podemos denotar os elementos

da base deH por |α, ki, em que α∈ {0,1}N_{, e} _k _{= 1}_,₂_{, ...d}_{, de maneira que a a¸c˜}_{ao de}_a j ea†j deixam k invariante, e atuam em |αi da maneira descrita acima. Assim, o espa¸co de Hilbert H

pode ser considerado como um produto tensorialC2N

⊗Cd_{, com a a¸c˜}_{ao de}_a

j ea†j sendo trivial na componenteCd_.

(27)

por exemplo, os orbitais de um átomo. O estado |vacicorresponderia ao estado de “vácuo”, sem nenhum férmion. Aplicando um operadora†_j, “cria-se” um férmion ocupando o modoj. As RAC garantem que haverá no máximo um férmion de um mesmo tipo em cada modo.

´

E importante notar que quando temos um sistema quântico cujo Hamiltoniano é descrito em termos dos operadores de spin das part´ıculas do sistema, ao realizar a transforma¸cão de Jordan-Wigner passamos a considerar um novo sistema, constitu´ıdo por modos fermiônicos. Se algum modo fermiônico estiver ocupado, dizemos que há uma “quasipart´ıcula” fermiônica ocupando tal modo. Dizemos assim ao invés de afirmar que há uma par´ıcula no sistema porque na realidade o sistema original não possui tais part´ıculas fermiônicas, mas possui outro tipo de part´ıculas cujos operadores de spin são importantes no estudo do Hamiltoniano e são mapeados em operadores fermiônicos através da transforma¸cão utilizada.

2.7 Diagonaliza¸c˜

ao de Formas Quadr´

aticas de Operadores

Fermiˆ

onicos

Nesta se¸cão também seguimos a referência [6]. Suponha que {a1, a2, ..., aN} seja um conjunto de operadores fermiônicos e que temos o Hamiltoniano

Hlivre=

N

X

j=1

αja†jaj. (2.48)

´

E f´acil perceber que os vetores |φi = (a†1)φ1...(a†N)φN|vaci, que podem ser representados por

φ= (φ1, ..., φN), formam uma base ortonormal de autovetores de Hlivre. Se αj ≥0 para todoj, comoa†_jaj é semidefinido positivo, temos hψ|H|ψi ≥0 para qualquer estado |ψi, de maneira que a energia do estado fundamental é não negativa. Contudo, de acordo com nossa constru¸cão acima para a base de H, existe um estado |vaci =|0,0, ...,0ipara o qual a†_jaj|vaci= 0 para todo j, e entãoHlivre|vaci= 0, de onde conclu´ımos que a energia do estado fundamental é 0.

A seguir temos um exemplo que nos ajudar´a na compreens˜ao do lema que o segue.

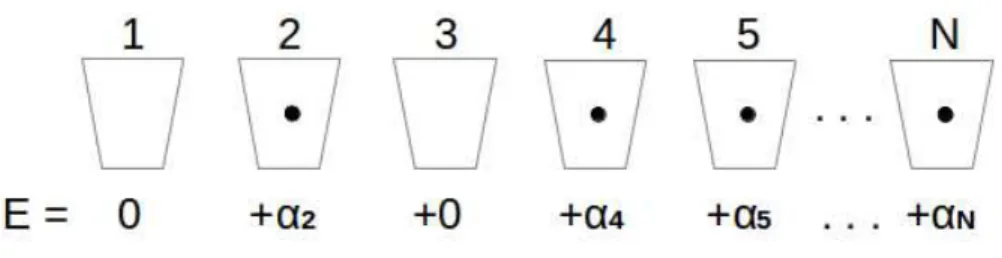
Exemplo 2.4. Consideremos agora o caso em que os αj do Hamiltoniano (2.48) n˜ao

necessari-amente são positivos. Tome, como exemplo, um sistema no estado |φi=|0,1,0,1,1, ...,1i, repre-sentado na figura 2.1. Tal vetor representa um sistema deN modos fermiônicos em que apenas o primeiro e o terceiro modos se encontram vazios, e os modos2,4,5, ..., N se encontram populados por férmions, cujas energias são, respectivamente, α2, α4, α5, ..., αN. Logo, a energia total deste

sistema ´e dada porE=α2+α4+α5+...+αN. Generalizando o exemplo acima, temos o lema:

Lema 2.2. Dado o Hamiltoniano (2.48), a energia do estado fundamental ser´aP

jmin(0, αj), e o

estado fundamental é obtido aplicando simultaneamente os operadores cria¸cão a†_j sobre|vaci, para todoj tal queαj <0. O estado fundamental é não degenerado se, e somente se,αj6= 0, ∀j. Além

(28)

Figura 2.1:Sistema deN modos fermiônicos e sua respectiva energia, em que apenas os modo 1 e 3 estão vazios, enquanto os modos2,4,5, ..., N estão ocupados.

Defini¸cão 2.15. Dizemos que um HamiltonianoH é um “Hamiltoniano Fermi quadrático” se ele puder ser escrito da forma

H = n

X

j,k=1

αjka†jak+ξjkaja†k+βjkajak+θjka†ja†k

, (2.49)

em queαjk, ξjk, βjk eθjk∈C e os operadoresaj s˜ao fermiˆonicos.

Teorema 2.3. Dado um Hamiltoniano Fermi quadr´atico H, existe um conjunto de operadores fermiˆonicos {bj}e coeficientesαj, j= 1, ..., n, em termos dos quaisH pode ser reescrito na forma

H = N

X

j=1

αjb†jbj. (2.50)

Assim, quando reescrevemos um Hamiltoniano no formato acima dizemos que o “diagonaliza-mos”, no sentido que seus autovalores e autovetores podem ser facilmente identificados. A fim de provar este teorema iremos mostrar alguns resultados.

Proposi¸cão 2.5. Dado um Hamiltoniano Fermi quadrático qualquer podemos, a menos de uma constante aditiva+ς1_{, ς}_∈R_{, reescrevê-lo na forma}

H = n

X

j,k=1

αjka†jak−α∗jkaja†k+βjkajak−βjk∗ a†ja†k

, (2.51)

onde αjk = (α)jk são os elementos de α, que é uma matriz hermitiana, e βjk = (β)jk são os

elementos deβ, que ´e uma matriz antissim´etrica.

Por se tratar de um resultado simples, não expomos a demonstra¸cão da proposi¸cão acima nesta disserta¸cão.

Agora, dado o Hamiltoniano (2.51), iremos procurar constantes γjk, µjk ∈C, j, k = 1, ..., n, de forma que os operadores

bj = n

X

k=1

γjkak+µjka†k

, j= 1, ..., n,

satisfa¸cam as rela¸cões de anticomuta¸cão canônicas e que quando H é expresso em termos dosbj,

(29)

Escrevendo as rela¸cões de anticomuta¸cão para osbj, vemos que elas são equivalentes às equa¸cões

γγ†+µµ†=1_, _(2.52)

γµT +µγT = 0, (2.53)

em queγ eµsão as matrizes cujos elementos são (γ)jk=γjk,(µ)jk=µjk. Podemos reescrever a rela¸cão entre osaj e osbj utilizando a matriz em blocos

T :=

"

γ µ

µ∗ _γ∗

#

, (2.54)

em queγ∗_{´e a matriz cujos elementos (}_γ∗_)ij _{s˜ao os complexos conjugados de}_γ_{, i.e. (}_γ∗_)ij _{= (}_γ_ij₎∗_.

O mesmo vale paraµ∗_{. Assim,}

             b1 .. . bn

b†1

.. . b† n              = " γ µ

µ∗ _γ∗

#              a1 .. . an

a†1

.. . a† n              , (2.55)

onde as entradas dos vetores são operadores. As equa¸cões (2.52) e (2.53) são equivalentes a afirmar que a matriz de transforma¸cãoT dada por (2.54) é unitária. Uma vez queT é unitária, podemos escrever os operadoresaj em termos dosbj a partir da rela¸cão

             a1 .. . an

a†1

.. . a† n             

=T†

             b1 .. . bn

b†1

.. . b† n              , (2.56)

de onde temos

h

a†1 · · · a†n a1 · · · an

i

=hb†1 · · · b†n b1 · · · bn

i

T. (2.57)

O nosso HamiltonianoH pode ser reescrito, de acordo com essa nota¸c˜ao, na forma

H =ha†1 · · · a†n a1· · · an

i "

α −β∗

β −α∗

#              a1 .. . an

a†1

(30)

onde (α)jk =αjk e (β)jk=βjk. Para simplificar, denotaremos

[a† a] =ha†1 · · · a†n a1 · · · an

i

, [b† b] =hb1† · · · b†n b1 · · · bn

i

, M =

"

α −β∗

β −α∗

#

.

Assim, temos

H = [a† _a_]_M

"

a a†

#

= [b† _b_]_{T M T}†

"

b b†

#

. (2.59)

Agora, observamos queM é hermitiana e, consequentemente, é diagonalizável e seus autovalores são reais. Ademais, temos:

Lema 2.3. Se v =

"

v1

v2 #

, sendo v1 e v2 n-dimensionais, ´e um autovetor de M com autovalor

correspondenteλ, ent˜ao

" v∗ 2 v∗ 1 #

´e um autovetor deM com autovalor correspondente −λ.

Demonstra¸c˜ao. Sejaλum autovalor deM ev=

"

v1

v2 #

um autovetor correspondente. Logo,

M v=λv⇒

"

α −β∗

β −α∗

# " v1 v2 # =λ " v1 v2 #

⇒ αv1−β

∗_v

2=λv1

βv1−α∗v2=λv2

.

Tomando o complexo conjugado dos dois lados das ´ultimas igualdades, e multiplicando por−1, e depois invertendo a primeira e a segunda linha, chegamos em

αv∗

2−β∗v1∗=−λ∗v2∗

βv∗

2−α∗v1∗=−λ∗v1∗

⇒

"

α −β∗

β −α∗

# " v∗ 2 v∗ 1 #

=−λ∗

" v∗ 2 v∗ 1 # ,

de onde se conclui que−λ∗ _{é um autovalor. Como}_λ_{é real, temos que}₋_λ_{é autovalor de}_M_.

Proposi¸c˜ao 2.6. Existe uma matriz T unit´aria da forma (2.54) que diagonaliza M, ou seja,

T M T† ₌_D_{, em que} _D_{´e uma matriz diagonal.}

Demonstra¸cão. Como consequência do lema anterior, podemos encontrar uma matriz T unitária tal que

T M T† =D=

"

d 0

0 −d

#

,

em que D ´e um bloco de matrizes, e d e −d s˜ao matrizes diagonais contendo os autovalores

d1, ..., dn e −d1, ...,−dn de H, respectivamente. Para isso, é necessário que a j-ésima coluna de

T† _{seja o autovetor correspondente ao autovalor que se encontra na} _j_{-´esima coluna de}_D_{. Assim,}

se v1 = "

v11

v12 #

, v2 = "

v21

v22 #

, ..., vn =

"

vn1

vn2 #

s˜ao autovetores correspondentes aos

autova-lores d1, d2, ..., dn, ent˜ao pelo lema anterior u1 = " v∗ 12 v∗ 11 #

, u2 = " v∗ 22 v∗ 21 #

, ..., un =

" v∗ n2 v∗ n1 # s˜ao

autovetores correspondentes aos autovalores−d1,−d2, ...,−dn e temos

T†_{= [}_v

1, ..., vn, u1, ..., un] = "

v11 · · · vn1 v12∗ · · · v∗n2

v12 · · · vn2 v11∗ · · · v∗n1 #

(31)

Definimos, agora, as matrizesγ eµtais que

γ†= [v11 · · · vn1], µ† = [v12 · · · vn2],

de forma que

T† =

"

γ† _µT

µ† _γT

#

⇒T=

"

γ µ

µ∗ _γ∗

#

.

Assim, encontramos uma matrizT unitária que satisfaz as condi¸cões necessárias para que os ope-radoresbj sejam fermiônicos e, além disso, quandoH é expresso em termos dosbj, temos:

H = [b†b]T M T†

"

b b†

#

= [b†b]D

"

b b†

#

= n

X

j=1

b†_jdjbj−bjdjb†j.

Como consequência das rela¸cões de anticomuta¸cão que osbj obedecem, podemos escrever:

H = n

X

j=1

djb†jbj+djb†jbj−dj1=r1+ n

X

j=1

2djb†jbj,

onder=−Pn

j=1dj.

Logo, a menos de um fator aditivo +(ς+r)1_{, quando}_H_{´e expresso na forma (2.49), conseguimos}

(32)

O Modelo XY

O modelo XY unidimensional em um campo magnético transverso, o qual estudaremos neste cap´ıtulo, é um modelo rico mas que pode ser diagonalizado exatamente. Devido a isso, ele tem sido estudado intensamente ao longo dos anos e utilizado para compreender o comportamento universal de sistemas de pequenas dimensões. Nos últimos anos o interesse neste modelo foi renovado pelo fato de que realiza¸cões laboratoriais deste sistema estão progredindo[12]. Lieb, Schultz e Mattis [7] diagonalizaram o Hamiltoniano do modelo utilizando, pela primeira vez, o método descrito no cap´ıtulo anterior.

Apesar da simplicidade do modelo XY transverso unidimensional, ele possui um diagrama de fase que depende do parâmetro de “anisotropia” γ e do campo magnético externo B, e é caracterizado por duas transi¸cões de fase. Seu Hamiltoniano, atuando no espa¸co de N spins-1

2,

pode ser escrito como:

H = J 2

N

X

j=1

1 +γ

2

σxjσjx+1+

1−γ

2

σyjσ y

j+1+Bσjz

, (3.1)

ondeσα

j, α=x, y, z, são os operadores de Pauli dados pela rela¸cão (2.28) e no qual consideramos condi¸cões periódicas de contorno, fazendo σα

j+N = σjα, α = x, y, z. Este Hamiltoniano descreve um sistema de spins magnéticos com intera¸cões entre vizinhos com constantes de acoplamento distintas ao longo das dire¸cõesxey, submetido a um campo magnético de móduloB ao longo da dire¸cãoz. Se tivermos J <0,−1≤γ ≤1, este Hamiltoniano modela um sistema ferromagnético, em que as componentes nas dire¸cões x e y dos spins vizinhos tendem a se alinhar no mesmo sentido para minimizar a energia. Por outro lado, seJ >0,−1≤γ≤1, o sistema pode ter uma fase antiferromagnética, em que os spins vizinhos tendem a se alinhar em sentidos opostos para minimizar a energia.

Observe no Hamiltoniano (3.1) que seγ= 0 o acoplamento dos spins na dire¸cãoxeypossuem a mesma intensidade, enquanto não há acoplamento na dire¸cãoz. Chamamos esse caso particular do modelo XY de “modelo XX”. Por outro lado, se fizermos γ = 1, o acoplamento na dire¸cãoy

desaparece, restando apenas na dire¸cãox. Esse caso particular é conhecido como “modelo de Ising transverso”. Um número considerável de sistemas de matéria condensada pode ser modelado pelo

(33)

modelo de Ising transverso [12], o qual é o modelo mais simples que apresenta uma transi¸cão de fase quântica à temperatura nula.

Neste trabalho considera-se os parâmetrosγ eB como sendo adimensionais e, como o foco é o caso ferromagnético, toma-seJ =−1. Assim, nos restringimos ao Hamiltoniano

H =−1

2 N

X

j=1

_{1 +}_γ

2

σx jσjx+1+

₁

−γ

2

σy_jσ_jy₊₁+Bσz j

(3.2)

no caso em que γ ≥ 0 e B ≥ 0, embora nos outros casos o Hamiltoniano também possa ser diagonalizado. Uma das transi¸cões de fase ocorre no ponto cr´ıtico B = 1 e é uma transi¸cão de uma fase ferromagnética (B < 1) para uma fase paramagnética (B > 1). A outra transi¸cão de fase ocorre quandoγ = 0 (veja mais detalhes em [5]). As correla¸cões entre pares de s´ıtios foram calculadas no trabalho de McCoyet al [13].

A seguir, iremos diagonalizar o Hamiltoniano (3.2) e, no fim do cap´ıtulo, também iremos obter algumas propriedades termodinâmicas do modelo. Neste cap´ıtulo seguimos a referência [5] para efetuar a diagonaliza¸cão do Hamiltoniano. Porém, a se¸cão de propriedades termodinâmicas foi basicamente desenvolvida pelo autor da disserta¸cão.

3.1 Diagonaliza¸c˜

ao Exata

Proposi¸cão 3.1. Se H é um Hamiltoniano do modelo XY ferromagnético dado por (3.2) atu-ando no espa¸co de HilbertH, existem operadores fermiônicos aj, j = 1,· · ·, N, e dois subespa¸cos

ortogonais entre si, e que geram todo oH, nos quais o Hamiltoniano atua segundo os operadores abaixo

H±=−1

2 N

X

j=1

a†_jaj+1+a†j+1aj+γa†ja†j+1+γaj+1aj−2Ba†jaj

−BN

2 , (3.3)

onde H+ _{´e definido com condi¸c˜}_{oes de contorno antiperi´}_{odicas sobre os operadores fermiˆ}_onicos,

aj+N =−aj, enquantoH− com condi¸c˜oes de contorno peri´odicas, aj+N =aj.

Este é um resultado importante pois, uma vez que escrevemos o Hamiltoniano numa forma quadrática de operadores fermiônicos em cada um dos subespa¸cos, de acordo com os resultados da se¸cão 2.7, podemos diagonalizá-lo.

Demonstra¸cão. Podemos utilizar as rela¸cões (2.30), (2.31) e (2.32) para reescrever o Hamiltoniano em fun¸cão dos operadores de abaixamento e levantamento:

H =−1₂

N

X

j=1 "

_{1 +}_γ

2

(σ+_j +σ−_j )(σ+_j₊₁+σ_j−₊₁) +

₁

−γ

2

_σ+

j −σj−

i

!

σ_j+₊₁−σ_j−₊₁ i

!

+B(2σ+jσ−j −1)

#

=−1

2 N

X

j=1

(σ+_jσ−_j₊₁+σ_j−σ_j+₊₁) +γ(σ+_jσ+_j₊₁+σ−_jσ_j−₊₁) + 2Bσ+_jσ−_j −B

(34)

Para reescrever o Hamiltoniano acima em fun¸cão de operadores fermiônicos, utilizamos a trans-forma¸cão de Jordan-Wigner (ver defini¸cão 2.14) e definimos o operador

µN := N

Y

l=1

σlz= N

Y

l=1

1−2a†lal

. (3.5)

Assim, obtemos as seguintes rela¸c˜oes, v´alidas paraj= 1,2, ..., N−1:

σ_j+σ_j−₊₁=a†_j₊₁aj, (3.6a)

σj−σ+j+1=a†jaj+1, (3.6b)

σj+σj++1=aj+1aj, (3.6c)

σj−σ−j+1=a†ja†j+1, (3.6d)

σ_N+σ₁−=σz

NσN+σ1−=µNaNa†1=−µNa†1aN, (3.6e)

σ_N−σ₁+=−σz Nσ−Nσ

+

1 =−σNza†N

Y

l<N

σz l

!

a1=−µNa†Na1, (3.6f)

σ_N+σ1+=σNzσN+σ

+

1 =µNaNa1=−µNa1aN, (3.6g)

σ_N−σ1−=−σNzσ−Nσ−1 =−µNa†_Na†1. (3.6h)

A rela¸cão abaixo também é necessária, e é válida paraj= 1,2, ..., N:

σ+_jσ−_j =ajaj† =1−a†jaj, (3.7)

Utilizando as express˜oes anteriores, que relacionam os operadores fermiˆonicos com operadores de levantamento e abaixamento, e substituindo os termos no Hamiltoniano (3.4), chegamos a:

H =−1

2 N−1

X

j=1

a†_jaj+1+a†j+1aj+γa†ja†j+1+γaj+1aj

+µN 2

a†_Na1+a†1aN +γa†_Na†1+γa1aN

+B

N

X

j=1

a†jaj−BN

2 , (3.8)

ondeµN é o observável cujos autovalores (+1 e −1) fornecem a “paridade” do número de quasi-part´ıculas fermiônicas no sistema. O operador abaixo pode ser interpretado como um observável que conta o número de férmions do sistema:

NN := N

X

l=1

a†_lal

. (3.9)

´

E poss´ıvel mostrar que, em geral, [H, NN]6= 0. Isso significa que o Hamiltoniano não conserva o número de férmions do sistema (ver equa¸cões (2.18) e (2.19)). Por outro lado [H, µN] = 0, o que implica que a paridade do número de férmions é conservada, isto é, férmions são criados/destru´ıdos em pares. Assim sendo, podemos considerar dois subespa¸cos poss´ıveis para o sistema, correspon-dentes aos autovalores +1 e −1 de µN. Sejam P+ e P− os projetores que atuam no espa¸co de

(35)

em mente que o Hamiltoniano conserva a paridade e comuta comP+ eP−, temos

H =1_H1_{= (}_P₊₊_P₋₎_H₍_P₊₊_P₋_{) =}_P₊_HP₊₊_P₋_HP₋₊_P₊_HP₋₊_P₋_HP₊

=P+HP++P−HP−=HP++HP−=H+P++H−P−, (3.10)

em queH+ _{descreve a atua¸c˜}_{ao do Hamiltoniano no subespa¸co onde}_P

+ projeta, enquantoH− no

subespa¸co ondeP₋projeta. Logo, podemos simplesmente nos restringir ao estudo deH nesses dois subespa¸cos. Definimos agora condi¸cões de contorno antiperiódicas para os férmions para o caso em que o autovalor de µN for +1, i.e, aj+N = −aj. Inversamente, para o autovalor −1, definimos condi¸cões de contorno periódicasaj+N =aj. Assim, para ambos os casos, chegamos a:

H±=−1₂

N

X

j=1

a†jaj+1+a†j+1aj+γa†ja†j+1+γaj+1aj−2Ba†jaj

−BN₂ . (3.11)

3.1.1 N´

umero Par de Quasipart´ıculas

Teorema 3.1. Seja H+ _{o operador dado por (3.11). Existem constantes} _c _e _α

q e operadores

χq, q= 0,· · · , N−1, tais que:

{χq, χk}= 0,

{χ†

q, χk}=δq,k1,

tais que

H+= N−1

X

q=0

αq χ†qχq−c. (3.12)

Uma consequência direta deste teorema é que essa expressão paraH+ _{nos permitirá}

identifi-car todas suas autoenergias, bem como todos os autoestados, conforme mostrado no exemplo 2.4 e no lema 2.2, no in´ıcio da se¸cão 2.7. O mesmo será feito com H−_{, o que nos permitirá}

diago-nalizar H como um todo e obter a fun¸cão de parti¸cão do sistema a partir da equa¸cão (2.35) e, consequentemente, extrair várias informa¸cões termodinâmicas deste modelo.

Demonstra¸cão. ParaµN = +1, como temos condi¸cões de contorno antiperiódicas, realizamos uma transformada discreta de Fourier antiperiódica:

ˆ

aq =e

−iπ/4

√

N

X

j=1

e−i2Nπ(q+

1 2)ja

j, q= 0,1,· · · , N−1, (3.13a)

aj =

eiπ/4

√

N

N−1 X

q=0

ei2Nπ(q+

1 2)jˆa

q, j= 1,· · ·, N. (3.13b)

Estes novos operadores satisfazem as seguintes rela¸c˜oes de anticomuta¸c˜ao:

{ˆaq,ˆak}= 0, (3.14a)

(36)

Vamos, agora, escrever o HamiltonianoH+ _{em termos destes novos operadores. Substituindo os}

operadores ˆaq na soma abaixo, temos:

N

X

j=1

a†_jaj+1=

N

X

j=1

1

N

N−1 X

q=0

e−i2Nπ(q+

1 2)jˆa†

q N−1

X

k=0

ei2Nπ(k+

1 2)(j+1)aˆ

k

= 1

N

N−1 X

k=0

ei2Nπ(k+

1 2)

N−1 X

q=0

ˆ

a†qˆak N

X

j=1

ei2Nπ(k−q)j. (3.15)

A fim de simplificar o resultado acima, considerew∈C_{e a soma}

SN =w+w2+· · ·+wN,

de forma que, sew6= 1, vale:

SN =

w−wN+1

1−w . (3.16)

Portanto, sew6= 1 ewN _{= 1 teremos} _S

N = 0. Por outro lado, se w= 1 temosSN =N. Assim, podemos escrever

N

X

j=1

a†jaj+1= 1

N

N−1 X

k=0

ei2Nπ(k+

1 2)

N−1 X

q=0

ˆ

a†qˆakN δq,k= N−1

X

k=0

ei2Nπ(k+

1 2)ˆa†

kˆak. (3.17a)

Semelhantemente,

N

X

j=1

a†_j₊₁aj = N−1

X

k=0

e−i2Nπ(k+

1 2)ˆa†

kˆak, (3.17b)

N

X

j=1

a†jaj = N−1

X

k=0

ˆ

a†_kˆak, (3.17c)

N

X

j=1

a†_ja†_j₊₁=−i

N−1 X

k=0

ei2Nπ(k+

1 2)ˆa†

kˆa†−k−1, (3.17d)

N

X

j=1

aj+1aj =i N−1

X

k=0

ei2Nπ(k+

1 2)ˆa

kaˆ−k−1. (3.17e)

Substituindo os termos acima no HamiltonianoH+ _{dado por (3.11), chegamos em:}

H+ = N−1

X

q=0

B−cos

2π N

q+1 2

ˆ

a†qˆaq+γ 2

N−1 X

q=0

−iei2Nπ(q+

1 2)[ˆaqˆa

−q−1+ ˆa†₋q−1ˆa†q]−

BN

2 . (3.18)

Por´em, temos as rela¸c˜oes:

−iei2Nπ(q+

1

2)=−icos ₂_π

N

q+1 2 + sin ₂_π N

q+1 2 , cos 2π N

q+1 2

ˆ

aqˆaN−q−1+ cos

2π N

N−q−1 +1 2

ˆ