Estimação clássica e Bayesiana em modelos de sobrevida com fração de cura

(1)

Universidade Federal do Rio Grande do Norte

Centro de Ciˆencias Exatas e da Terra

Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica

Josemir Ramos de Almeida

Estima¸c˜

ao Cl´

assica e Bayesiana em Modelos de

Sobrevida com Fra¸c˜

ao de Cura

(2)

Josemir Ramos de Almeida

Estima¸c˜

ao Cl´

assica e Bayesiana em Modelos de

Sobrevida com Fra¸c˜

ao de Cura

Disserta¸cão apresentada ao Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica da Universidade Federal do Rio Grande do Norte, em cumprimento com as exigências legais para obten¸cão do t´ıtulo de Mestre.

´

Area de Concentra¸c˜ao: Probabilidade e Estat´ıstica

Orientador:

Prof. Dr. Bernardo Borba de Andrade

Co-orientador:

Prof. Dr. Heleno Bolfarine

(3)

Catalogação da Publicação na Fonte. UFRN / SISBI / Biblioteca Setorial Centro de Ciências Exatas e da Terra – CCET.

Almeida, Josemir Ramos de.

Estimação clássica e bayesiana em modelos de sobrevida com fração de cura / Josemir Ramos de Almeida. - Natal, 2013.

86 f. il.:

Orientador: Prof. Dr. Bernardo Borba de Andrade. Co-orientador: Prof. Dr. Heleno Bolfarine.

Dissertação (Mestrado) – Universidade Federal do Rio Grande do Norte. Centro de Ciências Exatas e da Terra. Programa de Pós-Graduação em Matemática Aplicada e Estatística.

1. Análise de sobrevivência – Dissertação. 2. Modelos de longa duração – Dissertação. 3. Método de Laplace – Dissertação. 4. Método de Monte Carlo – Dissertação. 5. Cadeias de Markov – Dissertação. I. Andrade, Bernardo Borba de. II. Bolfarine, Heleno. III. Título.

(4)

(5)

Dedicat´

oria

Aos meus pais Maria de Lourdes R. de Almeida e Josafá P. de Almeida pela forma¸cão de caráter que eles me proporcionaram, pois sem eles não teria alcan¸cado meus objetivos pessoais e profissionais.

A minha irm˜a Mercicleide R. de Almeida, pela for¸ca, apoio e incentivo.

A minha noiva Elisˆangela da S. Rodrigues, pelo companheirismo e paciˆencia de estar ao meu lado todos esses anos.

Aos meus av´os maternos,in memoriam, Corina M. de Oliveira e Jeov´a R. de Oliveira.

(6)

Agradecimentos

A Deus, pois sem ele n˜ao faria sentido a existˆencia.

Aos meus pais, pelo apoio de todas as horas.

A minha irm˜a, pela for¸ca e incentivo.

A minha noiva, pelo companheirismo, dedica¸c˜ao e paciˆencia.

Aos professores Bernardo B. de Andrade e Heleno Bolfarine pelo conhecimento a mim oferecido, pela oportunidade de poder trabalhar com eles e pela paciˆencia e dedica¸c˜ao ao me orientar.

A banca examinadora pelo aceite do convite em avaliar este trabalho de dis-serta¸c˜ao, bem como pelas sugest˜oes e cr´ıticas que foram de grande valia para o aperfei¸coamento do mesmo.

Aos professores do PPGMAE, a citar: Carla Vivacqua, Pledson Guedes, Andr´e Pinho, D´ebora Borges e Nir Cohen.

A todos os colegas de mestrado do PPGMAE.

Aos meus professores de gradua¸cão da Universidade Federal da Para´ıba (UFPB), pois de forma direta e indireta foi devido ao conhecimento dos mesmos que fui capaz de trilhar o caminho até o mestrado. Em particular ao professor Dr. Eufrásio de A. Lima Neto.

(7)

Resumo

Em Análise de Sobrevivência, os modelos de longa dura¸cão permitem a es-tima¸cão da fra¸cão de cura, que representa uma parcela da popula¸cão imune ao evento de interesse. No referido trabalho abordamos os enfoques clássico e Bayesiano com base nos modelos de mistura padrão e de tempo de promo¸cão, utilizando diferentes distribui¸cões (exponencial, Weibull e Pareto) para modelar os tempos de falhas. A base de dados utilizada para ilustrar as implementa¸cões é descrita em Kersey et al. (1987) e consiste em um grupo de pacientes com leucemia que foram submetidos a um certo tipo de transplante. As implementa¸cões espec´ıficas utilizadas foram de otimiza¸cão numérica por BFGS implementado em R (base::optim), aproxima¸cão de Laplace (implementa¸cão própria) e o amostrador de Gibbs implementado no Open-Bugs. Descrevemos as principais caracter´ısticas dos modelos utilizados, os métodos de estima¸cão e os aspectos computacionais. Também discutimos como diferentes prioris podem afetar nas estimativas Bayesianas.

(8)

Abstract

In Survival Analysis, long duration models allow for the estimation of the he-aling fraction, which represents a portion of the population immune to the event of interest. Here we address classical and Bayesian estimation based on mixture models and promotion time models, using different distributions (exponential, Weibull and Pareto) to model failure time. The database used to illustrate the implementations is described in Kersey et al. (1987) and it consists of a group of leukemia patients who underwent a certain type of transplant. The specific implementations used were numeric optimization by BFGS as implemented in R (base::optim), Laplace appro-ximation (own implementation) and Gibbs sampling as implemented in Winbugs. We describe the main features of the models used, the estimation methods and the computational aspects. We also discuss how different prior information can affect the Bayesian estimates.

(9)

Lista de Figuras

2.1 Formas da densidade da Pareto(p;k). . . 22

2.2 Formas da densidade da Weibull(γ;α).. . . 23

5.1 Gráficos das estimativas das sobrevivências estimadas por Kaplan-Meier versus as sobrevivências estimadas pelos modelos exponencial, Weibull e Pareto. . . 47

5.2 Curvas de sobrevivˆencia estimadas por Kaplan-Meier versus as sobre-vivˆencias estimadas pelos modelos exponencial, Weibull e Pareto. . . 47

5.3 Densidades a priori, a posteriori e verossimilhan¸ca perfilada dadas as especifica¸c˜oes 1), 2) e 3), respectivamente, para o MMPexp. . . 50

5.4 Histórico das itera¸cões dadas as especifica¸cões 1), 2) e 3), respectiva-mente, para o MMPexp. . . 51

5.5 Autocorrela¸cões das itera¸cões dadas as especifica¸cões 1), 2) e 3), res-pectivamente, para o MMPexp. . . 51

5.6 Densidades a priori, a posteriori e verossimilhan¸ca perfilada dadas as especifica¸c˜oes 1), 2) e 3), respectivamente (por linha), para o MTPexp. 54

5.7 Histórico das itera¸cões dadas as especifica¸cões 1), 2) e 3), respectiva-mente, para o MTPexp. . . 55

5.8 Autocorrela¸cões das itera¸cões dadas as especifica¸cões 1), 2) e 3), res-pectivamente, para o MTPexp. . . 55

5.9 Curvas de sobrevivência dos modelos de mistura padrão e tempo de promo¸cão exponencial. . . 55

(10)

9

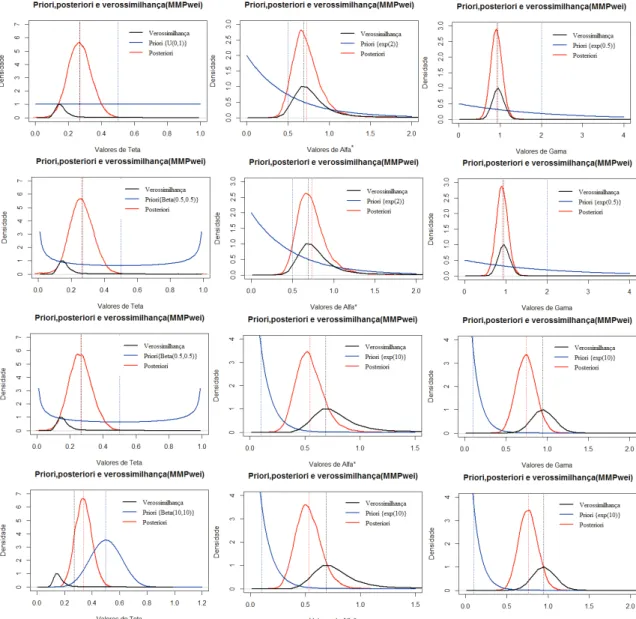
5.11 Histórico das itera¸cões dadas as especifica¸cões 1), 2) (superior), 3) e 4) (inferior), respectivamente, para o MMPwei. . . 59

5.12 Autocorrela¸cões das itera¸cões dadas as especifica¸cões 1), 2) (superior), 3) e 4) (inferior), respectivamente, para o MMPwei. . . 59

5.13 Densidades a priori, a posteriori e verossimilhan¸ca perfilada dadas as especifica¸c˜oes 1), 2), 3) e 4), respectivamente (por linha), para o MTPwei. . . 62

5.14 Histórico das itera¸cões dadas as especifica¸cões 1), 2) (superior), 3) e 4) (inferior), respectivamente, para o MTPwei. . . 63

5.15 Autocorrela¸cões das itera¸cões dadas as especifica¸cões 1), 2), 3) e 4) (por coluna), respectivamente, para o MTPwei. . . 63

5.16 Curvas de sobrevivência dos modelos de mistura padrão e tempo de promo¸cão Weibull. . . 64

5.17 Densidades a priori, a posteriori e verossimilhan¸ca perfilada dadas as especifica¸c˜oes 1), 2) e 3), respectivamente (por linha), para o MMPpar. 66

5.18 Histórico das itera¸cões dadas as especifica¸cões 1), 2) e 3), respectiva-mente (por coluna), para o MMPpar. . . 67

5.19 Autocorrela¸cões das itera¸cões dadas as especifica¸cões 1), 2) e 3), res-pectivamente (por coluna), para o MMPpar. . . 68

5.20 Densidades a priori, a posteriori e verossimilhan¸ca perfilada dadas as especifica¸c˜oes 1), 2) e 3), respectivamente (por linha), para o MTPpar. 71

5.21 Histórico das itera¸cões dadas as especifica¸cões 1), 2) (superiores) e 3) (inferior), respectivamente, para o MTPpar. . . 72

5.22 Autocorrela¸cões das itera¸cões dadas as especifica¸cões 1), 2) e 3), res-pectivamente (por coluna), para o MTPpar. . . 72

(11)

Lista de Tabelas

5.1 Estimativas dos parˆametros para o MMPexp. . . 49

5.2 Estimativas dos parˆametros para o MTPexp. . . 52

5.3 Estimativas dos parˆametros para o MMPwei. . . 57

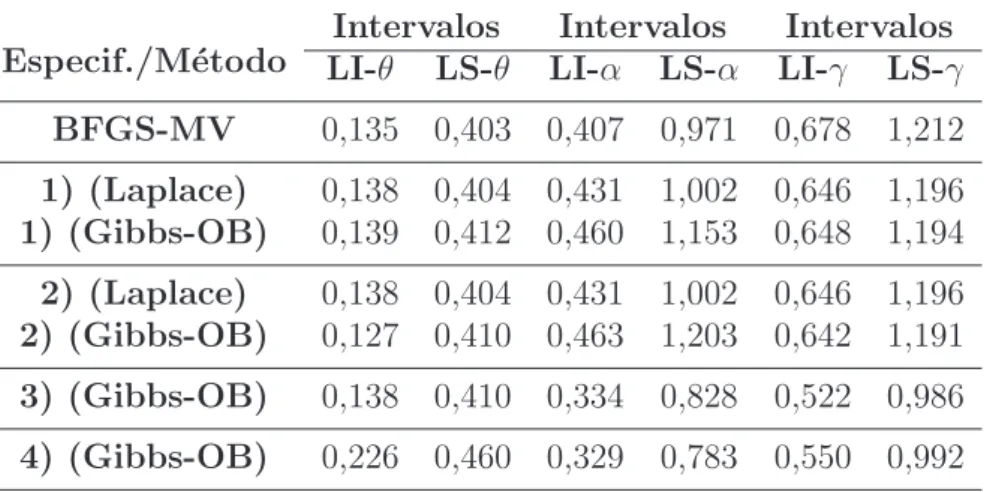
5.4 Intervalos das estimativas dos parˆametros para o MMPwei. . . 57

5.5 Estimativas dos parˆametros para o MTPwei. . . 61

5.6 Intervalos das estimativas dos parˆametros para o MTPwei. . . 61

5.7 Estimativas dos parˆametros para o MMPpar. . . 66

5.8 intervalos das estimativas dos parˆametros para o MMPpar. . . 67

5.9 Estimativas dos parˆametros para o MTPpar. . . 70

(12)

Conte´

udo

1 Introdu¸c˜ao 14

1.1 Revis˜ao Bibliogr´afica . . . 14

1.2 Objetivos . . . 16

2 Conceitos Básicos em Análise de Sobrevivência 18 2.1 Introdu¸cão . . . 18

2.2 Fun¸c˜ao de Sobrevivˆencia . . . 19

2.3 Estimador de Kaplan-Meier . . . 20

2.4 Distribui¸c˜oes Probabil´ısticas . . . 21

2.4.1 Distribui¸c˜ao Pareto . . . 21

2.4.2 Distribui¸c˜ao Weibull . . . 22

2.4.3 Distribui¸c˜ao Exponencial . . . 23

3 Modelos de Longa Dura¸c˜ao 24 3.1 Introdu¸c˜ao . . . 24

3.2 Modelo de Mistura Padr˜ao (MMP) . . . 24

3.2.1 Modelo de Mistura Padr˜ao Exponencial (MMPexp) . . . 26

3.2.2 Modelo de Mistura Padr˜ao Pareto (MMPpar) . . . 26

3.2.3 Modelo de Mistura Padr˜ao Weibull (MMPwei) . . . 27

3.3 Modelo de Tempo de Promo¸c˜ao (MTP) . . . 27

3.3.1 Modelo de Tempo de Promo¸c˜ao Exponencial (MTPexp) . . . 30

(13)

12

3.3.3 Modelo de Tempo de Promo¸c˜ao Weibull (MTPwei) . . . 31

4 Métodos de Estima¸cão 33 4.1 Inferência Clássica . . . 33

4.1.1 Verossimilhan¸ca Perfilada . . . 34

4.2 Inferˆencia Bayesiana . . . 34

4.2.1 Teorema de Bayes . . . 35

4.2.2 Est´agios da Inferˆencia Bayesiana . . . 35

4.2.3 Distribui¸c˜oes de Probabilidade a Priori . . . 36

4.2.4 Distribui¸c˜ao de Probabilidade a Posteriori . . . 38

4.3 M´etodo de Laplace . . . 40

4.4 Métodos de Simula¸cão Estocástica . . . 42

4.4.1 Cadeias de Markov . . . 42

4.4.2 Diagn´ostico de Convergˆencia . . . 43

4.4.3 Amostrador de Gibbs . . . 43

5 Aplica¸c˜ao 45 5.1 Introdu¸c˜ao . . . 45

5.1.1 An´alise Convencional . . . 45

5.2 Diferentes modelos de fra¸c˜ao de cura . . . 48

5.2.1 Modelo de mistura padr˜ao exponencial (MMPexp) . . . 48

5.2.2 Modelo de tempo de promo¸c˜ao exponencial (MTPexp) . . . 52

5.2.3 Modelo de mistura padr˜ao Weibull (MMPwei) . . . 56

5.2.4 Modelo de tempo de promo¸c˜ao Weibull (MTPwei) . . . 60

5.2.5 Modelo de mistura padr˜ao Pareto (MMPpar) . . . 65

5.2.6 Modelo de tempo de promo¸c˜ao Pareto (MTPpar) . . . 69

6 Considera¸c˜oes Finais 74 6.1 Conclus˜oes . . . 74

(14)

13

A 79

A.1 M´etodo de Laplace . . . 79

A.2 Modelos de mistura padr˜ao . . . 81

A.2.1 Modelo de Mistura Padr˜ao Exponencial (MMPexp) . . . 81

A.2.2 Modelo de Mistura Padr˜ao Pareto (MMPpar) . . . 82

A.2.3 Modelo de Mistura Padr˜ao Weibull (MMPwei) . . . 83

A.3 Modelos de tempo de promo¸c˜ao . . . 84

A.3.1 Modelo de Tempo de Promo¸c˜ao Exponencial (MTPexp) . . . 84

A.3.2 Modelo de Tempo de Promo¸c˜ao Pareto (MTPpar) . . . 85

(15)

Cap´ıtulo 1

Introdu¸c˜

ao

Dados relacionados à sobrevivência de indiv´ıduos submetidos a certo trata-mento comumente envolvem um grupo de curados. Muitos dos modelos considerados na literatura não levam em conta tal caracter´ıstica, deixando portanto de explorar toda a informa¸cão contida nos dados. Este é o caso do modelo de Cox e do modelo de tempo de falha acelerado.

A análise de sobrevivência possui aplica¸cão na maioria das áreas do conhe-cimento, no entanto a área médica é a que mais se destaca, tanto pela aplica¸cão quanto pela necessidade cada vez maior de métodos estat´ısticos que permitam uma análise adequada dos dados.

1.1 Revis˜

ao Bibliogr´

afica

A incorpora¸cão de um componente de cura nos modelos de sobrevivência já vem sendo estudado, desde o final dos anos 40, com os trabalhos de Boag (1949) e Berkson e Gage (1952). Os autores trabalharam sobre o problema de estimar a propor¸cão de indiv´ıduos curados de câncer. Nesta se¸cão, traremos algumas contri-bui¸cões em diversas áreas do conhecimento que seguiram a mesma proposta dos autores.

(16)

1.1 Revis˜ao Bibliogr´afica 15

Com o objetivo de estimar a propor¸cão de curados de um conjunto de da-dos composto por 2682 pacientes acometida-dos de câncer do estômago, e utilizando o método de m´ınimos quadrados, Berkson e Gage (1952) utilizaram um modelo com-posto por uma combina¸cão de duas distribui¸cões, uma distribui¸cão exponencial e uma distribui¸cão degenerada. Com este modelo, os autores obtiveram sucesso no ajuste de outras bases de dados, como por exemplo, nos dados utilizados no estudo de Boag (1949).

Maller e Zhou (1996) fazem uma introdu¸cão a análise de dados de sobre-vivência, com ênfase em popula¸cões que apresentam indiv´ıduos “imunes”ao evento de interesse. O livro traz outras abordagens como por exemplo, formula¸cão de testes para a presen¸ca de imunes, propriedades do estimador de Kaplan-Meier, estima¸cão não paramétrica, modelos paramétricos para uma amostra, propriedades para gran-des amostras em modelos com covariáveis, entre outros temas.

Yakovlev e Tsodikov (1996), discutem pesquisas desenvolvidas e métodos de inferência com significado biológico a respeito de latência de câncer. O material oferece novas abordagens na descri¸cão estocástica do estudo do câncer, utilizando dados de recorrência do tumor. Nos últimos cap´ıtulos os autores abordam modelos de sobrevida com fra¸cão de curados, bem como a escolha do tratamento mais adequado, baseando-se em informa¸cões de covariáveis, além de inúmeras aplica¸cões em estudos reais.

Tsodikov (1998) apresenta o modelo de mistura padrão e tempo de promo¸cão, bem como um modelo de riscos proporcionais para dados de sobrevivência de longa dura¸cão. Apresenta também os métodos de estima¸cão via máxima verossimilhan¸ca parcial e marginal. Segundo o autor, os métodos de estima¸cão são equivalentes para o modelo de risco proporcional com fra¸cão de cura. Além disso, traz uma com-para¸cão da eficiência assintótica dos dois métodos de estima¸cão, e por fim sugere um algor´ıtimo para o ajuste do modelo de riscos proporcionais com fra¸cão de cura.

Chen et al. (1999) abordam métodos Bayesianos para dados de sobrevida com fra¸cão de cura. Propõem um modelo que difere do modelo de mistura padrão com uma estrutura de riscos proporcionais na presen¸ca de covariáveis. Estabele-cem rela¸cões matemáticas com o modelo de mistura padrão convencional, como por exemplo, apresentam uma fun¸cão própria de sobrevivência para os não curados. Por fim, fazem uma aplica¸cão a dados de melanoma.

(17)

pa-1.2 Objetivos 16

ramétricos e semi paramétricos, modelos de riscos proporcionais, modelos com fra-gilidade, modelos de longa dura¸cão, modelos de tempo de falha acelerado, modelos hierárquicos de sobrevivência, entre outros. Na abordagem Bayesiana os autores discutem especifica¸cões de prioris informativas e não informativas, distribui¸cões a posteriori, testes de hipóteses Bayesianos, métodos MCMC, entre outros.

Peng et al. (2001) fazem um estudo de simula¸cão para testar a presen¸ca de pacientes curados em dados de sobrevivência de longo prazo. Utilizam máxima ve-rossimilhan¸ca para o modelo de mistura padrão gama com dados de leucemia.

Chen et al. (2002) tratam de modelos de longa dura¸cão paramétricos e semi-paramétricos e propõem abordagens Bayesianas. Realizam uma aplica¸cão com dados cl´ınicos de melanoma conduzido pelo Eastern Cooperative Oncology Group.

Sinha et al. (2003) estudam um modelo de dois estágios para o desenvolvimento do câncer com um estrutura de riscos proporcionais na presen¸ca de covariáveis se-gundo uma abordagem Bayesiana. Trazem rela¸cões matemáticas do modelo proposto com os já existentes na literatura. Utilizam métodos MCMC para amostrar da distri-bui¸cão a posteriori dos parâmetros. Utilizam uma classe de prioris não informativas e destacam que o modelo proposto é flex´ıvel tanto para uma modelagem Bayesiana paramétrica como para uma modelagem semiparamétrica, bem como sua exten¸cão multivariada.

Rodrigues et al. (2008) propõem uma nova abordagem que unifica os modelos de sobrevivência usuais com os modelos de longa dura¸cão. O objetivo é fazer um estudo das teorias frequentista e Bayesiana, dada a inclusão de um cenário de riscos competitivos.

Existem inúmeras referências a respeito dos modelos de longa dura¸cão, no entanto, faremos uso apenas das expostas acima.

1.2 Objetivos

Os modelos que apresentam um componente de cura s˜ao conhecidos como

modelos de longa dura¸cão oumodelos com fra¸cão de cura. O tema de estudo surgiu com o objetivo de explorar os modelos de sobrevivência que tratam a presen¸ca de indiv´ıduos que, mesmo com a doen¸ca, após submetidos a algum tipo de tratamento passam a se caracterizar como indiv´ıduos não sucept´ıveis ao evento de interesse.

A proposta deste trabalho ´e estudar esses tipos de modelos, em particular os

(18)

1.2 Objetivos 17

propostos por Boag (1949) e Berkson e Gage (1952), conhecidos como modelos de mistura padrão e o modelo proposto por Yakovlev e Tsodikov (1996), conhecido como modelos de tempo de promo¸cão, e fazer uma discussão entre as abordagens clássica e Bayesiana para o ajuste dos referidos modelos.

(19)

Cap´ıtulo 2

Conceitos B´

asicos em An´

alise de

Sobrevivˆ

encia

2.1 Introdu¸c˜

ao

Pode-se definir a análise de sobrevivência como um conjunto de técnicas es-tat´ısticas voltadas para o estudo do “tempo”até a ocorrência de um evento de inte-resse.

Tais técnicas são utilizadas com mais frequência na área médica. No entanto, sua aplica¸cão se estende a problemas de outras áreas, por exemplo, aplica¸cões em falhas de equipamento, a¸cões e falhas de mercado, divórcios, aposentadorias, de-ten¸cões, etc.

Denotaremos porfalhaa ocorrência de um determinado evento de interesse. Tal ocorrência pode estar associada a uma observa¸cão parcial ou incompleta da variável resposta. Estas observa¸cões parciais ou imcompletas denotaremos por censura, e a presen¸ca das mesmas é a principal caracter´ıstica de dados de sobrevivência.

A análise de sobrevivência difere dos métodos convencionais, pois estes não oferecem suporte para tratar dados com presen¸ca de censura. Além disso, é poss´ıvel considerar no estudo os dados censurados e os não censurados de forma a produ-zir boas estimativas dos parâmetros para o modelo em estudo. A estima¸cão dos parâmetros pode ser através do método de máxima verossimilha¸ca ou de métodos de simula¸cão estocástica. Tais abordagens serão discutidas com mais detalhes nos próximos cap´ıtulos.

Devido a presen¸ca de censura nos dados, a variável resposta do modelo deve incorporar duas informa¸cões: o tempo até a falha e o tempo de censura.

(20)

2.2 Fun¸c˜ao de Sobrevivˆencia 19

apresentada na forma (ti, δi), i= 1, ..., k, sendoti representado por ti = min(Ti;Ci), ondeTirepresenta o tempo de falha eCio tempo de censura, al´em dissoδirepresenta a vari´avel indicadora de falha ou censura, ou seja,

δi =1(Ti≤Ci), (2.1)

sendo1(·) a fun¸c˜ao indicadora.

2.2 Fun¸c˜

ao de Sobrevivˆ

encia

SejaT uma variável aleatória cont´ınua não negativa, com fun¸cão de densidade de probabilidade fT(t). Então sua fun¸cão de sobrevivência é dada por:

ST(t) =P(T > t) =

Z ∞

t

fT(t)dt= 1−FT(t), t≥0. (2.2)

Tomando como exemplo um enfoque biológico, pode-se descrever a fun¸cão de sobrevivência como a probabilidade de um indiv´ıduo sobreviver além de um tempo t especificado. Observe que a fun¸cão de sobrevivência pode ser escrita como o complementar da fun¸cão de distribui¸cão deT,FT(t).

O que nos leva as seguintes propriedades para ST(·):

P1) Mon´otona decrescente;

P2) Cont´ınua a esquerda;

P3) ST(0)=1;

P4) limt→∞ST(t)=0.

Por P4), a fun¸cão de sobrevivência decai para zero quando o tempo t tende a infinito. Tal comportamento caracteriza uma fun¸cão própria.

A fun¸cão de densidade de probabilidade pode ser encontrada através da fun¸cão de sobrevivência, ou seja,

dST(t) dt =

d(1₋FT(t)) dt =−

dFT(t)

(21)

2.3 Estimador de Kaplan-Meier 20

2.3 Estimador de Kaplan-Meier

Como já mencionado, a presen¸ca de censuras inviabiliza a análise dos dados por meio de técnicas convencionais, como por exemplo, uma análise descritiva dos dados. Uma análise descritiva para dados de sobrevivência tem como componente principal a estima¸cão da fun¸cão de sobrevivência. Existem vários procedimentos para encontrar a fun¸cão de sobrevivência, dentre eles podemos citar, o estimador de Nelson-Aalen (Nelson, 1972 e Aalen, 1978), o método atuarial, que corresponde a uma das mais antigas técnicas estat´ısticas para tratar tempos de falhas, e é indicado para grandes bases de dados. Este é um dos métodos mais utilizados em demo-grafia, cujo objetivo é descrever a mortalidade humana. Por fim, o estimador de Kaplan-Meier (Kaplan e Meier, 1958) também conhecido como estimador produto-limite. Os autores mostraram que este estimador é o estimador não paramétrico que maximizava a fun¸cão verossimilhan¸ca de ST(t). Devido a sua facilidade de uso e baixo custo computacional, este estimador se tornou o mais difundido em análise de sobrevivência, em particular nas ciências biológicas. Vale salientar que este es-timador possui boas propriedades estat´ısticas, como mostradas por Maller e Zhou (1996) e Lawlles (2003) e está implementado na maioria dos softwares estat´ısticos. A discussão de tais propriedades foge ao escopo deste trabalho.

Considere um estudo com n observa¸c˜oes ek tempos de falhas distintos, sendo k_≤n. Seja ti, i= 1, ..., k, os tempos da i-´esima falha, tal quet1< t2< ... < tk.

Logo, pode-se definir o estimador de Kaplan-Meier para tm ≤t < tm+1 como sendo:

ˆ ST(t) =

    

1 , se t < t1 m

Y

i=1

1₋ di ni

, se tm ≤t < tm+1, m= 1, ..., k.

(2.3)

Sendo,

• t1, t2, ..., tk os k tempos distintos de falhas ordenados;

• di os n´umeros de falhas no instante ti;

• ni o número de observa¸cões sob risco nos tempos ti, ou seja, as observa¸cões que não falharam nem foram censuradas até o instante anterior ati.

(22)

2.4 Distribui¸c˜oes Probabil´ısticas 21

2.4 Distribui¸c˜

oes Probabil´ısticas

Dentre as distribui¸c˜oes de probabilidade utilizadas para descrever os tempos de falhas, podemos citar a exponencial, Weibull, log-normal, log´ıstica, log-log´ıstica, Pareto, gama, gama generalizada, Rayleigh, normal inversa e Gompertz.

Neste trabalho utilizaremos as distribui¸c˜oes Pareto, Weibull e exponencial.

2.4.1 Distribui¸c˜

ao Pareto

A distribui¸cão Pareto, tem esse nome em homenagem ao economista italiano Vilfredo Pareto. Nascido em Paris em 15 de julho de 1848, suas contribui¸cões na Economia moderna e na Sociologia são vastas.

Também chamada de distribui¸cão de Bradford, foi originalmente criada para descrever a distribui¸cão de renda entre indiv´ıduos. Com uma vasta área de aplica¸cão, é utilizada não só na economia como também nas ciências sociais, na atuária e na geof´ısica.

Seja T uma variável aleatória com distribui¸cão Pareto(p;k), p, k >0, então, suas fun¸cões de densidade de probabilidade, fT(·), e de sobrevivência, ST(·), são dadas, respectivamente, por:

fT(t) =

pkp

(k+t)p+11(0,∞)(t), (2.4)

ST(t) =

k k+t

p

1(0,∞)(t). (2.5)

Note-se que é comum que se defina como Pareto a variável aleatória u = t+k, visto que pode acarretar problemas na otimiza¸cão quando não considera-se tal transforma¸cão, ou seja, t estaria no intervalo p < t <_∞. Esta parametriza¸cão é similar a implementada no software R (base::actuar).

A esperan¸ca e a variˆancia de T s˜ao dadas respectivamente por:

E(T) = 1

p₋1, p > 1 ; V ar(T) = pk2 p₋2−

pk p₋1

2

, p >2.

(23)

Figura 2.1 Formas da densidade da Pareto(p;k).

2.4.2 Distribui¸c˜

ao Weibull

A distribui¸cão Weibull foi proposta originalmente por Fisher e Tippett em 1928, no estudo de valores extremos. Posteriormente, foi também desenvolvida de modo independente por Waloddi Weibull em 1939 em seus estudos sobre a resistência de materiais. Após o fim da II Guerra Mundial, as pesquisas no per´ıodo pós-guerra deram ênfase às análises de resistência de materiais, o que resultou na associa¸cão do nome de Waloddi Weibull a esta distribui¸cão (Bailey e Dell, 1973).

SejaT uma variável aleatória com distribui¸cão Weibull (γ;α), γ, α >0. Então sua fun¸cão densidade de probabilidade e de sobrevivência são dadas, respectiva-mente, por:

fT(t) = γ αγt

γ−1_exp

−

t α

γ

1(0,∞)(t), (2.6)

ST(t) = exp

−

_t

α

γ

1(0,∞)(t). (2.7)

Tem-se também que a esperan¸ca e a variância deT, são dadas, respectivamente, por:

E(T) =αΓ

1 + 1 γ

; V ar(T) =α2

(

Γ

1 + 2 γ

−Γ

1 +1 γ

2) .

Sendo Γ(_·) a fun¸c˜ao gama, dada por: Γ(z) =R₀∞xz−1_exp(₋_x)dx.

Devido à sua flexibilidade, a distribui¸cão de Weibull é amplamente utilizada

(24)

não só em estudos industriais, por exemplo, na modelagem de falhas de equipa-mentos, como também em estudos cl´ınicos. A sua flexibilidade permite o ajuste de diversas formas, como pode ser visto na Figura 2.2.

Figura 2.2 Formas da densidade da Weibull(γ;α).

2.4.3 Distribui¸c˜

ao Exponencial

Corresponde a um modelo simples de apenas um parâmetro apresentando uma fun¸cão de taxa de falha constante que caracteriza a falta de memória da distribui¸cão. ´

E bastante utilizada tanto na área industrial quanto na área médica. Cox e Snell (1981) aplicam este modelo com o objetivo de descrever o tempo de vida de pacientes com leucemia.

Seja T uma variável aleatória com distribui¸cão exponencial(λ), λ >0, então, suas fun¸cões de densidade e de sobrevivência são dadas, respectivamente, por:

fT(t) =λexp(−λt)1(0,∞)(t), (2.8)

ST(t) = exp(−λt)1(0,∞)(t). (2.9)

(25)

Cap´ıtulo 3

Modelos de Longa Dura¸c˜

ao

3.1 Introdu¸c˜

ao

Modelos de fra¸cão de cura, estão se tornando cada vez mais populares na análise de dados provenientes de ensaios cl´ınicos de câncer. Os modelos que incor-poram uma taxa de cura tem sido utilizados para modelar o tempo de eventos para vários tipos de câncer nos quais uma propor¸cão de pacientes são “curados”, incluindo o cancêr da mama, linfoma no-Hodgkins, leucemia, câncer da próstata, melanoma, e câncer de cabe¸ca e pesco¸co. Dentre o mais popular desses modelos está omodelo de mistura padrão introduzido por Berkson e Gage (1952). Neste modelo, assumimos que uma certa fra¸cãoθ da popula¸cão são de “curados”e o restante 1₋θsão de não curados (Chen et al. 1999).

3.2 Modelo de Mistura Padr˜

ao (MMP)

Uma abordagem para a análise de dados de sobrevivência com imunes é ajustar um modelo paramétrico que é uma mistura de duas distribui¸cões, uma representando o tempo de falha para o grupo de suscet´ıvel e a outra que permite uma distribui¸cão degenerada para os tempos de sobrevivência dos imunes. Vamos nos referir a esses tipos de modelos como modelos de mistura. Em contraste com Boag (1949), Berkson e Gage (1952) utilizaram um modelo constitu´ıdo por uma mistura de uma distri-bui¸cão exponencial e uma distridistri-bui¸cão degenerada, para permitir uma propor¸cão de curados. Eles utilizaram este modelo para um grande conjunto de dados consistindo de 2682 pacientes acometidos de câncer de estômago (Maller e Zhou, 1996).

(26)

3.2 Modelo de Mistura Padr˜ao (MMP) 25

suscet´ıveis ao evento de interesse. Um indiv´ıduo ser´a suscet´ıvel ao evento seM = 1 com probabilidade 1₋θ, e imune se M = 0, com probabilidade igual aθ (fra¸c˜ao de cura).

Observe que, teoricamente, os tempos de vida para os indiv´ıduos imunes são infinitos, então estes terão fun¸cão de distribui¸cão igual a zero. Simplificando, tem-se:

P(T _≤t_|M = 1) = FT(t) e P(T ≤t|M = 0) = 0.

Logo, obtém-se uma mistura das duas subpopula¸cões e pode-se escrever a fun¸cão de sobrevivência para a popula¸cão, como sendo:

Spop(t) = P(T ≥t) = 1−P(T ≤t)

= 1₋[P(T _≤t_|M = 1)P(M = 1) +P(T _≤t_|M = 0)P(M = 0)] = 1₋[FT(t)(1−θ) + 0] = 1−[(1−ST(t))−θ(1−ST(t))]

= θ+ (1₋θ)ST(t). (3.1)

Aqui,ST(t) é a fun¸cão de sobrevivência para o grupo dos não curados eθa propor¸cão de curados.

Portanto, o modelo de mistura padrão é caracterizado pela fun¸cão de sobre-vivência dado por (3.1) e pela fun¸cão de densidade dada por:

fpop(t) =− ∂

∂tSpop(t) = (1−θ)fT(t), (3.2)

Para a constru¸cão da fun¸cão de verossimilhan¸ca do modelo de mistura, consi-dere ti = min(Ti;Ci) o tempo observado do i-ésimo indiv´ıduo, Mi = mi e p(mi) = P(Mi = mi) a fun¸cão de probabilidade de Mi e δi a fun¸cão indicadora de falha ou censura dada por (2.1).

Dessa maneira podemos escrever os seguintes vetores:

t=       t1 t2 ... tn      

, δ ₌

      δ1 δ2 ... δn      

, M=

      M1 M2 ... Mn      

(27)

3.2 Modelo de Mistura Padr˜ao (MMP) 26

completos no modelo de mistura padr˜ao, ´e dada por:

L∗_{M M P}(θ_;_D_c_{) =}

n

Y

i=1

[mifpop(ti;ψ)]δi[Spop(ti;ψ)]mi−δip(mi). (3.3)

Sendoψ o parâmetro, ou vetor de parâmetros associado à distribui¸cão deTi.

Como (3.3) é não observável, pois depende das variáveis latentes Mi, então utiliza-se uma fun¸cão de verossimilhan¸ca marginal, que é dada por:

LM M P(θ;D) = n

Y

i=1

[fpop(ti;ψ)]δi[Spop(ti;ψ)]1−δi. (3.4)

3.2.1 Modelo de Mistura Padr˜

ao Exponencial (MMPexp)

Assumindo uma distribui¸cão exponencial (λ), com fun¸cões de densidade, (2.8), e sobrevivência, (2.9), então as fun¸cões de verossimilhan¸ca e log-verossimilhan¸ca de

θ_{= (θ;}_λ)′ _{para o modelo de mistura padr˜ao exponencial s˜ao dadas, respectivamente,}

por:

LM M P exp(θ;D) = [λ(1−θ)]

Pn

i=1δi_exp

(

−λ n

X

i=1 δiti

)

×

n

Y

i=1

[θ+ (1₋θ) exp(₋λti)]1−δi, (3.5)

ℓM M P exp(θ;D) = log{λ(1−θ)} n

X

i=1 δi−λ

n

X

i=1 [δiti]

+ n

X

i=1

[(1₋δi) log{θ+ (1−θ) exp(−λti)}]. (3.6)

3.2.2 Modelo de Mistura Padr˜

ao Pareto (MMPpar)

Seja T _∼ Pareto(p;k), p, k > 0, com fun¸cões de densidade, (2.4), e de so-brevivência, (2.5), então as fun¸cões de verossimilhan¸ca e log-verossimilhan¸ca de

θ_{= (θ;}_p;_k)′ _{para o modelo de mistura padr˜ao Pareto, s˜ao dadas, respectivamente,}

(28)

3.3 Modelo de Tempo de Promo¸c˜ao (MTP) 27

por:

LM M P par(θ;D) = ((1−θ)pkp)

Pn i=1δi

n

Y

i=1

" ₁

k+ti

p+1#δi

×

n

Y

i=1

θ+ (1₋θ)

_k

k+ti

p1−δi

, (3.7)

ℓM M P par(θ;D) = n

X

i=1

δi[log(1−θ) +plog(pk)−(p+ 1) log(k+ti)]

+ n

X

i=1

(1₋δi) log

θ+ (1₋θ)

k k+ti

p

. (3.8)

3.2.3 Modelo de Mistura Padr˜

ao Weibull (MMPwei)

Seja T _∼Weibull(γ;α), γ, α >0, com fun¸cões de densidade, (2.6), e de sobre-vivência, (2.7), então teremos as fun¸cões de verossimilhan¸ca e log-verossimilhan¸ca deθ _{= (θ;}_α;_γ)′ _{para o modelo de mistura padrão Weibull, dadas, respectivamente,}

por:

LM M P wei(θ;D) =

(1₋θ)α−γγ

Pn i=1δi

n

Y

i=1

tγ_i−1exp

−

ti α

γδi

×

n

Y

i=1

θ+ (1₋θ) exp

−

ti α

γ1−δi

, (3.9)

ℓM M P wei(θ;D) = log

(1₋θ)α−γγ n

X

i=1 δi+

n

X

i=1 δi

(γ₋1) log(ti)−

_t i α γ + n X i=1

(1₋δi) log

θ+ (1₋θ) exp

− _t i α γ . (3.10)

3.3 Modelo de Tempo de Promo¸c˜

ao (MTP)

(29)

Embora o modelo de mistura padrão seja simples e bastante utilizado, o mesmo possui alguns inconvenientes. Primeiramente, os modelos de mistura padrão não são capazes de modelar o mecanismo biológico envolvido no processo cl´ınico. O que não ocorre, por exemplo, nos modelos de tempo de promo¸cão (Yakovlev e Tsodikov, 1996), os quais são capazes de modelar o número de causas, que competem entre si, para que ocorra o evento de interesse.

Em segundo lugar, na presen¸ca de covariáveis, não se pode ter uma estrutura de riscos proporcionais, que é uma propriedade desejável para realizar análises nas covariáveis. Além disso, quando inclu´ıdo covariáveis através do parâmetroθ, via um modelo de regressão binomial padrão, a equa¸cão (3.1) produz distribui¸cões a poste-riori impróprias para muitos tipos de priores impróprias não-informativas, incluindo prioris uniformes para os coeficientes de regressão (Chen et al. 2002).

Uma vantagem do critério de riscos proporcionais, citado por Chen et al. (1999), é que a partir de uma perspectiva frequentista muitos resultados assintóticos e computacionais exigem esse tipo de estrutura.

Yakovlev e Tsodikov (1996) propuseram o modelo de tempo de promo¸cão, no qual os tempos de sobrevivência de pacientes curados e não curados são incorporados simultaneamente.

Para constru¸cão do referido modelo, suponha que tenhamos um número de células potencialmente cancer´ıgenas associadas a uma variável aleatória M com distribui¸cão de Poisson (ϕ), ϕ > 0, dada por, P(M = m) = ϕmexp_m_!{−ϕ}, m = 0,1,2, .... Tais células são denominadasfatores latentes e portanto não observáveis. Seja também, um conjunto de variáveis aleatórias latentesKj, j = 1,2, ..., M, repre-sentando o tempo até a ocorrência do evento de interesse devido a j-ésima célula. Considerando as variáveis aleatórias Kj, condicionadas a M, independentes e iden-ticamente distribu´ıdas.Definimos o tempo até a ocorrência do evento de interesse, como sendo:

T = min_{K0, K1, K2, ..., KM}, (3.11)

sendo K0, tal que P(K0 = ∞) = 1. Pode-se observar o tempo até o surgimento do tumor, sendo que, se um indiv´ıduo não apresentar células potencialmente can-cer´ıgenas, mesmo que o tempo de acompanhamento para este indiv´ıduo seja longo, o mesmo não desenvolverá o tumor.

(30)

Portanto, a fun¸cão de sobrevivência de T é dada por:

Spop(t) =P(T > t) =

X

m≥0

P(T > t, M =m)

= P(T > t, M = 0) +X m≥1

P(T > t, M =m)

= P(T > t_|M = 0)P(M = 0)

+ X

m≥1

P(T > t_|M =m)P(M =m).

Como, P(T > t_|M = 0) é a sobrevivência dado o número de células igual a zero, então, o indiv´ıduo não apresentou células potencialmente cancer´ıgenas e o mesmo não será acometido pelo evento de interesse, ou seja, P(T > t_|M = 0) = 1. Então,

Spop(t) = P(M = 0) +

X

m≥1

P(T > t_|M =m)P(M =m)

= P(M = 0) +X m≥1

P(min_{K1, K2, ..., Km}> t|M = m)P(M =m)

= P(M = 0) +X m≥1

P(K1 > t)P(K2 > t).· · · .P(Km> t)P(M =m)

= ϕ

0_{exp (}₋_ϕ)

0! +

X

m≥1

[ST(t)]m

ϕm_{exp (}₋_ϕ) m!

= exp (₋ϕ)

" _∞ X

m=0

[ST(t)ϕ]m m!

#

.

Aproximando a express˜aoP∞_m₌₀[ST(t)ϕ]m

m! em fun¸c˜ao de s´erie de Taylor, tem-se que,

P∞

m=0

[ST(t)ϕ]m

m! = exp (ST(t)ϕ).

Portanto, pode-se escrever a fun¸cão de sobrevivência associada ao modelo de tempo de promo¸cão como sendo:

Spop(t) = exp (−ϕ) exp (ST(t)ϕ) = exp (−ϕFT(t)). (3.12)

Sendo, a fun¸c˜ao de densidade dada por:

fpop(t) =−

dSpop(t)

(31)

De modo que a fra¸c˜ao de cura ´e expressa como sendo:

θ= exp(₋ϕ). (3.14)

Assim como no modelo de mistura padrão M é não observável, então utiliza-remos a fun¸cão de verossimilhan¸ca de θ _{= (ψ;}_ϕ)′_{, relativa à distribui¸cão marginal}

de teδ_{, associados aos tempos} _K_j_{, dada por:}

LM T P(θ;D) = n

Y

i=1

[ϕfT(ti;ψ) exp{−ϕFT(ti;ψ)}]δi[exp{−ϕFT(ti;ψ)}]1−δi. (3.15)

Segundo Sinha et al. (2003), as fun¸cões de sobrevivência e densidade para os não curados, são fun¸cões próprias dadas, respectivamente, por:

S_T∗(t) = exp(−ϕFT(t))−exp(−ϕ) 1₋exp(ϕ) ,

f_T∗(t) =ϕf(t)exp(−ϕFT(t)) 1₋exp(₋ϕ) ,

Mesmo que os modelos de mistura padrão e de tempo de promo¸cão tenham sido formulados em diferentes situa¸cões, é poss´ıvel escrever o modelo de tempo de promo¸cão como um modelo de mistura padrão (Sumathi e Aruna Rao, 2008). Com θ= exp(₋ϕ) temos,

Spop(t) = exp (−ϕ) + (1−exp (−ϕ))

exp (₋ϕFT(t))−exp (−ϕ) 1₋exp (₋ϕ) ,

e a fun¸cão de sobrevivência para os não curados é dada por:

S_T∗(t) =P(T > t_|M _≥1) = exp (−ϕFT(t))−exp (−ϕ) 1₋exp (₋ϕ) .

3.3.1 Modelo de Tempo de Promo¸c˜

ao Exponencial (MTPexp)

Seja T _∼ exponencial (λ), λ > 0, então as fun¸cões de verossimilhan¸ca e log-verossimilhan¸ca de θ_{= (ϕ;}_λ)′_{, para o referido modelo, são dadas, respectivamente,}

(32)

por:

LM T P exp(θ;D) = (ϕλ)

Pn

i=1δi_exp

(

−λ n

X

i=1 δiti

)

× exp

(

−ϕ[1₋exp(₋λti)] n

X

i=1 δi+

n

X

i=1

(1₋δi)

!)

,(3.16)

ℓM T P exp(θ;D) = log(ϕλ) n

X

i=1 δi−λ

n

X

i=1 δiti

− ϕ[1₋exp(₋λti)] n

X

i=1 δi+

n

X

i=1

(1₋δi)

!

. (3.17)

3.3.2 Modelo de Tempo de Promo¸c˜

ao Pareto (MTPpar)

Seja T _∼ Pareto(p;k), p, k > 0, então as fun¸cões de verossimilhan¸ca e log-verossimilhan¸ca deθ_{= (θ;}_p;_k)′_{, para o referido modelo, são dadas, respectivamente,}

por:

LM T P par(θ;D) = (ϕpkp)

Pn i=1δi

n

Y

i=1

" ₁

k+ti

p+1#δi

× exp ( −ϕ 1₋ k k+ti

p "_Xn

i=1 δi+

n

X

i=1

(1₋δi)

#)

,(3.18)

ℓM T P par(θ;D) = n

X

i=1

δilog(ϕpkp) + n

X

i=1

(p+ 1)δilog

k k+ti

p − ϕ 1₋ k k+ti

p "_Xn

i=1 δi+

n

X

i=1

(1₋δi)

#

. (3.19)

3.3.3 Modelo de Tempo de Promo¸c˜

ao Weibull (MTPwei)

(33)

respectiva-3.3 Modelo de Tempo de Promo¸c˜ao (MTP) 32

mente, por:

LM T P wei(θ;D) =

ϕγα−γ

Pn i=1δi

n

Y

i=1

tγ_i−1δi

× exp ( _n X i=1 δi − _t i α γ −ϕ

1₋exp

− _t i α γ) × exp ( −ϕ n X i=1

(1₋δi)

1₋exp

− _t i α γ) , (3.20)

ℓM T P wei(θ;D) = log

ϕγα−γ n

X

i=1 δi+

n

X

i=1

δi[(γ−1) log(ti)]

+ n X i=1 δi − ti α γ −ϕ

1₋exp

− ti α γ − ϕ n X i=1

(1₋δi)

1₋exp

− _t i α γ . (3.21)

(34)

Cap´ıtulo 4

M´

etodos de Estima¸c˜

ao

4.1 Inferˆ

encia Cl´

assica

Seja T1, ..., Tn uma amostra aleatória de tamanho n da variável aleatória T com fun¸cão de densidade (ou de probabilidade) f(t_|θ_{), com} θ _∈ _{Θ, onde Θ é o}

espa¸co paramétrico. A fun¸cão de verossimilhan¸ca de θ _{correspondente à amostra}

aleat´oria observada, D = (n,t,δ_{), ´e dada por:}

L(θ_;_D_{) =}

n

Y

i=1

f(ti|θ).

Observe que, em análise de sobrevivência, a contribui¸cão das observa¸cões não censuradas é dada pela fun¸cão de densidade, f(t_|θ_{). O que não acontece com as}

observa¸cões censuradas, que por sua vez têm contribui¸cão para L(θ_;_D_{) dada pela}

fun¸cão de sobrevivência,S(t_|θ_{). Logo, teremos que reescrever a fun¸cão de}

verossimi-lhan¸ca de tal forma que possamos modelar adequadamente dados de sobrevivˆencia. Sendo, a fun¸c˜ao de verossimilhan¸ca para modelar dados com presen¸ca de censura dada por:

L(θ_;_D_{) =}

n

Y

i=1

[f(ti|θ)]δi[S(ti|θ)]1−δi. (4.1)

Portanto, o estimador de m´axima verossimilhan¸ca de θ_{´e o valor de ˆ}θ_∈_{Θ que}

maximiza a fun¸c˜ao de verossimilhan¸ca L(θ_;_D_{). O estimador de m´axima}

verossimi-lhan¸ca pode ser encontrado como a raiz da equa¸c˜ao de verossimiverossimi-lhan¸ca ℓ(θ_;_D_{) =}

∂ℓ(θ;D)

∂θ = 0. No qualℓ(θ;D) ´e o logaritmo natural da fun¸c˜ao de verossimilhan¸ca de

θ _{(Bolfarine e Sandoval, 2010).}

Para a maximiza¸c˜ao das fun¸c˜oes, ℓ(θ_;_D_{), nos modelos abordados no Cap´ıtulo}

(35)

4.2 Inferˆencia Bayesiana 34

4.1.1 Verossimilhan¸ca Perfilada

Na estima¸cão de um vetor de parâmetros via verossimilhan¸ca perfilada encontra-se as estimativas de máxima verossimilhan¸ca dos demais parâmetros substituindo-os na fun¸cão de verossimilhan¸ca e em seguida calcula-se a verossimilhan¸ca em cada ponto do parâmetro de interesse.

Considere um modelo estat´ıstico, em que θ _{´e um vetor de parˆametros}

desco-nhecidos, sendo θ _{= (θ;}_{ψ) e suponha que inferˆencias realizadas no modelo envolva}

apenas θ. Então, a fun¸cão de verossimilhan¸ca perfilada é obtida substituindo, na fun¸cão de verossimilhan¸ca original, o parâmetros ψ por sua estimativa de máxima verossimilhan¸ca,ψbθ, para um conjunto de valores fixados deθ.

Dessa forma pode-se escrever θb₀ _{= (θ;}_ψb_θ_{), sendo}_ψb_θ_{a solu¸c˜ao de} ∂log[L(θ)]

∂ψ = 0. Assim, a fun¸c˜ao de verossimilhan¸ca perfilada pode ser definida como:

Lper(θ) =L(θ;ψbθ). (4.2)

Sendoℓ(θ;ψ) = log[L(θ;ψ)], então a fun¸cão de log-verossimilhan¸ca perfilada paraθ é definida por:

ℓper(θ) =ℓ(θ;ψbθ) = sup ψ

[ℓ(θ;ψ)]. (4.3)

Logo, o estimador de máxima verossimilhan¸ca perfilada, θbp, é encontrado como solu¸cão da equa¸cão:

∂ℓper(θ) ∂θ = 0.

4.2 Inferˆ

encia Bayesiana

Na inferência Bayesiana admitimos que as incertezas são pass´ıveis de serem descritas, coerentemente, por uma distribui¸cão de probabilidade. Assim, o procedi-mento de estima¸cão consiste em descrever a incerteza inicial do pesquisador sobre o parâmetro, através da distribui¸cão a priori, π(_·), e em seguida, combinar essa informa¸cão com aquela proveniente dos dados, resumida na fun¸cão de verossimi-lhan¸ca. O resultado deste procedimento é uma distribui¸cão de probabilidade,π(_·|x), (distribui¸cão a posteriori) e a inferência sobre o parâmetro é feita feita através da caracteriza¸cão dessa distribui¸cão (Migon et al., 2008).

(36)

4.2.1 Teorema de Bayes

Pode-se dizer ainda que, o conhecimento inicial que se tem a respeito do parâmetro, expresso porπ(_·), transforma-se em conhecimento final, dado pela distri-bui¸cão a posteriori, π(_·|x). Esta transforma¸cão se deve ao Teorema de Bayes, dado as quantidades observadas.

A atualiza¸cão da informa¸cão se dá através do Teorema de Bayes,

π(θ_|_{x) =} f(x;θ)

f(x) =

f(x_|θ_)π(θ₎

f(x) =

f(x_|θ_)π(θ₎

R

f(θ_{, x)d}θ =

f(x_|θ_)π(θ₎

R

f(x_|θ_)π(θ_)dθ, (4.4)

sendoπ(θ_|_{x) a distribui¸c˜ao} _{a posteriori} _de θ _e_π(θ_{) a distribui¸c˜ao a} _priori _de θ_.

Observe que 1/f(x) funciona como uma constante normalizadora não depen-dendo do parâmetro. Assim, utilizando o teorema de Bayes, podemos reescrever a distribui¸cão a posteriori como sendo:

π(θ_|_x)_∝_f_(x_|θ_)π(θ_). _(4.5)

4.2.2 Est´

agios da Inferˆ

encia Bayesiana

A metodologia Bayesiana fornece não só a possibilidade de atualiza¸cão do co-nhecimento dos parâmetros do modelo, e posteriormente a tomada de decisões, como também é um ferramental simples e flex´ıvel a partir do qual faz-se inferências usando modelos paramétricos. No entanto, esta flexibilidade traz alguns obstáculos compu-tacionais. Basicamente, tais problemas computacionais se resumem em opera¸cões de integra¸cão, que muitas vezes possui alto grau de complexidade.

Nas últimas décadas muitos algoritmos de resolu¸cões de integrais foram pro-postos, e outros modificados, com o objetivo de contornar tais dificuldades. Vale salientar que, a utliza¸cão de muitos destes algor´ıtmos só foi poss´ıvel devido aos avan¸cos computacionais, e foi devido a isto que a inferência Bayesiana progrediu tanto nos últimos anos.

(37)

a implementa¸cão computacional, nem restri¸cões quanto ao número de parâmetros a serem estimados.

A distribui¸cão a posteriori é convenientemente resumida em termos da espe-ran¸ca condicional de uma fun¸cão deθ_{, ou seja,}

E[g(θ₎_|_{x] =}

Z

g(θ_)π(θ_|_x)dθ_. _(4.6)

Se o parâmetro for multidimensional pode-se encontrar as distribui¸cões mar-ginais a posteriori. Sejaθ_{= (}θ₁_,θ₂_{), então,}

π(θ₁_|_{x) =}

Z

π(θ_|_x)dθ₂_. _(4.7)

4.2.3 Distribui¸c˜

oes de Probabilidade a Priori

A distribui¸cão a priori constitui-se em um importante elemento na análise Bayesiana e a determina¸cão desta distribui¸cão é subjetiva. Espera-se que a distri-bui¸cão de probabilidade a priori represente o estado atual de conhecimento sobre os parâmetros, antes de serem analisados os resultados experimentais.

Pode-se ter propostas para a obten¸cão da distribui¸cão a priori de diversas formas, como por exemplo, prioris conjugadas, prioris não informativas e prioris hierárquicas.

Prioris N˜ao Informativas

Em alguns problemas práticos, podemos nos deparar com situa¸cões em que não temos informa¸cões suficientes para a tomada de decisão a respeito da distribui¸cão a priori do parâmetro do modelo. Nesses casos, sugere-se propor uma distribui¸cão a priori que reflita no m´ınimo de influência sobre a posteriori resultante. Observe que, neste caso, o maior peso da distribui¸cão a posteriori será dado pela fun¸cão de verossimilhan¸ca.

Reconhece-se a necessidade de análise que consiga captar esta no¸cão de uma priori que tenha um efeito m´ınimo, relativamente aos dados, na inferência final. Tal análise pode ser pensada como um ponto de partida quando não se consegue fazer uma elicita¸cão detalhada do conhecimento a priori (Ehlers, 2011).

(38)

Uma poss´ıvel fam´ılia de distribui¸c˜ao a priori informativas

Para o modelo de tempo de promo¸cão foi visto que a fra¸cão de curados era dada por θ = exp(₋ϕ). No entanto, o parâmetro de interesse está vinculado na interpreta¸cão direta de θ e não de ϕ. Logo, como ϕ > 0 é viável pensar para a distribui¸cão de probabilidade a priori deϕ, uma distribui¸cão Uniforme.

Seja ϕ _∼ Unif(0;A), A > 0 “grande”, com f.d.p. fϕ(φ) = 1[0,A] (φ)

A . Como o interesse é uma interpreta¸cão em θ, vejamos o comportamento da distribui¸cão de probabilidade a priori para θ.

Seja,θ= exp(₋ϕ)_⇒ϕ=₋log(θ) e Π(_·) a fun¸c˜ao de distribui¸c˜ao deθ. Logo, teremos que:

Π(θ∗) = P(θ_≤θ∗) =P(exp(₋ϕ)_≤θ∗) =P(ϕ >₋log(θ∗)) = 1₋

Z −log(θ∗₎

0

1 Adϕ

= 1₋ 1 Aϕ

−log(θ

∗₎

0 = 1− 1

A(−log(θ

∗₎

−0) = 1 + log(θ

∗₎

A .

Então, a distribui¸cão a priori deθ é dada por:

π(θ) = dΠ(θ) dθ =

1 θ

1[0,A](φ) A .

Note ainda que:

Z 1 0 π(θ)dθ= Z 1 0 1 A 1 θdθ=

1

Alog(θ)

1

0 = 0− ∞,

ou seja, a escolha de uma distribui¸cão Uniforme (0;A), como sendo uma distribui¸cão de probabilidade a priori para ϕ, nos remete a uma distribui¸cão de probabilidade a priori imprópria para θ.

Vale salientar que, uma distribui¸cão a priori imprópria não implica, necessari-amente, em uma distribui¸cão a posteriori também imprópria.

Uma outra distribui¸cão natural a se pensar para θé a distribui¸cão Beta, visto que esta modela variáveis no intervalo (0;1). Vejamos então, como se comporta ϕ com tal proposta paraθ.

Tomemosθ_∼Beta(α;β), ou seja,π(θ) = _Γ(Γ(_αα_)Γ(+β_β)₎θα−1₍₁₋_θ)β−1_,₀_{< θ <}_{1, α >} 0, β > 0.

Seja ϕ = ₋log(θ) e dθ

(39)

sendo:

π(ϕ) = π(θ)

dθ dϕ

=

Γ(α+β) Γ(α)Γ(β)θ

α−1₍₁

−θ)β−1_|−exp(₋ϕ)_|

= Γ(α+β)

Γ(α)Γ(β)[exp(−ϕ)] α−1_[1

−exp(₋ϕ)]β−1exp(₋ϕ)

= Γ(α+β)

Γ(α)Γ(β)[exp(−ϕ)] α_[1

−exp(₋ϕ)]β−1;ϕ >0.

Portanto, a distribui¸cão de probabilidade a priori para ϕ é uma distribui¸cão Beta(α+ 1, β) analisada em exp(-ϕ).

Como casos particulares, observe que:

i) com α livre e β= 1, temos θ_∼Beta(α,1) e ϕ_∼ Exp(α);

ii) com α= 1 eβ = 1, temosθ _∼Unif(0,1) eϕ_∼ Exp(1).

4.2.4 Distribui¸c˜

ao de Probabilidade

a Posteriori

A seguir descrevemos as distribui¸c˜oes de probabilidade a posteriori para os modelos de longa dura¸c˜ao descritos no Cap´ıtulo 3.

• Distribui¸c˜ao de probabilidade a posteriori para o Modelo de Mistura Padr˜ao Exponencial (MMPexp).

π(θ_|_t) _∝ _π(θ₎_×_[λ(1₋_θ)]Pni=1_exp

(

−λ

n

X

i=1 δiti

)

×

n

Y

i=1

[θ+ (1₋θ) exp(₋λti)]1−δi, (4.8)

sendoθ _{= (θ, λ).}

• Distribui¸c˜ao de probabilidade a posteriori para o Modelo de Mistura Padr˜ao Pareto (MMPpar).

(40)

π(θ_|_t) _∝ _π(θ₎_×₍₍₁₋_θ)pkp₎Pni=1δi

n

Y

i=1

"

1 k+ti

p+1#δi

×

n

Y

i=1

θ+ (1₋θ)

_k

k+ti

p1−δi

, (4.9)

sendoθ _{= (θ, p, k).}

• Distribui¸c˜ao de probabilidade a posteriori para o Modelo de Mistura Padr˜ao Weibull (MMPwei).

π(θ_|_t) _∝ _π(θ₎_×₍₁₋_θ)α−γ_γ

Pn i=1δi

n

Y

i=1

tγ_i−1exp

−

ti α

γδi

×

n

Y

i=1

θ+ (1₋θ) exp

−

ti α

γ1−δi

, (4.10)

sendoθ _{= (θ, α, γ).}

• Distribui¸c˜ao de probabilidadea posterioripara o Modelo de Tempo de Promo¸c˜ao Exponencial (MTPexp).

π(θ_|_t) _∝ _π(θ₎_×_(ϕλ)Pni=1δi_exp

(

−λ

n

X

i=1 δiti

)

× exp

(

−ϕ[1₋exp(₋λti)] n

X

i=1 δi+

n

X

i=1

(1₋δi)

!)

, (4.11)

sendoθ _{= (ϕ, λ).}

• Distribui¸c˜ao de probabilidadea posterioripara o Modelo de Tempo de Promo¸c˜ao Pareto (MTPpar).

π(θ_|_t) _∝ _π(θ₎_×_(ϕpkp₎Pni=1δi

n

Y

i=1

"

1 k+ti

p+1#δi

× exp ( −ϕ 1₋ _k

k+ti

p "_Xn

i=1 δi+

n

X

i=1

(1₋δi)

#)

, (4.12)

(41)

4.3 M´etodo de Laplace 40

• Distribui¸c˜ao de probabilidadea posterioripara o Modelo de Tempo de Promo¸c˜ao Weibull (MTPwei).

π(θ_|_t) _∝ _π(θ₎_×_ϕγα−γ

Pn i=1δi

n

Y

i=1

tγ_i−1δi

× exp ( _n X i=1 δi − ti α γ −ϕ

1₋exp

− ti α γ) × exp ( −ϕ n X i=1

(1₋δi)

1₋exp

− ti α γ) , (4.13)

sendoθ _{= (ϕ, γ, α).}

As distribui¸c˜oes de probabilidade a prioriπ(θ_{) de cada modelo s˜ao destacadas}

na aplica¸c˜ao (Cap´ıtulo 5).

4.3 M´

etodo de Laplace

No referido trabalho utilizaremos a abordagem proposta por Tierney e Kadane (1986) para o cálculo de integrais através do método de Laplace. Os fundamentos do método de Laplace, datam do século XIII (Laplace, 1774). Consideremos integrais da forma

I =

Z

f(θ_{) exp(}₋_nΨ(θ_))dθ_. _(4.14)

Seja Ψ uma fun¸cão regular de um parâmetro n-dimensional, θ_{, e} _θb_{o máximo}

de ₋Ψ(_·). A aproxima¸cão para a integral acima é dada através do desenvolvimento em série de Taylor de Ψ(θ_{) e f(}θ_{) em torno de} θˆ_.

Queremos encontrar a esperan¸ca condicional a posteriori de uma fun¸c˜ao do parˆametro, ou seja,

E[g(θ₎_|_{x] =}

R

g(θ_)f_(x_|θ_)π(θ_)dθ

R

f(x_|θ_)π(θ_)dθ , (4.15)

sendo esta obtida pela substitui¸c˜ao de (4.14) em (4.16).

Para aplicar o m´etodo de Laplace a integral deve estar na forma (4.14). Con-sideremos ent˜ao:

i) exp(₋nΨ(θ_{)) =}_f_(x_|θ_)π(θ_),

ii) g(θ_{) =}_f₍θ_{) no numerador e} _f₍θ_{) = 1 no denominador.}

(42)

4.3 M´etodo de Laplace 41

Logo, a equa¸c˜ao (4.15) pode ser reescrita na forma:

E[g(θ₎_|_{x] =}

R

exp(₋nΨ∗₍_θ_))d_θ

R

exp(₋nΨ(θ_))dθ. (4.16)

sendo,

−nΨ(θ_{) = ln}_f_(x_|θ_{) + ln}_π(θ_),

−nΨ∗₍_θ_{) = ln}_g(_θ_{) + ln}_f_(x_|_θ_{) + ln}_π(_θ_).

Tomemos agora, ˆθ _e θ∗ _{com sendo argumentos m´aximo das fun¸c˜oes} ₋_Ψ(θ_{) e} −Ψ∗₍_θ_).

O que nos leva as aproxima¸c˜oes para as respectivas integrais:

Z

exp(₋nΨ∗₍_θ_))d_θ_≈√_2πσ∗_n−1/2_exp(₋_nΨ∗₍_θ∗_)), _(4.17)

Z

exp(₋nΨ(θ_))dθ _≈√_2πˆ_σn−1/2_exp(₋_nΨ(ˆθ_)). _(4.18)

Portanto, uma aproxima¸c˜ao para esperan¸ca a posteriori (4.16) ´e dada por:

E[g(θ₎_|_{x] =}

R

exp(₋nΨ∗₍_θ_))d_θ

R

exp(₋nΨ(θ_))dθ ≈ √

2πσ∗_n−1/2_exp(₋_nΨ∗₍_θ∗₎₎

√

2πˆσn−1/2_exp(₋_nΨ(ˆθ₎₎

≈ σ

∗

ˆ

σ exp(−n[Ψ

∗₍_θ∗₎

−Ψ(ˆθ_)]). _(4.19)

No qual, σ∗ _{= [det(}_∇2_Ψ∗₍_θ∗_))]−1/2_{; ˆ}_σ _{= [det(}_∇2_Ψ(ˆ_θ_))]−1/2_{, sendo} _∇2 _{a matriz} Hessiana.

A idéia da integra¸cão via método de Laplace, está em aplicar separadamente o método nas integrais do numerador e do denominador. Tierney e Kadane (1986) ressaltam que o esfor¸co computacional é reduzido, visto que só é necessário encontrar as derivadas de ordem 1 e 2, e maximizar as duas fun¸cões integrantes, que em resumo são apenas fun¸cões de verossimilhan¸ca ligeiramente modificadas.

Outra contribui¸cão deste método é em rela¸cão ao erro de aproxima¸cão, pois tanto no numerado como no denominador deE[g(θ₎_|_{x] o erro é da ordem de}_n−1_.

(43)

4.4 Métodos de Simula¸cão Estocástica 42

4.4 M´

etodos de Simula¸c˜

ao Estoc´

astica

O objetivo dos métodos de Monte Carlo via cadeias de Markov é simular uma cadeia de Markov no espa¸co do parâmetro que tenha como distribui¸cão estacionária a distribui¸cão a posteriori, π(θ_|·).

Nos métodos de simula¸cão estocástica, cada valor obtido na simula¸cão depende do valor gerado anteriormente, ou seja, cria-se uma cadeia de valores dependentes entre si. Um maneira de evitar a forte dependência dos valores gerados, com rela¸cão ao valor inicial fornecido para gera¸cão da cadeia, é descartando os primeiros valores simulados. Dada a convergência da cadeia, dizemos que foi obtido a distribui¸cão estacionária objetivo.

As amostras iniciais descartadas são obtidas no per´ıodo de aquecimento da cadeia também conhecido comoburn-in. Na simula¸cão pode-se optar por gerar uma longa cadeia e a seguir tomar valores apenas a cada certo número de amostras simuladas, tal procedimento é conhecido comoraleamento, saltos outhinning.

4.4.1 Cadeias de Markov

Pode-se definir uma cadeia de Markov, como sendo uma sequˆencia,θ₀_,θ₁_{, ...,}θ_n_,

tal queP(θ_i _∈_A_|θ₀_,θ₁_{, ...,}θ_i₋₁_)=P₍θ_i _∈_A_|θ_i₋₁_), _i_{= 1, ..., n, para qualquer evento}

A, ou seja, o valor seguinte da sequˆencia gerada,θ_i_{, depende apenas do valor atual}

da cadeia,θ_i₋₁_{, e n˜ao dos valores anteriores a}θ_i₋₁_.

Dada uma sequência de Markov com distribui¸cão estacionária π(_·|x), note-se que θ _∼_p_i₍_·|θ_i₋₁_{) e sob condi¸cões de regularidade (Robert e Casella, 2004) tem-se}

quepi se aproxima de π(·|x) à medida que i→ ∞, e ainda temos, segundo a lei dos grandes números que, definindoµg =E(g(θ|x)) e bµn = 1_nPni=1g(θi), então:

b

µn q.c

→µg, n→ ∞. (4.20)

Há também condi¸cão para Normalidade assintótica (Robert e Casella, 2004), ou seja,

√

n(_bµn−µg)→D N(0;σ2g), (4.21)

sendo σ2

g a variância assintótica de g(θ), que pode ser estimada por diferentes métodos (Robert e Casella, 2004).

(44)

4.4.2 Diagn´

ostico de Convergˆ

encia

Um método preliminar para verificar a convergência da cadeia simulada é feito analisando os gráficos das quantidades estimadas ao longo das itera¸cões, bem como o gráfico da distribui¸cão marginal a posteriori do parâmetro. Além da análise gráfica, outras técnicas de convergências podem ser utilizadas. Tais técnicas podem ser vistas com mais detalhes em Gelman e Rubin (1992) e Geweke (1992).

Para verificar a convergência das cadeias fez-se uso do programaCODA( Conver-gence Diagnosis and Output Analysis Software for Gibbs Sampling Output) (Best, et al. (1997)). Tal programa consiste em um conjunto de fun¸cões utilizadas para análise estat´ıstica e gráfica das cadeias geradas pelo método de Monte Carlo via Cadeias de Markov.

Os métodos gráficos podem ser utilizados em conjunto com outros métodos para verificar a convergência da cadeia. Este procedimento em conjunto é prefer´ıvel à escolha de apenas um deles. Inclusive, segundo Best et al. (1997), Cowles e Carlin (1996) testaram alguns dos métodos implementados no CODA e verificaram que em alguns exemplos em espec´ıfico o software falhou na deteçcão da convergência.

4.4.3 Amostrador de Gibbs

O amostrador de Gibbs está caracterizado como um método de simula¸cão de Monte Carlo via cadeias de Markov. O nome do método se deve a distribui¸cão de Gibbs, que é bastante utilizada nas áreas da Mecânica estat´ıstica e F´ısica Estat´ıstica. O amostrador de Gibbs foi originalmente proposto por Geman e Geman(1984) na área de processamento de imagens, mas somente em 1990 com o trabalho de Gel-fand e Smith (1990) que este método se tornou mais conhecido na comunidade estat´ıstica. Mais detalhes a respeito deste método são encontrados em Gamerman e Lopes (2006). O referido método está implementado no software OpenBugs e WinBugs, e Lunn et al. (2009) discutem conceitos básicos, estrutura e extensão do software.

Este algoritmo é utilizado para simular distribui¸cões desconhecidas de um vetor de parâmetros θ _{= (θ}₁_{, θ}₂_{, ..., θ}_k_{), a partir de simula¸cões de distribui¸cões}

condicio-nais, π(θj|θ−j), j= 1,2, ..., k. Pode-se descrever o algoritmo nos seguinte passos:

1o_{) considere um vetor inicial do tipo(θ}(0) 1 , θ

(0) 2 , ..., θ

(45)

• simuleθ₁(i) de π(θ₁(i−1)_|θ₂(i−1), θ(₃i−1), ..., θ(_ki−1)),

• simuleθ₂(i) de π(θ(₂i−1)_|θ₁(i), θ(₃i−1), ..., θ_k(i−1)), ...

• simuleθ_k(i) de π(θ(_ki−1)_|θ₁(i), θ(₂i), ..., θ_k(i₋)₁).

O algoritmo acima ainda pode ser descrito como segue. Suponha que πθ(θ) =

π(θ1, θ2, ..., θk). Seja a fun¸c˜ao de densidade de probabilidade do vetorθ = (θ1, θ2, ..., θk), al´em disso represente θ

−j = (θ1, θ2, ..., θj−1, θj+1, ..., θk) o vetor obtido a partir de θ

com exclusão da j-ésima variável, e por fim, sejaπθj|θ−j(θj|θ−j) a fun¸cão de densidade

de θ_j _{condicionada a} θ₋_j_{. Portanto para gerar uma amostra de} θ _{= (θ}₁_{, θ}₂_{, ..., θ}_k₎

realiza-se os passos descritos acima.

Este algoritmo fornece uma cadeia de Markov com espa¸co de estado E, onde a fun¸cão de transi¸cão deθ(i−1) _para _θ(i) _{é dada por:}

p(θ(i−1)_{, θ}(i)_{) =} k

Y

j=1

π(θ(_ji−1)_|θ₁(i), ..., θ_j(i₋)₁, θ(_j₊₁i−1), ..., θ(_ki−1)).

(46)

Cap´ıtulo 5

Aplica¸c˜

ao

5.1 Introdu¸c˜

ao

Neste trabalho foi utilizado uma base de dados com 28,26% de censura, corres-pondente a um grupo de 46 pacientes acometidos por leucemia e submetidos a um transplante de medula óssea, conhecido como transplante alogênico, ou seja, quando o paciente recebe, de um familiar, material genético compat´ıvel. Os tempos foram medidos em anos, que variam de 0,03 a 5 anos. Mais detalhes a respeito da base de dados podem ser encontrados em Maller e Zhou (1996) e em Kersey et al. (1987).

Fez-se uma análise de sobrevivência convencional, sem a suposi¸cão da fra¸cão de cura, para verificar qual modelo probabil´ıstico se adequava melhor ao ajuste dos dados utilizando-se as distribui¸cões de probabilidade usuais para tempos de sobre-vida (exponencial, Weibull e Pareto). Em seguida, ajustou-se os modelos demistura padrão e detempo de promo¸cão, considerando as mesmas distribui¸cões para os tem-pos de falhas. Os métodos numéricos para as estima¸cões foram: BFGS (máxima verossimilhan¸ca - MV), método de Laplace e amostrador de Gibbs.

As análises foram realizadas utilizando os pacotes R versão 2.15 (MV e Laplace) e OpenBUGS versão 3.2.1 (Gibbs).

5.1.1 An´

alise Convencional

Para a aplica¸cão em estudo, as expressões das estimativas das fun¸cões de so-brevivência dos modelos exponencial, Weibull e Pareto, obtidos pelo método da máxima verossimilhan¸ca são, respectivamente:

ˆ