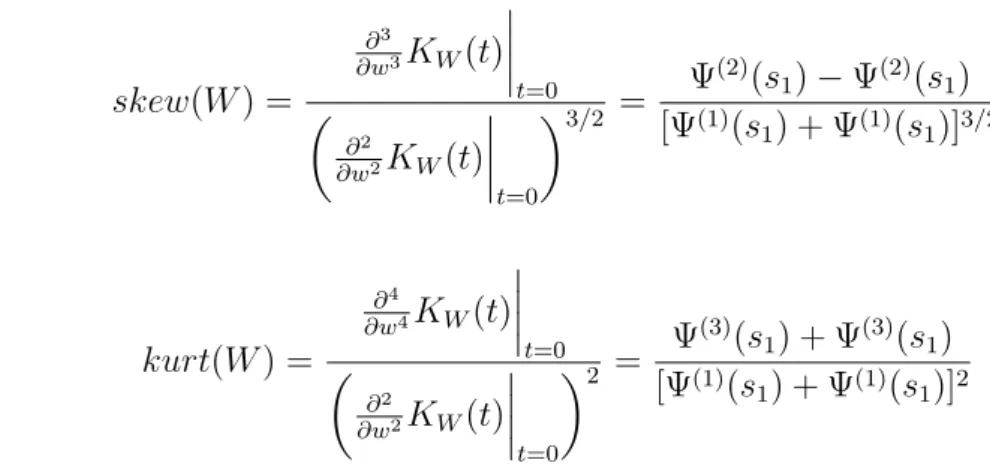A distribuição F generalizada para selecionar modelos de sobrevivência com fração de cura

(1)

Universidade Federal do Rio Grande do Norte

Centro de Ciˆencias Exata e da Terra

Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica

Allyson Fernandes Liandro

A Distribui¸c˜

ao F Generalizada para Selecionar

Modelos de Sobrevivˆ

encia com Fra¸c˜

ao de Cura

(2)

Allyson Fernandes Liandro

A Distribui¸c˜

ao F Generalizada para Selecionar

Modelos de Sobrevivˆ

encia com Fra¸c˜

ao de Cura

Trabalho apresentado ao Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica da Universidade Federal do Rio Grande do Norte, em cumprimento com as exigências legais para obten¸cão do t´ıtulo de Mestre.

´

Area de Concentra¸c˜ao: Probabilidade e Estat´ıstica

Orientadora:

Prof

a

. Dr

a

. Dione Maria Valen¸ca

(3)

Allyson Fernandes Liandro

A Distribui¸c˜

ao F Generalizada para Selecionar

Modelos de Sobrevivˆ

encia com Fra¸c˜

ao de Cura

Trabalho apresentado ao Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica da Universidade Federal do Rio Grande do Norte, em cumprimento com as exigências legais para obten¸cão do t´ıtulo de Mestre.

´

Area de Concentra¸c˜ao: Probabilidade e Estat´ıstica

Aprovado em: / /

Banca Examinadora:

Profa_{. Dr}a_{. Dione Maria Valen¸ca} Departamento de Estat´ıstica - CCET/UFRN

Orientadora

Prof. Dr. Bernado Borba de Andrade Departamento de Estat´ıstica - CCET/UFRN

Examinador Interno

Prof. Dr. Juvˆencio Santos Nobre

(4)

Dedicat´

oria

A todos que me ajudaram nessa conquista.

(5)

Agradecimentos

Primeiramente, agrade¸co a Deus por me dar for¸cas de onde `as vezes nem tinha. Foi mais uma etapa rumo ao meu sonho vencida.

Agrade¸co tamb´em a Nossa Senhora do Carmo. Sei que sempre esteve comigo me protegendo. Obrigado!

Agradecer a minha mãe Rainete pela paciência e por sempre me incentivar até mesmo na minha decisão de ir a Natal cursar o mestrado. Sei que foi dif´ıcil me ver longe, mas sempre voltei quando pude. E ao meu pai Francisco por sempre me orientar a continuar estudando e fazer por onde ser o melhor.

Agrade¸co aos meus irm˜aos Anderson e Adson por todo o apoio e ajuda que sempre me deram. Obrigado por tudo!

Agrade¸co a minha noiva Izabele, por sempre acreditar em mim quando eu nem tinha mais esperan¸cas. Mesmo longe, estavamos sempre juntos. A cada dia acredito mais que você é a pessoa certa! Essa vitória é para você e meu filho, Pedro Emanuel.

`

A minha orientadora Dione Maria Valen¸ca pela rigidez e carinho de uma mãe. Nunca irei esquecer aquelas palavras da Defesa! Você acreditou em mim até nos mo-mentos em que eu não fiz por onde. Obrigado por tudo! Espero ainda trabalhar com você por mais vezes, se assim me permitir.

Ao Professor Bernado Borba de Andrade, pela contribui¸cão desde a Pré-Qualifica¸cão até a Defesa desse trabalho. Mais do que isso, pela forma¸cão acadêmica e pela paciência. Sei que nos veremos novamente algum dia.

Ao Professor Juvêncio Santos Nobre por despertar meu interesse pela Estat´ıstica na época da gradua¸cão na UFC. Não sei o que viu em mim, mas sei que me ajudou o suficiente para não desistir e terminar o curso. Obrigado também por ter aceitado a estar na minha banca de Defesa. Farei o poss´ıvel para atender suas expectativas em mim.

(6)

Aos meus amigos George e Romualdo por tantos momentos vividos na infˆancia. Mesmo nos vendo pouco, sei que nossa amizade vai durar muito!

Aos meus amigos da GC (galera da cal¸cada):

Henrique, por várias vezes me ajudando a continuar em frente e pelas conversas jogadas fora sobre vários assuntos. Ainda é só o come¸co da nossa caminhada!

João, por vários momentos que um deu for¸ca ao outro. Sei que a estrada é ardua, mas seremos recompensandos, tenho certeza!

Hemerson, pelos conselhos e principalmente o incentivo. Sempre jogaremos, al´em de conversa fora, v´arias partidas de video game.

Jo˜ao Felipe, pela amizade de sempre e v´arios papos sobre todos os assuntos. ´

Atila e Saulo por tudo!

Sei que nossos caminhos se separaram, mas sei que um dia nos reuniremos novamente naquela cal¸cada!

A todos os professores que eu tive aula na UFC, em especial ao Professor João Maur´ıcio Araújo Mota pelo incentivo e pela paciência em vários momentos. Obrigado por me auxiliar sempre que precisei, principalmente no momento que procurei um mestrado. Você mostrou a porta e ainda me incentivou a entrar. E agrade¸co também a Professora Silvia Maria de Freitas pela forma¸cão profissional e pessoal. Obrigado também por me ajudar com meu mestrado. Serei grato a todos vocês!

Aos professores do PPGMAE - UFRN, pela amizade e por sempre se preocupar com o aluno: Pledson, Andr´e Pinho, Andr´e Gustavo, Carla Vivacqua e Nir Cohen.

Agrade¸co também a Professora Ivone Salsa pela orienta¸cão na Inicia¸cão a Docência. Me ensinou que a arte de ensinar é tão bela quanto a arte de estudar.

Agrade¸co também aos funcionários do CCET, em especial o Russinho. Quero te ver um dia aqui no Ceará para comer um bom peixe!

Agrade¸co aos meus amigos do PPGMAE, em especial a Antônio Marcos e Anna Rafaella por estar ao meu lado sempre que precisei. Por muitos dias dif´ıceis e muitas alegrias conquistadas. Choramos e rimos juntos! Sei que vocês não puderam ir a minha Defesa, mas sei que estiveram comigo em pensamento e cora¸cão. Agrade¸co ao Rumenick por me ajudar sempre que precisei, principalmente no término desse trabalho! Também agrade¸co a Andressa, Bruno, Jocelânio, Hérica, Alysson L´ıvio, Wênia, Fábio Azevedo (não esquecerei aquelas palavras que me disse antes de ir embora para Fortaleza), Renato, Eduardo, July e tantos outros que estiveram comigo nesse tempo em Natal. Quero ver todos vocês novamente algum dia.

`

A CAPES pelo apoio financeiro.

(7)

“Não há vergonha em errar, vergonha é não ter dado tudo de si por medo de errar.”

(8)

Resumo

A análise de sobrevivência paramétrica modela o tempo até a ocorrência de um evento com base no ajuste de modelos probabil´ısticos fazendo uso frequente de modelos flex´ıveis para a escolha de um modelo mais simples e fácil de interpretar. Nesse sentido, a distribui¸cão F generalizada tem a vantagem de incluir várias distribui¸cões importantes como casos especiais, com Weibull, log-normal, log-log´ıstica, entre outras. Modelos de sobrevivência que tratam de estudos em que um percentual dos indiv´ıduos não apresentam a ocorrência do evento de interesse, mesmo acompanhados por um longo per´ıodo de tempo, são chamados de modelos de longa dura¸cão ou modelos com fra¸cão de cura e vem sendo estudados nos ultimos anos por diversos autores. Neste contexto, este trabalho tem como objetivo o estudo de caracter´ısticas teóricas e computacionais associadas ao ajuste do modelo F generalizado com fra¸cão de cura.

Palavras-chave: Análise de sobrevivência, fra¸cão de cura, F generalizada.

(9)

Abstract

The parametric analysis of survival models the time until the occurrence of an event based on the setting of probabilistic models making frequent use of flexible models for choosing a simpler and easier to interpret model. In this sense, the generalized F distribution has the advantage to include several important distributions as special cases, with Weibull, lognormal, log-logistic and others. Survival models dealing with a study on percentage of individuals do not have the occurrence of the event of interest, whether or not accompanied by a long period of time, they are called long-term survival models or cure rate models and has been studied in recent years by several authors. In this context, this work aims to study theoretical and computational characteristics associated with fitting the generalized F cure rate models.

Keywords: Survival analysis, cure rate, generalized F.

(10)

Sum´

ario

1 Introdu¸c˜ao 1

1.1 Objetivo . . . 2

1.2 Descri¸c˜ao dos cap´ıtulos . . . 2

2 Análise de Sobrevivência 3 2.1 Conceitos básicos . . . 3

2.1.1 Modelo de posi¸c˜ao e escala . . . 4

2.1.2 Censura . . . 5

2.2 Modelos de sobrevivˆencia com fra¸c˜ao de cura . . . 5

2.2.1 Abordagem unificada . . . 6

2.2.2 Modelo de mistura padr˜ao . . . 7

2.2.3 Modelo de tempo de promo¸c˜ao . . . 7

2.2.4 Fun¸c˜ao de verossimilhan¸ca . . . 8

3 A Distribui¸cão F Generalizada com Fra¸cão de Cura 10 3.1 A distribui¸cão F generalizada . . . 10

3.1.1 Reparametriza¸c˜ao proposta em Prentice (1975) . . . 14

3.1.2 Casos particulares da F generalizada . . . 15

3.2 Distribui¸c˜ao F generalizada com fra¸c˜ao de cura . . . 15

3.2.1 Inferˆencia para o modelo FG com fra¸c˜ao de cura . . . 17

4 Aplica¸cões 21 4.1 Câncer de ovário . . . 21

4.2 Cˆancer de Col´on . . . 24

4.3 Dados simulados no R . . . 26

5 Conclus˜oes 29

(11)

A Algumas defini¸c˜oes e demonstra¸c˜oes 31

A.1 Fun¸c˜ao gama e fun¸c˜ao poligama . . . 31

A.2 Fun¸c˜oes beta e beta incompleta . . . 31

A.3 Obten¸c˜ao da fun¸c˜ao de verossimilhan¸ca marginal . . . 32

A.4 Demonstra¸c˜ao para a equa¸c˜ao 3.2 . . . 33

B Comandos no R 36

(12)

Cap´ıtulo 1

Introdu¸c˜

ao

Em modelos de sobrevivência, estamos interessados no tempo até a ocorrência de um evento de interesse, comumente denominado tempo de sobrevivência ou de vida. Em alguns casos, um percentual dos indiv´ıduos pode não apresentar o evento de interesse, mesmo acompanhados por um longo per´ıodo de tempo. Esses modelos são chamados de modelos de sobrevivência com fra¸cão de cura. Os modelos mais conhecidos nesta classe são o modelo de mistura padrão, desenvolvido em Berkson & Gage (1952) e um modelo proposto por Yakovlev et al. (1993), mais tarde chamado demodelo de tempo de promo¸cão. Rodrigues et al. (2009) propõem uma extensão dos modelos de longa dura¸cão na qual os modelos anteriores são casos particulares.

A escolha de submodelos por um modelo mais amplo é de grande importância em várias áreas da estat´ıstica, como, por exemplo, em análise de sobrevivência. A distribui¸cão F generalizada é utilizada por incluir várias outras distribui¸cões muito importantes em modelos de sobrevivência, como a gama generalizada, a log-log´ıstica, a Weibull e a log-normal. Neste sentido, Prentice (1975) discutiu a utiliza¸cão da fam´ılia F generalizada para dados sem censura e uma reparametriza¸cão de forma a facilitar a escolha de submodelos. Kalbfleisch & Prentice (2002) estudam algumas propriedades importantes da distribui¸cão F generalizada. Alguns autores como Hogg & Ciampi (1985) e Brown et al. (1992) relatam problemas na maximiza¸cão da verossimilhan¸ca da F generalizada.

Peng et al. (1998), que representa a principal referência deste trabalho, propõem um modelo de tempo de falha acelerado F generalizado com fra¸cão de cura, com base em um modelo de mistura padrão. Neste artigo o modelo proposto foi utilizado para ajustar dados de sobrevivência de pacientes portadores de linfoma não-Hodgkin. Peng (1999) desenvolve um pacote, chamado gfcure, desenvolvido para ajuste de modelos de sobrevivência F generalizado (e diversos casos particulares) com e sem fra¸cão de

(13)

1.1 Objetivo 2

cura, com base no software estat´ıstico R (R Development Core Team, 2013). Peng et al. (1998) comentam que podem ocorrer problemas de máximos locais na maximiza¸cão da verossimilhan¸ca do modelo de mistura padrão F generalizada.

1.1 Objetivo

O objetivo deste trabalho é estudar o modelo log-F generalizado com fra¸cão de cura com base na extensão proposta por Rodrigues et al. (2009). Especificamente temos como objetivos:

1. Descrever as propriedades te´oricas do modelo log-F generalizada com fra¸c˜ao de cura via abordagem unificada e de alguns submodelos;

2. Estudar os procedimentos de máxima verossimilhan¸ca para a estima¸cão dos pa-râmetros, a implementa¸cão computacional e os procedimentos para a sele¸cão de submodelos;

3. Por fim, usar o modelo de mistura padr˜ao F generalizada para selecionar sub-modelos com fra¸c˜ao de cura, adequados ao ajuste de dados reais, dispon´ıveis na literatura.

1.2 Descri¸c˜

ao dos cap´ıtulos

(14)

Cap´ıtulo 2

An´

alise de Sobrevivˆ

encia

Neste cap´ıtulo fazemos uma breve introdu¸cão aos principais conceitos de análise de sobrevivência. Informa¸cões mais detalhadas podem ser obtidas em Lawless (2003) e Colosimo & Giolo (2006), por exemplo.

2.1 Conceitos b´

asicos

Seja T uma variável aleatória absolutamente cont´ınua e positiva, com fun¸cão de distribui¸cão F, representando o tempo até a ocorrência de um evento.

Definimos a fun¸c˜ao de sobrevivˆencia de T como sendo

S(t) = P(T > t) = Z ∞

t

f(x)dx= 1₋F(t). (2.1) Esta fun¸cão representa a probabilidade de um ´ıtem (ou indiv´ıduo) sobreviver pelo menost unidades de tempo. Algumas vezes S(t) é referida como fun¸cão de confiabili-dade. Por defini¸cão, temos que S(t) é uma fun¸cão decrescente cont´ınua, com S(0) = 1 e S(_∞) = limt→∞S(t) = 0.

A fun¸cão densidade pode ser obtida através da fun¸cão de sobrevivência, da seguinte forma:

f(t) = ₋dS(t)

dt . (2.2)

O risco ou taxa de falha em um intervalo [t, t+ ∆t) ´e definido como sendo a pro-babilidade do evento ocorrer neste intervalo, dado que n˜ao ocorreu antes det, dividida pelo comprimento do intervalo, ∆t.

(15)

2.1 Conceitos b´asicos 4

vência até o tempo t. Então, a fun¸cão de risco associada a T é definida como

h(t) = lim

∆t→0

P(t_≤T < t+ ∆t_|T _≥t)

∆t =

f(t)

S(t). (2.3)

Existem vários modelos paramétricos usados para análise de dados de sobrevivência. Lawless (2003), entre outros autores, descreve estes modelos, onde os principais são a Weibull, log-normal, log-log´ıstica e gama generalizada.

2.1.1 Modelo de posi¸c˜

ao e escala

Uma classe ampla de modelos, apresentado em Lawless (2003), ´e chamada de modelo de posi¸c˜ao de escala, usada para modelar o logaritmo dos tempos de falha. Seja,

Y = logT. Definindo,

Y =µ+σǫ, (2.4)

comµ_∈Reσ > 0, temos queY pertence à fam´ılia de posi¸cão e escala com parâmetros de posi¸cãoµe escalaσ, considerando queǫ tem uma distribui¸cão que não depende dos parâmetros desconhecidos.

Podemos ent˜ao representar a fun¸c˜ao densidade de Y por

fY(y;µ, σ) = 1

σf

y₋µ σ

, y _∈R (2.5)

em que af(_·) é uma fun¸cão densidade associado a ǫ. A fun¸cão de sobrevivência de Y é

SY(y;µ, σ) =S

y₋µ σ

, y _∈R (2.6)

com S(_·) representando a fun¸c˜ao de sobrevivˆencia associado a ǫ.

Podemos tamb´em representar a fun¸c˜ao risco desse modelo a partir de (2.3). Logo

hY(y;µ, σ) =

fY(y;µ, σ)

SY(y;µ, σ)

.

(16)

2.2 Modelos de sobrevivˆencia com fra¸c˜ao de cura 5

2.1.2 Censura

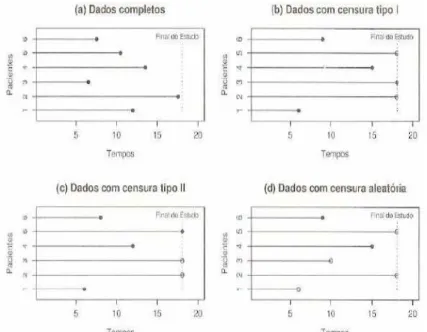
Geralmente dados de tempo de vida apresentam caracteristicas especiais, devido a presen¸ca de observa¸cões censuradas, isto é, para alguns indiv´ıduos em estudo não sabemos seu tempo exato de vida. O tipo mais comum de censura é à direita, em que o tempo até a ocorrência do evento de interesse é superior ao que foi registrado. Consideramos três mecanismos de censura à direita:

• Tipo I: Oberva¸cões são acompanhadas até um per´ıdodo pré-estabelecido de tempo.

• Tipo II: Observa¸cões são acompanhadas até obter-se um número pré-determinado de falhas.

• Aleatório: Observa-se este tipo de censura quando um indiv´ıduo é retirado do estudo por uma causa alheia ao próprio estudo.

Figura 2.1: Tipos de censura, sendo as esferas negras as falhas e as brancas as censuras. (Colosimo & Giolo, 2006)

Neste trabalho consideramos a censura aleat´oria.

2.2 Modelos de sobrevivˆ

encia com fra¸c˜

ao de cura

(17)

e os modelos de sobrevivência com presen¸ca de indiv´ıduos imunes são chamados de modelos com fra¸cão de cura (também chamados de modelos de longa dura¸cão).

2.2.1 Abordagem unificada

Rodrigues et al. (2009) propõem uma extensão dos modelos de longa dura¸cão. Para uma visão geral do modelo supomos que, para cada indiv´ıduo em um determinado estudo,N denota o número de causas ou fatores de risco competindo para a ocorrência do evento de interesse, com distribui¸cão de probabilidadepθ(n) =Pθ(N =n), sendo θ

o parâmetro da distribui¸cão. Seja também, Ri os tempos até a ocorrência do evento devido à i-ésima causa em que R1, ..., RN são i.i.d., com fun¸cão de sobrevivência

SR(_·) = 1₋FR(_·).

SejaT o tempo at´e a ocorrˆencia do evento de interesse, definido como

T = min_{R0, R1, . . . , RN},

com P(R0 = ∞) = 1. Com isso se N = 0 o evento de interesse nunca ocorrer´a. As

variáveis aleatóriasRi eN são variáveis latentes, ou seja, não observáveis, enquantoT é uma variável observável. A fun¸cão de sobrevivência nesse caso é dada por:

Sp(t) = P(T > t)

= P(T > t, N = 0) +P(T > t, N _≥1)

= P(T > t_|N = 0)Pθ(N = 0) +P(T > t_|N _≥1)Pθ(N _≥1) = pθ(0) +

∞

X

n=1

pθ(n)S(t)n (2.7)

em que, P(T > t_|N = 0) = 1 e Pθ(N = 0) = pθ(0). A fun¸cão de sobrevivência Sp(t) é dita imprópria, pois o limt→∞Sp(t)>0.

A fra¸c˜ao de cura ´e definida como:

lim

t→∞Sp(t) =Pθ(N = 0) =pθ(0)

que é também interpretado como a propor¸cão de indiv´ıduos em que nunca vai ocorrer o evento de interesse.

(18)

em (2.8), de acordo com (2.2):

fp(t) =

∞

X

n=1

npθ(n)f(t)S(t)n−1

. (2.8)

Em análise de sobrevivência com fra¸cão de cura os modelos mais conhecidos são os modelos de mistura padrão e tempo de promo¸cão. O modelo unificado possui ambos como casos particulares (Rodrigues et al., 2009).

2.2.2 Modelo de mistura padr˜

ao

Esse modelo paramétrico consiste em uma mistura de distribui¸cões representando a fun¸cão de sobrevivência dos indiv´ıduos suscet´ıveis ao evento de interesse, que irão falhar, e a outra uma fun¸cão degenerada que permite tempos de vida infinitos para os imunes.

Então, sejaN uma variável aleatória seguindo a distribui¸cão Bernoulli com parâme-tro (1 - θ). O modelo de sobrevivência com fra¸cão de cura, visto como caso particular de (2.8) (Rodrigues et al., 2009), é dado por:

Sp(t) =θ+ (1₋θ)S(t) (2.9)

sendopθ(0) =θ a fra¸c˜ao de cura.

As fun¸c˜oes densidade e risco para este modelo s˜ao dadas, respectivamente, por

fp(t) = (1₋θ)f(t) e

hp(t) =f(t) 1−θ

θ+ (1₋θ)S(t). Ver Maller & Zhou (1996) para mais informa¸c˜oes.

2.2.3 Modelo de tempo de promo¸c˜

ao

Esse modelo consiste em pressupor a existência de várias causas que competem entre si para ocorrer no indiv´ıduo o evento de interesse, em que o número de causas é considerada uma variável latenteN com distribui¸cão Poisson com parâmetro θ. Então pode-se mostrar (Fonseca, 2009) que neste caso (2.8) se reduza a:

Sp(t) = e

−_θ₍₁−_S₍_t₎₎

(19)

em que S(t) é uma fun¸cão de sobrevivência dos temposRi, comi= 1, ..., N epθ =e

−_θ

a fra¸c˜ao de cura.

As fun¸c˜oes densidade e risco para este modelo s˜ao dadas, respectivamente, por:

fp(t) =θf(t)e

−_θ₍₁−_S₍_t₎₎

e

hp(t) =θf(t).

Ver Ibrahim, Chen & Sinha (2001) para mais informa¸c˜oes.

Figura 2.2: Compara¸cão entre a fun¸cão de sobrevivência da Weibull, Weibull com modelo de mistura padrão e tempo de promo¸cão.

2.2.4 Fun¸c˜

ao de verossimilhan¸ca

Suponha uma amostra com n indiv´ıduos e para cada indiv´ıduo i, i = 1, ..., n, s˜ao associados essas vari´aveis:

• Ni: Variável aleatória discreta com fun¸cão de probabilidadePθ(Ni =ni) = pθ(ni), sendo θ um vetor de parâmetros desconhecidos;

(20)

• T∗

i: Tempo de falha observado, dado por T

∗

i = min{Ti;Ci}, com Ti = min{Ri0,

Ri1, ..., RiNi} eCi o tempo de censura para o indiv´ıduoi; • δi: Indicador de falha, sendo δi =

(

1, seTi ≤Ci; 0, seTi > Ci.

O conjunto dos dados completos ´e representado por Dc = (n,T

∗′

,δ′,N)′

, sendo

T∗

= (T∗

1, ..., T

∗

n)

′

,δ = (δ1, ..., δn)

′

eN= (N1, ..., Nn)

′

e o conjunto de dados observados porD= (n,T∗′

,δ′)′

. Seja φ = (ψ′

, θ′

)′

o vetor de parâmetros. A fun¸cão de verossimilhan¸ca de φ, cor-respondente ao conjunto dos dados completos Dc, admitindo censura não-informativa, é dada por:

L(φ;Dc) = n Y

i=1

[S(ti;ψ)ni]1−δi

[nif(ti;ψ)S(ti;ψ)ni

−1

]δipθ(ni) =

n Y

i=1

S(ti;ψ)ni−niδi

[nif(ti;ψ)]δiS(ti;ψ)niδi

−δi

pθ(ni) =

n Y

i=1

[S(ti;ψ)]ni−δi

[nif(ti;ψ)]δipθ(ni).

Como a equa¸cão anterior depende das variáveis latentesNiutiliza-se na prática uma verossimilhan¸ca marginal, fazendo o somatório da distribui¸cão conjunta (T∗

i , δi, Ni) com rela¸cão às variáveis não observáveis Ni.

Então a fun¸cão de verossimilhan¸ca marginal (Ver Apêndice A.3) é dada por

L(φ;D) = n Y

i=1

[Sp(ti;φ)ni]1−δi

[fp(ti;φ)]δi. (2.11) Por razões teóricas e computacionais, é prefer´ıvel trabalhar com o logaritmo da fun¸cão de verossimilhan¸ca para a estima¸cão dos parâmetros, como dada abaixo:

l(φ;D) = logL(φ;D) = log

( _n Y

i=1

[Sp(ti;φ)ni]1

−δi

[fp(ti;φ)]δi )

= n X

i=1

(21)

Cap´ıtulo 3

A Distribui¸c˜

ao F Generalizada com

Fra¸c˜

ao de Cura

Nesse cap´ıtulo apresentamos a fun¸cão de distribui¸cão F generalizada conforme mos-trado no artigo de Peng et al. (1998), suas propriedades, uma outra parametriza¸cão sugerida em Prentice (1975), além dos seus submodelos. As demonstra¸cões para alguns resultados encontram-se no Apêndice A.

3.1 A distribui¸c˜

ao F generalizada

Segundo Johnson, Kotz & Balakrishnan (1992), várias “generaliza¸cões” e diferen-tes parametriza¸cões da distribui¸cão F foram estudadas ao longo do tempo. A forma descrita no livro de Kalbflesh & Prentice (2002) é a mais utilizada, pois leva em con-sidera¸cão o modelo de posi¸cão e escala para se construir a distribui¸cão.

SejaT0 uma v.a. seguindo a distribui¸c˜ao F com 2s1 e 2s2 graus de liberdade (Mood,

Graybill & Boes, 1974) cuja a fun¸c˜ao densidade ´e dada por:

fT0(t0) =

s1

s2

s1

ts1−1

0

B(s1, s2)

1 +

s1

s2

t0

s1+s2 t0 ∈R

+_, _(3.1)

com s1, s2 >0 e B(s1,s2) a fun¸c˜ao beta (ver Apˆendice A.2).

Defini¸c˜ao

Seja T = aTb

0 (Johnson, Kotz & Balakrishnan, 1992). A v. a. T ´e dita ter

distri-bui¸cão F generalizada com os parâmetros a, b, s1 e s2, com a ∈ R e b > 0. A fun¸cão

(22)

3.1 A distribui¸c˜ao F generalizada 11

densidade de T é dada a seguir (ver demonstra¸cão no Apêndice A.4)

fT(t) =

s1

s2

s1

(ab)−₁

t a

s1

b−1

B(s1, s2)

1 + s1 s2 t a 1

b(s1+s2)

, t >0. (3.2) A distribui¸cão F generalizada, que foi descrita em Prentice (1975), tem como uma das vantagens incluir outras distribui¸cões bastante conhecidas na literatura como casos particulares, a Weibull, log-normal, log-logistica e a gama generalizada, dentre outras. Pode-se escreverY = logT na forma do modelo de posi¸cão e escala, como dada em (2.4). Dessa maneira,

Y =µ+σW

em que µ = loga, o parâmetro de posi¸cão, σ = b, o parâmetro de escala e sendo

W = logT0.

A vari´avel W = logT0 representa uma log-F com parˆametros s1 e s2 (ver Peng et

al., 1998 e Apêndice A.5), com fun¸cões de densidade, sobrevivência e de risco dadas, respectivamente, por

fW(w) =

s1

s2

s1

ews1

B(s1, s2)

1 + s1 s2 ew

(s1+s2), w ∈R, (3.3)

SW(w) =Ik(s2, s1) (3.4)

e

hW(w) =

us2(1

−u)s1

B(s1, s2)Ik(s2, s1)

,

com u= 1

1+s1

s2

ew e k = s2(s2+s1e w₎−1

, sendo Ix(a, b) a fun¸c˜ao beta incompleta (ver Apˆendice A.2).

Algumas varia¸c˜oes de s1 e s2 refletem no comportamento das fun¸c˜oes de

sobrevi-vˆencia e de risco, como podem ser vistos nas Figuras 3.1 e 3.2.

A fun¸c˜ao geradora de momentos de W (Kalbfleisch & Prentice, 2002) ´e dada por

MW(t) =

Γ(s1 +t)Γ(s2 −t)

Γ(s1)Γ(s2)

s1

s2

(23)

Figura 3.1: Gráficos da fun¸cão de sobrevivência de W.

Figura 3.2: Gr´aficos da fun¸c˜ao risco de W.

A partir da fun¸c˜ao geradora de momentos podemos encontrar a fun¸c˜ao geradora de cumulantes:

KW(t) = logMW(t)

= log(Γ(s1 +t)) + log(Γ(s2+t))−log Γ(s1)−log Γ(s2) +tlog

s2

s1

A esperan¸ca e variˆancia de W podem ser definidas a partir da fun¸c˜ao geradora de cumulantes:

E(W) = ∂

∂wKW(t)

t=0

= Ψ(s1)−Ψ(s2) + log

s2

s1

e

V ar(W) = ∂

2

∂w2KW(t)

t=0

= Ψ(1)(s1) + Ψ(1)(s2)

com Ψ(a) e Ψ(1)₍_a_{) são decorrentes da fun¸cão poligama (ver Apêndice A.1).}

(24)

fun¸c˜ao geradora de cumulantes:

skew(W) = ∂3

∂w3KW(t)

t=0 ∂2

∂w2KW(t)

t=0

3/2 =

Ψ(2)₍_s

1)−Ψ(2)(s1)

[Ψ(1)₍_s

1) + Ψ(1)(s1)]3/2

e

kurt(W) = ∂4

∂w4KW(t)

t=0 ∂2

∂w2KW(t)

t=0 2 =

Ψ(3)₍_s

1) + Ψ(3)(s1)

[Ψ(1)₍_s

1) + Ψ(1)(s1)]2

com Ψ(2)₍_a_{) e Ψ}(3)₍_a_{) s˜ao decorrentes da fun¸c˜ao poligama.}

Os parˆametros s1 e s2 controlam a assimetria e curtose da distribui¸c˜ao. Quando

s1 > s2 a distribui¸cão é assimétrica a direita e se s1 < s2 a assimetria é a esquerda. No

caso des1 =s2 a distribui¸cão é simétrica. A Figura 3.3 mostra como fica a densidade

de acordo com a varia¸cão dos parâmetros de forma da distribui¸cãoW.

Figura 3.3: Gr´aficos da fun¸c˜ao densidade de W.

(25)

generaliza¸c˜ao do modelo de posi¸c˜ao e escala:

fY(y) = 1

σfW

y₋µ σ = s1 s2 s1

e(y−σµ)s1

σB(s1, s2)

1 + s1 s2

e(y−σµ)

(s1+s2), y ∈R (3.5)

e

SY(y) = SW

y₋µ σ

=Ik(s2, s1) (3.6)

sendok =s2

s2+s1e

y−µ σ

−1

.

Dizemos que Y tem distribui¸c˜ao log-F generalizada e consideramos com nota¸c˜ao

Y _∼logF G(µ, σ, s1, s2).

3.1.1 Reparametriza¸c˜

ao proposta em Prentice (1975)

Prentice (1975) propõe uma nova parametriza¸cão para o modelo logFG para fa-cilitar a discrimina¸cão entre modelos. Nesta proposta s1 e s2 são substitu´ıdos pelos

parˆametrosq ep, sendoq _∈R ep_≥0, em que

q=

1

s1 −

1 s2 1 s1 + 1 s2

−1/2

e p= 2

s1+s2

.

Equivalentemente:

s1 =

2

q2_{+ 2}_p₊_q₍_q2_{+ 2}_p₎1/2 e s2 =

2

q2_{+ 2}_p₋_q₍_q2_{+ 2}_p₎1/2.

Para completar a parametriza¸c˜ao, definimosδ = (s−1

1 +s

−1

2 )1/2 = (q2+ 2p)1/2.

Definimos σ=η/δ. A forma do modelo de posi¸c˜ao e escala para este caso ´e:

Y =µ+ η

δW

A fun¸c˜ao densidade de probabilidade e de sobrevivˆencia de Y ficam:

fY(y) =

δ ηfW

(y₋µ)δ η

(26)

3.2 Distribui¸c˜ao F generalizada com fra¸c˜ao de cura 15

e

SY(y) =SW

(y₋µ)δ η

. (3.8)

Segundo Cox (2008), a substitui¸cão final deσ=η/δnão é necessária, mas tem uma vantagem de garantir que tanto a F generalizada e a gama generalizada vão estimar o mesmo parâmetro de escala, que é útil para a interpreta¸cão do modelo. Por outro lado, a parametriza¸cão da forma da fun¸cão risco da F generalizada depende da razão

η/δ no lugar deσ.

3.1.2 Casos particulares da F generalizada

A distribui¸cão F generalizada é vista como uma grande fam´ılia de modelos co-nhecidos em análise de sobrevivência. Peng et al. (1998) e Cox (2008) abordam os relacionamentos da F generalizada com outros modelos, como descritos na tabela a seguir:

Tabela 3.1: Modelos obtidos atrav´es do modelo F generalizado

Restri¸c˜oes nos parˆametros

Modelo para T Densidade padr˜ao Original Prentice (1975)

gama generalizada s2→ ∞ p = 0 fW(w) = | q|

Γ(q−₂₎(q −₂

)q−2

e[q−1

w−_q−2

exp(qw)]_{, se}_q₆_{= 0}

log´ıstica s1=s2 = 1 p = 1 e q = 0 fW(w) = ew

(1 +ew₎2

log-normal s1, s2→ ∞ p = q = 0 fW(w) =

1

√

2πe −w

2 2

Weibull s1= 1 es2→ ∞ p = 0 e q = 1 fW(w) =ew−e w

3.2 Distribui¸c˜

ao F generalizada com fra¸c˜

ao de cura

Considere uma amostra de tamanho n. Para o i-´esimo individuo da amostra, com

(27)

ocorrência do evento devido àj-ésima causa e considere aqui que logRij, são variáveis aleatórias i.i.d. seguindo a distribui¸cão logF generalizada com parâmetrosµ,σ,s1 es2,

com fun¸cão de densidade e de sobrevivência denotadas porfR(·) e fun¸cãoSR(·), dadas respectivamente pelas expressões (3.5) e (3.6).

Definimos tamb´em Ti = min{Ri0, Ri1, ..., RiNi}, sendo Ri0 tal que P(R0 =∞) = 1

eYi = log(Ti). Então, de acordo com abordagem unificada para modelos com fra¸cão de cura descrita no Cap´ıtulo 2, as fun¸cões de sobrevivência e densidade de Yi , são dadas respectivamente por

Sp(yi;φ) = pθ(0) +

∞

X

ni=1

pθ(ni)SR(y)ni (3.9) e

fp(yi;φ) = fR(y)

∞

X

ni=1

nipθ(ni)SR(y)ni

−1

, (3.10)

sendoφ= (µ, σ, s1, s2,θ) o vetor de parametros efR(·) eSR(·) as fun¸c˜oes de densidade

e sobrevivˆencia das vari´aveis latentesRij.

Para os casos particulares em que Ni tem distribui¸cão Bernoulli(1 - θ) (modelo de mistura) e Ni tem distribui¸cão de Poisson(θ) podemos mostrar que as fun¸cões de sobrevivência e densidade são:

• Modelo de mistura padr˜ao

Sp(y;φ) = θ+ (1₋θ)SR(y) (3.11) e

fp(y;φ) = (1₋θ)fR(y). (3.12) • Modelo de tempo de promo¸c˜ao

Sp(y;φ) = exp[₋θ(1₋SR(y))] e

(28)

3.2.1 Inferˆ

encia para o modelo FG com fra¸c˜

ao de cura

Considere o conjunto dos dados observ´aveis representados por D = (n,Y∗′

,δ′)′

, em que Y∗

= (Y∗

1, ..., Y

∗

n)

′

, sendo Y∗

i = min{logTi,logCi} e Ci o tempo de censura,

i-´esimo indiv´ıduo, eδ = (δ1, ..., δn)

′

representa o vetor de indicadores de falha/censura. De acordo com a descri¸cão dada na Se¸cão 2.2.4, obtemos o logaritmo da fun¸cão de verossimilhan¸ca marginal para o vetor de parâmetros desconhecidosφ= (µ, σ, s1, s2,θ)

′

como

l(φ;D) = n X

i=1

(1₋δi) log[Sp(yi;φ)] +δilog[fp(yi;φ)]. (3.13)

Estima¸c˜ao dos Parˆametros

Com base em (3.13) podemos usar o método da máxima verossimilhan¸ca, que con-siste em obter estimativas dos parâmetros do modelo os valores que maximizam o logaritmo da fun¸cão de verossimilhan¸ca. Desejamos então resolver o sistema de equa-¸cões:

U(φ) = ∂l(φ;D)

∂φ =0

Segundo Peng et al. (1998) algumas dificuldades computacionais surgem em maxi-mizar a fun¸cão de verossimilhan¸ca no modelo de mistura F generalizado. As fun¸cões de densidade e sobrevivência de uma distribui¸cão F generalizada dependem de uma fun¸cão beta e uma rela¸cão de beta incompleta, o que as torna dif´ıcil avaliar com preci-são quando s1, s2 e σ tem valores extremos. Outros problemas são de máximos locais

e a obten¸c˜ao das derivadas da verossimilhan¸ca em rela¸c˜ao a s1 e s2 para maximizar a

verossimilhan¸ca do modelo de mistura padr˜ao.

Peng et al. (1998) descrevem em seu artigo um pacote do S-Plus chamadogfcure, desenvolvido para ajustar o modelo F generalizado com fra¸cão de cura no caso parti-cular do modelo de mistura padrão. Em 2005 o pacote é disponibilizado no software

R e é usado em conjunto com o pacote survival. Além de estimar os parâmetros relacionados ao modelo de tempo de falha acelerado, também estima os parâmetros re-lacionados a fra¸cão de cura. As distribui¸cões que podem ser utilizadas nogfcure são, além da F generalizada: exponencial, Weibull, log-normal, gama, rayleigh, log-log´ıstica, log-log´ıstica generalizada e a gama generalizada estendida.

(29)

doR, sendo necessário fazer um download dos arquivos para utilizá-lo, o que dificulta o acesso pelo usuário comum. Não houve atualiza¸cão desde de 2005, o que deixa o programa um pouco defasado.

Contudo, o pacote gfcure vem sendo utilizado por diversos autores para ajuste modelos em aplica¸cões a dados de sobrevivência com fra¸cão de cura: Peng & Carrier (2002) fazem um estudo de simula¸cão que compara os modelos paramétricos e semipa-ramétricos de fra¸cão de cura. Le et al. (2007) ajustam modelos com fra¸cão de cura em dados sobre a leucemia linfoblástica aguda em adultos. Martinez et al. (2007) estudam dados relativos ao retorno de doadores voluntários de sangue e ajustam ao modelo gama generalizada estendida com fra¸cão de cura. Hubben et al. (2008) estudam o tratamento de pacientes infectados com HIV na Itália usando para isso o modelo log-normal. Con-lon et al. (2011) propõem um método de imputa¸cão múltipla para dados censurados em estudos de câncer colorretal com base no modelo log-normal com fra¸cão de cura. Em todos os casos, as estimativas foram feitas com o aux´ılio do pacote gfcure.

Sele¸c˜ao de Modelos com Fra¸c˜ao de Cura

A distribui¸c˜ao F generalizada tem como uma de suas vantagens a possibilidade de escolha de submodelos, que facilitam na an´alise de dados. Para isso, desejamos selecionar o modelo mais adequado para o ajuste.

O teste da razão de verossimilhan¸cas é bastante utilizado para a escolha de mode-los. Contudo, para testar alguns submodelos da F generalizada a hipótese nula coloca o parâmetro na fronteira do espa¸co paramétrico (Peng et al., 1998), mesmo com a para-metriza¸cão proposta por Prentice (1975), e isso representa uma viola¸cão das condi¸cões de regularidade. Logo, não se pode garantir a distribui¸cão assintótica qui-quadrado da estat´ıstica da razão de verossimilhan¸cas.

Desta forma, alternativas para o teste da raz˜ao de verossimilhan¸cas s˜ao:

• Método gráfico: Um método bastante conhecido em análise de sobrevivência compara a curva estimada de Kaplan-Meier (Kaplan & Meier, 1958) com as curvas de sobrevivência estimadas conforme os modelos propostos. O modelo mais adequado é aquele em que sua curva de sobrevivência mais se aproximar da curva do estimador Kaplan-Meier.

• AIC: Chamado de critério de informa¸cão Akaike, desenvolvido por Akaike (1974). AIC é um ´ındice de ajuste que leva em considera¸cão a parcimônia do modelo com uma penaliza¸cão pelo número de parâmetros no modelo. O critério é definido por

(30)

sendo k é o número de parâmetros. O AIC, no entanto, não funciona bem na presen¸ca de efeitos aleatórios.

Quanto menor for o valor do AIC, mais adequado ´e o modelo para um determi-nado conjunto de dados.

• BIC: Chamado de critério de informa¸cão Bayesiano, desenvolvido por Schwarz (1978), leva em considera¸cão tanto a parcimônia do modelo quanto o número de parâmetros que deve ser estimados para atingir esse grau particular de ajuste, através da imposi¸cão de uma penalidade para o aumento do número de parâ-metros. Diferentemente do AIC, a penalidade para o aumento do número de parâmetros no BIC é maior. O critério é definido por

BIC =₋2lφ, Db +klog(n) sendo k é o número de parâmetros e n o tamanho da amostra.

Da mesma forma que o AIC, quanto menor o valor do BIC, mais adequado ´e o modelo.

Uma simula¸cão foi feita a fim de avaliar a eficácia dos métodos AIC e BIC para o modelo F generalizado com fra¸cão de cura, com parâmetros µ = 3, σ = 5, s1 = 10 e

s2 = 7. Os tamanhos da amostra variam entre 50, 100, 500, 1000 e 5000. As fra¸c˜oes

de cura s˜ao, para esse caso, de 10%, 30% e 50%. E as censuras s˜ao: 30% e 50% de censura. Os resultados seguem na Tabela 3.2.

Tabela 3.2: Simula¸c˜ao para avaliar o desempenho do AIC e BIC para o modelo F generalizado com fra¸c˜ao de cura.

Tempos 50 100 500 1000 5000 30% censura

π(%) AIC BIC AIC BIC AIC BIC AIC BIC AIC BIC

10 172.92 182.48 384.91 397.94 1915.50 1936.57 3796.33 3820.87 19380.40 19412.99 30 205.45 215.01 384.28 397.31 2052.38 2073.45 4208.03 4232.56 20995.23 21027.81 50 227.63 237.19 410.12 423.14 1904.93 1926 3876.36 3900.90 18062.57 18095.16 50% censura

π(%) AIC BIC AIC BIC AIC BIC AIC BIC AIC BIC

10 160.13 169.69 314.67 327.69 1578.48 1599.55 3135.80 3160.34 14408.55 14441.14 30 200.77 210.33 353.83 366.86 2113.40 2134.47 3280.83 3305.36 15568.88 15601.46 50 195.37 204.93 365.18 378.20 1884.68 1905.76 3867.39 3891.93 18896.60 18929.19

(31)

(32)

Cap´ıtulo 4

Aplica¸c˜

oes

Neste cap´ıtulo usamos o modelo de mistura padrão F generalizada para a escolha de submodelos entre gama generalizada, log-log´ıstica, log-normal e Weibull, para ajustar dois conjuntos de dados dispon´ıveis no R. O ajuste dos modelos foi realizado com base no logaritmo da fun¸cão de verossimilhan¸ca (3.13) considerando as fun¸cões populacionais de sobrevivênciaSp e de densidadefp dadas respectivamente em (3.11) e (3.12). Foram utilizados os métodos de sele¸cão descritos na Se¸cão 3.2.1 para cada conjunto de dados. Após a escolha do modelo mais adequado, as estimativas desse modelo são apresentadas. Todos os procedimentos foram realizados com base no no softwareR 3.02, com o aux´ılio do pacotegfcure.

Na primeira aplica¸cão o tamanho da amostra é bastante pequeno. Como os resul-tados são assintóticos e com o cuidado já dito na Se¸cão 3.2.1, essa aplica¸cão será um exemplo de como é feito o procedimento de escolha de modelos.

4.1 Cˆ

ancer de ov´

ario

O estudo a seguir trata sobre os tempos de vida ou censura em dias de 26 pacientes com câncer de ovário, dispon´ıveis no R com o nome ovarian. O estudo foi realizado por uma Cooperativa de Oncologia Ocidental e publicado por Edmunson et al. (1979). O percentual de censura dos dados é de 56%.

Os tempos m´ınimos e m´aximos observados no estudo foram de 59 dias e 1227 dias. Segue abaixo algumas estat´ısticas descritivas dos tempos em rela¸c˜ao ao “status” de falha ou censura.

(33)

4.1 Cˆancer de ov´ario 22

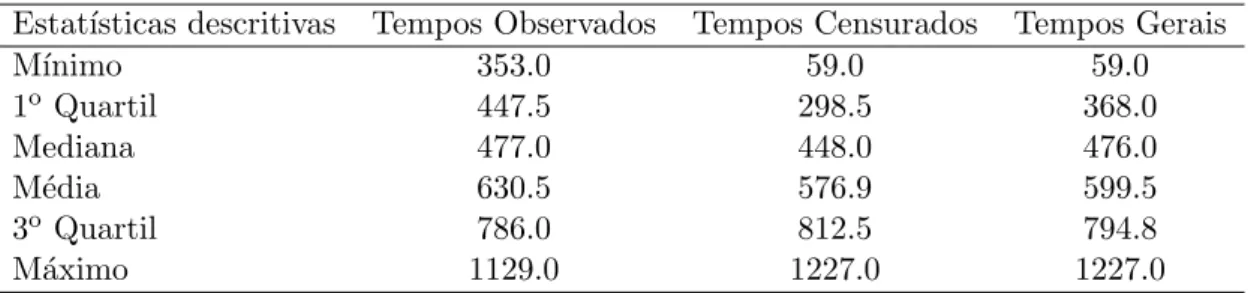
Tabela 4.1: Estat´ısticas descritivas para os tempos de vida de pacientes com cˆancer de ov´ario, em dias.

Estat´ısticas descritivas Tempos Observados Tempos Censurados Tempos Gerais

M´ınimo 353.0 59.0 59.0

1o Quartil 447.5 298.5 368.0

Mediana 477.0 448.0 476.0

M´edia 630.5 576.9 599.5

3o Quartil 786.0 812.5 794.8

M´aximo 1129.0 1227.0 1227.0

Na Figura abaixo, tem-se o histograma e boxplot dos tempos até a falha ou censura das pacientes com câncer de ovário. No boxplot verifica-se uma maior presen¸ca de dados censurados, indicando uma que pode haver uma parcela de pacientes curados ou imunes ao evento de interesse.

Figura 4.1: Histograma e boxplot para os tempos de vida de pacientes com cˆancer de ov´ario, em dias.

Verificaremos alguns modelos na tentativa de saber qual que se melhor ajusta aos dados. Inicialmente consideramos o ajuste de um modelo Weibull sem fra¸c˜ao de cura e notamos (Figura 4.2) que este modelo parece n˜ao se ajustar bem aos dados.

(34)

4.1 Cˆancer de ov´ario 23

Figura 4.2: Compara¸cão entre Kaplan-Meier e a fun¸cão de sobrevivência Weibull.

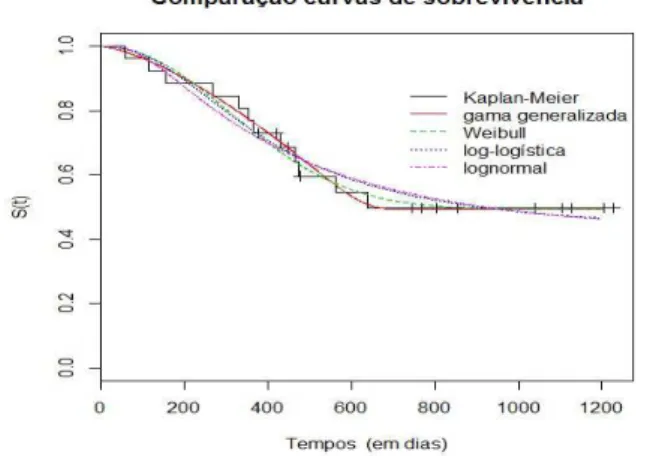
Figura 4.3: Compara¸c˜ao entre modelos.

A Figura 4.3 mostra que os modelos de mistura gama generalizada e Weibull aderem bem aos dados, observando a presen¸ca de uma longa dura¸c˜ao em uma parcela dos parcientes.

A partir da Tabela 4.2 podemos notar que os valores das estat´ısticas AIC e o BIC apontam para o modelo de mistura padrão Weibull como melhor modelo neste caso, o que está de acordo com o resultado da análise gráfica.

Tabela 4.2: Compara¸c˜ao entre os modelos.

Modelo No_{de Parˆametros} _AIC _BIC

F Generalizada 5 63.71 76.73 gama generalizada 4 60.57 70.99 log-normal 3 62.82 70.64 log-log´ıstica 3 62.27 70.09 Weibull 3 60.57 68.39

(35)

4.2 Cˆancer de Col´on 24

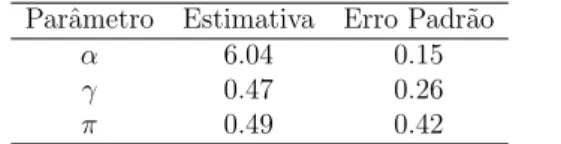
Tabela 4.3: Estimativas para o modelo Weibull.

Parˆametro Estimativa Erro Padr˜ao

α 6.04 0.15

γ 0.47 0.26

π 0.49 0.42

A fra¸c˜ao de cura estimada para este caso ´e de aproximadamente 49%.

4.2 Cˆ

ancer de Col´

on

O estudo a seguir publicado em Moertel et al. (1990) considera dados sobre trata-mento quimioterápico para câncer de colón. Foram observados os tempos de vida de 1858 pacientes onde registrou-se os tempos até a ocorrência do evento ou até a censura (em dias). O percentual de censura dos dados é de 50%.

Os tempos m´ınimos e m´aximos observados no estudo foram de 8 dias e 3329 dias. Segue na Tabela 4.4 algumas estat´ısticas descritivas dos tempos em rela¸c˜ao ao “status” de falha ou censura.

Tabela 4.4: Estat´ısticas descritivas para os tempos de vida de pacientes com cˆancer de col´on, em dias.

Estat´ısticas descritivas Tempos Observados Tempos Censurados Tempos Gerais

M´ınimo 8 19 8

1o _Quartil ₅₂₆ ₅₉₁ ₅₆₆

Mediana 1814 1937 1855 M´edia 1503 1582 1538 3o _Quartil ₂₂₉₇ ₂₃₅₆ ₂₃₃₁

M´aximo 3309 3329 3329

Na Figura 4.4 tem-se o histograma e boxplot dos tempos até a falha ou censura das pacientes com câncer de cólon. No boxplot verifica-se uma grande presen¸ca de dados at´ıpicos.

(36)

4.2 Cˆancer de Col´on 25

Figura 4.4: Histograma e boxplot para os tempos de vida de pacientes com cˆancer de col´on, em dias.

Os valores das estat´ısticas AIC e BIC são apresentados na Tabela 4.5, onde podemos concluir que o modelo que melhor ajusta aos dados é o modelo de mistura log-log´ıstica, apesar dos valores de quase todos os outros modelos estarem bem próximos.

Modelo No _{de Parˆametros} _AIC _BIC

Na Figura 4.6, é observado que o risco do paciente vir a óbito cresce até o 500o _dia

(37)

4.3 Dados simulados no R 26

Figura 4.6: Fun¸cão de risco ajustada pelo modelo log-log´ıstica para os dados de câncer de colón.

Na Tabela 4.6 temos as estimativas dos parˆametros e erros padr˜oes para o modelo log-log´ıstico.

Tabela 4.6: Estimativas para o modelo log-log´ıstico.

α 6.53 0.05

γ 0.65 0.03

π 0.41 0.06

A fra¸c˜ao de cura estimada para este caso ´e de aproximadamente 41%.

4.3 Dados simulados no R

Nesse caso, o conjunto de dados foi gerado a partir da F generalizada com os parˆametros: µ = 3, σ = 5, s1 = 10 e s2 = 7. O tamanho da amostra ´e de 200 e a

porcentagem de censura nos dados ficaram em torno de 30%.

Os tempos min´ımos e m´aximos que foram gerados s˜ao: 0.03 unidades de tempo e 596.40 unidades de tempo. Na Tabela abaixo, tem-se as estat´ısticas descritivas do tempos de vida simulados:

Tabela 4.7: Estat´ısticas descritivas para os tempos de vida simulados, em unidades de tempo.

Estat´ısticas descritivas Tempos Observados Tempos Censurados Tempos Gerais M´ınimo 0.03 2.50 0.03 1o _Quartil _3.86 _74.95 _10.42

Mediana 15.54 233.40 43.61 M´edia 48.89 254.40 137.30 3o _Quartil _42.10 _417.30 _229.80

(38)

Na Figura 4.7 tem-se o histograma e boxplot dos tempos at´e a falha ou censura. No boxplot verifica-se alguns dados at´ıpicos.

Figura 4.7: Histograma e boxplot para os tempos de vida simulados, em unidades de tempo.

Assim como na aplica¸cão anterior, a Figura 4.8 mostra que, inicialmente, nenhum modelo pode ser descartado. Assim, novamente, se faz necessário verificar qual o melhor modelo através do AIC e BIC.

(39)

Modelo No_{de Parˆametros} _AIC _BIC

Nesse caso, o modelo escolhido é o modelo de mistura Weibull. As estimativas dos parâmetos e dos erros padrões são dadas na Tabela 4.9.

Tabela 4.9: Estimativas para o modelo log-log´ıstico.

µ 0.57 0.04

σ 0.02 0.004

π 0.34 0.19

(40)

Cap´ıtulo 5

Conclus˜

oes

Neste trabalho estudamos a distribui¸cão F generalizada com fra¸cão de cura (FGfc), com base na abordagem estendida proposta por Rodrigues et al. (2009), que inclui como caso particular o modelo de mistura padrão F Generalizado proposto em Peng et al. (1998), sem a inclusão de covariáveis. Apresentamos a forma da verossimilhan¸ca marginal da FGfc no caso geral e nos dois casos particulares mais conhecidos que são os modelos de mistura padrão e o modelo de tempo de promo¸cão. Discutimos alguns procedimentos alternativos ao teste da razão de verossimilhan¸cas, para a sele¸cão de submodelos da FGfc sem covariáveis. Consideramos aplica¸cões com base em dados disponibilizados no software R. Usamos para ajuste dos dados o pacotegfcure (Peng, 1999) e consequentemente assumimos nestas aplica¸cões os modelos de mistura padrão em que a fun¸cão densidade e de sobrevivência são apresentados em (3.11) e (3.12).

Em trabalhos futuros consideramos que uma extensão importante seria o estudo e implementa¸cão computacional do modelo FGfc unificado com a inclusão de covariáveis no parâmetro de posi¸cão e no parâmetro associado à fra¸cão de cura. Além disso, per-cebemos que apesar do pacote gfcure ter se mostrado preciso no ajuste dos submodelos da FGfc nas aplica¸cões, identificamos (em simula¸cões não apresentadas neste traba-lho) que as estimativas dos parâmetros da FGfc podem apresentar muitas oscila¸cões em seus resultados com o uso deste pacote. Não encontramos descri¸cões suficientes na literatura para implementar adapta¸cões no sentido de reduzir estas oscila¸cões. Assim um estudo de simula¸cão detalhado se faz necessário para avaliar a performance deste pacote principalmente no ajuste da FGfc.

Uma outra extensão de interesse seria o estudo/implementa¸cão de procedimentos computacionais que possam ser utilizados com facilidade na estima¸cão e teste em mo-delos FGfc em sua abordagem mais unificada, incluindo principalmente modelo de tempo de promo¸cão. Neste sentido Silva (2013) vem desenvolvendo uma adapta¸cão

(41)

30

(42)

Apˆ

endice A

Algumas defini¸c˜

oes e demonstra¸c˜

oes

A.1 Fun¸c˜

ao gama e fun¸c˜

ao poligama

A fun¸c˜ao gama (Mood, Graybill & Boes, 1974), denotada por Γ(a), ´e definida por Γ(a) =

Z ∞

0

xa−1

exdx, t >0.

Se a = n for inteiro, temos

Γ(n+ 1) =n!.

A fun¸c˜ao poligama (Abramowitz & Stegun, 1964) de ordem m ´e definido como:

Ψ(m)₍_a_{) =} ∂m+1

∂am+1 log Γ(a).

A.2 Fun¸c˜

oes beta e beta incompleta

A fun¸c˜ao beta (Mood, Graybill & Boes, 1974), denotada por B(a, b), ´e definida como

B(a, b) = Z 1

0

xa−1

(1₋x)b−1

dx

sendo a e b positivos.

Uma outra forma da fun¸c˜ao beta ´e apresentada por Abramowitz & Stegun (1964), onde

B(a, b) = Z ∞

0

xa−1

(1 +x)a+bdx.

(43)

A.3 Obten¸c˜ao da fun¸c˜ao de verossimilhan¸ca marginal 32

Podemos definir a fun¸cão beta em rela¸cão a fun¸cão gama, como segue abaixo:

B(a, b) = Γ(a)Γ(b) Γ(a+b).

Definimos a fun¸c˜ao beta incompleta padronizada (Johnson, Kotz & Balakrishnan, 1992), denotada por Ix(a, b), como

Ix(a, b) = 1

B(a, b) Z x

0

ua−1

(1₋u)b−1

du

A.3 Obten¸c˜

ao da fun¸c˜

ao de verossimilhan¸ca

margi-nal

A demonstra¸c˜ao tamb´em pode ser vista em Carneiro (2012).

A fun¸cão de verossimilhan¸ca marginal é obtida fazendo-se o somatório de L(φ;Dc) em rela¸cão a Ni. Ou seja,

L(φ;D) =

∞

X

ni=0

L(φ;Dc) = ∞ X ni=0 n Y i=1

[S(ti;ψ)ni]1

−δi

−1

]δipθ(ni) Como o somat´orio depende de i, ent˜ao

L(φ;D) = n Y i=1 ∞ X ni=0

[S(ti;ψ)ni]1−δi

−1

]δipθ(ni).

Podemos separar a fun¸c˜ao anterior em duas,δi = 0 e δi = 1. Seδi = 0:

L(φ;D) = n Y i=1 ∞ X ni=0

S(ti;ψ)nipθ(ni).

De (2.7), temos que

L(φ;D) = n Y

i=1

Sp(ti;φ).

Seδi = 1:

L(φ;D) = n Y i=1 ∞ X ni=0

nif(ti;ψ)S(ti;ψ)ni

−1

(44)

A.4 Demonstra¸c˜ao para a equa¸c˜ao 3.2 33

De (2.8), temos que

L(φ;D) = n Y

i=1

fp(ti;φ).

Logo, a fun¸c˜ao marginal ´e dada por:

L(φ;D) = n Y

i=1

[Sp(ti;φ)ni]1−δi

[fp(ti;φ)]δi.

A.4 Demonstra¸c˜

ao para a equa¸c˜

ao 3.2

Seja T0 uma v.a. seguindo distribui¸c˜ao F com 2s1 e 2s2 graus de liberdade, ambos

positivos, com densidade dada em (3.1). Fazendo T = aTb

0 temos que a v. a. T tem

distribui¸c˜ao F generalizada com os parˆametros a, b, s1 e s2, sendo b > 0. :

FT(t) = P(T < t) =P(aT0b < t) =P

T0 <

t a

1/b

=FT0

t a

1/b

Derivando a fun¸c˜ao fica:

fT(t) =

t a

1

b−1 1

abfT0

t a

1

b

fT(t) =

t a

1

b−1 1

ab s1 s2 s1 t a 1

bs1−1

B(s1, s2)

1 + s1 s2 t a 1

b(s1+s2)

fT(t) =

t a

1

b−1 ₁

ab s1 s2 s1 t a s1 b− 1 b

B(s1, s2)

1 + s1 s2 t a 1

b(s1+s2)

fT(t) =

s1

s2

s1

(ab)−1

t a

s1

b−1

B(s1, s2)

1 + s1 s2 t a 1

(45)

A.5 Demonstra¸c˜

ao para a equa¸c˜

ao 3.3

Seja W = logT −µ

σ , onde W ´e o logaritmo da v. a. T0. A fun¸c˜ao densidade de

probabilidade de W ´e dada por:

FW(w) = P(W < w) = P

logT ₋µ σ < w

=

=P(logT < µ+σw) =P(T < eµ+σw) = FT(µ+σw) Derivando a fun¸c˜ao em rela¸c˜ao a W, temos:

fW(w) = σeµ+σwfT(eµ+σw)

fW(w) = σeµ+σw

s1

s2

s1

(eµ_σ₎−1

eµ+σw

eµ s1

σ−1

B(s1, s2)

" 1 +

s1

s2

eµ+σw

eµ 1

σ#s

1+s2

fW(w) =

σ σ

eµ+σw−µ

s1

s2

s1

(eµ+σw−µ

)sσ1−1

B(s1, s2)

1 + s1 s2

(eµ+σw−µ

)σ1 s1+s2

fW(w) =

eσw

s1

s2

s1

eσwsσ1−σw

B(s1, s2)

1 + s1 s2

eσwσ s1+s2

fW(w) =

s1

s2

s1

ews1

B(s1, s2)

1 + s1 s2 ew

(s1+s2)

A.6 Demonstra¸c˜

ao para a equa¸c˜

ao 3.4

A fun¸cão de sobrevivência da variável W ficará dessa forma:

SW(w) = Z ∞

w

(s1

s2)

s1evs1

B(s1, s2)[1 + (s_s12)e

(46)

SW(w) = Z ∞

w

₍s1

s2)e

v

1 + (s1

s2)e

v s1

1 1 + (s1

s2)e

v s2

B(s1, s2)

−1

dv

Fazendo u = 1

1 +s1

s2

ev =

s2

s2+s1ev

e du = ₋ 

 1

1 +s1

s2 ev     s1 s2 ev 1 +s1

s2

ev  dv, temos que:

SW(w) = − Z 0

s2(s2+s1ew)−1

us2−1

(1₋u)s1−1

B(s1, s2)

−1

du SW(w) =

Z s2(s2+s1ew)−1

0

us2−1

(1₋u)s1−1

B(s1, s2)

−1

du SW(w) =Ik(s2, s1)

(47)

Apˆ

endice B

Comandos no R

Nessa se¸cão mostramos a rotina utilizada para a obten¸cão das estimativas tanto da simula¸cão da Se¸cão 3, quanto da Se¸cão 4. Para isso, é preciso que baixe o pacote gfcure e execute no software R 32-bits. Para mais informa¸cões de onde está dispon´ıvel o pacote, consulte Peng (1999).

require(flexsurv) # Chamar o pacote flexsurv, j´a com o survival incluso. attach("SUA_BIBLIOTECA_DO_R _\\ gfcure_\\.RData")

load.gfcure("SUA_BIBLIOTECA_DO_R _\\ gfcure")

#### Rotina para a simula¸c~ao na Se¸c~ao 3.2.1

### Fun¸c~ao a partir da gera¸c~ao de n´umeros aleat´orios da F ## a = 20 (mu = 3), b = 5, s1 = 10 e s2 = 7

rm(list = ls())

D = function(n, a, b, s1, s2, p, tau){ N <- rbinom(n, 1, 1-p)

C <- runif(n, 0, tau)

T <- vector(); y <- vector(); d <- vector(); cv <- vector() T[N==1] <- a*rf(sum(N),2*s1,2*s2)_bb

T[N==0] <- C[N==0]

y <- apply(cbind(T,C), 1, min) d <- ifelse(T < C, 1, 0)

cv <- ifelse(y = C, 1, 0)

return(list(y = y, d = d, pc1=sum(cv)/sum(1-d),pc2=mean(1-d))) }

(48)

37

#### n = 50 ### Censura = 30 ## % de cura = 10

d <- D(50, 20, 5, 10, 7, 0.1, 250);d$pc1;d$pc2 # Verificar a censura. n=50 # Escolha do tamanho da amostra

mod=gfcure(Surv(d$y, d$d)_∼1, cureform=_∼1, dist="gf", sait = 0, temp = 10, ntemp = 100);mod

(AIC=-2*mod$log+2*5) (BIC=-2*mod$log+5*log(n))

## % de cura = 30

d <- D(50, 20, 5, 10, 7, 0.3, 450);d$pc1;d$pc2 n=50

## % de cura = 50

d <- D(50, 20, 5, 10, 7, 0.5, 500000);d$pc1;d$pc2 n=50

### Censura = 50 ## % de cura = 10

d <- D(50, 20, 5, 10, 7, 0.1, 100);d$pc1;d$pc2 n=50

(49)

38

## % de cura = 30

d <- D(50, 20, 5, 10, 7, 0.3, 500);d$pc1;d$pc2 n=50

## % de cura = 50

d <- D(50, 20, 5, 10, 7, 0.5, 500000);d$pc1;d$pc2 n=50

#### Rotina para a Se¸c~ao 4.1 ### Dados sobre c^ancer de ov´ario str(ovarian)

t=seq(0:1200)

### Ajuste usando o Kaplan-Meier

ekm=survfit(Surv(futime, fustat)_∼1, conf.type="none", data=ovarian) plot(ekm, main="Estimador de Kaplan-Meier",ylab="S(t)", xlab="Tempos (em dias)")

##### Modelos a serem considerados no estudo #### Gama Generalizada

### Ajuste usando o gfcure

(50)

39

mod1

s=mod1$coef[1]

sigma=exp(mod1$coef[2]) mu=mod1$coef[3]

y1=(1-pegg(t, s, sigma, mu))*(1-mod1$cure)+mod1$cure

#### Weibull

mod2=gfcure(Surv(futime, fustat)_∼1, cureform=_∼1, data=ovarian) mod2

a=1/exp(mod2$coef[1]);a b=exp(mod2$coef[2]);b

y2=(exp(-(t/b)_ba)*(1-mod2$cure))+mod2$cure

#### log-log´ıstica

mod3=gfcure(Surv(futime, fustat)_∼1, cureform=_∼1, data=ovarian, dist="loglogistic")

mod3

y3=(1/(1+(t/b)_ba))*(1-mod3$cure)+mod3$cure

#### F Generalizada

mod4=gfcure(Surv(futime, fustat)_∼1, cureform=_∼1, data=ovarian, dist="gf", sait = 0, temp = 0, ntemp = 0)

mod4

#### log-normal

mod5=gfcure(Surv(futime, fustat)_∼1, cureform=_∼1, data=ovarian, dist="lognormal")

mod5

mu=mod5$coef[2]

(51)

40

w = (log(t)-mu)/sigma

y5=pnorm(w, 0, 1, lower.tail=F)*(1-mod5$cure)+mod5$cure

### Gr´afico da figura 4.1

plot(ekm, main="Compara¸c~ao curvas de sobreviv^encia", ylab="S(t)", xlab="Tempos (em dias)")

lines(t,y1, col=2, lty=1) lines(t,y2, col=3, lty=2) lines(t,y3, col=4, lty=3) lines(t,y5, col=6, lty=4)

legend(700,0.9,col=c(1,2,3,4,6),lty=c(1,1,2,3,4), c("Kaplan-Meier", "gama generalizada","Weibull","log-log´ıstica","lognormal"),lwd=1, bty="n")

#### Crit´erios de Informa¸c~ao da tabela 4.1 ### AIC

(AIC1=-2*mod1$log+2*4) # Gama generalizada (AIC2=-2*mod2$log+2*3) # Weibull

(AIC3=-2*mod3$log+2*3) # log-log´ıstica (AIC4=-2*mod4$log+2*5) # F generalizada (AIC5=-2*mod5$log+2*3) # log-normal

### BIC n=100

(BIC1=-2*mod1$log+4*log(n)) # Gama generalizada (BIC2=-2*mod2$log+3*log(n)) # Weibull

(BIC3=-2*mod3$log+3*log(n)) # log-log´ıstica (BIC4=-2*mod4$log+5*log(n)) # F generalizada (BIC5=-2*mod5$log+3*log(n)) # log-normal

####### Rotina para a se¸c~ao 4.2 ##### Inserir os dados

str(colon) t=seq(0:3500)

(52)

41

ekm=survfit(Surv(time, status)_∼1, conf.type="none", data=colon)

#### Gama generalizada ### Ajuste usando o gfcure

mod1=gfcure(Surv(time, status)_∼1, cureform=_∼1, dist="egg", data=colon, sait = 0, temp = 10, ntemp = 10)

mod1

s=mod1$coef[1]

sigma=exp(mod1$coef[2]) mu=mod1$coef[3]

y1=(1-pegg(t, s, sigma, mu))*(1-mod1$cure)+mod1$cure

##### Usando a distribui¸c~ao Weibull ### Ajuste usando o gfcure

mod2=gfcure(Surv(time, status)_∼1, cureform=_∼1, data=colon) mod2

y2=(exp(-(t/b)_ba)*(1-mod2$cure))+mod2$cure

#### log-log´ıstica

mod3=gfcure(Surv(time, status)_∼1, cureform=_∼1, dist="loglogistic", data=colon)

mod3

y3=(1/(1+(t/b)_ba))*(1-mod3$cure)+mod3$cure

#### F Generalizada

mod4=gfcure(Surv(time, status)_∼1, cureform=_∼1, dist="gf", data=colon, sait = 10, temp = 10, ntemp = 10)

mod4

(53)

42

mod5=gfcure(Surv(time, status)_∼1, cureform=_∼1, dist="lognormal", data =colon)

mod5

mu=mod5$coef[2]

sigma=exp(mod5$coef[1]) w = (log(t)-mu)/sigma

y5=pnorm(w, 0, 1, lower.tail=F)*(1-mod5$cure)+mod5$cure

### Gr´afico para a figura 4.3

plot(ekm, main="Compara¸c~ao curvas de sobreviv^encia", ylab="S(t)", xlab="Tempos (em dias)")

lines(t,y1, col=2, lty=1) lines(t,y2, col=3, lty=2) lines(t,y3, col=4, lty=3) lines(t,y5, col=6, lty=4)

legend(1500,0.9,col=c(1,2,3,4,6),lty=c(1,1,2,3,4), c("Kaplan-Meier", "gama generalizada","Weibull","log-log´ıstica","lognormal"),lwd=1,bty="n")

#### Crit´erios de Informa¸c~ao da tabela 4.3 ### AIC

(AIC1=-2*mod1$log+2*4) # Gama generalizada (AIC2=-2*mod2$log+2*3) # Weibull

(AIC3=-2*mod3$log+2*3) # log-log´ıstica (AIC4=-2*mod4$log+2*5) # F generalizada (AIC5=-2*mod5$log+2*3) # log-normal

### BIC n=100

(BIC1=-2*mod1$log+4*log(n)) # Gama generalizada (BIC2=-2*mod2$log+3*log(n)) # Weibull

(54)

Referˆ

encias

Abramowitz, M. and Stegun, I.A. (1964).Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover Publications, New York.

Akaike, H. (1974). A New Look at the Statistical Model Identification. IEEE Tran-sactions on Automatic Control, Vol. 19, No. 6, pp. 716-723.

Berkson, J. and Gage, R.P. (1952). The likelihood ratio, Wald, and Lagrange mul-tiplier tests: an expository note. Journal of American Statistical Association, Vol. 47, No. 259, pp. 501-515.

Brown, B.W., Levy, L.B., Lovato, J., Russell, K. and Spears, F.M. (1992).Algorithm 762: LLDRLF, Log-likelihood and Some Derivatives for log-F Models. ACM Transactions on Mathematical Software, Vol. 22, No. 3, pp. 372-382.

Carneiro, H.P. de A. (2012).Testes de Hipóteses em Modelos de Sobrevivência com Fra¸cão de Cura. Disserta¸cão de Mestrado - PPGMAE - UFRN.

Cox, C (2008). A generalized F distribution: An umbrella for parametric survival analysis. Statistics in medicine, Vol. 27, pp. 4301-4312.

Colon, A.S.C., Taylor, J.M.G., Sargent, D.J. and Yothers, G. (2011). Using cure models and multiple imputation to utilize recurrence as an auxiliary variable for overall survival. Clinical trials, Vol. 8, pp. 581-590.

Colosimo, E.A. e Giolo, S.R. (2006). Análise de Sobrevivência Aplicada. Edgard Blücher, São Paulo, SP.

Edmunson, J.H., Fleming, T.R., Decker, D.G., Malkasian, G.D., Jefferies, J.A., Webb, M.J., and Kvols, L.K. (1979). Different Chemotherapeutic Sensitivities and Host Factors Affecting Prognosis in Advanced Ovarian Carcinoma vs. Mi-nimal Residual Disease. Cancer Treatment Reports, Vol. 63, pp. 241-247.

Fonseca, R.S. (2011).Modelos de Sobrevivência com Fra¸cão de Cura e Omissão nas Variáveis. Disserta¸cão de Mestrado - PPGMAE - UFRN.

(55)

44

Hogg, S.A. and Ciampi, A. (1985). GFREG: A computer program for maximum likelihood regression using the generalized F distribution. Computer Methods and Programs in Biomedicine, Vol. 20, pp. 201-215.

Hubben, G.A.A., Bishai, D., Pechlivanoglou, P., Cattelan, A.M., Grisetti, R., Fac-chin, C., Compostella, F.A., Bos, J.M., Postma, M.J. and Tramarin, A. (2008).

The societal burden of HIV/AIDS in Northern Italy: An analysis of costs and quality of life. AIDS Care, Vol. 20, No. 4, pp. 449-455.

Ibrahim, J.G., Chen, M.H. and Sinha, B. (1992).Bayesian Survival Analysis. Sprin-ger, New York.

Jackson, C. (2013). Flexible parametric survival models. URL: http://cran.r-project.org/web/packages/flexsurv/index.html. Acesso: 09 de julho de 2014.

Johnson, N.L., Kotz, S. and Balakrishnan, N. (1992). Continuous Univariate Dis-tributions. Wiley, Vol.2, New York.

Kalbfleisch, J.D. and Prentice, R.L. (2002).The Statistical Analysis of Failure Time Data. Wiley, New York.

Kaplam, E.L. and Meier, P. (1958). Nonparametric Estimation from Incomplete Observation. Journal of the American Statistical Association, Vol.58, No. 282, pp. 457-481.

Lawless, J.F. (2003).Statistical Models and Methods for Lifetime Data.Wiley, New York.

Le, Q.H., Thomas, X., Ecochard, R., Iwaz, J., Lhe´eritier, V., Michallet, M., Fiere, D. (2007). Proportion of long-term event-free survivors and lifetime of adult patients not cured after a standard acute lymphoblastic leukemia therapeutic program. American Cancer Society, Vol. 109, No. 10, pp. 2058-2067.

Maller, R.A., Zhou, X. (1974). Survival analysis with long-term survivors. Wiley, New York.

Martinez, E.Z., Louren¸con, A.F., Mazucheli, J. e Ferreira, O. (2007). Modelos de Sobrevivência de Longa Dura¸cão Aplicados ao Estudo do Comportamento de Retorno do Doador de Sangue Voluntário.Revista de Matemática e Estat´ıstica. Vol 25, No. 1, pp. 137-154.

(56)

The-45

rapy of Resected Colon Carcinoma. The New England Journal of Medicine, Vol.8, pp. 322-352.

Mood, A.M., Graybill, F.A., Boes, D.C. (1974). Introduction To The Theory of Statistics. McGraw - Hill International Editions, 3th Edition.

Peng, Y. (1999) GFCURE - An S-PLUS Package for Parametric

Analysis of Survival Data with Possible Cured Fraction. URL:

http://www.math.mun.ca/_∼ypeng/research/gfcure/. Acesso: 09 de junho de 2014.

Peng, Y. and Carrier, K.C. (2002). An Empirical Comparison of Parametric and Semiparametric Cure Models.Biometrical Journal, Vol. 44, No. 8, pp. 1002-1014.

Peng, Y. and Dear, K.B.G. and Denham, J.W. and others (1998). A generalized F mixture model for cure rate estimation. Statistics in medicine, Vol. 17, No. 8, pp. 813-830.

Prentice, R.L. (1975). Discrimination Among Some Parametric Models. Statistics in medicine, Vol. 62, No. 3, pp. 607-614.

R Development Core Team (2013). R: A Language and Environment of Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. URL: http://www.r-project.org/.

Rodrigues, J., Cancho, V.G., de Castro, M. and Louzada-Neto, F. (2009). On the unification of long-term survival models. Statistics and Probability Letters Vol. 79, pp. 753-759.

Schwartz, G. (1978).Estimating the Dimension of a Model.The Annals of Statistics Vol. 6, No. 2, pp. 461-464.

Silva, R. P. da (2013). Modelo Gama Generalizado com Longa Dura¸cão: Teoria e Prática. Monografia de Gradua¸cão (Forma¸cão em Estat´ıstica) - Curso de Esta-t´ıstica, Departamento de EstaEsta-t´ıstica, Universidade Federal do Rio Grande do Norte, Natal-RN. 50 f.