3 Função de transferência em tempo discreto

(1)

Capítulo 3

3 Função de transferência em tempo discreto

3.1 Amostragem impulsiva

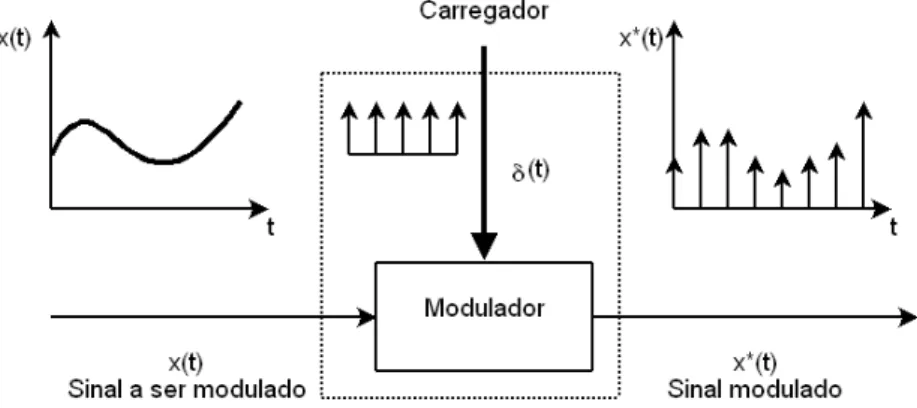
Considerando um sinal x(t) que será amostrado por um amostrador, conhecido como sampler, de tal modo que a intervalos de tempo T, conhecido como tempo de amostragem ou tempo de discretização, ocorra uma leitura, este sinal é dado pela Figura 3.1, e pode ser representado por,

∑

∞

=

− δ =

0 k *

) kT t ( ) kT ( x ) t ( x

Figura 3.1: Amostrador impulsivo

Supondo que não são medidos tempos negativos, devido a causalidade, então a equação acima pode ser expandida como,

L

L+ δ − +

+ − δ + δ

=x(0) (t) x(T) (t T) x(kT) (t kT) )

t ( x*

Observe que o δ representa um trem de impulsos e, uma das formas de entender o fenômeno da amostragem é que o sinal x(t) modula o trem de impulsos para formar o sinal amostrado conforme apresentado pela Figura 3.2.

(2)

Agora aplicando a Transformada de Laplace no sinal amostrado,

[ ]

[

]

[

]

∑

∞

=

−

− −

=

+ +

+ =

+ − δ +

− δ +

δ =

=

0 k

kTs

Ts 2 Ts

* *

e ) kT ( x

e ) T 2 ( x e ) T ( x ) 0 ( x

) T 2 t ( L ) T 2 ( x ) T t ( L ) T ( x ) t ( L ) 0 ( x ) t ( x L ) s ( X

L

Sabendo-se que a Transformada de laplace de um impulso defasado de a é,

[

]

as

e ) a t (

Lδ − = − Então,

∑

∞

=

− −

− ₊ ₊ ₌

+ =

0 k

kTs Ts

2 Ts

*

e ) kT ( x e

) T 2 ( x e ) T ( x ) 0 ( x ) s (

X L

Definindo,

z ln T 1 s z

eTs = ⇒ =

Então,

( )

∑

∞

=

−

= =

0 k

k z

ln T 1 s *

z kT x )

s ( X

O lado direito desta equação é a definição de transformada Z da seqüência x(t), então,

) z ( X )

s ( X

z ln T 1 s

* =

=

Desta forma,

) z ( X z ln T 1

X* ⎟=

⎠ ⎞ ⎜

⎝ ⎛

3.2 Circuito Data-Hold

A saída de um amostrador é um trem de impulsos, mas em alguns casos isso não é desejável, e o necessário seria um sinal contínuo, a transformação de um sinal na forma de trem de impulsos em um sinal contínuo pode ser feito por um circuito tipo Data-Hold, que nada mais é do que o processo de se obter um sinal contínuo x(t) de uma seqüência discreta x(kT).

O circuito Data-Hold nada mais é do que um interpolador, isto é, ele gera ou mantém um sinal entre dois impulsos seguindo uma interpolação polinomial na forma,

0 1 1

n 1 n n

n a a a

a ) kT (

h +τ = τ + ₋τ − +L+ τ+

onde h(kT+τ) é a saída do circuito data-hold. Assumindo x(kT) como o sinal que passará pelo circuito, neste caso, h(kT) deve ser igual a x(kT) para que os sinais sejam os mesmos, então,

) kT ( x a a

a ) kT (

h +τ = _nτn + _n₋₁τn−1 +L+ ₁τ+

3.2.1 Segurador de Ordem Zero - ZOH

(3)

) kT ( x ) kT (

h +τ =

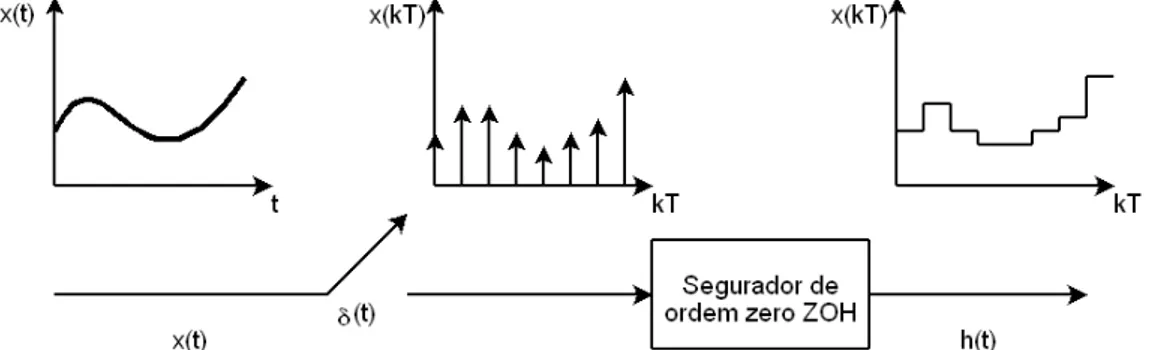
Na Figura 3.3:, observa-se o resultado de um segurador de ordem zero.

Figura 3.3: Exemplo de sinal amostrado com uma reconstrução utilizando o ZOH O ZOH mantém o sinal anterior até que um novo sinal apareça, então,

) kT ( x ) t kT (

h + =

Significando que a saída do circuito será igual à entrada até que ocorra outro sinal de entrada, então,

[

]

[

]

[

1(t 2T) 1(t 3T)

]

) T 2 ( x ) t T 2 ( h 2 k

) T 2 t ( 1 ) T t ( 1 ) T ( x ) t T ( h 1 k

) T t ( 1 ) t ( 1 ) 0 ( x ) t ( h 0 k

− − − =

+ ⇒

=

− − − =

+ ⇒ =

− − =

⇒ =

Então a resposta temporal do ZOH será definida como,

[

]

[

]

[

]

∑

∞

=

+ − − − =

+ − − − +

− − =

0 k

) T ) 1 k ( t ( 1 ) kT t ( 1 ) kT ( x

) T 2 t ( 1 ) T t ( 1 ) T ( x ) T t ( 1 ) t ( 1 ) 0 ( x ) t (

h L

Como a Transformada de Laplace do degrau unitário atrasada de kT é dada por,

[

]

s e ) kT t ( 1 L

kTs

−

= −

Então a Transformada de Laplace da resposta do ZOH torna-se,

( )

∑

∞

=

− −

∞

=

+ −

− ₋

= ⎥ ⎦ ⎤ ⎢

⎣ ⎡

− =

0 k

kTs Ts

0 k

Ts 1 k kTs

e ) kT ( x s

e 1 s

e s e ) kT ( x ) s ( H

Como,

∑

∞

=

−

= 0 k

kTs *

e ) kT ( x )

s ( X Então,

) s ( X s e 1 ) s (

H *

Ts

−

− =

Consequentemente, a função de transferência o ZOH é dada por, s

e 1 ) s ( X

) s ( H ) s ( G

Ts

* ZOH

−

− = =

3.2.2 Segurador de primeira ordem

(4)

) kT ( x a ) kT (

h +τ = ₁τ+

Aplicando a condição que,

) T ) 1 k (( x ) T ) 1 k ((

h − = −

Então, ) T ) 1 k (( x ) kT ( x T a ) T ) 1 k ((

h − = ₁ + = −

Portanto, T ) T ) 1 k (( x ) kT ( x

a₁ = − −

Consequentemente, a equação do segurador de primeira ordem fica, ) kT ( x T ) T ) 1 k (( x ) kT ( x ) kT (

h +τ = − − τ+

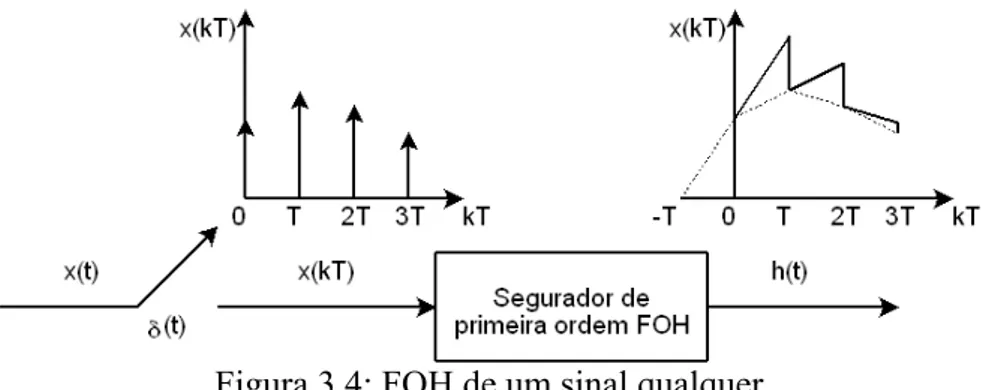
Como o FOH utiliza uma extrapolação linear utilizando o valor anterior e o atual para predizer o valor do próximo e, além disso, o valor h(kT) deve ser igual a x(kT). então, ) T ( x T ) T 2 ( x T 1 ) T 2 ( x T ) T ( x ) T 2 ( x ) T 2 ( h 2 k ) 0 ( x T ) T ( x T 1 ) T ( x T ) 0 ( x ) T ( x ) T ( h 1 k ) 0 ( x T 1 ) 0 ( x T ) T ( x ) 0 ( x ) ( h 0 k τ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ τ = + τ − = τ + ⇒ = τ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ τ = + τ − = τ + ⇒ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ τ + = + τ − − = τ ⇒ =

Que pode ser expressa convenientemente como,

) T ) 1 k (( x T ) T ( x T 1 ) kT (

h ⎟ − τ −

⎠ ⎞ ⎜ ⎝ ⎛ τ + = τ +

Fica difícil escrever a equação sem assumir uma entrada conhecida, utilizando uma entrada degrau para x(t),

) T t ( 1 T t ) t ( 1 T t 1 ) t (

h ⎟ − −

⎠ ⎞ ⎜ ⎝ ⎛ + =

Somando e subtraindo 1(t-T),

) T t ( 1 ) T t ( 1 T T t ) t ( 1 T t 1 ) t (

h ⎟ − − − − −

⎠ ⎞ ⎜ ⎝ ⎛ + =

Aplicando a transformada de Laplace a cada um dos termos da equação acima,

(

Ts

)

₂

Ts Ts 2 2 Ts 1 Ts e 1 e s 1 e Ts 1 Ts 1 s 1 ) s (

H ⎟− − = − +

⎠ ⎞ ⎜ ⎝ ⎛ + = − − −

Agora, a transformada de Laplace da entrada x*(t) do FOH é,

∑

∞ = − − − = = 0 k Ts kTs * e 1 1 e ) kT ( 1 ) s ( X

Então a função de transferência do segurador de primeira ordem FOH fica,

(

_Ts

)

2 ₂ * FOH Ts 1 Ts e 1 ) s ( X ) s ( H ) s (

G = = − − +

(5)

Figura 3.4: FOH de um sinal qualquer

3.2.3 Funções de Transferência em Tempo Discreto com ZOH

Supondo que antes da função G(s) há um ZOH, então a convolução de G(s) com o ZOH é dada por,

) s ( G s e 1 ) s ( X

Ts

−

− = Fazendo,

(

)

(

1 e

)

G (s) G (s) e G (s) s

) s ( G e 1 ) s ( G s e 1 ) s (

X Ts Ts ₁ ₁ Ts ₁

Ts

− −

− =

− = −

= −

=

Pegando apenas o último termo,

) s ( G e ) s (

X₁ = −Ts ₁ Aplicando o teorema da convolução,

∫

−τ τ τ = t

0

1 0

1(t) g (t )g ( )d

x

onde,

[ ]

(

)

[

G (s)

]

L ) t ( g

T t e

L ) t ( g

1 1 1

Ts 1 0

− − −

=

− δ = =

Então,

∫

δ − −τ τ τ = t

0

1 1(t) (t T )g ( )d

x

Como o delta extrai o valor da função,

) T t ( g ) t (

x₁ = ₁ −

Além disso, Z[g1(t)]=G1(Z), então, por definição,

[

x (t)

] [

Zg (t T)

]

z G (z)

Z ₁ = ₁ − = −1 ₁

Porém, o desejado é,

[

]

[

] [

]

(

)

(

)

_⎥⎦⎤

⎢⎣ ⎡ − = −

= −

=

− =

− −

s ) s ( G Z z 1 ) z ( G z 1 ) z ( G z ) z ( G

) t ( x Z ) t ( g Z ) s ( G e ) s ( G Z ) z ( X

1 1

1 Ts 1

No caso do FOH preceder a função G(s), tem-se

(

)

G(s)

Ts 1 Ts e

1 ) s ( X

2 2

Ts +

−

= −

(6)

(

)

(

)

_⎥⎦⎤

⎢⎣ ⎡ + −

=

⎥⎦ ⎤ ⎢⎣

⎡ +

− =

− −

) s ( G Ts

1 Ts Z z 1

) s ( G Ts

1 Ts e

1 Z ) z ( X

2 2

1

2 2 Ts

Exemplo 3.1: Obter a transformada Z de, 1 s

1 s e 1 ) s ( X

Ts

+ −

= −

Solução: Como representa um ZOH,

(

)

(

)

(

)

(

T_T

)

₁1

1 T 1

1 1

1 Ts

z e 1

z e 1 z

e 1

1 z

1 1 z

1 1 s

1 s 1 Z z 1

1 s

1 s 1 Z z 1 1 s

1 s e 1 Z ) z ( X

− −

− − −

− −

− − = ⎥⎦ ⎤ ⎢⎣

⎡

− − − −

= ⎥⎦ ⎤ ⎢⎣

⎡ + − −

=

= ⎥⎦ ⎤ ⎢⎣

⎡ + −

= ⎥ ⎦ ⎤ ⎢

⎣ ⎡

+ −

=

3.2.4 Resposta em Freqüência do ZOH

A função de transferência do ZOH é dada por, s e 1 G

Ts

ZOH

−

− =

A resposta em freqüência, que é o diagrama de bode, pode ser encontrada substituindo s por jω,

(

)

( )

(

( ) ( )

)

( )

(

( ) ( )

)

₍

₎

2 / T

2 / T sin Te

j 2

e e

e 2

j 2

e e

e 2 j

2 e 1 2 j

e 1 ) j ( G

Tj 2 / 1 Tj

2 / 1 Tj 2 / 1 Tj 2 / 1

Tj 2 / 1 Tj 2 / 1 Tj 2 / 1 Tj

Tj

ZOH

ω ω =

ω − =

ω − = ω − = ω

ω − ω

− ω ω

−

ω − ω ω

− ω

−

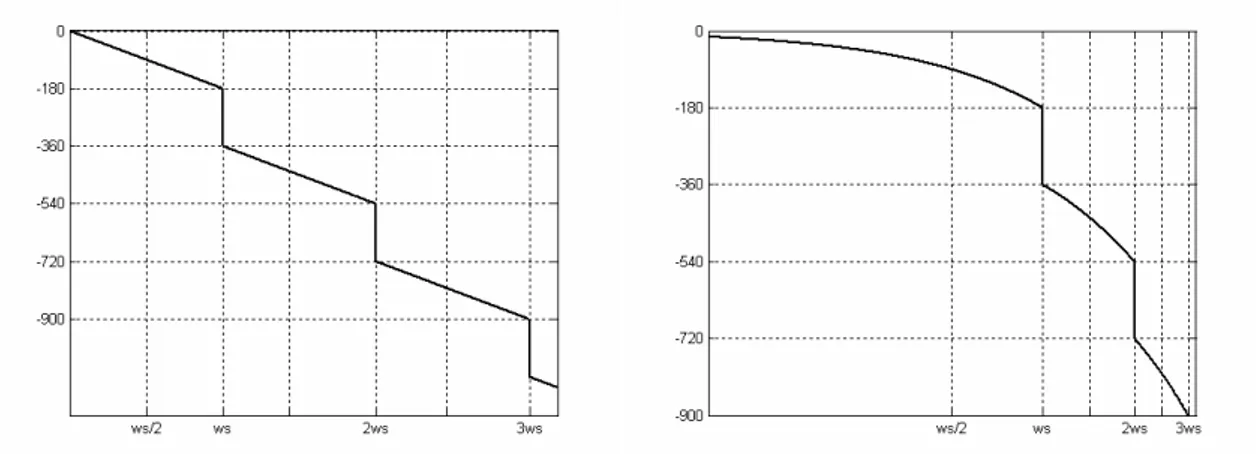
Nas figuras abaixo, ωs representa a freqüência de Nyquist, isto é a máxima freqüência que o sinal ainda pode ser reconstruído adequadamente. Caso o sinal amostrado apresente freqüências acima da freqüência de Nyquist o sinal discretizado apresentará erro de aliasing.

(7)

Figura 3.5: Resposta em freqüência do ZOH

O ZOH pode ser entendido como um filtro de reconstrução do sinal amostrado e ele não é um filtro passa-baixo ideal. Como a magnitude muda com a freqüência, atenuando o sinal a medida que a freqüência aumenta, o ZOH distorce o sinal, isto é, ele muda a amplitude e a fase do sinal de saída.

3.3 Função de Transferência Pulsada

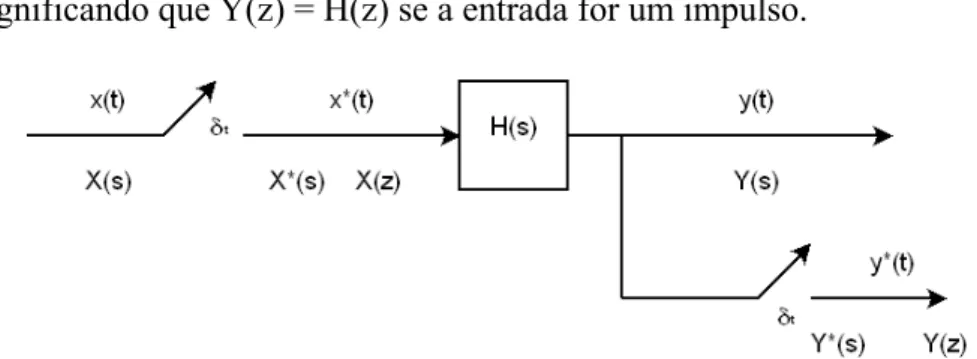
A função de transferência, FT, pulsada é a função de transferência em Laplace envolvendo o amostrador. Supondo que um sistema cuja resposta ao impulso seja h(t) tenha a entrada x(t) e a saída seja y(t), cujas transformadas de Laplace são H(s), X(s) e Y(s) respectivamente. Pelo teorema da convolução tem-se,

( )

= =

_∫

(

−τ

) ( )

τ τ=

_∫

t

(

−τ

) ( )

τ τ 0

t

0

d h t x d x t h ) t ( x * ) t ( h t y

Que no domínio de Laplace é dada por, ) s ( X ) s ( H ) s (

Y =

Adicionando um amostrador em x(t), este é dado por,

(

)

_∑

(

)

∑

∞

= ∞

=

− δ =

0 k 0

k *

kT t ) kT ( x kT

t ) t ( x ) t ( x

Aplicando esta entrada no sistema, tem-se que a resposta y(t) será a combinação de cada impulso gerado por x*(t) em h(t), sendo assim,

( )

kT t 0 )

nT ( x ) nT t ( h

kT x ) kT t ( h T

2 x ) T 2 t ( h T x ) T t ( h 0 x ) t ( h ) t ( y

k

0 n

≤ ≤ −

=

= −

+ + −

+ −

+ =

∑

=

L

Amostrando também a saída do sistema, tem-se a Soma de Convolução dada por,

) kT ( x * ) kT ( h ) nT ( h ) nT kT ( x )

nT ( x ) nT kT ( h ) kT ( y

0 n 0

n

= −

=

∑

∞

= ∞

=

O procedimento feito até aqui é exatamente o que ocorre na Figura 3.6. Deve-se notar que H(z) é a resposta do sistema ao delta de Kronecker, pois se,

⎩ ⎨ ⎧

≠ = =

δ =

0 k 0

(8)

[

(kT)

]

x(kT)z 1 Z

) z ( X

0 k

k = =

δ

=

∑

∞

=

−

Significando que Y(z) = H(z) se a entrada for um impulso.

Figura 3.6 : Sistema em tempo contínuo com amostradores

3.3.1 Transformada de Z de FTs incluindo o amostrador

Em sistemas em tempo discreto, alguns sinais do sistema são amostrados enquanto outros continuam representados em tempo contínuo, que é exatamente o que ocorre na Figura 3.6. Sendo assim, será útil calcular a função de transferência pulsada contendo amostradores em várias posições.

Note que na Figura 3.6, a resposta do sistema, Y(s), é dada por: )

s ( X ) s ( H ) s (

Y = *

A Transformada de Laplace Inversa de Y(s) é dada por,

[

]

∑

∫

∑

∫

∞

= ∞

= −

= τ − τ δ τ τ

− =

τ τ τ − =

=

0 k t

0 k 0

t

0

* *

1

) kT ( x ) kT ( h d

) kT ( ) ( x ) t ( h

d ) ( x ) t ( h ) s ( X ) s ( H L ) t ( y

Aplicando a transformada Z,

∑ ∑

∞

=

− ∞

= ⎥⎦

⎤ ⎢

⎣ ⎡ =

0 n

n

0 k

z ) kT ( x ) kT ( h )

z ( Y Fazendo m = n - k,

( )

) z ( X ) z ( H

z ) kT ( x z ) mT ( h

z ) kT ( x ) mT ( h )

z ( Y

k

0 k m

0 m

m k

0 k

= = =

− ∞

= − ∞

= ∞

=

+ − ∞

=

∑

∑∑

Significando que,

[

H(s)X (s)

]

H (s)X (s) )

s (

Y* = * * = * *

Aplicando transformada Z, torna-se,

) z ( H ) z ( X

) z ( Y ) z ( X ) z ( H ) z (

Y = ⇒ =

(9)

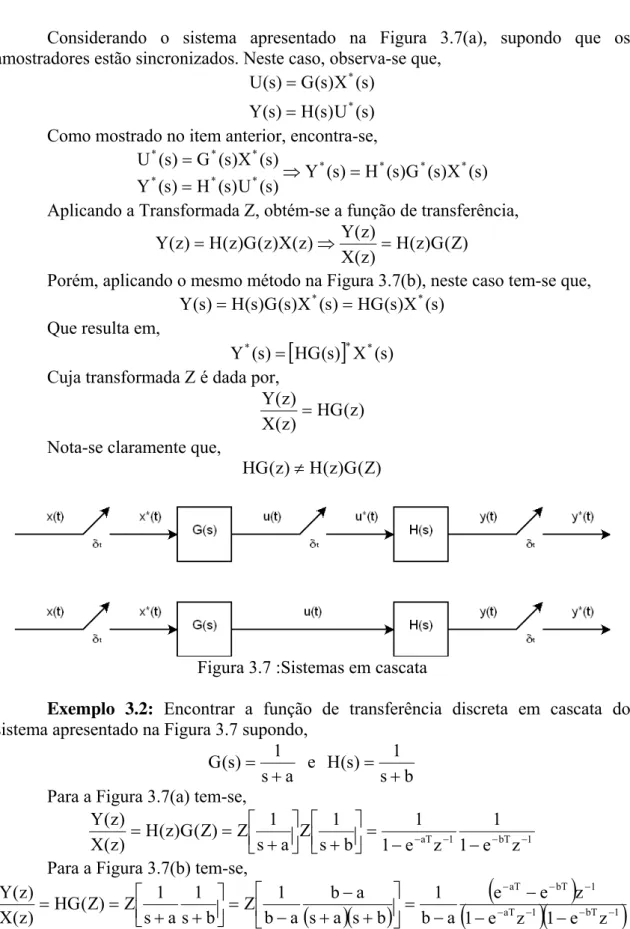
Considerando o sistema apresentado na Figura 3.7(a), supondo que os amostradores estão sincronizados. Neste caso, observa-se que,

) s ( U ) s ( H ) s ( Y

) s ( X ) s ( G ) s ( U

* *

= =

Como mostrado no item anterior, encontra-se,

) s ( X ) s ( G ) s ( H ) s ( Y ) s ( U ) s ( H ) s ( Y

) s ( X ) s ( G ) s (

U _* _* _* _*

* * *

= ⇒

= =

Aplicando a Transformada Z, obtém-se a função de transferência, )

Z ( G ) z ( H ) z ( X

) z ( Y ) z ( X ) z ( G ) z ( H ) z (

Y = ⇒ =

Porém, aplicando o mesmo método na Figura 3.7(b), neste caso tem-se que, )

s ( X ) s ( HG ) s ( X ) s ( G ) s ( H ) s (

Y = * = *

Que resulta em,

[

HG(s)

]

X (s) )

s (

Y* = * *

Cuja transformada Z é dada por,

) z ( HG ) z ( X

) z ( Y

=

Nota-se claramente que,

) Z ( G ) z ( H ) z (

HG ≠

Figura 3.7 :Sistemas em cascata

Exemplo 3.2: Encontrar a função de transferência discreta em cascata do sistema apresentado na Figura 3.7 supondo,

a s

1 ) s ( G

+ = e

b s

1 ) s ( H

+ = Para a Figura 3.7(a) tem-se,

1 bT 1

aT

z e 1

1 z

e 1

1 b

s 1 Z a s

1 Z ) Z ( G ) z ( H ) z ( X

) z ( Y

− − −

− ₋

− = ⎥⎦ ⎤ ⎢⎣ ⎡

+ ⎥⎦ ⎤ ⎢⎣ ⎡

+ = =

Para a Figura 3.7(b) tem-se,

(

)(

)

(

aT 1

)(

)

bT 1

)

1 bT aT

z e 1 z e 1

z e e a b

1 b

s a s

a b a b

1 Z b s

1 a s

1 Z ) Z ( HG ) z ( X

) z ( Y

− − −

−

− − −

− −

= ⎥ ⎦ ⎤ ⎢

⎣ ⎡

+ +

− −

= ⎥⎦ ⎤ ⎢⎣

⎡

+ + = =

Este exemplo mostra claramente que ambos são diferentes.

(10)

Como mencionado anteriormente, a amostragem pode ocorrer em qualquer etapa do processo de controle. Supondo um sistema em malha fechada como o descrito na Figura 3.8.

Figura 3.8: sistema em malha fechada envolvendo amostador Consequentemente,

) s ( E ) s ( HG ) s ( R ) s ( E ) s ( G ) s ( H ) s ( R ) s (

E = − * = − *

Que pode ser reescrito utilizando FT pulsada para todos os termos como,

[

]

) s ( GH 1

) s ( R )

s ( E ) s ( E ) s ( HG ) s ( R ) s ( E

* * *

*

+ = ⇒

− =

Como,

) s ( E ) s ( G ) s (

C* = * *

Então, a função de transferência pulsada de malha fechada é dada por, ) s ( GH 1

) s ( G )

s ( R

) s ( C ) s ( GH 1

) s ( R ) s ( G ) s ( E ) s ( G ) s (

C _*

*

* *

* * *

+ = ⇒

+ =

=

Aplicando a transformada Z, encontra-se a função de transferência discreta em malha fechada,

) z ( GH 1

) z ( G )

z ( R

) z ( C

+ =

3.3.4 Função de transferência em malha fechada de controladores digitais

(11)

Figura 3.9: sistema em malha fechada envolvendo amostador No caso, a função de transferência em malha fechada é dada por,

) s ( E ) s ( G ) s ( G ) s ( C ) s ( E ) s ( G ) s ( G ) s (

C * *

D * *

* *

D ⇒ =

=

Aplicando a transformada Z,

) z ( E ) z ( G ) z ( G ) z (

C = D

Como,

[

R(z) C(z)

]

) z ( G ) z ( G ) z ( C ) z ( C ) z ( R ) z (

E = − ⇒ = _D −

Chegando a,

) z ( G ) z ( G 1 ) z ( G ) z ( G ) z ( R ) z ( C D D + =

3.3.5 Função de transferência pulsada de um controlador PID digital

A resposta de um controlador PID no domínio do tempo é dada por, ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + +

=

_∫

e(t)

dt d T dt ) t ( e T 1 ) t ( e K ) t ( m _d t 0 i

onde e(t) é a entrada do controlador dada pela diferença da resposta da planta e pela referência a ser seguida, K é o ganho proporcional, Ti é a constante de tempo do controle integral e Td a constante de tempo do controle proporcional.

Para se obter a função de transferência pulsada do controlador PID, é necessário realizar a discretização da resposta temporal. A integral será aproximada pela soma trapezoidal e a derivada será aproximada pela derivada da interpolação utilizando 2 pontos. Assim,

(

)

(

)

⎥⎦ ⎤ − − + ⎢ ⎣ ⎡ + ⎥⎦ ⎤ ⎢⎣ ⎡ + ₊ + ₊ ₊ − + + = T T ) 1 k ( e ) kT ( e T 2 ) kT ( e T ) 1 k ( e 2 ) T 2 ( e ) T ( e 2 ) T ( e ) 0 ( e T T ) kT ( e K ) kT ( m d i L

Ou então,

(

)

_[

₍

₎

_]

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − − + + − + =

∑

= T ) 1 k ( e ) kT ( e T T 2 ) hT ( e T ) 1 h ( e T T ) kT ( e K ) kT ( m d k 1 h i

Para resolver o problema, deve-se primeiro notar que, ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡

_∑

− = − − = 1 i 0 h h 1 k i h z ) h ( x ) z ( X z 1 1 ) h ( x Z

Prova: esta transformada é comprovada fazendo,

(12)

A transformada Z de cada um dos termos utilizando a propriedade da translação real, k ) 1 i ( i z ) k ( x z ) 1 i ( x z ) i ( x ) z (

Y~ = − + + − + +L+ −

Porém, observe que, definindo,

L

L+ +

+ +

+

= −i −(i+1) −k

z ) k ( x z ) 1 i ( x z ) i ( x ) z ( X~

E da definição de transformada Z,

L + + + = = = ∞ − − = −

∑

1 2

0 k k z ) 2 ( x z ) 1 ( x ) 0 ( x z ) k ( x )] k ( x [ Z ) z ( X

Então, obtêm-se,

∑

−

=

−

= i1

0 h h z ) h ( x ) z ( X ) z ( X~ Por outro lado,

) z ( X~ z 1 1 ) z ( Y~ ) z ( X~ ) z ( Y~ z ) z ( Y~ ) k ( x ) 1 k ( y ~ ) k ( y ~ 1 1 − − − = ⇒ = − ⇒ = − −

Pois a transformada Z de x(k) que começa em k = i é X~(z), finalmente, ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ₋ − = − = = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡

_∑

− = − − − = 1 i 0 h h 1 1 k i h z ) h ( x ) z ( X z 1 1 ) z ( X~ z 1 1 ) z ( Y~ ) h ( x Z

Voltando ao problema original utilizando o resultado acima e assumindo a causalidade, isto é, que para o tempo t = 0 não há resposta do erro,

[

]

E(z)

z 1 1 ) 0 ( E ) z ( E z 1 1 ) hT ( e

Z ₁ ₁

k 1 h − − = − = − − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡

_∑

(

)

[

]

E(z)

z 1 z ) 0 ( E ) z ( E z 1 1 z ) T 1 h ( e Z ₁ 1 1 1 k 1 h − − − − = − = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ₋ − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡

_∑

₋

Agora, para

[

]

(

)

[

e(k 1T)

]

z E(z) Z ) z ( E ) kT ( e Z 1 − = − =

Então, a transformada Z do controlador PID é dada por,

[

]

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + = − − −

− _T E(z) z E(z)

T z 1 z z 1 1 2 1 T T ) z ( E K ) z (

M d 1

1 1

1 i

Resultando em,

(

)

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + − + + = − − − 1 d 1 1 i z 1 T T z 1 z 1 T 2 T 1 K ) z ( E ) z ( M

Rearranjando os termos,

(

)

(

)

_⎥⎦⎤ ⎢⎣ ⎡ ₊ ₋ − + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + − + − = − − − − 1 D 1 I P 1 d 1 i i z 1 K z 1 K K z 1 T T z 1 1 T T T 2 T 1 K ) z ( E ) z ( M Onde = − = − = 2 K K T 2 KT K K I i

(13)

= =

i I

T KT

K ganho integral

= =

T KT

K D

D ganho derivativo

A equação acima é referenciada como sendo a forma em posição.

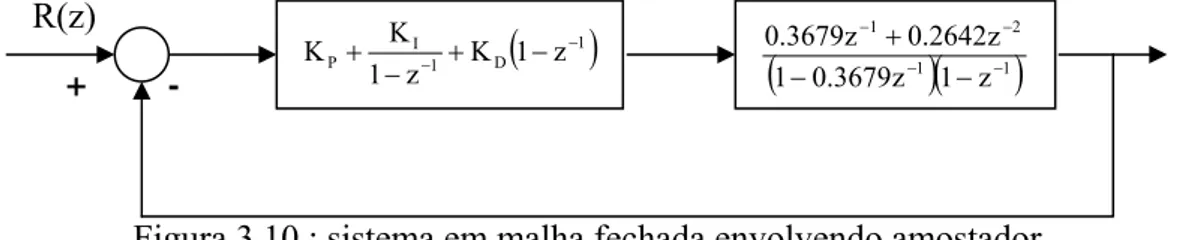
Exemplo 3.3: Comparar a resposta ao degrau do sistema abaixo considerando o sistema com e sem o controlador PID digital na forma como apresentado na Figura 3.10.

Figura 3.10 : sistema em malha fechada envolvendo amostador

Assumindo que o tempo de amostragem T é de 1 segundo, os ganhos do controlador sejam KP = 1, KI=0.2, KD = 0.2 e que a planta seja dada por,

(

s 1

)

s 1 G_p

+ =

Solução: Primeiro deve-se calcular a função de transferência pulsada entre o ZOH e a planta. A convolução da planta e o ZOH é dada por,

(

s 1

)

s 1 s

e 1 G G

s

p

ZOH ₊

−

= −

Aplicando a transformada de Z,

[

]

₍

₎

(

)

₍

₎

(

)

₍

₎

(

) (

[

₍

) (

_{) (}

₎

)

]

1 T 2

1

1 1 T T

T 1

2 1

2 1 s

p ZOH

z e 1 z 1

z z Te e

1 e

1 T z 1 1 s s

1 Z z 1

1 s s

1 Z z 1 1 s s

1 s

e 1 Z G G Z

− − −

− − − −

− −

−

− −

− − + + − −

= ⎥ ⎦ ⎤ ⎢

⎣ ⎡

+ −

=

= ⎥ ⎦ ⎤ ⎢

⎣ ⎡

+ −

= ⎥ ⎦ ⎤ ⎢

⎣ ⎡

+ −

=

Esta transformada foi obtida através de tabela de transformação. Item 13 fazendo a = 1. Para comparar com o resultado do Exemplo 2.7, deve-se lembrar que naquele ponto estava-se trabalhando com sinais, que são as respostas, e não as Funções de Transferência como tratadas aqui. No Exemplo 2.7, a resposta é convolução da FT com entrada. Agora substituindo os valores de T = 1 e simplificando, obtêm-se,

[

]

₍

1

₎₍

1

₎

2 1

p ZOH

z 3679 . 0 1 z 1

z 2642 . 0 z 3679 . 0 ) z ( G G G

Z ₋ ₋

− −

+ =

=

A função de transferência do controlador PID é dada por

(

)

(

)

1 2 1

1

2 D 1 D P

D I P

1 D 1 I P

D

z 1

z 2 . 0 z 4 . 1 4 . 1 z

1

z K z K 2 K K K K

z 1 K z 1

K K

) z ( G ) z ( E

) z ( M

− − −

−

− −

− + −

= −

+ +

− + + =

= − +

− + = =

Agora a função de transferência em malha fechada é dada por,

(

1

)

D 1 I

P K 1 z

z 1

K

K ₋ + − − −

+

₍

₎₍

₎

1 1

2 1

z 1 z 3679 . 0 1

z 2642 . 0 z 3679 . 0

− −

+

R(z)

(14)

(

)(

)

(

)(

)

4 3

2 1

4 3

2 1

3 2

1

4 3

2 1

3 2

1

4 3

2 1

1 1

2 1

1 2 1

1 1

2 1

1 2 1

D D

z 0528 . 0 z 6642 . 0 z 5906 . 1 z 8528 . 1 1

z 0528 . 0 z 2963 . 0 z 1452 . 0 z 5151 . 0

z 3679 . 0 z 7358 . 1 z 3679 . 2 1

z 0528 . 0 z 2963 . 0 z 1452 . 0 z 5151 . 0 1

z 3679 . 0 z 7358 . 1 z 3679 . 2 1

z 0528 . 0 z 2963 . 0 z 1452 . 0 z 5151 . 0

z 3679 . 0 1 z 1

z 2642 . 0 z 3679 . 0 z

1

z 2 . 0 z 4 . 1 4 . 1 1

z 3679 . 0 1 z 1

z 2642 . 0 z 3679 . 0 z

1

z 2 . 0 z 4 . 1 4 . 1 ) z ( G ) z ( G 1

) z ( G ) z ( G ) z ( R

) z ( C

− −

−

− −

−

− −

− − −

− −

− − −

+ −

− =

− +

−

+ −

− +

−

+ −

− =

=

− −

+ −

+

− −

+ −

= +

=

Programa em Matlab

clear all;close all;clc

% planta sem o sistema de controle discreto % significando que a simulação é tempo contínuo

num=[1]; % numerador contínuo

den=[1 1 0]; % denominador contínuo

figure('Color',[1 1 1])

step(num,den) % resposta ao degrau

% Planta controlada com PID digital

numd=[0 0.5151 -0.1452 -0.2963 0.0528]; dend=[1 -1.8528 1.5906 -0.6642 0.0528];

kT=[0:1:40]; % vetor de tempo discreto com T=1

r=ones(1,41); % criação do degrau unitário

c=filter(numd,dend,r); % simulação do sistema

figure('Color',[1 1 1]);plot(kT,c,'ko',kT,c,'k-')

title('Unit-Step Response');xlabel('kT [s]');ylabel('Output C')

(a) sem controle (b) controlado

Figura 3.11: Resposta do sistema

3.3.6 Simulação de sistemas em tempo discreto

(15)

( ) ( ) n 1 n 1 n m 1 m n 1 m n 0 n n 1 1 n m 1 m n 1 m n 0 a z a z b z b z b z a z a 1 z b z b z b ) z ( X ) z ( Y + + + + + + = + + + + + + = − − ₋− − + ₋ − − ₋− − L L L L

n ≥ m Que também pode ser expressa na forma de pólos e zeros,

(

)(

) (

)

(

1

)(

2

) (

n

)

m 2 1 0 p z p z p z z z z z z z b ) z ( X ) z ( Y − − − − − − = L L

n ≥ m

Observe que,

n n 1 1 m m 1 1 0 z a z a 1 z b z b b ) z ( X ) z ( Y − − − − + + + + + + = L L

Que pode ser reescrita como,

(

1+a₁z−1 +L+a_nz−n

)

Y(z)=

(

b₀ +b₁z−1+L+b_mz−m

)

X(z) Aplicando a transformada inversa de Z, obtém-se,

) mT kT ( x b ) T kT ( x b ) kT ( x b ) nT kT ( y a ) T 2 kT ( y a ) T kT ( y a ) kT ( y m 1 0 n 2 1 − + + − + = − + + − + − + L L

Significando que a resposta atual y(kT) é obtida fazendo, ) mT kT ( x b ) T kT ( x b ) kT ( x b ) nT kT ( y a ) T 2 kT ( y a ) T kT ( y a ) kT ( y m 1 0 n 2 1 − + + − + + + − − − − − − − = L L

Deve ser lembrado que para kT < 0 a resposta do sistema será zero, isto é y(-T) = 0 devido à condição de causalidade.

Exemplo 3.4: Calcular a resposta ao degrau unitário em tempo discreto com T = 0.5 para o sistema dado em tempo contínuo,

(

)

2

1 s s ) s ( G + =

Solução: Das tabelas de transformada Z,

(

)

(

)

3679 . 0 z 2131 . 1 z z 9098 . 0 z ) z ( U ) z ( Y z 3679 . 0 z 2131 . 1 1 z 9098 . 0 1 z e 1 z e ) T 1 ( 1 1 s s Z 2 2 2 1 1 2 1 T 1 T 2 + − − = + − − = − + − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − − − − − − −

Então, o sistema a ser simulado é,

(1 – 1.2131z-1 + 0.3679z-2)Y(z) = (1 – 0.9098z-1)U(z) Aplicando a Transformada Z inversa,

y(kT) – 1.2131y((k-1)T) + 0.3679y((k-2)T) = u(kT) – 0.9098u((k-1)T) Rearranjando, ) T ) 1 k (( u 9098 . 0 ) kT ( u ) T ) 2 k (( y 3679 . 0 ) T ) 1 k (( y 2131 . 1 ) kT (

y = − − − + − −

Como x(kT)=1(kT), então, começando o processo de iteração, Para k = 0 u(kT) = u(0) = 1

y(kT) = y(0) = u(0) = 1 Para k = 1 u(kT) = u(0.5) = 1; u(0)=1

y(kT) = y(0.5) = 1.2131y(0) + u(0.5) - 0.9098u(0) = 1.2131 +1 - 0.9098 = 1.3033 Para k=2 u(kT) = u(1) = 1; u(0.5) = 1;

(16)

= 1.2131*1.3033 - 0.3679 + 1 - 0.9098 = 1.3033 Para k=3 u(kT) = u(1.5) = 1; u(1) = 1;

y(kT) = y(1.5) = 1.2131y(1.5) - 0.3679y(1) + u(1.5) - 0.9098u(1) = 1.2131*1.3033 - 0.3679*1.3033 + 1 - 0.9098 = 1.1917 Para k=4 x(kT) = u(2) = 1; u(1.5) = 1; u(1) = 1

y(kT) = y(2)=1.2131y(1.5)-0.3679y(1)+u(2)-0.9098u(1.5) = 1.2131*1.191-0.3679*1.3033+1 - 0.9098 = 1.0564 E assim por diante.

3.3.7 Realização de Controladores digitais e filtros digitais

Considerando o sistema abaixo,

n n 1

1

m m 1

1 0

z a z

a 1

z b z

b b ) z ( X

) z ( Y

− −

+ + +

=

L L

A sua representação em diagramas de bloco, ou utilizando o Simulink do Matlab, é dada na Figura 3.12, esta realização é conhecida como padrão, pois o sistema pode ser alterado para se obter outras realizações.

Figura 3.12 : Função de transferência

Exemplo 3.5: Implementar em Simulink o exemplo da Figura 3.10. Utilizando funções de transferência para o controlador e para a planta e finalmente a função de transferência de malha fechada.

Solução: a função de transferência da planta é dada por,

2 1

z 3679 . 0 z 3679 . 1 1

z 2642 . 0 z 3679 . 0 ) z (

G ₋ ₋

− −

+ −

+ =

Função de transferência do controlador PID digital,

1 2 1

PID

z 1

z 2 . 0 z 4 . 1 4 . 1 ) z (

G ₋

− −

(17)

Para implementar esta função de transferência da planta e do controlador utiliza-se o bloco denominado “Discrete Filter”, mas poderia utiliza-ser utilizado os blocos “Discrete Transfer Fcn” ou “Discrete Zero-Pole”. A implementação do sistema está apresentada na Figura 3.13:.

Figura 3.13: Diagrama de blocos implementado em Simulink utilizando funções de transferência

Para a implementação da função de transferência de malha fechada, optou-se pela expansão em blocos ao invés de se utilizar função de transferência, para tanto, deve-se observar que a função de transferência de malha fechada é dada por,

4 3

2 1

4 3

2 1

z 0528 . 0 z 6642 . 0 z 5906 . 1 z 8528 . 1 1

z 0528 . 0 z 2963 . 0 z 1452 . 0 z 5151 . 0 ) z ( R

) z ( C

− −

+ −

− =

Observe que neste caso, observa-se que o termo b0 é zero, pois sua representação é,

4 4 3 3 2 2 1 1

4 3 3 3 2 2 1 1 0 MF

z a z a z a z a 1

z b z b z b z b b ) z (

G ₋ ₋ ₋ ₋

− −

+ +

=

Para este caso, a solução se encontra na Figura 3.14.

(18)

(19)

(20)

3.5 Exercícios Propostos

Exercício 3.1: Obter a transformada Z das seguintes funções de transferência, e comparar os resultados com os valores obtidos no Matlab com T = 1 e a = 3.

a)

(

s 1

)(

s 2

)

3 s )

s ( G

+ +

+ =

b)

(

)

2 Ts

a s

1 s

e 1 ) s ( G

+ −

= −

Dica:

clear all;close all;clc

% denifindo os dados da planta

T=0.2; num=[1 3];

den=conv([1 1 ],[1 2]);

Gs=tf(num,den) % planta contínua

Gz=c2d(Gs,T) % planta discreta

Exercício 3.2: Calcular a Transformada Z do seguinte sinal,

(

)

2 st

2 s

e 1 ) s ( G

+ −

= −

Exercício 3.3: Calcular a Transformada Z da seguinte função de transferência,

2 s 3 s

1 )

s ( G

2 + + =

Exercício 3.4: Calcular a resposta c(kT) para k = 0,1,2,3,4,5, rupondo que a entrada r(kT) seja um impulso e o tempo de amostragem T = 1 segundo,

(

₁

)

2

1

z 5 . 0 1

z 2 1 ) z ( R

) z ( C

− −

− + =

Exercício 3.5: Obter a função de transferência discreta em malha fechada dos seguintes diagramas de bloco,

(21)

(b)

Exercício 3.6: Calcular a função de transferência em malha fechada do seguinte diagrama de blocos,