Conceções de alunos do 11º ano acerca dos conceitos de taxa de variação e reta tangente ao gráfico de uma função num ponto

Universidade do Minho

Instituto de Educação

outubro de 2016

Conceções de alunos do 11º ano

acerca dos conceitos de taxa de

variação e reta tangente ao gráfico

de uma função num ponto

P

aula Ale

xandra da Costa Figueir

edo

Conceções de alunos do 1

1º ano acerca dos conceitos de t

axa de v

ariação e ret

a t

angente ao gráfico de uma função num ponto

UMinho|20

16

Paula Alexandra da Costa Figueiredo

Conceções de alunos do 11º ano

acerca dos conceitos de taxa de

variação e reta tangente ao gráfico

de uma função num ponto

Universidade do Minho

Instituto de Educação

Trabalho realizado sob a orientação do

Doutor José António Fernandes

Relatório de Estágio

Mestrado em Ensino de Matemática no 3º ciclo

do Ensino Básico e no Ensino Secundário

AGRADECIMENTOS

Neste relatório quero deixar expresso o meu profundo agradecimento ao meu supervisor de estágio Professor Doutor José António Fernandes por toda a orientação, apoio e disponibilidade durante o estágio profissional e na realização deste relatório.

À professora Margarida, orientadora cooperante do estágio agradeço a dedicação e amizade ao longo deste ano. Agradeço também às minha colegas de estágio, Cláudia e Joana pela amizade e partilha.

À escola na qual fiz o estágio e seus professores, funcionários e queridos alunos agradeço o acolhimento e colaboração ao longo de um ano de trabalho.

Não posso deixar de agradecer os meus pais pelo apoio, incentivo e sacrifício ao longo destes árduos anos na universidade. Aos meus melhores amigos, Paulo e Rita agradeço pela compreensão, encorajamento e carinho durante todo este percurso.

CONCEÇÕES DE ALUNOS DE 11.º ANO ACERCA DOS CONCEITOS DE TAXA DE VARIAÇÃO E RETA TANGENTE AO GRÁFICO DE UMA FUNÇÃO NUM PONTO

Paula Alexandra da Costa Figueiredo

Mestrado em Ensino de Matemática no 3.º ciclo do Ensino Básico e no Ensino Secundário Universidade do Minho, 2016

RESUMO

No âmbito do Estágio Profissional do Mestrado em Ensino de Matemática no 3.º Ciclo do Ensino Básico e no Ensino Secundário foi desenvolvido um projeto em que pretendia analisar as conceções dos alunos de uma turma do 11º ano de escolaridade relativamente aos conceitos de reta tangente ao gráfico de uma função e de taxa de variação de uma função num ponto.

Esta investigação estruturou-se a partir dos três seguintes objetivos: (1) identificar conceções dos alunos acerca da taxa de variação e reta tangente ao gráfico de uma função num ponto; (2) explorar as conceções dos alunos no ensino do conceito de taxa de variação e (3) avaliar o impacto do ensino nas conceções dos alunos sobre taxa de variação e reta tangente ao gráfico de uma função num ponto. Tendo em vista atingir os objetivos propostos, foi realizado um teste diagnóstico, que foi aplicado no início e no final da intervenção; foi realizada uma intervenção pedagógica, em que foram feitas gravações em áudio e vídeo das aulas e fotocopiados os cadernos dos alunos; e, finalmente, avaliaram-se as aprendizagens dos alunos através da realização de uma questão-aula e algumas questões incluídas num teste sumativo.

Na avaliação diagnóstica constata-se que, geralmente, os alunos apresentaram conceções erradas acerca do conceito de reta tangente, relacionando-o com o conceito de reta tangente à circunferência. Após a implementação da intervenção pedagógica observaram-se progressos nos resultados alcançados, embora alguns alunos continuem a manter as dificuldades antes identificadas.

Os alunos adquiriram uma noção intuitiva sobre se uma reta é ou não tangente ao gráfico num ponto, mas, em geral, não visualizaram a reta tangente ao gráfico de uma função num ponto como o limite de retas secantes traçadas em torno desse ponto, nem associaram o declive da reta tangente ao valor da derivada no ponto. Relativamente ao conceito de taxa de variação, os alunos apresentaram dificuldades em interpretar geometricamente o conceito, não recorrendo a uma visualização gráfica para resolver tarefas ou para confirmar geometricamente os resultados obtidos.

Em geral, às dificuldades referidas acrescentam-se aquelas que resultaram de relacionar os diferentes conceitos estudados, o que revela a natureza complexa destes conceitos. Face a estas dificuldades, a linearização do gráfico da função no ponto pode constituir uma estratégia complementar ao limite das retas secantes para explorar o conceito de reta tangente.

CONCEPTIONS D’ÉLÈVES DE 11.º ANNÉE À PROPOS DE CONCEPTS DE TAUX DE VARIATION ET LIGNE TANGENTE AU GRAPHIQUE D’UNE FONCTION SUR UN POINT

Paula Alexandra da Costa Figueiredo

Maitrise en Enseignement de Mathématique 3.º cycle de l’Enseignement base et Enseignement Secondaire

Universidade do Minho, 2016 RÉSUMÉ

Dans le cadre du stage proffissionnel dans le domaine de Maitrise en Enseignement de Mathématique 3.º cycle de l’Enseignement base et Enseignement Secondaire un projet a été mis au point, qui vise analyser les conceptions des élèves dans une classe de 11.º année par rapport aux concepts de la tangente au graphique d'une fonction et au taux de variation d'une fonction en un point.

Cette recherche a été structuré à partir des trois objectifs suivants: (1) identifier les conceptions des élèves sur le taux de changement et tangente à une fonction à un tableau de points; (2) explorer les conceptions des élèves dans l'enseignement sur la notion de taux de changement et (3) évaluer l'impact de l'éducation dans les conceptions des élèves sur le taux de croissance et tangente à la représentation graphique d'une fonction en un point. Afin d'atteindre les objectifs proposés, un test de diagnostic appliqué au début et à la fin de l'intervention a été effectué; une intervention éducative, ils ont fait des enregistrements audio et vidéo des cours et photocipié les cahiers des élèves; et enfin on a évalué les apprentissages des élèves en procédant à une question de classe et quelques questions incluses dans un test sommatif.

Atravers de l'évaluation diagnostique on constate que, en général, les étudiants ont présenté des idées incorrectes à propos du concept de ligne tangente, reliant à la notion de tangente au cercle. Après la mise en pratique de l'éducation intervention on a pu observer des progrès dans les résultats obtenus, bien que certains élèves continuent à manifester les difficultés auparavant identifiées.

Les étudiants ont acquis un sens intuitif si une ligne est ou non tangente au graphique en un point, mais en général, ils n’ont pas vu la ligne tangente au graphique d'une fonction en un point comme le limite de lignes droites autour de ce point, ni associés la pente de la ligne tangente à la valeur du dérivé au point. En ce qui concerne la notion de taux de changement, les élèves ont eu des difficultés dans l'interprétation du concept géométriquement, n’ayant eux utiliser une vuasualisation graphique pour résoudre des tâches ou pour confirmer les résultats obtenus géométriquement.

En général, ces difficultés sont ajoutées à celles qui ont conduit à relier les différents concepts étudiés, qui révèle la nature complexe de ces concepts. Compte tenu de ces difficultés, la fonction de linéarisation graphique au point peut être une stratégie complémentaire à la limite de lignes sécantes à explorer le concept de la tangente.

Mots-clés: Apprentissage; Conceptions; Linhe tangente et le taux de changement; 11.º année.

ÍNDICE DECLARAÇÃO ... ii AGRADECIMENTOS ... iii RESUMO ... v RÉSUMÉ ... vii ÍNDICE ... ix

ÍNDICE DE TABELAS ... xii

ÍNDICE DE FIGURAS ... xiii

CAPÍTULO I — INTRODUÇÃO ... 1

1.1. Tema e objetivos ... 1

1.2. Pertinência do Estudo ... 3

1.3. Estrutura do Relatório ... 3

CAPÍTULO II — ENQUADRAMENTO TEÓRICO ... 5

2.1. O conceito de taxa de variação e o seu ensino ... 5

2.1.1. Perspetiva histórica do conceito de taxa de variação ... 5

2.1.2. O ensino de conceito de taxa de variação no currículo do Ensino Secundário ... 6

2.1.3. Significados do conceito de derivada ... 8

2.2. O ensino do conceito de reta tangente a uma curva num ponto no currículo escolar ... 10

2.3. As conceções dos alunos ... 11

CAPÍTULO III — ENQUADRAMENTO CONTEXTUAL ... 15

3.1. Caracterização da escola ... 15

3.2. Caracterização da turma... 16

3.3. Estratégias de Intervenção ... 18

3.4. Métodos de recolha de dados ... 19

4.1. Avaliação diagnóstica... 21

Questão 1 ... 21

Questão 2 ... 24

4.2. Implementação da intervenção pedagógica ... 26

4.2.1. Reta tangente ao gráfico de uma função num ponto ... 28

4.2.2. Taxa de Variação ... 32

4.2.3. Função derivada ... 34

4.2.4. Relação entre os intervalos de monotonia de uma função e o sinal da função derivada ... 36

4.3. Avaliação das aprendizagens ... 40

4.3.1. Questão – Aula ... 41

Questão 1 ... 41

Questão 2 ... 42

Questão 3 ... 44

4.3.2. Teste de avaliação sumativa ... 47

Questão de escolha múltipla ... 47

Questão de desenvolvimento ... 48

Questão 1.1 ... 49

Questão 1.2a) ... 51

Questão 1.2b) ... 52

4.3.3. Segunda aplicação do teste diagnóstico ... 53

Questão 1 ... 53

Questão 2 ... 56

CAPÍTULO V — CONCLUSÕES, IMPLICAÇÕES, RECOMENDAÇÕES E LIMITAÇÕES ... 59

5.3. Objetivo 2: Explorar as conceções dos alunos no ensino do conceito de taxa de variação .. 61

5.4. Objetivo 3: Impacto do ensino nas conceções dos alunos ... 63

5.5. Limitações, Recomendações e Implicações ... 65

BIBLIOGRAFIA ... 69

ANEXO I — Teste diagnóstico ... 73

ANEXO II — Elementos de Avaliação ... 79

Questão-Aula ... 81

Teste de avaliação sumativa ... 82

ÍNDICE DE TABELAS

Tabela 1 – Frequência absoluta das classificações dos alunos no final do 10.º ano e no 1.º, 2.º e

3.º período do 11.º ano ... 17

Tabela 2 — Objetivos e métodos de recolha de dados ... 20

Tabela 3 – Percentagem dos tipos de resposta e das justificações na questão 1 ... 21

Tabela 4 – Percentagem de alunos em cada uma das opções de resposta das alíneas a) e b) da questão 2 ... 25

Tabela 5 – Aulas lecionadas na intervenção pedagógica ... 27

Tabela 6 — Tipo de justificação apresentada pelos alunos na questão 1 ... 42

Tabela 7 — Percentagem de alunos em cada uma das opções de resposta à questão 3 da questão-aula ... 45

Tabela 8 — Justificações dos alunos para a exclusão das opções (A), (B) e (C) ... 46

Tabela 9 — Percentagens de alunos em cada uma das opções de escolha ... 48

Tabela 10 — Tipos de erros cometidos pelos alunos na questão 1.1 ... 49

Tabela 11 – Percentagem dos tipos de resposta e das justificações na questão 1 ... 53

Tabela 12 – Percentagem de alunos em cada uma das opções de resposta das alíneas a) e b) da questão 2 ... 56

ÍNDICE DE FIGURAS

Figura 1. Relação entre uma reta e uma circunferência (Marques & Ferreira, 2012, p. 33). ... 10 Figura 2. Definição de reta tangente à circunferência recorrendo ao produto escalar (Neves,

Pereira & Silva, 2015a, p. 103). ... 11 Figura 3. Interpretação geométrica de derivada de uma função num ponto (Neves, Pereira &

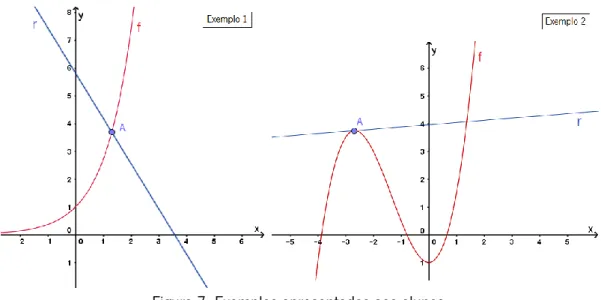
Silva, 2015b, p. 131). ... 11 Figura 4. Questões do estudo realizado por Castela (1995). ... 13 Figura 5. Resposta do aluno A ao gráfico 1 da questão 1. ... 23₁₅ Figura 6. Justificação do aluno A na alínea b) da questão 2. ... 26₂ Figura 7. Exemplos apresentados aos alunos. ... 28 Figura 8. Representação realizada pelo aluno A , no caderno diário. ... 293 Figura 9. Exemplo apresentado aos alunos para determinarem a reta tangente em

A

. ... 30 Figura 10. Exemplo apresentado aos alunos para determinarem a reta tangente em

A

. ... 31 Figura 11. Resolução da questão 1.3 pelo aluno A . ... 32₅ Figura 12. Resolução da questão 1.3 pelo aluno A . ... 32₁₀ Figura 13. Representação gráfica utilizada para introduzir o conceito de taxa de variação. ... 33 Figura 14. Representação efetuada pelo aluno A no caderno. ... 341 Figura 15. Apontamento efetuado pelo aluno A no caderno. ... 354 Figura 16. Resolução efetuada pelo aluno A no caderno. ... 36₁₉ Figura 17. Resolução efetuada pelo aluno A no caderno. ... 37₆ Figura 18. Resolução efetuada pelo aluno A no caderno. ... 40₄ Figura 19. Resolução efetuada pelo aluno A no caderno. ... 40₁₀ Figura 20. Resolução efetuada pelo aluno A no caderno. ... 40₁₅ Figura 21. Resolução da questão 1, da questão-aula, pelo aluno A . ... 42₆ Figura 22. Resolução da questão 1, da questão-aula, pelo aluno A . ... 42₅ Figura 23. Resolução da questão 2, da questão-aula, pelo aluno A . ... 432 Figura 24. Resolução da questão 2, da questão-aula, pelo aluno A . ... 448 Figura 25. Resolução da questão 3, da questão-aula, pelo aluno A . ... 4517 Figura 26. Resolução da questão 3, da questão-aula, pelo aluno A . ... 47₁

Figura 27. Resolução da questão 1.1, do teste de avaliação, pelo aluno A . ... 507 Figura 28. Resolução da questão 1.1, do teste de avaliação, pelo aluno A . ... 5118 Figura 29. Resolução da questão 1.2a), do teste de avaliação, pelo aluno A . ... 52₅ Figura 30. Resolução da questão 1.2b), do teste de avaliação, pelo aluno A . ... 52₂₀ Figura 31. Resolução da questão 1, gráfico 6, na segunda aplicação do teste diagnóstico, pelo

aluno A . ... 5620 Figura 32. Resolução da questão 2b), na segunda aplicação do teste diagnóstico, pelo aluno

. 17

CAPÍTULO I INTRODUÇÃO

No capítulo inicial, dividido em três secções, são apresentados o tema e objetivos deste Relatório de Estágio, bem como a sua pertinência e, finalmente, é apresentada também, de forma sucinta, a estrutura geral do Relatório.

1.1. Tema e objetivos

O tema escolhido para o Projeto de Intervenção Pedagógica Supervisionada centra-se nas conceções de alunos de uma turma de 11.º ano de Matemática A acerca dos conceitos de taxa de variação e de reta tangente ao gráfico de uma função num ponto. Assim, a intervenção de ensino incidirá no Tema II – Introdução ao Cálculo Diferencial I do programa de 11º ano do ensino secundário (Ministério da Educação, 2002).

A álgebra é um ramo importante da Matemática, e o reconhecimento desta importância é visível através da ênfase que é dada à álgebra nos programas de ensino básico e secundário. Assim, “considerando a álgebra como um fio condutor curricular desde os primeiros anos de escolaridade, os professores poderão ajudar os alunos a construir uma base sólida baseada na compreensão e nas suas experiências” (NCTM, 2008, p. 39). O que muitas vezes acontece é que os alunos chegam ao ensino secundário sem esta base sólida, e com conceções erradas ou pouco fundamentadas sobre determinados objetos matemáticos.

Perceber as conceções dos alunos implica saber “o que a pessoa pensa sobre determinada coisa, que entendimento tem dessa coisa, qual é a forma como ela a vê ou encara” (Guimarães, 2010, p. 84). Este é um processo extremamente difícil para o professor, principalmente quando está perante uma turma heterogénea. As conceções de cada aluno sobre determinado objeto são diferentes já que “os alunos não aprendem apenas um subconjunto do que lhes foi mostrado. Em vez disso, utilizam nova informação para modificar as suas próprias conceções. Em consequência, o conhecimento de cada aluno em matemática é único e pessoal” (NCTM, 1994, p. 3).

Conceitos como taxa de variação, reta tangente e outros a eles associados, como função derivada, são fundamentais para a compreensão de várias situações do dia-a-dia. Tal como salienta o NCTM, “a compreensão da variação é essencial à compreensão das funções e à compreensão de muitas ideias transmitidas nas notícias” (2008, p. 42); no entanto, refere-se ainda que este é um conceito que não está devidamente consolidado para a maioria dos alunos.

Já Finney, Thomas, Demana e Waits (1994) evidenciam a importância da noção de derivada no cálculo, reforçando a ideia de que é um conceito com diversas aplicações.

O que me levou a escolher este tema foi a necessidade de entender a forma como os alunos encaram determinados objetos matemáticos e de que forma podem ser exploradas essas conceções de modo a tornar o processo de ensino-aprendizagem mais eficaz.

Note-se que, maioritariamente, os professores não conhecem as conceções que os alunos têm sobre um determinado tema, antes de começarem a sua lecionação. Desta forma, não podem usar esse conhecimento como ponto de partida no processo de ensino-aprendizagem, de modo a tirar partido das conceções dos alunos, quer sejam estas corretas ou não.

Guimarães (2010, p. 81) destaca que “não há ensino se não existir aprendizagem, entendido o ensino como processo de interação entre o professor e o(s) aluno(s), pelo qual o professor promove e dirige a aquisição e o desenvolvimento do referido conhecimento no(s) aluno(s)”. Tendo em conta este facto, o que se pretende principalmente é que os alunos desenvolvam o seu conhecimento, neste caso específico, no que diz respeito ao tema Taxa de Variação. Desta forma, o professor torna-se responsável por fornecer aos alunos os meios necessários para que eles sejam capazes de lidar com as suas conceções prévias e com os novos conhecimentos, de modo a que haja de facto aprendizagem por parte dos alunos. Também Vrancken e Engler (2014) salientam que:

O ensino deve contribuir para que o estudante desenvolva as suas potencialidades e alcance a formação de um pensamento produtivo, criador e científico. É importante criar no estudante a necessidade de aprender e gerar um ambiente onde se possibilite e se motive a exploração do significado pessoal dos conceitos. (p. 452)

Assim, tendo em conta a importância das conceções dos alunos, especificamente do 11.º ano, estabeleceram-se para o presente estudo os três objetivos seguintes:

1. Identificar conceções dos alunos acerca da taxa de variação e reta tangente ao gráfico de uma função num ponto;

2. Explorar as conceções dos alunos no ensino do conceito de taxa de variação;

3. Avaliar o impacto do ensino nas conceções dos alunos sobre taxa de variação e reta tangente ao gráfico de uma função num ponto.

1.2. Pertinência do Estudo

O conceito de taxa de variação, e consequentemente o conceito de reta tangente ao gráfico de uma função num ponto, que é maioritariamente usado para chegar à definição de Taxa de Variação num ponto, são conceitos de extrema importância no currículo da Matemática.

Estes dois conceitos têm aplicações em diversas ciências além da Matemática, como a Física, por exemplo, onde a Taxa de Variação corresponde à velocidade instantânea de um corpo num determinado momento, ou na Biologia onde é usada para determinar a taxa de crescimento de bactérias. O conceito de Taxa de Variação também é amplamente utilizado e estudado em diversos cursos de Ensino Superior, principalmente em cursos de Engenharia e de ciências exatas, como a Matemática, Física ou Química, entre outros.

Para além das aplicações do conceito de taxa de variação a outras áreas, também do ponto de vista estritamente matemático, o conceito de taxa de variação mantém relações com outros conceitos, destacando-se as noções de monotonia, de otimização e de vários aspetos ligados ao cálculo integral. Assim, as muitas aplicações deste conceito, quer dentro da matemática quer fora, no âmbito de outras ciências, conferem-lhe uma importância fundamental, que se verifica com poucos conceitos matemáticos.

Tendo em contas estes aspetos, é imprescindível que os alunos tenham uma correta compreensão destes conceitos. Segundo Viseu (2000, pp. 4-5) “uma forma de ampliar esta compreensão é o trabalho com diferentes representações dos conceitos e as relações entre essas representações, evidenciando que os procedimentos se aprendem não só de uma forma mecânica, como também conhecendo como funcionam”.

Desta forma, é notável a importância de conhecer e explorar as conceções que os alunos têm acerca destes dois conceitos, para que construam ideias e conceções corretas e devidamente estruturadas ao longo do seu percurso escolar.

1.3. Estrutura do Relatório

Este relatório encontra-se dividido em cinco capítulos: Capítulo I — Introdução; Capítulo II — Enquadramento teórico; Capítulo III — Enquadramento contextual, Capítulo IV — Intervenção pedagógica e Capítulo V — Conclusões, implicações, recomendações e limitações.

O Capítulo I, de Introdução, que acabámos de apresentar, encontra-se dividido em três subcapítulos, em que são abordados o tema e objetivos deste projeto, a sua pertinência e, por fim, a estrutura do mesmo.

O Capítulo II, de Enquadramento teórico, encontra-se dividido em três subcapítulos, que são o suporte teórico deste relatório. Assim, faz-se uma breve referência à evolução histórica à luz da matemática e dos programas de ensino dos principais conceitos abordados neste relatório, que são os conceitos de Taxa de Variação, de reta tangente, aborda-se o ensino do conceito de reta tangente ao gráfico de uma função num ponto no currículo escolar atual e, por último, aborda-se a problemática das conceções dos alunos.

No Capítulo III, de Enquadramento contextual, dividido em quatro subcapítulos, apresenta-se a caracterização da escola e da turma onde foi realizada a intervenção pedagógica, bem como as estratégias de intervenção utilizadas, finalizando com os métodos utilizados para a recolha de dados usados na realização deste relatório.

O Capítulo IV, da Intervenção pedagógica, sendo o mais amplo, está organizado em três subcapítulos, especificamente sobre a análise da avaliação diagnóstica, da implementação da intervenção pedagógica e, por fim, da avaliação das aprendizagens.

No Capítulo V, de Conclusões, implicações, recomendações e limitações, apresentam-se as conclusões, implicações, recomendações e limitações do estudo realizado, e encontra-se dividido em cinco subcapítulos que apresentam uma síntese do projeto e dão resposta aos três objetivos propostos no estudo, finalizando com algumas sugestões e recomendações a partir dos resultados obtidos.

CAPÍTULO II

ENQUADRAMENTO TEÓRICO

Neste capítulo é apresentado o fundamento teórico deste relatório, que se organiza em três subcapítulos: (1) o conceito de taxa de variação e o seu ensino, (2) o ensino do conceito de reta tangente ao gráfico de uma função num ponto no currículo escolar e (3) as conceções dos alunos. 2.1. O conceito de taxa de variação e o seu ensino

Este subcapítulo apresenta-se dividido em três secções, sendo a primeira dedicada a uma perspetiva histórica do conceito de derivada, onde são apresentadas algumas contribuições de Descartes, Fermat e Newton para o Cálculo. Depois é apresentada a evolução do ensino do conceito de derivada nos currículos desde que ele foi introduzido, pela primeira vez, em 1905, até ao programa atual. E finalmente são abordadas algumas representações da taxa de variação, bem como a sua interpretação gráfica.

2.1.1. Perspetiva histórica do conceito de taxa de variação

Foram vários os autores que contribuíram para a evolução do conceito de derivada, não sendo claro, na literatura, a atribuição da sua descoberta apenas a uma pessoa.

Um dos matemáticos que contribuiu para o descobrimento deste conceito foi Descartes (1596 — 1650), que em 1637 escreveu um tratado intitulado “Discurso do método para bem conduzir a razão e procurar a verdade das ciências”. Este tratado tinha três apêndices, sendo que o terceiro — “A Geometria” — era dedicado à Matemática. Neste apêndice, ele inclui “uma classificação de curvas e um método de construir tangentes a curvas” (Santos, 2011, p. 73).

Pela mesma altura, Fermat (1601 — 1665) escreveu o tratado “Método para achar máximos e mínimos”, no qual mostra que, além da descoberta de um método para determinar máximos e mínimos de curvas polinomiais, “descobriu como aplicar seu processo de valores vizinhos para achar a tangente a uma curva algébrica da forma y f(x)” (Boyer, 1974, p. 255).

Para Boyer (1992, p. 15) “há plena razão para se reconhecer, […] que Fermat foi o “inventor” do Cálculo Diferencial”, utilizando um método semelhante ao usado atualmente para determinar o declive da reta tangente ao gráfico de uma função num ponto.

Mais tarde, Newton (1643 — 1727) e Leibniz (1646 — 1716), de forma independente, também deram grandes contributos para o Cálculo Diferencial.

Embora só no século XIX Cauchy introduza formalmente o conceito de limite e o conceito de derivada, a partir do século XVII, com Leibniz e Newton, o Cálculo Diferencial torna-se um instrumento cada vez mais indispensável pela sua aplicabilidade aos mais diversos campos da Ciência. (Viseu, 2000, p. 18)

Segundo Stewart (2006) foi Newton o primeiro matemático a abordar as ideias de limite como base do Cálculo Diferencial. Por sua vez Leibniz concluiu que para determinar a reta tangente a uma curva teria de recorrer à razão das diferenças das ordenadas e das abcissas, quando estas diferenças se tornam infinitamente pequenas (Boyer, 1974). Contudo, o conceito de limite apresentado por Leibniz e Newton não era muito claro, e só mais tarde surge uma definição mais desenvolvida de limite apresentada por d’Alembert.

2.1.2. O ensino de conceito de taxa de variação no currículo do Ensino Secundário A Taxa de Variação é um dos temas integrantes do programa de 11.º ano de Matemática A do Ensino Secundário.

A breve evolução do ensino do conceito de derivada, aqui apresentada, baseia-se no texto intitulado “O conceito de derivada no ensino secundário ao longo do século XX”, de Aires e Vásquez (2004), onde são apresentadas em pormenor as várias reformas implementadas no ensino ao longo do século passado, focando o conceito de derivada.

Este tema, integrado no capítulo da Álgebra, foi introduzido no programa de Matemática, na VI classe do curso complementar de Ciências, no ano de 1905, numa reforma feita no ensino liceal por Eduardo José Coelho, que nessa altura era Ministro e Secretário de Estado dos Negócios do Reino.

Em 1918, numa reforma feita por Alfredo Magalhães, o Cálculo Infinitesimal ganha autonomia, passando o tema das derivadas a ser precedido da noção de limite. Anos mais tarde, em 1936, verifica-se um retrocesso no ensino da Matemática e o tema das derivadas é excluído do programa de Matemática. Só em 1947 este tema volta a fazer parte do programa.

Na reforma implementada em 1974 foram feitas alterações que visavam a aproximação entre a Matemática lecionada no Ensino Secundário e no Ensino Superior e o tema Derivadas passou a ter um capítulo a ele dedicado, tanto no 11.º como no 12.º ano.

A partir daqui foram feitas várias reformas, sempre mantendo o ensino do tema Derivadas Desde a introdução da noção de derivada no plano de estudo do ensino liceal, no ano

1936, em que aquela foi suprimida, assistimos a uma afirmação e aumento do espaço dedicado ao ensino de derivadas. (Aires & Vázquez, 2004, p. 120)

O programa de 11.º ano de Matemática A, de 2002, que esteve em vigor pela última vez este ano, está dividido em três temas: (1) Geometria no Plano e no Espaço II, (2) Introdução ao Cálculo Diferencial, Funções racionais e com radicais, Taxa de Variação e Derivada e (3) Sucessões Reais (Ministério da Educação, 2002).

O subtema Taxa de Variação inclui-se no segundo tema que tem como tempo previsto de lecionação 30 aulas de 90 minutos, o que representa cerca de um terço do ano escolar.

O programa inclui a introdução do conceito de limite, salientando-se o facto de que ele deve ser introduzido de forma intuitiva e só no 12.º ano será formalizado. Prosseguindo com a taxa média de variação, preconiza-se que este conceito seja introduzido através da noção de velocidade média que os alunos conhecem da Física.

A taxa média de variação de uma função f no intervalo

 

a, é dada por: b   f b_{b a}f a v m t _ab    ( ) ( ) . . . _,

Posteriormente, introduz-se a taxa de variação, fazendo a sua interpretação geométrica recorrendo à noção intuitiva de limite. Passa-se depois à função derivada da função afim e de funções polinomiais de 2.º e 3.º graus, função racional de 1.º grau e função módulo, sugerindo-se que sugerindo-sejam propostos aos alunos alguns problemas simples envolvendo aplicações das derivadas. Finaliza-se este subtema relacionando os intervalos de monotonia da função com o sinal da sua respetiva derivada, sem deixar de apresentar alguns contraexemplos de “funções que têm derivada nula num ponto sem que nele haja extremo e que há funções com extremo que não têm derivada real no ponto em que tal acontece” (Ministério da Educação, 2002).

O cálculo diferencial também é um tema de enorme relevância no 12.º ano de escolaridade, onde representa também cerca de um terço do programa. Neste ano de escolaridade, tal como no 11.º ano, o ensino do cálculo diferencial é precedido do ensino do conceito de limite. No entanto, aqui o conceito de limite é introduzido não de forma intuitiva, mas formalmente, sendo apresentado aos alunos a definição de limite de função segunde Heine. São exploradas as operações com limites, limites notáveis, indeterminações, assintotas, continuidade e ainda o Teorema de Bolzano-Cauchy.

Prossegue-se com o Cálculo Diferencial onde os alunos aprendem regras de derivação de diferente tipo de funções, incluindo as funções trigonométricas, exponenciais e logarítmicas, e ainda a derivada da função composta. Segue-se o ensino da segunda derivada e concavidades, o que permite aos alunos fazer o estudo de funções em casos simples. É também sugerido no programa que seja dado aos alunos uma perspetiva histórica do Cálculo Diferencial. Finaliza-se o tema propondo-se problemas de otimização o mais completo possíveis, devendo salientar-se as suas aplicações e importância no mundo atual.

2.1.3. Significados do conceito de derivada

O conceito de derivada tem vários significados, quer ao nível teórico, no âmbito da matemática, quer ao nível prático, no âmbito das suas aplicações a outras ciências, destacando-se os destacando-seguintes significados de derivada da função f em x : 0

 O limite h x f h x f h ) ( ) ( lim 0 0 0    ;  O limite 0 0) ( ) ( lim x x x f x f o x x    ;

 Declive da reta tangente ao gráfico de f no ponto de abcissa x ; 0

 O declive da reta que melhor aproxima a função f na vizinhança do ponto x ; 0  A tangente do ângulo que a reta tangente ao gráfico de f no ponto x faz com o 0

eixo horizontal;

 Velocidade instantânea em x ; 0

 Taxa de crescimento populacional no instante x . 0

Tal (2000) sugere que a abordagem à noção de derivada deve ser planeada de forma a que sejam abordados o maior número de significados e representações do conceito, de modo a criar uma imagem concetual rica nos alunos. A este propósito, Dolores (2007) salienta que os alunos dificilmente reconhecem as ideias associadas ao conceito de derivada na resolução de problemas sobre variação.

Relativamente à interpretação gráfica do conceito de taxa de variação, são vários os autores que defendem que “o estudo das funções – Introdução ao Cálculo Diferencial I – deve ser feito colocando em primeiro plano as abordagens gráficas e intuitivas e relacionando de forma

Apesar das várias advertências neste sentido, muitas vezes devido ao tempo previsto nos programas para a abordagem deste tema, privilegia-se a componente analítica em vez da componente gráfica, introduzindo-se a noção de derivada e realizando-se tarefas sem qualquer contexto real e sem salientar a importância da sua interpretação gráfica (Pimentel, 1995).

Orton (1983), num estudo com 110 alunos ingleses entre os 16 e os 22 anos, todos com pelo menos um ano de Cálculo, verificou que a maioria dos alunos aplica corretamente os algoritmos de derivação, mas não interpreta geometricamente a noção de limite que está na base do conceito de derivada. Também González e Flores (2016), num estudo realizado com 45 alunos entre os 17 e os 25 anos, da Licenciatura em Matemática, concluíram que a maioria dos estudantes tem uma ideia da noção de derivada, enquanto fórmula, mas apenas 15% a identificam como o declive da reta tangente ou taxa de variação. A partir destes estudos torna-se evidente que os alunos demonstram facilidade nos procedimentos analíticos, contudo o mesmo não acontece com a compreensão concetual e geométrica.

Segundo Ferrini-Mundi e Lauten (1993), os alunos apresentam, em termos mais específicos, dificuldades em entender de que forma as retas secantes ao deslizarem ao longo de uma curva em torno de um ponto, no limite dão origem à reta tangente à curva nesse ponto.

Outra dificuldade identificada, neste caso num estudo realizado por Viseu (2000), com 19 professores estagiários de matemática, foi uma interpretação incorreta da informação proveniente do gráfico de uma função para efetuar um possível esboço gráfico da sua derivada ou vice-versa. Segundo o autor, de um modo geral, os estagiários apresentam dificuldades em relacionar a monotonia de uma função com o sinal da respetiva derivada em situações gráficas sem dados concretos.

Riddle (1994) apresenta como principal causa para estas dificuldades o facto de só se explorarem as representações gráficas na introdução do conceito de taxa de variação, passando-se posteriormente às regras de derivação. Mais tarde, esta abordagem pode passando-ser geradora de conflitos cognitivos:

Os alunos aprendem os processos de cálculo (limites, derivadas, etc…) a um nível puramente algorítmico, com poucas imagens do conceito. (…) Quando se recorre à visualização, a ligação entre representações visual/ gráfica e analítica/ algébrica é geradora de conflitos cognitivos (Dreyfus, 1990, p. 125)

Atendendo aos resultados obtidos nos diferentes estudos referidos acima, torna-se evidente a necessidade de adotar uma metodologia de ensino onde as componentes analítica e gráfica se

complementam, proporcionado aos alunos a oportunidade de criarem uma imagem conceptual de taxa de variação adequada.

2.2. O ensino do conceito de reta tangente a uma curva no currículo escolar

O conceito de reta tangente começa por surgir associado à circunferência e só mais tarde passa a ser associado a uma curva qualquer. Pensa-se que “foi na civilização grega que primeiramente surgiu a noção de tangente a uma curva que não a circunferência” (Boyer, 1974, p. 94). Também Arquimedes e Apolónio determinaram retas tangentes a hipérboles, parábolas e elipses. Posteriormente, Descartes e Fermat, no século XVII, generalizaram o conceito de tangente a qualquer curva (Viseu & Almeida, 2003).

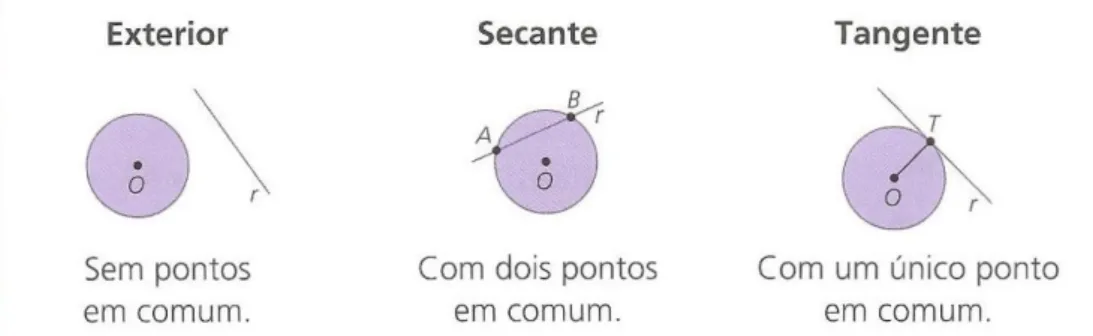
O ensino do conceito de reta tangente, segundo o programa de Matemática (Ministério da Educação, 2002), surge no 9.º ano de escolaridade associado à circunferência (Figura 1).

Figura 1. Relação entre uma reta e uma circunferência (Marques & Ferreira, 2012, p. 33). Como observamos pela Figura 1, a tangente é considerada como uma reta que tem um único ponto em comum com a circunferência. Isto é verdade para a relação entre a circunferência e a reta, mas não pode ser generalizado para qualquer curva. No entanto, em muitos alunos prevalece esta conceção quando chegam ao Ensino Secundário, a qual se revela correta em certas situações e errada noutras.

O conceito de tangente é posteriormente abordado no 11.º ano no tema Geometria no Plano e no Espaço II, mais uma vez relacionado com a circunferência. Nesta altura, é ensinado aos alunos a determinar a equação da reta tangente à circunferência recorrendo ao produto escalar (Figura 2).

Figura 2. Definição de reta tangente à circunferência recorrendo ao produto escalar (Neves, Pereira & Silva, 2015a, p. 103).

Ainda no 11.º ano, este conceito é abordado a propósito do conceito de derivada de uma função num ponto. É feita uma interpretação geométrica do conceito de derivada no ponto, como sendo o declive da reta tangente ao gráfico da função nesse mesmo ponto (Figura 3).

Figura 3. Interpretação geométrica de derivada de uma função num ponto (Neves, Pereira & Silva, 2015b, p. 1311).

A interpretação geométrica do conceito de derivada de uma função num ponto pode ser vantajosa, no sentido em que os alunos podem confirmar geometricamente os resultados obtidos de forma analítica. No entanto, segundo Tall (1994), os alunos geralmente não fazem ligação entre o pensamento analítico e o pensamento visual, principalmente por esta ligação ser ignorada no ensino.

Por outro lado, a interpretação geométrica pode constituir um problema considerando que os alunos nem sempre conseguem identificar corretamente a reta tangente ao gráfico de uma função num ponto, além de que “uma compreensão gráfica demasiado viva pode contribuir para ofuscar aspetos analíticos essenciais dos conceitos” (Almeida & Viseu, 2002).

2.3. As conceções dos alunos

O ensino é fortemente subordinado a aspetos árduos de captar como as conceções dos professores, mas também das conceções dos alunos face à Matemática, e ao seu ensino e aprendizagem (Christiansen & Walther, 1986).

As conceções, segundo Barbosa (2011, p. 11) “funcionam como lentes pelas quais os sujeitos dão significado às suas experiências”. Partindo desta perspetiva, é essencial ter

1_{Observa-se que na citação do livro de texto os parênteses curvos não estão corretos, existe um parentese curvo à}

consciência das conceções dos alunos sobre determinados temas matemáticos pois só desta forma poderemos entender através de que “lentes” os alunos dão significado aos conceitos que são abordados na sala de aula.

Perceber as conceções dos alunos implica saber “o que a pessoa pensa sobre determinada coisa, que entendimento tem dessa coisa, qual é a forma como ela a vê ou encara” (Guimarães, 2010, p. 84), o que nem sempre é um processo fácil, devido ao aumento de heterogeneidade das turmas. Além disso, é importante perceber que as conceções podem decorrer das nossas experiências ou do confronto com as experiências dos outros (Ponte, 1992). Assim, é preciso entender a origem das conceções dos alunos para que o processo de ensino-aprendizagem seja mais eficaz, contrariando possíveis conceções erradas ou fortalecendo conceções corretas manifestadas pelos alunos (Fernandes, 1990). Guimarães (2010) salienta, ainda, que uma vez que o aluno desenvolva uma conceção, ela será usada em compreensões futuras e os alunos irão aplicá-la a novas situações, o que reforça ainda mais a importância da compreensão e análise das conceções dos alunos.

São vários os autores que abordam questões relacionadas com as conceções dos alunos e a forma como se desenvolve o seu conhecimento matemático. Cantoral e Montiel (2001, p. v) referem que

Os alunos constroem conhecimento com certa independência do discurso matemático do ensino. Com frequência, constroem explicações inadequadas e inclusive erradas do ponto de vista matemático, uma vez que descobrem profundas relações entre peças do saber matemático, sem que isso tenha sido parte explícita do seu ensino.

No que diz respeito às conceções dos alunos acerca da reta tangente ao gráfico de uma função num ponto, muitos alunos têm dificuldades em identificar a reta tangente num ponto de inflexão ou em entender o significado de uma reta tangente intersetar um gráfico de uma função em mais do que um ponto, em consequência de não terem construído uma conceção adequada do conceito de reta tangente num ponto (Biza & Zachariades, 2010). No mesmo sentido, Vinner (1991) salienta que o conceito de tangente à circunferência tende a prevalecer, mesmo quando se trata de outro tipo de curvas. Em consequência, “tornam-se geradoras de conflito cognitivo as situações em que a reta tem vários pontos em comum com a curva, ou em que a reta “corta” a curva, o que nunca acontece com a circunferência” (Viseu & Almeida, 2003, p. 197).

Para Tall (1991) estes conflitos surgem devido ao facto de as abordagens pedagógicas não levarem em consideração as intuições dos alunos relativamente a este conceito, o que destaca a importância da avaliação dessas intuições prévias dos alunos.

Num estudo realizado por Vinner (1991), com 278 alunos de Análise, pediu-se aos alunos para traçar retas tangentes a diferentes gráficos num determinado ponto e conclui-se que 85% dos alunos apresentou representações erradas, sendo que em 35% dessas representações erradas era evidente a influência da noção de tangente à circunferência.

Castela (1995), num estudo realizado com alunos do ensino secundário sobre o conceito de reta tangente a uma curva num ponto, detetou diferentes conceções, o que a levou a questionar-se sobre a forma como o vocabulário utilizado no ensino pode influenciar essas conceções. A autora avança ainda com a hipótese de que os alunos têm diferentes capacidades para contextualizar novos conhecimentos que diferem dos que estabeleceram previamente, devido à existência de inconsistências entre as antigas conceções, antes adquiridas, e aquelas que se pretende que adquiram de novo.

Com este estudo, realizado com alunos franceses no decorrer de três anos letivos, pretendia-se avaliar as conceções dos alunos acerca do conceito de reta tangente a uma curva. O estudo foi realizado com 228 alunos que já tinham estudado o conceito de derivada e 144 que nunca o tinham estudado. Aos alunos foi pedido que respondessem a um questionário com oito questões, onde em cada uma se representava uma curva e uma reta e os alunos tinham que indicar, justificando, se a reta era ou não tangente à curva no ponto A assinalado na curva (Figura 4).

Relativamente aos resultados dos alunos que nunca tinham estudado derivadas, observou-se uma baixa taxa de sucesso. Estes apreobservou-sentaram maiores dificuldades nos gráficos 1, 2, 4 e 6, onde mais de 50% dos alunos apresentou respostas incorretas. Segundo a autora, as dificuldades apresentadas devem-se, no gráfico 1, ao facto de a reta cortar a curva; no gráfico 2, ao facto de A ser um ponto anguloso: no gráfico 4, ao facto de a curva se confundir localmente com a reta; e no gráfico 6, ao facto de se tratar de um ponto de inflexão.

No que diz respeito aos alunos que já tinham estudado derivadas, nos gráficos 1, 2, 3, 5, 6, 7 e 8 as percentagens de respostas corretas ultrapassou os 75%, o que não se verificou na questão 4, onde a percentagem de respostas corretas não ultrapassou os 50%. A maioria dos alunos que errou na questão 4 justificou alegando que a curva se confunde localmente com a reta, donde não é tangente.

Viseu (2000) utilizou o mesmo questionário, num estudo realizado com 19 professores estagiários da Licenciatura em Ensino de Matemática da Universidade do Minho, concluindo que a maioria dos estagiários generalizou a noção de tangente à circunferência a outras situações, desenvolvendo uma perspetiva global deste conceito. Nas respostas obtidas observa-se a referência ao número de pontos de interseção entre a curva e a reta e ao facto de a reta “cortar” ou não a curva, revelando assim uma conceção pouco clara de reta tangente por parte dos estagiários.

Através dos resultados obtidos nos estudos acima referidos, conclui-se que a maioria dos alunos apresenta conceções erradas acerca do conceito de reta tangente ao gráfico de uma função, principalmente devido ao facto de generalizarem o conceito de reta tangente à circunferência a outras situações.

CAPÍTULO III

ENQUADRAMENTO CONTEXTUAL

Neste capítulo será caracterizado o enquadramento contextual da intervenção pedagógica, onde será apresentada a caracterização da escola onde foi feito o estágio, bem como da turma onde lecionei. Apresentam-se ainda as estratégias de intervenção utilizadas e os diferentes métodos de recolha de dados.

3.1. Caracterização da escola

Relativamente ao enquadramento contextual, a intervenção pedagógica foi realizada numa turma do 11.º ano de escolaridade de uma escola do concelho de Braga.

Esta escola pertence a um agrupamento de escolas constituído por doze estabelecimentos de ensino, abrangendo cerca de 2277 alunos distribuídos por diferentes níveis de ensino, desde o ensino pré-escolar até ao ensino secundário, e 235 professores.

Tendo já muitos anos de existência, a escola acumulou um vasto espólio a nível bibliográfico, biológico e de equipamento científico, que em parte está exposto no museu da escola e na biblioteca. A escola possui ainda um teatro e uma quinta e foi submetida a uma profunda remodelação no ano letivo de 2010/2011.

A escola está munida de diversos espaços para os professores e para os alunos, como por exemplo salas de convívio e salas de trabalho e estudo.

Os pontos fulcrais do Plano Anual de Atividades (PAA) são a promoção do sucesso educativo e do sentido de pertença ao agrupamento no qual está inserida a escola, a valorização profissional de docentes e não docentes e o aumento da interação com a comunidade educativa. Neste sentido, o PAA está repleto de atividades que visam atingir as metas acima descritas.

Aos alunos é disponibilizado apoio educativo às disciplinas que vão ter exame, e o horário desse apoio consta do horário dos alunos e dos professores. Este apoio consta do Plano de Ação para a Promoção do Sucesso Educativo elaborado pela escola, o qual salienta a criação de grupos de trabalho no apoio educativo de acordo com níveis de aprendizagem e graus de dificuldade.

A escola tem em conta a diversidade de estatutos sociais e económicos dos seus alunos, oferecendo um apoio diversificado e uma oferta educativa variada. Nesta escola podemos encontrar, essencialmente, um ensino secundário regular, mas também existem cursos

profissionais e algumas turmas do ensino básico. Desta forma, a oferta educativa da escola neste ano letivo inclui os cursos científico-humanísticos de Ciências e Tecnologias, Línguas e Humanidades, Artes Visuais e Ciências Socioeconómicas. Como cursos profissionais funcionaram o de Técnico de Gestão e Programação de Sistemas Informáticos, Técnico de Multimédia, Técnico de Apoio à Infância, Técnico de Receção, Técnico de Eletrónica, Automação e Computadores e Técnico de Auxiliar Psicossocial. Existem ainda Percursos Vocacionais (de equivalência ao 9.º ano) e de Educação e Formação de Adultos.

Existem ainda na escola vários projetos como um Clube de Robótica, um Centro de Criatividade e Mudança, uma Oficina de Leitores, uma Oficina de Teatro, um Programa de Educação para a Saúde, entre outros.

Esta escola procura ainda aprofundar nos alunos o respeito pelos outros, o espírito de solidariedade, o humanismo e a convivência democrática. Espera desta forma, formar jovens cidadãos críticos e interventivos na sociedade. Estes objetivos presentes no Projeto Educativo vêm seguidos de pontos de partida atuais e planos de melhoria para cada um dos objetivos pretendidos, bem como dos indicadores a ter em conta para avaliar cada objetivo.

Na avaliação externa, feita à escola em fevereiro de 2010, a escola foi avaliada com o nível Bom nos cinco critérios: (1) resultados, (2) prestação do serviço educativo, (3) organização e gestão escolar, (4) liderança e (5) capacidade de autorregulação e melhoria da escola. Numa nova avaliação feita em 2016, os resultados obtidos melhoraram substancialmente, atingindo o nível de Muito Bom em todas as categorias.

Por fim, salienta-se a inexistência de casos graves de violência, existindo um bom relacionamento entre todos os membros da comunidade escolar, com respeito e atenção pelos direitos e deveres mútuos.

3.2. Caracterização da turma

A turma, na qual realizei a intervenção pedagógica era uma turma de 11.º ano do curso Científico-Humanístico de Ciências e Tecnologias, constituída por 20 alunos (A₁, A , …, ₂

A

20),

sendo que 13 (65%) eram rapazes e 7 (35%) raparigas, com idades compreendidas entre 16 e 18 anos, e uma média de idades de 16,7 anos.Desta turma faziam parte 10 alunos repetentes, dos quais 3 já tinham duas retenções e uma aluna com Necessidades Educativas Especiais (NEE).

referiram que Matemática era a disciplina na qual tinham mais dificuldades. Havia ainda 6 alunos com explicações a Matemática e salienta-se ainda o facto de que 19 alunos pretendiam ingressar no ensino superior.

No respeitante ao desempenho da turma no 10.º ano de escolaridade, 35% dos alunos terminaram o 10.º ano com negativa na disciplina de Matemática. No 1.º período do 11.º ano houve uma descida das notas, sendo que a média foi 8.5 valores. No segundo e terceiro períodos as notas subiram ligeiramente, no entanto observando-se uma média final de 11.º ano de apenas 9.5 e a classificação mais elevada de 12 valores.

Tabela 1 – Frequência absoluta das classificações dos alunos no final do 10.º ano e no 1.º, 2.º e 3.º período do 11.º ano

10.º Ano 11.º Ano

Classificação 3.º Período 1.º Período 2.º Período 3.º Período

5 0 0 0 1 6 0 1 3 2 7 0 7 4 0 8 3 2 2 5 9 4 5 1 0 10 6 3 7 5 11 2 1 2 2 12 4 0 0 5 13 1 1 1 0 Média 10.2 8.5 8.8 9.5

A turma, além das aulas de Matemática, teve um bloco de 90 minutos de apoio educativo semanal a esta disciplina, que constava do seu horário. A participação no apoio não era obrigatória, mas a comparência dos alunos foi razoável ao longo do ano.

No teste diagnóstico realizado pela turma, logo na primeira aula do 1.º período, foram constatadas diversas dificuldades dos alunos. Evidenciou-se a existência de uma enorme falta de bases, denotando-se falta de conhecimento de diversos conceitos que já deveriam estar consolidados.

Durante as aulas, a turma sempre foi bastante apática. Em geral, os alunos não questionavam o que lhes era dito, nem apresentavam espírito crítico face ao que a professora ensinava e face à sua própria aprendizagem. A turma mostrou falta de autonomia, e a maioria dos alunos também não recorria ao professor para esclarecer dúvidas. Salienta-se ainda que, de um modo geral, eram alunos que demonstravam falta de hábitos de estudo, principalmente em casa, embora, com o passar das aulas, alguns alunos tenham começado a trabalhar mais, revelando maior autonomia.

Neste contexto, era evidente a necessidade da intervenção pedagógica ser motivadora, proporcionando aos alunos a possibilidade de, além de desenvolverem trabalho autónomo, questionarem as suas aprendizagens anteriores, confrontando-os com conceções diferentes daquelas que já tinham estabelecido.

3.3. Estratégias de Intervenção

Ao longo do ano escolar os alunos trabalharam individualmente, pelo que durante a minha intervenção pedagógica foi mantido esse formato de organização dos alunos, pois considerei que seria mais vantajoso para o meu estudo. Visto que o que se pretende é identificar as conceções dos alunos e explorá-las, o trabalho individual é mais indicado, já que assim se diminuem as interferências entre as possíveis diferentes conceções dos alunos, o que poderá contribuir para aumentar o rigor e a fiabilidade do estudo. Esta opção também se relacionou com o tempo previsto para a intervenção pois como a turma já estava um pouco atrasada, de acordo com a planificação feita pela orientadora no início do ano letivo, o trabalho individual dos alunos constituiu uma forma de contribuir para o cumprimento da planificação.

Durante o estágio profissional, e em particular durante a intervenção pedagógica, adotei uma filosofia de ensino construtivista. Tendo como ator principal o aluno, tentei que ao longo das aulas eles fossem construindo o seu conhecimento, dando-lhes tarefas adequadas e que apresentassem algum desafio.

O modelo construtivista caracteriza-se pela deteção de conceções existentes no aluno, colocando-as à prova para as modificar ou construir outras novas. As conceções prévias dos alunos podem ser problemáticas, uma vez que uma imagem mental contraditória pré-existente na mente do aluno pode constituir um obstáculo na definição formal (Tall, 2000). Desta forma, esforcei-me no sentido de conscientizar os alunos para algumas contradições, confrontando-os com conceções erradas, com as quais me deparei no teste diagnóstico e também no decorrer das aulas.

A intervenção pedagógica iniciou-se com uma tarefa de diagnóstico (ver Anexo I), cujo objetivo foi permitir conhecer as conceções que os alunos tinham acerca dos conceitos de reta tangente ao gráfico de uma função num ponto. Esta tarefa foi realizada logo na primeira aula da intervenção pedagógica e influenciou a posterior implementação da intervenção, no sentido em que, através da análise das respostas dos alunos, fiquei com informação para adaptar o meu ensino às conceções estabelecidas pelos alunos e, de seguida, explorá-las nas aulas.

contraditavam as suas. Pretendia desta forma, que os alunos interiorizassem novas conceções, que são fundamentais para futuras aprendizagens.

Outra estratégia usada consistiu em confrontar os alunos com determinados conceitos que aprenderam em outras disciplinas, mais especificamente na Física, e que estão relacionados com o tema aqui explorado. Nesse sentido,Sebastião e Silva defende:

De resto o estudo das derivadas deve ser feito em estreita conexão com o dos movimentos, na física. Introduzir o conceito matemático de derivada sem ter partido do conceito mecânico de velocidade, e sem depois apresentar as múltiplas concretizações da mesma ideia na geometria e na física – é um erro grave de pedagogia (1951, p. 4).

Foi aplicada ainda uma questão-aula (ver Anexo II) perto do final da intervenção, para verificar as aprendizagens dos alunos e dar-lhes algum feedback acerca do seu desempenho.

Finalmente, terminada a intervenção, foi feita a avaliação final, que consistiu num teste de avaliação sumativa. Este teste, do qual apenas uma parte correspondia à matéria que lecionei (ver Anexo II), já estava marcado pela professora da turma desde o início do ano letivo e teve por finalidade avaliar os conhecimentos dos alunos após a intervenção de ensino.

Para finalizar a intervenção pedagógica foi aplicado novamente aos alunos o teste diagnóstico que realizaram no início da intervenção. Através dos resultados obtidos nestas avaliações e da sua análise pude avaliar o impacto do ensino nas conceções dos alunos sobre taxa de variação e reta tangente ao gráfico de uma função num ponto.

3.4. Métodos de recolha de dados

No decorrer da intervenção pedagógica foram várias as formas utilizadas para a recolha dos dados necessários à execução deste relatório.

Antes de iniciar a intervenção pedagógica foi pedida, através da orientadora, à escola e, posteriormente aos encarregados de educação dos alunos da turma, por escrito, autorização para a realização da gravação em vídeo e áudio das aulas a lecionar por mim (ver Anexo III).

Desta forma, em todas as aulas, foi colocada uma câmara de filmar no fundo da sala para registar a aula. Foi usado também um telemóvel, como gravador áudio, que estava pousado sobre a mesa do professor ou então levava na mão quando os alunos chamavam por mim para colocar dúvidas. No final de cada aula, descarregava o ficheiro áudio e vídeo para o meu computador pessoal.

De salientar que houve dois Encarregados de Educação que não autorizaram a gravação dos seus filhos e então os respetivos alunos passaram para o fundo da sala de modo a não serem captados pela máquina de filmar.

Uma das fontes de recolha de dados utilizadas para dar resposta ao primeiro objetivo da intervenção pedagógica foi o teste diagnóstico.

Para dar resposta aos outros dois objetivos propostos, no decorrer das aulas, tendo em conta que a gestão de tempo é difícil, principalmente numa fase inicial, as minhas colegas de estágio, bem como a orientadora fizeram observações das minhas aulas.

No final da intervenção pedagógica pedi aos alunos os seus cadernos diários, que fotocopiei e posteriormente devolvi.

Através dos cadernos, foi possível ter uma ideia mais clara daquilo que os alunos escreviam nas aulas, que tarefas realizavam em casa, se passavam corretamente o que era escrito no quadro e também se tiraram apontamentos importantes durante as aulas. Desta forma percebi também os principais erros e dificuldades sentidas pelos alunos.

Posteriormente, a avaliação das aprendizagens dos alunos foi feita através de: (1) uma questão-aula, constituída por três questões; (2) parte do teste de avaliação sumativa, constituída por uma questão de escolha múltipla e uma questão de desenvolvimento com três alíneas; (3) um teste diagnóstico, aplicado aos alunos no final da intervenção com o intuito de verificar se, relativamente à sua aplicação antes da intervenção, houve melhoria nas suas respostas após a intervenção pedagógica.

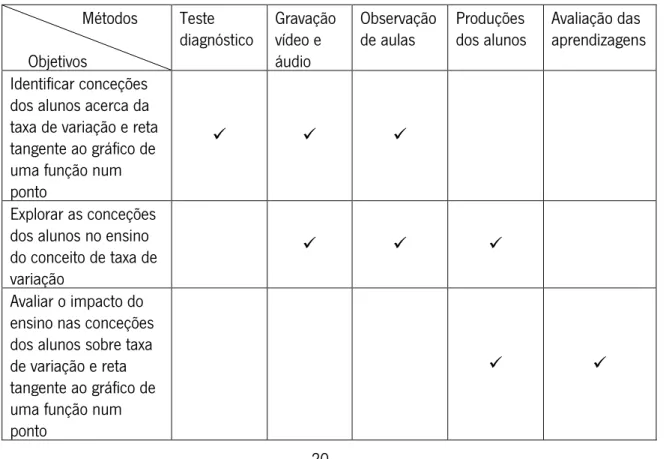
Na Tabela 2 discriminam-se os diferentes métodos de recolha de dados segundo cada um dos objetivos da intervenção pedagógica.

Tabela 2 — Objetivos e métodos de recolha de dados Métodos Objetivos Teste diagnóstico Gravação vídeo e áudio Observação de aulas Produções dos alunos Avaliação das aprendizagens Identificar conceções

dos alunos acerca da taxa de variação e reta tangente ao gráfico de uma função num ponto

  

Explorar as conceções dos alunos no ensino do conceito de taxa de variação

  

Avaliar o impacto do ensino nas conceções dos alunos sobre taxa

CAPÍTULO IV

INTERVENÇÃO PEDAGÓGICA

O Capítulo IV deste relatório, intitulado Intervenção Pedagógica divide-se em três subcapítulos: (1) Avaliação Diagnóstica, (2) Implementação da Intervenção Pedagógica e (3) Avaliação das Aprendizagens. Neste capítulo são aprofundadas questões relativas à minha intervenção pedagógica e tendo em conta que não é possível esmiuçar todos os pormenores, foi feita uma seleção rigorosa dos elementos mais importantes que deveriam estar presentes neste relatório.

A escolha dos elementos e partes da intervenção a analisar foi feita tendo em vista os objetivos propostos para a minha intervenção. Desta forma foram eleitos os elementos que visam dar resposta a cada um dos objetivos delineados para a intervenção pedagógica.

4.1. Avaliação diagnóstica

Nesta secção será feita uma análise dos resultados obtidos no teste de avaliação diagnóstica, que foi realizado na primeira aula da intervenção pedagógica (ver Anexo I). Relativamente ao teste, constituído por duas questões, na questão 1 foi feita uma análise das respostas corretas (C) e incorretas (I), bem como das justificações apresentadas pelos alunos, e na questão 2 é apresentada a percentagem de alunos que escolheram cada uma das opções das alíneas a) e b) e a análise das justificações referentes à alínea b).

Questão 1

Em cada um dos oito gráficos seguintes indica (assinalando uma das opções Sim/Não) e justifica se a reta r é tangente à curva 𝓒 no ponto A .

Na Tabela 3 apresentam-se as percentagens das respostas dos alunos, bem como as justificações dessas respostas.

Tabela 3 – Percentagem dos tipos de resposta e das justificações na questão 1

Gráficos Respostas: Justificações:

C I

50 50

Não, porque r interseta C em dois pontos 40 Sim, porque r interseta C na “parte curva” 10 Sim, porque r passa no ponto de máximo da curva

5 Sim, porque r é perpendicular a s * 5

Justificação irrelevante 35

35 65

Sim, porque r interceta

C

num só ponto 35 Não, porque r não interseta

C

numa parte

curva 10

Sim, porque r é perpendicular a s * 5 Sim, porque r passa no ponto de máximo da

curva 5

Justificação irrelevante 30

Não justifica 15

90 10

Sim, porque r interseta

C

num só ponto. ₁₀ Não, porque r “atravessa”

C

50 Justificação irrelevante

30

Não justifica ₁₀

90 10

Sim, porque r interseta

C

num só ponto 30 Sim, porque r interseta

C

numa “parte

curva” 5

Sim porque r é perpendicular a s * 5 Sim, porque r passa no ponto de máximo da

curva 5

Justificação irrelevante 40

Não justifica 15

80 20

Não, porque r interceta

C

em dois pontos 35 Não, porque r não interceta

C

na “parte

curva” 20

Justificação irrelevante ₁₅

Não justifica ₃₀

25 75

Sim, porque r interseta

C

num só ponto

10 Não, porque r “atravessa” a curva

C

₄₅ Justificação irrelevante

35

Não justifica ₁₀

60 40

Não, porque r interceta

C

em dois pontos ₃₀ Sim, porque passa nos pontos de máximo da

curva

C

10

Sim, porque r interceta

C

_{na “parte curva” 5} Sim, porque r é perpendicular a s * ₅

90 10

Sim, porque r interceta

C

num só ponto ₃₅ Sim, porque r interceta

C

_{na “parte curva” 5} Sim, porque r é perpendicular a s * ₅

Justificação irrelevante ₃₅

Não justifica ₂₀

Na questão 1 do teste diagnóstico, é notável que muitos alunos ligam o conceito de reta tangente ao conceito de reta tangente à circunferência, onde a reta apenas interceta a circunferência num ponto e não atravessa a curva.

Para muitos alunos a decisão sobre a reta r ser, ou não, tangente à curva

C

no ponto

A

baseou-se exclusivamente no facto de a reta r intersetar a curva

C

num único ponto, sendo assim tangente à curva, ou em mais do que um ponto, não sendo tangente à curva. Surgem também alguns alunos, que usando este critério na maioria das alíneas, nos gráficos 3 e 6 usam um critério diferente, justificando que r não é tangente á curva

C

no ponto

A

porque r atravessa a curva.

Um dos alunos, nos gráficos onde considera que a reta r é tangente á curva

C

, desenhou uma reta s , perpendicular a r , justificando a sua opção de r ser tangente a

C

com o facto de

r e s serem perpendiculares (Figura 5). Esta opção pode estar também relacionada com o conceito de reta tangente à circunferência, já que no decorrer deste ano letivo um dos conteúdos lecionados foi o conceito de reta tangente à circunferência com recurso ao produto escalar.

Figura 5. Resposta do aluno A ao gráfico 1 da questão 1. ₁₅

Tendo em conta esta conceção dos alunos, é natural que a maioria dos alunos responda corretamente nos gráficos aos quais a noção de reta tangente à circunferência pode ser aplicada, como por exemplo os gráficos 3, 4 e 8, o que acontece.

Alguns dos alunos que responderam corretamente nos gráficos 2 e 5, apesar de não referirem explicitamente que não existe reta tangente à curva em pontos angulosos, referem que

r não pode ser tangente à curva

C

no ponto A, já que r não passa numa parte curva, apresentando assim uma justificação mais próxima da noção de reta tangente à curva.

A percentagem de alunos que não justificaram a sua opção varia entre os 5% e os 30%. Uma das razões para a não justificação poderia ser o facto de serem gráficos onde era mais difícil perceber se a reta r era tangente à curva ou não, no entanto não parece existir nenhuma relação destas percentagens com as percentagens de respostas erradas.

As justificações irrelevantes variam entre os 15% e os 40%. Estes alunos justificam as suas escolhas referindo, por exemplo, que r é tangente a

C

porque está bem posicionada, ou não é tangente porque está mal posicionada, ou dizendo que a reta r é tangente porque está na mesma direção da curva, entre outras.

Questão 2

Velocidade de um carro de corrida. O gráfico seguinte mostra a variação da velocidade de um carro de corrida num circuito plano de 3 quilómetros, durante a segunda volta.

a) Qual das quatro opções seguintes corresponde, aproximadamente, à distância da linha de partida até ao início da reta mais longa do circuito?

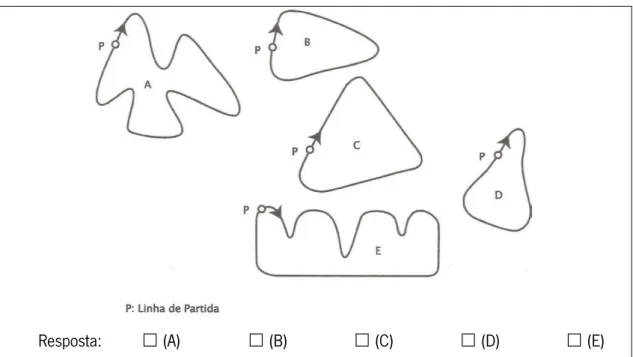
Resposta:  (A) 0,5 km  (B) 1,5 km  (C) 2,3 km  (D) 2,6 km b) Eis o traçado de cinco circuitos. Em qual deles (A, B, C, D ou E) poderá ter circulado o

Resposta:  (A)  (B)  (C)  (D)  (E) Num pequeno texto, apresenta as razões que fundamentam a resposta selecionada.

Na Tabela 4 apresentam-se as frequências (em %) de alunos nas diferentes opções de resposta de cada uma das alíneas a) e b) desta questão.

Tabela 4 – Percentagem de alunos em cada uma das opções de resposta das alíneas a) e b) da questão 2 Opção Respostas a) b) A 0% 15% B 90% 45% C 10% 0% D 0% 5% E – 35%

Na alínea a) da questão 2 a maioria dos alunos (90%) escolheu a opção B, que é a opção correta; os dois alunos que erraram esta questão optaram pela opção C. Relativamente à alínea b), 45 % dos alunos responderam corretamente, elegendo a opção B. Houve sete alunos que escolheram a opção E, três optaram pela opção A, apenas um aluno elegeu a opção D e ninguém optou pela C.

Na alínea b) todos os alunos justificaram, de alguma forma, a opção que escolheram, sendo que apenas dois apresentam uma justificação irrelevante.

Na opção A, escolhida por 15% dos alunos, dois alunos justificaram a sua escolha com o facto de o percurso ter que apresentar três curvas. Estes alunos podem ter transportado o gráfico velocidade-distância para a forma do circuito escolhido.

Dos nove alunos que optaram pelo gráfico B, que é o gráfico que melhor se adequa ao circuito, as justificações baseiam-se no facto de que como existem três reduções de velocidade, terão que existir três curvas no circuito. Adicionalmente, como existem mais gráficos que satisfazem esta condição (gráficos C e D), alguns destes alunos apresentaram razões para excluir esses gráficos, referindo a acentuação das curvas e o comprimento das retas (Figura 6).

Figura 6. Justificação do aluno A na alínea b) da questão 2. ₂ A opção C não foi escolhida por nenhum aluno.

O único aluno que optou pelo circuito D apresenta como justificação as variações de velocidade, que teriam que ser constante nas retas e variável nas curvas.

Por fim, sete alunos escolheram a opção E com diferentes justificações. Uma delas baseia-se no facto de que como existem variações de velocidade, então o circuito tem que aprebaseia-sentar várias curvas. Outros alunos alegaram que como o carro começa com uma diminuição da velocidade, então o circuito teria que iniciar com uma descida. Houve ainda um aluno que justificou que como existe uma reta que é maior que as restantes, o único circuito que destaca essa reta é o E.

4.2. Implementação da intervenção pedagógica

Nesta secção será feita uma análise das aulas lecionadas ao longo da intervenção pedagógica. A intervenção foi feita ao longo de nove blocos de 90 minutos cada, nos quais foi lecionado o tema “Taxa de Variação”, incluído no programa de 11.º ano de Matemática A de 2002. Na Tabela 5 são apresentadas as aulas lecionadas e os conteúdos abordados em cada uma delas.