UM MODELO NUMÉRICO PARA ANÁLISE ELASTOPLÁSTICA DE MACIÇOS ROCHOSOS COM BASE NO CRITÉRIO DE RUPTURA DE HOEK-BROWN

MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO Escola de Minas da Universidade Federal de Ouro Preto

Departamento de Engenharia de Minas

Programa de Pós-Graduação em Engenharia Mineral – PPGEM

UM MODELO NUMÉRICO PARA ANÁLISE ELASTOPLÁSTICA DE

MACIÇOS ROCHOSOS COM BASE NO CRITÉRIO DE RUPTURA DE

HOEK-BROWN

Autor:

JEFFERSON TALES SIMÃO

Orientadora: Profa_{. Dr}a_{. CHRISTIANNE DE}

LYRA NOGUEIRA

Dissertação apresentada ao Programa de Pós- Graduação do Departamento de Engenharia de Minas da Escola de Minas da Universidade Federal de Ouro Preto, como parte integrante dos requisitos para obtenção do título de Mestre em Engenharia Mineral.

Área de concentração:

Lavra de Minas

Catalogação: sisbin@sisbin.ufop.br

S593m Simão, Jefferson Tales.

Um modelo numérico para análise elastoplástica de maciços rochosos com base no critério de ruptura de Hoek-Brown [manuscrito] / Jefferson Tales Simão. - 2014.

90f.: il. color; grafs.; tabs.

Orientador: Profa. Dra. Christianne de Lyra Nogueira.

Dissertação (Mestrado) - Universidade Federal de Ouro Preto. Escola de Minas. Departamento de Engenharia de Minas. Programa de Pós-Graduação em Engenharia Mineral – PPGEM.

Área de concentração: Lavra de Minas.

1. Método dos elementos finitos - Teses. 2. Elastoplasticidade - Teses. 3. Análise funcional não linear - Teses. 4. Solos - Compactação - Teses. I. Nogueira, Christianne de Lyra. II. Universidade Federal de Ouro Preto. III. Título.

iii

AGRADECIMENTOS

À Universidade Federal de Ouro Preto e a CAPES pela contribuição à minha formação acadêmica e apoio financeiro.

À minha orientadora, professora Dra. Christianne de Lyra Nogueira, pela transmissão de conhecimentos, discussões, sugestões e contribuições técnicas a este trabalho.

Aos meus familiares, pela sustentação e apoio em todas as etapas da vida.

iv

RESUMO

Esta dissertação tem como objetivo a implementação computacional do modelo constitutivo elástico perfeitamente plástico com base no critério de ruptura de Hoek-Brown e com plasticidade associada para análise não linear tensão deformação de obras geotécnicas, tais como escavações e fundações superficiais, em maciços rochosos. As implementação computacionais foram realizadas no programa ANLOG com base na formulação em deslocamento do método dos elementos finitos. Em função da natureza não linear do modelo constitutivo adota-se um processo de solução em nível global incremental interativo do tipo Newton-Raphson com incrementos automáticos de carga de modo a garantir o equilíbrio. Além disto, um algoritmo explícito com sub-incrementos automáticos de deformação é adotado para integração de tensão em nível local de modo a garantir a condição de consistência. Os resultados de simulações numéricas de ensaios triaxiais convencionais, adotando diferentes trajetórias de tensão, confirmam a implementação computacional. Exemplos relacionados com abertura de cavidades e capacidade de suporte em maciços rochosos foram usados para validar as implementações computacionais e demonstrar a aplicabilidade do modelo numérico gerado.

v

ABSTRACT

This dissertation aims the computational implementation of an elastic perfectly plastic constitutive model based on the Hoek-Brown failure criterion and with non-associative plasticity in order to be applied to non-linear analysis of geotechnical problems as excavation and shallow foundation in rock mass. The computational implementation was carried out into ANLOG system based on the finite element method displacement formulation. Due to the non-linear nature of the constitutive model an incremental iterative Newton-Raphson procedure with automatic increments of load is adopted in order to guarantee the equilibrium in global level. Besides, in order to guarantee the consistency condition in local level, an explicit algorithm with automatic sub increment of strain is adopted for the stress integration. Results from the numerical simulation of conventional triaxial test, following different stress path, have confirmed the computational implementation. Examples related to circular opening and bearing capacity in rock mass were used in order to validate the computational implementation and the applicability of the numerical model developed.

vi

Sumário

Página

Lista de Figuras ... vii

Lista de Tabelas ... ix

Lista de Quadros ... x

Lista de Símbolos ... xi

Capítulo 1 – INTRODUÇÃO ... 1

1.1 - Considerações preliminares ... 1

1.2 - Objetivo e descrição do trabalho ... 2

Capítulo 2 – FORMULAÇÃO DO MEF PARA PROBLEMAS ELASTOPLÁSTICOS ... 4

2.1 - Equações de equilíbrio estático ... 5

2.2 - Estratégias de solução de sistemas de equações não lineares ... 6

2.3 - Estratégias de integração de tensão ... 12

Capítulo 3 – MODELO ELÁSTICO PERFEITAMENTE PLÁSTICO DE HOEK-BROWN ... 21

3.1 - Conceitos da plasticidade... 22

3.2 - O Modelo Hoek Brown... 25

Capítulo 4 – O PROGRAMA ANLOG ... 34

4.1 - Macro comando ... 37

4.2 - Elementos finitos e aproximações ... 38

4.3 - Matriz constitutiva ... 41

4.4 - Implementações computacionais ... 44

Capítulo 5 – EXEMPLOS DE VERIFICAÇÃO ... 52

5.1 - Simulação de um ensaio CTC ... 53

5.2 - Cavidade cilíndrica em meio elastoplástico ... 57

5.3 - Capacidade de suporte de fundação superficial ... 63

Capítulo 6 – CONCLUSÕES ... 70

vii

Lista de Figuras

Capítulo 2 - FORMULAÇÃO DO MEF PARA PROBLEMAS ELASTOPLÁSTICOS

Figura 2.1 - Ilustração do método puramente incremental ... 10

Figura 2.2 - Processo de Newton Raphson ... 11

Figura 2.3 - Algorítmo de integração de tensão genérico (Adaptado de Oliveira 2006) ... 15

Capítulo 3 - MODELO ELÁSTICO PERFEITAMENTE PLÁSTICO DE HOEK-BROWN Figura 3.1 - Tipos de comportamento tensão deformação ... 22

Figura 3.2 - Comportamento linear elastoplástico bidimensional em meio isotrópico ... 24

Figura 3.3 - Modelo constitutivo geral ... 24

Figura 3.4 - Relação tensão deformação para um modelo elástico perfeitamente plástico ... 25

Figura 3.5 - Influência da resistência à compressão uniaxial (ζci) ... 28

Figura 3.6 - Influência constante petrográfica (mb) ... 29

Figura 3.7 - Influência do parâmetro s ... 29

Figura 3.8 - Influência do parâmetro a ... 30

Figura 3.9 - Critério de Hoek-Brown (adaptado Benz, 2008) ... 31

Capítulo 4 - O PROGRAMA ANLOG Figura 4.1 - Ambiente de trabalho do FORTRAN (Nogueira, 2010) ... 36

Figura 4.2 - Mtool - TecGraf® (Nogueira, 2010) ... 36

Figura 4.3 - Elemento finito quadrangular quadrático (Q8) ... 38

Capítulo 5 - EXEMPLOS DE VERIFICAÇÃO Figura 5.1 - Simulação de ensaios triaxiais CTC ... 53

Figura 5.2 - Malha de elementos finitos – trajetórias de tensão ... 54

Figura 5.3 - Curva tensão-deformação – ensaio CTC ... 55

Figura 5.4 - Trajetórias de tensão no espaço p-q... 57

Figura 5.5 - Abertura de uma cavidade cilíndrica a grande profundidade ... 58

Figura 5.6 - Malha de elementos finitos - cavidade cilíndrica em meio elastoplástico ... 60

Figura 5.7 - Distribuição das tensões ao redor da abertura circular ... 61

Figura 5.8 - Distribuição de tensão ... 62

Figura 5.9 - Regiões elásticas e plásticas ... 62

viii

Figura 5.11 - Curva carga-recalque - fundação corrida rígida e lisa - meio puramente coesivo .. 65

Figura 5.12 - Curva carga-recalque – fundação rígida – meio puramente coesivo - corrida versus circular ... 66

Figura 5.13 - Curva carga-recalque – fundação rígida e rugosa - filito ... 68

Figura 5.14 - Curva carga-recalque – fundação rígida e rugosa - basalto ... 68

ix

Lista de Tabelas

Capítulo 2 - FORMULAÇÃO DO MEF PARA PROBLEMAS ELASTOPLÁSTICOS

Tabela 2.1 - Fator de incremento de carga ( λ) ... 8

Tabela 2.2 - Critérios de convergência –ratio ≤ tolerância ... 11

Tabela 2.3 - Definição da ocorrência de fluxo plástico ... 16

Capítulo 3 - MODELO ELÁSTICO PERFEITAMENTE PLÁSTICO DE HOEK-BROWN Tabela 3.1 - Valores da constante mi para rocha intacta (Hoek e Brown 1997) ... 26

Tabela 3.2 - Resistência à compressão uniaxial (Hoek e Brown 1977) ... 26

Capítulo 4 - O PROGRAMA ANLOG Tabela 4.1 - Alterações no código computacional ANLOG ... 44

Capítulo 5 - EXEMPLOS DE VERIFICAÇÃO Tabela 5.1 - Parâmetros do modelo Hoek-Brown - CTC ... 53

Tabela 5.2 - Parâmetros da solução incremental-iterativa - CTC ... 54

Tabela 5.3 - Valores da resistência ao cisalhamento e deformação axial máxima... 56

Tabela 5.4 - Parâmetros do modelo Hoek-Brown - cavidade ... 60

Tabela 5.5 - Raio de transição e tensões (pi=5MPa e ri=5m) ... 60

Tabela 5.6 - Parâmetros da solução incremental-iterativa - fundação ... 64

Tabela 5.7 - Parâmetros da solução incremental-iterativa – efeito GSI ... 67

x

Lista de Quadros

Capítulo 4 - O PROGRAMA ANLOG

Quadro 4.1 – Sub-rotina DATNPROP ... 45

Quadro 4.2 – Sub-rotina DATIMAT ... 45

Quadro 4.3 – Sub-rotina PROPERTIES ... 46

Quadro 4.4 – Sub-rotina MATDE_ALL ... 47

Quadro 4.5 – Sub-rotina MATDEP_ALL ... 47

Quadro 4.6 – Sub-rotina TCALCG_ALL ... 47

Quadro 4.7 – Sub-rotina TCALC_2 ... 48

Quadro 4.8 – Sub-rotina TCALC_71 ... 48

Quadro 4.9 – Sub-rotina DHB ... 49

Quadro 4.10 – Sub-rotina DHB_GAGB ... 50

Quadro 4.11 _– Sub-rotina YIELD_FUNC_HB ... 50

Quadro 4.12 – Sub-rotina COEF_GRAD_YIELD_HB ... 50

xi

Lista de Símbolos

a - gradiente da função de plastificação a - parâmetro do critério de Hoek-Brown

ah - função do incremento de deformação plástica

b - gradiente da função potencial plástico B - matriz cinemática

bp - vetor de forças de corpo

D - fator de perturbação De - matriz constitutiva elástica

Dep - matriz constitutiva elastoplástica

E - módulo de Young F - função de plastificação

Fext - vetor de forças externas global

e

δ

F - parcela de força externa devido aos deslocamentos prescritos não nulos

e b

F - parcela de força externa devido às forças de peso próprio

e s

F - parcela de força externa devido às forças de superfície

e ext

F - vetor de forças externas do elemento Fint -vetor de força interna global

e int

F -vetor de força nodal

G - função potencial plástico

GSI - índice geológico de resistência I1- primeiro invariante do tensor de tensão

I2D - segundo invariante do tensor de tensão desviadora

I3D - terceiro invariante do tensor de tensão desviadora

J - matriz jacobiana K - matriz de rigidez global Ke _{-matriz de rigidez elementar}

mb - parâmetro do critério de Hoek-Brown

xii

N - matriz que contém as funções de interpolação Ni - função de interpolação

Q - força de reação

qn - vetor de forças de superfície

R - erro relativo local

RMR - classificação do maciço rochoso s - parâmetro do critério de Hoek-Brown ST0L - tolerância para o erro relativo local T - pseudo tempo

U - vetor de deslocamentos nodais

û - vetor do incremento de deslocamento em cada elemento x - vetor das coordenadas locais

- operador diferencial de primeira ordem  - coeficiente de Poisson

 - fator de carga  - vetor de deformação

ci - resistência à compressão uniaxial da rocha intacta

p - ângulo que define a relação entre a deformação axial e volumétrica plástica (ζ1–ζ3) - diferença de tensão

d - multiplicador escalar

δ - valor do deslocamento nodal prescrito

δΔUk _{- correção iterativa do incremento de deslocamento a nível global} Δλi- fator de incremento de carga

ε1 - deformação axial

εvol - deformação volumétrica θ - ângulo de Lode

κ - fator de carga

ζ - vetor das componentes de tensão

1

Capítulo 1

INTRODUÇÃO

1.1. Considerações preliminares

Esta dissertação de mestrado está inserida na linha de pesquisa de Geomecânica e Geotecnia da área de concentração de Lavra de Minas do Programa de Pós-Graduação em Engenharia de Mineral (PPGEM) da Escola de Minas (EM) da Universidade Federal de Ouro Preto (UFOP). Ela se justifica pela contribuição ao entendimento do comportamento mecânico de obras geotécnicas em equilíbrio estático e em estados de deformação plana e axissimétrica, com base na simulação numérica, via método dos elementos finitos (MEF).

Esta dissertação está relacionada ao desenvolvimento do sistema computacional ANLOG que se constitui num código aberto, escrito em linguagem de programação FORTRAN, inicialmente desenvolvido na PUC-Rio (Zornberg, 1989) e que vem sendo atualizado sob a supervisão da professora Christianne de Lyra Nogueira desde o final de sua tese de doutorado na PUC-Rio em 1998 (Nogueira, 1998). Este programa contou com a colaboração de vários alunos de iniciação científica, mestrado e doutorado (Zornberg, 1989; Nogueira, 1992 e 1998; Machado Jr., 2000; Pereira, 2003; Pinto, 2004; Silva, 2005; Oliveira, 2006; Yang, 2009; Valverde, 2010; Armond e Nogueira, 2013).

2

Vários modelos constitutivos podem ser encontrados na literatura. No entanto, os que melhor representam o comportamento tensão deformação são os modelos não lineares, tais como o elástico (Duncan e Chang, 1970), elástico perfeitamente plástico (Sloan e Booker, 1986) e elastoplástico (Lade e Kim, 1990).

As grandes dificuldades encontradas na ampla utilização de análises tensão deformação não lineares estão: no controle do processo de solução não linear, tanto em nível global quanto local; e, na definição dos parâmetros dos modelos constitutivos, os quais, em sua maioria são definidos a partir de resultados de ensaios de laboratórios tal como o ensaio de compressão triaxial convencional (CTC).

Um modelo constitutivo que vem sendo cada vez mais adotado nas análises tensão deformação de maciços rochosos e que considera parâmetros empíricos que podem ser determinados a partir de observações do levantamento geológico-geotécnico é o modelo elástico perfeitamente plástico com base no critério de resistência de Hoek-Brown (Hoek, 2006).

O critério de resistência de Hoek-Brown foi inicialmente desenvolvido para estimar a resistência de maciços rochosos não fraturados e em seguida foi modificado levando em conta a condição de fraturamento do maciço (Hoek e Brown, 1980, 1988 e 1997; Hoek, 1980 e 1994; Hoek et al, 1992; 1995 e 2002). As dificuldades associadas aos processos de integração de tensão e de solução de equação não linear também tem sido objeto de estudo de alguns autores no âmbito da aplicação do critério de Hoek-Brown (Clausen e Damkilde, 2008; Choi e Deb, 2005) e é objeto de estudo desta dissertação.

1.2. Objetivo e descrição do trabalho

Esta dissertação de mestrado tem como objetivo o desenvolvimento de um modelo numérico, com base no MEF, para análise tensão deformação em condição de deformação plana e axissimétrica de obras geotécnicas realizadas em maciços rochosos, considerando o modelo elástico perfeitamente plástico com plasticidade associada de Hoek-Brown (Clausen e Damkilde, 2008).

3

deslocamento do MEF e do algoritmo de integração de tensão para o modelo Hoek-Brown.

4

Capítulo 2

FORMULAÇÃO DO MEF PARA PROBLEMAS

ELASTOPLÁSTICOS

A aplicação do MEF na análise de problemas mecânicos em equilíbrio estático levando em conta a natureza elastoplástica das relações constitutivas conduz a um sistema de equações não lineares cuja solução deverá garantir a condição de equilíbrio, em nível global, e a condição de consistência, em nível local, pela qual todo estado de tensão deve permanecer no interior ou no máximo sob a superfície de plastificação definida pelo modelo constitutivo adotado.

Neste capítulo apresenta-se o sistema de equação, na forma matricial com base na formulação em deslocamento do MEF, que governa esse problema mecânico para um estado generalizado de tensão e deformação juntamente com as estratégias de solução da equação de equilíbrio e da integração de tensão ao longo de uma trajetória de deformação qualquer.

5

2.1. Equações de equilíbrio estático

O sistema de equação diferencial que governa um problema mecânico de equilíbrio estático é dado por:

0 b

ζ 

T _p

em V (2.1)

em que é um operador diferencial de primeira ordem, ζ é o vetor das componentes de tensão, bp é o vetor de forças de corpo (peso próprio) e V é o domínio do problema.

Esse sistema de equação deverá atender às seguintes condições de contorno:

n n q

ζ  em Sq (condição de contorno natural) (2.2a)

δ

Ui  em Su (condição de contorno essencial) (2.2b)

em que qn é o vetor de forças de superfície, U é o vetor de deslocamentos nodais e δ é o

valor do deslocamento nodal prescrito (nulo ou não) num ponto do contorno do domínio do problema. Sq e Su são, respectivamente, os contornos do domínio do problema com

força e deslocamentos prescritos.

Com base na formulação em deslocamento do MEF o sistema de equação de equilíbrio (Equação 2.1) pode ser reescrito na seguinte forma simplificada:

ext int F

F  (2.3)

em que

F

forças nodais equivalentes às forças externas do elemento

F

e e b e s e

ext F F F

F (2.4)

em que

qe e e

s 



qe

S

T_q

N

6

representa a parcela de força externa devido às forças de superfície;

e

V_e

T e_dV

p e

b  N b

F (2.5b)

representa a parcela de força externa devido às forças de peso próprio; e por fim,

δ K

Fe _ e

 (2.5c)

representa a parcela de força devido aos deslocamentos prescritos não nulos .

As Equações 2.5a e 2.5b são integradas, respectivamente, ao longo de uma face

(Sqe) e do volume (Ve) de um dado elemento finito. Ke é a matriz de rigidez elementar

e N é a matriz que contém as funções de interpolação Ni que dependem do tipo de

elemento (Nogueira, 1998).

O vetor de força interna F_int representa o arranjo global do vetor de força nodal

e int

F equivalente ao estado de tensão em um dado elemento, o qual é definido como:



e

V

e T e

int B ζdV

F (2.6)

O operador B é a matriz cinemática que relaciona as componentes de deformação e deslocamento e, portanto, contém as derivadas das funções de interpolação Ni.

As matrizes de rigidez, de interpolação e cinemática são descritas no Capitulo 4 juntamente com a descrição do programa ANLOG (Nogueira, 2010).

2.2. Estratégias de solução de sistemas de equações não lineares

7

alguma estratégia de solução deve ser adotada de modo a garantir a condição de equilíbrio global (Equação 2.3).

Dentre as estratégias de solução de sistemas de equação não lineares as que adotam um procedimento puramente incremental ou incremental iterativo são as mais difundidas.

Nessas estratégias, a trajetória de equilíbrio é controlada pelo fator de carga, , que é atualizado a cada passo de carga i ao longo desta trajetória fazendo:

i 1 i i  

 _ (2.7)

em que _i é o fator de incremento de carga. O fator de carga varia de zero à unidade

ao longo de uma dada trajetória de equilíbrio.

Para problemas fortemente não lineares o tamanho do passo de carga pode conduzir a uma resposta numérica que se afasta da resposta real, no caso do procedimento puramente incremental, ou pode inviabilizar a convergência do processo iterativo, no caso do procedimento incremental-iterativo. Incrementos de carga muito pequenos podem tornar o processo de solução muito lento. Desta forma, a seleção automática do tamanho do incremento de carga é fator importante para o sucesso do processo de solução do sistema de equação (Nogueira, 1998).

Uma estratégia eficiente de incremento automático de carga deve fornecer grandes incrementos quando a resposta da estrutura for quase linear e conduzir a pequenos incrementos quando a resposta da estrutura for fortemente não linear. A Tabela 2.1 apresenta os valores dos fatores de incrementos de carga tal como sugerido por Crisfield (1991 e 1997) os quais podem ser usados juntamente com um procedimento de solução incremental-iterativo partindo de um valor inicial para o fator

8

Tabela 2.1 - Fator de incremento de carga ()

Numa solução incremental-iterativa com incrementos automáticos de carga, os fatores de incrementos de carga calculados automaticamente não poderão ser maiores

ou menores que valores máximos e mínimos (max e mín) fornecidos pelo usuário

para que o programa não entre num “loop” infinito. Se a convergência não é verificada para um número máximo de iterações num dado passo, uma simples estratégia de corte do tamanho do passo é utilizada.

Nas estratégias puramente incremental e incremental iterativa atualizam-se, no final de cada passo de carga, a nível global (ou da estrutura), os vetores de deslocamento, U, de força externa, Fext, e de força interna, Fint; e a nível local (ou do

elemento), os vetores de deformação, , e tensão, , de modo que:

i 1 i

i U U

U    (2.8)

i 1

i

i ext ext

ext F F

F  

 (2.9)

i 1

i

i int int

int F F

F  

 (2.10)

i 1 i

i ε ε

ε    (2.11)

i 1 i

i ζ ζ

ζ  _  (2.12)

O incremento de deformação, , avaliado a nível do elemento depende da

relação cinemática e do incremento de deslocamento em cada elemento, uˆ . O

Estratégia

1 2

1 i 1 i d I I            1 i ratio toler          ninc / 1 0   

9

incremento de tensão, , depende, além do modelo constitutivo, do algoritmo de integração de tensão adotado.

O incremento de deslocamento, U, em cada passo de carga i depende da

estratégia de solução adotada em resposta ao incremento de força externa:

ext i exti F

F 

 (2.13)

No procedimento puramente incremental o vetor de incremento de deslocamento nodal é obtido a nível global resolvendo o seguinte sistema de equação:

 

U 

  _(2.14)

em que

K

rigidez de cada elemento

K



e

v

e ep T

e _{B D BdV}

K (2.15)

que depende da matriz constitutiva elastoplástica, D_ep, a qual é avaliada em função do

estado de tensão em cada elemento. Este procedimento pode ainda ter algumas variações em função do estado de tensão adotado na avaliação da matriz de rigidez, quais sejam: método da rigidez inicial (Figura 2.1a) e método da rigidez tangente (Figura 2.1b).

10

a) Método da rigidez inicial b) Método da rigidez tangente

Figura 2.1 - Ilustração do método puramente incremental

A eficiência deste método (entendida como a capacidade de reproduzir uma dada trajetória de equilíbrio) é altamente influenciada pelo tamanho dos incrementos utilizados e pelo grau de não linearidade da relação constitutiva do material.

No procedimento incremental iterativo o vetor de incremento de deslocamento nodal é obtido a nível global resolvendo a seguinte lei de recorrência:





    

 iter

1 k

k

0 _U

U

U (2.16)

em que



U

 

k _{K Ψ}

U  



 (2.17)

é a correção iterativa do incremento de deslocamento a nível global, do tipo Newton-Raphson, em que:

k k

ext int

 

Ψ F F (2.18)

11

Tabela 2.2 - Critérios de convergência – ratio  tolerância

Critério ratio

Força FextFint Fext

Deslocamento U U

Energia ext

0 _F

U Ψ

U  

 

O símbolo  indica produto escalar

O método de correção iterativa de Newton Raphson caracteriza-se por manter o nível de força externa constante durante o ciclo iterativo. Com relação à matriz de rigidez, dois procedimentos podem ser adotados: o padrão e o modificado. O procedimento incremental-iterativo de Newton-Raphson é chamado de padrão quando a matriz de rigidez é atualizada em cada ciclo iterativo (ver Figura 2.2a) ou de modificado quando a matriz de rigidez é mantida constante durante o ciclo iterativo (ver Figura 2.2b). O procedimento modificado, apesar de ser mais lento é mais estável que o procedimento padrão e, por isso é adotado neste trabalho.

a) Padrão b) Modificado

Figura 2.2 - Processo de Newton Raphson

12

2.3. Estratégias de integração de tensão

Os procedimentos apresentados anteriormente envolvem a avaliação do estado de tensão em cada elemento e a cada ciclo iterativo. Esta avaliação é feita atualizando-se o estado de tensão no início do passo corrente uma vez obtido as variáveis incrementais:

u B ε  

 i (2.19)

i ep i D ε ζ  

 (2.20)

As Equações 2.11 e 2.12 (ou ainda, as Equações 2.19 e 2.20) só são válidas para incrementos infinitesimais de tensões, dζ, e deformações, dε. No entanto, como estes incrementos não são infinitesimais e erros podem ser cometidos e acumulados durante a integração das tensões, algum esquema de integração de tensão em nível local deverá ser adotado a fim de o critério de plastificação não seja violado.

Em uma situação multiaxial, ou generalizada em termos do estado tensão-deformação, a variação infinitesimal do vetor de componentes de deformação experimentado pelo corpo ao longo de uma determinada trajetória de deformação e/ou tensão, pode ser escrito como a soma das componentes de natureza elástica e plástica desta deformação, ou seja:

p e

_d

d

d

ε



ε



ε

em que

d

ε

p

d

ε

 

ε d

d e _{ e} 1

(2.22)

em que De é matriz constitutiva elástica cujos coeficientes são funções dos parâmetros

13

b

ε



d



d

(2.23)

em que

ζ b

 

 G (2.24)

em que d é um multiplicador escalar positivo que depende do acúmulo de deformação

plástica a ser definida por uma lei de endurecimento e b é o gradiente da função potencial plástico, G(). A função potencial plástico define a direção do incremento de deformação.

Ao longo de uma dada trajetória de equilíbrio os estados de tensão devem permanecer dentro ou, no máximo, sobre a superfície de plastificação. Desta forma, tem-se que:

0 d a d d

h h F d F

dF T _h

p   

      

  

 ε b a (2.25)

ou ainda:

   a d

d _h

T _

a (2.26)

em que

    F

a (2.27)

é o gradiente da função de plastificação, F(,h), e

b εp h

h h F a

   

 (2.28)

14

Substituindo-se as Equações 2.22 e 2.23 na Equação 2.21, pré multiplicando-se ambos os termos por _aT_{De, e em seguida substituindo-se o resultado na Equação 2.26,}

chega-se a:





D a

d a d

h e T

e T

 

 (2.29)

Usando a definição da Equação 2.29 e considerando a decomposição aditiva da Equação 2.21, pode-se definir a variação infinitesimal do vetor de componentes de tensão, como sendo:

ε

D

ζ

d

d



em que





h e T

T T

e e ep

a D

b D a

b a D

D D

 

 (2.31)

é a matriz elastoplástica que deverá ser adota para avaliação da matriz de rigidez durante o processo de solução incremental a nível global e para a integração de tensão a nível local.

Nos casos em que a função potencial plástico, G, é tomada como igual à função de plastificação, F, tem-se uma plasticidade associada e uma matriz elastoplástica simétrica uma vez que o vetor b é idêntico ao vetor a. Caso contrário, quando a função potencial plástico é diferente da função de plastificação, tem-se uma plasticidade não associada e uma matriz elastoplástica não simétrica uma vez que os vetores a e b são diferentes.

15

Vários algoritmos para integração de tensão têm sido propostos e tem sido observado que eles interferem diretamente na precisão da solução numérica, induzindo erros que podem se propagar ao longo da solução incremental.

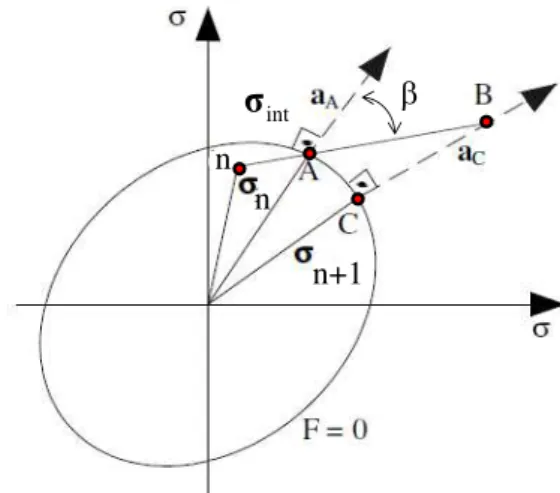
Desta forma, considerando a situação indicada na Figura 2.3 a qual representa um fluxo plástico para uma condição de plasticidade associada, diferentes algoritmos para integração das equações constitutivas podem ser representados através da seguinte regra:

)

Δ

(_Δ p

e int 1

n ζ D ε ε

ζ _    (2.32)

ou ainda,

p e *

1 n 1

n ζ D Δε

ζ _  _  (2.33)

em que

[0,1]

], )

Δλ[(1

Δεp   aAaC  (2.34)

e

ε

D

ζ

ζ n eΔ

* 1

n   (2.35)

é a tensão elástica predita obtida no ponto B.

n

n+1 n

int

ζ 

16

Quando =1, tem-se um algoritmo do tipo backward Euler ou completamente implícito. Neste caso, como as tensões no ponto C não são conhecidas é necessário a adoção de um processo iterativo. Quando =0, tem-se um algoritmo tipo forward Euler, ou completamente explícito. Neste caso, é necessário calcular as tensões no limite da

região elástica no ponto A, ζ_int, assim como o gradiente da função de plastificação neste

ponto, aA.

A e e

int 1

n ζ DΔε DΔλa

ζ _    (2.36)

Durante uma dada trajetória de deformação incremental ε e partindo de um

estado de tensão inicial ζn quatro situações podem ser observadas tal como indicada na

Tabela 2.3.

Tabela 2.3 – Definição da ocorrência de fluxo plástico

Caso Observação

1 o estado de tensão é inicialmente elástico e _{permanece elástico} F(ζ_n)FTOL e F( * ) FTOL

1 n 

ζ

2 o estado de tensão inicial muda de elástico para _plástico F(ζ_n)FTOL e F(ζ*_n1)FTOL 3 o estado de tensão é inicialmenete plástico e _{permanece plástico} F(ζ_n)FTOL e F(ζ*_n1)FTOL 4 o estado de tensão é inicialmente plástico e experimenta um descarregamento elástico

seguido de um fluxo plástico

FTOL )

(

Fζ_n  e F( * ) FTOL

1 n 

ζ

2 /

  

FTOL é uma pequena tolerância positiva. Sloan et al. (2001) sugerem _FTOL





No caso 1 o incremento de tensão é completamente elástico e a tensão atualizada considerando um incremento de tensão puramente elástico adotando a matriz constitutiva elástica, ou seja, fazendo:

ε D ζ

ζ_n1 _n  _e (2.37)

O caso 4 ocorre quando o ângulo β entre o vetor gradiente da função de plastificação no ponto A, aA, e o vetor de incremento de tensão elástica, ζDeε, é

17 

   

    

ζ a

ζ a

Δ Δ

cos

β

A T A

1 _(2.38)

Nos casos 2 e 3, é necessário determinar a porção elástica do incremento de deformação, Δε. Isto pode ser feito, determinando-se o valor de  que satisfaz a seguinte equação:

FTOL )

h ,

αΔ

F(ζ_n  ζ _n  (2.39)

em que α é um escalar que varia de 0 a unidade e é obtido resolvendo a inequação 2.39 iterativamente. Quando =0 o incremento de deformação gera apenas incremento de

tensão de natureza elastoplástica (caso 3). Quando =1 o incremento de deformação gera variações de tensão apenas de natureza elástica (caso 1).

Uma vez conhecido o valor de , as parcelas do incremento de tensão elástica, do incremento de deformação elástica e o valor da tensão no limite da região elástica são avaliadas fazendo-se:

ζ

ζe αΔ

 (2.40)

ε

ε αΔ

Δ e  (2.41)

e n int ζ Δζ

ζ   (2.42)

Partindo-se de um estado de tensão na superfície de plastificação, ζ_int, e

assumindo-se a hipótese de que a direção do fluxo plástico permanece constante ao longo do incremento de deformação de natureza elastoplástica, ε_ep, pode-se atualizar

o estado de tensão no final do incremento fazendo:

ep int

1

n ζ ζ

ζ _   (2.43)

em que

ep int ep

ep D (ζ ) ε

ζ  

18

ε ε   

 _ep (1 ) (2.45)

Com o intuito de tornar mais precisa a integração de tensão ao longo de uma trajetória incremental finita o incremento de deformação elastoplástica pode ser dividido em subincrementos (nsub) de tal forma que:

k ep 1 k k _{ζ dζ} ζ   

(2.46)

/nsub)

(

Δ

)

(

d

1 k

1 -k ep k

ep

D

ζ

ε

ζ







A tensão é atualizada no final de cada subincremento, partindo-se do estado de tensão corresponde ao ponto na superfície de plastificação (_ζ0 _ζint).

Este procedimento é mais eficiente quando o número de subincrementos é calculado de forma automática, considerando-se o grau de não-linearidade do comportamento tensão-deformação e/ou o erro cometido durante o processo.

Desta forma, vários critérios têm sido sugeridos para a definição do seu tamanho. Sloan et al. (2001) sugeriram uma estratégia em que o tamanho do

subincremento de deformação de natureza elastoplástica,

d

ε

trajetória incremental,



ε

ep k k

ep

ΔT

Δ

d

ε



ε

em que ΔTk _{é um escalar chamado de incremento de pseudotempo. O incremento de}

pseudotempo varia de zero a unidade e é obtido em função do erro relativo local cometido na avaliação das tensões. A primeira aproximação para o pseudotempo é feita

considerando-se um incremento unitário, ΔT=1. O processo é controlado pelo

pseudotempo T (0≤T≤1) que é atualizado a cada subincremento, ΣΔT=T=1.

Para um dado subincremento k de deformação (Equação 2.48), são calculadas

19 k ep 1 -k ep

1

(

)d

Δ

ζ



D

ζ

ε

k ep 1 1 -k ep

2

(

Δ

)d

Δ

ζ



D

ζ



ζ

ε

A partir destas duas estimativas, dois estados de tensão aproximados são definidos:

1 1 -k

k _{ζ Δζ}

ζ   (2.51)

) Δ Δ ( 2 / 1 ~ 2 1 1 k

k _{ζ ζ ζ}

ζ     _(2.52)

Sloan et al. (2001) sugeriram o cálculo do erro relativo local, R, cometido ao longo do subincremento corrente k, em função da diferença entre os estado de tensão

aproximados

ζ



ζ

~

STOL

~

)

Δ

Δ

(

5

.

0

~

~

R

k k k

k

_



_



_

ζ

ζ

ζ

ζ

ζ

ζ



em que ST0L é uma dada tolerância adotada. Sloan et al. (2001) sugerem uma tolerância em torno de 10-6 a 10-2.

Se o erro local relativo no subincremento corrente for menor que uma dada tolerância o subincremento corrente será aceito, ou seja: a tensão aproximada será

atualizada,

ζ



~

ζ

Se o erro local relativo no subincremento corrente for maior que uma dada tolerância o subincremento corrente não será aceito, ou seja: a tensão aproximada não será atualiazada, o pseudotempo, T, não será atualizado e um novo valor (menor que o corrente) de incremento de pseudotempo, ΔT, será calculado.

Independentemente de o subincremento corrente ser aceito ou não, os próximos valores de ΔT são dados pela expressão:

k 1

k _qΔT

20

em que

k

STOL/R

0.9

q



O incremento de pseudotempo pode aumentar ou diminuir ao longo da trajetória ade incremento de deformação em função da tolerância adotada. Assim, de acordo com Sloan et al. (2001), para acelerar o processo o incremento de psuedotempo pode ser

ampliado em até 10% do valor anterior, ou seja,

ΔT



1

.

1

ΔT

21

Capítulo 3

MODELO ELÁSTICO PERFEITAMENTE PLÁSTICO

DE HOEK-BROWN

Em uma análise tensão-deformação elastoplástica as variações nos campos de deslocamento, tensão e deformação dependem do nível de tensão e deformação, mas também, do histórico de tensões e deformações experimentadas ao longo de uma trajetória de equilíbrio.

A formulação de um modelo de comportamento elastoplástico envolve invariavelmente três conceitos: condição de plastificação, que define o estado de tensão que corresponde ao início do fluxo plástico; a lei de fluxo plástico, que relaciona o incremento de deformação plástica com as tensões correntes; e a lei de endurecimento, que define como a condição de plastificação modifica durante o fluxo plástico.

22

3.1. Conceitos da plasticidade

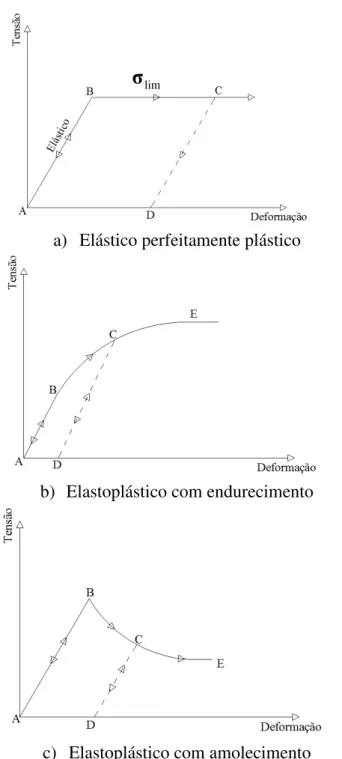
A fim de explicar o comportamento típico de alguns materiais inelásticos, ou plásticos, considere a situação de compressão uniaxial ilustrada na Figura 3.1.

lim

ζ

a) Elástico perfeitamente plástico

b) Elastoplástico com endurecimento

c) Elastoplástico com amolecimento

23

Na Figura 3.1a tem-se um material com comportamento elástico perfeitamente plástico. Neste caso, para valores de tensão inferiores à tensão limite ou de escoamento,

lim

ζ , o corpo experimenta deformações de natureza elástica. Para um valor de tensão igual à tensão limite o corpo experimenta uma deformação de natureza plástica.

A Figura 3.1b ilustra o comportamento de um material com endurecimento plástico (strain hardening). Nesse caso a relação tensão-deformação é linear e elástica até certo ponto (ponto B) a partir do qual se torna não linear com o material experimentando acúmulos de deformação plástica.

A Figura 3.1c ilustra o comportamento de um material com amolecimento plástico (strain softening). Neste caso, o material comporta-se como linear e elástico até o limite de escoamento a partir do qual se inicia uma diminuição de tensão com o aumento da deformação.

O conceito de tensão limite ou de escoamento é adotado apenas em situações uniaxiais. Para situações multiaxiais deve-se usar o conceito de função de escoamento ou plastificação (F).

A função de plastificação, que define uma superfície no espaço das tensões, é uma função do estado de tensão e de deformação plástica. Sob a superfície de plastificação, a função de plastificação é nula (F=0) e no interior desta superfície tem-se um valor negativo (F<0) indicando que nesta região o comportamento do material é elástico.

Uma vez alcançado o primeiro nível de plastificação, a superfície de plastificação pode expandir na medida em que acumula deformação plástica. Este fenômeno, ilustrado na Figura 3.2a, caracteriza um comportamento com endurecimento. No caso do material que apresenta um amolecimento (Figura 3.2b) observa-se uma contração da superfície de plastificação. Nestes casos a função de plastificação é uma função do tipo:

)) ( h ( F ) ( F )) ( h , ( F

F_{  ε}p _{   ε}p _(3.1)

24

a) Endurecimento b) Amolecimento

Figura 3.2 - Comportamento linear elastoplástico bidimensional em meio isotrópico

A Figura 3.3 apresenta uma curva tensão versus deformação típica para um modelo constitutivo que leva em conta tanto endurecimento quanto o amolecimento.

Figura 3.3 - Modelo constitutivo geral.

Num modelo elástico perfeitamente plástico a função, ou superfície, de plastificação se confunde com a superfície de ruptura. Este modelo não adota o endurecimento e, portanto, a função de plastificação depende apenas no nível de tensão, ou seja,

0 ) ( F

F   (3.2)

Uma curva tensão s deformação típica de um modelo constitutivo com

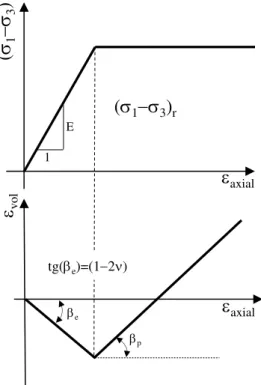
25

tensão, ₁ é a deformação axial, _vol é a deformação volumétrica, E é o módulo de

Young,  é o coeficiente de Poisson, (₁₃)_r é a resistência à compressão e p é um

ângulo que define a relação entre a deformação axial e volumétrica plástica que dependem do critério de resistência adotado.

_axial E

1

(₁₃)_r

(

1 3

)

_axial vol

e

_p

tg(e)=(12)

Figura 3.4 - Relação tensão-deformação para um modelo elástico perfeitamente plástico

3.2. O Modelo Hoek Brown

O critério de resistência de Hoek-Brown (Hoek e Brown, 1980) foi desenvolvido na década de 80, com base em observações empíricas, originalmente para estimar a resistência de rochas duras. No espaço das tensões principais, o critério descreve uma relação não linear, originalmente definida como:

s

σ σ

m

σ σ σ

ci 3 i ci 3

1   (3.3)

em que ci é a resistência à compressão uniaxial, mi é a constante petrográfica e s é um

26

intactas. As Tabelas 3.1 e 3.2 apresentam, respectivamente, valores padrões para a constante petrográfica e a resistência à compressão uniaxial de algumas rochas.

Ao longo das últimas décadas várias atualizações foram propostas, motivadas pelo número crescente obras geotécnicas realizadas em maciços rochosos de qualidade muito baixa, a fim de se considerar a condição do maciço.

Tabela 3.1 - Valores da constante mi para rocha intacta (Hoek e Brown, 1997)

Rocha mi

Mármore 9

Quartzito 24

Granito 33

Gnaisse 33

Tabela 3.2 - Resistência à compressão uniaxial (Hoek e Brown, 1997)

Rocha Condição ci (MPa)

Granito Extremamente forte >250

Gnaisse Muito forte 100-250

Filito Forte 50-100

Concreto Média 25-50

Gesso Fraco 5-25

Rochas alteradas 1-5

Solo Extremamente fraco 0.25-1

Em 1988, Hoek e Brown (Hoek e Brown, 1988) propuseram uma atualização de modo a se levar em conta a qualidade da rocha utilizando o conceito do RMR proposto por Bieniawski. Nesta nova versão tem-se que:

s

σ σ

m

σ σ σ

c 3 b i c 3

1   (3.4)

em que, para um maciço não perturbado:

28 / ) 100 RMR ( i b me

m   (3.5)

8 / ) 100 RMR (

e

s



27 14 / ) 100 RMR ( i b me

m _  _(3.7)

6 / ) 100 RMR (

e

s



Em 1992, uma nova modificação foi proposta para aplicação em maciços rochosos altamente fraturados e sem resistência à tração (Hoek et al, 1992). Nesta nova versão, um novo parâmetro, a, é introduzido:

a c 3 b i c 3 1 σ σ m σ σ σ _        (3.9)

Na década de 90, Hoek (Hoek, 1994) introduziu o conceito do índice geológico de resistência (GSI) como uma forma de reduzir a resistência do maciço rochoso com base nas condições geológicas. O índice geológico de resistência varia de 0 a 100 e depende da análise geológica estrutural levando em conta a existência de fraturas, o estado da rocha e o grau de intemperização.

A partir daí uma nova versão do critério de Hoek-Brown é proposto (Hoek et al, 1995): a c 3 b i c 3

1 _σ s

σ m σ σ σ _       

 (3.10)

onde 28 / ) 100 GSI ( i b me

m   (3.11)

e para um maciço com GSI>25

8 / ) 100 GSI (

e

s



5 . 0

a (3.13)

e para GSI<25

0

28

200 GSI 65 . 0

a  (3.15)

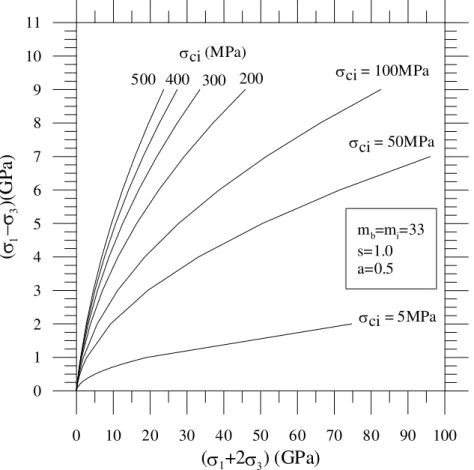
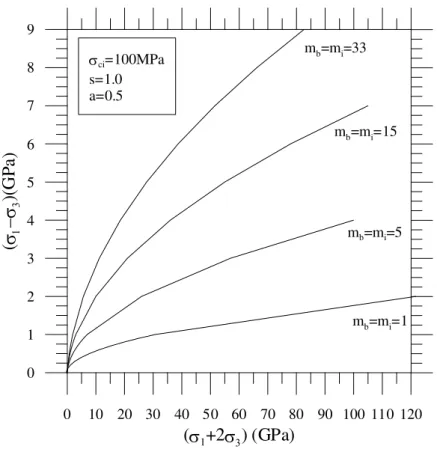
As Figuras 3.5 a 3.8 ilustram a influência dos parâmetros do critério de resistência. Da Figura 3.5 podemos observar que quanto maior a resistência à compressão maior o nível de tensão admissível. Da Figura 3.6 pode-se observar que a constante petrográfica afeta a inclinação da superfície de modo que quanto maior o mb

mais íngreme é a superfície. O parâmetro s afeta a resistência à tração de modo que quanto maior o s maior a resistência à tração (Figura 3.7). A curvatura da superfície é comandada pelo parâmetro a (Figura 3.8) de modo que quanto menor o valor do parâmetro a maior a curvatura.

0 10 20 30 40 50 60 70 80 90 100

(1+23) (GPa)

0 1 2 3 4 5 6 7 8 9 10 11

( 3

)(

G

Pa

)

_{ci = 5MPa} _{ci = 50MPa} _{ci = 100MPa} 200

300 500 400

_{ci (MPa)}

m_b=m_i=33 s=1.0 a=0.5

29

0 10 20 30 40 50 60 70 80 90 100 110 120

(1+23) (GPa)

0 1 2 3 4 5 6 7 8 9

(

3

)(

G

Pa

)

mb=mi=1

ci=100MPa s=1.0 a=0.5

mb=mi=5 mb=mi=15 m_b=m_i=33

Figura 3.6 - Influência constante petrográfica (mb).

-500 -400 -300 -200 -100 0 100 200 300 (1+2₃) (GPa)

0 10 20 30 40 50 60 70 80 90 100 110 120

(

3

)(

G

Pa

)

s=0.1

_ci=200MPa m_b=2.0 a=0.5 s=0.5

s=1.0 s=1.5

30

-100 0 100 200 300 400 500 600 700 800

(1+23) (GPa)

0 25 50 75 100 125 150 175 200 225 250

(

3

)(

G

Pa

)

a=1

ci=200MPa mb=2.0 s=0.1 a=0.5

a=0.3 a=0.1

a=0.1 a=0.3 a=0.5 a=1.0

Figura 3.8 - Influência do parâmetro a

Recentemente, Hoek et al (2002) propuseram uma modificação na definição dos parâmetros mb, s, e a, de tal forma que:

) D 14 28 /( ) 100 GSI ( i b me

m _   _(3.16)

) D 3 9 /( ) 100 GSI (

e

s







. 0

a_{ } GSI/15_ 20/3 _(3.18)

D é fator de perturbação obtido em função do dano provocado pelo desmonte do maciço e pela relaxação das tensões. Hoek et al (2002) apresenta alguns valores para D em função da condição do maciço e do processo construtivo.

A Equação 3.10 pode ser considerada uma forma geral do critério de Hoek-Brown. As diferentes versões apresentadas afetam os parâmetros mb, s e a, tal como

31

modelo de comportamento tensão deformação linear elástico perfeitamente plástico com plasticidade associada.

Assim sendo, a superfície de plastificação (e potencial plástico) do modelo elástico perfeitamente plástico de Hoek-Brown é definida no espaço das tensões principais, como:





σ σ m σ σ σ ) G( ) F( a ci 3 b ci 3

1  

          

 (3.19)

A Figura 3.9 ilustra a superfície de plastificação no espaço das tensões principais e no plano desviador. No plano desviador, a superfície de plastificação é um hexágono irregular.

compressão extensão

a) Espaço das tensões

principais

b) Plano desviador

Figura 3.9 - Critério de Hoek-Brown (adaptado Benz et al, 2008).

As tensões principais podem ser escritas em termos dos invariantes de tensão tal como (Owen e Hinton, 1980):

3 I sen 3 1 cosθ I 3 I 3 I 3 2 θ sen 3 I 2 ₁ 2D 1 1 2D

1 

     _{ }             

 (3.20)

 

2 2D ₁

2  

 (3.21)

3 I sen 3 1 cosθ I 3 I 3 4 θ sen 3 I 2 ₁ 2D 1 2D

3 

           _{ }            

32 em que               D 2 D 2 D 3 1 D 3 D 2 I I I 2 3 3 sen 3 1 ) I , I

( (3.23)

é o ângulo de Lode (/6/6 ); I1é o primeiro invariante do tensor de tensão; e, I2D

e I3D são, respectivamente, o segundo e o terceiro invariante do tensor de tensão

desviadora. Estes invariantes de tensão podem ser definidos em termos das componentes cartesianas do tensor de tensão num estado de deformação plana e axissimétrica como:

z y x 1

I    (3.24)

) ( ) ( 3 1 ) ( 3 1

I_2D  _x2 _y2 _z2  _x_y _y_z_z_x  _xy2 (3.25)





Substituindo as Equações 3.20 e 3.22 na Equação 3.19 obtém-se a o critério de plastificação do modelo de Hoek-Brown generalizado definido em termos dos invariantes de tensão:





F 2D b b 1 ci

a / 1 ci 2D ci D 2

1   

     _{ }            

 (3.27)

Como pode ser observado na Figura 3.9, o modelo de Hoek-Brown apresenta singularidades nas arestas. Assim, a seguinte modificação é sugerida para esses pontos:

Para θ = – 30° (na compressão):

0 = s σ 3 I m 3 3I m σ 3I σ

F 1 _ci

b 2D b 1/a ci 2D

ci    

     

 (3.28)

33

0 = s

σ

3 I m 3

3I 2m

σ

3I

σ

F 1 _ci

b 2D b 1/a

ci 2D

ci    

  

  

 (3.29)

O critério de resistência de Hoek-Brown tem sido largamente utilizado para estimar a capacidade de suporte e a deformação de maciços rochosos (Sharan, 2003; Choi e Deb, 2005; Benz et al., 2008; Clausen, 2013 e Wang et al., 2011). Uma das razões da popularidade do critério é a possibilidade de estimar os parâmetros do material através de simples observações de campo e da resistência à compressão uniaxial da rocha intacta

Com relação o módulo de deformabilidade elástico várias sugestões foram indicadas. Serafim e Pereira (1983) sugeriram a seguinte relação em termos do RMR:

) 40 / 10 RMR (

10

E(GPa)_  _(3.30)

Hoek e Brown (1997) a presentam a seguinte modificação:

100 10

E(GPa)_ (GSI10/40) ci

(3.31)

Em seguida, levando em conta a influência da perturbação do maciço, tem-se que:

7525DGSI/11 5

e 1

D/2)10 (1

E(MPa) _{ }

 

 (3.32)

ou ainda, em função do módulo de deformabilidade da rocha intacta, Ei, fazendo:

  _

  

  

 _{i 6015DGSI/11}

e 1

D/2 1 0.02

E

34

Capítulo 4

O PROGRAMA ANLOG

O programa computacional ANLOG (Análise não linear de obras geotécnicas) é escrito em linguagem de programação FORTRAN 90. Sua primeira versão foi desenvolvida por Zornberg (1989) tendo sido utilizada na análise de problemas mecânicos de equilíbrio estático, envolvendo a simulação de aterros e escavações, em condição de deformação plana e axissimétrica e levando em conta comportamento tensão-deformação elastoplástico.

35

simulações 3D (ANLOG v.2010). Armond e Nogueira (2013) incorporaram os modelos constitutivos Brooks e Corey (1964) e Fredlund e Xing (1994) para análise de problemas de fluxo em meio não saturado (ANLOG v.2013).

De uma forma geral o programa ANLOG pode ser usado para análise de problemas sem ou com acoplamento de fluxo e deformação (em condições saturadas); análise de problemas de fluxo em meio poroso saturado e não saturado; simulação de problemas mecânicos em condições de tensão plana e deformação plana, axissimétrica e tri-dimensional; e, simulação de problemas acoplados em condições de deformação e fluxo planos.

Do ponto de vista da aproximação por elementos finitos, o ANLOG apresenta os seguintes elementos finitos: elementos unidimensionais (linear e quadrático); elementos planos triangulares e quadrangulares (linear e quadrático); elementos sólidos (linear e quadrático); elementos de interface de espessura nula e elementos específicos para reforço; e, elementos finitos para análises acopladas: elementos planos (triangulares e quadrangulares).

Em relação aos modelos constitutivos os seguintes modelos constitutivos encontram-se implementados no ANLOG: modelos constitutivos para solos - elásticos (Linear e Hiperbólico), elastoplásticos (CamClay Modificado, Lade 77, Lade & Kim, Lade & Kim modificado) e elásticos perfeitamente plástico (Mohr-Coulomb e Drucker&Prager, originais e modificados); modelos constitutivos para reforços - elástico linear e elástico perfeitamente plástico von Mises; modelos constitutivos para junta/interface solo-reforço - elástico linear e elástico perfeitamente plástico baseado no critério de Coulomb; e, modelos constitutivos para fluxo não saturado - modelo exponencial, modelo de van Genuchten, interpolação linear e por spline cúbica de dados de ensaios.

Do ponto de vista de procedimento de solução de sistemas de equações algébricas, os seguintes algoritmos encontram-se implementados no ANLOG: algoritmo puramente incremental; algoritmo incremental-iterativo (Newton-Raphson); e, algoritmo incremental-iterativo (Newton-Raphson) incluindo a estratégia de

36

No que diz respeito ao procedimento de integração de tensão, tem-se os seguintes algoritmos: algoritmos de integração de tensão puramente explícitos; algoritmos de integração de tensão puramente explícitos com sub-incremento; e, algoritmos de integração de tensão explícitos com sub-incremento e controle do erro na avaliação das tensões.

O ANLOG roda numa plataforma Windows (Figura 4.1) e o programa MTOOL (Figura 4.2) desenvolvido pelo grupo de tecnologia em computação gráfica da PUC-Rio (TecGraf®) é usado como pré e pós processadores gráficos.

Figura 4.1 - Ambiente de trabalho do FORTRAN (Nogueira, 2010).

37

O programa ANLOG adota uma estrutura em macro comando que permite a simulação de processos construtivos de forma relativamente simplificada. Além disto, ele adota, no mínimo, 2 arquivos de dados para análise tensão deformação acoplada ou não: um arquivo com extensão “.D” contendo a sequência de macro-comandos e seus respectivos conjunto de dados, e outro com extensão “.NF” contendo as informações da malha de elementos finitos. Para uma análise de fluxo em meio não saturado se faz necessário, além dos arquivos “.D” e “.NF”, um arquivo de dados com extensão “.INI”.

Os resultados são registrados em arquivos com extensões “.OUT” e “.POS”. O

arquivo com extensão “.POS” é compatível com o pós-processador gráfico através do programa MTOOL.

4.1. Macro comando

Um macro comando é uma palavra chave utilizada para controlar a execução de blocos de rotinas que devem ser acionadas para realização de uma tarefa específica. O usuário deverá fornecer a sequência de macro comandos e todos os dados relacionados a eles. Esta sequência de macro comandos define o fluxo de informação que deverá ser usado na solução de um problema específico.

Para solução de um problema mecânico de equilíbrio estático se adota, de uma forma geral, os seguintes macros comando: DADOS; CEDGE e/ou CPOINT e/ou CGRAV; SOLVE; e FEXEC (Nogueira, 2010).

O macro comando DADOS ativa um bloco de rotinas as quais são responsáveis pela leitura dos dados geométricos (coordenadas e conectividades), materiais (modelos constitutivos e parâmetros) e condições de contorno (essencial).

Os macros comandos CPOIN, CEDGE e CGRAV ativam um bloco de rotinas que fornecem o carregamento nodal devido às forças pontuais, de superfície e de volume (ou corpo), respectivamente.

38

variáveis secundárias (deformação, tensão, gradiente hidráulico, velocidade de fluxo, etc.) são também obtidas através deste macro comando.

Além destes macros comando, ainda podem ser usados os seguintes macro comando para definição de um estado de tensão inicial diferente de zero considerando nulo o estado de deformação inicial: TINIS e TINK0. O macro comando TINK0 é usado para se obter um estado de tensão geoestático e o TINIS para um estado de tensão isotrópico.

4.2. Elementos finitos e aproximações

No âmbito desta dissertação foi adotado o elemento isoparamétrico: quadrangular quadrático Q8, tal como ilustrado na Figura 4.3.

1

(-1,-1) 2 (0;-1) 6 (0,1)

ξ

3 (1;-1) 8

(-1,0)

5 (1;1) 7

(-1,1)

4 (1;0)

1

(-1,-1) 2 (0;-1) 6 (0,1)

ξ

3 (1;-1) 8

(-1,0)

5 (1;1) 7

(-1,1)

4 (1;0) 

Figura 4.3 - Elemento finito quadrangular quadrático (Q8)

Relacionado a este elemento finito tem-se as seguintes funções de forma/interpolação escritas em termos das coordenadas naturais (, ):

1

N ( , ) 0.25(1         )(1 )( 1) (4.1a)

2 2

N ( , ) 0.5(1      )(1 ) (4.1b)

3

N ( , ) 0.25(1       )(1 )( 1) (4.1c)

2 4

N ( , ) 0.5(1      )(1 ) (4.1d)

5

N ( , ) 0.25(1         )(1 )( 1) (4.1e)

2 6

N ( , ) 0.5(1      )(1 ) (4.1f)

7

N ( , ) 0.25(1         )(1 )( 1) (4.1g)

2 8

39

Para problemas em estado plano de deformação e axissimétrico, abordados no âmbito desta dissertação, os deslocamentos em qualquer ponto do domínio do elemento pode ser escrito em função dos deslocamentos nodais como:

u N u ˆ v u         (4.2) onde





nno nno 1

1 v ... u v

u

ˆ 

u (4.3)

é o vetor de deslocamentos nodais com u e v sendo, respectivamente, as componentes do vetor de deslocamento nas direções x e y;

       nno nno 1 1 16 x 2 N 0 0 N ... N 0 0 N N (4.4)

é a matriz das funções de interpolação quadráticas, definidas pelas Equações 4.1, e nno é o número de pontos nodais de cada elemento. Para o elemento Q8, nno é igual a 8.

Usando o conceito de elemento isoparamétrico, as coordenadas cartesianas de um ponto qualquer no domínio do elemento podem ser escritas em termos das coordenadas dos pontos nodais tal como:

x N x ˆ y x         (4.5) em que





nno nno 1

1 y ... x y

x



x (4.6)

é o vetor das coordenadas locais dos pontos nodais em relação ao sistema cartesiano (x,y).

A matriz jacobiana J é utilizada na transformação de sistemas de coordenadas