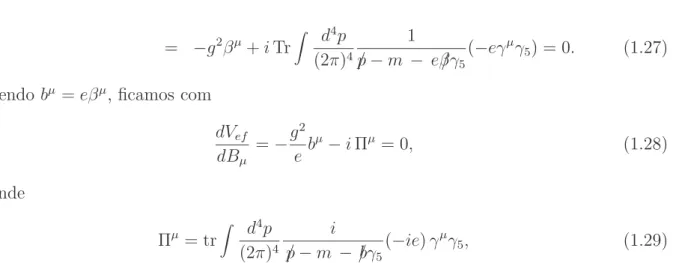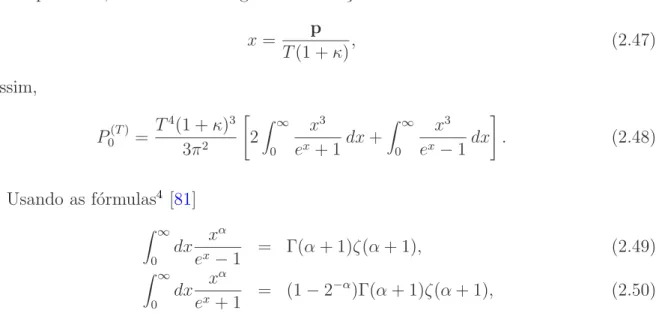Violação de Lorentz e teoria de gravitação modificada

(1)

Centro de Ciˆencias Exatas e da Natureza

Programa de P´os-Gradua¸c˜ao em F´ısica

TESE DE DOUTORADO 2010

VIOLAC

¸ ˜

AO DE LORENTZ E

TEORIA DE GRAVITAC

¸ ˜

AO MODIFICADA

Alesandro Ferreira dos Santos

Orientador:

Prof. Dr. Jos´e Roberto Soares do Nascimento

Co-Orientador:

Prof. Dr. Albert Petrov

(2)

Alesandro Ferreira dos Santos

VIOLAC

¸ ˜

AO DE LORENTZ E

TEORIA DE GRAVITAC

¸ ˜

AO MODIFICADA

Tese apresentada ao Programa de P´os-Gradua¸c˜ao em F´ısica da Universidade

Fede-ral da Para´ıba como parte dos requisitos ne-cess´arios para a obten¸c˜ao do t´ıtulo de Doutor em F´ısica.

Orientador:

Prof. Dr. Jos´e Roberto Soares do Nascimento

Co-Orientador:

Prof. Dr. Albert Petrov

(3)

(4)

(5)

(6)

“Você ganha for¸ca, coragem e confian¸ca a cada experiência em que enfrenta o medo. Você tem de fazer

exatamente aquilo que acha que n˜ao consegue.”

(7)

• Ao professor José Roberto pela orienta¸cão, dedica¸cão e motiva¸cão na realiza¸cão deste trabalho.

• A minha esposa pelo apoio e confian¸ca.`

• Ao colega e colaborador Tiago Mariz, assim como aos demais professores que cola-boraram com este trabalho, Cl´audio, Albert, Marcelo e Adilson.

• Aos professores e funcion´arios do departamento de f´ısica da UFPB que contribu´ıram de alguma forma para a realiza¸c˜ao deste trabalho.

• Aos colegas e amigos do departamento de f´ısica da UFPB, em especial aos que dividiram sala comigo nesse per´ıodo.

(8)

Resumo

Nesta tese estudamos a quebra espontˆanea das simetrias de Lorentz e CPT em um modelo de quatro f´ermions quadridimensional em temperatura zero e em temperatura

finita. Em temperatura zero encontramos que essas simetrias podem ser violadas, já em temperatura finita mostramos que pode existir uma temperatura para a qual essas mesmas simetrias que foram quebradas em temperatura zero podem ser restauradas. Mos-tramos que é poss´ıvel obter uma equa¸cão de Friedmann em cinco dimensões na presen¸ca

de termos que violam as simetrias de Lorentz, e como solu¸cão dessa equa¸cão encontramos que a evolu¸cão do universo pode ter um comportamento não usual, oscilando entre fases aceleradas e desaceleradas. Analisamos a eletrodinâmica quântica estendida no limite de altas temperaturas. Nosso objetivo é estudar as modifica¸cões que a viola¸cão de Lorentz

pode causar na energia livre da eletrodinâmica quântica e com isso usar dados experi-mentais relacionados a energia livre para estimar um valor numérico para o parâmetro de quebra das simetrias de Lorentz. Estudamos uma proposta de modifica¸cão da gravita¸cão, esta proposta consiste em adicionarmos o termo de Chern-Simons a gravita¸cão usual. O

assunto com maior destaque nesta nova teoria de gravita¸cão é a busca por solu¸cões que ocorrem na relatividade geral e que de algum modo persistem nesta teoria modificada. Mostramos que para uma determinada escolha do campo escalar que é introduzido junto ao termo de Chern-Simons na teoria, é poss´ıvel termos importantes solu¸cões da

relativi-dade geral nesta nova teoria de gravita¸cão, como a solu¸cão de Schwarzschild, a métrica de Gödel, entre outras. Estudamos com maior ênfase a solu¸cão de Gödel, mostrando que é poss´ıvel termos essa solu¸cão na teoria modificada tanto no caso em que interpretamos o campo escalar como um campo externo, quanto no caso em que o interpretamos como

um campo dinâmico, esta última interpreta¸cão nos conduz a modifica¸cões importantes em parâmetros da teoria.

Palavras-chave: viola¸c˜ao das simetrias de Lorentz e CPT, energia livre, gravita¸c˜ao

modificada e m´etrica de G¨odel.

´

(9)

In this thesis we study the Lorentz and CPT symmetries breaking in a 4D four-fermions model at zero and at finite temperature. At zero temperature we find that these

symmetries can be violated, but at finite temperature we show that there is a critical temperature at which the Lorentz and CPT symmetries are restored. We show that it is possible obtain the Friedmann equation in five dimensions in the presence of terms that violate the Lorentz symmetries , and as solution of this equation we find that the evolution

of the universe is not usual, oscillating between accelerated phases and desaccelerated phases. We analyse the extension of the quantum eletrodynamics in the limit of high temperatures. Our aim is study the modifications that the Lorentz violation can cause in the free energy of the quantum eletrodynamics and with this to use experimental data

related the free energy to estimate a numeric value to the parameter of Lorentz violation. We study a proposal of modification of the gravitation, this proposal consist in adding the Chern-Simons term to the usual gravitation. The issue most notable in this theory of gravitation is the search for solutions that occur in the general relativity and that

somehow persist in this new theory. We show that for a given choice of scalar field that is introduced together with the Chern-Simons term, it is possible to find important solutions of the general relativity in this new theory of gravitation, as the Schwarzschild solution, the G¨odel metric, among others. We study with emphasis the G¨odel solution, showing

that it is possible the existence this solution in the modified theory when we interpret the scalar field as a external field and when we interpret this same field as a dynamic field, this last interpretation leads the important modifications in parameter of the theory.

Keywords: violation of Lorentz symmetries and CPT, free energy, modified gravitation

(10)

viii

Conte´

udo

Lista de Figuras x

Introdu¸c˜ao 1

1 Quebra Espontˆanea de Simetria 7

1.1 Um simples exemplo de quebra espontˆanea de simetria . . . 7

1.2 O mecanismo de Higgs . . . 8

1.3 O Modelo Bumblebee . . . 10

1.4 Quebra dinâmica da simetria de Lorentz em um modelo de quatro-férmions 12 1.5 Restaura¸cão da simetria de Lorentz em temperatura finita . . . 20

1.6 Equa¸c˜ao de Friedmann com quebra espontˆanea da simetria de Lorentz. . . 26

2 Eletrodinâmica quântica estendida 34 2.1 Modelo padrão estendido . . . 34

2.2 Energia livre da eletrodinˆamica quˆantica estendida em altas temperaturas . 36 2.2.1 A energia livre . . . 40

2.2.1.1 Contribui¸c˜ao de um loop . . . 41

2.2.1.2 Contribui¸c˜ao de dois loops . . . 44

2.2.2 Estimativa num´erica . . . 47

3 Gravita¸cão modificada pelo termo de Chern-Simons 50 3.1 Algumas motiva¸cões que podem levar a modifica¸cões . . . 50

(11)

3.3 Solu¸c˜ao de Schwarzschild . . . 55

4 Solu¸cão de Gödel na gravita¸cão modificada 58

4.1 O universo de G¨odel . . . 58

4.2 Introduzindo a métrica de Gödel na gravita¸cão de Chern-Simons . . . 61

4.3 Campo escalar θ dinˆamico . . . 63

Conclus˜oes e perspectivas 69

Apˆendice A -- Integrais em D dimens˜oes 72

Apˆendice B -- Algumas ferramentas da relatividade geral 73

Apˆendice C -- Tensor de Cotton para a solu¸c˜ao de Schwarzschild 75

Apêndice D -- Tensor de Cotton para a métrica de Gödel 79

(12)

x

Lista de Figuras

1 Se µ2 _>₀ _⇒_φ _{= 0} _{. . . .} ₈

2 Se µ2 _<₀ _⇒_φ ₌_±_φ 0. . . 8

3 Contribui¸c˜oes para o tadpole Πµ _{. . . 14}

4 Comportamento da fun¸c˜ao FI(ξ). . . 21

5 Comportamento da fun¸c˜ao FII(ξ) . . . 22

6 Comportamento da fun¸c˜ao FIII(ξ) . . . 23

7 Comportamento da fun¸c˜ao FIV(ξ) . . . 24

8 Comportamento da fun¸c˜ao FVI(ξ) . . . 25

9 Dinˆamica do fator de escala . . . 32

10 Dinˆamica da velocidade . . . 32

11 Diagramas de um loop . . . 41

(13)

Introdu¸

c˜

ao

A simetria na natureza é um fenômeno único e fascinante. Esta idéia

surge naturalmente ao esp´ırito humano, remetendo-o para um equil´ıbrio

e propor¸c˜ao, padr˜ao e regularidade, harmonia e beleza, ordem e

per-fei¸cão. Estes são alguns dos vocábulos que resumem rea¸cões que temos

inerentes `as simetrias que abundam na natureza, nas formas vivas e

inanimadas.

Autor desconhecido

Na natureza como um todo, em particular na f´ısica, as simetrias desempenham um papel muito importante, pois elas podem nos dar informa¸c˜oes a cerca de processos e/ou problemas que estamos interessados em estudar e/ou resolver.

O modelo padr˜ao de f´ısica de part´ıculas e a teoria da relatividade de Einstein s˜ao duas teorias de grande sucesso que preservam duas importantes simetrias, as simetrias de Lorentz e a simetria CPT. Podemos nos perguntar, o que significa um sistema f´ısico ser

invariante perante as simetrias de Lorentz e CPT? Antes de responder a essa pergunta é interessante e se faz necessário entendermos de maneira clara o que são as transforma¸cões de Lorentz e a transforma¸cão CPT.

As simetrias de Lorentz ou transforma¸cões de Lorentz são divididas em dois tipos, rota¸cões e boosts. O que caracteriza cada uma dessas transforma¸cões? As rota¸cões

podem existir em três formas, uma ao longo de cada uma das três dire¸cões espaciais; um boost é uma mudan¸ca de velocidade de um sistema inercial. Há três tipos de boosts, um ao longo de cada uma das três dire¸cões espaciais.

A transforma¸cão CPT é a combina¸cão de três transforma¸cões: conjuga¸cão de carga (C), paridade (P) e reversão temporal (T). A simetria de conjuga¸cão de carga (C) trans-forma uma part´ıcula em sua antipart´ıcula. A simetria de paridade (P) converte um objeto

(14)

Introdu¸c˜ao 2

Assim, um sistema f´ısico é dito invariante perante as simetrias de Lorentz e CPT se as leis f´ısicas envolvidas permanecem inalteradas após sofrerem a a¸cão de qualquer uma dessas transforma¸cões.

As simetrias de Lorentz e CPT são simetrias que já passaram por vários testes expe-rimentais e possuem uma excelente precisão experimental. No entanto, no fim dos anos

80 e in´ıcio dos anos 90, a partir de um trabalho realizado por Kostelecky e Samuel [1], surgiu a idéia que as simetrias de Lorentz e CPT podem ser violadas no contexto de teoria de cordas. Desde então, essa idéia foi intensamente discutida e surgiram vários grupos de pesquisadores espalhados pelo mundo estudando a possibilidade de que as simetrias

fundamentais da f´ısica possam ser violadas, vários experimentos foram constru´ıdos com a inten¸cão de se verificar tal viola¸cão, experimentos envolvendo mésons neutros, oscila¸cões de neutrinos, entre vários outros. Contudo, se a quebra dessas simetrias realmente ocor-rem na natureza, devem ser extocor-remamente pequenas, de modo que precisamos de aparatos

experimentais extremamente sens´ıveis para tal deteçcão. A deteçcão de algum ind´ıcio de viola¸cão das simetrias de Lorentz e CPT, por menor que seja, pode ser uma forte indica¸cão de uma nova f´ısica, que provavelmente vem da escala Planck [2].

Motivados pela possibilidade que as simetrias de Lorentz e CPT possam ser violadas, Kostelecky e Colladay [3] constru´ıram uma extens˜ao do modelo padr˜ao que inclui todos os

termos que violam Lorentz e CPT, uma vez que o modelo padrão usual como o conhecemos descreve todas as part´ıculas fundamentais e suas intera¸cões não gravitacionais, porém preservando tanto as simetrias de Lorentz como a simetria CPT. Esses novos termos que surgem na extensão do modelo padrão podem violar apenas as simetrias de Lorentz ou as

simetrias de Lorentz e CPT.

O mecanismo utilizado para gerar o modelo padrão estendido é a quebra espontânea

de simetria, tido por muitos como o mais elegante mecanismo de quebra de simetria, no qual um campo tensorial que contém ´ındices de Lorentz adquire um valor esperado no vácuo não nulo, < Tµ >6= 0, que seleciona uma dire¸cão preferencial no espa¸co-tempo e

assim, quebra espontaneamente a simetria de Lorentz.

Por constru¸cão, o modelo padrão estendido é invariante diante das transforma¸cões de

Lorentz de observador. Aqui ressaltamos que as transforma¸cões de Lorentz podem ser classificadas em transforma¸cão de Lorentz de observador e transforma¸cão de Lorentz de part´ıcula, sendo que uma transforma¸cão de Lorentz de observador é uma mudan¸ca de sistema de observa¸cão, já uma transforma¸cão de Lorentz de part´ıcula é uma rota¸cão ou

(15)

Portanto, se existe viola¸c˜ao, a f´ısica pode ser alterada diante de uma transforma¸c˜ao de part´ıcula.

A extensão do modelo padrão é composta por inúmeros termos, mas para preservar algumas caracter´ısticas importantes limita-se o modelo a um subconjunto onde a in-variância de gauge usual e a renormalizabilidade da teoria são mantidas, esse subconjunto

é denominado de extensão m´ınima do modelo padrão.

Assim como o modelo padrão é uma teoria que descreve muito bem uma grande quan-tidade de fenômenos f´ısicos e por outro lado não consegue explicar alguns fenômenos, te-mos a teoria da relatividade geral de Einstein, que dá conta de explicar muito bem vários fenômenos gravitacionais, mas nos últimos anos tem-se notado que essa teoria não dá

conta de explicar alguns dados observacionais importantes. De acordo com dados obser-vacionais obtidos por Supernovas do tipo Ia, estrutura de grande escala, curva de rota¸cão de galáxias, entre outros, temos um universo dominado por algo que não conhecemos e que a relatividade geral não consegue explicar. Observa-se que a matéria do universo é

muito maior que a matéria bariônica que conhecemos, ou seja, a maior parte de matéria do universo é formada por uma componente chamada de matéria escura, cujo a composi¸cão não conhecemos, detecta-se a sua existência pela influência gravitacional causada pela mesma. Outro importante dado observacional é a confirma¸cão de que o universo está se

expandindo de forma acelerada, e a componente responsável por tal acelera¸cão é deno-minada de energia escura, que tem como principal caracter´ıstica atuar como uma espécie de antigravidade com pressão negativa. Esses dados observacionais nos levam a um uni-verso dominado por componentes escuras, as quais sabemos muito pouco, ou nada sobre

sua forma¸cão. Outro ponto em aberto está relacionado a quantiza¸cão da gravidade, há algumas teorias que tem tido algum desenvolvimento nesse sentido, como teoria de cordas e gravidade quântica em la¸co (loop quantum gravity), mas nenhuma resposta definitiva sobre uma teoria de gravita¸cão quântica.

Diante desses problemas muitos se perguntam, seriam matéria e energia escura algum efeito quântico da gravita¸cão ou apenas uma modifica¸cão da relatividade geral? Dada a

ausência de uma teoria quântica para a gravita¸cão, nos últimos anos houve um grande interesse em se propor alguma modifica¸cão para a teoria da relatividade geral, entre essas modifica¸cões podemos destacar as teorias F(R) e a modifica¸cão causada pelo termo de Chern-Simons gravitacional. No decorrer do trabalho fizemos alguns estudos para esse

´

ultimo caso.

(16)

Introdu¸c˜ao 4

foi inicialmente motivada por modifica¸cão semelhante feita na eletrodinâmica quântica. Na eletrodinâmica quântica, tal modifica¸cão leva para viola¸cão das simetrias de Lorentz e viola¸cão de paridade. A modifica¸cão na relatividade geral consiste de adicionarmos o termo de Chern-Simons quadridimensional a a¸cão de Einstein-Hilbert usual. Esse termo

faz com que a teoria tenha viola¸cão de paridade, porém conservando as simetrias de Lorentz. Essa modifica¸cão não consiste em uma manipula¸cão arbitrária, ela é vista como uma teoria efetiva de uma teoria de cordas. Essa teoria efetiva é motivada por cancelar anomalias em f´ısica de part´ıculas e em teoria de cordas. O que tem se destacado nessa

modifica¸cão é a possibilidade de que solu¸cões bem determinadas na relatividade usual, como a solu¸cão de Schwarzschild, podem persistir nessa nova teoria de gravita¸cão para a escolha de algum parâmetro espec´ıfico.

Apresentaremos esta Tese da seguinte maneira: no cap´ıtulo 1 iremos estudar o me-canismo de quebra espontˆanea das simetrias de Lorentz. Para ilustrar esse meme-canismo

iniciamos com um exemplo simples, a teoriaλφ4_{, e analisamos quando a quebra de}

sime-tria ocorre. Como estamos interessados em estudar a quebra espontânea das simesime-trias de Lorentz nas se¸cões seguintes, que ocorre de modo semelhante ao mecanismo de Higgs, aqui analisamos rapidamente o mecanismo de Higgs, mecanismo responsável por dar massa as

part´ıculas do modelo padr˜ao. Em seguida estudamos o modelo bumblebee, um modelo de quebra espontˆanea das simetrias de Lorentz e CPT. Nesse modelo um campo vetorial

Bµ adquire um valor esperado no vácuo não nulo, < Bµ >=bµ, que escolhe uma dire¸cão

preferencial no espa¸co-tempo e assim as simetrias de Lorentz s˜ao quebradas

espontanea-mente. Na próxima se¸cão iremos estudar a quebra dinâmica das simetrias de Lorentz e CPT em um modelo de quatro-férmions, onde induziremos dinamicamente um potencial bumblebee por corre¸cões radiativas. A equa¸cão de gap será obtida e analisada para tem-peratura zero e temtem-peratura finita. Em temtem-peratura zero observamos que a equa¸cão de

gap tem uma solu¸cão não trivial que nos leva a viola¸cão das simetrias de Lorentz e CPT, já em temperatura finita surge a possibilidade de que essas simetrias possam ser restaura-das para uma dada temperatura cr´ıtica. Finalizamos esse cap´ıtulo estudando a equa¸cão de Friedmann em cinco dimensões no contexto de quebra espontânea das simetrias de

Lo-rentz com o objetivo de verificar quais os efeitos que a viola¸cão das simetrias de LoLo-rentz podem trazer para o cenário cosmológico. Como uma primeira tentativa encontramos resultados altamente não-triviais.

No cap´ıtulo 2 fazemos uma breve discussão do modelo padrão estendido dando ênfase a eletrodinâmica quântica estendida, em seguida estudamos a energia livre da

(17)

que violam as simetrias de Lorentz e CPT que possuem dimensão de massa podem ser negligenciados de modo que os únicos termos interessantes para o nosso estudo são cµν,

dµν e (kF)µνλρ. Logo ap´os, estudamos os efeitos que a viola¸c˜ao de Lorentz pode produzir

na energia livre, que é uma quantidade de grande interesse, pois nos dá informa¸cões

so-bre a nucleoss´ıntese primordial, f´ısica de plasma entre outros assuntos em f´ısica. Nossos cálculos para a energia livre se estendem até a segunda ordem na constante de acopla-mento, ou seja, calculamos as contribui¸cões de um e dois loops. E por fim, fazemos uma estimativa numérica para o parâmetro de quebra das simetrias de Lorentz usando dados

da abundância primordial de hélio, onde a diferen¸ca entre valores teóricos e experimentais talvez possa ser resolvido pela contribui¸cão vinda da quebra das simetrias de Lorentz.

A teoria de gravita¸cão modificada pelo termo de Chern-Simons é discutida no cap´ıtulo 3. Inicialmente damos algumas motiva¸cões que nos levam a idéias de modifica¸cões à teoria da relatividade de Einstein, e fazemos uma discussão de algumas aplica¸cões dessa nova

teoria. Na próxima se¸cão estudamos a modifica¸cão em si, discutindo os novos termos que surgem na teoria ao adicionarmos o termo de Chern-Simons à a¸cão de Einstein-Hilbert. Logo após, passamos a discutir o ponto que mais tem chamado aten¸cão em torno dessa teoria, que é a possibilidade de solu¸cões conhecidas na relatividade geral persistirem na

teoria modificada, como exemplo, estudamos a possibilidade da solu¸c˜ao de Schwarzschild persistir nessa nova teoria de gravita¸c˜ao.

No cap´ıtulo 4 introduzimos o universo Gödel, universo que tem com principal ca-racter´ıstica a possibilidade de curvas tipo-tempo fechadas, sendo o primeiro modelo cos-mológico com matéria em rota¸cão. Introduzido o modelo, mostramos que a métrica de

Gödel é solu¸cão das equa¸cões de Einstein, como o próprio Kurt Gödel mostrou em 1949. Em seguida vamos verificar se a métrica de Gödel também é solu¸cão na gravita¸cão mo-dificada pelo termo de Chern-Simons. Em nossa primeira análise consideraremos que o campo escalar θ introduzido junto ao termo de Chern-Simons na a¸cão é um campo ex-terno. Com essa interpreta¸cão observamos que, se θ é uma fun¸cão das coordenadas x e

y a solu¸cão de Gödel é solu¸cão da teoria modificada. Nossa segunda interpreta¸cão será feita para o caso em que o campo escalar θ é um campo dinâmico. Neste caso a análise precisa ser feita com mais cuidado, pois para a métrica de Gödel ser solu¸cão das equa¸cões

(18)

Introdu¸c˜ao 6

(19)

1 Quebra Espontˆ

anea de Simetria

Se minha vis˜ao estiver correta, o universo pode ter um tipo de

estru-tura dominante. Em uma parte do universo, vocˆe pode ter uma dire¸c˜ao

preferencial dos eixos; em outra parte, as dire¸c˜oes dos eixos podem ser

diferentes.

Y. Nambu

A natureza exibe fascinantes e exuberantes formas de simetrias. Contudo, existem

vários exemplos na natureza de simetrias que são quebradas. Um simples exemplo vem da f´ısica de estado sólido. No ferromagneto os átomos interagem através da intera¸cão spin-spin que é um escalar e invariante por simetrias de rota¸cão. No entanto, no estado fundamental todos os spins estão alinhados e a simetria sob rota¸cão é quebrada. Existem

vários fenômenos em que a teoria, a lagrangiana, é invariante diante de alguma simetria, porém apresentam solu¸cões no vácuo que violam essa simetria, quando isso ocorre dizemos que temos uma quebra espontânea de simetria.

1.1 Um simples exemplo de quebra espontˆ

anea de

simetria

Para ilustrar o fenômeno da quebra espontânea de simetria vamos considerar um campo escalar com intera¸cão do tipo λφ4_{. Esta teoria admite a simetria} _φ _{→ −}_φ_{. A}

lagrangiana que descreve tal modelo ´e dada por

L= 1

2(∂µφ)(∂

µ_φ₎

−1₂µ2φ2₋ 1

4!λφ

4_, _(1.1)

onde λé positivo e µ2 _{é um parâmetro que pode ser positivo ou negativo. O potencial é}

dado por

V(φ) = 1 2µ

2_φ2₊ 1

4!λφ

(20)

1.2 O mecanismo de Higgs 8

O estado fundamental ´e obtido ao tomarmos o m´ınimo do potencial,

dV dφ =µ

2_φ₊1

6λφ

3 _{= 0}_. _(1.3)

Da equa¸c˜ao (1.3) temos duas situa¸c˜oes a serem analisadas:

(i) se µ2 _>_{0, temos apenas a solu¸c˜ao} _φ_{= 0, que est´a mostrada na Figura 1 e a simetria}

de paridade (φ_{→ −}φ) ´e mantida;

(ii) se µ2 _<_{0, temos dois m´ınimos,} _φ ₌ _±q₋6µ2

λ = ±φ0 e um m´aximo local em φ = 0,

que est˜ao mostrados na Figura 2.

Figura 1: Se µ2 _>₀ _⇒ _φ_{= 0} _{Figura 2: Se} _µ2 _<₀ _⇒ _φ₌_±_φ0

Uma vez que escolhemos um valor de φ0, a simetria ´e quebrada pelo v´acuo da teoria.

As consequˆencias f´ısicas s˜ao independentes dessa escolha.

Portanto, esse ´e um exemplo simples de uma teoria em que a quebra espontˆanea de simetria ocorre.

1.2 O mecanismo de Higgs

Agora vamos ver o que ocorre quando a simetria em questão é a simetria de gauge. Usando esta simetria poderemos analisar como ocorre o fenômeno de Higgs, fenômeno este que é responsável por dar massa às part´ıculas do modelo padrão. Nosso interesse

(21)

estudar a eletrodinâmica quântica escalar1 _{cuja lagrangiana é dada por}

L = (Dµφ)†(Dµφ)−µ2φ2−λφ4−

1 4FµνF

µν_, _(1.4)

ondeDµ=∂µ−ieAµ´e a derivada covariante eFµν =∂µAν−∂νAµ.Esta teoria ´e invariante

pelas transforma¸c˜oes

φ(x)_→eiα(x)_φ₍_x₎_,

Aµ→Aµ+∂µα. (1.5)

Do mesmo modo que vimos na se¸c˜ao anterior, pode-se verificar que para µ2 _> ₀

o potencial apresenta apenas um m´ınimo, ou seja, φ0 = 0. J´a para µ2 < 0, ocorre o

fenˆomeno da quebra espontˆanea de simetria e o potencial tem como m´ınimo

φ2₀ =₋µ

2

2λ ≡ v2

2. (1.6)

Para analisarmos o espectro de part´ıculas, podemos escolher φ0 = √v

2 e o campo φ

pode ser convenientemente parametrizado como

φ = e

iξ v

√

2(v+η),

≈ √1

2(v+η+iξ), (1.7)

para pequenas oscila¸c˜oes em torno do v´acuo. Assim, podemos reescrever a lagrangiana (1.4) como

L= 1 2 h

(∂µη)(∂µη) + 2µ2η2

i +1

2(∂µξ)(∂

µ_ξ₎

− 1₄FµνFµν −evAµ(∂µξ) +

e2_v2

2 AµA

µ₊_{. . . .}

(1.8)

Agora podemos fazer algumas observa¸c˜oes sobre esta nova lagrangiana:

• O campoη ´e um campo massivo com massa m2

η =−2µ2;

• O campoξ ´e um escalar sem massa;

• O ´ultimo termo indica que o f´oton adquiriu uma massa, m2

γ =e2v2;

• O pen´ultimo termo indica que existe uma mistura entre os campos Aµ eξ.

1

(22)

1.3 O Modelo Bumblebee 10

´

E poss´ıvel fazer uma escolha de gauge para a qual o espectro de part´ıculas seja evi-dente. Para tal escolha ´e conveniente reescrevermos

1

2(∂µξ)(∂

µ_ξ₎

−evAµ(∂µξ) +

e2_v2

2 AµA

µ ₌ e2v2

2

Aµ−

1

ev∂µξ A

µ

− 1

ev∂

µ_ξ_. _(1.9)

Como temos a liberdade de escolher um gauge qualquer, ´e conveniente escolher

Aµ → Aµ−

1

ev∂µξ

φ _→ e−iξvφ= (v√+η)

2 . (1.10)

Sabendo que a lagrangiana ´e localmente invariante de gauge, podemos usar esses campos na lagrangiana original e obtermos

L= 1 2 h

(∂µη)(∂µη) + 2µ2η2

i

− 1₄FµνFµν+

e2_v2

2 AµA

µ₊ _ctes. _(1.11)

O gauge que usamos ´e chamado degauge unit´ario ou f´ısico. Nesse gauge notamos que:

• O campoη tem massa m2 ₌₋₂_µ2_;

• Os f´otons s˜ao massivos, mγ =ev;

• O campoξ desapareceu do espectro.

Então, o campoξsem massa desapareceu e o fóton tornou-se massivo2_{. Esse fenômeno}

é conhecido como o mecanismo de Higgs. Esse é o mecanismo responsável por dar massa a todas as part´ıculas do modelo padrão. Mais detalhes desse mecanismo podem ser

encontrados em livros texto como [4, 5, 6, 7].

1.3 O Modelo Bumblebee

Vamos estudar a possibilidade da quebra espontˆanea das simetrias de Lorentz e CPT. A id´eia de que essas simetrias possam ser espontaneamente violadas tem sido sugerida como um poss´ıvel mecanismo que pode ocorrer no contexto de uma teoria fundamental na

escala Planck, como teoria de cordas e teorias de gravita¸cão quântica [1]. O mecanismo de quebra espontânea das simetrias de Lorentz tem sido intensivamente estudado na literatura [8, 9,10, 11, 12,13].

2

(23)

Um dos mais elegantes e interessantes mecanismos de quebra de simetria se dá através da quebra espontânea, que como já vimos, a lagrangiana respeita a simetria em questão, mas as solu¸cões no vácuo de tal teoria não respeitam. O fenômeno da viola¸cão espontânea de simetria tem consequências bem conhecidas em teorias de campos. Quando estudamos

teorias de gauge temos o teorema de Goldstone, que afirma que, quando uma simetria global é quebrada espontaneamente, podem aparecer modos Nambu-Goldstone sem massa (part´ıculas sem massa). Por outro lado, se a simetria é local o mecanismo envolvido é o mecanismo de Higgs, responsável por dar massa aos campos de gauge. Mais informa¸cões

a respeito do teorema Goldstone e do mecanismo de Higgs podem ser encontradas em [14, 15, 16, 17, 18, 19, 20]. Esses processos também já foram estudados para o caso em que a simetria é a simetria de Lorentz [9, 21, 22, 23, 24, 25].

Um simples exemplo de uma teoria com quebra espontânea das simetrias de Lorentz é o modelo bumblebee [8, 9, 26], onde um campo vetorial adquire um valor esperado no vácuo (VEV) diferente de zero,

< Bµ>=bµ, (1.12)

sendoBµ um campo vetorial e bµ seu valor esperado no v´acuo. Assim, o v´acuo da teoria

escolhe uma dire¸c˜ao preferencial no espa¸co-tempo.

Existem várias versões do modelo bumblebee que podem ser definidas com diferentes formas para os termos cinéticos e para o potencial. Este modelo também pode ser estudado

em geometrias diferentes do espa¸co-tempo, tais como no espa¸co-tempo de Minkowski3_,

espa¸co-tempo de Riemann4 _{e no espa¸co-tempo de Riemann-Cartan}5 _[8, _{21]. Uma vers˜ao}

generalizada do modelo bumblebee tem sido discutida em [27].

Para introduzirmos o modelo bumblebee vamos considerar o caso em que o campo bumblebeeBµest´a acoplado com a gravidade e com a mat´eria, de modo que consideramos

termos quadr´aticos em Bµ e at´e segunda ordem na derivada deste campo. A densidade

de lagrangiana que descreve esse modelo ´e dada por

LB =

1

16πG(R−2Λ)−

1

4τ1BµνB

µν₊ 1

2τ2DµBνD

µ_Bν ₊1

2τ3DµB

µ_D νBν

+ σ1BµBνRµν +σ2BµBµR−V(BµBµ±b2) +LM, (1.13)

ondeGé a constante gravitacional de Newton, Λ é a constante cosmológica, Ré o escalar de Ricci (B.8),Rµν é o tensor de Ricci (B.5) eDµé a derivada covariante. As quantidade

3

Espa¸co-tempo plano 4

Espa¸co-tempo curvo 5

(24)

1.4 Quebra dinˆamica da simetria de Lorentz em um modelo de quatro-f´ermions 12

τ1, τ2, τ3, σ1 eσ2são constantes que determinam a forma dos termos cinéticos para o campo bumblebee. O tensorBµν é definido como

Bµν =∂µBν −∂νBµ, (1.14)

no espa¸co-tempo de Riemann. Já_LM representa os termos de intera¸cão com a matéria ou

correntes externas. O potencialV(BµBµ±b2) que tem m´ınimos não triviais é o responsável

pela viola¸c˜ao das simetrias de Lorentz. O m´ınimo do potencial ocorre quando

BµBµ±b2 = 0. (1.15)

Essa condi¸cão é satisfeita quando o campo vetorial adquiri um valor esperado no vácuo diferente de zero, ou seja,< Bµ>=bµ, logo

bµbµ=∓b2. (1.16)

Assim, observamos que esse resultado quebra espontaneamente a invariˆancia de Lorentz.

Na literatura existem v´arias formas para o potencial, entre elas as mais estudadas s˜ao

V =λ(BµBµ∓b2), (1.17)

que envolve um campo multiplicador de Lagrangeλ e ´e linear emBµBµ,

V = 1

2λ(BµB

µ

∓b2)2, (1.18)

que também envolve λ, porém é quadrático em BµBµ e,

V = 1

2κ(BµB

µ

∓b2)2, (1.19)

tamb´em quadr´atico em BµBµ e com κ sendo uma constante.

1.4 Quebra dinˆ

amica da simetria de Lorentz em um

modelo de quatro-f´

ermions

Em um modelo de quatro-férmions quadridimensional, vamos estudar a quebra es-pontânea das simetrias de Lorentz e CPT via o mecanismo de Coleman e Weinberg [28], isto é, induziremos um potencial bumblebee dinamicamente por corre¸cões radiativas.

(25)

Consideremos uma teoria fermiˆonica dada por

L0 = ¯ψ(i∂/−m)ψ− G

2( ¯ψγµγ5ψ)( ¯ψγ

µ_γ5ψ₎_, _(1.20)

onde ψ é um campo espinorial de Dirac e G = e_g22. Essa teoria é não renormalizável e

pode ser entendida como uma teoria efetiva em baixas energias surgindo de uma teoria mais fundamental, como foi pensado inicialmente em [29].

Para eliminar o termo de auto-intera¸c˜ao de (1.20), vamos introduzir um campo auxiliar

Bµ de modo que podemos escrever

L = _L0+ g2

2 Bµ−

e

g2ψγ¯ µγ5ψ

!2

= g

2

2 BµB

µ_{+ ¯}_ψ₍_i∂/

−m ₋ eB/γ5)ψ. (1.21)

Para encontrarmos o potencial efetivo vamos usar o funcional gerador que ´e dado por

Z(¯η, η) = Z

DBµDψ Dψ¯exp

i

Z

d4x(_L+ ¯ηψ+ ¯ψη)

. (1.22)

Vamos inicialmente fazer a integra¸c˜ao sobre os f´ermions,

Z

Dψ Dψ¯exphψ¯(i∂/₋m ₋ eB/γ5)ψ+ ¯ηψ+ ¯ψηi=eη M¯ −1η detM, (1.23)

ondeM =i∂/₋m ₋ eB/γ5. Dessa maneira, podemos reescrever o funcional gerador como

Z(¯η, η) = Z

DBµ exp

"

iSef[B] +i

Z

d4x η¯ 1

i∂/₋m ₋ eB/γ5η

!#

, (1.24)

onde Sef[B] ´e a a¸c˜ao efetiva definida como

Sef[B] = g

2

2 Z

d4x BµBµ−iTr ln(i∂/−m − eB/γ5), (1.25)

e Tr ´e o tra¸co sobre as matrizes de Dirac. O potencial efetivo para este caso fica

Vef =₋g

2

2BµB

µ₊_i_TrZ d4p

(2π)4 ln (p/−m − eB/γ5). (1.26)

Nós estamos interessados em investigar o m´ınimo do potencial, e com isso verificar se há m´ınimos não nulos que nos levam a viola¸cão de simetrias, no caso, simetrias de Lorentz

e CPT. Assim, devemos analisar as solu¸c˜oes da equa¸c˜ao

dVef dBµ

(26)

= ₋g2βµ+iTr

Z d4p (2π)4

1

p

/₋m ₋ eβ/γ5

(₋eγµγ5) = 0. (1.27)

Sendobµ₌_eβµ_{, ficamos com}

dVef

dBµ

=₋g

2 e b

µ

−iΠµ= 0, (1.28)

onde

Πµ= tr

Z d4p (2π)4

i p

/₋m ₋/γ5b (−ie)γ

µ_γ5, _(1.29)

´e a amplitude do tadpole. Para calcularmos essa integral, vamos usar as seguintes regras de Feynman:

(i) o propagador do f´ermion

= i

p

/₋m; (1.30)

(ii) a inser¸c˜ao ao propagador do f´ermion

= ₋ib/γ5; (1.31)

(iii) e o vértice férmion-fóton

= ₋ie γµγ5. (1.32)

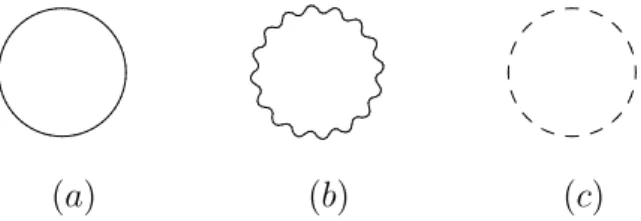
Com essas regras de Feynman as contribui¸c˜oes para Πµ_{s˜ao mostradas na figura abaixo.}

Figura 3: Contribui¸c˜oes para o tadpole Πµ

Levando em conta as propriedades de simetrias ao calcular as integrais, e as

(27)

contribui¸c˜oes relevantes separadamente. Para o segundo gr´afico da Figura3 temos que

Πµ_b = Tr

Z d4p

(2π)4 (−ieγ

µ_γ5₎_S₍_p₎₍

−ib/γ5)S(p), (1.33)

onde S(p) = i

p/−m ´e o propagador usual. Substituindo o valor de S(p) ficamos com

Πµ_b =eTr

Z d4p (2π)4

γµ_γ5₍_/_p₋_m₎_/γ5_b ₍_p_/₋_m₎

(p2₋_m2₎2 . (1.34)

Calculando o tra¸co sobre as matrizes de Dirac temos

Πµ_b = 4e

Z d4p (2π)4

2(b_·p)pµ₋₍_p2₊_m2₎_bµ

(p2₋_m2₎2 . (1.35)

Agora vamos mudar do espa¸co de Minkowski para o espa¸co Euclidiano realizando uma

rota¸c˜ao de Wick p0 = ip4, x0 = ₋ix4, b0 = ib4, b2 ₌ ₋_b2

E, p2 = −p2E, p2E = ~p2 +p24, d4_p ₌ _id4_p

E e d4x = −id4xE. Assim, podemos reescrever (1.35) no espa¸co Euclidiano

como

Πµ_b = 4ie

Z d4pE (2π)4

(~p2₊_p2

4 −m2)b

µ

E−2(pE·bE)p

µ

E

(~p2₊_p2

4+m2)2

. (1.36)

Para implementar transla¸c˜ao somente na componente espacial de pµ_E = (p4, ~p) n´os decompomos opµ_E como segue [30]

pµ_E = ˆpµ+p4δµ0, (1.37)

e como uma consequˆencia ˆpµ _{= (0}_{, ~p}_{). Devido a simetria da integral sob rota¸c˜ao espacial,}

n´os podemos usar

ˆ

pµpˆν _→ ~p

2 D(δ

µν

−δµ0δν0). (1.38)

Usando (1.37) e (1.38) podemos escrever

(pE_·bE)pµ_E= ~p

2 Db µ E− ~p2 Db4δ

µ0₊_p2

4b4δµ0. (1.39)

Substituindo (1.39) em (1.36) n´os encontramos que

Πµ_b = Π1bµE+ Π2b4δµ0, (1.40)

com

Π1 = 4ie

Z dp4 2π(µ

2₎3−D

2

Z dD~p (2π)D

"

1

~p2₊_p2

4+m2 − 2

D~p2+ 2m2

(~p2₊_p2

4+m2)2

#

(28)

e

Π2 =−8ie

Z dp4 2π(µ

2₎3−D

2

Z dD~p (2π)D

"

1

~p2₊_p2

4+m2 − 1+D

D ~p

2₊_m2

(~p2₊_p2

4+m2)2

#

, (1.42)

onde temos transformado o espa¸co tridimensional para D-dimensional e introduzimos um parâmetro arbitrário µ que identifica a escala de massa. Agora, ao integrarmos em D dimensões, com aux´ılio das expressões dadas no APÊNDICE A, obtemos

Π1 =−

8ie(µ2₎3−D

2

(4π)D2

Γ

2₋ D 2

Z dp4 2πm

2₍_p2

4 +m2)

D

2−2 (1.43)

e

Π2 =

4ie(µ2₎3−D

2

(4π)D2

Γ

1₋D 2

Z dp4 2π

h

(D₋1)(p2₄+m2)D2−1−(D−2)m2(p2

4+m2)

D

2−2

i

.

(1.44)

Por fim, integrando sobre o momento p4 encontramos

Π1 =−

8ie(µ2₎3−D

2

(4π)D+12

Γ

3−D 2

mD−1, (1.45)

e Π2 = 0. Expandindo (1.45) em torno de D= 3 ficamos com

Π1 =− iem2

π2_ǫ + iem2

2π2 ln m2 µ′2

!

, (1.46)

onde ǫ= 3₋D e µ′2 _{= 4}_π2_µ2_e−γ_.

Portanto, a contribui¸c˜ao (1.40) ´e dada por

Πµ_b = "

−iem

2 π2_ǫ +

iem2

2π2 ln m2 µ′2

!#

bµ_E. (1.47)

Nesse momento, vamos analisar o gráfico com três inser¸cões na Figura 3. Esse gráfico

nos fornece

Πµ_bbb = Tr

Z d4p

(2π)4(−ieγ

µ_γ5₎_S₍_p₎₍

−ib/γ5)S(p)(₋ib/γ5)S(p)(₋ib/γ5)S(p). (1.48)

Substituindo o propagador ficamos com

Πµ_bbb =eTr

Z d4p (2π)4

γµ_γ5₍_p_/₋_m₎_/γ5_b ₍_p_/₋_m₎_/γ5_b ₍_p_/₋_m₎_/γ5_b ₍_p_/₋_m₎

(29)

e ao calcularmos o tra¸co sobre as matrizes de Dirac

Πµ_bbb = 4e

Z d4p (2π)4

4(₋p2₋_m2₎₍_p_·_b₎2_{+ (}_p4 _{+ 6}_p2_m2₊_m4₎_b2

(p2₋_m2₎4 b

µ₊

+ 16e

Z d4p (2π)4

(₋p2₋_m2₎₍_p_·_b₎_b2 _{+ 2(}_p_·_b₎3

(p2₋_m2₎4 p

µ_. _(1.50)

Transformando para o espa¸co Euclidiano,

Πµ_bbb = 4ie

Z d4pE (2π)4

4(p2

E−m2)(pE·bE)2−(pE4 −6p2Em2 +m4)b2E

(p2

E+m2)4

bµ_E

+16ie

Z d4pE (2π)4

(p2

E−m2)(pE·bE)b2E−2(pE·bE)3

(p2

E+m2)4

pµ_E. (1.51)

Seguindo passos semelhantes ao que fizemos para Πµ_b, usando tamb´em a simetria rotacional do integrando que justifica a troca

ˆ

pµ_p_ˆν_p_ˆλ_p_ˆρ _→ ~p4

D(D+ 2)[(δ

µν₋_δµ0_δν0₎₍_δλρ₋_δλ0_δρ0_{) + (}_δµλ₋_δµ0_δλ0₎₍_δνρ₋_δν0_δρ0₎

+(δµρ₋δµ0δρ0)(δλν₋δλ0δν0)], (1.52)

podemos escrever

(pE·bE)2 = ~p2 D(b

2

E−b24) +p24b24, (1.53)

(pE_·bE)3pµE =

3~p4 D(D+ 2)b

µ

Eb2E+

3~p2 D p

2 4−

3~p4 D(D+ 2)

!

b24bµE+p44b34δµ0

+ 3~p

2 D p

2 4−

3~p4 D(D+ 2)

!

b2

Eb4δµ0−

6~p2 D p

2 4−

3~p4 D(D+ 2)

!

b3

4δµ0.(1.54)

Substituindo esses resultados em (1.51) obtemos que

Πµ_bbb = Π3b2Eb

µ

E+ Π4b24b

µ

E+ Π5b2Eb4δµ0+ Π6b34δµ0, (1.55)

onde

Π3 = 16ie

Z dp

4

2π(µ 2₎3−D

2

Z dD~p (2π)D

"

−4mD2~p2 −

6~p4

D(D+2) −2m4

(p2

E+m2)4

+

2~p2

D + 2m2

(pE+m2₎3

− 1

4(p2

E+m2)2

#

, (1.56)

Π4 = Π5 = 16ie

Z dp4 2π(µ

2₎3−D

2

Z dD~p (2π)D

"2D+8

D ~p

2_m2 _{+ 2}_m4 ₊6~p4₍_D₊₃₎ D(D+2)

(p2

E+m2)4

−

D+7

D ~p2+ 3m2

(p2

E+m2)3

+ 1

(p2

E+m2)2

#

(30)

Π6 = 16ie

Z dp4 2π(µ

2₎3−D

2

Z dD~p (2π)D

"

−2~p4₋₆ 2D+5

D(D+2)~p

4₋₂_m4₋₄D+3

D ~p

2_m2

(p2

E+m2)4

+4

D+3

D ~p

2_{+ 4}_m2

(p2

E+m2)3

− ₍_p2 2 E+m2)2

#

. (1.58)

Calculando a integral em D dimens˜oes, novamente usando o APˆENDICE A, ficamos com

Π3 =

8ie(µ2₎3−D

2

3(4π)D2

Γ

3₋ D 2

Z dp4 2πm

2h

4(p2₄+m2)D2−3+ (D−6)m2(p2

4+m2)

D

2−4

i

,

(1.59)

Π4 = Π5 =

8ie(µ2₎3−D

2

3(4π)D2

Γ

3₋ D 2

Z dp4 2πm

2h

(D₋5)(p24+m2)

D

2−3

−(D₋6)m2(p24+m2)

D

2−4

i

, (1.60)

Π6 = −

4ie(µ2₎3−D

2

3(4π)D2

Γ

2₋ D 2

Z dp

4

2π

h

(D₋1)(D₋3)(p2

4+m2)

D

2−2

−2(D₋3)(D₋4)m2(p2₄+m2)D2−3+ (D−4)(D−6)m4(p2

4+m2)

D

2−4

i

. (1.61)

Agora, ao realizarmos a integra¸c˜ao emp4 obtemos

Π3 =

8ie(µ2₎3−D

2

3(4π)D2+1

Γ

5−D

2

(D₋1)mD−3, (1.62)

e

Π4 = Π5 = Π6 = 0. (1.63)

Ao expandirmos (1.62) em torno de D= 3 encontramos,

Π3 = ie

3π2. (1.64)

Assim, a contribui¸c˜ao (1.55) ´e dada por

Πµ_bbb = ie 3π2b

µ

Eb2E. (1.65)

Portanto, a equa¸c˜ao (1.29) pode ser escrita como

Πµ = Πµb + Πµbbb

= "

−im

2_e π2_ǫ +

im2_e

2π2 ln m2 µ′2

! +ieb

2 E

3π2

#

(31)

Dessa maneira, a equa¸c˜ao de gap (1.28) se torna −g 2 e b µ −i " −im 2 π2_ǫ +

im2

2π2 ln m2 µ′2

!

− ib

2

3π2

#

ebµ = 0, (1.67)

onde temos voltado para o espa¸co de Minkowski. Lembrando que G = e2_/g2_{, podemos}

reescrever essa ´ultima equa¸c˜ao como

"

−_G1 − m

2 π2_ǫ +

m2

2π2 ln m2 µ′2

!

− b

2

3π2

#

ebµ = 0. (1.68)

Introduzindo a constante de acoplamento renormalizada,

1

GR

= 1

G + m2

π2_ǫ, (1.69)

a equa¸c˜ao de gap que iremos analisar fica

"

−_G1

R

+ m

2

2π2 ln m2 µ′2

!

− b

2

3π2

#

bµ= 0. (1.70)

Assim, nós observamos que uma solu¸cão não-trivial é

b2 =₋3π2

" 1

GR − m2

2π2 ln m2 µ′2

!#

. (1.71)

Dessa equa¸cão notamos que um m´ınimo não-trivial, para o caso em que bµ é do

tipo-tempo6 _{´e poss´ıvel somente se}

1

GR < m2

2π2 ln m2 µ′2

!

=_⇒GR > 2π 2 m2_lnm2

µ′2

, (1.72)

e se bµ ´e do tipo-espa¸co7

1

GR > m2

2π2 ln m2 µ′2

!

=_⇒GR < 2π 2 m2_lnm2

µ′2

. (1.73)

Portanto, para esse modelo de quatro-f´ermions quadridimensional obtivemos que o potencial tem um m´ınimo diferente de zero, dado pela equa¸c˜ao (1.71), ou seja, um valor

esperado no vácuo não nulo parab2_{, como consequência temos que a invariância de Lorentz}

´e quebrada. Essa an´alise foi desenvolvida nos trabalhos [31, 135].

6

Um vetor ser do tipo-tempo implica que bµbνgµν >0.

7

(32)

1.5 Restaura¸c˜ao da simetria de Lorentz em temperatura finita 20

1.5 Restaura¸

c˜

ao da simetria de Lorentz em

tempera-tura finita

Nesta se¸cão iremos estudar o mesmo modelo que estudamos na se¸cão anterior, quatro-férmions quadridimensional, porém, iremos estudar no contexto de temperatura finita.

Nosso objetivo é investigar se há alguma possibilidade para que as simetrias de Lorentz, que foram quebradas no caso de temperatura zero (se¸cão anterior), sejam restauradas no limite de altas temperaturas. Para tal estudo, iremos considerar que o nosso sistema esteja em equil´ıbrio térmico com uma dada temperatura T. Usaremos o formalismo de

Matsubara, que consiste em tomarmos

p4 =

n+ 1 2

2πT, (1.74)

e na seguinte mudan¸ca

Z dp4 2π =T

X

n

. (1.75)

Agora, devemos fazer tais substitui¸cões nas equa¸cões (1.43), (1.44), (1.59), (1.60) e (1.61). Analisaremos essas equa¸cões separadamente. Iniciaremos com (1.43) que se torna

Π1 =−

8ie(µ2₎3−D

2

(4π)D2

Γ

2₋ D 2

TX

n

m2(p2₄+m2)D2−2. (1.76)

Para calcularmos esse somatório usaremos uma representa¸cão explicita sobre as frequências de Matsubara dada por [30, 33]

X

n

[(n+b)2₊_a2_]−λ

=

√

πΓ(λ₋1/2)

Γ(λ)(a2₎λ−1/2 + 4 sin(πλ)fλ(a, b), (1.77)

onde

fλ(a, b) =

Z ∞

|a|

dz

(z2₋_a2₎λRe

1

e2π(z+ib)₋₁

!

, (1.78)

que é válida para λ <1 e possui pólos em λ = 1₂,₋1₂,₋3₂, . . .. Usando (1.74), a equa¸cão (1.76) pode ser reescrita como

Π1 =−

8ie(µ2₎3−D

2

(4π)D2

Γ

2₋ D 2 m 2πξ ! ξ m

!4−D

m2X

n

"

n+1 2

2 +ξ2

#2−D₂

, (1.79)

comξ= βm₂_π, ondeβ = _T1. Se tomamosD= 3 em nossa ´ultima equa¸c˜ao, podemos ver que

λ <1, mas em λ = 1

(33)

que

Π1 =

"

−im

2 π2_ǫ +

im2

2π2 ln m2 µ′2

!

+im2_F I(ξ)

#

e, (1.80)

onde

FI(ξ) =

Z ∞

|ξ| dz

1₋tanh(πz)

π2√_z2₋_ξ2 . (1.81)

O comportamento dessa fun¸c˜ao ´e mostrado na Figura 4.

Figura 4: Comportamento da fun¸c˜ao FI(ξ)

Observamos que o comportamento assintótico da fun¸cãoFI(ξ) em altas temperaturas é8 _FI₍_ξ_→₀₎_≈₁_/_2.

Substituindo (1.74) e (1.75) na equa¸c˜ao (1.44) obtemos que

Π2 =

4ie(µ2₎3−D

2

(4π)D2

Γ

1₋ D 2

(

(D₋1) m 2πξ

!

ξ2 m2

!1−D₂ X

n

"

n+1 2

2 +ξ2

#1−D₂

− (D₋2)m2 m

2πξ

!

ξ2 m2

!2−D₂ X

n

"

n+ 1 2

2 +ξ2

#2−D₂ )

. (1.82)

Comoλ= 1₋ D

2 e λ= 2−

D

2 satisfazem a condi¸c˜ao λ <1 para D→3, esses somat´orios

podem ser resolvidos usando (1.77) e nos fornecem

Π2 =ieT2FII(ξ), (1.83)

com

FII(ξ) = ₋ Z ∞

|ξ| dz

4(ξ2₋₂_z2_)[tanh(_πz₎₋_1]

√

z2₋_ξ2 . (1.84)

No limite de altas temperaturas a fun¸c˜aoFII(ξ) tem o comportamento mostrado na Figura

8

(34)

5. Neste limite, T _{→ ∞}, a fun¸c˜ao FII(ξ _→0) =₋1/3.

Figura 5: Comportamento da fun¸c˜ao FII(ξ)

Com esses resultados, a equa¸c˜ao (1.40) se torna

Πµ_b = "

−im

2 π2_ǫ +

im2

2π2 ln m2 µ′2

!

+im2FI(ξ) #

ebµ_E+ieT2FII(ξ)b4δµ0. (1.85)

Observamos que no limite T _→0 recuperamos o resultado obtido em (1.40).

Nosso próximo passo é verificar as contribui¸cões com três inser¸cões ao propagador no

contexto de temperatura finita. Fazendo as substitui¸c˜oes (1.74) e (1.75) na equa¸c˜ao (1.59) obtemos

Π3 =

8ie(µ2₎3−D

2

3(4π)D2

Γ

3₋ D 2 m2 ( 4 m 2πξ ! ξ2 m2

!3−D₂ X

n

"

n+ 1 2

2 +ξ2

#3−D₂

+ (D₋6)m2 m

2πξ

!

ξ2 m2

!4−D₂ X

n

"

n+ 1 2

2 +ξ2

#4−D₂ )

. (1.86)

Note que, para D = 3 temos λ = 3

2 e λ = 5

2, ou seja, λ > 1. Assim, precisaremos usar

uma rela¸c˜ao de recorrˆencia para a integral fλ(a, b) da seguinte forma

fλ(a, b) =−

1 2a2

2λ₋3

λ₋1fλ−1(a, b)− 1 4a2

1

(λ₋2)(λ₋1)

∂2

∂b2fλ−2(a, b). (1.87)

Usando essa rela¸cão para λ = 3₂, voltamos a condi¸cão em que o somatório sobre as frequências de Matsubara é válido. Já quando olhamos para o caso em que λ= 5₂, não é suficiente usarmos essa rela¸cão apenas uma vez, pois ainda ter´ıamosλ >1. Para resolver esse problema podemos usar esta rela¸cão de recorrência duas vezes e assim obtemosλ= 1₂ eλ=₋1₂ como exigido pela equa¸cão (1.77). Procedendo dessa maneira encontramos que

Π3 = ie

(35)

onde

FIII(ξ) = Z ∞

|ξ| dz

(3ξ2₋₂_z2_{) sech}2

(πz) tanh(πz)

3√z2₋_ξ2 . (1.89)

O comportamento da fun¸c˜aoFIII(ξ) ´e exibido na Figura6. No limite de altas temperaturas

FIII(ξ_→0) = ₋1/3π2_.

Figura 6: Comportamento da fun¸c˜ao FIII(ξ)

Agora, vamos substituir (1.74) e (1.75) na equa¸c˜ao (1.60), fazendo isso ficamos com

Π4 = Π5 =

8ie(µ2₎3−D

2

3(4π)D2

Γ

3₋D 2

m2

(

(D₋5) m 2πξ

!

ξ2 m2

!3−D₂ X

n

"

n+1 2

2 +ξ2

#3−D₂

− (D₋6)m2 m

2πξ

!

ξ2 m2

!4−D₂ X

n

"

n+1 2

2 +ξ2

#4−D₂ )

. (1.90)

Procedendo de maneira análoga ao que fizemos em (1.86), usando as rela¸cões de re-corrência encontramos que

Π4 = Π5 =ieFIV(ξ), (1.91)

com

FIV(ξ) = −

Z ∞

|ξ| dz

ξ2_sech2₍_πz_{) tanh(}_πz₎

3√z2₋_ξ2 . (1.92)

Na Figura7 temos o comportamento da fun¸c˜ao FIV(ξ). Nesta figura observamos que no limite de altas temperaturas FIV(ξ_→0) = 0.

Por fim, vamos usar o formalismo de Matsubara na equa¸c˜ao (1.61), e como resultado essa equa¸c˜ao se torna

Π6 = −

4ie(µ2₎3−D

2

3(4π)D2

Γ

2₋ D 2

(

(D₋1)(D₋3) m 2πξ

!

ξ2 m2

!2−D₂ X

n

"

n+1 2

2 +ξ2

(36)

Figura 7: Comportamento da fun¸c˜ao FIV(ξ)

− 2(D₋3)(D₋4)m2 m

2πξ

!

ξ2 m2

!3−D₂ X

n

"

n+ 1 2

2 +ξ2

#3−D₂

+ (D₋4)(D₋6)m4 m

2πξ

!

ξ2 m2

!4−D₂ X

n

"

n+ 1 2

2 +ξ2

#4−D₂ )

. (1.93)

Procedendo como fizemos para resolver os somat´orios em (1.90) encontramos que

Π6 =ieFVI(ξ), (1.94)

sendo

FVI(ξ) =

Z ∞

|ξ| dz

(2z2₋_ξ2_{) sech}2₍_πz_{) tanh(}_πz₎

3√z2 ₋_ξ2 , (1.95)

com seu comportamento mostrado na Figura 8. No limite de altas temperaturas temos queFVI(ξ _→0) = ₃_π12.

Usando as equa¸c˜oes (1.88), (1.91) e (1.94) podemos reescrever a equa¸c˜ao (1.55) no contexto de temperatura finita como

Πµ_bbb = "

ib2E

3π2 +ib 2

EFIII(ξ) +ib24FIV(ξ)

#

ebµE+

h

ib2_EFIV(ξ) +ib2₄FVI(ξ)ieb4δµ0. (1.96)

Com as equa¸c˜oes (1.85) e (1.96) podemos escrever

Πµ =

"

−im

2 π2_ǫ +

im2

2π2 ln m2 µ′2

!

+im2FI(ξ) + ib2

E

3π2 +ib 2

EFIII(ξ) +ib24FIV(ξ)

#

(37)

Figura 8: Comportamento da fun¸c˜ao FVI(ξ)

+ hib2_EFIV(ξ) +ib2₄FVI(ξ) +iT2FII(ξ)ieb4δµ0, (1.97)

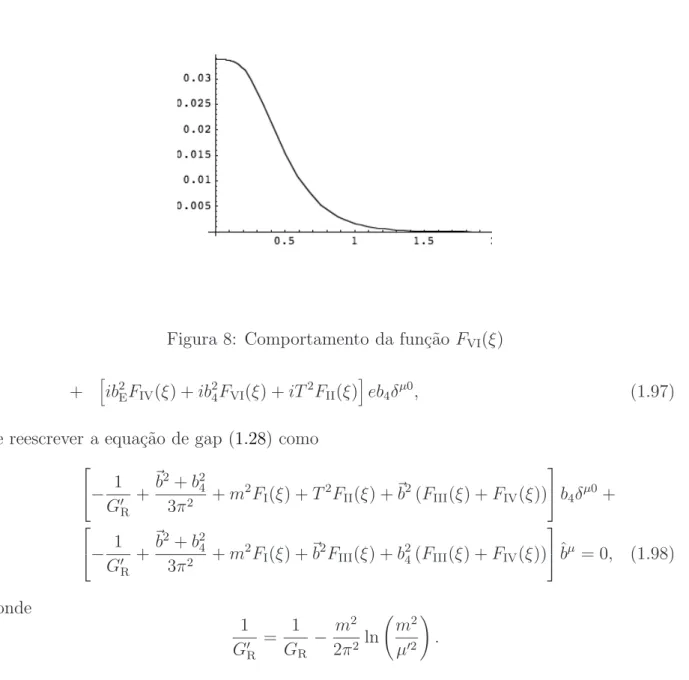
e reescrever a equa¸c˜ao de gap (1.28) como



− 1

G′

R

+~b

2₊_b2 4

3π2 +m

2_FI₍_ξ_{) +}_T2_FII₍_ξ_{) +}_~b2₍_FIII₍_ξ_{) +}_FIV₍_ξ₎₎



b4δµ0+



− 1

G′

R

+~b

2₊_b2 4

3π2 +m

2_FI₍_ξ_{) +}_~b2_FIII₍_ξ_{) +}_b2

4(FIII(ξ) +FIV(ξ))



ˆbµ = 0, (1.98)

onde

1

G′

R

= 1

GR − m2

2π2 ln m2 µ′2

!

.

Analisando essa equa¸c˜ao, encontramos as seguintes possibilidades:

1. b4 =bi = 0 é uma solu¸cão trivial onde as simetrias de Lorentz não são quebradas.

2. b4 ₆= 0 e bi 6= 0. Neste caso b4 e/ou bi cresce quadraticamente com a temperatura,

ent˜ao, a quebra das simetrias de Lorentz cresce.

3. b4 ₆= 0 e bi = 0. Neste caso, a equa¸c˜ao de gap se reduz para

−b2₄ =b2₀ = 3π2 1

|G′

R| −

T2_|FII(ξ)_|+m2FI(ξ) !

, (1.99)

onde n´os temos usadoG′

R =−|G′R|, porquebµ´e tipo-tempo e ambasFI(ξ) e|FII(ξ)|

crescem monotonamente com T. Em particular, com T _{→ ∞}, FI(ξ) → 1/2 e

(38)

1.6 Equa¸c˜ao de Friedmann com quebra espontˆanea da simetria de Lorentz 26

cr´ıtica, a condi¸cão b4 = 0 é satisfeita e as simetrias de Lorentz serão restauradas.

4. b4 = 0 andbi 6= 0. Neste caso a equa¸c˜ao de gap ´e

− _G1_′

R

+m2FI(ξ) +~b2

1

3π2 +FIII(ξ)

= 0. (1.100)

Ent˜ao, como ₃_π12+FIII(ξ)≥0 eFI(ξ)≤1/2 existir´a uma temperatura cr´ıtica em que

as simetrias de Lorentz ser˜ao restauradas somente se 1

m2_G′

R ≤1/2. Por outro lado,

para 1

m2_G′

R >1/2, a viola¸c˜ao das simetrias de Lorentz cresce com a temperatura.

Portanto, nosso objetivo principal foi mostrar que o modelo de quatro-f´ermions

quadri-dimensional apresenta quebra espontˆanea das simetrias de Lorentz e CPT em temperatura zero, e no contexto de temperatura finita observamos que para b4 ₆= 0 e bi = 0, existe

uma temperatura cr´ıtica na qual as simetrias de Lorentz e CPT podem ser restauradas. E que por outro lado, para b4 = 0, bi 6= 0, e _m21_G′

R > 1/2, as simetrias de Lorentz s˜ao

quebradas pelo aparecimento de um vetor tipo-espa¸co bµ _{e n˜ao ocorre restaura¸c˜ao para}

nenhuma temperatura.

1.6 Equa¸

c˜

ao de Friedmann com quebra espontˆ

anea

da simetria de Lorentz

Nesta se¸cão iremos estudar quais os efeitos que a viola¸cão das simetrias de Lorentz pode trazer para o cenário cosmológico. O interesse em quebra das simetrias de Lorentz naturalmente inspira a idéia de estudar os impactos em cosmologia, onde o problema

chave hoje é entender o fenômeno que está causando a expansão acelerado do universo. Algumas estimativas experimentais preliminares da quebra das simetrias de Lorentz em escala cosmológica são apresentadas em [34], alguns tópicos relevantes em viola¸cão das simetrias de Lorentz em cosmologia podem ser encontrados em [35].

´

E natural esperar que a presen¸ca da quebra das simetrias de Lorentz pode modificar o cenário cosmológico. Um caminho para se estudar a viola¸cão de tais simetrias em

cosmologia é através da quebra espontânea dessas simetrias. Neste estudo usaremos o modelo bumblebee em um espa¸co tempo de cinco dimensões [36, 37]. A importância de se estudar esse modelo em cinco dimensões surge a partir do grande interesse no conceito

de dimens˜oes extras motivado por teorias de cordas e branas [38].

N´os aplicaremos esse mecanismo para implementar a modifica¸c˜ao causada pela

(39)

Friedmann-Robertson-Walker, e assim estudar seus impactos. Nós mostraremos que a dinâmica de expansão do universo devido à presen¸ca da quebra das simetrias de Lorentz é altamente não trivial.

Agora vamos descrever a teoria. Um teoria geral em cinco dimens˜oes que descreve o modelo bumblebee pode ser dada por

S = Z

d5x√₋g(_LB+LG+LM), (1.101)

onde _LG é o termo gravitacional de Einstein-Hilbert, LM é o termo de matéria e LB é o

termo tipo-bumblebee:

LB =−

1 4BµνB

µν

−V(BµBµ±b2), (1.102)

com o tensor Bµν definido como Bµν = ∂µBν −∂νBµ. O V(BµBµ± b2) ´e o potencial

bumblebee que escolhemos como

V = 1

2κ(BµB

µ

±b2)2 = 1 2κ(Bµg

µν_B

ν ±b2)2. (1.103)

Assim, a a¸c˜ao (1.101) toma a forma

S = Z

d5_x√₋_g

" 1 16πGR−

1 4BµνB

µν₋ 1

2κ(BµB

µ_±_b2₎2₊_L

M

#

. (1.104)

Variando a a¸cão (1.104) com respeito à métrica, obtemos as equa¸cões de Einstein:

Gµν = 8πGTµν, (1.105)

onde Gµν ´e o tensor de Einstein e Tµν ´e o tensor energia momento composto por dois

termos

Tµν =Tµν(M)+Tµν(B), (1.106)

comT(M)

µν sendo o tensor energia momento associado ao setor de mat´eria eTµν(B) ´e o tensor

energia momento associado ao campo bumblebee,

T_µν(B) =T_µν(B)K +T_µν(B)V, (1.107)

comTµν(B)K gerado pela parte cin´etica da a¸c˜ao do campo bumblebee eTµν(B)V pela parte do

potencial. Usando a defini¸c˜ao do tensor energia momento

Tµν =−

2

√ −g

δ_LB

(40)

n´os obtemos

T_µν(B)k =BµαBνα−

1

4gµνBαβB

αβ _(1.109)

e

T_µν(B)V =₋V gµν+ 2V′BµBν, (1.110)

ondeV′ ₌ δV

δX, comX =Bµg µν_B

ν±b2. Ent˜ao, podemos escrever o tensor energia momento

total para o campo bumblebee como

T_µν(B)=BµαBνα−

1

4gµνBαβB

αβ

−V gµν+ 2V′BµBν. (1.111)

A mat´eria aqui ´e considerada como sendo um fluido perfeito com densidade de energia

ρe press˜ao p, cujo tensor energia momento ´e dado por

T_µν(M) = (ρ+p)UµUν +p gµν, (1.112)

onde Uµ = (1,0,0,0,0) ´e a velocidade do fluido.

Seguindo o princ´ıpio cosmológico, nós assumimos que o universo é homogêneo e isotrópico, com o elemento de linha de Friedmann-Robertson-walker (FRW) em cinco

dimens˜oes dado por [39]

ds2 = gµνdxµdxν

= ₋dt2+a2(t) "

dr2

1₋kr2 +r

2₍_dθ2_{+ sin}2_θdφ2₎

#

+ǫΦ2(t)dy2, (1.113)

onde k =₋1,0,1 é o parâmetro de curvatura para um universo aberto, plano e fechado, respectivamente, y é a dimensão extra e o fator ǫ é₋1 ou +1 para uma dimensão extra tipo-tempo ou tipo-espa¸co, respectivamente. Em nossa análise nós sugerimos que a di-mensão extra seja tipo-espa¸co, então ǫ = +1. A assinatura para o espa¸co-tempo usual em quatro dimensões é escolhida como sendo (₋+ ++), a(t) é o fator de escala do usual espa¸co tri-dimensional e Φ(t) é o fator de escala da dimensão extra.

Agora, vamos calcular as componentes do tensor energia momento correspondentes ao campo bumblebee Bµ. De maneira similar a [40], n´os escolhemos Bµ na dire¸c˜ao da

dimens˜ao extra, assim, ficamos com

B0 = 0, B1 = 0, B2 = 0, B3 = 0, B4 =B(t). (1.114)

No v´acuo o campo bumblebee deve satisfazer a condi¸c˜aogµν_B

(41)

para fornecer o valor m´ınimo para a energia [40]. Entretanto, no caso geral o campo bumblebee pode ser diferente. As componentes n˜ao nulas para o tensor energia momento do campo bumblebee s˜ao

T00(B) =

˙

B2

2Φ2 +

1 2κ

B2

Φ2 −b 2

!2

, (1.115)

T11(B) =

a2₍_t₎

2(1₋kr2₎

" ˙

B2

Φ2 −κ B2

Φ2 −b 2

!2#

, (1.116)

T₂₂(B) = a

2₍_t₎_r2

2 " ˙

B2

Φ2 −κ B2

Φ2 −b 2

!2#

, (1.117)

T₃₃(B) = a

2₍_t₎_r2_sin2_θ

2

" ˙

B2

Φ2 −κ B2

Φ2 −b 2

!2#

, (1.118)

T44(B) = −

1 2B˙

2₊ 3

2κ

B4

Φ2 −κB 2_b2

− 1₂κb4Φ2. (1.119)

Voltando para as equa¸c˜oes de Einstein, e tomando a componente com µ = ν = 0 n´os temos

G00= 8π(T₀₀M +T₀₀B), (1.120)

onde TM

00 =ρ e

G00= 3 a˙

2 a2 +

˙

a˙Φ aΦ

! +3 k

a2. (1.121)

Assim, a correspondente equa¸c˜ao de Einstein toma a forma

˙

a a

!2 +k

a2 +

˙

a˙Φ aΦ =

8π

3 ρ+ 4π

3 " ˙

B2

Φ2 +κ B2

Φ2 −b 2

!2#

. (1.122)

Este é o análogo em cinco dimensões da equa¸cão de Friedmann envolvendo quebra

es-pontânea das simetrias de Lorentz. Podemos verificar que no caso b = 0 eB = 0, isto é, sem viola¸cão de Lorentz, essa equa¸cão reproduz os resultados conhecidos [41,42].

Agora, vamos resolver a equa¸cão de Friedmann com quebra espontânea das simetrias de Lorentz (1.122). Vamos considerar o caso Φ(t) =const, ou seja, dimensão extra estática [42, 43]. Nesta situa¸cão o fator de escala da dimensão extra não muda, e a evolu¸cão do universo é dada pela cosmologia padrão em quatro dimensões. No entanto, os efeitos da

viola¸c˜ao de Lorentz persistem. A equa¸c˜ao (1.122) se torna

˙

a a

!2 +k

a2 =

8π

3 ρ+ 4π

3 " ˙

B2

Φ2 +κ B2

Φ2 −b 2

!2#

. (1.123)

(42)

campo B. Outra equa¸cão que relaciona essas variáveis é a lei de conserva¸cão de energia que pode ser encontrada a partir de

∇µTµν = 0. (1.124)

Para a componenteν = 0, usando as propriedades das derivadas covariantes [44], obtemos

∇µTµ0 =∂µTµ0+ ΓµµλTλ0+ Γ0µλTµλ = 0. (1.125)

Os s´ımbolos de Christoffel9 _{relevantes no caso geral, ou seja, incluindo o caso Φ n˜ao}

constante, s˜ao

Γ0₀₀ = 0,

Γ1₁₀ = Γ2₂₀ = Γ3₃₀ = a˙

a,

Γ4₄₀ = ˙Φ Φ, Γ0₁₁ = aa˙

1₋kr2,

Γ0₂₂ = aar˙ 2,

Γ033 = aar˙ 2sin2θ,

Γ0₄₄ = Φ ˙Φ. (1.126)

Assim, usando as componentes do tensor energia-momento para o campo bumblebee e os

s´ımbolos de Christoffel em (1.125), nós obtemos a equa¸cão de conserva¸cão de energia em cinco dimensões com quebra espontânea das simetrias de Lorentz

˙

ρ+ 3a˙

a

"

ρ+p+B˙

2

Φ2

# +1

2∂0 "

κ B 2

Φ2 −b 2

!2 +B˙

2

Φ2

# +˙Φ

Φ "

ρ+p+ 2κB 4

Φ4 −2κ B2_b2

Φ2

# = 0.

(1.127)

Notamos que para Φ(t) = const e B = 0, temos a equa¸c˜ao de conserva¸c˜ao de energia usual, ˙ρ+ 3a_a˙(ρ+p) = 0.

Nós podemos adicionar às equa¸cões (1.123, 1.127) a equa¸cão de movimento para o

campo B dada por,

¨

BΦ2+ 2κB(B2₋b2Φ2) + 3a˙

aB˙Φ

2 _{= 0}_. _(1.128)

O último termo nessa equa¸cão é gerado pela derivada temporal de √₋g. Aqui nós já impomos a condi¸cão de dimensão extra estática, Φ(t) = const. Então, vamos resolver

9