Modelos epidemiológicos em redes

(1)

ANNA PATRICIA PACHAS MANRIQUE

MODELOS EPIDEMIOLÓGICOS EM REDES

Brasil

2016, Julho

(2)

(3)

ANNA PATRICIA PACHAS MANRIQUE

MODELOS EPIDEMIOLÓGICOS EM REDES

Dissertação apresentada ao Departamento de Matematica Aplicada da Fundação Getulio Vargas como requisito final para a obtencão do título de Mestre em Matemática Aplicada

Fundação Getulio Vargas – FGV Matematica Aplicada Programa de Pós-Graduação

Orientador: Moacyr Alvim Horta

Brasil

2016, Julho

(4)

Ficha catalográfica elaborada pela Biblioteca Mario Henrique Simonsen/FGV

Pachas Manrique, Anna Patricia

Modelos epidemiológicos em redes / Anna Patricia Pachas Manrique. – 2016. 70 f.

Dissertação (mestrado) – Fundação Getulio Vargas, Escola de Matemática Aplicada.

Orientador: Moacyr Alvim Horta. Inclui bibliografia.

1. Epidemiologia – Modelos matemáticos. 2. Teoria dos grafos. 3. Redes sociais. I. Silva, Moacyr Alvim Horta Barbosa da. II. Fundação Getulio Vargas. Escola de Matemática Aplicada. III. Título.

(5)

(6)

(7)

Agradecimentos

A Deus, por me dar forças e vontade de sempre aprender algo novo A Emap-FGV , pela oportunidade

Agradeço a meu orientador , pela tranquilidade que transmite e por ter me dado muitas dicas em todo momento da dissertação

E um agradecimento imenso a minha filha , por ela existir.

(8)

(9)

O ser humano vivencia a si mesmo, seus pensamentos como algo separado do resto do universo - numa espécie de ilusão de ótica de sua consciência. E essa ilusão é uma espécie de prisão que nos restringe a nossos desejos pessoais, conceitos e ao afeto por pessoas mais próximas. Nossa principal tarefa é a de nos livrarmos dessa prisão, ampliando o nosso círculo de compaixão, para que ele abranja todos os seres vivos e toda a natureza em sua beleza. Ninguém conseguirá alcançar completamente esse objetivo, mas lutar pela sua realização já é por si só parte de nossa liberação e o alicerce de nossa segurança interior. (Albert Einstein)

(10)

(11)

Resumo

A velocidade e a abrangência a nivel mundial com que os agentes patogénicos tem se disseminado nos últimos anos tem chamado a atenção para a importância da estrutura da rede social de contato . De fato, a topologia das redes na qual os membros da sociedade interagem têm influenciado na dinâmica das epidemias.

Estudos têm demostrado que os agentes patogénicos ao se disiparem em redes livres de escala tem efeitos diferentes se comparado quando difundidos em redes aleatorias, como nos modelos clássicos. Nestes existiam limiar de epidemia , podendo de alguma forma as entidades de saúde ter um controle sobre a dissipação das enfermidades , aplicando certas medidas como as vacinas por exemplo. Já nos modelos nos quais são consideradas as redes , especificamente a rede livre de escala ,este limiar desaparece. Desta forma, o limiar de epidemia ao depender da topologia se faz necessario incluir esta estrutura dentro dos modelos epidemiológicos. Devido a importancia destas redes , redes aleatórias e principalmente redes livres de escala foram implementadas junto a modelos de propagação de epidemias para verificar o limiar de epidemia e o tempo caracteristico , verificando que o limiar de epidemia desaparece.

Palavras-chaves: Epidemiologia, modelo SI, modelo SIS, modelo SIR ,redes livre

(12)

(13)

Abstract

The speed and comprehensiveness global level with the pathogen has spread in recent years has drawn attention to the importance of the contact’s social network structure. In fact, the topology of the networks in which members of society interact has influenced the dynamics of epidemics.

Studies have shown that pathogens when disiparem in scale-free networks have different effects when compared broadcast in random networks, such as the classic models.

In these there were epidemic threshold, may somehow the health ministry have a control on the dissipation of diseases by applying certain measures such as vaccines. Already in models in which are considered the networks, specifically the free network scale, the threshold disappears. Thus, the epidemic threshold depends on the topology is required to include within this structure models

Because of the importance of these networks, random networks and scale-free have been implemented along the epidemics of propagation models to check the epidemic threshold and the characteristic time, noting that the epidemic threshold disappears

Key-words: Epidemiology, SI model, model SIS, SIR model, scale-free networks,

(14)

(15)

Lista de ilustrações

Figura 1 – redes. . . 23

Figura 2 – Pontes de Konisgberg. . . 24

Figura 3 – Distribuição de Grau. . . 25

Figura 4 – Matriz de Adjacência. . . 26

Figura 5 – Distribuicão Binomial e Poisson. . . 28

Figura 6 – Redes aleatorias e Redes livres de escala . . . 31

Figura 7 – Modelos Epidemiológicos. . . 34

Figura 8 – Modelo SI. . . 37

Figura 9 – Modelo SIS. . . 38

Figura 10 – Modelo SIR. . . 39

Figura 11 – Bloco de Aproximaçao de Grau. . . 42

Figura 12 – Modelo SI com diferentes k . . . 44

Figura 13 – Mediana e Quartis de Redes Aleatórias e Livres de Escala (𝜆 > 𝜆𝑐). . . 50

Figura 14 – Comportamento do Agente Patogênico em Redes Aleatórias e Livre de Escala.(𝜆 > 𝜆𝑐). . . 50

Figura 15 – Mediana e Quartis de Redes Aleatórias e Livres de Escala . . . 50

Figura 16 – Comportamento do Agente Patogênico em Redes Aleatórias e Livre de Escala. . . 51

Figura 17 – Redes formadas com series predefinidas. . . 59

Figura 18 – Função Acumulada da Lei de Potencia. . . 60

(16)

(17)

Lista de tabelas

Tabela 1 – Doenças com suas respectivas formas de transmissão e R0 . . . 39 Tabela 2 – modelo SIS (𝜆 > 𝜆𝑐). . . 49

(18)

(19)

Lista de abreviaturas e siglas

N Número de Nós L Número de Arestas K𝑖 Grau do Nó i P𝑘 Distribuição de Grau n Momento de ordem n

<K> primeiro momento ou grau medio <K2 _> _{segundo momento}

S Total de Indivíduo Suscetíveis I Total de Indivíduo Infetados R Total de Indivíduo Recuperados s Proporção de Indivíduos suscetíveis i Proporção de Indivíduos Infetados

𝛽 Probabilidade de transmissão da doença

𝜇 Probabilidade de cura do infetado

𝜏 Tempo característico

SI Modelo S-I

SIS Modelo S-I-S

SIR Modelo S-I-R

Θ𝑘 Função Densidade

𝜆 Limiar de Epidemia

(20)

(21)

Sumário

1 Introdução. . . 21 1.1 Relevância . . . 21 1.2 Motivação . . . 21 1.3 Objetivo . . . 21 1.4 Estrutura do Texto . . . 22 2 Redes . . . 23 2.1 Breve Historia . . . 23 2.2 Conceitos Básicos . . . 24 2.2.1 Número de nodos (N) . . . 24 2.2.2 Núumero de Arestas(L) . . . 24 2.2.3 Grau do nó i(k𝑖) . . . 25 2.2.4 Distribuição de graus(P𝑘) . . . 25 2.2.5 O momento de ordem n . . . 25 2.2.6 matriz de adjacência . . . 26 2.3 Tipos de Redes . . . 26 2.3.1 Redes Aleatorias . . . 27

2.3.2 Redes Livre de Escala . . . 29

3 Modelos Epidemiológicos . . . 33 3.1 Hipótese . . . 33 3.2 Conceitos importantes . . . 34 3.2.1 Tempo caraterístico (𝜏 ). . . 34 3.2.2 Numero Basico (R0) . . . 34 3.2.3 Taxa de Transmissibilidade . . . 35 3.2.4 Taxa de Propagação (𝜆) . . . 35 3.2.5 limiar de epidemia (𝜆𝑐) . . . 35 3.3 Modelos . . . 35 3.3.1 Modelo SI . . . 35 3.3.2 Modelo SIS . . . 36 3.3.2.1 estado endemico ( 𝜇 < 𝛽 < 𝑘 >) . . . 37

3.3.2.2 estado livre de doença( 𝜇 > 𝛽 < 𝑘 >) . . . 38

3.3.3 Modelo SIR . . . 39

4 Modelos Epidemiológicos em Redes . . . 41

(22)

4.2 Conceitos Novos . . . 41 4.2.1 Bloco de Aproximação de Grau . . . 41 4.2.2 Função Densidade . . . 42 4.3 Modelos . . . 43 4.3.1 SI em redes . . . 43 4.3.2 SIS em redes , e o desaparecimiento do limiar de epidemia . . . 45 4.4 Aplicações e Discussões . . . 48 5 Testes e Resultados . . . 49 5.1 Teste 1 . . . 49 5.2 Teste 2 . . . 50 Conclusão . . . 53 Referências . . . 55

Apêndices

57

APÊNDICE A Criação de uma rede com distribuiçao livre de escala . . . 59

APÊNDICE B Pseudocodigo de criação de uma rede livre de escala e o

mo-delo SIS . . . 63

APÊNDICE C Codigo Fonte em Matlab de uma rede livre de escala e o

(23)

21

1 Introdução

1.1 Relevância

Ao estudar as doenças infecciosas , verifica-se que algumas delas devastaram po-pulações em diversas épocas da historia da humanidade, desde a antiguidade até os días atuais.Elas não só ocasionam perdas humanas mas também ocasionam grande prejuízo econômico para as nações .Sendo muitas vezes consideradas como causadoras de morte muito maiores do que as guerras (ANDERSON; MAY, )

Ao relatar as consequências das epidemias desde a antiguidade até a atualidade , que ocasionaram danos enormes na população, desde um número elevado de mortes até grande prejuízo económico , observa-se a relevância do estudo das doenças epidêmicas. Portanto, os governos e a população em geral precisam tomar medidas adequadas, sendo assim, imprescindível mais estudos referentes ao assunto.

1.2 Motivação

Em 1770 , com Bernoulli surge o estudo da epidemiología matemática ,e desde então tem crescido o interesse em modelar doenças infecciosas. Ter maior compreensão do comportamento dinâmico das epidemias é o primeiro passo para controlá-lo. Modelos matemáticos da dissipação de doenças em diferentes tipos de redes da sociedades é um fator importante na modelagem de epidemia e tem sido objeto de estudo de diversos autores(SANTORRAS; VESPIGNANI,2001) (BARABASI, 1999)

Ao estudar os modelos epidemiológicos e conhecer as redes sociais da população , pode-se saber o tempo caraterístico da doença.Dessa forma pode-se adotar campanhas de vacinação eficientes , levando em conta o tempo certo para evitar a disseminação da doença em questão.

Assim , uma motivação dos estudos de redes e de modelos epidemiológicos em redes sociais de contato é em certa forma uma ajuda para os governos para impedir a disseminação da doença em grande escala e assim as medidas governamentais serem mais eficazes

1.3 Objetivo

O objetivo deste trabalho é fazer um estudo sobre os modelos epidemiológicos básicos SI,SIS, SIR e entender pontos como o tempo caraterístico, limiar epidemiológico,

(24)

22 Capítulo 1. Introdução

Número básico. Além disso, fazer um estudo sobre alguns tipos de redes , como redes aleatórias e livres de escala. E verificar se existe diferença na difusão das doenças nos modelos epidemiológicos em redes diferentes e se o limiar de epidemia é igual em todas as redes. Será feita uma implementação que simule a disseminação das doenças em redes aleatórias e livres de escala e verificaçao do limiar de epidemia.

1.4 Estrutura do Texto

A estrutura deste trabalho esta dividido em :

Capıtulo 2, será referente às redes , fazendo uma breve Historia, abordando os conceitos básicos e alguns tipos de Redes ,

Capítulo 3,será apresentado algums modelos epidemiológicos

Capıtulo 4, será abordado os modelos epidemiológicos em Redes ,se tratará novos conceitos e como esses modelos mudam quando se considera estes novos conceitos

Capítulo 5, serão feito os testes e a verificaçao de que o limiar desaparece Capítulo 6, Se fará a conclusão

No Apéndice A abordaremos como é criado uma rede com distribuição livre de escala , descrevendo o modelo de configuração e a geração de uma sequencia de números com grau de distribuição livre de escala

No apéndice B ,o pseudocódigo de criação de uma rede livre de escala e o modelo SIS

No apéndice C o código Fonte em Matlab de uma rede livre de escala e o modelo SIR

(25)

23

2 Redes

Uma rede ou grafo é formada por um conjunto de pontos chamados vertices ou nós com conexões entre eles , chamadas links ou arestas. (NEWMAN, 2003).Póde-se observar as redes no cotidiano, representando diversas estruturas em diversos níveis , desde níveis moleculares , como na molécula de uma proteína de levedura até em complexos sociais de diversas dimensões , como uma rede de amizade.Como observado na figura 1

Figura 1: a)Ligações da levedura ;b)Redes sociais

Neste capitulo será abordado o tema redes complexas, na primeira seção se fará uma breve historia do surgimento das redes , focando nos principais eventos. Na segunda seção , será tratado os principais conceitos que englobam as redes. Já a terceira seção abordará os tipos de redes mais usados.

2.1 Breve Historia

1736 - Euler,matemático e físico , resolveu o problema das Pontes de Königsberg, dessa forma foi fundamentada a teoría dos grafos. O problema das pontes era saber se seria possível atravessar as sete pontes da cidade , sem ter que passar duas vezes pela mesma ponte. Euler provou através de um grafo que seria impossível (EULER, 1741);criando , dessa forma , uma regra para aplicar a qualquer cidade, como mostrado na figura 2

1847- Gustav Robert Kirchhoff, físico russo, estudando circuitos eletricos, iniciou os estudos da teoria das Arvores. As árvores são um tipo de grafo.

1852 - Francis Guthrie, matemático inglês, criou a conjectura das 4 cores, a qual estabelece que qualquer mapa desenhado no plano,dividido com um numero qualquer de regiões pode ser colorido de forma que só usando quatro cores se possa colorir regiões fronterizas com cores diferentes.

(26)

24 Capítulo 2. Redes

Figura 2: Pontes de Konisgberg , proposta Euler

1859 - William Rowan Hamiltin, matemático, físico e astrônomo irlandés,inventou um jogo cujo objetivo era percorrer uma única vez os vértices de um decaedro, trazendo dessa forma conceitos novos como ciclo e caminho euleriano e hamiltoniano.

1959 - Erdős e Rényi , estudaram os grafos aleatórios,com o propósito de que através de métodos probabilísticos , estudar as propriedades dos grafos em função do crescimento de conexões aleatorias entre vértices.(ERDOS; RENYI, 1959)

1967 - Stanley Milgram, psicólogo, promoveu uma experiência para estudar o con-ceito de Mundo Pequeno,ao avaliar o grau de ligação entre as pessoas. Através do envio de cartas, para certos destinatários, foi determinado que existem seis graus de separação entre pessoas, demonstrando assim, que existe uma grande probabilidade de que pessoas desconhecidas tenham amigos em comúm.

1998 - Steven Strogatz e Duncan Watts, desenvolveram um algoritmo com base em grafos aleatórios, para estudarem o conceito de Mundo Pequeno.

1999 - Albert László Barabási e Réka Albert criaram um modelo genérico de construção de redes, semelhantes as redes encontradas em redes da internet. Estas redes foram denominadas redes livres de escala.(BARABASI, 1999)

2.2 Conceitos Básicos

2.2.1 Número de nodos (N)

Representa o número de componentes no sistema ou o tamanho da rede. Assim,por exemplo o número de pessoas numa determinada sociedade pode ser representada por N nós . Assim,i=1,2,... N.

2.2.2 Núumero de Arestas(L)

Número de ligações, ou L, representa o número total de interações entre os nós. Cada aresta liga ou conecta os nós (ROSEN, 2009)

(27)

2.2. Conceitos Básicos 25

2.2.3 Grau do nó i(k

𝑖

)

Cada nó tem um grau, representando o número de ligações que tem com outros nós. O grau de um nó pode representar o numero de amigos que uma pessoa tem numa rede de amizade , por exemplo.

O numero total de ligações L, pode ser expressa como a soma dos graus dos nós dividido por 2, como mostrado na fórmula :

𝐿 = 1 2 𝑁 ∑︁ 𝑖=1 𝑘𝑖 (2.1)

2.2.4 Distribuição de graus(P

𝑘

)

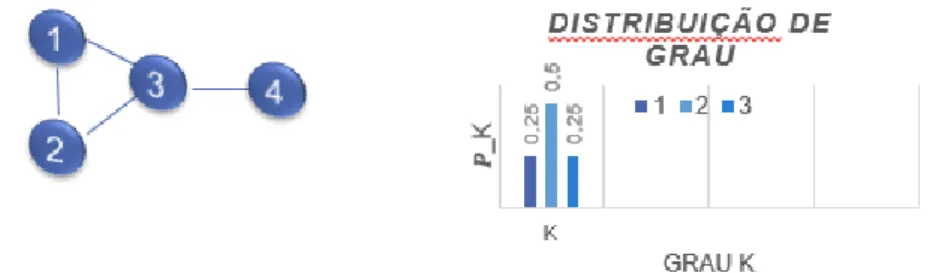
Fornece a probabilidade de que um nó selecionado aleatoriamente na rede tenha grau k.

𝑃𝑘=

𝑁𝑘

𝑁 (2.2)

Por ser uma probabilidade, ele deve ser normalizado, isto é,

∑︁

𝑘=1

𝑃𝑘 = 1 (2.3)

Para uma rede com N nós o grau de distribuição do histograma é normalizada. Como mostrado no grafico 3

Figura 3: a)Rede com 4 nós ,b)distribuição de graus

2.2.5 O momento de ordem n

Do grau de distribuição é definida como:

< 𝑘𝑛 >=

∞

∑︁

𝑘𝑚𝑖𝑛

𝐾𝑛𝑃𝑘 (2.4)

Primeiro momento(< 𝑘1 _{>); 𝑛 = 1 Chamado de o grau médio ,expressa a media} dos graus de todos os nós e pode ser expresa pela seguinte formula

(28)

26 Capítulo 2. Redes < 𝑘 >= 1 𝑁 𝑁 ∑︁ 𝑖=1 𝐾𝑖 = 2𝐿 𝑁 (2.5)

Segundo momento(< 𝑘2 _{>), 𝑛 = 2 Está relacionado com a variância}

𝜎2 =< 𝑘2 > − < 𝑘 >2 (2.6)

Medindo a propagação nos graus. Sua raiz quadrada, 𝜎, é o desvio padrão.

2.2.6 matriz de adjacência

É uma matriz NxN na qual :

⎧ ⎨ ⎩

𝐴𝑖𝑗 = 1,se existe a aresta entre o nó i e j

𝐴𝑖𝑗 = 0,se não existe a aresta entre o nó i e j

A matriz de adjacência proporciona informações dos nós e suas respectivas arestas O grau de nó i pode ser obtida diretamente dos elementos da matriz de adjacência. Assim, ela é obtida somando a linha i ou coluna j da matriz,quando se trata de uma rede não direcionada ou simetrica.Para obter o grau do nó i , pode-se usar

𝐾𝑖 = 𝑁 ∑︁ 𝑗=1 𝐴𝑗𝑖 = 𝑁 ∑︁ 𝑖=1 𝐴𝑗𝑖 (2.7)

Um exemplo de uma rede com 4 nós com sua respectiva matriz de adjacência é mostrada na figura 4

Figura 4: matriz de adjac˜encia

2.3 Tipos de Redes

Existem diversos tipos de redes,com variações dos números de nós, número de arestas e distribuição de graus. Assim , por exemplo existem redes com estrutura regular, na qual a distribuição de grau é uniforme como redes nas quais poucos nós tem muitas arestas e muitos nós poucas arestas. O objetivo do estudo de redes sociais é reproduzir

(29)

2.3. Tipos de Redes 27

uma rede real que representem a sociedade estudada e seus contatos e analisar como esto afeta os processos que ocorrem nestas redes.

2.3.1 Redes Aleatorias

São chamadas de redes de Erdős-Rényi devido a contribuição destes autores, os quais sao considerados os fundadores da teoria dos grafos (ERDOS; RENYI,1959). Assim como eles outro autor que estudou as redes aleatorias foi Gilbert (GILBERT, 1959)

Redes aleatorias sao geradas aleatoriamente . Assim, dada uma quantidade de nós ,que podem ser pessoas, cidades, locais, etc; se colocam aleatoriamente as ligações entre os nós de forma que reproduza um sistema real , como relações de amizade, ligações entre cidades,etc. Assim, a rede aleatoria é formada de N nós, onde cada par de nó esta conectado com probabilidade p

A distribuição dos graus em redes aleatórias segue uma distribuição binomial. Quando o número de nós é grande esta distribuição é muito bem aproximada pela dis-tribuição de Poisson. Será estudada uma rede que segue uma disdis-tribuição Binomial, en-seguida uma rede com distribuiçao de Poisson , e logo a demonstração de por que é a distribuição de Poisson se aproxima da distribuição Binomial

Distribuição Binomial.

Para estabelecer a probabilidade de que um nó 𝑖 numa rede com N nós tenha k ligações se faz o produto dos seguintes termos:

∙ A probabilidade de que k de suas ligações estão presentes, ou 𝑝𝑘

∙ A probabilidade de que o restante (𝑁 − 1 − 𝑘) as ligações estão faltando, ou (1 −

𝑝)(𝑁 −1−𝐾)

∙ O número de maneiras que se pode selecionar k ligações em (𝑁 − 1) ligações 𝐶_𝑘(𝑁 −1)

Dessa forma o grau de distribuição de uma rede aleatoria tem a seguinte distribui-ção binomial

𝑝𝑘 = 𝐶

(𝑁 −1)

𝑘 𝑝

𝑘_{(1 − 𝑝)}𝑁 −1−𝐾 _(2.8)

A forma desta distribuição depende do tamanho do sistema N e probabilidade p. A distribuição binomial permite-nos calcular o grau médio de rede <K>,bem como a sua variancia

(30)

A maioria das redes reais são esparsas, o que significa que para eles <k> «N Neste limite, o grau de distribuição é bem aproximada pela distribuição de Poisson

𝑃𝑘=

𝑒−<𝑘>< 𝑘 >𝑘

𝑘! (2.9)

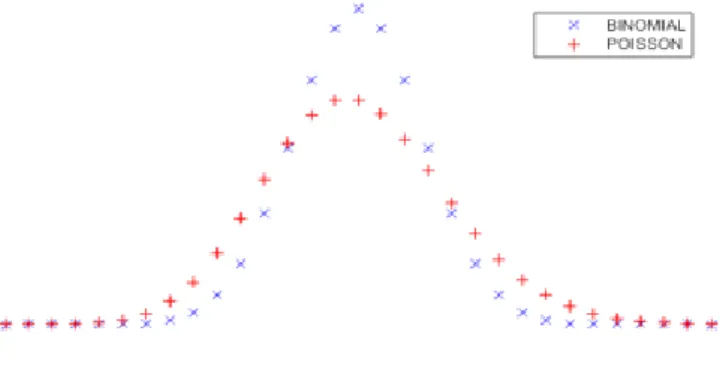
A distribuição binomial e a distribuição de Poisson têm propriedades semelhantes: Ambas as distribuições têm um pico por volta de <k> como mostrado na figura 5

Figura 5: Binomial e poisson

Ao usar uma forma de Poisson , para representar uma rede aleatoria, é necesario considerar:

∙ O resultado exato para o grau de distribuição é a forma binomial, assim a forma de Poisson representa apenas uma aproximação valido para <k>«N. Como a maioria das redes de importância prática são esparsas, esta condição é satisfeita.

∙ A vantagem da forma de Poisson é que as características-chave da rede, como<

𝑘 >, < 𝑘2 _{>e 𝑘, têm uma forma muito mais simples , dependendo em um único} parâmetro, <k>.

∙ A distribuição de Poisson não depende explicitamente do número de nodos N. Deste modo, prevê que o grau de distribuição de redes de tamanhos diferentes, mas o mesmo grau médio <k> são indistinguível uma da outra

Porém os dois tipos de redes devem ser usadas dependendo do caso assim:

∙ Redes pequenas: binomial. Para pequena redes com 𝑁 = 102 _{por exemplo o grau de} distribuição Binomial desvia significativamente da distribuição de Poisson. Portanto, para pequenas redes usar a forma binomial

∙ Grandes Redes: Poisson.Para redes maiores 𝑁 = 103_{, 10}4_{, a distribuição de graus} torna-se semelhantes.Dessa forma , para o N grande o grau de distribuição é inde-pendente da tamanho da rede.

(31)

Aproximação binomial para Poisson

Através de manipulações matemáticas chegaremos à distribuição de Poisson, apartir da distribuição Binomial. 𝑃 (𝑘) = 𝑃 (𝑥 = 𝑘) = (︃ 𝑛 𝑘 )︃ 𝑝𝑘(1 − 𝑝)𝑛−𝑘 (2.10) Reescrevendo a equação: 𝑃 (𝑥 = 𝑘) = 𝑛! 𝑘!(𝑛 − 𝑘)!𝑝 𝑘𝑛𝑘 𝑛𝑘(1 − 𝑛𝑝 𝑛 ) 𝑛−𝑘 _(2.11) = 𝑛! 𝑘!(𝑛 − 𝑘)! (𝑛𝑝)𝑘 𝑛𝑘 (1 − 𝑛𝑝 𝑛 ) 𝑛−𝑘 _(2.12) tendo 𝜆 = 𝑛𝑝 𝑃 (𝑥 = 𝑘) = 𝑛(𝑛 − 1)....(𝑛 − 𝑘 + 1) 𝑘! 𝜆𝑘 𝑛𝑘(1 − 𝜆 𝑛) 𝑛−𝑘 _(2.13) = 𝜆 𝑘 𝑘!1(1 − 1 𝑛)...(1 − 𝑘 − 1 𝑛 )(1 − 𝜆 𝑛) 𝑛−𝑘 _(2.14)

se tomarmos o limite quando n → ∞

lim 𝑛→∞(1 − 1 𝑛)...(1 − (𝑘 − 1) 𝑛 ) = 1 (2.15) e em: lim 𝑛→∞(1 − 𝜆 𝑛) 𝑛−𝑘 _{= lim} 𝑛→∞(1 − 𝜆 𝑛) 𝑛 _{= 𝑒}−𝜆 (2.16)

obtendo dessa forma:

lim

𝑛→∞𝑃 (𝑥 = 𝑘) =

𝑒−𝜆𝜆𝑘

𝑘! (2.17)

Esta é a distribuiçao de Poisson

2.3.2 Redes Livre de Escala

Pareto, um economista do século 19, notou que na Itália alguns indivíduos ricos ganhavam a maior parte do dinheiro, enquanto a maioria da população ganhava pouco. Observou , assim, que a distribuição de riqueza era bem aproximada por uma lei de potência. (PARETO, 1964)

(32)

Ao mapear a World Wide Web , realizado no estudo liderado por Laszlo Barabási, se pode verificar que 80 % das páginas web tinham apenas 4 hiperligações e que aproximadamente 0,001 % das páginas tinha mais de 1000 hiperligações.Dessa forma, ele também verificou que a distribuição das hiperligações era bem aproximada por uma lei de potência

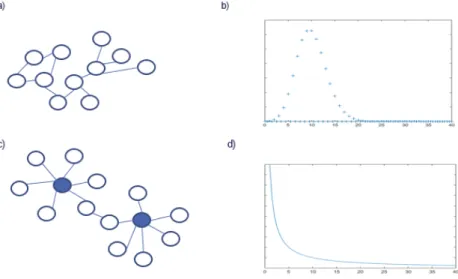
Dessa forma,as redes livres de escala são um tipo de rede cuja distribuição dos graus tem (teóricamente) variancia infinita , como a lei de potencia, com expoente entre 2 e 3 .Neste caso, a maioria dos nós(vértices) tem poucas ligações, contrastando com a existência de alguns nós que apresentam um elevado número de ligações. Este último grupo de nós são designados de "Hubs", os quais tem um papel fundamental dentro da rede.

Este tipo de rede , denominadas redes livre de escala, justamente por que alguns nós não tem escala , sendo muito diferente da média <k>

As redes de livre escala são bastante comuns e podem ser identificadas nos mais vari-ados contextos tais como: World Wide Web, as redes biológicas, as redes sociais, redes metabolicas, entre outras.

A distribuição dos graus em redes livres de escala seguem a lei de potencia :

𝑝𝑘 ≈ 𝑘−𝛾 (2.18)

Onde o expoente é o seu expoente de grau. Na lei de potencia , os graus dos nós são inteiros positivos, k = 0, 1, 2, ..., o formalismo discreto fornece a probabilidade 𝑝𝑘 que

um nó tenha exatamente k ligações

𝑝𝑘= 𝑐𝑘−𝛾 (2.19)

A constante c é determinada pela condição de normalização ∞

∑︁

𝑘=1

𝑃𝑘 = 1

Das duas equações anteriores obtemos:

𝑐∑︁ 𝑘=1 𝑘−𝛾 = 1 (2.20) 𝑐 = _∑︀ 1 𝑘=1𝑘−𝛾 (2.21)

Sendo o denominador a funçao zeta. Dessa forma, se obtem:

𝑐 = 1

(33)

De (2.19) e (2.22):

𝑃𝑘 =

𝑘−𝛾

𝜁(𝛾) (2.23)

Pode-se observar na figura 6 uma rede aleatoria e sua distribuição binomial assim como uma rede livre de escala e sua distribuição de potencia. No grafico a diferença de uma pequena rede aleatória e uma rede livre de escala. Uma caraterística da distribuição de potencia é a presencia da "cauda gorda"quando o grau aumenta, enquanto na distribuição binomial não existe nós com graus altos e portanto,não existe a presença desta "cauda gorda". Esta "cauda gorda"na rede livre de escala representa portanto a existencia de nós com alto grau

Figura 6: a)rede aleatoria; b)grafico da distribuiçao binomial ; c)rede livre de escala d)grafico da distri-buiçao livre de escala

(34)

(35)

33

3 Modelos Epidemiológicos

A palavra epidemiologia é derivada do grego (epi = sobre; demos = populacão, povo; logos = estudo). Desta forma, epidemiologia é o estudo do que ocorre em uma população. Epidemiologia é a ciencia que estuda o processo saude-enfermidade na sociedade, levando em consideração fatores determinantes dos riscos de doenças, propondo medidas especifi-cas para prevenir, controlar e erradicar as enfermidades (FILHO; M, 2006)

O estudo matemático da epidemiologia começou a ser realizado em 1760 por Bernoulli quando estudou a varıola(BERNOULLI, 1760). Somente a partir da metade do seculo XIX,com o avanço do conhecimento médico sobre microorganismos e doenças infeccio-sas,começou a surgir teorias matemáticas para fenômenos epidemiolgicos.

O epidemiologista ingles Sir William Heaton Hamer, construiu em 1906 a curva epidemica do sarampo. Hamer desenvolveu a expresão matemática do comportamento epidemioló-gico do sarampo tendo por base a sua teoria mecânica de números e densidade. Ele for-mulou matematicamente o comportamento epidémico como uma dinâmica dos contatos entre indivíduos sadios e infectados, conhecido como principio de ação de massas.

Pelo princípio de ação de massas se estabelece que a taxa de transmissão da doençã é proporcional ao produto da densidade de indivíduos não infectados e infectados. Em 1927, Kermack e McKendrick desenvolveram uma teoria relacionando o surgimento de uma epidemia a um valor crítico do núumero de suscetíveis (W; KENDRICK,1927). O princípio de acão de massas e a teoria do valor crítico são os dois marcos nos estudos da epidemiologia moderna.

Neste capitulo será abordado modelos epidemiologicos , na primeira seção trataremos as hipótesis nas quais se baseiam os modelos ; já na segunda seção será abordado os modelos de epidemiologia , sendo eles o modelo SI , SIS e SIR.Cave mencionar que existem outros modelos os quais não serão abordados nesta dissertação.

3.1 Hipótese

hipóteses na modelagem da disseminação de agentes patogénicos ∙ Compartimentalização

A classificação é feita com base na fase da doença que os afeta , assim um individuo pode estar em um dos três estados ou compartimentos:

– Susceptíveis (S): Indivíduos que ainda nao tiveram contato com o agente

(36)

34 Capítulo 3. Modelos Epidemiológicos

– Infectados (I): indivíduos que entraram em contato com o patógeno e se

infec-taram e, portanto, estão contagiados podendo infectar outras pessoas.

– Recuperado (R): indivíduos que foram infectados antes, mas se recuperaram

da doença, portanto, não podem se infectar assim como nao podem infectar outros indivíduos

Os indivíduos podem se deslocar entre os compartimentos. Assim , quando um individuo suscetível entra em contato com um infectado , o primeiro pode se tornar infectado e posteriormente graças ao seu sistema imunológico se recuperar e se tornar imune.

Algumas doenças precisam mais classificações , com mais estados adicionais, como indiví-duos imunes, que não podem ser infectados, ou indivíindiví-duos latentes, que têm sido expostos à doença, mas ainda não são contagiosos.

∙ Mistura Homogênea A hipótese de mistura homogênea (Ação de aproximação de mas-sas) assume que cada indivíduo tem a mesma chance de entrar em contacto com um indivíduo infectado. Esta hipótese é equivalente a hipótese de que a rede de contatos é aleatória.

Sob estas duas hipotesis se erge a estrutura de modelagem de epidemias. Na seguinte seção detalharemos os modelos de epidemia básicos o SI, SIS e SIR. Como mostrado na figura 7

Figura 7: a)modelo SI, b)Modelo SIS ,c)Modelo SIR

3.2 Conceitos importantes

3.2.1 Tempo caraterístico (𝜏 )

É o tempo necessário para atingir a fracção de 1/e é dizer cerca de 63 % de todos indivíduos susceptíveis 𝜏 é o inverso da velocidade com que se propagam os patogenos, através da população, é dizer o inverso da taxa de transmissibilidade

3.2.2 Numero Basico (R

0

)

Representa o número médio de indivíduos susceptível infectados por um indivíduo infec-tado durante o período de infecção . O número básico de reprodução é valiosa para seu

(37)

3.3. Modelos 35

poder de previsão

3.2.3 Taxa de Transmissibilidade

É a velocidade com que a doença se espalha

3.2.4 Taxa de Propagação (𝜆)

Ela depende apenas das características biológicas do agente patogénico,ou seja, a proba-bilidade de transmissão 𝑏𝑒𝑡𝑎 e da taxa de recuperação 𝑚𝑢 É definida para prever quando um agente patogénico na população persiste no modelo SIS

3.2.5 limiar de epidemia (𝜆

𝑐

)

O agente patogénico pode se espalhar somente se a sua taxa de propagação exceda um limiar de epidemia

3.3 Modelos

Nos modelos serão considerado N constante e sem dinâmica vital o que significa que na população não se considerarão nascimentos nem mortes.

3.3.1 Modelo SI

Considere uma doença que se propaga numa população de 𝑁 indivíduos e que cada individuo tem < 𝑘 > contatos. Considerando 𝛽 a taxa de transmissão da doença e essa transmissão se dá com o encontro entre indivíduos suscetíveis e infectados . A proporção de vizinhos suscetíveis de um indivíduo infetado é < 𝑘 > 𝑆/𝑁 logo a taxa de transmissão da doença gerada por este indivíduo infetado é de 𝛽 < 𝑘 > 𝑆/𝑁 .Considerando todos os indivíduos infetados obtemos a seguinte equação:

𝑑𝐼(𝑡) 𝑑𝑡 = 𝛽 < 𝑘 > 𝑆(𝑡) 𝑁 𝐼(𝑡) (3.1) considerando 𝑠(𝑡) = 𝑆(𝑡) 𝑁 (3.2) 𝑖(𝑡) = 𝐼(𝑡) 𝑁 (3.3)

(38)

𝑑𝑖

𝑑𝑡 = 𝛽 < 𝑘 > 𝑖(1 − 𝑖) (3.4)

Esta equação tem a mesma expressão já conhecida como Modelo Logístico , usada como modelo de crescimento populacional. (VERHULST,1838)

onde o produto 𝛽 < 𝑘 > é a taxa de transmissibilidade.

𝑑𝑖 𝑖 +

𝑑𝑖

(1 − 𝑖) = 𝛽 < 𝑘 > 𝑑𝑡 (3.5) integrando os dois lados da equação, obtemos:

𝑙𝑛𝑖 − 𝑙𝑛(1 − 𝑖) = 𝛽 < 𝑘 > 𝑡 + 𝐶 (3.6)

Com condiçao iniciao 𝑖𝑜 = 𝑖(𝑡 = 0) , obtemos 𝐶 = _(1−𝑖𝑖𝑜_𝑜₎

𝑖 = 𝑖𝑜𝑒

<𝐾>𝑡

1 − 𝑖𝑜+ 𝑖𝑜𝑒<𝑘>𝑡

(3.7)

Esta equação prevê que:

– No início ,a fracção dos indivíduos infectados aumenta exponencialmente , como

vemos na figura 8. Na verdade, desde o início um indivíduo infectado encontra só indivíduos suscetíveis, portanto, o patógeno pode facilmente se dissipar. Com o tempo um indivíduo infectado encontra cada vez menos indivíduos suscetíveis. Por isso, o crescimento de i diminui quando t cresce ,como mostrado na figura 8. A epidemia termina quando todos foram infectado, ou seja, quando

𝑖(𝑡 → ∞) = 1 e 𝑠(𝑡 → ∞) = 0

– O tempo caracteristico necessário para atingir cerca de 63 % de todos

in-divíduos susceptíveis .Ele é representado pela seguinte equação

𝜏 = 1

𝛽 < 𝑘 > (3.8)

A equação prevê que o aumento ou a densidade de ligações <k> ou 𝛽 aumenta a velocidade do agente patogênico e reduz o tempo característico.

3.3.2 Modelo SIS

No modelo SI o indivíduo suscetível pode se tornar infectado quando entra em contato com o agente infeccioso , porém não mostra o sentido inverso , é dizer quando um infectado volta para o estado suscetível. No entanto , a maioria dos patógenos são eventualmente

(39)

3.3. Modelos 37

Figura 8: A evolução no tempo da fração de infectados.

No inicio cresce exponencialmente. No final, 𝑠(𝑡 = ∞) = 0; 𝑖(𝑡 = ∞) = 1 , tendo toda a populaçao infetada.

Implementado no matlab, usando ODE45,o qual usa o método Runge kutta

derrotados pelo organismo ,e o individuo volta a ser suscetível após o tratamento , sendo suscetível ele não infectara nenhum outro individuo , até ele ser infectado novamente. No modelo SI existe a probabilidade 𝛽 de um infectado infetar um suscetivel , já no modelo SIS também existe a taxa 𝜇 de recuperação da doença , tornando-se suscetível novamente o indivíduo . A equação que descreve esta dinâmica é

𝑑𝑖

𝑑𝑡 = 𝛽 < 𝑘 > 𝑖(1 − 𝑖) − 𝜇𝑖 (3.9)

em que 𝜇 é a taxa de recuperação e o termo 𝜇𝑖 capta a taxa à qual a população se recupera da doença. Integrando os dos lados da equaçao obtemos:

𝑖 = (1 − 𝜇 𝛽 < 𝑘 >)

𝐶𝑒(𝛽<𝑘>−𝜇)𝑡

1 + 𝐶𝑒(𝛽<𝑘>−𝜇)𝑡 (3.10) onde a condiçao inicial 𝑖𝑜 = 𝑖(𝑡 = 0) , dado 𝐶 = 𝑖𝑜/(1 − 𝑖𝑜− 𝜇/𝛽 < 𝑘 >).

Enquanto no modelo SI,toda a população fica infetada ,em um tempo grande , no modelo SIS obtem-se dois resultados possíveis

3.3.2.1 estado endemico ( 𝜇 < 𝛽 < 𝑘 >)

Para baixa taxa de recuperação da fracção dos indivíduos infectados, i, segue uma curva logística semelhante ao observado no modelo SI. No entanto, não todos os indivíduos estão infectados, mas i atinge uma constante 𝑖(∞) < 1 como mostrado na figura 9 . Isto significa que apartir de um determinado t, apenas uma fracção finita da população está infectada. Neste estado estacionário ou endêmico o número de pessoas infectadas é igual ao número de indivíduos que se recuperam da doença, daí a fração infectado da população não muda com o tempo , como observamos na figura 9

(40)

Figura 9: A evolução no tempo da fração de infectados no modelo SIS, no estado endêmico Implementado no matlab, usando ODE45,o qual usa o método Runge kutta

3.3.2.2 estado livre de doença( 𝜇 > 𝛽 < 𝑘 >)

Nesse estado, o número de pessoas curadas por unidade de tempo excede o número de indivíduos recém-infectados. Dessa forma, o agente patogenico desaparece da população. Assim, o modelo SIS prevê que alguns agentes patogénicos persistirão na população, já outros irão morrer para algúm t

Para prever se a população estará livre da doença ou será estado endêmico é necessário entender o número básico de Reprodução 𝑅0

Numero básico de Reprodução

O número básico de Reprodução representa o número médio de novos indivíduos infecta-dos gerainfecta-dos diretamente por um único indivíduo infectado quando a população é quase inteiramente suscetível. Ele é representado pela seguinte fórmula:

𝑅0 =

𝛽 < 𝑘 >

𝜇 (3.11)

O número básico de reprodução é valiosa para seu poder de previsão:

– Se 𝑅0 > 1 a epidemia evolui para um estado endêmico. Com efeito, se cada in-divíduo infectado infecta mais de uma pessoa saudável, o patógeno está prestes a se espalhar e persistir na população.

– Se 𝑅0 < 1 a epidemia morre. Assim, se cada indivíduo infectado infecta menos de uma pessoa adicional, o patógeno não pode persistir na população, e morre

Portanto , o número de reprodução é um dos primeiros parâmetros epidemiológicos para estimar um novo agente patogénico, avaliando a gravidade do problema que enfrentam. Quanto maior é 𝑅0, mais rápido a doença se espalha. Na tabela observa-se 𝑅0 para vários patógenos.(PRICE, 1965)

(41)

3.3. Modelos 39

Tabela 1: Doenças com suas respectivas formas de transmissão e R0

DOENÇA TRANSMISSÃO R0

Sarampo Transportado pelo Ar 12-18 Pertussis Gotículas no Ar 12-17

Difteria Saliva 6-7

Variola Contato 5-7

Poliomielite Rota Fecal 5-7 Caxumba Gotículas no Ar 4-7

HIV Contato sexual 2-5

Sars Gotículas no Ar 2-5

Gripe Gotículas no Ar 2-3

3.3.3 Modelo SIR

Neste modelo um novo grupo é inserido: recuperados. Eles não serão infetados novamente , devido ao sistema inmune assim como não transmitirão a doença . A taxa de variação de infetados , de suscetíveis e de recuperados com relação ao tempo são respetivamente:

𝑑𝑖 𝑑𝑡 = 𝛽 < 𝑘 > 𝑠𝑖 − 𝜇𝑖 (3.12) 𝑑𝑠 𝑑𝑡 = −𝛽𝑠𝑖 < 𝑘 > (3.13) 𝑑𝑟 𝑑𝑡 = 𝜇𝑖 (3.14)

Assim, neste modelo com T grande o numero de infectados desaparece . Como mostrado na figura 11

Figura 10: Modelo SIR.levando em consideração proporção de infetados, suscetíveis e recuperados Implementado no matlab, usando ODE45,o qual usa o método Runge kutta

(42)

(43)

41

4 Modelos Epidemiológicos em Redes

A velocidade com que os agentes patogênicos se difundem na população aumentou signi-ficativamente , o que antigamente era uma barreira geográfica atualmente ela diminuiu drásticamente , diversos avanços tecnológicos permitiram diminuir as barreiras que im-pediam o contato entre os indivíduos de diversos continentes , este avanço trouxe muitos benefícios para a sociedade, porém algums problemas , principalmente no âmbito da saúde pública dos governos. Assim por exemplo , na antiguedade um virus levava anos para se espalhar num continente. Atualmente um virus pode atingir varios continentes em ques-tão de días, devido a diminuição do tempo de viagem de um continente para outro , por exemplo. Portanto, se faz necessario comprender estas mudanças e inserí-las nos modelos epidemiológicos.

Os modelos clássicos, modelos expostos no capitulo 3 considera a hipótese de mistura homogênea , assumindo uma estrutura de rede simples ou seja sem considerar a topología presente em redes de contato reais. Só em 2001 Romualdo Pastor-Satorras e Alessandro Vespignani, incorporaram as características topológicas da rede nos modelos epidemioló-gicos.

Neste capitulo se fará uma abordagem dos modelos epidemiológicos que levam em consi-deração o tipo de redes de contato real na qual a doença se espalha. Na primeira seção consideramos as hipótesis , segunda seção serão abordados algums dos novos conceitos que serão usados e por último , os modelos de epidemiologia em redes.

4.1 Hipótese

– Compartimentalização: Considera-se a mesma divisão dos individuos feita nos

modelos de epidemiologia ,vistas no capitulo anterior. Assim ,os individuos sao classificados como Suscetiveis, Infetados e Recuperados

– Onde a característica considerada desta rede é a sua distribuição dos graus

4.2 Conceitos Novos

4.2.1 Bloco de Aproximação de Grau

Os nós são separados por graus e se assume que nós que tenham o mesmo grau são estatisticamente equivalente . Sendo, assim, deve-se considerar o grau de cada nó como uma variável implícita dentro dos modelos epidemiológicos. O bloco de aproximação com 7 nós , de grau 1, 2 e 3 são mostrados na figura 12

(44)

42 Capítulo 4. Modelos Epidemiológicos em Redes

Figura 11: Bloco de Aproximação de Grau

4.2.2 Função Densidade

A função de densidade Θ𝑘 fornece a fracção de nós infectados na vizinhança de um nó

suscetível com grau k.

Na hipótese de mistura homogênea Θ𝑘é simplesmente a fração dos nós infectados, i. Numa

rede não homogênea, no entanto , a fraçao de nós infectados na vizinhança de um nó pode depender do grau k do nó e do tempo t. Faremos a suposição de que a probabilidade de que uma ligação de um nó com grau k para um nó com grau 𝑘′é independente de k, o que quer dizer que a rede não tem correlação de grau . Por isso, a probabilidade de que uma aresta escolhido aleatoriamente tenha uma ligação com o nó 𝑘′ _{é representado por}

𝑘′𝑝′_𝑘 ∑︀𝑁 𝑘=1𝑘𝑝𝑘 = 𝑘 ′_𝑝′ 𝑘 < 𝑘 > (4.1)

Pelo menos uma ligação de cada nó infectado é ligado a outro nó infectado aquele que transmitiu o patogeno. Portanto, o número de ligações disponível para a transmissão futuro é (𝐾′ − 1), o que nos permite escrever:

Θ𝑘 =

∑︀

𝑘′(𝑘′ − 1)𝑝_𝑘′𝑖_𝑘′

< 𝑘 > = Θ (4.2)

A segunda igualdade se deve a que a densidade não depende de k Diferenciando (4.2) obtemos 𝑑Θ 𝑑𝑡 = ∑︀ 𝑘(𝑘 − 1)𝑝𝑘 < 𝑘 > 𝑑𝑖𝑘 𝑑𝑡 (4.3)

Para progredir, é preciso considerar o modelo específico na qual o patógeno se insere.Portanto, será visto os modelos em Redes

(45)

4.3. Modelos 43

4.3 Modelos

4.3.1 SI em redes

Se um patógeno se espalha em uma rede, os indivíduos com mais ligações são mais sus-ceptíveis de estar em contacto com um indivíduo infectado, portanto, eles tem mais pro-babilidade de serem infectadas. Assim, no formalismo matemático se deve considerar o grau de cada nó como uma variável implícita. Isto é conseguido pelo bloco de aproximação grau, que distingue os nós com base no seu grau e assume que os nós com o mesmo grau são estatisticamente equivalente .figura 12. Dessa forma obtemos

𝑖𝑘 =

𝐼𝑘

𝑁𝑘

(4.4)

onde 𝑖𝑘 representa a fração de nós com grau k que estão infectados entre todos os nós de

grau k

A fracção total de nós infectados, é a soma de todos nós infetados com graus k

𝑖 =

𝑘𝑚𝑎𝑥

∑︁

1

𝑝𝑘𝑖𝑘 (4.5)

Tendo em conta os diferentes graus de nós, podemos escrever o modelo SI para cada grau k separadamente:

𝑑𝑖𝑘

𝑑𝑡 = 𝛽(1 − 𝑖𝑘)𝑘Θ𝑘 (4.6)

Esta equação tem a mesma estrutura que (3.6), A taxa de infecção é proporcional a 𝛽 e a fração de nós de grau k que ainda não estão infectadas,o qual é (1 − 𝑖𝑘) . No entanto,

existem algumas diferenças fundamentais:

– O grau medio em (3.6) é substituído com cada nó de grau k real

– A função densidade Θ𝑘 representa a fração de vizinhos infectados de um nó

susceptível k. Na hipótese de mistura homogênea Θ𝑘 é simplesmente a fracção

dos nós infectados, i. Numa rede não homogênea, no entanto, a fracção de nós infectados na vizinhança de um nó pode depender do grau k do nó e do tempo t

– Enquanto (3.6) capta com uma única equação o tempo dependente do

com-portamento de todo o sistema, (4,6) representa um sistema de k equações acopladas, uma equação para cada grau presente na rede.

(46)

44 Capítulo 4. Modelos Epidemiológicos em Redes 𝑑Θ 𝑑𝑡 = 𝛽 ∑︀ 𝑘(𝑘2− 𝑘)𝑝𝑘 < 𝑘 > [1 − 𝑖𝑘]Θ (4.7)

Considerando 𝑖𝑘muito pequeno, é dizer no início da epidemia

integrando : Θ(𝑡) = 𝐶𝑒𝜏𝑡 (4.8) considerando: 𝜏 = < 𝑘 > 𝛽 < 𝑘2 _{> − < 𝑘 >}; 𝐶 = 𝑖0 (< 𝑘 > −1) < 𝑘 > (4.9) Obtemos: Θ(𝑡) = 𝑖0 < 𝑘 > −1 < 𝑘 > 𝑒 𝑡 𝜏 (4.10)

para t pequeno , (3.6) fica:

𝑑𝑖𝑘 𝑑𝑡 = 𝛽𝑘Θ𝑘 (4.11) De(4.10) e (4.11), chegamos: 𝑑𝑖𝑘 𝑑𝑡 = 𝑖0 < 𝑘 > −1 < 𝑘 > 𝑒 𝑡 𝜏 (4.12) integrando: 𝑖𝑘= 𝑖0(1 + 𝑘 < 𝑘 > −1 < 𝑘2 _{> − < 𝑘 >})𝑒 𝑡 𝜏−1 (4.13)

Pode-se expressar esta equaçao como: 𝑦 = 𝑓 (𝑡) + 𝑘(𝑔(𝑡) o que quer dizer que quanto maior o k , mais rápido o nó fica infectado como mostrado na figura 13

(47)

4.3. Modelos 45

O Tempo Carateriscico (𝜏 ) em Redes

Considerando o tempo Carateristico como :

𝜏 = < 𝑘 >

(𝛽 < 𝑘2 _{> − < 𝑘 >)} (4.14) Pode-se achar o tempo Caraterístico aproximado, tanto em Redes aleatórias como em redes livre de escala

1) Redes aleatorias

– Podendo escrever o segundo momento como:

< 𝑘2 >≈< 𝑘 > (< 𝑘 > +1) (4.15)

– Podemos obter o tempo carateristico como:

𝜏 ≈ 1

𝛽 < 𝑘 > (4.16)

– Obtendo dessa forma um resultado similar á rede homogênea

Redes Livre de escala 𝛾 >= 3

– Considerando < 𝑘2 _{> e < 𝑘 > finitos ,obtemos}

𝜏 = 1

𝛽 < 𝑘 > (4.17)

– Resultado igual a rede aleatoria

3) Redes Livre de escala 𝛾<=3

– considerando 𝑁 → ∞ ,𝑙𝑖𝑚 < 𝑘2 _{>→ ∞}

𝜏 → 0 (4.18)

– Este resultado é bassicamente a presença dos Hubbs

4.3.2 SIS em redes , e o desaparecimiento do limiar de epidemia

Ao modelo SI acrescenta-se 𝜇𝑖𝑘 obtendo:

𝑑𝑖𝑘

𝑑𝑡 = 𝛽(1 − 𝑖𝑘)𝑘𝑘− 𝜇𝑖𝑘 (4.19)

(48)

𝜏 = < 𝑘 >

(𝛽 < 𝑘2 _{> −𝜇 < 𝑘 >)} (4.20) Para suficientemente grande 𝜇 o tempo característico é decaimentos negativos,

Taxa de espalhamento(𝜆)

𝜆 = 𝛽

𝜇 (4.21)

a qual depende apenas das características biológicas do agente patogénico,ou seja, da probabilidade de transmissão 𝛽 e da taxa de recuperação 𝜇. Quanto maior é 𝜆, o mais provável é que a doença se espalhe. No entanto, o número de infectado não aumenta gradualmente com 𝜆,em vez disso, o agente patogênico pode se espalhar somente se a sua taxa de propagação excede um 𝜆𝑐 limiar de epidemia. Se fará uma análise de como

varia 𝜆𝑐 para redes aleatórias e sem escala.

1)Redes Aleatorias

Se um patógeno se espalha em uma rede aleatória, podemos usar < 𝑘2 >=< 𝑘 >< 𝑘 +1 >

em (4.20) , obtendo-se que o agente patogénico na população persistir se

𝜏 = < 𝑘 >

𝛽 < 𝑘 >< 𝑘 + 1 > −𝜇 < 𝑘 > (4.22)

obtemos

𝜏 ≈ 1

𝛽(< 𝑘 > +1) − 𝜇 (4.23)

Considerando: 𝜏 > 0 para verificar que a doença se espalha. Déve-se considerar o deno-minador >0, obtendo-se:

𝜆 = 𝛽 𝜇 >

1

< 𝑘 > +1 (4.24)

obtendo o limiar de epidemia de uma rede aleatória como:

𝜆𝑐=

1

< 𝑘 > +1 (4.25)

como k é sempre finito, uma rede aleatória diferente de zero tem sempre um limiar de epidemia ,com consequências importantes:

(49)

4.3. Modelos 47

– Se 𝜆 > 𝜆𝑐 o patógeno vai se espalhar até que ele atinja um estado endêmico,

onde uma fracção finito 𝑖(𝜆) da população está infectada em qualquer momento

𝜆 > 𝜆𝑐

– Se 𝜆 < 𝜆𝑐, o patógeno morre, ou seja, 𝑖(𝜆) = 0

Por isso, o limiar de epidemia nos permite decidir se um agente patogénico permane-cerá ou não na população. Esta transição do ausência à presença de um surto epidémico, aumentando o 𝜆 taxa de propagação está na base da maior parte das campanhas para combater um patógeno

1)Redes livre de escala

Já se um patôgeno se espalha numa rede com grau de distribuição arbitrária não pode-remos usar < 𝑘2 >=< 𝑘 >< 𝑘 + 1 >no tempo caraterístico(4.20).Dessa forma devemos

considerar o denominador de 𝜏 > 0 para obter o limiar 𝜆𝑐 de epidemia.Assim:

𝛽 < 𝑘2 > −𝜇 < 𝑘 > > 0 (4.26) 𝛽 < 𝑘2 >> 𝜇 < 𝑘 > (4.27) 𝜆 = 𝛽 𝜇 > < 𝑘 > < 𝑘2 _> (4.28)

como n tende ao infinito entao <k2 _{> 𝑡𝑒𝑛𝑑𝑒𝑎𝑜𝑖𝑛𝑓 𝑖𝑛𝑖𝑡𝑜}

, não podemos considerar:< 𝑘2 _{>=< 𝑘 >< 𝑘 + 1 >, pois o segundo momento <k}2 _> o tempo carateristico dado por :

𝜏 = < 𝑘 >

(𝛽 < 𝑘2 _{> −𝜇 < 𝑘 >)} (4.29) (10,21), obtendo-se o limiar de epidemia como

𝑐 = < 𝑘 >

< 𝑘2 _> (4.30)

Quanto a uma rede sem escala , com N grande, diverge, portanto, para grandes redes é esperado que o limiar de epidemia desapareça isto significa que mesmo patógenos que são difíceis de passar de indivíduo para indivíduo pode se espalhar com sucesso,a qual representa a segunda previsão fundamental da rede de epidemias.

O limiar de epidemia de fuga é uma consequência direta dos hubbs. Com efeito, um patogéno que não consegue infectar outros nós antes do indivíduo infectado se recuperar,

(50)

lentamente vai desaparecer da população. Em uma rede aleatória todos nós têm grau comparável, kk, portanto, se a taxa de espalhamento está sob o limiar de epidemia, o patógeno não tem como se espalhar. Numa rede sem escala, no entanto, mesmo se um agente patogénico é apenas fracamente infecciosa, se infecta um hubb, o hubb pode passá-lo para um grande número de outros nós, permitindo que persistam na população

4.4 Aplicações e Discussões

Algumas doenças que foram rapidamente espalhadas em algumas populações específicas podem ter uma explicação plausível baseado no tipo de rede social na qual a doença se transmitiu.

Assim por exemplo a Síndrome da Imunodeficiência Adquirida, AIDS , em São Francisco nos EUA , na década dos 80 do século passado , se difundiu rapidamente na populacão de homosexuais . Isto pode ter acontecido ao ser infectado um ou vários "hubs"provavelmente os quais tiveram contatos sexuais com vários indivíduos fazendo com que a doença se espalhe rapidamente nesta comunidade. Um caso parecido de difusão rápida da AIDS ocorreu na Inglaterra , onde se verificou um alto índice de contaminação de usuários de drogas na troca de seringas. Este grupo também pode ter sido rapidamente atingido ao ser contaminado um "Hub"deste grupo.Dessa forma, para a transmissão da AIDS podem-se considerar redes de contato como a rede sexual ou a rede social de transfusão sanguínea. Outro caso onde a rapidez do espalhamento da doença pode ser explicado pela existência de redes livre de escala é o Cólera , o qual até o século XIX só existia na Asia e na India. Na América do Sul , aparece em 1991 em Chancay no Perú , e se espalhou rapidamente para outras cidades como Lima e algumas cidades do litoral, e logo para todo América. Em muitas destas cidades pode -se ter a presença de Hubs os quais podem ter sido a ligação entre algumas cidades. Como a doença é transmitida basicamente pela batéria Vibrio cholerae a qual tem a capacidade de se multiplicar em grande velocidade dentro do intestino ; o contato físico de mãos por exemplo pode causar rapidamente uma difusão desta bactéria , o que pode explicar de alguma forma a difusão entre regiões e logo entre países.

(51)

49

5 Testes e Resultados

O objetivo dos testes é simular uma rede de contato aleatória e outra rede livre de escala nas quais se infectam algums nós e se tenta reproduzir o modelo SIS , para analisar o limiar de epidemia nos dois tipos de redes.

No algoritmo , primeiro se cria uma sequencia de números que tenham a distribuiçao de Poisson(para simular redes aleatórias) e outrass que tenham a distribuição de pareto(para simular redes livres de escala) ,estas sequencias representarão a distribuição de grau de cada rede. Logo, a partir desta sequencia se estabelece a matriz de adjacencia. Por último se simula o modelo SIS , através desta matriz de adjacencia.A forma como foi implemen-tado encontra-se no apêndice.

Foram realizados dos tipos de testes , no primeiro considerando (𝜆 > 𝜆𝑐) tanto nas redes

aleatórias quanto nas redes livre de escala. Já no segundo teste considerou-se (𝜆 < 𝜆𝑐) ,

em ambas as redes

Para a realização dos Testes foi implementado um algoritmo no matlab , o qual se simula 1000 vezes a difusão da doença

5.1 Teste 1

Para analisar se o patógeno persiste ou morre na rede aleatória e livre de escala , no modelo SIS , levando em consideração (𝜆 > 𝜆𝑐). Se obteve que em todas as experiencias o

patôgeno persistiu , tanto nas redes de contato com distribuição aleatória como nas redes de contato livre de escala.

Na tabela 2 encontra-se os dados , e na figura 13 os resultados expressos através dos quartis e a mediana dos resultados . Já na figura 13, um exemplo de como o agente se comporta em redes aleatórias e livres de escala através do tempo

Tabela 2: Modelo SIS (𝜆 > 𝜆𝑐). )

Rede Aleatoria Rede livre de escala Rede livre de escala

n=10000 n=10000 n=10000 𝛽 = 0.8 𝛽 = 0.8 𝛽 = 0.8 <k>=20 <k>=12 <k>=12 - X𝑚𝑖𝑛 = 4 X𝑚𝑖𝑛 = 4 𝜇 = 0.1 𝜇 = 0.1 𝜇 = 0.1 - y=3.1 y=2.5

(52)

50 Capítulo 5. Testes e Resultados

Figura 13: Mediana e Quartis de Redes Aleatórias e Livres de Escala

Figura 14: Comportamento do Agente Patogênico em Redes Aleatórias e Livre de Escala

5.2 Teste 2

A diferença do teste 1 , será considerado (𝜆 < 𝜆𝑐), em Redes Aleatórias e Livres de

Escala. Nas redes aleatórias , em 100% das repetiçoes o patôgeno não se espalhou, assim como nas redes livre de escala com 𝛾 =3.1. Já nas redes livre de escala com 𝛾=2.5 em aproximadamente 10% dos casos o agente patogênico se espalhou.Desses 10% dos casos que se espalharam foi analisado a mediana e calculado os quartis . Na Tabela 3 observa-se os dados utilizados para a implementação.Já na figura 15 observa-se colocou os resultados das Redes aleatórias , na qual observa-se que sempre se obteve resultado 0 , é dizer a doença desaparece, da mesma forma obten-se o mesmo resultados em Redes livres de Escala para 𝛾= 3.1. Já para 𝛾= 2.5 , só em aproximadamente 10% dos casos o resultado foi diferente de zero , como mencionado anteriormente. Desses 10% de casos , no qual a doença sobreviveu, se obteve os quartis e a mediana , como observado na figura 15. Já na figura 16 , observa-se um exemplo de como o agente se comporta em redes aleatórias e livres de escala através do tempo , quando 𝜆 > 𝜆𝑐

(53)

5.2. Teste 2 51

Tabela 3: Modelo SIS (𝜆 > 𝜆𝑐). )

Rede Aleatoria Rede livre de escala Rede livre de escala

n=10000 n=10000 n=10000 𝛽 = 0.1 𝛽 = 0.1 𝛽 = 0.1 <k>=6 <k>=6 <k>=6 - X𝑚𝑖𝑛 = 2 X𝑚𝑖𝑛 = 2 𝜇 = 0.8 𝜇 = 0.8 𝜇 = 0.8 - y=3.1 y=2.5

morre morre morre ou persiste

(54)

(55)

53

Conclusão

Os modelos Epidemiologicos SI, SIS e SIR se assemelham nas fases iniciais de uma epi-demia: Quando o número de indivíduos infectados é pequeno, a doença propaga-se livre-mente e o número de indivíduos infectados aumenta exponenciallivre-mente.Já para grandes momentos : No modelo SI todos torna-se infectados; no modelo SIS ou atinge um estado endêmico, em que uma fracção dos indivíduos são sempre infectados, ou um estado livre da doença em que a infecção morre; no modelo SIR todos os indivíduos se recuperam no final.

Já o número reprodutivo prevê o destino a longo prazo de uma epidemia: para 𝑅0 > 1 o patógeno persiste na população, enquanto que para 𝑅0 < 1 morre naturalmente.

Até agora os modelos consideraram a hipótese de mistura homogênea o que significa que todos os indivíduos tem em media <k> ligações , ou seja sem considerar a topología presente em redes de contato reais.

Dessa forma , para prever com precisão a dinâmica de uma epidemia, é preciso considerar o papel de uma rede de contatos. Ao considerar uma rede de contatos aleatorias, com dis-tribuição de poisson para grandes número de nós , a difusão da doença se comporta como nos modelos clássicos. Porém , as redes sociais, nas quais os patógenos se difundem apre-sentam uma distribuição da lei de Potencia,com 2>𝛾>3 na qual muitos nós tem poucas interações , enquanto poucos nós apresentam muitas ligações os quais são chamados de Hubbs. A presença destes nós requer que a modelagem matemática das doenças os incluía para assim ser analisados o limiar de epidemia. O desaparecimento do limiar de epidemia é uma consequência direta dos hubs. Se consideramos uma rede aleatória todos nós têm grau comparável, 𝑘 ≈< 𝑘 > , portanto, se a taxa de espalhamento está sob o limiar de epidemia, o patógeno não tem como se espalhar na população já que um patogéno que não consegue infectar outros nós antes o indivíduo infectado se recuperar, lentamente vai desaparecer da população. Numa rede sem escala, no entanto, mesmo se um patógeno é pouco infeccioso, se infecta um hubb, o hubb pode passá-lo para um grande número de outros nós, permitindo que o patógeno continue na população , verificando-se desta forma o desaparecimento do limiar de epidemia.

(56)

(57)

55

Referências

ANDERSON, R.; MAY, R. Infectious diseases of humans:dynamics and control.

Oxford University. Citado na página 21.

BARABASI. Emergence of scaling in random network. science, n. 286, p. 509–512, 1999. Citado 2 vezes nas páginas 21e 24.

BERNOULLI, D. Essai d’une nouvelle analyse de la mortalité causée par la petite vérole et de advantages de l’inoculation pour la prévenir. Mémorires de

Mathématiques et de Psique, 1760. Citado na página 33.

ERDOS; RENYI. On randon graphs. Publicationes Mathematicae, n. 6, p. 290–297, 1959. Citado 2 vezes nas páginas 24e 27.

EULER. Solutio problemat is ad geometriam situs pertinentis. Academiae

Scientiarum Imperialis, n. 8, p. 128–140, 1741. Citado na página 23.

FILHO, A.; M, R. Introdução á epidemiologia. 4a ed Guanabara Koogam, 2006. Citado na página 33.

GILBERT, . Randon graphs. The Annals of Mathematical Statistics, n. 30, p. 1141–1144, 1959. Citado na página 27.

NEWMAN, M. The structure and function of complex networks. Siam Review, n. 45, p. 11–19, 2003. Citado na página 23.

PARETO, . Cours d’economie politique. Librairie Droz, p. 299–345, 1964. Citado na página 29.

PRICE, D. S. Networks of scientific papers. Sciencie, n. 149, p. 510–515, 1965. Citado na página 38.

ROSEN. Matematica discreta e suas aplicaçoes. 2009. Citado na página 24. SANTORRAS, P.; VESPIGNANI. Epidemic spreading in scalefree. Physical

Review Letters, n. 86, p. 3200–3203, 2001. Citado na página 21.

VERHULST, P. F. Notice sur la loi que la population poursuit dans son

accroissement. Correspondance mathématique et physique, n. 10, p. 113–121, 1838. Citado na página 36.

W, K.; KENDRICK, M. A contribution to the mathematical theory of epidemics.

Proccedings of the Royal Society of London Series A Mathematical and Physical Sciences, n. 115, p. 700–721, 1927. Citado na página 33.

(58)

(59)

(60)

(61)

59

APÊNDICE A – Criação de uma rede com

distribuiçao livre de escala

para criar uma rede com distribuiçao livre de escala será usado o modelo de Configuração. Será explicado este modelo e logo como foi gerado uma sequencia de numeros que sigam a distribuição da lei de potencia

Modelo de Configuração com uma sequencia pre definida pode-se construir uma rede

livre de escala , como mostrado na figura 14.a Na rede gerada pelo modelo de configuração cada no tem um grau 𝐾𝑖 predefinido , passando a se fazer as conexoes aleatoriamente.

Dessa forma , ao aplicar este procedimento varias vezes com a mesma sequencia de graus dos nós pre definida se pode obter diferentes redes como mostrado na figura 14.b

Figura 17: a)serie predefinida; b)redes formadas com a series predefinidas em a

A probabilidade de ter uma ligaçao entre os nós de grau 𝑘𝑖 e 𝑘𝑗 é

𝑃𝑖𝑗 =

𝐾𝑖𝐾𝑗

(2𝐿 − 1) (A.1)

Obtemos uma rede com nós ligados a si mesmos e ligaçoes multiplas entre os mesmos nós , podemos rejeitar isso , porém isso significa que nem todos os emparelhamentos possíveis aparecem com igual probabilidade e dessa forma a igualdade encima nao será valida. Além disso ao aumentar 𝑁 a quantidade de auto-ligaçoes e multi-ligaçoes serão insignificantes. Dessa forma não será excluído

Geração de uma sequencia de numeros com Graus de distrituição livre de Escala

Sequência de grau de uma rede é uma sequência de graus de nó. Assim, na figura 6.a temos a sequencia 3,2,2,1. Com essa sequencia podemos formar diversas redes como mostrado na figura

(62)

60 APÊNDICE A. Criação de uma rede com distribuiçao livre de escala

Para gerar uma sequência de grau a partir de um grau de distribuição pré-definida que começam a partir de um grau de distribuição pré-definida analiticamente, como

𝑝𝑘= 𝑘−𝑦 (A.2)

mostrada na Figura 4.16a.

Nosso objetivo é gerar uma sequência grau 𝑘1, 𝑘2, ..., 𝑘𝑁 que seguem o 𝑝𝑘 distribuição.

Começamos por calcular a função Acumulada , a qual é :

𝑦 = 1 − 𝑥𝑚𝑖𝑛𝑒𝑥𝑝−1𝑥1−𝑒𝑥𝑝 (A.3)

cujo gráfico concontramos na figura 5.3.1 cuja funçao inversa é:

𝑦 = [(1 − 𝑥)(𝑥𝑚𝑖𝑛

1−𝑒𝑥𝑝

)]1−𝑒𝑥𝑝 (A.4)

cujo grafico encontramos na figura 5.3.2. na qual o dominio é [0,1]

geramos N números aleatórios ri, i = 1, ..., n, escolhido de modo uniforme a partir da (0, 1) intervalo. Para cada ri colocamos na funçao inversa para assim obter o y que é o grau do nó . Note-se que a sequência de grau atribuído a um pk não é única - que pode gerar vários conjuntos de 𝑘1, ..., 𝑘𝑛 sequências compatíveis com o mesmo pk.

(63)

61

(64)

(65)

63

APÊNDICE B – Pseudocodigo de criação de

uma rede livre de escala e o

modelo SIS

Criando uma sequencia de numeros com grau de distribuição livre de escala

Criando uma matriz de adjacencia

(66)

(67)

65

APÊNDICE C – Codigo Fonte em Matlab de

uma rede livre de escala e o

modelo SIR

//CRIANDO UMA SERIE //xmin= minimo grau //exp =expoente n="entrar valor" xmin="entrar valor" exp= "entrar valor" D=rand(1,n) E=zeros(1,n); for i=1:n x=D(1,i); y=((1-x)*(xmin.(_{1 − 𝑒𝑥𝑝))).}(_{1/(1 − 𝑒𝑥𝑝));} E(1,i)=round(y); end E

//ACHANDO A MATRIZ ADJACENCIA //L numero de arestas

//F matriz 1 tem aresta, 0 nao tem aresta

//E vetor que informa o numero de aresta de cada no //M=2L=somatoria da quantidades de arestar(sempre par) E; n=length(E); F=zeros(n,n); G=zeros(n,n); M=0; for i=1:n

(68)

66 APÊNDICE C. Codigo Fonte em Matlab de uma rede livre de escala e o modelo SIR

M=E(1,i)+ M; end

//criando uma matriz F com probabilidades de conexão for i=1:n for j=(i+1):n F(i,j)= (E(1,i)*E(1,j))/(M-1); b=rand ; if F(i,j)>b G(i,j)=1; G(j,i)=1;//colocar na simetrica end end end F G //MODELO SIR //B taxa infeçao //t tempo(iteraçoes) //i vetor infetados //u taxa recuperaçao t="Entrar valor" B="entrar valor; I="entrar valores; u="entrar valor; G; V= zeros(1,length(G)); for i=1:length(I) m=I(1,i); V(1,m)=1; end