Grafos eulerianos e identidades polinomiais na álgebra Mn(K)

CENTRO DE CIÊNCIAS EXATAS E DE TECNOLOGIA

PROGRAMA DE PÓS GRADUAÇO EM MATEMÁTICA

Fernanda Sabio Gonçalves

Grafos Eulerianos e Identidades Polinomiais na

Álgebra

M

n

(

K

)

São Carlos - SP

CENTRO DE CIÊNCIAS EXATAS E DE TECNOLOGIA

PROGRAMA DE PÓS GRADUAÇO EM MATEMÁTICA

Grafos Eulerianos e Identidades Polinomiais na

Álgebra

M

n

(

K

)

Fernanda Sabio Gonçalves

Orientador: Prof Dr. Humberto Luiz Talpo

Bolsista CAPES

Dissertação apresentada ao Programa de

Pós-Graduação em Matemátia da UFSCar

omo parte dos requisitos para a obtenção

do título de Mestre emMatemátia.

São Carlos - SP

Ficha catalográfica elaborada pelo DePT da

Biblioteca Comunitária da UFSCar

G635ge

Gonçalves, Fernanda Scabio.

Grafos eulerianos e identidades polinomiais na álgebra

M

n

(K)

/ Fernanda Scabio Gonçalves. -- São Carlos :

UFSCar, 2013.

81 f.

Dissertação (Mestrado) -- Universidade Federal de São

Carlos, 2013.

1. Álgebra. 2. Identidades polinomiais. 3. Matrizes

(Matemática). 4. Grafos eulerianos. I. Título.

Agradeço,primeiramente,aDeuspelavidaepelasinúmerasbênçãosreebidas.

AosmeuspaisAdrianoeMargarete, meuirmãoVitoremeunamoradoHélio,

peloapoio,inentivo e ompreensão.

A meu orientador, Prof. Humberto Luiz Talpo, pelapaiênia e dediação.

A todos os meus amigos matemátios,pelaonvivênia tão agradável e pelas

horas de estudo.

A meus amigos não matemátios, que, mesmo não entendendo muito bem o

queestudo,sempreforampaientes emeenorajavamnosmomentosde diuldade.

Aos professores do Departamento de Matemátia, pelos ensinamentos e por

despertar em mimodesejo de ontinuar estudando Matemátia.

Porm, agradeço àCAPES e aoProgramade ApoioaoPlano de

Neste trabalhoapresentamos algumasapliaçõesde Teoria de Grafosemproblemas

envolvendoidentidadespolinomiaisparaaálgebradasmatrizes

M

n

(

K

)

. Umabreve apresentação de PI-teoria e de alguns oneitos de Teoria de Grafos, omo a

de-nição de grafos eulerianos, que são os elementos básios desta abordagem, foram

apresentadaspara tornarotextoautoontido. São expliitadasduas demonstrações

distintas do Teorema de Amitsur-Levitzki, a de Razmyslov e uma deorrente do

Teorema de Swan - um resultado importante a respeito de grafos eulerianos. Por

m, um resultado semelhanteaoTeorema de Amitsur-Levitzkipara matrizes

antis-simétrias é demonstrado utilizando elementos de Teoria de Grafos. Ressaltamos

que o entendimento da ténia utilizada torna possível a simpliação de diversos

resultadose temsemostrado uma importanteferramentanoestudode PI-álgebras.

Palavras-have: Identidades polinomiais. Álgebra das matrizes. Grafos

In this work we present some appliations of graph theory in problems involving

polynomialidentitiesfor thealgebra

M

n

(

K

)

. A briefpresentationof PI-theoryand some onepts of graph theory, suh asthe denition of Eulerian graphs,whihare

the basielements ofthis work, were presented tomakethe textself-ontained. We

showtwo dierent proofs of the Amitsur-Levitzki theorem, the proof of Razmyslov

andother duetoSwan's theorem -animportantresultonEuleriangraphs. Finally,

a similar result of the Amitsur-Levitzki's theorem for skew-symmetri matries is

proved usingelementsofgraphtheory. Weemphasizethatthe understandingofthe

tehniquemakesitpossibletosimplifymanyresultsandhasbeen animportanttool

inthe study of PI-algebras.

Introdução 11

1 Álgebras om Identidades Polinomiais 13

1.1 Propriedades Básias de Álgebras . . . 13

1.2 Identidades Polinomiais. . . 18

1.3 PolinmiosMulti-homogêneos e Multilineares . . . 22

1.4 PolinmiosPróprios. . . 28

1.5 O Teorema de Amitsur-Levitzki . . . 29

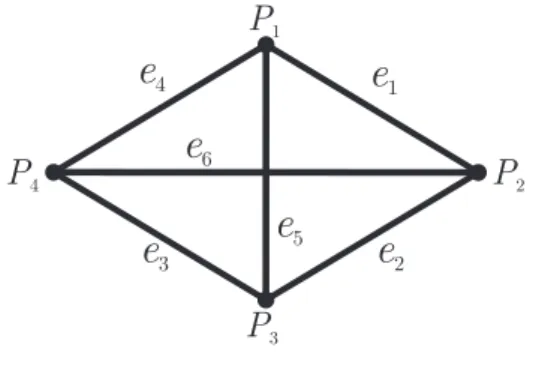
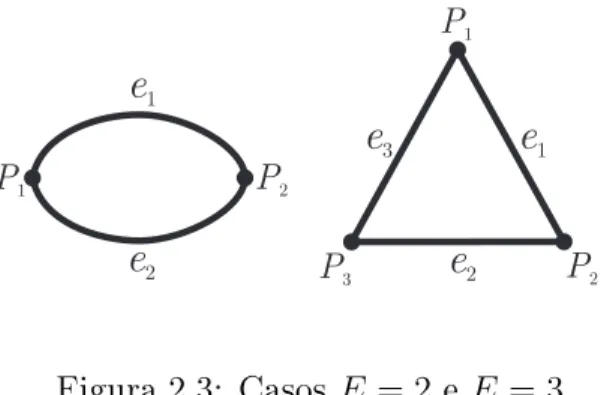
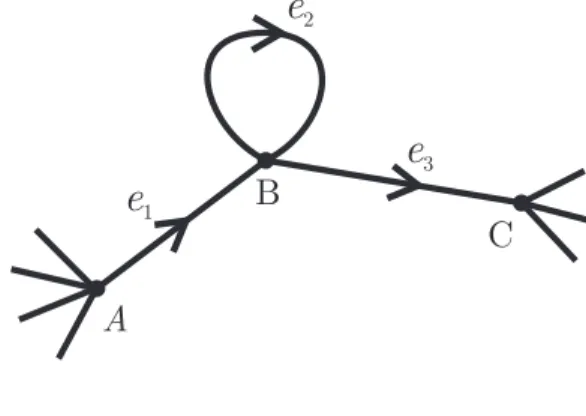
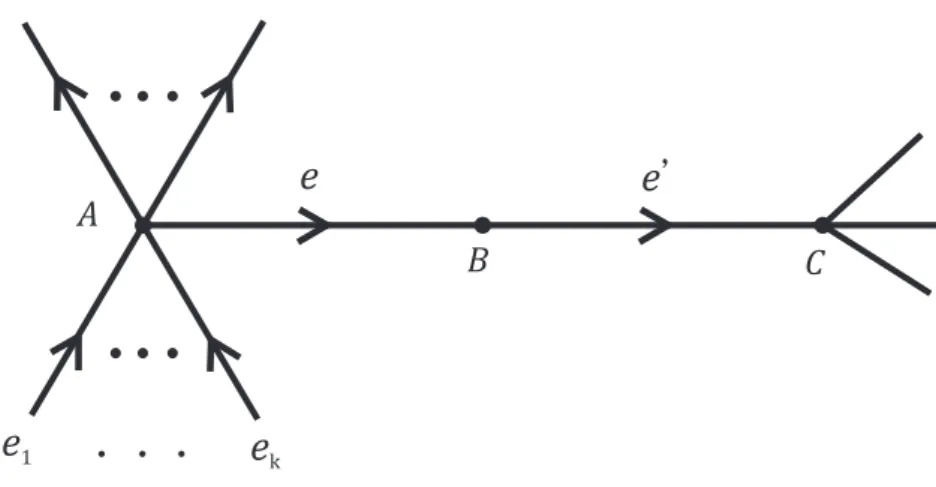
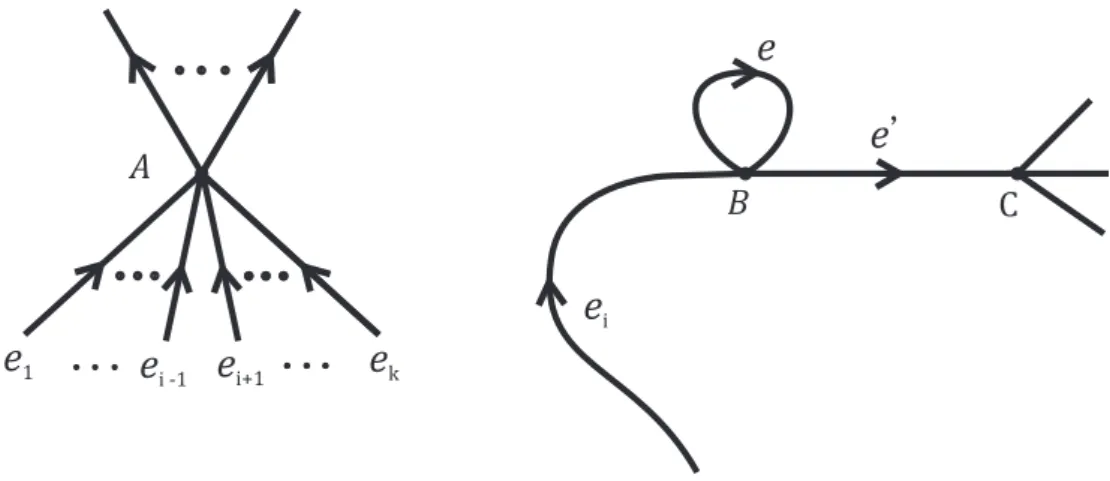
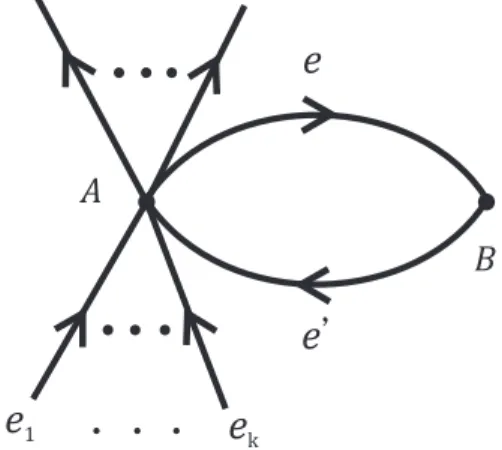
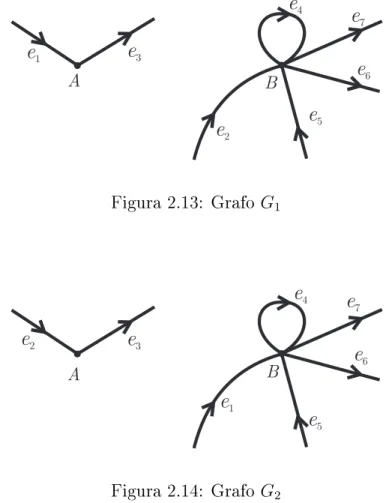
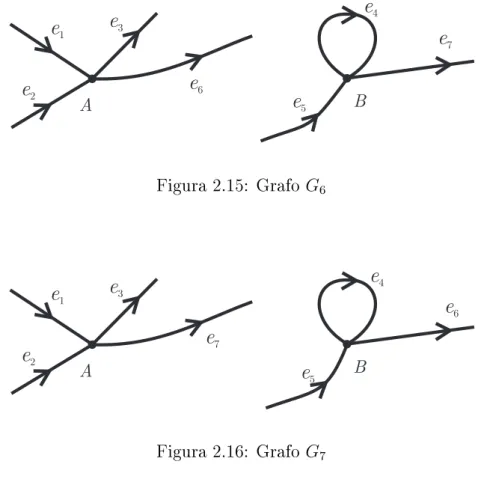
2 Grafos Eulerianos 38 2.1 Teoria de Grafos . . . 38

2.2 O Teorema de Swan . . . 44

3 Apliações da Teoria de Grafos à PI-álgebra 54 3.1 O Teorema de Amitsur-Levitzki . . . 55

3.2 Identidades Polinomiaispara Matrizes Antissimétrias. . . 57

O estudo das álgebras om identidades polinomiais (ou PI-álgebras) é algo

onsiderado reente na história da matemátia. Teve iníio na déada de 40,om

a publiação de alguns trabalhos de matemátios omo Jaobson, Kaplansky e

Le-vitzki, mas se intensiou por volta de 1950, quando foi provado o Teorema de

Amitsur-Levitzki, que garante a existênia de uma identidade polinomial de grau

2

n

para a álgebra das matrizes

n

×

n

sobre um orpo

K

. Este resultado possui

diversas demonstrações, baseadas emténias distintas. A demonstração original é

baseada em argumentos ombinatórios e, posteriormente, surgiram outras versões,

omoasde Razmyslov([10℄)ede Rosset([11℄),queutilizamargumentosalgébrios.

Entretanto, estas demonstrações são trabalhosas, apesar de envolverem

on-eitos elementares. Na tentativa de simpliá-las, Swan ([13℄) enontrou, em 1963,

uma demonstração bastantelara utilizandoTeoria de Grafos. A grande vantagem

desta ténia é que argumentos algébrios mais elaborados podem ser vistos omo

oneitos geométrios básios, apenas identiando o grafo adequado aoproblema.

Desde então, a Teoria de Grafos vem sendo uma importanteferramenta no estudo

de identidadespolinomiaspara matrizes.

Este trabalho tem omo objetivo estudar a apliação de Teoria de Grafos à

PI-álgebras. A m de ilustrar a importâniadesta abordagem, o primeiroapítulo

traz a demonstração de Razmyslov para o Teorema de Amitsur-Levitzki, e

algu-mas observações importantes aera deste resultado. Também é feita uma breve

exposição de alguns oneitos básios de PI-teoria.

No segundo apítulo denimosos elementosde Teoria de Grafosutilizadosao

polinomiaisdematrizes, queinluiademonstraçãodoTeoremadeAmitsur-Levitzki

feitaporSwan ([13℄ e[14℄),e de um resultado semelhantepara matrizes

Álgebras om Identidades

Polinomiais

Nesteapítuloapresentamosalgunsoneitoseresultadosbásiosarespeitode

identidadespolinomiais,tendoomoreferêniasoslivrosdeDrensky[3℄eGiambruno

e Zaiev [5℄, e as notas do miniurso Introdução às PI-álgebras, ministrado por

Brandão [2℄durante o Verão de 2013, naUniversidade Federal de São Carlos.

Grande parte do que abordamosnesta primeira etapa do trabalho não é

uti-lizada nos apítulos seguintes. No entanto, são onteúdos lássios e optamos por

inluí-lospara possíveis onsultas.

1.1 Propriedades Básias de Álgebras

Esta primeiraseção introduz o objetobásio deste estudo: álgebrassobre um

orpo

K

esuaspropriedades. Veremosdiversosexemploslássiosdeálgebras,omo aálgebra tensoriale a de Grassmann.

Denição1.1.1. Seja

K

umorpoe

A

umespaçovetorialsobre

K

. Dizemosque

A

éumaálgebra(ou

K

-álgebra)se estádenidaumaoperaçãobinária

∗

:

A×A

−→

A

, hamadade multipliação, tal que para quaisquer

a, b, c

∈

A

e qualquer

λ

∈

K

(

a

+

b

)

∗

c

=

a

∗

c

+

b

∗

c,

λ

(

a

∗

b

) = (

λa

)

∗

b

=

a

∗

(

λb

)

.

Neste texto, denotaremos

a

∗

b

por

ab

para simpliar a notação. O produto

a

1

a

2

a

3

é denido por

(

a

1

a

2

)

a

3

e, indutivamente,

a

1

a

2

· · ·

a

n

é o produto

(

a

1

a

2

· · ·

a

n

−

1

)

a

n

. Dizemos que um subonjunto

β

é uma base da álgebra

A

se é

base de

A

omo espaço vetorial e a dimensão de

A

é sua dimensão omo espaço vetorial. Se aálgebra

A

for umespaçovetorialde dimensão nitasobre

K

,dizemos que

A

é uma álgebrade dimensão nita. Emgeral, os resultados de álgebra linear para espaçosvetoriais tambémsão válidospara álgebras.

Observemos que se a álgebra

A

possui base

{e

i;

i

∈

I}

, então a multipliação em

A

é obtidaa partir damultipliação dos elementos dabase:

e

i

∗

e

j

=

X

k

∈

I

α

k

ij

e

k

, α

k

ij

∈

K

onde, para

i

e

j

xados, apenas um número nito de

α

k

ij

são não nulos. Por outro

lado, dados uma base arbitrária

{e

i;

i

∈

I}

do espaço vetorial

A

e um onjunto de elementos

α

k

ij

∈

K

tais que, para

i

e

j

xados, apenas um número nito de

α

k

ij

são

não nulos, podemosdenir a multipliação em

A

por

X

i

∈

I

ξ

i

e

i

!

∗

X

j

∈

I

η

j

e

j

!

=

X

i,j

∈

I

ξ

i

η

j

(

e

i

∗

e

j

)

, e

i

∗

e

j

=

X

k

∈

I

α

k

ij

e

k

.

A álgebra

A

é assoiativa se

(

ab

)

c

=

a

(

bc

)

para quaisquer

a, b, c

∈

A

, e é omutativa se

ab

=

ba

para quaisquer

a, b

∈

A

. Dizemos ainda que

A

é unitária se a multipliação possuir elemento neutro, isto é, se existe elemento

1A

∈

A

tal que

1A

a

=

a

1A

=

a

para qualquer elemento

a

∈

A

.

Quandoaálgebra

A

satisfazasondições

a

2

₌

_aa

_{= 0}

e

(

ab

)

c

+(

bc

)

a

+(

ca

)

b

= 0

(identidade de Jaobi),

A

é hamada de álgebra de Lie. Se existe

n

∈

N

tal que o produtode quaisquer

n

+ 1

elementosde

A

(omqualquerdisposiçãode parênteses) é igual a zero,

A

é nilpotente. Neste aso, o menor

n

que satisfaz esta ondição é dito índie de nilpotênia de

A

. Para o aso de existir

n

∈

N

tal que

a

n

_{= 0}

para

qualquer

a

∈

A

, dizemosque

A

é um álgebra nil de índie limitado.

Exemplo1.1.2. Oespaçodospolinmiosem

n

variáveisomutativas, denotadopor

K

[

x

1

, x

2

, . . . , x

n]

, é uma

K

-álgebra assoiativa, omutativa e unitária, om relação

Exemplo1.1.3. O espaçodas matrizes

n

×

n

omoeientesem

K

, denotadopor

M

n(

K

)

, é uma

K

-álgebra assoiativa e unitária, om relação ao produto usual de

matrizes. Notemos que esta álgebra não é omutativa. Nesta álgebra, destaamos

as matrizes unitárias

E

ij

, para

1

≤

i, j

≤

n

, onde

E

ij

é a matriz uja únia entrada não nula é

1

na

i

-ésima linha e

j

-ésima oluna. Estas matrizes formam uma base para

M

n(

K

)

, onde dim

M

n(

K

) =

n

2

.

De maneira geral, pode-se veriar queo espaço vetorial

M

n(

A

)

, o espaço das matrizes

n

×

n

sobre uma álgebra

A

, é uma álgebra om as operações usuais de matrizes.

Exemplo 1.1.4 (Álgebra de Grassmann). Seja

V

um espaço vetorial om base ordenada

{e

1

, e

2

. . .}

. Denimos a álgebra de Grassmann (ou álgebra exterior) de

V

, denotadapor

E

=

E

(

V

)

, omo sendo a álgebra om base

{

1E

, e

i

1

e

i

2

. . . e

i

k

|i

1

< i

2

< . . . < i

k

, k

≥

1

}

e om produto denido pela relação

e

i

e

i

= 0

e

e

i

e

j

=

−e

j

e

i

.

É onveniente esrever

E

=

E

(0)

_⊕

_E

(1)

, onde

E

(0)

=

he

i

1

. . . e

i

2

k

|

1

≤

i

1

< . . . < i

2

k

, k

≥

0

i

,

E

(1)

=

e

i

1

. . . e

i

2

k

+1

|

1

≤

i

1

< . . . < i

2

k

+1

, k

≥

0

.

Como

e

i

e

j

=

−e

j

e

i

, temos que

(

e

i

1

. . . e

i

r

)(

e

j

1

. . . e

j

s

) = (

−

1)

rs

₍

_e

j

1

. . . e

j

s

)(

e

i

1

. . . e

i

r

)

para quaisquer

r, s

∈

N

. Logo,

ax

=

xa

para quaisquer elementos

a

∈

E

(0)

e

x

∈

E

, e

bc

=

−cb

para quaisquer elementos

b, c

∈

E

(1)

. Com o mesmo argumento, é fáil

veriar que

E

(0)

_E

(0)

₊

_E

(1)

_E

(1)

_⊆

_E

(0)

e

E

(0)

_E

(1)

₊

_E

(1)

_E

(0)

_⊆

_E

(1)

.

Exemplo 1.1.5 (Álgebra Tensorial). Sejam

V

e

W

espaços vetoriais de dimensão nita sobre um mesmo orpo

K

. O produto tensorial entre

V

e

W

,

V

⊗

W

, é o espaço vetorial das apliações bilineares

Dados

v

∈

V

e

w

∈

W

, o produto tensorial

v

⊗

w

é o funional bilinear ujo valor em

(

α, β

)

∈

V

∗

_×

_W

∗

é dado por

(

v

⊗

w

)(

α, β

) =

α

(

v

)

·

β

(

w

)

.

Demaneirageral,se

V

1

, V

2

, . . . , V

s

sãoespaçosvetoriaissobreummesmoorpo

K

, o produto tensorial

V

1

⊗

V

2

⊗

. . .

⊗

V

s

é o espaço das apliações multilineares

denidas em

V

∗

1

⊗

V

2

∗

⊗

. . .

⊗

V

s

∗

f

:

V

₁

∗

⊗

V

₂

∗

⊗

. . .

⊗

V

s

∗

−→

K

tal que

(

v

1

⊗

v

2

⊗

. . .

⊗

v

s)(

α

1

, α

2

, . . . , α

s) =

α

1

(

v

1

)

·

α

2

(

v

2

)

. . . α

s(

v

s)

.

Quando os fatores deum produto tensorial sãotodos iguais, denotamos o

pro-duto de

s

ópias de

V

por

N

s

V

ou

V

⊗

s

. A somadesses produtos dene o espaço

T

(

V

) =

X

s

≥

0

V

⊗

s

_,

onde

V

⊗

0

=

K

e

V

⊗

1

=

V

. Comoprodutotensorial,

T

(

V

)

éumaálgebraassoiativa om unidade.

Sejam

B

umalasse deálgebrase

A

∈ B

uma álgebragerada porumonjunto

X

. Dizemos que

A

é livremente geradapor

X

na lasse

B

se, paraqualquer álgebra

B

∈ B

, toda apliação

X

→

B

pode ser estendida a um homomorsmo

A

→

B

.

Exemplo 1.1.6. Para qualquer onjunto

X

, a álgebra polinomial

K

[

X

]

é livre na lasse de todas as álgebras assoiativas omutativas unitárias.

O oneito de álgebra generaliza as noções de espaços vetoriais e de anéis.

Assim, também podemosonsiderar subálgebras e ideaisde uma álgebra,onforme

adenição aseguir.

Denição 1.1.7. O subespaço

S

da álgebra

A

é uma subálgebra se é fehado em relaçãoàmultipliação,isto é,se paraquaisquer

s

1

, s

2

∈

S

,

s

1

∗s

2

∈

S

. Asubálgebra

I

é hamada de ideal à esquerda de

A

se

A

∗

I

⊆

I

, isto é, se

a

∗

i

∈

I

para todo

a

∈

A, i

∈

I

. Analogamente, denimos ideal à direita e ideal bilateral, geralmente

Exemplo 1.1.8. O subespaço das matrizes triangulares superior,

U

n(

K

)

, é uma subálgebra de

M

n(

K

)

.

Tambémde maneiraanálogaàsdemaisestruturasalgébrias,denimos

homo-morsmos entre

K

-álgebras, omosegue.

Denição 1.1.9. O homomorsmo de espaços vetoriais

φ

:

A

−→

B

das álgebras

A, B

é um homomorsmo (de álgebras) se

φ

(

a

∗

b

) =

φ

(

a

)

∗

φ

(

b

)

. Analogamente,

introduzimosos oneitos de isomorsmo, automorsmo, endomorsmo,et.

Os resultados usuais referentes a homomorsmosde espaços vetoriais,grupos

e anéis ontinuam válidos para homomorsmosde álgebras. Por exemplo, sendo

A

uma álgebra e

I

um ideal de

A

, denimos a álgebra quoiente de

A

por

I

, onde o produtoédadopor

(

a

+

I

)(

b

+

I

) =

ab

+

I

,para

a, b

∈

A

. TambémtemosoTeorema doIsomorsmo, enuniado aseguir.

Teorema 1.1.10. Seja

φ

:

A

−→

B

um homomorsmodeálgebras. Entãoo núleo de

φ

ker(

φ

) =

{a

∈

A|φ

(

a

) = 0

}

é um ideal bilateral de

A

e a álgebra quoiente

A/

ker

φ

é isomorfa à imagem Im

(

φ

) =

{φ

(

a

)

|a

∈

A}

.

O exemplo a seguir mostra omo obter uma álgebra om unidade a partir de

uma álgebra

A

dada. Esta onstrução é hamada de adjunção formal da unidade a

A

.

Exemplo 1.1.11. Seja

A

uma álgebra e onsideremos o espaço vetorial

K

⊕

A

=

{

(

λ, a

)

|λ

∈

K, a

∈

A}

.

Denindo em

K

⊕

A

a multipliação

(

λ

1

, a

1

)(

λ

2

, a

2

) = (

λ

1

λ

2

, λ

1

a

2

+

λ

2

a

1

+

a

1

a

2

)

,

Emtodaálgebra

A

om unidade, identiamos

λ

1A

om

λ

para todo

λ

∈

K

e

K

é onsideradoo subespaço vetorial de

A

gerado por

K

.

Denição 1.1.12. O omutador de omprimento

n

, om

n >

1

, é denido induti-vamente omo

[

a

1

, a

2

] =

a

1

a

2

−

a

2

a

1

,

[

a

1

, . . . , a

n

−

1

, a

n] = [[

a

1

, . . . , a

n

−

1

]

, a

n]

.

É laro que

[

a, b

] = 0

se,e somentese,

ab

=

ba

. Empartiular

[

a, a

] = 0

. Utili-zando apenas adenição de omutador,veriamos failmenteque,para quaisquer

a, b, c

∈

A

, vale

[

ab, c

] =

a

[

b, c

] + [

a, c

]

b.

De maneira mais geral, usando induçãonita e a igualdade aima, mostra-se

que

[

a

1

. . . a

n

, c

] =

n

X

i

=1

a

1

. . . a

i

−

1

[

a

i

, c

]

a

i

+1

. . . a

n

.

Tambémé fáilveriarque

[

a, b, c

] + [

b, c, a

] + [

c, a, b

] = 0

para quaisquer

a, b, c

∈

A

. Assim, ao onsiderarmos a multipliação no anel

A

denida por

[

,

] :

A

×

A

−→

A

(

a, b

)

7−→

[

a, b

] =

ab

−

ba

temos que

(

A,

[

,

])

é uma álgebra de Lie.

1.2 Identidades Polinomiais

Fixemos um onjuntoinnito (enumerável)

X

=

{x

1

, x

2

, . . .}

,ujos elementos serão hamados de variáveis. Uma palavra em

X

é uma sequênia

x

i

de elementos de

X

, onde

n

é o tamanho da palavra e,aso

n

= 0

, temos a palavra vazia denotada por

1

.

Seja

K

umorpoedenotemospor

S

(

X

)

oonjuntode todasaspalavrasem

X

, inlusive a palavra vazia

1

. Tais palavras são hamadas de monmios e o produto

de dois monmios é dado por justaposição. Duas palavras

x

i

1

. . . x

i

n

e

x

j

1

. . . x

j

m

são iguais se

n

=

m

e

i

k

=

j

k

para

k

= 1

, . . . , n

. Denimos

K

hXi

omo sendo o

K

-espaço vetorial om base

S

(

X

)

, isto é, é o onjunto dos polinmios om

oei-entes em

K

e variáveis não omutativas

x

i

∈

X

.

K

hXi

é uma álgebra, hamada de álgebra assoiativa livre, livremente gerada por

X

sobre

K

. Se

f

∈

K

hXi

, es-revemos

f

(

x

1

, . . . , x

n)

para indiar que

x

1

, . . . , x

n

∈

X

são as únias variáveis que apareem em

f

.

A álgebra

K

hXi

é denida, a menos de isomorsmos, pela seguinte proprie-dade universal: dada uma

K

-álgebraassoiativa

A

, qualquer apliação

h

:

X

→

A

, om

h

(

x

i) =

a

i

, pode ser estendida de formaúniaaum homomorsmode álgebras

φ

h

:

K

hXi →

A

, tal que

φ

h(

x

i

1

. . . x

i

n

) =

a

i

1

. . . a

i

n

. No aso de

A

ser unitária, temos também a ondição

φ

h(1) = 1A

. Assim, se

f

=

f

(

x

1

, . . . , x

n)

∈

K

hXi

, deno-tamos por

f

(

a

1

, . . . , a

n)

a imagem de

f

por

φ

h

, ou seja, basta substituir

x

i

por

a

i

em

f

.

Denição 1.2.1. Seja

f

=

f

(

x

1

, . . . , x

n)

∈

K

hXi

e seja

A

uma álgebra (assoia-tiva). Dizemosque

f

é uma identidade polinomial para

A

se

f

(

a

1

, . . . , a

n) = 0

, para todos

a

1

, . . . , a

n

∈

A

,

que denotaremos por

f

(

x

1

, . . . , x

n)

≡

0

.

Se a álgebra

A

satisfaz uma identidade polinomial não trivial

f

, dizemos que

A

é uma álgebraom identidade polinomial ou PI-álgebra.

É interessante observar que se

f

=

f

(

x

1

, . . . , x

n)

∈

K

hXi

é uma identidade polinomial, então

f

tem termo onstante nulo. Além disso,

f

é uma identidade polinomialde

A

se,esomentese,

f

pertene aosnúleosdetodososhomomorsmos de

K

hXi

em

A

.

Exemplo 1.2.2. Se

A

é uma álgebra omutativa, então o polinmio

f

(

x

1

, x

2

) = [

x

1

, x

2

]

é uma identidade polinomial de

A

.

Exemplo 1.2.3. Qualquer álgebra nilpotente é uma PI-álgebra. Com efeito, se

A

n

_{= 0}

para algum

n

≥

1

, então o polinmio

x

1

. . . x

n

é uma identidade polinomial de

A

.

Exemplo 1.2.4. Se

A

é uma álgebra nil de índie limitado, digamos

n

, então o polinmio

x

n

é uma identidadepolinomial de

A

.

Exemplo 1.2.5. Seja

U

n(

K

)

a álgebra das matrizes triangulares superior om oe-ientes em

K

.

U

n(

K

)

é uma PI-álgebra, pois satisfaz a identidade

[

x

1

, x

2

]

. . .

[

x

2

n

−

1

, x

2

n]

≡

0

.

De fato, o omutador de quaisquer duas matrizes triangulares superior é uma

matriztriangular superior om diagonal nula,que éumamatriz nilpotentede índie

n

.

Exemplo1.2.6. A álgebra

M

2

(

K

)

satisfaz aidentidade

[[

x

1

, x

2

]

2

_{, x}

3

]

≡

0

, hamada

de identidadedeHall. Comefeito,bastanotarmosque,se

a

∈

M

2

(

K

)

,seupolinmio araterísitoé

x

2

₋

tr

(

a

)

x

+ det (

a

)

, onde tr

(

a

)

é o traço de

a

e

det(

a

)

seu determi-nante. Então, noasode

a

serumomutador,temos tr

(

a

) = 0

e

a

2

_{+det (}

_a

₎

_·I

2

= 0

,

de onde

a

2

₌

₋

_{det (}

_a

₎

_·

_I

2

. Logo

a

2

é uma matriz esalar, que omutaom qualquer

outra matriz.

Exemplo1.2.7. O polinmio

[

x

1

, x

2

, x

3

]

éuma identidadepolinomialda álgebrade Grassmann

E

. Basta observarque

[

a, b

]

∈

E

(0)

paraquaisquer

a

,

b

∈

E

, logoomuta om qualquer elemento de

E

.

Consideremos opolinmio

s

n(

x

1

, . . . , x

n) =

X

σ

∈

S

n

(

−

1)

σ

x

σ

(1)

. . . x

σ

(

n

)

,

onde

S

n

éogruposimétriosobre

n

elementose

(

−

1)

σ

Exemplo1.2.8. Em 1950, AmitsureLevitzki provaram que

s

2

n(

x

1

, . . . , x

2

n)

é uma identidadepolinomial da álgebra

M

n(

K

)

. Este resultado é onheidoomo Teorema de Amitsur-Levitzki, que será abordado om maiores detalhes adiante.

Tendoemvistaosexemplosaima,seria possívelpensarqueasálgebrasmais

onheidas sãoPI-álgebras. Entretanto,éfáilverqueaálgebra

K

hXi

nãopossui identidadespolinomiaisnão nulas.

Dadauma álgebra

A

,denotamos por

T

(

A

)

oonjuntode todasasidentidades polinomiais de

A

. É laro que

A

é PI-álgebra se

T

(

A

)

6

=

{

0

}

. Se

A

1

e

A

2

são álgebras, dizemos que

A

1

e

A

2

são PI-equivalentes se

T

(

A

1

) =

T

(

A

2

)

. Álgebras isomorfas são semprePI-equivalentes, mas areíproanão é verdadeira.

O onjunto

T

(

A

)

é um ideal de

K

hXi

e, além disso, se

f

=

f

(

x

1

, . . . , x

n)

é umpolinmioem

T

(

A

)

,e

g

1

, . . . , g

n

são polinmiosarbitráriosem

K

hXi

,segueque

f

(

g

1

, . . . , g

n)

∈

T

(

A

)

.

Denotamos o onjunto de todos os endomorsmos de

K

hXi

por

End K

hXi

. Como qualquer elemento de

End K

hXi

é determinado pela apliação

x

7→

g

,

x

∈

X, g

∈

K

hXi

, segue que

T

(

A

)

é um ideal invariante sob todos os

endomor-smos de

K

hXi

. Osideais om esta propriedade são hamados de

T

-ideais.

Denição 1.2.9. Dizemos que um ideal

I

de

K

hXi

é um T-ideal se

ϕ

(

I

)

⊆

I

para todo

ϕ

∈

End KhXi

, ou equivalentemente, se

f

(

g

1

, . . . , g

n)

∈

I

para quaisquer

f

(

x

1

, . . . , x

n)

∈

I

e

g

1

, ...,

g

n

∈

K

hXi

.

Assim

T

(

A

)

é um

T

-ideal de

K

hXi

. Na verdade, todo

T

-ideal de

K

hXi

é o onjunto de identidadespolinomiaisde algumaálgebra. De fato, se

I

éum

T

-ideal, temos que

I

=

T

_K

_h

_X

_i

I

.

A interseção de uma famíliaqualquer de T-ideais éainda um T-ideal. Dessa

forma,dado um subonjunto

S

qualquer de

K

hXi

, denimos o T-ideal gerado por

S

, usualmente denotado por

hSi

T

, omo sendo a interseção de todos os T-ideais

de

K

hXi

queontêm

S

. Então

hSi

T

é o menorT-ideal de

K

hXi

ontendo

S

e, se

f

∈ hSi

T

, dizemosque

f

é onsequênia de

S

.

Se

A

é uma álgebra e

S

⊆

T

(

A

)

é tal que

T

(

A

) =

hSi

T

omo problema de Speht. Em 1987, Kemer deu uma resposta positiva para este

problema, mas seu trabalho não mostra omo determinar uma tal base nita e

portantonãoresolve oproblemadadesrição das identidadesde uma álgebra. Esta

questão ontinua em aberto até hoje, tendo sido resolvido apenas para algumas

álgebrasem partiular. Vejamos alguns exemplos.

Exemplo 1.2.10. Se

A

é uma álgebra omutativa e unitária qualquer e

K

é um orpoinnito, então

T

(

A

) =

h

[

x

1

, x

2

]

i

T

. Dizemosentão quetodas as identidades de

A

são onsequênias do polinmio

[

x

1

, x

2

]

.

Este exemplonos garanteaexistêniade álgebrasPI-equivalentesque nãosão

isomorfas.

Exemplo 1.2.11. Se

K

é um orpo innito de araterístia diferente de 2, então

T

(

E

) =

h

[

x

1

, x

2

, x

3

]

i

T

, onde

E

éa álgebra de Grassmann. (ver [2℄,Exemplo 4.0.40)

Exemplo 1.2.12. Em 1981 Drensky ([4℄) mostrou que as identidades polinomiais

s

4

(

x

1

, x

2

, x

3

, x

4

)

≡

0

,

[[

x

1

, x

2

]

2

, x

3

]

≡

0

formam umabase minimal para as identidades polinomiais de

M

2

(

K

)

.

Exemplo 1.2.13. Considere a álgebra

E

⊗

E

, onde

E

é a álgebra de Grassmann. Os polinmios

f

(

x

1

, x

2

, x

3

, x

4

, x

5

) = [[

x

1

, x

2

]

,

[

x

3

, x

4

]

, x

5

]

e

g

(

x

1

, x

2

) =

[

x

1

, x

2

]

2

, x

1

são identidades polinomiais de

E

⊗

E

. Em 1982, Popov ([9℄) mostrou que, em araterístia0, estes doispolinmiosformamuma base para as identidadesde

E

⊗

E

.

1.3 Polinmios Multi-homogêneos e Multilineares

Nesta seção generalizamos oneitos básios a respeito de polinmios, omo

grau e linearidade. Veremos também que, quando o orpo base

K

é innito, o estudodeidentidadespolinomiaisdeuma dadaálgebrapode serreduzida aoestudo

Denição 1.3.1. Sejam

u

∈

KhXi

um monmio,

f

∈

KhXi

um polinmio e

x

i

∈

X

. Denimos:

(a) O grau de

u

em

x

i

, denotado por

deg

x

i

u

, omo sendo o número de oorrênias de

x

i

em

u

.

(b) O grau de

f

em

x

i

, denotado por

deg

x

i

f

, omo sendo o maior grau em

x

i

de algum monmio de

f

.

Dizemos que um polinmio

f

∈

KhXi

é homogêneo em

x

i

se todos os seus monmiostêm omesmograuem

x

i

. Opolinmio

f

éditomulti-homogêneo quando é homogêneoem todas as variáveis. Se

u

=

u

(

x

1

, . . . , x

n)

é um monmiode

KhXi

, denimosomultigrau de

u

omosendoa

n

-upla

(

a

1

, . . . , a

n)

onde

a

i

= deg

x

i

u

. Para

f

∈

KhXi

,aomponente multi-homogênea de

f

é asoma de todos osmonmiosde

f

om um dado multigrau. Assim,

f

é multi-homogêneo se, e somente se, possui

uma únia omponente multi-homogênea. É laro que se

f

(

x

1

, . . . , x

n)

∈

K

hXi

é homogêneo de grau

k

em

x

i

e

λ

∈

K

,temos

f

(

x

1

, . . . , x

i

−

1

, λx

i

, x

i

+1

, . . . , x

n) =

λ

k

f

(

x

1

, . . . , x

i

−

1

, x

i

, x

i

+1

, . . . , x

n)

.

Em partiular, se

f

élinear em

x

i

,isto é,homogêneo de grau 1 em

x

i

, temos

f

(

x

1

, . . . , x

i

−

1

, λ

1

y

1

+

. . .

+

λ

m

y

m

, x

i

+1

, . . . , x

n) =

m

X

j

=1

λ

i

f

(

x

1

, . . . , x

i

−

1

, y

j

, x

i

+1

, . . . , x

n)

.

Quando

f

(

x

1

, . . . , x

n)

∈

K

hXi

é multi-homogêneo om multigrau

(1

, . . . ,

1)

, oumelhor, emada monmioada variável tem grau exatamente 1, dizemosque

f

é multilinear. Neste aso,

f

éda forma

X

σ

∈

S

n

α

σ

x

σ

(1)

. . . x

σ

(

n

)

,

om

α

σ

∈

K.

Denotamospor

P

n

osubespaçode todos ospolinmiosmultilinearesde

KhXi

nasvariáveis

x

1

,

x

2

,...,

x

n

. Éfáilverqueoonjunto

x

σ

(1)

x

σ

(2)

. . . x

σ

(

n

)

|

σ

∈

S

n

é umabase de

P

n

eassim

dimK

P

n

=

n

!

.

Consideremos agora

f

(

x

1

, x

2

, . . . , x

n)

∈

P

n

,

A

uma

K

-álgebrae

β

umonjunto gerador de

A

, omo espaço vetorial. Dados

a

1

,

a

2

, ...,

a

n

∈

A

, observemos que

onde

e

1

,

e

2

, ...,

e

n

∈

β

. Com isso, podemos onluir que

f

(

x

1

, x

2

, . . . , x

n)

é uma identidade polinomial de

A

se, e somente se,

f

(

e

1

, e

2

, . . . , e

n) = 0

para quaisquer

e

1

, e

2

, . . . , e

n

∈

β

. Emoutraspalavras,para veriarse um polinmiomultilinear

f

éuma identidade polinomialde

A

,basta veriar se

f

seanulaquandoavaliadoem elementosgeradores de

A

.

Este argumento nos permite mostrar que toda álgebra de dimensão nita é

uma PI-álgebra. Com efeito, se

A

é uma álgebra om

dim

A < n

, então

s

n

= 0

é uma identidade polinomial de

A

. Na verdade, omo a identidade standard é um polinmio multilinear, basta veriar que

s

n

= 0

para os elementos da base de

A

. Como

dim

A < n

, é neessário que

x

i

=

x

j

para algum

i

6

=

j

. Com isso, os termos de

s

n

(

x

1

, . . . , x

i

, . . . , x

i

, . . . , x

n)

se anulam dois a dois. Para ada

σ

∈

S

n

, existe

τ

∈

S

n

obtidaa partir de

σ

permutandoas posições de

x

i

. É laro que

σ

e

τ

tem

sinais opostos e, assim, ada termo

(

−

1)

σ

_x

σ

(1)

. . . x

σ

(

i

)

. . . x

σ

(

i

)

. . . x

σ

(

n

)

, é anulado por

(

−

1)

τ

_x

τ

(1)

. . . x

τ

(

i

)

. . . x

τ

(

i

)

. . . x

τ

(

n

)

. Logo,

s

n

= 0

. Oexemploabaixo ilustraesta situação.

Exemplo 1.3.2. Considere

n

= 3

e

dim

A

= 2

, om base

{a, b}

. Temos

S

3

(

x

1

, x

2

, x

3

) =

x

1

x

2

x

3

+ (

−

1)

(132)

x

3

x

1

x

2

+ (

−

1)

(123)

x

2

x

3

x

1

+ (

−

1)

(13)

_x

3

x

2

x

1

+ (

−

1)

(23)

x

1

x

3

x

2

+ (

−

1)

(12)

x

2

x

1

x

3

S

3

(

a, b, c

) =

aba

+

aab

+

baa

−

aba

−

aab

−

baa

= 0

.

Reordemos que uma identidade polinomial

f

≡

0

é onsequênia de

hSi

T

se

f

∈ hSi

T

. Dois onjuntos de identidades polinomiais que geram o mesmo

T

-ideal

são ditos equivalentes.

Teorema 1.3.3. Sejam

I

umT-idealde

KhX

i

e

f

(

x

1

, . . . , x

n)

∈

I

. Se

K

éinnito, entãoadaomponente multi-homogênea de

f

pertenea

I

. Consequentemente,

I

é gerado por seus polinmiosmulti-homogêneos.

Demonstração: Suponhamos

m

= deg

x

1

f

. Para ada

i

= 0

, 1, ...,

n

, tomemos

f

i

(

x

1

, . . . , x

n)

omo sendo a soma de todos os monmiosque têm grau

i

em

x

1

, ou

seja,

f

i

é aomponente homogêneade grau

i

em

x

1

. Temos então

f

=

Seja

V

=

hf

i

T

o

T

-ideal de

K

hXi

geradopor

f

. Como

K

éinnito,podemos esolher

λ

0

,

λ

1

,...,

λ

m

∈

K

todos distintos. Sendo

V

um

T

-ideal, temos

g

j

=

f

(

λ

j

x

1

, x

2

, . . . , x

n) =

f

0

+

λ

j

f

1

+

. . .

+

λ

m

j

f

m

∈

V,

para ada

j

= 0

,

1

, . . . , m.

Considerando estas equações omo um sistema linear om variáveis

f

i

,

i

= 0

,

1

, . . . , m

, temos

















1

λ

0

· · ·

λ

m

0

1

λ

1

· · ·

λ

m

1

. . . . . . . . . . . .

1

λ

m

· · ·

λ

m

m

































f

0

f

1

. . .

f

m

















=

















g

0

g

1

. . .

g

m

















.

Como

I

é um

T

-ideal, garantimos que

g

j

∈

I

, para

j

= 0

,

1

, . . . , m

. Além disso, a primeira matriz aima é a matriz de Vandermonde, ujo determinante é

Q

i<j

(

λ

j

−

λ

i)

6

= 0

. Logo, tal matriz é invertível, de onde obtemos que

f

0

, f

1

, . . . , f

m

∈

I

.

Agora, para ada

i

= 0

, 1, ...,

m

e ada

t

= 0

, 1, 2, ..., tomemos

f

it

omo sendoaomponentehomogêneaem

f

i

de grau

t

em

x

2

. Usandoosmesmos argumen-tosaima, onluímos que

f

it

∈

I

. Repetindo o proesso para ada variável, temos a primeira armação. Por m, observamos que

f

é a soma de suas omponentes multi-homogêneas e,portanto,

I

é gerado porseus polinmiosmulti-homogêneos.

Na prova doteorema abaixo utilizamosoproesso de multilinearização.

Teorema 1.3.4. Se aálgebra

A

satisfazumaidentidadepolinomialdegrau

k

, então satisfazumaidentidademultilineardegrau

≤

k

. Emoutraspalavras,todaPI-álgebra satisfaz alguma identidademultilinear não nula.

Demonstração: Seja

f

(

x

1

, . . . , x

n)

∈

KhXi

uma identidade polinomialde

A

. Se adavariável

x

i

satisfaz

deg

x

i

f

≤

1

,podemosrenomearasvariáveis(eventualmente, identiandoalgumasdelas om

0

),obtendo umaidentidadepolinomialmultilinear

Suponhamosentão quealgumavariável,digamos

x

1

,satisfaz

m

= deg

x

1

f >

1

. Tomemos

y

1

e

y

2

variáveis de

X

distintas de

x

1

, . . . , x

n

, e onsideramos um novo polinmioem

n

+ 1

variáveis, dado por

g

(

y

1

, y

2

, x

2

, . . . , x

n) =

f

(

y

1

+

y

2

, x

2

, . . . , x

n)

−

f

(

y

1

, x

2

, . . . , x

n)

−

f

(

y

2

, x

2

, . . . , x

n)

.

Este polinmio ainda é uma identidade polinomial de

A

. Basta veriar que é não nulo. Suponhamos que

g

= 0

. Como qualquer apliação

X

→

X

pode ser estendida a um endomorsmo de

KhXi

, substituindo

y

1

e

y

2

por

x

1

em

g

, ainda obtemosuma identidade polinomial,ouseja

g

(

x

1

, x

1

, x

2

, . . . , x

n) =

f

(2

x

1

, x

2

, . . . , x

n)

−

2

f

(

x

1

, . . . , x

n) = 0

.

Como

f

=

f

0

+

f

1

+

. . .

+

f

m

, onde

f

i

éasoma dos monmiosde grau

i

em

x

1

, temos

f

i(2

x

1

, x

2

, . . . , x

n) = 2

i

f

i(

x

1

, x

2

, . . . , x

n)

.

Assim,

f

0

+ 2

f

1

+

. . .

+ 2

m

f

m

= 2 (

f

0

+

f

1

+

. . .

+

f

m)

e

f

0

= (2

2

−

2)

f

2

+

. . .

+ (2

m

−

2)

f

m

,

ontradizendo

m

= deg

x

1

f >

1

. Então, omo

deg

y

1

g

=

m

−

1

, podemos repetir este proesso até queo polin-mioresultantesejalinearem

x

1

. Setalpolinmionãoformultilinear,om,digamos,

deg

x

2

=

d

≥

2

, apliamos o proesso para

x

2

, obtendo um polinmio linear em

x

1

e

x

2

. Proedendo desta maneira para todas as variáveis, obtemos uma identidade

polinmialmultilinearde

A

.

Este métodode multilinearizaçãotemuma importanteonsequênia,

apresen-tada noteoremaa seguir.

Demonstração: Como

K

é innito, pelo Teorema 1.3.3,

f

é equivalente ao onjunto de suas omponentes multi-homogêneas. Assim, podemos assumir que

f

=

f

(

x

1

, . . . , x

n)

é multi-homogêneo.

Apliaremos o proesso de multilinearizaçãoa

f

. Se

deg

x

1

f

=

m >

1

, esre-vemos

f

(

y

1

+

y

2

, x

2

, . . . , x

n) =

m

X

i

=0

f

i(

y

1

, y

2

, x

2

, . . . , x

n)

,

onde

f

i

é a omponente homogênea de grau

i

em

y

1

. Então todos os polin-mios

f

i

=

f

i(

y

1

, y

2

x

2

, . . . , x

n)

são onsequênias de

f

. Como

deg

y

j

f

i

< m

para

i

= 1

, . . . , d

−

1

e

j

= 1

,

2

, podemos repetir os argumentos e obter um onjunto de

polinmiosmultilineares que são onsequênias de

f

. Como

deg

y

1

f

i

=

i

,

deg

y

2

f

i

=

m

−

i

e

deg

x

k

f

i

= deg

x

k

f

, para

k

= 2

, . . . , n

, temos:

f

0

(

y

1

, y

1

, x

2

, . . . , x

n) =

f

(

y

1

, x

2

, . . . , x

n)

,

f

1

(

y

1

, y

1

, x

2

, . . . , x

n) =

mf

(

y

1

, x

2

, . . . , x

n)

,

.

.

.

f

m

−

1

(

y

1

, y

1

, x

2

, . . . , x

n) =

mf

(

y

1

, x

2

, . . . , x

n)

,

f

m(

y

1

, y

1

, x

2

, . . . , x

n) =

f

(

y

1

, x

2

, . . . , x

n)

.

Assim

f

i(

y

1

, y

1

, x

2

, . . . , x

m) =





m

i





f

(

y

1

, x

2

, . . . , x

m)

,

e os oeientes binomiaissão não nulos, pois har

K

= 0

. Logo, estas identidades multilineares são equivalentes a

f

.

O orolárioabaixo segue diretamentedoteorema.

Corolário 1.3.6. Se

I

é um T-ideal de

K

hXi

e har

K

= 0

, então

I

é gerado por seus polinmios multilineares.

portantequando trabalhamosomPI-álgebras,uma vez quesimpliaoestudodos

T

-ideais.

1.4 Polinmios Próprios

Sendo

X

=

{x

1

, x

2

, . . .}

, denotamos porCom

(

X

)

o onjunto

[

x

i

1

, x

i

2

, . . . , x

i

k

]

|

k

≥

2

, x

i

j

∈

X

,

onde

1

éoprodutodeumonjuntovaziodeomutadores. Seja

B

(

X

)

asubálgebrade

K

hXi

gerada por Com

(

X

)

. Ospolinmios

f

∈

B

(

X

)

são hamadosde polinmios

próprios.

O resultado a seguir garante que os elementos de

X

e de

B

(

X

)

formam uma base para

K

hXi

. A demonstração deste fato pode ser enontrada em[3, pág. 42℄.

Teorema 1.4.1. Se

f

(

x

1

, . . . , x

n)

∈

KhXi

, então existem polinmios

w

a(

x

1

, . . . , x

n)

∈

B

(

X

)

, onde

a

= (

a

1

, . . . , a

n)

∈

N

n

, tais que

f

(

x

1

, . . . , x

n) =

X

a

x

a

1

1

. . . x

a

n

n

w

a(

x

1

, . . . , x

n)

.

Isto signia que, dado um polinmioqualquer, podemos esrevê-lo naforma

apresentada no teorema, utilizando as propriedades do omutador. Vejamos um

exemplo.

Exemplo 1.4.2. Considere o polinmio

f

(

x

1

, x

2

, x

3

)

=

x

2

x

2

1

x

3

. Como

ab

=

ba

+ [

a, b

]

e

[

ab, c

] = [

a, c

]

b

+

a

[

b, c

]

, temos

x

2

x

2

1

x

3

=

x

2

1

x

2

x

3

+

x

2

, x

2

1

x

3

=

x

2

1

x

2

x

3

+ [

x

2

, x

1

]

x

1

x

3

+

x

1

[

x

2

, x

1

]

x

3

.

Agora, notemos que

[

x

2

, x

1

]

x

1

x

3

=

x

1

[

x

2

, x

1

]

x

3

+ [

x

2

, x

1

, x

1

]

x

3

x

1

[

x

2

, x

1

]

x

3

=

x

1

x

3

[

x

2

, x

1

] +

x

1

[

x

2

, x

1

, x

3

]

.

Então

x

2

x

2

1

x

3

=

x

2

1

x

2

x

3

+ 2

x

1

x

3

[

x

2

, x

1

] + 2

x

1

[

x

2

, x

1

, x

3

]

+

x

3

[

x

2

, x

1

, x

1

] + [

x

2

, x

1

, x

1

, x

3

]

Observemos que, onsiderando

a

1

=

. . .

=

a

n

= 0

no Teorema 1.4.1, temos uma base para

B

(

X

)

.

O teorema abaixo garante que as identidades polinomiais de uma

K

-álgebra, om

K

innito, são onsequênias das identidades próprias. Em partiular, se har

K

= 0

, então as identidades polinomiaisde uma

K

-álgebra são onsequênias das identidadesmultilinearespróprias.

Teorema 1.4.3. Se

K

é um orpo innito e

I

é um idealde

KhXi

, então

I

=

hI

∩

B

(

X

)

i

T

,

ou seja,

I

é gerado (omo T-ideal)por seus polinmios próprios.

Esta demonstração tambémpode ser enontrada em[3℄, na seção 4.3.

1.5 O Teorema de Amitsur-Levitzki

Para nalizar o primeiro apítulo, abordaremos om maiores detalhes o T

eo-rema de Amitsur-Levitzki.

Consideremos

s

n(

x

1

, . . . , x

n)

,opolinmiostandarddegrau

n

. Observemosque o polinmiostandard de grau

n

+ 1

é onsequênia do polinmiostandard de grau

n

, ou seja,se

s

n

éuma identidade polinomialpara uma álgebra

A

,

s

n

+1

tambémé.

Com efeito, basta ver que

s

n

+1

(

x

1

, . . . , x

n

+1

) =

n

+1

X

i

=1

(

−

1)

i

−

1

_x

i

s

n

(

x

1

, . . . ,

x

b

i

, . . . , x

n

+1

)

,

Reordemos também que, se

A

é uma álgebra nitamente gerada om

dim

A < n

, então

s

n

= 0

é uma identidade polinomial para

A

. Em partiular,

a dimensão de

M

n(

K

)

é

n

2

, então esta álgebra satisfaz qualquer identidade

stan-dard de grau

m

≥

n

2

_{+ 1}

. Entretanto, este não é o grau mínimo para que um

polinmiostandard seja identidadepolinomialde

M

n(

K

)

. Amitsure Levitzki mos-traram,em1950, queopolinmiostandard de grau

2

n

éuma identidadepolinomial para a álgebra das matrizes

n

×

n

sobre um orpo

K

. Tal resultado é onheido omo Teoremade Amitsur-Levitzki.

Teorema 1.5.1 (Teorema de Amitsur-Levitzki). A álgebra das matrizes

M

n(

K

)

satisfaz a identidade standard de grau

2

n

s

2

n(

x

1

, . . . , x

2

n) = 0

.

A demonstração original deste resultado é baseada em argumentos

ombina-tórios e, em [3℄, são enontrada mais duas demonstrações distintas, de Razmyslov

e de Rosset, ambas utilizandoargumentos algébrios. Neste texto, apresentaremos

apenas a demonstração de Razmyslov, om o objetivo de ompará-la à

demonstra-ção utilizandooteoremade Swan, que veremos nopróximoapítulo,mas antes são

neessárias algumasonsiderações.

Notemos queavalidadedoTeoremade Amitsur-Levitzkipara

M

n(

Q

)

implia a validade do resultado para

M

n(

K

)

, om

K

um orpo qualquer. De fato, sejam

A

1

, . . . , A

2

n

matrizesem

M

n(

K

)

. Podemos esrevê-las omo

A

k

=

n

X

i,j

=1

λ

(

_ij

k

)

E

ij

,

onde

E

ij

são matrizes elementares (possuem 0 em todas as entradas, exeto na posição

(

i, j

)

,quetemvalor1),e

λ

(

k

)

i,j

∈

K

. Dessaforma,omoaidentidadestandard éumpolinmiomultilinear,temosque

s

2

n(

A

1

, . . . , A

2

n)

éumaombinaçãolinearde

s

2

n(

E

i

1

j

1

, . . . , E

i

2

n

j

2

n

)

. Cada termo

s

2

n(

E

i

1

j

1

, . . . , E

i

2

n

j

2

n

)

é igual a

0

, uma vez que assumimos avalidadedo teoremapara

M

n(

Q

)

, eportanto,

s

2

n(

A

1

, . . . , A

2

n) = 0

.

O resultado a seguir utilizao proesso de multilinearização para garantir que

Proposição 1.5.2. A álgebra

M

n(

K

)

não satisfaz uma identidade polinomial de grau menor que

2

n

.

Demonstração: Seja

f

(

x

1

, . . . , x

k)

umaidentidadepolinomialem

M

n(

K

)

degrau

k <

2

n

. Pelo Teorema 1.3.4, podemos assumir que

f

(

x

1

, . . . , x

k)

é multilinear, e

pode ser esrito omo

f

(

x

1

, . . . , x

k) =

X

σ

∈

S

k

α

σ

x

σ

(1)

. . . x

σ

(

k

)

om

α

σ

∈

K

.

Vejamos que

α

σ

= 0

,para qualquer

σ

∈

S

k

, elogo

f

(

x

1

, . . . , x

k)

éopolinmio nulo. Consideremos asmatrizes

E

11

, E

12

, E

22

, E

23

, . . . , E

pq

,onde

p

=

q

se

k

éímpar, e

p

=

q

−

1

se

k

é par.

Como o produtode matrizeselementares satisfaz

E

ij

E

hk

=







0

,

se

j

6

=

h

E

ik

,

se

j

=

h

,

temos que

f

(

E

11

, E

12

, E

22

, E

23

, . . . , E

pq) =

α

ǫ

E

1

q

,

onde

ǫ

éa permutação identidade de

S

k

. Logo

α

ǫ

= 0

. Para qualquer

σ

∈

S

k

, existe

σ

−

1

_∈

_S

k

talque

σ

◦

σ

−

1

₌

_ǫ

. Consideremos

f x

σ

−

1

₍₁₎

, x

_σ

−

1

₍₂₎

, . . . , x

_σ

−

1

₍

_k

₎

.

Fazendo assubstituições

x

σ

−

1

₍₁₎

7→

E

₁₁

,

x

σ

−

1

₍₂₎

7→

E

₁₂

,

x

σ

−

1

₍₃₎

7→

E

₂₂

,

.

.

.

x

σ

−

1

₍

_k

₎

7→

E

_pq

,

obtemos

α

σ

E

1

q

,

de onde onluímos que

α

σ

= 0

para qualquer

σ

∈

S

k

.

Opróximoresultadogaranteque,amenosdemultipliaçãoporonstantes,não