Mercados de risco e a teoria dos valores extremos: estudo empírico de casos

ALANE SIQUEIRA ROCHA

MERCADOS DE RISCO E A TEORIA DOS VALORES

EXTREMOS: ESTUDO EMPÍRICO DE CASOS

ALANE SIQUEIRA ROCHA

MERCADOS DE RISCO E A TEORIA DOS VALORES

EXTREMOS: ESTUDO EMPÍRICO DE CASOS

Dissertação aprovada como requisito parcial para obtenção do grau de mestre no curso de Pós-Graduação em Economia, Área de Concentração em Economia de Empresas, da Universidade Federal do Ceará - CAEN.

Orientador: Prof. Dr. Ronaldo de Albuquerque e Arraes.

Rocha, Alane Siqueira

Mercados de risco e a Teoria dos Valores Extremos: estudo empírico de casos / Alane Siqueira Rocha - Fortaleza, 2004.

80 f.

Dissertação (Mestrado) - Universidade Federal do Ceará, Curso de Pós-Graduação em Economia - CAEN.

1.Teoria dos Valores Extremos. 2. Mercados de Risco. I. Título.

ii

ALANE SIQUEIRA ROCHA

MERCADOS DE RISCO E A TEORIA DOS VALORES

EXTREMOS: ESTUDO EMPÍRICO DE CASOS

Dissertação aprovada como requisito parcial para obtenção do grau de mestre no curso de Pós-Graduação em Economia, Área de Concentração em Economia de Empresas, da Universidade Federal do Ceará - CAEN.

Aprovada em 30 de abril de 2004.

BANCA EXAMINADORA

______________________________________________________ Prof. Dr. Ronaldo de Albuquerque e Arraes (Orientador)

Universidade Federal do Ceará - UFC

_____________________________________________________ Prof. Dr. Emerson Luís Lemos Marinho

Universidade Federal do Ceará - UFC

_____________________________________________ Prof. Dr. Emílio Recamonde Capelo

iii

iv

AGRADECIMENTOS

Ao Professor Ronaldo de Albuquerque e Arraes pelo esmero, competência e dedicação como professor do curso de mestrado e como orientador deste trabalho.

Aos membros da banca examinadora, Emerson Luís Lemos Marinho e Emílio Recamonde Capelo, que contribuíram com sugestões valiosas ao trabalho.

v

SUMÁRIO

INTRODUÇÃO ... 1

CAPÍTULO 1. A TEORIA DOS VALORES EXTREMOS ... 4

1.1.INTRODUÇÃO ... 4

1.2.DISTRIBUIÇÃOGENERALIZADADOSVALORESEXTREMOS-GVE... 6

1.3.ESTIMAÇÃODOSPARÂMETROSDADISTRIBUIÇÃOGVE ... 11

1.4.ESTIMATIVADEQUANTISDADISTRIBUIÇÃOGVE ... 14

1.5.TEORIADOSVALORESEXTREMOSAPLICADAAOVALUE-AT-RISK(VaR) ... 15

1.6.TEORIADOSVALORESEXTREMOSAPLICADAAOMERCADODESEGUROS ... 17

CAPÍTULO 2. DESCRIÇÃO DAS SÉRIES UTILIZADAS... 21

2.1.INTRODUÇÃO ... 21

2.2.QUALIDADEDOSAJUSTESDEDISTRIBUIÇÕESTEÓRICAS ... 22

2.2.1. Procedimentos gráficos... 23

2.2.1.1. Comparação de freqüências ... 23

2.2.1.2. Gráfico Probabilidade-Probabilidade (P-P) ... 23

2.2.1.3. Gráfico Quantil-Quantil (Q-Q) ... 23

2.2.2. Teste de Adequação dos Ajustes ... 24

2.2.2.1 Teste Kolmogorov-Smirnov (K-S) ... 25

2.2.2.2 Teste Anderson-Darling (A-D)... 25

2.3.SÉRIEIBOVESPA ... 26

2.4.SÉRIEMERVAL ... 29

2.5.SÉRIEDOWNJONES ... 33

2.6.SÉRIEDEPERDASCOMSEGURODEINCÊNDIO... 37

CAPÍTULO 3. APLICAÇÃO NUMÉRICA DA TVE ... 40

3.1.INTRODUÇÃO ... 40

3.2.ESTIMATIVASDEPERDASPARAASSÉRIESFINANCEIRAS ... 40

3.2.1. Metodologias Tradicionais para o cálculo do VaR ... 40

3.2.1.1.VaR Simulação Histórica ... 40

3.2.1.2.VaR Normal... 42

3.2.1.3. VaR Paramétrico... 42

3.2.2. TVE para o cálculo da Perda Máxima Esperada - VaR ... 44

3.3.ESTIMATIVASDEPERDASPARAASÉRIESDEINDENIZAÇÕESDESEGURODE INCÊNDIO ... 51

CAPÍTULO 4. RESULTADOS EMPÍRICOS PARA VERIFICAÇÃO DA TEORIA DOS VALORES EXTREMOS ... 56

4.1.INTRODUÇÃO ... 56

4.2.VERIFICAÇÃODASESTIMATIVASDEPERDAS ... 56

4.3.ANÁLISEDOSRESULTADOSPARAASTRÊSPIORESPERDASDASAMOSTRAS ... 62

CAPÍTULO 5. CONCLUSÃO ... 67

vi

RESUMO

O objetivo deste trabalho é inferir o comportamento de valores extremos de uma variável aleatória contínua, sejam eles valores extremos pertencentes à cauda inferior de uma função densidade de probabilidade (fdp), como as severas perdas diárias em investimentos financeiros, ou valores extremos pertencentes à cauda superior de uma fdp, como os elevados dispêndios com indenizações na indústria de seguros. A Teoria dos Valores Extremos (TVE) desempenha papel fundamental na modelagem de eventos gravosos raros, com expressivas conseqüências econômicas associadas a probabilidades muito pequenas de ocorrerem. Uma das grandes preocupações na administração de riscos é desenvolver técnicas de análise para prever essas ocorrências excepcionais. Dessa forma, as caudas da fdp das variáveis que representam esses eventos raros são de grande importância para o estudo do risco, tornando a TVE uma ferramenta de grande valia para a estimação mais acurada do risco dessas perdas elevadas. Investigou-se, neste trabalho, a estimação de perdas máximas esperadas para séries financeiras e para seguros, empregando-se: i) métodos tradicionais, que utilizaram todos os dados amostrais para analisar a variável aleatória em questão; e ii) a metodologia dos Valores Extremos, particularmente a da Distribuição Generalizada dos Valores Extremos (GVE), que utilizou apenas um conjunto de máximos amostrais para a estimação das perdas máximas esperadas. Verificou-se que os métodos tradicionais subestimaram as perdas esperadas, sobretudo nas proximidades dos limites das caudas das distribuições, e que a distribuição GVE mostrou-se bem mais eficiente na previsão dessas perdas extremas em todas as séries analisadas.

vii

ABSTRACT

The objective of this work is to infer the behavior of extremes values of a continuous random variable, either extreme values in the down left tail of the probability density function (pdf), like the great daily losses in financial markets investments, or extreme values in the pdf upper right tail, like some great claim sizes in the insurance industry. The Extreme Value Theory (EVT) plays a fundamental role in modeling rare events associated with great losses and very small probabilities of occurrence. One of the great concerns in the risk management is to develop analytic techniques to foresee those exceptions. In that way, the tails of the pdf rare losses are of great importance in evaluating that kind of risk, turning the EVT a valuable tool for an accurate evaluation of high losses risk. In this work, the estimates of expected maximum losses in financial series and in insurance payments were investigated using: i) the traditional methods, that used all the sample data in fitting the random variable pdf; and, ii) the Extreme Value methodology, particularly the Generalized Extreme Value distribution (GEV), that used only a set of maximum values detected in the sample data in estimating the pdf of expected maximum losses. The findings of this study indicate, firstly, an important underestimation of extreme losses with the traditional methods, mainly in the pdf tails limits, and, secondly, that the GEV distribution proved to be more efficient in forecasting the extreme losses in all the analyzed series.

INTRODUÇÃO

O homem sempre buscou segurança e proteção contra acontecimentos

indesejáveis. Em tempos pré-históricos, as pessoas preocupavam-se com sua integridade

física em decorrência da agressão das forças brutas da natureza. Com o progresso da

civilização, a questão da segurança tem se tornado mais complexa, envolvendo numerosos

riscos novos e incorporando sofisticadas técnicas de estruturação de proteções a esses

riscos.

Há dois tipos principais de riscos econômicos, 1) o risco dos investidores, que

envolve a chance de perda ou de ganho e o 2) risco puro, quando há apenas a chance de

perda. Os negócios de seguro são do tipo riscos econômicos puros, porquanto perder a

vida, ou o carro ou o apartamento não tem a contrapartida de nenhum ganho.

A Teoria dos Valores Extremos – TVE desempenha papel fundamental na

modelagem de eventos associados a probabilidades muito pequenas ou eventos raros para

a quantificação, dentre outras, de grandes riscos econômicos. Vários são os domínios de

aplicação da TVE, tendo como exemplo, as companhias resseguradoras1 que necessitam

prever adequadamente os montantes de grandes indenizações com seguros. O comentário

abaixo evidencia a necessidade do aprimoramento na quantificação de riscos econômicos.

For the first time in the history of our planet, mankind is about to change the climate significantly and possibly irreversibly, without having any idea of the consequences that will have.... With economic and insured losses increasing in volume by a factor of 3 and 5 respectively since the 1960s, we definitely have a trend which, without exaggeration, may be regarded as dramatic. (Munich Re, 1990)2

1

O resseguro pode ser resumidamente definido como o seguro do seguro. É um instrumento de transferência de risco das seguradoras para as resseguradoras com a finalidade de evitar o comprometimento de sua saúde financeira.

2

CHAVEZ, V.; ROEHRL, A. Extreme Value Theory can save your neck, 2004. Disponível em <http://www.approximity.com/papers/TVE_wp.pdf>. Acesso em: 25 de janeiro de 2004.

A ocorrência de eventos com valores elevados implica certos custos para

remediar suas conseqüências. O terremoto de Kobe, por exemplo, acarretou pagamento de

indenizações entre $100 e $150 bilhões de dólares pelas companhias de seguro.

Souza (1999, p. 41) evidencia a importância da TVE no estudo e

dimensionamento de infra-estrutura de apoio a catástrofes naturais:

(...) Um caso bastante citado é o dimensionamento dos diques construídos nos Países Baixos para controlar o avanço do mar. O último grande transbordamento registrado teve conseqüências desastrosas, matando mais de 1800 pessoas em 1953. O trabalho de matemáticos holandeses como Van Dantzig foi decisivo para o avanço tanto da TVE como para o dimensionamento da altura dos diques. O problema nesse caso é: dadas as observações do nível máximo anual observado (o maior deles antes de 1953, quando o nível atingiu 3.85m acima do normal, tinha sido na enchente de 1570, de 4m) qual a maior altura que o nível do mar atingirá nos próximos 10.000 anos (quantil associado à probabilidade de 1-10-4)? Van Dantzig estimou como sendo 5.14m acima do nível de referência Trata-se de um exemplo típico onde é necessário se fazer inferência para eventos de fora do conjunto amostral (...)

O desenvolvimento do mercado financeiro intensificou-se na década de 90

impulsionando a implementação de instrumentos de acompanhamento gerenciais voltados à

nova realidade da globalização. As conseqüências de eventos específicos, como a crise da

Rússia, são difundidas rapidamente no mercado financeiro mundial.

As instituições financeiras mantêm modelo interno de análise de risco de

mercado, com destaque especial para o RiskMetrics, desenvolvido pelo banco americano

J.P. Morgan, que teve como resultado final a técnica de mensuração de riscos conhecida

como Value-at-Risk (VaR).

Morgan (1996, p. 5) refere-se a medida Valor em Risco (VaR) como sinônimo de

risco de mercado: "Over the last few years measures of market risk have become

synonymous with the term Value-at-Risk."

Jorion (1997, p. 18) apresenta o seguinte conceito para o VaR: " O VaR sintetiza

a maior (ou pior) perda esperada dentro de determinado período de tempo e intervalo de

confiança."

Em 1993, o Grupo dos Trinta (G-30), uma equipe composta por banqueiros,

agentes financeiros e acadêmicos importantes das maiores nações industriais, emitiu

relatório contendo uma recomendação importante: a avaliação de posições no mercado e

Sua capacidade de sintetizar, em um único número, a perda financeira esperada

com determinado grau de confiança, foi decisivo para sua recomendação pelo Comitê da

Basiléia como metodologia para alocação de capital em instituições financeiras.

A Teoria dos Valores Extremos contribuiu para o aprimoramento dos modelos de

VaR por concentrar-se no ajuste da distribuição apenas sobre os valores extremos da

variável aleatória, diminuindo, portanto, a influência dos valores centrais. A TVE nos auxilia,

portanto, na estimação das perdas máximas esperadas em momentos de instabilidade. Em

suma, o resultado fundamental da TVE consiste na convergência da distribuição assintótica

de uma série de mínimos (máximos) padronizados.

Objetiva-se, então, neste trabalho: i) aplicar a TVE a amostras de dados financeiros

e dados de pagamento de elevadas indenizações de seguro; e ii) comparar as estimativas

de perdas máximas encontradas a partir da TVE com as estimativas de perdas máximas

encontradas pelas metodologias tradicionais. As metodologias tradicionais, diferentemente

da TVE, estimam perdas esperadas utilizando a amostra total de dados.

O trabalho está organizado da seguinte forma: a esta introdução segue-se no

capítulo 1 uma primeira abordagem geral sobre a TVE. No capítulo 2 são apresentadas as

séries utilizadas para a estimação das perdas esperadas. O capítulo 3 aplica as

metodologias de estimação de perdas máximas discutidas nos capítulos anteriores às

amostras apresentadas no capítulo 2. No capítulo 4 comparam-se as estimativas de perdas

máximas esperadas com as perdas efetivamente ocorridas. Um quinto e último capítulo é

0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45

-3 -2 -1 0 1 2 3

0,0 0,2 0,4 0,6 0,8 1,0 1,2 1,4

0,

0

0,

5

1,

0

1,

5

2,

0

2,

5

3,

0

CAPÍTULO 1. A TEORIA DOS VALORES EXTREMOS

1.1. INTRODUÇÃO

O objetivo deste trabalho é fazer inferências sobre os extremos de uma variável

aleatória, sejam extremos pertencentes à cauda inferior da variável, como mínimos de

retornos diários de ativos financeiros, ou extremos pertencentes a sua cauda superior, como

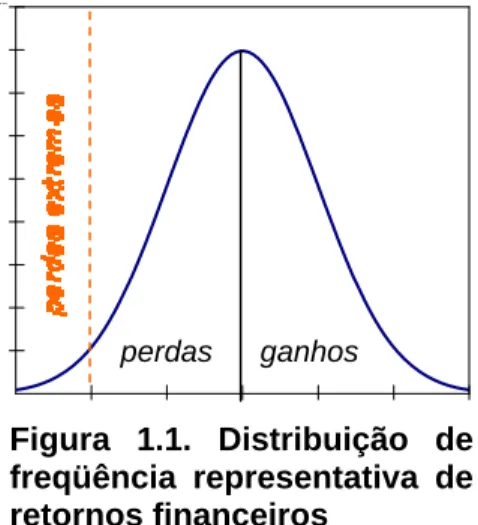
o valor de uma indenização de sinistro. As figuras 1.1 e 1.2, abaixo, exemplificam situações

diversas para a análise de valores extremos, com baixa probabilidade de ocorrência, que

podem ser mínimos ou máximos de uma variável aleatória em análise.

O propósito do administrador de risco é constituir reservas suficientes para se

resguardar contra esses eventos extremos.

Bautista (2002, p. 3) revela que:

Os fundamentos da teoria dos valores extremos foram inicialmente expostos por Fisher & Tippett (1928), que definiram os três tipos possíveis (I,II, III) de distribuições assintóticas dos valores extremos, conhecidas como de Gumbel, Fréchet e Weibull, respectivamente.

ganhos

perdas perdas

Figura 1.1. Distribuição de freqüência representativa de retornos financeiros

Fonte: Concepção da autora.

Figura 1.2. Distribuição de freqüência representativa da Severidade das perdas com Indenizações de seguro.

O resultado fundamental da Teoria dos Valores Extremos consiste na

convergência da distribuição assintótica de uma série de mínimos ou máximos padronizados

para distribuições pertencentes às seguintes classes de distribuições: i) Distribuição

Generalizada do Valor Extremo - GVE ; ou ii) Distribuição Generalizada de Pareto - DGP.

A Teoria de Valores Extremos, portanto, concentra-se em classes especiais de

distribuições de probabilidade: as distribuições GVE, classe que inclui as distribuições de

Gumbel, de Fréchet e de Weibull, e as distribuições DGP, como a Exponencial, a Pareto e a

Beta. Na forma padronizada, a GVE e a DGP dependem apenas de um parâmetro,

chamado de índice de cauda.

Para as distribuições GVE e DGP utilizam-se, respectivamente, as seguintes

formas de tratar os valores extremos: a primeira abordagem considera máximos (ou

mínimos) selecionados em períodos sucessivos, por exemplo, meses ou anos. Estas

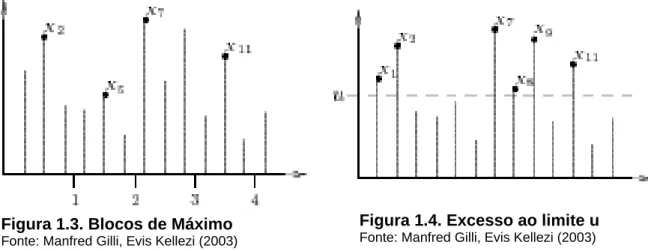
observações selecionadas constituem os eventos extremos. Na figura 1.3, as observações

X2, X5, X7 e X11 representam os máximos para quatro blocos com períodos de três

observações. A segunda abordagem seleciona extremos que excedem um determinado

limite. As observações X1, X2, X7, X8, X9 e X11 na figura 1.4, excedem o limite u e constituem

eventos extremos.

A primeira técnica apresenta a desvantagem da possibilidade, dependendo do

tamanho do bloco, de perder observações extremas dentro do mesmo bloco. Observa-se,

na figura 1.3, que no terceiro bloco desconsidera-se um valor maior que os máximos x2, x5 e

x11. A escolha do tamanho do bloco pode, entretanto, ser realizada de forma objetiva como,

por exemplo, blocos de meses, blocos de anos.

Figura 1.3. Blocos de Máximo

Fonte: Manfred Gilli, Evis Kellezi (2003)

Figura 1.4. Excesso ao limite u

Na segunda técnica, a escolha de um limite suficientemente alto é menos

objetiva. A escolha está sujeita a um trade-off entre variância e viés. Aumentando o número

de observações para as séries de máximos (baixo limite) são introduzidas nas séries

algumas observações do centro da distribuição, tornando a estimativa do parâmetro índice

de cauda mais consistente, porém mais viesada. Por outro lado, escolhendo um limite alto

reduz-se o viés do estimador, tornando-o, entretanto, mais impreciso, em virtude da

utilização de uma menor quantidade de observações para a sua estimação.

Os comentários, a partir deste ponto, referem-se ao máximo, pois os resultados

para o mínimo podem ser obtidos pela relação

mínimo(X1,...,Xn) = - máximo( - X1,..., - Xn) .

Neste trabalho particularizamos a TVE aplicando apenas a distribuição GVE.

1.2. DISTRIBUIÇÃO GENERALIZADA DOS VALORES EXTREMOS - GVE

A Distribuição Normal é uma importante distribuição limite para soma de médias

amostrais, como explicitado no Teorema do Limite Central. Similarmente, a família de

distribuições de valores extremos representa as distribuições limite para os máximos

amostrais, como determinado pelo Teorema de Fisher & Tippett.

Essa família de distribuições de valores extremos determina a forma da

distribuição limite (assintótica) do máximo à medida que a extensão do intervalo de tempo, a

partir do qual o máximo é selecionado, tende para infinito. Segundo Mendes (2004, p. 45), a

função repartição Fx dos máximos GVE, admitindo a hipótese i.i.d para os máximos, foi

introduzida por Jenkinson (1955) e é denotada, em sua forma não padronizada, por,

Teorema de Fisher&Tippett3 : Seja (Xn) uma seqüência de variáveis aleatórias

i.i.d., se existirem seqüências constantes normalizadoras cn>0 e dn

∈

ℜ e uma distribuição

não degenerada4 H tal que

onde, d

→ representa convergência em distribuição; e Mn o máximo selecionada de n

variáveis aleatórias i.i.d, Mn = máx(X1, X2, ... , Xn), então H é do tipo Gumbel, Fréchet ou

Weibull.

Segundo Mendes (2004, p. 34) a prova do teorema pode ser verificada em

Embrechts, Klüppelberg e Mikosch (1997), baseando-se, esta, em propriedades de

transformadas afins, convergência em distribuição e conceito de distribuição do mesmo tipo.

Considerando que, i) valores de máximos são aqueles que se localizam

próximos do limite superior da distribuição de uma variável aleatória X; ii) o comportamento

assintótico de Mn está relacionado com a cauda da distribuição Fx próxima do limite superior

xFx de Fx; e iii) para x<xFx tem-se

{

}

( )

( )

n

n

x

F

x

M

Pr

≤

=

. Segue, abaixo, um exemplo de

convergência da distribuição Exponencial para a distribuição de Gumbel retirado de Mendes

(2004, p.34) :

Exemplo: Convergência da distribuição Exponencial unitária para a Gumbel. Suponha que FX seja a distribuição exponencial unitária. Isto é,

x

X

(

x

)

e

F

=

1

−

− . Então

F

_X

(

x

)

n

=

(

1

−

e

−x

)

n e assim,

{

M c x d

}

(

F

(

c x d

)

)

. Pr

x c

d M

Pr _{n n n n n} n

n n

n = ≤ ⋅ + = ⋅ +

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − _≤

Fazendo

c

_n

=

1

e

d

_n

=

ln(

n

)

obtemos

(

)

(

)

(

)

e

exp

{ }

e

.

n

e

)

n

ln(

x

F

x n n x n ) n ln( x

n − − − →∞ −

−

→

⎟

⎠

⎞

⎜

⎝

⎛

₋

_⋅

=

−

=

+

1

1

1

vemos que tomando como constantes normalizadoras cn=1 e dn=ln(n), a distribuição assintótica do máximo coletado em bloco de tamanho n de observações oriundas de uma exponencial unitária será, quando n →∞ uma distribuição de Gumbel.

3

Para mais detalhes sobre a Teoria dos Valores Extremos ver: MENDES, Beatriz V. de M. Uma Introdução à Analise de Valores Extremos. Rio de Janeiro: E-papers Serviços Editoriais, 2004.

4

f(x )

A função densidade de probabilidade da distribuição GVE, para ξ≠0, é

encontrada derivando-se a equação (1.1) acima e para ξ=0 derivando-se a equação (1.2),

logo:

definidas em, -∞ < x < μ - σ/ξ para ξ<0; μ - σ/ξ < x < +∞ para ξ>0 e -∞ < x < +∞ para ξ→0.

Os parâmetros μ e σ correspondem, respectivamente, a parâmetros de escala e

de tendência; o terceiro parâmetro, ξ, também representado por α=1/ξ, indica a densidade

da cauda. O índice da cauda, α, mede a velocidade com que a cauda da distribuição se

aproxima de zero.

Como já exposto, o parâmetro α, designado de índice da cauda, modela a cauda da distribuição. De acordo com o valor do índice da cauda, três tipos de distribuições do

valor extremo são obtidos: a distribuição Fréchet (α>0), a distribuição de Gumbel (α=0) e a

distribuição de Weibull (α<0). Este resultado é muito significativo, pois como a distribuição assintótica do máximo sempre pertence a uma destas três distribuições, qualquer que seja a

distribuição original, nenhuma suposição é necessária sobre a natureza da distribuição

original das observações. Apresentam-se, no Apêndice A, as características das

distribuições GVE.

⎪⎪

⎪

⎪

⎩

⎪⎪

⎪

⎪

⎨

⎧

=

⎭

⎬

⎫

⎩

⎨

⎧

⎥⎦

⎤

⎢⎣

⎡

_⎟

⎠

⎞

⎜

⎝

⎛

₋

−

−

⎟

⎠

⎞

⎜

⎝

⎛

₋

−

≠

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

⎥⎦

⎤

⎢⎣

⎡

_⎟

⎠

⎞

⎜

⎝

⎛ −

+

−

⎥⎦

⎤

⎢⎣

⎡

_⎟

⎠

⎞

⎜

⎝

⎛ −

+

=

− ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + −

0

se

x

exp

exp

x

exp

0

se

x

exp

x

)

x

(

f

_x

ξ

σ

μ

σ

μ

σ

ξ

σ

μ

ξ

σ

μ

ξ

σ

ξ ξ ξ

1

1

1

1

1 1 (1.3) (1.4)

Figura 1.5. Função densidade de probabilidade GVE para ξ = - 0,5 (Weibull), ξ→ 0 (Gumbel) e ξ = 0,5 (Fréchet) com μ=0 e σ=1.

25 , 1 | 8 , 0 5 , 2 | 4 , 0 5 | 2 , 0 = = = = = = α ξ α ξ α ξ 25 , 1 | 8 , 0 5 , 2 | 4 , 0 5 | 2 , 0 = = = = = = α ξ α ξ α ξ

Figura 1.6. Funções densidade de probabilidade Fréchet com μ=0 e σ=1.

Fonte: Concepção da autora.

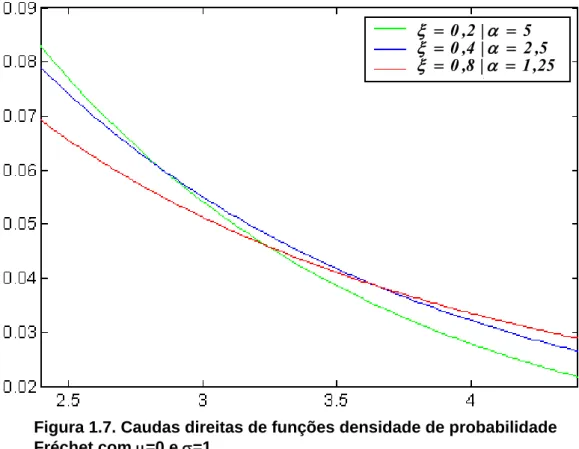
Figura 1.7. Caudas direitas de funções densidade de probabilidade Fréchet com μ=0 e σ=1.

Fonte: Concepção da autora.

5 | 2 , 0

5 , 2 | 4 , 0

25 , 1 | 8 , 0

− = −

=− =−

=− =−

=

α

ξ α

ξ α

ξ

As figuras 1.6 e 1.7 apresentam os gráficos das funções densidade de

probabilidade Fréchet para ξ = 0,2 ( α = 5), ξ = 0,4 ( α = 2,5) e ξ = 0,8 (α = 1,25) com μ=0 e

σ=1. A figura 1.7 plota, para melhor visualização, as caudas das distribuições de Fréchet apresentadas na figura 1.6.

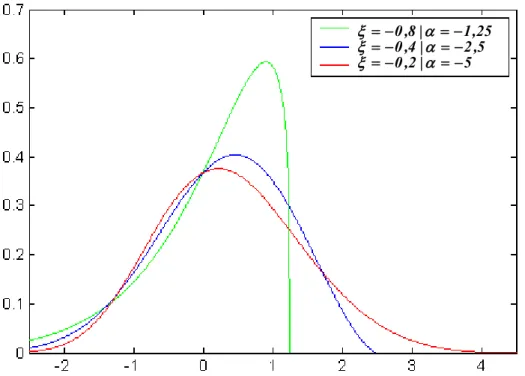
A figura 1.8 apresenta as funções densidade de probabilidade Weibull para ξ =

-0,8 ( α = -1,25), ξ = -0,4 ( α =-2,5) e ξ = -0,2 (α = -5) com μ=0 e σ=1.

Observando-se as caudas das distribuições apresentadas nas figuras 1.6, 1.7 e

1.8 nota-se que o índice α determina a velocidade com que as caudas se aproximam de

zero. Observa-se que, quanto menor o índice de cauda α, mais lentamente a cauda da

distribuição se aproxima de zero, possuindo, assim, as distribuições com menores índices α, caudas mais densas.

Gnedenko5 (1943) apud Bautista (2002, p. 3) afirmou que as caudas das

distribuições GVE podem ser representadas por distribuições contínuas. A cauda da

distribuição de Gumbel corresponde às distribuições exponencial, gama, normal ou

5

GNEDENKO, B. V. Sur la distribution limite du terme maximum d´une série aleatoire. Annales des Mathématiques, v.44,p.423-453, 1943.

Figura 1.8. Funções densidade de probabilidade Weibull com μ=0 e σ=1.

∏

₌

=

n

j

j

(

)

L

)

(

L

1

θ

θ

normal, a cauda da distribuição de Fréchet segue uma distribuição de Cauchy, Pareto ou

t-Student e a da distribuição de Weibull segue uma distribuição Uniforme.

Sobre a hipótese de independência dos máximos acrescenta-se a afirmação de

Souza (1999, p. 12):

Os retornos extremos, por definição, ocorrem a baixíssimas freqüências, e não seria de se esperar que exibissem dependência temporal. Eventos raros em geral são determinados por circunstâncias muito particulares, e que dificilmente se reproduziriam no futuro. São imprevisíveis e típicos de momentos de crises.

1.3. ESTIMAÇÃO DOS PARÂMETROS DA DISTRIBUIÇÃO GVE

Para a estimação dos parâmetros

ξ

,

μ

,

σ

da distribuição GVE, utiliza-se, neste trabalho, a metodologia da função de máxima verossimilhança6.

O método da máxima verossimilhança consiste em adotar como estimador a

estatística que maximiza a probabilidade, ou a densidade de probabilidade de ser

encontrada a amostra observada.

A função de verossimilhança para um conjunto de n observações independentes

é dada por,

onde

L

_j

(

θ

)

é a contribuição da j-ésima observação para a verossimilhança. Se a j-ésima observação é um evento com probabilidade positiva (como de uma

distribuição discreta ou de um intervalo), então a contribuição é aquela probabilidade – p(x).

Se a j-ésima observação for um valor de uma distribuição contínua, a contribuição é a f.d.p

daquele valor – f(x).

Os estimadores de máxima verossimilhança – EMV são encontrados pela

maximização da função de verossimilhança em relação aos parâmetros desconhecidos da

distribuição GVE. O máximo da função de verossimilhança –

L

(

θ

)

ocorre no mesmo ponto

(

)

=

(

(

)

)

=

_⎜⎜⎝

⎛

∏

_⎟⎟⎠

⎞

i i

)

x

(

f

ln

x

;

,

,

L

ln

x

;

,

,

μ

σ

ξ

μ

σ

ξ

l

(

)

∑

∑

∑

∏

∏

= − − = = = − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + −

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

⎥⎦

⎤

⎢⎣

⎡

_⎟

⎠

⎞

⎜

⎝

⎛ −

+

−

⎥⎦

⎤

⎢⎣

⎡

_⎟

⎠

⎞

⎜

⎝

⎛ −

+

⋅

⎟

⎠

⎞

⎜

⎝

⎛ +

−

−

=

⎥⎦

⎤

⎢⎣

⎡

_⎟

⎠

⎞

⎜

⎝

⎛ −

+

−

⎥⎦

⎤

⎢⎣

⎡

_⎟

⎠

⎞

⎜

⎝

⎛ −

+

⎟

⎠

⎞

⎜

⎝

⎛ +

−

−

=

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

⎥⎦

⎤

⎢⎣

⎡

_⎟

⎠

⎞

⎜

⎝

⎛ −

+

−

⎥⎦

⎤

⎢⎣

⎡

_⎟

⎠

⎞

⎜

⎝

⎛ −

+

=

⎟⎟⎠

⎞

⎜⎜⎝

⎛

=

n i i i n i i n i i n i i i

x

x

ln

ln

x

x

ln

ln

n

x

exp

x

ln

)

x

(

f

ln

x

;

,

,

1 1 1 1 1 1 1 1

1

1

1

1

1

1

1

1

1

ξ ξ ξ ξ ξ

σ

μ

ξ

σ

μ

ξ

ξ

ξ

σ

σ

μ

ξ

σ

μ

ξ

ξ

ξ

σ

σ

μ

ξ

σ

μ

ξ

σ

σ

μ

ξ

l

As estimativas dos parâmetros são, para a distribuição GVE, encontradas

utilizando-se a função de log-verossimilhança dada por:

onde:

f

(

x

_i

)

é dada pela equação (1.3) ou (1.4).

Para as distribuições de Fréchet e Weibull, representadas pela equação (1.3),

desenvolve-se a seguinte função log-verossimilhança:

Os estimadores de máxima verossimilhança são, então, obtidos pela solução do

sistema de equações não lineares formado pelas derivadas de primeira ordem da equação

(1.6), em relação a cada parâmetro

ξ

,

μ

,

σ

, derivadas estas igualadas a zero. Referido sistema de equações está apresentado abaixo.

6

O princípio da verossimilhança afirma que devemos escolher aquele valor do parâmetro desconhecido que maximiza a probabilidade de se obter a amostra particular observada, ou seja, o valor que torna aquela amostra a “mais provável”.

(1.5)

(

)

∑

∏

∏

= =

⎭

⎬

⎫

⎩

⎨

⎧

_⎟

⎠

⎞

⎜

⎝

⎛

₋

−

−

⎟

⎠

⎞

⎜

⎝

⎛ −

−

−

=

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

⎭

⎬

⎫

⎩

⎨

⎧

⎥⎦

⎤

⎢⎣

⎡

_⎟

⎠

⎞

⎜

⎝

⎛

₋

−

−

⎟

⎠

⎞

⎜

⎝

⎛

₋

−

⋅

=

⎟⎟⎠

⎞

⎜⎜⎝

⎛

=

n i i i n i i i

x

exp

x

ln

x

exp

exp

x

exp

ln

)

x

(

f

ln

x

;

,

,

1 1

1

σ

μ

σ

μ

σ

σ

μ

σ

μ

σ

σ

μ

ξ

l

(

) ( )

(

) (

)

∑

∑

∑

= − = − = −

=

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

⋅

−

−

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⋅

−

−

⎟

⎟

⎠

⎞

⎜

⎜

⎝

⎛

−

=

⎪

⎪

⎭

⎪⎪

⎬

⎫

⎪

⎪

⎩

⎪⎪

⎨

⎧

⎥⎦

⎤

⎢⎣

⎡

₊

₋

−

+

−

=

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

₊

₋

n i i i i i i ˆ i n i i ˆ i i n i i

w

ˆ

ˆ

x

w

ˆ

ˆ

ˆ

x

w

ln

ˆ

w

w

w

ˆ

ˆ

x

ˆ

ˆ

n

ˆ

w

ˆ

ˆ

1 2 1 1 1 2 1 1

0

1

1

0

1

1

0

1

1

σ

μ

σ

ξ

μ

ξ

ξ

μ

σ

σ

σ

ξ

σ

ξ ξ ξ onde: ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ − + = σ μ ξˆ x _ˆ ˆ

w_i 1 i

Como o sistema de equações acima não possui solução analítica, devem-se

utilizar métodos numéricos para obtenção da solução.

Para a distribuição de Gumbel, representada pela equação (1.4), temos a seguir

i) a função log-verossimilhança, e ii) o sistema de equações para estimação dos parâmetros

μ e σ.

i) função log-verossimilhança:

ii) sistema de equações não-lineares para estimação dos parâmetros da

distribuição GVE ⎯ Gumbel:

x

f(x)

x =Q(p)

área p

Figura 1.9. Representação gráfica do p-quantil Q(p).

Fonte: Concepção da autora.

A estimação dos parâmetros da distribuição GVE é, neste trabalho, realizada

utilizando-se uma rotina do software EVIM7 desenvolvida em MATLAB R11. Referida rotina

encontra os parâmetros da distribuição GVE pelo método numérico de Newton-Raphson.

Podem, entretanto, ocorrer situações de não convergência na estimação dos parâmetros da

distribuição GVE, sendo que Smith8 (1985) apud Mendes (2004, p.46), afirma que os

Estimadores de Máxima Verossimilhança – EMV mantém boas qualidades quando ξ > -0,5.

Esta afirmação é importante, pois, segundo EMBRECHTS (1999) é comum em aplicações

de seguro encontrarem-se valores de α no intervalo (1;2) – que corresponde ao intervalo

(0,5;1) para ξ – enquanto em Finanças, α situa-se no intervalo (2;5) – que corresponde ao

intervalo (0,20;0,5) para ξ , cujas áreas são objeto deste estudo.

1.4. ESTIMATIVA DE QUANTIS DA DISTRIBUIÇÃO GVE

Define-se a medida estatística quantil ou p-quantil da variável aleatória X,

indicada por Q(p), como o valor que satisfaz as relações,

P

(

X

≤

Q

(

p

))

≥

p

e

p

))

p

(

Q

X

(

P

≥

≥

1

−

, onde 0<p<1.

O p-quantil é, então, o valor tal que a soma das probabilidades dos valores

menores do que ele é igual a p. A figura 1.9, a seguir, representa graficamente a estatística

p-quantil para uma distribuição contínua.

7

EVIM v1.0 é um pacote gratuito contendo funções, desenvolvidas em MATLAB, para a análise de valores extremos. Este pacote pode ser encontrado em http://www.bilkent.edu.tr/ ~faruk.

8

( )

p

F

xˆ

_p

=

_ξˆ−_,μˆ1_,σˆ

(

)

[

1

]

1

1

1

1 1 1

−

−

+

=

⎟

⎟

⎠

⎞

⎜

⎜

⎝

⎛

⎟⎟⎠

⎞

⎜⎜⎝

⎛

−

+

=

−

⎟

⎟

⎠

⎞

⎜

⎜

⎝

⎛

⎟⎟⎠

⎞

⎜⎜⎝

⎛

−

+

−

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

⎟

⎟

⎠

⎞

⎜

⎜

⎝

⎛

⎟⎟⎠

⎞

⎜⎜⎝

⎛

−

+

−

=

− − − − ξ ξ ξ ξ

ξ

σ

μ

σ

μ

ξ

σ

μ

ξ

σ

μ

ξ

)

p

ln(

ˆ

ˆ

ˆ

xˆ

ˆ

ˆ

xˆ

ˆ

)

p

ln(

ˆ

ˆ

xˆ

ˆ

)

p

ln(

ˆ

ˆ

xˆ

ˆ

exp

p

p ˆ p ˆ p ˆ p

Considerando que as observações extremas seguem uma distribuição GVE, o

p-quantil da distribuição GVE é definido como

Para a equação (1.1) apresentada anteriormente temos

1.5. TEORIA DOS VALORES EXTREMOS APLICADA AO VALUE-AT-RISK (VaR)

O final da última década caracterizou-se pela ocorrência de significativas crises

financeiras no mercado financeiro internacional. Esses acontecimentos demandaram a

existência de sistemas de gerenciamento de risco que utilizem metodologias apropriadas

para a estimação de eventos raros e com conseqüências financeiras elevadas. Com isso, a

TVE experimentou um boom no campo financeiro nos últimos tempos.

As instituições financeiras mantêm um modelo interno de análise de risco de

mercado, com destaque especial para o RiskMetrics, desenvolvido pelo banco americano

J.P. Morgan, que teve como resultado final a técnica de mensuração de riscos conhecida

como Value-at-Risk (VaR).

O VaR — valor em risco — é a perda máxima esperada, em valor monetário, e

sob condições normais de mercado, de um título, de uma carteira ou de uma instituição,

dado um determinado nível de confiança e um horizonte de tempo especificado.

(

)

[

−

−

1

]

+

=

−ξ

ξ

σ

μ

ln(

p

)

ˆ

ˆ

ˆ

VaR

_extremo

Segundo JORION (1998, p. vii), o VaR pode ser descrito como:

“VaR é um método de mensuração de risco que utiliza técnicas estatísticas padrões, comumente usadas em outras áreas técnicas. Em linguagem formal, o VaR mede a pior perda esperada ao longo de determinado intervalo de tempo,

sob condições normais de mercado e dentro de determinado nível de confiança.

Com base em fundamentos científicos, o VaR fornece aos usuários uma medida concisa do risco de mercado”.

Para MORGAN (1996, p. 6) "VaR answers the question: how much can I lose

with x% probability over a given time horizon."

A Teoria de Valores Extremos contribuiu para o aprimoramento dos modelos de

VaR por concentrar-se no ajuste da distribuição apenas sobre os valores extremos da

variável aleatória, diminuindo, portanto, a influência dos valores centrais. A TVE vem ao

encontro da necessidade de se possuir um sistema adequado de controle de risco para

prevenir catástrofes financeiras em momentos de crise. Estudos empíricos verificaram o fato

de que distribuições de retornos de séries financeiras costumam apresentar caudas mais

pesadas do que as de uma distribuição normal. As metodologias tradicionais de cálculo do

VaR, contudo, em geral supõem normalidade, seja condicional ou não condicional, e não

acomodam satisfatoriamente as ocorrências extremas da distribuição dos retornos.

Pelo exposto, o VaR é determinado pelo p-quantil da distribuição dos retornos de

um ativo ou de uma carteira de ativos financeiros. Utilizando a TVE para representar a

distribuição dos retornos extremos, o VaR Extremo é definido como o p-quantil estimado a

partir da distribuição dos valores extremos, GVE.

De forma particular, o VaR, estimado utilizando-se a Teoria dos Valores

Extremos e presumindo-se que a distribuição dos retornos extremos segue uma distribuição

GVE, é encontrado a partir da equação (1.7), que determina o p-quantil da distribuição GVE.

A equação para o VaR extremo é, então,

1.6. TEORIA DOS VALORES EXTREMOS APLICADA AO MERCADO DE

SEGUROS

O risco associado a um contrato de seguros deve ser estudado através da

variável aleatória, S, que compõe a equação 1.9, representando o montante total dos

desembolsos a que o segurador está exposto em decorrência dos eventuais sinistros

garantidos pelo contrato de seguro. No Modelo de Risco Coletivo, o montante agregado das

indenizações, S, é representado por

onde:

N(t) representa o número de pagamentos de indenizações até o tempo t, e

Xi o valor do pagamento da i-ésima indenização de seguro.

O modelo de risco coletivo gera reclamações de indenizações para o conjunto

das apólices de um portfólio. Para aplicar os modelos de risco coletivo necessitamos de

informações sobre a distribuição do número de indenizações, N, e da distribuição da

severidade individual dessas indenizações, X.

Dessa forma, a variável perda agregada para grupos fechados, S(t), é

representada pela soma dos montantes, Xi’s, do número total de reclamações de

indenizações de sinistros, N(t), em cada período de cobertura.

A variável aleatória S(t) representa, assim, o montante agregado periódico das

indenizações de sinistros gerados por um portfólio. O número de indenizações, N(t), é a

variável aleatória associada com a freqüência de reclamações de indenizações, e os Xi’s,

são, também, variáveis aleatórias que representam a severidade das indenizações.

A distribuição de severidade individual das reclamações de indenizações de

sinistros é costumeiramente descrita por uma distribuição contínua, com as seguintes

características:1) as indenizações de sinistros são sempre positivas; e 2) possuem forma

assimétrica positiva.

Como exemplo da variável aleatória X, têm-se a linha de seguros de incêndio, na

qual os eventos são incêndios em uma edificação segurada, que resultam em perdas

.

t

,

X

X

X

)

t

(

econômicas. Devido aos incêndios causarem geralmente grandes danos, devem ser

escolhidas distribuições de severidade adequadas para esta situação. Segundo Bowers

(1997, p. 436), na literatura atuarial, algumas distribuições padrão são sugeridas:

Distribuição Lognormal – bastante utilizada para representar a severidade das

perdas. Sua cauda medianamente espessa à direita pode ajustar-se

satisfatoriamente a diversas situações.

Distribuição de Pareto – A distribuição de Pareto é utilizada para grandes

dispersões devido a sua cauda acentuadamente espessa.

O segurador deve conhecer o comportamento de suas perdas aleatórias futuras,

S(t), para quantificar de forma adequada o valor a ser cobrado como prêmio. Como

comentado acima, a variável aleatória Xi, montante da indenização de sinistro, pode ser

representada, por exemplo, por distribuições contínuas de caudas espessas e

medianamente espessas como a Pareto e a Lognormal, as caudas das referidas

distribuições determinam a probabilidade de perdas elevadas ou extremas. Referidas perdas

extremas podem acarretar a insolvência do segurador, se não existir capital suficiente. O

segurador preocupa-se, portanto, em estimar de forma adequada a distribuição de

severidade das perdas para manter sua atividade seguradora solvente.

O modelo clássico de risco para a atividade seguradora em tempo contínuo é um

processo estocástico {U(t),t ≥0}:

onde:

U(t) = reserva de risco (capital do segurador) de uma carteira no instante t;

u = U(0) = capital inicial do segurador;

p = prêmio com carregamento por unidade de tempo.

A figura 1.10, a seguir, representa uma possível trajetória do processo de risco.

.

t

),

t

(

S

pt

u

)

t

(

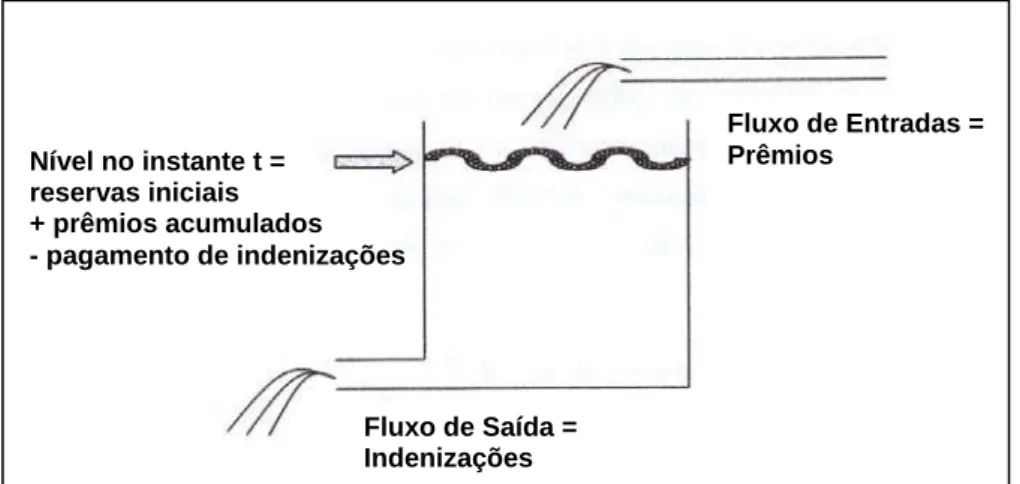
A figura 1.11 traz uma analogia simplificada do processo de risco descrito na

equação 1.10. A Reserva, U(t), é representada pelo nível do reservatório, nível este que se

deseja manter sempre positivo. Com esse propósito, deve-se quantificar de forma adequada

as entradas determinísticas, os prêmios e as saídas probabilísticas, que são os pagamentos

de indenizações. Ressalte-se que a quantificação adequada dos prêmios depende da

estimação das indenizações. São ignorados, no modelo em tela, outros fatores distintos dos

prêmios e do pagamento das indenizações, tais como o retorno dos investimentos em

mercado e as despesas administrativas.

As distribuições de perdas Xi são tradicionalmente ajustadas utilizando-se a

amostra completa de dados. A TVE, como já se verificou, ajusta uma distribuição de

probabilidades apenas aos valores extremos da amostra de dados, buscando, assim,

Figura 1.10. Realização do Processo de Risco U(t).

Fonte: KAAS et al. Modern Actuarial Risk Theory. P. 84.

Figura 1.11. Analogia Simplificada do Processo de Reserva de Risco.

Fonte: STRAUB, Erwin. Non-life Insurance Mathematics. p.8.

Nível no instante t = reservas iniciais + prêmios acumulados - pagamento de indenizações

Fluxo de Saída = Indenizações

Fluxo de Entradas = Prêmios

U(t)

T1 T2 T3 T4=T T5

0 u

melhores estimativas para as indenizações catastróficas. A estimação da perda aleatória X,

pela Teoria dos Valores Extremos, para um determinado percentil, é encontrada

aplicando-se uma distribuição GVE pela equação 1.7 acima.

As indenizações catastróficas são, entretanto, geralmente repassadas em parte,

ou no todo, para companhias resseguradoras, que operam contratos de resseguro. O

resseguro é a operação na qual um segurador,,denominado ressegurado ou companhia

cedente, transfere a outro segurador, o ressegurador, uma parte do risco assumido em um

contrato de seguro, pagando por esta cobertura um valor previamente combinado, o prêmio.

O ressegurador está sujeito ao mesmo processo de risco, apresentado na figura 1.10, com

pagamentos de indenizações agora determinados por indenizações vultosas.

Uma companhia seguradora possui limites para aceitação de riscos definidos

pela própria entidade ou por normas governamentais. Para não prejudicar sua atividade

comercial, a seguradora retém riscos superiores a estes limites, transferindo parte das suas

responsabilidades para companhias resseguradoras.

Com a contratação de resseguro, o segurador pode absorver com maior

facilidade os impactos negativos advindos da ocorrência de eventos catastróficos, como

furacões, tornados, que poderiam levar a entidade à insolvência. Após a contratação do

resseguro as indenizações catastróficas ficam na responsabilidade do ressegurador de

acordo com o determinado em contrato. O ressegurador, portanto, necessita de forma mais

premente da quantificação adequada de perdas extremas, tornando a TVE de vital

importância para a atividade resseguradora.

A aplicação mais importante da TVE no campo de seguro é provavelmente na

área de resseguro.

Pelo exposto, podemos afirmar que, no mercado financeiro e no mercado de

seguros, revela-se uma preocupação comum: a necessidade premente de quantificar de

CAPÍTULO 2. DESCRIÇÃO DAS SÉRIES UTILIZADAS

2.1. INTRODUÇÃO

Neste trabalho, utilizam-se as seguintes amostras de dados:

ƒ Séries financeiras referentes a índices de bolsa, no período compreendido

entre 30/12/1993 e 20/11/2003 inclusive, adquiridas na base de dados do

Economática:

1. Ibovespa: série de 2.447 índices diários de fechamento da Bovespa;

2. Merval: série de 2.451 índices diários de fechamento Merval;

3. Down Jones: série de 2.491 índices diários de fechamento Down

Jones.

A partir dos índices diários das três séries em pauta determinaram-se seus

retornos diários respectivos pela equação: Rt=ln(Pt/Pt-1), onde Pt

corresponde ao índice no instante t.

ƒ Série de dados de seguro de incêndio da indústria de seguros da

Dinamarca, no período compreendido entre 1980 e 1990 inclusive,

consistindo em 2.167 perdas acima de 1 milhão de Coroas Dinamarquesas,

adquirida na base de dados do Software Evim.

As séries de retornos e a série de perdas serão analisadas neste capítulo, no

qual se apresenta seu comportamento gráfico, suas estatísticas descritivas e, por fim,

busca-se encontrar a distribuição contínua de probabilidades que melhor se ajusta aos

dados amostrais. Os resultados aqui presentes foram realizados com o auxílio do Software

O Software Bestfit disponibiliza várias distribuições discretas e contínuas de

probabilidade para realização de ajuste aos dados amostrais, estimando seus parâmetros e

testando a adequação do ajuste. Dentre as distribuições contínuas ⎯ área de interesse para

este trabalho ⎯ as mais conhecidas contidas nesse software são:

1. Beta

2. Erlang

3. Exponencial

4. Gamma

5. Logística

6. Loglogística

7. Lognormal

8. Normal

9. Pareto

10.Pearson tipo V e VI

11.Qui-quadrado

12.Rayleigh

13.t-Student

14.Triangular

15.Uniforme

16.Weibull

O Bestfit realiza o rank dos ajustes das distribuições utilizando os testes

estatísticos: Qui-quadrado, Kolmogorov-Smirnov(K-S) e o Anderson-Darling(A-D).

Apresentam-se, a seguir, os ajustes utilizando o rank decorrente dos testes K-S e A-D.

Referidos testes são os mais apropriados a dados contínuos, ressaltando que: i) o teste K-S

foca o centro da distribuição, não detectando muito bem discrepâncias nas caudas;

enquanto o teste A-D realça as diferenças nas caudas entre a distribuição ajustada e a

distribuição empírica.

Para as séries supra referidas apresenta-se a distribuição que obteve o 1º lugar

no rank pelos testes K-S e A-D, quando os resultados para os dois testes são discrepantes

dá-se preferência ao teste A-D, pois, o propósito deste trabalho é a estimação de valores

pertencentes à cauda da distribuição sob análise. Para as séries financeiras, apresenta-se

adicionalmente, o ajuste pela distribuição Normal, por ser esta uma aproximação largamente

utilizada para representar retornos de séries financeiras.

2.2. QUALIDADE DOS AJUSTES DE DISTRIBUIÇÕES TEÓRICAS

A qualidade dos ajustes de distribuições teóricas aos dados amostrais será

analisada, no decorrer deste trabalho, por i) procedimentos gráficos como : gráfico da

distribuição empírica versus teórica ajustada; gráfico Probabilidade-Probabilidade (P-P);

gráfico Quantil-Quantil (Q-Q); e ii) testes de adequação como: teste Kolmogorov-Smirnov e

2.2.1. Procedimentos gráficos 2.2.1.1. Comparação de freqüências

Para dados contínuos, a comparação de freqüências é uma comparação gráfica

do histograma dos dados amostrais, distribuição empírica, com a função densidade

fˆ

(

x

)

da distribuição contínua ajustada. Se a distribuição ajustada representa bem o

comportamento dos dados amostrais, o gráfico da distribuição teórica ajustada deve ser

semelhante ao gráfico da distribuição empírica.

2.2.1.2. Gráfico Probabilidade-Probabilidade (P-P)

Um gráfico P-P é a representação gráfica da função distribuição ajustada

Fˆ

(

x

)

versus a probabilidade acumulada amostral

F

~

(

x

)

. Se

Fˆ

(

x

)

e

F

~

(

x

)

possuem o mesmo

comportamento, então o gráfico P-P será linear.

2.2.1.3. Gráfico Quantil-Quantil (Q-Q)

Um gráfico Q-Q é a representação gráfica dos quantis advindos da distribuição

ajustada

Fˆ

(

x

)

versus os quantis da distribuição amostral

F

~

(

x

)

. Se

Fˆ

(

x

)

e

F

~

(

x

)

possuem

o mesmo comportamento, então o gráfico Q-Q será linear.

O gráfico Q-Q amplifica as diferenças existentes entre as caudas das

distribuições teóricas ajustadas e as caudas das distribuições empíricas amostrais, o gráfico

P-P, diferentemente, amplifica as diferenças existentes no centro das distribuições

Fˆ

(

x

)

e

)

x

(

F

~

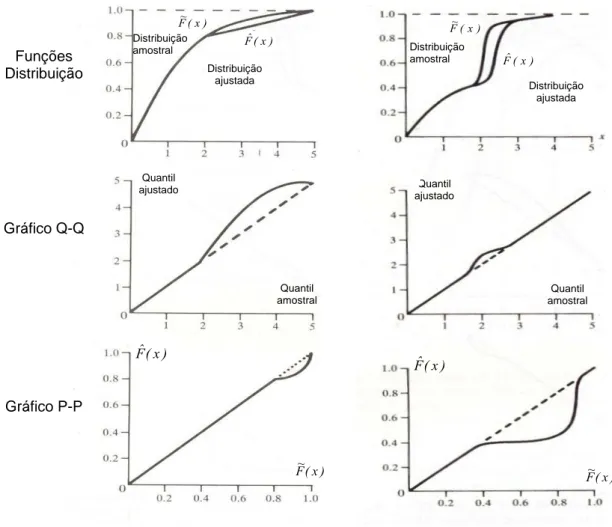
. A figura 2.1 mostra, no painel esquerdo, a diferença existente na cauda direita das distribuições ser amplificada no gráfico Q-Q, o que não ocorre no gráfico P-P.Como outro

exemplo, temos o painel direito da figura 2.1 que apresenta a diferença existente no centro

2.2.2. Teste de Adequação dos Ajustes9

Apresentam-se, nesta seção, dois testes de aderência para avaliar a adequação

do ajuste de uma determinada distribuição teórica aos dados amostrais. As hipóteses dos

testes são:

Hipótese nula: A distribuição teórica populacional representa o comportamento

da distribuição amostral;

Hipótese alternativa: A amostra não provém da distribuição teórica ajustada.

9

Mais detalhes sobre os testes podem ser encontrados em: LAW, A. M. e KELTON W. D. Simulation Modeling & Analysis.1991. p. 387.

) x ( Fˆ ) x ( F~

Distribuição ajustada Distribuição

amostral

) x ( Fˆ ) x ( F~

Distribuição amostral

Distribuição ajustada

Funções Distribuição

Gráfico Q-Q

Gráfico P-P

Figura 2.1. Exemplos de gráficos P-P e Q-Q.

Fonte: LAW, A. M. e KELTON W. D. Simulation Modeling & Analysis.1991. p. 377 e 378. Quantil

amostral Quantil

ajustado

Quantil amostral Quantil

ajustado

) x ( Fˆ

) x (

F~ _F~_(x)

2.2.2.1 Teste Kolmogorov-Smirnov (K-S)

O teste Kolmogorov-Smirnov é um teste de aderência que compara a função

distribuição empírica acumulada

F

~

(

x

)

com a função distribuição teórica ajustada

F

ˆ

(

x

)

, ou

seja, mede o grau de concordância entre a distribuição de um conjunto de valores amostrais

e determinada distribuição teórica específica. O teste determina, então, se os valores da

amostra podem ser considerados como provenientes de uma população com determinada

distribuição teórica. A distribuição teórica representa o que se poderia esperar sob Ho.

A estatística do teste K-S será obtida pela maior distância vertical entre as

distribuições observada

F

~

(

x

)

e teórica

F

ˆ

(

x

)

para todos valores de x, e a definição formal

é dada por D_n =max|F~_n(x)−Fˆ(x)|. O valor calculado

D

_n é confrontado com o valor crítico

tabeladoc, caso

D

_n seja menor que c não se pode rejeitar

H

₀ a um nível de significância

α

, ou seja, a diferença máxima pode ser atribuída ao acaso. De igual forma, se o p-value for superior ao nível α de significância não se pode rejeitar a hipótese H0. O p-value

representa a probabilidade de ocorrer valores da estatística mais extremos que o observado

sob a hipótese de H0 ser verdadeira,p−value=Prob

(

D >D_n H₀

)

. O p-value, o nível de

significância observado, é uma medida de plausibilidade dos resultados da amostra

considerando a hipótese nula como verdadeira. Quanto menor o valor do p-value, menor é a

possibilidade da amostra provir de uma população onde a hipótese nula é verdadeira. A

maioria dos softwares fornece o p-value associado a um teste de hipóteses, com isso é

possível obter uma conclusão sobre o teste sem se referir a uma tabela estatística.

A utilização do teste Kolmogorov-Smirnov apresenta algumas características

relevantes: i) não requer agrupamento de dados, ou seja, nenhuma informação é perdida;

ii) possui desempenho satisfatório com qualquer número de informações; e iii) é poderoso

para o trabalho com distribuições contínuas.

2.2.2.2 Teste Anderson-Darling (A-D)

O teste Anderson-Darling também é um teste de aderência que compara a

função distribuição empírica acumulada

F

~

(

x

)

com a função distribuição teórica

ajustada

F

ˆ

(

x

)

, ou seja, determina se os valores da amostra podem ser considerados como

provenientes de uma população com determinada distribuição teórica. Como apresentado

valores de x. O teste A-D, de outra forma, é desenhado para detectar discrepâncias nas

caudas com maior poder que o teste K-S, pois atribui maior peso as diferenças próximas às

caudas das distribuições. A estatística do teste é dada por:

[

F

~

(

x

)

Fˆ

(

x

)

]

(

x

)

fˆ

(

x

)

dx

n

A

_n2

∫

∞ _n 2

ψ

∞

−

−

=

onde:

[

]

(

Fˆ(x) 1 Fˆ(x)

)

1

) x (

− ⋅ =

ψ é a função de ponderação das diferenças;

) x (

F~_n é a função distribuição ou função de probabilidade acumulada da amostra

de tamanho n;

)

x

(

Fˆ

é a função distribuição ou função de probabilidade acumulada da

distribuição teórica ajustada;

)

x

(

fˆ

é a função densidade de probabilidade da distribuição teórica ajustada.

O valor calculado

A

_n2 é confrontado com o valor crítico tabelado

a

_n,1−α, caso o

valor da estatística calculado seja menor que o valor crítico, não se pode rejeitar

H

₀ a um

nível de significância

α

. Alternativamente, a conclusão sobre o teste pode ser realizada

através do p-value. Se o p-value for superior ao nível α de significância não se pode rejeitar a hipótese H0. As conclusões sobre os testes de hipóteses, neste trabalho, são realizadas

comparando-se o p-value com o nível de significância estipulado previamente.

2.3. SÉRIE IBOVESPA

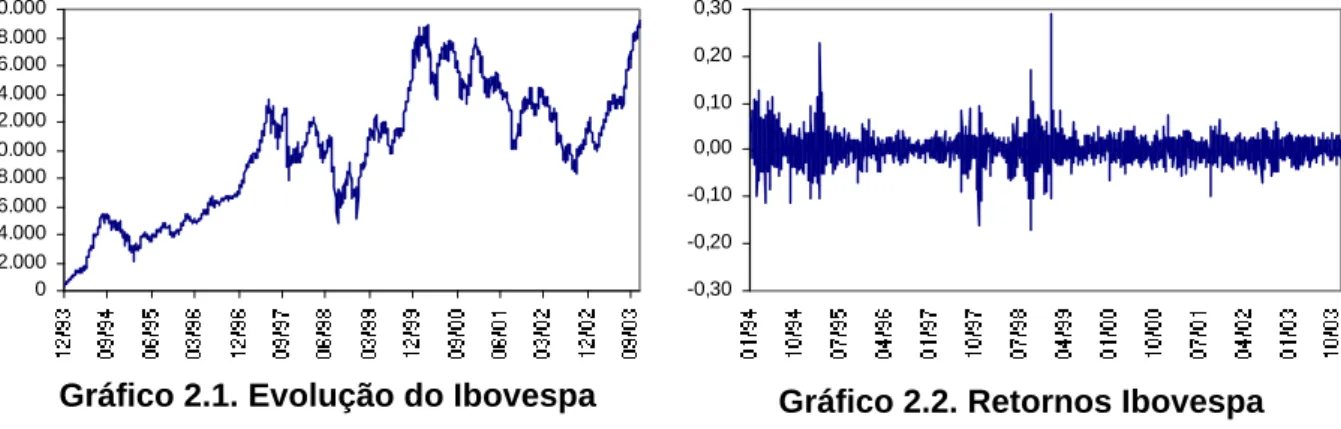
Nos Gráficos 2.1 e 2.2 plotam-se, respectivamente, a evolução do Ibovespa e o

comportamento dos retornos no período sob análise. Os retornos diários oscilam no

intervalo de -17,2% a 28,8%.

0 2.000 4.000 6.000 8.000 10.000 12.000 14.000 16.000 18.000 20.000

-0,30 -0,20 -0,10 0,00 0,10 0,20 0,30

A Tabela 2.1 revela que a distribuição Logística foi classifica como o melhor

ajuste pelos testes K-S e A-D, apresentando esta dentre todas as distribuições contidas no

Software Bestfit menor discrepância em relação à distribuição amostral. O ajuste da

distribuição Normal aos dados empíricos obteve apenas o 11º lugar, o último lugar, pois

apenas 11 distribuições apresentaram ajustes válidos. Todas as distribuições contínuas

ajustadas, incluindo-se a distribuição Logística, que obteve as menores discrepâncias, foram

rejeitadas pelos testes em questão considerando que todos os valores da estatística p-value

resultaram menores que 5%.

Na tabela 2.2, observam-se as estatísticas descritivas da amostra e das

distribuições ajustadas, revelando que a distribuição Normal possui curtose bem inferior em

relação à curtose apresentada pelos dados amostrais. Ressalte-se que a hipótese de

Normalidade dos retornos, amplamente utilizada como aproximação para distribuição de

retornos no cálculo do VaR, apresentou-se como inadequada.

Tabela 2.1. Resultados Ajuste Ibovespa

Descrição Ajuste Logística Ajuste Normal

A-D K-S A-D K-S

Test Value 3,214 0,02421 +∞ 0,06708

P Value <0,05 <0,05 <0,05 <0,05

Rank 1 1 11 5

Fonte : Cálculos realizados no Software Bestfit.

Tabela 2.2. Estatísticas Ajuste Ibovespa

Descrição Amostra Ajuste Logística Ajuste Normal

Média 0,0016 0,0016 0,0016

Desvio-padrão 0,0279 0,0255 0,0279

Assimetria 0,5739 0 0

Curtose 12,563 4,2 3

Fonte: Cálculos realizados no Software Bestfit

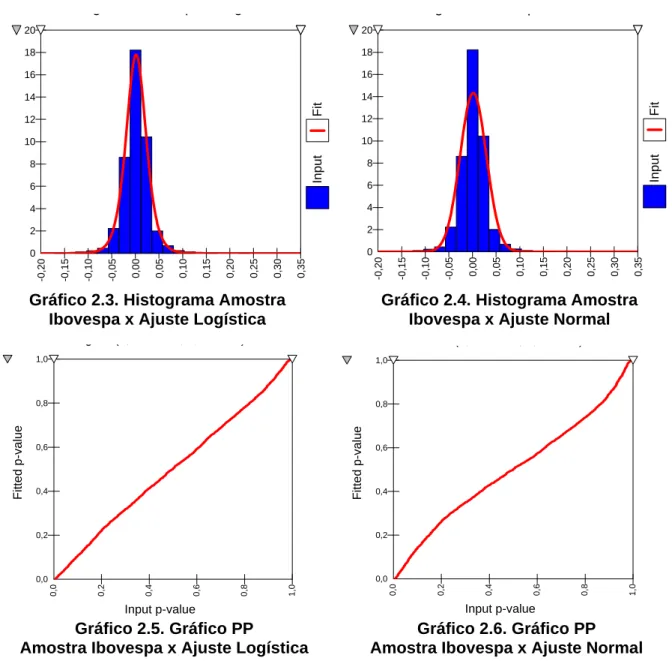
Os gráficos 2.3 e 2.4 apresentam visualmente o ajuste pela distribuição Logística

e Normal. Verifica-se, como revelado acima, um melhor ajuste da distribuição Logística em

detrimento à distribuição Normal.

A forma quase linear, apresentada no gráfico 2.5, revela o melhor ajuste nas

caudas pela distribuição Logística comparado ao gráfico 2.6, que apresenta um elevado