Teoria geométrica da medida e aplicações

CENTRO DE CIÊNCIAS

DEPARTAMENTO DE MATEMÁTICA

CURSO DE PÓS-GRADUAÇÃO EM MATEMÁTICA .

João Vítor da Silva

Teoria Geométrica da Medida e Aplicações

João Vítor da Silva

Teoria Geométrica da Medida e Aplicações

Dissertação submetida à Coordenação do Curso de Pós-graduação em Matemática da Universadade Federal do Ceará, como requisito para obtenção do grau de Mestre em Matemática.

Área de concentação: Matemática.

Orientador: Prof. Dr. Eduardo Vasconcelos Oliveira Teixeira.

S58t Teoria geométrica da medida e aplicações/ João Vítor da Sil-va.- - Fortaleza, 2011.

193f.

Orientador: Prof. Dr. Eduardo Vasconcelos Oliveira Teixeira Área de concentração : Matemática

Dissertação(Mestrado) - Universidade Federal do Ceará, Centro de ciências, Departamento de Matemática, Fortaleza,

2011.

Dedicatória

Dedico este trabalho aos meus pais, Maria Socorro Mendonça Silva e João Virgínio da Silva, e, a Maria Selene Bezerra de Carvalho todos estes os quais amo muito.

Tarde demais eu te amei!

Eis que habitavas dentro de mim e eu te procurava do lado de fora! Eu, disforme, lançava-me sobre as belas formas das tuas criaturas. Estavas comigo, mas eu não estava contigo.

Retinham-me longe de ti as tuas criaturas, que não existiriam se em ti não existissem.

Tu me chamaste, e teu grito rompeu a minha surdez.

Fulguraste e brilhaste e tua luz afugentou a minha cegueira. Espargiste tua fragrância e, respirando-a, suspirei por ti. Tu me tocaste, e agora estou ardendo no desejo de tua paz...

Santo Agostinho

Agradecimentos

Aos meus pais: Maria Socorro Mendonça Silva e João Vígínio da Silva pela criação, amor, carinho, confiança e oportunidade de me oferecerem uma educação dígna e o caráter o qual possuo hoje. Aos meus quatro irmão: Antônio Ednaldo da Silva, Eliana Mendonça da Silva Lemos, Juliana Virgínia da Silva e Cícero Leond Mendonça da Silva por sempre estarem do meu lado me apoiando em todos os momentos.

Aos amigos de graduação que estarão sempre em meu coração: Fabiano Luiz da Silva, Antônio Emiliano Ribeiro, Cícera Ferreira dos Santos e Rosilda Benício de Sousa. Aos professores do ensino Fundamental e Médio que contribuiram de maneira significativa para minha formação: Ivone, Lurdes, Inês, Solange, Carlos Sérgio, Joana Angélica, Valdênia, Raimundo Porfílio, Vanda Caciano e Rosa Maria. Aos professores da graduação na Universidade Regional do Cariri e no IFCE os quais me estimularam a dar continuidade em meus estudos: Evandro Carlos Ferreira dos Santos, Carlos Humberto Soares Júnior, Mário de Assis Oliveira, Zeláber Gondim Guimarães, Carlos Alberto Soares de Almeida, Pedro Ferreira de Lima, Fernando Luis e Juscelino Pereira Silva. Aqueles meus companheiros os quais estiveram mais presentes em meu mestrado: Cícero Tiarlos Nogueira Cruz, Francisco Pereira Chaves, Priscila Rodrigues de Alcântara, Maria de Fátima Cruz Tavares, Júnio Moreira de Alencar, Francisco de Assis Benjamim Filho, Maria Wanderlândia Coriolano de Lavor, José Loester Sá Carneiro, Antonio Wilson Rodrigues da Cunha, Filipe Mendonça de Lima, Francisco Calvi da Cruz Júnior, João Francisco da Silva Filho, Antonio Edinardo de Oliveira, José Deibsom da Silva, José Ederson Melo Braga, Leon Denis da Silva, Raimundo de Araújo Bastos Júnior, Rondinelle Marcolino Batista, Tiago Mendonça Lucena de Veras, Valéria Gerônimo Pedrosa, Ana Shirley Monteiro da Silva, Disson, Adriano e aqueles os quais não tive a oportunidade de ser colega de turma, mas me tornara amigo: do doutorado: Flávio França Cruz, José Nazareno Vieira Gomes, Kelton Silva Bezerra, Marco Antonio Lázaro Velásquez ,e, do mestrado: Rachel Costa da Silva, Elaine Sampaio, Robério Alexandre Coelho, André, Renato e Leonardo.

e Marcelo Dário dos Santos Amaral, que foram incentivadores e contribuiram de várias formas para o sucesso, conclusão e aperfeiçoamento deste trabalho.

Aos funcionários do departamento de matemática, principalmente a secretária da Pós-Graduação Andrea Costa Dantas pela sua atenção e eficiente trabalho, e, aos funcionários da biblioteca: Seu Erivan, Dona Fernanda e dona Rosilda, todos estes pelo auxílio prestado durante todo o curso de mestrado.

A meu orientador Eduardo Vasconcelos Oliveira Teixeira pelo incentivo e confiança na conclusão deste trabalho.

Aos professores do curso de mestrado em matemática: Luquésio Petrola de Melo Jorge, Silvano Dias Bezerra de Menezes, Cleon da Silva Barroso, Antônio Caminha Muniz Neto, Jorge Herbert Soares de Lira, José Othon Dantas Lopes, Aldir Chaves Brasil Júnior, Marcos Ferreira de Melo, João Lucas Marques Barbosa, José Fábio Bezerra Montenegro, Diego Ribeiro Moreira e Eduardo Vasconcelos Oliveira Teixeira, pela ímpar e incomensurável contribuição, experiência e exemplo que todos esses me forneceram.

À minha querida Maria Selene Bezerra de Carvalho pelo amor, dedicação, incentivo e compreensão nas horas mais necessárias e difíceis as quais esteve sempre do meu lado.

À FUNCAP pelo suporte financeiro. Aos membros da banca.

A nossa Mãe do Céu, Nossa Senhora, a quem devo agradecer por sua constante vigilância e interseção por mim perante seu amadíssimo filho, Nosso Senhor Jesus Cristo. E acima de Tudo a Deus, o Pai e criador; Jesus Cristo, o Filho Salvador e o Espírito Santo, santificador e luz do mundo. A Este(s) não enumero os motivos pela simples razão de não ser possível caberem todos estes em nenhum livro.

Resumo

O

presente trabalho de mestrado visa estudar alguns dos trabalhos do matemático italiano Ennio De Giorgi, os quais fazem referência a existência e regularidade de superfícies mínimas, mas estas não contextualizadas integralmente no âmbito da Geometria Diferencial, mas sim voltadas a um campo da matemática a algumas décadas implementada que a Teoria Geométrica da Medida. Segundo as definições de Ennio De Giorge iremos estudar superfícies, que para o mesmo se davam como bordos de certos conjuntos, os quais são denotados de conjuntos de Caccioppoli, homenagem esta dada por De Giorgi a o matemático italiano Renato Caccioppoli, tais conjuntos tem muitas propriedades geométricas interessantes, como por exemplo adimetem plano tangente canônico em quase todo ponto, e, possuem “perímetro” finito. Os resultados expostos constatarão que até a dimensão 7 todas as soluções do problema de Plateau são regulares e em geral sua classe de regularidade é C1,α_.

Nossos esforços se concentrarão em:

i. Definir o que é uma superfície, em geral de modo a ter-se um conceito mais amplo que variedades, mas com alguma Geometria Diferencial;

ii. Mostrar que existem superfícies mínimas que minimizam área via um Teorema de Compacidade;

iii. Provar a regularidade da superfície, ou seja, a superfície é uma variedade suave. Enfim, os resultados deste trabalho em sua maioria serão baseados na obra: M

¯inimal Surface and Function of Bounded Variation do autor Enrico Giusti, o qual resume bem as técnicas de Teoria Geométrica da Medida referentes aos trabalhos de Ennio De Girogi sobre teoria de regularidade de superfícios mínimas.

Esta obra tratará do problema de Plateau, que é encontrar uma hipersuperfície de área mínima que abrange determinado limite. Foi somente em 1930-1931 que uma solução deste problema foi encontrada por Douglas e Radó para superfícies em R3_{, e levou mais 30 anos}

teoria da medida. Pioneiros destes novos métodos foram De Giorgi, Reifenberg, Almgren, Fleming, e Federer.

Este trabalho é dedicado à representação e abordagem de Ennio De Giorgi ao estudo de superfícies mínimas paramétricas. De Giorgi definiu hipersuperfícies admissíveis para o problema de Plateau como limite de sequências de conjuntos de Caccioppoli. Estes últimos são conjuntos de Borel Eem Rn _{com a propriedade que a derivada distribucional}

DχE, ou seja, no sentido das distribuições, da função característica χE é uma medida de

Radon de variação total localmente limitada. O perímetro de um conjunto de Caccioppoli E em um aberto limitado Ω_⊂Rn é definido como a variação total de DχE em Ω:

Per(E;Ω) = Z

Ω

|DχE|=sup

Z

Ω

divg(x)dx;g_∈C10(Ω;R n_),|

g|_L∞_(Ω)≤1

Com esta noção enfraquecida de “superfície” o problema de Plateau é fácilmente solucionado no seguinte sentido: Teorema (Existência de uma solução fraca): Sejam Ω aberto e limitado, e, Lum conjunto de Caccioppoli emRn. Então, na classe dos conjuntos de Caccioppoli{E;E−Ω=L−Ω}existe um conjunto de Perímetro mínimo emΩ, o qual

denotaremos conjunto minimal em Ω. A prova da regularidade em quase toda parte, no entanto, exige um trabalho bastante difícil. Por isso, o noção de fronteira reduzida ∂∗E de um conjunto E é introduzida como o conjunto dos pontos x_∈Rn _{para os quais existe}

um vetor normal unitário generalizado ν(x) como o limite de quandoρ_→0 dos vetores

νρ(x) =

Z

B(x,ρ)

DχE

Z

B(x,ρ)

|DχE|

.

Teorema (Regularidade parcial): Para qualquer conjunto mínimalE em Ωa fronteira reduzida Ω_∩∂∗Eé uma hipersuperfície analíticaC1,α _{e o conjunto singularΩ∩(∂E−∂}∗_E)

tem dimensão(n−1)−dimensional de Hausdorff nula. As ferramentas para a prova destes resultados são fornecidas a partir do capítulo 5. Nos capítulos 2-3 serão tratadas algumas propriedades das funções de variação limitada:compacidade, semicontinuidade da variação total, aproximação por funções suaves e traços. A prova de regularidade se encontra no capítulo 8. Trataremos algumas poucas sessões à investigação do conjunto singular. Para cada ponto x0 ∈ ∂E existe um cone tangente C como limite em L1loc de uma seqüência

adequada de conjuntos de expansão Et ={x ∈Rn :x0+t(x−x0)∈E} quando t →0. O

cone tangente é mínimo se E é mínimal numa vizinhança de x0 e x0 pertence à fronteira

reduzida se e somente se ∂C é um hiperplano.

Teorema (Almgren, Simons): Seja F um cone em Rn cujo fronteira é suave fora do

≥

0, então ∂F é um hiperplano para n _≤ 7. n = 7 é a dimensão ótima (Bombieri, De Giorgi, Giusti). Portanto, para n _≤ 7 a fronteira de todo conjunto mínimal E em Ω _⊂ Rn é analítica. Este resultado é completado por outro teorema (Federer): A medida s-dimensional de Hausdorff do conjunto singular é nula para qualquer s > n−8.

A leitura deste trabalho exige um conhecimento “razoavelmente” bom em teoria da medida e alguma familiaridade com a teoria das equações diferenciais parciais elípticas. Em sua totalidade, o trabalho é, em sua grande maioria uma obra de representação e exposição de Teoria Geométrica da Medida a qual é um novo ramo da Análise altamente não trivial.

Palavras-Chaves: Funções de varição limitada, conjuntos de Perímetro finito (conjuntos de Caccioppoli), conjuntos minimais, Superfícies Mínimas, Regularidade de Superfícies Mínimas, Problema de Plateau, Problema de Bernstein, Teoria de De Giorgi-Nash-Moser.

T

his master thesis aims to study some of the work of mathematician Italian Ennio De Giorgi, which refer to the existence and regularity of minimal surfaces, but these do not fully contextualized within the Differential Geometry, but focused on a field of mathematics within a few decades implemented which is the Geometric Measure Theory. According to the definitions of Ennio De Giorgi will study surfaces, which gave to the same as maples certain sets, which are denoted Caccioppoli sets , its have many interesting geometric properties, such as tangent adimetem canonical almost everywhere, and have finite "perimeter". The above results found that up to size 7 all the solutions to the problem of Plateau are regular and in general their class of regularity is C1,α Our efforts will focus on:

i. Defining what is a surface in general to take up a broader concept that varieties, but with some differential geometry;

ii. Show that there are minimal surfaces which minimize area via a compactness theorem;

iii. Prove the regularity of the surface, ie, the surface is a smooth manifold.

Finally the results of this study are mostly based on the work: Minimal Surface and Function of Bounded Variation of the author Enrico Giusti, which summarizes the techniques of Geometric Measure Theory relating to the work of Ennio De Girogi on a regularity theory of minimal surfaces.

This work will address the problem of Plateau, which is to find a hypersurface of least area that covers certain threshold. It was only in 1930-1931 that a solution to this problem was found by Douglas and Radó for surfaces in R3_{, and it took another 30 years until the}

case could be in higher-dimensions attacked by methods of measure- theorteic. Pioneers of these new methods were De Giorgi, Reifenberg, Almgren, Fleming, and Federer.

This work is dedicated to representation and Ennio De Giorgi approach to the study of minimal surfaces parameteric. De Giorgi defined hypersurfaces admissible for the problem

sets EenRn_{with the property that the distributional derivativeDχE, i.e., in the sense of}

distributions, the characteristic function χE is a Radon measure of locally bounded total variation. The perimeter of a Caccioppoli set E in a limited open ΩRn is defined as the total variation of DχE inΩ:

Per(E;Ω) = Z

Ω

|DχE|=sup

Z

Ω

divg(x)dx;g_∈C10(Ω;Rn),|g|L∞_(Ω)≤1

With this weakened notion of “surface” the Plateau problem is easily solved in the following sense: Theorem (existence of a weak solution): Let Ω open and bounded and L on a set of Caccioppoli Rn_{. Then the class of sets Caccioppoli {E, E−Ω =L−Ω} is}

a set of minimal perimeter in Ω, which denote the minimal set in Ω. The proof of the regularity almost everywhere, however, requires a very difficult job. Therefore, the notion of reduced boundary ∂∗E of a set E is introduced as the set of points x _∈ Rn for which there exists a generalized unit normal vector ν(x)as the limit when ρ_→0 of the vectors

νρ(x) =

Z

B(x,ρ)

DχE

Z

B(x,ρ)

|DχE|

.

Theorem (partial regularity): For any minimal set EinΩthe reduced boundaryΩ_∩∂∗_E

is an analytic hypersurface and the singular set Ω_∩(∂E−∂∗E)has (n−1)−dimensional Hausdorff measure 0.

Tools for the proof of these results are provided from Chapter 5. In chapters 2-3 will address some properties of functions of bounded variation: compactness, semicontinuity of the total variation, approximation by smooth functions and trace. The proof of regularity found in Chapter 8. We will try a few sessions to the investigation of the singular set. For every point x0 ∈ ∂E there exists a tangent cone C as the limit at Lloc1 for proper

sequence of sets of expansion Et ={x ∈Rn :x0+t(x−x0)∈E}whent →0. The tangent

cone is minimal if E is minimal in a neighborhood of x0 and x0 belongs to the reduced

boundary if and only if ∂C is a hyperplane.

Theorem (Almgren, Simons): LetFbe a cone inRn_{whose boundary is smooth outside}

the vertex. If the first and second variations of area of ∂F satisfy δA= 0 and δ2_{A ≥ 0,}

then ∂F is a hyperplane for n _≤ 7. n = 7 is optimal (Bombieri, De Giorgi, Giusti). Therefore, for n_≤7 the boundaryΩ_∩∂E of every minimal set E inΩ_⊂Rn is analytic. This result is completed by another theorem (Federer): The s−dimensional Hausdorff measure of the singular set vanishes for any s > n−8.

familiarity with the theory of elliptic partial differential equations. In their totality, the work is mostly a work of representation and exhibition of Geometric Measure Theory which a new branch of highly nontrivial analysis.

Key Words: Functions of Bounded variation, sets of finite perimeter (Caccioppoli sets), minimal sets, Minimal Surfaces, Regularity of Minimal Surfaces, Problem’s Plateau, Bernstein’s Problem, Theory of De Giorgi-Nash-Moser.

Conteúdo

1 Introdução 1

1.1 Um pouco de História e alguns comentários . . . 1

1.2 As Grandes Personalidades e o Legado destas . . . 4

2 Preliminares 5 2.1 Algumas noções de Teoria da Medida . . . 6

2.2 Medida de Hausdorff . . . 12

2.3 Funções de variação limitada e conjuntos de Caccioppoli . . . 19

2.3.1 Propriedades dos conjuntos de Caccioppoli . . . 25

2.3.2 A fórmula de Gauss-Green e o Teorema Estrutural . . . 27

2.4 Regularizantes Simétricos (Mollifiers) . . . 32

2.4.1 Propriedades dos Regularizantes Simétricos (Mollifiers) . . . 33

2.5 Aproximação de Funções BV . . . 34

2.6 Existência de Superfícies Mínimas . . . 38

2.6.1 Teoremas de compacidade . . . 38

2.7 Aproximação de conjuntos de Caccioppoli por funções C∞ . . . 42

2.8 Desigualdade de Sobolev e consequências . . . 46

3 Teoria do Traço para Funções de Variação Limitada 49 3.1 Traço de Funções em W1,p_{(Ω) . . . 49}

3.2 Traço de Funções de Variação Limitada . . . 51

3.2.1 O Teorema de Lebesgue-Besicovitch e o Lema de Recobrimento de Vitali . . . 51

3.2.2 O Teorema do Traço e a Fórmula de Gauss-Green para C+_R . . . 54

4 A Fronteira Reduzida 63 4.1 Fronteira Reduzida . . . 63

4.2 Blow-up da Fronteira Reduzida . . . 72

4.3 Semi-Espaço Tangente . . . 76

5 Regularidade da Fronteira Reduzida 79 5.1 Resultados preliminares . . . 80

5.1.1 A classe Γn−1 . . . 81

5.2 O Teorema Estrutural . . . 82

5.2.1 Conjuntos contavelmente rectificáveis e puramente não-rectificáveis 86 5.3 Regularidade C1 da Fronteira Reduzida . . . 90

5.3.1 Representação localmente Lipschitz de ∂E . . . 93

5.4 A medida Teórica da fronteira e o Teorema de Gauss-Green . . . 97

5.4.1 Medida Teórica da Fronteira . . . 97

5.4.2 Teorema de Gauss-Green Generalizado . . . 98

5.4.3 Comentários sobre Densidade-Rectificabilidade de conjuntos . . . . 100

6 Algumas Desigualdades 102 6.1 Alguns Lemas Técnicos . . . 102

6.1.1 O Desvio de Minimalidade . . . 102

7 Aproximação de conjuntos minimais 113 7.1 O Lema de decaimento de De Giorgi . . . 114

7.1.1 O Desvio de Planridade (Flatness) - O excesso de área . . . 114

7.1.2 A Filosofia do Lema de Decaimento de De Giorgi . . . 120

7.2 Superfícies Mínimas e Harmônicas . . . 121

7.2.1 Comentários sobre Espaços de Campanato . . . 121

7.2.2 O lema de decaimento de De Giorgi para superfícies harmônicas . . 122

7.3 Aproximação de conjuntos de Caccioppoli . . . 131

8 Regularidade de Superfícies Mínimas 141 8.1 Teoria de Regularidade Básica (Analiticidade) . . . 142

8.1.1 Hölder continuidade da fronteira reduzida . . . 147

8.2 O Teorema de Regularidade C0,α _{. . . 150}

8.3 Pontos Singulares e Cones Mínimos . . . 157

8.3.1 O Teorema de Simon e a regularidade em dimensões baixas (n_≤7) 158 8.4 Estimativa de Federer da dimensão do conjunto singular . . . 159

8.5 Regularidade C1,α _{para hipersuperfícies Minimas . . . 160}

8.5.1 O Teorema de De Giorgi-Federer-Massari-Miranda . . . 160

8.5.3 Comentários Finais . . . 164

9 Teoria de De Giorgi-Nash-Moser 166 9.1 De Giorgi e o 19o problema de Hilbert . . . 166

9.1.1 Subsoluções são limitadas . . . 168

9.1.2 O Lema de Oscilação de De Gorgi . . . 171

9.2 A equivalência entre as Teorias de De Giorgi e Nash-Moser . . . 175

9.2.1 A Desigualdade de Harnack e o Teorema de De Giorgi-Nash-Moser 175 9.3 Uma Aplicação geométrica do Teorema de De Giorgi-Nash-Moser . . . 176

9.4 Regularidade básica das soluções de divA(x, Du) =0 em Ω . . . 177

10 Aplicação à Teoria de Variedades Mínimas 181 10.1 Teorema de Regularidade . . . 181

10.2 Cones Mínimos . . . 183

10.3 Problema de Bernstein . . . 184

11 Aplicações à Problemas de Fronteira Livre 186 11.1 Problemas de Fronteira Livre . . . 186

11.1.1 Motivação: Problema de obstáculo . . . 187

11.1.2 Existência e unicidade . . . 187

11.1.3 Regularidade C1,α _{da fronteira livre . . . 189}

11.2 Melhoramentos dos resultados de regularidade . . . 191

11.2.1 Soluções Q-fracas . . . 191

11.2.2 A Classe de planaridade . . . 192

11.2.3 Regularidade da Fronteira Livre . . . 193

Capítulo

1

Introdução

Conteúdo

1.1 Um pouco de História e alguns comentários . . . 1 1.2 As Grandes Personalidades e o Legado destas . . . 4

1.1 Um pouco de História e alguns comentários

Em matemática Teoria Geométrica da Medida é o estudo das propriedades geométricas das medidas de conjuntos (geralmente em espaços euclidianos), incluindo-se coisas como comprimento de arco e área. A mesma utiliza-se de teoria da medida a fim de generalizar Geometria Diferencial em superfícies com singularidades suaves chamadas conjuntos rectificáveis.

Contribuições significativas surgiram ao se utilizarem técnicas de Teoria Geométrica da Medida, as quais podemos citar: Richard Shoen e Shing Tung Yau1 _{provaram de}

maneira original a conjectura de positividade da massa em Cosmologia, a mesma está relacionada a conjectura de Yamabe. Em 2000 Hutchings-Morgan-Ritoré e Ros provaram a conjectura da Bolha Dupla: A Bolha dupla de sabão é a maneira mais economica de se compacatar dois volumes descritos a priori. E soluções regulares para o Problema de Plateau.

Na interface entre Geometria e Equações Diferenciais Parciais, a Teoria Geométrica da Medida tem sido extensivamente desenvolvida desde a década de 60, iniciando com contribuições básicas devido aos matemáticos Herbert Federer, Ennio De Giorgi, A.I. Volpert e F. Almgren, em conexão com questões resultantes de cálculo das variações, desigualdades isoperimétricas, etc. Tem numerosas aplicações no estudo de conjuntos

1

Este trabalho (somado a outras importantes contribuições) levou Yau a ganhar a medalha Fields em

singulares, fenômenos e problemas físicos: formação de bolhas de sabão, buracos negros, cristais, defeitos de materiais, transisão de fase, fissura em mecânica, linhas de vórtices em cristais líquidos, supercondutores e superfluidos; Sistemas Dinâmicos, processamento de imagens e Teoria de regularidade de problemas de fronteira livre.

O problema de encontrar superfícies mínimas, isto é, de encontrar a superfície de área mínima entre todas as quais estão delimitadas por uma dada curva, foi um das primeiras considerações a respeito da fundamentação do cálculo das varições, e somente teve uma resposta satisfatória a algumas décadas. Conhecido como o Problema de Plateau, após o físico cego que fez belas experiências com películas de sabão e bolhas, tal problema impôs resistência aos esforços de muitos matemáticos por mais de um século. Foi somente na década de trinta que uma solução fora dada ao problema de Plateau em Espaços Euclidianos tri-dimensionais, com o paper de Jesse Douglas[58] e Tibor Radó [59],[60]. O método aplicado por Douglas2 _{e Radó foi desenvolvido e extendido em dimensão 3}

por vários outros, mas nenhum destes resultados se mostrou eficaz para hipersuperfícies mínimas em dimensões elevadas, como também superfícies de dimensão e codimensão quaisquer.

Somente 30 anos mais tarde que o problema de Plateau fora atacado com ênfase em toda a sua generalidade, por vários matemáticos usando técnicas de medida-teórica; em particular podemos citar De Giorgi [50][51][52][53], Reifenberg [61], Federer e Fleming [30] e Almgren [49],[62]. Com respeito a alguns desses matemáticos temos que Federer e Fleming definiram um superfíciek−dimensional emRn_{como umak−corrente, isto é, um}

funcional linear emk−formas. Tal método é tratado com detalhes no livro de Federer [63]. Quanto a Almgren e Allard tiveram uma visão diferenciada de superfície, introduziram a noção de varifold k−dimensional, isto é, medidas de Radon em Rn_{× G}(n, k), onde

G(n, k) denota a variedade Grassmanniana de k−planos em Rn. Por outro lado as idéias

de De Giorgi [53] nunca foram publicadas em revistas de grande circulação. Segundo o formalismo de Ennio De Giorgi uma hipersuperfície em Rn _{era o bordo de um conjunto}

mensurável E _⊂ Rn_{, cuja função característica χ}

E possui derivadas distribucionais que

são medidas de Radon de variação total localmente finita, a esses conjuntos Ennio De Giorgi em homenagem póstuma a Renato Caccioppoli denotou de conjuntos de Caccioppoli (em teoria dos perímetros,conjuntos de perímetro localmente finito). Nesse contexto a área (n−1)−dimensional é dada como a variação total deDχE.

Com respeito a teoria dos perímetros desenvolvida segundo as idéias de Ennio De Giorgi, é possível mostrar, sem grandes dificuldades, com o auxílio de alguns resultados de compacidade a existência de uma solução para o problema de Plateau em algum

2

senso mais fraco (este é o teorema de existência de superfícies mínimas, conjuntos de fronteira minimal). Em contrapartida é uma tarefa nada simples mostrar que tais hipersuperfícies (e em geral toda hipersuperfície minimizante de área) são de fato regulares (hipersuperfícies analíticas), como também com um pouco mais de esforço e uma maquinária de teoremas sofisticados em mãos pode-se mostrar os teoremas de regularidade de De Giorgi: A fronteira reduzida ∂∗Ede um conjunto minimal E_⊂Rn é uma variedade (n−1)−dimensional C1,α_{, exceto possivelmente em um conjunto singular fechado. As}

idéias para a prova da analiticidade e da Hölder continuidade estão concentradas no paper de De Giorgi [53], o qual fora posteriormente simplificado e completado por Miranda [74] onde este mostrou que o conjunto singularΣtem medida de Hausdorff(n−1)−dimensional nula.

Referente ao trabalho de Ennio de Giorgi [53]: O mesmo mostrou que para todox _∈∂E é possível definir um vetor normal aproximado.

νρ(x) =

Z

Bρ

DχE

Z

Bρ

|DχE|

.

Podendo-se mostrar que se, para algum x _∈ ∂E e algum ρ > 0 , o vetor νρ(x) tem

comprimento sufientemente próximo de 1, então a diferença 1−νr(x) converge a zero

quando r _→ 0. Está caracteriza-se como a parte mais difícil da prova, com isso se concretiza algo relativamente fácil mostrar que ∂E é regular (analítica) na vizinhança de x. Tal método se torna muito eficaz para o estudo regularidade em quase todo ponto.

Uma vez estabelecida a regularidade em quase todo ponto, é natural se pensar quando o conjunto singular Σ pode existir. Dessa forma, podemos nos dirigir ao estudo do comportamento de ∂E nas proximidades de um ponto, digamos a origem, e este é em geral feito através de técnicas de Blow-up, isto é, por considerar os conjuntos

Ek={x ∈Rn;

x

k ∈E} k=1, 2, ...

Devido a invariância geométrica da área, todos esse conjuntosEksão minimais, existirá

dessa forma uma subsequência desses conjuntos convergindo em medida para um conjunto C, o qual também será minimal. Além dissoCé um cone, grosseiramente falando um cone tangente aEem 0. Dessa forma podemos observar que Eé regular em uma vizinhança de 0 se e somente se ∂Cé um hiperplano, com isso, segue que a existência de singularidades em ∂Eé reduzida a existência de cones mínimos singulares.

Em [49] Almgren provou a não existência de cones mínimos singulares em Rn_{, e em}

de hipersuperfícies mínimas em Rn_{, para n ≤ 7. Este resultado é ótimo pois o cone de}

Simons

S={x _∈R8;x2₁+x2₂+x2₃+x2₄< x2₅+x₆2+x2₇+x4₈}

é cone mínimo singular em R8_{. Tal resultado fora demonstrado por Enrico Bombieri}3_,

Ennio De Giorgi e Enrico Giusti [43].

Por final, baseado nos trabalhos de Simons , Herbert Federer [4] provou que a dimensão de Hausdorff do conjunto singular não excede n−8, e esta estimativa é ótima.

1.2 As Grandes Personalidades e o Legado destas

O legado que a Teoria Geométrica da Medida proporcionou e ainda proporciona é substancialmente incalculável. Muitos matemáticos foram influenciados pelas escolas matemáticas de H. Federer, E. De Giorgi, Almgren, Allard entre outros grandes nomes, entre esse podemos citar: Luis A. Caffarelli desenvolveu o estudo de regularidade de fronsteira livre como também conjuntos singulares de fronsteira livre [87], [88]; J. Cheeger e T. Colding desenvolveram trabalhos na direção de variedades Riemannianas com curvatura de Ricci não-negativa [89]; L. Simon desenvolveu trabalhos em conjuntos singulares de aplicações harmônicas minimizantes de energia ou correntes minimizantes de área [90], [91] ; Outros trabalhos se concentram no estudo de aplicações harmônicas estacionárias [92], campos de Yang-Mills [93], [94], equações de Seiberg-Witten [95], [96], [97] , e, equações de Ginzburg-Landau em dimensões mais elevadas [98], [99].

3

Capítulo

2

Preliminares

Conteúdo

2.1 Algumas noções de Teoria da Medida . . . 6

2.2 Medida de Hausdorff . . . 12

2.3 Funções de Variação Limitada e conjuntos de Caccioppoli . . . 19

2.3.1 Propriedades dos conjuntos de Caccioppoli . . . 25

2.3.2 A Fórmula de Gauss-Green e o Teorema Estrutural . . . 27

2.4 Regularizantes Simétricos (Mollifiers) . . . 32

2.4.1 Propriedades dos Regularizantes Simétricos (Mollifiers) . . . 33

2.5 Aproximação de Funções BV . . . 34

2.6 Existência de Superfícies Mínimas . . . 38

2.6.1 Teoremas de Compacidade . . . 38

2.7 Aproximação de conjuntos de Caccioppoli por funções C∞ . . . . 42 2.8 Desigualdade de Sobolev e consequências . . . 46

N

este cápítulo estudademos algumas ferramentas essenciais para o desenvolvimento de teoria de regularidade para conjuntos minimais: funções de variação limitada e conjuntos de Caccioppoli. Obteremos muitas propriedades destes, em particular o Teorema de existência de conjuntos minimais (superfícies mínimas). Estaremos em geral a utilizar a noção de medida de Hausdorff (n−1)−dimensional a qual é a mais apropriada para nossos objetivos.

2.1 Algumas noções de Teoria da Medida

Nesta seção estará uma exposição sucinta de alguns resultados de Teoria da Medida, os quais serão utilizados no transcorrer desse texto e servirão de subsídios para a demonstração de muitos outros.

Medidas e Funções µ−mensuráveis SejaX um conjunto , e 2X _{o conjunto de partes de X.}

Definição 2.1. Uma coleçãoF de subconjuntos deX, F ⊂2X_{, é chamado umaσ−álgebra}

se

i. _{∅, X∈ F};

ii. Se _{A∈ F} então _X−A∈F; e

iii. Se _{Ak ∈ F}, _{k =1, ...}, então [

k_≥1

Ak ∈ F. Além disso, uma σ−álgebra de Borel do

Rn é a menor σ−álgebra contendo os subconjuntos abertos do Rn.

Definição 2.2. Uma aplicação µ : 2X _→ [0,+_∞] é chamada uma medida em X se satisfizer

i. _{µ(∅) = 0}; e

ii. _µ(A)≤X

k_≥1

µ(Ak) sempre que A⊂

[

k_≥1

Ak.

Além disso, seja µ uma medida sobre X e A_⊂X. Então µ restrita a A, escreveremos da

seguinte forma, µ_⌊A, será a medida definida por (µ_⌊A)(B) =µ(A_∩B) para todo B_⊂X.

Nota 2.1. A definição (2.2) é usualmente denotada de Medida Exterior.

Definição 2.3. Um conjunto A _⊂ X é µ−mensurável (no sentido de Carathéodory) se

para cada B_⊂X.

µ(B) =µ(B_∩A) +µ(B−A).

Definição 2.4. i. Uma medida _µ sobre _X é regular se para cada conjunto _{A ⊂ X}, existe um conjunto µ−mensuravel B tal que A_⊂B e µ(A) =µ(B).

ii. Uma medida_µsobre_Rn é chamada Borel se todo conjunto de Borel é_µ−mensurável.

iii. Uma medida _µ sobre o _Rn _{é Borel regular se µ é Borel e para cada A⊂R}n_{, existe}

Definição 2.5. Uma medida µ sobreRn _{é uma medida deRadon se µ é uma medida de}

Borel regular e µ(K)<_∞ para todo conjunto compacto K_⊂Rn_.

Definição 2.6. Seja µ uma medida sobre X, e Y um espaço topológico. Uma função f:X_→Y é µ−mensurável se f−1_{(U) é µ−mensurável para cada conjunto aberto U⊂Y.}

Teorema 2.1.1. (Egoroff ) Seja µ uma medida em Rn e suponha que fk:Rn →Rm com

(k =1, 2, ...) são µ− mensuráveis. Assuma também que A _⊆ Rn é µ− mensurável com

µ(A) <_∞ e fk→g µ− quase sempre em A. Então para cada ε > 0 existe um conjunto

µ mensurável B_⊆A tal que

i. _{µ(A−B)< ε}

ii. _fk→g uniformemente em_B.

Proof: Veja Evans-Gariepy [6] pag. 16.

Teorema 2.1.2. (Lusin) Sejam µ uma medida de Borel regular em Rn e f :Rn _→ Rm uma função µ-mensurável. Assuma que A_⊂ Rn é µ-mensurável com µ(A) <_∞. Então

para cada ε > 0 fixado existe um conjunto compacto K_⊂A tal que

i. _{µ(A−K)< ε} e

ii. _f|K é contínua.

Proof: Veja Evans-Gariepy [6] pag. 15.

Integrais e Teoremas de Limites

Definição 2.7. i. Dizemos que _ν é uma medida com sinal sobre _Rn, e denotaremos por ν _{∈ M}(Rn) se existe uma medida de Radon µ sobre o Rn e uma função f _∈ L1

loc(Rn;µ) tal que ν=µ⌊f

ii. Dizemos que _ν é uma medida vetorial sobre o _Rn _{em R}m_{, e denotaremos por ν ∈} M(Rn_;Rm_{), se existe uma medida de Radonµ e uma função vetorialf= (f}

1, ..., fm)

com fi ∈L1loc(Rn;µ) tal que νi =µ⌊fi (i=1, ..., m).

Teorema 2.1.3. (Lema de Fatou) Sejam fk :X→[0,∞] funçõs µ−mensuráveis (k=

1, ...). Então _Z

lim inf

k→∞

fkdµ≤lim inf k→∞

Z fkdµ

Proof: Veja Evans-Gariepy [6], Teorema 1, p.19.

Teorema de Fubini

Definição 2.8. Seja µ uma medida sobre um conjunto X e ν uma medida sobre um

conjunto Y. Para cada M_⊂X_×Y definimos

(µ_×ν)(M) :=inf

X

k≥1

µ(Ak)ν(Bk)

,

onde o ínfimo é tomado sobre toda sequência de conjuntos µ−mensurável Ak ⊂ X e

conjunto ν−mensurável Bk ⊂ Y (k =1, ...) tal que M⊂

[

k_≥1

Ak×Bk. A medida µ×ν é

chamada a medida produto de µ e ν.

Teorema 2.1.4. (Fubini) Seja µuma medida sobre um conjuntoXe seja νuma medida sobre um conjunto Y.

i. _µ×ν é uma medida regular em _X×Y.

ii. Se_A⊂Xé_µ−mensurável e_B⊂Yé_ν−mensurável, então_A×Bé_µ×ν-mensurável

e (µ_×ν)(A_×B) =µ(A)ν(B).

iii. Se _{M ⊂ X×Y} é _σ−finita com respeito a _µ×ν (isto é, _{M =} [

k≥1

Mk, onde Mk é

µ_×ν−mensurável e(µ_×ν)(Mk)<∞para k=1, ...), entãoMy ={x: (x, y)∈M}

e µ−mensurável para ν em quase todo x é µ(My) é ν−integrável. Além disso,

(µ_×ν)(M) = Z

Y

µ(My)dν(y).

Analogamente para x e Mx ={y: (x, y)∈M}.

iv. Se _{f : X×Y → [−∞,∞]} é _µ×ν−integrável e _f é _σ−finita com respeito a _µ×ν (em particular, se f é µ _×ν−somável), então a aplicação y _7→ R_Xf(x, y)dν(x) é ν−integrável, a aplicação x_7→R_Yf(x, y)dν(y) é ν−integrável, e ainda,

Z

X×Y

fd(µ_×ν) = Z

X

Z

Y

f(x, y)dµ(x)

dν(y) = Z

Y

Z

X

f(x, y)dν(y)

dµ(y)

Proof: Veja Evans-Gariepy [6], Teorema 1, p.22.

Definição 2.9. i. A medida de Lebesgue 1-dimensional _L1 em R é definida por

L1_{(A) :=inf}

X

i_≥1

diamCi :A⊂

[

i_≥1

Ci, Ci ⊂R

para todo A_⊂R.

ii. A medida de Lebesgue n-dimensional _Ln sobre _Rn é definida indutivamente por

Ln _{:= L}n−1

×L1_{= L}1

×..._×L1_,

ou equivalentemente,

Ln:= Ln−k_×Lk

para qualquer k_∈{1, ..., n−1}. Às vezes usaremos a notação |E|, alguns autores se

utilizam da notação meas E para a medida de Lebesgue de um conjunto genérico E

de Rn.

Diferenciação de Medidas de Radon

Definição 2.10. Sejamµe νmedidas de Radon sobreRn_{. Dizemos que νé diferenciável}

com respeito a µ em x se

Dµν(x) :=lim r→0

ν(B[x, r]) µ(B[x, r])

sempre que este limite existe e é finito. Ainda, diremos que Dµνé a densidade de ν com

respeito a µ.

Definição 2.11. i. A medida _ν é absolutamente contínua com respeito _µ, e escreveremos ν_≪µ, se µ(A) =0 implica que ν(A) = 0 para todo A_⊂Rn.

ii. As medidas _ν e _µ são multuamente singulares, e escreveremos _ν⊥µ, se existe um

conjunto de Borel B_⊂Rn _{tal que µ(R}n_{−B) =ν(B) =0.}

Teorema 2.1.5. (Radon-Nikodym) Sejamµ, ν medidas de Radon sobre Rn _{com µ ≪}

ν. Então

ν(A) = Z

A

Dµνdµ

para todo conjunto µ-mensurável A_⊂Rn_.

Proof: Veja Evans-Gariepy [6], Teorema 2, p.40.

Teorema 2.1.6. (Lebesgue-Besicovitch)

i. Seja _µ uma medida de Radon sobre _Rn e _f∈L1_loc(Rn_;µ). Então

lim

r→₀

1 µ(B(x, r))

Z

B(x,r)

fdµ =f(x)

ii. Seja _µ uma medida de Radon sobre _Rn_{, 1≤p <}

∞ e f_∈Lp_loc(Rn_{;µ). Então}

lim

r→₀

1 µ(B(x, r))

Z

B(x,r)

|f−f(x)|pdµ=0 (2.1)

para x _∈Rn _{µ−quase sempre.}

Proof: Veja Evans-Gariepy [6], Teorema 1, p.43, e Corolário 1, p.44.

Definição 2.12. Um ponto x é dito ser um ponto de Lebesgue de f com respeito a µ, se (2.1) é satisfeita.

Teorema de Representação de Riesz-Markov Teorema 2.1.7. (Representação de Riesz- Markov)

i. Seja _L:C0(Rn_;Rm₎

→R um funcional linear satisfazendo

sup{L(φ) :φ_∈C0(Rn,Rm),|φ|≤1, spt(φ)⊂K}<∞

para cada conjunto compacto K _⊂ Rn_{. Então existe uma única medida de Radon}

vetorial µ=σ||µ||_{∈ M}(Rn_;Rm_{) tal que}

L(φ) = Z

Rn

φ.dµ= Z

Rn

φ.σd||µ|| _(2.2)

para toda φ_∈C0(Rn,Rm), onde σ:Rn →Rm é tal que |σ|=1 ||µ||−q.s.

ii. Seja _{L : C0(R}n_{) → R} um funcional linear tal que _{L(φ) ≥ 0} para toda _{φ ∈} C0(Rn), φ≥0. Então existe uma medida de Radon µ em Rn tal que

L(φ) = Z

Rn

φ.dµ

para toda φ_∈C0(Rn)

Proof: Veja Evans-Gariepy [6], Teorema 1, p.49, e Corolário 1, p.53.

Definição 2.13. Diremos que λ é uma medida de variação se para cada conjunto aberto

V _⊂Rn,

λ(V) =sup{L(φ) :φ_∈C0(Rn,Rm),|φ|≤1, spt(φ)⊂V},

onde L : C0(Rn,Rm) → R é um funcional linear limitado. Se L é como em (2.2), então

Convergência Fraca SejaU um conjunto aberto do Rn

Definição 2.14. Sejam µ e µk, k = 1, ..., medidas de Radon sobre Rn. Diremos que

µk converge fracamente a µ no sentido de medida de Radon, e escrevemos µk ⇀ µ em M(Rn), se

lim

k→∞

Z Rn

φ.dµk=

Z Rn

φ.dµ

para toda φ_∈C0(Rn).

Teorema 2.1.8. Sejam µ, µ1, µ2, ... medidas de Radon em U. Então as seguintes

afirmações são equivalentes:

i. _{µk ⇀µ} em _M(U);

ii. lim supµk(C)≤µ(C) para cada compacto C⊂U e µ(O)≤lim infµk(O) para cada

aberto O_⊂U;

iii. _lim

k→∞

µk(B) =µ(B) para cada B⊂Rn conjunto Boreliano limitado comµ(∂B) = 0.

Proof: Veja Evans-Gariepy [6] Teorema 1, pag. 54.

Teorema 2.1.9. (Compacidade fraca para Medidas de Radon) Seja {µk}k≥1 em M(Rn_{) tal que sup}

k

µk(K)<∞ para todo conjunto compacto K do Rn. Então existe uma

subsequência {µkj}j≥1 e uma medida de Radon µ tal que µkj ⇀µ em M(R

n_).

Proof: Veja Evans-Gariepy [6],pag. 55.

Definição 2.15. Sejamf, fk ∈Lp(U), k=1, ..., e seja 1≤p <∞.

i. Diremos que _fk converge fracamente em _Lp_(U) para _f, e escrevemos _{fk ⇀ f} em Lp_{(U), se}

Z

U

fkφdx→

Z

U

fφdx

para toda φ_∈Lq_{(U), onde} 1 p +

1

q =1, 1 < q≤∞.

ii. Diremos que _fk converge fracamente em medida, ou como medida, para _f se

Z

U

fkφdx→

Z

U

fφdx

iii. Diremos que _fk converge fracamente no sentido das distribuições, ou como

distribuição, para fse _Z

U

fkφdx→

Z

U

fφdx

para toda φ_∈C∞

0 (U)

Definição 2.16. Sejam f, fk ∈ L

∞

(U), k = 1, .... Diremos que fk converge fraco estrela

em L∞

(U) para f, e escreveremos fk−→⋆f em L∞(U), se

Z

U

fkφdx→

Z

U

fφdx

para toda φ_∈L∞

(U).

2.2 Medida de Hausdorff

Há no Rn uma “boa” medida m−dimensinal introduzida em 1918 pelo matemático alemão Felix Hausdorff, chamada Medida de Hausdorff, a qual coincide com a noção clássica de área para variedades mergulhadas, ou seja, subvariedades , porém está definida para todos os subconjuntos de Rn_{. Quando n = m a medida de Hausdorff}

coincide com a medida de Lebesgue. A medida de Hausdorff é a medida natural para trabalhar com conjuntos que não são regulares no sentido da Geometria Diferencial. A medida de Hausdorff _Hs _{é o resultado de uma construção conhecida como construção de}

Carathéodory (Veja Gianquinta-Modica-Soucek [82]). Sejam A_⊂Rn _{, 0≤s <}

∞ e 0 < δ_≤∞. Defina

Hsδ(A) = inf

X

j>1

α(s)

_{diam C}

j

2

s

;A_⊂[

j>1

Cj, diam Cj6δ

onde α(s) = π

s/2

Γ(s 2 +1)

e Γ(s) = Z∞

0

e−xxs−1dx é a função Gama de Euler.

Observação 2.1. Para δ > δ′ tem-se _Hs_δ(A) 6 _Hs

δ′(A). Portanto H

s

δ(.) é uma função

monótona não-crescente de δ_∈[0,_∞).

Para A e s como acima, faz sentido definirmos o limite

Hs_{(A) :=}

lim

δ→₀H

s_{(A) =}

sup

δ>0 H s_(A).

Claramente 06_Hs(A)6_∞.

Assim, denotaremos_Hs _{a s-dimensional Medida de Hausdorff em R}n_{. Por H}s δ(.)

subconjunto A_⊂Rn_{, δ > 0 e s≥0}

Hs_(A) ≥ Hs

δ(A)≥ H s

∞(A)

Notemos que é necessário requerer δ_→0 na ordem de forçar a cobertura “concordar”

com a geometria local do conjunto A, como é ilustrado nas figuras abaixo.

Figura 2.1: A medida de Hausdorff (área) de um pedaço da superfície sendo aproximada pela interseção de pequenas bolas as quais a recobrem.

Teorema 2.2.1. _Hs _{é uma Medida de Borel regular se 0 ≤ s <}

∞. Além disso, se A_⊂Rn _{é H}s_{−mensurável com H}s_(A)<

∞ então Hs_{⌊A é uma medida de Radon.}

Proof.: Veja Evans-Gariepy [6], pag. 61 e Fanghua-Xiaoping [8], pag. 6 para a

primeira parte, e veja Evans-Gariepy [6], p.5. para a segunda parte.

Observação 2.2. _Hs _{não é uma medida de Radon se 0≤ s < n, uma vez que a mesma}

não é σ-finita

Teorema 2.2.2. Propriedades elementares da Medida de Hausdorff.

i. _H0_{(.) é uma medida de contagem, ou seja, a mesma fornece a "cardinalidade" do}

conjunto;

ii. _H1_{= L}1 _{em R, onde L}1 _{denota a medida de Lebesgue;}

iii. _Hs _{=0 em R}n _{se s>n;}

iv. _Hs_{(λA) =λ}s_Hs_(A). para todo _{λ > 0} e _A⊂Rn. (Homogeneidade de grau s);

v. _Hs_{(I(A)) = H}s_(A) para cada _{I :R}n _−→Rn isometria linear e _{A ⊂ R}n, ou seja, a

mesma é em particular invariante por rotações e tranlações.

vi. Se _f:Rn _→Rm Lipschitziana, _A⊂Rn_{, 0≤s <∞}. Então

Hs_(f(A))

≤(Lip(f))s

Hs_(A).

onde

Lip(f) :=sup

_{|f(x) −f(y)|}

|x−y| ;x, y∈R n_{, x}

6

=y

Proof.: Evans-Gariepy [6], pag. 63. para (i)-(v) e pag. 75 para (vi).

Lema 2.1. Sejam A_⊂Rn _{e 0≤s < t <}

∞. i. Se _Hs_(A)<_∞ então _Ht_(A)=₀;

ii. Se _Ht_{(A)> 0} então _Hs_{(A) = ∞}. Proof.: Evans-Gariepy [6], pag. 65.

Motivados pelo conteúdo do Lema acima podemos então tratar da

Definição 2.17. A Dimensão de Hausdorff de um conjunto A_⊂Rn é definida como

Hdim(A) = inf{s≥0;Hs(A)<∞} =inf{s;Hs(A) =0}

=sup{s;_Hs_{(A)> 0}}

=sup{s;_Hs_{(A) =}

∞}_≤n.

Observação 2.3. A dimensão de Hausdorff de um conjunto E _⊂ Rn _{coincide com a}

dimensão topológica do mesmo, quando este for uma variedade topolóligica mergulhada, ou seja, uma subvariedade.

Exemplo 2.1. (Self-similar fractals)

Ilustremos com alguns exemplos o cálculo da dimensão de Hausdorff de conjuntos fractais.

O conjunto de Cantor clássico

O conjunto de Cantor é um fractal bem-conhecido e facilmente construtível. Podemos construí-lo indutivamente como segue: Sejam

E0 = [0, 1],

E1 = [01₃]∪[2₃, 1],

E2 = [0,1₉]∪[₉2,1₃]∪[8₉, 1],

· · ·

Ek = [0,₃1k]∪[

2 3k,

1

3k−1]∪ · · · ∪[

3k₋₁

3k , 1].

Então o conjunto E = \

k≥0

Ek é conhecido como conjunto de Cantor (Veja figura

abaixo.)

Observe que

i. Seja _{ψ1(x) =} x

3, ψ2(x) = 2 3+

1

3x. Então E=ψ1(E)∪ψ2(E);

ii. E é construído de um modo muito simples, mas as propriedades geométricas locais

são complicadas e difíceis de serem descritas em linguagem matemática clássica;

iii. Não obstante o mesmo é um conjunto bastante importante em vários sentidos:este

é não-enumerável e perfeito, isto é, E′ = E, entretanto não é conveniente medir

seu comprimento no senso normal dado que L1_{(E) =0. De qualquer forma podemos}

averiguar que _Hdim(E) =

Figura 2.3: Conjunto de Cantor

A curva de Von Koch

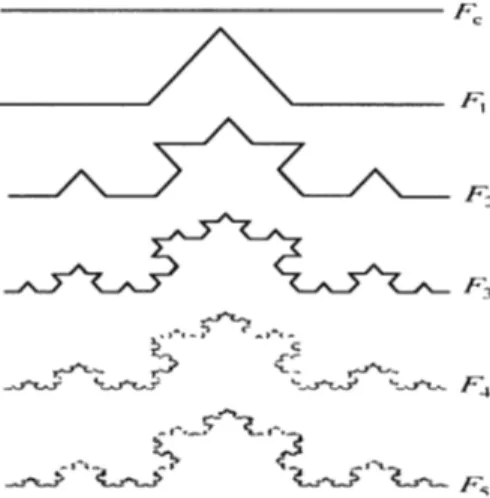
Seja F0 um segmento unitário de reta. F1 é um conjunto obtido pela remoção do terço

médio da parte de F0 e a reposição deste por outros dois lados de um triângulo equilátero

cuja base é a parte removida. Assim F1 contém 4 segmentos. Aplicando-se o mesmo

procedimento a cada parte de F1 contruiremos F2. Deduzimos similarmente a obtenção de

Fk pela reposição dos terços médios de cada segmento deFk−1 por outros dois lados de um

triângulo equilátero correspondente. Então a curva limite F = lim

k→∞

Fk é referida como a

curva de Von Koch (Veja figura abaixo.)

Figura 2.4: A curva de Von Koch ou Snowflake (Floco de neve)

Então temos as seguintes propriedades para a cuva de Von Koch:

i. Se puzermos _{ψ1(x) =} x

3, ψ2(x) = 1

√

6x+ 1

3, ψ3(x) = 1

√

6x+ 1

√

6 + 1

6, ψ4x = 2 3 +

1 3x,

então F= 4

[

j=1 ψj(F).

iii. Um cálculo direto indica que o comprimento de _Fk é 4 3

k

, assim o comprimento de F é infinito. Porém a área de F no plano 2−dimensional é zero. Portanto

o comprimento e a área de F não são objetos matemáticos covenientes a fim de descrever a “forma” de F efetivamente. De qualquer forma podemos também averiguar que Hdim(F) = log3

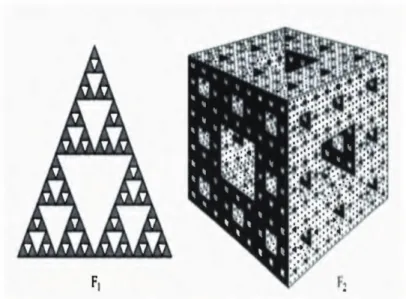
log4 Mais self-similar fractals.

Figura 2.5: F2 é conhecido como a Esponja de Sierpinski, o memo é um exemplo de um

conjunto de dimensão fracionária. Sua dimensão de Hausdorff é log_log20₃, cerca de 2,7. F1 é obtido por homotetias com fator de escalonamento 1₂. Iniciando com um

triângulo equilátero com lado 1, na n−ésima etapa removemos3n _{triângulos com}

lados2−n. Portanto a dimensão de Hausdorff deF1 é log_log3₂.(De Studies in Geometry

by Blumenthal and Manger c1970 by W.H. Freeman and Company.)

Exemplo 2.2. O conjunto de Cantor em R (Bis)

Para qualquer intervalo J= [a, b] em R e qualquer t _∈(2,_∞), definimos

Φ(J) =

a, a+b−a t

∪

b−b−a t , b

.

Temos a seguinte importante identidade

|J|m = X S∈Φ(J)

|S|m para m= log2 logt.

De fato a expressão do lado direito é 2|J_t|mm. Portanto 2=t

m_{. Iniciemos com}

e tome indutivamente para j=1, 2, ...,

Hj=∪{Φ(J);J∈Hj−1}

Então definimos o conjunto de Cantor por

Ct =

\

j≥0 Hj

Pode-se checar que

Hdim(Ct) =m= log2 logt, e

Hm_(C t) =

wm 2m.

Note que C3 é o conjunto de Cantor estudado em Análise Real.

Para mais informações sobre conjuntos fractais e dimensão de Hausdorff consulte Rataj [13], Albertini [19] e Waiezsäcker [20].

Teorema 2.2.3. Hn_=Ln _{em R}n_.

Proof Veja Evans-Gariepy [6] pag. 70 ou Fanghua-Xiaoping [8] pag. 11

Exemplo 2.3. Conforme os resultados acima podemos inferir que

Figura 2.6: A medida de Hausdorff Hn−1 _{da esfera coincide com a medida de Lebesgue da}

mesma, ou seja, sua área.

Além disso, temos também conforme os resultados acima expostos que _Hs_(Sn−1_{) =0}

se s > n e _Hs_(Sn−1_{) =}

∞ se s < n. Analogamente para o n−toro,_Hs_(Tn_{) = 0, se s > n}

e _Hs_(Tn_{) =}

Figura 2.7: Sendo o 2−toro uma subvariedade topológia, sua medida de Hausdorff _Hn−1

coincide com a medida de Lebesgue, istó é, sua área.

2.3 Funções de variação limitada e conjuntos de

Caccioppoli

Funções de Variação Limitada(Funções BV, do inglêsBounded Variation) são funções cuja derivada distribucional é uma medida de Radon finita. Isto é essencialmente a forma enfraquecida para teoria da medida de uma função ser diferenciável.

Definição 2.18. Seja Ω_⊂Rn, n_≥2.

i. Uma função _{f ∈ L}1_{(Ω) é dita ser de Varição Limitada e escreveremos f ∈} BV(Ω), mais adiante esclareceremos o que seria tal conjunto, se o gradiente Df

, distribucional, ou seja, no sentido das distribuições é uma medida de Radon finita em Ω.

ii. Diremos que _f é uma função de variação limitada local, e denotamos_{f∈BVloc(Ω)}, se f_∈BV(V) para todo conjunto aberto V _⊂⊂U.

Em outras palavras, f_∈ BV(Ω) se, e somente, existe Df _{∈ M}(Ω;Rn) finita tal que para i =1, ..., n, _Z

Ω

fφxi = −

Z Ω

φd(Dif),

para toda φ_∈C1

0(Ω), onde Df = (D1f, ..., Dnf) em Ω; ou equivalentemente, Z

Ω

fdivφdx= − Z

Ω

para toda φ_∈C1

0(Ω). Além disso, para simplificar escreveremos Z

Ω

fdivφdx= − Z

Ω φ.Df

para toda φ_∈C1 0(Ω).

Df portanto representa o gradiente fraco distribucional da função f. Em termos mais gerais estamos exigindo que a função f satisfaça em um certo sentido o clássico Teorema da Divergência (Gauss-Green).

Definição 2.19. Seja f _∈ L1

loc(Ω) , definimos a Variação Total de f em Ω conjunto

aberto do Rn como: Z

Ω

|Df|=V(f;Ω) = sup Z

Ω

f(x)divg(x)dx;g _∈C1₀(Ω;Rn),|g|L∞_(Ω)≤1

.

Definição 2.20.

BV(Ω) =

f_∈L1(Ω); _∃ Df_{∈ M}(Ω;Rn), Z

Ω

fdivφdx= − Z

Ω

φ.Df _∀ φ_∈C1₀(Ω)

.

Se munirmos BV(Ω)com a norma _kf_kBV(Ω)=kfkL1_(Ω)+

Z Ω

|Df|então este se tornará um

Espaço de Banach. Ademais

Z Ω

|Df| define uma seminorma em BV(Ω). Analogamente

se define

BVloc(Ω) =

f_∈L1(V); _∃ Df_{∈ M}(V;Rn), Z

V

fdivφdx= − Z

V

φ.Df _∀ φ_∈C1₀(V)

com V _⊂⊂Ω

No exemplo a seguir, observaremos que para toda função f _∈ W1,1(Ω) tem variação total finita. Em particular, veremos que toda função de Sobolev tem localmente variação limitada.

Exemplo 2.4. Sejafuma função de Sobolev, isto é,f_∈W1,1_{(Ω), então temos a seguinte}

igualdade _Z

Ω

|Df|= Z

Ω

|_∇f|dx.

Para cada V _⊂⊂Ω e g_∈C1

0(V;Rn), com |g|≤1 temos Z

V

fdivg= − Z

Ω∇

fgdx_≤ Z

V

|_∇f|dx <_∞

Agora ao aplicarmos a definição de variação total concluiremos que

Z Ω

|Df|_≤

Z Ω

Aqui se tem _∇f = (f1, ..., fn) e f1....fn são as derivadas generalizadas de f. Agora é

suficiente provar a desigualdade oposta, para tanto fixe ε > 0, e escolha φ como (|∇f|)ε

|_∇f|

onde |_∇f|ε=ηε∗Df, ou seja, a convolução de Df com um regularizante simétricoηcomo

veremos nas seções seguintes; então

Z Ω

|Df|_≥

Z Ω

fdivφdx= Z

Ω

(|_∇f|)ε.|_∇f| |_∇f|

Passando o limite quando ε_→0, obtemos Z

Ω

|Df|_≥

Z Ω

|_∇f|dx.

Observe também que a mesma igualdade é válida se f é de classeC1_.

Mediante a definição de variação total de uma funçãof_∈L1

loc(Ω), note que a variação

da mesma pode ser infinita. Neste caso, veremos através do Teorema (2.3.1), que pode ser encontrado em Ambrosio-Fusco-Pallara [10], que esta não será uma função de variação limitada.

Teorema 2.3.1. Seja f_∈L1_{(Ω). Então f∈BV(Ω) se, e somente se,} Z

Ω

|Df|<_∞. Além disso,

Z Ω

|Df|=||_∇f||(Ω).

Proof: Suponhamos que fseja uma função de variação limitada, ou seja, f_∈BV(Ω).

Fixemos φ_∈C1

0(Ω;Rn),|φ|≤1, então temos que

− Z

Ω

fdivφdx= Z

Ω

φ._∇f_≤ Z

Ω

d||_∇f||.

Uma vez que |φ|_≤1, segue segundo a definição que

Z Ω

|Df|_≤||_∇f||(Ω)<_∞. Reciprocamente, definamos um funcional linear L:C1

0(Ω;Rn)→R por L(φ) := −

Z Ω

fdivφdx,

para toda φ _∈ C1

0(Ω;Rn). Observemos que |L(φ)| ≤ V(f;Ω)||φ||L∞. Agora fixemos um conjunto compacto K_⊂Ω, e seja V um conjunto aberto tal que K_⊂V _⊂⊂Ω. Para cada φ _∈C0(Ω;Rn) com spt(φ) ⊂K, existe uma sequência φk∈ C10(V;Rn), k=1, ..., tal que φk → φ uniformente em V. Definimos bL(φ) := lim

k→∞

L(φk), para todo φ _∈ C0(Ω;Rn_).

pode ser estendido a um operador linear bL:C0(Ω;Rn)→R tal que

supbL(φ) :φ_∈C0(Ω;Rn),|φ|_≤1, spt(φ)_⊂K<_∞.

Finalmente, pelo Teorema de Riesz-Markov, existe uma única medida de Radon vetorial µ tal que

b

L(φ) := Z

Ω φ.dµ.

Portanto, f é uma função de variação limitada, isto é, f_∈BV(Ω). Ainda, para cada φ _∈C1

0(Ω;Rn),|φ|≤ 1, tem-se |bL(φ)|≤V(f;Ω), logo ||∇f||(Ω) ≤V(f;Ω), e isto finaliza

a demonstração do Teorema.

Exemplo 2.5. Suponhamos que f _∈ W1,1_{(Ω), então pelo Exemplo (2.4) e o Teorema}

anterior (2.3.1), f _∈ BV(Ω), logo W1,1_{(Ω) ⊂ BV(Ω), e analogamente, W}1,1

loc(Ω) ⊂ BVloc(Ω). Em particular, W_loc1,p(Ω) _⊂ BVloc(Ω) para 1 _≤ p _{≤ ∞}. Consequentemente, toda função de Sobolev tem variação localmente limitada.

Exemplo 2.6. Sejam g _∈ C1

0(Ω;Rn), E ⊆ Rn com fronteira C2 e χE a função

característica de E. Então pelo Teorema de Gauss-Green (Teorema da Divergência) segue que

Z Ω

χEdivg(x)dx= Z

∂E

gνd_Hn−1 _{≤ H}n−1(∂E_∩Ω)

onde |ν(x)|=1, sendo este o vetor normal exterior a ∂E . Se em acréscimo assumirmos

|g(x)|_≤1, teremos via definição de variação total que Z

Ω

|Df|=sup Z

Ω

f(x)divg(x)dx;g_∈C10(Ω;R n₎

,|g|_L∞_(Ω)≤1

≤ Hn−1(∂E_∩Ω)<_∞. Portanto χE ∈BV(Ω). De fato se tem

Z Ω

|Df|=_Hn−1(∂E_∩Ω). (2.3)

Vejamos: Do fato de E ter fronteira C2 , ν(x) será uma função de classe C1 com

|ν(x)| = 1 . Dessa forma invocando o Teorema de Tietze diferenciável, ou Teorema da Extensão de Whitney ou mesmo o Teorema para Aproximação de funções Lipschitz por funções C1 _{(Veja Apêndice), existe uma função N, definida em todo o R}n _{, tal que} N _∈ C1_(Rn_;Rn_{) e |N(x)|≤ 1 para todo x. Se escolhermos η ∈ C}∞

0 (Ω) com |η| ≤ 1 e se

puzermos g=Nη teremos via o Teorema de Gauss-Green,

Z E

divg(x)dx= Z

∂E

Assim se nos utilizarmos das definições de Variação Total e Medida de Hausdorff na última igualdade seguirá que

Z Ω

|DχE|≥sup Z

∂E

νd_Hn−1;η_∈C∞

0 (Ω),|η|≤1

=_Hn−1(∂E_∩Ω)

Observação 2.4. Pelo Exemplo (2.5) acima tem-se W1,1_{(Ω)⊆BV(Ω). Entertanto não}

se terá BV(Ω) =W1,1_{(Ω), vejamos: Suponha que E⊆R}n _{tenha fronteira C}2 _{e seja χ} E a

função característica de E. Adimitindo que E seja limitado então teremos

Z Ω

χEdx = Ln(E∩Ω)

onde Ln _{denota a medida de Lebesgue de E}

∩Ω em Rn e consequentemente χE ∈L1(Ω).

Em contrapartida χE ∈/ W1,1(Ω), pois se o fosse, por χE ∈ BV(Ω), χE deveria ser

absolutamente contínua, o que facilmente é constatado sua negativa. Para mais detalhes consute Evans-Gariepy [6] pag. 164.

Motivados pelo exemplo (2.6) acima juntamente com a observação subsequente podemos então falar na seguinte

Definição 2.21. Sejam E um conjunto Boreliano e Ω _⊂ Rn aberto. Definimos o Perímetro de E em Ω como:

Per(E;Ω) = Z

Ω

|DχE|=sup Z

Ω

divg(x)dx;g_∈C1₀(Ω;Rn),|g|_L∞_(Ω)≤1

Nota 2.2. A definição acima pode ser extendida a qualquer conjunto Boreliano B_⊂ Rn ao tomarmos

Per(E;B) =inf{Per(E;Ω) :B_⊂Ω, Ω_⊂ Aberto}

Moralmente, o Perímetro de um conjuntoEserá a medida generalizada de sua fronteira e esta, como vimos no exemplo anterior, coincidirá com a noção clássica de área quando a fornteira do mesmo for suficientemente regular, ou seja, suave.

Observação 2.5. Por consequência das exposições temos

i. |Df| é a medida de variação de f; |DχE| é a medida de perímetro de E; |DχE|(Ω) é

o perímetro de E em Ω;

ii. Se _{f∈BVloc(Ω)∩L}1_{, então f∈BV(Ω) se, e somente se, |Df|(Ω) <}

∞ neste caso

podemos definir

iii. Podemos conseguir via o Teorema de Riesz-Markov a seguinte representação

|Df|(V) = sup Z

V

fdivφdx;φ_∈C1₀(V;Rn),|φ|_≤1

,

|DχE|(V) = sup Z

E

divφdx;φ_∈C1₀(V;Rn),|φ|_≤1

para cada V _⊂⊂Ω.

A última observação ressalta nossa escolha de variação total e Perímetro do um conjunto E.

Exemplo 2.7. Seja E_⊂⊂Ω um conjunto aberto limitado.Suponhamos que ∂E seja uma fronteira Lipschitz, entãoEtem perímetro finito. Com efeito, fixadoϕ_∈C1

0(Ω;Rn),|ϕ|≤ 1, pela Fórmula de Gauss-Green versão para campos suaves em domínios cujas fronteiras são localmente o gráfico de funções Lipschitz (Veja Apêndice),

Z E

divϕdx = Z

∂E

ϕ.νd_Hn−1 <_∞,

onde ν é a normal exterior a ∂E. Logo χE ∈BV(Ω), o que implica queE é um conjunto

de perímetro finito.

Definição 2.22. Diremos que um conjunto BorelianoEé umconjunto de Caccioppoli

se, e somente se, para todo Ω _⊂ Rn _{aberto e limitado, este tiver Perímetro localmente}

finito, isto é, Per(E;Ω)<_∞.

Nota 2.3. Originalmente, conjuntos de perímetro finito foram definidos como conjuntos

que podem ser aproximados por domínios poliedrais , E _{∈ P}, o qual é definido como qualquer conjunto E _⊂ Rn no qual é o fecho de um conjunto aberto cuja fronteira topológica, ∂E, está contida em uma união finita de hiperplanos do Rn. Essa definição é similar a definição de Lebesgue da área de uma superficie. Mais geralmente, o perímetro de qualquer conjunto, não necessariamente mensurável, foi definido como

Per(E;Rn) :=inflim inf h→₀ H

n−1_(∂Eh);E

h ∈ P,|(E−Eh)∪(Eh −E)|→0

então mostra-se que E é um conjunto mensurável, se Per(E;Rn_{) <}

∞, e, neste caso,

2.3.1 Propriedades dos conjuntos de Caccioppoli

i. SeΩ_⊆Ω1 entãoPer(E;Ω)≤Per(E;Ω1)com igualdade quandoE⊂⊂Ω(isto é, E é um subconjunto compacto de Ω);

ii. Per(E1∪E2;Ω)≤Per(E1;Ω) +Per(E2;Ω) com igualdade quandodist(E1, E2)> 0; iii. De fato o item acima pode ser melhorado da seguinte forma

Per(E1∪E2;Ω) +Per(E1∩E2;Ω)≤Per(E1, Ω) +Per(E2, Ω)

iv. Se|E|=0então Per(E) =0. Em particular se |E1△E2|=|(E1−E2)∪(E2−E1)|=0 então Per(E1) =Per(E2).

Para uma demonstração de tais propriedades consulte Pacheco [12], pag. 39. e Ennio de Giorgi Selected Papers. [29] pag. 221.

Vejamos uma contextualização de conjuntos de Caccioppoli:

Definição 2.23. (Partições de Caccioppoli)SejaΩ_⊂Rn _{um conjunto aberto eI⊂N;}

Diremos que uma partição {Ei}i_∈N de Ω é uma partição de Caccioppoli se X

i∈I

P(Ei, Ω)<

∞. Se diz que a partição {Ei}i_∈N é ordenada se |Ei|≥|Ej| sempre que i≤j. Vejamos o seguinte exemplo de partição de Caccioppoli

Figura 2.8: A partição {Eh} do retângulo (0, x1)×(0, y1) é uma partição de Caccioppoli se e