UM CURSO DE GEOMETRIA ANAL´ITICA E ´

(1)

GEOMETRIA ANAL´ITICA E ´

ALGEBRA LINEAR

Reginaldo J. Santos

Departamento de Matem ´atica-ICEx

Universidade Federal de Minas Gerais

http://www.mat.ufmg.br/~regi

(2)

´

E proibida a reproduç ão desta publicaç ão, ou parte dela, por qualquer meio, sem a pr évia autorizaç ão, por escrito, do autor.

Editor, Coordenador de Revis ão, Supervisor de Produç ão, Capa e Ilustraç ões: Reginaldo J. Santos

ISBN 85-7470-006-1

Ficha Catalogr ´afica

Santos, Reginaldo J.

S237u Um Curso de Geometria Anal´ıtica e ´Algebra Linear / Reginaldo J. Santos - Belo Horizonte: Imprensa Universit ´aria da UFMG, 2007.

1. ´Algebra Linear 2. Geometria Anal´ıtica I. T´ıtulo

(3)

Pref ´acio vii

1 Matrizes e Sistemas Lineares 1

1.1 Matrizes . . . 1

1.1.1 Operac¸ ˜oes com Matrizes . . . 3

1.1.2 Propriedades da ´Algebra Matricial . . . 10

1.1.3 Aplicac¸ ˜ao: Cadeias de Markov . . . 16

Ap êndice I: Notaç ão de Somat ório . . . 33

1.2 Sistemas de Equac¸ ˜oes Lineares . . . 35

1.2.1 M ´etodo de Gauss-Jordan. . . 39

1.2.2 Matrizes Equivalentes por Linhas . . . 50

1.2.3 Sistemas Lineares Homog ˆeneos . . . 52

(4)

2 Invers ˜ao de Matrizes e Determinantes 77

2.1 Matriz Inversa . . . 77

2.1.1 Propriedades da Inversa . . . 79

2.1.2 Matrizes Elementares e Invers ˜ao (opcional) . . . 82

2.1.3 M ´etodo para Invers ˜ao de Matrizes . . . 86

2.1.4 Aplicaç ão: Interpolação Polinomial . . . 96

2.1.5 Aplicac¸ ˜ao: Criptografia . . . 98

2.2 Determinantes . . . 107

2.2.1 Propriedades do Determinante . . . 113

2.2.2 Matrizes Elementares e o Determinante (opcional) . . . 128

Ap êndice II: Demonstraç ão do Teorema 2.11 . . . 136

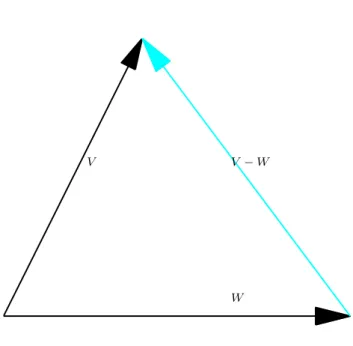
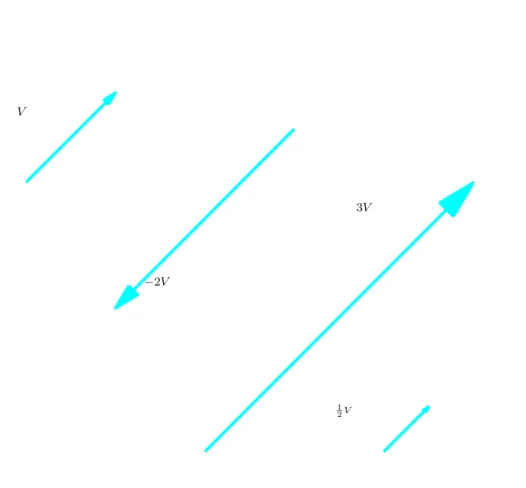
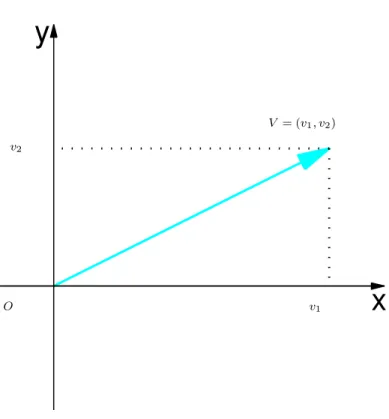
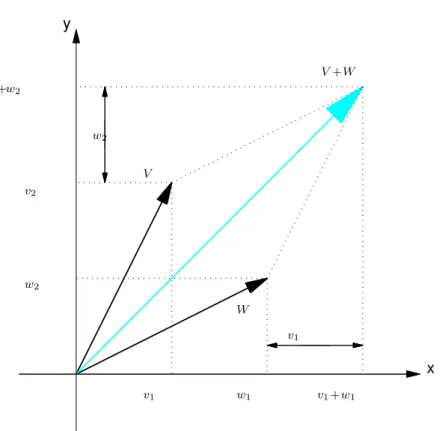
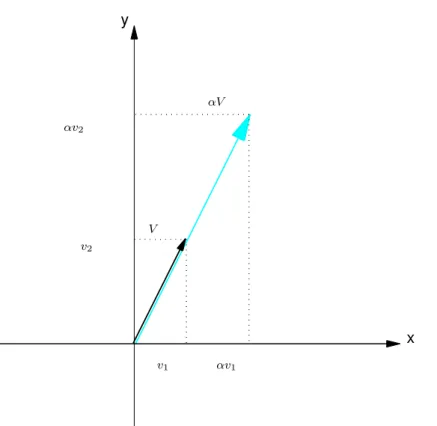
3 Vetores no Plano e no Espaço 142 3.1 Soma de Vetores e Multiplicaç ão por Escalar . . . 144

3.2 Produtos de Vetores . . . 180

3.2.1 Norma e Produto Escalar . . . 180

3.2.2 Projec¸ ˜ao Ortogonal . . . 194

3.2.3 Produto Vetorial . . . 197

3.2.4 Produto Misto . . . 209

Ap êndice III: Demonstraç ão do item (e) do Teorema 3.5 . . . 226

4 Retas e Planos 229 4.1 Equac¸ ˜oes de Retas e Planos . . . 229

4.1.1 Equac¸ ˜oes do Plano . . . 229

4.1.2 Equac¸ ˜oes da Reta . . . 244

(5)

4.2.1 Angulosˆ . . . 270

4.2.2 Dist ˆancias . . . 277

5 Espac¸osRn ₃₀₀ 5.1 Independ ˆencia Linear . . . 300

5.1.1 Os Espac¸osRn _{. . . .} ₃₀₀

5.1.2 Combinac¸˜ao Linear . . . 305

5.1.3 Independ ˆencia Linear. . . 311

5.1.4 Posic¸˜oes Relativas de Retas e Planos . . . 322

5.2 Subespac¸os, Base e Dimens ˜ao . . . 329

Ap ˆendice IV: Outros Resultados . . . 355

5.3 Produto Escalar emRn _{. . . .} ₃₆₃

5.3.1 Produto Interno . . . 363

5.3.2 Bases Ortogonais e Ortonormais . . . 372

5.4 Mudanc¸a de Coordenadas . . . 382

5.4.1 Rotac¸ ˜ao . . . 388

5.4.2 Translac¸ ˜ao . . . 390

5.4.3 Aplicaç ão: Computaç ão Gr áfica - Projeç ão Ortogr áfica . . . 393

6 Diagonalizaç ão 405 6.1 Diagonalizaç ão de Matrizes . . . 405

6.1.1 Motivac¸˜ao . . . 405

6.1.2 Autovalores e Autovetores . . . 408

6.1.3 Diagonalizac¸ ˜ao . . . 418

6.2 Diagonalizaç ão de Matrizes Sim étricas . . . 440

(6)

6.2.2 Matrizes Ortogonais . . . 443

Ap ˆendice V: Autovalores Complexos . . . 454

6.3 Aplicaç ão: Identificaç ão de C ônicas . . . 458

6.3.1 Elipse . . . 458

6.3.2 Hip ´erbole . . . 465

6.3.3 Par ´abola . . . 472

Respostas dos Exerc´ıcios 500

Bibliografia 683

(7)

Este texto cobre o material para um curso de um semestre de Geometria Anal´ıtica e Álgebra Linear ministrado nos primeiros semestres para estudantes da área de Ci ências Exatas. O texto pode, mas n ão é necess ário, ser acompanhado de um programa como o MATLABr∗, SciLab ou o Maxima.

O conte údo é dividido em seis cap´ıtulos. O Cap´ıtulo 1 trata das matrizes e sistemas lineares. Aqui todas as propriedades da álgebra matricial s ão demonstradas. A resoluç ão de sistemas lineares é feita usando somente o m étodo de Gauss-Jordan (transformando a matriz at é que ela esteja na forma escalonada reduzida). Este m étodo requer mais trabalho do que o m étodo de Gauss (transformando a matriz, apenas, at é que ela esteja na forma escalonada). Ele foi o escolhido, por que tamb ém é usado no estudo da invers ão de matrizes no Cap´ıtulo 2. Neste Cap´ıtulo é tamb ém estudado o determinante, que é definido usando cofatores. As demonstraç ões dos resultados deste cap´ıtulo podem ser, a crit ério do leitor, feitas somente para matrizes3_×3.

O Cap´ıtulo 3 trata de vetores no plano e no espaço. Os vetores s ão definidos de forma geom étrica,

(8)

assim como a soma e a multiplicaç ão por escalar. S ão provadas algumas propriedades geometrica-mente. Depois s ão introduzidos sistemas de coordenadas de forma natural sem a necessidade da definiç ão de base. Os produtos escalar e vetorial s ão definidos tamb ém geometricamente. O Cap´ıtulo 4 trata de retas e planos no espaço. S ão estudados ângulos e dist âncias entre retas e planos.

O Cap´ıtulo 5 cobre a teoria dos espaços euclidianos. O conceito de depend ência e independ ência linear é introduzido de forma alg ébrica, acompanhado da interpretaç ão geom étrica para os casos de R2_eR3_{. Aqui s ão estudadas as posiç ões relativas de retas e planos como uma aplicaç ão do conceito}

de depend ência linear. S ão tamb ém tratados os conceitos de geradores e de base de subespaços. S ão abordados tamb ém o produto escalar e bases ortonormais. O Cap´ıtulo é terminado com mudança de coordenadas preparando para o Cap´ıtulo de diagonalizaç ão.

O Cap´ıtulo 6 traz um estudo da diagonalizaç ão de matrizes em geral e diagonalizaç ão de matrizes sim étricas atrav és de um matriz ortogonal. É feita uma aplicaç ão ao estudo das seç ões c ônicas.

Os exerc´ıcios est ão agrupados em tr ês classes. Os “Exerc´ıcios Num éricos”, que cont ém exerc´ıcios que s ão resolvidos fazendo c álculos, que podem ser realizados sem a ajuda de um com-putador ou de uma m áquina de calcular. Os “Exerc´ıcios Te óricos”, que cont ém exerc´ıcios que reque-rem demonstrações. Alguns s ão simples, outros s ão mais complexos. Os mais dif´ıceis complemen-tam a teoria e geralmente s ão acompanhados de sugest ões. Os “Exerc´ıcios usando o MATLABr”, que cont ém exerc´ıcios para serem resolvidos usando o MATLABr ou outro software. Os comandos necess ários a resoluç ão destes exerc´ıcios s ão tamb ém fornecidos juntamente com uma explicaç ão r ápida do uso. Os exerc´ıcios num éricos s ão imprescind´ıveis, enquanto a resoluç ão dos outros, de-pende do n´ıvel e dos objetivos pretendidos para o curso.

(9)

direci-onadas para o estudo de Geometria Anal´ıtica e Álgebra Linear pode ser obtido na web na p ágina do autor, assim como um texto com uma introduç ão ao MATLABre instruç ões de como instalar o pacote gaal. O MATLABr n ão é um software gratuito, embora antes a vers ão estudante vinha gr átis ao se comprar o guia do usu ário. Atualmente o SciLab é uma alternativa gratuita, mas que n ão faz c álculo simb ólico. O Maxima é um programa de computaç ão alg ébrica gratuito. Ambos podem ser usados como ferramenta auxiliar na aprendizagem de Geometria Anal´ıtica e Álgebra Linear. Na p ágina do autor na web podem ser encontrados pacotes de funç ões para estes programas al ém de links para as p áginas do SciLab e do Maxima e v árias p áginas interativas que podem auxiliar na aprendizagem.

No fim de cada cap´ıtulo temos um “Teste do Cap´ıtulo” para que o aluno possa avaliar os seus conhecimentos. Os Exerc´ıcios Num éricos e os Exerc´ıcios usando o MATLABr est ão resolvidos ap ós o último cap´ıtulo utilizando o MATLABr. Desta forma o leitor que n ão estiver interessado em usar o software pode obter apenas as respostas dos exerc´ıcios, enquanto aquele que tiver algum interesse, pode ficar sabendo como os exerc´ıcios poderiam ser resolvidos fazendo uso do MATLABre do pacote gaal.

(10)

Hist ´orico

Julho 2007 Algumas correc¸ ˜oes. As respostas de alguns exerc´ıcios foram reescritas.

Março 2007 V árias figuras foram refeitas e outras acrescentadas. Foram reescritos o Exemplo 3.12 e o Corol ário 3.10. Na seç ão 5.2 um exemplo foi reescrito e acrescentado mais um. Os Exemplos 5.25e 5.26 foram reescritos, sa´ıram do ap êndice e voltaram ao texto normal. A seç ão 5.4 de Mudança de Coordenadas foi reescrita e acrescentada uma aplicaç ão à computaç ão gr áfica. Foram acrescentados dois exerc´ıcios na seç ão de Matrizes, um na de Invers ão de Matrizes, um na seç ão de Determinantes, dois na de Produto de Vetores, um na de Subespaços, um na de Produto Escalar emRn_{, tr ês na de Mudança de Coordenadas, quatro na de Diagonalizaç ão e} um na de Diagonalizaç ão de Matrizes Sim étricas. Foram corrigidos alguns erros.

Julho 2006 Foi acrescentado o Exemplo 2.16 na p ágina 124. A seç ão 3.2 ’Produtos de Vetores’ foi reescrita. Foi acrescentado um exerc´ıcio na seç ão 4.2. O Cap´ıtulo 5 foi reescrito. Foram corrigidos alguns erros.

Março 2006 A Seç ão 1.1 de Matrizes e a Seç ão 2.2 de Determinantes foram reescritas. Na seç ão 1.2 o Teorema 1.4 voltou a ser que toda matriz é equivalente por linhas a uma única matriz na forma escalonada reduzida. Foram acrescentados v ários exerc´ıcios aos Cap´ıtulos 3 e 4. O Cap´ıtulo 5 foi reescrito. Foram acrescentados exerc´ıcios te óricos à seç ão ’Aplicaç ão à C ônicas’.

(11)

equivalente por linhas” com a demonstraç ão. O que antes era Exemplo 1.14 passou para o lugar do Exemplo 1.10. O Exemplo 2.5 foi modificado. No Cap´ıtulo 3 foram acrescentados 2 exerc´ıcios na seç ão 3.1, 1 exerc´ıcio na seç ão 3.2. No Cap´ıtulo 4 a seç ão 4.1 foi reescrita e foram acrescentados 2 exerc´ıcios. O Cap´ıtulo 5 foi reescrito. Foi inclu´ıda no Ap êndice III da seç ão 5.2. a demonstraç ão de que a forma escalonada reduzida de uma matriz é única. A seç ão ’Diagonalização de Matrizes’ ganhou mais um exerc´ıcio te órico.

Setembro 2003 Foi acrescentada a regra de Cramer na seç ão ’Determinantes’ (Exemplo 2.20). A seç ão ’Subespaços, Base e Dimens ão’ foi reescrita. Foi acrescentado um ap êndice a esta seç ão com ’Outros resultados’. A Proposiç ão 5.15 da seç ão ’Produto Escalar em Rn _foi re-escrita. A seç ão ’Diagonalizaç ão de Matrizes’ ganhou mais dois exerc´ıcios te óricos. A seç ão ’Diagonalização de Matrizes Sim étricas’ ganhou um ap êndice sobre ’Autovalores Complexos’.

Novembro 2002 V árias correç ões incluindo respostas de exerc´ıcios. A seç ão ’Subespaços, Base e Dimens ão’ ganhou mais um exemplo e um exerc´ıcio. A seç ão ’Diagonalização de Matrizes Sim étricas’ ganhou mais um exemplo.

Julho 2001 Revis ão completa no texto. Novos exerc´ıcios nas seç ões ’Matrizes’ e ’Sistemas Lineares’. As seç ões ’Subespaços’ e ’Base e Dimens ão’ tornaram-se uma s ó. A seç ão ’Mudança de Coordenadas’ passou do Cap´ıtulo 6 para o Cap´ıtulo 5.

(12)

Sugest ˜ao de Cronograma

Cap´ıtulo 1 8 aulas

Cap´ıtulo 5 16 (12) aulas

(13)

Matrizes e Sistemas Lineares

1.1 Matrizes

UmamatrizA,m_×n(mporn), ´e uma tabela demnn ´umeros dispostos emmlinhas encolunas

A=



   

a11 a12 . . . a1n

a21 a22 . . . a2n

..

. . . . ...

am1 am2 . . . amn



   

.

Ai- ´esima linhadeA ´e

ai1 ai2 . . . ain

(14)

parai= 1, . . . , me aj- ´esima colunadeA ´e 

   

a1j

a2j

.. .

amj



   

,

paraj = 1, . . . , n. Usamos tamb ém a notaç ãoA = (aij)m×n. Dizemos queaij ou[A]ij é oelemento

ou aentradade posic¸ ˜aoi, jda matrizA.

Sem=n, dizemos queA ´e umamatriz quadrada de ordemne os elementosa11, a22, . . . , ann

formam adiagonal (principal)deA.

Exemplo 1.1. Considere as seguintes matrizes:

A=

1 2 3 4

, B =

−2 1 0 3

, C =

1 3 0 2 4 ₋2

,

D= 1 3 ₋2 , E =





1 4

−3



 eF = 3 .

As matrizesA eB s ão 2_×2. A matrizC é 2_×3, D é 1_×3, E é 3_×1e F é1_×1. De acordo com a notaç ão que introduzimos, exemplos de elementos de algumas das matrizes dadas acima s ão

a12= 2,c23 =−2,e21 = 4,[A]22= 4,[D]12= 3.

(15)

matriz coluna. Matrizes linha e matrizes coluna s ão chamadas devetores. O motivo ficar á claro na Seç ão5.1na p ágina300.

Dizemos que duas matrizes s ão iguais se elas t êm o mesmo tamanho e os elementos correspon-dentes s ão iguais, ou seja,A = (aij)m×n eB = (bij)p×q s ãoiguaissem = p, n = q eaij = bij

parai= 1, . . . , mej = 1, . . . , n.

Vamos definir operaç ões matriciais an álogas às operaç ões com n úmeros e provar propriedades que s ão v álidas para essas operaç ões. Veremos, mais tarde, que um sistema de equaç ões lineares pode ser escrito em termos de uma única equaç ão matricial.

Vamos, agora, introduzir as operac¸ ˜oes matriciais.

1.1.1 Operac¸ ˜oes com Matrizes

Definiç ão 1.1. A soma de duas matrizes de mesmo tamanho A = (aij)m×n e B = (bij)m×n é

definida como sendo a matrizm_×n

C =A+B

obtida somando-se os elementos correspondentes deAeB, ou seja,

cij =aij +bij,

(16)

Exemplo 1.2. Considere as matrizes:

A=

1 2 ₋3

3 4 0

, B =

−2 1 5

0 3 ₋4

Se chamamos deCa soma das duas matrizesAeB, ent ˜ao

C=A+B =

1 + (₋2) 2 + 1 ₋3 + 5 3 + 0 4 + 3 0 + (₋4)

=

−1 3 2

3 7 ₋4

(17)

Definiç ão 1.2. Amultiplicaç ão de uma matrizA = (aij)m×npor um escalar(n úmero)α é definida

pela matrizm_×n

B =αA

obtida multiplicando-se cada elemento da matrizApelo escalarα, ou seja,

bij =α aij,

parai = 1, . . . , mej = 1, . . . , n. Escrevemos tamb ´em[αA]ij = α aij. Dizemos que a matrizB ´e

umm ´ultiplo escalarda matrizA.

Exemplo 1.3. O produto da matrizA=





−2 1

0 3

5 ₋4



pelo escalar₋3 ´e dado por

−3A=





(₋3)(₋2) (₋3) 1 (₋3) 0 (₋3) 3 (₋3) 5 (₋3)(₋4)



= 



6 ₋3 0 ₋9

−15 12



(18)

Definiç ão 1.3. Oprodutode duas matrizes, tais que o n úmero de colunas da primeira matriz é igual ao n úmero de linhas da segunda,A= (aij)m×p eB = (bij)p×n é definido pela matrizm×n

C =AB

obtida da seguinte forma:

cij = ai1b1j+ai2b2j +. . .+aipbpj, (1.1)

parai= 1, . . . , mej = 1, . . . , n. Escrevemos tamb ´em[AB]ij =ai1b1j +ai2b2j+. . .+aipbpj.

A equaç ão (1.1) est á dizendo que o elemento i, j do produto é igual à soma dos produtos dos elementos dai- ésima linha deApelos elementos correspondentes daj- ésima coluna deB.



 

c11 . . . c1n

..

. cij ...

cm1 . . . cmn

  =        

a11 a12 . . . a1p

..

. . . . ...

ai1 ai2 . . . aip

..

. . . . ...

am1 am2 . . . amp

             b11 b21 .. .

bp1

. . . . . . . . . . . .

b1j

b2j

.. . bpj . . . . . . . . . . . .

b1n

b2n

.. . bpn     

A equaç ão (1.1) pode ser escrita de forma compacta usando anotaç ão de somat ório.

[AB]ij =ai1b1j+ai2b2j +. . .+aipbpj = p

X

k=1

(19)

e dizemos “somat ´orio dekvariando de1apdeaikbkj”. O s´ımbolo p

X

k=1

significa que estamos fazendo

uma soma em que o ´ındicek est á variando dek = 1at ék =p. Algumas propriedades da notaç ão de somat ório est ão explicadas noAp êndice I na p ágina33.

Exemplo 1.4. Considere as matrizes:

A=

1 2 ₋3

3 4 0

, B =





−2 1 0

0 3 0

5 ₋4 0



 .

Se chamamos deCo produto das duas matrizesAeB, ent ˜ao

C=AB =

1 (₋2) + 2_·0 + (₋3) 5 1_·1 + 2_·3 + (₋3) (₋4) 0 3 (₋2) + 4_·0 + 0_·5 3_·1 + 4_·3 + 0 (₋4) 0

=

−17 19 0

−6 15 0

.

(20)

Exemplo 1.5. SejamA =

1 2 3 4

eB =

−2 1 0 3

. Ent ˜ao,

AB =

−2 7

−6 15

e BA=

1 0 9 12

.

Vamos ver no pr óximo exemplo como as matrizes podem ser usadas para descrever quantitativa-mente um processo de produç ão.

Exemplo 1.6. Uma ind ústria produz tr ês produtos, X, Y e Z, utilizando dois tipos de insumo, A e B. Para a manufatura de cada kg de X s ão utilizados 1 grama do insumo A e 2 gramas do insumo B; para cada kg de Y, 1 grama de insumo A e 1 grama de insumo B e, para cada kg de Z, 1 grama de A e 4 gramas de B. Usando matrizes podemos determinar quantos gramas dos insumos A e B s ão necess ários na produç ão dexkg do produto X,ykg do produto Y ezkg do produto Z.

X Y Z gramas de A/kg

gramas de B/kg

1 1 1 2 1 4

= A X =





x y z





kg de X produzidos kg de Y produzidos kg de Z produzidos

AX =

x+y+z

2x+y+ 4z

(21)

Definiç ão 1.4. Atranspostade uma matrizA= (aij)m×n é definida pela matrizn×m

B =At

obtida trocando-se as linhas com as colunas, ou seja,

bij =aji,

parai= 1, . . . , nej = 1, . . . , m. Escrevemos tamb ´em[At_]

ij =aji.

Exemplo 1.7. As transpostas das matrizes

A=

1 2 3 4

, B =

−2 1 0 3

e C=

1 3 0 2 4 ₋2

s ˜ao

At=

1 3 2 4

, Bt =

−2 0 1 3

e Ct=





1 2

3 4

0 ₋2



 .

(22)

1.1.2 Propriedades da ´

Algebra Matricial

Teorema 1.1. SejamA,B eCmatrizes com tamanhos apropriados,αeβescalares. S ão v álidas as seguintes propriedades para as operaç ões matriciais:

(a) (comutatividade)A+B =B+A;

(b) (associatividade)A+ (B+C) = (A+B) +C;

(c) (elemento neutro) A matriz¯0,m_×n, definida por[¯0]ij = 0, parai= 1, . . . , m,j = 1, . . . , n ´e

tal que

A+ ¯0 =A,

para toda matrizA,m_×n. A matriz¯0 ´e chamadamatriz nulam_×n.

(d) (elemento sim ´etrico) Para cada matrizA, existe uma ´unica matriz ₋A, definida por[₋A]ij =

−aij tal que

A+ (₋A) = ¯0.

(e) (associatividade)α(βA) = (αβ)A;

(f) (distributividade)(α+β)A=αA+βA;

(g) (distributividade)α(A+B) =αA+αB;

(23)

(i) (elemento neutro) Para cada inteiro positivopa matriz,p_×p,

Ip =



   

1 0 . . . 0 0 1 . . . 0

..

. . . . ...

0 0 . . . 1



   

,

chamadamatriz identidade ´e tal que

A In=ImA =A, para toda matrizA= (aij)m×n.

(j) (distributividade)A(B+C) =AB +AC e(B+C)A=BA+CA;

(k) α(AB) = (αA)B =A(αB);

(l) (At₎t₌_A_;

(m) (A+B)t ₌_At₊_Bt_; (n) (αA)t₌_{α A}t_;

(o) (AB)t₌_Bt_At_;

(24)

(a) [A+B]ij =aij +bij =bij +aij = [B +A]ij;

(b) [A+ (B+C)]ij =aij+ [B+C]ij =aij + (bij +cij) = (aij+bij) +cij = [A+B]ij +cij = [(A+B) +C]ij;

(c) SejaX uma matrizm_×ntal que

A+X =A (1.2)

para qualquer matriz A,m_×n. Comparando os elementos correspondentes, temos que

aij +xij =aij,

ou seja,xij = 0, parai = 1. . . , mej = 1. . . , n. Portanto, a ´unica matriz que satisfaz (1.2) ´e

a matriz em que todos os seus elementos s ˜ao iguais a zero. Denotamos a matrizXpor ¯0. (d) Dada uma matrizA,m_×n, sejaXuma matrizm_×n, tal que

A+X = ¯0. (1.3)

Comparando os elementos correspondentes, temos que

aij +xij = 0,

ou seja,xij = −aij, parai = 1. . . , me j = 1. . . , n. Portanto, a ´unica matriz que satisfaz

(1.3) é a matriz em que todos os seus elementos s ão iguais aos sim étricos dos elementos de

A. Denotamos a matrizXpor₋A.

(25)

(f) [(α+β)A]ij = (α+β)aij = (αaij) + (βaij) = [αA]ij + [βA]ij = [αA+βA]ij.

(g) _[_α₍_A₊_B_)]_ij ₌ _α_[_A₊_B_]_ij ₌_α₍_a_ij ₊_b_ij_{) =}_αa_ij ₊_αb_ij _{= [}_αA_]_ij _{+ [}_αB_]_ij

= [αA+αB]ij.

(h) A demonstraç ão deste item é a mais trabalhosa. SejamA,BeCmatrizesm_×p,p_×qeq_×n

respectivamente. A notaç ão de somat ório aqui pode ser muito útil, pelo fato de ser compacta.

[A(BC)]ij = p

X

k=1

aik[BC]kj = p

X

k=1

aik( q

X

l=1

bklclj) = p X k=1 q X l=1

aik(bklclj) =

= p X k=1 q X l=1

(aikbkl)clj = q X l=1 p X k=1

(aikbkl)clj = q X l=1 ( p X k=1

aikbkl)clj =

= q

X

l=1

[AB]ilclj = [(AB)C]ij.

(i) Podemos escrever a matriz identidade em termos do delta de Kronecker que ´e definido por

δij =

1, sei=j

0, sei₆=j

como[In]ij =δij. Assim,

[AIn]ij = n

X

k=1

aik[In]kj = n

X

k=1

aikδkj =aij.

(26)

(j) [A(B+C)]ij =

X

k=1

aik[B+C]kj =

X

k=1

aik(bkj+ckj) =

X

k=1

(aikbkj +aikckj) =

= p

X

k=1

aikbkj + p

X

k=1

aikckj = [AB]ij + [AC]ij = [AB +AC]ij.

A outra igualdade ´e inteiramente an ´aloga a anterior e deixamos como exerc´ıcio.

(k) [α(AB)]ij =α p

X

k=1

aikbkj = p

X

k=1

(αaik)bkj = [(αA)B]ij e

[α(AB)]ij =α p

X

k=1

aikbkj = p

X

k=1

aik(αbkj) = [A(αB)]ij.

(l) [(At₎t_]

ij = [At]ji =aij.

(m) [(A+B)t_]

ij = [A+B]ji =aji+bji = [At]ij + [Bt]ij.

(n) [(αA)t]ij = [αA]ji=αaji=α[At]ij = [αAt]ij.

(o) [(AB)t_]

ij = [AB]ji =

p

X

k=1

ajkbki = p

X

k=1

[At]kj[Bt]ik = p

X

k=1

[Bt]ik[At]kj = [BtAt]ij.

Adiferenc¸aentre duas matrizes de mesmo tamanhoAeB ´e definida por

(27)

ou seja, ´e a soma da matrizAcom a sim ´etrica da matrizB.

SejamAuma matrizn_×nepum inteiro positivo. Definimos apot ˆenciapdeA, porAp ₌_{A . . . A}

| {z }

pvezes .

E parap= 0, definimosA0 ₌_I

n.

Exemplo 1.8. Vamos verificar se para matrizesAeB, quadradas, vale a igualdade

(A+B)(A₋B) =A2₋B2. (1.4)

Usando a propriedade (i) do teorema anterior obtemos

(A+B)(A₋B) = (A+B)A+ (A+B)(₋B)

= AA+BA₋AB₋BB=A2+BA₋AB ₋B2

Assim,(A+B)(A₋B) =A2₋_B2 _{se, e somente se,}_BA₋_AB _{= 0}_{, ou seja, se, e somente se,}

AB =BA. Como o produto de matrizes n ão é comutativo, a conclus ão é que a igualdade (1.4),n ão vale para matrizes em geral. Como contra-exemplo basta tomarmos duas matrizes que n ão comutem entre si. Sejam

A =

0 0 1 1

e B =

1 0 1 0

.

Para estas matrizes

A+B =

1 0 2 1

, A₋B =

−1 0 0 1

, A2 =A=

0 0 1 1

, B2 =B =

1 0 1 0 . Assim,

(A+B)(A₋B) =

−1 0

−2 1

6

=

−1 0 0 1

(28)

1.1.3 Aplicac¸ ˜ao: Cadeias de Markov

Vamos supor que uma populaç ão é dividida em tr ês estados (por exemplo: ricos, classe m édia e pobres) e que em cada unidade de tempo a probabilidade de mudança de um estado para outro seja constante no tempo, s ó dependa dos estados. Este processo é chamadocadeia de Markov.

Seja tij a probabilidade de mudanc¸a do estado j para o estado i em uma unidade de tempo

(gerac¸ ˜ao). Tome cuidado com a ordem dos ´ındices. A matriz

T = 1

2

3





t11 t12 t13

t21 t22 t23

t31 t32 t33 

 1

2

3

é chamadamatriz de transiç ão. A distribuiç ão da populaç ão inicial entre os tr ês estados pode ser descrita pela seguinte matriz:

P0 = 



p1

p2

p3 



est á no estado 1 est á no estado 2 est á no estado 3

A matrizP0caracteriza a distribuiç ão inicial da populaç ão entre os tr ês estados e é chamadavetor de estado. Ap ós uma unidade de tempo a populaç ão estar á dividida entre os tr ês estados da seguinte forma

P1 = 



t11p1+t12p2+t13p3

t21p1+t22p2+t23p3

t31p1+t32p2+t33p3 



(29)

Lembre-se quetij ´e a probabilidade de mudanc¸a do estadojpara o estadoi. Assim o vetor de estado

ap ´os uma unidade de tempo ´e dada pelo produto de matrizes:

P1 =T P0. Exemplo 1.9. Vamos considerar a matriz de transic¸ ˜ao

T = 1

2

3

   1 2 1 4 0 1 2 1 2 1 2 0 1 4 1 2    1

2

3

(1.5)

e o vetor de estados inicial

P0 =   1 3 1 3 1 3  

est á no estado 1 est á no estado 2 est á no estado 3

(1.6)

que representa uma populaç ão dividida de forma que1/3da populaç ão est á em cada estado. Ap ós uma unidade de tempo a matriz de estado ser á dada por

P1 =T P0 =    1 2 1 4 0 1 2 1 2 1 2

0 1₄ 1₂

      1 3 1 3 1 3   =    1 4 1 2 1 4   

Como estamos assumindo que em cada unidade de tempo a matriz de transiç ão é a mesma, ent ão ap ósk unidades de tempo a populaç ão estar á dividida entre os tr ês estados segundo a matriz de estado

(30)

Assim a matrizTk_{d á a transiç ão entre}_k_{unidades de tempo.}

Veremos naSeç ão6.1na p ágina405como calcular rapidamente pot ênciaskde matrizes e assim como determinar a distribuiç ão da populaç ão ap ósk unidades de tempo parak um inteiro positivo qualquer.

Exerc´ıcios Num ´ericos

(respostas na p ´agina

501)

1.1.1. Considere as seguintes matrizes

A=

2 0 6 7

, B =

0 4 2 ₋8

, C =

−6 9 ₋7 7 ₋3 ₋2

D =





−6 4 0 1 1 4

−6 0 6



, E = 



6 9 ₋9

−1 0 ₋4

−6 0 ₋1





Se for poss´ıvel calcule:

(a) AB ₋BA, (b) 2C₋D, (c) (2Dt₋₃_Et₎t_,

(31)

1.1.2. Conhecendo-se somente os produtosAB e AC, como podemos calcularA(B +C), Bt_At_,

Ct_At_e₍_ABA₎_C_?

1.1.3. Considere as seguintes matrizes

A=

−3 2 1

1 2 ₋1

, B =





2 ₋1 2 0 0 3   C =  

−2 1 ₋1 0 1 1

−1 0 1



, D= 



d1 0 0

0 d2 0

0 0 d3 



E1 =   1 0 0 

, E₂ =   0 1 0 

, E₃ =   0 0 1   Verifique que:

(a) AB ´e diferente deBA.

(b) AEj é a j- ésima coluna de A, para j = 1,2,3 e EitB é a i- ésima linha de B, para

i= 1,2,3(o caso geral est ´a noExerc´ıcio1.1.16na p ´agina26).

(c) CD = [ d1C1 d2C2 d3C3 ], em queC1 =   −2 0 −1 

,C2 =   1 1 0 

eC3 =   −1 1 1 

, s ˜ao as

(32)

(d) DC =





d1C1

d2C2

d3C3 

, em que C1 =

−2 1 ₋1 , C2 =

0 1 1 e

C3 =

−1 0 1 s ão as linhas de C (o caso geral est á noExerc´ıcio 1.1.17 (b) na p ágina27).

(e) Escrevendo B em termos das suas colunas, B = [ B1 B2 ], em que B1 =   2 2 0   e

B2 =   −1 0 3 

, o produtoAB pode ser escrito comoAB = A[B1 B2 ] = [AB1 AB2 ] (o caso geral est ´a noExerc´ıcio1.1.18(a) na p ´agina28).

(f) escrevendoAem termos das suas linhas,A1 =

−3 2 1 eA2 =

1 2 ₋1 , o produtoAB pode ser escrito como AB =

A1 A2 B =

A1B

A2B

(o caso geral est ´a no

Exerc´ıcio1.1.18(b) na p ´agina28).

1.1.4. Sejam

A =

1 ₋3 0 0 4 ₋2

e X =

  x y z  .

Verifique quexA1+yA2+zA3 =AX, em queAj ´e aj- ´esima coluna deA, paraj = 1,2,3

(33)

1.1.5. Encontre um valor dextal queABt_{= 0}_{, em que}

A= x 4 ₋2 e B = 2 ₋3 5 .

1.1.6. Mostre que as matrizesA =

1 1_y

y 1

, em que y é uma n úmero real n ão nulo, verificam a equaç ãoX2 _{= 2}_X_.

1.1.7. Mostre que seAeB s ˜ao matrizes que comutam com a matrizM =

0 1

−1 0

, ent ˜aoAB =

BA.

1.1.8. (a) Determine todas as matrizesA,2_×2,diagonais(os elementos que est ˜ao fora da diagonal s ˜ao iguais a zero) que comutam com toda matrizB,2_×2, ou seja, tais queAB =BA, para toda matrizB,2_×2.

(b) Determine todas as matrizesA, 2_×2, que comutam com toda matrizB, 2_×2, ou seja, tais queAB =BA, para toda matrizB,2_×2.

1.1.9. Verifique queA3 _{= ¯0}_{, para}

A=





0 1 0 0 0 1 0 0 0



.

O caso geral est ´a noExerc´ıcio1.1.29na p ´agina32.

(34)

Uma vez inicializado o MATLABr, aparecer á na janela de comandos um prompt>> ouEDU>>. O prompt significa que o MATLABr est á esperando um comando. Todo comando deve ser finalizado teclando-se Enter. Comandos que foram dados anteriormente podem ser obtidos novamente usando as teclas_↑e _↓. Enquanto se estiver escrevendo um comando, este pode ser corrigido usando as teclas_←, _→, Deletee Backspace. O MATLABr faz diferença entre letras mai úsculas e min úsculas.

No MATLABr, pode-se obter ajuda sobre qualquer comando ou func¸ ˜ao. O comando >> help

(sem o prompt >>) mostra uma listagem de todos os pacotes dispon´ıveis. Ajuda sobre um pacote espec´ıfico ou sobre um comando ou func¸ ˜ao espec´ıfica pode ser obtida com o comando >> help nome,

(sem a v´ırgula e sem o prompt>>) em quenomepode ser o nome de um pacote ou o nome de um comando ou func¸ ˜ao.

Al ém dos comandos e funç ões pr é-definidas, escrevemos um pacote chamado gaal com funç ões espec´ıficas para a aprendizagem de Geometria Anal´ıtica e Álgebra Li-near. Este pacote pode ser obtido gratuitamente atrav és da internet no endereço http://www.mat.ufmg.br/~regi, assim como um texto com uma introduç ão ao MATLABre instruç ões de como instalar o pacotegaal. Depois deste pacote ser devidamente instalado, o comandohelp gaalno prompt do MATLABrd á informaç ões sobre este pacote.

Mais informac¸ ˜oes sobre as capacidades do MATLABrpodem ser obtidas em [4,28].

Vamos descrever aqui alguns comandos que podem ser usados para a manipulaç ão de matri-zes. Outros comandos ser ão introduzidos a medida que forem necess ários.

(35)

>> A=[a11,a12,...,a1n;a21,a22,...; ...,amn] cria uma matriz, m por n, usando os elementosa11, a12, ..., amn e a armazena numa vari ´avel de nome A. Por exemplo, >>

A=[1,2,3;4,5,6]cria a matrizA=

1 2 3 4 5 6

;

>> I=eye(n)cria a matriz identidadenporne a armazena numa vari ´avelI;

>> O=zeros(n)ou>> O=zeros(m,n)cria a matriz nulanpornoumporn, respectivamente, e a armazena numa vari ´avelO;

>> A+B é a soma deAeB, >> A*B é o produto deAporB, >> A.’ é a transposta deA,

>> A-B ´e a diferenc¸aAmenosB,

>> num*A é o produto do escalarnumporA, >> A^k é a pot ênciaAelevado ak.

>> A(:,j) ´e a colunaj da matrizA,>> A(i,:) ´e a linhaida matrizA.

>> diag([d1,...,dn])cria uma matriz diagonal, cujos elementos da diagonal s ˜ao iguais aos elementos da matriz[d1,...,dn], ou seja, s ˜aod1,...,dn.

>> A=sym(A) converte a matriz A numa matriz em que os elementos s ão armazenados no formato simb ólico. A funç ãonumericfaz o processo inverso.

>> solve(expr) determina a soluç ão da equaç ão expr=0. Por exemplo, >> solve(x^2-4)determina as soluç ões da equaç ãox2₋_{4 = 0}_;

Comando do pacote GAAL:

>> A=randi(n) ou >> A=randi(m,n)cria uma matriz npor n oum por n, respectivamente, com elementos inteiros aleat ´orios entre₋5e5.

1.1.10. Use o MATLABrpara calcular alguns membros da seq ¨u ˆenciaA, A2_{, . . . , A}k_{, . . .}_{, para}

(a) A=

1 1₂ 0 1₃

; (b) A =

₁ 2

1 3

0 ₋1₅

(36)

A seq ¨u ˆencia parece estar convergindo para alguma matriz? Se estiver, para qual?

1.1.11. Calcule as pot ˆencias das matrizes dadas a seguir e encontre experimentalmente (por tentativa!) o menor inteirok > 1tal que (use o comando>> A=sym(A) depois de armazenar a matriz na vari ´avelA):

(a) Ak ₌_I

3, em que

A =





0 0 1 1 0 0 0 1 0



;

(b) Ak ₌_I

4, em que

A =



  

0 1 0 0

−1 0 0 0 0 0 0 1 0 0 1 0



  ;

(c) Ak _{= ¯0}_{, em que}

A =



  

0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0



  .

1.1.12. Vamos fazer um experimento no MATLABrpara tentar ter uma id éia do qu ão comum é encontrar matrizes cujo produto comuta. No prompt do MATLABrdigite a seguinte linha:

(37)

(n ão esqueça das v´ırgulas e pontos e v´ırgulas!). O que esta linha est á mandando o MATLABr fazer é o seguinte:

• Criar um contadorce atribuir a ele o valor zero.

• Atribuir às vari áveisAeB,1000matrizes3_×3com entradas inteiras e aleat órias entre₋5

e5.

• SeAB=BA, ou seja,AeBcomutarem, ent ão o contadorc é acrescido de1. • No final o valor existente na vari ávelc é escrito.

Qual a conclus ão que voc ê tira do valor obtido na vari ávelc?

1.1.13. Faça um experimento semelhante ao anterior, mas para o caso em que cada uma das matrizes édiagonal, isto é, os elementos que est ão fora da diagonal s ão iguais a zero. Use a seta para cima_↑para obter novamente a linha digitada e edite a linha no prompt do MATLABrde forma a obter algo semelhante à linha:

>> c=0; for n=1:1000,A=diag(randi(1,3));B=diag(randi(1,3));if( ....

Qual a conclus ão que voc ê tira do valor obtido na vari ávelc?

1.1.14. Fac¸a um experimento semelhante ao anterior, mas para o caso em que uma das matrizes ´e diagonal. Use a seta para cima _↑ para obter novamente a linha digitada e edite a linha no prompt do MATLABrde forma a obter a seguinte linha:

>> c=0; for n=1:1000,A=diag(randi(1,3));B=randi(3);if(A*B==B*A),c=c+1;A,B,end,end,c

(38)

1.1.15. Use o MATLABrpara resolver osExerc´ıcios Num ´ericos.

Exerc´ıcios Te ´oricos

1.1.16. SejamE1 =        1 0 0 .. . 0       

, E2 =        0 1 0 .. . 0       

,. . . ,En =

       0 0 .. . 0 1       

matrizesn_×1.

(a) Mostre que se

A =     

a11 a12 . . . a1n

a21 a22 . . . a2n

..

. . . . ...

am1 am2 . . . amn



   

é uma matrizm_×n, ent ãoAEj é igual à colunajda matrizA.

(b) Mostre que se

B =     

b11 b12 . . . b1m

b21 b22 . . . b2m

..

. . . . ...

bn1 bn2 . . . bnm

     ,

´e uma matrizn_×ment ˜aoEt

(39)

1.1.17. Seja

D=



   

λ1 0 . . . 0

0 λ2 . . . 0 ..

. . .. ...

0 . . . 0 λn



   

umamatriz diagonaln_×n, isto é, os elementos que est ão fora da diagonal s ão iguais a zero. Seja

A =



   

a11 a12 . . . a1n

a21 a22 . . . a2n

..

. . . . ...

an1 an2 . . . ann



   

.

(a) Mostre que o produtoAD ´e obtido da matrizAmultiplicando-se cada colunaj porλj, ou

seja, seA= [A1 A2 . . . An ], em queAj =



 

a1j

.. .

anj





 ´e a colunaj deA, ent ˜ao

AD= [λ1A1 λ2A2 . . . λnAn].

(40)

seja, seA=



   

A1

A2 .. .

An



   

, em queAi = [ai1 . . . ain ] ´e a linhaideA, ent ˜ao

DA=



   

λ1A1

λ2A2 .. .

λnAn



   

.

1.1.18. SejamAeB matrizesm_×pep_×n, respectivamente.

(a) Mostre que a j- ´esima coluna do produto AB ´e igual ao produto ABj, em que Bj =



 

b1j

.. .

bpj





 é aj- ésima coluna deB, ou seja, seB = [B1 . . . Bn ], ent ão

AB =A[B1 . . . Bn] = [ AB1 . . . ABn ];

(41)

[ai1 . . . aip] ´e ai- ´esima linha deA, ou seja, seA=      A1 A2 .. . Am     

, ent ˜ao

AB =      A1 A2 .. . Am      B =     

A1B

A2B .. .

AmB

     .

1.1.19. Seja A uma matriz m _× n e X =

   x1 .. . xn  

 uma matriz n × 1. Prove que

AX = n

X

j=1

xjAj, em queAj é aj- ésima coluna deA. (Sugest ão: Desenvolva o lado direito e

chegue ao lado esquerdo.)

1.1.20. (a) Mostre que seA ´e uma matrizm_×ntal queAX = ¯0, para toda matrizX,n_×1, ent ˜ao

A= ¯0. (Sugest ˜ao: use oExerc´ıcio16na p ´agina26.)

(b) SejamB eC matrizesm_×n, taisBX =CX, para todoX, n_×1. Mostre queB =C. (Sugest ˜ao: use o item anterior.)

1.1.21. Mostre que a matriz identidade In ´e a ´unica matriz tal que A In = InA = A para qualquer

matriz A, n _× n. (Sugest ˜ao: Seja Jn uma matriz tal que A Jn = JnA = A. Mostre que

(42)

1.1.22. SeAB =BAep ´e um inteiro positivo, mostre que(AB)p ₌_Ap_Bp_.

1.1.23. SejamA, B eCmatrizesn_×n.

(a) (A+B)2 ₌_A2_{+ 2}_AB ₊_B2_{? E se}_AB ₌_BA_{? Justifique.} (b) (AB)C =C(AB)? E seAC =CAeBC =CB? Justifique. (Sugest ˜ao: Veja oExemplo1.8na p ´agina15.)

1.1.24. (a) SeAeB s ão duas matrizes tais queAB = ¯0, ent ãoA= ¯0ouB = ¯0? Justifique. (b) SeAB = ¯0, ent ãoBA= ¯0? Justifique.

(c) SeA ´e uma matriz tal queA2 _{= ¯0}_{, ent ˜ao}_A_{= ¯0}_{? Justifique.}

1.1.25. Dizemos que uma matrizA,n_×n, ésim étricaseAt₌_A_{e é}_{anti-sim étrica}_se_At₌₋_A_.

(a) Mostre que se A é sim étrica, ent ão aij = aji, para i, j = 1, . . . n e que se A é

anti-sim ´etrica, ent ˜ao aij = −aji, para i, j = 1, . . . n. Portanto, os elementos da diagonal

principal de uma matriz anti-sim ´etrica s ˜ao iguais a zero.

(b) Mostre que seAeBs ão sim étricas, ent ãoA+B eαAs ão sim étricas, para todo escalar

α.

(c) Mostre que seAeB s ão sim étricas, ent ãoAB é sim étrica se, e somente se,AB =BA. (d) Mostre que seAeBs ão anti-sim étricas, ent ãoA+BeαAs ão anti-sim étricas, para todo

escalarα.

(43)

(f) Mostre que toda matriz quadradaApode ser escrita como a soma de uma matriz sim étrica e uma anti-sim étrica. (Sugest ão: Observe o resultado da soma deA+At_com_A₋_At_.)

1.1.26. Para matrizes quadradasA = (aij)n×ndefinimos o trac¸o deA como sendo a soma dos

ele-mentos da diagonal (principal) deA, ou seja,tr(A) = n

X

i=1

aii.

(a) Mostre quetr(A+B) = tr(A) + tr(B). (b) Mostre quetr(αA) = αtr(A).

(c) Mostre quetr(At_{) = tr(}_A₎_.

(d) Mostre quetr(AB) = tr(BA). (Sugest ão: Prove inicialmente para matrizes2_×2.) 1.1.27. SejaAuma matrizn_×n. Mostre que seAAt_{= ¯0}_{, ent ão}_A_{= ¯0}_{. (Sugest ão: use o traço.) E se}

a matrizAform_×n, comm₆=n?

1.1.28. J á vimos que o produto de matrizes n ão é comutativo. Entretanto, certos conjuntos de matrizes s ão comutativos. Mostre que:

(a) SeD1 eD2s ão matrizes diagonaisn×n, ent ãoD1D2 =D2D1. (b) SeA é uma matrizn_×ne

B =a0In+a1A+a2A2+. . .+akAk,

(44)

1.1.29. Uma matrizA ´e chamadanilpotenteseAk _{= ¯0}_{, para algum inteiro positivo}_k_{. Verifique que a}

matriz

A=



     

0 1 0 _{· · ·} 0 0 0 1 _{· · ·} 0

..

. ... . .. ... ...

0 0 0 _{· · ·} 1 0 0 0 _{· · ·} 0



     

n×n

,

(45)

Ap êndice I: Notaç ão de Somat ório

S ão v álidas algumas propriedades para a notaç ão de somat ório:

(a) O ´ındice do somat ório é uma vari ável muda que pode ser substitu´ıda por qualquer letra:

n

X

i=1

fi = n

X

j=1

fj.

(b) O somat ´orio de uma soma pode ser escrito como uma soma de dois somat ´orios:

n

X

i=1

(fi+gi) = n

X

i=1

fi+ n

X

i=1

gi.

Pois,

n

X

i=1

(fi+gi) = (f1+g1) +. . .+ (fn+gn) = (f1+. . .+fn) + (g1+. . .+gn) = n

X

i=1

fi+ n

X

i=1

gi.

Aqui foram aplicadas as propriedades associativa e comutativa da soma de n ´umeros.

(c) Se no termo geral do somat ório aparece um produto, em que um fator n ão depende do ´ındice do somat ório, ent ão este fator pode “sair” do somat ório:

n

X

i=1

figk =gk n

X

i=1

fi.

Pois,

n

X

i=1

figk = f1gk +. . .+fngk = gk(f1 +. . . +fn) = gk n

X

i=1

fi. Aqui foram aplicadas as

(46)

(d) Num somat ´orio duplo, a ordem dos somat ´orios pode ser trocada:

n

X

i=1

m

X

j=1

fij = m

X

j=1

n

X

i=1

fij.

Pois,

n

X

i=1

m

X

j=1

fij = n

X

i=1

(fi1+. . .+fim) = (f11+. . .+f1m) +. . .+ (fn1+. . .+fnm) = (f11+. . .+

fn1) +. . .+ (f1m+. . .+fnm) = m

X

j=1

(f1j +. . .+fnj) = m

X

j=1

n

X

i=1

fij. Aqui foram aplicadas as

(47)

1.2 Sistemas de Equac¸ ˜oes Lineares

Muitos problemas em v árias áreas da Ci ência recaem na soluç ão de sistemas lineares. Vamos ver como a álgebra matricial pode simplificar o estudo dos sistemas lineares.

Umaequaç ão linearemnvari áveisx1, x2, . . . , xn é uma equaç ão da forma

a1x1+a2x2+. . .+anxn =b ,

em quea1, a2, . . . , aneb s ˜ao constantes reais;

Umsistema de equaç ões linearesou simplesmentesistema linear é um conjunto de equaç ões lineares, ou seja, é um conjunto de equaç ões da forma

    

   

a11x1 + a12x2 + . . . + a1nxn = b1

a21x1 + a22x2 + . . . + a2nxn = b2 ..

. ... = ...

am1x1 + am2x2 + . . . + amnxn = bm

em queaij ebk s ˜ao constantes reais, parai, k= 1, . . . , mej = 1, . . . , n.

Usando o produto de matrizes que definimos na seç ão anterior, o sistema linear acima pode ser escrito como uma equaç ão matricial

(48)

em que A=     

a11 a12 . . . a1n

a21 a22 . . . a2n

..

. . . . ...

am1 am2 . . . amn



   

, X =

     x1 x2 .. . xn     

e B =

     b1 b2 .. . bm      .

Umasoluç ãode um sistema linear é uma matrizS =

     s1 s2 .. . sn     

tal que as equaç ões do sistema s ão

satisfeitas quando substitu´ımosx1 =s1, x2 = s2, . . . , xn = sn. O conjunto de todas as soluc¸ ˜oes do

sistema é chamadoconjunto soluç ão ousoluç ão geraldo sistema. A matrizA é chamadamatriz do sistema linear.

Exemplo 1.10. O sistema linear de duas equaç ões e duas inc ógnitas

x + 2y = 1 2x + y = 0

pode ser escrito como

1 2 2 1 x y = 1 0 .

A soluç ão (geral) do sistema acima éx=₋1/3ey= 2/3(verifique!) ou

X =

−13

2 3

(49)

Uma forma de resolver um sistema linear é substituir o sistema inicial por outro que tenha o mesmo conjunto soluç ão do primeiro, mas que seja mais f ácil de resolver. O outro sistema é obtido depois de aplicar sucessivamente uma s érie de operaç ões, que n ão alteram a soluç ão do sistema, sobre as equaç ões. As operaç ões que s ão usadas s ão:

• Trocar a posiç ão de duas equaç ões do sistema;

• Multiplicar uma equac¸ ˜ao por um escalar diferente de zero;

• Somar a uma equaç ão outra equaç ão multiplicada por um escalar.

Estas operaç ões s ão chamadas deoperaç ões elementares. Quando aplicamos operaç ões ele-mentares sobre as equaç ões de um sistema linear somente os coeficientes do sistema s ão alterados, assim podemos aplicar as operaç ões sobre a matriz de coeficientes do sistema, que chamamos de matriz aumentada, ou seja, a matriz

[A_|B] =



   

a11 a12 . . . a1n b1

a21 a22 . . . a2n b2 ..

. . . . ... ...

am1 am2 . . . amn bm



   

(50)

Definiç ão 1.5. Uma operaç ão elementar sobre as linhas de uma matriz é uma das seguintes operaç ões:

(a) Trocar a posic¸ ˜ao de duas linhas da matriz;

(b) Multiplicar uma linha da matriz por um escalar diferente de zero;

(c) Somar a uma linha da matriz um m ´ultiplo escalar de outra linha.

O pr óximo teorema garante que ao aplicarmos operaç ões elementares às equaç ões de um sis-tema o conjunto soluç ão n ão é alterado.

Teorema 1.2. Se dois sistemas lineares AX = B e CX = D, s ˜ao tais que a matriz aumentada

[C _|D] é obtida de[A _| B]aplicando-se uma operaç ão elementar, ent ão os dois sistemas possuem as mesmas soluç ões.

Demonstração. A demonstraç ão deste teorema segue-se de duas observaç ões:

(51)

(b) Se o sistema CX = D, é obtido de AX = B aplicando-se uma operaç ão elementar às suas equaç ões (ou equivalentemente às linhas da sua matriz aumentada), ent ão o sistema

AX =B tamb ém pode ser obtido deCX =Daplicando-se uma operaç ão elementar às suas equaç ões, pois cada operaç ão elementar possui uma operaç ão elementar inversa do mesmo tipo, que desfaz o que a anterior fez (verifique!).

Pela observação (b),AX =BeCX =Dpodem ser obtidos um do outro aplicando-se uma operaç ão elementar sobre as suas equaç ões. E pela observaç ão (a), os dois possuem as mesmas soluç ões.

Dois sistemas que possuem o mesmo conjunto soluç ão s ão chamadossistemas equivalentes. Portanto, segue-se do Teorema 1.2 que aplicando-se operaç ões elementares às equaç ões de um sistema linear obtemos sistemas equivalentes.

1.2.1 M ´etodo de Gauss-Jordan

O m étodo que vamos usar para resolver sistemas lineares consiste na aplicaç ão de operaç ões elementares às linhas da matriz aumentada do sistema at é que obtenhamos uma matriz numa forma em que o sistema associado a esta matriz seja de f ácil resoluç ão.

(52)

Exemplo 1.11. Uma ind ústria produz tr ês produtos, X, Y e Z, utilizando dois tipos de insumo, A e B. Para a manufatura de cada kg de X s ão utilizados 1 grama do insumo A e 2 gramas do insumo B; para cada kg de Y, 1 grama de insumo A e 1 grama de insumo B e, para cada kg de Z, 1 grama de A e 4 gramas de B. O preço de venda do kg de cada um dos produtos X, Y e Z é R$ 2,00, R$ 3,00 e R$ 5,00, respectivamente. Com a venda de toda a produç ão de X, Y e Z manufaturada com 1 kg de A e 2 kg de B, essa ind ústria arrecadou R$ 2500,00. Vamos determinar quantos kg de cada um dos produtos X, Y e Z foram vendidos. Como vimos noExemplo1.6na p ágina 8, usando matrizes o esquema de produç ão pode ser descrito da seguinte forma:

X Y Z gramas de A/kg

gramas de B/kg prec¸o/kg





1 1 1 2 1 4 2 3 5



 = A X =

  x y z  

kg de X produzidos kg de Y produzidos kg de Z produzidos

AX =





x+y+z

2x+y+ 4z

2x+ 3y+ 5z

 =   1000 2000 2500  

gramas de A usados gramas de B usados arrecadac¸ ˜ao

Assim precisamos resolver o sistema linear 





x + y + z = 1000 2x + y + 4z = 2000 2x + 3y + 5z = 2500

cuja matriz aumentada ´e





1

1 1 1000 2 1 4 2000 2 3 5 2500



(53)

1a._{eliminac¸ ˜ao:}

Vamos procurar para piv ô da 1a._{linha um elemento n ão nulo da primeira coluna n ão nula (se for o caso,} podemos usar a troca de linhas para “traz ê-lo” para a primeira linha). Como o primeiro elemento da primeira coluna é igual a1ele ser á o primeiro piv ô. Agora, precisamos “zerar” os outros elementos da 1a._{coluna, que é a coluna do piv ô, para isto, adicionamos à 2}a._linha,₋₂_{vezes a 1}a._{linha e adicionamos}

`a 3a._{linha, tamb ´em,}₋₂_{vezes a 1}a. _linha. −2_×1a.linha+2a.linha_−→2a.linha −2_×1a._linha₊₃a._linha_−→₃a._linha



 

1 1 1 1000 0

−1 2 0 0 1 3 500



 

Olhamos para a sub-matriz obtida eliminando-se a 1a. _{linha. Escolhemos para piv ô um elemento} diferente de zero na 1a.coluna n ão nula desta sub-matriz. Vamos escolher o elemento de posiç ão 2,2. Como temos que “fazer” o piv ô igual a um, vamos multiplicar a 2a. _{linha por}₋₁_.

−1_×2a._linha_−→₂a._linha





1 1 1 1000 0 1 ₋2 0 0 1 3 500





Agora, precisamos “zerar” os outros elementos da 2a.coluna, que é a coluna do piv ô, para isto, soma-mos à 1a._linha,₋₁_{vezes a 2}a._{e somamos à 3}a._{linha, tamb ém,}₋₁_{vezes a 2}a._.

−1_×2a.linha+1a.linha_−→1a.linha −1_×2a._linha₊₃a._linha_−→₃a._linha





1 0 3 1000 0 1 ₋2 0 0 0

5 500





(54)

Olhamos para a sub-matriz obtida eliminando-se a 1a._{e a 2}a._{linha. Escolhemos para piv ô um elemento} diferente de zero na 1a. coluna n ão nula desta sub-matriz. Temos de escolher o elemento de posiç ão 3,3 e como temos de “fazer” o piv ô igual a1, vamos multiplicar a 3a.linha por1/5.

1

5×3a.linha−→3a.linha





1 0 3 1000 0 1 ₋2 0 0 0 1 100





Agora, precisamos “zerar” os outros elementos da 3a._{coluna, que é a coluna do piv ô, para isto,} soma-mos à 1a._linha,₋₃_{vezes a 3}a._{e somamos à 2}a._linha,₂_{vezes a 2}a._.

−3_×3a.linha+1a.linha_−→1a.linha

2_×3a._linha₊₂a._linha_−→₂a._linha





1 0 0 700 0 1 0 200 0 0 1 100





Portanto o sistema dado ´e equivalente ao sistema

 



x = 700

y = 200

z = 100

que possui soluc¸ ˜ao geral dada por

X =





x y z



= 



700 200 100



.

(55)

A ´ultima matriz que obtivemos no exemplo anterior est ´a na forma que chamamos deescalonada reduzida.

Definiç ão 1.6. Uma matriz A = (aij)m×n est á na forma escalonada reduzida quando satisfaz as

seguintes condic¸ ˜oes:

(a) Todas as linhas nulas (formadas inteiramente por zeros) ocorrem abaixo das linhas n ˜ao nulas;

(b) Opiv ô(1o._{elemento n ão nulo de uma linha) de cada linha n ão nula é igual a}₁_;

(c) O piv ô de cada linha n ão nula ocorre à direita do piv ô da linha anterior.

(d) Se uma coluna cont ém um piv ô, ent ão todos os seus outros elementos s ão iguais a zero.

Se uma matriz satisfaz as propriedades (a) e (c), mas n ˜ao necessariamente (b) e (d), dizemos que ela est ´a na formaescalonada.

Exemplo 1.12. As matrizes 



1 0 0 0 1 0 0 0 1



 e





1 3 0 2

0 0 1 ₋3

0 0 0 0



(56)

s ˜ao escalonadas reduzidas, enquanto 



1 1 1 0 ₋1 2 0 0 5



 e





1 3 ₋1 5 0 0 ₋5 15

0 0 0 0





s ão escalonadas, masn ãos ão escalonadas reduzidas.

Este m étodo de resoluç ão de sistemas, que consiste em aplicar operaç ões elementares às linhas da matriz aumentada at é que a matriz do sistema esteja na forma escalonada reduzida, é conhecido comom étodo de Gauss-Jordan.

Exemplo 1.13. Considere o seguinte sistema 





x + 3y + 13z = 9

y + 5z = 2

−2y ₋ 10z = ₋8

A sua matriz aumentada ´e _



1

3 13 9

0 1 5 2

0 ₋2 ₋10 ₋8





Como o piv ô da 1a._{linha é igual a}₁_{e os outros elementos da 1}a._{coluna s ão iguais a zero, n ão h á nada} o que fazer na 1a.eliminaç ão.



 

1 3 13 9

0

1 5 2

0 ₋2 ₋10 ₋8



(57)

Olhamos para submatriz obtida eliminando-se a 1a. linha. Escolhemos para piv ô um elemento n ão nulo da 1a.coluna n ão nula da submatriz. Escolhemos o elemento de posiç ão 2,2. Como ele é igual a

1, precisamos, agora, “zerar” os outros elementos da coluna do piv ô. Para isto somamos à 1a. _linha, −3vezes a 2a. e somamos à 3a.linha,2vezes a 2a..

−3_×2a. _linha₊₁a. _linha_−→₁a._linha

2_×2a._linha₊₃a._linha_−→₃a._linha 



1 0 ₋2 3

0 1 5 2

0 0 0 ₋4





Portanto o sistema dado ´e equivalente ao sistema

 



x ₋ 2z = 3

y + 5z = 2 0 = ₋4

quen ãopossui soluç ão.

Em geral, um sistema linear n ão tem soluç ão se, e somente se, a última linha n ão nula da forma escalonada reduzida da sua matriz aumentada for da forma[ 0 . . . 0_|b′

m], comb′m 6= 0.

Exemplo 1.14. Considere o seguinte sistema 





3z ₋ 9w = 6 5x + 15y ₋ 10z + 40w = ₋45

(58)

A sua matriz aumentada ´e





0 0 3 ₋9 6

5 15 ₋10 40 ₋45 1

3 ₋1 5 ₋7





Como temos que “fazer” o piv ô igual a um, escolhemos para piv ô o elemento de posiç ão 3,1. Preci-samos “coloc á-lo” na primeira linha, para isto, trocamos a 3a._{linha com a 1}a. _.

1a._linha_←→₄a._linha 



1

3 ₋1 5 ₋7

5 15 ₋10 40 ₋45

0 0 3 ₋9 6





Agora, precisamos “zerar” os outros elementos da 1a._{coluna, que é a coluna do piv ô, para isto,} adici-onamos à 2a.linha,₋5vezes a 1a..

−5_×1a. _linha₊₂a._linha_−→₂a._linha 

 

1 3 ₋1 5 ₋7 0 0

−5 15 ₋10 0 0 3 ₋9 6



 

(59)

−(1/5)_×2a._linha_−→₂a._linha





1 3 ₋1 5 ₋7 0 0

1 ₋3 2 0 0 3 ₋9 6





Agora, precisamos “zerar” os outros elementos da 2a._{coluna, que é a coluna do piv ô, para isto,} adici-onamos à 1a._{linha a 2}a. _{e à 4}a. _linha,₋₃_{vezes a 2}a._.

2a.linha+1a.linha_−→1a.linha −3_×2a. _linha₊₄a. _linha_−→₄a._linha





1 3 0 2 ₋5 0 0 1 ₋3 2

0 0 0 0 0





Esta matriz ´e escalonada reduzida. Portanto o sistema dado ´e equivalente ao sistema seguinte

x + 3y + 2w = ₋5

z ₋ 3w = 2.

A matriz deste sistema possui duas colunas sem piv ôs. As vari áveis que n ão est ão associadas a piv ôs podem ser consideradasvari áveis livres, isto é, podem assumir valores arbitr ários. Neste exemplo as vari áveisyewn ão est ão associadas a piv ôs e podem ser consideradas vari áveis livres. Sejamw = α ey = β. As vari áveis associadas aos piv ôs ter ão os seus valores dependentes das vari áveis livres,z = 2 + 3α,x=₋5₋2α₋3β. Assim, a soluç ão geral do sistema é

X =



  

x y z w



  =



  

−5₋2α₋3β β

2 + 3α α



 

(60)

Em geral, se o sistema linear tiver soluç ão e a forma escalonada reduzida da matriz aumentada possuir colunas sem piv ôs, as vari áveis quen ãoest ão associadas a piv ôs podem ser consideradas vari áveis livres, isto é, podem assumir valores arbitr ários. As vari áveis associadas aos piv ôs ter ão os seus valores dependentes das vari áveis livres.

Lembramos que o sistema linear n ão tem soluç ão se a última linha n ão nula da forma escalonada reduzida da matriz aumentada do sistema for da forma[ 0. . . 0_|b′

m], comb′m 6= 0, como noExemplo

1.13na p ´agina44.

Observaç ão. Para se encontrar a soluç ão de um sistema linear n ão é necess ário transformar a matriz aumentada do sistema na sua forma escalonada reduzida, mas se a matriz est á nesta forma, o sistema associado é o mais simples poss´ıvel. Um outro m étodo de resolver sistemas lineares consiste em, atrav és da aplicaç ão de operaç ões elementares à matriz aumentada do sistema, se chegar a uma matriz que é somenteescalonada (isto é, uma matriz que satisfaz as condiç ões(a)e (c), mas n ão necessariamente(b)e(d)daDefiniç ão1.6). Este m étodo é conhecido comom étodo de Gauss.

O pr óximo resultado mostra que um sistema linear que tenha mais de uma soluç ão n ão pode ter um n úmero finito de soluç ões.

Proposic¸ ˜ao 1.3. SejamAuma matrizm_×neB uma matrizm_×1. Se o sistema linearA X =B

(61)

Demonstrac¸˜ao. Seja

Xλ = (1−λ)X0 +λX1, paraλ∈R.

Vamos mostrar que Xλ é soluç ão do sistema A X = B, para qualquer λ ∈ R. Para isto vamos

mostrar queA Xλ =B.

Aplicando as propriedades (i), (j) das operaç ões matriciais (Teorema1.1na p ágina10) obtemos

A Xλ =A[(1−λ)X0+λX1] =A(1−λ)X0+AλX1 = (1−λ)A X0+λA X1

ComoX0eX1 s ão soluç ões deA X =B, ent ãoA X0 =BeA X1 =B, portanto

A Xλ = (1−λ)B+λB= [(1−λ) +λ]B =B,

pela propriedade (f) doTeorema1.1.

Assim o sistemaA X =B tem infinitas soluç ões, pois para todo valor deλ_∈ R_,_X_λ _{é soluç ão e}

Xλ−Xλ′ = (λ−λ′)(X₁−X₀), ou seja,X_λ 6=X_λ′, paraλ6=λ′. Observe que paraλ= 0,X_λ =X₀,

paraλ = 1, Xλ = X1, para λ = 1/2, Xλ = 1₂X0 + 1₂X1, para λ = 3, Xλ = −2X0 + 3X1 e para

λ=₋2,Xλ = 3X0−2X1.

NoExemplo3.4na p ágina168temos uma interpretaç ão geom étrica desta demonstraç ão.

(62)

1.2.2 Matrizes Equivalentes por Linhas

Definiç ão 1.7. Uma matrizA = (aij)m×n éequivalente por linhasa uma matrizB = (bij)m×n, se

Bpode ser obtida deAaplicando-se uma seq ü ência de operaç ões elementares sobre as suas linhas.

Exemplo 1.15. Observando osExemplos1.11,1.14e1.13, vemos que as matrizes 



1 1 1 2 1 4 2 3 5



, 



0 0 3 ₋9 5 15 ₋10 40 1 3 ₋1 5



, 



1 3 13

0 1 5

0 ₋2 ₋10





s ˜ao equivalentes por linhas `as matrizes





1 0 0 0 1 0 0 0 1



, 



1 3 0 2

0 0 1 ₋3

0 0 0 0



, 



1 0 ₋2 0 1 5 0 0 0



,

respectivamente. Matrizes estas que s ˜ao escalonadas reduzidas.

Cuidado:elas s ão equivalentes por linhas,n ãos ão iguais!

A relaç ão “ser equivalente por linhas” satisfaz as seguintes propriedades, cuja verificaç ão deixa-mos como exerc´ıcio para o leitor:

(63)

• SeA é equivalente por linhas aB, ent ãoB é equivalente por linhas aA(simetria);

• SeA é equivalente por linhas aB eB é equivalente por linhas aC, ent ãoA é equivalente por linhas aC(transitividade).

(64)

Teorema 1.4. Toda matriz A = (aij)m×n ´e equivalente por linhas a uma ´unica matriz escalonada

reduzidaR= (rij)m×n.

O pr óximo resultado ser á usado para provar alguns resultados no cap´ıtulo de invers ão de matrizes.

Proposiç ão 1.5. SejaR uma matrizn_×n, na forma escalonada reduzida. SeR₆=In, ent ãoRtem

uma linha nula.

Demonstração. Observe que o piv ô de uma linhaiest á sempre numa colunajcomj _≥i. Portanto, ou a última linha de R é nula ou o piv ô da linhan est á na posiç ão n, n. Mas, neste caso todas as linhas anteriores s ão n ão nulas e os piv ôs de cada linhaiest á na colunai, ou seja,R=In.