UNIVERSIDAD AUTÓNOMA DE BAJA CALIFORNIA FACULTAD DE INGENIERÍA MEXICALI
SISTEMAS LINEALES 2
Dr. Lars Lindner
I
Contenido
5 Representación en el Espacio de Estado 3
Introducción ... 3
5.1 Transformación al Espacio de Estado ... 4
5.2 Solución de la Ecuación de Estado en el Tiempo ... 15
5.3 Solución de la Ecuación de Estado en el Dominio de la Frecuencia ... 18
5.4 Matriz de la Respuesta al Impulso ... 22
5.5 Algunos principios básicos de la teoría de matrices para el cálculo de la matriz de 5.6 transición ... 27
5.6.1 Teorema de Cayley-Hamilton ... 27
5.6.2 Aplicación a funciones de matrices ... 32
5.6.3 La Regla de Sylvester ... 35
Formas Normales para Sistemas univariables ... 37
5.7 5.7.1 Forma Canónica Controlable (FCC) ... 37
5.7.2 Forma Canónica Observable (FCO) ... 42
5.7.3 Forma Diagonal y Forma Canónica de Jordan ... 46
Transformación de Ecuaciones de Estado a Formas Normales ... 56
5.8 5.8.1 Transformación de Semejanza ... 56
5.8.2 Transformación a Forma Diagonal ... 59
5.8.3 Transformación a Forma Canónica de Jordan ... 65
5.8.4 Aplicación de Transformaciones canónicas ... 68
Controlabilidad y Observabilidad ... 71
5.9 5.9.1 Controlabilidad ... 73
5.9.2 Observabilidad ... 78
5.9.3 Aplicación y Ejemplos ... 80
Estabilizabilidad y Reconstructibilidad ... 87
5.10 5.10.1 Estabilizabilidad ... 87
5.10.2 Reconstructibilidad ... 87
Sintonización de Sistemas lineales en el Espacio de Estado ... 88
5.11 5.11.1 Introducción ... 88
5.11.2 Procedimientos para la Sintonización del Controlador ... 94
5.11.3 Sintonización de Controladores usando Colocación de Polos ... 97
Reconstrucción del Estado usando Observadores lineales ... 119
5.12 5.12.1 Diseño de Observadores de Orden completo usando Colocación de Polos 119 5.12.2 Diseño de un Observador de Orden reducido ... 134
5
Representación en el Espacio de Estado
Introducción
5.1
Desde el punto de vista matemático y en el caso más simple, la representación de sistemas dinámicos en el espacio de estado corresponde a una conversión de una ecuación diferencial de orden 𝑛 a un sistema equivalente de 𝑛 ecuaciones diferenciales de primer orden. La aplicación de esta representación a problemas de ingeniería de control dio lugar a una expansión tremenda de la teoría de control desde aproximado 1957, de modo que a veces se distinguen entre los métodos
“clásicos” y modernos” de la teoría de control. La razón de este desarrollo se encuentra
principalmente en el hecho que por primera vez existían computadoras digitales eficientes, cuales permitieron una amplia aplicación de los métodos de espacio de estado, como hacer posible la solución numérica de problemas muy complejos. Particularmente en el tratamiento de sistemas con múltiples entradas y salidas, sistemas no-lineales y sistemas variantes en el tiempo, la representación de espacio de estado es muy útil y apropiada. Esta representación de sistema también permite una formulación sencilla de problemas de optimización dinámica en el dominio del tiempo, cuales se pueden resolver de manera analítica y algunos solamente por manera numérica. Una segunda razón importante para la aplicación de esta forma de representación es el significado fundamental del término estado de un sistema dinámico. Físicamente, el estado de un sistema dinámico se determina por el contenido de energía presente en los acumuladores de energía del sistema. Solo por el conocimiento del estado del sistema en un momento arbitrario
𝑡 = 𝑡0 sigue el comportamiento del sistema para todos los otros momentos. Por supuesto, la
influencia de magnitudes externo, por ejemplo el comportamiento en el tiempo de la entrada
𝑢(𝑡), debe ser conocida. El estado de un sistema con 𝑛 acumuladores de energía se define usando
Transformación al Espacio de Estado
5.2
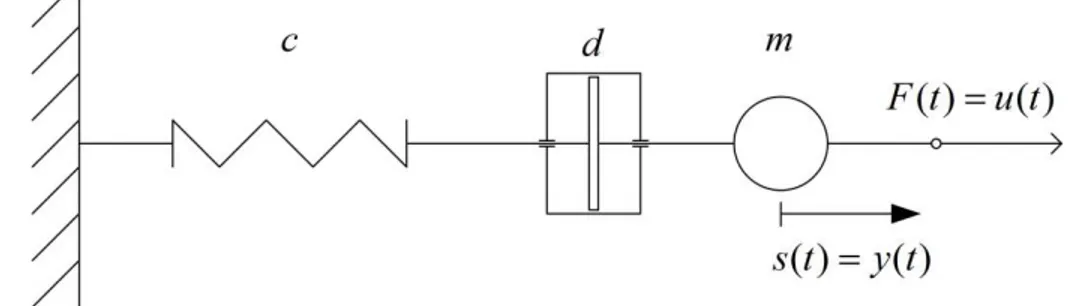
Antes que se especifica la representación en espacio de estado para sistemas lineales y continuos, se usa un ejemplo para mostrar la conversión de una ecuación diferencial (ED) de segundo orden a dos ecuaciones diferenciales de primer orden. Para eso, se considere el siguiente oscilador armónico mecánico de la Figura 1, con la masa 𝑚, la constante de amortiguación 𝑑 y la constante de resorte 𝑐, cual se excita con una fuerza externa 𝑢(𝑡) = 𝐹(𝑡).
Figura 1: Sistema resorte-masa-amortiguador (RMA)
La ED para el desplazamiento 𝑦(𝑡) = 𝑠(𝑡) como salida es:
𝑚𝑦̈(𝑡) + 𝑑𝑦̇(𝑡) + 𝑐𝑦(𝑡) = 𝑢(𝑡) ( 1 )
y usando la ecuación convertida:
𝑦̈(𝑡) = 1
𝑚[𝑢(𝑡) − 𝑑𝑦̇(𝑡) − 𝑐𝑦(𝑡)] ( 2 )
se puede derivar un diagrama de bloque, integrando 𝑦̈(𝑡) dos veces y retroalimentando 𝑦(𝑡) y
𝑦̇(𝑡), ilustrado en la Figura 2. Ahora es evidente, definir las salidas de los elementos integrales como variables de estado 𝑥1(𝑡) y 𝑥2(𝑡), entonces hacer las siguientes sustituciones en la ecuación
( 1 ) y ( 2 ):
𝑥1(𝑡) = 𝑦(𝑡) ( 3 )
Estas variables de estado también tienen una interpretación física y directa: 𝑥1(𝑡) describe el desplazamiento y por ende representa una medida de la energía potencial del resorte, mientras la velocidad 𝑥2(𝑡) representa una medida de la energía cinética de la masa.
Figura 2: Diagrama de bloque del sistema RMA
Del diagrama del bloque o respectivamente de las ecuaciones resulta ahora el sistema de ED de primer orden buscado:
𝑥̇1(𝑡) = 𝑥2
𝑥̇2(𝑡) = −𝑚 𝑥𝑐 1−𝑚 𝑥𝑑 2+𝑚 𝑢(𝑡)1
( 5 )
Si se representa ese sistema de ecuaciones en forma matricial, resulta la ecuación de estado:
[𝑥̇𝑥̇1(𝑡) 2(𝑡)] = [
0 1
−𝑚 −𝑐 𝑚𝑑] ⋅ [𝑥𝑥12(𝑡)(𝑡)] + [ 0 1 𝑚] 𝑢(𝑡)
( 6 )
o respectivamente:
𝑥̇(𝑡) = 𝐴 𝑥(𝑡) + 𝑏 𝑢(𝑡) ( 7 )
con:
𝑥(𝑡) = [𝑥𝑥1(𝑡)
2(𝑡)] 𝐴 = [
0 1
La magnitud de salida está dada por ecuación ( 3 ), con esta resulta la ecuación de salida:
𝑦(𝑡) = 𝑐𝑇𝑥(𝑡) ( 8 )
, con 𝑐𝑇 = [1 0].
Hay que notar, que en lo siguiente se usan letras minúsculas subrayadas (por ej. 𝑏) para vectores de columna y letras mayúsculas subrayadas (por ej. 𝐴) para matrices. El ejemplo solo tiene una variable de entrada 𝑢(𝑡) y una variable de salida 𝑦(𝑡), por ende será denominado un sistema univariable (SISO). Un sistema multivariable (MIMO) con 𝑟 variables de entrada
𝑢1(𝑡), 𝑢2(𝑡), … , 𝑢𝑟(𝑡) y 𝑚 variables de salida 𝑦1(𝑡), 𝑦2(𝑡), … , 𝑦𝑚(𝑡) se representa con 𝑢(𝑡) y 𝑦(𝑡).
Por lo tanto, la forma general de la representación de estado de un sistema lineal, invariante en el tiempo, dinámico de orden 𝑛 resulta:
𝑥̇(𝑡) = 𝐴 𝑥(𝑡) + 𝐵 𝑢(𝑡) ( 9 )
𝑦(𝑡) = 𝐶 𝑥(𝑡) + 𝐷 𝑢(𝑡) ( 10 )
, con 𝑥(𝑡0) = 𝑥0. Aquí significan:
𝑥(𝑡) Vector de estado con dimensión 𝑛
𝑢(𝑡) Vector de entrada con dimensión 𝑟
𝑦(𝑡) Vector de salida con dimensión 𝑚
𝐴 Matriz del sistema con dimensión 𝑛 𝑥 𝑛
𝐵 Matriz de entrada con dimensión 𝑛 𝑥 𝑟
𝐶 Matriz de salida con dimensión 𝑚 𝑥 𝑛
𝐷 Matriz de entrada-salida con dimensión 𝑚 𝑥 𝑟
La ecuación ( 9 ) representa la ecuación de estado vectorial (o ecuación diferencial de estado) y describe la dinámica del sistema. Si 𝑢(𝑡) = 0, resulta la ecuación homogénea 𝑥̇(𝑡) = 𝐴 𝑥(𝑡) con
𝑥(𝑡0) = 𝑥0, que define el movimiento libre (sistema autónomo). La matriz del sistema 𝐴 por lo
la excitación externa. Ecuación ( 10 ) representa la ecuación de salida vectorial (o ecuación de observación), que describe esencialmente la relación entre las variables de estado y variables de salida, cual está dada por la matriz 𝐶 como combinaciones lineales y estáticos de las variables de estado. Además, hay sistemas, donde las variables de entrada 𝑢(𝑡) tienen una influencia proporcional directa hacia las variables de salida 𝑦(𝑡) por la matriz de entrada-salida 𝐷. Se dice, que esos sistemas pueden brincar en la variable de salida 𝑦(𝑡).
La próxima figura ilustra un diagrama de bloque de la representación de estado de un sistema lineal multivariable:
Figura 3: Diagrama de bloque de la representación de estado de un sistema multivariable
La representación de estado también se puede usar para sistemas variante en el tiempo:
𝑥̇(𝑡) = 𝐴(𝑡) 𝑥(𝑡) + 𝐵(𝑡) 𝑢(𝑡) ( 11 )
𝑦(𝑡) = 𝐶(𝑡) 𝑥(𝑡) + 𝐷(𝑡) 𝑢(𝑡) ( 12 )
o para sistemas no-lineales variante o invariante en el tiempo:
𝑥̇(𝑡) = 𝑓 [𝑥(𝑡), 𝑢(𝑡), 𝑡] ( 13 )
Ejemplo 5-1: Ecuacion de Estado Circuito RLC
Se busca la representación de estado del siguiente circuito RLC, con entrada 𝑢 = 𝑢𝑒(𝑡) y salida
𝑦 = 𝑢𝐶(𝑡):
Figura 4: Circuito RLC
La primera posibilidad de solución (PS1) usa la ecuación diferencial del sistema para derivar la representación de estado:
𝑢𝑒= 𝑢𝑅+ 𝑢𝐿+ 𝑢𝐶
𝑢𝑒= 𝑅𝑖𝐿+ 𝐿𝑑𝑖𝑑𝑡 + 𝑢𝐿 𝐶 𝑢𝑒= 𝑅𝐶𝑢̇𝐶+ 𝐿𝐶𝑢̈𝐶+ 𝑢𝐶
𝑢 = 𝐿𝐶𝑦̈ + 𝑅𝐶𝑦̇ + 𝑦
𝑦̈ = 𝑥̇2 =𝐿𝐶1 [𝑢 − 𝑅𝐶𝑥2− 𝑥1]
𝑥̇1= 𝑥2
Ahora resulta la representación de estado:
𝑥̇ = [𝑥̇𝑥̇1 2] = [
0 1
−𝐿𝐶1 −𝑅𝐿] ⋅ 𝑥 + [ 0 1 𝐿𝐶] 𝑢(𝑡)
( 15 )
La segunda posibilidad de solución (PS2) usa las derivadas ya existentes y definidas por los elementos dinámicos del circuito para definir las variables de estado directo. En este caso será
𝑥1= 𝑢𝐶 y 𝑥2= 𝑖𝐿:
𝑑𝑢𝐶
𝑑𝑡 = 𝑥̇1= 1 𝐶 𝑖𝐿=
1 𝐶 𝑥2
𝑑𝑖𝐿
𝑑𝑡 = 𝑥̇2= 1 𝐿 𝑢𝐿=
1
𝐿[𝑢𝑒− 𝑢𝑅− 𝑢𝐶] = −𝑅𝐿 𝑖𝐿−1𝐿 𝑢𝐶+1𝐿 𝑢𝑒
= −1𝐿 𝑥1−𝑅𝐿 𝑥2+1𝐿 𝑢
Ahora resulta la representación de estado:
𝑥̇ = [𝑥̇𝑥̇1 2] = [
0 1𝐶
−1𝐿 −𝑅𝐿] ⋅ 𝑥 + [ 0 1 𝐿] 𝑢(𝑡)
( 17 )
𝑦 = [1 0] ⋅ 𝑥 ( 18 )
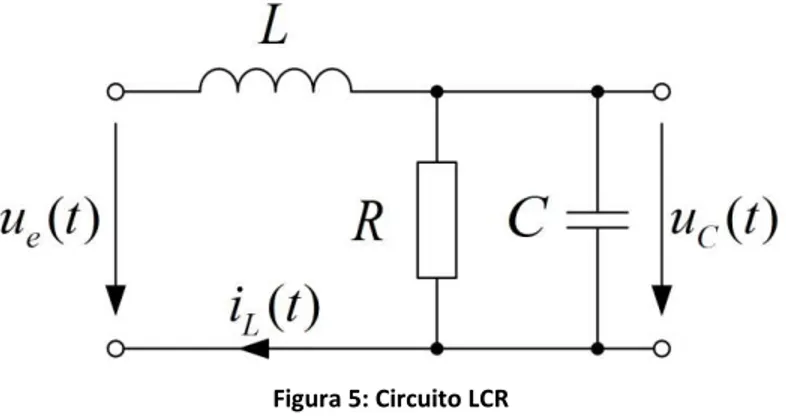
Ejemplo 5-2: Ecuacion de Estado Circuito LCR
Se busca la representación de estado del siguiente circuito LCR, con entrada 𝑢 = 𝑢𝑒(𝑡) y salida
𝑦 = 𝑢𝐶(𝑡):
Figura 5: Circuito LCR
Primero se usa PS1 para determinar la ecuación de estado, cual usa la ED del sistema y las siguientes variables de estado 𝑥1= 𝑦 y 𝑥2= 𝑦̇:
𝑢𝑒= 𝑢𝐿+ 𝑢𝐶 = 𝐿𝑑𝑖𝑑𝑡 + 𝑢𝐿 𝐶
𝑢𝑒= 𝐿𝑑𝑡𝑑 [𝑖𝑅+ 𝑖𝐶] + 𝑢𝐶 = 𝐿𝑑𝑡 [𝑑 𝑅 𝑢1 𝐶+ 𝐶𝑢̇𝐶] + 𝑢𝐶
𝑢(𝑡) = 𝐿𝐶𝑦̈ +𝑅 𝑦̇ + 𝑦𝐿
Se determinan las ecuaciones para las variables de estado:
𝑥̇1= 𝑥2
𝑥̇2= −𝐿𝐶 𝑥1 1−𝑅𝐶 𝑥1 2+𝐿𝐶 𝑢1
, que se agrupan en forma matricial:
𝑥̇ = [𝑥̇𝑥̇1 2] = [
0 1
−𝐿𝐶 −1 𝑅𝐶1 ] ⋅ 𝑥 + [ 0 1 𝐿𝐶] 𝑢(𝑡)
( 19 )
Después se usa PS2 para determinar la ecuación de estado, usando las variables de estado convenientes 𝑥1 = 𝑢𝐶 y 𝑥2= 𝑖𝐿:
𝑥̇1= 𝑢̇𝐶 =𝐶 𝑖1 𝐶 =1𝐶[𝑖𝐿− 𝑖𝑅] =1𝐶 [𝑖𝐿−𝑅 𝑢1 𝐶]
𝑥̇1= −𝑅𝐶 𝑥1 1+𝐶 𝑥1 2
𝑥̇2=𝑑𝑖𝑑𝑡 =𝐿 1𝐿 𝑢𝐿=1𝐿[𝑢𝑒− 𝑢𝐶]
𝑥̇2= −1𝐿𝑥1+1𝐿𝑢
Ahora resulta la representación de estado:
𝑥̇ = [𝑥̇𝑥̇1 2] = [
−𝑅𝐶1 𝐶1
−1𝐿 0] ⋅ 𝑥 + [ 0 1 𝐿] 𝑢(𝑡)
( 21 )
𝑦 = [1 0] ⋅ 𝑥 ( 22 )
Ejemplo 5-3: Ecuacion de Estado Circuito RRCC
Se busca la representación de estado del siguiente circuito RRCC, con entrada 𝑢 = 𝑢𝑒(𝑡) y salida
𝑦 = 𝑢𝐶2(𝑡):
Figura 6: Circuito RRCC
Usando PS1, que usa la ED del sistema, resulta en:
𝑢𝑒= 𝑢𝑅1+ 𝑢𝑅2+ 𝑢𝐶2
𝑢𝑒= 𝑅1[𝑖𝐶1+ 𝑖𝐶2] + 𝑅2𝑖𝐶2+ 𝑢𝐶2
𝑢𝑒= 𝑅1𝐶1𝑢̇𝐶1+ [𝑅1+ 𝑅2]𝐶2𝑢̇𝐶2+ 𝑢𝐶2
Ahora hay que encontrar una definición para 𝑢̇𝐶1, usando la ley de Kirchhoff de las mayas y las leyes de los componentes electrónicos:
𝑢̇𝐶1= 𝑢̇𝑅2+ 𝑢̇𝐶2 = 𝑅2
𝑑𝑖𝐶2
𝑑𝑡 + 𝑢̇𝐶2 = 𝑅2𝐶2𝑢̈𝐶2+ 𝑢̇𝐶2
Sustituyéndolo en la ED del circuito RRCC y usando variables estándares, resulta:
𝑢(𝑡) = 𝑅1𝑅2𝐶1𝐶2𝑦̈ + [𝑅1𝐶1+ 𝑅1𝐶2+ 𝑅2𝐶2]𝑦̇ + 𝑦
Se despeja la derivada mayor y se usan las variables de estado 𝑥1= 𝑦 y 𝑥2 = 𝑦̇ y las siguientes constantes 𝛼 = 𝑅1𝑅2𝐶1𝐶2 y 𝛽 = 𝑅1𝐶1+ 𝑅1𝐶2+ 𝑅2𝐶2:
𝑥̇1= 𝑥2
Ahora resulta la representación de estado:
𝑥̇ = [𝑥̇𝑥̇1 2] = [
0 1
−𝛼 −1 𝛽𝛼] ⋅ 𝑥 + [ 0 1 𝛼] 𝑢(𝑡)
( 23 )
𝑦 = [1 0] ⋅ 𝑥 ( 24 )
Usando PS2 para las variables de estado convenientes 𝑥1= 𝑢𝐶1 y 𝑥2= 𝑢𝐶2:
𝑢̇𝐶1= 𝑥̇1=
1 𝐶1𝑖𝐶1 =
1
𝐶1[𝑖𝑅1− 𝑖𝐶2] 𝑥̇1=𝐶1
1[ 1 𝑅1𝑢𝑅1−
1
𝑅2𝑢𝑅2] = 1
𝑅1𝐶1[𝑢𝑒− 𝑢𝐶1] − 1
𝑅2𝐶1[𝑢𝐶1− 𝑢𝐶2] 𝑥̇1= − [𝑅1
1𝐶1+ 1
𝑅2𝐶1] 𝑥1+ 1 𝑅2𝐶1𝑥2+
1 𝑅1𝐶1𝑢
𝑢̇𝐶2= 𝑥̇2=
1 𝐶2𝑖𝐶2 =
1 𝑅2𝐶2𝑢𝑅2 𝑥̇2=𝑅1
2𝐶2[𝑢𝐶1− 𝑢𝐶2] = 1
𝑅2𝐶2[𝑥1− 𝑥2]
Ahora resulta la representación de estado:
𝑥̇ = [𝑥̇𝑥̇1 2] =
[ − [𝑅1
1𝐶1+ 1 𝑅2𝐶1]
1 𝑅2𝐶1 1
𝑅2𝐶2 − 1 𝑅2𝐶2]
⋅ 𝑥 + [𝑅11𝐶1 0
] 𝑢(𝑡) ( 25 )
𝑦 = [0 1] ⋅ 𝑥 ( 26 )
Ejemplo 5-4: Ecuacion de Estado Circuito RRLLC
Se busca la representación de estado del siguiente circuito RRLLC, con entrada 𝑢 = 𝑢𝑒(𝑡) y salida
𝑦 = 𝑢𝐶(𝑡):
Figura 7: Circuito RRLLC
Este problema se resuelve como ejercicio en la casa. Usa valores 𝑅1= 2Ω, 𝑅2= 1Ω,
𝐿1= 0.5𝐻, 𝐿2= 0.1𝐻 y 𝐶 =121 𝐹 para la simulación.
Solución de la Ecuación de Estado en el Tiempo
5.3
Inicialmente se considere un sistema de primer orden, cual se representa por la siguiente ecuación diferencial escalar:
𝑥̇(𝑡) = 𝑎𝑥(𝑡) + 𝑏𝑢(𝑡) ( 27 )
, con valor inicial 𝑥(0) = 𝑥0. Usando la transformación de Laplace, ecuación ( 27 ) resulta en:
𝑠𝑋(𝑠) − 𝑥0= 𝑎𝑋(𝑠) + 𝑏𝑈(𝑠)
y despejando la variable dependiente:
𝑋(𝑠) =𝑠 − 𝑎 𝑥1 0+𝑠 − 𝑎 𝑏𝑈(𝑠)1 ( 28 )
Usando la transformación inversa de Laplace y el teorema de convolución, ecuación ( 28 ) resulta en la solución de ( 27 ):
𝑥(𝑡) = ℒ−1{𝑋(𝑠)} = 𝑒𝑎𝑡𝑥
0+ ∫ 𝑒𝑎(𝑡−𝜏) 𝑡
0 𝑏𝑢(𝜏) 𝑑𝜏
( 29 )
Ahora es evidente para el caso vectorial, usar la misma estructura de la solución y formalmente cambiar todas las variables escalares con vectores y matrices:
𝑥(𝑡) = 𝑒𝐴𝑡𝑥
0+ ∫ 𝑒𝐴(𝑡−𝜏) 𝑡
0 𝐵 𝑢(𝜏) 𝑑𝜏
( 30 )
𝑑
𝑑𝑡 𝑒𝐴𝑡= 𝐴𝑒𝐴𝑡 ( 31 )
Esta condición se cumple, cuando se aplica la función exponencial 𝑓(𝑥) = 𝑒𝑥 como una serie infinita (serie de potencias) a la matriz exponencial ( 31 ), que resulta en:
𝑒𝐴𝑡 = 𝐼 + 𝐴𝑡 + 𝐴2𝑡2 2! + 𝐴3
𝑡3 3! + 𝐴4
𝑡4 4! + ⋯
= ∑ 𝐴𝑘𝑡𝑘 𝑘! ∞
𝑘=0
( 32 )
Se puede mostrar, que esa serie converge absolutamente para todas matrices 𝐴 y para todos
|𝑡| < ∞. Por lo tanto, la diferenciación por partes de esa serie con respeto al tiempo es pertinente y resulta en:
𝑑
𝑑𝑡 𝑒𝐴𝑡 = 𝐴 + 𝐴2𝑡 + 𝐴3 𝑡2 2! + 𝐴4
𝑡3 3! + ⋯
= 𝐴 [𝐼 + 𝐴𝑡 + 𝐴2𝑡2 2! + 𝐴3
𝑡3 3! + ⋯ ] = 𝐴𝑒𝐴𝑡
Por ende, se cumple la condición en la ecuación ( 31 ) y se puede usar ecuación ( 32 ) como la definición para la matriz exponencial ( 31 ). Ahora se comprueba, que la ecuación ( 30 ) es solución de la ecuación de estado, por eso se deriva, usando la siguiente forma:
𝑥(𝑡) = 𝑒𝐴𝑡𝑥
0+ 𝑒𝐴𝑡∫ 𝑒−𝐴𝜏 𝑡
0 𝐵 𝑢(𝜏) 𝑑𝜏
𝑥̇(𝑡) = 𝐴𝑒𝐴𝑡𝑥
0+ 𝐴𝑒𝐴𝑡∫ 𝑒−𝐴𝜏 𝑡
0 𝐵 𝑢(𝜏) 𝑑𝜏 + 𝑒
𝐴𝑡𝑒−𝐴𝑡𝐵 𝑢(𝑡)
= 𝐴 [𝑒𝐴𝑡𝑥
0+ 𝑒𝐴𝑡∫ 𝑒−𝐴𝜏 𝑡
En general, ecuación ( 30 ) se representa también en la forma:
𝑥(𝑡) = Φ(𝑡) 𝑥0+ ∫ Φ(𝑡 − 𝜏) 𝑡
0 𝐵 𝑢(𝜏) 𝑑𝜏
( 33 )
, con Φ(𝑡) = 𝑒𝐴𝑡 la matriz de transición. La primera parte de la solución 𝑥ℎ(𝑡) = Φ(𝑡) 𝑥0 representa la solución homogénea, es decir el movimiento libre. La segunda parte de la solución
𝑥𝑝(𝑡) = ∫ Φ(𝑡 − 𝜏)0𝑡 𝐵 𝑢(𝜏) 𝑑𝜏 representa la solución particular y por ende el movimiento forzado
del sistema.
Propiedades de la Matriz de Transición:
a) Φ(0) = 𝑒𝐴⋅0= 𝐼, la matriz de identidad
b) Φ−1(𝑡) = (𝑒𝐴𝑡)−1= 𝑒𝐴(−𝑡)= Φ(−𝑡), la matriz de transición siempre es invertible
c) Φ𝑘(𝑡) = 𝑒𝐴𝑡𝑘= Φ(𝑘𝑡), para sistemas discretas en el tiempo
d) Φ(𝑡1)Φ(𝑡2) = Φ(𝑡2)Φ(𝑡1) = 𝑒𝐴(𝑡1+𝑡2)= Φ(𝑡1+ 𝑡2)
Solución de la Ecuación de Estado en el Dominio de la
5.4
Frecuencia
Para poder usar las ecuaciones de estado en el dominio de frecuencia se requiere la transformada de Laplace de vectores y matrices, que son dependientes del tiempo. Para eso se transforma la representación de estado ( 9 ) y ( 10 ) usando Laplace:
𝑠𝑋(𝑠) − 𝑥(0) = 𝐴 𝑋(𝑠) + 𝐵 𝑈(𝑠) ( 34 )
𝑌(𝑠) = 𝐶 𝑋(𝑠) + 𝐷 𝑈(𝑠) ( 35 )
Ecuación ( 34 ) se convierte en:
(𝑠𝐼 − 𝐴)𝑋(𝑠) = 𝑥(0) + 𝐵 𝑈
𝑋(𝑠) = (𝑠𝐼 − 𝐴)−1𝑥(0) + (𝑠𝐼 − 𝐴)−1𝐵 𝑈(𝑠) ( 36 )
, debido a que (𝑠𝐼 − 𝐴) es no-singular y por eso se puede invertir. Ecuación ( 36 ) representa la transformada de Laplace de la ecuación ( 33 ) para 𝑡0= 0 y por eso la solución en el dominio de frecuencia. Comparando ecuación ( 33 ) con ( 36 ) resulta en:
Φ(𝑡) = ℒ−1{(𝑠𝐼 − 𝐴)−1} ( 37 )
o respectivamente
ℒ{Φ(𝑡)} = Φ(𝑠) = (𝑠𝐼 − 𝐴)−1 ( 38 )
Para calcular la inversa (𝑠𝐼 − 𝐴)−1, se necesita la matriz adjunta adj(𝑠𝐼 − 𝐴):
Φ(𝑠) = 1
La matriz adjunta de una matriz 𝑀 con:
𝑀 =
[
11 12 1
21 22 2
1 2
k k
i i ik
m
m
m
m
m
m
m
m
m
L
M
M
M
M
K
], resulta del hecho de que cada elemento 𝑚𝑖𝑘 es reemplazado por su cofactor cof𝑖𝑘 𝑀 y que se transpone la matriz resultante:
adj 𝑀 =
[
11 21 1
12 22 2
1 2
i i
k k ik
cof M
cof M
cof M
cof M
cof M
cof M
cof M
cof M
cof M
L
M
M
M
M
K
], con cof𝑖𝑘 𝑀 = (−1)𝑖+𝑘⋅ det 𝑀𝑖𝑘 para 𝑖 = 𝑘 = 1,2, … , 𝑛. Se puede usar la regla del “tablero de
ajedrez” para determinar los signos de los subdeterminantes det 𝑀𝑖𝑘:
+det 𝑀11 − det 𝑀12 + det 𝑀13 …
− det 𝑀21 + det 𝑀22 − det 𝑀23 …
+ det 𝑀31 − det 𝑀32 + det 𝑀33 …
⋮ ⋮ ⋮
Ejemplo 5-5:
Dado la siguiente matriz del sistema 𝐴 = [ 0 6
−1 −5] y se busca la matriz de transición en el
tiempo:
(𝑠𝐼 − 𝐴) = [𝑠1 𝑠 + 5]−6
adj(𝑠𝐼 − 𝐴) = [ det 𝑀− det 𝑀11 − det 𝑀21
12 det 𝑀22 ] = [𝑠 + 5 6−1 𝑠]
Φ(𝑠) =(𝑠 + 2)(𝑠 + 3) [1 𝑠 + 5 6−1 𝑠]
Transformando cada elemento inverso:
Φ(𝑡) = [(3𝑒(−𝑒−2𝑡−2𝑡− 2𝑒+ 𝑒−3𝑡−3𝑡) (−2𝑒) (6𝑒−2𝑡−2𝑡− 6𝑒+ 3𝑒−3𝑡−3𝑡))]
Ejemplo 5-6:
Dado la ecuación de estado:
𝑥̇(𝑡) = [ 0−1 −5] 𝑥(𝑡) + [6 01] 𝑢(𝑡)
, con 𝑥(0) = 𝑥0= [31]. Del Ejemplo 5-5 se calculó la matriz de transición:
Φ(𝑡) = [(3𝑒(−𝑒−2𝑡−2𝑡− 2𝑒+ 𝑒−3𝑡−3𝑡) (−2𝑒) (6𝑒−2𝑡−2𝑡− 6𝑒+ 3𝑒−3𝑡−3𝑡))]
Se debe calcular el vector de estado 𝑥(𝑡) usando ( 33 ) para un escalón unitario en la entrada
𝑢(𝑡) = 𝜎(𝑡) para 𝑡 ≥ 0. Con Φ(𝑡 − 𝜏) 𝐵 𝑢(𝜏) resulta la segunda columna de Φ(𝑡):
𝑥(𝑡) = [(3𝑒(−𝑒−2𝑡−2𝑡− 2𝑒+ 𝑒−3𝑡−3𝑡) (−2𝑒) (6𝑒−2𝑡−2𝑡− 6𝑒+ 3𝑒−3𝑡−3𝑡))] [31] + ∫ [ (6𝑒−2(𝑡−𝜏)− 6𝑒−3(𝑡−𝜏)) (−2𝑒−2(𝑡−𝜏)+ 3𝑒−3(𝑡−𝜏))] 𝑡
0 𝑑𝜏
Después de multiplicación e integración resulta:
𝑥(𝑡) = [15𝑒6𝑒−2𝑡−3𝑡− 12𝑒− 5𝑒−2𝑡−3𝑡] + [1 − 3𝑒𝑒−2𝑡−2𝑡− 𝑒+ 2𝑒−3𝑡−3𝑡]
Ejemplo 5-7:
Del Ejemplo 5-6 se debe calcular el vector de estado 𝑥(𝑡) para una rampa unitaria 𝑢(𝑡) = 𝜌(𝑡) con
𝑥0= 0 para 𝑡 ≥ 0. Este problema se puede resolver como ejercicio en la casa.
Matriz de la Respuesta al Impulso
5.5
Al analizar los sistemas de control, no solo interesa el comportamiento de las variables de estado, sino también la relación entre la entrada 𝑢(𝑡) y la salida 𝑦(𝑡). Si en la ecuación de salida
𝑦(𝑡) = 𝐶 𝑥(𝑡) + 𝐷 𝑢(𝑡) se sustituye la relación ( 30 ) para 𝑥(𝑡), entonces resulta en:
𝑦(𝑡) = 𝐶𝑒𝐴𝑡𝑥(0) + ∫ 𝐶𝑒𝑡 𝐴(𝑡−𝜏)𝐵 𝑢(𝜏)
0 𝑑𝜏 + 𝐷 𝑢(𝑡)
( 40 )
Ahora se define la siguiente matriz (𝑚 𝑥 𝑟):
𝐺(𝑡) = 𝐶𝑒𝐴𝑡𝐵 + 𝐷 𝛿(𝑡) ( 41 )
o respectivamente:
𝐺(𝑡 − 𝜏) = 𝐶𝑒𝐴(𝑡−𝜏)𝐵 + 𝐷 𝛿(𝑡 − 𝜏) ( 42 )
, cual a integrarla con 𝑢(𝜏) da:
∫ 𝐺(𝑡 − 𝜏)𝑡
0 𝑢(𝜏)𝑑𝜏 = ∫ 𝐶𝑒
𝐴(𝑡−𝜏)𝐵 𝑢(𝜏) 𝑡
0 𝑑𝜏 + ∫ 𝐷 𝑢(𝜏)𝛿(𝑡 − 𝜏)
𝑡
0 𝑑𝜏
= ∫ 𝐶𝑒𝑡 𝐴(𝑡−𝜏)𝐵 𝑢(𝜏)
0 𝑑𝜏 + 𝐷 𝑢(𝑡)
( 43 )
Por lo tanto, la ecuación ( 40 ) se puede expresar como:
𝑦(𝑡) = 𝐶𝑒𝐴𝑡𝑥(0) + ∫ 𝐺(𝑡 − 𝜏)𝑡
0 𝑢(𝜏)𝑑𝜏
( 44 )
𝑦ℎ(𝑡) = 𝐶𝑒𝐴𝑡𝑥(0) = 𝐶 Φ(𝑡) 𝑥(0) ( 45 )
y la solución particular:
𝑦𝑝(𝑡) = ∫ 𝐺(𝑡 − 𝜏) 𝑡
0 𝑢(𝜏)𝑑𝜏
( 46 )
La solución particular también se deriva usando el teorema de convolución:
𝑌𝑝(𝑠) = 𝐺(𝑠) ⋅ 𝑈(𝑠) = ℒ {∫ 𝐺(𝑡 − 𝜏)𝑢(𝜏) 𝑡
0 𝑑𝜏}
( 47 )
Por lo tanto, la matriz
𝐺(𝑡) = 𝐶 Φ(𝑡) 𝐵 + 𝐷 𝛿(𝑡) ( 48 )
representa la matriz de la respuesta al impulso, respectivo 𝑔(𝑡) representa la respuesta al impulso para un sistema SISO. Esa matriz de la respuesta al impulso 𝐺(𝑡) contiene 𝑟 variables de entrada y
𝑚 variables de salida.
Ejemplo 5-8:
Para el sistema lineal del Ejemplo 5-6 con 𝑥(0) = 0:
𝑥̇(𝑡) = [ 0−1 −5] 𝑥(𝑡) + [6 01] 𝑢(𝑡) 𝑦 = [1 0] 𝑥
, se había calculado la matriz de transición Φ(𝑡). Usando ecuación ( 48 ) resulta en:
𝐺(𝑡) = [1 0] [(3𝑒(−𝑒−2𝑡−2𝑡− 2𝑒+ 𝑒−3𝑡−3𝑡) (−2𝑒) (6𝑒−2𝑡−2𝑡− 6𝑒+ 3𝑒−3𝑡−3𝑡))] [01]
Debido a que el sistema es un sistema de una sola variable, la matriz resulta solo un escalar, que es idéntico con 𝑔(𝑡).
Ejercicios “Matriz de la Respuesta al Impulso”
A continuación se deriva la matriz de transferencia𝐺(𝑠) a partir de la representación de estados de un sistema multivariable, con cual se representa la transformada de Laplace del vector de salida 𝑌(𝑠).
𝑌(𝑠) = 𝐺(𝑠) ⋅ 𝑈(𝑠) ( 49 )
, con 𝐺(𝑠) = [𝐺𝑖𝑗(𝑠)] e 𝑖 = 1,2, … , 𝑚 y 𝑗 = 1,2, … . , 𝑟. Esta relación solo es válida para valores iniciales ceros 𝑥(0) = 0. Sustituyendo ecuación ( 36 ) en ( 35 ) resulta en:
𝑌(𝑠) = 𝐶 (𝑠𝐼 − 𝐴)−1𝐵 𝑈(𝑠) + 𝐷 𝑈(𝑠)
= [𝐶 (𝑠𝐼 − 𝐴)−1𝐵 + 𝐷] 𝑈(𝑠) ( 50 )
Por ende resulta para la matriz de transferencia:
𝐺(𝑠) = 𝐶 (𝑠𝐼 − 𝐴)−1𝐵 + 𝐷 ( 51 )
𝐺(𝑠) = 𝐶 Φ(𝑠)𝐵 + 𝐷 ( 52 )
Comparando ( 52 ) con ( 48 ), se concluye:
𝐺(𝑠) = ℒ{𝐺(𝑡)} = ℒ{𝐶 Φ(𝑡) 𝐵 + 𝐷 𝛿(𝑡)}
𝑠𝑋(𝑠) = 𝐴 𝑋(𝑠) + 𝐵 𝑈(𝑠) 𝑠𝑋(𝑠) − 𝐴 𝑋(𝑠) − 𝐵 𝑈(𝑠) = 0
(𝑠𝐼 − 𝐴)𝑋(𝑠) − 𝐵 𝑈(𝑠) = 0
−𝐶 𝑋(𝑠) − 𝐷 𝑈(𝑠) = −𝑌(𝑠)
Ahora se pueden agrupar las dos ecuaciones en forma matricial:
[𝑠𝐼 − 𝐴 𝐵−𝐶 𝐷] [−𝑈(𝑠)] = [𝑋(𝑠) −𝑌(𝑠)]0
La primera matriz representa la matriz de Rosenbrock 𝑃(𝑠) = [𝑠𝐼 − 𝐴 𝐵
−𝐶 𝐷]. Para un sistema
univariable (𝑚 = 𝑟 = 1), la matriz resulta:
𝑃(𝑠) = [𝑠𝐼 − 𝐴 𝑏−𝑐𝑇 𝑑]
Se calcula el determinante de esta matriz cuadrada:
|𝑃(𝑠)| = 𝑐𝑇adj(𝑠𝐼 − 𝐴) 𝑏 + 𝑑|𝑠𝐼 − 𝐴|
Ahora, se puede expresar ecuación ( 52 ) como:
𝐺(𝑠) =𝑐𝑇adj(𝑠𝐼 − 𝐴) 𝑏 + 𝑑|𝑠𝐼 − 𝐴|
|𝑠𝐼 − 𝐴| ( 53 )
𝐺(𝑠) = |𝑃(𝑠)| |𝑠𝐼 − 𝐴|=
𝑁(𝑠)
Ejemplo 5-9:
Se busca la función de transferencia 𝐺(𝑠) del siguiente sistema lineal univariable:
𝑥̇(𝑡) = [ 0−12 7] 𝑥(𝑡) + [1 01] 𝑢(𝑡) 𝑦 = [−10 4] 𝑥 + 𝑢(𝑡)
Primero se calcula el siguiente determinante:
|𝑠𝐼 − 𝐴| = | 𝑠12 𝑠 − 7| = 𝑠(𝑠 − 7) + 12 = (𝑠 − 3)(𝑠 − 4)−1
Se determina la matriz de Rosenbrock:
𝑃(𝑠) = [12 𝑠 − 7 1𝑠 −1 0 10 −4 1]
y su respectiva determinante:
|𝑃(𝑠)| = 𝑠(𝑠 − 7) − 10 + 4𝑠 + 12 = (𝑠 − 1)(𝑠 − 2)
Usando ecuación ( 52 ) se calcula 𝐺(𝑠):
𝐺(𝑠) = |𝑃(𝑠)| |𝑠𝐼 − 𝐴|=
(𝑠 − 1)(𝑠 − 2) (𝑠 − 3)(𝑠 − 4)
Como ejercicio en la casa, comprueba 𝐺(𝑠) usando ecuación ( 52 ).
Algunos principios básicos de la teoría de matrices para
5.6
el cálculo de la matriz de transición
5.6.1
Teorema de Cayley-Hamilton
En la introducción de la representación de estado, se encontró que la matriz 𝐴 del sistema contiene toda la información completa sobre el comportamiento propio del sistema. En particular debe contener los polos del sistema entonces. En la matriz de transferencia según ecuación ( 52 ), solo la matriz de transición Φ(𝑠) aparece como dependiente de 𝑠. Según ecuación ( 39 ), esa matriz contiene como denominador común el determinante |𝑠𝐼 − 𝐴|, un polinomio del orden 𝑛, cuales raíces resultan los polos del sistema. En consecuencia, a la matriz real cuadrática 𝐴 con dimensión (𝑛 𝑥 𝑛) se pueden asignar exactamente 𝑛 valores propios reales o complejos, cuales resultan de la ecuación característica:
𝑃∗(𝑠) = |𝑠𝐼 − 𝐴| = 0 ( 55 )
𝑃∗(𝑠) es un polinomio del orden 𝑛 en función de 𝑠 y representa el polinomio característico de la
matriz 𝐴. Ecuación ( 55 ) entonces tiene la siguiente forma, con 𝑎𝑛= 1:
𝑃∗(𝑠) = 𝑎
0+ 𝑎1𝑠 + 𝑎2𝑠2+ ⋯ + 𝑠𝑛= ∑ 𝑎𝑖𝑠𝑖 𝑛
𝑖=0
( 56 )
De esa ecuación se pueden determinar los valores propios. Para un sistema univariable se puede calcular la función de transferencia 𝐺(𝑠), según ecuación ( 54 ). Si se quieren determinar los polos del sistema, se tiene que considerar, que cada polo de 𝐺(𝑠) tiene que ser un valor propio de 𝐴 según ecuación ( 55 ), pero no todos los valores propios de 𝐴 tienen que ser también polos de
clásico (por ejemplo el criterio de Hurwitz o Routh). En el caso de un sistema multivariable, se garantiza estabilidad asintótica, si los polos de cada función de transferencia particular o todos los valores propios de 𝐴 están ubicados en el semiplano izquierdo de 𝑠. Se puede comprobar fácil, que en una matriz diagonal o matriz triangular, los elementos diagonales representan los valores propios. Para las siguientes consideraciones se necesita usar el Teorema de Cayley-Hamilton:
Cada matriz cuadrática 𝐴 cumple su ecuación característica.
Si por ejemplo 𝑃∗(𝑠) es el polinomio característico de 𝐴 según ecuación ( 56 ), entonces resulta:
𝑃∗(𝐴) = 𝑎
0𝐼 + 𝑎1𝐴 + 𝑎2𝐴2+ ⋯ + 𝐴𝑛 = 0 ( 57 )
Cabe señalar, que se conserve el mismo nombre 𝑃∗ como en ecuación ( 56 ), pero que 𝑃∗(𝐴) ahora representa una matriz. Para demostrar el teorema, se usa la inversa de la matriz (𝑠𝐼 − 𝐴) en la siguiente forma:
(𝑠𝐼 − 𝐴)−1= 1
|𝑠𝐼 − 𝐴|adj(𝑠𝐼 − 𝐴) =
adj(𝑠𝐼 − 𝐴)
𝑃∗(𝑠) ( 58 )
, cuando vale para la matriz polinomial con dimensión (𝑛 𝑥 𝑛):
adj(𝑠𝐼 − 𝐴) = ∑ 𝐴𝑖𝑠𝑖 𝑛−1
𝑖=0
( 59 )
Ejemplo 5-10:
a) Se busca la adjunta adj(𝑠𝐼 − 𝐴) con la matriz del sistema 𝐴 = [ 0 1
−4 −4]:
adj(𝑠𝐼 − 𝐴) = [𝑠 + 4 1−4 𝑠] = [−4 0] + [4 1 1 00 1] 𝑠 = adj(−𝐴) + 𝐼𝑠 = 𝐴0+ 𝐴1𝑠 = ∑ 𝐴𝑖𝑠𝑖 1
𝑖=0
Entonces, 𝐴0 = adj(−𝐴) y 𝐴1= 𝐼.
b) Se busca la adjunta adj(𝑠𝐼 − 𝐴) con la matriz del sistema 𝐴 = [0 2 11 0 3
0 2 0]
:
adj(𝑠𝐼 − 𝐴) = [𝑠
2− 6 2𝑠 + 2 𝑠 + 6
𝑠 𝑠2 3𝑠 + 1
2 2𝑠 𝑠2− 2]
= [−6 20 0 61 2 0 −2] + [
0 2 1 1 0 3
0 2 0] 𝑠 + 𝐼𝑠 2
= 𝐴0+ 𝐴1𝑠 + 𝐴2𝑠2= ∑ 𝐴𝑖𝑠𝑖 2
𝑖=0
Entonces,. 𝐴0= [−6 20 0 61
2 0 −2]
, 𝐴1= [0 2 11 0 3
0 2 0] = 𝐴
y 𝐴2 = 𝐼.
Multiplicando ( 58 ) desde izquierda con 𝑃∗(𝑠)(𝑠𝐼 − 𝐴) resulta:
𝑃∗(𝑠)𝐼 = (𝑠𝐼 − 𝐴) adj(𝑠𝐼 − 𝐴)
Sustituyendo ( 56 ) y ( 59 ) en esa expresión resulta:
∑ 𝑎𝑖𝑠𝑖 𝑛
𝑖=0
𝐼 = (𝑠𝐼 − 𝐴) ∑ 𝐴𝑖𝑠𝑖 𝑛−1
Después de aplicar las sumas y comparar los coeficientes de las mismas potencias 𝑠 resulta:
𝑎0𝐼 = −𝐴 𝐴0 𝑎1𝐼 = −𝐴 𝐴1+ 𝐴0 𝑎2𝐼 = −𝐴 𝐴2+ 𝐴1
⋮
𝑎𝑛−1𝐼 = −𝐴 𝐴𝑛−1+ 𝐴𝑛−2 𝐼 = 𝐴𝑛−1
Ahora se multiplica la primera ecuación con 𝐼, la segunda con 𝐴, la tercera con 𝐴2, etcétera y y la última ecuación con 𝐴𝑛. Sumando todas las ecuaciones resultantes, se obtiene el polinomio característico de 𝐴:
𝑎0𝐼 + 𝑎1𝐴 + 𝑎2𝐴2+ ⋯ + 𝐴𝑛= 0
La comprobación de esta derivación de demostración para 𝑛 = 2 queda como ejercicio en la casa. También este teorema importante se discutirá un poco más usando un ejemplo.
Ejemplo 5-11:
Dado la matriz del sistema 𝐴 = [1 1
0 −2]. Con (𝑠𝐼 − 𝐴) = [𝑠 − 10 𝑠 + 2]−1 se obtiene la ecuación
característica:
𝑃∗(𝑠) = (𝑠 − 1)(𝑠 + 2) = 𝑠2+ 𝑠 − 2 = 0
Sustituyendo la matriz del sistema 𝐴 a la educación característica se obtiene:
𝑃∗(𝐴) = 𝐴2+ 𝐴 − 2𝐼 = 0
, que se compruebe mediante:
𝑃∗(𝐴) = [1 −1
Usando dos ejemplos, en lo siguiente se quiere mostrar cómo se calculan potencias de 𝐴 usando el teorema de Cayley-Hamilton:
Ejemplo 5-12:
a) Desde ecuación ( 60 ) resulta por multiplicación con 𝐴−1:
𝐴 + 𝐼 − 2𝐴−1= 0
, y con eso:
𝐴−1=1
2 (𝐴 + 𝐼) = [10 −0.5]0.5
b) Si por ejemplo se quiere calcular la suma 𝐴3+ 2𝐴2, se usa 𝐴2 de la ecuación ( 60 ):
𝐴2= 2𝐼 − 𝐴
𝐴3 resulta por multiplicación de esa expresión con 𝐴 y después de sustituir 𝐴2 sigue:
𝐴3= 2𝐴 − 𝐴2= 2𝐴 − 2𝐼 + 𝐴 = −2𝐼 + 3𝐴
Por ende se calcula la suma buscada:
5.6.2
Aplicación a funciones de matrices
Primero, se considera un polinomio general 𝐹(𝑠) de orden 𝑝:
𝐹(𝑠) = 𝑓0+ 𝑓1𝑠 + ⋯ + 𝑓𝑝𝑠𝑝 ( 61 )
Además, está dado el siguiente polinomio de orden 𝑛 con 𝑛 < 𝑝:
𝑃∗(𝑠) = 𝑎
0+ 𝑎1𝑠 + ⋯ + 𝑎𝑛𝑠𝑛 ( 62 )
Se puede dividir 𝐹(𝑠) con 𝑃∗(𝑠) y resulta en la siguiente representación para 𝐹(𝑠) entonces:
𝐹(𝑠) = 𝑄(𝑠)𝑃∗(𝑠) + 𝑅(𝑠) ( 63 )
Aquí, 𝑄(𝑠) es el resultado de la división y 𝑅(𝑠) un polinomio residual del orden máximo (𝑛 − 1). Sustituyendo una matriz cuadrática 𝐴 con dimensión (𝑛 𝑥 𝑛) a la ecuación ( 61 ), resulta en la siguiente función matricial:
𝐹(𝐴) = 𝑓0𝐼 + 𝑓1𝐴 + ⋯ + 𝑓𝑝𝐴𝑝 ( 64 )
Aquí, el polinomio característico de la matriz cuadrática 𝐴 es justamente 𝑃∗(𝑠). Ahora, esa función matricial ( 64 ) se puede representar análogo a ( 63 ):
𝐹(𝐴) = 𝑄(𝐴)𝑃∗(𝐴) + 𝑅(𝐴) ( 65 )
Sin embargo y de acuerdo al teorema de Cayley-Hamilton, dado que 𝑃∗(𝐴) = 0, se sigue:
𝐹(𝐴) = 𝑅(𝐴) = 𝛼0𝐼 + 𝛼1𝐴+. . +𝛼𝑛−1𝐴𝑛−1 ( 66 )
Cada (𝑛 𝑥 𝑛) función matricial 𝐹(𝐴) del orden 𝑝 ≥ 𝑛, según ecuación ( 64 ), se puede representar
por una función 𝑅(𝐴) del orden máximo (𝑛 − 1).
Un ejemplo de esto se ha calculado previamente (Ejemplo 5-11), eliminando todas las potencias 𝐴𝑖 con 𝑖 ≥ 𝑛 usando el polinomio característico.
Se puede mostrar, que ecuación ( 66 ) valga también para 𝑝 → ∞ , es decir si 𝐹(𝐴) representa una suma infinita, siempre y cuando existe el valor límite para 𝑝 → ∞. Por lo tanto, esta relación también se puede usar para calcular la matriz exponencial 𝐹(𝐴) = 𝑒𝐴𝑡 según ecuación ( 32 ), y así la matriz de transición Φ(𝑡) se puede representar en la forma:
Φ(𝑡) = 𝑒𝐴𝑡 = 𝑅(𝐴) = 𝛼
0(𝑡)𝐼 + 𝛼1(𝑡)𝐴+. . +𝛼𝑛−1(𝑡)𝐴𝑛−1 ( 67 )
Aquí los coeficientes 𝛼𝑗(𝑡) para 𝑗 = 0,1, … 𝑛 − 1 son funciones del tiempo, porque el tiempo también se manifiesta explícitamente en la serie de potencias. Para calcular esos coeficientes, se considere otra vez ecuación ( 65 ). Si se sustituyen para 𝑠 los valores propios 𝑠𝑖 de la matriz 𝐴, entonces por la relación 𝑃∗(𝑠𝑖) = 0 sigue:
𝐹(𝑠𝑖) = 𝑅(𝑠𝑖) ( 68 )
Los dos polinomios entonces son iguales para los valores propios. Por lo tanto vale con 𝐹(𝑠𝑖) =
𝑒𝑠𝑖𝑡 análoga a la ecuación ( 67 ) para 𝑖 = 1,2, … 𝑛:
𝑒𝑠𝑖𝑡 = 𝛼0(𝑡) + 𝛼1(𝑡)𝑠𝑖+ ⋯ + 𝛼𝑛−1(𝑡)𝑠𝑖𝑛−1 ( 69 )
Esto da como resultado exactamente 𝑛 ecuaciones para los 𝑛 valores propios 𝑠𝑖, para calcular los
𝑛 coeficientes desconocidos. Sin embargo, aquí se supone que todos 𝑛 valores propios 𝑠𝑖 son diferentes. Sin embargo, si hay valores propios repetidos, entonces para cada valor propio 𝑠𝑘 de la multiplicidad 𝑚𝑘 resultan 𝑚𝑘 ecuaciones de la forma, para 𝜇 = 0,1, … , 𝑚𝑘−1:
𝑑𝜇
𝑑𝑠𝜇𝑒𝑠𝑡|𝑠=𝑠
𝑘
=𝑑𝑠𝑑𝜇𝜇[𝛼0(𝑡) + 𝛼1(𝑡)𝑠 + ⋯ + 𝛼𝑛−1(𝑡)𝑠𝑛−1]| 𝑠=𝑠𝑘
Ejemplo 5-13:
Se quiere calcular la matriz de transición del Ejemplo 5-5 con la siguiente matriz del sistema:
𝐴 = [ 0−1 −5]6
La ecuación característica resulta:
𝑃∗(𝑠) = |𝑠𝐼 − 𝐴| = |𝑠 −6
1 𝑠 + 5| = 𝑠2+ 5𝑠 + 6 = 0
, con los valores propios 𝑠1= −2 y 𝑠2= −3. Ahora se hace el siguiente acercamiento según ecuación ( 67 ):
Φ(𝑡) = 𝑒𝐴𝑡 = 𝛼
0(𝑡)𝐼 + 𝛼1(𝑡)𝐴 = [𝛼00(𝑡) 𝛼0 0(𝑡)] + [
0 6𝛼1(𝑡) −𝛼1(𝑡) −5𝛼1(𝑡)]
Después se determinan los coeficientes 𝛼0(𝑡) y 𝛼1(𝑡) usando ecuación ( 69 ):
𝑒−2𝑡= 𝛼
0(𝑡) − 2𝛼1(𝑡) 𝑒−3𝑡= 𝛼
0(𝑡) − 3𝛼1(𝑡)
La solución de esas dos ecuaciones resultan los dos coeficientes 𝛼0(𝑡) y 𝛼1(𝑡):
𝛼0(𝑡) = 3𝑒−2𝑡− 2𝑒−3𝑡 𝛼1(𝑡) = 𝑒−2𝑡− 𝑒−3𝑡
Por lo tanto, finalmente se obtiene la matriz de transición:
Φ(𝑡) = [ 𝛼−𝛼0 6𝛼1
1 𝛼0− 5𝛼1] = [(3𝑒
5.6.3
La Regla de Sylvester
Por la ecuación ( 68 ), la tarea de determinar un "polinomio de sustitución" 𝑅(𝐴) para una función matricial 𝐹(𝐴), se puede reducir al siguiente problema:
Se determina un polinomio 𝑅(𝑠) del orden 𝑛 − 1, cual está igual a los valores de la función 𝐹(𝑠) predeterminados en los 𝑛“puntos de apoyo” 𝑠𝑖 (nodos):
𝐹(𝑠𝑖) = 𝑅(𝑠𝑖)
Si 𝑠𝑖 son los valores propios de la matriz 𝐴, entonces 𝑅(𝐴) es el polinomio buscado y se aplica lo siguiente:
𝐹(𝐴) = 𝑅(𝐴)
Entonces, esto representa un problema de interpolación que tiene una solución definitiva (única). Para la solución de este problema, se puede usar la fórmula de Interpolación de Lagrange:
𝑅(𝑠) = ∑ [
𝐹(𝑠𝑗) ∏𝑠𝑠𝑖− 𝑠 𝑖− 𝑠𝑗 𝑛
𝑖=1
𝑖≠𝑗 ] 𝑛
𝑗=1
( 71 )
Aplicando ( 71 ) para interpolar un polinomio de orden 𝑛 = 3 por ejemplo, resulta en:
𝑅(𝑠) = 𝐹(𝑠1)(𝑠(𝑠2− 𝑠)(𝑠3− 𝑠)
2− 𝑠1)(𝑠3− 𝑠1) + 𝐹(𝑠2)
(𝑠1− 𝑠)(𝑠3− 𝑠)
(𝑠1− 𝑠2)(𝑠3− 𝑠2) + 𝐹(𝑠3)
(𝑠1− 𝑠)(𝑠2− 𝑠) (𝑠1− 𝑠3)(𝑠2− 𝑠3)
Si en ( 71 ) se sustituye la variable 𝑠 por la matriz 𝐴 y también 𝑠𝑖 por 𝑠𝑖𝐼 en el nominador, entonces se obtiene la Regla de Sylvester de manera directa:
𝑅(𝐴) = ∑ [
𝐹(𝑠𝑗) ∏𝑠𝑠𝑖𝐼 − 𝐴 𝑖− 𝑠𝑗 𝑛
𝑖=1
𝑖≠𝑗 ] 𝑛
𝑗=1
( 72 )
Φ(𝑡) = ∑ [
𝑒𝑠𝑗𝑡∏𝑠𝑖𝐼 − 𝐴
𝑠𝑖− 𝑠𝑗 𝑛
𝑖=1
𝑖≠𝑗 ] 𝑛
𝑗=1
( 73 )
Aquí, las magnitudes 𝑠𝑖 son los valores propios de 𝐴, que a su vez deben ser todos diferentes. Esta relación corresponde al sistema de ecuaciones según la ecuación ( 69 ) e incluye la ecuación ( 67 ). Su evaluación se hace en 3 pasos:
1. Determinación de los valores propios de 𝐴.
2. Determinación de los productos en los paréntesis de ( 73 ). 3. Computación de Φ(𝑡) y sumando esos productos.
Ejemplo 5-14:
Usando la matriz del sistema del Ejemplo 5-5:
𝐴 = [ 0−1 −5]6
, con los valores propios 𝑠1− 2 y 𝑠2= −3, se obtienen los siguientes productos:
𝑠1𝐼 − 𝐴 𝑠1− 𝑠2 =
1
−2 − (−3) [−21 −2 + 5] = [−6 −2 −61 3 ] 𝑠2𝐼 − 𝐴
𝑠2− 𝑠1 = 1
−3 − (−2) [−31 −3 + 5] = [−6 −1 −2]3 6
Con esos resulta la matriz de transición usando la regla de Sylvester:
Φ(𝑡) = 𝑒−2𝑡[ 3 6
−1 −2] + 𝑒−3𝑡[−2 −61 3 ] = [(3𝑒(−𝑒−2𝑡−2𝑡− 2𝑒+ 𝑒−3𝑡−3𝑡) (−2𝑒) (6𝑒−2𝑡−2𝑡− 6𝑒+ 3𝑒−3𝑡−3𝑡))]
Formas Normales para Sistemas univariables
5.7
En lo siguiente se quiere mostrar, como se puede derivar la representación del espacio de estado a través de la función de transferencia de un sistema univariable. De la elección de las variables de estado depende la estructura de la matriz 𝐴 y los vectores 𝑏 y 𝑐 en las ecuaciones ( 7 ) y ( 8 ). Dado la función de transferencia:
𝐺(𝑠) =𝑈(𝑠) =𝑌(𝑠) 𝑏𝑎0+ 𝑏1𝑠 + ⋯ + 𝑏𝑛−1𝑠𝑛−1+ 𝑏𝑛𝑠𝑛 0+ 𝑎1𝑠 + ⋯ + 𝑎𝑛−1𝑠𝑛−1+ 𝑠𝑛 =
𝑁(𝑠)
𝐷(𝑠) ( 74 )
, cual siempre se puede normalizar a que 𝑎𝑛= 1. Nota, que el orden del nominador 𝑁(𝑠) es igual del denominador 𝐷(𝑠). Se supone, que el nominador no es cero, resulta que hay mínimo un coeficiente 𝑏𝑖 ≠ 0 y por lo tanto 𝑁(𝑠) ≠ 0. Como es de conocimiento breve, esa función de transferencia 𝐺(𝑠) se forma por aplicar la transformación de Laplace a la siguiente ED:
𝑑𝑛𝑦
𝑑𝑡𝑛 + 𝑎𝑛−1∙𝑑 𝑛−1𝑦
𝑑𝑡𝑛−1+ ⋯ + 𝑎1𝑦̇ + 𝑎0𝑦 = 𝑏𝑛∙𝑑 𝑛𝑢
𝑑𝑡𝑛 + 𝑏𝑛−1∙𝑑 𝑛−1𝑢
𝑑𝑡𝑛−1 + ⋯ + 𝑏1𝑢̇ + 𝑏0𝑢 ( 75 )
La tarea ahora consiste en convertir esta ED de orden 𝑛 a un sistema de 𝑛 ecuaciones diferenciales de orden 1. Para eso y en lo siguiente, se consideran tres posibilidades con diferentes opciones de las variables de estado.
5.7.1
Forma Canónica Controlable (FCC)
a) Caso Especial
Primero se supone, que no aparecen derivadas en la variable de entrada, es decir la ecuación
( 75 ) se convierte a:
𝑑𝑛𝑦
𝑑𝑡𝑛+ 𝑎𝑛−1∙𝑑 𝑛−1𝑦
Si se despeja la derivada más alta de 𝑦:
𝑑𝑛𝑦
𝑑𝑡𝑛 = 𝑏0𝑢 − [𝑎𝑛−1∙𝑑 𝑛−1𝑦
𝑑𝑡𝑛−1+ ⋯ + 𝑎1𝑦̇ + 𝑎0𝑦] ( 77 )
resulta sale una representación directa en forma de un diagrama de bloques, que según la siguiente figura consiste de 𝑛 elementos integrales en serie con sus respectivas retroalimentaciones:
Figura 8: Diagrama de bloques para FCC para el caso especial
Como 𝑏0 representa un elemento lineal, se puede desplazar a la salida de 𝑦. Eso es conveniente para el caso general. Si las salidas de los integradores se definen como variables de estado, resultan las ecuaciones de estado directo:
𝑥̇1= 𝑥2 𝑥̇2= 𝑥3
⋮
𝑥̇𝑛 = 𝑢 − 𝑎0𝑥1− 𝑎1𝑥2− ⋯ − 𝑎𝑛−1𝑥𝑛
( 78 )
𝑦 = 𝑏0𝑥1 ( 79 )
𝐴 =
[ 0 1 2 3 1
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
n
a
a
a
a
a
K
K
K
M
M
M
M O
M
K
K
]𝑩 = 𝒃 =
[
0
0
0
0
1
M
]( 80 )
𝐶 = 𝑐𝑇 = [
0
0
0
0
0
b
L
] 𝑫 = 𝒅 = 𝟎La estructura de 𝐴 se llama Forma Normal de Frobenius o Forma Normal Controlable. Se caracteriza por ello, que en el último renglón contiene los coeficientes negativos de su polinomio característico y normalizados a 𝑎𝑛= 1.
b) Caso General
Ahora se usa ecuación ( 75 ), donde también aparecen derivadas de la entrada. El planteamiento del diagrama de bloques de la manera anterior ahora no es posible usarlo de manera directa. Sin embargo, si se elige la primera variable de estado 𝑥1 así, que para la magnitud de la salida resulta:
𝑦 = 𝑏0𝑥1+ 𝑏1𝑥̇1+ ⋯ + 𝑏𝑛𝑑 𝑛𝑥
1
𝑑𝑡𝑛 ( 81 )
, entonces se obtiene también la misma estructura de la matriz 𝐴, como ( 80 ). Para mostrar eso, se aplica la transformada de Laplace a ecuación ( 81 ):
𝑌(𝑠) = 𝑋1(𝑠)[𝑏0+ 𝑏1𝑠 + ⋯ + 𝑏𝑛𝑠𝑛] ( 82 )
Esa relación se sustituye en ecuación ( 74 ) y simplificando, resulta:
𝐺(𝑠) =𝑋1(𝑠)[𝑏0+ 𝑏𝑈(𝑠)1𝑠 + ⋯ + 𝑏𝑛𝑠𝑛]=𝑏𝑎0+ 𝑏1𝑠 + ⋯ + 𝑏𝑛−1𝑠𝑛−1+ 𝑏𝑛𝑠𝑛 0+ 𝑎1𝑠 + ⋯ + 𝑎𝑛−1𝑠𝑛−1+ 𝑠𝑛
=𝑋1(𝑠) 𝑈(𝑠) =
1
𝑎0+ 𝑎1𝑠 + ⋯ + 𝑎𝑛−1𝑠𝑛−1+ 𝑠𝑛
las ecuaciones ( 78 ) representan también las ecuaciones de estado para el caso general. La matriz del sistema 𝐴 y la matriz de entrada 𝐵 de ( 80 ) siguen igual. Si a la Figura 8 se agrega la ecuación
( 81 ), se obtiene el diagrama de bloques para el caso general:
Figura 9: Diagrama de bloques para FCC para el caso general
Para la ecuación de salida sale usando ( 78 ) y ( 81 ):
𝑦 = 𝑏0𝑥1+ 𝑏1𝑥2+ ⋯ + 𝑏𝑛−1 𝑥𝑛+ 𝑏𝑛𝑥̇𝑛
= 𝑏0𝑥1+ 𝑏1𝑥2+ ⋯ + 𝑏𝑛−1 𝑥𝑛+ 𝑏𝑛[𝑢 − 𝑎0𝑥1− 𝑎1𝑥2− ⋯ − 𝑎𝑛−1𝑥𝑛] = (𝑏0− 𝑏𝑛𝑎0)𝑥1+ (𝑏1− 𝑏𝑛𝑎1)𝑥2+ ⋯ + (𝑏𝑛−1− 𝑏𝑛𝑎𝑛−1)𝑥𝑛+ 𝑏𝑛𝑢
( 83 )
Al sistema ( 80 ) solo se cambian las matrices 𝐶 y 𝐷. En resumen, el resultado del caso general es lo siguiente. Para un sistema univariable del orden 𝑛 con la función de transferencia:
𝐺(𝑠) =𝑈(𝑠) =𝑌(𝑠) 𝑏𝑎0+ 𝑏1𝑠 + ⋯ + 𝑏𝑛−1𝑠𝑛−1+ 𝑏𝑛𝑠𝑛 0+ 𝑎1𝑠 + ⋯ + 𝑎𝑛−1𝑠𝑛−1+ 𝑠𝑛
, resultan las matrices de la representación de estado:
𝐴 =
[ 0 1 2 3 1
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
n
a
a
a
a
a
K
K
K
M
M
M
M O
M
K
K
]𝑩 = 𝒃 =
[
0
0
0
0
1
M
]
( 85 )
𝐶 = 𝑐𝑇 = [
0 n 0 1 n 1 n1 n n1
b
b a
b
b a
L
b
b a
] 𝑫 = 𝒅 = 𝒃𝒏Por lo tanto, la forma canónica controlable es muy fácil de identificar desde la función de transferencia. En particular para 𝑏𝑛= 0, contiene, además de ceros y unos, sólo los coeficientes de 𝐺(𝑠). La matriz entrada-salida 𝐷 solo existe para 𝑏𝑛≠ 0, esto es cuando el orden del nominador 𝑁(𝑠) es igual al orden del denominador 𝐷(𝑠). La salida del sistema puede brincar, si
5.7.2
Forma Canónica Observable (FCO)
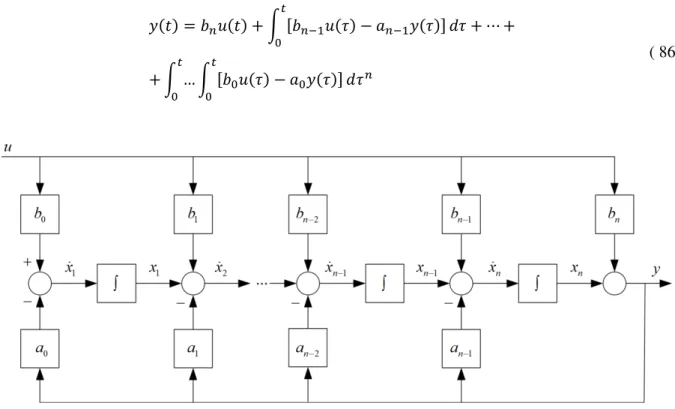
Se obtiene otra definición de las variables de estado para el caso general del sistema univariable ( 75 ), si en lugar del acercamiento ( 81 ) se integra la ED n-veces, para que ya no aparezcan derivadas en la entrada 𝑢:
𝑦(𝑡) = 𝑏𝑛𝑢(𝑡) + ∫ [𝑏𝑛−1𝑢(𝜏) − 𝑎𝑛−1𝑦(𝜏)] 𝑡
0 𝑑𝜏 + ⋯ +
+ ∫ …𝑡
0 ∫ [𝑏0𝑢(𝜏) − 𝑎0𝑦(𝜏)] 𝑡
0 𝑑𝜏
𝑛
( 86 )
Figura 10: Diagrama de bloques para FCO
Si las salidas de los integradores se definen como variables d estado, resulta:
𝑥̇1= −𝑎0𝑦 + 𝑏0𝑢 𝑥̇2= 𝑥1− 𝑎1𝑦 + 𝑏1𝑢 𝑥̇3= 𝑥2− 𝑎2𝑦 + 𝑏2𝑢
⋮
𝑥̇𝑛 = 𝑥𝑛−1− 𝑎𝑛−1𝑦 + 𝑏𝑛−1𝑢
( 87 )
La ecuación de salida es:
Sustituyendo la ecuación de salida a las ecuaciones de estado:
𝑥̇1= −𝑎0𝑥𝑛+ (𝑏0− 𝑏𝑛𝑎0)𝑢 𝑥̇2= −𝑎1𝑥𝑛+ 𝑥1+ (𝑏1− 𝑏𝑛𝑎1)𝑢 𝑥̇3= −𝑎2𝑥𝑛+ 𝑥2+ (𝑏2− 𝑏𝑛𝑎2)𝑢
⋮
𝑥̇𝑛 = −𝑎𝑛−1𝑥𝑛+ 𝑥𝑛−1+ (𝑏𝑛−1− 𝑏𝑛𝑎𝑛−1)𝑢
( 89 )
Inmediatamente de esa forma se pueden determinar las matrices de la forma canónica observable
𝐴 = [ 0 3 2 1
0
0
0
0
1
0
0
1
0
0
0
0
1
0
0
0
0
1
n n n
a
a
a
a
L
M M M
M
M M
M
O
M M M
L
]𝑩 = 𝒃 =
[ 0 0 3 3 2 2 1 1 n
n n n n n n n n n
b b a
b b a
b b a
b b a
M M ]
( 90 )
𝐶 = 𝑐𝑇 = [
0
0
L
0 1
] 𝑫 = 𝒅 = 𝒃𝒏
Ejemplo 5-15:
Se busca la forma canónica controlable y observable de la siguiente ED:
𝑦̈ + 5𝑦̇ + 6𝑦 = 𝑢
Primero, se determinan los coeficientes:
𝑎0= 6 𝑏0= 1 𝑎1= 5 𝑏1= 0 𝑎2= 1 𝑏2= 0
Para la forma FCC:
𝐴 = [ 0−6 −5]1 𝑏 = [01] 𝑐𝑇 = [1 0]
, se determina la función de transferencia:
Φ(𝑠) =(𝑠 + 2)(𝑠 + 3) [1 𝑠 + 5 16 𝑠]
𝐺(𝑠) = 𝑐𝑇
⋅ Φ(𝑠) ⋅ 𝑏 = [1 0] ⋅ Φ(𝑠) ⋅ [01] =(𝑠 + 2)(𝑠 + 3)1
Para la forma FCO:
𝐴 = [0 −61 −5] 𝑏 = [10] 𝑐𝑇 = [0 1]
, se determina la función de transferencia:
Φ(𝑠) =(𝑠 + 2)(𝑠 + 3) [1 𝑠 + 5 −61 𝑠 ]
𝐺(𝑠) = 𝑐𝑇
Ejemplo 5-16:
Se busca la forma FCC y el diagrama de bloques del sistema dinámico:
𝑦̈ + 𝑎1𝑦̇ + 𝑎0𝑦 = 𝑏0𝑢 + 𝑏1𝑢̇
Usando los coeficientes de la ED, se determina la forma FCC:
𝐴 = [ 0−𝑎 1
0 −𝑎1] 𝑏 = [01] 𝑐
𝑇 = [𝑏
0 𝑏1] 𝑑 = 0
y el diagrama de bloque:
Figura 11: Diagrama de bloques para el Ejemplo 5-16
De la forma FCC y del diagrama se hallan las ecuaciones del sistema:
𝑥̇1= 𝑥2
𝑥̇2= −𝑎0𝑥1− 𝑎1𝑥2+ 𝑢 𝑦 = 𝑏0𝑥1+ 𝑏1𝑥2
Usando el diagrama y las reglas del bucle cerrado, se determina la función de transferencia:
𝐺(𝑠) =𝑌(𝑠)𝑈(𝑠) = 𝑏0 1
𝑠2+ 𝑏11𝑠 1 − (−𝑎11𝑠 + 𝑎0𝑠12)
=𝑎 𝑏0+ 𝑏1𝑠 0+ 𝑎1𝑠 + 𝑠2
Transformando inversa usando Laplace, se regresa a la ED original.
5.7.3
Forma Diagonal y Forma Canónica de Jordan
Para la tercera posibilidad de la representación de sistemas lineales univariables, se definen las variables de estado usando la descomposición en fracciones parciales de la función de transferencia 𝐺(𝑠). Para eso se supone, que los polos de 𝐺(𝑠) están conocidos y que el grado 𝑚 del nominador 𝑁(𝑠) es menor, que el grado 𝑛 del denominador 𝐷(𝑠). Esto siempre se puede lograr dividiendo un elemento proporcional con la amplificación 𝑏𝑛 de la ecuación ( 74 ), es decir por una división polinomial, de modo que en lo siguiente sólo se contempla la función de transferencia en la forma:
𝐺(𝑠) =𝑏0𝑎+ 𝑏1𝑠 + ⋯ + 𝑏𝑚𝑠𝑚 0+ 𝑎1𝑠 + ⋯ + 𝑠𝑛 =
𝑁(𝑠)
𝐷(𝑠) 𝑚 < 𝑛 ( 91 )
En lo siguiente se distinguen tres casos.
a) Polos reales distintos
Si todos los polos 𝑠𝑖 de 𝐺(𝑠) son distintos y reales, entonces se puede descomponer 𝐺(𝑠) en 𝑛 fracciones parciales:
𝐺(𝑠) = ∑𝑠 − 𝑠𝑐𝑖 𝑖 𝑛
𝑖=1
( 92 )
La salida 𝑌(𝑠) resulta entonces:
𝑌(𝑠) = ∑𝑠 − 𝑠𝑐𝑖 𝑖 𝑛
𝑖=1
𝑈(𝑠) ( 93 )
Figura 12: Diagrama de bloques para la forma diagonal con polos reales distintos
Como variables de estado 𝑥𝑖 se eligen las magnitudes de la Figura 12:
𝑋𝑖(𝑠) =𝑠 − 𝑠1
𝑖𝑈(𝑠) ( 94 )
, de las cuales resultan las ecuaciones de estado por transformación inversa al dominio del tiempo:
𝑥̇𝑖 = 𝑠𝑖𝑥 𝑖+ 𝑢 ( 95 )
para 𝑖 = 1,2, … , 𝑛. Para la variable de salida vale:
𝑦 = 𝑐1𝑥1+ 𝑐2𝑥2+ ⋯ + 𝑐𝑛𝑥𝑛 ( 96 )
Resumiendo los componentes 𝑥𝑖 al vector de estado 𝑥, se obtiene la representación de estado:
𝑥̇ = 𝐴 𝑥 + 𝑏 𝑢 𝑦 = 𝑐𝑇 𝑥
𝐴 =
[ 1
2
0
0
0
0
0
0
ns
s
s
L
M
M
O
L
]𝑩 = 𝒃 =
[
1
1
1
M
]
( 97 )
𝒄𝑻= [
1 2 n
c
c
L
c
]b) Polos reales repetidos
Cuando hay polos reales y repetidos en 𝐺(𝑠), entonces el denominador 𝐷(𝑠) se puede representar con 𝑝 diferentes polos:
𝐷(𝑠) = (𝑠 − 𝑠1)𝑟1(𝑠 − 𝑠2)𝑟2… (𝑠 − 𝑠𝑝)𝑟𝑝 ( 98 )
, con 𝑟𝑖 (𝑖 = 1,2, … , 𝑝) la multiplicidad del polo 𝑠𝑖. Debido a que el orden del sistema es 𝑛, tiene que valer:
∑ 𝑟𝑖 𝑝
𝑖=1
= 𝑛 ( 99 )
, por supuesto con 𝑝 ≤ 𝑛. Para ese caso la descomposición en fracciones parciales de 𝐺(𝑠) es:
𝐺(𝑠) = ∑ [𝑠 − 𝑠𝑐𝑖,1 𝑖+
𝑐𝑖,2
(𝑠 − 𝑠𝑖)2+ ⋯ + 𝑐𝑖,𝑟𝑖
(𝑠 − 𝑠𝑖)𝑟𝑖] 𝑝
𝑖=1
( 100 )
De esta representación se pueden sacar las siguientes conclusiones:
- La suma de ( 100 ) consiste de 𝑛 términos / fracciones como en el caso a)
- Si se desarrolla un diagrama de bloques como en a) y se usa cada termino como subsistema, resulta la suma de los órdenes:
∑(1 + 2 + 3 + ⋯ + 𝑟𝑖) 𝑝
𝑖=1
= ∑𝑟𝑖(1 + 𝑟𝑖) 2 𝑝
𝑖=1
> 𝑛 ( 101 )
, debido a que:
∑𝑟𝑖(1 + 𝑟2 𝑖) 𝑝
𝑖=1
=12 ∑ 𝑟𝑖 𝑝
𝑖=1
+12 ∑ 𝑟𝑖2 𝑝
𝑖=1
en total es mayor 𝑛. Entonces se representaría el sistema lineal de orden 𝑛 por un sistema de orden mayor 𝑛, cual tendría más que 𝑛 variables de estado. Sin embargo, tal representación sería redundante, debido a que una descripción completa de un sistema de orden 𝑛 solo requiere 𝑛 variables de estado independientes. Entonces, se busca una realización de 𝐺(𝑠) de acuerdo con la ecuación ( 100 ) con el orden mínimo 𝑛, cual se denomina realización mínima de 𝐺(𝑠). Considerando un término de la suma en la ecuación ( 100 ), por ejemplo para 𝑖 = 1:
𝑐1,1 𝑠 − 𝑠1+
𝑐1,2
(𝑠 − 𝑠1)2+ ⋯ +
𝑐1,𝑟1
(𝑠 − 𝑠1)𝑟1
, es fácil ver, que esta expresión puede ser realizada por 𝑟1 elementos de primer orden, es decir con el orden global 𝑟1, mediante un arreglo según el diagrama de bloques mostrado en la Figura 13.
Figura 13: Diagrama de bloques para la forma canónica de Jordan con polos reales repetidos
Para los 𝑟1 variables de estado de este sistema parcial resultan las ecuaciones de estado:
𝑥̇𝑖 = 𝑠1𝑥𝑖+ 𝑥𝑖+1 𝑥̇𝑟1 = 𝑠1𝑥𝑟1+ 𝑢
( 102 )
Ejemplo 5-17:
Dado el denominador de un sistema de orden 𝑛 = 5:
𝐷(𝑠) = (𝑠 − 𝑠1)2(𝑠 − 𝑠2)3
La descomposición en fracciones parciales para 𝐺(𝑠) da:
𝐺(𝑠) =𝑠 − 𝑠𝑐1,1 1+
𝑐1,2 (𝑠 − 𝑠1)2+
𝑐2,1 𝑠 − 𝑠2+
𝑐2,2 (𝑠 − 𝑠2)2+
𝑐2,3 (𝑠 − 𝑠2)3
y resulta el siguiente diagrama de bloques:
Figura 14: Diagrama de bloques para el Ejemplo 5-17
Utilizando las variables de estado definidas en este diagrama, se obtiene:
𝑥̇1= 𝑠1𝑥1+ 𝑥2 𝑥̇2= 𝑠1𝑥2+ 𝑢 𝑥̇3= 𝑠2𝑥3+ 𝑥4 𝑥̇4= 𝑠2𝑥4+ 𝑥5 𝑥̇5= 𝑠2𝑥5+ 𝑢
y
o como representación en matrices:
𝑥̇ = 𝐴 𝑥 + 𝑏 𝑢 𝑦 = 𝑐𝑇 𝑥
, con los siguientes matrices y vectores:
𝐴 ≡ 𝐽 =
[ 1 1 2 2 2
1 0 0 0
0 0 0 0
0 0 1 0
0 0 0 1
0 0 0 0
s s s s s ] 𝒃 = [
0
1
0
0
1
]( 103 )
𝒄𝑻= [
1,2 1,1 2,3 2,2 2,1
c c c c c ]
En el caso de polos reales repetidos, como se muestra en este ejemplo, los polos aparecen en la diagonal de la matriz del sistema 𝐴 según su multiplicidad 𝑟𝑖 y adicionalmente en la diagonal secundaria superior generalmente aparecen elementos con el valor 1. Se agregan 1 en la diagonal
secundaria, donde la variable de estado no es una “inicial” en el diagrama de bloques. Donde la
variable es “inicial”, aparecen elementos 1 en el vector 𝑏. Tal matriz se denomina Matriz de
Jordan. La matriz 𝐴 ya no tiene forma diagonal, sino forma canónica de Jordan.
c) Polos complejos conjugados
Por supuesto la descomposición según ecuación ( 92 ) y ( 100 ) también es válida para polos complejos conjugados. Sin embargo, en este caso saldrían incógnitas complejas 𝑐𝑖,1, que llevarían a una representación de estado compleja, con variables de estado y matrices 𝐴, 𝐵, 𝐶 complejas. Típicamente en este caso no se separan los dos polos complejos conjugados y se recibe un polinomio de segundo grado. Una simple posibilidad para esto se tratará en lo siguiente. Para dos polos complejos conjugados 𝑠1,2 = 𝜎 ± 𝑗𝜔 se obtiene un sistema parcial 𝐺12(𝑠), que consiste de dos fracciones parciales:
𝑐1,2= 𝛿 ± 𝑗𝜀
Si se combinan ambas fracciones parciales, resulta una función de transferencia de segundo orden para el sistema parcial:
𝐺12(𝑠) =𝑐1(𝑠 − 𝜎 + 𝑗𝜔) + 𝑐(𝑠 − 𝜎)2+ 𝜔2(𝑠 − 𝜎 − 𝑗𝜔)2 =𝑠(𝑐1+ 𝑐2𝑠) − 𝜎(𝑐2− 2𝑠𝜎 + 𝜎1+ 𝑐22) + 𝑗𝜔(𝑐+ 𝜔2 1− 𝑐2)=𝑁𝐷12(𝑠) 12(𝑠)
Usando 𝑐1+ 𝑐2= 2𝛿 y 𝑐1− 𝑐2= 2𝑗𝜀, resulta:
𝐺12(𝑠) =(𝜎−2(𝜎𝛿 + 𝜔𝜀) + 2𝛿𝑠2+ 𝜔2) − 2𝜎𝑠 + 𝑠2 =𝑎 𝑏0+ 𝑏1𝑠 0+ 𝑎1𝑠 + 𝑠2
, con los coeficientes reales:
𝑏0= −2(𝜎𝛿 + 𝜔𝜀) 𝑎0= 𝜎2+ 𝜔2
𝑏1= 2𝛿 𝑎1= −2𝜎
Este sistema parcial 𝐺12(𝑠) se puede representar en forma canónica controlable, por ejemplo:
𝐴 = [ 0−𝑎 1
0 −𝑎1] 𝒃 = [𝟎𝟏]
( 105 )
𝑐𝑇 = [𝑏 0 𝑏1]
Ejemplo 5-18:
Dado para un sistema de orden 𝑛 = 6 los polos y las incógnitas:
Polos 𝑠1 𝜎 + 𝑗𝜔 𝜎 − 𝑗𝜔 𝑠2 doble 𝑠3
Incógnitas 𝑐1 𝛿 + 𝑗𝜀 𝛿 − 𝑗𝜀 𝑐2,1 𝑐2,2 𝑐3
A partir de esto, se puede determinar directamente un diagrama de bloques para la forma canónica de Jordan y a través de la definición de las variables de estado en esta forma se obtienen las matrices y vectores correspondientes:
𝐴 = [ 1 0 1 2 2 3
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
s
a
a
s
s
s
] 𝒃 = [1
0
1
0
1
1
]𝒄𝑻= [
1 0 1 2,2 2,1 3
c b b c c c ]
Como resumen se puede observar, que la representación de un sistema univariable en el caso de polos simples de 𝐺(𝑠) (valores propios distintos de 𝐴) resulta en la forma diagonal y en el caso de polos múltiples de 𝐺(𝑠) (valores propios repetidos de 𝐴) resulta en la forma canónica de Jordan. En el caso de polos complejos, se obtiene una representación de estado compleja, o juntando pares de polos complejos conjugados, una matriz del sistema real 𝐴, con una estructura tipo diagonal. Las 3 formas normales presentadas aquí se distinguen, que la matriz del sistema 𝐴 solo tiene pocos elementos diferentes de cero y que esos están directamente conectados con los coeficientes de la función de transferencia. Esas formas simples también se denominan formas canonícas.