Ficha catalográfica elaborada pelo DePT da Biblioteca Comunitária da UFSCar

(1)

CENTRO DE CIÊNCIAS EXATAS E DE TECNOLOGIA

PROGRAMA DE PÓS GRADUAÇO EM MATEMÁTICA

Karen Regina Panzarin

Reobrimentos Ramiados entre Superfíies e

Dessins d'Enfants

São Carlos - SP

(2)

CENTRO DE CIÊNCIAS EXATAS E DE TECNOLOGIA

PROGRAMA DE PÓS GRADUAÇO EM MATEMÁTICA

Reobrimentos Ramiados entre Superfíies e

Dessins d'Enfants

Karen Regina Panzarin

Orientador: Prof. Dr. Daniel Vendrúsolo

Dissertação apresentada ao Programa de

Pós-Graduação em Matemátia da UFSCar

omo parte dos requisitos para a obtenção

do título de Mestre emMatemátia.

São Carlos - SP

(3)

Ficha catalográfica elaborada pelo DePT da

Biblioteca Comunitária da UFSCar

P199rr

Panzarin, Karen Regina.

Recobrimentos ramificados entre superfícies e dessins

d’enfants / Karen Regina Panzarin. -- São Carlos : UFSCar,

2012.

54 f.

Dissertação (Mestrado) -- Universidade Federal de São

Carlos, 2012.

1. Topologia. 2. Recobrimento ramificado. 3. Superfícies

(Matemática). I. Título.

(4)

(5)

Em primeirolugar à Deus, pois sem Ele,nada disso teria sido possível.

À minha família que sempre me ajudou e me apoiou em meus momentos de

desespero, por areditarem emmim e nuna me deixarem desistir de meus sonhos;

em espeial, minha mãe e avó por todas as orações, e ao Leandro por se dispor a

meajudar om as guras,portodo arinho,paiênia edediação.

Ao professorDaniel Vendrúsolo porter aeitado meorientar.

À professoraAlieKimieMiwa Libardiporter mepreparadoeporme ajudar

sempreque neessitei.

Aos meus pouos, mas sineros, amigos queestiveram omigonesta batalha.

Por m, à todos que já passaram por minha vida e que de alguma maneira

(6)

Considere duas superfíies fehadas, onexas,

X

e

Y

, inteiros

n

≥

0

e

d

≥

2

, e para

i

= 1

, . . . , n

uma partição

(

dij

)

j

=1

,...,m

i

de

d

. A 5-upla

(

X, Y, n, d,

(

dij

))

é o

dado de ramiação de um andidato a reobrimento ramiado.

Em muitos trabalhos disute-se quando um dado de ramiação pode ser

re-alizado por um reobrimento ramiado

f

:

X

→

Y

de grau

d

, om

n

pontos de ramiaçãoe graus loais na pré-imagemdos pontosde ramiaçãodados por

dij

.

Hurwitz estabeleeu uma equivalênia algébria para este problema

geomé-trio, esta equivalênia tem sido utilizada para tratar do tema. Neste trabalho

apresentamos a denição de dessin d'enfant, um grafo na superfíie

X

, relaionado

om um reobrimentoramiado eutilizamosesta ferramenta paraobter ondições

que estabeleem quando um dado de ramiação é exepional (não pode ser

re-alizado). Abordamos também uma versão alternativa para a denição de dessin

(7)

Given losed onneted surfaes

X

and

Y

, integers

n

≥

0

and

d

≥

2

, and for

i

= 1

, . . . , n

partitions

(

dij

)

j

=1

,...,m

i

of

d

. The 5-tuple

(

X, Y, n, d,

(

dij

))

is alled the

branh datumof a andidate branhed overing.

Many worksdisusswhenagivenbranhdatumanberealizedbyabranhed

overing

f

:

X

→

Y

of degree

d

, with

n

branhing points and loal degree in the pre-images of branhing points given by

dij

.

Hurwitz has established an algebrai equivalene to this geometri problem,

this equivalene has been used to treat the subjet. In this dissertation we dene

dessin d'enfant, a graph on the surfae

X

, related to a branhed overing and use

this tool to obtain onditions for a given branh datum be exeptional (i.e. an

not be realized). We also dene an alternative and more expliit version for the

(8)

Agradeimentos iii

Resumo iv

Abstrat v

Introdução vii

1 Pré-requisitos 1

1.1 Reobrimentos Ramiados . . . 1

1.2 Problema de Existênia de Hurwitz . . . 4

1.3 Dessins d'Enfants . . . 5

2 De Dessins d'Enfants para Permutações e Vie-Versa 8

3 Exeções via Dessin d'Enfant 18

(9)

Considere duas superfíies fehadas, onexas,

X

e

Y

,inteiros

n

≥

0

e

d

≥

2

, e para

i

= 1

, . . . , n

umapartição

(

dij

)

j

=1

,...,m

i

de

d

. A5-upla

(

X, Y, n, d,

(

dij

))

éodado

de ramiação de um andidato a reobrimento ramiado. Para a existênia de

talreobrimento,existem algumasondiçõesneessárias em termosde

χ

(

X

)

, χ

(

Y

)

, orientabilidade, grau total e grau loaldos pontosde ramiação.

O Problema de Existênia de Hurwitz é um problema lássio que questiona

quando essas ondições também são suientes. Existem várias maneiras

equiva-lentes de seformular esse problema bemomo várias ténias desenvolvidas, om o

passar do tempo, para tentar soluioná-lo. O únio aso que ainda permanee em

aberto é quando

Y

éa esfera e éneste aso tambémqueapareem as exeções.

Hurwitz reformulou o problema em termos de permutações e esta é a

fer-ramenta lássia para a abordagem do mesmo. Uma outra ténia reentemente

abordadapor[7℄,éanoção de dessind'enfant. Elafoi introduzidadentrodoestudo

de apliações algébrias entre superfíies Riemannianas e remonta à Grothendiek.

Essa é uma ténia quenão haviasido empregadadiretamenteantes pra resolver o

problema em si.

Neste trabalho apresentamos a denição de dessin d'enfant e nos utilizamos

desta ferramenta para obter ondições que estabeleem quando um dado de

rami-ação é exepional (não pode ser realizado). Abordamos também uma versão

alternativapara a denição de dessin d'enfant,mais ompleta.

O desenvolvimento dos apítulosdeste trabahoé feitadoseguintemodo:

(10)

O apítulo 2 é omposto de resultados previamente onheidos e que são

en-ontradosem [2℄e[5℄. Em[4℄oautortambémtrabalhaomresultadossemelhantes.

Empartiular, é neste apítuloque aparee o Teoremade Hurwitz.

Porm, noapítulo3apresentamosresultadosbaseados em[7℄e[3℄que

forne-emondiçõesparadizerquandoumdadoompatívelérealizávelporalgum

reobri-mentoramiado. Outrostrabalhos quetratamderealizabilidadede reobrimentos

(11)

Pré-requisitos

Neste apítulo apresentamos as denições básias, notações e exemplos das

ferramentasque utilizaremos durante todoo trabalho.

1.1 Reobrimentos Ramiados

Denição 1.1.1. Um reobrimento é uma apliação

f

:

X

→

Y

, onde

X

e

Y

são espaçostopológios,

f

ésobrejetorae, paraada

p

∈

Y

,existeumavizinhançaaberta

de

p

,

Up

⊂

Y

, tal que

f

−

1

₍

_Up

₎

pode ser esrita omo união disjunta de onjuntos

abertos

Vα

⊂

X

e a restrição de

f

à

Vα

é um homeomorsmo de

Vα

em

Up

.

(12)

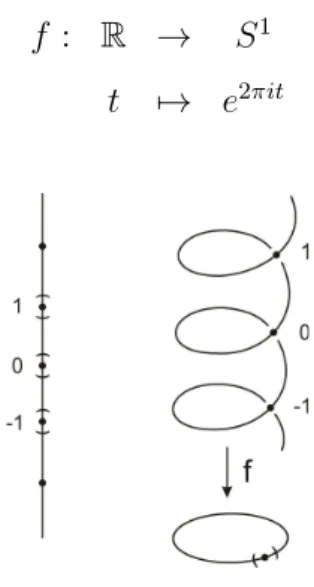
f

:

R

_→

_S

1

t

7→

e

2 πit

Figura1.1: Reobrimentotendoomoespaçodereobrimentoaretareal,

R

,eomo

espaçobase aesfera,

S

1

; observe queada

p

∈

S

1

possui innitaspré-imagens.

Neste trabalho, sempre que nos referirmos a um reobrimento

f

:

X

→

Y

, faremos uso da Denição 1.1.1 oloando

X

e

Y

omo sendo superfíies fehadas

(isto é,ompatas e sem bordo) e onexas.

Exemplo 1.1.3.

f

:

T

→

K

Figura 1.2: Reobrimento tendo omo espaço de reobrimento o toro,

T

, e omo

espaçobaseagarrafadeKlein,

K

;observequeada

p

∈

K

possuiduaspré-imagens.

Denição 1.1.4. Um reobrimento ramiado é uma apliação

f

:

X

→

Y

, onde

(13)

Ux

om

x

∈

Ux

de modo que a restrição de

f

a

Ux

se omporta loalmente omo a

apliação

C

∋

z

7→

z

k

_∈

_C

para algum

k

∈

Z

,

k

≥

1

.

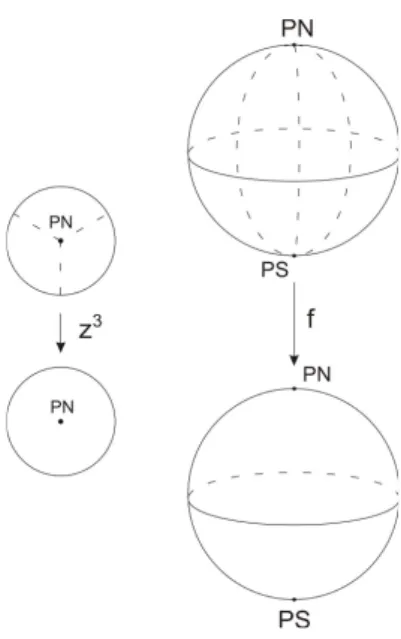
Exemplo 1.1.5. Seja

f

:

S

2

_→

_S

2

e onsidere a esfera

S

2

entrada na origem

0 ∈

R

3

. Geometriamente, podemos desrever

f

omo a apliação que assoia ada

urva quedá uma volta num íruloda

S

2

de altura no ponto

(0

,

0 , t

)

, t

∈

(

−

1 ,

1)

, a uma urva que dá três voltas no mesmo írulo da

S

2

.

Figura 1.3: Reobrimento ramiado tendo omo espaço de reobrimento e espaço

base aesfera,

S

2

.

Observemos quea apliação

f

:

S

2

_→

_S

2

doexemplo1.1.5 é um reobrimento

ramiado pois os pólos,

P N

e

P S

, não possuem três pré-imagens omo todos os

outros pontos da esfera. Se onsiderarmos

f

:

S

2

_{\ {}

_{P N, P S}

_{} →}

_S

2

_{\ {}

_{P N, P S}

_}

teremosum reobrimentonão-ramiado.

Denição 1.1.6. Considere

k

∈

Z

omo na Denição 1.1.4. Se

x

∈

X

é tal que

k >

1

, dizemos que

f

(

x

)

é um ponto de ramiação e o inteiro

k

é o grau loal do

reobrimento.

Notemos que ada

x

∈

f

−

1

₍

_xj

₎

, onde

xj

é ponto de ramiação, é isolado.

(14)

quedenotaremos por

n

, de taispontos.

Denição1.1.7. Consideremosoonjunto

R

=

{

xi

∈

Y

;

xi

é pontode ramiação

}

.

f

′

₌

_f

_|

X

\

f

−

1 (

R

)

:

X

\

f

−

1

₍

_R

₎

_→

_Y

_\

_R

é umreobrimentoeo númerode pré-imagens

é onstante e nito, denotado por

d

e hamado grau do reobrimento.

Com essa denição, vemos que o Exemplo 1.1.3 é um reobrimento de grau 2

e oExemplo 1.1.5 é um reobrimento de grau 3.

Denição 1.1.8. Se o

i

-ésimo ponto de ramiação em

Y

possui

mi

pré-imagens,

os graus loais

(

dij

)

j

=1

,...,m

i

desse ponto nos dão uma partição de

d

, om

dij

≥

1

e

m

i

X

j

=1

dij

=

d

.

Denição1.1.9. Suponhamosdadosassuperfíiesfehadasonexas

X

e

Y

, inteiros

n

≥

0

e

d

≥

2

e, para

i

= 1

, . . . , n

, uma partição

(

dij

)

j

=1

,...,m

i

de

d

. A

5

-upla

(

X, Y, n, d,

(

dij

))

será hamadadado de ramiação ou dado de reobrimento de um

andidato a reobrimento ramiado.

Para tal dado, sempre assoiaremoso inteiro

n

˜

=

m

1

+

. . .

+

mn

.

Exemplo 1.1.10.

(

T,

RP

2

_,

₅

_,

₈

_,

₍₄

_,

_{4); (3}

_,

₁

_,

_{4); (5}

_,

_{3); (2}

_,

₂

_,

₂

_,

_{2); (2}

_,

₃

_,

₃₎₎

é um dado

de ramiação de um andidato à reobrimento ramiado do toro,

T

, no plano

projetivo,

RP

2

, que possui

n

= 5

pontos de ramiação, grau

d

= 8

e

n

˜

= 2 + 3 +

2 + 4 + 3

.

1.2 Problema de Existênia de Hurwitz

A seguir apresentamos uma denição que nos diz quando um dado de

rami-ação éompatível. A maioriados itens desta denição deorrem dofato de que se

tirarmosospontosderamiaçãoesuasrespetivaspré-imagensdeumreobrimento

ramiado, oresultado ainda será um reobrimento,porémnão-ramiado.

Denição 1.2.1. Um dado de ramiação é ompatível se as seguintes ondições

(15)

(1)

χ

(

X

)

−

n

˜

=

d.

(

χ

(

Y

)

−

n

)

;

(2)

n.d

−

n

˜

é par;

(3) Se

Y

é orientável,então

X

é também orientável;

(4) Se

Y

é não-orientável e

d

é ímpar, então

X

é também não-orientável;

(5) Se

Y

é não-orientável mas

X

é orientável, então ada partição

(

dij

)

j

=1

,...,m

i

de

d

rena a partição

(

d/

2 , d/

2)

. (Note que

d

é par pela ondição (4).)

Denição 1.2.2. Um dado

(

X, Y, n, d,

(

dij

))

é realizávelse existir um reobrimento ramiado tendo-o omo dado de ramiação.

Denição 1.2.3. Um dado de ramiaçãoé exepional se elefor ompatível, mas

não for realizávelpor nenhum reobrimento ramiado.

Surge assim, uma questão: quando um dado de ramiação ompatível é

rea-lizávelpor algumreobrimentoramiado?

Essa pergunta é onheida omo o Problema de Existênia de Hurwitz.

Exis-tem várias maneiras equivalentes de se formular esse problema bem omo várias

ténias desenvolvidas, om o passar do tempo, para tentar soluioná-lo. A

ferra-mentalássiafoio próprioHurwitzquem introduziu,reformulandoalgebriamente

um problema geométrio emtermos de permutações.

No apítulo 3 apresentaremos alguns resultados que respondem

geometria-menteà essa questão para ertos asos espeíos.

1.3 Dessins d'Enfants

Denição 1.3.1. Um dessin d'enfant em uma superfíie fehada onexa

X

é um

grafo

D

⊂

X

onde:

(16)

(2) Para

i

= 1

, . . . , n

−

2

ada aresta em

Ei

une um vértie de

Vi

a um de

Vi

+1

;

(3) Para

i

= 2

, . . . , n

−

2

, ada vértie de

Vi

possui grau par e ao redor dele se

enontram, alternadamente, arestas de

Ei

−

1

e arestas de

Ei

;

(4)

X

\

D

onsiste de disos abertos.

Denição 1.3.2. O omprimento dos disos em

X

\

D

é o número de arestas que

delimitam a fronteira dos disos (om multipliidade).

Exemplo 1.3.3. .

Figura1.4: Dessind'enfant notoro. (Este dessin d'enfant será, mais adiante,

asso-iado aodado de ramiação

(

T, S

2

_,

₃

_,

₈

_,

₍₂

_,

₂

_,

₂

_,

₂₎

_,

₍₃

_,

₅₎

_,

₍₅

_,

₃₎₎

).

Denição 1.3.4. Um dessin d'enfant ompleto em uma superfíie fehada onexa

(17)

(1) Para algum

n

≥

3

, oonjunto de vérties de

D

se deompõeomo

V

1

⊔

. . .

⊔

Vn

e o onjunto de arestas de

D

se deompõe omo

E

1

⊔

. . .

⊔

En

−

1

;

(2) Para

i

= 1

, . . . , n

−

1

ada aresta em

Ei

une um vértie de

Vi

a um de

Vi

+1

;

(3) Para

i

= 2

, . . . , n

−

1

, ada vértie de

Vi

possui grau par e ao redor dele se

enontram, alternadamente, arestas de

Ei

−

1

e arestas de

Ei

;

(4)

X

\

D

onsiste de disos abertos.

Exemplo 1.3.5. .

Figura 1.5: Dessin d'enfant ompleto no toro. (Este dessin d'enfant

ompleto também será, mais adiante, assoiado ao dado de ramiação

(

T, S

2

_,

₃

_,

₈

_,

₍₂

_,

₂

_,

₂

_,

₂₎

_,

₍₃

_,

₅₎

_,

₍₅

_,

₃₎₎

(18)

De Dessins d'Enfants para

Permutações e Vie-Versa

Neste apítulo introduzimos alguns resultados básios que são demonstrados

em[2℄e [5℄. Como onentramosnosso trabalho emdessins d'enfants,optamos por

não demonstrá-los.

Seja

(

X, Y, n, d,

(

dij

))

um dado de ramiação de um reobrimento ramiado

f

, onde

Y

= ˜

Y

∪

B

éuma superfíieonexaeloalmenteonexaporaminhos (logo

onexaporaminhos),

Y

˜

éumasuperfíiesembordoeasomponentesonexasde

B

, obordode

Y

,sãohomeomorfasa

S

1

oua

R

;

X

éumasuperfíienãoneessariamente

onexa;

R

=

{

xi

∈

Y

;

xi

é pontode ramiação

}

,

Y

ˆ

=

Y

\

R

,

i

= 1

, . . . , n

e

j

=

1 , . . . , mi

. Considere

Vx

i

uma vizinhança de

xi

tal que

f

restrita às omponentes

onexas de

f

−

1

₍

_Vx

i

)

é dotipo

z

7→

z

d

ij

;

Vx

ˆ

i

=

Vx

i

\

R

.

Seja

z

ˆ

∈

Y

ˆ

. Como

Y

ˆ

é onexo por aminhos, existe um aminho

vi

queune

z

ˆ

a

xi

ˆ

, onde

xi

ˆ

∈

Vx

ˆ

i

. Seja

αx

i

um laço em

Vx

ˆ

i

om pontobase

xi

ˆ

e onsidere

{

v

∗

i

}

a

lasse de homotopia do aminho

v

∗

i

=

vi.αx

i

.v

−

1 i

. Considere também

{

w

∗

q

}

a lasse

de homotopia do aminho

w

∗

q

=

wq.

{

C

q

}

.w

q

−

1

, onde

wq

é um aminho em

Y

ˆ

e é tal

que

wq

(0) = ˆ

z

,

wq

(1) = ˆ

xq

(

xq

ˆ

∈

C

q

_∈

_B

,

C

q

omponenteonexa de

B

homeomorfa

à

S

1

(19)

Teorema 2.0.6 (Hurwitz). 1

Um dado de ramiação

(

X, Y, n, d,

(

dij

))

é realizável se, e somente se,é possível deniro homomorsmo

Ψ :

π

1

( ˆ

Y ,

z

ˆ

)

→

Sd

{

v

∗

i

}

7→

σx

i

{

w

∗

q

}

7→

λq

onde o onjunto dos omprimentos dos ilos dados pela deomposição únia das

permutações

σx

i

e

λq

derevem a ramiação sobre

xi

e

C

q

, respetivamente.

Mais ainda,

X

é onexo se, e somente se, a ação que orresponde a

Ψ

é transitiva.

Observação 2.0.7. Dado um dessin d'enfant

D

, om notação omo na denição

1.3.1, orrespondendo à realização de um dado de ramiação

(

X, S

2

_{, n, d,}

₍

_dij

₎₎

,

podemos onstruir permutações orrespondendo à mesma realização,omo segue:

•

Enumereasarestasde

Ei

omo

e

(1)

i

, . . . , e

(

d

)

i

, omeçandodeummodoarbitrário

para

E

1

e de modoque para

i

≥

2

, ao redor de ada vértie de

Vi

, ada aresta

e

(

_i

k

)

é seguida pelaaresta

e

(

k

)

i

−

1

om o mesmo número

k

;

•

Para

i

≤

n

−

2

e

k

∈ {

1 , . . . , d

}

seleione o vértie de

Vi

no qual

e

(

k

)

i

está

ligadoe dena

τi

(

k

)

omo sendo

h

tal que opróximo

e

(

∗

)

i

ao redor do vértieé

e

(

i

h

)

;

•

Para

k

∈ {

1 , . . . , d

}

seleione o vértie de

Vn

−

1

no qual

e

(

k

)

n

−

2

está ligado e

dena

τn

−

1

(

k

)

omo sendo

h

talqueo próximo

e

(

∗

)

n

−

2

aoredordo vértie é

e

(

h

)

n

−

2

.

Lembremos que

X

está orientada e observemos que os seguintes fatos sobre

a aresta

e

(

h

)

i

são neessários para denir

τi

(

k

)

: para

i

= 1

, esta aresta vem logo

depois de

e

(

k

)

i

, enquanto que para

i

= 2

, . . . , n

−

2

, existea aresta

e

(

k

)

i

−

1

situadaentre

elas. Observemos também que a aresta

e

(

h

)

n

−

2

quando usada na denição de

τn

−

1

(

k

)

novamente vem logo depois da

e

(

k

)

n

−

2

.

1

(20)

Paradesreveraorrespondêniaoposta, dados

τ

1

, . . . , τn

−

1

∈

Sd

, onstruímos

um grafo

D

(

τ

1

, . . . , τn

−

1

)

om vérties

V

1

⊔

. . .

⊔

Vn

−

1

, onde

Vi

é o onjunto dos

ilos de

τi

, e para

i

= 1

, . . . , n

−

2

e

k

= 1

, . . . , d

uma aresta

e

(

k

)

i

une os ilos de

τi

e

τi

+1

o qual ontém

k

. Observe que

D

(

τ

1

, . . . , τn

−

1

)

é onexo se, e somente se,

< τ

1

, . . . , τn

−

1

>

é transitivo. Deste modo, usaremos as permutações para onstruir

laços que garantem a onexidade do grafo. Estes laços são onstruídos da seguinte

maneira:

Começamos om algum vértie de

V

1

e seguimos o aminho

e

(

k

)

1

, . . . , e

(

k

)

n

−

2

.

Tendo assim hegado a um vértie de

Vn

−

1

, nós seguimos o aminho:

e

(

τ

−

1 n

−

1 (

k

))

n

−

2

, e

(

τ

−

1 n

−

2 τ

−

1 n

−

1 (

k

))

n

−

3

, . . . , e

(

τ

−

1

3 ...τ

−

1 n

−

1 (

k

))

2

, e

(

τ

−

1

2 τ

−

1

3 ...τ

−

1 n

−

1 (

k

))

1

o qual nos leva a um vértie de

V

1

. De lá, nós proedemos do mesmo modo

ome-çando de

e

(

τ

−

1

1 τ

2 −

1 τ

3 −

1 ...τ

n

−

1

1 (

k

))

1

até enontrarmos a aresta

e

(

k

)

1

novamente.

Deste modo,temos que, dados

τ

1

, . . . , τn

−

1

∈

Sd

orrespondendoà uma

realiza-çãodeumdadoderamiação

(

X, S

2

_{, n, d,}

₍

_dij

₎₎

, oespaçoobtidode

D

(

τ

1

, . . . , τn

−

1

)

anexandodisosaosilosdistintosdesritosanteriormenteé

X

,e

D

(

τ

1

, . . . , τn

−

1

)

⊂

X

é um dessind'enfant orrespondente àmesma realização do dadode ramiação.

Observemos que oloando

n

no lugarde

n

−

1

noproedimentoaima, ons-truímos o grafo

D

(

τ

1

, . . . , τn

)

⊂

X

o qual é o dessin d'enfant ompleto orrespon-dente à mesmarealização do dado de ramiação.

Exemplo 2.0.8. Construção do reobrimento ramiado, do dessin d'enfant e do

dessin d'enfant ompletodadas as permutações:

τ

1

= (12)(34)(56)(78)

τ

2

= (135)(27468)

τ

3

= (16327)(485)

.

Para omeçar, temos que:

V

1

=

{

(12)

,

(34)

,

(56)

,

(78)

}

=

{

v

11

, v

12

, v

13

, v

14

}

(21)

V

3

=

{

(16327)(485)

}

=

{

v

31

, v

32

}

Apenas olhando para esses onjuntos, podemos dizer que

d

= 8

,

n

= 3

,

(

d

1 j

)

j

=1

,...,

4

= (2

,

2 ,

2)

,

(

d

2 j

)

j

=1

,

2

= (3

,

5)

e

(

d

3 j

)

j

=1

,

2

= (5

,

3)

.

Vamos agora onstruir as arestas

e

(

k

)

i

. Devemos observar que na onstrução

do dessind'enfant ompleto apareeum onjunto de arestas a mais se ompararmos

om a onstrução do dessin d'enfant lássio.

Faremos primeiramente o grafo

D

(

τ

1

, τ

2

)

e em seguida o grafo

D

(

τ

1

, τ

2

, τ

3

)

.

Oonjuntodearestasdoprimeirografoé

E

1

=

{

e

(1)

1

, e

(2)

1

, e

(3)

1

, e

(4)

1

, e

(5)

1

, e

(6)

1

, e

(7)

1

, e

(8)

1

}

,

onde:

e

(1)

₁

une os ilos

(12)

∈

τ

1

e

(135)

∈

τ

2

;

e

(2)

₁

une os ilos

(12)

∈

τ

1

e

(27468)

∈

τ

2

;

e

(3)

₁

une os ilos

(34)

∈

τ

1

e

(135)

∈

τ

2

;

e

(4)

₁

une os ilos

(34)

∈

τ

1

e

(27468)

∈

τ

2

;

e

(5)

₁

une os ilos

(56)

∈

τ

1

e

(135)

∈

τ

2

;

e

(6)

₁

une os ilos

(56)

∈

τ

1

e

(27468)

∈

τ

2

;

e

(7)

₁

une os ilos

(78)

∈

τ

1

e

(27468)

∈

τ

2

;

e

(8)

₁

une os ilos

(78)

∈

τ

1

e

(27468)

∈

τ

2

.

Os laços do grafo

D

(

τ

1

, τ

2

)

é onstruído omo segue:

Começamosom o vértie

v

11

∈

V

1

e seguimos o aminho

e

(1)

1

o qual nos leva

aovértie

v

21

∈

V

2

. Dessevértie, nósseguimos oaminho

e

(

τ

−

1

2 (1))

1

=

e

(5)

1

oqual nos

leva aovértie

v

13

∈

V

1

. Devemos agora seguir o aminho

e

(

τ

−

1

1 τ

2 −

1 (1))

1

=

e

(6)

1

que nos

levaao vértie

v

22

∈

V

2

e seguir por

e

(

τ

−

1

2 (6))

1

=

e

(4)

1

hegandoem

v

12

∈

V

1

. Seguimos

agora por

e

(

τ

−

1

1 τ

2 −

1 (6))

1

=

e

(3)

1

que nos leva a

v

21

∈

V

2

; passamos novamente por

e

(

τ

2 −

1 (3))

1

=

e

(1)

1

hegando em

v

11

∈

V

1

e seguimos por

e

(

τ

−

1

1 τ

2 −

1 (3))

1

=

e

(2)

1

que nos leva

a

v

22

∈

V

2

epor

e

(

τ

−

1

2 (2))

1

=

e

(8)

1

hegando em

v

14

∈

V

1

. Daqui seguimos peloaminho

e

(

τ

1 −

1 τ

2 −

1 (2))

1

=

e

(7)

1

que hega em

v

22

∈

V

2

e, por último, seguimos

e

(

τ

−

1

2 (7))

1

=

e

(2)

1

que

nalmente ompleta o laço hegando em

v

11

∈

V

1

, já que o próximo aminho seria

e

(

τ

1 −

1 τ

−

1

2 (7))

1

=

e

(22)

Temos,portanto, olaço

L

1

:

v

11

−

v

21

−

v

13

−

v

22

−

v

12

−

v

21

−

v

11

−

v

22

−

v

14

−

v

22

−

v

11

.

Proedendodomesmo modoomofeitoaimaparaosvérties

v

12

, v

13

, v

14

∈

V

1

obtemos, respetivamente, os laços:

L

2

:

v

12

−

v

21

−

v

11

−

v

22

−

v

14

−

v

22

−

v

11

−

v

21

−

v

13

−

v

22

−

v

12

,

L

3

:

v

13

−

v

21

−

v

12

−

v

22

−

v

14

−

v

22

−

v

13

,

L

4

:

v

14

−

v

22

−

v

11

−

v

21

−

v

13

−

v

22

−

v

12

−

v

21

−

v

11

−

v

22

−

v

14

.

Como

L

1

, L

2

e

L

4

orrespondem aomesmo laço, onsideramosapenas um

de-les, digamos

L

1

.

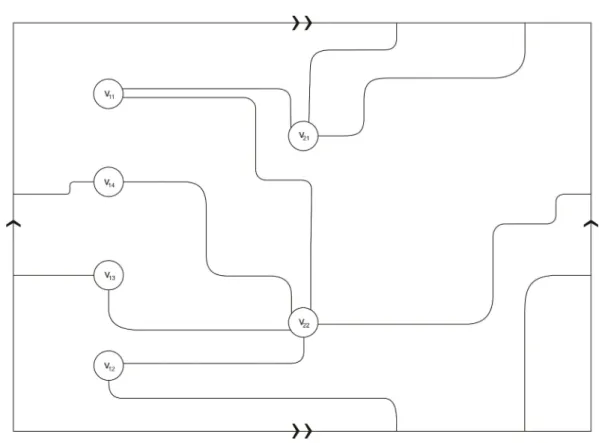
Figura2.1: Laços

L

1

e

L

3

quetornam ografo onexo vistoomo polígonos.

Como existem arestas em omum a ambos os laços, podemos identiar as

arestas

v

22 e

(7)

₁

←→

v

14 e

(8)

₁

(23)

Figura 2.2: Polígono orrespondente aos laços

L

1

e

L

3

depois da primeira

identi-ação das arestas.

Identiando as arestas

v

22 e

(4)

₁

←→

v

12 e

(3)

₁

←→

v

21

obtemos o ilindro:

Figura2.3: Polígonoorrespondente aos laços

L

1

e

L

3

depoisdasegunda

identia-ção das arestas.

Por m, identiamos as arestas

v

22 e

(2)

₁

←→

v

11 e

(1)

₁

←→

v

21 e

(5)

₁

←→

v

13 e

(6)

₁

←→

v

22

e

obtemos o toro.

Deste modo,obtemosqueoespaçodereobrimentoé otoro. Fazendooálulo

de ompatibilidade, obtemosque

χ

(

Y

) = 2

e, portanto, o espaço base é a esfera

S

2

.

(24)

11

12

13

14

21

22

11

13

14

21

22

12

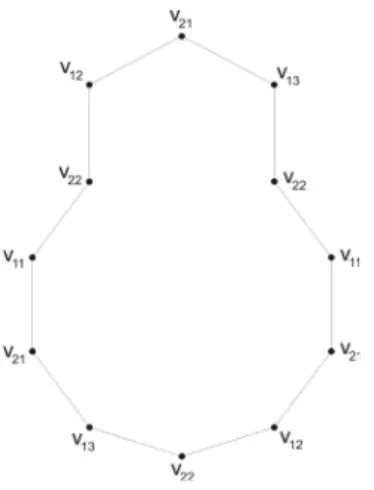
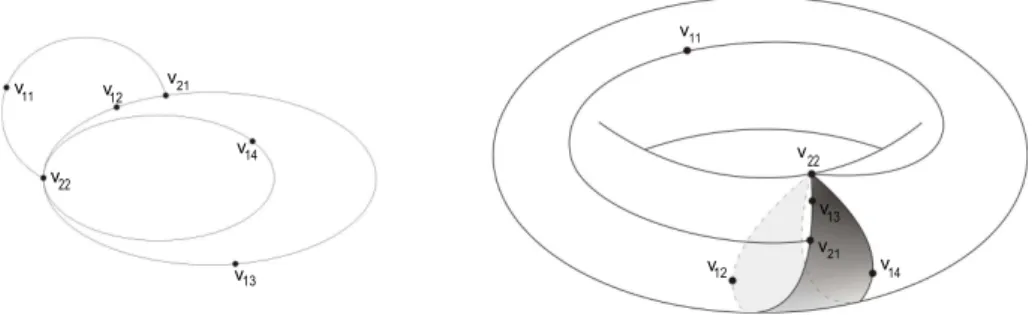
Figura2.4: No desenho da esquerda temos uma outra representação dos dois laços

L

1

e

L

3

; no desenho dadireita, quando oloadosno toro.

.

(25)

(26)

E

1

=

{

e

(1)

1

, e

(2)

1

, e

(3)

1

, e

(4)

1

, e

(5)

1

, e

(6)

1

, e

(7)

1

, e

(8)

1

}

e

E

2

=

{

e

(1)

2

, e

(2)

2

, e

(3)

2

, e

(4)

2

, e

(5)

2

, e

(6)

2

, e

(7)

2

, e

(8)

2

}

,

onde:

e

(1)

₂

une os ilos

(135)

∈

τ

2

e

(16327)

∈

τ

3

;

e

(2)

2

une os ilos

(27468)

∈

τ

2

e

(16327)

∈

τ

3

;

e

(3)

₂

une os ilos

(135)

∈

τ

2

e

(16327)

∈

τ

3

;

e

(4)

₂

une os ilos

(27468)

∈

τ

2

e

(485)

∈

τ

3

;

e

(5)

₂

une os ilos

(135)

∈

τ

2

e

(485)

∈

τ

3

;

e

(6)

₂

une os ilos

(27468)

∈

τ

2

e

(16327)

∈

τ

3

;

e

(7)

₂

une os ilos

(27468)

∈

τ

2

e

(16327)

∈

τ

3

;

e

(8)

2

une os ilos

(27468)

∈

τ

2

e

(485)

∈

τ

3

.

e o onjunto

E

1

é o mesmo utilizado na onstrução anterior.

Construindo os laços do grafo

D

(

τ

1

, τ

2

, τ

3

)

de modo análogo ao feito anterior-mente, obteremos os laços:

l

1

=

v

11

−

v

21

−

v

31

−

v

22

−

v

11

,

l

2

=

v

12

−

v

21

−

v

31

−

v

22

−

v

12

,

l

3

=

v

13

−

v

21

−

v

32

−

v

22

−

v

13

,

l

4

=

v

14

−

v

22

−

v

31

−

v

22

−

v

14

.

(27)

Conluímos assim,que o dado de ramiação possui a forma:

(28)

Exeções via Dessin d'Enfant

Nesteapítuloapresentamosresultadosbaseadosem[3℄e[7℄queforneem

on-diçõespara dizer quando um dado ompatívelé realizável por algum reobrimento

ramiado.

Proposição 3.0.9. Um dado de ramiação

(

X, S

2

_{, n, d,}

₍

_dij

₎₎

é realizável se, e

somentese,existeumdessind'enfant

D

⊂

X

omoonjuntodevértiesdeomposto

omo

V

1

, . . . , Vn

−

1

tal que:

(i) Para

i

= 1

e

i

=

n

−

1

, os vérties em

Vi

possuem grau

(

dij

)

j

=1

,...,m

i

;

(ii) Para

i

= 2

, . . . , n

−

2

,

n >

3

, os vérties em

Vi

possuem grau

(2

dij

)

j

=1

,...,m

i

;

(iii) Os disos em

X

\

D

possuem omprimento

(2(

n

−

2)

dnj

)

j

=1

,...,m

n

.

Dem.:

Para a primeira impliação, suponhamos que exista um reobrimento

rami-ado

f

:

X

→

S

2

om pontos de ramiação

x

1

, . . . , xn

que realiza o dado

(

X, S

2

_{, n, d,}

₍

_dij

₎₎

, e vamos onstruir um dessin d'enfant

D

⊂

X

que satisfaça (i),

(ii)e (iii).

Para

i

= 1

, . . . , n

−

2

esolha um aro simples

αi

que une

xi

a

xi

+1

. Suponha

(29)

Considere

α

=

n

−

2

[

i

=1

αi

.

Figura3.1: Construção daurva

α

.

Dena

D

=

f

−

1

₍

_α

₎

eoloque

Vi

=

f

−

1

₍

_xi

₎

e

Ei

=

f

−

1

₍

_αi

₎

.

Observemos quepelomodoque

D

foionstruído, asondições(1), (2), (3)da

deniçãode dessind'enfanteositens(i)e(ii)daproposiçãoestãosatisfeitos. Deste

modo, faltaapenas provarmos osdois fatos sobre asomponentes de

X

\

D

.

S

2

_\

_α

éumdisoabertoe,aorestringirmos

f

aqualqueromponentede

X

\

D

,

teremosum reobrimentosobreessedisoomumúniopontode ramiação,o

xn

.

Tal reobrimento é sempre modelado no reobrimento

z

7→

z

d

nj

do diso unitário

abertonelemesmo. Assim,asomponentesde

X

\

D

sãodisosabertoseaondição

(4)dadenição de dessin d'enfant está satisfeita.

Para ser mais preiso, existe um desses disospara ada elementode

f

−

1

₍

_xn

₎

e o

j

-ésimo possui o omprimentodesejado:

(2(

n

−

2)

dnj

)

j

=1

,...,m

(30)

Figura 3.2:

j

-ésimo diso de omprimento

(2(

n

−

2)

dnj

)

j

=1

,...,m

n

.

Paraareíproa, suponhamosdados

S

2

omosuperfíiebasee

D

⊂

X

odessin

d'enfant om o onjunto de vérties deomposto omo

V

1

, . . . , Vn

−

1

satisfazendo as

ondições(i), (ii)e (iii).

Observemos que om essas informações onseguimos obter o dado

(

X, S

2

_{, n, d,}

₍

_dij

₎₎

; para mostrar que é realizável, vamos onstruir um reobrimento

ramiado

f

:

X

→

S

2

quetenha este dado omo dado de ramiação.

Esolha

n

pontosdistintos

x

1

, . . . , xn

naesferae

n

−

2

arossimples

α

1

, . . . , αn

−

2

talque

αi

une

xi

a

xi

+1

ede modoqueseenontrem apenasemseusextremosenão

passem por

xn

.

Denotemos:

Vi

=

{

x

(

_i

j

)

∈

X

;

j

= 1

, . . . , mi

}

, i

= 1

, . . . , n

−

1

.

Ei

=

{

γ

l

i,j

: [0

,

1]

→

X

;

γ

i,j

l

(0) =

x

(

j

)

i

e

γ

l

i,j

(1) =

x

(

l

)

i

+1

,

om

j

= 1

, . . . , mi, l

=

1 , . . . , mi

+1

}

, i

= 1

. . . , n

−

2

.

α

=

n

−

2

[

i

=1

αi

.

Denamos

f

:

D

→

S

2

oloando

f

(

x

(

j

)

(31)

e

f

(

γ

l

i,j

(

t

)) =

αi

(

t

)

,

i

= 1

, . . . , n

−

2

,

j

= 1

, . . . , mi

,

l

= 1

, . . . , mi

+1

.

Resta denir

f

em

X

\

D

.

Notemosque

X

\

D

onsiste, amenosdehomeomorsmo,de

mn

disosabertos

Cj

,

j

= 1

, . . . , mn

.

Vamos então denir

f

em ada

Cj

,

j

= 1

, . . . , mn

.

Observemos que

S

2

_\

_α

é homeomorfo a um diso aberto

U

uja fronteira é

omposta pelas urvas

αi

'se que as fronteiras dos disos abertos

Cj

são ompostas

pelas urvas

γ

l

i,j

.

Assim, existeumaapliação

Ψ :

D

2

_→

_S

2

om

Ψ

|

˚

D

2

: ˚

D

2

→

U

homeomorsmo

de modo que, a orrespondênia ontrária de

Ψ

seria ortar a esfera

S

2

em

α

abrindo-a num diso uja fronteira são duas ópias de

α

:

α

1

e

α

2

. Ou seja,

Ψ

identia

α

1

e

α

2

fehando odiso em

α

etransformando-o naesfera.

Figura3.3: Desrição geométria daapliação

Ψ

.

Vamosolhar oqueaontee nasfronteirasdas omponentes de

X

\

D

,ouseja,

amenos de homeomorsmo,nas fronteiras dos disos

Cj

's.

Paramanteraonexidadedografo,afronteirade

Cj

,paraada

j

= 1

, . . . , mn

, deve onter pontos das pré-imagens de todos os pontos de ramiação, exeto

xn

,

poisos pontos

x

(

j

)

n

de

f

−

1

₍

_xn

₎

estarãono interior de

Cj

.

Vamos denir

f

′

_:

_Cj

_→

_D

2

de modo que, para ada aro da fronteira de

Cj

que se iniia em um vértie de

V

1

e termina no vértie de

Vn

−

1

(o primeiro que

aparee depois de

V

1

), seu orrespondente pela

f

′

seja

α

1

; e o aro seguinte que

(32)

orrespondente, pela

f

′

, oaro

α

2

.

Lembremos que existem

dnj

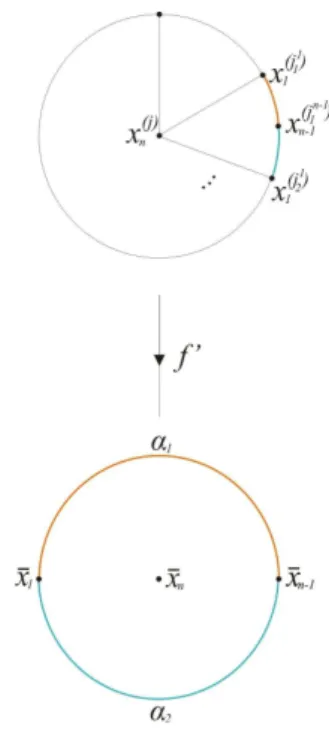
de ambos osaros itados.

Figura3.4: Desriçãogeométria da apliação

f

′

.

Vamos exigirtambémque

f

′

₍

_x

(

j

)

n

) =

xn

∈

D

˚

2

om

Ψ(

xn

) =

xn

.

Deste modo, resta denir

f

′

nos pontosde

Cj

˚

\ {

x

(

j

)

n

}

.

Dado

y

∈

Cj

˚

\ {

x

(

j

)

n

}

, omo

Cj

é estrelado, podemos parametrizaro segmento

dereta queomeçaem

x

(

j

)

n

∈

Cj

,passapor

y

eterminaem

γ

l

i,j

(

t

1

) =

yn

∈

∂Cj

,para

algum

t

1

∈

[0

,

1]

. Assim,

y

= (1

−

ty

)

x

(

j

)

n

+

ty

yn

, paraalgum

ty

∈

[0

,

1]

.

Dena

f

′

₍

_y

_{) = (1}

₋

_ty

₎

_xn

₊

_ty

_f

′

₍

_yn

₎

. (Observemos que

f

′

₍

_yn

₎

já está denido

já que

yn

∈

∂Cj

).

Portanto, podemos denir

f

:

Cj

→

S

2

oloando

f

= Ψ

◦

f

′

.

(33)

Figura3.5: Desrição geométria daapliação

f

= Ψ

◦

f

′

.

Como uma onsequênia da demonstração da proposição anterior, podemos

enuniar oseguinte

Corolário 3.0.10. A ada realização de um dado de ramiação

(

X, S

2

_{, n, d,}

₍

_dij

₎₎

orresponde um dessin d'enfant

D

⊂

X

.

Se usarmosa Denição1.3.4 aoinvés daDenição 1.3.1na proposição aima,

teremoso seguinte resultado:

Proposição 3.0.9.' As realizações de um dado de ramiação

(

X, S

2

_{, n, d,}

₍

_dij

₎₎

orrespondem aos dessins d'enfants

D

⊂

X

om o onjunto de vérties deomposto

omo

V

1

, . . . , Vn

tal que:

(i) Para

i

= 1

e

i

=

n

, os vérties em

Vi

possuem grau

(

dij

)

j

=1

,...,m

i

;

(ii) Para

i

= 2

, . . . , n

−

1

, os vérties em

Vi

possuem grau

(2

dij

)

j

=1

,...,m

i

;

(iii) Os disos em

X

\

D

possuem omprimento onstante

2(

n

−

1)

.

(34)

Corolário 3.0.11. As realizações de um dado de ramiação

(

X, S

2

_{, n, d,}

₍

_dij

₎₎

orrespondem às esolhas de

τi

= Ψ(

vi

)

em

Sd

para

i

= 1

, . . . , n

−

1

tal que

< τ

1

, . . . , τn

−

1

>

é transitivo e, oloando

τn

=

τ

−

1 n

−

1

· · ·

τ

1 −

1

, a lasse de

onjuga-ção de

τi

é dada por

(

dij

)

j

=1

,...,m

i

, onde

i

= 1

, . . . , n

.

Proposição 3.0.12. Um dado de ramiação

D

= (

S

2

_{, Y,}

₃

_{, d,}

₍

_{x, d}

₋

_x

₎

_,

₍₂

_{, . . . ,}

₂₎

_,

(2

, . . . ,

2))

, om

d

par, é realizável se, e somente se,

x

=

d

2

.

Dem.:

Suponhamos que

D

seja realizável. Então

(

S

2

_{, Y,}

₃

_{, d,}

₍₂

_{, . . . ,}

₂₎

_,

₍₂

_{, . . . ,}

₂₎

_,

(

x, d

−

x

))

étambémrealizávele,pelaProposição3.0.9,eleorrespondeaum dessin

d'enfant

D

⊂

S

2

om o onjunto de vérties deomposto omo

V

1

⊔

V

2

tal que os

vértiesem

V

1

possuem grau 2e osvérties em

V

2

possuemgrau

x

e

d

−

x

.

Na demonstração da Proposição 3.0.9, vemos que devemos ter o vértie de

grau

x

em uma omponente de

S

2

_\

_D

e o outro vértie, de grau

d

−

x

, em outra

omponente. Comotodasasomponentesdevemonterumelementodapré-imagem

de

x

3

, onluímos quetemos apenas duas omponentes, oque mostra que

D

éuma

urvasimplesfehadaimersaem

S

2

eportanto,osdisosem

S

2

_\

_D

possuemmesmo

omprimento,ou seja,

2(3

−

2)

x

= 2(3

−

2)(

d

−

x

)

, logo,

x

=

d

−

x

e,assim,

x

=

d

2

.

Reiproamente, suponhamos que

x

=

d

2

e mostremos que

D

= (

S

2

_{, Y,}

₃

_{, d,}

(

d/

2 , d/

2)

,

(2

, . . . ,

2)

,

(2

, . . . ,

2))

é realizável. Para isso, vamos onstruir um dessin

d'enfant,

D

, queorresponda àrealização desse dado de ramiação.

Consideremos odado

(

S

2

_{, Y,}

₃

_{, d,}

₍₂

_{, . . . ,}

₂₎

_,

₍₂

_{, . . . ,}

₂₎

_,

₍

_d/

₂

_{, d/}

₂₎₎

eobservemos

que, sendo

(2

, . . . ,

2)

,

(2

, . . . ,

2)

,

(

d/

2 , d/

2)

partições de

d

, teremos

m

1

=

k

=

m

2

, paraalgum

k

∈

Z

e

d

1 j

= 2 =

d

2 j

paratodo

j

= 1

, . . . , m

1

. Portanto,oúnio dessin que orresponde à essas araterístias é o ilustrado na gura 3.6, onde os pontos

ilustrados na primeira leira orrespondem a pré-imagem de

x

1

e os da segunda

(35)

(

S

2

_{, Y,}

₃

_{, d,}

₍₂

_{, . . . ,}

₂₎

_,

₍₂

_{, . . . ,}

₂₎

_,

₍

_d/

₂

_{, d/}

₂₎₎

.

Observe que

D

satisfaz todas as propriedades da Denição 1.3.1 e da

Pro-posição 3.0.9. Além disso, ressaltamos o fato de ter duas omponentes onexas