UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE BIOCIÊNCIAS
PROGRAMA DE PÓS-GRADUAÇÃO EM CIÊNCIAS BIOLÓGICAS
Estudo das Propriedades Críticas do Processo Epidêmico por Par com Difusão de Pares
FREDERICO LEMOS DOS SANTOS
ORIENTADOR: PROF. DOUTOR UMBERTO LAINO FULCO
Natal / RN
FREDERICO LEMOS DOS SANTOS
Estudo das Propriedades Críticas do Processo Epidêmico por Par com Difusão de Pares
Dissertação apresentada ao Programa de Pós-Graduação em Ciências Biológicas do Centro de Biociências, da Universidade Federal do Rio Grande do Norte, como requisito parcial para obtenção do grau de mestre em Ciências Biológicas.
ORIENTADOR: DR. UMBERTO LAINO FULCO
Natal / RN
UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE BIOCIÊNCIAS
PROGRAMA DE PÓS-GRADUAÇÃO EM CIÊNCIAS BIOLÓGICAS
TERMO DE APROVAÇÃO
Estudo das Propriedades Críticas do Processo Epidêmico por Par com Difusão de Pares
FREDERICO LEMOS DOS SANTOS
Esta versão da dissertação, apresentada pelo aluno Frederico Lemos dos Santos
ao Programa de Pós-Graduação em Ciências Biológicas do Centro de Biociências da Universidade Federal do Rio Grande do Norte, foi julgada adequada e aprovada pelos Membros da Banca Examinadora na sua redação final para a conclusão do Curso de Mestrado em Ciências Biológicas.
MEMBROS DA BANCA EXAMINADORA
______________________________________ Prof. Dr. Umberto Laino Fulco
DBF/CB/UFRN
______________________________________ Prof. Dr. Gilberto Corso
DBF/CB/UFRN
______________________________________ Prof. Dr. Marcelo Martins de Oliveira
CAP/UFSJ
AGRADECIMENTOS
A Gilberto Corso que me deu a oportunidade de conhecer a Biofísica, ousando em novos conhecimentos interdisciplinares, atrelados a uma prática muito difícil chamada de Know How.
Ao meu orientador Umberto que me propôs os desafios os quais me movem na vida e que acreditou na realização de cada um deles. E que ainda acredita...
A Macedo que, sem ter nada a ver com isso, sempre esteve muito disponível para compartilhar e discutir sistemas de não-equilíbrio comigo.
A Alexandre Queiroz que deu forma a esse sonho.
Ao Ronald Dickman que nos posicionou dentro do meio científico das partículas que compõem um todo.
A minha esposa, filhas e filhos pela paciência, apoio e incentivo nas horas difíceis em que se pensa em desistir de tudo.
RESUMO
O processo de contato por par -PCP é um modelo estocástico de não equilíbrio que se inspira no processo de contato simples -PC e que exibe uma transição de fase para um estado absorvente. Embora que o estado absorvente para o PC corresponda a uma única configuração (estado vazio), o PCP possui infinitas configurações. No entanto, estudos numéricos e teóricos indicam que o PCP pertence a mesma classe de universalidade do PC (classe da percolação direcionada), mas apresenta uma anomalia na dinâmica de propagação. Um número infinito de configurações de estados absorventes surge no PCP, devido a todos os processos de criação e aniquilação que requererem um par de partículas de vizinhos mais próximos. O processo de contato por par difusivo - PCPD foi proposto por Grassberger em 1982. Porém, o interesse neste problema segue com a redescoberta por Howard; Täuber (1997), que questionaram a validade da descrição de Langevin. Com base nos resultados numéricos e em grupo de renormalização, Carlon; Henkel ; Schollwöck, (2001), observaram que alguns expoentes críticos no PCPD apresentam valores similares ao da classe PC. Porem, Hinrichsen (2001), mostrou resultados diferentes do caso PCPD, através da simulação, para o caso PC, propondo uma nova classe de universalidade. Até hoje existe uma controvérsia em relação a classe de universalidade do PCPD. No PCPD é necessário um par de partículas vizinhas para os processos de criação e aniquilação, embora as partículas difundam individualmente. Neste trabalho, estudamos o PCPDP com difusão de pares, no qual partículas isoladas não podem difundir. Pares vizinhos difundem juntos. Usando simulação quase-estacionária, determinamos com boa precisão o ponto crítico e os expoentes para dois valores da probabilidade de difusão: D=0.5, e 0.1. Para D=0.5: PC=0.89007(3), z=1.573(1), =1.10(2), m=1.1758(24). Para D=0.1: PC=0.9172(1), z=1.579(11), =1.11(4), m=1.173(4).
Palavras chaves: Sistema Epidêmico Difusivo, Propriedades Críticas,
ABSTRACT
The pair contact process - PCP is a nonequilibrium stochastic model which, like the basic contact process - CP, exhibits a phase transition to an absorbing state. While the absorbing state CP corresponds to a unique configuration (empty lattice), the PCP process infinitely many. Numerical and theoretical studies, nevertheless, indicate that the PCP belongs to the same universality class as the CP (direct percolation class), but with anomalies in the critical spreading dynamics. An infinite number of absorbing configurations arise in the PCP because all process (creation and annihilation) require a nearest-neighbor pair of particles. The diffusive pair contact process - PCPD) was proposed by Grassberger in 1982. But the interest in the problem follows its rediscovery by the Langevin description. On the basis of numerical results and renormalization group arguments, Carlon, Henkel and Schollwöck (2001), suggested that certain critical exponents in the PCPD had values similar to those of the party-conserving - PC class. On the other hand, Hinrichsen (2001), reported simulation results inconsistent with the PC class, and proposed that the PCPD belongs to a new universality class. The controversy regarding the universality of the PCPD remains unresolved. In the PCPD, a nearest-neighbor pair of particles is necessary for the process of creation and annihilation, but the particles to diffuse individually. In this work we study the PCPD with diffusion of pair, in which isolated particles cannot move; a nearest-neighbor pair diffuses as a unit. Using quasistationary simulation, we determined with good precision the critical point and critical exponents for three values of the diffusive probability: D=0.5 and D=0.1. For D=0.5: PC=0.89007(3), z=1.573(1), =1.10(2), m=1.1758(24). For D=0.1: PC=0.9172(1), z=1.579(11), =1.11(4), m=1.173(4).
Key-words: Diffusive Epidemic System, Critical Properties, Quasistationary,
LISTA DE ABREVIATURAS
D,vp - Parâmetro de difusão L - Comprimento da Rede m21 - Cumulante
≡ - Por definição
≈ - Escalonada
rep - Número de ensaios independentes tr - Tempo total
MC - Monte Carlo
ME - Mecânica Estatística MS - Ministério da Saúde
Ƭ - Tempo de vida do estado QS nts - Tamanho do sistema
np - Número de partículas
npar Número de pares de partículas OMS - Organização Mundial de Saúde QS - Quase-estacionária
tr - Tempo total
rep - Número de ensaios independentes SVS - Secretaria de Vigilância em Saúde
prep Probabilidade de reposição na lista de configurações pc
PC
- -
Ponto crítico
Processo de Contato
PCP - Processo de Contato por Par PD - Percolação Direcionada
PCPD - Processo de Contato por Par Difusivo
LISTA DE FIGURAS
Figura 1: Rede unidimensional de comprimento L= N sítios. ... 29
Figura 2: Regras para o processo de contato (PC). As caras escuras correspondem a partículas contaminadas. As caras claras a partículas curadas. ... 29
Figura 3: Processo de Contato por Par (PCP), onde "p" é a probabilidade de cura e (1-p) a de contaminação, tanto a direita como a esquerda do par ... 30
Figura 4: Processo de Contato por Par com Difusão de partículas (PCPD). ... 31
Figura 5: Regras para o PCPDP, onde pares de partículas difundem juntos. Essa difusão pode ser tanto para direita quanto para a esquerda. ... 31
Figura 6: Número de pares de partículas versos tempo, para L=640 e D=0.5 ... 35
Figura 7: Razão entre os momentos versus a probabilidade de aniquilação de pares. A curva inferior se refere a L=10 e a curva superior a L=20, para D=0.5. O ponto onde existe o cruzamento é equivalente a probabilidade crítica, o valor de pc está
entre 0.85 e 0.90. ... 36
Figura 8: Razão entre os momentos versus a probabilidade de aniquilação de pares. Utilizamos para calcular o ponto crítico, diversos tamanhos de rede: L=40, 80, 160, 320 e 640. O ponto onde existe o cruzamento é equivalente a probabilidade crítica pc≈0.917. ... 36
Figura 9: O quarto cumulante reduzido versus a probabilidade de aniquilação de pares, para L=160 e D=0.5. O ponto mínimo é equivalente ao ponto crítico, pc≈0.890. ... 37
Figura 10: O quarto cumulante reduzido versus a probabilidade de aniquilação de pares, para L=320 e D=0.1. O ponto mínimo é equivalente ao ponto crítico,
pc≈0.9172. ... 37
Figura 11: A probabilidade crítica versus 1/L, para D=0.5. A curva inferior com quadrados refere-se aos cruzamentos de m21. A curva superior com triângulos
refere-se aos mínimos de q4.Os dois conjuntos de valores convergem para um valor
muito perto de 0.890. ... 38
Figura 12: O ajuste do expoente para , para e para uma rede unidimensional, calculados a partir das curvas de densidade de par versus . A inclinação desses ajustes mostra o valor que calculamos para o expoente
. ... 39
inclinação desses ajustes mostra o valor que calculamos para o expoente /
... 40
Figura 14: O ajuste do expoente para , para e para uma rede unidimensional, calculados a partir das curvas do tempo da vida versus . A
inclinação desses ajustes mostra o valor que calculamos para o expoente
. ... 41
Figura 15: O ajuste do expoente para , para e para uma rede unidimensional, calculados a partir das curvas do tempo da vida versus . A
inclinação desses ajustes mostra o valor que calculamos para o expoente
. ... 41
Figura 16: A razão do momento versus 1/L, para e . ... 42
Figura 17: A razão do momento versus 1/L, para e . A
extrapolação linear nos dar . ... 43
Figura 18: A razão do momento versus 1/L, para e . ... 44
Figura 19: A razão do momento versus 1/L, para e . A
extrapolação linear nos dá . ... 44
Figura 20: O logaritmo de |dx/dp| versus L, para e . A curva inferior com cruzes é a derivada |dm/dp|, a curva do meio com quadrados é a
derivada e a curva superior com triângulos é a derivada . ... 46
Figura 21: O logaritmo de |dx/dp| versus L, para D=0.1 e . A curva inferior com cruzes é a derivada |dm/dp|, a curva do meio com quadrados é a
LISTA DE TABELAS
Tabela 1 – Tabela com os valores usados na difusão D=0.5 e nc=100 (tamanho da lista) para todos os casos...34
SUMÁRIO
RESUMO ... 5
ABSTRACT ... 6
LISTA DE ABREVIATURAS ... 7
LISTA DE FIGURAS ... 8
LISTA DE TABELAS ... 10
1 INTRODUÇÃO ... 12
1.1 SISTEMAS COMPLEXOS ... 14
1.2 TRANSIÇÕES DE FASE, FENÔMENOS CRÍTICOS E CLASSES DE UNIVERSALIDADE ... 16
2 RELAÇÃO ENTRE EPIDEMIA E SISTEMAS COMPLEXOS ... 18
3 OBJETIVOS ... 19
3.1 OBJETIVO GERAL ... 19
3.2 OBJETIVOS ESPECÍFICOS ... 19
4 MATERIAL E MÉTODOS ... 20
4.1 MATERIAL ... 20
4.2 MÉTODOS ... 20
4.2.1 Métodos Computacionais ... 20
4.2.2 Processos markovianos ... 22
4.2.3 Método Quase-Estacionário ... 23
5 O MODELO ... 27
5.3 A SIMULAÇÃO ... 32
6 RESULTADOS E DISCUSSÃO ... 35
7 CONCLUSÕES ... 48
REFERÊNCIAS ... 50
ANEXO A – PROGRAMA FRED2.F ... 53
ANEXO B – PROGRAMA PCPDPQ.F ... 59
1 INTRODUÇÃO
Uma doença é considerada endêmica quando ocorre em uma dada região específica ou em uma população, com taxas de prevalência e incidência relativamente altas em comparação com as observadas em outras populações ou regiões. São determinadas condições do meio ambiente ou do próprio hospedeiro que se modificam e aí uma doença endêmica pode evoluir para epidêmica. O que caracteriza uma epidemia é a rápida ocorrência da doença, em grande número de habitantes, numa comunidade ou região, em um dado momento. As epidemias ocorrem geralmente quando a população de uma determinada região entra em contato, pela primeira vez, com um novo agente patogênico (vírus, bactéria) que provoca um desequilíbrio do sistema, conferindo-lhe vantagem. Uma epidemia pode acontecer também quando ocorre uma mutação do agente patogênico, surpreendendo o sistema imunológico das pessoas.
um número grande de mortes, mas não é considerada uma pandemia porque a doença não é contagiosa.
A ciência que estuda quantitativamente a distribuição dos fenômenos de saúde/doença, seus fatores condicionantes e determinantes, nas populações humanas é a epidemiologia. A análise de determinação causal das doenças em uma dada população dividida em espécies, classes sociais e/ou grupos específicos de populações (étnicos, religiosos, etc.) exige da epidemiologia uma interação interdisciplinar e estabelece sua dependência de outras ciências a exemplo das ciências sociais, ciência política, estatística, economia, demografia, ecologia e história.
O uso da informática no cotidiano e na pesquisa transformou hábitos, costumes e valores, além de acumular bancos de dados, que subsidiaram a geração de informações e que contribuíram para a construção de conhecimento em nível local, regional e global. Atualmente os sistemas informatizados de posicionamento geográfico, bem como as simulações em computadores, estão se tornando importantes ferramentas para os estudos epidemiológicos, por permitirem o inter-relacionamento das informações obtidas a partir dessas simulações com os dados da Biologia e da saúde pública/coletiva (RODRIGUES, 2007). Dessa forma, cresce nos pesquisadores a tendência de procurar novos resultados de simulações em computadores, softwares especialistas e a validação de novos modelos.
1.1 SISTEMAS COMPLEXOS
Até a presente data, ainda não se tem uma definição precisa do que venha a ser um sistema complexo. O que existe são características típicas que perfazem esse sistema. Suas características principais são (SOCIEDADE BRASILEIRA DE FÍSICA, 2005).
(i) Os sistemas complexos, em sua maioria, são compostos de componentes extremamente simples, mas que em conjunto, geram um comportamento cooperativo extremamente complicado. O comportamento do todo é bastante diferente do comportamento das partes.
(ii) A evolução temporal é geralmente controlada por uma dinâmica não linear, eventualmente levando a um comportamento caótico. A isso significa que o sistema responde de uma maneira altamente não linear a qualquer estímulo externo como, por exemplo, o calor específico e a susceptibilidade inerente a um sistema magnético. Outro exemplo é um sistema que apresenta transição de fase a uma dada temperatura. Próximo à transição, o efeito cooperativo gera ordem de longo alcance. Devemos considerar amostras do sistema da ordem de grandeza do comprimento de correlação, que diverge na temperatura de transição.
(iii) O sistema como um todo (macroscópico), geralmente apresenta um grande número de configurações metaestáveis (ou de tempo de vida relativamente longo) com propriedades consideravelmente diferentes daquelas de seus elementos isolados;
(iv) Eles freqüentemente apresentam padrões espaço-temporais fractais ou multifractais, que, às vezes, se constituem de modo auto-organizados;
de potências, por exemplo, se desejarmos prever o tamanho de uma maré, temos uma noção clara da resposta, no entanto se quisermos saber qual será o tamanho de um terremoto a resposta não é tão clara assim.
A maior contribuição para a compreensão dos sistemas complexos adveio do desenvolvimento da Mecânica Quântica, mais precisamente depois de 1926, quando os pesquisadores passaram a elaborar uma teoria para a descrição de átomos e moléculas, a qual abriu o caminho para a teoria da Mecânica Estatística – ME, que é a teoria física que trata os sistemas de muitos corpos a partir de uma visão microscópica.
O esquema teórico geral da teoria ME consiste em encontrar as interações relevantes (microscópicas) entre os constituintes (átomos, moléculas, etc.) do sistema e a partir destas interações, calcular o Hamiltoniano do mesmo. Uma vez conhecido o Hamiltoniano, o formalismo permite, analiticamente ou numericamente, calcular todas as grandezas físicas de interesse. Os valores médios obtidos a partir da ME são os observáveis físicos de interesse, que devem concordar com os valores obtidos através de uma análise macroscópica (Termodinâmica) do sistema. Através de sua análise microscópica a ME nos permite ter acesso às informações do sistema, que nos propiciem, por exemplo, a determinação das transições de fase (GREINER; NEISE; STÖCKER, 1995).
1.2 TRANSIÇÕES DE FASE, FENÔMENOS CRÍTICOS E CLASSES DE UNIVERSALIDADE
Na natureza existem muitos sistemas que exibem transições de fase. Dentre eles incluam-se os fluidos, materiais magnéticos, ligas metálicas, cristais líquidos, etc. A transição de fase consiste em uma transformação entre os estados desses sistemas em função dos parâmetros externos como pressão, temperatura, campo magnético, etc.
Os primeiros estudos sobre as transições de fase remontam ao ano de 1873, quando Van Der Wall publicou sua tese de doutorado com a primeira teoria de sucesso a respeito de uma transição líquido-vapor. Já outra teoria de igual relevância, com pontos em comum com a teoria de Van Der Walls, é a teoria desenvolvida por Curie-Weiss que explica a transição de fase entre o estado ferromagnético e o paramagnético. Essas teorias são conhecidas como teorias clássicas das transições de fase ou Teorias de campo médio (SALINAS, 1999).
Foi a partir da década de 60 que as teorias clássicas passaram por um processo de analiticidade mais acurada, o que levou ao desenvolvimento de novas técnicas para realizações de experimentos em torno dos pontos críticos. Desta feita, o comportamento peculiar com divergências assintóticas foi caracterizado pelos chamados expoentes críticos. Foi a partir dessa caracterização que se percebeu que o comportamento crítico de grandezas termodinâmicas tais como a compressibilidade de um fluido e a suscetibilidade de um ferromagnético, exibiam um caráter universal, caracterizado pelo mesmo valor de um expoente crítico bem definido, o que deu origem ao conceito de classe de universalidade (SALINAS, 1999).
Para se descrever a transição de fase é necessário introduzir a noção de
parâmetro de ordem, cujo objetivo é assumir valor nulo na fase desordenada e
ferromagnético, as diferenças entre as densidades do cobre e do zinco num sítio da rede cristalina de uma liga binária de cobre e zinco, a polarização espontânea de um material ferromagnético, a magnetização espontânea de uma sub-rede ou magnetização alternada de um sistema anti-ferromagnético (TOMÉ; OLIVEIRA, 1997).
É importante ainda entender, no estudo das transições de fase, o surgimento de uma quebra espontânea de simetria em um sistema descrito por um processo estocástico.
Tomando-se, como exemplo, um sistema que sofre transição de fase ordem-desordem, é observado que quando se varia um parâmetro externo como temperatura, o sistema passa de uma fase desordenada para uma ordenada, surgindo dois estados ordenados. Estes dois estados ordenados levam a uma quebra espontânea de simetria que se relaciona com a existência de mais de um estado ordenado. É necessário examinar, portanto, quais são as condições para que exista mais de um estado ordenado em um processo estocástico.
2 RELAÇÃO ENTRE EPIDEMIA E SISTEMAS COMPLEXOS
Para se estudar uma epidemia, não basta a pura e simples observação de um único indivíduo ou pequeno grupo, mas sim de um conjunto bem amplo, o que torna a observação muito mais complexa. Esse efeito produzido pela coletividade e cooperação entre as partes é uma das características dos Sistemas Complexos.
3 OBJETIVOS
3.1 OBJETIVO GERAL
O presente trabalho tem como objetivo estudar a propagação de uma
epidemia, através do método quase-estacionário. O modelo epidêmico utilizado foi o processo de contato por par com difusão de pares.
Sabemos que até hoje existe uma controvérsia em relação à classe de universalidade do PCPD. O que estamos interessados neste trabalho é estudamos o PCPD com uma variação na difusão de partícula. A difusão é através de pares de partícula, não existindo difusão de partículas isoladas. Por esse motivo neste trabalho determinamos com boa precisão o ponto crítico e os expoentes críticos e comparamos os nossos resultados com os já estabelecidos na literatura e ver e conseguimos ajudar a explicar a controvérsia que existe. Utilizaremos dois valores da probabilidade de difusão e .
3.2 OBJETIVOS ESPECÍFICOS
Calcular o ponto crítico para as taxas de difusão D=0.5 e D=0.1;
Calcular os expoentes críticos para as taxas de D= 0.5 e D= 0.1;
4 MATERIAL E MÉTODOS
4.1 MATERIAL
COMPUTADORES: Para o desenvolvimento do presente trabalho foi utilizado um cluster de 16 computadores com processadores Pentium Core 2 Duo 2.5 GHz, com 4 Gb de memória RAM, executando sistema operacional LINUX (distribuição FEDORA CORE versão 10.0). Interconectados em rede privada via protocolo SSH (Security Shell).
SOFTWARES: Foram desenvolvidas duas rotinas na linguagem FORTRAN, sendo o FRED2.f para uma primeira aproximação do ponto crítico pc e o PCPDPQ.f para determinar com maior precisão o ponto
crítico.
4.2 MÉTODOS
4.2.1 Métodos Computacionais
É através dos métodos numéricos que se fazem as simulações estatísticas as quais são conjuntos de algoritmos que fazem uso de seqüências aleatórias para realização das simulações. Um dos métodos mais conhecidos para simulações estatísticas é o método de Monte Carlo – MC (BINDER; HEERMANN,1986) que vem sendo usado por décadas em muitas aplicações complexas.
O nome Monte Carlo foi cunhado por Metropolis por causa da semelhança das simulações estatísticas com os jogos de sorte e porque Monte Carlo, era a cidade do principado de Mônaco, centro de jogos de sorte e atividades similares.
Atualmente o método MC é utilizado em diversos campos de pesquisa para simular fenômenos críticos complexos como em reações químicas propostas em (ZIFF; GULARI; BARSHAD,1986), e em (ALBANO, 2000). As dinâmicas populacionais também usam MC como pode ser visto em (SATULOVSKY; TOMÉ.,1994), bem como a proliferação de epidemias em (CARLON; HENKEL; SCHOLLWÖCK, 2001), e a criação e aniquilação de partículas em (GRASSBERGER, 1989), entre outras.
Não fossem as limitações computacionais como velocidade de processamento e quantidade de memória usada, bem como os erros estatísticos inerentes ao próprio processo, o método MC poderia ser mais amplamente utilizado. É que certas simulações, dependendo da natureza do simulado, pode levar horas, dias, meses ou até anos de processamento. Assim, um problema que leva anos de simulação é simplesmente impraticável.
Quanto ao erro estatístico, é uma característica das simulações, uma vez que para gerar nossas médias, o método gera uma seqüência de números aleatórios que são diferentes para cada passo de MC. Dependendo do número de amostras geradas, o erro estatístico pode macular os resultados.
De acordo com o que se deseja simular, a aplicação do método MC passa por algumas aproximações para torná-lo exeqüível na prática: Uma delas é tomar uma representação do que se deseja simular de tal forma que esteja dentro da capacidade de processamento dos computadores disponíveis. A segunda é a representação de forma discreta do processo que se deseja simular e por último, a representação do processo em uma dimensão Ld , onde d é a dimensão espacial
Pelo exposto acima a respeito do método MC, emergem duas questões fundamentais para o sucesso do método: uma diz respeito a geração de seqüências aleatórias adequadas, enquanto a outra se apóia na trilogia descrita no parágrafo anterior. Quanto à geração de seqüências aleatórias adequadas, o método MC apóia-se nos processos markovianos, descritos no tópico a seguir. Já em relação a adequação ao tipo de simulação, estudiosos têm se empenhado na construção de dinâmicas capazes de dar a eficiência ao método. Para os propósitos desse trabalho, o método que empregamos é o Quase-estacionário, descrito logo após a descrição dos processos markovianos.
4.2.2 Processos Markovianos
Os sistemas dinâmicos são caracterizados por estados examinados em instantes de tempo. Se um dado estado depender só, e exclusivamente do estado imediatamente anterior, dizemos que esse sistema obedece a um processo markoviano. Se os referidos estados forem descritos por funções de variáveis estocásticas, então o conjunto desses estados, vem a ser uma cadeia de Markov (TOME; OLIVEIRA, 2001).
Assim, dada a definição de probabilidade condicional:
E que pode ser generalizada para:
E assim podemos escrever:
Ou seja, um processo markoviano fica completamente definido pelas probabilidades condicionais.
Ou seja, a probabilidade de ocorrência de dado evento A é dada por:
Assim, para gerar novas configurações para um sistema que dependam somente da configuração atual, usa-se um processo markoviano. Em outras palavras, dada uma seqüência de estados, uma nova seqüência de estados pode ser gerada a partir da anterior, sem a necessidade do conhecimento dos estados anteriores. Dizemos que se trata de um processo sem memória.
4.2.3 Método Quase-Estacionário
Os estados absorventes são irreversíveis, ou seja, uma vez atingido este estado o sistema nunca mais irá sair dele. Em modelos de processos de contato o parâmetro de ordem, geralmente, é a densidade de sítios ativos, o qual é zero no estado absorvente.
desprezando, em suas médias, as amostras para os quais o parâmetro de ordem se anula completamente.
O método QS busca contornar esta dificuldade de simulação através da atualização gradativamente de uma lista de configurações visitadas durante a evolução, após a sua relaxação. Quando uma flutuação gera uma transição que levaria o sistema ao estado absorvente, coloca-se o sistema em uma das configurações salvas anteriormente escolhidas aleatoriamente na lista. O conjunto de configurações salvas é atualizado a cada intervalo de tempo, substituindo-se uma das configurações salvas pela atual, com uma pequena probabilidade prep.
A vantagem do método está no fato de que a realização do processo pode rodar por um tempo indefinidamente longo, enquanto em simulações convencionais um grande número de ensaios devem ser realizados para que se obtenha uma amostragem decente do estado “estacionário”. Como na simulação QS o tempo de relaxação só precisa ser esperado uma vez, ela é uma ordem de grandeza mais rápida na região crítica.
O método se baseia em uma função de distribuição denominada quase-estacionária, muito útil na caracterização dos sistemas que sofrem transições de fase para estados absorventes, no sentido de determinar suas propriedades como pontos críticos e expoentes críticos. Este método consiste em um processo Markoviano de tempo contínuo , onde seus estados tomam valores . Para o estado do sistema é inativo (estado absorvente) enquanto que para o estado do sistema é ativo. Dada uma configuração inicial a probabilidade de ser igual a é representada por . Para o processo apresenta uma probabilidade de não ir para o estado absorvente até o tempo . Tal probabilidade é definida como probabilidade de sobrevivência e é dada por:
. (1)
, (2)
com . A distribuição quase-estacionária é normalizada, ou seja, .
A distribuição QS consiste na solução da equação de movimento
, (3)
onde é taxa de transição para fora do estado n e é o fluxo de probabilidade nesse mesmo estado. Para ver isto, consideremos a equação (3), sem o termo , no regime QS. Substituindo e observando que no regime QS
. (4)
É possível ver na equação (4) que seu lado direito é identicamente zero se para O termo final da equação (3) representa uma redistribuição da probabilidade para o sub-espaço não absorvente. Cada estado não absorvente recebe uma quota igual de probabilidade.
Para simular o processo QS, consideramos um processo , relacionado a , cuja distribuição de probabilidade estacionária é a distribuição QS de A distribuição de probabilidade de é governada pela equação (3), que implica que para a evolução de é idêntica a aquela de .
Um aspecto sutil da equação (3) é que a distribuição é usada para determinar o valor de quando visita o estado absorvente. Apesar de que, apriori, não conhecemos , podemos, em uma simulação, usar a história
destas configurações com a corrente. Desta forma, a distribuição para o processo convergirá para a distribuição QS em tempos longos.
5 O MODELO
O processo de contato básico – PC é modelo estocástico de não-equilíbrio que exibe uma transição de fase para um único estado absorvente que é o vazio. (HARRIS,1974). Já o PCP originalmente proposto por Dickman; Jensen (1993), apresenta múltiplos estados absorventes e tem sido bastante estudado na tentativa de se confirmar novas classes de universalidade.
Estudos numéricos e teóricos indicam que o PCP pertence a mesma classe de universalidade do PC, isto é, a classe da percolação direcionada - PD, mesmo possuindo os múltiplos estados absorventes. Esses múltiplos estados absorventes originam-se de sua dinâmica de propagação que necessita de um par de partículas vizinhas para a criação e aniquilação das partículas vizinhas.
Muitos estudos têm sido feitos em cima das modificações propostas a esse modelo, como por exemplo, uma adição de uma fonte de partículas (DICKMAN; RABÊLO; ÓDOR, 2001). Pesquisadores como Kim; Park (1994) já haviam estudado o PCP com uma fonte de partículas e demonstraram que a fonte altera o ponto crítico, mas mantém consistentes os valores dos expoentes críticos consistentes
com os valores da PD, com exceção de β que aparece com um desvio de 4% do valor da PD.
Trabalhos recentes passaram a estudar o PCP com a difusão das partículas, o processo de contato por par com difusão - PCPD, originalmente proposto por Grassberger (1982). Alguns pesquisadores como Carlon; Henkel; Shollwöck (2001), sugerem que o PCPD esteja na mesma classe de universalidade do PC, enquanto outros dizem que não, e que talvez pertença a uma nova classe de universalidade (HINRICHSEN, 2001; ÓDOR, 2003; PARK; HINRICHSEN; KIM, 2001; DICKMAN; MENEZES, 2002).
2001). Eles observaram que alguns expoentes críticos no PCPD apresentavam valores similares ao da classe da PC. Porém Hinrichsen (2001) mostrou resultados diferentes entre o caso PCPD e o caso PC através da simulação, propondo uma nova classe de universalidade. O comportamento distinto do PCPD foi confirmado em simulações de Ódor (2000)que apresentou evidências para a existência de duas classes de universalidade (probabilidades de difusão superior ou inferior a 0.3). Henkel e Schollwöck (2001) sugeriram, com base em um estudo de efeito de tamanho finito, que para as taxas de difusão, o comportamento crítico do PCPD pertence a uma única classe de universalidade. Em uma variante do PCPD, os expoentes críticos são encontrados variando de acordo com a probabilidade de sobrevivência de pares recém-criados (NOH, 2004).
Finalmente, ainda não foi esclarecida a classe de universalidade do PCPD, existindo uma controvérsia. Neste PCPD tradicional as partículas difundem individualmente. Para os processos de criação e aniquilação é necessário um par de partículas vizinhas.
Neste nosso trabalho estudamos o PCPD com uma variação na forma da difusão das partículas. As partículas são difundidas aos pares ficando um processo de contato por par com difusão de pares de partículas - PCPDP.
O objetivo desse nosso trabalho foi a determinação do ponto crítico com seus respectivos expoentes críticos e comparamos com aqueles existentes na literatura. Isso ajuda explicar a controvérsia existente nesse modelo. Utilizamos a simulação quase-estacionária proposta por Dickman; Martins (2005) para o estudo dos dois casos de difusão: D=0.5 e D=0.1.
5.1 IMPLEMENTAÇÃO DO MODELO
ao sítio como ocupado por partículas que podem estar contaminadas (ativas, doentes) ou saudáveis (inativas, curadas), conforme mostra a rede unidimensional de comprimento L=N onde N=15, figura 1, abaixo.
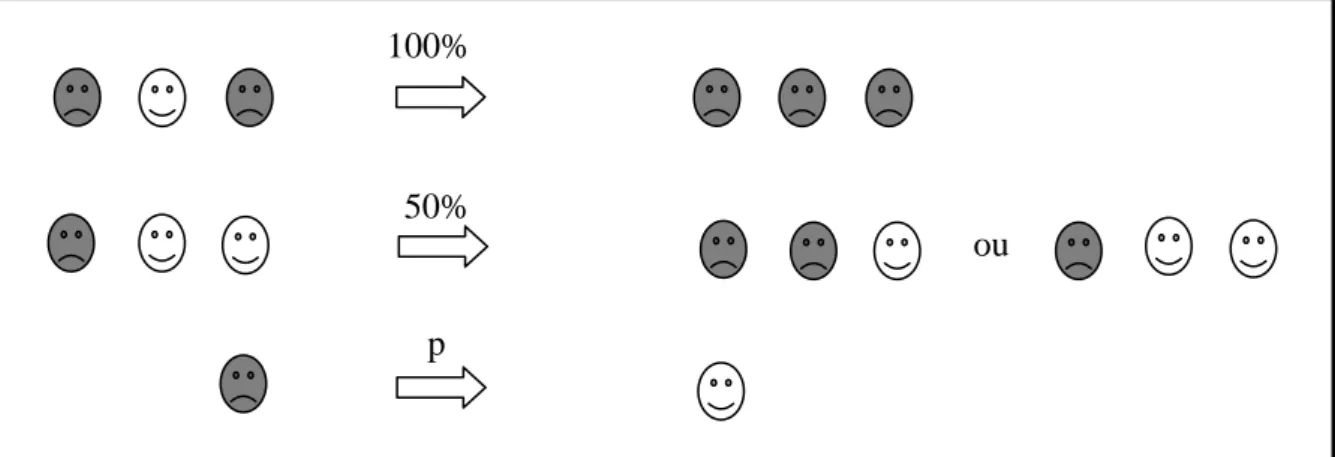
As regras para o PC, ilustradas pela figura 2 abaixo, consiste em visitas aleatórias aos sítios com intuito de contaminar ou curar as partículas.
A contaminação de uma partícula se dá quando ela é visitada e tem como vizinhos tanto da direita como da esquerda, partículas contaminadas. Caso um dos sítios vizinhos não contenha uma partícula contaminada, ela terá uma chance de 50% de ser contaminada ou não, independente de que lado esteja o sitio contaminado.
A cura de uma partícula se dá mediante a probabilidade “p”, chamada probabilidade de cura. A cura independe da condição das partículas vizinhas. Caso o sítio visitado já contenha uma partícula curada, nada acontece.
Figura 1: Rede unidimensional de comprimento L= N sítios.
ou p
50% 100%
O parâmetro de ordem do PC é a densidade de partículas contaminadas que vai a zero no estado absorvente (estado sem atividade). Para o PC, este estado acontece quando todas as partículas foram curadas.
Já no Processo de Contato por Par (PCP), apenas os pares de partículas contaminadas (sítios vizinhos contendo partículas contaminadas) exibem atividade. Cada um tem uma taxa de cura mútua, e uma taxa ) para contaminar uma nova partícula em um sítio vizinho, caso esse sítio (escolhido aleatoriamente) esteja saudável. Em uma dimensão para , o sistema vai para o estado absorvente (estado sem atividade) (DICKMAN; KAMPHORST, SILVA,1998). O parâmetro de ordem para esse modelo é a densidade de pares de partículas. Esquematicamente temos a figura 3, abaixo:
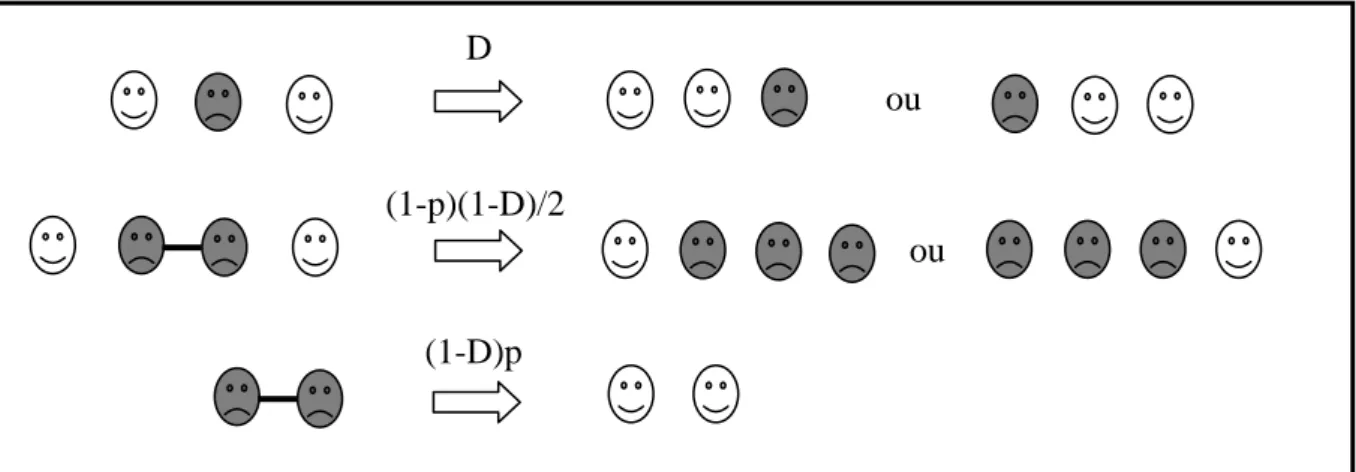
Agora vamos mostrar o nosso modelo estudado. No PCPD tradicional, além da criação e aniquilação de processos descritos acima, cada partícula pode difundir individualmente, com taxa D, para um sítio vizinho escolhido aleatoriamente. O movimento é concretizado se os sítios de destino estiverem vazios.
(1-p) p
ou
Com já foi dito anteriormente, o PCPDP, é similar ao PCPD tradicional com uma diferença na maneira de difundir.que é feita por pares de partículas e não por partículas individuais, ou seja, pares de vizinhas difundem juntas. Esse modelo apresentou uma transição contínua para o estado absorvente, quando usada uma taxa de aniquilação crítica , que como pode ser vista, varia com a taxa de difusão. Uma vez que as partículas sejam autorizadas a difundir, a natureza do sistema mudou radicalmente.
Em contraste com os modelos mais simples como o PC, em que a difusão não altera o comportamento crítico (DICKMAN; JENSEN, 1993); a difusão representa uma perturbação singular no PCP. As regras dinâmicas para o nosso caso unidimensional, estão na figura 5 abaixo:
ou ou
Figura 4: Processo de Contato por Par com Difusão de partículas (PCPD).
(1-D)p (1-p)(1-D)/2
D
Figura 5: Regras para o PCPDP, onde pares de partículas difundem juntos. Essa difusão pode ser tanto para direita quanto para a esquerda.
D
(1-p)(1-D)/2
ou ou
Simulamos o nosso modelo PCPDP unidimensional utilizando redes de diferentes tamanhos (L=40, 80, 160, 320 e 640), cada uma com 10000 amostras. Inicialmente, todos os sítios são ocupados. Determinamos a densidade de partículas média , a densidade de pares de partículas média , a taxa de momento
, e a probabilidade de sobrevivência (onde denota uma média estacionária).
5.3 A SIMULAÇÃO
Para a simulação usamos duas rotinas em anexo nessa dissertação. Primeira, chamada de fred2.f serviu para dar uma estimativa grosseira do ponto critico, através do gráfico do cumulante m21 versos p para as redes de L=40, L=80, L=160,
L=320 e L=640, mostrado na figura 7, onde os cruzamentos das curvas indicam o ponto crítico.
Já a segunda pcpdpq.f que incorpora o método quase estacionário descrito anteriormente e é responsável pela densidade de pares e de partículas, fornecendo a razão (razão entre o segundo momento e o primeiro momento ao quadrado) e o quarto cumulante reduzido, , onde:
e os são cumulantes da distribuição de probabilidade. Esses resultados são calculados na base de histogramas, um para a probabilidade de ter exatamente np
pares, outra para ter exatamente npart partículas, no estado QS.
prep: é a probabilidade de reposição na lista de configurações . Normalmente ≤
0.001. É indicado reduzir prep a medida que o tamanho L é aumentado. O critério é
que o tempo de residência na lista, , seja pelo menos duas vezes maior que o tempo de vida , e ainda pequeno em relação ao tempo total tr. Já na fase de relaxação tomamos essa probabilidade como prepr, dez vezes maior que prep,
para acelerar a atualização da lista (isto serve para esquecer a condição inicial).
ithst: é o tempo para relaxação. Normalmente entre 0.1 e 0.01 do tempo total. Durante essa fase inicial não acumulamos os histogramas, nem calculamos o .
rep: é o número de ensaios independentes. O método QS permite rodar o processo por tempos arbitrários. Mesmo assim, é conveniente realizar certo número de ensaios independentes, para estimar as incertezas.
A rotina gera dois arquivos de saída: O primeiro contém a história do processo, a saber: tempo, número de pares, número de partículas, número de visitas ao estado absorvente. O segundo arquivo contém os histogramas e outras informações sobre cada ensaio, e no final as médias e incertezas calculadas sobre o conjunto de ensaios (rep). A linha final contém todas as informações usadas na análise do problema, de tal forma que pode montar um arquivo dessas grandezas em função do parâmetro p.
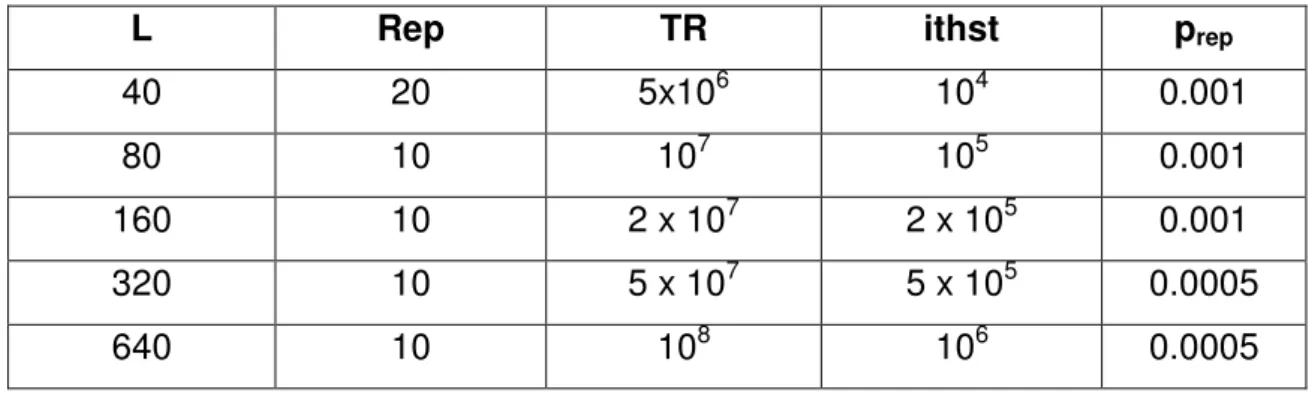
Utilizamos valores de rep e tr tais que a incerteza em par seja de 0.0001. Para
Tabela 1: Valores usados na difusão D=0.5 e nc=100 (tamanho da lista) para
todos os casos.
L Rep TR ithst prep
40 20 5x106 104 0.001
80 10 107 105 0.001
160 10 2 x 107 2 x 105 0.001
320 10 5 x 107 5 x 105 0.0005
6 RESULTADOS E DISCUSSÃO
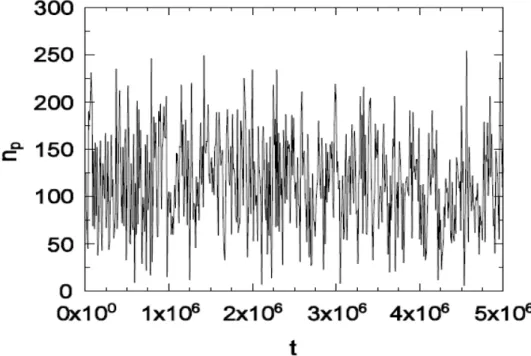
Para cada novo tamanho L que estudamos, é preciso verificar se a densidade de pares relaxou até o tempo ithst. Para observamos isto, fazemos um gráfico do tempo versus número de partícula conforme mostra a figura 6 abaixo, para L=640. Notamos por essa figura, que o número de pares de partículas está relaxado ao redor de um valor médio (np=125).
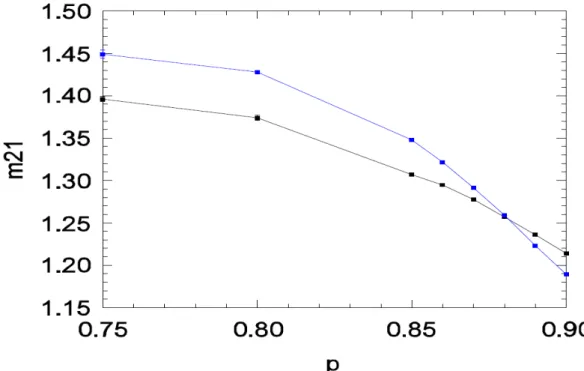
Inicialmente para calcularmos a probabilidade crítica, estudamos sistemas pequenos (L =10, 20, 40), calculando a razão entre os momentos 21. Os
cruzamentos de 21 fornecem estimativas do valor crítico pc. Fizemos isso tanto para
D=0.5 como para D=0.1. Para D=0.5, usamos a priori tamanhos pequenos: L=10 e 20. Na ausência de qualquer informação sobre pc experimentamos p = 0.75, 0.8, 0.9.
A partir desses dados preliminares, observamos evidências no cruzamento dos 21
em torno de 0.85 a 0.9, ver Figura7. Então realizamos estudos adicionais para p=0.86, 0.87,...,0,89, para tamanhos maiores.
Para o caso D=0.1, realizamos os mesmos procedimentos com redes pequenas, e depois para redes maiores como L=40, 80, 160, 320 e 640 dentro de um intervalo de p=0.912, 0.914,..., 0.920, ver Figura 8.
Figura 8: Razão entre os momentos versus a probabilidade de aniquilação de pares. Utilizamos para calcular o ponto crítico, diversos tamanhos de rede: L=40, 80, 160, 320 e 640. O ponto onde existe o cruzamento é equivalente a probabilidade crítica pc≈0.917.
Para cada par consecutivo de tamanhos de rede, L e 2L, foi encontrado o valor pc dos cruzamentos de 21.
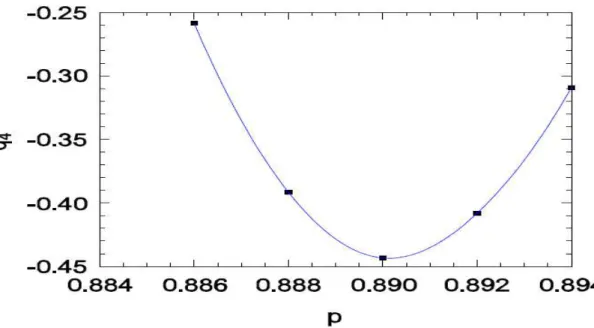
Existe outra maneira empírica de estimar pc, que consiste em localizar o
mínimo do quarto cumulante reduzido. Isso é feito ajustando-se um polinômio de quarto grau aos pontos dos dados mais próximos ao mínimo, como mostra a Figura 9 para D=0.5 com L = 160 e a Figura 10, com D=0.1 e L=320.
Figura 9: O quarto cumulante reduzido versus a probabilidade de aniquilação de pares, para L=160 e D=0.5. O ponto mínimo é equivalente ao ponto crítico, pc≈0.890.
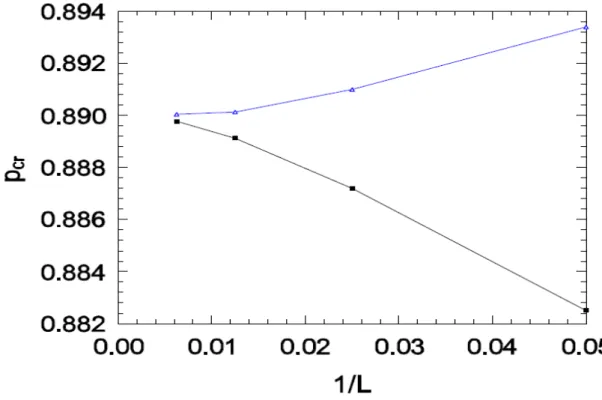
A figura 11, mostra os dados dos valores de pc, associados aos cruzamentos
e aos mínimos de q4, versus 1/L. A curva inferior com os pontos quadrados é
referente aos cruzamentos de 21. O ponto em 1/160 corresponde ao cruzamento
das curvas para L = 160 e L = 320, e assim por diante. A superior com os pontos triangulares é dos mínimos de q4, com o ponto em 1/160 o valor para L = 160 e
assim por diante. Os dois conjuntos de valores convergem rapidamente para um valor muito perto de 0.890. As extrapolações quadráticas dos valores dos cruzamentos fornecem e 0.8900, quando extrapolamos em função de e respectivamente. A extrapolação dos valores dos mínimos de q4 também
nos fornece .
Terminado a etapa de análise dos cruzamentos e dos mínimos, temos uma estimativa muito boa para o pc. Então podemos usar os dados obtidos, utilizando as
redes de tamanho L= 40, 80, 160, 320 e 640, para estimar a razão entre os expoentes , o expoente dinâmico e o valor crítico mc através das leis de
Figura 11: A probabilidade crítica versus 1/L, para D=0.5. A curva inferior com quadrados refere-se aos cruzamentos de m21. A curva superior com triângulos refere-se aos mínimos de q4.Os dois
escalas e enquanto . Alguns desvios dessas leis de potência e a ausência de um limite finito para sinalizam que o valor de p escolhido não é o ponto crítico. Em particular, uma curvatura não-nula dos gráficos
log-log de versus L (ver Fig. 12 e 13), ou de versus L (ver Fig. 14 e 15) indica um desvio do ponto crítico. Porém, no nosso caso as figuras citadas apresentam boas retas. Os ajustes quadráticos aos dados mostram que não existem curvaturas significativas.
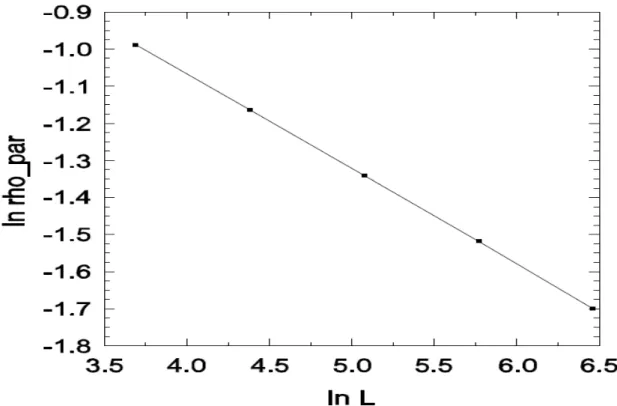
Dessa forma podemos fazer os ajustes lineares aos dados e obter os expoentes desejados. A priori, calculamos o expoente a partir de duas diferentes difusões: D=0.5 (Fig. 12) e D=0.1 (Fig. 13).. O ajuste linear do gráfico logaritmo da densidade de par de partículas versus o log L nos mostra que o valor do expoente, para D=0.5 (Fig. 12), e para D=0.1 (Fig. 13).
Para o calculo do expoente , fizemos um ajuste linear na figura do logaritmo do tempo da vida versus logaritmo de L. Utilizamos também dois tipos de difusões
a D=0.5, onde calculamos , ver Figura 14, e a D=0.1, onde calculamos
, ver Figura 15.
Figura 14: O ajuste do expoente para , para e para uma rede unidimensional, calculados a partir das curvas do tempo da vida versus . A inclinação desses ajustes mostra o valor que calculamos para o expoente .
ln (
τ
)
L
Figura 15: O ajuste do expoente para , para e para uma rede unidimensional, calculados a partir das curvas do tempo da vida versus . A inclinação desses ajustes mostra o valor que calculamos para o expoente .
Observamos que os valores dos expoentes calculados acima são muito próximos aos valores da percolação direcionada (DP) em uma dimensão espacial. A figura 16 de versus também fornece um valor limite.
Fizemos uma extrapolação linear para o caso (ver Fig. 16) e notamos que esse ponto está abaixo do valor crítico, pois a figura mostra uma pequena curvatura para cima. Desse modo fizemos outra extrapolação para um valor maior, (ver Fig. 17). Notamos uma maior linearidade e encontramos , isso tudo para D=0.5.
Para fizemos a figura para (ver Fig.18) e notamos uma curvatura para cima. Refizemos o gráfico para (ver Fig.19) e encontramos . Todos os dois valores de mc estão próximos ao valor da DP.
Infelizmente os dados obtidos não são suficientes para determinarmos os valores críticos de q4 e ρpart. Para tanto, seriam necessários sistemas maiores e
muito mais tempo de computação.
Figura 18: A razão do momento versus 1/L, para e .
Figura 19: A razão do momento versus 1/L, para e . A extrapolação linear nos
Para dar uma maior confiabilidade ao nosso trabalho, vamos a incerteza para e levá-la aos expoentes críticos.
Sabemos que o sistema na proximidade da transição de fase é altamente instável e por esse motivo, uma variação no ponto crítico produz mudanças nos expoentes críticos. Logo é muito importante adicionarmos essa incerteza do nos valores dos expoentes críticos e do .
A incerteza em é estimada da seguinte forma: inicialmente procuramos o valor de p para o qual exista uma curvatura significativa e em seguida utilizamos para esse procedimento um ajuste quadrático. Interpolamos valores próximos de p e calculamos as curvaturas deles. Fazemos os gráficos das curvaturas em função de p no intervalo escolhido.
Observamos nas figuras, curvaturas significativas para e para e então calculamos a incerteza para o valor crítico de para e para . A partir do valor crítico de pc e sua incerteza, podemos
calcular a incerteza de para e para
, onde estimamos essa incerteza fazendo um ajuste linear no intervalo do ponto crítico. Análises semelhantes fornecem para , e
para ; e para , e para
. Para estes casos, as estimativas estão muito próximas dos valores da PD,
a saber, , , e .
Com os dados que dispomos podemos calcular mais um expoente, muito embora com precisão menor. Na teoria de escala de tamanho finito as derivadas , e avaliadas no ponto crítico, seguem a relação
, onde x é qualquer uma das grandezas mencionadas acima. Usando um intervalo que inclua o valor de pc e sua incerteza mais baixa, estimamos
nossas retas lineares para os três últimos pontos de cada conjunto estudado, encontramos os seguintes valores:
Para temos, , 0.940(26) e 0.891(7), para os casos , e respectivamente, onde a estimativa de ; Para temos, , 0.850(17) e 0.902(20), para os casos , e respectivamente, onde a estimativa de .
Os valores de para as duas diluições, embora não tão precisos como os demais, ainda apresentam uma boa consistência com o valor da literatura que é
.
7 CONCLUSÕES
Encontramos com boa precisão o valor da probabilidade crítica para
, e para .
A partir do valor da probabilidade crítica calculamos os expoentes
críticos , para e , para .
Estimamos também o expoente , para , e para . Calculamos o para e
para . Para estes casos, as estimativas ficaram muito próximas dos valores conhecidos para a classe de percolação
direcionada, a saber, , , e
.
Encontramos o expoente || para as seguintes difusões: Para
temos, , 0.940(26) e 0.891(7), para os casos , e respectivamente, onde a estimativa de ; Para temos, , 0.850(17) e 0.902(20), para os casos , e respectivamente, onde a estimativa de . Onde o valor de na literatura é
.
Para as duas difusões ensaiadas, o PCPDP está dentro da classe da Percolação Direcionada, conforme a tabela 2. Em outras palavras, podemos tratar problemas epidêmicos complexos que utilizam essas difusões da mesma forma que uma epidemia simples.
Tabela dos resultados
pc ⊥ z m
D=0.5 0.89007(3) 0.252(2) 1.573(10) 1.10(2) 1.758(2)
D=0.1 0.9172(1) 0.252(9) 1.579(11) 1.11(4) 1.173(4)
PD --- 0.25208(5) 1.5807(1) 1.096854(4) 1.1736(1)
REFERÊNCIAS
ALBANO, V. Ezequiel. The Monte Carlo simulation method: a powerful tool for the study of reaction process. Heterogeneous Chemistry Reviews, v. 3, n. 4, p. 389-418, dec. 1996.
BINDER, Kurt; HEERMANN, Dieter W. Monte Carlo Simulation in Statistical
Physics an introdution, 4. ed. Berlim: Springer-Verlag, 1986.v.7.
CARLON, Enrico; HENKEL, Malte; SCHOLLWÖCK, Ulrich. Critical properties of the reaction-diffusion model 2A 3A, 2A 0. Physical Review E, Maryland, v. 63, n. 3, p. 10, feb. 2001.
DICKMAN, Ronald. Universality and diffusion in nonequilibrium critical phenomena.
Physical Review B, Maryland, v. 40, n. 10, p. 5 (7005 - 7010), oct. 1989.
DICKMAN, Ronald; SILVA, Jeferson Kamphorst Leal da. Moment ratios for absorbing-state phase transitions. Physical Review E, Maryland, v. 58, n. 4, p. 4 (4266-4270), oct. 1998.
DICKMAN, Ronald; JENSEN, Iwan. Time-dependent perturbation theory for diffusive non-equilibrium lattice models. Journal of Physics A: Mathematical and General, Maryland, v.,26, n. 4, p. L151 - L157, fev. 1993.
DICKMAN, Ronald; MENEZES, Marcio Argollo Ferreira de,. Nonuniversality in the pair contact process with diffusion. Physical Review E, Maryland, v. 66, n. 4, p. 4, oct. 2002. DOI (9045101)
DICKMAN, Ronald; OLIVEIRA, Marcelo Martins de. How to simulate the
quasistationary state. Physical Review E, Maryland , v. 71, n. 1, p. 5, jan. 2005. DICKMAN, Ronald; RABELO, Wilson R. M.;ODOR, Géza. Pair contact process with a particle source. Physical Review E, Maryland, v. 65, n. 1, p. 8, dec. 2001. DOI (10.1103/PhysRevE.65.016118).
GABINETE Permanente de Emergências. Disponível em : <
http://portal.saude.gov.br/portal/arquivos/pdf/informe_influenza_ae_34_2009.pdf>. Acesso em: 16 set. 2009.
GRASSBERGER, Peter. Directed percolation in 2+1 dimensions. Journal of
Physics A: Mathematical and General, Maryland, v. 22, n. 17, p. 6 (3673-3679),
sep 1989.
______. On phase transitions in Schlögl's second model. Zeitschrift für Physik B
Condensed Matter, Maryland, v. 47, n. 4, p. 9 (365-374), dec. 1982.
GREINER, W.; NEISE, L.; STÖCKER, H. Thermodynamics an Statistical
Mechanics. New York: Springer-Verlag, 1995.
HARRIS, T. E. Contact Interactions on a Lattice. Annals of Probability, Beachwood, v. 2, n. 6, p. 968-988, dec. 1994.
HENKEL, Malte; SCHOLLWÖCK, Ulrich. Universal finite-size scaling amplitudes in anisotropic scaling. Journal of Physical A: Mathematical and General, Maryland, v. 34, n. 16, p. (3333 - 33350), apr. 2001
HINRICHSEN, Haye. Pair contact process with diffusion: A new type of
nonequilibrium critical behavior?, Physical Review E, Maryland, v. 63, n. 3, p. 3 (036102), fev. 2001.
HOWARD, Martins J.;TÄUBER, Uwe C.;.'Real' versus `imaginary' noise in diffusion-limited reactions. Journal of Fhysics A: Mathematical and General, v.30,n. 22, nov. 1997.
KIM, Mann Ho; PARK, Hyunggyu. Critical Behavior of an Interacting Monomer-Dimer Model. Physical Review Letter, Maryland, v. 73, n. 19, p. 13 (2579--2582), nov. 1994.
LÉVY, Paul Pierre. Théorie de l'addition des variables aléatoires. Paris: Gauthier-Villars, 1937.
MANDELBROT, Bonoit B. Fractais: Form, Change and Dimension. San Francisco: H W Freeman and Company, 1977.
______. The Fractal Geometry of Nature. New York: W. H. Freeman and Company, 1982.
NEUMANN, J. Von. Theory of Self Reproduction Automata. London: University of Illinois Press, 1966.
NOH, Jae Dong; PARK, Hyunggyu. Universality class of absorbing transitions with continuously varying critical exponents. Physical Review E, v. 69, n. 1, p. 12, jan. 2004.
ÓDOR, Géza. Critical behavior of the one-dimensional annihilation-fission process 2A Ø, 2A 3A. Physical Review E, Maryland, v. 62, n. 3, p. R3027-R3030, sep. 2000. ______. Critical behavior of the one-dimensional diffusive pair contact process.
Physical Review E, Maryland, v. 67, n. 1, p. 6, jan. 2003.
PARK, Kwangho; HINRICHSEN, Haye; KIM, In-mook. Binary spreading process with parity conservation. Physical Review E, Maryland, v. 63, n. 3, p. 4, may. 2001. RODRIGUES, A. L. Junior. Geoepidemiologia da aids e das doenças
oportunistas transmissíveis na Faixa de Fronteira Brasileira. Tese ( Livre
Docência) – Universidade de São Paulo, Ribeirão Preto, 2007.
SATULOVSKY, Javier E.; TOMÉ, Tânia. Stochastic lattice gas model for a predator-prey system. Physical Review E, Maryland, v. 49, n. 6, p. 6, jun. 1994
SOCIEDADE BRASILEIRA DE FÍSICA. Física para o Brasil: pensando o futuro. 2005. ed. São Paulo: Editora Livraria da Física, 2005..
TOMÉ, Tânia; OLIVEIRA, Mário J. De. Dinâmica Estocástica e Irreversibilidade. São Paulo: Editora da Universidade de São Paulo, 2001. v.1.
______. Stochastic mechanics of nonequilibrium systems. Brazilian Journal of
Physics, v. 27, n. 4, p. 525-532, 1997.
VISWANATHAN, S.; NAIK, N.; NEUBERGER, A. Trade disclosure regulation in
markets with negotiated trades. 4. ed. New York: Oxford University Press, v. 12,
1999.
ANEXOS
ANEXO A – PROGRAMA FRED2.F
Abaixo, o programa fred2.f, escrito em Fortran 77, que simula processos epidêmicos difusívos por pares. Uma primeira aproximação ao encontro dos pontos críticos.
c////////////////////////////////////////////////////////////////////////// /////////////////////
c programa simulador de processos epidemicos difusivos - VERSAO TESTE! c////////////////////////////////////////////////////////////////////////// /////////////////////
program pcp_dif
c////////////////////////////////////////////////////////////////////////// /////////////////////
c declaracao das variaveis set/2008
c////////////////////////////////////////////////////////////////////////// ///////////////////// implicit none integer ns,nts,tr,i,j,k,nb,na,rep,r,nsi,nsf,dn,idum,jj,kk,np,w, > a(10000),q,rep0,selec,dsd,ip,ipn, > soma,ar,ap,ig,iseed,jseed,mseed,nseed,ia,ib,m,npart,inew real y,pcont,pcura,f,z1
double precision r231, p,vp, th1, x,ants,rnts,m1,m2,m4,u,z,np1, > npm2(100000),npm4(100000),l(100000),ps(100000),rps,m21,alr231, > sp
parameter(nts=640,
> IA=843314861, IB=453816693, M=1073741824)
character*30 arquivo1,arquivo2
c////////////////////////////////////////////////////////////////////////// /////////////////////
c descricao das variaveis
c////////////////////////////////////////////////////////////////////////// /////////////////////
c p : probabilidade de criar (dada que nao ha difusao) c 1-p : probabilidade de aniquilar (dad que nao ha difusao) c vp : probabilidade de difusao
c nts : numero de sitios c rep : numero de ensaios c tr : tempo maximo
c np : numero de pares
c write(*,*)'nome do arquivo de dados' c read(*,*)arquivo2
c write(*,*)'nome do arquivo das amostras' c read(*,*) arquivo1
c write(*,*)'selecao das amostras 0 ou 1' c read(*,*) selec
c open (unit=1, file='dp1.dat',status='old') open (unit=2, file='l640_920.dat',status='new')
c sementes do gerador:
nseed = 506060543 mseed = 760274711 iseed = 566042033 jseed = 179394569
r231 = 1.d0/2147483647.d0
c////////////////////////////////////////////////////////////////////////// //////////////// ////
c constantes
c////////////////////////////////////////////////////////////////////////// /////////////////////
p = 0.920d0 vp= 0.1d0
th1 = vp + (1.d0-vp)*p
rep=12000 tr=12000 selec=0
ants=dfloat(nts) rnts=1.d0/ants alr231 = r231*ants
do j = 1, tr ps(j) = 0.d0 l(j) = 0.d0 npm2(j) = 0.d0 npm4(j) = 0.d0 enddo
c////////////////////////////////////////////////////////////////////////// ////////////////////
c selecao inicial das amostras
c////////////////////////////////////////////////////////////////////////// ////////////////////
c if(selec.eq.0)then
rep0=0
do 48 i=1,rep l(i)=0
c else
c open(unit=1,file=arquivo1) c read(1,*)rep0
c read(1,*)a c read(1,*)b c read(1,*)l c close(1) c end if
c////////////////////////////////////////////////////////////////////////// /////////////////////
c iniciando o programa
c////////////////////////////////////////////////////////////////////////// /////////////////////
c////////////////////////////////////////////////////////////////////////// /////////////////////
c Numero de amostras
c////////////////////////////////////////////////////////////////////////// /////////////////////
do 3500 r=rep0+1,rep
c////////////////////////////////////////////////////////////////////////// /////////////////////
c configuracao inicial aleatoria
c////////////////////////////////////////////////////////////////////////// /////////////////////
do i=1, nts a(i)=1 enddo np = nts npart = nts
c////////////////////////////////////////////////////////////////////////// /////////////////////
c evolucao do processo
c////////////////////////////////////////////////////////////////////////// /////////////////////
do 500 j=1,tr
c////////////////////////////////////////////////////////////////////////// /////////////////////
c um passo
c////////////////////////////////////////////////////////////////////////// /////////////////////
do 600 ig=1,nts
c////////////////////////////////////////////////////////////////////////// /////////////////////
c criacao, aniquiliacao e difusao
c////////////////////////////////////////////////////////////////////////// /////////////////////
c escolher um sitio:
if (nseed.lt.0) nseed = (nseed+M) + M i = alr231*nseed + 1
if(i.gt.nts) i=nts
c verificar se esta ocupado: if (a(i).eq.0) go to 600
c verificar se o vizinho a direita esta ocupado: ip = i + 1
if (i.eq.nts) ip = 1 if (a(ip).eq.0) go to 600
c escolher o processo:
iseed = IB + IA*iseed
if (iseed.lt.0) iseed = (iseed+M) + M z = iseed*r231
if (z.lt.vp) then
c difusao:
mseed = IB + IA*mseed
if (mseed.lt.0) mseed = (mseed+M) + M if (mseed.lt.1073741824) then
c par difunde a direita:
inew = ip + 1
if (ip.eq.nts) inew = 1 if (a(inew).eq.1) go to 600 a(i) = 0
a(inew) = 1 ipn = inew + 1
if (inew.eq.nts) ipn = 1 if (a(ipn).eq.1) np = np + 1 ipn = i - 1
if (i.eq.1) ipn = nts
if (a(ipn).eq.1) np = np - 1 else
c par difunde a esquerda:
inew = i - 1
if (i.eq.1) inew = nts if (a(inew).eq.1) go to 600 a(ip) = 0
a(inew) = 1 ipn = inew - 1
if (inew.eq.1) ipn = nts if (a(ipn).eq.1) np = np + 1 ipn = ip + 1
if (ip.eq.nts) ipn = 1
if (a(ipn).eq.1) np = np - 1 endif
else if (z.lt.th1) then
c criacao:
mseed = IB + IA*mseed
if (mseed.lt.1073741824) then
c tente criar na direita:
inew = ip + 1
if (ip.eq.nts) inew = 1 if (a(inew).eq.1) go to 600 a(inew) = 1
np = np + 1
npart = npart + 1 ipn = inew + 1
if (inew.eq.nts) ipn = 1 if (a(ipn).eq.1) np = np + 1 else
c tente criar na esquerda:
inew = i - 1
if (i.eq.1) inew = nts if (a(inew).eq.1) go to 600 a(inew) = 1
np = np + 1
npart = npart + 1 ipn = inew - 1
if (inew.eq.1) ipn = nts if (a(ipn).eq.1) np = np + 1 endif
else
c aniquilacao:
a(i) = 0 a(ip) = 0 np = np - 1
npart = npart - 2 inew = ip + 1
if (ip.eq.nts) inew = 1
if (a(inew).eq.1) np = np - 1 inew = i - 1
if (i.eq.1) inew = nts
if (a(inew).eq.1) np = np - 1 if (np.eq.0) go to 3500
endif
600 continue
if (np.eq.0) write (1,*) r, j, np, z, th1 ps(j) = ps(j) + 1.d0
np1 = dfloat(np)*rnts l(j)=l(j)+np1
npm2(j)=npm2(j)+np1**2 npm4(j)=npm4(j)+np1**4
c if (j.eq.24) write (1,*) j, npart, np, ps(j) c write (1,*) (a(i), i=1, nts)
c write (1,*)
3500 continue
c////////////////////////////////////////////////////////////////////////// /////////////////////
c escrevendo os resultados
c////////////////////////////////////////////////////////////////////////// /////////////////////
do j = 1, tr
if (ps(j).gt.0.) then sp = ps(j)/rep
rps = 1.d0/ps(j) m1 = l(j)*rps m2 = npm2(j)*rps m4 = npm4(j)*rps
c u = 1.d0-m4/(3.*m2**2) m21 = m2/(m1*m1)
write(2,11) j, sp, m1, m21 endif
enddo
11 format (i5,1x,f9.5,1x,f9.5,1x,f9.5,1x,f9.5)
ANEXO B – PROGRAMA PCPDPQ.F
Abaixo, o programa fonte pcpdpq.f, escrito em Fortran 77, que simula uma distribuição Quase-estacionária do processo de contato por para com difusão de pares.
c////////////////////////////////////////////////////////////////////////// /////////////////////
c QS simulacao do PCP com difusao de pares
c////////////////////////////////////////////////////////////////////////// /////////////////////
program pcpdpq
c////////////////////////////////////////////////////////////////////////// /////////////////////
c declaracao das variaveis
c////////////////////////////////////////////////////////////////////////// ///////////////////// implicit none integer ns,nts,tr,i,j,k,rep,r,nsi,nsf,dn,idum,jj,kk,np,w, > a(10000),q,rep0,iqq,dsd,ip,ipn,nc,nlst,lst,iprp,iprpr,ithst, > nabs,ig,iseed,jseed,mseed,nseed,ia,ib,m,npart,inew,ipr, > nrep,nrm real y,pcont,pcura,f,z1
double precision h,ht,r231, p,vp, th1, x,ants,rnts,m1,m2,m4,u, > z,np1,anrp,anrt,rhp,rht,rhp2,rht2,ai,pr,aip,ait,al,rmp,rmt, > l(100000),rps,m21,alr231,qq,qql,prt,prep,prepr,rhp3,rhp4, > sp,aip2,aip3,rL,rL2,rL3,rL4,rhrh,r4,ak2,ak4,qk,anrn,anrnm, > avrp,varp,avmp,vamp,avqk,vaqk,avt,vat,avrt,vart,avmt,vamt, > x1,x2,x3,x4,x5,x6 parameter(nts=320,nc=100,tr=100000000,ithst=1000000,rep=10, > prep=0.0005d0,prepr=10.d0*prep,al=nts,rL=1.d0/al,rL2=rL*rL, > rL3=rL*rL2,rL4=rL*rL3,anrn=rep,anrnm=anrn-1.d0,
> IA=843314861, IB=453816693, M=1073741824)
dimension lst(nc,nts), h(nts), ht(nts)
c////////////////////////////////////////////////////////////////////////// /////////////////////
c descricao das variaveis
c////////////////////////////////////////////////////////////////////////// /////////////////////
c p : probabilidade de criar (dada que nao ha difusao)
c 1-p : probabilidade de aniquilar (dada que nao ha difusao) c vp : probabilidade de difusao
c nts : numero de sitios c rep : numero de ensaios c tr : tempo maximo
C npart: numero de particulas c nc : numero de copias
c prep: probabilidade de reposicao na lista de configuracoes c prepr: " " " durante relaxacao
c h: histgrama do numero de pares
c ht: histgrama do numero de particulas
open (unit=1, file='dp1_320_974.dat',status='new') open (unit=2, file='cf1_320_974.dat',status='new')
c sementes do gerador:
nseed = 506060543 mseed = 760274711 iseed = 566042033 jseed = 179394569
r231 = 1.d0/2147483647.d0 iprp = prep*2147483647.d0 iprpr = prepr*2147483647.d0
c////////////////////////////////////////////////////////////////////////// //////////////// ////
c constantes
c////////////////////////////////////////////////////////////////////////// /////////////////////
p = 0.9174d0 vp= 0.1d0
th1 = vp + (1.d0-vp)*p
ants=dfloat(nts) rnts=1.d0/ants alr231 = r231*ants
avrp = 0.d0 varp = 0.d0 avmp = 0.d0 vamp = 0.d0 avqk = 0.d0 vaqk = 0.d0 avt = 0.d0 vat = 0.d0
avrt = 0.d0 vart = 0.d0 avmt = 0.d0 vamt = 0.d0
c////////////////////////////////////////////////////////////////////////// /////////////////////
c loop sobre realizacoes
c////////////////////////////////////////////////////////////////////////// /////////////////////