Domínios Fundamentais de Ford para Grupos de Isometrias Hiperbólicas Complexas

(1)

DOM´INIOS FUNDAMENTAIS DE FORD PARA GRUPOS DISCRETOS

DE ISOMETRIAS HIPERB ´

OLICAS COMPLEXAS

Seme Gebara Neto

Orientador:

Prof. Dr. Nikolai Alexandrovitch Goussevskii

Tese apresentada ao Departamento de Matem´

atica do Instituto de Ciˆ

encias Exatas

da Universidade Federal de Minas Gerais, como parte dos requisitos para

obten¸c˜

ao do grau de Doutor em Matem´

atica

(2)

`

(3)

Agradecimentos

Ao Nikolai, meu orientador.

Ao Chico, meu irm˜

ao.

(4)

Sum´

ario

Introdu¸c˜ao 1

1 O Espa¸co Hiperb´olico Complexo HnC 4

1.1 O modelo projetivo . . . 4

1.2 O dom´ınio de Siegel e o grupo de Heisenberg . . . 5

1.3 Classifica¸c˜ao das Isometrias Holomorfas . . . 7

1.4 Subvariedades totalmente geod´esicas e hipersuperf´ıcies equidistantes . . . 9

1.5 A estrutura CR para o espa¸co de Heisenberg . . . 13

1.6 Esferas isom´etricas . . . 14

1.6.1 Esferas isom´etricas de Dirichlet . . . 15

1.6.2 Esferas isom´etricas de Ford . . . 15

2 Dom´ınios fundamentais para grupos discretos de isometrias holomorfas 18 2.1 O dom´ınio fundamental de Ford em geometria hiperb´olica complexa . . . 18

2.2 O dom´ınio fundamental de Ford em geometria CR-esf´erica . . . 19

2.3 O Teorema dos Poliedros de Poincar´e . . . 20

2.4 O teorema de Giraud . . . 22

2.5 Finite dihedral groups . . . 23

2.6 Superposi¸c˜ao de grupos grupos diedrais . . . 27

2.7 Grupos gerados por trˆes transla¸c˜oes . . . 31

2.8 Grupos gerados por duas transla¸c˜oes . . . 35

(5)

Introdu¸

c˜

ao

O objetivo principal deste trabalho é descrever a estrutura combinatória dos poliedros fundamentais de Ford para alguns grupos discretos de isometrias holomorfas complexas. Entre os grupos estudados, estão os grupos c´ıclicos e alguns outros grupos elementares (isto é, cujo conjunto limite é finito).

O entendimento dos dom´ınios fundamentais é ferramenta importante para a constru¸cão de grupos discretos de isometrias. Muitos exemplos podem ser obtidos a partir de grupos elementares (grupos c´ıclicos, diedrais, abelianos, nilpotentes, solúveis, etc.), uma vez conhecida a estrutura combinatória de seus poliedros fundamentais de Dirichlet ou Ford, usando os teoremas de combina¸cão de Klein-Maskit.

Em geometria hiperbólica real, os poliedros fundamentais de Dirichlet e Ford para grupos elementares são bastante conhecidos. Mais do que isso, têm estrutura combinatória simples. Por exemplo, para grupos c´ıclicos onde o gerador é el´ıptico, parabólico ou hiperbólico, qualquer que seja a ordem do gerador (no caso el´ıptico) e qualquer que seja a dimensão do espa¸co hiperbólico real, os dom´ınios de Dirichlet ou Ford têm sempre duas faces.

Em geometria hiperbólica complexa novas dificuldades surgem, devido à natureza diferente desta ge-ometria. Uma dificuldade central diz respeito ao comprimento dos ciclos de arestas que aparecem nos poliedros de Dirichlet e Ford: o teorema de Giraud (veja o teorema 2.4.1) garante que cada ciclo de arestas não-planas de um poliedro de Dirichlet ou Ford para um grupo discreto de isometrias holomorfas complexas tem comprimento no máximo três. Este fato implica que a estrutura combinatória de um poliedro fundamental de Dirichlet ou Ford pode ser bastante complicada.

Isto se reflete j´a para grupos c´ıclicos gerados por um elemento el´ıptico de ordem finita. Considere um elemento el´ıptico g agindo no espa¸co hiperbolico complexo de dimens˜ao dois H2C, que deixa invariante

um R_-plano _R_{. Se} _G _{´e o grupo c´ıclico gerado por} _g_{, o poliedro de Ford para} _G _{´e o exterior comum}

entre as esferas isométricas dos elementos não-triviais do grupo. Olhando para a interse¸cão destas esferas com oR_{-plano invariante}_R_{, vemos que somente as esferas de}_g _e_g−1_{definem faces do dom´ınio de Ford,}

pois o exterior de cada uma das outras esferas isom´etricas cont´em o exterior comum entre esferas do gerador e de seu inverso. Mas em H2

C uma configura¸c˜ao bem diferente ocorre: cada uma destas esferas

isométricas contém (na verdade duas) faces do poliedro de Ford para G, chamadas por Giraud ([6]) de “lados invis´ıveis”, por não aparecerem na restri¸cão aR.

Os estudos sobre dom´ınios fundamentais de Ford para geometria hiperbólica complexa come¸cam com a generaliza¸cão do conceito de esfera isométrica de uma isometria holomorfa complexa, proposto por Goldman [7] (que provou também serem as esferas isométricas esferas espinais verticais) e passam pela demonstra¸cão de que o exterior comum a todas as esferas isométricas de elementos não-triviais de um grupo discreto define um dom´ınio fundamental para a a¸cão do grupo (o dom´ınio de Ford). Estudos nesta dire¸cão são encontrados em Goldman ([7]), Kamyia ([12]) e, de uma forma mais completa, em Dutenhefner ([3]).

(6)

• Phillips [18], onde é demosntrado que dom´ınios de Dirichlet para grupos c´ıclicos onde o gerador ou é um elemento hiperbólico ou um elemento parabólico unipotente, têm duas faces, independentemente da localiza¸cão do ponto base;

• Goldman e Parker [9], que caracterizaram os poliedros de Dirichlet para grupos diedrais, gerados por inversões em duas linhas complexas assintóticas: se Γ denota este grupo, foi mostrado que existe uma hipersuperf´ıcie real Γ-invarianteF tal que se o ponto base está em F o poliedro de Dirichlet tem exatamente duas faces, e, caso contrário, tem infinitas faces, e

• Parker [16], que estudou detalhadamente grupos c´ıclicos gerados por um elemento elipto-parabólico, concluindo que, se o ponto base está no eixo do gerador, então o poliedro de Dirichlet tem exatamente duas faces e, caso contrário, tem infinitas faces.

Por outro lado, trabalhos sobre a estrutura combinatória dos poliedros de Ford para grupos elementares de isometrias hiperbólicas complexas ainda são poucos e os casos conhecidos são apenas os mais simples. Esta tese caminha na dire¸cão de cobrir parte desta lacuna, estudando grupos c´ıclicos e alguns outros grupos elementares.

Um estudo bastante amplo sobre os poliedros de Ford para grupos c´ıclicos ´e apresentado. Os resultados aqui demonstrados s˜ao os seguintes:

?? Sejag_∈PU(2,1)um elemento elipto-parab´olico, que n˜ao fixa o ponto idealq, e sejaFG o dom´ınio

de Ford do grupoG=_hg_icom rela¸c˜ao aq. Ent˜ao

1. Seq pertence ao eixo deg,FG tem precisamente duas faces.

2. Seq n˜ao pertence ao eixo deg,FG tem infinitas faces.

?? Seja Go grupo gerado por um elemento el´ıptico regular g∈PU(2,1) de ordem finitan >2, com

g(q)6=q, que deixa invariante umR_-plano.

1. Seqpertence a um eixo deg, ent˜aoFGtem precisamente duas faces, contidas nas esferas isom´etricas

deg e de seu inverso.

2. Seqn˜ao pertence a nenhum eixo deg, ent˜aoFG tem2 + 2(n−3) = 2n−4faces: as duas primeiras

estão contidas nas esferas isométricas de g e de seu inverso, cada uma das demais esferas isométricas contém duas faces.

?? Sejag_∈PU(2,1)um elemento loxodrˆomico, que n˜ao fixa o ponto ideal q, e sejaFG o dom´ınio de

Ford do grupo G=_hg_icom rela¸c˜ao a q. Ent˜ao

1. Seg é hiperbólico, então FG tem precisamente duas faces.

2. Seg não é hiperbólico eqpertence ao eixo de g, entãoFG tem precisamente duas faces.

3. Segnão é hiperbólico e seqnão pertence ao eixo deg, então o número de faces deFGé finito, mas

pode ficar arbitrariamente grande.

Para que esta classifica¸cão sobre gurpos c´ıclicos esteja completa, falta apenas um caso, onde o gerador é um elemento el´ıptico regular que não preserva umR_{-plano. A diferen¸ca entre tais elementos e aqueles}

que preservam umR_{-plano pode ser descrita como segue: se}_g _{um elemento el´ıptico regular que preserva}

umR_-plano_R_{, então}_g_{é a composi¸c˜}_{ao das inversões em duas linhas complexas}_L₁_e_L₂_{perpendiculares a}

R. J´a um elementohque n˜ao preserva umR_{-plano pode ser obtido compondo-se}_g _{com uma rota¸c˜}_{ao (de}

ordem maior que dois) em torno deL2. Depende portanto de dois parˆametros reais. Grupos gerados por

este tipo de elemento s˜ao objetos de estudos futuros.

Sobre grupos c´ıclicos gerados por elementos el´ıpticos podemos observar tamb´em que o teorema ??

(7)

de Dirichlet para um grupo c´ıclico gerado por um elemento el´ıptico preservando um R_{-plano em} _H2 C:

podemos representar H2

C como a bola unit´ariaB2 ⊂C2 e sua fronteira como a esfera unit´ariaS3 ⊂C2.

Ent˜ao, qualquer vizinhan¸ca do ponto ideal q ∈ ∂H2

C em C2 cont´em pontos de H2C. Se a vizinhan¸ca

´e suficientemente pequena, para pontos base nesta vizinhan¸ca a estrutrua do dom´ınio de Dirichlet ´e exatamente a mesma daquela dos dom´ınios de Ford.

Como conseqüência das técnicas utilizadas nas demonstra¸cões dos resultados acima, caracterizamos também os poliedros de Ford para alguns outros grupos discretos de isometrias, provando os seguintes resultados

2.5.1O poliedro de FordFDn para o grupo diedral finito de ordem 2n,n≥2, tem exatamente 6n−6

faces. Cada esfera isométrica de um elemento não trivial contém duas faces (caso o elemento seja um ge-rador ou perten¸ca ao subgrupo c´ıclico gerado pelo produto dos gege-radores) ou quatro faces (caso o elemento seja uma inversão, exceto para os geradores). Pensado simplesmente como um poliedro emH2

C(ou emH),

isto é, como interse¸cão de semi-espa¸cos definidos pelas esferas isométricas,FDn tem2+2(2n−3) = 4n−4

faces. As duas primeiras contidas nas esferas isométricas dos geradores. Cada uma das outras esferas isométricas intercepta o exterior comum das esferas isométricas dos geradores em duas componentes co-nexas.

Há também um estudo sobre grupos gerados por inversões em três linhas complexas, duas delas ul-traparalelas e a terceira sua perpendicular comum, formando dois diedros, ambos com ângulo reto (se¸cão 2.6). Este é um exemplo de um grupo não-elementar. É mostrado que, sob certas condi¸cões, a estrutura do poliedro de Ford contém a estrutura dos poliedros de Ford de cada um dos diedros, no sentido que não há novas faces e arestas além daquelas que aparecem em cada um dos diedros quando observado isoladamente.

Finalmente, nas se¸cões 2.7 e 2.8 são estudados grupos gerados por duas ou três transla¸cões de Heisenberg, encontrando infinitas faces para o poliedro de Ford do grupo gerado por duas transla¸cões e 18 faces (48 arestas) para o poliedro de Ford do grupo gerado por três transla¸cões. Este último grupo pode ser visto como grupo fundamental de uma variedade tridimensional modelada na geometria do Grupo de Heisenberg (uma das oito geometrias existentes em dimensão três, também chamada Nil). Esta variedade é um fi-brado de c´ırculos sobre o toro e as rela¸cões entre os geradores deste grupo definem o número de Eulere

desta fibra¸cão e vice-versa. No exemplo estudado aqui, foi pré-fixadoe= 2. Um próximo trabalho pode caracterizar a estrutura combinatória do poliedro de Ford para estes grupos, em fun¸cão do númeroe.

(8)

Cap´ıtulo 1

O Espa¸

co Hiperb´

olico Complexo H

n

C

A seguir, uma descri¸cão do espa¸co hiperbólico complexo, que é o ambiente dos objetos deste trabalho. Os resultados enunciados neste cap´ıtulo podem ser encontrados, numa análise detalhada no livro de Goldman,

Complex Hyperbolic Geometry[7].

1.1 O modelo projetivo

O espa¸co hiperb´olico complexoHn

C n-dimensional ´e uma variedade de K¨ahler simplesmente conexa

com-pleta de curvatura seccional holomorfa negativa e constante. A métrica pode ser normalizada para que a curvatura holomorfa seja igual a -1. Os modelos apresentados a seguir estão normalizados desta ma-neira. Nessas condi¸cões, a curvatura seccional real deHn

Cvaria entre -1 e -1/4. O primeiro modelo a ser

apresentado ´e omodelo projetivo.

Vamos denotar porCn,1 _{o espa¸co vetorial complexo de dimens˜ao}_n_{+ 1 com a forma Hermitiana n˜ao}

degenerada_h·,_·idefinida por

hZ, W_i = z1w1 + · · · + znwn − zn+1wn+1,

sendo que

Z =



   

z1

.. .

zn

zn+1



   

e W =



   

w1

.. .

wn

wn+1



    .

Considere os seguintes sub-espa¸cos deCn,1_:

V0 = {Z ∈Cn+1: hZ, Zi= 0}

V− = {Z ∈Cn+1: hZ, Zi<0}

V+ = {Z∈Cn+1: hZ, Zi>0}.

Os vetores em V0,V− ouV+ s˜ao respectivamente chamados denulos,negativosoupositivos.

Seja P _: Cn,1_{\ {}₀_{} →} CPn _{a proje¸c˜}_{ao natural sobre o espa¸co projetivo. O} _espa¸_{co hiperb´}_olico complexo ´e definido como Hn

C = P(V−), munido da m´etrica Riemannina induzida da forma h·,·i pela

proje¸cãoP_{. Esta métrica é chamada de}_m´_{etrica de Bergman}_.

Visto que vetores negativosZpossuem a ´ultima coordenadazn+1diferente de zero, podemos normalizar

esta coordenada como 1. AssimHn

(9)

Bn ₌ ©

z = (z1, z2, . . . , zn), ∈ Cn : hhz, zii<1ª,

sendo que hh·,·ii denota o produto escalar usual emCn_.

O grupo de isometrias biholomorfas deHn

C´e PU(n,1) que age no espa¸co hiperb´olico complexo como

transforma¸cões lineares projetivas. Assim PU(n,1) é a projetiviza¸cão do grupo unitário U(n,1) com respeito à forma Hermitiana definida acima em Cn,1_{. Todo o grupo de isometrias de} _Hn_C _{é gerado por}

PU(n,1) e por conjuga¸cões complexas. Adistância de Bergmanρentre dois pontosz, w_∈Hn Cé dada

por

cosh2

µ_ρ₍_{z, w}₎

2

¶

= hZ, WihW, Zi

hZ, ZihW, Wi

sendo que Z eW s˜ao quaisquer vetores negativos emCn,1 _{que se projetam em}_z_e_w_{respectivamente.}

1.2 O dom´ınio de Siegel e o grupo de Heisenberg

A fronteira de Hn

C ´e a esfera S2n−1 =P(V0). Do mesmo modo, como a fronteira do espa¸co hiperb´olico

real pode ser identificada com a compactifica¸cão em um ponto do espa¸co Euclidiano, a fronteira do espa¸co hiperbólico complexo pode ser identificada com a compactifica¸cão em um ponto do grupo de Heisenberg.

Antes disso, vejamos odom´ınio de Siegelhn para o espa¸co hiperb´olico complexo. Este ´e o seguinte subconjunto deCn_:

hn={(w′, wn)∈Cn |2Re(wn)− hhw′, w′ii >0}

sendo que w′ _{= (}_w

1, . . . , wn−1)∈Cn−1. Astransforma¸c˜oes de Cayley

z∈Bn _←→ _w_∈_hn

zj= 2wj

1 + 2wn wj=

zj

1 +zn (1≤j < n)

zn= 1−2wn

1 + 2wn

wn=1

2 1−zn

1 +zn

relacionam o modelo da bola com o dom´ınio de Siegel.

O espa¸co hiperbólico complexo também pode ser parametrizado porcoordenadas horoesféricas[9, página 522]. Para definir coordenadas horoesféricas, é necessário escolher um ponto ideal q na fronteira do espa¸co hiperbólico complexo. Feito isso, cada ponto x_∈ Hn

C estar´a na interse¸c˜ao de uma horoesfera

centrada em qcom uma geod´esica real partindo de (ou chegando em) q. O ponto usualmente escolhido para definir coordendas horoesf´ericas tem no modelo projetivo coordenadas Q∞ =





0

−1 1



, e ´e denotado

q∞. Estas coordenadas s˜ao (ζ, v, u), pertencentes ao conjuntoS =Cn−1×R×R+, e parametrizamHnC,

no modelo projetivo e no dom´ınio de Siegel, por

ψ: Cn−1_×R_×R₊ _−→ _Hn_C

(ζ, v, u) _−→





2ζ

1_{− hh}ζ, ζ_{ii −}u+iv

1 +_hhζ, ζ_ii+u₋iv 



(10)

Cn−1_×_R_×_R

+ −→ hn

(ζ, v, u) −→

" _ζ

hhζ, ζ_ii+u₋iv

2

#

onde_hh·,_·iidenota a forma Hermitiana usual definida positiva emCn−1_.

A correspondˆencia inversaψ−1 _{assinala, a cada vetor negativo}



 z′

zn

zn+1



, emCn,1, as seguintes

coorde-nadas horoesf´ericas:

ζ= z

′

zn+zn+1

, v= Im

µ_z

n−zn+1

zn+zn+1

¶ ,

u=₋Re

µ

zn−zn+1

zn+zn+1

¶

− hhz

′_{, z}′

ii |zn+zn+1|2

.

(1.2)

Esta equa¸c˜ao pode ser escrita como a seguinte igualdade de vetores emCn,1_:



 z′

zn

zn+1



 =

1

2(zn+zn+1)





2ζ

1_{− hh}ζ, ζ_{ii −}u+iv

1 +_hhζ, ζ_ii+u₋iv 

 =

1

2(zn+zn+1)ψ(ζ, v, u) (1.3)

Por outro lado, cada pontow= (w′_{, w}

n) no dom´ınio de Siegel hn, define coordenadas horoesf´ericas por

ζ = w′ , v = ₋2 Im(wn) e u = 2 Re(wn)− hhw′, w′ii.

A fronteira do espa¸co hiperb´olico complexo∂Hn

C≃S2n−1, est´a em correspondˆencia biun´ıvoca com o

conjunto

∂HnC ≃ Cn−1×R× {0} ∪ {q∞},

ondeq∞´e o ponto distinguido no infinito. Para simplificar, vamos utilizar coordenadas (ζ, v), ao inv´es de

(ζ, v,0), para denotar pontos na fronteira.

A identifica¸c˜ao acima, entre o espa¸co hiperb´olico complexo e o dom´ınio de Siegel_S=Cn−1_×R_×R₊_,

pode ser estendida `a fronteira destes espa¸cos simplesmente adicionando que

ψ: q∞ 7→ Q∞=





0

−1 1



.

Deste modo, podemos identificar a fronteira do espa¸co hiperbólico complexo com a compactifica¸cão em um ponto dogrupo de Heisenberg_H=Cn−1_×R_{. A opera¸c˜}_{ao deste grupo é definida por}

(ζ, v)_∗ (ζ′, v′) = (ζ+ζ′, v+v′+ 2 Im_hhζ, ζ′_ii).

As coordenadas horoesféricas também são utilizadas para se definir anorma de Heisenberg_{| · |}0no

dom´ınio de Siegel. Esta norma ´e definida por

|ζ, v, u_|0 = | kζk2+u−iv|1/2 = 4

p

(11)

Amétrica de Cygan[15, página 297] emS é definida por

ρ0((ζ1, v1, u1),(ζ2, v2, u2)) = |ζ1−ζ2, v1−v2+ 2Imhhζ1, ζ2ii, |u1−u2| |0 (1.5)

1.3 Classifica¸

c˜

ao das Isometrias Holomorfas

Um automorfismo g de Hn

Cé representado por uma transforma¸cão unitária ˜g de Cn,1, e os pontos fixos

de g em Hn

C correspondem a autovetores do levantamento ˜g. Pelo teorema do ponto fixo de Brouwer,

todo automorfismo deHn

Cpossui um ponto fixo emHnC ∪ ∂HnC. Ent˜ao, podemos dividir os elementos do

grupo PU(n,1), de isometrias holomorfas deHn

C, em três categorias básicas (veja [2] ou [7, página 203]).

Dizemos que g_∈PU(n,1) ´e

• el´ıpticosegpossui, pelo menos, um ponto ponto fixo emHn C,

• parab´olico seg possui exatamente um ponto fixo na fronteira deHn C,

• loxodrˆomicosegpossui exatamente dois pontos fixos na fronteira deHn C.

Em dimensãon = 2, se um elemento g em PU(2,1) é loxodrômico, então o levantamento ˜g possui autovalores da forma eiθ_, _k _{e 1}_/k_{, para um certo n´}_{umero real} _θ _{e um outro n´}_{umero real positivo} _k_.

Dizemos que este elemento ´ehiperb´olicoseθ= 0.

Um elementogé el´ıptico se, e somente se,ggera um grupo c´ıclico cujo fecho é compacto. Os autovalores da matriz correspondente têm sempre norma 1. Dizemos também que um elemento el´ıpticogé el´ıptico-regularse todos os autovalores da correspondente matriz degsão distintos. Por outro lado, um elemento el´ıpticog éel´ıptico-especialsegpossui pontos fixos na fronteira do espa¸co hiperbólico complexo.

Um elemento parabólicogéunipotenteseg puder ser representado por um elemento unipotente em U(n,1); isto é, uma transforma¸cão linear tendo 1 como seus únicos autovalores. Este elemento parabólico

géel´ıptico-parabólicosegnão é unipotente. Neste caso,gpossui uma única linha complexa invariante Σ na qualg age como um automorfismo parabólico (de H1

C) e g age como um automorfismo n˜ao trivial

no fibrado normal `a Σ.

Em [7, p´agina 204], Goldman definiu umafun¸c˜ao discriminante

f :C _−→ R

f(z) = _|z_|4 ₋ 8Re(z3) + 18_|z_|2 ₋ 27.

que pode ser usada para se determinar a classe de conjuga¸c˜ao de elementos em SU(2,1), o conjunto das matrizes em U(2,1) com determinante igual a 1. De fato, seω3 denota a ra´ız c´ubica primitiva de 1 emC,

podemos enunciar

Teorema 1.3.1 Sejaτ : SU(2,1) −→ C_{a fun¸c˜}_{ao que associa a cada matriz o seu tra¸co. Se}_A_∈_SU(2_,₁₎ ent˜ao

1. Aé el´ıptico-regular se, e somente se,f(τ(A)) < 0; 2. Aé loxodrômico se, e somente se,f(τ(A)) > 0;

3. Aé el´ıptico-parabólico se, e somente se, A não é el´ıptico e τ(A)_∈f−1₍₀₎

− {1, ω3, ω23}.

4. Aé uma reflexão complexa (isto é, de ordem 2 que fixa ou um ponto ou uma linha complexa emH2 C

se, e somente se,A´e el´ıptico e τ(A)_∈f−1₍₀₎

(12)

5. A´e parab´olico unipotente se, e somente se,τ(A)∈ {1, ω3, ω32}.

Vejamos agora alguns exemplos importantes de isometrias holomorfas do espa¸co hiperb´olico complexo

H2

C. [7, se¸c˜ao 4.2.2, p´agina 120]

Fixado um ponto (ζ0, v0) do grupo de Heisenberg H = C×R, a transla¸c˜ao de Heisenberg por

(ζ0, v0) é a aplica¸cãoT(ζ0,v0) em PU(2,1) representada pela seguinte matriz unitária

T(ζ0,v0) =





1 ζ0 ζ0

−ζ0 1−1₂(kζ0k2−iv0) −1₂(kζ0k2−iv0)

ζ0 1₂(kζ0k2−iv0) 1 +1₂(kζ0k2−iv0)



.

Em coordenadas horoesf´ericas, esta isometria age como:

T(ζ0,v0)(ζ, v, u) = (ζ0+ζ , v0+v+ 2 Imhhζ0, ζii, u).

Esta aplica¸cão é parabólica, com ponto fixo o ponto idealq∞, e age transitivamente em cada horoesfera,

centrada emq∞, deH2C.

Adilata¸cão de Heisenbergde fatork >0 é representada pela matriz unitária

Dk =





1 0 0 0 1+k_2k2 1−k_2k2 0 1−k2

2k

1+k2 2k



.

Em coordenadas horoesf´ericas,Dk age como:

Dk(ζ, v, u) = (k ζ , k2v , k2u).

Esta aplica¸cão é hiperbólica com pontos fixos (0,0) _{∈ H} e q∞. Mais ainda, Dk age transitivamente no

conjunto de horoesferas, centradas emq∞, deH2C.

Umacadeia verticalsobre um pontoζ0∈Cno grupo de Heisenberg ´e o conjunto (veja mais detalhes

na se¸c˜ao 1.4)

{ (ζ0, v) : v∈R} ∈ H

A rota¸c˜ao de Heisenbergao redor da cadeia vertical sobre 0∈C_{´e representada pela seguinte matriz}

unit´aria:

A =





eiθ _{0 0}

0 1 0 0 0 1



,

e age, em coordenadas horoesf´ericas, como

A(ζ, v, u) = (eiθ_{ζ , v , u}₎_.

Esta aplica¸c˜ao ´e el´ıptica-especial e tem como conjunto de pontos fixos emH2

C∪∂H2C:

½ · z1

z2

¸

∈ B2 _{tal que} _z₁_{= 0 e}_|_z₂_{| ≤} ₁

¾ .

Um elemento loxodrômico, não hiperbólico,g é conjugado a uma rota¸cão de Heisenberg ao redor da cadeia vertical seguida de uma dilata¸cão de Heisenberg. Portanto g age em coordenadas horoesféricas como:

(13)

1.4 Subvariedades totalmente geod´

esicas e hipersuperf´ıcies

equi-distantes

Defini¸c˜ao 1.4.1 O produto vetorial Hermitiano

⊠ :C2,1_×C2,1_−→C2,1

´e definido por(veja [7, p´agina 45])

v⊠w =



 v1

v2

v3



 ⊠ 

 w1

w2

w3



 = 



v3w2 − v2w3

v1w3 − v3w1

v1w2 − v2w1





Este produto vetorial Hermitiano ⊠ desempenha, no espa¸co vetorial complexo 3-dimensional C2,1_{, um}

papel parecido ao do produto vetorial usual_×, no espa¸co EuclidianoR3_{. Isto ´e, o produto vetorial de dois}

vetores ´e um vetor perpendicular aos vetores originais, ou seja,

hv, v⊠w_i = _hw, v⊠w_i = 0.

As subvariedades totalmente geod´esicas do espa¸co hiperb´olico complexoHn

C podem ser listadas (veja

o artigo [2] para mais detalhes); h´a dois tipos: seja J a estrutura quase-complexa de Hn

C herdada da

estrutura usual em Cn,1 _{pela proje¸c˜}_{ao natural}_P_{. As subvariedades totalmente geod´esicas de} _Hn C ou s˜ao

holomorfas(seu espa¸co tangente em cada ponto ´e invariante pela estrutura quase-complexaJ deHn Cou

sãototalmente reais(cujo espa¸co tangente em cada ponto é ortogonal à sua imagem por J).

Por isometrias do espa¸co hiperb´olico complexo, as subvariedades totalmente geod´esicas holomorfas de

Hn

C s˜ao equivalentes a HkC, para todo inteiro k, 1≤k ≤n, onde este espa¸co hiperb´olico pode ser visto

como um subconjunto de Hn

C, simplemente considerando-se as ´ultimas n−k coordenadas iguais a zero.

Se a codimensão complexa é 1, esta subvariedade é chamada dehiperplano complexoe se a dimensão complexa é 1, delinha complexa.

Os hiperplanos complexos deHn

C possuem uma descri¸c˜ao simples (veja [7, p´agina 99]). Se H ⊂HnC

é um hiperplano complexo, entãoH =P_{( ˜}_H_{) onde ˜}_H _⊂Cn,1 _{é um hiperplano linear complexo de}Cn,1_.

Ent˜ao, ˜H⊥_{´e uma linha positiva. Assim, para qualquer vetor positivo}_P

∈H˜⊥_{, temos que}

H = _{z_∈HnC : hz, P˜ i= 0 sendo ˜z∈C

n,1 _{um levantamento de} _z

}

Um tal vetorP ´e chamado devetor polar ao hiperplano complexoH.

Em dimens˜aon= 2, os conceitos de hiperplano complexo e linha complexa coincidem. Portanto, toda linha complexa em H2

Cpode ser dada por um vetor polar.

Proposi¸c˜ao 1.4.1 Seja Σ uma linha complexa em H2C e sejam xe y dois pontos distintos de Σ. Para

quaisquer representantes,X eY, destes pontos emC2,1_{, um vetor polar a esta linha complexa ´e dado por}

PΣ = X⊠Y.

As posi¸c˜oes relativas de duas linhas complexas Σ1 e Σ2, emH2C, s˜ao nomeadas da seguinte maneira:

• Σ1e Σ2sãoconcorrentesse elas se encontram em um único ponto no interior do espa¸co hiperbólico

complexo.

• Σ1e Σ2sãoassintóticasse elas se encontram em um único ponto na fronteira do espa¸co hiperbólico

(14)

• Σ1 e Σ2 s˜aoultraparalelasse elas n˜ao se encontram emH2C∪∂H2C.

Defini¸c˜ao 1.4.2 Sejam Σ1 e Σ2 duas linhas complexas em H2C concorrentes em um ponto z ∈ H2C. O

ˆ

anguloφ=∠(Σ1,Σ2)entreΣ1 eΣ2é definido como o menor ângulo Riemanniano entre duas geodésicas

γ1⊂Σ1 e γ2⊂Σ2 que passam porz.

Da defini¸cão acima, é claro que o ângulo∠(Σ1,Σ2) pertence ao intervalo 0≤∠(Σ1,Σ2)≤π/2.

Defini¸cão 1.4.3 Sejam Σ1 e Σ2 duas linhas complexas ultraparalelas em H2C. Então, existe uma única

linha complexa Σortogonal comum àΣ1 e àΣ2. AdistânciaentreΣ1 eΣ2 é definida como a distância

entre os pontosΣ∩Σ1 e Σ∩Σ2 do espa¸co hiperb´olico complexo.

Em [7, página 100], foi apresentada uma maneira para se determinar o ângulo e a distância entre duas linhas complexas, em fun¸cão de vetores polares a elas.

Proposi¸c˜ao 1.4.2 Sejam Σ1 e Σ2 duas linhas complexas emH2C, com respectivos vetores polares P1 e

P2, normalizados de modo que hP1, P1i = hP2, P2i = 1. Neste caso,

1. se _|hP1, P2i| < 1, então Σ1 e Σ2 são concorrentes e |hP1, P2i| = cos(φ), onde φ é o ângulo entre

estas linhas complexas. Neste caso,P1⊠P2´e um vetor negativo, que representa o pontoΣ1∩Σ2.

2. se_|hP1, P2i|= 1, entãoΣ1eΣ2são assintóticas. Neste caso,P1⊠P2é um vetor nulo, que representa

o pontoΣ1∩Σ2, contido na fronteira do espa¸co hiperb´olico complexo.

3. se _|hP1, P2i| >1, então Σ1 e Σ2 são ultraparalelas e |hP1, P2i|= cosh(ρ/2), onde ρ é a distância

entre estas linhas complexas. Neste caso,P1⊠P2 é um vetor positivo, polar à única linha complexa

ortogonal comum aΣ1 e Σ2.

Associado a uma subvariedade totalmente geod´esica complexaF ⊂Hn

C est´a o conceito de proje¸c˜ao

ortogonalΠF :HnC−→F (veja [7, p´agina 75]). De fato, temos queHnC ´e uma variedade Riemanniana

completa e simplesmente conexa de curvatura n˜ao positiva e F ⊂ Hn

C ´e uma subvariedade totalmente

geod´esica e completa. Para todo x∈Hn

C, a fun¸c˜ao distˆancia

Hn C−→R

u _7→ ρ(u, x) é uma fun¸cão estritamente convexa ao longo de geodésicas emHn

C. Visto queF ´e totalmente geod´esica, a

restri¸cão desta fun¸cão àFtambém é estritamente convexa e, portanto, possui um único m´ınimo. Definimos então ΠF(x)∈ F como sendo o ponto de F mais próximo de x. É claro que, a linha geodésica de xa

ΠF(x) ´e ortogonal `aF em ΠF(x).

Mais ainda, existe umainversãoiF :HnC−→HnCemF. Esta inversão é uma aplica¸cão em PU(n,1),

de ordem 2, cujo conjunto de pontos fixos ´e precisamente F e que pode ser definida do seguinte modo: para todox_∈Hn

C, ΠF(x) é o ponto médio, na métrica de Bergman, entrexeiF(x).

SeF ⊂Hn

Cé um hiperplano complexo com vetor polarP, então a proje¸cão ortogonal ΠF :HnC−→F

sobreF e a invers˜aoiF :HnC−→HnCemF s˜ao dadas por

iF(Z) = −Z + 2h

Z, P_i

hP, PiP ΠF(Z) = Z −

hZ, P_i

(15)

sendo que estamos considerandoZ um vetor negativo e P um vetor positivo emCn,1_.

Passemos agora a estudar as subvariedades totalmente geodésicas e totalmente reais. Por isometrias do espa¸co hiperbólico complexo, elas são equivalentes a Hk

R, para k inteiro tal que, 1 ≤ k ≤ n, onde

este espa¸co hiperb´olico real pode ser visto como um subconjunto de Hn

C simplesmente considerando-se

as últimasn₋k coordenadas iguais à zero e as primeiraskcoordenadas números reais. A subvariedade totalmente geodésica Hk

R ´e chamada de puramente real. Uma tal subvariedade totalmente geod´esica

e totalmente real de dimensão maximal n é chamada de Rn_-plano_{. Neste caso, também temos que,}

associado a um Rn_{-plano está o conceito de}_invers˜_ao_{. Esta inversão é uma isometria anti-holomorfa de} Hn

C, de ordem 2, cujo conjunto de pontos fixos é precisamente oRn-plano. Em dimensãon= 2, a inversão

J noR2_{-plano puramente real}_H2_R_{´e dada por}

J :



 z1

z2

z3



 7−→ 



1 0 0 0 1 0 0 0 1



 

 z1

z2

z3



 = 

 z1

z2

z3



.

Em dimens˜ao n= 2, a interse¸c˜ao de uma linha complexa com a fronteira de H2

C´e uma cadeia e a

interse¸c˜ao de umR2_{-plano com} _∂_H2

C´e umR-c´ırculo. No grupo de HeisenbergH=C×R, estas curvas

possuem uma descri¸cão geométrica simples (veja [7, se¸cões 4.3 e 4.4]). Uma cadeia ou é uma reta vertical ou é uma elipse que se projeta, no plano complexo C_{× {}₀_}_{, em uma circunferência. Um} R_{-c´ırculo ou}

é uma reta Euclidiana horizontal ou é o levantamento horizontal de uma leminiscata contida no plano complexo C_{× {}₀_}_{. ´}_{E claro que as inversões em linhas complexas e em} R2_{-planos definem inversões nas}

respectivas cadeias eR_{-c´ırculos em}_H_.

´

E importante observar que no espa¸co hiperbólico complexo não existem subvariedades totalmente geodésicas de codimensão real 1.

Lembre-se do conceito de superf´ıcies equidistantes no espa¸co hiperb´olico complexo (veja os detalhes em [7, cap´ıtulo 5]): sejam z1 e z2 dois pontos distintos emHCn. Obissetor equidistante dez1 ez2 ´e

definido por

B = B{z1, z2} = {z∈H2C|ρ(z, z1) =ρ(z, z2)}

Seja Σ _⊂ Hn

C a ´unica linha complexa contendo z1 e z2 e seja σ ⊂ Σ a geod´esica de Σ que bissecta o

segmento geod´esico que liga z1 a z2. Chamamos Σ de espinha complexa e σ de espinha real do

bissetorB.

Um bissetor ´e uma subvariedade de codimens˜ao real 1 emHn

C; portanto não é totalmente geodésico.

Mas ele possui duas decomposi¸cões em subvariedades totalmente geodésicas: uma por subvariedades holo-morfas e outra por subvariedades totalmente reais. Estas decomposi¸cões são chamadas dedecomposi¸cão em fatias de Mostowedecomposi¸cão em meridianos de Goldman.

Teorema 1.4.1 (decomposi¸c˜ao em fatias) Seja B um bissetor em Hn

C com espinha complexa Σ e

espinha real σ. SeΠΣ:HnC→Σdenota a proje¸c˜ao ortogonal sobreΣ, ent˜ao

B = Π−1_Σ (σ) = [

s∈σ

(16)

Na igualdade acima, é claro que, para cada s ∈ σ, Π−1Σ (s) é uma linha complexa ortogonal à Σ em s.

Estas linhas complexas s˜ao asfatiasdo bissetorB.

Teorema 1.4.2 (decomposi¸c˜ao em meridianos) Seja B um bissetor em Hn

C com espinha real σ.

Então, para cadak satisfazendo 2_≤k_≤n,B é a união de todos osRk_{-planos contendo}_σ_.

OsRn_{-planos contendo a espinha real de um bissetor s˜ao chamados de}_meridianos_.

´

E claro que uma linha geod´esica completaσemHn

Cdefine um ´unico bissetor. Assim, os pontos finais

V1 e V2 desta geodésica em ∂HnC também definem, de maneira única, este bissetor. Este pontos são os

v´erticesdo bissetor de espinha realσ.

A interse¸cão de um bissetor com a fronteira do espa¸co hiperbólico complexo é chamada de esfera espinal. Do mesmo que bissetores, uma esfera espinal também se decompõe em fatias e meridianos, que são fronteiras das fatias e meridianos do bissetor, e também fica unicamente definida pela escolha dos seus vértices.

As invers˜oes em fatias e meridianos de um bissetor deixam o bissetor invariante.

Teorema 1.4.3 Seja B um bissetor emHn C.

1. SeF é uma fatia deB, então a inversãoiF permuta os vértices deB, portanto deixaB invariante

e tamb´em deixa invariante cada meridiano deB.

2. SeM é um meridiano de B, então os vértices deB são fixados pela inversãoiM, logo iM deixaB

invariante. iM tamb´em deixa invariante cada fatia de B.

Os exemplos mais simples de bissetores em H2

C, s˜ao aqueles que tˆem como fronteira as esferas de

Heisenbergou osplanos de contato, que definimos a seguir, usando no grupo de HeisenbergH=C_×R

coordenadas horoesf´ericas (ζ, v),ζ=x+iy.

Sejap0 = (ζ0, v0) um ponto qualquer no grupo de Heisenberg e sejaR um n´umero real positivo. A

esfera de HeisenbergI de centrop0 = (ζ0, v0) e raioR ´e a esfera, na m´etrica de Cygan, com este centro

e este raio, isto é, I = {p∈ H |ρ0(p, p0) = R}. Se p= (ζ, v), então I é caracterizada pela seguinte

equa¸c˜ao:

|ζ−ζ0|4 +

·

v −v0 − 2 Im

µ ζ0ζ

¶¸2

= R4

Os v´ertices desta esfera de Heisenberg s˜ao os pontosV1= (ζ0, v0+R2) eV2= (ζ0, v0−R2). Portanto, a

espinha complexa da esfera de HeisenbergI´e a cadeia vertical sobre o seu centro.

Sejap0= (ζ0, v0) um ponto qualquer no grupo de Heisenberg. O plano de contatoE(ζ0,v0), definido por

p0, é a esfera espinal que tem como vértices o ponto idealq∞e o pontop0. Em coordenadas horoesféricas,

esta esfera espinal ´e dada pela equa¸c˜ao

v = v0 − 2 Im

µ ζ ζ0

¶

= v0 + 2y0x −2x0y,

ondeζ0=x0+iy0 e (ζ=x+iy, v) ´e um ponto emE(ζ0,v0). ´E claro que a espinha complexa desta esfera

(17)

1.5 A estrutura CR para o espa¸

co de Heisenberg

A fronteira do espa¸co hiperb´olico complexoHn

C´e a compactifica¸c˜ao em um ponto do grupo de Heisenberg

H =Cn−1_×R_{e admite uma estrutura natural de Cauchy-Riemann (CR-estrutura), isto ´e, um campo}

de hiperplanos E _⊂ T ∂Hn

C possuindo uma estrutura complexa satisfazendo v´arias propriedades. Esta

estrutura de Cauchy-Riemann define a estrutura do espa¸co hiperb´olico complexo no sentido que um CR-automorfismo holomorfo da ∂Hn

C se estende unicamente como uma isometria holomorfa de HnC e,

reciprocamente, cada isometria do espa¸co hiperb´olico complexo define um automorfismo de contato desta CR-estrutura.

Em geral, uma hipersuperf´ıcie realH, bastante regular, em uma variedade complexaM, admite uma tal estrutura. Para todox_∈H, lembramos que esta estrutura CR emx´e definida por: [9, p´agina 523]

Ex = TxH ∩ J(TxH)

sendo que J:TxH →TxH denota a estrutura quase-complexa deM.

Neste sentido ent˜ao, toda horoesferaHu⊂HnCadmite uma tal estrutura de Cauchy-Riemann. Mais

ainda, veremos que a perspectiva geod´esica preserva o campo de hiperplanos que define a estrutura CR deHn

C. Desta propriedade, poderemos definir uma estrutura CR na fronteira∂HnC do espa¸co hiperb´olico

complexo.

Para isso vamos fazer uso do operador diferencial realdc_{, definido como sendo a parte imagin´aria do}

operador diferencial complexo 2∂, isto ´e,

dc= 2Im(∂) =−i(∂−∂).

Lema 1.5.1 Seja M uma variedade complexa e seja H uma hipersuperf´ıcie real de M definida por

H =f−1₍₀₎_sendo_O_{um valor regular de uma fun¸c˜}_{ao diferenci´}_avel_f _:_M _→_R_{. Ent˜}_ao,_ω₌_dc_f _:_{T M} _→_R

é uma calibra¸cãopara a estrutura CR de H induzida do seu mergulho na variedade complexaM. Isto é, para todox∈H, temos queEx= Ker{dcfx:TxH→R}.[7, página 59]

Vamos determinar agora uma 1-forma que calibra a estrutura de Cauchy-Riemann da fronteira do espa¸co hiperb´olico complexo. Esta 1-forma de contato ω depende do potencial de K¨ahler associado ao ponto q∞, no infinito do grupo de Heisenberg. Para este fim, considere agora o dom´ınio de Siegel

hn=_{(w1, . . . , wn)∈Cn |2Re(wn)− hhw′, w′ii >0}

para o espa¸co hiperbólico complexo. Cada horoesferaHu, do espa¸co hiperbólico complexo, é definida como

o conjunto de n´ıvelf−1₍_u_{) da fun¸c˜}_ao_f₍_w_{) = 2Re(}_w

n)− hhw′, w′ii.Deste modo, estas horoesferas tamb´em

s˜ao os conjuntos de n´ıvel do potencial de K¨ahler associado a q∞, ψq∞(w) = ln(2Re(wn)− hhw

′_{, w}′

ii). O potêncial de Kähler é invariante pelo estabilizador de q∞ em PU(n,1), mas a fun¸cão f, acima, não é

invariante por este grupo de isotropia. Então, para definirmos a estrutura de Cauchy-Riemann em cada horoesfera, é melhor utilizarmos o potencial de Kähler ao invés da fun¸cãof. Pelo lema anterior, a estrutura de Cauchy-Riemann em cada horoesfera é calibrada pela 1-forma ω =dc_ψ

q∞ no sentido que para cada

x_∈Hn

C, se Hu é a única horoesfera contendo x, então o campo de hiperplanos Ex⊂Tx(Hu) é o núcleo

do funcional linearωx|TxHu :TxHu → R.

Em coordenadas horoesf´ericas (ζ, v, u) _∈ Cn−1_×R_×R₊ _{para o espa¸co hiperb´olico complexo, esta}

1-forma de contatoω´e dada por: [7, p´agina 123]

ω = 1

u(dv − 2Imhhζ, dζii) =

1

u(dv + 2xdy−2ydx) =

1

u 

dv + 2

n−1

X

j=1

(xjdyj −yjdxj)



(18)

ondeζ= (ζ1, . . . , ζn−1) eζj=xj+iyj.

Finalmente, vejamos como definir uma estrutura de Cauchy-Riemann para o grupo de Heisenberg

H = ∂HnC− {q∞}. De maneira geométrica, a fun¸cão que identifica as diversas horoesferas de H n C é a

perspectiva geod´esica [9, p´agina 522]

Πu:Ht −→ Hu

(ζ, v, t) _7→ (ζ, v, u).

Claramente, esta aplica¸c˜ao preserva este campo de hiperplanos emHn

C. Daqui, podemos dizer que este

campo de hiperplanos ´e paralelo ao longo de geod´esicas que terminam no ponto ideal q∞. De maneira

anal´ıtica, vimos que para cadax= (ζ, v, u)_{∈ S}, a estrutura CR em x´e o hiperplano real deTxHu dado

por

Ex = Kerωx = Ker

µ

1

u(dv + 2xdy−2ydx) ¶

= Ker (dv + 2xdy₋2ydx)

o qual é independente da coordenada horoesféricau. Isto demonstra a afirma¸cão acima, de que este campo de hiperplanos é paralelo ao longo de perspectivas geodésicas. Então, no grupo de Heisenberg_Htambém podemos definir uma estrutura de Cauchy-Riemnann, como o campo de hiperplanos

Ker (dv + 2xdy−2ydx).

Mais ainda, a 1-forma de contato que calibra esta estrutura de Cauchy-Riemann ´e dada por

ω = dv + 2xdy−2ydx , ∀(ζ, v)∈ H onde ζ=x+iy.

1.6 Esferas isom´

etricas

Nesta se¸cão, os bissetores serão relacionados com calibra¸cões da estrutura de Cauchy-Riemann da fronteira do espa¸co hiperbólico complexo. Lembre-se, pelo lema 1.5.1, que se_U é uma vizinhan¸ca de∂Hn

C⊂P(Cn,1)

e sef :_{U →}R_{é uma fun¸c˜}_{ao diferenciável com valor regular 0 e se} _f−1_{(0) =}_∂_Hn_C_{, então a restri¸c˜}_{ao de}

dc_f _`_a _∂_Hn

C ´e uma 1-forma de contato calibrando a estrutura CR na∂HnC. O espa¸co das calibra¸c˜oes da

estrutura CR da∂Hn

C ´e denotado por Cal(∂HnC). Observe que este conjunto ´e 1-dimensional no sentido

que seω1, ω2∈Cal(∂HnC), ent˜ao existe uma fun¸c˜aoλ:∂HnC→Rtal queω1=λω2.

Seg´e um autormorfismo da estrutura CR da ∂Hn

Ce se ω ∈Cal(∂HnC), tem-se queg∗ω∈Cal(∂HnC).

Isto implica que existe uma fun¸c˜aoJg,ω :∂HnC→Rtal que

g∗ω = Jg,ωω.

Esta fun¸cãoJg,ω é chamada dedistor¸cãode g com respeito aω [7, página 179]. A esfera isométrica

degcom respeito aω, denotada porIg,ω, é o conjunto dos pontos para os quais a calibra¸cãoω não muda

porg, isto ´e,

Ig,ω = {z∈∂HCn : Jg,ω(z) = 1}.

Portanto, associadas a diferentes calibra¸cões podem ser definidas diferentes esferas isométricas para um mesmo automorfismo g. Vejamos agora alguns casos particulares de calibra¸cões, associadas a entidades geométricas deHn

C, que irão definir esferas isométricas de interesse geométrico: as esferas isométricas de

(19)

1.6.1 Esferas isom´

etricas de Dirichlet

A esfera isom´etrica de Dirichlet de um automorfismogdeHn

Cser´a definida como a esfera isom´etrica deg

com respeito a uma 1-forma de contatoωxdefinida por um potencial de K¨ahlerψxassociado a um ponto

xno interior do espa¸co hiperb´olico complexo.

Precisamente, sejaxqualquer ponto no interior do espa¸co hiperb´olico complexo. O potencial de K¨ahler

ψx:HnC→Rassociado ax´e dado por

ψx(z) = 2 ln sech

µ ρ(z, x)

2

¶

= lnhX, XihZ, Zi

hX, Z_ihZ, X_i,

sendo que X eZ s˜ao quaisquer vetores negativos emCn,1 _{que se projetam, respectivamente, em}_x_e_z_.

Este potencial de Kähler define uma fun¸cão diferenciável Ψx= expψx:HnC→Rdada por

Ψx(z) = sech2

µ_ρ₍_{z, x}₎

2

¶

= hX, XihZ, Zi

hX, ZihZ, Xi,

que pode ser estendida a uma fun¸c˜ao diferenci´avel numa vizinhan¸ca _U de Hn

C ⊂ P(Cn,1) e que define a

fronteira do espa¸co hiperb´olico complexo como∂Hn

C= Ψ−1x (0). Ent˜ao,

ωx = dcΨx|∂Hn

C

define uma calibra¸c˜ao para a estrutura de Cauchy-Riemann de∂Hn

C, isto ´e,ωx∈Cal(∂HnC).

Agora, seja g um automorfismo qualquer da estrutura CR da ∂Hn

C. Se x∈ HnC, a esfera isom´etrica

Ig,xdeg com respeito a 1-forma de contatoωx´e chamada deesfera isom´etrica de Dirichletdegcom

respeito ax. ´

E poss´ıvel provar, veja [3, se¸cão 1.5] que esta esfera isométrica é caracterizada por uma equa¸cão envolvendo forma hermitiana de assinatura (n,1) em Cn,1 _{e, uma vez que o ponto base} _x _∈ _Hn

C, esta

equa¸cão é equivalente a uma equa¸cão envolvendo a fun¸cão distânciaρda métrica de Bergaman deHn C:

Ig,x = {z∈∂HnC : |hZ, Xi| = |hZ, g−1(X)i| }

= _{z_∈Hn

C : ρ(z, x) = ρ(z, g−1(x))}.

Ou seja,Ig,xé a interse¸cão de um bissetor equidistante com a fronteira do espa¸co hiperbólico complexo.

Observe ainda que, se x é um ponto fixo do automorfismo g, então esta esfera isométrica Ig,x se

degenera a todo o espa¸co hiperb´olico complexo.

1.6.2 Esferas isom´

etricas de Ford

Vamos agora definir esfera isom´etrica de Ford de um automorfismog deHn

C. Ser´a definida como a esfera

isométrica deg com respeito a uma calibra¸cão associada a um pontoqna fronteira do espa¸co hiperbólico complexo.

Sejaq _∈ ∂Hn

C um ponto qualquer na fronteira do espa¸co hiperb´olico complexo, e seja Q∈ Cn,1 um

vetor nulo representandoq. O potencial de K¨ahlerψQ:HnC→Rassociado aQ´e dado por

ψQ(z) = ln− h

Z, Z_i

hZ, Q_ihQ, Z_i,

(20)

Este potencial de Kähler define uma fun¸cão diferenciável ΨQ= expψQ :HnC→Rdada por

ΨQ(z) = − h

Z, Z_i

hZ, Q_ihQ, Z_i,

que pode ser estendida a uma fun¸c˜ao diferenci´avel numa vizinhan¸ca_U deHn

C emP(Cn,1) e que define a

fronteira do espa¸co hiperb´olico complexo como∂Hn C= Ψ

−1

Q (0). Ent˜ao,

ωQ = dcΨQ|∂Hn

C

define uma calibra¸c˜ao para a estrutura de Cauchy-Riemann de∂Hn

C, isto ´e,ωQ ∈Cal(∂HnC).

Agora, sejagum automorfismo qualquer da estrutura CR da fronteira deHn

C. A esfera isom´etricaIg,q

de g com respeito a esta 1-forma de contato ωQ ´e chamada de esfera isom´etrica de Ford de g com

respeito ao ponto da fronteiraq [7, se¸cão 5.4.4]. Para isto fazer sentido, precisamos demonstrar que esta defini¸cão independe do representanteQdo pontoq. De fato, vamos demonstrar que a fun¸cão de distor¸cão

Jg,Q degcom respeito a 1-formaωQ não depende deQ, isto é, que para todo número complexo não nulo

λ nós temos queJg,λQ = Jg,Q. Para este fim, observe que o potencial de Kähler ψQ, a fun¸cão ΨQ e

a forma de contato ωQ dependem do representante Q para o ponto da fronteira q. De fato, para todo

n´umero complexoλ₆= 0, tem-se

ψλQ = ψQ − ln|λ|2,

ΨλQ =

1

|λ_|2ΨQ ,

ωλQ = 1

|λ_|2ωQ .

Como as fun¸cões de distor¸cão deg, Jg,Q e Jg,λQ, com respeito as formas de contato ωQ eωλQ, são

respectivamente definidas pelas equa¸c˜oes

g∗ωQ = Jg,QωQ e g∗ωλQ = Jg,λQωλQ,

podemos concluir que

g∗ωλQ = g∗

µ ₁

|λ|2ωQ

¶

= 1

|λ|2g ∗_ω

Q =

1

|λ|2Jg,QωQ =

1

|λ|2Jg,Q|λ| 2_ω

λQ = Jg,QωλQ.

Destas equa¸cões, segue a nossa afirma¸cão Jg,λQ = Jg,Q. De agora em diante então, podemos nos

referir a fun¸cão de distor¸cão Jg,q deg com respeito a um ponto da fronteiraq e também, para definir a

esfera isom´etrica de Ford de g, podemos utilizar a forma de contato ωQ, para qualquer representanteQ

deqemCn,1_.

´

E poss´ıvel demonstrar, veja [3, se¸c˜ao 1.5], as seguintes propriedades:

• A esfera isométrica de Ford é caracterizada por uma equa¸cão envolvendo a forma hermitiana de assinatura (n,1) emHn

C:

Ig,q = {z∈∂HnC : |hZ, Qi| = |hZ, g−1(Q)i| };

• Embora esta equa¸cão não possa ser traduzida em termos da fun¸cão distância ρ da métrica de Bergman deHn

C, pois o ponto base q est´a agora na fronteira ∂HnC, a fun¸c˜ao de Busemann [7]

hQ(z) =ln−h

Z, Q_ihQ, Z_i

hZ, Zi pode ser utilizada:

(21)

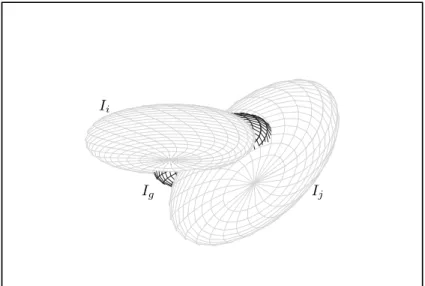
• A esfera isométrica de Ford de um automorfismogcom rela¸cão ao ponto idealqé uma esfera espinal (isto é, a interse¸cão de um bissetor equidistante com a fronteira do espa¸co hiperbólico complexo) cuja espinha complexa passa porq. Quando trabalhamos com coordenadas horoesféricas definidas a partir do pontoq, esferas espinais cujas espinhas complexas passam porq recebem o nome especial deesferas espinais verticais.

• [15] A esfera isométrica de Ford é uma esfera na métrica de Cygan para∂Hn

C. Para isto, fixemos

coordenadas horoesf´ericas usuais, a partir do ponto idealq∞=





0

−1 1



. Sejagum automorfismo que

n˜ao fixaq∞, representado pela seguinte matriz em SU(n,1):





A α β γ∗ _a _b

δ∗ _c _d



,

sendo queA_∈U(n₋1) eα, β, γ, δs˜ao vetores coluna emCn−1_{e que}∗_{denota a transposta conjugada}

de uma matriz. A esfera isométrica de Ford dehé a esfera, na métricaρ0, com centroqg=g−1(q∞)

e raioRg =

s

2

|a₋b+c₋d_|. Isto ´e,Ig,q∞ = {z∈H

n

C : ρ0(z, qg) =Rh}.

Isto significa em particular queIg,q∞pode ser vista como a imagem da esfera de Heisenberg unit´aria

centrada na origem de_H(dada pela equa¸c˜ao_kζ_k4₊_v2_{= 1) por uma similaridade: primeiro aplique}

a dilata¸c˜ao de Heisenberg de fatorRg seguida por uma transla¸c˜ao de Heisenberg pelo vetorqg.

• Como em geometria hiperbólica real, aqui também o dom´ınio fundamental de Ford para um grupo discreto de isometrias será definido como o exterior comum das esferas isométricas dos elementos não triviais do grupo. Sendo a interse¸cão de um bissetor equidistante com∂Hn

C, cada esfera isom´etrica

Ig,q de um automorfismo g que n˜ao fixa q divide ∂HnC em dois semi-espa¸cos, um deles contendo

o ponto ideal q, que ser´a chamado de exterior de Ig,q. Assim sendo, fixando q =q∞ para definir

coordenadas horoesféricas e utilizar a métrica de Cygan, ointeriore oexteriordeIg,q∞ =Ig estão

definidos por:

Int (Ig) ={z∈∂HnC: ρ0(z, g−1(q∞))< Rg} = {z∈∂HnC: |hZ, Q∞i|>|hZ, g−1(Q∞i| },

Ext (Ig) ={z∈∂HnC: ρ0(z, g−1(q∞))> Rg} = {z∈∂HnC: |hZ, Q∞i|<|hZ, g−1(Q∞i| }.

Nesse caso, podemos enunciar, como no caso de geometria hiperb´olica real, o seguinte resultado [3, proposi¸c˜ao 1.5.4]

Proposi¸c˜ao 1.6.1 Seja g∈PU(n,1) tal queg(q∞)6=q∞. Ent˜ao

g(Int (Ig))⊂Ext¡Ig−1

¢

e g(Ext (Ig))⊂Int¡Ig−1

¢

Observa¸cão: As eferas isométricas de Dirichlet e de Ford são definidas na fronteira do espa¸co hiperbólico complexo. Mas, como mostram as propriedades enunciadas estas esferas são de fato esferas espinais em

∂Hn

C. Assim, podemos estender o conceito de esfera isom´etrica ao interior do espa¸co hiperb´olico complexo,

simplesmente considerando o bissetor que define esta esfera espinal. Deste modo as esferas isom´etricas de Dirichlet e de Ford podem ser consideradas emHn

Cou em∂HnC ou emHnC∪∂HnC. E todos os resultados

(22)

Cap´ıtulo 2

Dom´ınios fundamentais para grupos

discretos de isometrias holomorfas

Lembrando que um dos objetivos deste trabalho é caracterizar o poliedro de Ford para grupos c´ıclicos de isometrias holomorfas, neste cap´ıtulo vamos formalizar o conceito de dom´ınio fundamental para a a¸cão de subgrupos discretos de PU(2,1) tanto no espa¸co hiperbólico complexoHn

C como em sua fronteira∂HnC.

Tamb´em vamos enunciar os resultados que garantem que os poliedros de Ford e Dirichlet para grupos discretos s˜ao dom´ınios fundamentais.

Veremos ainda os teoremas de Poincar´e, relacionado com a constru¸c˜ao de grupos discretos a partir de poliedros fundamentais, e de Giraud, relacionado com os ciclos de arestas dos poliedros fundamentais de Ford e Dirichlet.

2.1 O dom´ınio fundamental de Ford em geometria hiperb´

olica

complexa

Phillips, [18] define um dom´ınio fundamental para a a¸c˜ao em Hn

C de um grupo discreto de isometrias

holomorfas (subgrupo discreto de PU(n,1)):

Defini¸c˜ao 2.1.1 Seja G um subgrupo discreto de PU(n,1). Um dom´ınio fundamental para G´e um subconjunto aberto e conexo F deHn

C tal que

1. vol(∂F) = 0 (volume Riemanniano),

2. F n˜ao cont´em pontosG-equivalentes e, para todoz_∈Hn

C, existeg∈Gtal queg(z)∈F,

3. F´elocalmente finito, isto ´e, cada subconjunto compacto deHn

Cintercepta somente uma quantidade

finita deG-imagens de F.

Um caso especial de dom´ınios fundamentais s˜ao os poliedros fundamentais, que aparecem naturalmente considerando esferas de Ford e Dirichlet.

Um subconjuntoF _⊂Hn

Cé umpoliedroseF é a interse¸cão de uma quantidade finita ou enumerável

de semi-espa¸cos abertos em Hn

C. Umsemi-espa¸coem HnC ´e uma componente conexa do complementar

de um bissetor emHn

C. O fecho deF possui então uma decomposi¸cão em células dada pelas interse¸cões

dos bissetores que definem F. Uma k-célula nesta decomposi¸cão é chamada de k-face deF. Também, as faces de codimensão um são chamadas deladosdeF, e as faces de codimensão dois são chamadas de

(23)

Defini¸c˜ao 2.1.2 SejaGum subgrupo discreto dePU(n,1). Um poliedroF ´e umpoliedro fundamental paraGem Hn

C se as seguintes condi¸c˜oes s˜ao satisfeitas:

1. Para todo elemento n˜ao trivialg_∈G,g(F)_∩F=_∅. 2. Para todoz_∈Hn

C, existe g∈G tal queg(z)∈F.

3. Os lados deF s˜ao, dois a dois, identificados por elementos deG; isto ´e, para cada ladosexiste um lados′_{, e existe um elemento}_g

s∈G, comgs(s) =s′. Esta identifica¸c˜ao deve satisfazer: gs′ =g−1

s

e(s′₎′₌_s._{O elemento} _g

s´e chamado de transforma¸c˜ao identificadora de lado.

4. F ´e localmente finito, isto ´e, qualquer subconjunto compacto deHn

Cintercepta somente uma

quanti-dade finita de imagens deF por elementos deG.

Como em geometria hiperb´olica real podemos caracterizar um subgrupoGde PU(n,1) discreto como aquele que age livre e descontinuamente em algum ponto de ∂Hn

C. Denotamos por Ω◦(G) ⊂ ∂HnC o

conjunto dos pontos ondeGage livre e descontinuamente. A demonstra¸cão do próximo teorema pode ser encontrada em [3, se¸cão 2.4]. Lembrando que esferas isométricas de Ford dependem da escolha de um ponto idealq∈∂HnC, fixamos aqui q=q∞.

Teorema 2.1.1 Seja Gum subgrupo de PU(n,1)tal queq∞∈Ω◦(G). Ent˜ao,

F(G) = \

g∈G−{id}

Ext (Ig)

´e um dom´ınio fundamental para a a¸c˜ao de GemHn C.

Uma propriedade importante de um poliedro fundamental é a que afirma que as aplica¸cões identificado-ras de lados geram o grupo originalG. No caso do espa¸co hiperbólico real, este teorema está demonstrado em [13, IV.F.6, página 70] ou em [1, teorema 9.3.3, página 220]. A demonstra¸cão do livro de Maskit pode ser aplicada para se demonstrar este mesmo fato no caso do espa¸co hiperbólico complexo. Assim, podemos enunciar o seguinte teorema.

Teorema 2.1.2 Seja F um poliedro fundamental para um subgrupo discreto G de PU(n,1). Ent˜ao, as aplica¸c˜oes identificadoras de lados deF geram G.

2.2 O dom´ınio fundamental de Ford em geometria CR-esf´

erica

Vamos considerar agora a a¸c˜ao de um subgrupo discreto de PU(n,1) na fronteira∂Hn

Cdo espa¸co hiperb´olico

complexo. Novamente o poliedro de Ford ser´a um dom´ınio fundamental.

A seguinte defini¸cão, para um poliedro fundamental, é uma generaliza¸cão da defini¸cão do livro do Maskit [13, página 29], para um dom´ınio fundamental para grupos de transforma¸cões conformes agindo no plano complexo estendido ˆC_{. Denotamos por Ω = Ω(}_G_{) o conjunto de pontos regulares de}_G_em_∂_Hn_C_,

isto ´e, o conjunto dos pontos ondeGage descontinuamente. Um subconjuntoF _⊂∂Hn

Cé umpoliedroseFé a interse¸cão de uma quantidade finita ou enumerável

de semi-espa¸cos abertos em∂Hn

C. Umsemi-espa¸coem∂HnC´e uma componente conexa do complementar

de uma esfera espinal em ∂Hn

C. O fecho de F possui então uma decomposi¸cão em células dada pelas

interse¸cões das esferas espinais que definemF. Umak-célula nesta decomposi¸cão é chamada dek-facede

(24)

Defini¸c˜ao 2.2.1 Seja G um subgrupo discreto de PU(n,1). Um poliedro F ⊂ ∂Hn

C ´e um poliedro

fundamental paraGem∂Hn

Cse as seguintes condi¸c˜oes s˜ao satisfeitas:

1. Para todo elemento n˜ao trivialg_∈G,g(F)_∩F=_∅. 2. Para todoz∈Ω⊂Hn

C, existeg∈Gtal queg(z)∈F.

3. A fronteira deF consiste de pontos limites e de uma cole¸cão finita ou enumerável de lados deF. 4. Os lados deF são, dois a dois, identificados por elementos deG; isto é, para cada ladosexiste um

lados′ _{e existe um elemento}_g

s∈G, comgs(s) =s′. Esta identifica¸c˜ao deve satisfazer: gs′ =g−1

s e

(s′₎′ ₌_s. _{O elemento} _g

s´e chamado detransforma¸c˜ao identificadora de lado.

5. Se _{sm} é uma sequência de lados de F então o diâmetro de Cygan dia0(sm) de sm tende a zero

quandom tende a infinito, isto ´e, os lados deF se acumulam somente em pontos limites.

6. Somente uma quantidade finita de imagens deF por elementos deGintercepta qualquer subconjunto compacto deΩ.

Fazendo referência novamente a [3], enunciamos os próximos resultados. Como usualmente, fixamos o ponto idealqem rela¸cão ao qual as esferas de Ford estão definidas comoq=q∞.

Teorema 2.2.1 Seja Gum subgrupo de PU(n,1)tal queq∞∈Ω◦(G). Ent˜ao,

F(G) = \

g∈G−{id}

µ

Ext (Ig) ∩∂HnC

¶

´e um poliedro fundamental para a a¸c˜ao de Gem∂Hn C.

Neste caso, também é verdadeira a afirma¸cão de que as aplica¸cões identificadoras de lado geram o grupo originalG.

Teorema 2.2.2 SejaGum subgrupo dePU(n,1)tal queq∞∈Ω◦(G), e sejaDum dom´ınio fundamental,

paraG, limitado por esferas isométricas de Ford de elementos emG. Então,D é o dom´ıno fundamental de Ford de G, isto é,

D = \

g∈G−{id}

Ext (Ig) = F(G).

Este último resultado significa que o poliedro de Ford de um grupo discreto G é o único dom´ınio fundamental para Gque é limitado por esferas isométricas de Ford

2.3 O Teorema dos Poliedros de Poincar´

e

Aqui é apresentada uma versão do Teorema dos Poliedros de Poincaré para geometria hiperbólica com-plexa. Este teorema fornece condi¸cões suficientes para que um dado poliedro D em Hn

C, com faces

identificadas por elementos de PU(n,1), seja um dom´ınio fundamental para o grupo gerado por estes identificadores de lados.

(25)

Considere um poliedro finitoD em H2

C (veja se¸c˜ao 2.1), sendo que os lados de D est˜ao, dois a dois,

identificados por elementos de PU(2,1). Vamos escrever condi¸c˜oes sobreDque v˜ao assegurar que o grupo

G, gerado por estes identificadores de lados, seja discreto, e queDseja um poliedro (dom´ınio) fundamental paraG.

A primeira condi¸cão é a de que os lados deDsejam, dois a dois, identificados por elementos de PU(2,1), isto é, para cada ladoadeD, existe um ladoa′_{, não necessariamente distinto de}_a_{, e existe um elemento}

ga ∈PU(2,1), satisfazendo as seguintes condi¸c˜oes:

(1)ga(a) =a′,

(2)ga′ =g−1

a .

As isometriasga s˜ao chamadas deaplica¸c˜oes identificadoras de lados.

(3)ga(D)∩D=∅.

(4)ga(D)∩D=a′.

SejaGo grupo gerado pelas aplica¸c˜oes identificadoras de lados. Observe que se existe um ladoa, com

a′₌_a_{, ent˜ao a condi¸c˜}_{ao (2) implica que}_g2

a = 1. Se isto ocorrer, a rela¸cãog2a= 1, é chamada derela¸cão

de reflex˜ao.

As próximas condi¸cões são relacionadas com as arestas deD. Em geral, a interse¸cão de dois bissetores é complicada. Em particular, ela pode ser desconexa [7]. Portanto, impomos que

(5)N˜ao existem lados deDtangentes na fronteira deH2

Ce, cada aresta deD´e uma subvariedade completa

deH2

Chomeomorfa a um disco aberto.

Observe que as identifica¸cões de lados definem uma rela¸cão de equivalência sobre as arestas deD; cada classe de equivalência de arestas pode ser ciclicamente ordenada como segue. Comece com uma arestae1.

Ela pertence `a fronteira de dois lados; vamos chamar um destes lados de s1. Ent˜ao, existe um lado s′1 e

existe uma aplica¸c˜ao identificadora de ladog1 tal queg1(s1) =s′1. Sejae2=g1(e1). Comoe1, a arestae2

pertence `a fronteira de exatamente dois lados, um deles ´es′

1, e o outro ser´a chamado des2. Novamente,

existe um lados′

2e uma aplica¸c˜ao identificadora de ladog2, comg2(s2) =s′2. Continuando desta maneira,

podemos gerar uma sequênciaej de arestas, uma sequênciagj de transforma¸cões identificadoras de lados,

e uma sequˆencia (sj, s′j) de pares de lados identificados. Visto que D possui um n´umero finito de lados,

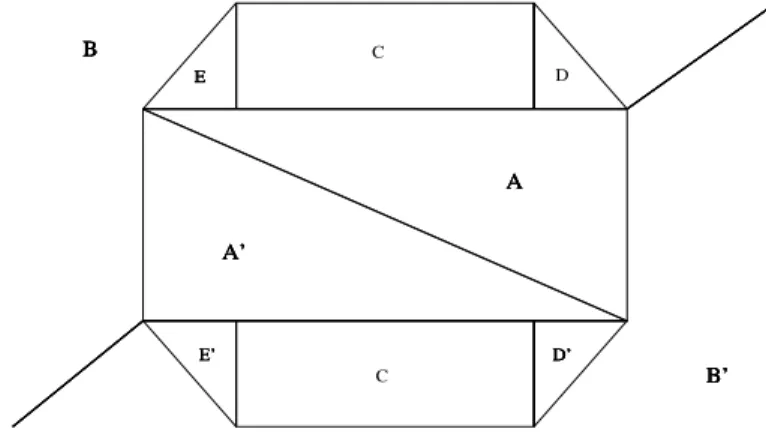
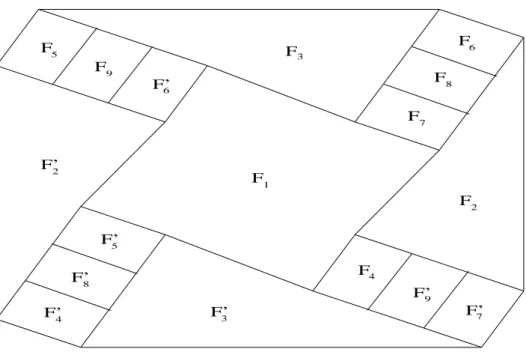
a sequência de arestas é periódica; assim todas estas três sequências também são periódicas. Seja k o menor per´ıodo de modo que estas três sequências sejam periódicas, com per´ıodok. A sequência ordenada ciclicamente de arestase1, e2, . . . , ek é chamada deciclo de arestas. O númeroké oper´ıododo ciclo.

Observe que

gk ◦ · · · ◦ g1(e1) = e1 .

O elementohe1 = gk ◦ · · · ◦ g1 ´e chamado detransforma¸c˜ao c´ıclicada arestae1.

Dada uma transforma¸c˜ao c´ıclica h, como acima, e dado um inteiro positivo m, defina a seguinte sequˆencia demkelementosh1, . . . , hmk deG:

h1=g1 , h2=g2g1 , h3=g3g2g1 , . . . , hk=h,

hk+1=g1h , hk+2=g2g1h , . . . , hmk−1=gk−1· · · g2g1hm−1 , hmk=hm.

SejaF(h) a seguinte fam´ılia de poliedros:

(26)

(6)A restri¸cão da transforma¸cão c´ıclicaheà arestaeé a identidade, e deve existir algum inteiro positivo

m tal que hm

e = 1, isto ´e, he tem ordem m. Mais ainda, os poliedros da fam´ıliaF(he) preenchem, sem

auto-interse¸c˜ao, uma vizinhan¸ca da arestae.

As rela¸c˜oes, no grupoG, da formahm_{= 1, s˜ao chamadas de}_rela¸_c˜_{oes c´ıclicas}_.

Teorema 2.3.1 (Poincar´e) Assuma que um poliedroD_⊂Hn

C, com um n´umero finito de lados, satisfa¸ca

as condi¸cões(1)-(6)enunciadas acima. Então, o grupoG, gerado pelas aplica¸cões identificadoras de lados de D, é discreto, D é um poliedro fundamental para G, e as rela¸cões c´ıclicas e de reflexão formam um sistema completo de rela¸cões paraG.

2.4 O teorema de Giraud

Como referˆencia aos resultados enunciados nesta se¸c˜ao, veja [3] ou [7].

Lados de poliedros estão contidos em bissetores equidistantes. Portanto arestas estão contidas em interse¸cões de dois bissetores. Nem sempre a interse¸cão de bissetores é bem comportada, pode ser por exemplo desconexa. Mas, quando tratamos com poliedros de Ford e Dirichlet, as esferas isométricas são respectivamente coverticais (as duas espinhas complexas passam pelo ponto ideal q∞ escolhido) ou

coequidistantes (definidos como bissetores equidistantes de um mesmo ponto w_∈Hn

C). Assim sendo, as

interse¸c˜oes entre duas delas s˜ao conexas.

Para entender poliedros fundamentais para grupos discretos de isometrias é necessário entender os ciclos de arestas que definirão as rela¸cões do grupo. Ferramenta importante no caso de geometria hiperbólica complexa é o teorema de Giraud ([7, se¸cão 8.3.5]):

Teorema 2.4.1 (Giraud) Suponhamos que B1 e B2 s˜ao dois bissetores com respectivas espinhas

com-plexas Σ1 e Σ2 tais que:

1. Σ1 e Σ2 s˜ao distintas;

2. Σ1∩B2 = Σ2∩B1 = ∅.

Então existe, no máximo, um outro bissetor, diferente de B1 eB2, que contém a interse¸cão B1∩B2.

Vamos pensar agora em dimensão complexa n = 2, onde lados (faces de codimensão real 1) são simplesmente chamados faces.

Uma consequência deste teorema é que, sendo ∆ um poliedro fundamental de Ford ou Dirichlet para a a¸cão de um grupo discreto de isometrias deH2

C, ent˜ao, exceto no caso de uma aresta plana (isto ´e, contida

numa linha complexa), todo ciclo de arestas de ∆ tem comprimento igual a 3 (veja [7, página 296]). Vamos supor então que temos para a a¸cão de um grupo discretoG, um poliedro desta natureza, isto é, um poliedro de Ford para determinado ponto idealq∞ou um poliedro de Dirichlet para determinado ponto

basew∈H2

C. Chamaremos a esfera isom´etrica de um elementog∈GdeIg e denotaremosIg′ =Ig−1.

Para identificar o ciclo de arestas ao qual pertence uma arestaa1 contida emIf∩Ig, usamos f para

identificarIf comIf′ =If−1. Assimf levaa₁numa arestaa₂, contida na intersec¸c˜ao deI_f′ com uma certa

esfera isométricaF1. No sentido inverso, gidentifica a1 com uma arestaa3, contida na interseçcão deIg′

com uma esfera isométricaF2. Pelo teorema de Giraud, o ciclo de arestas está completo, portanto há uma

isometriahtal queh(a3) =a1 eh(F2) =F1, isto ´e, Ih=F2 eIh′ =F1. Como este ciclo de arestas (como

todos os outros de arestas n˜ao-planas) tem comprimento exatamente trˆes, segueg_◦f−1

◦h= 1, ou seja,

h=f_◦g−1_{. Um outro modo de interpretar: sabemos, pelo teorema de Giraud que h´a exatamente trˆes}

bissetores contendoa1; s˜ao elesIf,Ig ef−1(F1) =g−1(F2). Desse modo, concluimos quef◦g−1(a3) =a1

ef_◦g−1₍_F

2) =F1. Portantoh=f◦g−1.

Observe a exce¸c˜ao que ocorre quandof3= 1 eg=f2.