UNIVERSIDADE DE TRÁS-OS-MONTES E ALTO DOURO
A Teoria dos Grafos e sua Aplicação
Dissertação de Mestrado em Ensino de Matemática no 3.º Ciclo do Ensino Básico e Secundário
Idília Maria Rocha Caetano
Universidade de Trás-os-Montes e Alto Douro II
UNIVERSIDADE DE TRÁS-OS-MONTES E ALTO DOURO
A Teoria dos Grafos e sua Aplicação
De:
Nome: Idília Maria Rocha Caetano.
Orientadores:
Professor Doutor José Luís Santos Cardoso.
Professora Doutora Ana Paula Aires Borges Teixeira.
Teoria de Grafos e sua aplicação
III Universidade de Trás-os-Montes e Alto Douro
Este trabalho foi elaborado como dissertação para efeito de obtenção do grau de Mestre no Ensino de Matemática do 3.º ciclo do Ensino Básico e Secundário, sendo apresentado na Universidade de Trás-os-Montes e Alto Douro.
Universidade de Trás-os-Montes e Alto Douro IV Aos meus pais.
À minha filha.
À minha irmã.
Teoria de Grafos e sua aplicação
V Universidade de Trás-os-Montes e Alto Douro
Agradecimentos
A realização desta investigação frutificou devido ao contributo de inúmeras pessoas, sem as quais não teria sido possível a sua concretização, e às quais quero deixar uma palavra de profunda gratidão e apreço:
À orientadora, Professora Doutora Ana Paula Aires Borges Teixeira pela orientação científica, pelo apoio, pela dedicação e total disponibilidade que sempre demonstrou durante este trabalho, sem o qual este trabalho não teria sido possível.
Ao orientador, Professor Doutor José Luís Santos Cardoso, pela sua disponibilidade na orientação, e pelas sugestões e valiosas críticas ao trabalho.
Aos meus pais, pela força concedida, e por me incentivarem perante os desafios a fazer mais e melhor. Agradeço-vos do fundo do coração pelo amor incondicional e pela forma como ao longo de todos estes anos, tão bem souberam ajudar-me.
À minha filha, Célia, fonte inesgotável de alegrias e força para que eu pudesse seguir adiante em mais uma fase de superação académica.
À minha irmã, pela confiança que sempre depositou no meu trabalho.
Ao meu marido, pelo apoio, pela confiança, pela paciência, pela compreensão, pelo total apoio, valorizando sempre o meu trabalho dando-me, força e coragem durante a sua realização.
Universidade de Trás-os-Montes e Alto Douro VI
Resumo
A Teoria dos Grafos é atualmente uma das áreas mais importantes da matemática discreta, tendo as suas raízes em jogos e recreações matemáticas. Atribui-se a sua origem/criação a Euler, ao resolver o problema das pontes de Königsberg (cidade da Prússia) em 1736, mas foram os problemas acerca de fórmulas de estrutura de compostos químicos, que A. Cayley resolveu na segunda metade do século XIX, que impulsionaram decisivamente o seu desenvolvimento.
A Teoria de Grafos é uma teoria relativamente recente, nascida no século XVIII. Com a reestruração de novas disciplinas no secundário, foi na disciplina de Matemática Aplicada às Ciências Sociais que a Teoria de Grafos ganhou relevância nos programas de Matemática, na vertente social, isto no final do século XX. Sendo abordado no 11.º ou 12.º ano (dependendo do ano que se iniciou MACS(2.º ano)).
No programa de Matemática aplicada às ciências sociais pretende-se que os estudantes interpretem situações de sistema de distribuição e explorem diversas soluções para problemas que lhe sejam postos em cada situação. Representar-se-á cada situação por um sistema de pontos e de linhas unindo alguns desses pontos. Deverão ser abordados os teoremas, problemas dos circuitos de Euler e Hamilton, bem como, definições e notações deverão ser introduzidas à medida que sejam necessárias por forma a clarificar a linguagem. Os modelos de grafos pretendem ser modelos úteis para enfrentar problemas de gestão e iniciar intervenções sociais ao nível da compreensão dos sistemas de distribuição e recolha (tanto nos sistemas de distribuição de bens alimentares, de correio ou de recolha de lixo como às decisões sobre a localização de serviços (segundo os programas de MACS homologados em 16/05/2001 [10]).
Teoria de Grafos e sua aplicação
VII Universidade de Trás-os-Montes e Alto Douro
Abstract
The Graph Theory is currently one of the most important areas of discrete mathematics, having their roots in mathematical games and recreations. Attributed to its origin / creation Euler, to solve the problem of the bridges of Königsberg (city of Prussia) in 1736, but were problems about structural formulas of chemical compounds that A. Cayley decided in the second half of the nineteenth century that decisively boosted its development.
Graph Theory is a relatively new theory, born in the eighteenth century. With restructuring new disciplines in the secondary, was in Mathematics Applied to Social Sciences that graph theory gained prominence in Mathematics programs, the social aspect, ie the end of the twentieth century. Being addressed in 11. º or 12. º year (depending on the year that began MACS (2. º year)).
Program in mathematics applied to social sciences is intended that students interpret situations of distribution system and explore solutions to several problems which put in every situation. Will represent each case by a system of points and lines connecting certain points. Theorems will be addressed problems Euler circuits and Hamilton, as well as definitions and notation will be introduced as necessary to clarify language. The graph models are intended to be useful models to address management problems and initiate social interventions at the level of understanding of the distribution and collection systems (both in the distribution systems of food, mail or garbage collection to decisions about location services (according to programs approved on 16/05/2001 MACS[10]).
Universidade de Trás-os-Montes e Alto Douro VIII
Índice
Agradecimentos ... V Resumo ... VI Abstract ... VII Índice ... VIII Índice das tabelas ... IX Índice de figuras ... XIntrodução ... 1
Capítulo 1 – Noções Fundamentais ... 3
As pontes de Königsberg ... 3
1.1- Grafos e Digrafos... 4
1.2- Adjacência e Incidência ... 7
1.3- Grau de um vértice, ordem e dimensão ... 10
1.4- Subgrafos ... 12
1.5- Grafos isomorfos ... 13
1.6- Operações com grafos ... 15
1.7- Grafos especiais ... 17
1.8- Caminhos e ciclos ... 26
Capítulo 2 – Grafos Eulerianos e Hamiltonianos ... 33
2.1- Grafos Eulerianos ... 33
2.2- Grafos Hamiltonianos ... 41
Capítulo 3 – Árvores ... 50
3.1- Definições e Propriedades ... 50
3.2- Árvores Geradoras ... 55
Capítulo 4 - Aplicações práticas ... 61
Conclusão ... 84
Teoria de Grafos e sua aplicação
IX Universidade de Trás-os-Montes e Alto Douro
Índice das tabelas
Tabela 1... 45
Tabela 2 - Os 24 ciclos de Hamilton do grafo da Figura 56. ... 46
Tabela 3 - Distância de B entre CB, F, L e S. ... 59
Tabela 4 - Distância de B e S entre CB, F, L. ... 59
Tabela 5 - Distância de B, S e L entre CB e F... 60
Tabela 6 - Distância de B, S, L e F com CB. ... 60
Tabela 7 - Graus dos vértices da Figura 64. ... 64
Tabela 8 - Distâncias entre as cidades. ... 79
Tabela 9... 83
Tabela 10 ... 83
Tabela 11 ... 83
Tabela 12 ... 83
Universidade de Trás-os-Montes e Alto Douro X
Índice de figuras
Figura 1 - Pontes de Konigsberg em 1736. ... 3
Figura 2 - Esquema construído por Euler para a cidade de Königsberg... 3
Figura 3 - Grafo dual das pontes de Königsberg. ... 4
Figura 4 - Mapa de estradas. ... 4
Figura 5 - Rede elétrica. ... 4
Figura 6 - Representação das secções da Figura 4 e da Figura 5. ... 5
Figura 7 - Diversas representações do grafo da Figura 6. ... 5
Figura 9 - Grafo subjacente ao grafo representado na Figura 8. ... 6
Figura 8 - Exemplo de grafo orientado. ... 6
Figura 10 - Exemplos de grafos. ... 6
Figura 11 - Grafo orientado com lacete no vértice C. ... 7
Figura 12 - Digrafo F e o seu grafo subjacente, G. ... 8
Figura 13 - Matrizes de adjacência e incidência de G. ... 10
Figura 14 - Matrizes de adjacência e incidência de F. ... 10
Figura 15 - Grafos G1 e G2. ... 11
Figura 16 - Diagramas semelhantes que não representam o mesmo grafo. ... 13
Figura 17 - Grafos Isomorfos. ... 14
Figura 18 - Grafos não isomorfos... 15
Figura 19 - Grafos Reunião, Interseção e Complementar. ... 16
Figura 20 - Grafo nulo com 5 vértices (N5). ... 17
Figura 21 - Grafos completos K5 e K6. ... 18
Figura 22 -O grafo G' é um grafo clique do grafo G. ... 19
Figura 23 - Grafo bipartido. ... 19
Figura 24 - Representações do grafo K3,3. ... 20
Figura 25 - Grafo estrela. ... 20
Figura 26 - Grafo bipartido completo K 3,2 ... 20
Figura 27 - Grafo complementar de K3,2. ... 21
Figura 28 ... 21
Figura 29 ... 21
Figura 30 - Sólidos Platónicos. ... 22
Figura 31 - Grafos platónicos do Tetraedro, Cubo, Octaedro, Dodecaedro e Icosaedro respetivamente. ... 22
Figura 32 - Grafos planar
K
4. ... 23Teoria de Grafos e sua aplicação
XI Universidade de Trás-os-Montes e Alto Douro
Figura 34 - Rede do metro de Lisboa. ... 24
Figura 35 - Digrafo conexo D. ... 24
Figura 36 - Grafo 1-Conexo. ... 25
Figura 37 - Grafo Ciclo C5. ... 25
Figura 38 - Grafo Roda com 6 vértices. ... 26
Figura 39 - Grafo G. ... 27
Figura 40 - Digrafo D. ... 28
Figura 41 - Digrafo conexo... 29
Figura 42 - Grafo orientável. ... 29
Figura 43 - Grafo com várias pontes. ... 30
Figura 44 - Grafo desconexo. ... 30
Figura 45 - G1 é Eureliano, G2 é semieuleriano e G3 nem é euleriano nem semieuleriano. ... 33
Figura 46 - D1 é euleriano, D2 é semieureliano e D3 nem é Euleriano nem semieuleriano. ... 34
Figura 47 - Grafo Euleriano obtido do Grafo não euleriano G2 da Figura 45. ... 36
Figura 48 - Exemplos de grafos eulerianos obtidos através de eulerizações do grafo G3 da Figura 45. ... 36
Figura 49 - Grafo Euleriano. ... 37
Figura 50 - Aplicação do Algoritmo de Fleury da Figura 49. ... 38
Figura 51 - Digrafo Eureliano. ... 40
Figura 52 - Aplicação do Algoritmo de Fleury ao digrafo da Figura 51. ... 40
Figura 53 ... 41
Figura 54 - Exemplo de Caminho Hamiltoniano para a demonstração do Teorema 8. 43 Figura 55 - Mapa de Portugal. ... 45
Figura 56 - Grafo relativo ao exemplo enunciado. ... 45
Figura 57 - Grafo Árvore. ... 50
Figura 58 - Grafo G. ... 51
Figura 59 - Árvores geradoras de G da Figura 58. ... 51
Figura 60 - Grafo G. ... 55
Figura 61 - Aplicação do Algoritmo de Corte ao grafo da Figura 60. ... 56
Figura 62 - Aplicação do Algoritmo de Construção ao grafo da Figura 60. ... 56
Figura 63 - Árvore geradora de menor peso do grafo G. ... 58
Figura 64 - Grafo S. ... 62
Figura 65 - Representação do subgrafo de S, S’. ... 65
Figura 66 - Grafo desconexo. ... 65
Universidade de Trás-os-Montes e Alto Douro XII
Figura 68 - Grafo completo k9... 67
Figura 69 - Grafo complementar de S. ... 67
Figura 70 - Subgrafo simples de S. ... 68
Figura 71 - Representação das cidades... 69
Figura 72 - Passeio da cidade A por um lacete em A. ... 69
Figura 73 - O percurso da cidade A para a cidade B pelo arco (A,B). ... 69
Figura 74 - O percurso da cidade B para a cidade D pelo arco (B,D). ... 70
Figura 75 - O percurso da cidade D para a cidade E pelo arco (D,E). ... 70
Figura 76 - O percurso da cidade E para a cidade F pelo arco (E,F). ... 70
Figura 77 - O percurso da cidade F para a cidade E pelo arco (F,E). ... 70
Figura 78 - O percurso da cidade E para a cidade D pelo arco (E,D). ... 71
Figura 79 - O percurso da cidade D para a cidade C pelo arco (D,C). ... 71
Figura 80 – Digrafo que representa o percurso do Jorge. ... 71
Figura 81 - Grafo subjacente ao digrafo da Figura 80. ... 71
Figura 82 - Grafo S. ... 73
Figura 83 – Subgrafo de S, S1. ... 74
Figura 84 - Grafo G. ... 75
Figura 85 ... 75
Figura 86 - Grafos G1, G2 e G3. ... 76
Figura 87 – Eulerização do grafo G2 ... 77
Figura 88 - Melhor eulerização do grafo G1... 77
Figura 89 – Grafo G ... 78
Figura 90 - Grafo pesado que representa o problema. ... 81
Figura 91 - Grafo da ligação das cidades em rede. ... 81
Figura 92 ... 82
Figura 93 ... 82
Figura 94 ... 82
Figura 95 ... 82
1
Introdução
Esta dissertação, foi realizada no âmbito do Mestrado em Ensino de Matemática no 3.º Ciclo do Ensino Básico e Secundário.
O tema da tese é "A Teoria de Grafos e a sua Aplicação".
A Teoria de Grafos, é uma área que nos permite obter uma relação entre a resolução de problemas e a modelação matemática. A investigação em Teoria de Grafos, suscitou-me bastante interesse e curiosidade.
Assim, esta dissertação é composta por três capítulos, cujo conteúdo se passa a descrever.
No primeiro capítulo, abordam-se as noções fundamentais, principais conceitos e resultados relativos à Teoria de Grafos, necessários para a compreensão dos capítulos seguintes. Serão abordados os seguintes conceitos: grafos e digrafos; Adjacência e Incidência; grau de um vértice, ordem e dimensão de um grafo; subgrafos; grafos isomorfos, operações com grafos; grafos especiais e ainda caminhos e ciclos.
No segundo capítulo introduz-se, as noções de Grafos Eulerianos e Grafos Hamiltonianos.
No terceiro capítulo descrevem-se, o estudo das árvores suas definições e propriedades e ainda árvore geradora.
Finalmente, no quarto capítulo apresentam-se, algumas aplicações que, pretendem ser uma ajuda aos docentes da disciplina de Matemática Aplicada às Ciências Sociais.
A Teoria dos Grafos estabeleceu-se, como uma importante ferramenta matemática, numa grande variedade de áreas do conhecimento e algumas áreas específicas, tais como, investigação operacional, indústria eletrónica, indústria de confeção, engenharia, economia, genética, sociologia, geografia, ecologia, análise numérica, computação paralela, telecomunicações e química, pois um grafo constitui o modelo matemático ideal para o estudo das relações entre objetos discretos de qualquer tipo. No programa de MACS pretende-se que, os estudantes interpretem situações de sistema de distribuição e explorem diversas soluções para problemas que lhe sejam
Universidade de Trás-os-Montes e Alto Douro 2 postos em cada situação. Representar-se-á cada situação por um sistema de pontos e de linhas unindo alguns desses pontos. Deverão ser abordados os teoremas, problemas dos circuitos de Euler e Hamilton, bem como, definições e notações, que deverão ser introduzidas à medida que sejam necessárias por forma a clarificar a linguagem. "Os modelos de grafos pretendem ser, modelos úteis para enfrentar problemas de gestão e iniciar intervenções sociais ao nível da compreensão dos sistemas de distribuição e recolha" [10].
Pela diversidade de aplicações, potencialidades e facilidade de exploração em contexto escolar, a teoria de grafos pode assumir um papel preponderante na criação e desenvolvimento dessas competências, contribuindo para que, os alunos adquiram uma cultura matemática mais rica que, os ajude a tornar-se cidadãos mais aptos a intervir na sociedade.
Como a teoria de grafos é uma área de matemática onde não são necessários grandes pré-requisitos, podemos abordar, praticamente, todos os conceitos básicos envolvidos em qualquer ano de escolaridade, sem ser necessário formalizar ou desenvolvê-los. É comum dizer-se que, muitos problemas em diversas ciências, podem ser modelizado por um grafo e resolvido com a teoria dos grafos. Por exemplo, é possível calcular as diferentes combinações de voos entre duas cidades, determinar se é ou não possível percorrer todas as ruas de uma cidade sem percorrer a mesma rua duas vezes e determinar o número de cores necessárias para colorir um mapa. Até à década de 90 do século transato, a teoria dos grafos era abordada somente no ensino universitário. Com o surgimento de novas disciplinas no ensino secundário, nomeadamente, da disciplina de MACS, a teoria dos grafos ganha um lugar nos programas de Matemática, na vertente.
O objetivo de fundo deste trabalho, é ser um manual de ajuda ao docente do Ensino Secundário.
Idília Caetano
3
Capítulo 1 – Noções Fundamentais
As pontes de Königsberg
Parte da cidade de Königsberg, localizava-se em duas ilhas do rio Pregel as quais estavam ligadas às margens e uma à outra através de 7 pontes, conforme ilustra a Figura 1.
Figura 1 - Pontes de Konigsberg em 1736.
De acordo com a tradição, ao domingo, os habitantes de Königsberg gostavam de dar passeios de modo a atravessar todas as pontes e um passatempo popular era tentar encontrar um trajeto que lhes permitissem atravessar toda a cidade passando em cada uma das pontes apenas uma vez.
Em 1736, o matemático suíço Leonard Euler (1707-1783), interessou-se por este problema e resolveu-o. As soluções de Euler para este problema e as técnicas por ele utilizadas, marcaram o início do estudo do tema atualmente designado por Teoria de Grafos. A técnica de Euler consistiu, essencialmente, em considerar as margens e as ilhas, no mapa da cidade, como pontos, que ligou por linhas, do mesmo modo que, aquelas eram unidas pelas referidas pontes. O esquema obtido por Euler, assemelha-se ao da Figura 2 e é habitualmente designado por Grafo. Assim, um grafo é um diagrama que consiste em pontos, designados por vértices, ligados uns aos outros por linhas, denominadas arestas; cada aresta une exatamente dois vértices.
Universidade de Trás-os-Montes e Alto Douro 4 O problema dual do problema das pontes de Königsberg, Figura 1, consiste em saber se um nadador poderia nadar naquele mesmo rio de modo a passar por baixo de todas as pontes sem repetir nenhuma. O grafo associado a este problema está representado na Figura 3.
Por exemplo, o grafo da Figura 3, determina cinco regiões. A região exterior que indicamos com o algarismo 1, e mais quatro regiões limitadas, as quais indicamos com os algarismos 2, 3, 4 e 5 na Figura 2.
Figura 3 - Grafo dual das pontes de Königsberg.
Um outro problema envolvendo o grafo da Figura 2, foi formulado e resolvido (em 1857-1859), pelo matemático irlandês Sir William Hamilton (1805-1865). Este problema, habitualmente conhecido por, viagem à volta do mundo, consistia em percorrer todos os vértices de um dodecaedro regular com vinte vértices, em que, cada vértice tem o nome de uma cidade e que passe uma única vez em cada vértice, iniciando e finalizando no mesmo vértice.
1.1- Grafos e Digrafos
As secções de um mapa de estradas e de uma rede elétrica são também exemplos de aplicação da teoria de grafos.
Consideremos, as secções de um mapa de estradas e de uma rede elétrica, representadas na Figura 4 e Figura 5, respetivamente.
Ambas as secções podem ser representadas, por meio de pontos e de segmentos de reta, tal como no esquema da Figura 6.
Figura 4 - Mapa de estradas.
Idília Caetano
5
Figura 6 - Representação das secções da Figura 4 e da Figura 5.
O esquema da Figura 6 diz-se um grafo. Notemos que, na passagem da situação real para o grafo, é irrelevante se as linhas são longas ou curtas, retilíneas ou curvas, ou do lado de onde partem. O importante é, conhecer os pontos e as linhas que os ligam. Assim, o mesmo grafo pode ser representado por diferentes esquemas. A título de exemplo, na Figura 7, apresentam-se outras quatro representações do grafo da figura 6. Os cinco esquemas, Figuras 6 e 7, representam o mesmo grafo, em virtude de possuírem os mesmos pontos, aqui designados por P, Q, R, S e T e serem constituídos por linhas que unem os mesmos pontos: PQ, PS, PT, QT, QS, QR, RS, ST.
Figura 7 - Diversas representações do grafo da Figura 6. Definição 1
Um grafo G é um par ordenado (V,E), em que V é um conjunto e E é um conjunto constituído por subconjuntos de V com dois elementos. A V dá-se o nome de
conjunto de vértices enquanto E denomina-se por conjunto de arestas.
Dizemos que os vértices A e B estão unidos por uma aresta se {A,B}≡AB pertence a E.
No caso particular de V=E=Ø, então a G=(V,E) dá-se o nome de grafo vazio. A Figura 6 representa o grafo G=(V,E):
cujo conjunto dos vértices é V={P, Q, R, S, T};
Universidade de Trás-os-Montes e Alto Douro 6 É indiferente escrever aresta PQ ou aresta QP, dado que ambas representam a existência de um caminho do vértice P para o vértice Q, que pode ser percorrido nos dois sentidos. Se o caminho tivesse um só sentido, por exemplo, apenas de P para Q, no grafo haveria uma seta com origem no vértice P e términus no vértice Q; neste caso, a aresta seria orientada e representar-se-ia por (P,Q).
A um grafo com arestas orientadas, chama-se grafo orientado, grafo dirigido ou
digrafo.
Definição 2
Um digrafo G é um par ordenado (V,E), em que V é um conjunto de vértices e E é um subconjunto de V×V. Ao conjunto E dá-se o nome conjunto de arcos. Dizemos que os vértices A e B estão unidos por um arco se (A,B) pertence a E. Ao grafo obtido substituindo cada arco de E por uma aresta chama-se grafo
subjacente a G.
O grafo da Figura 8 é orientado. Neste caso:
O conjunto dos vértices é V = {A, B, C, D, E};
O conjunto dos arcos é E = {(A,B), (B,A), (A,C), (C,E), (C,D)}.
Figura 9 - Grafo subjacente ao grafo representado na Figura 8.
Na Figura 10, apresentamos mais alguns exemplos de grafos.
Figura 8 - Exemplo de grafo orientado.
Idília Caetano
7
1.2- Adjacência e Incidência
De seguida introduzimos os conceitos de adjacência e incidência, que caracterizam os vértices dum grafo, dirigido ou não, e as respetivas ligações (arestas ou arcos). Na Figura 11, o digrafo apresenta um lacete no vértice C.
Definição 3
Seja G=(V,E) um grafo (digrafo). Se AB
E ((A,B)
E), A e B (distintos) dizem-sevértices adjacentes e AB ((A,B)) diz-se aresta (arco) incidente nos vértices A e
B (A diz-se vértice inicial e B vértice terminal). Se AV não é adjacente a qualquer vértice de V, então A diz-se um vértice isolado. No caso de dois vértices adjacentes serem coincidentes, a aresta (arco) correspondente designa-se por lacete.
No grafo da Figura 6, os vértices P e Q são adjacentes, enquanto P e R não o são; PQ é incidente nos vértices P e Q. Este grafo não apresenta lacetes.
O grafo da Figura 8, é orientado, isto é, é um digrafo. Por exemplo, os vértices A e C são adjacentes, assim como A e B, enquanto A e E não o são; o arco (A,B) é incidente nos vértices A e B (A é o vértice inicial e B é o vértice terminal); (A,C) é incidente nos vértices A e C (neste caso A é também o vértice inicial, mas C é o vértice terminal). Este grafo não apresenta lacetes.
Figura 11 - Grafo orientado com lacete no vértice C.
Quando o número de vértices do grafo é elevado e, em particular, quando o seu número de arestas é reduzido, isto é, quando o grafo é esparso, é também bastante prático representá-lo através de uma matriz.
Neste trabalho, abordaremos as representações matriciais relacionadas com as noções de adjacência e incidência.
Universidade de Trás-os-Montes e Alto Douro 8
Definição 4
Seja G=(V,E) um grafo (digrafo) com n vértices numerados de 1 a n. A matriz
adjacência de G é uma matriz quadrada de dimensão igual ao número de vértices
de G e cujo elemento da linha i e coluna j é igual ao número de arestas que unem os vértices
V
i e Vj(arcos que unemV
i a Vj, sendoV
i o vértice inicial e Vj ovértice terminal).
Observamos que:
i) como o nome indica, a matriz adjacência, especifica quais os vértices do grafo que são adjacentes;
ii) num grafo que não possui lacetes, a diagonal principal da matriz adjacência é nula;
iii) a matriz adjacência de um grafo é simétrica enquanto a de um digrafo, em geral, não o é.
Consideremos o digrafo F representado na Figura 12, e o respetivo grafo subjacente, G.
Figura 12 - Digrafo F e o seu grafo subjacente, G.
Como o grafo G tem quatro vértices, a matriz adjacência é de ordem 4. O procedimento para a construir é o seguinte:
Como G, apenas possui um lacete no vértice C, a diagonal principal é nula com exceção do elemento da posição (3,3) que terá o valor 1;
Como G, é não dirigido, a matriz de adjacência de G é simétrica relativamente à sua diagonal principal;
Os vértices A e B são ligados por uma aresta de G, assim a matriz conterá 1 na posição (1,2) e, consequentemente na posição (2,1);
Idília Caetano
9
Os vértices A e C também são ligados por uma aresta de G e, como tal, as posições (1,3) e (3,1) desta matriz conterá o valor 1;
Como os vértices A e D não estão ligados por uma aresta, as posições (1, 4) e (4, 1) da matriz adjacência são nulas.
Aplicando, o procedimento anterior, a todos os pares de vértices de G obtém-se a matriz adjacência de G.
Notemos que se, por exemplo, os vértices A estivessem ligados ao vértice B por 3 arcos na entrada (1, 2) estaria o valor 3.
Observemos ainda que, como a matriz adjacência dum grafo é simétrica em relação à diagonal principal, basta construir o seu triângulo superior (ou inferior) e preencher as restantes entradas de modo a obter uma matriz simétrica.
Para construir a matriz adjacência do digrafo F, dado um par de vértices, não só é necessário observar o número de ligações entre os vértices, mas também tem de ser tida em consideração, a informação referente aos vértices inicial e final. Assim, por exemplo, como os vértices A e B estão ligados por um arco (A, B), mas não por um arco (B, A), na posição (1, 2) da matriz de adjacência deve constar o valor 1, enquanto na posição (2,1) deve constar o valor 0. Procedendo deste modo, obtém-se a matriz adjacência de F.
Vejamos de seguida, a noção de matriz incidência.
Definição 5
Seja G=(V,E) um grafo sem lacetes e com n vértices numerados de 1 a n e m arestas (arcos) numerados de 1 até m. A matriz incidência de G é uma matriz de ordem nm, cujo elemento da linha
i
e colunaj
é igual a 1 se o vérticei
é incidente com a aresta (arco)j
e 0 no caso contrário.Para o digrafo, na construção da sua matriz de incidência, temos de ter atenção o sentido da orientação. Dá-se, o valor de 1 se a orientação for de saída, valor -1 se a orientação for de entrada e é de salientar que, no caso de existir um lacete no vértice
i
, a respetiva entrada na matriz de incidência quer no grafo ou no digrafo é igual a 2.Universidade de Trás-os-Montes e Alto Douro 10 Enquanto a matriz adjacência é quadrada, a matriz incidência, em geral, não o é; o seu número de linhas, coincide com o cardinal do conjunto de vértices, enquanto o seu número de colunas, com o número de arestas (arcos).
Figura 13 - Matrizes de adjacência e incidência de G.
Figura 14 - Matrizes de adjacência e incidência de F.
1.3- Grau de um vértice, ordem e dimensão
É útil ter nomenclatura que caracterize, por exemplo, num mapa de estradas, o número total de cidades e estradas que as ligam, existentes nesse mapa, bem como, para cada cidade, o número de vias que permitem partir e ou chegar a essa cidade. Com este intuito, introduziremos seguidamente, as noções de ordem dum grafo, dimensão dum grafo e grau dum vértice.
Definição 6
Dado um grafo (digrafo) G=(V,E), ao respetivo número de vértices chama-se
ordem de G e ao número de arestas (arcos) dimensão de G. Por sua vez, grau de um vértice é o número de arestas (arcos) que lhe são incidentes. Quando
todos os vértices têm o mesmo grau, r, G diz-se grafo regular de grau r.
Observamos que, como um lacete de um dado vértice, A, é duplamente incidente em A, contribui com duas unidades para o grau de A; um vértice de grau zero é um vértice
isolado.
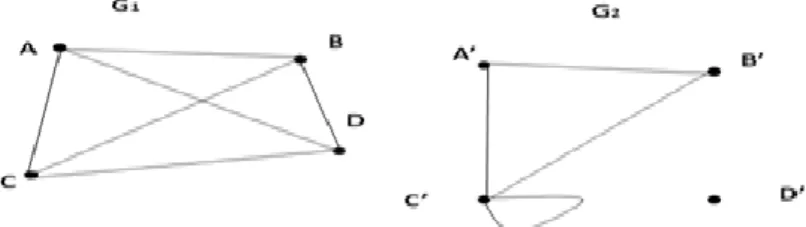
Consideremos os grafos da Figura 15, como ambos têm quatro vértices, a ordem de G1 e de G2 é 4. No entanto, G1 tem 6 arestas enquanto G2 possui apenas 5, assim a
Idília Caetano
11 dimensão de G1 é 6 e a dimensão de G2 é 5. Como todos os vértices de G1 têm grau 3, G1 é um grafo regular de grau 3. No caso de G2, este não é regular, pois o grau de D' é zero, isto é, D' é um vértice isolado; o grau de A' coincide com o de B' e é igual a 2 e, dado possuir um lacete em C', o grau de C' é 4.
Figura 15 - Grafos G1 e G2.
No grafo da Figura 11, os vértices A e C tem grau 3, mas o vértice B tem grau 2, assim, esse grafo não é regular. A ordem e a dimensão desse grafo são iguais a 3 e a 5, respetivamente.
Euler mostrou que, a soma dos graus de todos os vértices de um grafo é sempre um número par, igual ao dobro das arestas; este resultado, é conhecido como lema dos
apertos de mão, dado que, quando várias pessoas apertam as mãos, o número total
de mãos envolvidas é par (em cada aperto estão envolvidas duas mãos).
Teorema 1
(Lema dos apertos de mão): Sendo G=(V,E) um grafo, a soma dos graus de
todos os vértices é igual ao dobro do número de arestas.
Para provar este resultado, basta observar que cada aresta (arco) contribui exatamente com duas unidades para a soma dos graus.
Do Lema dos apertos de mão podemos concluir que em qualquer grafo (digrafo): i) a soma dos graus de todos os vértices é um número par;
ii) o número de vértices de grau ímpar é par;
iii) regular de grau r, com n vértices, o número de arestas (arcos) é igual a .
No grafo da Figura 12, a soma dos graus de todos os vértice é par ( 2+2+5+1=10), e o número de vértices de grau ímpar é par. O grafo G1 da Figura 15, é regular de grau 3 com 4 vértices e 6 arestas verificando o lema dos apertos de mão .
Universidade de Trás-os-Montes e Alto Douro 12
Definição 7
Seja D=(V,E) um digrafo e AV um dos seus vértices. O grau de entrada
(saída) de A é o número de arcos em que A é o vértice terminal (inicial).
Qualquer grafo orientado, satisfaz um resultado semelhante ao Lema do aperto de mão, chamado Di-lema dos apertos de mão.
Teorema 2
(Di-lema dos apertos de mão): Sendo D=(V,E) um digrafo, a soma de todos os
graus de saída (entrada) é igual ao número de arcos correspondentes.
Este resultado, é uma consequência direta do facto de, cada arco contribuir exatamente com uma unidade para a soma dos graus de saída (entrada).
No digrafo F, representado na Figura 12, os graus de saída são os seguintes: 2 em A, 1 em B, 3 em C e 1 em D, sendo a soma destes graus igual a 7; contando os seus arcos verificamos que, também são 7 dado que o lacete conta como 2 arcos. Consideramos, agora, os graus de entrada deste grafo: 0 em A; 2 em B; 4 em C e 1 em D, também, a sua soma 7.
1.4- Subgrafos
Por vezes, a resolução de um problema implica considerar apenas uma parte de um grafo. A título de exemplo, consideremos o caso de uma rota aérea envolvendo os aeroportos de Bragança, Vila Real, Porto, Lisboa e Faro. Se, em determinada situação, forem relevantes somente rotas envolvendo as cidades de Bragança, Vila Real e Lisboa, podemos ignorar os aeroportos das restantes cidades. Então, no grafo que modela a rede completa, podemos remover os vértices das cidades não relevantes para o problema e, também, as arestas que incidam nos vértices removidos; com este procedimento, obtemos um grafo com ordem inferior ao original e que, designamos por subgrafo do grafo original.
Definição 8
Seja G=(V,E) um grafo (digrafo). O Grafo G’=(V’,E’) diz-se um subgrafo
Idília Caetano
13 unem vértices de V’. Neste caso, G é um supergrafo (superdigrafo) de G’. Sendo W'V, o subgrafo (subdigrafo) induzido por W’ é o grafo (digrafo) cujo
conjunto de vértices é W’ e o conjunto de arestas (arcos) é formado por todas as arestas (arcos) em E que unem os vértices de W’.
Consideremos, o grafo G2 da Figura 17. O Grafo G3, Figura 18, é um subgrafo de G2. O grafo G5 é um subgrafo de G2 e é o subgrafo de G2 induzido por {1,2,3,4,5,7,8}. O grafo G2 é supergrafo dos grafos G3 e G5.
Sejam G=(V,E) um grafo, A e B dois dos seus vértices e AB uma aresta de G. Os grafos seguintes são subgrafos de G:
▪ o próprio G; ▪ o grafo (V, Ø);
▪ o grafo resultante de G por eliminação da aresta AB, isto é, o grafo (V,E\{AB}); ▪ o grafo ({A,B},{AB});
▪ qualquer subgrafo de um subgrafo de G;
▪ o grafo constituído apenas por um único vértice de G (em que E=Ø).
1.5- Grafos isomorfos
Como vimos na Secção 1.1, dois diagramas podem ser muito diferentes e representar o mesmo grafo; o caso contrário também pode acontecer, isto é, dois diagramas podem ser muito semelhantes e, no entanto, não representarem o mesmo grafo, como por exemplo na Figura 16.
Figura 16 - Diagramas semelhantes que não representam o mesmo grafo.
Observemos que, os diagramas da Figura 16, não representam o mesmo grafo, dado que, embora ambos possuam os mesmos vértices, BC é aresta do primeiro grafo, mas
Universidade de Trás-os-Montes e Alto Douro 14 não é do segundo. No entanto, se em G1 o vértice A for substituído pelo B e vice-versa, obtemos o grafo G2.
Definição 9
Dois grafos, G1 e G2, dizem-se isomorfos se existe uma correspondência unívoca entre os seus vértices e arestas de tal maneira que a relação de incidência seja preservada, isto é, se existe uma correspondência, de um para um, entre os vértices de G1 e os de G2, com a propriedade de o número de arestas que unem dois vértices de G1 ser igual ao número de arestas que unem os vértices correspondentes de G2.
G1 G2
Figura 17 - Grafos Isomorfos.
Os grafos G1 e G2 da Figura 17, embora apresentem formas muito distintas, são isomorfos. Basta, designar os vértices A, B, C, D, G, H, I e J do Grafo G1, respetivamente, por 1, 3, 6, 7, 2, 4, 5 e 8, para obter o grafo G2.
Como entre dois grafos de ordem
n
, há n! possibilidades de correspondências de um para um, para um valor den
elevado torna-se impraticável testar, se cada uma das!
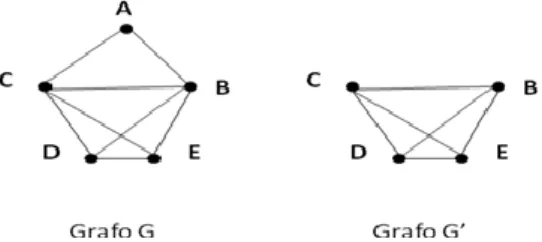
n correspondências preservam a adjacência. Assim, na prática, torna-se difícil determinar se dois grafos são ou não isomorfos. Para mostrar que, dois grafos não são isomorfos, uma forma de contornar esta dificuldade é mostrar que, estes não partilham, pelo menos, uma das propriedades que os grafos isomorfos partilham. Por exemplo, grafos isomorfos apresentam o mesmo número de vértices e de arestas; adicionalmente, os graus dos vértices correspondentes devem coincidir; caso contrário, concluímos que, os grafos não são isomorfos.
O grafo G3 da Figura 18, não é isomorfo aos grafos G1 e G2 da Figura 17, dado possuir menos uma aresta; G4 não é isomorfo nem a G1 nem a G2, visto possuir menos uma aresta; G5 é não isomorfo a G1 e a G2 pois, possui menos um vértice. Também é
Idília Caetano
15 simples concluir que, os grafos G3, G4 e G5 são não isomorfos entre si; para tal, basta observar que, o grafo G5 tem menos vértices que os grafos G3 e G4, logo não é isomorfo a nenhum destes. Por sua vez, os grafos G3 e G4 também não são isomorfos pois, por exemplo, o grau do vértice 6 em G3 é 2, enquanto em G4, o grau de B (vértice correspondente) é 3.
G3 G4 G5
Figura 18 - Grafos não isomorfos.
1.6- Operações com grafos
Existem várias operações que podemos efetuar com grafos, de modo a obter novos grafos. Aqui são focadas as mais utilizadas.
Na definição seguinte, usam-se as letras A e B para representar, genericamente, vértices de um dado grafo (digrafo).
Definição 10
Consideremos, os grafos (digrafos) Gi=(Vi,Ei), i=1,2. O grafo (digrafo) i) complementar de é o grafo (digrafo)
(
,
')
i
E
V
G
i
i tal que:
AB AB Ei AB Vi
E i : , '
E
A B A B Ei A B Vi
i ( , ):( , ) , ' ; ii) que resulta da interseção de G1 e G2 é definido por:) , ( 1 2 1 2 2 1 G V V E E G ;
iii) que resulta da reunião de G1 e G2 é definido por:
) , ( 1 2 1 2 2 1 G V V E E G .
Na Figura 19, apresentamos exemplos que, pretendem clarificar os conceitos introduzidos na Definição 10.
Universidade de Trás-os-Montes e Alto Douro 16
Idília Caetano
17
1.7- Grafos especiais
Nesta secção, são abordados alguns casos particulares de grafos que, pelas suas características especificas, justificam ser destacados dos demais.
Definição 11
Seja G=(V,E) um grafo (digrafo). Se V for um conjunto constituído por n vértices isolados, então G diz-se um grafo nulo e representa-se por Nn.
Na Figura 20, está representado N , isto é, o grafo nulo com 5 vértices. 5
Figura 20 - Grafo nulo com 5 vértices (N5).
Notemos que, todo o grafo nulo é regular de grau 0, visto todos os seus vértices terem grau zero. Observemos, adicionalmente, que o grafo nulo, Nn, é um subgrafo de qualquer grafo de ordem n.
Definição 12
Dado um grafo (digrafo) G, se dois dos seus vértices estiverem ligados por lacetes ou mais de uma aresta (arco), a G dá-se o nome de multigrafo. O grafo (digrafo) G diz-se simples se não contiver lacetes nem arestas (arcos) múltiplas(os) Se G for simples e todos os vértices de G forem adjacentes entre si, então G diz-se completo e representa-se por
K
n.Notemos que o grafo completo com
n
vértices (representado porK
n) é regular de grau n1.Na Figura 21, estão representados dois grafos completos e, na Figura 15 está representado
K
4. O grafo da, Figura 6, é simples, mas não é completo.Universidade de Trás-os-Montes e Alto Douro 18
K5 K6
Figura 21 - Grafos completos K5 e K6.
Observamos que, os grafos da Figura 19, são simples, enquanto os da Figura 10, são todos multigrafos, dado que todos eles apresentam lacetes no vértice A.
Conforme foi referido anteriormente, podemos representar três cidades pelos vértices A, B e C, e as estradas que as ligam por arestas. Assim, a correspondente rede viária pode ser representada por um grafo. Se, por exemplo, as cidades A e B têm duas estradas diferentes a uni-las, então, existem arestas múltiplas entre esses dois vértices e o grafo correspondente é um multigrafo.
Do Lema dos apertos de mão, podemos concluir que, em qualquer grafo (digrafo)
completo com n vértices, o número de arestas (arcos) é ( 1). 2
1
2 n n C
n Por exemplo,
uma vez que o grafo completo
K
6, da Figura 21, tem 6 vértices, pelo lema dos apertos de mão, concluímos que tem 15 arestas.O complementar de um grafo G com n vértices, pode ser construído utilizando o correspondente grafo
K
n. Basta, para tal, remover deK
n todas as arestas de G. O complementar de qualquer grafo completo, é o grafo nulo correspondente e vice-versa.Definição 13
Dado um grafo G, dá-se o nome de clique de G a qualquer subgrafo completo de G.
Idília Caetano
19 Consideremos, os grafos G e G' da Figura 22. O Grafo G' é um Grafo Clique do Grafo G.
Figura 22 -O grafo G' é um grafo clique do grafo G.
Definição 14
Seja G=(V,E) um grafo (digrafo). Se for possível encontrar um subconjunto A de V, de tal modo que cada aresta (arco) de G una um vértice de A a um vértice de V\ A, G diz-se bipartido.
Num grafo bipartido, podem existir vértices em A, que não estejam unidos a nenhum vértice de V\A.
Consideremos os grafos seguintes:
Figura 23 - Grafo bipartido.
Ambos os grafos são grafos bipartidos, embora no segundo grafo, o terceiro vértice preto não esteja unido ao nenhum vértice branco.
Definição 15
Seja G=(V,E) um grafo simples (digrafo). Se G for bipartido e se cada vértice de A estiver unido a cada um dos vértices de V\A, G designa-se por grafo bipartido
completo e representa-se por , onde r e s são o número de vértices em A e V\A, respetivamente. No caso particular de r=1 ou s=1, G diz-se grafo estrela.
Universidade de Trás-os-Montes e Alto Douro 20 De seguida, apresentamos dois exemplos de grafos bipartidos completos. O grafo que se pode representar da seguinte forma:
Figura 24 - Representações do grafo K3,3.
O grafo estrela com 8 vértices apresenta a forma seguinte:
Figura 25 - Grafo estrela.
Da Definição 15, concluímos que, qualquer grafo (digrafo) bipartido completo tem um número de arestas (arcos) exatamente igual a rs.
Observemos ainda que, o complementar de um grafo bipartido completo é a união de dois grafos completos.
Ilustremos esta ideia, com o caso do grafo bipartido completo K3,2 da Figura 26, o qual contém arestas.
Figura 26 - Grafo bipartido completo K 3,2
O complementar de K3,2 é o grafo da Figura 27, que é a união dos grafos das Figuras 28 e 29.
Idília Caetano
21
Figura 27 - Grafo complementar de K3,2.
Figura 28 Figura 29
Outros exemplos:
Consideremos, agora, um grafo que representa os casamentos entre as pessoas de uma cidade, onde cada pessoa é representada por um vértice e um casamento por uma aresta. Assumindo que, só se verificam casamentos entre pessoas de sexo diferente, o grafo será bipartido, já que os vértices a serem unidos por uma aresta são obtidos da seguinte forma: um do subconjunto dos vértices que representam o sexo masculino e o outro do subconjunto dos vértices que representam o sexo feminino;
O caso de uma rede local constituída por sete computadores e impressoras, todos ligados a um servidor central. Esta rede tem uma topologia em estrela, a qual pode ser representada pelo grafo bipartido completo K1,7, representado na Figura 25.
Universidade de Trás-os-Montes e Alto Douro 22 O tetraedro, o cubo, o octaedro, o dodecaedro e o icosaedro, Figura 30, são os cinco sólidos regulares, conhecidos como Sólidos Platónicos. Da projeção destes cinco sólidos no plano, obtêm-se os cinco grafos habitualmente conhecidos por grafos
Platónicos.
Figura 30 - Sólidos Platónicos.
Definição 16
Um grafo regular formado pelos vértices e arestas da projeção no plano de um dos sólidos regulares, tetraedro, cubo, octaedro, dodecaedro ou icosaedro, designa-se por grafo platónico.
Na Figura 31, encontram-se os cinco grafos platónicos referidos na Definição 16.
Figura 31 - Grafos platónicos do Tetraedro, Cubo, Octaedro, Dodecaedro e Icosaedro respetivamente.
Idília Caetano
23 Todos os grafos platónicos, têm a particularidade de poderem ser representados por grafos, de tal modo que, quaisquer duas das suas arestas nunca se cruzem. Em muitos problemas, é útil conseguir desenhar grafos que gozem desta particularidade e que são conhecidos por grafos planares.
Definição 17
Um grafo G diz-se planar se puder ser desenhado no plano de modo a que quaisquer duas das suas arestas nunca se cruzem, exceto nos vértices onde ambas são incidentes. Os esboços correspondentes designam-se por esboços
planos de G.
Contrariamente aos grafos platónicos, o grafo bipartido completo
K
3,3, Figura 24, não é planar, dado que, qualquer um dos seus esboços planos contêm pelo menos um cruzamento.O grafo
K
4 é planar, dado que admite os seguintes esboços planos:Figura 32 - Grafos planar
K
4.Definição 18
Qualquer grafo G que não possa ser expresso como a reunião de dois grafos com interseção vazia, é um grafo conexo; caso contrário, diz-se desconexo. Neste último caso, G pode ser expresso como a reunião de um número finito de grafos conexos, sendo cada um destes designado por componente de G.
Universidade de Trás-os-Montes e Alto Douro 24 Na Figura 33, constam um grafo conexo G1 e outro desconexo G2.
Figura 33 - Grafo conexo - G1 e Grafo desconexo- G2.
A rede do metro de Lisboa, Figura 34, pode ser representada por um grafo conexo, dado que, quaisquer duas das estações de metro estão ligadas pela rede.
Figura 34 - Rede do metro de Lisboa. Definição 19
Um digrafo D diz-se conexo, se o grafo subjacente a D é conexo.
Idília Caetano
25 Consideremos, o digrafo D da Figura 35. Como o grafo G1 da Figura 33, é o grafo subjacente a D, e G1 é conexo, pela Definição 19, concluímos que, o digrafo D da Figura 35, é conexo.
Definição 20
Um grafo G diz-se k-conexo, se dois quaisquer dos seus vértices estiverem ligados por, pelo menos, k arestas, onde k é o maior inteiro não negativo naquelas condições.
A título de exemplo, se após a remoção de, no mínimo, dois vértices, um grafo conexo G passa a ser desconexo, então G diz-se 2-conexo. O grafo G1 da Figura 33, transforma-se num grafo desconexo, se lhe for retirado o vértice B, logo G1 é 1-conexo. O mesmo acontece com o grafo da Figura 36 que, também fica desconexo quando se retira o vértice C.
.
Figura 36 - Grafo 1-Conexo.
Definição 21
Seja G um grafo simples com n vértices. Se G for conexo e regular de grau 2, então a G dá-se o nome de grafo ciclo ou grafo circuito de ordem n e representa-se por .
A Figura 37, representa o grafo circuito , isto é o grafo ciclo com 5 vértices.
Universidade de Trás-os-Montes e Alto Douro 26 Se considerarmos, agora uma rede de computadores, em que cada unidade está ligada a exatamente duas outras unidades e a informação circula de computador para computador, ao longo do circuito, até ao local pretendido, este tipo de rede pode ser modelada por um grafo circuito. No caso de essa rede ser formada por cinco computadores, pode ser modelada pelo grafo ciclo da Figura 37.
Algumas redes de computadores, estão organizadas de tal modo que, a informação é transferida ao longo do circuito ou através de um servidor central, podendo estas redes ser representadas por um misto de grafo estrela e grafo ciclo. Chega-se, assim, ao conceito de grafo roda. No caso de a rede ter seis computadores, o grafo roda correspondente é o da Figura 38.
Figura 38 - Grafo Roda com 6 vértices.
O grafo da Figura 38, obtém-se a partir do grafo ciclo C5, acrescentando um novo vértice e unindo este novo vértice a cada um dos vértices do grafo C5.
Definição 22
Consideremos o grafo ciclo , com n3. Ao grafo simples, de n+1 vértices, que se obtém acrescentando um vértice extra a e unindo, através de arestas, este novo vértice a cada um dos n vértices deste grafo ciclo, dá-se o nome de grafo
roda e representa-se por
.
1.8- Caminhos e ciclos
Várias aplicações da teoria de grafos envolvem ir de um vértice para outro, no grafo. O problema das pontes de Königsberg, já descrito anteriormente, é um exemplo; outro, será tentar encontrar o caminho mais curto entre uma dada escola e a estação de camionagem. De seguida, apresentamos alguns conceitos que, pretendem clarificar estas noções no contexto da teoria de grafos.
Idília Caetano
27
Definição 23
Seja G um grafo (digrafo). Um passeio de comprimento k em G, entre os vértices v1 e
v
k1, é uma sucessão de k arestas (arcos) de G da forma1 3 2 2 1
v
,
v
v
,
,
v
kv
kv
((
v
1,
v
2),
(
v
2,
v
3),
,
(
v
k,
v
k1)
) (1) e que se representa porv
1v
2v
3
v
kv
k1.No caso do grafo da Definição 23, não ser dirigido, o passeio (1) também pode representar o passeio entre os vértices
v
k1 e v1.Num passeio pode haver repetição de vértices e arestas; por exemplo,
6 7 5 4 2 5 4 2 3 1
v
v
v
v
v
v
v
v
v
v
é um passeio de comprimento 9, no grafo da Figura 39, entre os vérticesv
1 ev
6.Figura 39 - Grafo G.
No caso de não poder haver repetição de arestas (arcos), num dado passeio, este passa a chamar-se um trajeto.
Definição 24
Seja G um grafo (digrafo). Se todas as arestas (arcos) de um passeio em G são diferentes, então o passeio designa-se por trajeto. No caso de todas as arestas (arcos) e todos os vértices de um passeio em G serem diferentes, então o passeio designa-se por caminho.
Consideremos, o grafo da Figura 39. O passeio
v
1v
3v
2v
4v
5v
2v
4v
5v
7v
6 não é um trajeto no grafo da Figura 39, visto haver repetição da arestav
4v
5, enquanto o passeio6 7 5 4 3 2 5 3 1
v
v
v
v
v
v
v
v
Universidade de Trás-os-Montes e Alto Douro 28 repetidas), embora não seja um caminho (dado que, por exemplo, o vértice
v
3 ocorre duas vezes). Como, o passeiov
1v
3v
5v
7, não apresenta vértices nem arestas repetidos então, é um caminho no grafo da Figura 39.No caso do digrafo da Figura 40, o passeio
v
1v
2v
5v
6v
3 representa um caminho entre os vérticesv
1 ev
3, enquantov
1v
2v
5v
6v
3v
6 representa um trajeto, entre os vérticesv
1 e6
v
, mas não é um caminho, dado que o vérticev
6 ocorre mais do que uma vez.Figura 40 - Digrafo D.
Definição 25
Seja G um grafo (digrafo). Um passeio fechado em G, é uma sucessão de arestas (arcos) de G da forma:
1 1 3 2 2 1
v
,
v
v
,
,
v
v
v
konde o primeiro e o último vértices coincidem. Se todas as arestas (arcos) do passeio fechado são diferentes, então o passeio fechado designa-se por trajeto
fechado.
É de notar que, no trajeto fechado estamos também perante um circuito.
No caso de todos os vértices de um trajeto fechado, exceto o primeiro e o último, serem diferentes, então este trajeto designa-se por caminho fechado.
É de notar que, no caminho fechado estamos também perante um ciclo.
Na Figura 39, a sequência
v
2v
1v
3v
5v
2v
1v
5v
2é um passeio fechado, mas não um trajeto fechado (por exemplo, a arestav
2v
1aparece duas vezes). Por sua vez,2 1 5 4 3 5 2
v
v
v
v
v
v
v
é um trajeto fechado e não é um ciclo (o vérticev
5aparece mais de uma vez), enquantov
5v
3v
4v
5é um exemplo de um ciclo.Idília Caetano
29 A noção de caminho, permite caraterizar a conetividade de um grafo (digrafo). Das Definições 18 e 24, concluímos que um grafo G é conexo se existe um caminho em G entre qualquer par dos seus vértices.
Definição 26
Um digrafo G diz-se fortemente conexo, se existir um caminho em G entre quaisquer dois dos seus vértices.
O digrafo D da Figura 35, embora seja conexo, não é um digrafo fortemente conexo, pois não existe um caminho de C para B. O digrafo representado na Figura 41 é fortemente conexo, dado existir um caminho entre quaisquer par de vértices.
Figura 41 - Digrafo conexo.
Assim, embora qualquer digrafo fortemente conexo seja conexo, nem todo o digrafo conexo é fortemente conexo.
Definição 27
Um grafo G é orientável, se G for o grafo subjacente dum digrafo fortemente conexo, isto é, se for possível orientar (pelo menos num sentido) as arestas de G de modo que o digrafo resultante seja fortemente conexo.
O grafo da Figura 42 é orientável, dado ser o grafo subjacente ao digrafo da Figura 41 que é fortemente conexo.
Universidade de Trás-os-Montes e Alto Douro 30 Consideremos as Figuras 43 e 44. Observemos que, a remoção da aresta BE do grafo da Figura 43, transforma este grafo no grafo desconexo da Figura 44. A uma aresta com esta característica dá-se o nome de ponte.
Notemos que, se removermos, por exemplo, a aresta AB, o grafo resultante da Figura 43 é desconexo, ou seja AB também é uma ponte.
Figura 43 - Grafo com várias pontes. Figura 44 - Grafo desconexo.
Definição 28
Num grafo conexo, uma ponte é uma aresta cuja remoção deixa o grafo desconexo.
O exemplo a que se refere a Figura 43, permite concluir que, qualquer grafo que contenha uma ponte não pode ser orientável, isto é, não pode ser o grafo subjacente de um digrafo orientável, dado essa ponte ter de ser orientada ou num sentido ou no outro.
O próximo resultado, permite saber se, substituindo cada aresta por um arco, é possível transformar um grafo num digrafo fortemente conexo.
Teorema 3
Um grafo conexo é orientável se e só se não contiver pontes.
Demonstração:
O grafo da Figura 43, permite mostrar que, se um grafo é orientável então não pode possuir pontes.
Para demonstrar o recíproco, comecemos por supor que o grafo conexo G não possui qualquer ponte. Como não há pontes, cada aresta tem de pertencer a um ciclo. Consideremos, um qualquer ciclo C1 de G e orientemos as suas arestas de modo a
Idília Caetano
31 obter um ciclo dirigido; assim conseguimos ir de um dado vértice de C1 para outro qualquer vértice deste mesmo ciclo. Consideremos, agora, um arco, que não esteja contido em C1, mas que seja incidente num vértice de C1. Uma vez que, estamos a admitir que, o grafo G não tem pontes, este arco está obrigatoriamente contido num dado ciclo C2 de G. É possível orientar os arcos de C2 de modo, a obter um ciclo orientado, desde que se respeite a orientação já estabelecida nos arcos do ciclo C2 comuns ao ciclo C1. Deste modo, é possível ir de qualquer vértice de C1 ou C2 para qualquer outro vértice de C1 ou C2. Como G é conexo, é possível continuar este procedimento até que todos os arcos de G estejam orientados, obtendo, deste modo, um digrafo fortemente conexo. c.q.d.
O próximo teorema, fornece uma condição suficiente para que um grafo contenha um ciclo ou circuito.
Teorema 4
Se G é um grafo conexo tal que o grau de cada vértice é, no mínimo, 2, então G contém um circuito.
Demonstração:
No caso de G ter arestas múltiplas, o resultado é trivial. Seja G, um grafo simples e um dos seus vértices. Admitamos, agora, que é um vértice adjacente a ; de seguida, escolhamos um vértice , distinto de , adjacente a ; continuando este processo, escolhamos um vértice , distinto de , adjacente , onde
1
i (como o grau de cada vértice é, pelo menos, dois é sempre possível encontrar esse vértice). Este processo termina, quando se encontra um vértice que já foi escolhido anteriormente ( o que acontece sempre dado o número de vértices de G ser finito), obtendo-se assim, um ciclo e portanto um circuito. c.q.d.
Um grafo bipartido, pode ser caraterizado a partir do conceito de ciclo.
Teorema 5
Um grafo é bipartido se e só se não contiver nenhum ciclo ímpar, isto é, se não contiver qualquer ciclo com um número ímpar de vértices.
Universidade de Trás-os-Montes e Alto Douro 32
Demonstração:
Relativamente à condição necessária.
Consideremos, um grafo G bipartido que, contenha pelo menos um ciclo (o caso em que G não possui ciclos é trivial). Sejam,
X
e Y, os seus conjuntos partição eum seu ciclo arbitrário. Suponhamos que, ; então e com . Como é adjacente a , k é par e, assim, C é um ciclo par.
No que diz respeito à condição suficiente.
Seja G, um grafo conexo com pelo menos 2 vértices, isto é, cujo cardinal , e que não contém ciclos ímpares. Consideremos um vértice de G,
v
, fixo eX
como sendo o conjunto dos vértices de G cujo caminho mais curto entre x e v tem comprimento par, sendoY
V X
. Suponhamos, agora, que são adjacentes. Sex
v
, então o menor caminho entrev
e x' tem comprimento um, logo , o que é um absurdo. Assim,x
ev
têm de ser distintos bem como x' ev
. Sejam vv v v1 2 2k2 2vk1x o caminho de menor comprimento entrev
e x, vw w1 2...w2t2w2 1tx' o caminho de menor comprimento entrev
e x'. Consideremos, agora, o último vértice que os 2 caminhos anteriores têm em comum, Z vi wj, algum par
i j
,
. Comoi
ej
possuem a mesma paridade ex
e x' são adjacentes,v v
j j1...
v
2k2 2v
k1xx w
'
2t1w
2t2...
w
j é um ciclo decomprimento ímpar, o que é um absurdo. Logo, quaisquer dois vértices em
X
(ouY) não são adjacentes e, como tal, G é bipartido com os conjuntos de partição
X
e Y. c.q.d.Os temas abordados neste capítulo foram, baseados nas referências [12], [13], [14] e
Idília Caetano
33
Capítulo 2 – Grafos Eulerianos e Hamiltonianos
2.1- Grafos Eulerianos
Voltemos, agora, ao problema das pontes de Königsberg, resolvido por Euler; o grafo associado a este problema é o que consta na Figura 2. Neste problema, pretendemos encontrar um trajeto fechado que inclua todas as arestas do referido grafo. A um trajeto com estas caraterísticas, dá-se o nome de trajeto Euleriano.
Definição 29
Seja G, um grafo (digrafo) conexo. A G dá-se o nome de grafo (digrafo)
euleriano (semieuleriano), se existe um circuito (trajeto) que inclua todas as
arestas (arcos) de G; neste caso o circuito (trajeto) diz-se euleriano.
As Definições 25 e 29, permitem concluir que, qualquer grafo euleriano é também semieuleriano.
Figura 45 - G1 é Eureliano, G2 é semieuleriano e G3 nem é euleriano nem semieuleriano.
O grafo G1 é Euleriano, dado existir o circuito ABCDBEDAEFA, que contém todas as arestas de G1. Por sua vez, como em G2 existe o trajeto ABCDBEDAE que contém todas as arestas de G2 então este é semieuleriano; o grafo G3 não é euleriano nem semieuleriano porque, não é possível definir um trajeto euleriano.
Universidade de Trás-os-Montes e Alto Douro 34
Figura 46 - D1 é euleriano, D2 é semieureliano e D3 nem é Euleriano nem semieuleriano.
O digrafo D1 é Euleriano, dado existir o circuito FAEDCBDABEF; em D2 existe o trajeto AEDCBDABE, logo D2 é semieuleriano; o digrafo D3 não é euleriano nem semieuleriano porque não é possível definir nenhum circuito ou trajeto euleriano.
O resultado seguinte, conhecido por Teorema de Euler, fornece uma condição necessária e suficiente para que um grafo seja euleriano.
Teorema 6 (Teorema de Euler)
Um grafo conexo G é euleriano se e só se todos os vértices de G têm grau par.
Demonstração:
Seja G um grafo conexo euleriano, EVV1 2...V Vn 1 um circuito euleriano em G e
X
um vértice qualquer de G. Uma vez que G é conexo e E é euleriano entãoX
V
i para algum i ∈ {1,2,...,n −1,n}.Vejamos que Vi tem grau par. Cada vértice que figura na sequência de vértices do
circuito euleriano E, tem duas arestas nele incidentes. Como cada aresta ocorre precisamente uma vez em E, o grau de cada vértice é par.
Provaremos a recíproca por indução sobre o número de arestas de G. Suponhamos, então, que o grau de cada vértice de G é par. O caso em que G não possui arestas é trivial. Portanto, como hipótese de indução, admitiremos que o resultado é válido se G possuir menos n arestas e, nessas condições provaremos que o resultado é válido no caso de G possuir n arestas ( ). Admitamos, então, que G tem n arestas. Como G é conexo, cada vértice terá pelo menos grau 2 e, portanto, a partir de G, é possível obter um subgrafo regular onde cada vértice tem grau 2, ou seja, pela Definição 21, podemos obter, um subgrafo ciclo C de G. Se C contiver todas as arestas de G, a prova está terminada.
No caso contrário, removemos de G todas as arestas de C, resultando assim um novo subgrafo H de G, eventualmente desconexo, com menos arestas que G (logo com