Notas para o acompanhamento das aulas de

Notas para o acompanhamento das aulas de

C´

alculo Diferencial e Integral 1

Cap´ıtulo 1

N´

umeros Reais e Fun¸c˜

oes

1.1

Conjuntos Num´

ericos

A teoria envolvendo a constru¸c˜ao matem´atica rigorosa dos conjuntos num´ericos, suas opera¸c˜oes e propriedades foge aos objetivos deste curso introdut´orio. Tal estudo ´e visto em disciplinas mais avan¸cadas de Teoria dos N´umeros e

An´alise Real (ouAn´alise Complexa).

Abaixo segue um resumo de tais conjuntos.

Conjunto don´umeros naturais:

N={1, 2, 3, 4, 5, . . .}.

Alguns autores consideram0(zero) como n´umero natural.

Conjunto dosn´umeros inteiros:

Z={. . . ,−5,−4,−3,−2,−1, 0, 1, 2, 3, 4, 5, . . .}.

A palavran´umeros em alem˜ao ´e escrita comozahlen.

Conjunto dosn´umeros racionais:

Q=a

b :a, b∈Zeb6=0

.

Existe uma rela¸c˜ao de equivalˆencia importante emQ:

a b =

c

d ⇐⇒ad=bc.

Assim, por exemplo, 1 2=

3

6, pois1.6=2.3.

Todo n´umero racional pode ser escrito em uma forma decimal, sendo esta forma “finita” ou “infinita” formando uma d´ızima peri´odica. Por exemplo,

1 2 =0, 5

7

8 =0, 875 1

3 =0, 3333 . . .

41

333 =0, 123123123 . . .

Existem n´umeros que n˜ao s˜ao racionais. Por exemplo, o comprimento da hipotenusa de um triˆangulo retˆangulo cujos catetos medem uma unidade de comprimento. Tal n´umero ´e indicado por√2e ´e uma raiz da equa¸c˜aox2₌₁2₊₁2 (esta equa¸c˜ao ´e proveniente doTeorema de Pit´agoras), ou seja, x2=2.

Ö2

1 1

Mas como saber se√2n˜ao pode ser escrito na forma a

b coma, b∈Zeb6=0? Necessitamos de umademonstra¸c˜ao

matem´atica.

Suponhamos que existama, b_∈Zcomb₆=0 de tal modo que a b =

Sabemos que todo n´umero inteiro maior do que1pode ser fatorado em produto de n´umeros primos e tal fatora¸c˜ao ´e ´unica a menos de permuta¸c˜ao dos fatores (este ´e o conhecido Teorema Fundamental da Aritm´etica). Assim, a =

p1p2. . . pn eb=q1q2. . . qm compi, qjn´umeros primos. Logo,

a

b =

√

2_⇒ a

2

b2 =2⇒

(p1p2. . . pn)2

(q1q2. . . qm)2

=2_⇒ p1p1p2p2. . . pnpn q1q1q2q2. . . qmqm

=2_⇒p1p1p2p2. . . pnpn =2q1q1q2q2. . . qmqm.

Ocorre que na ´ultima igualdade, a quantidade de fatores iguais a 2 no primeiro membro ´e par, enquanto que no segundo membro ´e ´ımpar. Uma contradi¸c˜ao que surgiu do fato de supormos que √2 ´e um n´umero racional. Logo, conclu´ımos que √2 n˜ao ´e um n´umero racional.

Ali´as, o leitor perceber´a facilmente que o racioc´ınio desenvolvido acima pode ser repetido para qualquer n´umero da forma√pcompprimo.

Podemos associar os n´umeros racionais a pontos de uma reta. Para tanto, basta fixarmos dois pontos A e B

distintos na reta e associarmos os n´umeros0e1, respectivamente. Com isto, estabelecemos umaunidade de medida geom´etrica sobre a reta que, por meio de seus m´ultiplos e subm´ultiplos, permite a localiza¸c˜ao dos demais n´umeros racionais sobre a reta. Os n´umeros racionais positivos est˜ao associados a pontos da semirreta com origem emAque passa por B, enquanto que os n´umeros racionais negativos est˜ao associados a pontos da semirreta com origem emA

que n˜ao passa porB. A figura abaixo esclarece o procedimento acima.

0 1 2 3

-1 -2 -3

-0 5,

A B

2 5_, 5

2

Existem pontos da reta que n˜ao est˜ao associados a n´umeros racionais. Tais pontos est˜ao associados aos chamados

n´umeros irracionais. `

A reuni˜ao do conjunto dos n´umeros racionais e do conjunto dos n´umeros irracionais chamamos de conjunto dos

n´umeros reaise indicamos porR.

A reta associada ao conjunto dos n´umeros reais, conforme descrevemos acima, chamamos dereta realoueixo.

Todo n´umero irracional pode ser aproximado por n´umeros racionais e possui uma representa¸c˜ao decimal “infinita” que n˜ao formad´ızima peri´odica. Por exemplo,

√

2=1, 41421356 . . . √3=1, 73205080 . . . √5=2, 23606797 . . . π=3, 14159265 . . . e=2, 71828182 . . .

Ainda h´a o conjunto dos n´umeros complexos:

C=a+bi:a, b_∈Rei=√−1

Em resumo:

N Z Q R C

Neste curso trabalharemos apenas com o conjunto dos n´umeros reais, admitindo suas opera¸c˜oes usuais, bem como suas propriedades.

Exerc´ıcio. Representa¸c˜ao decimal de n´umeros racionais. Escreva os n´umeros racionais

0, 42 0, 888 . . . 0, 62555 . . . 0, 999 . . .

em forma de fra¸c˜ao com numerador e denominador inteiros.

1.2

Intervalos, Desigualdades e Valor Absoluto

H´a subconjuntos deRque s˜ao especiais para o desenvolvimento da teoria envolvendo C´alculo Diferencial e Integral. S˜ao osintervalos. Sejama < bn´umeros reais.

(1){x_∈R:a < x < b}= ]a, b[´e chamado de intervalo aberto de extremosaeb.

b a

R

(2){x_∈R:a_≤x_≤b}= [a, b]´e chamado de intervalo fechado de extremosaeb.

b a

R

De modo an´alogo:

(3){x_∈R:a < x_≤b}= ]a, b]

b a

R

(4){x_∈R:a_≤x < b}= [a, b[

b a

R

(5){x_∈R:a_≤x}= [a,+_∞[

a

R

(6){x_∈R:a < x}= ]a,+_∞[

a

R

(7){x_∈R:x < b}= ]−_∞, b[

b

R

(8){x_∈R:x_≤b}= ]−_∞, b]

b

R

(9)R= ]−_∞,+_∞[

R

Inequa¸c˜oes do 1o

. graus˜ao desigualdades redut´ıveis a uma das seguintes formas:

ax > b, ax_≥b, ax < b, ax_≤b.

Exemplo. Encontrar os valores de xtais que 2(x−1)< 5x+3.

Resolu¸c˜ao:

Temos2x−2 < 5x+3⇒−3x < 5⇒x >−5

3. Logo, os valores de xest˜ao no intervalo

−5 3,+∞

.

Definimos om´oduloouvalor absolutode um n´umero realxcomo sendo

|x|=

x, sex_≥0

−x, sex < 0 .

Por exemplo,|5|=5 e|−7|=7.

Propriedades. Sejak > 0.

(1)|x|=k_⇐⇒x=koux= −k.

(2)|x|< k_⇐⇒−k < x < k.

(3)|x|> k_⇐⇒x > koux <−k.

(4)√x2_=|x|.

Exerc´ıcio. Resolva|2x−3|> 7.

1.3

Fun¸c˜

oes

Sejam XeY conjuntos ex₇₋→yuma regra que associa acadaelementox_∈Xumunico´ elementoy_∈Y. `

A terna(X, Y, x_7−→y)chamamos defun¸c˜ao. Uma fun¸c˜ao pode ser indicada por

f:X_−→Y,f(x) =y

ou ainda

f: X _−→ Y x _7−→ y

.

O conjuntoX´e chamado dedom´ınioda fun¸c˜aof.

O conjuntoY ´e chamado decontra-dom´ınio da fun¸c˜aof.

O conjuntoI={f(x)_∈Y:x_∈X}_⊂Y ´e chamado deconjunto imagemda fun¸c˜aof. O elementof(x)_∈Y´e chamado deimagem do elementox_∈Xpela fun¸c˜aof.

Exemplos e contra-exemplo.

(1)X={0, 1, 2, 3, 4},Y={5, 6, 7, 8}ef:X_→Y tal que

x y=f(x)

0 8

1 8

2 5

3 5

4 6

0

1

2

3

4

5

6

7

8

X Y

0 1

1 2 3 4 5 6 7 8

2 3 4

(2)X=N,Y=Ze

f: N _−→ Z

x _7−→ 2x

4

3

2

4

3

2

1

0 1 1 2 3 4 5 6 7 8

2 3 4

1 0

-1

5 6

7 8

Z

N -1

(3)X={1, 2, 3}, Y={1, 2, 3}ef:X_→Y tal que

x y=f(x)

1 1

1 2

2 3

3 3

1

2

3

3

2

1 X

Y 0 1

1 2 3

Observemos quefn˜ao´e fun¸c˜ao, pois ao elemento1_∈Xn˜aoest´a associado um´unicoelemento deY.

Sejaf:X_→Y,f(x) =y, uma fun¸c˜ao.

Quando elementos distintos do dom´ınioXest˜ao associados a elementos distintos do contra-dom´ınioY dizemos que

f´e uma fun¸c˜aoinjetiva (ou injetora). Matematicamente:

x₆=y_⇒f(x)₆=f(y)

ou, equivalentemente,

f(x) =f(y)_⇒x=y.

Quando o conjunto imagem defcoincide com seu contra-dom´ınio, isto ´e,I=Y, dizemos quef´esobrejetiva(ou sobrejetora).

Quandof´e injetiva e sobrejetiva dizemos quef´ebijetiva(ou bijetora, ou ainda que f´e uma bije¸c˜ao).

Exemplos.

(1)A fun¸c˜ao

f: N _−→ N

x _7−→ x2 ´e injetiva.

De fato, sejamx1, x2∈Ntal que

f(x1) =f(x2)⇒x21=x22⇒ q

x2 1=

q

x2

2⇒|x1|=|x2|⇒x1=x2 pois x1, x2> 0.

A fun¸c˜aof n˜ao ´e sobrejetiva, pois, por exemplo, 2_∈Ne n˜ao ´e quadrado de n´umero natural, ou seja,6 ∃x_∈Ntal quef(x) =x2_{=2. Portanto, I6=N.}

Naturalmente,fn˜ao ´e bijetiva.

(2)A fun¸c˜ao

f: N_∪{0} _−→ N

x _7−→ x+1

´e bijetiva.

De fato, sejamx1, x2∈N∪{0}tal que

f(x1) =f(x2)⇒x1+1=x2+1⇒x1=x2.

Portanto,f´e injetiva.

Seja y _∈ N. Temos x = y−1 _∈ N_∪{0} e f(x) = f(y−1) = (y−1) +1 = y. Portanto, I = N, ou seja, f ´e sobrejetiva.

Sejam f: A_→B eg:C_→D fun¸c˜oes tais que B_⊂C. Podemos definir uma nova fun¸c˜aog_◦f:A_→D tal que

g_◦f(x) =g(f(x)), chamada defun¸c˜ao compostadegcomf.

x A

B _{C D}

f x( ) g(f x( ))

go_f

g f

Exemplo. Sejam

f: N _−→ N

x _7−→ x2

e g: N _−→ Q

x _{7−→ x+}x₁

.

Temos definida a composta degcomf pois o conjunto imagem defest´a contido no dom´ınio de g. Portanto.

g_◦f: N _−→ Q

x _7−→ x2 x2

pois g_◦f(x) =g(f(x)) =g x2 = x2

x2

+1.

Observemos quef_◦gn˜ao est´a definida, pois o conjunto imagem degn˜ao est´a contido no dom´ınio def.

Neste curso trabalharemos com fun¸c˜oes do tipo f : X _⊂ R _→ R, que s˜ao chamadas de fun¸c˜oes reais de uma vari´avel real. Observemos que o gr´afico de tais fun¸c˜oes pode ser representado no plano cartesiano:

G={(x, f(x)) :x_∈X}_⊂R_×R=R2_.

1.4

Algumas Fun¸c˜

oes Especiais

A menos que se diga o contr´ario, nas pr´oximas subse¸c˜oes trabalharemos sempre comdom´ınios maximaisemR, isto ´e, as fun¸c˜oesfque iremos definir ter˜ao sempre omaior dom´ınio poss´ıvel emRpara o qual a express˜ao anal´ıtica deffa¸ca sentido. Tamb´em trabalharemos com o contra-dom´ınio de fcomo sendoR. Assim, os coment´arios sobre injetividade, sobrejetividade e bijetividade def ser˜ao feitos tendo em mente essas considera¸c˜oes.

1.4.1

Fun¸c˜

oes Constantes

S˜ao fun¸c˜oes do tipof:R_→Rcomf(x) =b, sendob_∈Rconstante.

O gr´afico de uma fun¸c˜ao constante no plano cartesiano ´e uma reta paralela (ou coincidente) ao eixo das abscissas (eixox), passando pelo ponto de ordenadabdo eixo das ordenadas (eixoy).

x y

b

Observemos que fun¸c˜oes constantes n˜ao s˜ao injetivas e nem sobrejetivas (portanto, n˜ao s˜ao bijetivas).

1.4.2

Fun¸c˜

oes Lineares

S˜ao fun¸c˜oes do tipof:R_→Rcomf(x) =ax, sendoa_∈Rconstante.

O gr´afico de uma fun¸c˜ao linear no plano cartesiano ´e uma reta com coeficiente angular igual a a, passando pela origem do sistema de coordenadas.

x y

1

q

a

0

Observemos que fun¸c˜oes lineares s˜ao bijetivas quando a ₆= 0 (prove isso). Quando a = 0 temos a fun¸c˜ao linear nula, que ´e um caso particular de fun¸c˜ao constante.

Lembremos, tamb´em, que o coeficiente angularado gr´afico def´e tal quea=tg(θ), sendoθ a medida do ˆangulo orientado no sentido anti-hor´ario a partir do eixoxque o gr´afico def forma com esse eixo (veja figura acima).

1.4.3

Fun¸c˜

oes Afins

S˜ao fun¸c˜oes do tipof:R_→Rcomf(x) =ax+b, sendoa, b_∈Rconstantes. (1₎

O gr´afico de uma fun¸c˜ao afim no plano cartesiano ´e uma reta com coeficiente angular igual a a, passando pelo ponto de ordenada bdo eixoy(isto ´e,f(0)) e, quandoa₆=0, passando pelo ponto de abscissa−b_a do eixox(isto ´e, a raiz da equa¸c˜aof(x) =0).

x y

- /_{b a} b

Observemos que fun¸c˜oes afins s˜ao bijetivas quandoa₆=0(prove isso). Quandoa=0, fun¸c˜oes afins s˜ao, na verdade, fun¸c˜oes constantes. Quandob=0, temos fun¸c˜oes lineares.

1

1.4.4

Fun¸c˜

oes Quadr´

aticas

S˜ao fun¸c˜oes do tipof:R_→Rcomf(x) =ax2_{+bx+c, sendoa, b, c∈Rconstantes ea6=0.}

O gr´afico de uma fun¸c˜ao quadr´atica no plano cartesiano ´e uma par´abola com v´ertice no pontoV = −b 2a,−

∆ 4a

passando pelo ponto de ordenada cdo eixoy. Quandoa > 0 temos a concavidade da par´abola para cima e, quando

a < 0, para baixo. Quando o gr´afico de uma fun¸c˜ao quadr´atica intersecta o eixox, essa intersec¸c˜ao ocorre em pontos de abscissas iguais `as ra´ızes reais def(x) =0.

-D/_4a c

x1 _x

y

x2

- /_{b 2a}

V

-D/4a

c x1

x y

x2

- /_{b 2a}

V

0

c

x y

- /_{b 2a}

V

0

c

x y

- /_{b 2a}

V

-D/_4a

c

x y

- /b 2a

V

-D/_4a c

x y

- /_{b 2a}

V

a > 0 > 0 D

a > 0 0 D =

a > 0 < 0 D

a < 0 > 0 D

a < 0 0 D =

a < 0 < 0 D

Observemos que fun¸c˜oes quadr´aticas n˜ao s˜ao injetivas e nem sobrejetivas.

1.4.5

Fun¸c˜

oes Polinomiais

S˜ao fun¸c˜oes do tipo f : R _→ R com f(x) = anxn +an−1xn−1+· · ·+a1x+a0, sendo an, an−1, . . . , a1, a0 ∈ R constantes.

Fun¸c˜oes constantes, lineares, afins e quadr´aticas s˜ao casos particulares de fun¸c˜oes polinomiais.

Exemplos. Consideremos as seguintes fun¸c˜oes:

(i)f:R_→R, comf(x) =x3_{(gr´afico em preto na figura abaixo).}

(ii)g:R_→R, comg(x) = 1₂x3_−x2₋1

2x+1 (gr´afico em vermelho na figura abaixo);

(iii)h:R_→R, comh(x) = 1 2x4−

5

2x2+2(gr´afico em azul na figura abaixo).

y y y

x -1 1 2 x -2 -1 x

0 1 2

1

2

1

1

f g h

Observemos que os gr´aficos das fun¸c˜oes intersectam o eixos das abscissas (eixosx) nos pontos cujas abscissas s˜ao as ra´ızes das equa¸c˜oes polinomiaisf(x) =0,g(x) =0eh(x) =0(verifique!).

J´a os pontos onde os gr´aficos das fun¸c˜oes intersectam os eixos das ordenadas (eixosy) s˜ao os pontos cujas ordenadas s˜aof(0),g(0)eh(0)(verifique!).

1.4.6

Fun¸c˜

oes Racionais

S˜ao fun¸c˜oes do tipo f:X_⊂R_→Rcomf(x) = p_q(₍x_x)₎, sendo p(x)e q(x)polinˆonios de tal modo queq(x)₆= 0 para qualquer x_∈X.

Fun¸c˜oes polinomiais s˜ao casos particulares de fun¸c˜oes racionais. Neste caso,q(x) =1 para qualquerx_∈R.

Exemplo 1. Consideremos f:R∗ _{→R comf(x) =} 1

mesmo sistema de coordenadas, para que possamos entender melhor a dinˆamica de varia¸c˜ao de n para os valores considerados.

n=3

n=2

-1

-1 0 1

1 x

y

n=2

n=1

n=1

n= 4 n= 4

n=3 n=3

-1

-1 0 1

1 x

y

-1 0 1

1 x

y

n= 4 -1

-1 0

1 1

x y

n=1 - n=2

1 0 1

1

x y

No caso em quen=1o gr´afico def(x) = 1

x (em cor preta) ´e constituido pelos dois ramos de uma hip´erbole (provar isso ´e um bom exerc´ıcio!). J´a para n=2, a fun¸c˜aof(x) = _x12 possui imagens positivas apenas (gr´afico na cor verde).

Nos casosn=3,f(x) = _x13 possui gr´afico em azul en=4,f(x) = 1

x4 possui gr´afico em vermelho.

Observemos que os gr´aficos das fun¸c˜oes acima n˜ao intersectam os eixos das abscissas (eixosx). Isto significa que as equa¸c˜oesf(x) =0n˜ao possuem ra´ızes (verifique!).

Observemos tamb´em que os gr´aficos das fun¸c˜oes acima n˜ao intersectam os eixos das ordenadas (eixosy). Isto ´e decorrˆencia do fato dex=0n˜ao pertencer ao dom´ınio das fun¸c˜oes.

Exemplo 2. Consideremos f : X1 ⊂R→ R, comf(x) = _x23x+3

+2x−8 e g: X2⊂ R→ R, com g(x) = x−5 x2

+2x−15. Os gr´aficos def e degest˜ao ilustrados na figura abaixo (as retas pontilhadas verticais n˜ao fazem parte dos gr´aficos).

y

x x

y

-_{5 3}

-₄

2

f g

-1

- /3 8

1 3/

5

Notemos que o dom´ınioX1da fun¸c˜aofn˜ao pode conter as ra´ızes deq1(x) =x2+2x−8, que s˜ao−4 e2, ou seja,

X1=R−{−4, 2}. J´a o dom´ınioX2degn˜ao pode conter as ra´ızes deq2(x) =x2+2x−15, que s˜ao−5e3, ou seja,

X2=R−{−5, 3}.

Observemos que os gr´aficos das fun¸c˜oes f e g acima intersectam os eixos das abscissas (eixos x) nos pontos de abscissas iguais `as ra´ızes das equa¸c˜oes f(x) =0 eg(x) =0, enquanto que intersectam os eixos das ordenadas (eixos

y) nos pontos de ordenadas iguais a f(0)eg(0)(verifique essas afirma¸c˜oes).

1.4.7

Fun¸c˜

oes Potˆ

encias

Casos particulares de fun¸c˜oes potˆencia: Paraa=1 temos quef´e uma fun¸c˜ao linear. Paraa=2 temos quef´e uma fun¸c˜ao quadr´atica. Paraa_∈Z+ temos quef´e uma fun¸c˜ao polinomial.

Paraa_∈Z− temos quef´e uma fun¸c˜ao racional.

Exemplos. Consideremos f : X _⊂ R_→ R comf(x) = xa _{nos casos em que a = −}1 2, −

1 3, −

1 5,

1 5,

1 3 e

1

2. Os seis gr´aficos dessas fun¸c˜oes est˜ao ilustrados na figura abaixo, sendo um de cada cor. Na ´ultima figura todos os gr´aficos est˜ao em um mesmo sistema de coordenadas, para que possamos entender melhor a dinˆamica de varia¸c˜ao dea para os valores considerados.

a= /1 2 a= /1 3 a= /1 5

a= - /1 5 a= - /1 3 a= - /1 2

a = - /1 5 a= - /1 3

a= /1 3 a= /1 5

-₁

-₁ 0 1

1 x

y

a= /1 3 -₁

-_{1 0} 1

1 x

y

a= /1 2 0

1

1 x

y

a= - /1 5 -1

-₁

0 1

1

x y

a= /1 5 -1

-₁ 0 1

1 x

y

a= - /1 2 0

1

1 x

y

a= - /1 3 -₁

-₁

0 1

1

x y

No caso em quea= 1

2 o gr´afico def(x) =

√_{x(em cor magenta) ´e parte de uma par´abola, sendo queX= [0,+}

∞[. J´a para a = −1

2 o dom´ınio de f(x) = 1

√_x ´e X = ]0,+_∞[ = R+ (gr´afico em verde escuro). Nestes dois casos n˜ao

podemos estender o dom´ınio aos n´umeros reais negativos pois, caso contr´ario, ter´ıamos n´umeros complexos na imagem def.

Nos casosa= 1

3 (gr´afico em azul) ea= 1

5 (gr´afico em preto) o dom´ınio def´eX=R.

J´a nos casos em quea= −1₃ (gr´afico em vermelho) e a= −₅1 (gr´afico em verde claro), o dom´ınio def´eX=R∗_.

O exemplo acima permite algumas observa¸c˜oes interessantes. De um modo geral, quando a_∈Qest´a escrito em forma de fra¸c˜ao simplificada (isto ´e, numerador e donominador primos entre si) e com denominador par, ent˜ao o dom´ınio de f ´eX = [0,+_∞[ quandoa > 0, e X= ]0,+_∞[ quandoa < 0. Com denominador ´ımpar, X= Rquando

a > 0, eX=R∗ _{quandoa < 0.}

J´a nos casos em quea´e irracional positivo, temos X= [0,+_∞[, enquanto que paraa irracional negativo, temos

X= ]0,+_∞[.

1.4.8

Fun¸c˜

oes Exponenciais

S˜ao fun¸c˜oes do tipof:R_→Rcomf(x) =ax_{, sendoa > 0ea6=1 constante real.}

Constantesa negativas n˜ao s˜ao consideradas em nossos estudos para que evitemos valores complexos na imagem def, como por exemplo(−1)

1 2

J´a a = 1 oua = 0 (com x > 0) conduzem a fun¸c˜oes constantes que, por sua vez, n˜ao s˜ao consideradas fun¸c˜oes exponenciais.

Exemplos. Consideremosf:R_→Rcomf(x) =ax_{, com a=0, 2; a=0, 5;a=0, 7;a=1, 5; a=2ea=e, cujos} gr´aficos s˜ao dados abaixo.

a= ,0 5

0 x

y

1

a= ,1 5

0 x

y

1 _{a 2}

=

0 x

y

1 _{a e}

=

0 x

y

1

a = ,0 7

0 x

y

1

a= ,0 2

0 x

y

1

Observemos que quando0 < a < 1o gr´afico de f´e decrescente, sempre intersectando o eixo das ordenadas (eixo

y) no ponto de ordenada1. Observemos tamb´em que, quanto maisaest´a pr´oximo de1, tanto mais o gr´afico defest´a pr´oximo do gr´afico da fun¸c˜ao constanteg(x) =1,_∀x_∈R(que corresponde ao gr´afico def(x) =1x_).

De modo an´alogo, quando a > 1 o gr´afico de f ´e crescente, sempre intersectando o eixo das ordenadas (eixoy) tamb´em no ponto de ordenada1.

Um destaque especial para o ´ultimo gr´afico, que corresponde ao gr´afico da fun¸c˜ao exponencial de basee, ou seja,

f(x) =ex_{. Esta fun¸c˜ao ser´a muito importante para estudos posteriores.}

Por fim, observemos que se considerarmosf:R_→R+ as fun¸c˜oes exponenciais s˜ao bijetivas (prove isso!).

1.4.9

Fun¸c˜

oes Logar´ıtmicas

S˜ao fun¸c˜oes do tipof:R+→Rcomf(x) =loga(x), sendoa > 0ea6=1 constante real. Lembremos que

log_a(x) =y⇔ay=x.

Desta forma, para que trabalhemos restritos ao conjunto dos n´umeros reais e tenhamos a fun¸c˜ao logar´ıtmica bem definida, precisamos, de fato, da restri¸c˜aoa > 0ea₆=1.

Exemplos. Consideremosf:R+ →Rcomf(x) =loga(x), coma=0, 2; a=0, 5; a=0, 7;a=1, 5; a=2 ea=e, cujos gr´aficos s˜ao dados abaixo.

a= ,0 5

0 y

a= ,1 5 a =2 a=e

1

0 y

0 y

0 x

y

a = ,0 2

0 x

y

1 a= ,0 7

0 y

1

Observemos que quando0 < a < 1 o gr´afico def´e decrescente, sempre intersectando o eixo das abscissas (eixox) no ponto de abscissa 1. Observemos tamb´em que, quanto maisa est´a pr´oximo de 1, tanto mais o gr´afico def est´a pr´oximo da reta vertical que passa pelo ponto de abscissa1do eixox.

De modo an´alogo, quando a > 1 o gr´afico de f ´e crescente, sempre intersectando o eixo das abscissas (eixo x) tamb´em no ponto de abscissa 1.

Um destaque especial para o ´ultimo gr´afico, que corresponde ao gr´afico da fun¸c˜ao logar´ıtmica na basee, ou seja,

f(x) =loge(x), que ´e chamada de fun¸c˜ao logar´ıtmica natural e denotada porf(x) =ln(x). Esta fun¸c˜ao tamb´em ser´a muito importante para estudos posteriores.

Por fim, todas as fun¸c˜oes logar´ıtmicas s˜ao bijetivas (prove tamb´em isso!).

1.4.10

Fun¸c˜

oes Trigonom´

etricas

Seja uma fun¸c˜aof:X_⊂R_→Rtal que existe um n´umero real positivopque cumpre a condi¸c˜ao

f(x+p) =f(x) (1)

para qualquerx_∈X.

Naturalmente esta mesma condi¸c˜ao ´e cumprida para qualquer m´ultiplo positivomp(m_∈N)dep, pois

f(x+mp) =f(x+ (m−1)p+p) =f(x+ (m−1)p) =f(x+ (m−2)p+p) =f(x+ (m−2)p)

.. .

=f(x+2p) =f(x+p+p) =f(x+p) =f(x).

Uma fun¸c˜aofque cumpre a propriedade descrita acima ´e chamada de fun¸c˜ao peri´odicae o menor n´umero real positivo pque satisfaz(1)´e chamado deper´ıododa fun¸c˜aof.

Fun¸c˜ao Seno

´

E a fun¸c˜aof:R_→Rtal quef(x) =sen(x).

A fun¸c˜ao seno ´e peri´odica de per´ıodop=2π. Sua imagem ´e o intervalo I= [−1, 1]. Seu gr´afico esta esbo¸cado na figura abaixo.

x y

0 p/2

3 2p/

2p 5 2p/ p

-p/2

-p -3 2p/ -2p -5 2p/

1

-1

Fun¸c˜ao Cosseno

´

E a fun¸c˜aof:R_→Rtal quef(x) =cos(x).

A fun¸c˜ao cosseno ´e peri´odica de per´ıodo p=2π. Sua imagem ´e o intervaloI= [−1, 1]. Seu gr´afico esta esbo¸cado na figura abaixo.

x y

0 p/2 3 2p/ 2p 5 2p/ p

-p/2 -p -3 2p/ -2p -5 2p/

1

-1

Fun¸c˜ao Tangente

´

E a fun¸c˜aof:X_⊂R_→Rtal quef(x) =tg(x)sendoX=R−π

2 +kπ:k∈Z .

x y

0

p/2 3 2p/ 2p

5 2p/ p

-p/2 -p -3 2p/ -2p

-5 2p/

Tarefa Importante. Considere as fun¸c˜oes

f(x) =a+bsen(cx+d)

g(x) =a+bcos(cx+d)

h(x) =a+btg(cx+d)

Utilizando o software GeoGebra, estude o comportamento dinˆamico dos gr´aficos das fun¸c˜oes acima fazendo com que os parˆametrosa,b,cedvariem. Fa¸ca um resumo de suas conclus˜oes.

As conclus˜oes as quais vocˆe chegou valem apenas para as fun¸c˜oes trigonom´etricas?

1.5

Fun¸c˜

oes Inversas

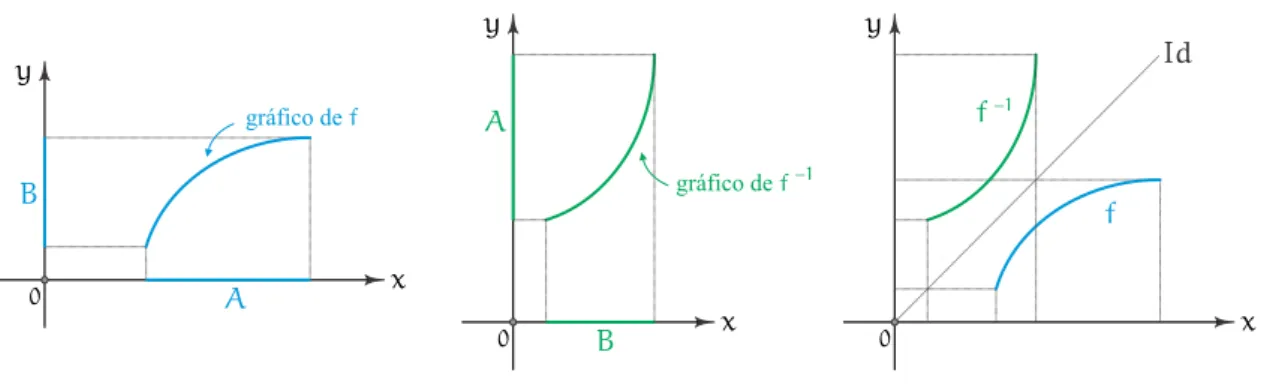
Sejaf:A_⊂R_→B_⊂Ruma fun¸c˜ao bijetiva. Logo, podemos definir a fun¸c˜aog:B_⊂R_→A_⊂Rtal que

f(a) =b_⇐⇒g(b) =a.

x y

0 A a=g b( )

B f a( )=b

gráfico def

A fun¸c˜aog´e chamada de inversada fun¸c˜aof e indicada porg=f−1_{. Assim, sef´e invert´ıvel (ou seja, bijetiva)} temos

f(x) =y_⇐⇒f−1_{(y) =x.} Com isso,

f_◦f−1_{(y) =f f}−1_(y)

=f(x) =y=Id(y)

e

f−1_◦f(x) =f−1(f(x)) =f−1(y) =x=Id(x)

sendo Id : R _→ R a fun¸c˜ao linear identidade, cujo gr´afico no plano cartesiano ´e a reta bissetriz dos quadrantes ´ımpares (portanto, coeficiente angular igual a1).

Propriedade geom´etrica das fun¸c˜oes invert´ıveis.

x y

0 _A

B

gráfico def

x y

0 x

y

0 B

A

gráfico def-1

f

f-1

Id

Exemplos.

(1)Sejamf:R+→R+comf(x) =x2(que ´e bijetiva com esse dom´ınio e contra-dom´ınio) e sua inversaf−1:R+→R+

comf−1_{(x) =}√_x. Temos

f_◦f−1(x) =f f−1(x)

=f √x

= √x2 =x

e

f−1_◦f(x) =f−1(f(x)) =f x2

=√x2_=|x|=x

gráfico def

x y

0 gráfico def-1

f

f-1 Id

1 1

x y

0 1

1

x y

0 1

1

(2)Sejamf:R_→R+ comf(x) =ax, sendoa > 0ea6=1 (que ´e bijetiva com esse dom´ınio e contra-dom´ınio) e sua

inversa f−1_:R

+→Rcomf−1(x) =loga(x). Temos

f_◦f−1(x) =f f−1(x)

=f(loga(x)) =a

loga(x)_=x e

f−1_◦f(x) =f−1(f(x)) =f(ax) =loga(ax) =x

Na figura abaixo temos os gr´aficos def(x) =ex_ef−1_{(x) =ln(x), ou seja, tomamosa=enas fun¸c˜oes acima.}

gráfico def

x y

gráfico def-1

Id

1

1 0

f

f-1

x y

1 0 x

y

1

0

1.6

Fun¸c˜

oes Pares e Fun¸c˜

oes ´Impares

Dizemos quef´e umafun¸c˜ao parquandof(−x) =f(x)para qualquerx_∈X. Dizemos quef´e umafun¸c˜ao ´ımparquandof(−x) = −f(x)para qualquerx_∈X.

Propriedade geom´etrica das fun¸c˜oes pares.

O gr´afico de uma fun¸c˜ao par ´e sim´etrico em rela¸c˜ao ao eixo das ordenadas (eixoy).

y

x

-x x

f x( ) = (f x- )

Propriedade geom´etrica das fun¸c˜oes ´ımpares.

O gr´afico de uma fun¸c˜ao ´ımpar ´e sim´etrico em rela¸c˜ao `a origem do sistemas de coordenadas.

y

x -x

x

f x( )

f x(- ) =-f x( )

Exemplos.

(1)Sejamf:R→Rtal quef(x) =cos(x)eg:R→Rtal queg(x) =x2_.

A fun¸c˜ao cosseno ´e par, poisf(−x) =cos(−x) =cos(x) =f(x)para qualquerx_∈R. De modo an´alogo,g(−x) = (−x)2=x2=g(x)para qualquerx_∈R.

x y

0 p/2 3 2p/ 2p

5 2p/ p

-p/2

-p

-3 2p/ -2p -5 2p/

1

-1

1

-₁ x

y

-2 1 2

4 f

g

(2)Sejamf:R_→Rtal quef(x) =sen(x)eg:R_→Rtal queg(x) =x3_.

A fun¸c˜ao seno ´e ´ımpar, poisf(−x) =sen(−x) = −sen(x) = −f(x)para qualquerx_∈R. De modo an´alogo,g(−x) = (−x)3= −x3_{= −g(x)para qualquerx∈R.}

x y

0 p/2

3 2p/

2p 5 2p/ p

-p/2

-p -3 2p/ -2p -5 2p/

1

-1

y

x 0

1 1

g

Cap´ıtulo 2

Limite e Continuidade

2.1

O Conceito de Limite

Consideremos a fun¸c˜aof:R∗_{→Rdada porf(x) =} x2+3x

x . Logo,∄f(0). Mas

f(x) = x(x+3)

x x=6=0x+3.

Logo, intuitivamente, para xpr´oximo de0,mas diferente de0,f(x)est´apr´oximo de3.

y

x 0

3 f x( )

gráfico def

-3 x

Quando x tende a 0 (x_→0), f(x) tende a 3 (f(x)_→3), ou seja, o limite de f(x) quando x tende a 0 ´e 3 e escrevemos

lim x→₀

x2_+3x

x =3.

Para escrever esta id´eia de modo mais rigoroso, recordemos que a no¸c˜ao de distˆancia entre pontosa, b_∈R´e dada pelo m´odulo da diferen¸ca entre estes pontos, ou seja,|a−b|. Assim, dizer quexest´apr´oximo de0significa que|x−0|

´e um valor pequeno. Analogamente, dizer que f(x) est´a pr´oximo de 3 significa que |f(x) −3|´e, tamb´em, um valor

pequeno.

Defini¸c˜ao. Sejam f:X_⊂R_→Ruma fun¸c˜ao real de uma vari´avel real e a_∈Rtal que ]a−r, a+r[_∩X₆=∅para qualquer r > 0. (1₎

Dizemos que f(x)tem limite L_∈R quando xtende a a,e escrevemos

lim

x→_af

(x) =L,

sempre que: para _∀ε > 0, _∃δ > 0tal que (2₎

0 <|x−a|< δ⇒|f(x) −L|< ε.

Desta forma, dizer que lim

x→_af(x) =L significa que podemos fazerf(x)arbitrariamente pr´oximo deL, tomando x

suficientemente pr´oximo dea, por´em, diferente dea.

1

Esta condi¸c˜ao garante que existem pontosxdo dom´ınio defarbitrariamente pr´oximos dea. 2

x

0 a

L

x y

a+d

a-d

L-e

L+e

f x( )

gráfico def

Exemplos. Sejam f, g : R _→ R tal que f(x) = k, sendo k constante real e g(x) = x. Seja a _∈ R. Mostremos, utilizando a defini¸c˜ao acima, que

lim

x→_af(x) =k

e

lim

x→_ag(x) =a.

De fato, no primeiro caso: dadoε > 0, tomando-se qualquer δ > 0, temos

0 <|x−a|< δ_⇒0 < ε_⇒|k−k|< ε_⇒|f(x) −k|< ε.

No segundo caso: |g(x) −a|< ε_⇐⇒|x−a|< ε_⇐⇒

x6=a 0 <|x−a|< εou seja, dadoε > 0, tomando-seδ=ε, temos por essa cadeia de equivalˆencias que

0 <|x−a|< δ_⇒|g(x) −a|< ε.

Proposi¸c˜ao. Sejam f:X_⊂R_→Re a_∈Rtais que exista lim

x→_af

(x). Ent˜ao, este limite ´e ´unico.

Proposi¸c˜ao. (regras para c´alculo de limites)Suponhamos f e gfun¸c˜oes tais que lim

x→_a

f(x) =L e lim

x→_a

g(x) =M.

(1) lim

x→_a

(f(x)_±g(x)) = lim

x→_a

f(x)_± lim

x→_a

g(x) =L_±M. (limite da soma ´e soma dos limites) (2) lim

x→_af(x)g(x) =_xlim→_af(x)_xlim→_ag(x) =LM. (limite do produto ´e produto dos limites)( 3₎

(3)Se M₆=0,ent˜ao lim

x→a

f(x)

g(x) = lim x→af(x)

lim x→ag(x)

= _ML. (limite do quociente ´e quociente dos limites, desde que o limite do

denominador seja diferente de zero)

Com o aux´ılio desta ´ultima proposi¸c˜ao e o conhecimento de alguns limites simples, como os do exemplo acima, ´e poss´ıvel calcular limites mais complexos. Vejamos alguns exemplos:

Exemplos.

(1)Consideremosf:R−{1}_→Rtal quef(x) = 2x3_x−₋2x₁ 2. Temos

lim x→₁

2x3−2x2 x−1 =xlim→₁

2x2(x−1)

x−1 =xlim→₁

2x2= lim x→₁

2lim x→₁

xlim x→₁

x=2.1.1=2.

1 x

y

2

gráfico def

3

Aqui temos um caso particular interessante: sef(x) =k,k∈R, temos

lim

x→akg(x) =kx→alimg(x) =kM,

pois lim

(2)Consideremosf:R−{a}_→Rtal quef(x) = x2−a2

x−a . Temos lim

x→_a

x2_−a2

x−a =xlim→_a

(x−a) (x+a)

x−a =xlim→_a

(x+a) = lim x→_ax

+ lim x→_aa

=a+a=2a.

(3)Consideremosf:R−{−1}_→Rtal que f(x) = x2−1

x+1. Temos lim

x→−₁ x2−1

x+1 =xlim→−₁

(x−1) (x+1)

x+1 =xlim→−₁

(x−1) = lim x→−₁

x− lim x→−₁

1= −1−1= −2.

(4)Consideremosf:R−{2}_→Rtal quef(x) = x3

−8

x−2. Temos lim

x→₂ x3₋₈

x−2 =xlim→₂

(x−2) x2_+2x+4

x−2 =xlim→₂

x2+2x+4 = lim

x→₂ xlim

x→₂ x+lim

x→₂ 2 lim

x→₂ x+lim

x→₂

4=2.2+2.2+4=12.

Observa¸c˜ao: x3_−a3_{= (x−a) x}2_+ax+a2 .

(5)Consideremosf:R_→Rtal quef(x) =x2_{+1. Temos}

lim x→₂

x2₊₁ = lim

x→₂ xlim

x→₂

x+ lim x→₂

1=2.2+1=5.

Exerc´ıcios.

(1)Sendoa₆=0, dˆe o dom´ınio def e calcule lim x→_a

f(x)para:

(i)f(x) =

1 x−

1 a

x−a;

(ii)f(x) =

1 x2 − 1

a2

x−a ;

(2)Dˆe o dom´ınio def(x) = x3−_x45x₋2+8x−4

5x−6 e calcule lim_x→₂ f(x).

(3)Calcule lim h→0

(a+h)3

−a3

h , sendoa∈R.

2.2

Limites laterais

Recordemos a defini¸c˜ao de limite lim x→a

f(x).

Se impusermos a restri¸c˜ao x > a, estamos fazendo x tender a a pela direita e denotamos este limite com esta restri¸c˜ao por

lim x→a+

f(x).

Se a restri¸c˜ao forx < a, estamos fazendo xtender aa pela esquerda e escrevemos

lim x→_a−f(x).

Os limites acima recebem o nome delimites laterais `a direita e `a esquerda de f, respectivamente, ema. Estes limites podem existir ou n˜ao. Caso um deles n˜ao exista ou caso difiram, ent˜ao lim

x→_a

f(x)n˜ao existe. Natural-mente,

lim x→_a

f(x) existe⇐⇒ lim x→_a+

f(x) = lim x→_a−

f(x) = lim x→_a

f(x).

Exemplos.

(1)Os limites laterais def(x) = |x_x| no ponto0 s˜ao:

lim x→0+

f(x) = lim x→0+

|x|

x =xlim→0+ x

x =xlim→0+ 1=1.

lim

x→₀−f(x) =_xlim→₀− |x|

x =xlim→₀− −x

x =xlim→₀−−1= −1.

Como lim

+

x y

gráfico def

-1 1

0

-Observa¸c˜ao:

|x|=x, sex_≥0

|x|= −x, sex < 0 .

(2)Os limites laterais def(x) =|x|no ponto0s˜ao:

lim

x→₀+f(x) =_xlim→₀+|x|=_xlim→₀+x=0.

lim

x→₀−f(x) =_xlim→₀−|x|=_xlim→₀−−x=0.

Como lim

x→₀+f(x) =_x→lim₀−f(x), temos que lim_x→₀

f(x) =0.

+ x

y

gráfico def

0

-Exerc´ıcios.

(1)Calcule os limites laterais defem−1 e1 sendof(x) =  



1sex <−1 x2_{se −1≤x≤1}

x+2sex > 1

.

(2)Calcule, caso exista, lim x→₀

x

√

x4

+4x2.

2.3

Fun¸c˜

oes Cont´ınuas

Defini¸c˜ao. Sejam f:X_⊂R_→R,p_∈Xe suponhamos que exista lim

x→_pf(x). Dizemos que f´e cont´ınua em pquando

lim

x→_p

f(x) =f(p).

Quando f for cont´ınua para qualquer p_∈X, dizemos que f ´e cont´ınua em X.

Caso pseja extremo de um intervalo fechado ou semifechado em X,o limite acima deve ser substituido pelo limite lateral conveniente em p.

Geometricamente, uma fun¸c˜ao cont´ınua possui gr´afico sem “saltos”em seu dom´ınio_.

Exemplos.

(1)A fun¸c˜aof(x) =x2_{´e cont´ınua emX=R. De fato: lim} x→_pf

(x) = lim x→_px

2_=p2_{=f(p)para qualquerp∈X.}

p x

y

p2

(2)A fun¸c˜aof(x) =

xsex₆=1

2sex=1 ´e descont´ınua emp=1, pois limx→1

f(x) = lim x→1

x=1₆=2=f(1). Nos demais pontos

f(x)´e cont´ınua pois, sep₆=1, lim x→_p

f(x) = lim x→_p

x=p=f(p).

x y

gráfico def

0 ₁

1 2

(3)A fun¸c˜aof(x) = |x_x| ´e cont´ınua emX=R∗ _pois: (i)Sep > 0, ent˜ao lim

x→_pf(x) =_xlim→_p

|x|

x =_xlim→_p

x

x =_xlim→_p1=1=f(p).

(ii)Sep < 0, ent˜ao lim

x→_pf(x) =_xlim→_p

|x|

x =_xlim→_p

−x

x =_xlim→_p−1= −1=f(p).

x y

gráfico def

-1

1

0

Observa¸c˜ao importante: N˜ao faz sentido analisar continuidade emp=0pois0 /_∈X.

(5)A fun¸c˜aof(x) =  



0, sex2_{> 1}

1, sex2_{< 1} 1

2, sex 2₌₁

´e descont´ınua emp=_±1e cont´ınua nos demais valores. De fato:

(i) Se p = −1, temos lim x→−1−

f(x) = lim x→−1−

0 = 0 e lim x→−1+

f(x) = lim x→−1+

1 = 1. Logo, lim x→−1

f(x) n˜ao existe. Portanto,f(x)´e descont´ınua emp= −1.

(ii)Sep=1, temos lim x→1−

f(x) = lim x→1−

1=1e lim x→1+

f(x) = lim x→1+

0=0. Logo, lim x→₁

f(x)n˜ao existe. Portanto,f(x)

´e descont´ınua emp=1.

(iii)Se p > 1 oup <−1 (ou seja, p2 _{> 1), temos lim} x→_p

f(x) = lim x→_p

0 = 0 =f(p). Logo, f(x)´e cont´ınua nesses pontos.

(iv) Se−1 < p < 1(ou seja,p2_{< 1), temos lim} x→_p

f(x) = lim x→_p

1=1=f(p). Logo,f(x)tamb´em ´e cont´ınua nesses pontos.

y

gráfico def

1 2/ 1

0 1 x

-₁

Exerc´ıcios.

(1)Analise a continuidade def(x) =

x2_{, sex} ≥1

x+1, sex < 1 em seu dom´ınio.

(2)Idem paraf(x) =

x2_{, sex≥1}

Proposi¸c˜ao. Sejam f, g:X_⊂R→R fun¸c˜oes cont´ınuas em X. Ent˜ao: (i)f_±g:X_⊂R_→Rtal que (f_±g) (x) =f(x)_±g(x)´e cont´ınua em X.

(ii) fg:X_⊂R_→Rtal que (fg) (x) =f(x)g(x)´e cont´ınua em X.

(iii) _gf :X_⊂R_→R tal que f g(x) =

f(x)

g(x) ´e cont´ınua em X=X−{x∈X:g(x) =0}.

(iv) Se Img_⊂X, ent˜ao f_◦g:X_⊂R→Rtal que f_◦g(x) =f(g(x))´e cont´ınua em X. (4₎

(v)Se existe f−1 _{(inversa de f) e X´e um intervalo, ent˜ao f}−1 _{´e cont´ınua em seu dom´ınio.}

Com o aux´ılio da proposi¸c˜ao anterior, a partir de continuidade de fun¸c˜oes simples, podemos concluir continuidade de fun¸c˜oes mais complexas. Por exemplo, as fun¸c˜oesf(x) =k, k_∈R ef(x) = xs˜ao cont´ınuas em R(verifique). A partir delas e da proposi¸c˜ao anterior, temos os seguintes exemplos de fun¸c˜oes cont´ınuas:

Exemplos.

(1)(polinˆomios s˜ao cont´ınuos). f(x) =a0+a1x+· · ·+anxn ´e cont´ınua emR, pois f´e soma e produto de fun¸c˜oes cont´ınuas.

(2)(fun¸c˜oes racionais s˜ao cont´ınuas). f(x) = _QP(₍x_x)₎, sendoP e Q polinˆomios, ´e cont´ınua em R−{x_∈R:Q(x) =0}, pois f´e quociente de fun¸c˜oes cont´ınuas.

(3)f(x) = √n

x´e cont´ınua em

R+, senfor par

R, senfor ´ımpar . (f´e a inversa degtal que g(x) =x

n _{que ´e cont´ınua emR}

+ ou

R)

(4)h(x) = √5

x2_{−5x´e cont´ınua emR. (hpode ser escrita como composta de f, tal que f(x) =} √5

x, com g, tal que

g(x) =x2_{−5x, que s˜ao cont´ınuas emR)}

(5)Consideremosf(x) = √_xx₋−₁1. TemosX=R+−{1}ef´e cont´ınua em seu dom´ınio. Al´em disso:

lim x→₁

√

x−1 x−1 =xlim→₁

√

x−1

√

x−1 √

x+1 = lim x→₁

1

√

x+1 = 1

lim x→₁

√

x+1 = 1 2.

2.4

Teorema do Confronto e Aplica¸c˜

oes

Teorema. (do confronto)Sejamf, g, h:X_⊂R_→Rea_∈Rtais que g(x)_≤f(x)_≤h(x)para x_∈X_∩(a−r, a+r),

sendo r > 0fixo (5_{). Nestas condi¸c˜oes, se lim}

x→_ag

(x) = lim

x→_ah

(x) =L,ent˜ao lim

x→_af

(x) =L.

y

gráfico def

L

0 a x

gráfico deh

gráfico de

1a

. Aplica¸c˜ao do TC:As fun¸c˜oesseno ecossenos˜ao cont´ınuas em R.

Sejaa_∈R. Devemos mostrar que lim x→_asen

(x) =sen(a)e lim x→_acos

(x) =cos(a).

4

O item(iv)desta proposi¸c˜ao pode ser enfraquecido, retirando-se a necessidade degser cont´ınua. O enunciado alternativo ´e: Sejam f:Y⊂R→Re g:X⊂R→Rfun¸c˜oes tais queImg⊂Y, lim

x→ag(x) =Lefcont´ınua emL.Ent˜ao,x→alimf(g(x)) =f(L). 5

y 1

0 1 x

sen a( )

sen x( )

cos a( ) cos x( )

x(o arco) a(o arco)

|cos x( ) -cos a( )| |sen x( ) -sen a( )|

| -x a| (o arco)

Inspirados na figura, temos paraxpr´oximo dea:

|sen(x) −sen(a)|<|x−a| |cos(x) −cos(a)|<|x−a|

ou seja (6_):

−|x−a|<sen(x) −sen(a)<|x−a| −|x−a|<cos(x) −cos(a)<|x−a|

que implica

sen(a) −|x−a|<sen(x)<|x−a|+sen(a)

cos(a) −|x−a|<cos(x)<|x−a|+cos(a)

Definindo:

g1(x) =sen(a) −|x−a|,

f1(x) =sen(x),

h1(x) =|x−a|+sen(a),

g2(x) =cos(a) −|x−a|,

f2(x) =cos(x)e

h2(x) =|x−a|+cos(a), temos:

g1(x)< f1(x)< h1(x)

g2(x)< f2(x)< h2(x)

e

lim

x→_ag1(x) =_xlim→_ah1(x) =sen(a)

lim

x→_ag2(x) =_xlim→_ah2(x) =cos(a)

Pelo Teorema do Confronto: lim x→_asen

(x) =sen(a)e lim x→_acos

(x) =cos(a), ou seja, sen(x) e cos(x)s˜ao cont´ınuas em R.

2a

. Aplica¸c˜ao do TC:O Limite lim x→0

sen(x)

x . (1

o_{. Limite Fundamental)}

Para0 < x < π

2 temos sen(x)< x <tg(x).

y

1

0 1 x

sen x( )

cos x( ) x

tg

tg x( )

6

Logo,

sen(x)< x <sen(x)

cos(x) ⇒

1 < x

sen(x) <

1

cos(x) ⇒

cos(x)< sen(x) x < 1.

Para−π₂ < x < 0 temos tg(x)< x <sen(x)e, procedendo de modo an´alogo, temos a mesma desigualdade acima: cos(x)< sen(_xx) < 1.

Definindog(x) =cos(x),f(x) = sen(_xx) eh(x) =1, temos

g(x)_≤f(x)_≤h(x) e lim x→₀

g(x) = lim x→₀

h(x) =1.

Logo, pelo Teorema do Confronto,

lim x→₀

f(x) =1,

ou seja,

lim x→₀

sen(x)

x =1.

Exemplos.

(1) lim x→₀

tg(x)

x =_xlim→₀

sen(x) cos(x)

x =xlim→₀

1

cos(x) sen(x)

x =_xlim→₀

1

cos(x)_xlim→₀

sen(x)

x =1.1=1.

(2) lim x→0

1−cos(x)

x =_xlim→0

(1−cos(x))(1+cos(x))

x(1+cos(x)) =_xlim→0

1−cos2

(x)

x(1+cos(x)) =_xlim→0

sen(x)

x

sen(x)

1+cos(x) =_xlim→0

sen(x)

x _xlim→0

sen(x)

1+cos(x) =1.

0 2=0.

(3) lim x→₀

1−cos(x)

x2 = lim x→₀

1−cos2

(x)

x2₍

1+cos(x))=_xlim→₀

sen(x)

x

sen(x)

x 1

1+cos(x) =1.1.12= 1 2.

(4) lim x→₀

sen(2x)

x =_xlim→₀

2sen(x)cos(x)

x =_xlim→₀

sen(x)

x 2cos(x) =1.2.1=2.

(5) lim x→₀

sen(x)

5x =_xlim→₀

1 5

sen(x)

x = 1 5.1=

1 5.

(6) lim x→₀

sen(x2) x =_xlim→₀

sen(x2) x2 x =

x2

=yylim→₀+ sen(y)

y ± √_y

=1._±√0=0.(7₎

Proposi¸c˜ao. Se lim

x→_af

(x) =0 e g(x)´e limitada (8_{), ent˜ao lim}

x→_af

(x)g(x) =0.

Demonstra¸c˜ao:

Comog(x)´e limitada, temos que_∃M > 0tal que|g(x)|_≤M. Logo:

|f(x)g(x)|=|f(x)|.|g(x)|_≤M|f(x)|_⇒

−M|f(x)|_≤f(x)g(x)_≤M|f(x)|.

Pelo Teorema do Confronto,

lim

x→_af

(x)g(x) =0

pois:

lim

x→_a

−M|f(x)|= −Mlim

x→_a

|f(x)|= −M.|0|=0e

lim

x→_aM

|f(x)|=Mlim

x→_a

|f(x)|=M.|0|=0.

Exemplos.

7

Observe que neste caso,x→0⇒x2_→0⇒y→0+_(poisx2_{> 0).} 8

(1) lim x→₀

xsen 1 x

=0, poisf(x) =x´e tal que lim x→₀

f(x) =0 eg(x) =sen 1 x

´e limitada. ( sen 1_x

≤1)

Observa¸c˜ao: lim x→₀

xsen 1 x

6

= lim x→₀

x.lim x→₀

sen 1 x

, pois lim x→₀

sen 1 x

n˜ao existe. (veremos isso adiante)

(2) lim x→0

x3_cos 1 x2

=0, pois f(x) =x3_{´e tal que lim} x→0

f(x) =0eg(x) =cos 1 x2

´e limitada. ( cos _x12

≤1)

(3) lim x→₀

|x|f(x) =0, sendof(x) =

1, sex_∈Q

−2, sex_∈R−Q . De fato: limx→₀

|x|=0 e|f(x)|_≤2.

Observa¸c˜ao: lim x→_a

|x|f(x)n˜ao existe sea₆=0.

(4) lim x→₀

xsen(_|x|x) =0.De fato: lim x→₀

x=0e

sen(x) |x|

=

|sen(x)| |x| ≤

|x| |x| =1.

Exerc´ıcio. Calcule:

(1) lim x→₀

sen3 x 2

x3 . (Resposta: 1 8)

(2) lim x→0

cos(2x)−cos(3x)

x2 . (Resposta: 5 2)

2.5

Limites no Infinito

Defini¸c˜ao. Seja f:X_⊂R_→Rtal que X n˜ao ´e limitado superiormente (9_{). Dizemos que o limite de f(x)quando x}

tende a infinito ´e L_∈R, e escrevemos

lim

x→+∞

f(x) =L,

quando: Dado ε > 0,_∃∆ > 0tal que

x > ∆⇒|f(x) −L|< ε.

x 0 D L y L-e L+e f x( )

gráfico def

x

De modo an´alogo,

lim

x→−∞

f(x) =L

quando: Dado ε > 0,_∃∆ > 0tal que

x <−∆_⇒|f(x) −L|< ε.

Exemplo. Demonstremos que lim x→₊∞

1

xn =0, paran∈Nfixo, utilizando a defini¸c˜ao. De fato, observemos que

|f(x) −L|< ε_⇐⇒

1 xn −0

< ε⇐⇒

x>0

1

xn < ε⇐⇒x > n r

1 ε.

Desta forma, dadoε > 0qualquer, fazendo∆= qn ₁

ε, temos pela cadeia de equivalˆencias acima:

x > ∆_⇒

1 xn −0

< ε,

9

que ´e exatamente a defini¸c˜ao de lim x→₊∞

1 xn =0. De modo an´alogo, demonstra-se que lim

x→−∞

1 xn =0.

Observa¸c˜ao. As regras operat´orias para calcular limites s˜ao v´alidas para calcular limites no infinito. Vamos a alguns exemplos:

(1) lim x→+∞

x3−2x+5 2x3

+10x2

−2x =_x→lim+∞

x3 ₁₋ 2x x3 + 5

x3

x3₂₊10x2 x3 −

2x x3

= lim x→+∞

1− 2 x2 + 5

x3

2+10_x − _x22 =

lim x→+∞

1− lim x→+∞

2

x2+ lim x→+∞

5 x3

lim

x→₊∞2+_x→lim₊∞

10

x −_x→lim₊∞

2 x2

= 1−0+0 2+0−0= 1

2.

(2) lim x→₋∞

2x5

−2x2

+3

3x5_+7x4_+x2 = lim x→₋∞

x5 2− 2 x3 + 3

x5

x5 ₃₊ 7 x+

1 x3

= lim x→₋∞

2− 2 x3 + 3

x5

3+7 x+

1 x3

= 2 3.

(3) lim x→₊∞

x4

−2x2

+3 3x5₊

7x2₋

2x =_x→lim₊∞ 1− 2

x2 + 3 x4

3x+ 7 x2 − 2

x3 =0.

(4) lim x→₊∞

sen(x)

x =0, pois lim_x→₊∞

1

x =0 e|sen(x)|≤1.

(5) lim x→−∞

5−cos(x)

x2 =0, pois lim x→−∞

1

x2 =0e|5−cos(x)|≤6.

(6) lim x→₊∞xsen

1 x

= lim x→₊∞

sen 1 x 1 x =

y=1 x

lim y→₀+

sen(y)

y =1. (1

o_{. limite fundamental)}

Observa¸c˜ao.: quandox_→+_{∞ ⇒} 1 x →0

+

⇒y_→0+_.

(7) lim x→0

sen 1 x

n˜ao existe. De fato:

Parax= 1

kπ,k∈Z, temos lim_x→₀sen

1 x

= lim k→₊∞sen

1

1 kπ

! = lim

k→₊∞sen

(kπ) = lim k→₊∞

0=0.

Parax= 1 π 2+2kπ,

k_∈Z, temos lim x→0

sen 1 x

= lim k→+∞

sen 1₁ π 2+2kπ

! = lim

k→+∞

sen π 2+2kπ

= lim

k→+∞ 1=1.

-₁ 1

x y

2/p - /p₂

gráfico def

Observa¸c˜ao. Seα > 0, ent˜ao lim x→₊∞

1 xα =0.

(8) lim x→₊∞

x√3 x+1 5x√3

x+3x−1 =_x→lim₊∞ x√3

x1+ 1 x√3

x

x√3

x5+ 3x x√3

x− 1 x√3 x

= lim x→₊∞

1+ 1 x43

5+ 3 x 1 3 − 1 x 4 3 = lim x→₊∞1

+ lim x→₊∞

1 x43 lim

x→+∞

5+ lim x→+∞

3 x

1 3

− lim x→+∞

1 x 4 3 = 1 5.

Exerc´ıcio. Calcule lim x→+∞

8−x

√

2.6

Limites Infinitos

Defini¸c˜ao. Sejam f:X_⊂R_→Re a_∈R tal que ]a−r, a+r[_∩X₆=∅para qualquer r > 0. Dizemos que o limite de f(x)quando xtende a a´e infinito, e escrevemos

lim

x→a

f(x) = +_∞,

quando: _∀M > 0,_∃δ > 0tal que

0 <|x−a|< δ_⇒f(x)> M.

x

0 a _x

y

a+d a-d

M f x( )

gráfico def

De modo an´alogo,

lim

x→_a

f(x) = −_∞ quando: _∀M > 0,_∃δ > 0tal que

0 <|x−a|< δ_⇒f(x)<−M.

Exemplo. Demonstremos que lim x→₁

1

(x−1)2 = +∞, utilizando a defini¸c˜ao. De fato, observemos que

f(x)> M_⇐⇒ 1

(x−1)2 > M⇐⇒x6=1

1

M>(x−1)

2

⇐⇒ r

1

M >|x−1|.

Desta forma, dadoM > 0qualquer, fazendoδ=q1

M, temos pela cadeia de equivalˆencias acima:

0 <|x−1|< δ_⇒ 1

(x−1)2 > M,

que ´e exatamente a defini¸c˜ao de lim x→₁

1

(x−1)2 = +∞.

Observa¸c˜ao 1. As regras operat´orias para calcular limites s˜ao v´alidas para calcular limites infinitos.

Observa¸c˜ao 2. O conceito de limite infinito pode ser considerado de forma a termos limite lateral a direita ou a esquerda de a. Exemplos: lim

x→₂+

1

(x−2)3 = +∞ e lim x→₂−

1

(x−2)3 = −∞. Naturalmente, para que exista lim

x→_af(x), os

limites laterais dever˜ao existir e coincidir.

Observa¸c˜ao 3. O conceito de limite infinito comxtendendo a+_∞ou−_∞tamb´em pode ser considerado. Exemplo: lim

x→−∞ x2_{= +}

∞.

Exemplos.

(1)Param, n_∈Nfixos, lim x→₀+

1 n

√

xm = lim x→₀+

1 x

m

n = +∞.

(2)Paran_∈Nfixo, lim x→0−

1 xn =

+_∞, senfor par

(3)Param, n_∈Nfixos, lim x→₊∞x

m

n = +_∞.

(4)Paran_∈Nfixo, lim x→₋∞x

n₌

+_∞, senfor par

−_∞, senfor ´ımpar .

Exerc´ıcios. Calcular:

(1) lim x→+∞

5x3_−2x2 .

(2) lim x→₋∞ 7x

5_+6x2 .

(3) lim x→₀

x3_+x√_x+ 1 x2

.

(4) lim x→₊∞

3x4

−1 2x3

−7x.

(5) lim x→₋∞

2x4

−3x

−x+1 .

(6) lim x→−₁

5x+2

|x+1|. (7) lim

x→₂

x2

+3x+1 x2

+x−6.

(8) lim x→₀

|x|

x2.

(9) lim x→+∞

x√x+1 x√3

x−x.

(10) lim x→₊∞

√

3x2_+2x+1−√_2x.

(11) lim x→₄

3−x x2

−2x−8.

2.7

Ass´ıntotas Horizontais e Verticais

Defini¸c˜ao. Dizemos que a reta x=ae uma ass´ıntota vertical do gr´afico de uma fun¸c˜ao f:X_⊂R_→Rquando pelo menos uma das seguintes condi¸c˜oes for verdadeira:

(i) lim

x→_a+f(x) = +∞. (ii) lim

x→_a−f(x) = +∞. (iii) lim

x→_a+f(x) = −∞. (iv) lim

x→a−

f(x) = −_∞.

Exemplo. A retax=0´e ass´ıntota vertical def(x) = _x1 pois lim

x→₀+f(x) = +∞. (ou lim_x→₀−f(x) = −∞)

-1

-1 0

1 1

x y

gráfico def

assíntotax=0(eixoy)

Defini¸c˜ao. Dizemos que a reta y=b´e uma ass´ıntota horizontal do gr´afico de uma fun¸c˜ao f: X_⊂R_→R quando pelo menos uma das seguintes condi¸c˜oes for verdadeira:

(i) lim

x→+∞

f(x) =b.

(ii) lim

x→−∞

f(x) =b.

Exemplo. A retay=0´e ass´ıntota horizontal def(x) = 1

x pois lim_x→+∞

f(x) =0. (ou lim x→−∞

-1 -1 0 1 1 x y

gráfico def

assíntotay=0(eixox)

Exerc´ıcios. Dˆe as ass´ıntotas (e trace os gr´aficos) de:

(1)f(x) = 1 x−2+3.

(2)f(x) =tg(x).

2.8

O Limite

lim

x_→+_∞

1

+

1

x

(2

. Limite Fundamental)

O valor deste limite segue de uma aplica¸c˜ao do Teorema do Confronto. Para apresent´a-lo, iremos abandonar um pouco o rigor matem´atico e assumir que a seq¨uˆencia de n´umeros reais

1+ 1

n

n

n∈N =

1+ 1

1

1

,

1+ 1

2

2

,

1+ 1

3

3

,

1+1

4

4

,

1+1

5

5

, . . . ,

1+ 1

n

n

, . . .

!

para n _∈ N ´e convergente. Intuitivamente, `a medida que n tende a infinito,

1+ 1

n

n

tende a um determinado

n´umero real irracional. Este n´umero ´e indicado poree seu valor aproximado ´e2, 718281828459045 . . .

Temos, desta forma, a motiva¸c˜ao para a seguintedefini¸c˜ao:

lim n→+∞

1+ 1

n

n

=e sendon_∈N.

Agora, mostremos que lim x→+∞

1+ 1

x

x

=e parax_∈R. Sejamx_∈Ren_∈Ntais que

n_≤x < n+1_⇒ 1 n+1 <

1 x ≤

1 n⇒1+

1

n+1 < 1+ 1 x≤1+

1 n.

Logo,

n_≤x < n+1_⇒

1+ 1

n+1

n

<

1+ 1

x

x ≤

1+ 1

n

n+1 .

Como

lim n→₊∞

1+ 1

n+1

n =

m=n+1mlim→₊∞

1+ 1

m

m−1

= lim m→₊∞

1+ 1

m

m

1+ 1

m

−1

=e.1−1=e

e

lim n→+∞

1+ 1

n

n+1

= lim n→+∞

1+ 1

n

n

1+ 1

n

1

=e.11=e,

temos, pelo Teorema do Confronto que

lim x→+∞

1+ 1

x

x =e.

Exerc´ıcios.

(1)Mostre que

lim x→−∞

1+ 1

x

Resolu¸c˜ao: ser´a feita em sala de aula.

(2)Mostre que

lim x→₀

(1+x) 1 x _=e.

Resolu¸c˜ao: ser´a feita em sala de aula.

(3)Mostre que

lim x→0

ax₋₁

x =ln(a),

sendoa > 0,a₆=1.

Resolu¸c˜ao: ser´a feita em sala de aula.

2.9

Teorema do Valor Intermedi´

ario, Teorema do Anulamento e

Teo-rema de Weierstrass.

Teorema do Valor Intermedi´ario. Se f: [a, b]_⊂R_→R´e cont´ınua (10_{)e γ´e um valor entre f(a)e f(b),ent˜ao}

existe c_∈[a, b]tal que f(c) =γ.

y

x

a c _b

f c( ) = g

f a( ) f b( )

gráfico def

Observa¸c˜ao. Casofn˜ao seja cont´ınua em[a, b], o teorema n˜ao vale. No exemplo abaixo n˜ao existec_∈[a, b]tal que

f(c) =γ.

y

x

a c b

g

f a( ) f b( )

gráfico def f c( )

?

Teorema do Anulamento. Seja f: [a, b]_⊂R_→Rcont´ınua. Se f(a)e f(b)possuirem sinais opostos, ent˜ao existe

c_∈]a, b[tal que f(c) =0.

10

y

x a

b c

0

f a( ) f b( )

gráfico def

Exemplos.

(1)Mostre que a equa¸c˜aox3_{−4x+8=0 admite ao menos uma raiz real.}

De fato,f(x) =x3_{−4x+8´e cont´ınua emR. Parax= −3 (por exemplo), temosf(−3) = −7 < 0e parax=0,}

temos f(0) =8 > 0. Logo, peloTeorema do Anulamento, existec_∈]−3, 0[tal que f(c) =0, ou seja,c´e raiz def.

(2)Mostre que a equa¸c˜aox3_{−4x+2=0 admite trˆes ra´ızes reais.}

De fato,f(x) =x3_{−4x+2´e cont´ınua emR.}

Parax= 0, temos f(0) =2 > 0 e para x= 1, temos f(1) = −1 < 0. Pelo Teorema do Anulamento, temos que

existec1∈]0, 1[tal quef(c1) =0.

Parax= −3, temosf(−3) = −13 < 0e parax= −2, temosf(−2) =2 > 0. Pelo Teorema do Anulamento, existe

c2∈]−3,−2[tal quef(c2) =0.

Conclus˜ao: f(x)admite trˆes ra´ızes reais. (Demonstramos a existˆencia de duas ra´ızes. A terceira raiz ´e obrigatori-amente real. Por quˆe?)

(3)Mostre que existex0∈

0,π₂

tal que cos(x0) =x0.

De fato, devemos mostrar quef(x) =cos(x) −x possui uma raiz no intervalo indicado. Observemos quef(x) =

cos(x) −x´e cont´ınua em R(em particular no intervalo

0,π 2

). Temos que f(0) =1 > 0e f π 2

= −π

2 < 0. Logo,

pelo Teorema do Anulamento, existe x0∈0,π₂tal quef(x0) =0, ou seja, cos(x0) =x0.

Exerc´ıcios.

(1)Mostre que a equa¸c˜aox3_+3x2_{−2x−6=0tem uma raiz entre1 e2.}

(2)Mostre que todo polinˆomio de grau ´ımpar tem pelo menos uma raiz real.

(3)SejaP(x) =a2nx2n+a2n−1x2n−1+· · ·+a1x+a0coma2n> 0 ea0< 0. Mostre que esse polinˆomio tem pelo menos duas ra´ızes reais: uma positiva e uma negativa.

(4)Sejama > 0en_∈N. Mostre que existe umα > 0tal que αn _=a.

Resolu¸c˜ao: ser´a feita em sala de aula.

Teorema de Weierstrass. Se f: [a, b]_⊂R_→R´e cont´ınua, ent˜ao existem xm, xM∈[a, b]tais quef(xm)≤f(x)≤

f(xM), ∀x∈[a, b].

y

x f x( _M)

f x( m)

a xM xmb gráfico def

Observa¸c˜ao:

xm: ponto de m´ınimo defem[a, b].

xM: ponto de m´aximo def em[a, b].

f(xm): valor m´ınimo defem[a, b].