Michelle Bandarra Marques Costa
Ensaios em matemática aplicada:
Estimação e trajetórias bootstrap de oferta de sangue e estudo
de desempenho de extensões do algoritmo de Programação
Dinâmica Dual Estocática
Rio de Janeiro 2017
Ensaios em matemática aplicada:
Estimação e trajetórias bootstrap de oferta de sangue e estudo
de desempenho de extensões do algoritmo de Programação
Dinâmica Dual Estocática
Dissertação para obtenção do grau de mes-tre apresentada à Escola de Matemática Aplicada
Área de concentração: Otimização Esto-cástica
Orientador: Vincent Guigues
Rio de Janeiro 2017
Costa, Michelle Bandarra Marques
Ensaios em matemática aplicada: estimação e trajetórias bootstrap de oferta de sangue e estudo de desempenho de extensões do algoritmo de Programação Dinâmica Dual Estocástica / Michelle Bandarra Marques Costa. - 2017.
132 f.
Dissertação (mestrado) - Fundação Getulio Vargas, Escola de Matemática Aplicada.
Orientador: Vincent Gérard Yannick Guigues. Inclui bibliografia.
1. Programação estocástica. 2. Otimização matemática. 3. Análise de séries temporais. 4. Bootstrap (Programa de computador). I. Guigues, Vincent Gérard Yannick. 11. Fundação Getulio Vargas. Escola de Matemática Aplicada. III. Título.
MICHELLE BANDARRA MARQUES COSTA
"ENSAIOS EM MATEMÁTICA APLICADA",
Dissertação apresentado(a) ao Curso de Mestrado em Modelagem Matemática da
Informação do(a) Escola de Matemática Aplicada para obtenção do grau de Mestra(a)
em Modelagem Matemática da nformação.
Data da defesa: 26/09/2017
ASSINATURA DOS MEMBROS DA BANCA EXAMINADORA
Vincent Gerard Yannick Guigues Orientador(a)
Eduardo Fonseca Mendes
Membro Interno
----= .
~ r
Adriart:~er
PizzingaMembro Externo
Agradeço ao meu orientador, Vincent Guigues, por toda a dedicação e atenção dedicada à conclusão deste trabalho. Também agradeço ao Adrian, sem o qual não saberia metade do que aprendi de estatística e econometria. Agradeço aos meus pais e minha irmã, que estiveram presentes por toda a minha vida, me apoiando e ajudando em todos os momentos, bons e ruins, e que eu nada seria sem eles.
Estudamos dois tópicos distintos da matemática aplicada. O primeiro tópico dedica-se à estima-ção e geraestima-ção de trajetórias futuras de séries de oferta de sangue, contribuindo para a literatura de gestão de estoque de bens perecíveis. São utilizados modelos de Vetores Autoregressivos (VAR) e as trajetórias são geradas por duas técnicas distintas de bootstrap presentes na litera-tura que consideram a não-normalidade dos erros do modelo. Conclui-se que ambas técnicas são adequadas e abordagens possíveis para melhorar a previsibilidade das séries de oferta de sangue. O segundo tópico dedica-se ao estudo de diferentes extensões do algoritmo de Programação Dinâ-mica Dual Estocástica (Stochastic Dual Dynamic Programming , SDDP). Sob a ótica de modelos de seleção de carteira, são comparados os desempenhos computacionais de dois algoritmos. O primeiro é uma modificação do SDDP que calcula múltiplos cortes por iteração, Multicut Decom-position Algorithm (MuDA). O segundo introduz estratégias de seleção de corte ao MuDA, no que denominamos de Cut Selection Multicut Decomposition Algorithm, CuSMuDA e, até onde sabemos, ainda não foi proposto pela literatura. São comparadas duas estratégias de seleção de corte distintas, CS1 e CS2. Foram rodadas simulações para 6 casos do problema de seleção de carteira e os resultados mostram a atratividade do modelo proposto CuSMuDA CS2, que obteve tempos computacionais entre 5,1 e 12,6 vezes menores que o MuDA e entre 10,3 e 21,9 vezes menores que o CuSMuDA CS1.
We study two topics of applied mathematics. The first topic is devoted to the estimation of blood supply time series and the generation of simulated trajectories. The main goal is to contribute to the literature of stock management of perishable goods. We use Autoregressive Vetors models and two bootstrap techniques when residuals are nonGaussian. We conclude that both techniques are suitable for the problem at hand and are good approaches to enhance predictability of the blood supply time series.
The second topic is devoted to the study of different extensions of the Stochastic Dual Dy-namic Programming algorithm (SDDP). We compare the computational performance of two algorithms applied to portfolio selection models. The first one is Multicut Decomposition Algo-rithm (MuDA) which modifies SDDP by including multiple cuts (instead of just one) per stage and per iteration. The second, Cut Selection Multicut Decomposition Algorithms (CuSMuDA), combines MuDA with cut selection strategies and, to the best of our knowledge, has not been proposed so far in the literature. We compare two Cut Selection strategies, CS1 and CS2. We run simulations for 6 different instances of the portfolio problem. The results show the attrac-tiveness of CuSMUDA CS2, which was much quicker than MuDA (between 5,1 and 12,6 times quicker) and much quicker than the other cut selection strategy, CuSMuDA CS 1 (between 10,3 and 21,9 times quicker).
2.1 Mapa da Hemorrede do Rio de Janeiro . . . 9 2.2 Gráficos de linha das séries teporais de ofertas de sangue . . . 11 3.1 Evolução dos limites superiores 𝑧𝑖
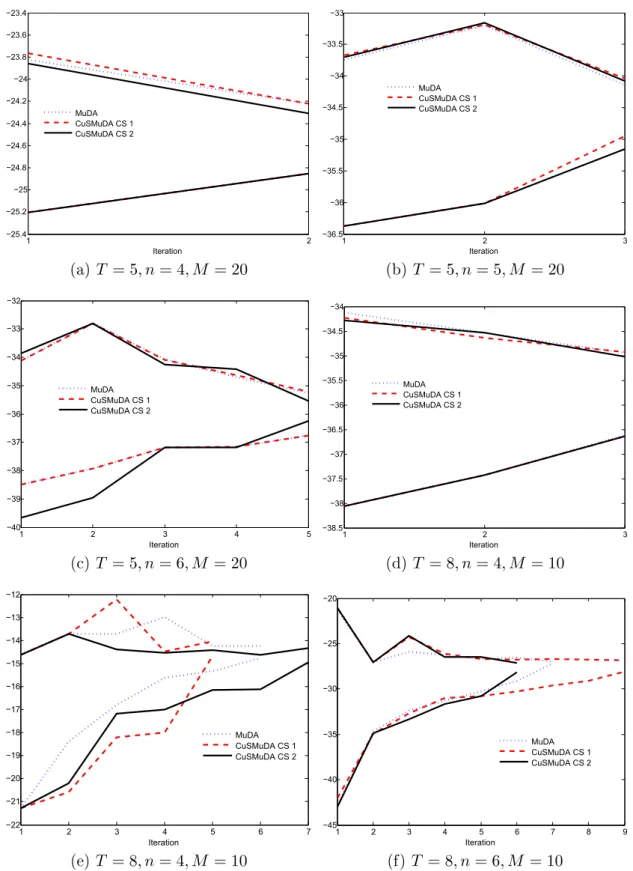
𝑠𝑢𝑝 e inferiores 𝑧𝑖𝑛𝑓𝑖 ao longo das 𝑖 iterações dos
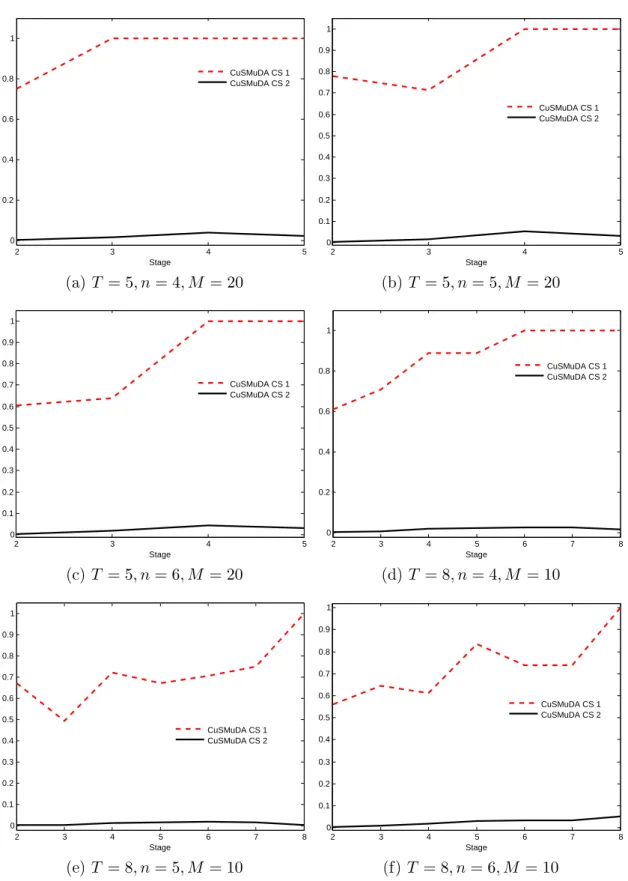
algoritmos . . . 27 3.2 Proporção média de cortes selecionados (ao longo das iterações do algoritmo) para
os estágios 𝑡 = 2,...,𝑇 pelos modelos CuSMuDA CS1 e CuSMuDA CS2 . . . 29 3.3 Representação para os estágios 𝑡 = 2,...,𝑇 , com 𝑇 = 5, da proporção média de
cortes (ao longo das iterações dos algoritmos) selecionados para Q𝑡(·,𝑟𝑡𝑗) como
função de 𝑗 = 1,...,𝑀 e 𝑀 = 20. Gráficos da esquerda consideram o modelo CuSMuDA CS 1 e gráficos da direita o modelo CuSMuDA CS 2. . . 30 3.4 Representação para os estágios 𝑡 = 2,...,𝑇 , com 𝑇 = 8, da proporção média de
cortes (ao longo das iterações dos algoritmos) selecionados para Q𝑡(·,𝑟𝑡𝑗) como
função de 𝑗 = 1,...,𝑀 e 𝑀 = 10. Gráficos da esquerda consideram o modelo CuSMuDA CS 1 e gráficos da direita o modelo CuSMuDA CS 2. . . 31
2.1 Estatísticas de teste nos resíduos do VAR(2) . . . 13 3.1 Subconjuntos de ativos escolhidos . . . 26 3.2 Tempo computacional (em minutos) para solucionar cada variação do
problema de portfólio com os algoritmos MuDA, CuSMuDA CS 1 e CuSMuDA CS 2 . . . 28
1 Introdução 1
1.1 Estudo em tópicos de estatística e econometria . . . 1
1.2 Estudo em tópicos de otimização estocástica e computação. . . 2
1.3 Organização e Estrutura do Trabalho . . . 2
2 Modelo de simulação para séries de oferta de sangue 3 2.1 Fundamentos teóricos . . . 3
2.2 Modelos . . . 4
2.2.1 Vetores auto-regressivos (VAR) . . . 5
2.2.2 Simulação de Bootstrap . . . 6
2.3 Dados e Resultados . . . 9
2.3.1 Dados e implementação . . . 9
2.3.2 Simulação Bootstrap . . . 13
3 Programação Dinâmica Dual Estocástica (PDDE) 15 3.1 Fundamentação Teórica . . . 15
3.1.1 Modelos probabilísticos . . . 15
3.1.2 Programação Dinâmica Estocástica . . . 16
3.1.3 Programação Dual Dinâmica Estocástica (PDDE ou SDDP em inglês) . . 18
3.1.4 Extensões do SDDP, Seleções de Corte e Algoritmos de decomposição mul-ticortes (MuDA) . . . 21 3.2 Modelos . . . 22 3.2.1 Seleção de carteira . . . 22 3.2.2 MuDA . . . 23 3.2.3 CuSMuDA . . . 24 3.3 Resultados. . . 25 4 Conclusão 33 Referências Bibliográficas 34
Introdução
O presente trabalho foi dividido em abordagens distintas a dois problemas matemáticos e eco-nométricos do mundo real. A primeira parte dedica-se ao estudo econométrico, onde foram realizadas estimações de modelos econométricos e gerações de trajetórias futuras a séries de oferta de sangue. A segunda parte dedica-se ao estudo de otimização estocástica, com aplicação de extensões de métodos de programação dinâmica a modelos de gestão de portfólio e formulação de uma nova estratégia para refinar os métodos atualmente utilizados pela literatura.
1.1 Estudo em tópicos de estatística e econometria
A gestão do banco de sangue nos postos de saúde e hospitais é uma tarefa complexa e de im-portância primordial para as políticas de saúde no Brasil e no mundo. Bolsas de sangue estão sujeitas a todo tipo de falhas desde o momento de sua coleta, passando pelo processamento da matéria até os testes de qualidade. Além disso, há o desafio atrelado a estocagem de um bem perecível como o sangue.1 A gestão bem sucedida de bolsas de sangue deve garantir o
equaciona-mento constante da oferta de sangue de hemocentros com a demanda por bolsas em hospitais e postos médicos na assistência de enfermos, portadores de doenças, acidentados e casos cirúrgicos. Para isto, é necessário controle do inventário e previsibilidade no fluxo de entrada e saída de bolsas de sangue nos hemocentros, evitando tanto o desperdício quanto a escassez de bolsas de sangue. Neste sentido, estudos buscando a melhora do processo são de grande importância, e este trabalho busca colaborar na discussão propondo uma modelagem para as séries de oferta de bolsas de sangue em hemocentros e um método para previsão de fluxos futuros.
Nosso trabalho propõe um método para modelagem, estimação e desenho de trajetórias fu-turas para as séries de oferta de sangue, ensejando colaborar com a literatura do tema e, mais amplamente, à literatura de gestão de estoque de bens perecíveis. Utilizamos séries diárias de doações ao hemocentro Instituto Estadual de Hematologia Arthur de Siqueira Cavalcanti (HE-MORIO), localizado no Rio de Janeiro, responsável por coletar, processar, armazenar e distribuir o sangue e seus derivados a hospitais e postos de saúde da rede pública do Estado, e modelamos as séries de oferta de sangue utilizando modelos econométricos consagrados, como Vetores Au-torregressivos (VAR), e duas técnicas distintas de Bootstrap para geração de trajetórias futuras e intervalos de confiança das previsões considerando erros não-Gaussianos. Conclui-se que ambas técnicas são adequadas e abordagens possíveis para melhorar a previsibilidade das séries de oferta de sangue.
1O prazo de validade de uma bolsa de sangue varia com a forma como ela foi coletada, estando estimado entre
1.2 Estudo em tópicos de otimização estocástica e computação
Problemas de otimização estocástica buscam solucionar de forma eficiente situações reais, através de modelos matemáticos onde os parâmetros estocásticos, i.e., os parâmetros cujo valor é incerto no momento de definição das ações a serem tomadas, são representados por variáveis aleatórias. Sendo bastante comuns em diversas áreas da ciência e engenharia, esses tipos de problemas são amplamente explorados pela literatura em variadas formulações possíveis, desde problemas de inventário ([62], [23]) até problemas de seleção de carteira ([5], [7], [34]).
Nosso trabalho dedica-se ao estudo de extensões do algoritmo de Programação Dinâmica Dual Estocástica (Stochastic Dual Dynamic Programming, SDDP), uma técnica de amostragem base-ada na Decomposição de Benders. Variantes do SDDP incluem modelos com múltiplos cortes adicionados por iteração (Multicut Decomposition Algorithm, MuDA), aumentando a comple-xidade de cada iteração do algoritmo, e estratégias de seleção de corte, aplicadas ao modelo multicorte (Cut Selection Multicut Decomposition Algorithm, CuSMuDA). Apesar de técnicas de seleção de corte aplicadas a modelos de multiplos cortes serem úteis para aceleração da conver-gência do algoritmo, até o nosso conhecimento não foi proposto na literatura uma combinação do método de MuDA com estratégias de seleção de corte. Além de estudarmos CuSMuDA com uma estratégia de seleção de cortes conhecida na literatura, Level 1, propusemos a aplicação ao caso estocástico da seleção de corte Limited Memory Level 1 apresentada em [32] para Dual Dynamic Programming (versão determinística do SDDP).
O trabalho teve como objetivo estudar problemas de otimização estocástica sob a ótica dos algoritmos de programação linear estocástica multiestágios, com atenção aos algoritmos MuDA, CuSMuDA com estratégia de seleção de cortes Level 1 (CuSMuDa CS1) e CuSMuDA com estraté-gia de seleção de cortes Limited Memory Level 1 (CuSMuDA CS2). Os modelos são formalmente apresentados e aplicados ao problema clássico de seleção de carteira. Também são expostos os resultados de experimentos numéricos em seis casos do problema de seleção de carteira, utili-zando os três algoritmos (MuDA, CuSMuDA CS1 e CuSMuDA CS2). Os resultados mostram a atratividade computacional da estratégia de seleção de cortes proposta CS2, que obteve tempos computacionais entre 5,1 e 12,6 vezes menores que MuDA e entre 10,3 e 21,9 vezes menores que CuSMuDA CS1.
1.3 Organização e Estrutura do Trabalho
O presente trabalho contém, além desta introdução, outros 3 capítulos.
O segundo capítulo apresenta todo o conteúdo do estudo em tópicos de estatística e econo-metria, incluindo os fundamentos teóricos utilizados para a modelagem e geração de trajetórias futuras das séries de oferta de sangue, os dados utilizados e resultados obtidos.
O terceiro capítulo apresenta todo o conteúdo do estudo em tópicos de otimização estocástica e computação, apresentando a fundamentação teórica de otimização estocástica e do algoritmo de SDDP e suas modificações principais na literatura, além de detalhar o desenvolvimento dos algoritmos aos três modelos tratados nas simulações (MuDA, CusMuDA CS1 e CuSMuDA CS2) aplicados ao problema de seleção de carteira e uma última seção com apresentação dos dados e dos resultados obtidos. Finalmente, o quarto capítulo conclui o trabalho.
Modelo de simulação para séries de
oferta de sangue
2.1 Fundamentos teóricos
Sangue é um recurso essencial para procedimentos médico-cirúrgios, sendo fundamental que esse valioso e limitado recurso esteja disponível a todos que precisam, sendo fundamental que se evite ao máximo seu desperdício.[44]. O sangue é composto principalmente por quatro tipos diferentes de hemocomponentes e hemoderivados, decorrentes de processos físicos e físico químicos realiza-dos no material, sendo eles: concentrado de hemácias, concentrado de plaquetas, plasma fresco congelado e crioprecipitado. Com exceção do plasma, todos os componentes são perecíveis, com tempo de vida útil que chega, no máximo, a 35 dias (Concentrado de hemácias).1
Em 1901, Karl Landsteiner descobriu o que ficou conhecido como o sistema ABO, que clas-sifica o sangue em quatro grupos principais, A, B, AB e O [50]. Em 1940, foi descoberto outro sistema de grupamento de sangue, o sistema Rh, dando origem aos tipos sanguíneos Rh positivo e Rh negativo. Seguindo os dois sistemas, há oito tipos sanguíneos: A+, A-, B+, B-, AB+, AB-, O+ e O-.[51]
No Brasil, a coleta de sangue é feita através de doações voluntárias. O grupo representado pelos doadores é diversificado, possuindo tanto doadores ocasionais quanto doadores frequentes, e cujas restrições são condições tais como idade entre 18 e 65 anos, peso acima de 50 quilos e aptidão médica. O tamanho usual de bolsa de sangue no Brasil é de cerca de 300 a 400 ml.[40]
Depois de coletado, o sangue é levado a laboratório, onde seu tipo sanguíneo é determinado e são executados diversos testes de triagem, além de poder ser separado em hemocomponentes. Caso seja considerado saudável, o sangue é estocado em um banco de sangue, onde ficará dispo-nível para atendimento da demanda de hospitais solicitando o material para transfusões. Uma única doação pode ajudar diversos pacientes, de acordo com quantos produtos foram processa-dos a partir de uma única bolsa, dentre concentrado de hemácias, concentrado de plaquetas e plasma.[40]2 A maior parte da literatura na área é restrita ao estudo das Hemácias, que
repre-sentam o maior volume de transfusões.
Como doações de sangue são feitas voluntariamente, a quantidade de sangue doado recebido
1O prazo de validade de uma bolsa de sangue varia com a forma como ela foi coletada, estando estimado entre
21 e 35 dias, segundo a Portaria 1.353 do Ministério da Saúde (Ministério de Saúde, 2013)
2Hemácias são utilizadas em cirurgias e acidentes envolvendo grandes perdas de sangue, em pacientes anêmicos
e em bebês prematuros. Plaquetas são utilizadas em cirurgias e acidentes envolvendo grandes perdas de sangue e no tratamento de câncer. Plasma é utilizado no tratamento de doenças do fígado e em casos de queimaduras.
por hemocentros para cada tipo sanguíneo é estocástica, assim como o número de transfusões demandadas por cada hospital para cada tipo sanguíneo, e estas duas variáveis - oferta e de-manda - devem ser levadas em conta pelo gestor de um banco de sangue. Parte fundamental do esforço de hospitais para melhorar a gestão de bancos de sangue está em compreender os padrões estatísticos dessas duas séries - através da análise estatística de dados históricos - de forma a aumentar sua previsibilidade ([63]).
Há uma ampla literatura em problemas de inventário de produtos perecíveis ([54], [55], [63], [29], [43], [56]). Alguns dos primeiros trabalhos que se concentraram na área de modelagem da oferta e demanda de sangue representaram as séries de demanda sanguínea como seguindo uma distribuição binomial negativa, com parâmetros que dependiam do tipo sanguíneo e dia da semana, dentre outros ([20] e [21]). [57] formularam uma cadeia de Markov para o problema; entretanto a abordagem foi posteriormente criticada, desde a alegação de violação da propriedade memoryless exigida em processos de Markov até a dificuldade em se determinar no mundo real as probabilidades de transição.3. Até o melhor de nosso conhecimento, não encontramos
traba-lhos que modelassem as séries sanguíneas como variáveis contínuas e nem, tampouco, trabatraba-lhos que modelassem conjuntamente as séries de sangue, capturando efeitos cruzados potencialmente gerados pela substitutibilidade entre alguns tipos sanguíneos. Nossa escolha por esse tipo de análise foi sua aplicação relativamente simples e com resultados bastante satisfatórios, com os modelos estimados tendo boas performances com a base de dados utilizada.
Além dos métodos para modelagem das séries de oferta e demanda de sangue, também é de interesse da literatura o desenho de trajetórias e modelos de previsão dos dados futuros. Por exemplo, [25] desenvolveram modelos sofisticados de previsão da oferta de sangue para o sistema regional de Albany, Nova Iorque, utilizando técnicas de suavização exponencial.
Nosso trabalho propõe um método para modelagem, estimação e desenho de trajetórias fu-turas para as séries de oferta de sangue, ensejando colaborar com a literatura do tema e, mais amplamente, à literatura de gestão de estoque de bens perecíveis. Utilizamos séries diárias de doações ao hemocentro Instituto Estadual de Hematologia Arthur de Siqueira Cavalcanti (HE-MORIO), localizado no Rio de Janeiro, responsável por coletar, processar, armazenar e distribuir o sangue e seus derivados a hospitais e postos de saúde da rede pública do Estado, e modela-mos as séries de oferta de sangue separadamente utilizando modelos econométricos consagrados, como Vetores Autorregressivos (VAR), e duas técnicas distintas de Bootstrap para geração de trajetórias futuras e intervalos de confiança das previsões considerando erros não-Gaussianos. Conclui-se que ambas técnicas são adequadas e abordagens possíveis para melhorar a previsibi-lidade das séries de oferta de sangue.
As próximas seções tratarão dos principais modelos utilizados no trabalho e apresentarão os resultados das estimações e das simulações.
2.2 Modelos
Nesta seção será apresentado o modelo de séries temporais utilizado no presente trabalho e a técnica utilizada para geração de trajetórias futuras. A metodologia consiste na estimação de modelo por vetores autorregressivos (VAR), modificado para considerar o impacto de fatores exógenos contemporâneos (VARX). Nosso modelo VARX é aplicado em duas etapas, a primeira consistindo na estimação por Mínimos quadrados ordinários (MQO) das séries regredidas em
fatores exógenos contemporâneos, e a segunda consistindo na estimação por VAR das séries cor-rigidas resultantes da primeira etapa. Ao longo de todo o processo são utilizados outros conceitos e técnicas estatísticas como, notadamente, análises gráficas e testes de hipóteses. Finalmente, é apresentado o conceito de bootstrap e as duas técnicas de bootstrap utilizadas para geração de trajetórias futuras das séries de oferta de sangue.
2.2.1 Vetores auto-regressivos (VAR)
Modelos de vetores auto-regressivos (VAR) examinam relações lineares entre variáveis tratadas como endógenas e os valores defasados delas próprias e das demais.
Seja 𝑌𝑡 = (𝑌1𝑡,...,𝑌𝐾𝑡)′ ∈ R𝑘 um vetor aleatório das variáveis de interesse. Seja o modelo
estrutural
𝐶𝑌𝑡= 𝐵0+ 𝐵1𝑌𝑡−1+ ... + 𝐵𝑝𝑇𝑡−𝑝+ 𝐵𝑣𝑡, 𝑡 = 0,1,2... (2.1)
no qual 𝐶 é uma matriz 𝐾 × 𝐾 que define as restrições contemporâneas entre as variaveis que constituem 𝑌𝑡, 𝐵0 é um vetor 𝐾 × 1 de termos de intercepto, 𝐵𝑖s são matrizes 𝐾 × 𝐾 de
coeficientes, 𝐵 é uma matriz diagonal 𝐾 ×𝐾 de desvios padrão e 𝑣𝑡é um vetor 𝑘×1 de
perturba-ções aleatórias não correlacionadas entre si contemporânea ou temporalmente, i.e., 𝑣𝑡𝑖.𝑖.𝑑(0; 𝐼𝐾).
O modelo VAR(p) na forma reduzida é dado por:
𝑌𝑡= 𝐶−1𝐵0+𝐶−1𝐵1𝑌𝑡−1+...+𝐶−1𝐵𝑝𝑇𝑡−𝑝+𝐶−1𝐵𝑣𝑡= 𝜈 +𝐴1𝑌𝑡−1+...+𝐴𝑝𝑌𝑡−𝑝+𝑢𝑡, 𝑡 = 0,1,2...
(2.2) no qual o vetor de erros i.i.d. 𝑢𝑡 é tal que 𝐸(𝑢𝑡) = 0 e 𝐸(𝑢𝑡𝑢
′
𝑡) = Σ𝑢, onde Σ𝑢 é uma matriz
simétrica positiva definida 𝐾 × 𝐾.
A condição de estacionariedade de um VAR estacionário diz que as raízes da equação carac-terísticas 𝑑𝑒𝑡(𝐼𝐾 − 𝐴1𝑧 − ... − 𝐴𝑝𝑍𝑝) = 0estão fora do círculo unitário, onde 𝐼𝐾 é uma matriz
identidade 𝐾 × 𝐾 e 𝑑𝑒𝑡(·) denota o determinante de uma matriz.
Dadas 𝑛 realizações de (2.2), podemos utilizar o método de MQO para estimar de forma eficiente os parâmetros, desde que incluidos lags suficientes de todas as variáveis e a equação satisfaça a hipótese de homocedasticidade para séries temporais (para maiores detalhes, ver [52])
Critérios de informação de Akaike e Schwarz
A determinação da ordem 𝑝 do modelo pode ser feita de duas formas: teste da razão de verossimilhanças ([13]) e critérios de informação.
Dois dos critérios de informação mais populares na literatura são Akaike [1] e Schwarz Baye-siano [24], dados por
Critério de informação de Akaike
𝐴𝐼𝐶(𝑞) = 𝑙𝑜𝑔|∑︁ˆ
𝑣
(𝑞) + 𝑞𝑚22 𝑇 Critério de informação de Schwarz
𝑆𝐵𝐼𝐶(𝑞) = 𝑙𝑜𝑔|∑︁ˆ
𝑣
(𝑞) + 𝑞𝑚2𝑙𝑜𝑔𝑇 𝑇
Previsão do modelo VAR
Dadas 𝑛 realizações (𝑌1,...,𝑌𝑛) de (2.2), é possível gerar previsões potenciais para o período
𝑛 + ℎ em 𝑛 da seguinte forma
ˆ
𝑌𝑛(ℎ) = ˆ𝜈 + ˆ𝐴1𝑌𝑛−1ˆ (ℎ) + ... + ˆ𝐴𝑝𝑌𝑛−𝑝ˆ (ℎ) (2.3)
onde ˆ𝑌𝑛(𝑗) = 𝑌𝑛+𝑗 para 𝑗 ≤ 0.
Modelo VARX(p,n) Em nosso trabalho, utilizamos uma modificação do modelo VAR tra-dicional que considera a inclusão de variáveis exógenas em (2.2), representadas por 𝑋𝑡 vetor
𝑛 × 1 contendo 𝑛 variáveis exógenas a 𝑌𝑡. A forma escolhida para estimação do nosso modelo
VARX(p,n) foi a realização de estimação em duas partes.4
Na primeira, estima-se o seguinte modelo MQO 5:
𝑦𝑖= 𝑐𝑖+ 𝑥𝑖𝛽 + 𝜖𝑖, 𝑖 = 1,...,8 (2.4)
no qual 𝑖 representa o tipo sanguíneo considerado, 𝑦𝑖 é um vetor 𝑇 × 1 da série de oferta do
i-ésimo tipo sanguíneo, 𝑐𝑖 é o intercepto, 𝑥𝑖 é um vetor 𝑇 × 𝑛𝑖 das 𝑛𝑖 variáveis exógenas a 𝑦𝑖
identificadas e 𝜖𝑖 é o vetor 𝑇 × 1 de resíduos do modelo.
Repare que podemos escrever (2.4) como 𝜖𝑖 = 𝑦𝑖− 𝑐𝑖− 𝑥𝑖𝛽, o que nos ajuda a compreender
a interpretação de 𝜖 como sendo a série de oferta do i-ésimo tipo sanguíneo, retirados os efeitos exógenos contemporâneos. Assim, a partir da estimação de (2.4) é possível obtermos ˆ𝜖𝑖∀𝑖.
Assim, definindo 𝑌𝑡= [(𝑦1𝑡− 𝑥1𝑡𝛽),...,(𝑦ˆ 8𝑡− 𝑥8𝑡𝛽)]ˆ ′ = [ ˆ𝜖1𝑡, ..., ˆ𝜖8𝑡]′, estimamos nosso modelo
VAR(p) seguinte a equação (2.2).
2.2.2 Simulação de Bootstrap
A técnica de Bootstrap é indicada para problemas nos quais os procedimentos estatísticos conven-cionais sejam de difícil aplicação. Por causa de sua generalidade, técnicas de Bootstrap têm sido aplicadas a uma classe extensa de problemas, desde a obtenção de estimativas de erros padrões e intervalos de confiança até a geração de cenários e trajetórias futuras. Em séries temporais, a utilização da técnica de Bootstrap surgiu em 1984, quando a metodologia foi aplicada num contexto econométrico para previsão de demanda de energia no mercado americano [67]. Mais tarde outros trabalhos surgiram e estudou-se a estimação do erro-padrão das estimativas dos parâmetros dos modelos de previsão.
Operacionalmente, o método de simulação por reamostragem de Bootstrap consiste em um sorteio com reposição dos elementos de uma amostra aleatória, gerando uma "amostra Boots-trap", de tamanho igual à original. Extrai-se um número suficiente de amostras6 a fim de se
obter a "distribuição Bootstrap"de qualquer estatística de interesse do pesquisador. Desta forma, o conjunto de observações Bootstrap corresponde a uma estimativa da verdadeira distribuição amostral da estatística em questão. Como mostrado em [19], a distribuição Bootstrap converge assintoticamente para a distribuição verdadeira da estatística.
4para maiores detalhes sobre a metodologia VARX, ver [22] 5Para maiores detalhes sobre o MQO, ver [18]
6Segundo [15], o número de reamostragens necessárias para se obter boas estimativas, em intervalos de confiança
Bootstrap para simulações VAR(p) com erros não Gaussianos
A maior parte da literatura de previsão de modelos VAR foca na previsão pontual de cada uma das variáveis do sistema. Dois problemas podem acarretar deste tipo de previsão: erro de previsão quando as variáveis do sistema são condicionais a valores das outras variáveis e o inte-resse de previsão múltiplos períodos a frente, que deve incorporar a incerteza acerca da evolução futura das variáveis de interesse [26].
Uma forma de solucionar esta questão é assumir erros de previsão Gaussianos em um modelo 𝑉 𝐴𝑅(𝑝), porém esta opção acarreta em problemas associados com a determinação de lag do modelo, como tratado em detalhes em [45]. Além disso, a evidência empírica sugere que séries temporais constantemente rompem com a hipótese Gaussiana ([39], [46]).
Uma forma de construir densidades de previsão multivariadas incorporando as incertezas dos parâmetros e da ordem do VAR, sem depender de hipóteses sobre a distribuição dos erros, é uti-lizando bootstraps não paramétricos (veja [6] para uma revisão de procedimentos de bootstrap em séries temporais). No presente trabalho, consideraremos dois métodos de bootstrap para geração de trajetórias futuras de modelo VAR: [48] e [26].
Bootstrap Backward [48]
O método de bootstrap para previsão de VAR(p) estacionários introduzido por [48] é uma extensão do procedimento proposto por [68] para processos univariados auto-regressivos 𝐴𝑅(𝑝). O método utiliza a representação backwards do modelo VAR para geração de pseudo dados amostrais in sample (trajetórias de bootstrap in sample), utilizados para replicar os parâmetros estimados. As trajetórias futuras são obtidas a partir de bootstrap no modelo VAR utilizando os estimadores obtidos pelo VAR backward particular de cada trajetória in sample e do sorteio com reposição dos resíduos originais no VAR.
Assim, considere o modelo 𝑉 𝐴𝑅(𝑝) dado pela equação (2.2). O modelo é estacionário, de modo que todas as raízes da equação característica 𝑑𝑒𝑡(𝐼𝐾− 𝐴1𝑧 − ... − 𝐴𝑝𝑧𝑝) = 0encontram-se
fora do círculo unitário.
Dadas 𝑛 realizações de (𝑌1,...,𝑌𝑝) de (2.2), podemos estimar os parâmetros do modelo pelo
método de mínimos quadrados, denotando por (ˆ𝜈, ˆ𝐴1, ..., ˆ𝐴𝑝) os estimadores de MQO para
(𝜈,𝐴1,...,𝐴𝑝) e ˆ𝑢𝑡 os resíduos de MQO.
Considere o modelo VAR backward associado ao modelo VAR da equação (2.2)
𝑌𝑡= 𝜇 + 𝐻1𝑌𝑡+1+ ... + 𝐻𝑝𝑌𝑡+𝑝+ 𝜔𝑡, 𝑡 = 0,1,... (2.5)
no qual 𝐻𝑖são matrizes 𝐾×𝐾 de coeficientes, 𝜔𝑡é um vetor aleatório 𝐾×𝐾 tal que 𝐸(𝜔𝑡) = 0
e 𝐸(𝜔𝑡𝜔
′
𝑡) =
∑︀
𝜔, onde ∑︀𝜔é uma matriz 𝐾×𝐾 simétrica positiva definida com elementos finitos.
Os modelos VAR ’forward’ (equação (2.2)) e VAR backward (equação (2.5)) são intimamente relacionados; por exemplo, 𝐻′
1 = Γ−1𝐴1Γ, onde Γ = 𝐸(𝑌𝑡𝑌
′
𝑡) para o caso VAR(1) (ver [47] para
maiores detalhes).
Denotamos os estimadores de MQO da equação (2.5) de (𝜇, 𝐻1, ..., 𝐻𝑝) por (ˆ𝜇, ˆ𝐻1,..., ˆ𝐻𝑝) e
ˆ
Podemos gerar um conjunto de pseudo-dados recursivamente baseado na equação (2.5) da seguinte forma:
𝑌𝑡*= 𝜇 + 𝐻1𝑌𝑡+1* + ... + 𝐻𝑝𝑌𝑡+𝑝* + 𝜔*𝑡, (2.6)
sendo que os 𝑝 primeiros valores da equação são definidos como idênticos aos 𝑝 últimos valores da série original e 𝜔*
𝑡 é retirado aleatoriamente de { ˆ𝜔𝑡}𝑛𝑡=1 com reposição.
Assim, é possível gerar conjuntos de pseudo-dados in sample cujas últimas p observações, nas quais as previsões do VAR se baseiam, são idênticas aos últimos p valores da série original.
A previsão de bootstrap para o período 𝑛 + ℎ no período 𝑛 pode ser gerada como
𝑌𝑛*(ℎ) = 𝜈*+ 𝐴*1𝑌𝑛*(ℎ − 1) + ... + 𝐴*𝑝𝑌𝑛*(ℎ − 𝑝) + 𝑢*𝑛+ℎ (2.7) sendo que 𝑌*
𝑛(𝑗) = 𝑌𝑛+𝑗 para 𝑗 ≤ 0, 𝑢*𝑛+ℎ é sorteado aleatoriamente de { ˆ𝑢*𝑡}𝑛𝑡=1 com
reposi-ção e (𝜈*,𝐴*
1, ..., 𝐴*𝑝) são os estimadores de MQO para (𝜈, 𝐴1, ..., 𝐴𝑝)obtidos pelos pseudo-dados
{𝑌𝑡*}𝑛
𝑡=1. A geração de 𝐵 conjuntos de pseudo-dados {𝑌𝑡*(ℎ,𝑖)}𝐵𝑖=1 permite, portanto, a geração
de 𝐵 previsões de bootstrap baseadas na equação (2.7). A partir das 𝐵 trajetórias futuras tam-bém é possível obter intervalos de previsão com (1 − 𝛼)100% de significância. Para tal, a cada ℎ ≥ 1, ordena-se em ordem crescente {𝑌𝑛*(ℎ,𝑖)}𝐵𝑖=1, de modo que 𝑌𝑛*(ℎ,1)possui o menor valor dentre as 𝐵 trajetórias em 𝑛 + ℎ e 𝑌*
𝑛(ℎ,𝐵)o maior valor. O intervalo de confiança de previsão
de 𝑌𝑛+ℎ a (1 − 𝛼)100% de significância é [𝑌𝑛*(ℎ, 𝛼 2100%𝐵),𝑌 * 𝑛(ℎ,1 − 𝛼 2100%𝐵)]. Bootstrap Forward [26]
O método de bootstrap proposto em [26] evita o uso da representação backward, o que o torna adequado para outras modelagens além do VAR, como modelos VARMA ou VAR-GARCH. O método utiliza as primeiras 𝑝 observações dos dados e sorteio com reposição dos resíduos esti-mados por MQO do modelo VAR para gerar trajetórias in sample. As trajetórias futuras são obtidas a partir de bootstrap no modelo VAR utilizando os últimos 𝑝 valores da amostra original, os parâmetros estimados por bootstrap nas trajetórias in sample e o sorteio com reposição dos resíduos originais no VAR.
Assim, da mesma forma que anteriormente, dadas 𝑛 realizações de (𝑌1,...,𝑌𝑝) de (2.2),
po-demos estimar os parâmetros do modelo pelo método de mínimos quadrados, denotando por (ˆ𝜈, ˆ𝐴1, ..., ˆ𝐴𝑝) os estimadores de MQO para (𝜈,𝐴1,...,𝐴𝑝) e ˆ𝑢𝑡 os resíduos de MQO.
Podemos gerar um conjunto de pseudo-dados recursivamente da seguinte forma:
𝑌𝑡* = 𝜈 + 𝐴1𝑌𝑡−1* + ... + 𝐴𝑝𝑌𝑡−𝑝* + 𝑢*𝑡, (2.8)
sendo que os 𝑝 primeiros valores da equação são definidos como idênticos aos 𝑝 primeiros valores da série original e 𝑢*
𝑡 é retirado aleatoriamente de { ˆ𝑢𝑡}𝑛𝑡=1 com reposição. A estimação
da equação (2.8) por MQO gera o conjunto de estimadores (𝜈*,𝐴*
1, ..., 𝐴*𝑝) para (𝜈, 𝐴1, ..., 𝐴𝑝).
A previsão de bootstrap para o período 𝑛 + ℎ no período 𝑛 pode ser gerada como
sendo que 𝑌*
𝑛(𝑗) = 𝑌𝑛+𝑗 para 𝑗 ≤ 0, 𝑢*𝑛+ℎ é sorteado aleatoriamente de { ˆ𝑢*𝑡}𝑛𝑡=1 com
reposi-ção. A geração de 𝐵 conjuntos de pseudo dados {𝑌*
𝑡 (ℎ,𝑖)}𝐵𝑖=1 permite, portanto, a geração de 𝐵
previsões de bootstrap baseadas na equação (2.9).
Da mesma forma que em [48], a partir das 𝐵 trajetórias futuras podemos obter intervalos de previsão, como descrito anteriormente.
As previsões bootstrap convergem estocasticamente quando 𝑛 cresce aos valores futuros ver-dadeiros da distribuição ([26]), o que torna o uso do bootstrap robusto para diversos enfoques, inclusive para o cálculo de intervalos de previsão do VAR.
2.3 Dados e Resultados
2.3.1 Dados e implementação
O presente estudo utilizou dados obtidos junto ao Hemocentro Instituto Estadual de Hematologia Arthur de Siqueira Cavalcanti (HEMORIO)7, Hemocentro coordenador da Rede de Hemoterapia
pública do Estado do Rio de Janeiro (figura 1), responsável por coletar, processar, armazenar e distribuir o sangue e seus derivados a hospitais e postos de saúde da rede pública do Estado.
Figura 2.1: Mapa da Hemorrede do Rio de Janeiro
Fundado em 1944 como o primeiro Banco de sangue do Brasil, o HEMORIO já distribuía sangue para hospitais de emergência desde sua fundação, apesar de o serviço de Hematologia só ter sido implantado em 1956. Atualmente, o HEMORIO abastece com sangue e derivados cerca de 200 unidades de saúde, e recebe em média cerca de 350 doadores voluntários de sangue por dia. Além disso, possui um serviço de Hematologia, com mais de 10 mil pacientes ativos, que realizam tratamentos de doenças hematológicas.
Os dados foram coletados do histórico de Expedição de componentes do HEMORIO. Este banco de dados registra diariamente as bolsas de sangue doadas à Rede de Hematologia do HE-MORIO, informando data de coleta, grupo ABO, fator Rh e componente. Toda bolsa de sangue coletada, independente do processamento utilizado, gera um bolsa de concentrado de hemácias, que é o hemocomponente de maior interesse para utilização em hospitais e centros cirúrgicos, tornando-se assim o foco do nosso estudo.
Todas as análises estatísticas, econométricas e simulações de bootstrap foram implementadas utilizando o software RStudio, baseado na linguagem de programação R.
Estatísticas descritivas
Designaremos as oito séries de oferta de sangue como as séries históricas diárias do total de unidades de bolsas de concentrado de hemácias resultantes das doações de sangue de cada um dos 8 tipos sanguíneos existentes (A positivo, A negativo, B positivo, B negativo, AB positivo, AB negativo, O positivo e O negativo). O período da amostra obtida compreende desde 1º de janeiro de 2013 até 09 de dezembro de 2015, totalizando 1.073 observações.
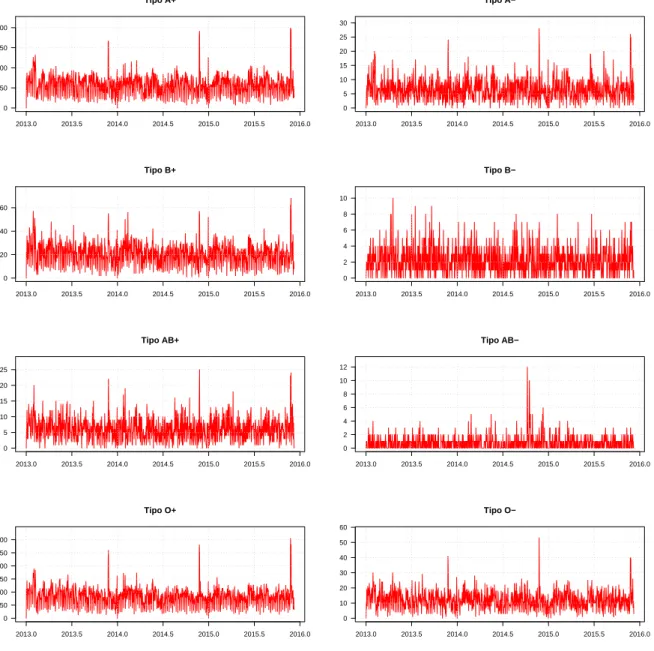
A figura 2.2registra a série histórica obtida para cada tipo sanguíneo As séries históricas de oferta de sangue podem ser observadas na figura2.2.
Através da análise do banco de dados e das funções de autocorrelação e autocorrelação parcial, foi possível tirar algumas conclusões a respeito das séries de oferta. Primeiramente, observar que os tipos sanguíneos O positivo e A positivo são os mais frequentes entre os doadores da amostra, com médias diárias de 81,8 bolsas e 57,0 bolsas, respectivamente. Entre os tipos sanguíneos de menor frequência da amostra estão B negativo e AB negativo, o último consistindo basicamente de valores 0 e 1.
Mínimos Quadrados Ordinários
A observação dos dados das séries de oferta, além da consideração das funções de autocorrelação e autocorrelação parcial (FAC e FACP) das séries individuais de oferta de sangue, mostraram que elas possuem sazonalidade semanal, com dias de semana possuindo maior fluxo de doadores que finais de semana. Além disso, há períodos das séries considerados outliers negativos - pe-ríodos com menor fluxo de doações, como Natal, Ano novo e o período que compreende a Copa do Mundo no Brasil - e períodos considerados outliers positivos - períodos com maior fluxo de doações, como os de Campanhas de doação. Estas descobertas estão em linha com estudos ante-riores, como o de [16], que conclui que as séries de sangue não aparentam sazonalidade no ano, mas apresentam variações ao longo dos dias da semana, com maiores taxas sendo registradas usualmente nas segundas, terças e quartas feiras e menores taxas nos finais de semana e feriados. Ainda, o tipo sanguíneo AB- parece não responder adequadamente aos mesmos estímulos que os outros, não possuindo sazonalidade aparente nem outliers consistentes ao longo dos anos da amostra8.
Tipo A+ 2013.0 2013.5 2014.0 2014.5 2015.0 2015.5 2016.0 0 50 100 150 200 Tipo A− 2013.0 2013.5 2014.0 2014.5 2015.0 2015.5 2016.0 0 5 10 15 20 25 30 Tipo B+ 2013.0 2013.5 2014.0 2014.5 2015.0 2015.5 2016.0 0 20 40 60 Tipo B− 2013.0 2013.5 2014.0 2014.5 2015.0 2015.5 2016.0 0 2 4 6 8 10 Tipo AB+ 2013.0 2013.5 2014.0 2014.5 2015.0 2015.5 2016.0 0 5 10 15 20 25 Tipo AB− 2013.0 2013.5 2014.0 2014.5 2015.0 2015.5 2016.0 0 2 4 6 8 10 12 Tipo O+ 2013.0 2013.5 2014.0 2014.5 2015.0 2015.5 2016.0 0 50 100 150 200 250 300 Tipo O− 2013.0 2013.5 2014.0 2014.5 2015.0 2015.5 2016.0 0 10 20 30 40 50 60
Portanto, o primeiro passo para a estimação do modelo envolveu a dessazonalização das séries e controle dos efeitos contemporâneos incidentes. Para isso, estimaram-se regressões lineares individuais pelo método de Mínimos Quadrados Ordinários, como o modelo descrito abaixo
𝑦𝑡𝑖= 𝑥𝑡𝑖𝛽𝑖+ 𝜖𝑡, 𝑡 = 1,...,𝑇, 𝑖 ∈ 𝐴 + ,𝐴 − ,𝐵 + ,𝐵 − ,𝐴𝐵 + ,𝑂 + ,𝑂− (2.10)
no qual 𝑇 é o tamanho da amostra (1.073 observações), 𝑖 designa o tipo sanguíneo, e o vetor 𝑥𝑡𝑖 de variáveis explicativas possui, além do intercepto, 6 dummies referentes a diferentes dias
da semana, uma dummy de tendência para o período entre 1º janeiro e o início do Carnaval
9, uma dummy para os dois dias da campanha nacional de doação de sangue, que ocorre em
novembro anualmente, e dummies para os feriados ocorridos no período, o que compreende uma dummy Copa do Mundo, que controla pelos diversos feriados que a cidade teve em dias de jogos do campeonato ocorridos na cidade do Rio de Janeiro, uma dummy para o dia 1º de janeiro, quando o Hemorio não coleta doações, uma dummy para o Natal, uma dummy para o Reveillon. Nossa hipótese é de que há dependência temporal nas séries, de modo que a estimação dos modelos individuais de regressão linear por MQO apresentou o problema de autocorrelação dos resíduos, comprometendo as estatísticas de testes de hipóteses.10 Para correção do problema, foi
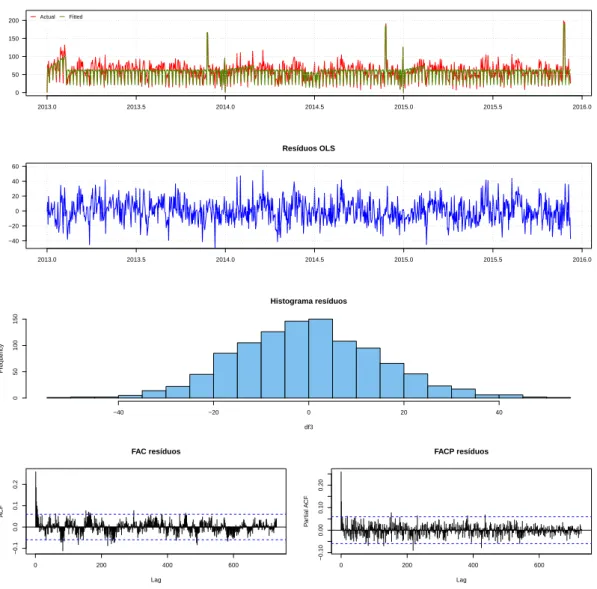
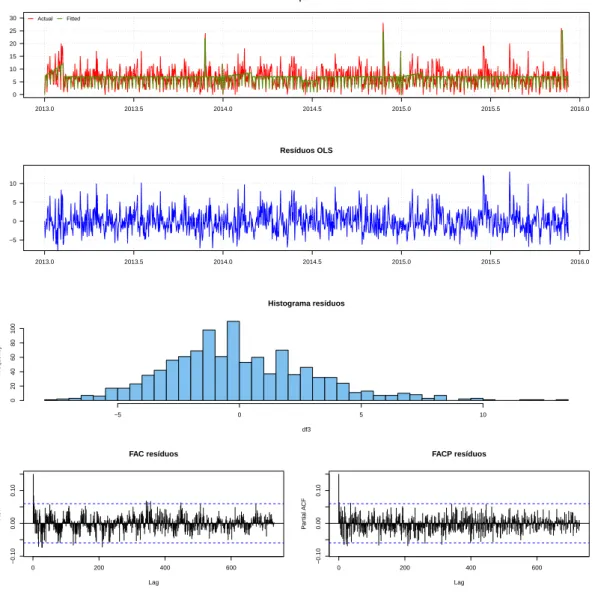
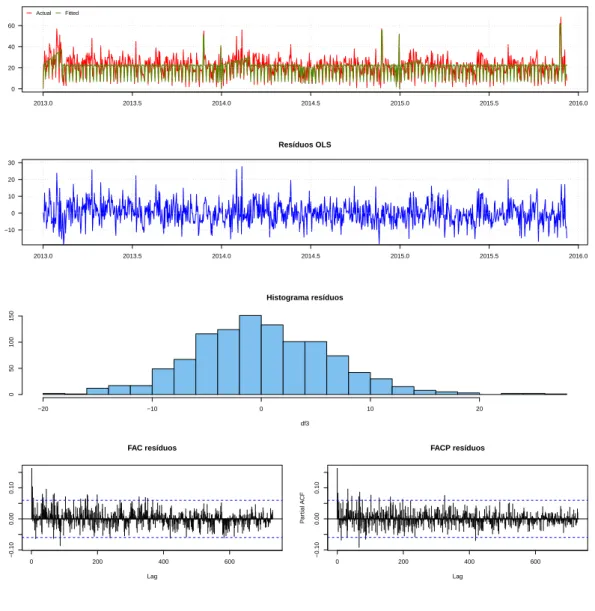
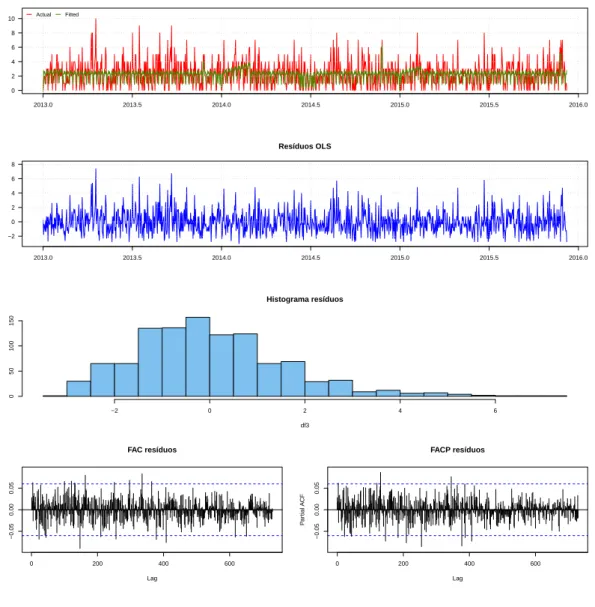
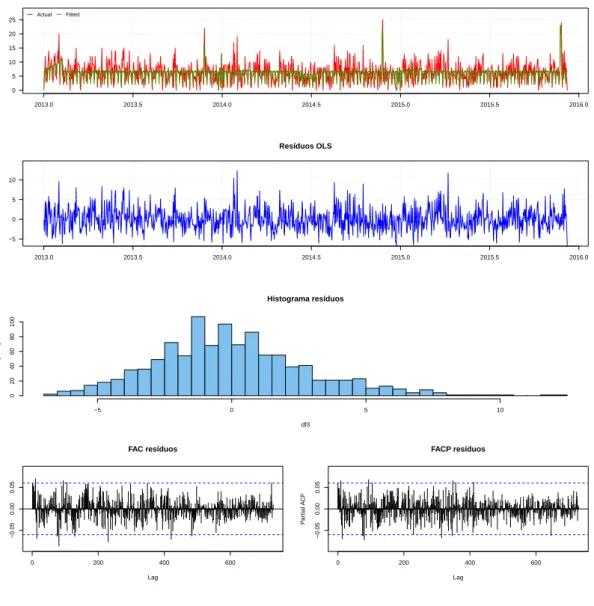
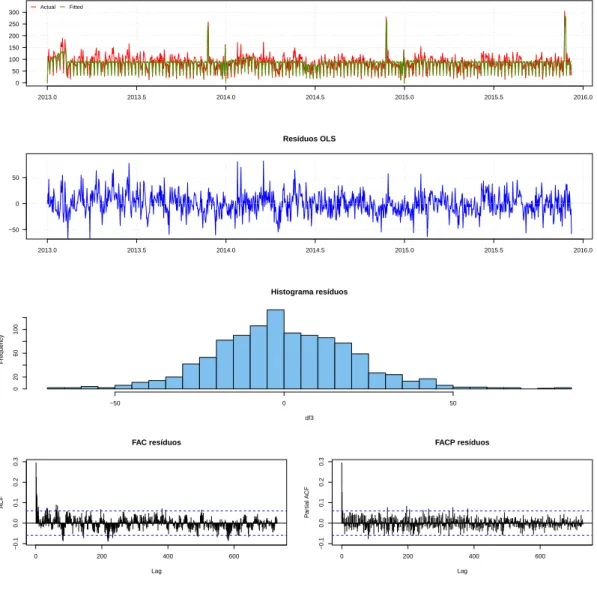
feita a estimativa da variância dos estimadores de MQO pelo método de Newey-West. No Anexo I estão os gráficos das séries amostrais e estimadas pelo modelo da equação (2.10), além dos gráficos dos resíduos estimados por MQO. Também podem ser vistos em detalhes os sumários das regressões de cada série.
Vetores Autorregressivos
Do primeiro passo de MQO, obtemos séries dessazonalizadas e corrigidas para os efeitos descritos e podemos passar para a definição de defasagem do VAR a ser considerado, que utiliza como variáveis dependentes os resíduos estimados de MQO dos sete tipos sanguíneos A+, A-, AB+, B+, B-, O+ e O-.
Os critérios de informação Akaike e Schwartz indicaram defasagem apropriada de um lag, i.e., que o modelo apropriado seria o VAR(1). Foi feita a estimação do VAR(1) e posterior análise dos gráficos de FAC e FACP, onde se verificou que o modelo não estava bem especificado, tendo sido observados resíduos autocorrelacionados para as regressões das séries A+ e O+.
Portanto, aumentou-se a defasagem, estimando-se o modelo VAR(2). Apesar de menos par-cimonioso que o modelo VAR(1), o modelo VAR(2) estimado controlou a autocorrelação serial dos erros observada no VAR(1) pela inclusão de mais um lag das séries explicativas. Os valores estimados do modelo encontram-se na tabela2.1 abaixo.
O anexo II mostra os gráficos dos resíduos de cada série proveniente do VAR(2), além de seus histogramas, qq plot, FAC e FACP. Com o auxílio dos gráficos e com as estatísticas dos testes Jarque-Bera ([41]), feitas em cada série de resíduos, para verificação de normalidade, pôde-se
9Em função do aumento da demanda por sangue no período que compreende o Carnaval no Rio de Janeiro,
o Hemorio faz um esforço de campanha desde o começo do ano para abastecimento dos estoques de sangue da instituição
10Um ajuste fino feito inicialmente no modelo considerou a significância dos estimadores obtidos, dada pela
estatística t, para fazer regressões personalizadas por tipo sanguíneo, incluindo conjunto possivelmente menor dos estimadores inicialmente considerados. Com as estatísticas Wald, foram feitos testes de restrição dos coeficientes para entender se os efeitos das dummies explicativas eram diferentes em anos distintos. Como ambas análises pro-duziram pouca diferença em relação às regressões sem restrições, por simplicidade e automatização computacional elas foram desconsideradas.
Tabela 2.1: Estatísticas de teste nos resíduos do VAR(2)
Média Dp Kurtose skewness JB estatística JB p valor
A+ -0.03 14.21 0.34 0.14 8.76 0.013 A- 0.00 2.94 0.73 0.56 81.09 0.000 B+ -0.00 6.24 0.86 0.36 56.61 0.000 B- 0.00 1.56 1.14 0.78 168.19 0.000 AB+ 0.00 2.78 0.76 0.54 78.62 0.000 O+ -0.04 19.21 0.98 0.19 180.54 0.000 O- -0.00 4.41 0.33 0.37 49.62 0.000 AB- 0.78 1.06 19.14 2.99 29.81 0.000
comprovar que tais séries, com fracas exceções, não poderiam ser consideradas como advindas de distribuições Gaussianas.
Apesar de não seguirem distribuição normal, as séries de resíduo estimadas do VAR(2) são independentes e identicamente distribuídas (iid), como verificado pelo teste BDS([11]). 11 No
Anexo III é possível acessar as estatísticas dos testes Jarque-Bera e BDS a cada uma das séries.
2.3.2 Simulação Bootstrap
Foram seguidas três metodologias para simulação de cenários futuros de cada série de oferta sanguínea (com exceção do AB-).
A primeira considera, erroneamente, que os resíduos advindos da estimação do VAR(2) são Gaussianos. A segunda e terceira metodologia utilizam o bootstrap backward [48] e o bootstrap forward [26] citados anteriormente, que tratam de simulações com erros não-Gaussianos.
Em todas as três metodologias, as trajetórias futuras para a série de oferta de sangue do tipo sanguíneo AB- foram obtidas por processo de Monte Carlo ([53]), através do sorteio sequencial, com reposição, de valores amostrais da série.
Para as três metodologias consideraram-se 𝐵 = 2.000 trajetórias com horizonte de previsão ℎ = 30 dias para cada tipo sanguíneo, a começar imediatamente ao fim da amostra disponível, i.e., 𝑛 = 𝑇 . A média das trajetórias dá a estimativa futura 1 a 30 dias a frente, e os 2,5% valores mais baixos e os 2,5% valores mais altos em cada momento 𝑡 a frente determinam o intervalo de confiança da previsão.
Neste momento, faz-se necessário um comentário acerca da escolha pela modelagem contínua das séries. Como consequência da escolha de modelagem feita das séries nesse trabalho, em al-gumas das trajetórias calculadas foram obtidos valores negativos às variáveis de oferta. A forma escolhida para tratar a questão foi a imposição de mínimo zero para todas as observações gera-das, de forma que todas as observações negativas foram artificialmente substituídas por valores nulos.
Bootstrap Gaussiano
Usada como base de comparação para as outras duas metodologias, a simulação Gaussiana consiste na geração de trajetórias de bootstrap futuras utilizando os parâmetros estimados no modelo VAR(2) e da hipótese que os erros são Gaussianos. Este é um bootstrap paramétrico, onde ao invés de se sortear da distribuição amostral dos erros, se sorteia da distribuição teórica
no caso, 𝑁(0, ˆ∑︀
𝑢), onde ˆ
∑︀
𝑢 é a matriz variância covariância dos erros amostrais. Após a geração
das trajetórias futuras do VAR(2), é realizado processo de recuperação dos valores de interesse, que são estimações para as séries de oferta de sangue. Assim, percorre-se o caminho inverso à estimação, construindo as trajetórias ao modelo de MQO a partir das trajetórias do modelo VAR e, posteriormente, discretizando os valores obtidos para conversão das trajetórias em trajetórias de número de bolsas de sangue ofertadas por dia, por tipo sanguíneo.
Os gráficos finais de cada tipo sanguíneo, contendo as 2.000 trajetórias, a previsão da série (média das trajetórias em cada 𝑡, 𝑡 = {1,...,30}), e o intervalo de confiança de 95% encontram-se no Anexo IV.
Bootstrap backward [48]
Seguindo [48], tal simulação é utilizada para quando os resíduos são não-Gaussianos. O mé-todo envolve a estimação de um VAR(2) backwards, utilizado posteriormente na geração de novas trajetórias in sample, que por sua vez servirão para uma nova estimação de parâmetros do mo-delo VAR(2) tradicional e geração de trajetórias futuras pelo sorteio com reposição dos resíduos originais no VAR (2) calculados sob os novos estimadores obtidos pelo VAR(2) particular de cada trajetória.12
Os gráficos de cada tipo sanguíneo, contendo as 2.000 trajetórias, a previsão da série (média das trajetórias em cada 𝑡, 𝑡 = {1,...,30}), e o intervalo de confiança de 95% encontram-se no Anexo V.
Bootstrap forward [26]
Também utilizada quando os resíduos não são Gaussianos, tal bootstrap difere do método de [48] por não exigir uma estimação de um VAR(2) backwards. Em [26], as trajetórias in sample possuem todas os mesmos 2 primeiros valores e são geradas através dos estimadores já estimados no VAR(2) tradicional e de sorteio dos resíduos originais do VAR(2). O resto do processo é idên-tico a [48], utilizando tais trajetórias para novas estimações dos parâmetros do modelo VAR(2) tradicional e geração de trajetórias futuras pelo sorteio com reposição dos resíduos originais no VAR (2) calculados sob os novos estimadores obtidos pelo VAR(2) particular de cada trajetória. Os gráficos de cada tipo sanguíneo, contendo as 2.000 trajetórias, a previsão da série (média das trajetórias em cada 𝑡, 𝑡 = {1,...,30}) e o intervalo de confiança de 95%, juntamente com a comparação com o método de [48], encontram-se no Anexo VI.
Para todos os tipos sanguíneos considerados, os resultados de Bootstrap dos métodos não Gaussianos são similares sob o modelo VAR(2). Em ambos métodos observam-se valores espera-dos dado pelas trajetórias como similares ao encontrado pelo Bootstrap Gaussiano. A principal diferença entre este e os dois métodos não Gaussianos está na construção dos intervalos de con-fiança, que são mais ruidosos, em linha com o esperado. Conclui-se que ambas metodologias de Bootstrap não Gaussiano são adequadas e abordagens possíveis para melhorar a previsibilidade das séries de oferta de sangue.
Programação Dinâmica Dual
Estocástica (PDDE)
3.1 Fundamentação Teórica
Problemas de otimização estocástica buscam solucionar de forma eficiente situações reais, através de modelos matemáticos onde os parâmetros estocásticos, i.e., os parâmetros cujo valor é incerto no momento de definição das ações a serem tomadas, são representados por variáveis aleatórias. Sendo bastante comuns em diversas áreas da ciência e engenharia, esses tipos de problemas são amplamente explorados pela literatura em variadas formulações possíveis, desde problemas de inventário ([62], [23], [66]) até problemas de seleção de carteira ([5], [7], [34], [66]).
Tipicamente, um problema de otimização estocástica busca minimizar o valor esperado de uma função objetivo ao longo de um horizonte de planejamento em um espaço de probabilidade determinado. O horizonte de planejamento se divide em estágios, períodos de tempo onde os parâmetros estocásticos adquirem valores específicos para o estágio, revelando assim parte da incerteza do problema. Em problemas com múltiplos estágios, é comum representar por uma árvore de cenários o conjunto de todos os valores possíveis às variáveis aleatórias assumirem em todo o horizonte de planejamento, onde cada cenário representa uma realização possível às variáveis aleatórias ao longo dos estágios do problema. O objetivo do problema de otimização estocástica é determinar a melhor decisão a ser tomada diante da incertezas apresentadas pelas variáveis aleatórias e os vários cenários.
3.1.1 Modelos probabilísticos
Na literatura é possível encontrar diferentes métodos para abordagem do problema de otimiza-ção estocástica de forma a incorporar e tratar as incertezas, dentre eles métodos de programaotimiza-ção estocástica. A programação estocástica trata de problemas de otimização com parâmetros que assumem uma distribuição de probabilidade discreta ou contínua e pode ser dividida em Mo-delos de Recurso (recourse models) e MoMo-delos Probabilísticos (chance-constrained programming). Enquanto Modelos de Recurso ([17], [4], [66]) utilizam abordagem reativa, corrigindo viola-ções a restriviola-ções após a realização das incerteza, Modelos Probabilísticos ([14], [66]) expressam restrições de estágios futuros em termos de declarações probabilísticas sobre as decisões de pri-meiro estágio. Os modelos probabilísticos são particularmente úteis quando os custos e benefícios associados às decisões futuras são difíceis de serem avaliados.
com o modelo linear abaixo ⎧ ⎨ ⎩ min 𝑐𝑇𝑥 𝐴𝑥 ≥ 𝑏 𝑥 ≥ 0, (3.1)
onde 𝑥 ∈ R𝑛, 𝑐 ∈ R𝑛 e 𝐴 é uma matrix real 𝑚 × 𝑛.
Assume-se que 𝑐 e 𝐴 são parâmetros determinísticos e 𝑏 é um vetor aleatório com função de distribuição acumulada marginal Θ conhecida. Nesta abordagem simplista, define-se o nível de confiança 𝛼 ∈ R𝑛, de modo a reescrever a restrição 𝐴𝑥 ≥ 𝑏 como
𝑃{︀
𝑚
∑︁
𝑗=1
𝐴𝑖𝑗𝑥𝑗 ≥ 𝑏𝑖}︀ ≥ 𝛼𝑖, 𝑖 = 1,...,𝑛 (3.2)
onde P é a medida de probabilidade e 𝐴𝑖𝑗 é o elemento da i-ésima linha e j-ésima coluna da
matriz 𝐴.
Aplicando a função de distribuição acumulada de 𝑏𝑖 à restrição (3.2), esta pode ser
reformu-lada como
𝑚
∑︁
𝑗=1
𝐴𝑖𝑗𝑥𝑗 ≥ Θ−1𝑖 (𝛼𝑖), 𝑖 = 1,...,𝑛, (3.3)
onde 𝛼𝑖e Θ−1𝑖 são conhecidos. Desta forma a restrição (3.2) é reduzida a uma restrição linear
comum e o modelo probabilístico se transforma em um modelo de programação linear determi-nístico.
É também possível considerar restrições em probabilidade conjunta do tipo P(𝐴𝑥 ≥ 𝑏) com 𝐴 e 𝑏 aleatórios para o problema (3.1) ([66]). Recentemente restrições em probabilidade conjunta em modelos dinâmicos em que sequencias de decisões sob incerteza devem ser tomadas foram também propostos, ver [2], [33].
3.1.2 Programação Dinâmica Estocástica
Algoritmos de Programação Dinâmica Estocástica (Stochastic Dynamic Programming, SDP) ([38], [12], [69]) podem ser utilizados para resolver processos de decisão sequenciais. Esse tipo de algoritmo utiliza técnicas de decomposição para, como o nome sugere, decompor o problema original em subproblemas menores, permitindo assim a representação desde modelos lineares até modelos mais complexos não lineares.
Considere o problema linear abaixo ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ min 𝑥1,𝑥2 𝑐𝑇1𝑥1+ 𝑐𝑇2𝑥2 𝐴1𝑥1= 𝑏1 𝐴2𝑥2+ 𝐵2𝑥1= 𝑏2 𝑥1 ≥ 0 𝑥2 ≥ 0, (3.4)
O problema (3.4) pode ser interpretado como um processo de dois estágios, onde no primeiro estágio deve-se decidir um valor para a variável 𝑥1 que obedeça à restrição 𝐴1𝑥1 = 𝑏1 e no
se-gundo estágio se otimiza o valor da variável 𝑥2, que depende da decisão 𝑥1 tomada no primeiro
estágio e dos parâmetros 𝑐2, 𝐴2, 𝑏2, 𝐵2.
Dessa forma, o problema de primeiro estágio seria definido como ⎧ ⎪ ⎨ ⎪ ⎩ min 𝑥1 𝑐𝑇1𝑥1+ 𝒬(𝑥1) 𝐴1𝑥1 = 𝑏1 𝑥1≥ 0 (3.5) onde 𝑥1 é a variável de decisão de primeiro estágio, também chamada de variável de estado,
𝐴1, 𝑐1 e 𝑏1 são os dados associados ao problema de primeiro estágio, 𝑐𝑇1𝑥1 é o custo imediato e
𝒬(𝑥1) é a função de custo futuro e representa o valor ótimo esperado do problema de segundo estágio.
O problema de segundo estágio, por sua vez, é definido como 𝒬(𝑥1) = ⎧ ⎪ ⎨ ⎪ ⎩ min 𝑥2 𝑐𝑇 2𝑥2 𝐴2𝑥2 = 𝑏2− 𝐵2𝑥1 𝑥2≥ 0. (3.6) No caso em que o vetor 𝜉 = (𝑐2,𝐵2,𝐴2,𝑏2) dos parâmetros deste problema de segundo estágio
são aleatórios, o problema de segundo estágio depende das realizações desses parâmetros e neste caso, denotaremos por
Q(𝑥1, ˜𝜉) = ⎧ ⎪ ⎨ ⎪ ⎩ min 𝑥2 ˜ 𝑐𝑇 2𝑥2 ˜ 𝐴2𝑥2= ˜𝑏2− ˜𝐵2𝑥1 𝑥2 ≥ 0 (3.7) o custo de segundo estágio para a realização ˜𝜉 = (˜𝑐2, ˜𝐵2, ˜𝐴2,˜𝑏2))dos parâmetros aleatórios.
Aqui, assume-se que o vetor aleatório 𝜉 possui um número finito de realizações conhecidas independentes 𝜉1,...,𝜉𝑀 chamadas de cenários, cada cenário com sua respectiva probabilidade
𝑝1,...,𝑝𝑀: ∑︀𝑀𝑖=1𝑝𝑖 = 1.
Neste caso, para o problema de segundo estágio minimiza-se o valor esperado 𝒬(𝑥1) =
𝐸𝜉[Q(𝑥1,𝜉)] do custo que pode ser escrito em função do somatório
𝒬(𝑥1) = 𝑀
∑︁
𝑖=1
𝑝𝑖Q(𝑥1,𝜉𝑖) (3.8)
Assumindo o modelo discreto, pode-se reescrever (3.4) de forma a chegarmos ao modelo ⎧ ⎪ ⎨ ⎪ ⎩ min 𝑥1 𝑐𝑇 1𝑥1+∑︀𝑀𝑖=1𝑝𝑖Q(𝑥1,𝜉𝑖) 𝐴1𝑥1 = 𝑏1 𝑥1 ≥ 0 (3.9) onde Q(𝑥1,𝜉𝑖)é o valor ótimo do problema de segundo estágio para cada realização 𝑖 = 1,...,𝑀:
Q(𝑥1,𝜉𝑖) = ⎧ ⎪ ⎨ ⎪ ⎩ min 𝑥2 𝑐𝑇2𝑖𝑥2 𝐴2𝑖𝑥2 = 𝑏2𝑖− 𝐵2𝑖𝑥1 𝑥2≥ 0. (3.10) No primeiro estágio, é tomada a decisão quanto ao valor do vetor 𝑥1, antes da realização
das incertezas representadas por 𝜉 desconhecido. Para isso, minimiza-se o custo 𝑐𝑇
do valor esperado do custo do problema de segundo estágio. No segundo estágio, onde as in-formações sobre 𝜉 já estão disponíveis, é tomada a decisão sobre o valor do vetor 𝑥2, refletindo
o comportamento sob informação completa, compensando qualquer decisão inadequada tomada no primeiro estágio.
Como a decisão de primeiro estágio 𝑥1 depende apenas da informação disponível até aquele
momento (princípio de não antecipatividade), ela independe das realizações do segundo estágio e, sendo assim, o vetor 𝑥1 é o mesmo para todos os possíveis eventos que venham a ocorrer no
segundo estágio do problema ([10]).
A forma com que algoritmos de SDP solucionam o problema é através da discretização da variável de estado 𝑥1 em diversos valores de teste {ˆ𝑥1𝑖, 𝑖 = 1,...,𝑚}e da resolução do problema
(3.10) para cada valor de teste e para cada realização 𝜉𝑖. Assim, são construídas aproximações
da função de custo futuro 𝒬(𝑥1) a partir desses valores de teste e da interpolação entre valores
de teste vizinhos.
O algoritmo pode ser generalizado para o caso multiestágios. De forma equivalente a equação (3.5) do problema de dois estágios, o problema para o estágio 𝑡 = 1,...,𝑇 em um modelo de múltiplos estágios pode ser representado por
Q𝑡(𝑥𝑡−1, 𝜉𝑡) = ⎧ ⎪ ⎨ ⎪ ⎩ min 𝑥𝑡∈R𝑛 𝑐𝑇𝑡𝑥𝑡+ 𝒬𝑡+1(𝑥𝑡) 𝐴𝑡𝑥𝑡+ 𝐵𝑡𝑥𝑡−1= 𝑏𝑡 𝑥𝑡≥ 0 (3.11) onde 𝑏𝑡 e 𝑐𝑡 são vetores aleatórios, as matrizes 𝐴𝑡 e 𝐵𝑡 são aleatórias (com um número finito e
conhecido de linhas), e 𝜉𝑡é um vetor aleatório correspondendo a concatenação dos elementos das
matrizes aleatórias 𝐴𝑡 e 𝐵𝑡e dos vetores 𝑏𝑡, 𝑐𝑡.
Assume-se que 𝜉𝑡,𝑡 = 2,...,𝑇 são independentes, com distribuição discreta e suporte finito
Θ𝑡= {𝜉𝑡1,...,𝜉𝑡𝑀𝑡} e 𝜉1 é determinístico.
Neste caso, a função de custo futuro para o estágio 𝑡 − 1 é 𝒬𝑡(𝑥𝑡−1) = E𝜉
[︁
Q𝑡(𝑥𝑡−1, 𝜉𝑡)]︁, com
𝒬1(𝑥0) = Q1(𝑥0, 𝜉1). Convenciona-se que 𝒬𝑇 +1 é nulo e 𝑥0 é dado.
Por conveniência, denotaremos
𝑋𝑡(𝑥𝑡−1,𝜉𝑡) := {𝑥𝑡∈ R𝑛: 𝐴𝑡𝑥𝑡+ 𝐵𝑡𝑥𝑡−1= 𝑏𝑡, 𝑥𝑡≥ 0}. (3.12)
3.1.3 Programação Dual Dinâmica Estocástica (PDDE ou SDDP em inglês)
A estratégia dos algoritmos de SDP de aproximação das funções de custo futuro através da discre-tização das variáveis de estágio e a consideração dos múltiplos cenários das variáveis estocásticas acarreta em aumento exponencial de complexidade à medida que se acrescentam componentes nas variáveis de estado (maldição da dimensionalidade), o que impede a aplicação prática da técnica a problemas com vetores de estado de grande tamanho e muitos estágios ([58]).
Deste modo, houve a necessidade de se propor alternativas ou melhorias para solucionar a limitação do método de SDP a problemas de grande escala. Dentre os métodos propostos está o PDDE ou Stochastic Dual Dynamic Programming (SDDP) em inglês ([58]), um algoritmo de amostragem variante de técnicas de decomposição aninhada ([8], [9]) que utiliza um número finito de cenários. Consideraremos a aplicação do SDDP para resolver problemas risco neutros. Para
a extensão do método para resolver problemas envolvendo medidas de risco ver [65], [35], [36], [30]. O SDDP soluciona uma pequena parte dos cenários de uma árvore de cenários, construindo a política ótima com base em aproximações das funções de custo futuro, definidas através de funções afim construídas por hiperplanos de suporte conhecidos como cortes de Benders (ou, simplesmente, cortes). Os hiperplanos são obtidos pela solução dual do problema de otimização de cada estágio e são adicionados a função custo a cada iteração do algoritmo. Esta abordagem evita a necessidade de construção de aproximações da função custo com base em um conjunto de valores discretos das variáveis de estado, contornando a maldição da dimensionalidade do SDP. Para entender melhor o algoritmo, considere o problema (3.9), com 𝑀 cenários possíveis para o vetor aleatório 𝜉 e cada cenário com probabilidade {𝑝𝑖, 𝑖 = 1,...,𝑀 }, tal que ∑︀𝑀𝑖=1𝑝𝑖 = 1.
Pereira e Pinto demonstram que as funções de custo futuro Q(𝑥1)são construídas exatamente
por funções lineares afim (cortes). Assim, utilizando apenas uma sub-amostra de valores para 𝑥1, é possível construir cortes que podem ser utilizados no estágio anterior para prover valores da
função de custo esperada 𝒬(𝑥1) para qualquer valor de teste de 𝑥1. Para calcular esses cortes, o
algoritmo performa duas iterações principais, conhecidas como passo Forward e passo Backward. No passo Forward, um cenário para a variável aleatória é sorteado da árvore de cenários, e as decisões são tomadas com base neste cenário, começando do primeiro estágio. Nesta etapa, são calculados o valor final da função objetivo e as políticas escolhidas (pontos de teste para 𝑥1).
Após a definição de pontos de teste, o algoritmo prossegue para o passo Backward, onde se refina a política ótima sugerida adicionando um novo corte a cada estágio do problema, iniciando no último estágio e evoluindo para trás até o primeiro estágio.
Assim, a aproximação da função de custo futura é obtida pelo seguinte problema Q𝑗(𝑥1) =
{︂
min 𝑓
𝑓 ≥ 𝜋𝑖𝑗(𝑏2𝑗− 𝐸1𝑥1), 𝑖 = 1,...,𝑛 (3.13)
para todo 𝑗 = 1,...,𝑀, onde 𝜋𝑖𝑗 é o multiplicador simplex associado a restrição do problema
de segundo estágio do cenário 𝑗, calculado no ponto de teste ˆ𝑥1𝑖. Assim, dado o conjunto de
pontos de teste {𝑥1𝑖, 𝑖 = 1,...,𝑛}, é possível calcular os multiplicadores associados {𝜋𝑖𝑗, 𝑖 = 1,...,𝑛}
para todo 𝑗 = 1,...,𝑀, resolvendo (3.13) para todo 𝑗 com o conjunto de pontos de teste acima. Como a aproximação da função de custo futura obtida utiliza apenas parte da totalidade de hiperplanos de corte que definem a função de custo futuro de cada um dos M cenários, ela é o limite inferior da função de custo futuro de cada cenário, e o problema de primeiro estágio se torna
𝑧 = {︂
min 𝑐1𝑥1+ 𝒬(𝑥1)
𝐴1𝑥1 ≥ 𝑏1 (3.14)
Utilizando (3.13) podemos reescrever (3.14) como 𝑧 = ⎧ ⎨ ⎩ min 𝑐1𝑥1+ 𝑓 𝐴1𝑥1 ≥ 𝑏1 𝑓 − 𝜋𝑖𝑗(𝑏2𝑗 − 𝐸1𝑥1) ≥ 0, 𝑖 = 1,...,𝑛, 𝑗 = 1,...,𝑀 (3.15) onde a solução de (3.15) dá o limite inferior 𝑧 do custo ótimo verdadeiro, i.e., 𝑧 = 𝑐1𝑥1+ 𝑓.
Um limite inferior sobre o valor ótimo é assim definido como o custo esperado de primeiro estágio, que é a soma dos custo presente e custos esperados futuros aproximados. O limite su-perior ¯𝑧, por sua vez, é definido como a estimativa do custo esperado total obtido ao se avaliar a política ótima definida pelos cortes em diversos cenários. A proximidade estatística entre um limite inferior e superior observa a convergência entre os passos Backward e Forward, e é testada por algum tipo de critério de parada. Um candidato a critério de parada é a diferença entre ¯𝑧 e 𝑧 ser inferior a um farrafo. Caso o critério de parada não seja atendido após a realização de dados passos Forward e Backwards, deve ser feita nova iteração, determinando vértices adicionais para refinar a aproximação. Para a escolha dos pontos de teste, Pereira e Pinto sugerem simulações de Monte Carlo da amostra de cenários.
O método SDDP para problemas multiestágios pode ser vista em detalhe no algoritmo para 𝑇 estágios abaixo.
Passo Forward. A cada iteração 𝑘, o algoritmo aproxima 𝒬𝑡 por 𝒬𝑘𝑡(𝑥) = max1≤𝑗≤𝑘𝛼𝑗𝑡 +
⟨𝛽𝑡𝑗,𝑥⟩. No início de cada iteração é sorteado um cenário 𝜉𝑘
2,...,𝜉𝑘𝑇 a partir dos 𝑀 cenários
exis-tentes.
No passo Forward se resolve para 𝑡 = 1,...,𝑇 o problema 𝑧 = ⎧ ⎨ ⎩ min 𝑥𝑇𝑡𝑐𝑘𝑡 + 𝑓 𝑥𝑡∈ 𝑋𝑡(𝑥𝑘𝑡−1,𝜉𝑡𝑘) 𝑓 ≥ 𝛼𝑗𝑡+ < 𝛽𝑡+1𝑗 ,𝑥𝑡>, 𝑗 = 1,...,𝑘 − 1, (3.16) com (𝑥𝑘
0,𝜉1𝑘) = (𝑥0,𝜉1) dados e solução ótima 𝑥𝑘𝑡.
Como visto acima, no passo Forward, são calculados o valor final da função objetivo e as políticas escolhidas a cada estágio. O objetivo é determinar bons valores de teste com base nas políticas ótimas {𝑥𝑘
𝑡, 𝑡 = 1,...,𝑇 − 1}do problema (3.16). Esses valores seráo utilizados no passo
Backward seguinte do algoritmo, para gerar novo corte para aproximar a função de custo futura de cada estágio.
Na primeira iteração o algoritmo inicia tomando como pontos de teste qualquer política fac-tível, i.e., 𝑥1
𝑡 ∈ 𝑋𝑡(𝑥1𝑡−1,𝜉𝑡1).
Do passo Forward deve-se também computar a média ¯𝑧𝑁 e o desvio padrão 𝜎𝑁 do custo total
∑︀
𝑡=1,...,𝑇(𝑐𝑘𝑡)𝑇𝑥𝑘𝑡 dos últimos 𝑁 passos Forward.
Passo Backward. No passo Backward é calculado um novo corte para aproximação das funções de custo futuro.
Assim, para 𝑡 = 𝑇,...,2, resolve-se o problema abaixo para todos os cenários possíveis 𝑗 = 1, . . . ,𝑀, 𝑓𝑡𝑗𝑘 = ⎧ ⎨ ⎩ min 𝑐𝑇𝑡,𝑗𝑥𝑡+ 𝑓 𝑥𝑡∈ 𝑋𝑡(𝑥𝑘𝑡−1, 𝜉𝑡,𝑗), 𝑓 ≥ 𝛼ℓ𝑡+ ⟨𝛽𝑡+1ℓ , 𝑥𝑡⟩, ℓ = 1, . . . ,𝑘. (3.17) onde 𝛽 corresponde ao corte definido pela solução dual do problema acima. Denotando por 𝜋𝑘
𝑡𝑗
multiplicadores de Lagrange ótimos associados as restrições de igualdade para o problema acima, calculamos 𝛼𝑘𝑡 =∑︀𝑀 𝑗=1𝑝𝑡𝑗[𝑓 𝑗𝑘 𝑡 + ⟨𝐵𝑡𝑗𝑇𝜋𝑘𝑡𝑗, 𝑥𝑘𝑡−1⟩], 𝛽𝑡𝑘= ∑︀𝑀 𝑗=1𝑝𝑡𝑗𝐵𝑡𝑗𝑇𝜋𝑡𝑗𝑘. Para 𝑡 = 1, resolvemos
⎧ ⎨ ⎩ min 𝑐𝑇1𝑥𝑡+ 𝑓 𝑥1 ∈ 𝑋1(𝑥0, 𝜉1), 𝑓 ≥ 𝛼ℓ1+ ⟨𝛽ℓ2, 𝑥1⟩, ℓ = 1, . . . ,𝑘, (3.18) cujo valor ótimo é o novo limite inferior 𝑧inf da função objetivo.
Critério de parada. Há diversos critérios de parada possíveis. Uma sugestão é interromper o algoritmo quando 𝑧sup−𝑧inf
𝑧sup ≤ 0.05, onde 𝑧inf é o valor ótimo do primeiro estágio do problema
e 𝑧sup= ¯𝑧𝑁 + 1.65𝜎𝑁/
√ 𝑁.
3.1.4 Extensões do SDDP, Seleções de Corte e Algoritmos de decomposição multicortes (MuDA)
A prova de convergência do método de SDDP para problemas lineares foi feita em [61]. Diversos incrementos e extensões ao SDDP foram propostas, incluindo variantes para aversão ao risco ([35], [37], [49]), além de fórmulas de corte para problemas não lineares ([31]) e regularizações para problemas lineares ([3]) e não lineares ([34]). As provas de convergência para problemas não lineares foram feitas em [28] para problemas com neutralidade ao risco e em [31] para problemas risco-avesso.
Devido à caracterísitca do algoritmo de SDDP adicionar uma grande quantidade de cortes ao problema de otimização a cada iteração recursiva, estratégias de seleção de corte tornam-se úteis para acelerar a convergência do método. Diversas estratégias diferentes de seleção de corte já foram propostas na literatura ([64], [27]). Em [59] e [60], foi sugerida a estratégia de seleção que consistia em selecionar apenas os cortes que possuíssem o maior valor em pelo menos um dos pontos de teste computados. A estratégia é chamada de Level 1 em [60], tendo sido apresen-tada pela primeira vez em 2007 no Congresso ROADEF por David Game e Guillaume Le Roy (GDF-Suez), ver [59].
Uma outra variante possível do algoritmo clássico do SDDP adiciona múltiplos cortes a cada estágio, por iteração. Chamaremos essa técnica de Multicut Decomposition Algorithm (MuDA). Esse método possui a vantagem de diminuir a quantidade necessária de iterações para que se satisfaça o critério de parada, dado que cada iteração calcula centenas de cortes a mais que uma iteração do SDDP convencional, gerando mais rapidamente boas aproximações das funções de custo futuro. Por outro lado, a adição de cortes aumenta a complexidade de cada iteração, fazendo com que o tempo computacional despendido por iteração pode elevar o tempo total de convergência do algoritmo em relação ao SDDP convencional, mesmo com menos iterações. Para experimentos númericos ver [70].
Assim como são possíveis estratégias de seleção de corte para aceleração da convergência do método SDDP, também deveriam ser úteis estratégias de seleção de corte para MuDA. Ao aplicar seleção de cortes ao algoritmo, previne-se que cada iteração adicional resolva os subproblemas dos passos Backward e Forward com mais restrições do que o necessário, permitindo ganhos de eficiência nos cálculos de cada subproblema. Chamaremos de Cut Selection for Multicut De-composition Algorithms (CuSMuDA) os algoritmos que utilizam estratégias de seleção de corte acoplados com o método MuDA. Até o nosso conhecimento não foi proposto na literatura este tipo de combinação de técnicas.