218 Brazilian Journal of Physics, vol. 36, no. 1B, March, 2006
One-Dimensional Lattice Gas Models with Infinitely Many Absorbing States
Carlos E. Fiore and M´ario J. de Oliveira Instituto de F´ısica
Universidade de S˜ao Paulo Caixa Postal 66318
05315-970 S˜ao Paulo, S˜ao Paulo, Brazil
Received on 6 December, 2005
We determined, by numerical simulations, the critical behavior one-dimensional systems with infinitely many absorbing states. These models are modified versions of the conserved lattice gas model in which two adjacent active particles instead of just one can jump to their neighboring sites. The models studied here are examples of systems with many absorbing states and order parameter coupled to a nondiffusive conserved field that show nontrivial critical behavior.
Keywords: Self-organized criticality; Absorbing phase transitions; Many absorbing states
I. INTRODUCTION
One of the major tasks in the study of nonequilibrium phase transitions is to determine the basic ingredients that distin-guish the different universality classes. Nonequilibrium phase transitions to a unique absorbing state generically belong to the universality class of directed percolation. This conjecture has been proposed by Grassberger [1] and later extended by Grinstein et al [2]. It establishes that systems with a scalar order parameter exhibiting a continuous phase transition to a unique absorbing state generically belong to the universality class of directed percolation. Directed Percolation defines a precise universality class (described by the Reggeon field the-ory) which is very robust with respect to the introduction of microscopic modifications.
Subsequently Rossi at al [3] have proposed a new uni-versality class for the critical behavior of systems that pos-sess infinitely many absorbing states and a nondiffusive con-served field. Several models have been studied to check this new finding, as the fixed-energy sandpile (FES) models [4–6], the conservative lattice gas (CLG) model [3, 7, 8], the con-served transfer threshold process (CTTP) [3, 9] and reaction-diffusion systems [10]. More recently, the Langevin equation describing systems in which the order parameter is coupled to a conserved nondiffusive field [11] has been solved numeri-cally and the critical exponents have been determined [12, 13]. With the exception of the CLG, all models mentioned above present a nontrivial critical behavior in one dimension. The CLG model defined on a one-dimensional chain can be solved exactly [14] and shows a classical critical behavior. For in-stance, the order parameter vanishes linearly when half of the sites are occupied. In this paper, we consider three modified versions of the CLG model, two of them exhibiting nonclas-sical critical behavior, which is compatible with calculation from a Langevin equation [12, 13]. Whereas in the ordi-nary CLG models just one active particle jumps to a nearby empty site, in the modified versions two active particles jump to nearby empty sites. This process, that produces two-site instead of just one-site vacancies, together with the conserva-tion of particles enhances the creaconserva-tion of active sites specially
when the density of particles is less then but near 0.5 and may give rise to an active state for a density strictly less than 0.5.
II. MODELS
The models we have studied are defined on a chain of L sites with periodic boundary conditions. A configuration is specified by the occupation variableηithat assumes the value ηi=0 if the site i is empty andηi=1 if the site i is occupied
by a particle. Double or multiple occupancies are forbidden. Isolated particles (particles with empty next-nearest-neighbor sites) are inactive and do not move. Adjacent sites occupied by particles are active and repel each other via repulsive short-range interactions. As a product of this interaction, the two active particles may jump to their neighborhoods. The contin-uous time Markovian dynamics consists of a series of repul-sions events in active states.
Differently from the dynamics of the CLG model, in which just one particle jumps at each time step, in the present models both adjacent active particles may jump to their neighboring sites. Three versions are studied that are called model 1, 2 and 3, which differ by their neighborhood. In model 1 the neigh-borhood is composed by the first-neighbor site only. In model 2, by the first and second neighboring sites, and in model 3, by the first, second and third neighboring sites. In addition, the neighborhood of the right (left) particle is at its right (left). If there are n empty site in the neighborhood, the jumping prob-ability to an empty site equals 1/n. If all sites of the neighbor-hood are occupied the particle remains at its place. In model 2, we have also considered a simpler model that consists in for-bidding jumps to the second nearest-neighbor site when n=1. Thus, in this model, for n=1, active sites can only jump to their first nearest-neighbor site.
In all models studied here, the number of particles is con-served and the density of particlesρworks as the control para-meter. In the regime of small densities, the system falls in one of its many absorbing states (without repulsions). Increasing the density of particles, a phase transition takes place to the active state (with repulsions) at the critical densityρc. The
Carlos E. Fiore and M´ario J. de Oliveira 219
0.445 0.45 0.455 0.46 0.465 0.47
ρ 0
0.04 0.08 0.12
ρ p
L=1000 L=2000 L=4000 L=8000
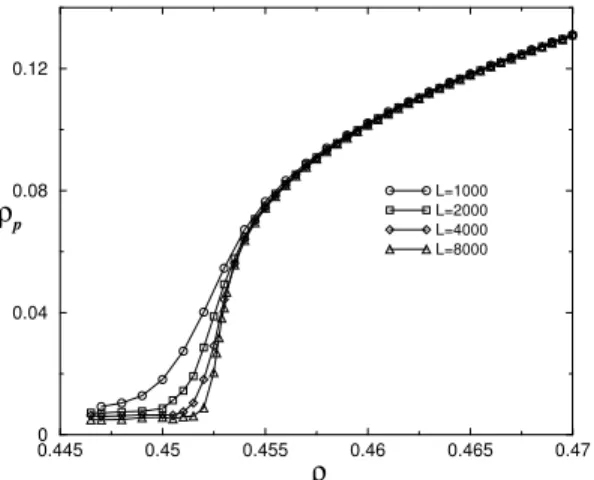
FIG. 1: Pair densityρpof model 2 as a function of particle densityρ
for several values of the system size L.
ρac. In actual calculation, we have used the density of pairs of
adjacent particlesρpdefined as the average
ρp= Np
L , (1)
where Npis the total number of adjacent particles.
III. METHODS
To locate the critical densityρcfor these models, we have
used three different methods. The first one consists in deter-mining the critical density by seeking a power-law behavior of the order parameter on the system size L. For sufficient large systems L and close to the critical point, finite-size scal-ing [15] establishes that the order parameter may be written in the form
ρp(∆,L) =L−β/νR(L1/ν∆), (2)
where∆≡ρ−ρcand the scaling function R(x)∼xβ, for large
x, since the behavior of the order parameter in this limit is given by [15]
ρp∼∆β. (3)
In the models studied where the tuning parameter is the den-sity of particles, we can only changeρin increments of 1/L. To get around this restriction, values ofρp for densities
be-tween those accessible for a given L were obtained via inter-polation.
A second criterion used to locate the critical point consists in determining the order parameter moment ratio m(ρ,L) =
N2
p/Np2. According to finite size scaling, m(ρ,L)obeys
the scaling relation
m(ρ,L) =φ(L1/ν∆), (4)
0.415 0.42 0.425 0.43 0.435
ρ 0
0.02 0.04 0.06 0.08 0.1
ρp
L=1000 L=2000 L=4000 L=8000
FIG. 2: Pair densityρpfor model 3 as a function of particle density
ρfor several values of the system size L.
whereφ(x)is a universal function. This criterion is very useful to determine the transition because it is invariant with respect to the system size L at the critical point.
A third criterion to locate the critical point consists in per-forming time-dependent simulations. This approach consists in studying the evolution of the system over a large number of independent trials (we have used from 5000 to 8000 trials), always starting with an initial configuration very close to an absorbing state with only a pair of particles. Each indepen-dent trial consists in choosing a different particle to become active and the system evolutes until a maximum time tM. At
each regular interval, we average the number of active pairs np=Npand the survival probability Ps(t) (defined as the
probability in each time unity the system does not reach the absorbing state). For long times in the critical point these vari-ables display power-law behavior, given by
np(t)∼tη, (5)
and
Ps(t)∼t−δ. (6)
In off-critical regimes (supercritical and subcritical) we ex-pect deviations from this power law behavior. Thus, this cri-terion is useful to locate the critical point.
IV. NUMERICAL RESULTS
220 Brazilian Journal of Physics, vol. 36, no. 1B, March, 2006
6 7 8
lnL
−3.6 −3.2 −2.8
ln
ρp
0.4525 0.4526 0.45265 0.4527 0.4528 0.453
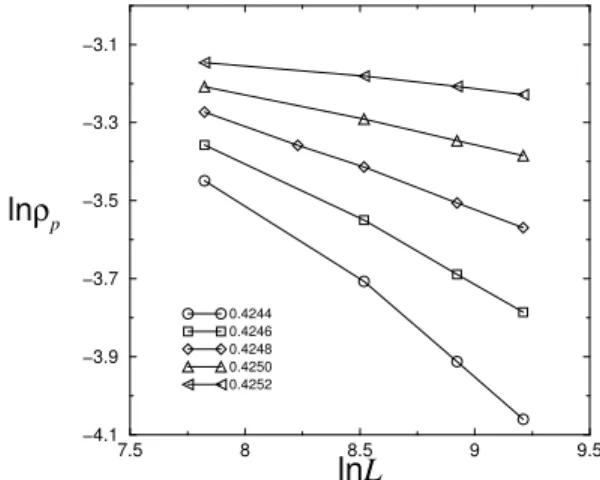
FIG. 3: Pair densityρpversus system size L for model 2, for various
values of the particle density.
steps. A Monte Carlo step occurs when all active sites on av-erage are visited. For these models, we did not permit that the system fall into the absorbing state by maintaining at least an active site.
The phase transition for model 1 occurs atρc=1/2 and
was found to be discontinuous with a jump equal to 0.125. For models 2 and 3, the transition is continuous. In Figs. 1 and 2, we show the behavior of the order parameter versus the density of particles for several values of the system size L. To locate the critical point we have used three methods as mentioned above. Using the cumulant method for lattices L=4000 and L=8000 the crossings occur atρc=0.4527(1)
and ρc=0.42475(5) for models 2 and 3 respectively. We
have also performed log-log plots ofρp versus L for several
values ofρ, as shown in Fig. 3 for model 2, and in Fig. 4 for model 3, to verify the dependence of the order parameter on the lattice size. Using this criterion we findρc=0.45270(5)
andβ/ν=0.223(5)for model 2. For model 3, considering the critical densityρc=0.4248, we obtained the critical
ex-ponentβ/ν=0.213(4), which agrees with the value obtained for model 2. It also agrees with the valueβ/ν=0.217(9)
obtained by Ramasco [12].
After obtaining the critical density, we used the values of
ρcto calculate the critical exponentsβ. In Figs. 5 and 6, we
have a log-log plot ofρpversus∆in the supercritical regime.
The slope of the straight line fitted to the data point for L=
8000 leads toβ=0.277(3), for model 2, andβ=0.278(2)for model 3.
We have also performed time-dependent simulations for models 2 and 3 to determine the exponentsδandηby means of equations (5) and (6).
¿From the power law behavior we found values forρcthat
are in agreement with the other methods. The following re-sults are found: δ=0.13(1) andη=0.36(2), for model 2, andδ=0.13(1)andη=0.33(3), for model 3. To calculate the averages at each time we have used from 5000 to 8000 trials on a lattice of size L=2000. For comparison we have used a different way to determine the exponentδfor model
7.5 8 8.5 9 9.5
lnL
−4.1−3.9 −3.7 −3.5 −3.3 −3.1
ln
ρ
p0.4244 0.4246 0.4248 0.4250 0.4252
FIG. 4: Pair densityρpversus system size L for model 3, for various
values of the particle density.
−8 −7 −6 −5 −4
ln∆ −3
−2.5 −2
ln
ρp
L=1000 L=2000 L=4000 L=8000
FIG. 5: Pair densityρpas function of∆≡ρ−ρcfor values of
sys-tem size L ranging from 1000 to 8000 in the supercritical regime for model 2.
−8 −7 −6 −5 −4
ln∆ −3.3
−2.8 −2.3
ln
ρp
L=1000 L=2000 L=4000 L=8000
FIG. 6: Pair densityρpas function of∆≡ρ−ρcfor values of
Carlos E. Fiore and M´ario J. de Oliveira 221
4 7 10 13
lnt −3.6
−3.2 −2.8 −2.4
ln
ρp
0.4255
0.4251
0.4248
0.4240
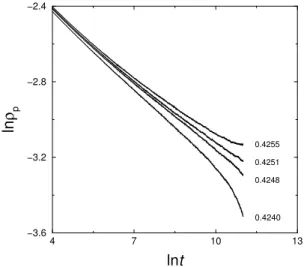
FIG. 7: Decay of the pair densityρpfor model 3 as function of time
for several values of the particle densityρand for L=10000.
3. In this approach, the density of pairsρp of particles was
measured as a function of time starting from a configuration obtained by distributing N particles randomly. At the critical point it behaves as [15]
ρp∼t−δ. (7)
The average pair density was calculated by using 5000 trials in a lattice of size L=10000. The data are shown in Fig. 7, from which we obtainδ=0.120(5), which is in fair agreement with the above result.
The critical exponents obtained for model 2 are presented in Table I. For comparison we also show in the same table the exponents obtained by Ramasco et al [12] and Dornic et al [13] for systems in which the order parameter is coupled
to a conserved nondiffusive field. The DP universality class exponents are also shown. The result forβ is close to the DP exponent as well as to the result obtained by Ramasco et al [12]. The values of the other exponents in Table I are, however, far from the DP values. The values forβ/νand for
ηare close to the results by Ramasco et al [12] and that ofδ
is very close to that found by Dornic et al [13].
TABLE I: Critical exponents of model 2 compared with results com-ing from the Langevin approach for systems with order parameter coupled to a conserved nondiffusive field [12, 13] and DP universal-ity class exponents [15] in one dimension.
β β/ν δ η Obs.
0.277(3) 0.223(5) 0.13(1) 0.36(2) model 2 0.29(2) 0.217(9) 0.140(5) 0.365(10) [12]
0.125(2) [13] 0.2765 0.2521 0.1595 0.3137 DP [15]
V. CONCLUSION
We have presented simple one-dimensional systems with infinitely many absorbing states and conserved particle num-ber that possess a non trivial critical behavior. These models are modified versions of the original CLG model. In model 1 the phase transition is discontinuous. The exponents deter-mined numerically for models 2 and 3 are in agreement with results by Ramasco et al [12] and by Dornic et al [13] for a one-dimensional system with the order parameter coupled to a conserved nondiffusive field.
Acknowledgment
C. E. F. acknowledges the financial support from Fundac¸˜ao de Amparo `a Pesquisa do Estado de S˜ao Paulo (FAPESP) un-der Grant No. 03/01073-0.
[1] P. Grassberger, Z. Phys. B 47, 365 (1982).
[2] G. Grinstein, Z.-W. Lai, and D. A. Browne, Phys. Rev. A 40, 4820 (1989).
[3] M. Rossi, R. Pastor-Satorras, and A. Vespignani, Phys. Rev. Lett. 85, 1803 (2000).
[4] R. Dickman, M. A. Mun˜oz, A. Vespignani, and S. Zaperi, Braz. J. Phys. 30, 27 (2000).
[5] A. Vespignani, R. Dickman, M. A. Mun ˜oz, and S. Zaperi, Phys. Rev. E 62, 4564 (2000).
[6] R. Dickman, T. Tom´e, and M. J. de Oliveira, Phys. Rev. E 66, 016111 (2002).
[7] S. L¨ubeck, Phys. Rev. E 64, 016123 (2001). [8] S. L¨ubeck and, Phys. Rev. E 68, 056102 (2003).
[9] S. L¨ubeck and P. C. Heger, Phys. Rev. E 66, 046114 (2002).
[10] R. Pastor-Satorras and A. Vespignani, Phys. Rev. E 62, R5875 (2000).
[11] A. Vespignani, R. Dickman, M. A. Mu ˜noz, and S. Zapperi, Phys. Rev. Lett. 81, 5676 (1998).
[12] J. J. Ramasco, M. A. Mun˜oz, and C. A. D. Santos, Phys. Rev. E 69, 045105 (2004).
[13] I. Dornic, H. Chat´e, and M. Mu˜noz, Phys. Rev. Lett. 94, 1000601 (2005).
[14] M. J. de Oliveira, Phys. Rev. E 71, 016112 (2005).