UNIVERSIDADE DE LISBOA FACULDADE DE CI ˆENCIAS
DEPARTAMENTO DE ESTAT´ISTICA E INVESTIGAC¸ ˜AO OPERACIONAL
Modelos para o Problema do Caixeiro Viajante Consistente
Mafalda Coutinho de Ponte
MESTRADO EM ESTAT´ISTICA E INVESTIGAC¸ ˜AO OPERACIONAL Especializac¸˜ao em Investigac¸˜ao Operacional
Dissertac¸˜ao orientada por:
Professor Doutor Lu´ıs Eduardo Neves Gouveia Professora Doutora Ana Maria Duarte Silva Alves Paias
Agradecimentos
Em primeiro lugar gostaria de agradecer aos meus orientadores, o Professor Doutor Lu´ıs Eduardo Neves Gouveia e a Professora Doutora Ana Maria Duarte Silva Alves Paias, por toda a disponibilidade, apoio e partilha de confianc¸a, que foram indispens´aveis `a elaborac¸˜ao da presente dissertac¸˜ao.
N˜ao menos importante, devo um agradecimento `a minha fam´ılia, em especial aos meus pais, pela educac¸˜ao que me proporcionaram, e por todo o apoio e motivac¸˜ao concedidos.
Esta dissertac¸˜ao foi financiada por fundos nacionais da FCT - Fundac˜ao para a Ciˆencia e a Tecnologia, ao abrigo do projecto: PTDC/MAT-NAN/2196/2014.
Resumo
Vamos considerar um conjunto de per´ıodos, dias por exemplo, que comp˜oem um horizonte temporal e um conjunto de clientes que tˆem que ser visitados em pelo menos um per´ıodo. Para cada per´ıodo deve ser gerada uma rota. Pretende-se determinar o conjunto de rotas de custo m´ınimo, todas com in´ıcio e fim num dep´osito, que permitem visitar todos os clientes nos per´ıodos em que estes requerem visita, e que garantem que os clientes que requerem consistˆencia ocupam posic¸˜oes relativas suficientemente pr´oximas em todas as rotas em que est˜ao inseridos. S˜ao conhecidos os custos de deslocac¸˜ao entre cada para de clientes e entre cada cliente e o dep´osito, quais os clientes a servir em cada per´ıodo e quais os clientes que requerem consistˆencia. Este problema resulta de uma adaptac¸˜ao do Consistent Travelling Salesman Problem(CTSP).
O CTSP constitui-se uma extens˜ao do TSP. Consequentemente, pertence `a classe de problemas NP-dif´ıcil.
No estudo realizado na presente dissertac¸˜ao foram comparados dois modelos principais. Um dos mo-delos resulta da adaptac¸˜ao do Modelo de Fluxos Agregados (MFA), e outro resulta da adaptac¸˜ao do modelo proposto por Picard e Queyranne (PQ). A utilizac¸˜ao de desigualdades v´alidas para fortalecer as relaxac¸˜oes lineares destes dois modelos permitiu construir outros dois modelos: o Modelo de Fluxos Agregados Forte (MFA Forte) e o Modelo de Picard e Queyranne Forte (PQ Forte). Numa primeira fase foram provadas v´arias relac¸˜oes relativamente `a qualidade das relaxac¸˜oes lineares dos quatro mo-delos. Numa segunda fase os modelos foram comparados com base nos resultados de uma experiˆencia computacional.
Para realizar a experiˆencia computacional foram geradas aleatoriamente 180 instˆancias de teste. Estas instˆancias podem considerar 20 ou 30 clientes, e 2 ou 3 per´ıodos, e diferem entre si quanto ao n´umero de clientes que tˆem que ser visitados em cada per´ıodo e o n´umero de clientes sujeito a restric¸˜oes de consistˆencia. A experiˆencia computacional permitiu avaliar n˜ao s´o a qualidade da relaxac¸˜ao linear de cada modelo, mas tamb´em o desempenho computacional dos modelos em estudo.
Palavras-chave: Algoritmos exatos; Traveling Salesman Problem; Consistˆencia
Abstract
We will suppose that we have a set of periods, days for instance, composing a time horizon, and a set of customers who need to be visited in at least one of those periods. For each period we need to generate a route. Our goal is to determine a minimum cost set of routes, all of those starting and finishing at a depot, such that every costumer is visited in all the periods he must be visited, ensuring that all customers requiring consistency are visited in similar relative positions in all the routes they are inserted in. All the travel costs between any pair of customers or any customer and the depot are known, as well as which customers must be visited in each period and which customers require consistency. The aforementioned problem is a variant of the Consistent Traveling Salesman Problem (CTSP).
The CTSP is an extension of the TSP. Consequently, it belongs to the class of NP-hard problems. In the study developed in this thesis two main models were compared. One of them results from adapting the Aggregated Flow Model (MFA), the second one was adapted from Picard and Queyranne Model (PQ). Using valid inequalities to strengthen the bounds provided by linear relaxations allowed us to build two other models: Strong Aggregated Flow Model (MFA Forte) and Strong Picard and Queyranne Model (PQ Forte). Firstly we were able to prove some relations concerning the quality of each model’s linear relaxation. Finally, a computational experiment was performed in order to compare the four models’ performance.
In order to carry out the computational experiment 180 instances were randomly generated. Such in-stances may consider 20 or 30 customers, as well as 2 or 3 periods. They may also differ in the number of customers to visit in each period and the number of customers subject to consistency restrictions. This experiment allowed us to evaluate not only the quality of each model’s linear relaxation, but also the four models’ computational performance.
Keywords: Exact Algorithms; Traveling Salesman Problem; Consistency
´Indice
Lista de Figuras ix
Lista de Tabelas xi
Lista de Siglas xv
1 Introduc¸˜ao 1
2 Problema do Caixeiro Viajante Consistente 3
2.1 Descric¸˜ao do Problema . . . 3
2.2 Revis˜ao Bibliogr´afica . . . 4
2.2.1 Period Traveling Salesman Problem . . . 4
2.2.2 Time-Dependent Traveling Salesman Problem . . . 5
2.2.3 Sincronizac¸˜ao e Consistˆencia . . . 6
3 Modelos 9 3.1 Definic¸˜ao do problema . . . 9
3.2 Formulac¸˜oes . . . 10
3.2.1 Modelo de Fluxos Agregados . . . 12
3.2.2 Modelo de Picard e Queyranne . . . 15
4 Experiˆencia Computacional 23 4.1 Gerac¸˜ao das Instˆancias de Teste . . . 23
4.2 Resultados Obtidos . . . 26
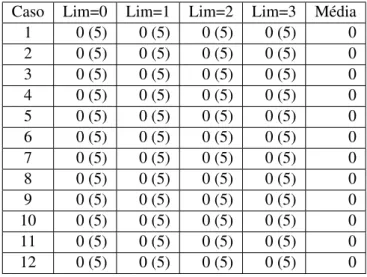
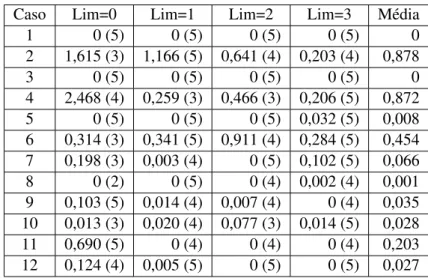
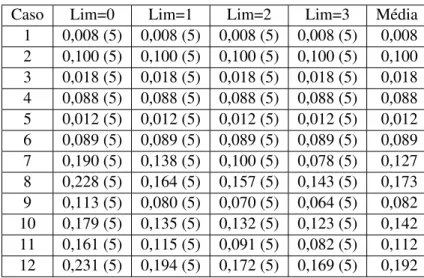
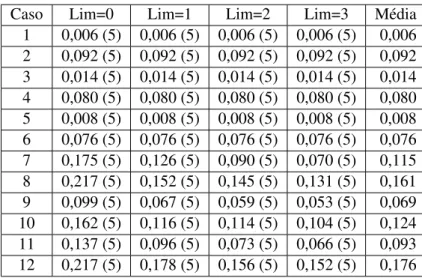
4.2.1 Desempenho Computacional . . . 27
4.2.2 Qualidade dos Limites . . . 35
4.3 Comparac¸˜ao dos Modelos . . . 45
4.3.1 Desempenho Computacional . . . 45
4.3.2 Qualidade dos Limites . . . 49
5 Conclus˜ao 55
Bibliografia 57
Lista de Figuras
3.1 Soluc¸˜ao n˜ao admiss´ıvel devido `as restric¸˜oes de consistˆencia . . . 10
3.2 Soluc¸˜ao admiss´ıvel . . . 11
3.3 Soluc¸˜ao n˜ao admiss´ıvel devido aos per´ıodos em que o servic¸o deve ser realizado . . . 11
3.4 Relac¸˜oes entre as relaxac¸˜oes lineares dos modelos propostos . . . 22
4.1 Esquema da distribuic¸˜ao dos nodos clientes quando m=2 . . . 23
4.2 Esquema da distribuic¸˜ao dos clientes quando m=3 . . . 25
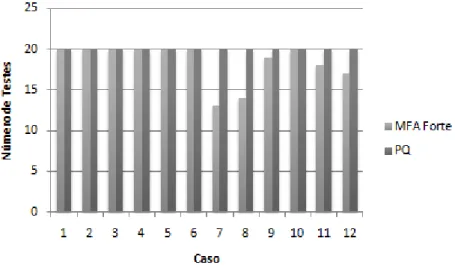
4.3 N´umero de testes que obtiveram a soluc¸˜ao ´otima, por caso e por modelo (m = 2 e n = 20) 45 4.4 N´umero de testes que obtiveram a soluc¸˜ao ´otima, por valor de Lim e por modelo (m = 2 e n = 20) . . . 45
4.5 N´umero de testes que obtiveram a soluc¸˜ao ´otima, por caso e por modelo (m = 2 e n = 30) 46 4.6 N´umero de testes que obtiveram a soluc¸˜ao ´otima, por valor de Lim e por modelo (m = 2 e n = 30) . . . 46
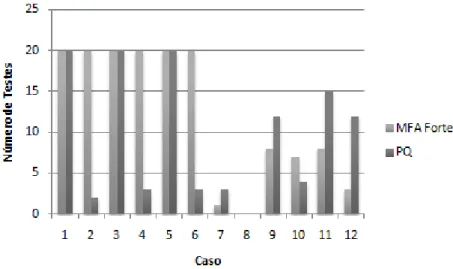
4.7 N´umero de testes que obtiveram a soluc¸˜ao ´otima, por caso e por modelo (m = 3 e n = 20) 46 4.8 N´umero de testes que obtiveram a soluc¸˜ao ´otima, por valor de Lim e por modelo (m = 3 e n = 20) . . . 47
4.9 M´edias dos tempos de processamento (segundos) para os problemas inteiros, por caso e por modelo (m = 2 e n = 20) . . . 47
4.10 M´edias dos tempos de processamento (segundos) para os problemas inteiros, por caso e por modelo (m = 2 e n = 30) . . . 48
4.11 M´edias dos tempos de processamento (segundos) para os problemas inteiros, por caso e por modelo (m = 3 e n = 20) . . . 48
4.12 M´edias dos tempos de execuc¸˜ao (segundos) das relaxac¸˜oes lineares, por caso e por mo-delo (m = 2 e n = 20) . . . 49
4.13 M´edias dos tempos de execuc¸˜ao (segundos) das relaxac¸˜oes lineares, por caso e por mo-delo (m = 2 e n = 30) . . . 49
4.14 M´edias dos tempos de execuc¸˜ao (segundos) das relaxac¸˜oes lineares, por caso e por mo-delo (m = 3 e n = 20) . . . 50
4.15 M´edias dos tempos de execuc¸˜ao (segundos) das relaxac¸˜oes lineares, por caso e por mo-delo (m = 3 e n = 30) . . . 50
4.16 M´edias dos valores da medida de desempenho dist, por caso e por modelo (m = 2 e n = 20) . . . 51
4.17 M´edias dos valores da medida de desempenho dist, por caso e por modelo (m = 2 e n = 30) . . . 51 4.18 M´edias dos valores da medida de desempenho dist, por caso e por modelo (m = 3 e
n = 20) . . . 52 4.19 M´edias dos valores do gap da Relaxac¸˜ao Linear, por caso e por modelo (m = 2 e n = 20) 52 4.20 M´edias dos valores do gap da Relaxac¸˜ao Linear, por caso e por modelo (m = 2 e n = 30) 52 4.21 M´edias dos valores do gap da Relaxac¸˜ao Linear, por caso e por modelo (m = 3 e n = 20) 53 4.22 M´edias dos valores do gap da Relaxac¸˜ao Linear, por caso e por modelo (m = 3 e n = 30) 53
Lista de Tabelas
4.1 Gerac¸˜ao das instˆancias de teste quando n = 20 e m = 2 . . . 24 4.2 Gerac¸˜ao das instˆancias de teste quando n = 20 e m = 3 . . . 25 4.3 M´edias dos tempos de execuc¸˜ao (segundos) dos problemas inteiros - Modelo de Fluxos
Agregados Forte (m = 2 e n = 20) . . . 27 4.4 M´edias dos tempos de execuc¸˜ao (segundos) dos problemas inteiros - Modelo de Fluxos
Agregados Forte (m = 2 e n = 30) . . . 28 4.5 M´edias dos tempos de execuc¸˜ao (segundos) dos problemas inteiros - Modelo de Fluxos
Agregados Forte (m = 3 e n = 20) . . . 28 4.6 M´edias dos tempos de execuc¸˜ao (segundos) dos problemas inteiros - Modelo de Picard e
Queyranne (m = 2 e n = 20) . . . 28 4.7 M´edias dos tempos de execuc¸˜ao (segundos) dos problemas inteiros - Modelo de Picard e
Queyranne (m = 2 e n = 30) . . . 29 4.8 M´edias dos tempos de execuc¸˜ao (segundos) dos problemas inteiros - Modelo de Picard e
Queyranne (m = 3 e n = 20) . . . 29 4.9 M´edias dos tempos de execuc¸˜ao (segundos) dos problemas inteiros - Modelo de Picard e
Queyranne (m = 3 e n = 30) . . . 29 4.10 M´edias dos tempos de execuc¸˜ao (segundos) dos problemas inteiros - Modelo de Picard e
Queyranne Forte (m = 2 e n = 20) . . . 30 4.11 M´edias dos tempos de execuc¸˜ao (segundos) dos problemas inteiros - Modelo de Picard e
Queyranne Forte (m = 2 e n = 30) . . . 30 4.12 M´edias dos tempos de execuc¸˜ao (segundos) dos problemas inteiros - Modelo de Picard e
Queyranne Forte (m = 3 e n = 20) . . . 30 4.13 M´edias dos tempos de execuc¸˜ao (segundos) das Relaxac¸˜oes Lineares - Modelo de Fluxos
Agregados Forte (m = 2 e n = 20) . . . 31 4.14 M´edias dos tempos de execuc¸˜ao (segundos) das Relaxac¸˜oes Lineares - Modelo de Fluxos
Agregados Forte (m = 2 e n = 30) . . . 32 4.15 M´edias dos tempos de execuc¸˜ao (segundos) das Relaxac¸˜oes Lineares - Modelo de Fluxos
Agregados Forte (m = 3 e n = 20) . . . 32 4.16 M´edias dos tempos de execuc¸˜ao (segundos) das Relaxac¸˜oes Lineares - Modelo de Fluxos
Agregados Forte (m = 3 e n = 30) . . . 32 4.17 M´edias dos tempos de execuc¸˜ao (segundos) das Relaxac¸˜oes Lineares - Modelo de Picard
e Queyranne (m = 2 e n = 20) . . . 33 xi
4.18 M´edias dos tempos de execuc¸˜ao (segundos) das Relaxac¸˜oes Lineares - Modelo de Picard e Queyranne (m = 2 e n = 30) . . . 33 4.19 M´edias dos tempos de execuc¸˜ao (segundos) das Relaxac¸˜oes Lineares - Modelo de Picard
e Queyranne (m = 3 e n = 20) . . . 33 4.20 M´edias dos tempos de execuc¸˜ao (segundos) das Relaxac¸˜oes Lineares - Modelo de Picard
e Queyranne (m = 3 e n = 30) . . . 34 4.21 M´edias dos tempos de execuc¸˜ao (segundos) das Relaxac¸˜oes Lineares - Modelo de Picard
e Queyranne Forte (m = 2 e n = 20) . . . 34 4.22 M´edias dos tempos de execuc¸˜ao (segundos) das Relaxac¸˜oes Lineares - Modelo de Picard
e Queyranne Forte (m = 2 e n = 30) . . . 34 4.23 M´edias dos tempos de execuc¸˜ao (segundos) das Relaxac¸˜oes Lineares - Modelo de Picard
e Queyranne Forte (m = 3 e n = 20) . . . 35 4.24 M´edias dos tempos de execuc¸˜ao (segundos) das Relaxac¸˜oes Lineares - Modelo de Picard
e Queyranne Forte (m = 3 e n = 30) . . . 35 4.25 M´edias das medidas de desempenho var - Modelo de Fluxos Agregados Forte (m = 2 e
n = 20) . . . 36 4.26 M´edias das medidas de desempenho var - Modelo de Fluxos Agregados Forte (m = 2 e
n = 30) . . . 36 4.27 M´edias das medidas de desempenho var - Modelo de Fluxos Agregados Forte (m = 3 e
n = 20) . . . 37 4.28 M´edias das medidas de desempenho dist - Modelo de Fluxos Agregados Forte (m = 2
e n = 20) . . . 37 4.29 M´edias das medidas de desempenho dist - Modelo de Fluxos Agregados Forte (m = 2
e n = 30) . . . 38 4.30 M´edias das medidas de desempenho dist - Modelo de Fluxos Agregados Forte (m = 3
e n = 20) . . . 38 4.31 M´edias das medidas de desempenho dist - Modelo de Picard e Queyranne (m = 2 e
n = 20) . . . 38 4.32 M´edias das medidas de desempenho dist - Modelo de Picard e Queyranne (m = 2 e
n = 30) . . . 39 4.33 M´edias das medidas de desempenho dist - Modelo de Picard e Queyranne (m = 3 e
n = 20) . . . 39 4.34 M´edias das medidas de desempenho dist - Modelo de Picard e Queyranne Forte (m = 2
e n = 20) . . . 39 4.35 M´edias das medidas de desempenho dist - Modelo de Picard e Queyranne Forte (m = 2
e n = 30) . . . 40 4.36 M´edias das medidas de desempenho dist - Modelo de Picard e Queyranne (m = 3 e
n = 20) . . . 40 4.37 M´edias do gap da Relaxac¸˜ao Linear - Modelo de Fluxos Agregados Forte (m = 2 e
n = 20) . . . 41 xii
4.38 M´edias do gap da Relaxac¸˜ao Linear - Modelo de Fluxos Agregados Forte (m = 2 e n = 30) . . . 41 4.39 M´edias do gap da Relaxac¸˜ao Linear - Modelo de Fluxos Agregados Forte (m = 3 e
n = 20) . . . 42 4.40 M´edias do gap da Relaxac¸˜ao Linear - Modelo de Fluxos Agregados Forte (m = 3 e
n = 30) . . . 42 4.41 M´edias do gap da Relaxac¸˜ao Linear - Modelo de Picard e Queyranne (m = 2 e n = 20) 42 4.42 M´edias do gap da Relaxac¸˜ao Linear - Modelo de Picard e Queyranne (m = 2 e n = 30) 42 4.43 M´edias do gap da Relaxac¸˜ao Linear - Modelo de Picard e Queyranne (m = 3 e n = 20) 43 4.44 M´edias do gap da Relaxac¸˜ao Linear - Modelo de Picard e Queyranne (m = 3 e n = 30) 43 4.45 M´edias do gap da Relaxac¸˜ao Linear - Modelo de Picard e Queyranne Forte (m = 2 e
n = 20) . . . 43 4.46 M´edias do gap da Relaxac¸˜ao Linear - Modelo de Picard e Queyranne Forte (m = 2 e
n = 30) . . . 43 4.47 M´edias do gap da Relaxac¸˜ao Linear - Modelo de Picard e Queyranne Forte (m = 3 e
n = 20) . . . 44 4.48 M´edias do gap da Relaxac¸˜ao Linear - Modelo de Picard e Queyranne Forte (m = 3 e
n = 30) . . . 44
Lista de Siglas
CTSP - Consistent Traveling Salesman Problem MFA - Modelo de Fluxos Agregados
PLIM - Programac¸˜ao Linear Inteira Mista PQ - Picard e Queyranne
PTSP - Period Traveling Salesman Problem RL - Relaxac¸˜ao Linear
TDTSP - Time-Dependent Traveling Salesman Problem TSP - Traveling Salesman Problem
VRP - Vehicle Routing Problem
Cap´ıtulo 1
Introduc¸˜ao
A gest˜ao e o planeamento de rotas assumem um papel essencial numa grande variedade de contextos. Para al´em dos casos mais ´obvios, como a distribuic¸˜ao de jornais e o transporte de crianc¸as, temos tamb´em a patrulha de seguranc¸a, e a ordenac¸˜ao de tarefas de maquinaria como sendo alguns dos in´umeros exem-plos de aplicac¸˜ao destas t´ecnicas `a tomada de decis˜ao.
Muitas vezes, mais do que planear uma ´unica rota, pretende-se planear todo um conjunto de rotas. Esta situac¸˜ao pode dever-se a dois motivos. Em primeiro lugar, podemos ter dispon´ıvel um conjunto de agentes ou ve´ıculos, cuja atividade queremos otimizar. Por outro lado, podemos ter apenas um ve´ıculo ou agente, mas pretendermos otimizar a sua atividade para um horizonte temporal composto por mais do que um per´ıodo.
Adicionalmente, podem existir quest˜oes de consistˆencia das rotas. Desta consistˆencia podem advir di-versos benef´ıcios. Para um condutor, por exemplo, a consistˆencia pode traduzir-se numa maior previsi-bilidade das diferentes rotas, o que resulta numa melhor eficiˆencia. Do ponto de vista do cliente, o facto de ser sempre servido pelo mesmo agente pode redundar num servic¸o mais personalizado, o que leva a uma maior satisfac¸˜ao do consumidor. Por fim, a consistˆencia temporal pode ser tamb´em uma forma de aumentar a satisfac¸˜ao do consumidor, ou mesmo um pr´e-requisito do pr´oprio servic¸o. A t´ıtulo ilustrativo, num hospital podem existir pacientes que tˆem que realizar um dado tratamento todos os dias `a mesma hora.
´
E neste contexto que surge o Problema do Caixeiro Viajante Consistente (Consistent Travelling Salesman Problem- CTSP). Neste problema temos um conjunto de clientes que tˆem que ser visitados uma ou mais vezes durante um horizonte temporal de m per´ıodos, de agora em diante designados por dias. Alguns dos clientes que s˜ao visitados em mais do que um dia possuem restric¸˜oes de consistˆencia, ou seja, nalguns ou mesmo em todos os dias em que s˜ao visitados, tˆem que o ser `a mesma hora, ou em horas suficientemente pr´oximas.
O presente documento tem como objetivo o estudo de uma adaptac¸˜ao do CTSP. A primeira diferenc¸a diz respeito `as restric¸˜oes de consistˆencia. Embora a forma mais ´obvia de garantir a consistˆencia tem-poral seja a criac¸˜ao de restric¸˜oes de consistˆencia que tenham em conta a hora de chegada do ve´ıculo a cada cliente, iremos construir estas restric¸˜oes apenas com base na consistˆencia da ordem relativa em que cada cliente ´e visitado em cada um dos circuitos. Mesmo esta consistˆencia n˜ao ser´a sempre abso-luta, na medida em que n˜ao ser´a obrigat´orio que um cliente ocupe sempre a mesma posic¸˜ao, mas sim
Cap´ıtulo 1. Introduc¸˜ao 2
posic¸˜oes suficientemente parecidas. Por outras palavras, teremos um limite superior pr´e-definido para as diferenc¸as entre posic¸˜oes. N˜ao estaremos a usar uma condic¸˜ao suficiente para garantir a consistˆencia temporal, mas este tipo de condic¸˜ao j´a constitui um primeiro passo na compreens˜ao e resoluc¸˜ao deste problema. A segunda adaptac¸˜ao prende-se com o facto de admitirmos que para al´em de conhecermos o n´umero de visitas que tˆem que ser feitas a cada cliente, tamb´em conhecemos exatamente os dias em que tais visitas tˆem de ocorrer, pelo que n˜ao existe o esforc¸o adicional para determinar a distribuic¸˜ao dos clientes pelos circuitos.
No ˆambito desta dissertac¸˜ao pretende-se estudar uma abordagem exata na resoluc¸˜ao do problema apre-sentado. Para o efeito ser˜ao propostos e comparados dois modelos de Programac¸˜ao Linear Inteira Mista (PLIM): o primeiro resulta da adaptac¸˜ao do Modelo de Fluxos Agregados (MFA), enquanto o segundo se baseia no Modelo de Piccard e Queyranne (PQ). Ser´a ainda proposto um conjunto de restric¸˜oes adici-onais com vista a fortalecer as relaxac¸˜oes lineares destes modelos. O desempenho de ambos os modelos ser´a avaliado com base na qualidade dos limites inferiores obtidos com as respetivas relaxac¸˜oes lineares e no tempo de execuc¸˜ao necess´ario para a resoluc¸˜ao do problema at´e `a otimalidade. Para o efeito foi utilizado o software FICO XPRESS.
Ap´os a introduc¸˜ao desta dissertac¸˜ao ´e feita uma descric¸˜ao geral do problema em estudo. A dita descric¸˜ao, bem como uma breve revis˜ao bibliogr´afica encontram-se no cap´ıtulo 2. S˜ao apresentadas na revis˜ao bi-bliogr´afica algumas variantes do TSP bastante pr´oximas do CTSP, tal como ele ´e considerado no pre-sente estudo, no entanto, n˜ao foi poss´ıvel encontrar nenhum trabalho que visasse o estudo e a resoluc¸˜ao deste problema com todas as adaptac¸˜oes j´a enunciadas. No cap´ıtulo 3 ´e feita uma definic¸˜ao detalhada do problema que est´a a ser estudado, com todas as suas especificidades. S˜ao ainda apresentados os modelos que ser˜ao considerados, bem como as desigualdades v´alidas que permitem fortalecer as respec-tivas relaxac¸˜oes lineares. No fim, s˜ao tamb´em provadas algumas relac¸˜oes relativamente `a qualidade das relaxac¸˜oes lineares destes modelos. Em seguida, no cap´ıtulo 4 ´e apresentada a experiˆencia computacio-nal realizada com vista a avaliar e comparar o desempenho dos diferentes modelos, recorrendo para tal a todo um conjunto de instˆancias de teste geradas aleatoriamente. Por fim, no cap´ıtulo 5, s˜ao apresentadas as principais conclus˜oes do estudo realizado.
Cap´ıtulo 2
Problema do Caixeiro Viajante
Consistente
No contexto do planeamento e gest˜ao de rotas, a consistˆencia de um conjunto de rotas pode ser um pr´e-requisito do servic¸o que se pretende oferecer. Mesmo que n˜ao o seja, a dita consistˆencia pode constituir uma mais-valia, aumentando o grau de satisfac¸˜ao dos consumidores e a eficiˆencia dos trabalhadores da empresa.
O problema que se prop˜oe resolver na presente dissertac¸˜ao visa a obtenc¸˜ao de um conjunto dos m cir-cuitos ´otimos, que passam por todos os clientes que devem ser visitados em cada dia e ainda respeita as restric¸˜oes de consistˆencia, ou seja, os clientes para os quais se empenham estas restric¸˜oes, nos dias em que s˜ao visitados, surgem no circuito em posic¸˜oes suficientemente parecidas.
Neste cap´ıtulo ser´a feita uma descric¸˜ao geral do problema em estudo, bem como das hip´oteses simpli-ficadoras que lhe est˜ao subjacentes. Em seguida, ´e feita uma breve revis˜ao bibliogr´afica sobre a ´area de investigac¸˜ao em que este se encontra inserido, alguns problemas relacionados e as respetivas propostas de resoluc¸˜ao.
2.1
Descric¸˜ao do Problema
Vamos considerar que existem n + 1 locais. O local 1, sem perda de generalidade, ´e o dep´osito, onde se encontra um ´unico ve´ıculo. Os restantes n locais correspondem a clientes, aos quais tem que ser prestado um servic¸o que envolve uma visita do ve´ıculo que est´a no dep´osito.
Vamos ainda considerar um horizonte temporal de m per´ıodos, por exemplo dias. Para cada dia conhece-mos exatamente quais os clientes que precisam do servic¸o, e portanto sabeconhece-mos tamb´em quantos clientes ´e preciso visitar, j´a que cada cliente n˜ao pode ser visitado mais do que uma vez por dia.
Conhecemos ainda, para cada par de locais, o custo de deslocac¸˜ao entre eles. Este custo pode estar medido em termos de distˆancia ou de tempo de deslocac¸˜ao.
Os clientes que s˜ao visitados mais do que uma vez est˜ao sujeitos a restric¸˜oes de consistˆencia. Tal significa que para cada um dos locais correspondentes existe um valor pr´e-definido que limita superiormente a diferenc¸a m´axima entre as posic¸˜oes que esse local ocupa em circuitos de dias diferentes. Num extremo
Cap´ıtulo 2. Problema do Caixeiro Viajante Consistente 4
esse valor ´e zero, o que significa que o respetivo local tem que ocupar a mesma posic¸˜ao em todos os circuitos em que est´a inserido. No outro extremo este valor ´e t˜ao elevado que n˜ao constitui qualquer tipo de restric¸˜ao `a variac¸˜ao de posic¸˜ao de circuito para circuito.
Tem-se como objetivo a minimizac¸˜ao dos custos totais associados ao conjunto dos m circuitos. O problema possui, ent˜ao, trˆes hip´oteses subjacentes que lhe s˜ao particulares.
Em primeiro lugar, estamos a lidar com um horizonte temporal composto, `a partida, por mais do que um per´ıodo. Tal significa que, ao inv´es de planear uma ´unica rota, estamos a planear um conjunto de rotas ao mesmo tempo. Este facto, s´o por si, torna o problema mais complexo do ponto de vista computacional. Em segundo lugar, estamos a admitir que sabemos quais os clientes que tˆem que ser visitados em cada per´ıodo, o que ´e simultaneamente vantajoso e desvantajoso. Por um lado, temos a vantagem da reduc¸˜ao do n´umero de soluc¸˜oes admiss´ıveis, n´umero esse que seria muito maior se apenas soub´essemos quantas vezes cada cliente deve ser visitado e tiv´essemos liberdade para distribuir os clientes pelos diferentes circuitos. No entanto, esta hip´otese traduz-se num elevado n´umero de restric¸˜oes adicionais, o que torna o problema ainda mais complexo. Adicionalmente, esta hip´otese pode ser demasiado restritiva em certas aplicac¸˜oes pr´aticas.
A ´ultima hip´otese prende-se com as restric¸˜oes de consistˆencia, que imp˜oem um limite superior para a variac¸˜ao da posic¸˜ao de cada local, para todos os pares de circuitos em que este est´a inserido.
2.2
Revis˜ao Bibliogr´afica
O objetivo do Traveling Salesman Problem (TSP) ´e a determinac¸˜ao de uma rota de custo m´ınimo, que se inicia e termina no dep´osito, e que permite passar por todos os clientes que ´e necess´ario servir uma s´o vez. Em geral, s˜ao conhecidos quais os clientes que tˆem que ser servidos, bem como os custos de deslocac¸˜ao entre quaisquer dois locais (geralmente expressos em tempo ou em distˆancia).
No problema em estudo nesta dissertac¸˜ao, pretende-se determinar, n˜ao uma rota, mas sim um conjunto de m rotas, cada uma referente a um per´ıodo do horizonte temporal considerado. Conhecemos `a partida todos os custos relevantes, bem como todos os clientes que tˆem que ser visitados em cada per´ıodo. Adi-cionalmente, os clientes podem estar sujeitos a restric¸˜oes de consistˆencia. Os clientes nestas condic¸˜oes devem ser visitados de forma a que a diferenc¸a m´axima entre as posic¸˜oes que ocupem em dois circui-tos diferentes nos quais estejam inseridos n˜ao ultrapasse um certo valor limite, tamb´em ele conhecido a priori.
N˜ao foi poss´ıvel encontrar na literatura trabalho sobre nenhum problema exatamente com estas carac-ter´ısticas. No entanto, j´a ´e poss´ıvel encontrar estudos sobre problemas fortemente relacionados com o nosso problema, que iremos analisar em seguida.
2.2.1 Period Traveling Salesman Problem
No Period Traveling Salesman Problem (PTSP), considera-se a existˆencia de um conjunto de clientes, sendo que cada um tem que ser visitado um n´umero pr´e-definido de vezes dentro do horizonte temporal considerado. O objetivo ´e, ent˜ao, distribuir os clientes entre as m rotas, de forma a que em cada rota cada cliente seja visitado no m´aximo uma vez; todos os clientes sejam visitados o n´umero desejado de
Cap´ıtulo 2. Problema do Caixeiro Viajante Consistente 5
vezes; e o custo total associado a todo o conjunto de rotas seja m´ınimo.
Consoante a abordagem utilizada, podem surgir restric¸˜oes adicionais. A t´ıtulo ilustrativo, no seu trabalho Chao, Golden e Wasil [3] consideram que para al´em de conhecermos o n´umero de vezes que cada cliente tem que ser visitado, tamb´em nos ´e dado a conhecer `a partida o conjunto de combinac¸˜oes admiss´ıveis de dias de visita, pelo que n˜ao h´a plena liberdade de escolha dos dias em que os clientes s˜ao visitados. Mais exemplos de abordagem, n˜ao s´o na interpretac¸˜ao e formulac¸˜ao deste problema, mas tamb´em na sua resoluc¸˜ao podem ser encontrados na revis˜ao realizada por Campbell e Wilson [2].
´
E de notar que o PTSP apresenta bastantes semelhanc¸as com o Vehicle Routing Problem (VRP). Embora os contextos sejam bastante diferentes, considerar um mesmo ve´ıculo que tenha que percorrer v´arias rotas, cada uma em seu per´ıodo, ou considerar mais do que um ve´ıculo, cada um a ter que percorrer uma rota pode conduzir a formulac¸˜oes an´alogas, principalmente se no caso do VRP estivermos a considerar que o mesmo cliente tem que ser visitado por mais do que um ve´ıculo, seja ao mesmo tempo ou n˜ao; ou se no PTSP estivermos a considerar um grande n´umero de clientes que tˆem que ser visitados apenas uma vez. Em particular, as restric¸˜oes que indicam que dois ve´ıculos tˆem que estar no mesmo local ao mesmo tempo e as restric¸˜oes que obrigam a que um mesmo ve´ıculo visite o mesmo local `a mesma hora em per´ıodos (por exemplo dias) diferentes podem ser formuladas de uma maneira bastante semelhante.
´
E esta a sugest˜ao dada por Cordeau, Gendreau e Laporte [5], que prop˜oem um ´unico procedimento heur´ıstico baseado em Tabu Search, capaz de gerar soluc¸˜oes admiss´ıveis para o Periodic Vehicle Routing Problem(PVRP), o Periodic Traveling Salesman Problem (PTSP) e o Multi Depot Vehicle Routing Pro-blem(MDVRP). Tamb´em Paletta [17] sugeriu um procedimento heur´ıstico para obter boas soluc¸˜oes para o PTSP, desta vez com base em pesquisa local.
2.2.2 Time-Dependent Traveling Salesman Problem
No Time-Dependent Traveling Salesman Problem (TDTSP), em geral, encontramos a particularidade de que os custos de deslocac¸˜ao dependem n˜ao s´o do local de origem e do local de destino do mesmo, mas tamb´em da posic¸˜ao que a deslocac¸˜ao ocupa no circuito no seu todo. No entanto, esta pode n˜ao ser a ´unica hip´otese a ter em conta neste problema. A t´ıtulo ilustrativo, ao inv´es de considerar o tipo de dependˆencia temporal supra-mencionado, Tas¸, Gendreau, Jabali e Laporte [19] consideram que ´e o tempo necess´ario para executar cada servic¸o que depende do instante temporal em que comec¸a a dita execuc¸˜ao. Consequentemente deixa de ser poss´ıvel representar estes custos de forma matricial, passando essa representac¸˜ao a ser feita atrav´es de uma func¸˜ao.
Uma forma de lidar com este tipo de problema ´e atrav´es de um procedimento heur´ıstico. Por exem-plo, Vander Wiel e Sahanidis [20] servem-se da decomposic¸˜ao de Benders para obter boas soluc¸˜oes admiss´ıveis para o problema.
Por outro lado, s˜ao v´arios os trabalhos sobre m´etodos exatos associados ao TDTSP. Os trabalhos desen-volvidos por Fox, Gavish e Graves [7], Picard e Queyranne [18], Gouveia e Voß [11], Godinho, Gouveia e Pesneau [10], Miranda-Bront, M´endez-D´ıaz e Zabala [16], e Bigras, Gamache e Savard [1], s˜ao ape-nas alguns exemplos de estudos cujo objetivo ´e apresentar novos modelos para o TDTSP, ou propor desigualdades v´alidas para fortalecer modelos j´a existentes. ´E de notar que um dos modelos propostos na presente dissertac¸˜ao resulta de uma adaptac¸˜ao do modelo de Picard e Queyranne [18], pelo que este
Cap´ıtulo 2. Problema do Caixeiro Viajante Consistente 6
modelo se reveste de particular importˆancia no estudo que ser´a realizado em seguida.
Este tipo de formulac¸˜oes n˜ao ´e ´util apenas para problemas de roteamento. Com efeito, alguns dos traba-lhos supra-citados, tais como Picard e Queyranne [18] e Bigras, Gamache e Savard [1], s˜ao aplicados a problemas de escalonamento de tarefas para m´aquinas.
Por fim, na revis˜ao feita por Gendreau, Ghiani e Guerriero [9] pode ser encontrada uma apresentac¸˜ao de v´arios casos especiais do Time-Dependent Traveling Salesman Problem j´a considerados na literatura, bem como de v´arios m´etodos de resoluc¸˜ao j´a propostos.
2.2.3 Sincronizac¸˜ao e Consistˆencia
´
E poss´ıvel encontrar na literatura v´arias menc¸˜oes a quest˜oes de sincronizac¸˜ao e de consistˆencia.
A sincronizac¸˜ao surge normalmente associada a problemas como o Vehicle Routing Problem (VRP), com mais de um ve´ıculo no dep´osito. Devido `as especificidades do servic¸o prestado, pode ser necess´ario que dois ve´ıculos estejam no mesmo local ao mesmo tempo. As respetivas rotas tˆem que ser planeadas de forma a garantir que tal acontece.
J´a a consistˆencia relaciona-se com os problemas em que se considera mais do que um per´ıodo, e pode manifestar-se de diversas formas. Uma das formas mais habituais prende-se com a consistˆencia temporal, que consiste em visitar um dado cliente `a mesma hora em todos os dias (per´ıodos) em que este tem que ser visitado. Tamb´em habitual ´e a consistˆencia quanto ao ve´ıculo, que consiste em garantir que o mesmo cliente ´e sempre visitado pelo mesmo ve´ıculo. Adicionalmente podemos ter consistˆencia posicional, que ´e semelhante `a consistˆencia temporal, mas em vez de considerar o tempo tem em conta a posic¸˜ao que o cliente ocupa em cada circuito. Todos estes tipos de consistˆencia apresentam vantagens, nomeadamente no que diz respeito `a satisfac¸˜ao do consumidor e `a eficiˆencia do servic¸o. Em particular, o primeiro tipo ´e visto como uma mais-valia, que permite a obtenc¸˜ao de uma maior confianc¸a por parte do cliente. O segundo tipo ´e visto como vantajoso, na medida em que o facto de ser sempre o mesmo ve´ıculo, e em particular o mesmo trabalhador, a servir o mesmo cliente permite que o trabalhador perceba melhor as caracter´ısticas do cliente, o que propicia um atendimento mais personalizado. O terceiro tipo, embora n˜ao t˜ao eficaz como o primeiro do ponto de vista da satisfac¸˜ao do consumidor, retira a sua importˆancia do facto de tornar os circuitos mais previs´ıveis para os trabalhadores, o que pode resultar numa maior eficiˆencia na prestac¸˜ao do servic¸o.
A elevada complexidade destes problemas leva a que seja mais comum o estudo de procedimentos heur´ısticos para a respetiva resoluc¸˜ao, em detrimento dos m´etodos exatos. Temos, como exemplo, o procedimento apresentado por Luo, Qin, Che e Lim [14], baseado na resoluc¸˜ao do VRP com janelas temporais, aplicac¸˜ao de um reparador e posterior aplicac¸˜ao de um algoritmo de Tabu Search. Este pro-cedimento foi utilizado no contexto do Vehicle Routing Problem com restric¸˜oes de consistˆencia quanto ao ve´ıculo, e permitiu retirar algumas conclus˜oes relevantes do ponto de vista da gest˜ao e da tomada de decis˜ao. De entre essas conclus˜oes destaca-se o facto de que, quando admitimos que a quantidade procurada por cada cliente pode apresentar flutuac¸˜oes significativas comparativamente `a capacidade de transporte do ve´ıculo, pode n˜ao ser vantajoso tentar garantir a consistˆencia quanto ao ve´ıculo. Nestes casos o aumento da satisfac¸˜ao do consumidor n˜ao compensa, muitas vezes, o aumento substancial dos custos de operac¸˜ao.
Cap´ıtulo 2. Problema do Caixeiro Viajante Consistente 7
Kovacs, Golden, Hartl e Parragh [12] tamb´em propuseram um procedimento heur´ıstico para este tipo de problema, admitindo n˜ao s´o a necessidade de consistˆencia ao n´ıvel do ve´ıculo, mas tamb´em de con-sistˆencia temporal. O primeiro tipo de concon-sistˆencia ´e regulado atrav´es de restric¸˜oes, enquanto o segundo tipo ´e encorajado atrav´es da func¸˜ao objetivo.
Existe, de facto, uma grande diversidade de abordagens que podem ser utilizadas para resolver quest˜oes ligadas `a consistˆencia. A utilizac¸˜ao de restric¸˜oes ´e uma abordagem mais inflex´ıvel, que permite garantir que a consistˆencia ´e efetivamente respeitada, o que, no entanto, pode causar um elevado aumento do custo total da soluc¸˜ao ´otima obtida. Por outro lado, ao inv´es de forc¸ar a consistˆencia atrav´es de restric¸˜oes, ´e poss´ıvel apenas incentiv´a-la, penalizando a inconsistˆencia na func¸˜ao objetivo. Esta abordagem possui a vantagem de permitir que seja alcanc¸ado um equil´ıbrio entre a consistˆencia e os custos totais de operac¸˜ao. Drexl [6] realizou uma revis˜ao das formulac¸˜oes e metodologias de resoluc¸˜ao do Vehicle Routing Problem com restric¸˜oes de sincronizac¸˜ao. A revis˜ao feita por Kovacs, Golden, Hartl e Parragh [13] incide sobre os VRP com restric¸˜oes de consistˆencia.
Embora n˜ao tenha sido abordada em profundidade na literatura, a consistˆencia a n´ıvel posicional ´e menci-onada como sendo um fator relevante. Em particular, este tipo de consistˆencia ´e visto como fundamental quando se procura obter consistˆencia temporal. A consistˆencia na posic¸˜ao do circuito, embora n˜ao seja suficiente para garantir a consistˆencia temporal, assume-se como um primeiro passo na obtenc¸˜ao da mesma.
Por fim, Kovacs, Golden, Hartl e Parragh [13] mencionam a poss´ıvel necessidade de, ao inv´es de ga-rantir a consistˆencia num conjunto de circuitos, tentar que estes sejam inconsistentes. Com efeito, a consistˆencia pode ser importante, nomeadamente em aplicac¸˜oes relacionadas com servic¸os de sa´ude ou entregas a clientes que se repitam com alguma frequˆencia, seja devido `as especificidades do servic¸o, ou para aumentar a satisfac¸˜ao do cliente. Contudo, podem existir situac¸˜oes em que a consistˆencia n˜ao ´e desej´avel. O transporte de mercadorias valiosas pode ver a sua seguranc¸a aumentada, e servic¸os de vi-gilˆancia e controlo podem ter a sua fiabilidade melhorada se `as rotas que lhes est˜ao associadas for acres-centada alguma inconsistˆencia, traduzida numa maior imprevisibilidade. Um exemplo relativo a este tipo de problemas ´e abordado por Constantino, Mour˜ao e Pinto [4]. No problema estudado pretendia-se criar um conjunto de rotas que permitisse minimizar o tempo total necess´ario, garantindo tamb´em a existˆencia de inconsistˆencia suficiente entre as rotas, de forma a desincentivar tentativas de assalto. Para mode-lar tal inconsistˆencia foi necess´ario dividir todos os dias do horizonte temporal em per´ıodos de tempo. Duas abordagens foram propostas para modelar as restric¸˜oes de inconsistˆencia. A primeira passa por garantir que uma mesma tarefa n˜ao ´e desempenhada no mesmo per´ıodo em dias consecutivos, possuindo como desvantagem o facto de n˜ao evitar que, por exemplo, duas rotas de dias n˜ao consecutivos sejam exatamente iguais. A segunda abordagem, aplicada numa perspetiva mais heur´ıstica, prende-se com a imposic¸˜ao de um limite superior para o n´umero de repetic¸˜oes de tarefas no mesmo per´ıodo de tempo, em todos os pass´ıveis pares de dias do horizonte temporal. A aplicac¸˜ao pr´atica deste trabalho relaciona-se com um estudo de caso referente `a recolha de dinheiro dos parqu´ımetros da cidade de Lisboa.
Cap´ıtulo 3
Modelos
Neste cap´ıtulo ´e feita uma descric¸˜ao detalhada do problema em estudo propriamente dito. Em seguida, s˜ao apresentados os modelos utilizados na presente dissertac¸˜ao. S˜ao ainda apresentadas as desigualdades v´alidas utilizadas para fortalecer as respetivas relaxac¸˜oes lineares.
3.1
Definic¸˜ao do problema
Vamos considerar um grafo, G = (V, A), onde V = {1, ..., n+1} ´e o conjunto dos nodos, e A = {(i, j) : i, j ∈ V ; i 6= j} ´e o conjunto dos arcos, que inclui as ligac¸˜oes entre quaisquer dois nodos. Admitimos que o nodo 1 ´e o dep´osito, enquanto os restantes nodos comp˜oem o conjunto Vc = {2, ..., n + 1} dos
nodos clientes. P = {1, ..., m} ´e o conjunto de per´ıodos considerados no horizonte temporal.
Conhecemos ainda, a priori, o custo de deslocac¸˜ao associado a cada arco (i, j), Ci,j; e o limite superior
para a variac¸˜ao m´axima das posic¸˜oes do nodo i em circuitos distintos, limi. O parˆametro Silassume o
valor 1 se o nodo i tem que ser visitado no per´ıodo l, e 0 no caso contr´ario. Associados a este ´ultimo parˆametro surgem os conjuntos N Cl = {i ∈ V : Sil = 1} dos nodos clientes que tˆem que ser visitados
no per´ıodo l.
A informac¸˜ao j´a apresentada nesta secc¸˜ao ´e suficiente para definir o problema que est´a a ser estudado. De facto, com a informac¸˜ao fornecida j´a ´e poss´ıvel contemplar a possibilidade de haver clientes que, mesmo sendo visitados mais do que uma vez, n˜ao est˜ao sujeitos a restric¸˜oes de consistˆencia. Basta, para o efeito, considerar um valor de limisuficientemente elevado. No entanto, procedendo desta forma, o resultado
pode ser um conjunto de restric¸˜oes redundantes que afetam a eficiˆencia computacional dos modelos a estudar.
Para evitar tal situac¸˜ao, ser´a introduzido um novo parˆametro cujo valor ´e conhecido `a partida, Li, que
assume o valor 1 se o cliente i est´a sujeito `as restric¸˜oes de consistˆencia, e 0 no caso contr´ario. Associado a este parˆametro surge o conjunto RC = {i ∈ V : Li = 1} de clientes para os quais existem restric¸˜oes
de consistˆencia.
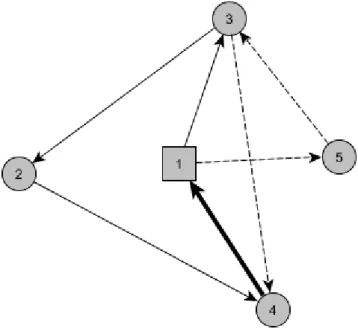
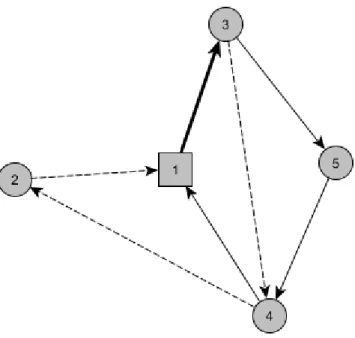
As figuras 3.1, 3.2 e 3.3 permitem ilustrar a forma como a consistˆencia em termos de posic¸˜ao ´e avaliada em circuitos que n˜ao partilham todos os nodos.
Vamos considerar uma rede com cinco nodos, onde o nodo 1 ´e o dep´osito e os restantes nodos s˜ao clientes. Suponhamos ainda que estamos a planear dois per´ıodos: no primeiro temos que visitar os
Cap´ıtulo 3. Modelos 10
Figura 3.1: Soluc¸˜ao n˜ao admiss´ıvel devido `as restric¸˜oes de consistˆencia
nodos 2, 3 e 4, e no segundo temos que visitar os nodos 3, 4 e 5. Temos que lim3 = 0, o que significa
que o nodo 3 tem que surgir na mesma posic¸˜ao em ambos os circuitos. O nodo 4 pode surgir em qualquer posic¸˜ao nos dois circuitos. Tal pode ser representado atrav´es de uma restric¸˜ao, com lim4a assumir um
valor suficientemente elevado, ou com base no parˆametro que distingue quais os nodos que tˆem que obedecer `as restric¸˜oes de consistˆencia. A existˆencia de limites de variac¸˜ao de posic¸˜ao para os nodos 2 e 5 ´e irrelevante, uma vez que estes aparecem em apenas um circuito.
Em cada uma das figuras, os arcos a cheio pertencem ao primeiro per´ıodo, e os arcos a tracejado con-cernem ao segundo. Se um arco surge a negrito, ent˜ao este ´e utilizado em ambas as rotas. A soluc¸˜ao da figura 3.1 n˜ao ´e admiss´ıvel, uma vez que no primeiro per´ıodo o nodo 3 ´e o primeiro a ser visitado, e no segundo per´ıodo ´e o segundo, sendo visitado apenas ap´os o nodo 5. J´a na figura 3.2 o nodo 3 ´e o primeiro a ser visitado em ambos os circuitos, pelo que a soluc¸˜ao ´e admiss´ıvel.
Note-se, ainda, que em ambas as figuras estamos a respeitar os per´ıodos de servic¸o de todos os nodos. Se assim n˜ao for, a soluc¸˜ao deixa de ser admiss´ıvel, mesmo que as restric¸˜oes de consistˆencia sejam respeitadas. ´E o que acontece na figura 3.3, onde o nodo 3 ´e sempre o primeiro a ser visitado, mas o nodo 5 ´e visitado no primeiro circuito, e o nodo 2 ´e visitado no segundo, o que leva a que a soluc¸˜ao n˜ao seja admiss´ıvel.
Pretende-se encontrar um conjunto de m circuitos de custo m´ınimo, onde todos os clientes s˜ao visitados em todos os per´ıodos nos quais requerem servic¸o, e as restric¸˜oes de consistˆencia em termos de posic¸˜ao s˜ao respeitadas.
3.2
Formulac¸˜oes
Nesta secc¸˜ao s˜ao apresentados os modelos utilizados para formular o problema em estudo, bem como as desigualdades v´alidas utilizadas na tentativa de fortalecer as suas relaxac¸˜oes lineares e obter melhores
Cap´ıtulo 3. Modelos 11
Figura 3.2: Soluc¸˜ao admiss´ıvel
Cap´ıtulo 3. Modelos 12
limites inferiores para o valor da soluc¸˜ao ´otima. Os modelos considerados na presente dissertac¸˜ao resul-tam de uma adaptac¸˜ao do Modelo de Fluxos Agregados (MFA), proposto por Gavish e Graves [8], e de uma adaptac¸˜ao do modelo proposto por Picard e Queyranne [18] (PQ).
As principais adaptac¸˜oes feitas aos modelos originais passam pelo facto de no nosso estudo estarmos a considerar m circuitos, e n˜ao apenas um, e pelo acr´escimo das restric¸˜oes de consistˆencia.
Nesta secc¸˜ao s˜ao ainda provadas algumas relac¸˜oes entre os valores ´otimos das relaxac¸˜oes lineares dos diferentes modelos.
3.2.1 Modelo de Fluxos Agregados
No modelo adaptado do MFA pretende-se minimizar a distˆancia total percorrida no conjunto dos m per´ıodos. Para o efeito, s˜ao utilizados dois conjuntos de vari´aveis de decis˜ao. Por um lado, temos as vari´aveis de decis˜ao xli,j, ∀(i, j) ∈ A, ∀l ∈ P , bin´arias, que assumem o valor 1 se o arco (i, j) ´e utilizado no per´ıodo l. Por outro lado temos as vari´aveis de fluxo yi,jl , ∀(i, j) ∈ A, ∀l ∈ P , que representam a quantidade de fluxo que passa pelo arco (i, j) no per´ıodo l. N˜ao foi necess´ario criar um conjunto de vari´aveis para representar a posic¸˜ao dos nodos nos circuitos, uma vez que essa posic¸˜ao pode ser obtida com base nos valores assumidos pelas vari´aveis de fluxo. Por fim, vamos ainda considerar um parˆametro simplificador, Nl = Pn+1
i=1 Sil, que representa o n´umero de nodos que comp˜oe cada circuito l. Note-se
que neste n´umero tamb´em ´e contabilizado o dep´osito.
O modelo baseado no MFA pode ser formulado da seguinte maneira:
M inimizar n+1 X i=1 n+1 X j=1 m X l=1 Cijxlij (3.1) Sujeito a : n+1 X j=1 xlij = Sil; ∀i ∈ V ; ∀l ∈ P (3.2) n+1 X j=1 xlji = Sil; ∀i ∈ V ; ∀l ∈ P (3.3) n+1 X j=2 yl1j = 1; ∀l ∈ P (3.4) n+1 X j=1 ylji− n X j=1 yijl = −Sil; ∀i ∈ Vc; ∀l ∈ P (3.5)
Cap´ıtulo 3. Modelos 13 yijl ≤ Nlxlij; ∀(i, j) ∈ A; ∀l ∈ P (3.6) n+1 X i=1 ysij− n+1 X i=1 yijt ≤ limj; ∀s ∈ P ; ∀t ∈ P ; ∀j ∈ RC ∩ N Cs∩ N Ct; s 6= t (3.7) xlij ∈ {0, 1}; ∀(i, j) ∈ A; ∀l ∈ P (3.8) yijl ≥ 0; ∀(i, j) ∈ A; ∀l ∈ P (3.9)
Na func¸˜ao objetivo (3.1) pretende-se minimizar o custo total associado ao conjunto dos m circuitos que vamos gerar. Este custo total resulta da soma dos produtos do custo de cada arco, j´a conhecido, pelo n´umero de vezes que esse mesmo arco ´e usado no conjunto de todos os circuitos.
As restric¸˜oes (3.2) e (3.3) designam-se por restric¸˜oes de afetac¸˜ao, e indicam que, se um determinado nodo faz parte de um dado circuito, ent˜ao nesse circuito tal nodo tem que ter um ´unico arco a entrar e um ´unico arco a sair. Da mesma forma, se determinado nodo n˜ao faz parte de um certo circuito, ent˜ao nesse mesmo circuito n˜ao pode haver qualquer arco a entrar ou a sair do dito nodo. As restric¸˜oes (3.4) fazem com que em cada circuito saia uma unidade de fluxo do dep´osito. As restric¸˜oes (3.5) implicam que, se um nodo faz parte de um circuito, a quantidade de fluxo que sai desse nodo nesse circuito ´e maior do que a quantidade de fluxo que entra nesse nodo no mesmo circuito em uma unidade. As restric¸˜oes (3.6) permitem-nos fazer a ligac¸˜ao entre os dois conjuntos de vari´aveis utilizados.
Como estamos a considerar que o fluxo num circuito ´e incrementado sempre que visitamos um nodo, a posic¸˜ao de um nodo no circuito pode ser obtida com base na quantidade de fluxo que entra no mesmo.
´
E com base nesta ideia que surgem as restric¸˜oes (3.7), que limitam superiormente a diferenc¸a de posic¸˜ao de um nodo em quaisquer dois circuitos em que este esteja inserido.
As restric¸˜oes (3.8) e (3.9) definem o dom´ınio das vari´aveis de decis˜ao. Sabemos que as vari´aveis xlij s˜ao vari´aveis bin´arias e que as vari´aveis ylij s˜ao n˜ao negativas. No entanto, e apesar de n˜ao ser imposta mais nenhuma restric¸˜ao sobre os valores assumidos pelas vari´aveis yijl , sabemos ainda que estas apenas assumem valores inteiros. Com efeito, como em cada circuito sai uma unidade de fluxo do dep´osito em (3.4), em cada circuito cada nodo tem no m´aximo um arco a sair do mesmo em (3.2), e como em cada nodo de um circuito o fluxo ´e incrementado em exatamente uma unidade segundo (3.7), temos a garantia de que tal acontece.
Se considerarmos o MFA tal como j´a foi apresentado, podemos concluir que, em cada circuito ad-miss´ıvel, ´e enviada uma unidade de fluxo a partir do dep´osito, e sempre que o ve´ıculo visita um cli-ente ´e-lhe acrescentada uma unidade de fluxo. Dada esta realidade, podemos admitir que a quantidade
Cap´ıtulo 3. Modelos 14
m´axima de fluxo ser´a obtida quando for visitado o ´ultimo cliente de um circuito, sendo que essa quan-tidade m´axima ´e precisamente Nl(recorde-se que este parˆametro contabiliza o dep´osito, uma e uma s´o vez). Assim, sabemos `a partida que estas restric¸˜oes apenas ser˜ao satisfeitas como igualdade nos arcos de retorno ao dep´osito. Para os restantes arcos podemos tornar a restric¸˜ao mais apertada.
Podemos, ent˜ao, escrever as seguintes desigualdades v´alidas:
yi1l ≤ Nlxli1; ∀i ∈ V ; ∀l ∈ P (3.10)
yijl ≤ (Nl− 1)xlij; ∀i ∈ V ; ∀j ∈ Vc; ∀l ∈ P (3.11)
O Modelo de Fluxos Agregados Forte que iremos considerar resulta da substituic¸˜ao das restric¸˜oes (3.6) do Modelo de Fluxos Agregados pelas desigualdades v´alidas (3.10) e (3.11) Tanto a func¸˜ao objetivo como as restantes restric¸˜oes permanecem inalteradas.
Lema 1: As restric¸˜oes (3.10) e (3.11) implicam as restric¸˜oes (3.6)
Demonstrac¸˜ao: No que diz respeito `as restric¸˜oes (3.10), estas s˜ao idˆenticas `as restric¸˜oes (3.6) nos valores dos ´ındices para os quais estas restric¸˜oes fazem sentido. Para os restantes valores dos ´ındices, basta apenas notar que (Nl− 1)xl
ij ≤ Nlxlij, j´a que xlij ≥ 0, tal como nos ´e dito nas restric¸˜oes (3.8)
Logo, verificando-se as restric¸˜oes (3.10) e (3.11), verificam-se tamb´em as restric¸˜oes (3.6). 2
Resultado 1:
i O valor ´otimo da relaxac¸˜ao linear do MFA Forte ´e igual ou superior ao valor ´otimo da relaxac¸˜ao linear do MFA.
ii Para algumas instˆancias o valor ´otimo da relaxac¸˜ao linear do MFA Forte ´e estritamente maior que o valor ´otimo da relaxac¸˜ao linear do MFA.
O lema 1 permitiu-nos mostrar que o conjunto formado pelas soluc¸˜oes admiss´ıveis da RL do Modelo de Fluxos Agregados Forte est´a contido no conjunto das soluc¸˜oes admiss´ıveis da RL do MFA, j´a que as restric¸˜oes (3.10) e (3.11) implicam (3.6), e as restantes restric¸˜oes s˜ao an´alogas para os dois modelos. Podemos ainda mostrar que podem existir instˆancias para as quais a soluc¸˜ao ´otima da RL do MFA Forte possui um valor maior do que o da soluc¸˜ao ´otima da RL do MFA. Basta apenas encontrar um exemplo de uma soluc¸˜ao que seja admiss´ıvel para o MFA, mas n˜ao para o MFA Forte.
Para o efeito, bem como para outros casos em que seja necess´ario fazer demonstrac¸˜oes semelhantes, ser´a considerado um pequeno exemplo com 2 per´ıodos e 4 clientes, sendo que em cada um dos per´ıodos tˆem que ser visitados 3 clientes. Dos dois clientes que tˆem que ser visitados nos dois per´ıodos, apenas um deles est´a sujeito a restric¸˜oes de consistˆencia. Em termos de informac¸˜oes deste exemplo temos que: N C1 = {2, 3, 4}, N C2 = {3, 4, 5}, RC = {3} e lim3 = 0.
Para este exemplo, considere-se, a t´ıtulo ilustrativo, a seguinte soluc¸˜ao:
Cap´ıtulo 3. Modelos 15
y132 = 1; y141 = 1; y123= 1; y134= 2; y234= 2; y141= 4; y452 = 3; y512 = 4. As restantes vari´aveis de decis˜ao tomam o valor 0.
´
E poss´ıvel verificar que esta soluc¸˜ao ´e admiss´ıvel para o Modelo de Fluxos Agregados. No entanto, j´a n˜ao ´e admiss´ıvel para o MFA Forte. Basta notar que N1= 4 e que, portanto, y1
14= 1 > (N1− 1) ∗ x114= 34.
Fica ent˜ao provado que existem instˆancias para as quais o valor ´otimo da RL do MFA Forte ´e estritamente maior do que o valor ´otimo da RL do MFA.
3.2.2 Modelo de Picard e Queyranne
Na adaptac¸˜ao do modelo de Picard e Queyranne (PQ) realizada na presente dissertac¸˜ao s˜ao utilizados os mesmos parˆametros que no Modelo de Fluxos Agregados.Temos, ent˜ao, o parˆametro Sil, que toma o valor 1 se o nodo i deve ser visitado na rota l; Nl, que define o n´umero de nodos em cada rota l; Cij,
que designa o custo de utilizac¸˜ao do arco (i, j); e limi, que representa o limite superior para a variac¸˜ao
de posic¸˜ao do nodo i nas diferentes rotas em que tem que ser visitado. Por outro lado, passamos a ter um ´unico grupo de vari´aveis de decis˜ao, zijkl, que tomam o valor 1 se o arco (i, j) est´a inserido na posic¸˜ao k da rota l.
O modelo adaptado do modelo PQ pode ser formulado da seguinte maneira:
M inimizar n+1 X i=1 n+1 X j=1 n+1 X k=1 m X l=1 Cijzijkl (3.12) Sujeito a : n+1 X i=1 n+1 X k=1 zklij = Sjl; ∀j ∈ V ; ∀l ∈ P (3.13) n+1 X j=2 z1j1l = 1; ∀l ∈ P (3.14) n+1 X i=1 zijkl= n+1 X i=1 zjik+1,l; ∀j ∈ Vc; ∀l ∈ P ; ∀k = 1, ..., Nl− 1 (3.15) n+1 X i=2 zi1Nl,l = 1; ∀l ∈ P (3.16) n+1 X k=1 k n+1 X i=1 zijks− n+1 X k=1 k n+1 X i=1 zijkt≤ limj; ∀s ∈ P ; ∀t ∈ P ; ∀j ∈ RC ∩ N Cs∩ N Ct; s 6= t (3.17)
Cap´ıtulo 3. Modelos 16
zijkl∈ {0, 1}; ∀(i, j) ∈ A; ∀k ∈ V ; ∀l ∈ P (3.18)
Uma vez mais pretendemos, na func¸˜ao objetivo (3.12), minimizar o custo total do conjunto de circuitos, que agora ´e escrito `a custa das novas vari´aveis de decis˜ao.
Nas restric¸˜oes (3.13) pretende-se garantir que todos os nodos clientes surgem nos circuitos associados a todos os per´ıodos em que tˆem que ser visitados. Para o efeito, garantimos que cada nodo, em cada circuito em que deve figurar, possui um e um s´o arco a entrar nele. Nas restric¸˜oes (3.14) procuramos garantir que em cada rota existe sempre um arco a partir da origem, arco esse que ocupa a primeira posic¸˜ao. Para cada um dos per´ıodos e cada nodo cliente temos as restric¸˜oes (3.15) que garantem que, se existe um arco incidente num nodo numa dada posic¸˜ao, nesse circuito existe um arco que parte desse mesmo nodo na posic¸˜ao seguinte. O ´ultimo arco de cada rota ´e sempre aquele que regressa ao dep´osito, o que ´e obtido atrav´es das restric¸˜oes (3.16)
Sabendo que o ´ındice k das vari´aveis de decis˜ao indica a posic¸˜ao que cada arco ocupa numa dada rota, e que as vari´aveis de decis˜ao s˜ao bin´arias, conclui-se que a posic¸˜ao de um nodo j num circuito l ´e dada por Pn+1
k=1k(
Pn+1
i=1 zklij). ´E com base neste conhecimento que s˜ao constru´ıdas as restric¸˜oes de consistˆencia
(3.17).
Por fim, as restric¸˜oes (3.18) definem o dom´ınio de variac¸˜ao da vari´aveis de decis˜ao, que se assumem como sendo vari´aveis bin´arias.
Foi ainda tido em conta todo um conjunto de hip´oteses, que em seguida se enunciam:
zijkl= 0; ∀(i, j) ∈ A; ∀k ∈ V ; ∀l ∈ P ; j /∈ N Cl (3.19)
zjikl= 0; ∀(j, i) ∈ A; ∀k ∈ V ; ∀l ∈ P ; j /∈ N Cl (3.20)
z1jkl= 0; ∀j ∈ V ; ∀k > 1; ∀l ∈ P (3.21)
zij1l= 0; ∀i ∈ Vc; ∀j ∈ V ; ∀l ∈ P (3.22)
Cap´ıtulo 3. Modelos 17
zijNll= 0; ∀i ∈ V ; ∀j ∈ Vc; ∀l ∈ P (3.24)
zijkl= 0; ∀(i, j) ∈ A; l ∈ P ; k > Nl (3.25)
Estas hip´oteses ir˜ao ser bastante relevantes para demonstrar que a relaxac¸˜ao linear do modelo PQ ´e mais forte que a relaxac¸˜ao linear do modelo MFA.
´
E poss´ıvel relacionar as vari´aveis de decis˜ao do Modelo de Fluxos Agregados com as do Modelo de Picard e Queyranne. Em particular, podemos escrever as seguintes express˜oes:
xlij = n+1 X k=1 zklij; ∀(i, j) ∈ A; ∀l ∈ P (3.26) yijl = n+1 X k=1 kzijkl; ∀(i, j) ∈ A; ∀l ∈ P (3.27) ´
E f´acil notar que, de acordo com estas condic¸˜oes, as vari´aveis xlijcontinuam a ser bin´arias, e as vari´aveis yijl continuam a ser inteiras. Para al´em disso, se usarmos as condic¸˜oes (3.26), podemos constatar que as func¸˜oes objetivo dos modelos MFA e PQ s˜ao equivalentes.
Lema 2: As restric¸˜oes (3.13) s˜ao equivalentes `as restric¸˜oes (3.3).
Demonstrac¸˜ao: Basta apenas usar as relac¸˜oes (3.26) e fazer as substituic¸˜oes nas restric¸˜oes (3.13), chegando ao resultado pretendido.
2
Lema 3: As restric¸˜oes (3.13), (3.14) e (3.15), juntamente com as condic¸˜oes (3.21), (3.22), (3.24), (3.25) e (3.26), implicam as restric¸˜oes (3.2).
Demonstrac¸˜ao: Para fazer esta demonstrac¸˜ao iremos definir dois casos distintos. Caso 1: j = 1
Se tivermos em conta as restric¸˜oes (3.14) e as condic¸˜oes (3.21), podemos concluir:
n+1 X i=1 n+1 X k=1 z1ikl= 1; ∀l ∈ P (3.28)
Foi ent˜ao provado o resultado pretendido, uma vez que assumimos que
Cap´ıtulo 3. Modelos 18
Caso 2: j ∈ Vc
Comec¸amos por somar as restric¸˜oes (3.15) para todos os valores de k para os quais estas est˜ao definidas, o que nos permite obter:
Nl−1 X k=1 n+1 X i=1 zijkl= Nl X k=2 n+1 X i=1 zjikl; ∀j ∈ Vc; ∀l ∈ P (3.30)
Se tivermos em conta as condic¸˜oes (3.22), (3.24) e (3.25), temos que:
n+1 X i=1 n+1 X k=1 zijkl= n+1 X i=1 n+1 X k=1 zjikl; ∀j ∈ Vc; ∀l ∈ P (3.31)
Como tal, pelas restric¸˜oes (3.13), podemos substituir o primeiro membro das equac¸˜oes anteriores, ficando com: Sjl = n+1 X i=1 n+1 X k=1 zklji; ∀j ∈ Vc; ∀l ∈ P (3.32)
Se depois fizermos as substituic¸˜oes necess´arias segundo as express˜oes (3.26), obtemos as restric¸˜oes desejadas.
2
Lema 4: As restric¸˜oes (3.14) e as condic¸˜oes (3.21) e (3.27) implicam as restric¸˜oes (3.4). Demonstrac¸˜ao: ´E f´acil verificar a seguinte express˜ao:
n+1 X j=1 z1jkl = n+1 X j=1 k ∗ z1jkl; ∀l ∈ P (3.33)
se k = 1. A esta express˜ao podemos somar as condic¸˜oes (3.21), cada uma multiplicada pelo respetivo valor de k, o que nos permite obter:
n+1 X j=1 n+1 X k=1 kz1jkl = 1; ∀l ∈ P (3.34)
Fazendo as devidas substituic¸˜oes com base nas relac¸˜oes (3.27), obtemos o resultado pretendido. 2
Lema 5: As restric¸˜oes (3.13) e (3.15), sob as hip´oteses (3.21), (3.24), (3.25) e (3.27), implicam as restric¸˜oes (3.5).
Cap´ıtulo 3. Modelos 19 seguinte express˜ao: Nl−1 X k=1 k ∗ n+1 X i=1 zklij = Nl X k=2 (k − 1) ∗ n+1 X i=1 zjikl; ∀j ∈ Vc; ∀l ∈ P (3.35)
De forma equivalente temos:
Nl−1 X k=1 k ∗ n+1 X i=1 zklij = Nl X k=2 k ∗ n+1 X i=1 zjikl− Nl X k=2 n+1 X i=1 zjikl; ∀j ∈ Vc; ∀l ∈ P (3.36)
Devido `as condic¸˜oes (3.21), (3.24) e (3.25), podemos escrever:
n+1 X k=1 k ∗ n+1 X i=1 zklij = n+1 X k=1 k ∗ n+1 X i=1 zjikl− n+1 X k=1 n+1 X i=1 zjikl; ∀j ∈ Vc; ∀l ∈ P (3.37)
Fazendo as devidas substituic¸˜oes com recurso `as igualdades (3.13) e (3.27), chegamos ao resultado pre-tendido.
2
Lema 6: As condic¸˜oes (3.26) e (3.27) implicam as restric¸˜oes (3.6.).
Demonstrac¸˜ao: Em primeiro lugar, ´e necess´ario notar que todas as vari´aveis de decis˜ao zijklassumem va-lores n˜ao negativos, e que k apenas assume vava-lores positivos. Se observarmos (3.26) e (3.27) conclu´ımos que, se ylij > 0, ent˜ao xlij > 0, e vice-versa. Como adicionalmente se tem xklij ≤ 1, podemos ent˜ao ver que o maior valor que yijl pode tomar ´e obtido quando, nas condic¸˜oes (3.27.), fazemos zijNl,l = xlij. Desta forma chegamos `as restric¸˜oes desejadas.
2
Observac¸˜ao: Considere-se agora que j ∈ Vc. Se relembrarmos as condic¸˜oes (3.24), conclui-se que o
maior valor de yijl ´e obtido fazendo zijNl−1,l = xlij, nas condic¸˜oes (3.27). Procedendo desta forma s˜ao obtidas as restric¸˜oes (3.11) do modelo MFA Forte.
Lema 7: As restric¸˜oes (3.17) s˜ao equivalentes `as restric¸˜oes (3.7).
Demonstrac¸˜ao: Para provar a equivalˆencia, basta fazer a substituic¸˜ao nas restric¸˜oes (3.17), segundo as igualdades (3.27), obtendo de imediato as restric¸˜oes (3.7).
2
Resultado 2:
i O valor ´otimo da relaxac¸˜ao linear do Modelo de Picard e Queyranne ´e igual ou superior ao valor ´otimo da relaxac¸˜ao linear do MFA.
ii Para algumas instˆancias o valor ´otimo da relaxac¸˜ao linear do Modelo de Picard e Queyranne ´e estritamente maior que o valor ´otimo da relaxac¸˜ao linear do MFA.
Cap´ıtulo 3. Modelos 20
Os lemas 2-7 permitiram provar que todas as soluc¸˜oes admiss´ıveis para a RL do modelo PQ s˜ao ad-miss´ıveis para a RL do MFA. Considere-se, agora, a seguinte soluc¸˜ao:
x1
12= 23; x213= 1; x114= 13; x123= 1; x132= 13; x134= 23; x234= 1; x141= 1; x245= 1; x251= 1.
y132 = 1; y141 = 1; y123= 1; y134= 2; y234= 2; y141= 4; y452 = 3; y512 = 4. As restantes vari´aveis de decis˜ao tomam o valor 0.
Esta soluc¸˜ao ´e admiss´ıvel para o modelo de Fluxos Agregados. No entanto, n˜ao ´e admiss´ıvel para o modelo de Picard e Queyranne. Basta notar que x112 > 0, mas y112 = 0, o que n˜ao ´e poss´ıvel j´a que, se yijl > 0, ent˜ao xlij > 0, e vice-versa. Conclui-se ent˜ao que nalgumas instˆancias podem existir soluc¸˜oes que s˜ao admiss´ıveis para o MFA, mas n˜ao para o modelo PQ, ou seja, nessas instˆancias o valor ´otimo do modelo PQ ´e maior que o valor ´otimo do MFA.
Observac¸˜ao: Nos lemas 2-7 tamb´em ficou provado que as restric¸˜oes do modelo PQ implicam todas as restric¸˜oes do modelo MFA Forte. Se a essa informac¸˜ao adicionarmos o facto de que a soluc¸˜ao acima mencionada tamb´em ´e admiss´ıvel para o MFA Forte, conclui-se que a relaxac¸˜ao linear do modelo PQ tamb´em ´e mais forte que a do MFA Forte.
Admitamos agora que todos os nodos sujeitos a restric¸˜oes de consistˆencia tˆem que ser visitados na mesma posic¸˜ao relativa em todos os circuitos em que est˜ao inseridos. Temos, ent˜ao, que limj = 0, ∀j ∈ RC.
Vamos comec¸ar por criar um conjunto de vari´aveis auxiliares, pkj, vari´aveis bin´arias que assumem o valor 1 se o cliente j ocupa a posic¸˜ao k em todos os circuitos onde deve ser visitado, e 0 no caso contr´ario. Devido `a forma como estas vari´aveis est˜ao definidas, podemos escrever as seguintes restric¸˜oes de ligac¸˜ao:
n+1
X
i=1
zijkl= pkj; ∀l ∈ P ; ∀k ∈ V ; ∀j ∈ RC; j ∈ N Cl (3.38) Precisamos ainda de garantir que a cada nodo sujeito `as restric¸˜oes de consistˆencia ´e atribu´ıda uma e uma s´o posic¸˜ao relativa. Tal garantia pode ser obtida atrav´es do seguinte conjunto de restric¸˜oes:
n+1
X
k=1
pkj = 1; ∀j ∈ RC (3.39)
´
E de salientar que as vari´aveis pkj n˜ao s˜ao imprescind´ıveis. ´E suficiente escrever o seguinte conjunto de restric¸˜oes: n+1 X i=1 n+1 X k=1 zijkl= 1; ∀l ∈ P ; ∀j ∈ RC; j ∈ N Cl (3.40)
No entanto, a utilizac¸˜ao das restric¸˜oes (3.38) e (3.39) ´e mais intuitiva.
O Modelo de Picard e Queyranne forte que iremos considerar resulta do modelo PQ j´a apresentado, retirando-lhe as restric¸˜oes de consistˆencia (3.17), e substituindo-as pelo conjunto das restric¸˜oes (3.38) e (3.39) ou, alternativamente, pelas restric¸˜oes (3.40). No estudo realizado para o presente trabalho optou-se
Cap´ıtulo 3. Modelos 21
pelo conjunto das restric¸˜oes (3.38) e (3.39).
Relativamente a este novo modelo surgem duas observac¸˜oes.
Em primeiro lugar, ´e de salientar que embora tenha sido criado um novo conjunto de vari´aveis para este novo modelo, n˜ao ´e necess´ario criar um conjunto de restric¸˜oes que definam o respetivo dom´ınio de variac¸˜ao. Por um lado, temos que a soma de vari´aveis bin´arias resulta sempre num valor inteiro n˜ao negativo. Como tal, as restric¸˜oes (3.38) implicam que as novas vari´aveis apenas assumam valores inteiros n˜ao negativos. Esta propriedade, associada ao conjunto das restric¸˜oes (3.39), leva a que todas as vari´aveis pkj relevantes para o nosso problema sejam vari´aveis bin´arias, tal como desejado.
Por fim, conv´em relembrar que este novo modelo apenas permite resolver um caso particular do problema em estudo, visto que uma das hip´oteses considerada nesta subsecc¸˜ao ´e a de que todos os clientes com restric¸˜ao de consistˆencia tˆem que ser visitados sempre na mesma posic¸˜ao relativa. No entanto, mesmo tendo um ˆambito mais limitado, iremos ver nos pr´oximos cap´ıtulos que este modelo reveste-se de grande importˆancia, uma vez que permite resolver casos particulares que se revelam mais problem´aticos para os outros modelos considerados nesta dissertac¸˜ao.
Lema 8: As restric¸˜oes (3.38) implicam as restric¸˜oes (3.17)
Demonstrac¸˜ao: Basta somar as restric¸˜oes (3.38), multiplicadas pelo respetivo valor de k, para obter as igualdades: n+1 X i=1 n+1 X k=1 k ∗ zklij = k ∗ pkj; ∀l ∈ P ; ∀j ∈ RC; j ∈ N Cl (3.41)
Como o segundo membro destas equac¸˜oes n˜ao depende de l, podemos escrever as condic¸˜oes pretendidas para cada par de per´ıodos relevante.
2
Resultado 3:
i O valor ´otimo da relaxac¸˜ao linear do Modelo de Picard e Queyranne Forte ´e igual ou superior ao valor ´otimo da relaxac¸˜ao linear do Modelo de Picard e Queyranne.
ii Para algumas instˆancias o valor ´otimo da relaxac¸˜ao linear do Modelo de Picard e Queyranne Forte ´e estritamente maior que o valor ´otimo da relaxac¸˜ao linear do Modelo de Picard e Queyranne. O lema 8 permitiu-nos provar que todas as soluc¸˜oes admiss´ıveis para o modelo PQ Forte s˜ao tamb´em admiss´ıveis para o modelo PQ. Considere-se agora a seguinte soluc¸˜ao:
z1211= z2123= z3431= z4141= 1
z1312= z1214= z3142= z2234= z4522= z4532= z5142= z5332= 12 As restantes vari´aveis de decis˜ao tomam o valor 0.
´
E f´acil verificar que esta soluc¸˜ao ´e admiss´ıvel para o modelo PQ. No entanto, j´a n˜ao o ´e para o modelo PQ Forte. Basta notar quePn
i=1zi311= 0, enquanto
Pn
i=1zi312= 12, o que vai contra as condic¸˜oes (3.38).
Fica ent˜ao provado que podem existir instˆancias para as quais o valor ´otimo no modelo PQ Forte ´e maior que o valor ´otimo do modelo PQ. Os resultados obtidos na experiˆencia computacional mostram que existem efetivamente instˆancias que verificam este resultado, bem como os dois resultados anteriores.
Cap´ıtulo 3. Modelos 22
Figura 3.4: Relac¸˜oes entre as relaxac¸˜oes lineares dos modelos propostos
A figura 3.4 permite sintetizar as relac¸˜oes deduzidas entre os diferentes modelos. Cada caixa representa um modelo. Uma seta com origem num modelo e destino noutro indica que a relaxac¸˜ao linear do modelo de destino ´e mais forte que a do modelo de origem.
Podemos concluir que ´e de esperar que os modelos de Picard e Queyranne (simples e forte) fornec¸am limites inferiores para o valor ´otimo de melhor qualidade que os obtidos nos modelos adaptados do MFA. Na pr´oxima secc¸˜ao iremos verificar as relac¸˜oes propostas na figura 3.4 com base nos resultados obtidos no teste computacional.
Cap´ıtulo 4
Experiˆencia Computacional
Neste cap´ıtulo apresenta-se a experiˆencia computacional realizada no ˆambito da presente dissertac¸˜ao, bem como os resultados obtidos. Na primeira secc¸˜ao ´e descrita a forma como as instˆancias de teste foram geradas aleatoriamente. Em seguida, s˜ao avaliados os resultados de uma forma geral e transversal aos diferentes modelos. Por fim, ´e feita a an´alise comparativa dos quatro modelos propostos.
Para o desenvolvimento de tal experiˆencia computacional foi utilizado o software Xpress IVE vers˜ao 1.24.18., quer ao n´ıvel da gerac¸˜ao das instˆancias de teste, quer ao n´ıvel da aplicac¸˜ao dos quatro modelos j´a mencionados, e com um computador com processador Intel CoreR TM2 Duo CPU E7400 @ 2.80GHz,
com 4GB de RAM.
Na presente dissertac¸˜ao n˜ao ser˜ao apresentados resultados discriminados por instˆancias de teste, mas sim m´edias de resultados. No entanto, os resultados completos, discriminados por instˆancia, encontram-se dispon´ıveis para consulta (http://mctsp.000webhostapp.com/).
4.1
Gerac¸˜ao das Instˆancias de Teste
Recorde-se que o parˆametro n indica o n´umero total de clientes da rede, enquanto m designa o n´umero de per´ıodos no horizonte temporal. Para efeitos de gerac¸˜ao das instˆancias de teste iremos considerar que n ∈ {20, 30} e que m ∈ {2, 3}.
Figura 4.1: Esquema da distribuic¸˜ao dos nodos clientes quando m=2
Cap´ıtulo 4. Experiˆencia Computacional 24
Comecemos por admitir que m = 2 e n = 20. Sabemos que N Cl representa o conjunto dos nodos
clientes que tˆem que ser visitados no per´ıodo l. Vamos designar por N C1&2a intersecc¸˜ao dos conjuntos
de nodos clientes de cada per´ıodo, ou seja, N C1&2= N C1∩ N C2, tal como ilustrado na figura 4.1.
Note-se que estamos a assumir que o conjunto N C1&2n˜ao ´e um conjunto vazio, caso contr´ario n˜ao faria
sentido a necessidade de restric¸˜oes de consistˆencia.
Para as hip´oteses consideradas foram definidos 12 casos, que diferem na composic¸˜ao dos conjuntos N C1,
N C2e N C1&2, quanto ao n´umero de clientes com restric¸˜oes de consistˆencia e quanto ao tipo de matriz
de custos considerado. Estes casos encontram-se descritos na tabela 4.1. Para cada caso ´e apresentado o n´umero de clientes pertencentes aos conjuntos N C1e N C2. A coluna NC1&2\#RC indica o n´umero de
clientes pertencentes a N C1&2, e o n´umero dos clientes deste grupo sujeitos a restric¸˜oes de consistˆencia,
por esta ordem. Por fim, ´e indicado se a matriz de custos em cada caso ´e sim´etrica ou assim´etrica.
Tabela 4.1: Gerac¸˜ao das instˆancias de teste quando n = 20 e m = 2
Caso NC1 NC2 NC1&2\#RC Assim´etrica Sim´etrica
1 20 20 20\15 D -2 20 20 20\15 - D 3 20 20 20\10 D -4 20 20 20\10 - D 5 20 20 20\5 D -6 20 20 20\5 - D 7 15 15 10\10 D -8 15 15 10\10 - D 9 15 15 10\5 D -10 15 15 10\5 - D 11 13 13 6\6 D -12 13 13 6\6 - D
Vamos agora considerar que n = 20 e m = 3. Designaremos por N C1&2, N C1&3 e N C2&3 as
intersecc¸˜oes dos conjuntos de clientes em pares de per´ıodos, enquanto o conjunto N C1&2&3 ´e
com-posto pelos clientes que tˆem que ser visitados nos trˆes per´ıodos, tal como se encontra ilustrado na figura 4.2. Note-se que nenhum dos conjuntos N C1&2, N C1&3 e N C2&3inclui o conjunto N C1&2&3. Uma
vez mais, nenhum destes quatro conjuntos de intersecc¸˜ao ´e vazio.
Nas instˆancias geradas com vinte clientes e trˆes per´ıodos admitiu-se que cada circuito ´e composto por 12 clientes, sendo que todos os clientes tˆem que ser visitados pelo menos uma vez. Os conjuntos N C1&2,
N C1&3e N C2&3contˆem dois clientes cada um. O conjunto N C1&2&3´e composto por quatro clientes.
Com base nas hip´oteses apresentadas, foram definidos seis casos distintos, que variam conforme a matriz de custos ´e sim´etrica ou assim´etrica, e com base nos conjuntos aos quais s˜ao aplicadas as restric¸˜oes de consistˆencia. Estes casos encontram-se descritos na tabela 4.2, que pode ser interpretada de forma an´aloga `a tabela 4.1.
A criac¸˜ao das instˆancias em que n = 30 foi feita com base em casos an´alogos aos apresentados, ap´os aplicac¸˜ao de proporcionalidade direta, procedendo-se aos arredondamentos interm´edios necess´arios. Para cada combinac¸˜ao de valores de n, m com cada caso pertinente ao valor de m foram geradas cinco instˆancias de teste, o que perfaz um total de 180 instˆancias de teste geradas aleatoriamente. ´E de salientar
Cap´ıtulo 4. Experiˆencia Computacional 25
Figura 4.2: Esquema da distribuic¸˜ao dos clientes quando m=3
Tabela 4.2: Gerac¸˜ao das instˆancias de teste quando n = 20 e m = 3
Caso NC1&2\#RC NC1&3\#RC NC2&3\#RC NC1&2&3\#RC Assim´etrica Sim´etrica
1 2\2 2\2 2\2 4\0 D -2 2\2 2\2 2\2 4\0 - D 3 2\0 2\0 2\0 4\4 D -4 2\0 2\0 2\0 4\4 - D 5 2\2 2\2 2\2 4\4 D -6 2\2 2\2 2\2 4\4 - D