André Gustavo Campos Pereira
Joaquim Elias de Freitas
Roosewelt Fonseca Soares
Cálculo I
D I S C I P L I N A
A integral definida
Autores
aula
Divisão de Serviços Técnicos
Catalogação da publicação na Fonte. UFRN/Biblioteca Central “Zila Mamede” Governo Federal
Presidente da República
Luiz Inácio Lula da Silva
Ministro da Educação
Fernando Haddad
Secretário de Educação a Distância – SEED
Carlos Eduardo Bielschowsky
Universidade Federal do Rio Grande do Norte
Reitor
José Ivonildo do Rêgo
Vice-Reitora
Ângela Maria Paiva Cruz
Secretária de Educação a Distância
Vera Lúcia do Amaral
Secretaria de Educação a Distância- SEDIS
Coordenadora da Produção dos Materiais
Marta Maria Castanho Almeida Pernambuco
Coordenador de Edição
Ary Sergio Braga Olinisky
Projeto Gráfico
Ivana Lima
Revisores de Estrutura e Linguagem
Eugenio Tavares Borges Jânio Gustavo Barbosa Thalyta Mabel Nobre Barbosa
Revisora das Normas da ABNT
Verônica Pinheiro da Silva
Revisoras de Língua Portuguesa
Janaina Tomaz Capistrano Sandra Cristinne Xavier da Câmara
Revisores Técnicos
Leonardo Chagas da Silva Thaísa Maria Simplício Lemos
Revisora Tipográfica
Nouraide Queiroz
Ilustradora
Carolina Costa
Editoração de Imagens
Adauto Harley Carolina Costa
Diagramadores
Bruno de Souza Melo Dimetrius de Carvalho Ferreira Ivana Lima Johann Jean Evangelista de Melo
Adaptação para Módulo Matemático
André Quintiliano Bezerra da Silva Kalinne Rayana Cavalcanti Pereira Thaísa Maria Simplício Lemos
Colaboradora
Viviane Simioli Medeiros Campos
Imagens Utilizadas
Apresentação
N
as aulas 8 (A primitiva) e 9 (Mais primitivas e as somas de Riemann), calculamos as primitivas de diversas funções, introduzimos as somas de Riemann e utilizamos em particularuma soma de Riemann para calcular a área sob o gráfico de uma função contínua positiva. Nesta aula, voltaremos a tratar das somas de Riemann no sentido de ampliar o cálculo de áreas sob o gráfico de funções não mais necessariamente positivas, definiremos a integral definida de uma função e, finalmente, faremos a conexão entre primitivas e a integral definida utilizando o importante teorema fundamental do cálculo.Objetivos
Somas de Riemann
Na aula 9, vimos que para calcular a área pretendida executamos os seguintes procedimentos:
1) subdividimos o intervalo fechado
a b] em n subintervalos usando um conjunto P x, x1, , x1, x, , xn1, xn} com n + 1 pontos, onde ax < x1 < < x1 < x< < xn1 < xnb, definindo n subintervalos x, x1], x1, x2], , x1, x], , xn1, xn]. O conjunto P é chamado de partição de a b];2) em cada subintervalo fechado
x x], com k= ,2, , n, escolhemos um ponto tal que . Denotamos por Sk a área do retângulo de base e altura (x), ou seja, =f(¯x)x;3)
denominamos por An a soma das áreas dos n sub-retângulos definidos anteriormente, isto é,n= n
= S=
n
=
f(¯x)x ;
4) fazemos a quantidade de pontos da partição crescer indefinidamente, ou seja, tender
para infinito.Observação 1 - Note que dizer que é equivalente a dizer que ∞, pois se o comprimento do maior intervalo está se aproximando de zero quer dizer que a quantidade de pontos da partição está crescendo indeterminadamente. Logo, podemos escrever
lim
n= limn∞n= limn∞ n
k=1
f(¯xk)xk.
Observação 2 - Vimos também na aula 9, que se considerarmos a norma como uma constante, todos os subintervalos x x] terão o mesmo comprimento e, se
f [a b]R for positiva e contínua em a b], então, a área sob a curva y=x) no intervalo a b] é definida por = lim
n∞n= limn∞ n
=
f(¯x)x.
Note que a observação 2 é um caso particular da observação 1, pois nesta nada foi dito sobre como é a partição e nenhuma suposição foi feita para a função em estudo. Ou seja, na 1. a partição e a função podem até ser iguais a 2, mas isso seria apenas um dos casos possíveis.
Na aula 6 (Aplicações da derivada), vimos o Teorema da Existência de Valores Extremos, de acordo com o qual se f é uma função contínua no intervalo fechado a b], então, f tem máximo absoluto e mínimo absoluto em a b]. Note que quando fazemos a primeira etapa das somas de Riemann, subdividimos o intervalo fechado a b] em n subintervalos usando a partição P x, x1, , x1, x, , xn1, xn} com n + 1 pontos, onde ax < x1 < < x1 < x < < xn1< xnb, definindo n subintervalos x, x1], x1, x2], , x1, x], , xn1, xn]. Portanto, se a função f com a qual estamos trabalhando for contínua, existirão em cada intervalo x x] dois pontos m, e k onde a função f tem máximo absoluto e mínimo absoluto em x x], sendo para esses pontos xmk )xk ).
Por 2) – soma de Reimann –, temos que é a largura do intervalo x x] e, portanto, um valor positivo. Assim, multiplicando ambos os lados da desigualdade
xmk)xk ) por , obtemos (x m
k)x(x
k )x; como isso vale para qualquer intervalo x, x1], x1, x2], , x1, x], , xn1, xn], teremos
(xm )x (x )x
(xm2 )x2 (x 2 )x2 ...
(xmn)x(x n )x.
Somando os membros da desigualdade anterior, obedecendo a desigualdade, teremos
n
=
(xmk)x n
=
a
4
3
2
1
0
0 1 2 3 4
x
4
3
2
1
0
0 1 2 3 4
b
4
3
2
1
0
0 1 2 3 4
4
3
2
1
0
0 1 2 3 4
x
Note ainda que qualquer outro ponto , tal que , temos
(xmk)(x)(x
k ), e repetindo o procedimento anterior, obteremos n
=
(xmk )x n
=
(¯x)x n
=
(xk )x.
A partir disso, podemos concluir que para qualquer partição do intervalo a b], P x, x1, , x1, x, , xn1, xn}, a desigualdade (Equação 1) ocorre quando f é
uma função contínua no intervalo fechado a b].
A soma que utiliza o valor xm) como altura do retângulo em cada subintervalo
x x] é chamada soma inferior. A soma que utiliza o valor x
k ) como altura do retângulo em cada subintervalo x x] é chamada soma superior.
Ilustramos nas Figuras 1a e 1b a seguir as somas inferior e superior, respectivamente, da função f : [4]R, definida por x) =x, utilizando uma partição com 10 pontos.
Figura 1 - (a) Área referente à soma inferior; (b) área referente à soma superior.
a b c
4
3
2
1
0
0 1 2 3 4
x
4
3
2
1
0
0 1 2 3 4
x
4
3
2
1
0
0 1 2 3 4
x
a b c
4
3
2
1
0
0 1 2 3 4
x
4
3
2
1
0
0 1 2 3 4
x
4
3
2
1
0
0 1 2 3 4
x A primeira observação que podemos fazer é que as somas superiores sempre são maiores ou iguais à área que desejamos aproximar e as somas inferiores sempre menores ou iguais; cabe ainda observar que as somas superiores são sempre maiores ou iguais a somas inferiores quando estamos calculando-as com base na mesma partição.
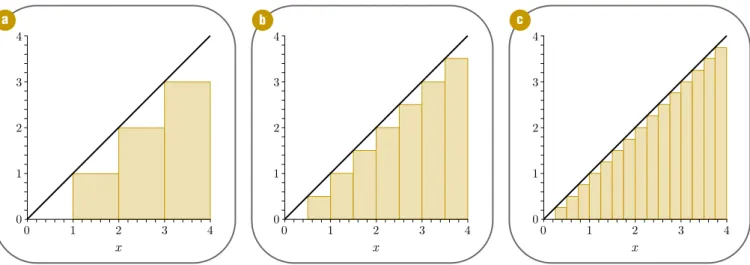
A segunda observação é que, se tomamos uma partição e vamos acrescentando cada vez mais pontos a ela, a soma superior vai diminuindo e a inferior vai aumentando. Ilustramos isso na Figura 2, na qual começamos com 4 pontos, depois acrescentamos os pontos médios aumentando para 8, e em seguida acrescentamos outra vez os pontos médios aumentando o número de pontos da partição para 16.
Figura 2 - (a) Área relativa à soma inferior de uma partição com 4 pontos; (b) acréscimo dos pontos médios à partição anterior, fazendo uma nova partição com 8 pontos; (c) acréscimo dos pontos médios à partição anterior, fazendo uma nova partição com 16 pontos.
Exemplo 1
Calcule a soma inferior da função f : [ b]R definida por
x) =x, utilizando a partição P x, x1, x2, , x1, x} do
intervalo [ b], tal que =x < x1< x2< < x1< x=b e com
x = , x1=
b n, x2=
2b n, x3 =
3b
n, , x =
n1)b n x=
nb n =b.
Solução
Note que o gráfico da função é o da Figura 5 da aula 9. Assim, se observarmos em cada subintervalo x x], o menor valor da função será assumido sempre no ponto inferior do intervalo, ou seja, em . Dessa forma, a soma inferior será
s(f, P) = n
=
f(xm)x= n
=
f(x)x= n
= x
b n = b1 n n =
x = b n
0 + b
n +
2b
n + +
(n1)b n
s(f, P) = b n
b
n+
2b
n + +
(n1)b n
= b2
n2(1 + 2 + + (n1))
= b2 n2
(n 1)n
2
= b2(n1)
2n .
Note que se quisermos saber o que acontece com essa soma inferior quando fizermos , temos que fazer ∞.
Para visualizarmos melhor, reescrevemos sf P) = b 2
1 1
n
. Pelo que
estudamos na aula 9, vemos que quando ∞ teremos lim
sf P) = b2
2 . Denotemos as somas superior e inferior de uma função f relativa a uma partição P por Sf P) e sf P), respectivamente. Pelo que vimos até o momento, temos que à medida que acrescentamos mais pontos à partição P, ou seja, que fazemos , Sf P) decresce e sf P) cresce. Além disso, sf P)Sf P). Com essas informações, podemos garantir que os limites lim
Atividade 1
a)
Calcule a soma superior da função f : [ b]R defi nida por x) =x, utilizando a partição PP xx, x, x11, x, x22, , x, , x11, x, x}} do intervalo[
[ b b]], tal que =x < x1< x2 < < x1< x=b e com
x= 0, x1 =
b n, x2 =
2b n, x3=
3b
n, ,x1 =
n1)b n , x=
nb n =b
b) Depois de calculada a soma superior, encontre
limSf P).
Se tomarmos outra partição lim
sf P
) lim
Sf P
) e fi zermos o mesmo procedimento, teremos que os
limites lim
sf P
) e lim
Sf P
) e existem.
Duas perguntas surgem naturalmente neste momento:
lim
sf P) = limsf P
)? lim
Sf P) = limSf P
)?
Caso as perguntas sejam respondidas positivamente, outra pergunta ainda pode surgir:
lim
sf P) = limSf P)?
Caso as perguntas sejam respondidas positivamente, para quaisquer que sejam as partições P,
lim
sf P
) lim
Sf P
) tomadas, temos pela equação 1 que
s(f P) = n
= f(xm
k)x n
=
f(¯xk)x n
=
f(xk )x=S(f P)
e pelo teorema do confronto visto na aula 2 (Funções contínuas)que
lim
s(f P) = limS(f P) = lim
n
k=1
A notação
b
fx)x foi introduzida por Leibniz, em que o símbolo
foi construído
a partir da letra S de soma, a f(x) denominamos de integrando, ao a, de limite inferior (da integral), e ao b, de limite superior (da integral); o dx indica que x é a variável independente que está assumindo valores no intervalo fechado a b] e é denominada variável de integração.
Agora, vem aquela pergunta que não quer calar: precisaremos calcular a soma superior e inferior de todas as partições possíveis e verifi car se, quando o número de pontos da partição crescer, os limites coincidirão? Mas não existem infi nitas partições?
Pois é!!!!
Mas não se desespere, agora vai entrar em ação o que estamos estudando este tempo todo, as primitivas. Socorro, primitivas!!!
E assim podemos defi nir
Defi nição 1
Integral defi nida – Dizemos que uma função f é integrável no intervalo fechado
a ba b]] se limlim
ssf Pf P) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = limSSf Pf P)), para qualquer partição P de
a ba b]]
(o que implicará limlim
ss((f Pf P) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = limSS((f Pf P) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim) = lim n
n
k
k=1=1
f
f(¯(¯(¯(¯(¯(¯xx))xxkk
para qualquer escolhido em xx x x]]. Representaremos esse limite por
bb
f
fxx))xx, que se lê integral defi nida de a até b de ffxx))xx. Temos então que
bb
a a f
f((xx))xx= lim= lim
n n k k=1=1
f
Teorema fundamental
do cálculo
Acabamos de definir a integral de uma função e constatamos que se f é integrável no
intervalo fechado a b] o valor do limite lim
n
k=1
(¯x)xk será sempre o mesmo para
qualquer escolhido em x x] e o valor desse limite será igual a
b
fx)x.
Suponhamos que f é integrável no intervalo fechado a b] e que f admita uma primitiva F em a b], isto é, x) =fx) em a b], seja P x, x1, x2, , x1, x} uma
partição qualquer do intervalo a b], com ax < x1< x2 < < x1< xb. Note que podemos escrever b)a) =
n
=
x)x)), pois
n
=1
Fx)Fx1)) = Fx1)Fx)) + Fx2)Fx1)) + Fx3)Fx2))+
+ Fxn)Fxn1))
Note também que o primeiro termo de cada parcela se cancela com o segundo termo da parcela seguinte. Fazendo esses cancelamentos, temos que a expressão anterior se reduz
a n
=1
x)x1)) =xn) =x) =b)a).
Como F é derivável x) =fx)), pelo teorema do valor médio estudado na aula 6, podemos garantir que existe um ponto , tal que
(x)(x) =(¯x)(xx) =(¯x)x=f(¯x)x.
Dessa forma,
(b)(a) = n
=
((x)(x)) = n
=
f(¯x)x.
Aplicando o limite quando , temos que
lim
((b)(a)) = lim
n
k=1
f(¯xk)xk= b
a
f(x)dx.
Note, entretanto, que b)a) é um número fixo, e é a diferença de dois números
b)a)), ou seja, é uma constante. Vimos na aula 1 (Limite de funções reais em um ponto)que o limite de uma constante é a própria constante, assim, a equação anterior pode ser reescrita da seguinte forma
b)a) =
b
Teorema 1 (Teorema fundamental do cálculo)
Se f for integrável no intervalo fechado a ba b]] e f admite uma primitiva F em
a ba b]], então,
bb))aa) =) =
bb
f fxx))dxdx.
Mostra-se que toda função contínua no intervalo fechado a b] é integrável nesse intervalo, assim podemos enunciar uma outra versão do teorema 1, a qual usaremos mais freqüentemente, já que as funções que trabalharemos nesta disciplina serão em sua maioria funções contínuas.
Teorema 2 (Teorema fundamental do cálculo)
Se f for contínua no intervalo fechado a ba b]] e f admite uma primitiva F em
a ba b]], então,
bb))aa) =) =
bb
f fxx))dxdx.
Exemplo 2
Calcule a integral defi nida /2
senx)x.
Solução
Identifi quemos cada elemento necessário à aplicação do teorema. Primeiro o intervalo a b], neste caso, temos que a= eb=
, logo, o intervalo é [/]. Sabemos da aula 2 que a função seno é contínua e sua primitiva é osx), logo, pelo teorema 2 temos que
/2
senx)dx=cos
2
Exemplo 3
Calcule a integral definida 3
ex.
Solução
Identifiquemos cada elemento necessário à aplicação do teorema. Primeiro o intervalo a b], neste caso, temos que = eb= 3, logo, o intervalo é [3].
Sabemos da aula 2 que a função exponencial é contínua e sua primitiva é , logo, pelo
teorema 2 temos que
3
exe3e.
Usaremos a notação x)xb
x ou simplesmente x)b para denotar b)a).
Assim, quando usarmos os teoremas anteriores, escreveremos
b
fx)dx=x)|xbx=x)|b=b)a).
Na aula 9, vimos que se f [a b]R for positiva e contínua em
a b], então, a área sob a curva y=x) no intervalo a b] é definida por
= lim
n∞n= limn∞
=
f(x)x. Vimos nesta aula que esse limite é um caso particular
das somas de Riemann estudadas nesta aula, ou seja, se a função tiver primitiva F, então,
= lim
n∞n= limn∞ k
k=
f(xk)·x= b
f(x)dx=F(b)F(a).
Exemplo 4
(Refazendo o exemplo 5 da aula 9)
Seja f : [ b]R a função definida por x) =x, a função identidade. Calcule a
área sob o gráfico da f.
Solução
Pelo que foi discutido, queremos calcular
fx)x. Como a função f é contínua e
tem primitiva x) = x
2 , temos pelo teorema 2 que
fx)dx=b)0) = b 2
2 02
2 =
b2
Atividade 2
Exemplo 5
(Refazendo o exemplo 6 da aula 9)
Vamos considerar agora a função f : [ b]R defi nida por y=x) =x. Calcule
a àrea sob o gráfi co da f.
Solução
Pelo que foi discutido, queremos calcular
fx)x. Como a função f é contínua e
tem primitiva x) = x
3 , temos pelo teorema 2 que
fx)dx=b)0) = b 3 3 03 3 = b3 3 .
Sabendo que todas as funções a seguir são contínuas no intervalo em que as estamos integrando, calcule as integrais defi nidas.
a)
22 x x55xx
b)
10 10 cos cos55xx))dxdx
c)
bb kdx k kdx kctecte
d)
1515 1 1 x xxx
e)
sensenxx))22 ososxx))dxdx
f)
sen
senxx+ 2+ 2))dxdx
g)
11
ee22xx
h)
22 55xx44x
x55 1 1xx
i)
22 xx+ 1)+ 1)xx
j)
bb Resumo
Nesta aula, revisamos as somas de Riemann, introduzimos as somas superior e inferior e vimos como elas foram utilizadas na definição da integral definida. Vimos o teorema fundamental do cálculo que fez a ligação da integral definida com as primitivas que estudamos nas aulas 8 e 9.
Auto-avaliação
Sabendo a primitiva de uma função contínua, vimos como é fácil calcular sua integral definida. Monte alguns exemplos utilizando a regra da cadeia, da soma, diferença, produto e quociente para calcular a integral definida, como o modelo seguinte.
Sabemos que a primitiva da soma é a soma das primitivas, assim, considerando
f g [a b]R funções contínuas com primitivas F G [a b]R, temos
b
fx) +gx))dx= x) +Gx))|b= b) +Gb))a) +Ga)) =
b)a)) + Gb)Ga))
= b c
fx)dx+ b
c
gx)dx.
Referências
ANTON, Howard. Cálculo: um novo horizonte. 6. ed. Porto Alegre: Bookman, 2000. v 1.