JONAS BORSETTI SILVA SANTOS ARGUMENTAÇÃO E PROVA: ANÁLISE DE ARGUMENTOS ALGÉBRICOS DE ALUNOS DA

(1)

JONAS BORSETTI SILVA SANTOS

ARGUMENTAÇÃO E PROVA: ANÁLISE DE

ARGUMENTOS ALGÉBRICOS DE ALUNOS DA

EDUCAÇÃO BÁSICA

MESTRADO PROFISSIONAL EM ENSINO DE MATEMÁTICA

PUC/SP

SÃO PAULO

(2)

JONAS BORSETTI SILVA SANTOS

ARGUMENTAÇÃO E PROVA: ANÁLISE DE

ARGUMENTOS ALGÉBRICOS DE ALUNOS DA

EDUCAÇÃO BÁSICA

Dissertação apresentada à Banca Examinadora da

Pontifícia Universidade Católica de São Paulo, como

exigência parcial para obtenção do título de MESTRE

PROFISSIONAL EM ENSINO DE MATEMÁTICA, sob

orientação da Profª Drª. Sônia Pitta Coelho.

PUC/SP

SÃO PAULO

(3)

Banca Examinadora

_______________________________________

(4)

Autorizo, exclusivamente para fins acadêmicos e científicos, a reprodução total ou parcial desta

Dissertação por processos de fotocopiadoras ou eletrônicos.

(5)

(6)

AGRADECIMENTOS

Primeiramente a Deus, que em nome de seu filho Jesus Cristo iluminou-me para a conclusão do iluminou-meu iluminou-mestrado.

À minha orientadora, Profª Drª Sonia Pitta Coelho, que com seus conselhos e sua amizade, fez com que eu me dedicasse de corpo e alma a esse trabalho.

Aos Drs. Lulu Healy e Luiz Gonzaga Xavier de Barros pelas sugestões dadas na qualificação e por fazerem parte de minha banca examinadora.

Aos meus pais Flávio e Maria José, que com seu amor e incentivo, pude concluir mais essa etapa de minha vida.

À minha avó Mariquinha, sem palavras para expressar o quanto você é importante para mim.

Aos meus irmãos Tadeu e Lucas, que, mais que meus irmãos, são meus grandes amigos. Também ao meu irmão Flávio (in memorian) – saudades.

À minha sogra Olívia, que me acolheu em sua família como seu verdadeiro filho.

Ao meu sogro Ricardo e à Mirtz, pela acolhida nos poucos feriados e pelo carinho.

Aos professores do Mestrado Profissional da PUC-SP, pelos ensinamentos, pelas cobranças e pelos conselhos dados em suas aulas.

Aos meus amigos Pedro Bigattão, Sérgio Alves, Ricardo Vasques e Ricardo Cardoso, companheiros do primeiro ao último dia do mestrado.

Aos meus cunhados Ângela, Viviane, Leonardo, Clarissa e Nadya, que se mostraram pacientes quando não pudemos nos encontrar, mas que agora poderemos.

A todos os alunos que ajudaram na conclusão realização desse trabalho. À Secretaria da Educação de São Paulo, pela ajuda financeira.

Aos colegas do Mestrado, pela amizade e companheirismo.

Aos colegas da E.E. Albino César, e da FIP, pelas palavras de incentivo, pela ajuda e pela amizade.

A toda minha família.

(7)

Principalmente, à minha esposa Priscila, pela sua paciência, compreensão e amor, por tudo isso e muito mais. Te amo hoje e sempre.

(8)

RESUMO

O presente trabalho trata de questões apresentadas no questionário de álgebra do projeto AprovaME (Argumentação e Prova na Matemática Escolar), da PUC-SP. Uma das metas do projeto é levantar um mapa sobre as concepções de argumentação e prova dos alunos brasileiros, mais precisamente dos alunos do Estado de São Paulo. Foram elaborados dois questionários, um de Álgebra e um de Geometria para esse levantamento, aplicados para uma amostra composta de 1998 alunos na faixa de 14 a 16 anos, matriculados na 8ª série do Ensino Fundamental e 1º ano do Ensino Médio. Após a análise descritiva dos dados coletados, pudemos verificar que a criação de argumentação e prova pelos alunos é falho, visto que muitos deles sequer viram qualquer tipo de argumentação ou prova em sua vida estudantil. Feita a análise descritiva, realizamos uma análise multidimensional, com o auxílio do software C.H.I.C. que também nos auxiliou na escolha dos alunos que seriam entrevistados. Ainda, para uma melhor análise, realizamos entrevistas com alguns professores acerca das questões que são objeto de nosso estudo, como também sobre o uso de argumentações e provas em sala de aula. Os mesmos valem-se muito pouco desse recurso. Em geral, nossas análises, tanto quantitativas quanto qualitativas, sugerem que os processos de argumentação e provas não estão sendo contemplados com esses alunos. Os alunos que responderam às questões apresentaram, na maioria das vezes, argumentos empíricos. Os que tentaram evidenciar alguma propriedade ou alguma estrutura para a argumentação e prova valeram-se muitas vezes da língua materna. Além disso, o uso da linguagem algébrica é pouco difundida nas escolas, fato evidenciado pelas argumentações apresentadas pelos alunos.

(9)

ABSTRACT

The present work focuses questions presented in the questionnaire of Algebra of the AProvaME project (Argumentation and Proof in the School Mathematics), of the PUC-SP. One of the goals of the project is to raise a map on the conceptions of argument and proof of the Brazilian pupils, more necessarily of the pupils of the State of São Paulo. Two questionnaires, one of Algebra and one of Geometry, had been elaborated for this survey, applied for a composed sample of 1998 pupils in the band of 14 the 16 years, registered in 8th series of Basic School and 1° year of Average School. After descriptive analysis of the collected data, we could verify that the creation of argumentation and proof for the pupils is defective, since many of them had never seen any type of argumentation or proof in its school life. Made the descriptive analysis, we carry through a multidimensional analysis, with the aid of the software C.H.I.C. that also assisted us in the choice of the pupils who would be interviewed. Still, for one better analysis, we carry through interviews with some teachers, concerning the questions that are object of our study, as also on the use of argumentations and proofs in classroom. The same ones are little used in their classes. In general, our analyses, in such a way quantitative how much qualitative, they suggest that the processes of argumentation and proofs are not being contemplated with these pupils. The pupils who had answered to the questions had presented, in the majority of the times, empirical arguments. The ones that had tried to evidence some property or some structure for the argumentations and proofs had used many times the narrative form. Moreover, the use of the algebraic language is little spread out in the schools, fact evidenced for the arguments presented for the pupils.

(10)

S

UMÁRIO

APRESENTAÇÃO ... 15

CAPÍTULO 1 ... 16

1.1 Justificativa ... 16

1.2 Um pouco sobre a história da Álgebra e das provas e demonstrações ... 17

1.3 As pesquisas em Educação Matemática sobre demonstração ... 19

1.4 O Projeto AProvaME – Argumentação e Prova na Matemática Escolar... 22

1.5 A amostra e o objetivo da pesquisa... 25

CAPÍTULO 2 ... 28

2.1 As idéias de Balacheff e o questionário de Álgebra... 28

2.2 Codificações utilizadas nas questões A3 e A4 ... 36

2.3 Alguns exemplos de codificações utilizadas ... 39

CAPÍTULO 3 – ANÁLISE QUANTITATIVA... 51

3.1 Introdução ... 51

3.2 As planilhas do Excel ... 51

3.3 Análises quantitativas da amostra... 53

3.4 Análises quantitativas do grupo em foco... 57

3.5 Análise Multidimensional, com o software CHIC... 65

3.6 Conclusões parciais acerca da análise quantitativa ... 76

CAPÍTULO 4 – ANÁLISE QUALITATIVA ... 80

4.1 Introdução ... 80

4.2 Respostas ilustrativas da questão A3 ... 81

4.3 Respostas ilustrativas da questão A4 ... 85

4.4 Protocolos da amostra codificados como 3... 89

4.5 Entrevistas ... 97

4.5.1 Alunos ... 97

4.5.2 Professores ... 111

4.5.3 Alunos e Professores ... 115

CONCLUSÃO ... 120

REFERÊNCIAS BIBLIOGRÁFICAS... 125

APÊNDICES ... 128

Apêndice 1 – Resultados do C.H.I.C. ... 128

ANEXOS ... 136

(11)

L

ISTA

D

E

Q

UADROS

Quadro 1 – Questão A1 do questionário de Álgebra ... 30

Quadro 2 – Continuação da questão A1 do questionário de Álgebra... 32

(12)

L

ISTA

D

E

T

ABELAS

Tabela 1 – Codificação das respostas dos alunos ... 39

Tabela 2 – Codificação das justificativas dos alunos ... 39

Tabela 3 – Recorte das questões A3 e A4 do grupo em foco ... 52

Tabela 4 – Questão A3 - amostra ... 53

Tabela 5 – Justificativa da questão A3 - Amostra ... 53

Tabela 6 – Questão A4 - Amostra ... 54

Tabela 7 – Justificativa da Questão A4 - Amostra ... 54

Tabela 8 – Questão A3 – Amostra – 8ª série EF... 55

Tabela 9 – Justificativa da Questão A3 – Amostra – 8ª série EF ... 56

Tabela 10 – Questão A3 – Amostra – 1ª série EM... 56

Tabela 11 – Justificativa da Questão A3 – Amostra – 1ª série EM ... 56

Tabela 12 – Questão A4 – Amostra – 8ª série EF... 57

Tabela 13 – Justificativa da Questão A4 – Amostra – 8ª série EF ... 57

Tabela 16 – Questão A3 – Grupo em Foco... 58

Tabela 17 – Sujeitos na Questão A3 – Grupo em Foco ... 58

Tabela 18 – Justificativas na Questão A3 – Grupo em Foco ... 58

Tabela 19 – Sujeitos e justificativas na Questão A3 – Grupo em Foco. 58 Tabela 20 – Questão A4 – Grupo em Foco... 59

Tabela 21 – Sujeitos na Questão A4 – Grupo em Foco ... 59

Tabela 22 – Justificativas na Questão A4 – Grupo em Foco ... 59

Tabela 23 – Sujeitos e justificativas na Questão A4 – Grupo em Foco. 59 Tabela 24 - Questão A3 – cruzamento dos dados: verdadeiro/falso e justificativas – Grupo em Foco ... 61

Tabela 25 - Questão A4 – cruzamento dos dados: verdadeiro/falso e justificativas – Grupo em Foco ... 62

(13)

L

ISTA

D

E

F

IGURAS

Figura 1 – Exemplo 1 falso para codificação de A3... 40

Figura 4 – Exemplo 1 verdadeiro para código 1 de A3... 41

Figura 8 – Exemplo 1 verdadeiro para código 2a de A3... 43

Figura 11 – Exemplo 1 verdadeiro para código 2b de A3... 44

Figura 13 – Exemplo verdadeiro para código 3 de A3... 45

Figura 14 – Exemplo 1 falso para A4... 46

Figura 15 – Exemplo 2 falso para A4... 47

Figura 22 - intersecção para análises do CHIC ... 66

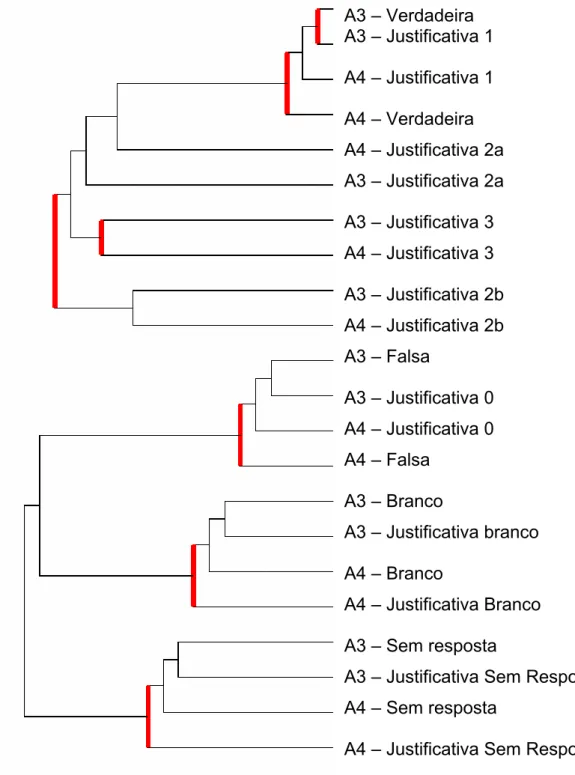
Figura 23 – Árvore de similaridades do C.H.I.C... 67

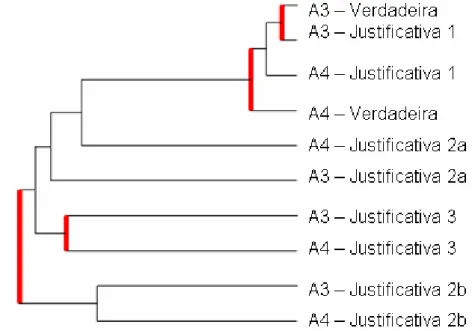
Figura 24 - Agrupamento 1 das similaridades referentes às respostas verdadeiras nas questões A3 e A4... 68

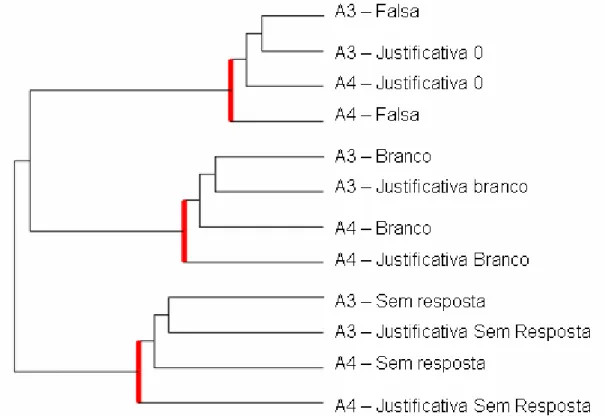
Figura 25 - Agrupamento 2 das similaridades referentes às respostas nas questões A3 e A4. ... 70

Figura 26 – Árvore Coesitiva do C.H.I.C... 72

Figura 27 – Subgrupo 1 da árvore coesitiva do C.H.I.C. ... 73

Figura 31 – Resposta do aluno 7 do Grupo em Foco para a questão A3... 81

(14)

Figura 49 – Resposta 1 com código 3 na Questão A3 ... 90

Figura 60 – Resposta do aluno 50 na Questão A3 ... 98

(15)

APRESENTAÇÃO

A coordenadora do projeto AProvaME (Argumentação e Prova na Matemática Escolar), Profª Drª. Siobhan Victoria (Lulu) Healy, propôs que um grupo de cinco mestrandos participantes desse projeto fizessem uma análise estatística das respostas dos questionários aplicados na primeira fase do projeto. Tal análise tem por objetivo criar um mapa das concepções dos alunos sobre argumentação e prova. Para tal, foram elaborados dois questionários, um de Álgebra e outro de Geometria, aplicados para 1998 estudantes da 8ª série do Ensino Fundamental e da 1ª série do Ensino Médio, com faixa etária entre 14 e 16 anos.

Este trabalho faz uma análise estatística descritiva das respostas obtidas no questionário de Álgebra, mais precisamente na questão que trata sobre a soma de dois números ímpares e na que trata da soma de um múltiplo de 3 com um múltiplo de 6.

Iniciamos o trabalho apresentando uma pequena visão histórica sobre os trabalhos existentes que tratam de argumentações e provas. Depois, explicamos o projeto em si e a nossa amostra.

Após, apresentamos o questionário, cuja investigação trata esse trabalho, a codificação utilizada para as questões e alguns exemplos de respostas dentro dessas codificações.

A seguir, apresentamos uma análise estatística descritiva da amostra e do grupo em foco e também algumas respostas ilustrativas do grupo em foco.

(16)

CAPÍTULO 1

Nesse capítulo, são abordados cinco itens. O primeiro é a justificativa, que explica porque escolhemos esse tema como trabalho final. O segundo faz um breve relato histórico sobre a história da álgebra e das demonstrações e provas. O terceiro faz um breve relato sobre as pesquisas em Educação Matemática sobre demonstrações. O quarto é sobre o projeto AProvaME, que explica o que é esse projeto e como surgiu no Programa de Estudos Pós-Graduados em Educação Matemática da PUC-SP. Por fim, o quinto descreve a amostra e o objetivo da pesquisa.

1.1 Justificativa

Desde a graduação, quando cursei a disciplina Álgebra, tenho me interessado sobre como provar e argumentar no contexto escolar. Quando comecei a lecionar para o Ensino Fundamental (EF) e Ensino Médio (EM), percebi que são pouquíssimos os livros que oferecem argumentos no tratamento expositivo. Normalmente, quando aparecem, essas argumentações se apresentam nos temas de geometria.

Além disso, a dificuldade do aluno em entender o problema, em diagnosticar em qual assunto está inserido tal problema e em argumentar sobre sua resolução faz com que tal questionamento venha sempre à mente do professor.

Esses fatos geraram meu interesse em investigar como os alunos justificam determinadas “verdades matemáticas”, como por exemplo, a afirmação: “a soma de dois números pares é sempre par”.

(17)

Tal projeto é patrocinado pela CNPq (Conselho Nacional de Desenvolvimento Científico) e conta entre seus participantes com vários professores do Programa e alunos do Mestrado Profissional em Ensino de Matemática da PUC-SP. Uma descrição mais completa encontra-se na terceira seção desse capítulo.

1.2 Um pouco sobre a história da Álgebra e das provas e demonstrações

A palavra PROVA teve vários significados durante a história da Matemática e em diferentes níveis e épocas. Sabe-se que as demonstrações matemáticas surgiram com Tales de Mileto e Pitágoras de Samos, mas não podemos afirmar que os povos pré-helênicos não tinham noção de prova, nem que sentissem a necessidade de prova. Há indícios de que esses povos percebiam ocasionalmente que certos modos de calcular áreas de volumes poderiam ser reduzidos a problemas mais simples. Além disso, os Escribas verificavam ou “provavam” que suas divisões estavam corretas através de multiplicações, como também verificavam que uma resposta era correta através da substituição do valor encontrado.

Tales (c.a. 600 a.C. – 525 a.C.) é considerado até hoje o primeiro matemático verdadeiro, pois lhe são atribuídos alguns teoremas, os quais este havia provado. Contudo, não há documentos antigos que podem ser apontados como provas desse feito, apenas menções datadas de 1.000 anos depois do tempo de Tales, por Proclo (410-485).

Apesar de Tales e Pitágoras terem tratado mais de Geometria que de Álgebra, não podemos deixar de notar que as provas matemáticas começaram assim, através de teoremas geométricos.

(18)

A primeira e talvez a maior obra matemática de todos os tempos são Os Elementos de Euclides (360 a.C. – 295 a.C.). Composto de 13 livros, Euclides os dividiu da seguinte forma: os seis primeiros tratam de geometria plana elementar, os três seguintes sobre teoria dos números, o livro X sobre incomensurabilidade e os três últimos versam principalmente sobre geometria no espaço. Não são atribuídas a Euclides as provas apresentadas em seus Elementos, mas sim a compilação de todo o conhecimento matemático da época.

O primeiro matemático que pensou em desenvolver uma característica universal para a simbologia matemática foi Leibinz, num artigo sobre análise combinatória de 1.666. Ele tinha visões acerca e uma lógica simbólica formal.

George Peacock (1791 – 1858) foi o primeiro matemático que produziu um importante trabalho escrito com a intenção de dar à álgebra o caráter demonstrativo. Para isso, Peacock propunha uma reavaliação da relação entre a aritmética e a álgebra. Separava a álgebra em duas partes: a álgebra aritmética e a álgebra simbólica. Procurou dar à álgebra um tratamento lógico equiparável aos Elementos de Euclides, ganhando o epíteto de “o Euclides da Álgebra”.

Para Peacock, a álgebra aritmética era considerada como o estudo resultante de uso de símbolos para denotar os números decimais positivos usuais, juntamente com os símbolos operatórios. Já a álgebra simbólica era uma ciência que olha somente as combinações de sinais e símbolos de acordo com certas leis, que são totalmente independentes dos valores específicos dos símbolos.

Outro que sustentava a nova visão da álgebra foi Augustus De Morgan (1806 – 1871). De Morgan insistia em que “com uma única exceção, nenhuma palavra ou sinal em álgebra ou aritmética tem um átomo de significado em todo este capítulo, cujos assuntos são símbolos e suas leis de combinação, dando uma álgebra simbólica que pode a partir daí tornar-se a gramática de cem álgebras diferentes significativas” (ibidem).

(19)

1.3 As pesquisas em Educação Matemática sobre demonstração

Para os pesquisadores em Educação Matemática, a prova ou demonstração é de suma importância, pois, sendo a prova um aspecto fundamental para a Matemática, esta deveria ser incluída no currículo da Escola Básica, na formação dos alunos, com o objetivo de desenvolver o raciocínio dedutivo.

Inclusive, podemos citar como exemplo o que aconteceu nos Estados Unidos, onde esse tema ficou completamente esquecido e a partir dos novos

Standards (2000), do National Council of Teachers of Mathematics, passou a ser um dos temas centrais dos currículos de Matemática.

Muitas são as pesquisas em torno desse tema. Alguns tratam da função da prova na Escola Básica (Hanna, 1990, apud Pietropaulo, 2005); outros estudaram os tipos de provas aceitos pelos matemáticos e por educadores matemáticos (Bell, 1976, apud Pietropaulo, 2005; Balacheff, 1988); outros ainda, pesquisaram o progresso dos alunos no desenvolvimento dedutivo (Hoyles, 1997). Destacaremos dois trabalhos: o primeiro, de Balacheff (1988), que analisou as dificuldades dos alunos no processo de aprendizagem de provas e o de Healy e Hoyles (2000) que estudaram as concepções dos alunos sobre provas. O trabalho de Balacheff para nós é de suma importância, pois através dele criamos os códigos para codificação dos protocolos, cuja explicação mais detalhada encontra-se no Capítulo 2.

Já o trabalho de Healy e Hoyles é o ponto de partida para a criação do projeto AProvaME. A partir dele criamos nossos questionários e todos os objetivos do projeto.

(20)

Para alguns, a argumentação não leva necessariamente à demonstração (Duval, 1991, apud Pietropaulo). Para outros, existe uma relação firmada entre esses termos, ou seja, através da argumentação chegaremos à demonstração. Como disse Balacheff (1999) “não haveria nem continuidade nem ruptura entre argumentação e demonstração, mas uma relação complexa e constitutiva de cada uma: a argumentação constitui um obstáculo epistemológico à aprendizagem da demonstração e em especial da prova em matemática”.

Inclusive, para nós, não haverá a distinção entre os termos demonstração e prova, pois o nosso foco são os alunos de 8ª série do Ensino Fundamental e 1º ano do Ensino Médio. Aqui, as palavras apresentadas serão sinônimas, pois são tratadas como explicações válidas matematicamente, não apenas em sua forma algébrica, axiomática.

Devemos ter cuidado ao pensar somente no resultado final obtido na prova. Não podemos deixar de considerar os processos utilizados pelo aluno para a obtenção da prova, no seu entender. Se olharmos somente o produto final, estaremos ocultando o processo demonstrativo criado por ele, a formulação de alguns teoremas que para ele levam à prova, a exploração do tema em si, que antecede o produto final. Esse processo todo conta com o raciocínio hipotético-indutivo, próprio de cada ser humano.

Dessa forma, os Parâmetros Curriculares para o Ensino Fundamental (1998) chamam a atenção para que o professor de matemática, quando da criação do conhecimento matemático pelo aluno

(21)

relevo ao aprendizado dessa ciência em todos os níveis de ensino.” (PCN, 1998, p. 28).

Como afirma Pietropaulo (2005), “A principal diferença entre as duas “espécies” de demonstração – a que apenas valida e a que também explica – é que a explicativa termina por utilizar raciocínios baseados em idéias matemáticas, enquanto a mera prova formal emprega basicamente regras de sintaxe.” Isso nos é importante, pois para o aluno, a principal prova é a que explica, é através desse tipo de prova que ele constrói seu conhecimento matemático, é através dessa que ele compreende o porquê de determinado fato matemático ocorrer, é através desse tipo de prova que se explica porque determinado teorema é verdadeiro.

Hanna (1995) procura diferenciar a função da prova para a Matemática e para a Educação Matemática: “enquanto na prática matemática a função da prova é justificar e verificar, a sua função principal na educação matemática é seguramente a da explicação” (p.47). Inclusive, no mesmo trabalho, Hanna diz que a prova deve incentivar a compreensão: “Uma boa prova, entretanto, não deveria ser somente correta e explicativa, a mesma poderia também levar em consideração, especialmente em seu nível de detalhe, o contexto da aula e a experiência dos estudantes.” (1995, p.48).

(22)

Ademais, o uso do computador hoje para a educação é cada vez mais atual, cada vez mais difundido, cada vez mais aceito. Nesse sentido, a apresentação de softwares educativos para a validação ou simplesmente para a verificação de resultados é tal, que em várias escolas de São Paulo, existe pelo menos uma sala de informática, onde o professor pode, com a ajuda do computador, tornar sua aula mais atrativa para o aluno e porque não, mais compreensível.

1.4 O Projeto AProvaME – Argumentação e Prova na Matemática Escolar

No Brasil, ainda é modesto o número de pesquisas sobre provas matemáticas, principalmente no âmbito escolar.

Entretanto, o número de pesquisadores interessados nesse tema vem aumentando nos últimos anos. Citamos PIETROPAULO (2005); GRAVINA, M.A. (2001); VAZ, R. de L. (2004), entre outros.

Uma grande pesquisa sobre esse assunto está sendo realizada pelo Programa de Estudos Pós-Graduados em Educação Matemática da Pontifícia Universidade Católica de São Paulo (PUC-SP), denominada projeto AProvaME, sob a coordenação da Profª Drª Siobhan Victoria (Lulu) Healy (a partir daqui, denominaremos o projeto AProvaME apenas por projeto).

O projeto tem por objetivo:

1. Levantar um mapa das concepções sobre argumentação e prova de alunos adolescentes em escolas do estado da São Paulo.

2. Formar grupos colaborativos compostos por pesquisadores e professores para a elaboração de situações de aprendizagem, visando envolver alunos em processos de construção de conjecturas e provas em contextos integrando ambientes informatizados.

(23)

aprendizagem, assim como na evolução de conhecimentos pedagógicos sobre prova em Matemática.

4. Avaliar situações de aprendizagem, em termos da compreensão dos alunos sobre a natureza e funções de prova em Matemática.

5. Investigar a implementação destas atividades por diferentes professores e assim identificar em que medida sua participação nos grupos colaborativos fornece uma apropriação desta abordagem para o ensino e aprendizagem de prova.

6. Formular recomendações relacionadas ao papel da argumentação e da prova no currículo de Matemática escolar.

7. Contribuir para o debate internacional sobre o ensino e aprendizagem de prova em Matemática.

O projeto, iniciado em Agosto/2005, com término previsto para Agosto/2007, é patrocinado pela CNPq. Conta com seis pesquisadores, que são professores doutores da PUC-SP e trinta e um colaboradores, mestrandos do curso de Mestrado Profissional em Ensino de Matemática da PUC-SP.

O projeto é composto de duas fases. Na primeira fase, já concluída, os pesquisadores e os colaboradores reuniram-se quinzenalmente para criarem dois questionários investigadores, um de álgebra e um de geometria, baseados nos questionários de uma pesquisa semelhante realizada na Inglaterra: “Justifying and Proving in School Mathematics” 1.

Tal pesquisa apresentou resultados nacionais sobre as concepções de provas de alunos de 14-15 anos, que seguiram uma nova maneira de provar, especificada no currículo nacional daquele país.

Apresentou também resultados interessantes, como:

• A grande maioria dos alunos usa argumentos empíricos para suas próprias construções de provas;

• Os estudantes com mais sucesso apresentaram provas em linguagem comum, não usando álgebra;

1_{HEALY, S. V. (L.)., & HOYLES, C. Justifying and Proving in School Mathematics. Technical}

(24)

• As respostas foram influenciadas principalmente pelas suas competências matemáticas, e também por fatores curriculares, sexo do aluno e o que eles entendiam por prova.

Diferentemente do que pretendemos com esse trabalho, o estudo de Healy e Hoyles levou em consideração alguns aspectos importantes, como o sexo dos alunos, a argumentação utilizada e ainda a concepção dos alunos sobre o que é uma prova.

Tal pesquisa concluiu que a grande maioria dos alunos não é capaz de construir provas válidas: em geral, valem-se de argumentos empíricos para construir uma prova, apesar de saberem que são mais pobres e não receberiam a melhor nota de seus professores, e também que esse tipo de prova não é geral, mas gera uma poderosa convicção para a afirmação que pretende ser provada. Ainda, as provas narrativas são populares entre os estudantes e estes têm mais sucesso ao construir provas valendo-se das narrativas.

Além disso, pouquíssimos estudantes tiveram sucesso ao tentarem construir provas sobre determinadas afirmações. Inclusive, as pesquisadoras levantaram uma questão ao concluirem a pesquisa: “If students do not see algebra as a language with which they can explain phenomena in mathematics

classrooms in which explanations are highly valued, what motivation can there

be for those who can successfully construct informal arguments to learn how to

reexpress them algebraically?” (Se os estudantes não vêem a Álgebra como

uma linguagem com a qual eles podem explicar fenômenos matemáticos em sala de aula, onde as explicações são altamente valorizadas, qual motivação pode haver para aqueles que podem com sucesso construir argumentos informais para aprender como re-expressá-los algebricamente?) 2.

Após a criação desses questionários, alguns colaboradores aplicaram-nos como questionários pilotos, para verificar a viabilidade das questões utilizadas, o número de questões, o tempo de aplicação, o formato, entre outras análises.

A partir dessas informações, os questionários foram re-elaborados e aplicados em várias escolas públicas e privadas do estado de São Paulo.

(25)

Após a aplicação, esses questionários foram codificados segundo uma classificação inspirada nos tipos de provas propostos por Balacheff3. Tal codificação será comentada posteriormente.

Depois de realizada a codificação, cada colaborador ficou responsável por inserir os dados relativos a essas codificações em uma planilha eletrônica do software MS-Excel.

Já a segunda fase contempla dois eixos inter-relacionados de investigação: a aprendizagem e o ensino.

No eixo da aprendizagem, o objetivo principal é a elaboração e avaliação de situações destinadas às áreas de dificuldades e limitações de compreensão. No eixo relativo ao ensino, a atenção se voltará ao professor e sua contribuição no processo de elaboração das situações de aprendizagem, e nas modificações destas em ação.

Esta segunda fase, já em andamento, tem como metodologia o design-based research (COBB et al. 2003), e foi dividida em duas etapas:

_ Na primeira etapa do design (etapa intra-grupos), as situações foram elaboradas por grupos de três a cinco colaboradores e dois pesquisadores e, em seguida, testadas/aplicadas em uma pequena amostra de alunos, e, por fim, discutidas e reformuladas em cada grupo.

_ Na segunda etapa (inter-grupos), as produções de cada grupo foram disponibilizadas no ambiente virtual, ambiente esse criado desde a primeira fase (TELEDUC), de maneira que cada professor-colaborador pôde desenvolver, pelo menos, duas atividades elaboradas pelos outros grupos (uma em geometria e outra em álgebra), em uma de suas turmas.

Esta é a fase em que o projeto encontra-se atualmente (leia-se primeira quinzena de março/2007), mais precisamente na segunda etapa desta.

1.5 A amostra e o objetivo da pesquisa

A aplicação dos questionários foi feita em vinte e oito escolas das redes particular e pública, sendo que seis dessas são particulares, três são municipais e o restante são escolas estaduais.

(26)

A nossa amostra é de 1.998 alunos, sendo que 277 (13,77%) são da Rede Particular de Ensino, 95 (4,75%) são da rede municipal de ensino e 1.626 (81,38%) são da Rede Estadual de Ensino. A grande maioria, portando, pertence à Rede Estadual de Ensino. Além disso, temos 60 turmas de 8ª série do Ensino Fundamental e 75 turmas da 1ª série do Ensino Médio. Com relação ao número de alunos, temos 896 alunos na 8ª série do Ensino Fundamental e 1.102 alunos na 1ª série do Ensino Médio.

Na Rede Municipal de Ensino, todos os alunos participantes são da 8ª série do Ensino Fundamental, correspondendo a 4,75% da amostra. Na Rede Particular de Ensino, temos 197 alunos na 8ª série do Ensino Fundamental e 80 alunos no 1º ano do Ensino Médio, correspondendo respectivamente a 9,86% e 4,00% da amostra. Já na Rede Estadual de Ensino, temos 604 alunos na 8ª série do Ensino Fundamental e 1.022 alunos no 1º ano do Ensino Médio, que correspondem a 30,23% e 51,15% da amostra, respectivamente. Podemos perceber que mais da metade da nossa amostra encontra-se no 1º ano do Ensino Médio da Rede Estadual de Ensino.

Os questionários foram aplicados nos três períodos de ensino, ou seja, matutino, vespertino e noturno. Tal aplicação ocorreu entre os meses de outubro e novembro de 2005.

As 28 escolas que participaram da pesquisa estão situadas em 14 municípios: Embu Guaçu, Itapecerica da Serra, Itaquaquecetuba, Itupeva, Jacareí, Jacupiranga, Jundiaí (2), Lorena, Osasco, Promissão, Santos, São Bernardo do Campo (3), São Paulo (12) e São Roque, sendo que oito escolas estão situadas no interior do estado de São Paulo (28,6%), uma no litoral (3,6%) e dezenove na região metropolitana (67,8%).

A partir de nossa amostra de 1.998 respondentes, foram obtidos aleatoriamente 50 alunos, conjunto esse denominado, em nosso trabalho, grupo em foco. Tal escolha foi feita de forma que cada aluno do grupo em foco correspondesse a aproximadamente 40 alunos da amostra.

Nosso trabalho investiga esse grupo em foco buscando identificar tendências da amostra.

(27)

cruzamento dos dados da questão A3 com os da questão A4 na grupo em foco. A partir dos dados e dos cruzamentos dessas questões, escolheremos de quatro a seis sujeitos para entrevistas, entrevistas estas baseadas nas respostas apresentadas pelos alunos em seus questionários.

Portanto, nosso trabalho será, num primeiro momento, quantitativo, apontando igualdades e divergências entre amostra e grupo em foco e depois dentro do próprio grupo em foco. Num segundo momento, nosso trabalho será qualitativo, com a realização de entrevistas com quatro a seis sujeitos escolhidos do grupo em foco e análise dessas entrevistas.

(28)

CAPÍTULO 2

2.1 As idéias de Balacheff e o questionário de Álgebra

Como já apontamos anteriormente, os questionários de Álgebra e Geometria foram baseados naqueles concebidos por Healy e Hoyles (1998) na Inglaterra e já utilizados em outros países, como França, Taiwan, Israel e Austrália.

Tais questionários compreenderam questões que visaram avaliar se os alunos conseguem distinguir evidências empíricas de argumentos matematicamente válidos, se compreendem e se são capazes de construir argumentos válidos e se conseguem estabelecer o domínio de validade de uma prova.

Os questionários estão estruturados e organizados em dois blocos: avaliação de cinco argumentos apresentados como provas de uma determinada afirmação e a construção de provas e argumentos.

Descrevemos a seguir o questionário de álgebra e suas estruturas e organizações do mesmo.

QUESTÃO A1

Nessa questão, os respondentes deveriam analisar cinco argumentações de supostos alunos sobre a afirmação de que “a soma de dois números pares é par”. Após esta análise, eles escolheriam qual das cinco mais se assemelharia à dele e para qual seu professor daria a maior nota.

Tais argumentações basearam-se nos tipos de provas apontados por Balacheff (1987):

_ O Empirismo Ingênuo que, para validar uma propriedade, toma alguns poucos casos, sem questionamento quanto à particularidade;

(29)

_ O Exemplo Genérico, que consiste na explicitação das razões que validam uma propriedade que encerra uma generalidade, mesmo fazendo uso de uma representação particular do objeto em estudo;

_ Experimento Mental, onde a argumentação flui através de pensamentos que controlam toda a generalização da situação, e não mais através de situações particulares.

Para Balacheff, as provas são divididas em duas categorias: pragmáticas e intelectuais. As primeiras apóiam-se sobre conhecimentos práticos, utilizam ações, como por exemplo, desenhos, observação de figuras para verificar que uma determinada afirmação é válida. Já as provas intelectuais envolvem formulações e relações entre determinadas propriedades em questão. A passagem das provas pragmáticas e intelectuais é marcada por uma evolução dos meios de linguagem.

Exemplificaremos a seguir as quatro etapas de Balacheff na seguinte situação:

O professor pede aos alunos para verificarem se o número de diagonais de um polígono de n lados é dado pela fórmula

2 ) 3 (n− n

.

Para validar tal resultado, os alunos poderiam valer-se de uma das quatro etapas de Balacheff:

_ No empirismo ingênuo, o aluno desenharia um polígono de 5 lados e traçaria as diagonais, encontrando 5 diagonais. Daí aplicaria a fórmula,

verificando que 5

2 ) 3 5 ( 5 = −

, e daí a fórmula é válida para qualquer polígono.

_ No experimento crucial, o aluno desenha um polígono com um

número de lados maior, por exemplo, 13 lados, e traça todas as suas diagonais, encontrando 65. Após desenhar, testa a fórmula e verifica

que o resultado é o mesmo, ou seja, 65

2 ) 10 13 ( 13 = −

(30)

_ No exemplo genérico, o aluno utiliza o caso particular do hexágono, verificando que de cada vértice partem 3 diagonais, obtendo um total de 18 diagonais. Mas, observa que cada diagonal é contada duas vezes, então divide o valor encontrado, ou seja, 18 por 2, encontrando 9 diagonais. O aluno percebe também que o mesmo acontece para outros polígonos, mudando apenas o número de diagonais que sai de cada vértice.

_ No experimento mental, o aluno mostra que para encontrar o número de diagonais de um polígono, basta considerar o número de diagonais que partem de cada vértice. Para isto, basta tomar o número de vértices e subtrair seus dois vizinhos e ele mesmo, ou seja, 3, multiplicar o resultado pelo número de vértices, e depois dividir por 2, pois cada diagonal é contada duas vezes. Daí se considerarmos n como sendo o número de vértices do polígono, teríamos

2 ) 3 (n− n

.

Apresentamos, a seguir, cada uma das provas apresentadas na questão e onde se encaixam nos tipos de provas de Balacheff.

Quadro 1 – Questão A1 do questionário de Álgebra

A1: Artur, Beth, Duda, Franklin e Hanna estavam tentando provar que a seguinte

afirmação é verdadeira:

Quando você soma dois números pares quaisquer, o resultado é sempre par.

Resposta de Artur

a é um número inteiro qualquer

b é um número inteiro qualquer

2a e 2b são números pares quaisquer

2a +2b = 2 (a + b)

Então Artur diz que a afirmação é verdadeira.

Resposta de Beth

2 + 2 = 4 4 + 2 = 6 2 + 4 = 6 4 + 4 = 8 2 + 6 = 8 4 + 6 = 10

(31)

Resposta de Duda

Números pares terminam em 0, 2, 4, 6 ou 8.

Quando você soma dois destes, a resposta

vai ainda terminar em 0, 2, 4, 6 ou 8.

Então Duda diz que a afirmação é verdadeira.

Resposta de Franklin

Então Franklin diz que a afirmação é verdadeira

Resposta de Hanna

8 + 6 = 14

8 = 2 x 4 6 = 2 x 3 14 = 2 x (4 + 3)

8 + 6 = 2 x 7

Então Hanna diz que a afirmação é verdadeira

Das respostas acima, escolha uma que é a mais parecida com a resposta que você daria se tivesse que resolver esta questão.

Das respostas acima, escolha aquela para a qual você acha que seu professor daria a melhor nota.

Na resposta de Arthur, temos o Experimento Mental, pois apresenta deduções lógicas, baseadas em propriedades.

Na resposta de Beth, temos o Empirismo Ingênuo, pois constata que a afirmação é válida para alguns casos particulares e afirma que é valida para todos os casos.

Na resposta de Duda, seria um caso de Exemplo Genérico, caracterizado pela verificação da afirmação e de algumas propriedades em um exemplo, mas sem considerá-lo particular.

(32)

Na resposta de Hanna, temos também uma evidência de Exemplo Genérico, pois usa um exemplo para verificação das propriedades e para verificar se a afirmação é verdadeira ou não, mas sem considerar esse exemplo tão particular, intenta construir uma generalidade usando esse exemplo.

Ainda a questão A1 tratava de obter dos alunos uma avaliação sobre a generalidade dos argumentos apresentados:

A afirmação é:

Quadro 2 – Continuação da questão A1 do questionário de Álgebra

Para cada resposta abaixo, circule SIM, NÃO ou NÃO SEI.

Mostra que a afirmação é

sempre verdadeira.

Mostra que a afirmação é verdadeira apenas

para

alguns números pares.

Resposta de Artur Sim Não Não sei Sim Não Não sei

Resposta de Beth: Sim Não Não sei Sim Não Não sei

Resposta de Duda: Sim Não Não sei Sim Não Não sei

Resposta de Franklin: Sim Não Não sei Sim Não Não sei

Resposta de Hanna: Sim Não Não sei Sim Não Não sei

Pretendíamos aqui que o aluno conseguisse determinar se as argumentações apresentadas são válidas sempre, em alguns casos ou nunca. Ainda, colocamos uma opção para quando não soubesse dizer (Não Sei).

QUESTÃO A2

(33)

O resultado era “QUANDO VOCÊ SOMA DOIS NÚMEROS PARES QUAISQUER, O RESULTADO É SEMPRE PAR” e o aluno teria que assinalar se a afirmação “QUANDO VOCÊ SOMA DOIS NÚMEROS PARES MAIORES QUE 100, O RESULTADO É SEMPRE PAR” já estaria provada a partir da afirmação anterior ou se ele teria que construir uma nova prova.

A2. Suponha que já foi provado que:

Zé pergunta o que precisa ser feito para provar que:

Quando você soma dois números pares maiores que 100, o resultado é sempre par.

Escolha A ou B:

(A) Zé não precisa fazer nada, pois a afirmação já foi provada.

(B) Zé precisa construir uma nova prova.

Iremos agora para a questão A5, pois as questões A3 e A4 são os objetos de estudo deste trabalho e serão detalhadas mais à frente.

QUESTÃO A5

Na questão A5, buscamos verificar a compreensão dos alunos sobre a noção de fatorial.

Iniciamos a questão colocando a definição de fatorial de um número natural e depois apresentamos cinco questões relativas ao fatorial

A5(a): Perguntamos: “5! É par? Justifique”. Como já havíamos colocado o que significava 5!, esperávamos que os alunos verificassem que 2 é um fator de 5!, e portanto 5! é par, ou que fizessem os cálculos e chegassem ao produto 120.

(34)

A5(c): Perguntamos: “8! é múltiplo de 21? Justifique”, e esperávamos que os alunos observassem que os termos 3 e 7 aparecem no produto de 8!

A5(d): Perguntamos: “62! é múltiplo de 37? Justifique”, e esperávamos que os alunos observassem que 37 é um dos fatores do produto de 62!. Vale notar que o cálculo nesse caso é totalmente inviável.

A5(e): Perguntamos: “Pedro calculou 23!. Sem calcular, determine o último algarismo do resultado encontrado por Pedro” e esperávamos que os alunos observassem que existe um fator 10 no produto de 23!, e, portanto, o último algarismo de 23! é 0.

Quadro 4 – Questão A5 do questionário de Álgebra

A5: Sabendo que:

4! significa 4 x 3 x 2 x 1

5! significa 5 x 4 x 3 x 2 x 1

Responda:

a) 5! é um número par? Justifique

b) O que significa 8! ?

c) 8! é um múltiplo de 21 ? Justifique

(35)

e) Pedro calculou 23!

Sem calcular, determine o último algarismo do resultado encontrado por Pedro. Justifique

As questões A3 e A4, objetos de estudo deste trabalho, serão explicadas a seguir.

Em ambas, intentamos verificar como os alunos constroem provas e argumentos. Pedimos para que eles respondessem se cada uma das afirmações apresentadas é verdadeira ou falsa e depois justificassem.

Para uma melhor compreensão do assunto tratado nessa questão, sugerimos a leitura da dissertação de Mestrado de Ednaldo José Leandro, que trata especificamente da questão A5 e também dos resultados obtidos.

A QUESTÃO A3

Nessa questão, a afirmação era: “QUANDO VOCÊ SOMA DOIS NÚMEROS ÍMPARES QUAISQUER, O RESULTADO É SEMPRE PAR”. Nossa intenção era verificar se os alunos conseguiriam, primeiramente, verificar se essa afirmação é verdadeira ou falsa, e após, se conseguiriam criar alguma justificativa para essa afirmação.

A3. A afirmação abaixo é verdadeira ou falsa?

Quando você soma dois números ímpares quaisquer, o resultado é sempre par.

(36)

A QUESTÃO A4

Nessa questão, afirmou-se: “QUANDO VOCÊ SOMA UM MÚLTIPLO DE TRÊS QUALQUER COM UM MÚLTIPLO DE SEIS QUALQUER, O RESULTADO É SEMPRE UM MÚLTIPLO DE TRÊS”.

Como na questão anterior, intentamos verificar se os alunos consideram a afirmação verdadeira ou falsa e, após, verificar se os alunos conseguiriam criar argumentos válidos para a justificativa de sua resposta.

A4. A afirmação abaixo é verdadeira ou falsa?

Quando você soma um múltiplo de três qualquer com um múltiplo de seis qualquer, o resultado é sempre um múltiplo de três.

Justifique sua resposta.

Na próxima seção, explicaremos os códigos criados para a codificação dos questionários e em quais questões tais códigos foram utilizados.

2.2 Codificações utilizadas nas questões A3 e A4

Os códigos utilizados em nosso trabalho basearam-se naqueles criados por Balacheff (1987):

• Empirismo Ingênuo;

• Experimento Crucial;

• Exemplo Genérico; e

• Experimento Mental,

(37)

Porém, antes de iniciarmos a criação dos códigos, deveríamos saber identificar claramente cada um dos itens acima. Com reuniões quinzenais, discutimos em algumas delas única e exclusivamente os questionários pilotos, aplicados por alguns dos colaboradores. Esse foi o ponto de partida para definirmos os códigos.

Numa primeira análise, pensamos na criação dos seguintes códigos:

0 – resposta errada ou EM BRANCO 1 – resposta com empirismo ingênuo

2 – resposta com alguma dedução, mas não completa 3 – resposta completa

Porém, após a análise mais detalhada dos questionários pilotos e as deduções acerca desses, percebemos que, nas respostas com algum tipo de dedução, mas não completas, umas eram mais completas que outras. Daí surgiu a idéia de criarmos uma divisão dentro do código 2:

2a – resposta com alguma dedução, mas falta muito para chegar à prova completa.

2b – resposta com alguma dedução e falta pouco para chegar à prova completa.

O código 2a seria para aquelas respostas que estão mais próximas do Empirismo Ingênuo de Balacheff e o código 2b para aquelas mais próximas do Experimento Mental. Podemos dizer, inclusive, que o código 2a seria para os casos de Experimento Crucial e o código 2b para os casos de Exemplo Genérico.

Além disso, concluímos que seria diferente o aluno deixar a resposta EM BRANCO ou escrever algo, mesmo que errado. E ainda, seria diferente o aluno deixar a resposta EM BRANCO e escrever algo como “NÃO SEI” ou “NÃO ENTENDI”, que para nós seriam os mesmos códigos.

(38)

Código -2 – respostas EM BRANCO

Código -1 – respostas do tipo “Não Sei” ou “Não entendi” Código 0 – respostas erradas

Código 1 – respostas com Empirismo Ingênuo Código 2a – respostas com Experimento Crucial Código 2b – respostas com Exemplo Genérico Código 3 – respostas com Experimento Mental

Após a criação e definição dos códigos que seriam usados para os questionários, em três das reuniões quinzenais, pegamos alguns dos questionários pilotos, codificamo-los e cada um dos colaboradores deu o seu parecer para o código adotado. Ao chegarmos a um consenso, colocamos a opinião daquele grupo no ambiente virtual (TELEDUC) para discussão de todos os participantes do projeto.

Depois, com os códigos criados e com a codificação definida para as respostas apresentadas, passamos à fase de criação de um caderno de codificações. Tal caderno serviria de base para todas as codificações dos colaboradores, tanto no questionário de Álgebra quanto no de Geometria.

Esses códigos serviram de base para a criação da planilha eletrônica do MS-Excel, para que todos os colaboradores pudessem inserir suas codificações dos questionários aplicados.

Lembramos que a codificação foi individual, e, portanto, cada um dos colaboradores teve o seu parecer único para a inserção dos dados. Isso é importante frisar, pois encontramos alguns erros nas tabelas enviadas por alguns dos colaboradores, para a criação de uma tabela geral com a codificação de todos os colaboradores. Esta tabela geral foi corrigida para nossa pesquisa pelos mestrandos que trabalharão com os questionários, como já dissemos na apresentação.

(39)

Ressaltamos que nas questões objetos de nosso estudo, o aluno teria antes que dizer se a afirmação é verdadeira ou falsa. Nossa codificação ficou, então, dividida em duas partes: a primeira, onde verificamos se o aluno respondeu se era verdadeira ou falsa e a segunda onde codificamos suas justificativas conforme exemplos apresentados mais à frente.

Tabela 1 – Codificação das respostas dos alunos

Descrição Código

Resposta: Falso 0 Resposta: Verdadeiro 1 Resposta em Branco -2 Respostas do tipo “Não Sei” ou “Não Entendi” -1

Tabela 2 – Codificação das justificativas dos alunos

Justificativas Código Justificativas Erradas ou que repetem o enunciado (ciclo

vicioso) 0

Justificativas sem deduções ou inferências, totalmente

empíricas 1

Justificativas com alguma dedução/inferência, explicitação de propriedades pertinentes, ou elementos que evidenciam uma estrutura matemática, sem, contudo, chegar à prova concreta. Dividida em:

- falta muito para chegar à prova (mais próxima de 1)

- falta pouco para chegar à prova (mais próxima de 3) 2a 2b Justificativas totalmente corretas, com todos os

passos necessários à prova. 3

Justificativas em Branco -2 Justificativas do tipo “Não Sei” ou “Não Entendi” -1

2.3 Alguns exemplos de codificações utilizadas

Apresentamos agora exemplos, tanto do grupo em foco quanto da amostra, em algumas categorias acima, com as respostas dos alunos para as questões que são objetos de nossa análise. Primeiramente, vejamos a questão A3 – A soma de dois números ímpares é par.

(40)

(Respostas totalmente erradas, respostas que não apresentam justificativas ou exemplos, ou respostas que simplesmente repetem o enunciado caracterizando um ciclo vicioso).

• Respostas justificando que a afirmação é falsa:

Figura 1 – Exemplo 1 falso para codificação de A3

(Falsa porque se somarmos 1 com 3 o resultado é 4 número par ou se somarmos 67 com 43 que dá 110 também número par.

3 67 1 43 4 110)

Esse aluno deve ter entendido que a soma de dois ímpares é ímpar, e, portanto, argumentou que a afirmação era falsa.

• Respostas que concordam, mas justificam uma outra afirmação:

Figura 2 – Exemplo 2 falso para codificação de A3

(Sim, porque ao multiplicar por 2 dará um número par)

Esse aluno justificou que a multiplicação por 2 é um número par, o que não era a pergunta.

• Respostas que apresentam casos empíricos que não envolvem dois números ímpares:

Figura 3 – Exemplo 3 falso para codificação de A3 (Sim porque já foi aprovada

(41)

Nesse caso, o aluno além de ter entendido, talvez, que era a soma de dois pares resultando em um par, também efetuou a soma de forma equivocada. Perceba que ele somou 104+104=108 e não 208.

RESPOSTAS QUE RECEBEM 1

(Alguma informação pertinente, mas sem deduções ou inferências – por exemplo, respostas que são completamente empíricas)

• Respostas apresentando 1 ou mais exemplos:

Figura 4 – Exemplo 1 verdadeiro para código 1 de A3

(Sim, pois independente dos números ímpares que são somados, a resposta é sempre par! Ex: 1+3=4 Æpar

3+9=12 Æ nº par )

Classificação segundo Balacheff: Empirismo Ingênuo

Esse aluno apenas colocou dois exemplos e daí afirmou que a era verdadeira.

(Sim, porque a soma de um nº ímpar somado com outro equivale o resultado par. Ex: 5+7=12, 3+1=4, 9+11=20 e assim por diante)

(42)

(Sim, porque se você soma dois números quaisquer ímpares; é divisor de 2, daria para dividir por 2 Por exemplo

+3 A partir que você soma dois números ímpares tem como resposta números pares 3 Ex: Se você vai á feira e compra 5 bananas e no supermercado você decide com- 6 prar mais 3 ao total terá =8)

6:2=3

Aqui, temos uma resposta interessante, pois o aluno cria um pequeno problema para justificar sua afirmação, porém não sai de um exemplo.

• A seguinte resposta recebeu codificação 1 porque não é claro se o aluno está fazendo mais que simplesmente adicionando 1 + 1:

(43)

Aqui, não ficou claro para nós se o aluno estava tentando explicar o que era um número ímpar ou simplesmente efetuando 1+1.

RESPOSTAS QUE RECEBEM 2A

(Respostas que usam exemplos empíricos, mas extrapolam estes exemplos, não sendo muito claros quanto a estrutura de números ímpares).

Figura 8 – Exemplo 1 verdadeiro para código 2a de A3

(Verdadeira pois sempre que você soma dois números ímpares o resultado é par. Exemplos: 3+3 = 6

15+15=30 1335+4579=5914

R. A resposta é par porque o número que sobra do ímpar se completa com o outro e os dois juntos são par) Classificação segundo Balacheff: Experimento Crucial

Perceba que esse aluno colocou alguns exemplos válidos, caracterizando um Empirismo Ingênuo, mas depois ele extrapola, colocando números muito diferentes e verificando que a soma desses daria um número par.

(44)

Aqui, o aluno tenta mostrar o que é um número ímpar, mas não nos é claro o que ele quis dizer com o “passa um número a mais do que se fosse par”.

(Verdadeira, 5+7=12

3+3=6 101+103=204 1+1=2)

Classificação segundo Balacheff: Experimento Crucial

Novamente, o aluno começa com alguns exemplos, nos evidenciando um Empirismo Ingênuo, mas depois esse exemplo é extrapolado, no caso, 101+103.

RESPOSTAS QUE RECEBEM 2B

(Respostas que dividem números impares em números pares +/- 1, mas usam o mesmo número duas vezes (ex: 3 + 3) em todos os exemplos).

Figura 11 – Exemplo 1 verdadeiro para código 2b de A3

(A afirmação é verdadeira.

Ao somar dois números ímpares, soma-se uma unidade ímpar de cada parcela: 3+3=(2+1)+(2+1)=(2+2)+(1+1)=6

35+35=(34+1)+(34+1)=(34+34)+(1+1)=70 97+97=(96+1)+(96+1)=(96+96)+(1+1)=194) Classificação segundo Balacheff: Exemplo Genérico

(45)

(ex.35+35). Nas nossas reuniões, decidimos que esse tipo de argumentação, apesar de ser muito boa, ainda não é uma prova completa, e, portanto, receberia o código 2b.

(Sim, porque 5+5=10

Ex.: tira o máximo de números pares do 5, é 4 então fica 4+4 e sobra 1+1. É 4+4 = 8 par

1+1 = 2 par O resultado é sempre par)

Classificação segundo Balacheff: Exemplo Genérico

Novamente temos o mesmo caso apresentado acima. O aluno usa o mesmo número ao efetuar a soma (5+5), evidência, para nós, de código 2b.

(Respostas que explicam bem a estrutura de números ímpares em termos gerais, mesmo ilustrando-os com dois números iguais).

Figura 13 – Exemplo verdadeiro para código 3 de A3

(46)

(Se um número é ímpar, conclui-se que este, ao ser desmembrado em pares (de 2 em 2), se agrupa, e sempre sobrará 1, independente do nº, pois é isso que o faz ser ímpar.

Podemos então agrupar parceladamente este número, para facilitar, da seguinte forma: transformando ambos em números pares, subtraindo 1 = PAR + PAR = PAR

que é o que o faz ser ímpar!

Sempre sobrarão então 1 de cada número. Estes, se unem e formam um par por si próprios, e então se juntam ao total, totalizando sempre então, um número par.)

Classificação segundo Balacheff: Experimento Mental

Aqui, não nos baseamos no exemplo que o aluno colocou (3+3) e sim na argumentação que ele usou. Ele escreve que, se o número é ímpar, ele pode ser desmembrado em números pares e sempre sobrará 1. Ao juntarmos esse 1 que sobra de cada um dos pares, esses se juntam e formam um par, que acrescido ao resultado da soma das parcelas pares formará um par. Em linguagem geral, sem usar a linguagem algébrica, esse aluno nos mostra o que é um número ímpar, a propriedade associativa e o que acontece com a soma de dois ímpares.

Vejamos agora alguns exemplos de questionários para a questão A4 – Quando somamos um múltiplo de 3 com um múltiplo de 6, o resultado é um múltiplo de 3.

(Respostas totalmente erradas, respostas que não apresentam justificativas ou exemplos, ou respostas que simplesmente repetem o enunciado caracterizando um ciclo vicioso).

Figura 14 – Exemplo 1 falso para A4

(Se multiplicar 3x6=18

(47)

Sim, se você multiplicar com os mesmos números dará o mesmo resultado)

Esse aluno argumentou, na verdade a propriedade comutativa, onde a ordem dos fatores não altera o produto. Apesar de ter colocado exemplos válidos, ele não afirmou que a soma de um múltiplo de 3 com um múltiplo de 3 resulta em um múltiplo de 3.

Figura 15 – Exemplo 2 falso para A4

(Não porque pode acontecer de não dar múltiplos diferentes.)

Aqui, o aluno concluiu que a afirmação era falsa, pois podem dar múltiplos diferentes, o que não é claro para nós.

(Respostas apresentando 1 ou mais exemplos)

(3 6 9 12 15 18 21 24 27 30 6 12 18 14 30 36 42 48 54 60

Verdadeira se somarmos por exemplo 15 com 60 obteremos 75 e se multiplicarmos 3 por 25 obteremos esse valor) Classificação segundo Balacheff: Empirismo Ingênuo

(48)

RESPOSTAS QUE RECEBEM 2A

(Respostas que explicam que múltiplos de seis são sempre múltiplos de três, em termos gerais, mas não apresentam informação sobre sua soma).

(porque seis é múltiplo de três desde então todos seus múltiplos são de três também) Classificação segundo Balacheff: Experimento Crucial

Esse aluno, além de ter afirmado que 6 é múltiplo de 3, ainda disse que todos os múltiplos de 6 são também de 3, mas não afirma nada sobre a soma dos múltiplos.

(A afirmação é verdadeira, pois todo múltiplo de seis é obrigatoriamente múltiplo de três (e dois) 6:3=2 660:3=220

6:6=1 660:6=110) Classificação segundo Balacheff: Experimento Crucial

(49)

RESPOSTAS QUE RECEBEM 2B

(Respostas que explicam que múltiplos de 6 são múltiplos de 3 e também fazem alguma menção à soma, porém com exemplos, sem generalização).

(Verdadeiro, pois todo número múltiplo de seis será sempre um número múltiplo de três. Com isso, podemos perceber que somados dão em um múltiplo de três

6 + 12 = 18

Múltiplo de 3 múltiplo de 3 e 6 múltiplo de 3) Classificação segundo Balacheff: Exemplo Genérico

Esse aluno argumentou que todo múltiplo de 6 é também de 3 e daí coloca um exemplo para evidenciar a afirmação de que a soma de um múltiplo de 3 com um múltiplo de 6 é um múltiplo de 3. Mas, como já dissemos, ele faz isso com um exemplo, não usa a propriedade associativa para comprovar o fato.

(Sim, pois 6 é múltiplo de 3, logo a soma de um múltiplo de 3 com um múltiplo de 6 é múltiplo de 3 (3a+6b = múltiplo de 3) )

(50)

Aqui, o aluno afirma que múltiplo de 6 é múltiplo de 3 e daí escreve que 3a + 6b é um múltiplo de 3. Novamente, o aluno não usa a propriedade associativa para comprovar sua afirmação, apesar de ter usado a linguagem algébrica para tentar fazê-lo.

(Respostas completas, com argumentos algébricos, valendo-se do algoritmo da divisão por 3, e da propriedade associativa, ou de recursos equivalentes).

(Verdadeira: múltiplos de 3 são do tipo 3.x e múltiplos de 6 são do tipo 6.y = 3.2.y Então, somando, temos: 3x + 3.2y = 3.(x+2y) Æmúltiplo de 3 )

Propriedade distributiva

Classificação segundo Balacheff: Experimento Mental

(51)

CAPÍTULO 3 – ANÁLISE QUANTITATIVA

3.1 Introdução

Nesse capítulo faremos uma análise descritiva dos dados e alguns comentários sobre a amostra e o grupo em foco. Levantaremos tendências da amostra a partir do grupo em foco e faremos ainda uma comparação entre ambas (amostra e grupo em foco).

Após essa análise, exibiremos algumas tabelas sobre o grupo em foco, apontando relações entre sujeito e resposta.

Com isso, teremos uma análise mais detalhada do grupo em foco, de como os alunos apresentam suas argumentações para essas questões.

3.2 As planilhas do Excel

Como já dissemos anteriormente, após a codificação dos protocolos, os dados foram colocados numa planilha do Excel padronizada para todos os aplicadores. Cada aplicador ficou responsável pela inserção dos dados de seus protocolos na planilha.

Descrevemos agora rapidamente a planilha e a inserção de dados. Esta planilha possui colunas com todas as questões e os códigos que estas poderiam receber.

Vejamos um exemplo: se o aluno respondeu que a afirmação A3 é verdadeira, colocaríamos 1 na coluna verdadeiro da questão A3 e 0 na coluna

falso. Se deixasse em branco, colocaríamos -2 em ambas as colunas e se

escrevesse algo como “não sei” ou “não entendi”, colocaríamos -1 em ambas as colunas.

(52)

colunas e se escrevesse algo como “não sei” ou “não entendi” colocaríamos -1 nessas colunas.

Foi criada, então, uma planilha geral, com as respostas de ambos os questionários de todos os 1998 alunos. Depois, feito o sorteio de nosso grupo em foco, recortamos as linhas correspondentes a esses alunos e colocamos em uma nova planilha.

Apresentamos abaixo o recorte dessa planilha de 50 alunos com os dados referentes às questões A3 e A4.

Tabela 3 – Recorte das questões A3 e A4 do grupo em foco

A3 A4

V ou F? Justificativa V ou F? Justificativa

Nº V F 0 1 2a 2b 3 V F 0 1 2a 2b 3

1 1 0 0 1 0 0 0 1 0 0 0 0 1 0

2 1 0 0 1 0 0 0 1 0 0 1 0 0 0

3 1 0 0 1 0 0 0 0 1 1 0 0 0 0

4 1 0 0 1 0 0 0 1 0 1 0 0 0 0

5 1 0 0 1 0 0 0 1 0 0 0 1 0 0

6 1 0 0 1 0 0 0 1 0 0 1 0 0 0

7 0 1 1 0 0 0 0 1 0 0 0 1 0 0