DETERMINAÇÃO DE DISTRIBUIÇÕES TRINOMIAIS E SUAS APLICAÇÕES

DETERMINAÇÃO DE DISTRIBUIÇÕES TRINOMIAIS E SUAS APLICAÇÕES

Trinomial distributions determination and its applications

André de Carvalho Caruzo1 Karina Ferreira Neves2 Prof. Dr. Ricardo Roberto Plaza Teixeira3

Resumo: O principal objetivo deste trabalho é apresentar um enfoque geométrico para o cálculo em problemas envolvendo distribuições de probabilidades trinomiais e a sua aplicação para a contagem de microestados de sistemas ideais. Para a compreensão desta idéia é útil a construção por meio de uma planilha eletrônica de triângulos numéricos semelhantes ao triângulo de Pascal. Estes triângulos numéricos podem contribuir para a descrição de sistemas físicos e econômicos.

Palavras-chave: probabilidade; distribuição binomial; distribuição trinomial.

Abstract: The main objective of this work is to present a geometric approach to the calculation in questions of trinomial probabilities distributions and its application for the counting of microstates of ideal systems. For the understanding of this idea it is useful the construction by a spreadsheet of numerical triangles similar to the Pascal triangle. These numerical triangles can contribute to the description of physical and economical systems.

Key-Words: probability; binomial distribution; trinomial distribution.

1 _{Curso de licenciatura em física do IFSP-SP.} 2

Curso de licenciatura em física do IFSP-SP.

3 _{Doutor em física pela USP e professor do Instituto Federal de Educação, Ciência e Tecnologia de São Paulo}

(IFSP, Rua Pedro Vicente, 625 – São Paulo – SP – CEP: 01109-010) e da Pontifícia Universidade Católica de São Paulo (PUCSP, Rua Monte Alegre, 984 – São Paulo – SP – CEP: 05014-001). E-mail:

1- Introdução

Os estudos sobre como o risco se manifesta em diferentes áreas do conhecimento vem se aprofundando nos últimos quatro séculos. O próprio estatuto da noção de acaso vem sendo discutido de modo crescente em diversos campos do conhecimento (Ruelle, 1993). A necessidade de tomar decisões em situações de risco envolvendo uma miríade de aspectos, fenômenos, variáveis e graus de liberdade fez com que a noção de probabilidade se desenvolvesse como uma poderosa ferramenta matemática para estas situações. O domínio das condições de risco, a partir de um conjunto de informações relevantes existentes, de modo a permitir uma tentativa de prospecção do que ocorrerá no futuro, foi uma das grandes revoluções científicas da história (Bernstein, 1997). O futuro – como fonte de oportunidades e perigos – sempre fascinou a humanidade: a importância dada aos oráculos na antiguidade grega, por exemplo, mostra como a previsão do destino de cada um atrai as atenções de todos. Deste modo, a probabilidade tem tanto o significado de prospecção das opiniões sobre o futuro quanto o sentido de interpretação das tendências do passado, interligando estes dois tempos a partir das informações que temos no presente. O conceito de probabilidade tenta quantificar deste modo o quão provável é a ocorrência de um determinado acontecimento incerto, ou seja, qual é a chance de um evento particular ocorrer (Macedo, 1976).

A gestão do risco pressupõe o trabalho numérico com diferentes possibilidades e a introdução na Europa do sistema de numeração indo-arábico de base decimal por Fibonacci no século XIII foi fundamental para permitir – séculos mais tarde – as manipulações matemáticas exigidas nesta área. Girolomo Cardano (1501-1576) – médico e jogador inveterado do século XVI – definiu a probabilidade de um evento como sendo a razão – uma fração menor que ou igual à unidade – entre os resultados favoráveis à ocorrência deste evento e o conjunto de todos os resultados possíveis. Blaise Pascal (1623-1662), um jogador e hedonista na juventude que se tornou muito religioso no fim da vida, propiciou um grande avanço para a área de previsão de resultados ao trabalhar com uma disposição geométrica de números já conhecida pelos chineses muitos séculos antes – denominada hoje de “triângulo de Pascal” (Boyer, 1974) – e que tem a propriedade algébrica simples de

que cada número deste triângulo é a soma dos números à direita e à esquerda que estão na linha superior. A análise de probabilidades em diversos eventos pode ser obtida a partir dos números existente neste triângulo que se tornou assim uma ferramenta importante de uso pelos matemáticos ao longo da história desta ciência. O próprio fato de Pascal ter nomeado uma de suas principais obras de “Tratado do Triângulo Aritmético” revela o modo como ele encarava suas intuições a respeito do cálculo de contagens para a determinação de probabilidades como uma “geometria do acaso”. O trabalho de Pierre de Fermat (1601-1665) na teoria dos números, assim como as cartas trocadas entre ele e Pascal, colaboraram bastante para a estruturação do moderno conceito de probabilidade (Eves, 2004). O primeiro livro inteiramente dedicado à teoria da probabilidade foi “Sobre o raciocínio em jogos de azar” escrito por Christian Huygens (1629-1695), indicando a forma pela qual o conceito de probabilidade se desenvolveu pela necessidade do cálculo de risco (Stewart, 1991). Finalmente, foi Jacques Bernoulli (1654-1705) quem estabeleceu a denominada visão frequentista de probabilidade (Coutinho, 1996), que a aproxima pela sua freqüência observada quando uma mesma experiência é repetida um número muito grande de vezes. Neste caso, a determinação das probabilidades é baseada nos dados históricos acumulados (Black, 2004): o caso das ações das bolsas de valores, no longo prazo, é um exemplo adequado desta situação.

A estatística probabilística é a ciência que tenta extrair padrões do acaso (Bennett, 2003) e dos eventos aleatórios e fortuitos que nos cercam na natureza e na sociedade. As probabilidades freqüentemente desafiam a intuição humana (Triola, 1999); deste modo, o estabelecimento das leis e regras envolvidas no seu cálculo foi um grande avanço para a matemática necessária para o cálculo de riscos. Os seguros de vida, por exemplo, baseiam-se em modelos estatísticos e em tabelas atuariais associados à probabilidade de determinados eventos (Seiter, 1999).

O estudo da aleatoriedade dos eventos do mundo não se contrapõe à busca de suas razões causais, visto que não há um conflito intransponível entre causalidade e aleatoriedade ou entre determinismo e probabilidade (Papoulis, 2002), existindo muito mais uma relação de complementaridade do que de dicotomia entre as duas abordagens. A

comportamento de sistemas com um grande número de constituintes, por outro lado, pode ser possível descobrir regularidades no comportamento comum usando a teoria das probabilidades (Stewart, 1991). Neste sentido, a probabilidade não pode ser associada à ignorância – da mesma forma como a razão estaria associada à certeza – mas sim à superação da ignorância (Prigogine, 1996). Além disso, enquanto que sistemas físicos geralmente são formados por elementos que interagem por leis bem conhecidas, os sistemas econômicos são formados por sujeitos que interagem de modo complexo; neste caso, em algumas situações, a abordagem probabilística pode ser a mais adequada (Cajueiro, 2008).

2- A distribuição trinomial

Muitos problemas que se enquadram em teorias em que algo está propagando-se no tempo podem ser resolvidos usando técnicas de distribuições probabilísticas. O conhecimento de certas distribuições teóricas de probabilidades é portanto essencial para a resolução de problemas em diversas áreas diferentes, inclusive na economia (Hoffmann, 2006). Um modelo amplamente usado é a distribuição binomial (Reza, 1961) que pode ser ilustrada – em uma dimensão – com o famoso modelo do bêbado que consiste em um indivíduo que caminha ao longo de uma reta u a partir da origem (u = 0), dando passos de comprimentos iguais e com probabilidade p para a direita e q=1-p para a esquerda, sendo p+q=1 (Reif, 1983). Sua função de distribuição de probabilidade pode ser assim representada (Salinas, 2005):

2 / ) ( 2 / ) ( 2

!

2

!

2

!

)

,

(

p

q

u

N

u

N

N

N

u

f













−













+

=

sendo que ƒ2 indica a probabilidade do macro-estado para esta configuração referente a

uma posição final u, com N sendo o número de passos dados. O índice 2 indica que para cada passo só há duas opções possíveis – para a direita e para a esquerda – e é esta a razão pela qual esta distribuição é denominada de binomial. É importante notar também que se N

for par então u será par e não maior que N e se N for ímpar, u será ímpar e não maior que N.

É possível, por exemplo, relacionar o problema da oscilação das bolsas de valores com os fenômenos da difusão, ou seja, simular um caminho aleatório envolvendo variáveis randômicas ou equações estocásticas de diferença, assim criando um espaço probabilístico que se adeque a problemas análogos. Para isto, deve-se criar um cenário ideal que permite analisar os estados possíveis de uma empresa que abre seu capital na bolsa valores. Sem levar em consideração fatores econômicos específicos, a bolsa de valores pode ser considerada como um sistema fechado e conseqüentemente em “equilíbrio financeiro”.

Os estados possíveis de uma empresa submetida a esse modelo são: (1) valorizar-se que será representado pelo símbolo ↑; (2) desvalorizar-se que será representado pelo símbolo ↓; (3) permanecer estável que será representado pelo símbolo →. Assim podemos criar um gráfico esquemático, como mostrado abaixo.

Figura 1- Eventos possíveis em cada passo de uma distribuição trinomial.

Analogamente à distribuição binomial, podemos construir um modelo de distribuição trinomial para obter uma função de probabilidade ƒ3 que é dependente de u, v

e N. O índice 3 indica que, neste caso, em cada passo há três opções possíveis – trata-se da denominada distribuição trinomial. O ponto de origem do “percurso” a ser realizado pelo indivíduo será denominado (0,0) e a partir dessa origem, os “passos” ocorrerão aos saltos em um semi-plano cartesiano, pois todos os direcionamentos possíveis - ↑(v ); ↓(v);

+ v

- v

→(u+) - terão “comprimentos” iguais: os “passos” terão, deste modo, a mesma unidade

pré-estabelecida.

Generalizando a idéia de Bernoulli (Branquinho, 2001) para acontecimentos eventuais com mais que duas possibilidades diferentes (Maletta, 2005), de modo geral, se em cada evento há três opções, a primeira com probabilidade p, a segunda com probabilidade q e a terceira com probabilidade r, a distribuição trinomial da probabilidade (Alves, 2004) de que após N eventos aconteçam N1 eventos com probabilidade p, N2

eventos com probabilidade q e N3 eventos com probabilidade r será:

3 2 1

!

!

!

!

)

,

,

(

r

q

p

N

N

N

N

N

N

N

P

=

Obviamente, as duas condições necessárias são que N1+N2+N3=N (Costa Neto,

2006) e que p+q+r=1. É importante notar que esta distribuição trinomial pode ser generalizada para uma distribuição multinomial – ou multivariada (Gibra, 1973) – para a qual existirá um conjunto de s variáveis N1, N2, N3, ..., Ns aleatórias; neste caso, a função de

probabilidade multinomial será uma generalização direta da função anterior (Beyer, 1966) para o caso trinomial.

Para este trabalho, os eventos acontecem em um semi-plano discreto, e os N passos possíveis ocorrem na vertical para cima +v (com probabilidade p), na horizontal para direita +u (com probabilidade q) ou na vertical para baixo –v (com probabilidade r). Assim a probabilidade associada a uma posição final específica (u,v) será:

2 2 3

!

2

!

!

2

!

)

,

,

(

r

q

p

v

u

N

u

v

u

N

N

N

v

u

f













−

−













−

+

=

Esta será a função de probabilidade trinomial adequada para este problema.

A conexão do presente trabalho com os problemas de difusão está na utilização das equações diferenciais apropriadas. Como cada passo é dado em um intervalo de tempo fixo, se este modelo está contido em um espaço bidimensional discreto (sendo u a variação entre

os pontos contidos na horizontal – somente para a direita – e v a variação entre os pontos contidos na vertical – para cima ou para baixo) e se o indivíduo encontra-se em (u,v) ele só poderá ter vindo de (u-1,v) ou de (u,v-1) ou de (u,v+1), ou seja, ou da esquerda ou de baixo ou de cima. Assim, pode-se escrever uma relação de recorrência:

ƒƒƒƒ3(u,v,N) = p.ƒƒƒƒ3(u,v-1,N-1) + q.ƒƒƒƒ3(u-1,v,N-1) + r.ƒƒƒƒ3(u,v+1,N-1) (4)

sendo p a probabilidade do indivíduo caminhar para a cima, q a probabilidade dele caminhar para direita e r a probabilidade de caminhar para baixo

O fenômeno da difusão para a densidade ψ de algo que se difunde pode ser descrito da seguinte forma diferencial:

( )

Supondo que o sistema seja fechado, pode-se escrever =0 ∂

Ψ ∂

t e, então, em duas dimensões, se a difusão for isotrópica, teremos:

0 2Ψ= ∇ ⇒ ₂ 0 2 2 2 = ∂ Ψ ∂ + ∂ Ψ ∂ v u (6)

As relações abaixo podem ser substituídas nesta equação:

2 , , 1 2 2 u u v u v u −Ψ Ψ ≈ ∂ Ψ ∂ − (7) 2 1 , , 1 , 2 2 2 v v v u v u v u + − Ψ +Ψ − Ψ ≈ ∂ Ψ ∂ (8)

0 2 2 1 , , 1 , 2 , , 1 −Ψ ₊Ψ − Ψ +Ψ ₌ Ψ− + − l l v u v u v u v u v u ⇒ 0 3 2 1 , 1 , 1 , , 1 +Ψ +Ψ − Ψ ₌ Ψ− + − − l v u v u v u v u (9) Finalmente, teremos: 1 , 1 , , 1 , 3 1 3 1 3 1 − + − + Ψ + Ψ Ψ = Ψuv u v uv uv (10)

Assim a probabilidade de o indivíduo estar em (u,v) no N-ésimo passo é a soma das probabilidades de ele ter estado no (N-1)-ésimo passo em (u-1,v), em (u,v+1) e em (u,v-1) ponderadas em cada caso pelo fator 1/3 – no caso de distribuições isotrópicas, como foi suposto anteriormente.

Desta forma, o espaço em questão poderá ser descrito como “quântico”, pois os “passos” ocorrerão aos saltos. Cada ponto é possível de ser ocupado no N-ésimo passo com a seguinte restrição: se N é par, então |u| + |v| é par; se N é impar, então |u| + |v| é impar. 3- O triângulo trinomial

A natureza não se comporta como um algoritmo, mas podemos construí-lo para forçar uma subsunção, uma adequação de fatos às normas criadas. A construção da ciência se dá desta forma, ou seja, pela simulação de situações ideais e, em seguida, pela sua extrapolação para situações mais gerais. Com a geometria foi assim, pois o espaço euclidiano apesar de adequado ao mundo clássico, não é um modelo muito realista de acordo com a física moderna: o edifício teórico é belo, mas trata-se de uma aproximação da realidade.

Imaginemos então a existência de um semi-plano euclidiano discreto, com valores distribuídos no semi-eixo horizontal (a partir da origem) que chamaremos de u e valores

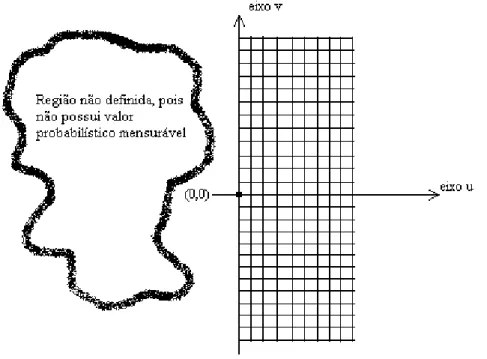
distribuídos na vertical que chamaremos de v. Então, teremos que u∈N e que v∈Z. Portanto o semi-plano em que este trabalho será realizado ficará da seguinte forma:

Figura 2 – Semi-plano discreto com os estados possíveis.

Repare que à esquerda, a região não está definida, pois para cada evento, as três possibilidades existentes são para cima, para a direita e para baixo. Portanto, a região à esquerda não poderá ser contemplada com valores probabilísticos. Somente existiria uma probabilidade associada a essa região se assumíssemos uma distribuição de probabilidades tetranomial com a existência de uma quarta possibilidade de “movimento” para a esquerda.

A situação trinomial mais simples na qual N=1 apresenta três opções possíveis de acordo com a figura 3. Esta figura será denominada de triângulo trinomial (Chappell, 1999) para N=1 e pode ser feita por um programa simples de “pintura” como o “paintbrush”.

Figura 3 – Triângulo trinomial para N=1.

No caso de N=2, há seis opções para os estados finais de acordo com a figura 4. Dentro dos círculos é apresentada a contagem de caminhos possíveis – que representam uma multiplicidade ou degenerescência de cada estado. Por exemplo, o estado u=1 e v=1, a partir da figura anterior para N=1, pode ser acessado de duas formas diferentes: a partir de baixo (ou seja, de u=1 e v=0) ou a partir da esquerda (ou seja, de u=0 e v=1). Desta forma, pode ser construído todo o triângulo trinomial para N=2, com as degenerescências de cada estado, conforme apresentado na figura 4.

Figura 4 – Triângulo trinomial para N=2.

Para N=3, as coordenadas possíveis e seus respectivos pesos probabilísticos estão apresentados no triângulo trinomial da figura 5.

Figura 5 – Triângulo trinomial para N=3.

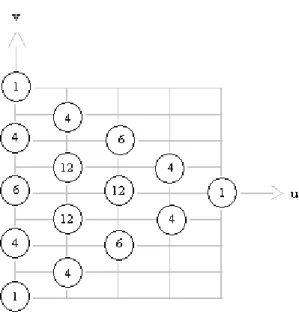
No caso de N=4, os estados possíveis com suas degenerescências são apresentados no triângulo trinomial da figura 6.

A mecânica quântica, uma das principais revoluções da ciência no século XX, incorporou o cálculo de probabilidades no seu âmago, visto que abandona a pretensão de que o mundo seja determinístico como pressupõe a mecânica clássica: assim, o cálculo probabilístico torna-se essencial para a sua compreensão. Imaginar qual seria o comportamento quântico de algo clássico pode se tornar um interessante exercício didático para a aprendizagem da física moderna. Robert Gilmore (1998), por exemplo, usa interessantes analogias deste tipo em seu livro de divulgação científica “Alice no país do quantum”: no mundo alternativo descrito no livro e que é visitado pela personagem principal – Alice –, uma destas analogias é o denominado “Banco de Heisenberg”, no qual empréstimos e pagamentos só podem ser feitos em pacotes de energia quantizados. Da mesma forma, em uma suposta “bolsa de valores quântica”, por exemplo, na qual a matemática a ser utilizada é aquela que trabalha com números discretos, uma ação só poderia realizar três movimentos ou “saltos” possíveis em um pregão: valorização ou desvalorização de uma mesma magnitude, ou manutenção de seu valor. Neste caso, as probabilidades são discretas, pois as probabilidades de todos os eventos só podem ser associadas usando-se somas e não integrais (Graham, 1989). Entretanto, o que pode ser observado no mundo real é apenas a projeção das contagens destes diagramas bidimensionais no eixo v, que informa, por exemplo, no caso desta ação, se e quanto o seu preço subiu ou desceu ou se manteve constante após N “pregões”. Esta projeção é necessária, porque com a distribuição trinomial estamos considerando uma terceira possibilidade que é a de a ação ficar estável, o que não é previsto pela distribuição binomial.

Para N=4, a projeção das contagens da figura no eixo vertical que pode variar de v=-4 até v=+4 fica sendo igual a: 1; 4; 10; 16; 19; 16; 10; 4; 1 (com um total de 81=34 contagens). O gráfico com estas contagens em função de v é apresentado na figura 7.

0

2

4

6

8

10

12

14

16

18

20

-4

-3

-2

-1

0

1

2

3

4

Estado v

D

e

g

e

n

e

re

s

c

ê

n

c

ia

Figura 7 – Degenerescência projetada no eixo v.

Supondo que as probabilidades dos três eventos possíveis (+v, +u, -v) em cada situação sejam as mesmas (p, q, r)=(1/3, 1/3, 1/3), a tabela 1 mostra as probabilidades fracionárias e percentuais associadas a cada estado v:

Tabela 1 – Probabilidades isotrópicas (p=q=r=1/3) e não isotrópicas (p=6/10; q=1/10; r=3/10) para distribuições trinomiais com N=4.

Estado final v Contagens Probabilidade fracionária para p=1/3, q=1/3 e r=1/3 Probabilidade percentual para p=1/3, q=1/3 e r=1/3 Probabilidade percentual para p=6/10, q=1/10 e r=3/10 4 1 1/81 1,23% 12,96% 3 4 4/81 4,93% 8,64%

2 10 10/81 12,34% 28,08% 1 16 16/81 19,75% 13,2% 0 19 19/81 23,46% 21,61% -1 16 16/81 19,75% 6,6% -2 10 10/81 12,34% 7,02% -3 4 4/81 4,93% 1,08% -4 1 1/81 1,23% 0,81%

Portanto, no caso em que as três probabilidades p, q e r são iguais a 1/3, a figura 8 apresenta a distribuição de probabilidades percentuais para os estados em função de v, com v variando entre -4 e +4. 0 5 10 15 20 25 -4 -3 -2 -1 0 1 2 3 4 Estado v P ro b a b il id a d e ( % )

Figura 8 – Soma das probabilidades de cada estado final v para a distribuição trinomial com N=4 e p=q=r=1/3.

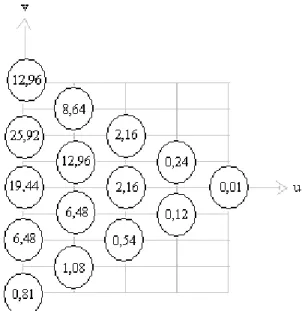
Uma outra situação possível para N=4, ocorre quando as probabilidades p, q e r não são iguais, por exemplo, no caso em que p=6/10, q=1/10 e r=3/10. Estas probabilidades não estão distantes daquelas encontradas na prática em muitos casos; por exemplo, há evidências históricas de que é de 65% a probabilidade de que um portfólio que contenha iguais quantidades em dólares de todas as ações comercializadas na Bolsa de Valores de Nova Iorque (Wall Street) suba de preço em um ano escolhido ao acaso (Moore, 2005). A figura 9 mostra o diagrama bidimensional com as probabilidades percentuais no lugar das contagens: note que a soma das porcentagens é igual a 100.

Figura 9 – Espaço probabilístico u versus v para N=4.

Percebe-se que as probabilidades são maiores para valores positivos de v do que para valores negativos de v, devido ao fato de que p>r. Somando todas as probabilidades no eixo v, ou seja, projetando-as no “mundo real”, obtém-se o gráfico da figura 10 que apresenta a distribuição de probabilidades percentuais em função de v, com v variando de – 4 até +4.

0 5 10 15 20 25 30 -4 -3 -2 -1 0 1 2 3 4 Estado v P ro b a b il id a d e ( % )

Figura 10 – Soma das probabilidades de cada estado final v para a distribuição trinomial com N=4 e p=6/10, q=1/10 e r=3/10.

Para realizar uma comparação, serão apresentados na tabela 2 os resultados obtidos para uma distribuição binomial com N=4 e apenas com duas opções para cada movimento: +v e –v, com probabilidades respectivamente de 2/3 e 1/3, que mantém entre si a mesma relação de 2 para 1 que mantém as probabilidades 6/10 e 3/10 da distribuição anterior trinomial para os casos em que v=+1 e v=-1. Neste caso o estado final v pode assumir apenas valores pares: as contagens e as probabilidades são apresentadas na tabela 2 (o número total de estados neste caso é 16).

Tabela 2 – Probabilidades isotrópicas (p=q=1/2) e não isotrópicas (p=2/3; q=1/3) para distribuições binomiais com N=4.

Estado final v Contagens Probabilidade fracionária para p=1/2 e Probabilidade percentual para p=1/2 e Probabilidade percentual para p=2/3 e

q=1/2 q=1/2 q=1/3 4 1 1/16 6,25% 19,75% 2 4 4/16 25,0% 39,51% 0 6 6/16 37,5% 29,63% -2 4 4/16 25,0% 9,88% -4 1 1/16 6,25% 1,23%

A figura 11 mostra como se comportam as probabilidades em função de v para o caso da distribuição binomial não-isotrópica (p=2/3; q=1/3) com N=4. É possível notar que o seu pico (o valor modal) que ocorre para v=+2, coincide com a posição do pico da figura 10 que apresenta a distribuição trinomial equivalente. Além disso, em ambos os casos a distribuição é assimétrica, o que é esperado visto que as probabilidades p, q e r (ou p e q, para a binomial) não são iguais. Entretanto, a distribuição trinomial apresenta vales que não aparecem no caso da binomial.

0 5 10 15 20 25 30 35 40 45 -4 -3 -2 -1 0 1 2 3 4 Estado v P ro b a b il id a d e ( % )

Figura 11 – Soma das probabilidades de cada estado final v para a distribuição binomial com N=4 e p=2/3 (para cima) e q=1/3 (para baixo).

Para efeito de comparação dos resultados referentes às projeções no eixo v para a distribuição binomial e para a distribuição trinomial equivalente, a tabela 3 apresenta os valores da média e do desvio padrão em cada caso. Tanto a média, quanto o desvio padrão são ligeiramente menores no caso da distribuição trinomial.

Tabela 3 – Média e desvio padrão para a distribuição binomial (N=4) não-isotrópica (p=2/3; q=1/3) e para a distribuição trinomial não-isotrópica (p=6/10; q=1/10; r=3/10).

Tipo de Distribuição Média Desvio Padrão Distribuição binomial 1,33 1,89

Distribuição trinomial 1,2 1,8

No caso em que temos um N genérico é possível obter os valores da distribuição trinomial facilmente usando uma planilha eletrônica, como o Excel. Por exemplo, suponha que N=10 e, portanto, par. Em uma planilha auxiliar (por exemplo, na planilha 2) serão inseridas apenas as três probabilidades básicas da distribuição trinomial: em A1, será inserido o valor de p (probabilidade de um “salto” para cima); em A2, será inserida o valor de q (probabilidade de um “salto” para a direita); em A3, será inserida a probabilidade de r (probabilidade de um “salto” para baixo). No caso presente serão utilizadas as probabilidades p=6/10, q=1/10 e r=3/10. A planilha 2 portanto se apresentará como na tabela 4.

Tabela 4 – Resultados a serem inseridos na planilha 2 referentes às probabilidades elementares p=0,6 (para cima), q=0,1 (para direita) e r=0,3

(para baixo), e que serão utilizadas na planilha 1.

A 1 0,6

2 0,1 3 0,3

Na planilha 1 será obtida a distribuição de probabilidade trinomial em uma disposição triangular. O número total de passos N=10 será colocado na célula A1 desta planilha, como referência para os cálculos das fórmulas que serão inseridas. Na coluna A, a partir de A2 e até A22, serão colocados os valores possíveis de v desde +10 até -10: por exemplo, na célula A2 coloca-se o número 10, na célula A3 coloca-se o número 9 e assim sucessivamente até que na célula A22 coloca-se o número -10. Na linha 1, a partir de B1 até L1 serão colocados os valores possíveis de u desde 0 até +10: por exemplo, na célula B1 coloca-se o número 0, na célula C1 coloca-se o número 1 e assim sucessivamente até que na célula L1 coloca-se o número 10. Esta disposição evidencia que u varia entre os números naturais e v varia entre os números inteiros. Posiciona-se o cursor na célula B2 e, no caso de N ser um número par, insere-se nesta célula a fórmula:

“=MOD(B$1+$A2+1;2)*SE(ABS($A2)+ABS(B$1)>$A$1;0;1)*FATORIAL($A$1)/(FAT ORIAL(B$1)*FATORIAL(ABS(($A$1-B$1+$A2))/2)*FATORIAL(ABS(($A$1-B$1- $A2)/2)))*Plan2!$A$1^(($A$1-B$1+$A2)/2)*Plan2!$A$2^(B$1)*Plan2!$A$3^(($A$1-B$1-$A2)/2)”

É importante notar que se N for impar, a fórmula a ser inserida será ligeiramente diferente (apenas por um 1 a menos na primeira função MOD da fórmula):

“=MOD(B$1+$A2;2)*SE(ABS($A2)+ABS(B$1)>$A$1;0;1)*FATORIAL($A$1)/(FATOR

IAL(B$1)*FATORIAL(ABS(($A$1-B$1+$A2))/2)*FATORIAL(ABS(($A$1-B$1- $A2)/2)))*Plan2!$A$1^(($A$1-B$1+$A2)/2)*Plan2!$A$2^(B$1)*Plan2!$A$3^(($A$1-B$1-$A2)/2)”

Finalmente, na coluna M podem ser encontradas as somas das probabilidades percentuais projetadas em v. Assim, insere-se na célula M2 a fórmula “=100*SOMA(B2:L2)” e arrasta-se está fórmula até a célula M22. A tabela 5 aprearrasta-senta os resultados que arrasta-serão obtidos com esta seqüência de comandos na planilha 1.

Tabela 5 – Resultados obtidos na planilha 1 para a distribuição trinomial com N=10 e p=6/10, q=1/10 e r=3/10, conforme a seqüência de comandos

A B C D E F G H I J K L M 1 10 0 1 2 3 4 5 6 7 8 9 10 2 10 0,00605 0 0 0 0 0 0 0 0 0 0 0,6047 3 9 0 0,01008 0 0 0 0 0 0 0 0 0 1,0078 4 8 0,03023 0 0,00756 0 0 0 0 0 0 0 0 3,7791 5 7 0 0,04535 0 0,00336 0 0 0 0 0 0 0 4,8709 6 6 0,06802 0 0,03023 0 0,0010 0 0 0 0 0 0 9,9237 7 5 0 0,09070 0 0,01176 0 0,00020 0 0 0 0 0 10,2653 8 4 0,09070 0 0,05291 0 0,00294 0 2,7E-05 0 0 0 0 14,6574 9 3 0 0,10582 0 0,01764 0 0,00049 0 2,6E-06 0 0 0 12,3944 10 2 0,07936 0 0,05291 0 0,00367 0 5,4E-05 0 1,6E-07 0 0 13,5999 11 1 0 0,07936 0 0,01470 0 0,00049 0 3,9E-06 0 6,0E-09 0 9,4552 12 0 0,04762 0 0,03307 0 0,0024 0 4,1E-05 0 1,6E-07 0 1,0E-10 8,3175 13 -1 0 0,03968 0 0,00735 0 0,00024 0 1,9E-06 0 0,00000 0 4,7276 14 -2 0,01984 0 0,01323 0 0,00092 0 1,4E-05 0 4,1E-08 0 0 3,4000 15 -3 0 0,01323 0 0,00220 0 6,1E-05 0 3,2E-07 0 0 0 1,5493 16 -4 0,00567 0 0,00331 0 0,00018 0 1,7E-06 0 0 0 0 0,9161 17 -5 0 0,00283 0 0,00037 0 6,1E-06 0 0 0 0 0 0,3208 18 -6 0,00106 0 0,00047 0 1,5E-05 0 0 0 0 0 0 0,1551 19 -7 0 0,00035 0 2,6E-05 0 0 0 0 0 0 0 0,0381 20 -8 0,00012 0 3,0E-05 0 0 0 0 0 0 0 0 0,0148 21 -9 0 2,0E-05 0 0 0 0 0 0 0 0 0 0,0020 22 -10 5,9E-06 0 0 0 0 0 0 0 0 0 0 0,0006

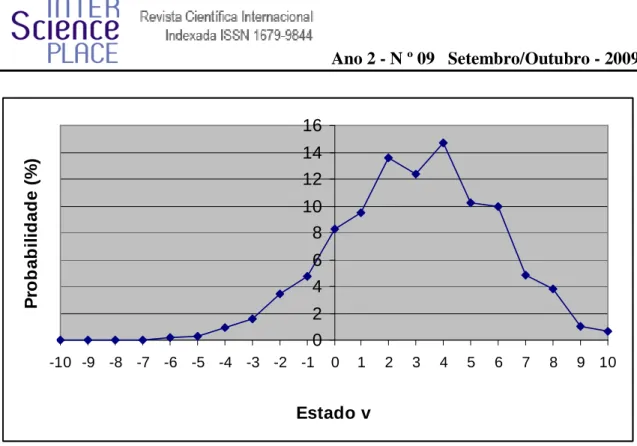
Com os resultados para as somas das probabilidades, pode-se construir o gráfico da figura 12 que apresenta a probabilidade percentual para cada estado final v, no caso em que N=10.

0 2 4 6 8 10 12 14 16 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 Estado v P ro b a b il id a d e ( % )

Figura 12 – Probabilidade de cada estado final v para a distribuição trinomial com N=10 e p=6/10, q=1/10 e r=3/10.

4- Conclusões finais

A análise de um caminho aleatório em uma dimensão é uma forma interessante para introduzir os conceitos básicos da teoria das probabilidades (Salinas, 2005) e para compreender as principais características das distribuições binomial e trinomial. Assim como entender a forma como o triângulo de Pascal é montado colabora para a compreensão do seu significado (Contador, 2005), o mesmo acontece por analogia com o triângulo trinomial. A premissa de que é “pecaminoso ensinar o abstrato antes do concreto” é com certeza válida no que diz respeito ao estudo da teoria das probabilidades (Melzak, 1973): as aplicações na economia podem ter deste modo um poder motivador bastante significativo para diversos públicos. A resolução de problemas quantitativos associados a um contexto concreto podem despertar o prazer pelo desafio que, quando bem utilizado, torna-se um instrumento didático poderoso nas mãos de um educador (Graham, 1989).

Apesar de estarmos lidando com um espaço ideal, com as técnicas apresentadas podemos inferir algo do comportamento real das ações lançadas no mercado aberto de valores. Durante apenas um dia, os “passos” que as ações das empresas dão são muitos e então podemos classificá-los como altamente degenerados, pois conforme visto neste artigo, acaba sendo pouco provável a ocorrência de muitas altas consecutivas, pouco provável a ocorrência de muitas baixas consecutivas, bem como pouco provável a inércia total. Os números indicam que trata-se um sistema altamente volátil e flutuante.

Por exemplo, altas como a das ações da Petrobrás que ocorreram em novembro de 2007 só acontecem quando há fatos imprevisíveis como a descoberta de mais petróleo na bacia de Santos. É interessante observar que estas ações sofreram quedas após esta forte alta, como uma tendência ao “status quo” anterior para devolvê-la ao seu “verdadeiro caminho”. Dessa forma, apesar das limitações existentes, o esquema aqui construído pode ser uma ferramenta útil para compreender, por exemplo, o comportamento das ações nas bolsas de valores, dentre muitos outros fenômenos nos quais existe um componente de aleatoriedade intrínseco.

Do ponto de vista teórico, os resultados obtidos neste trabalho permitem avaliar a expansão do universo financeiro em bolsas de valores ou qualquer outro fenômeno que ocorra a partir de três “estados de transição” possíveis. É interessante notar que foi desenvolvida uma função probabilística adequada às distribuições trinomiais, atrelando cada macro-estado final a uma coordenada de um espaço discreto u × v, ou seja, a cada coordenada desse espaço ideal está atrelada uma seqüência de eventos que não precisam ser isotrópicos.

Além da função adequada, obteve-se uma interface computacional para o cálculo das probabilidades, facilitando a construção de esquemas maiores. Por exemplo, a tabela 5 apresenta o espaço probabilístico para uma distribuição trinomial quando N=10, p=0,6, q=0,1 e r=0,3. Assim sendo, de forma genérica, o análogo matemático para a difusão que foi criado e que depende de u, v, N, p, q e r, permite responder perguntas específicas, como, por exemplo, sobre qual a probabilidade de um “indivíduo” se encontrar após o N-ésimo passo na posição final u e v. Tal resultado é possível de se obter usando a relação f3(u,v,N),

passos, por meio de uma planilha eletrônica. A fórmula apresentada f3(u,v,N) possui duas

partes distintas: a primeira é o contador de caminhos e a segunda parte é a normalização. Deste modo, as probabilidades não influem nas degenerescências: elas são apenas ponderações informando o quanto de cada estado elementar existe no macro-estado obtido.

Referências bibliográficas

- ALVES, Rafaela Cardoso e VIVANCO, Mário Javier Ferrua. Controle estatístico de qualidade em ensaios destrutivos via quantidades aleatórias. Uberlândia: Anais da 49ª Reunião da RBRAS, maio/2004.

- BERNSTEIN, P. L. Desafio aos deuses. Rio de Janeiro: Campus, 1997. - BENNETT, D. Aleatoriedade. São Paulo: Martins Fontes, 2003.

- BEYER, W. H. Handbook of tables for probability and statistics. Cleveland: The Chemical Rubber Co., 1966.

- BLACK, Ken. Business Statistics for contemporary decision. New Jersey: John Wiley & Sons Inc, 2004.

- BOYER, Carl B. História da matemática. Rio de Janeiro: Edgard Blûcher, 1974.

- BRANQUINHO, Carvalho. Metodologia de dimensionamento de canais para soft handoff em sistemas CDMA. Campinas: Tese de Doutoramento (Unicamp), 2001.

- CAJUEIRO, Daniel O. e BORGES, Ernesto P. O que há em comum entre a água fervente e os mercados financeiros? A econofísica responde. Ciência Hoje, vol. 42, no 248, pp. 32-37, maio/2008.

- CHAPPELL, James e OSLER, Thomas J. The trinomial triangle. The College Mathematics Journal, Vol. 30, No 2, 1999, pp. 141-142.

- CONTADOR, Paulo Roberto Martins. Matemática, uma breve história (Volume III). São Paulo: Editora Livraria da Física, 2005.

- COSTA NETO, Pedro Luiz de Oliveira e CYMBALISTA, Melvin. Probabilidades. São Paulo: Edgard Blücher, 2006.

- COUTINHO, C. Q. S. Introdução ao conceito de probabilidade: uma visão frequentista. São Paulo: Educ, 1996.

- EVES, Howard. Introdução à história da matemática. Campinas: Editora da Unicamp, 2004.

- GIBRA, I. N. Probability and statistical inference for scientists and engineers. New Jersey: Prentice-Hall, 1973.

- GILMORE, Robert. Alice no país do quantum. Rio de Janeiro: Jorge Zahar Editor, 1998.

- GRAHAM, R. L., KNUTH, D. E. e PATASHNIK, O. Concrete mathematics. New York: Addison-Wesley, 1989.

- HOFFMANN, Rodolfo. Estatística para economistas. São Paulo: Pioneira Thomson Learning, 2006.

- MACEDO, H. Dicionário de física. Rio de Janeiro: Editora Nova Fronteira, 1976.

- MALETTA, Bruno Vasques. Modelos baseados em simulação de Monte Carlo: Soluções para o cálculo de Value-at-Risk. Rio de Janeiro: Dissertação de mestrado (UFRJ), 2005.

- MELZAK, Z. A. Companion to concrete mathematics. New York: Wiley, 1973. - MOORE, David S. A estatística básica e sua prática. Rio de Janeiro: LTC, 2005.

- PAPOULIS, A. e PILLAI, S. U. Probability, random variables and stochastic process. New York: McGraw-Hill, 2002.

- PRIGOGINE, Ilya. O fim das certezas. São Paulo: Editora da Unesp, 1996. - REIF, F. Statistical and thermal physics. Tokyo: McGraw-Hill, 1983.

- REZA, F. M. Introduction to information theory. New York: McGraw-Hill Company, 1961.

- RUELLE, D. Acaso e caos. São Paulo: Editora da Unesp, 1993.

- SALINAS, S. R. A. Introdução à física estatística. São Paulo: Edusp, 2005. - SEITER, C. Matemática para o dia-a-dia. Rio de Janeiro: Campus, 1999.

- STEWART, I. Será que Deus joga dados? Rio de Janeiro: Jorge Zahar Editor, 1991. - TRIOLA, M. Introdução à estatística. Rio de Janeiro: LTC, 1999.