http://dx.doi.org/10.7494/OpMath.2013.33.3.565
THE PUTNAM-FUGLEDE PROPERTY
FOR PARANORMAL
AND
∗
-PARANORMAL OPERATORS
Patryk Pagacz
Communicated by P.A. Cojuhari
Abstract. An operator T ∈ B(H) is said to have the Putnam-Fuglede commutativity property (PF property for short) if T∗X = XJ for any X ∈ B(K,H) and any isometry J∈ B(K)such thatT X =XJ∗. The main purpose of this paper is to examine if
paranor-mal operators have the PF property. We prove thatk∗-paranormal operators have the PF property. Furthermore, we give an example of a paranormal without the PF property. Keywords: power-bounded operators, paranormal operators, ∗-paranormal operators,
k-paranormal operators,k∗-paranormal operators, the Putnam-Fuglede theorem. Mathematics Subject Classification:47B20, 47A05, 47A62.
1. TERMINOLOGY
Throughout what follows, Z stands for the set of all integers, Z− for the set of all negative integers, N for the set of all non-negative integers and N+ for the set of all positive integers. Complex Hilbert spaces are denoted byHandK and the inner product is denoted byh·,−i. Moreover, we denote byB(H,K)the set of all bounded operators fromHintoK. To simplify, we putB(H) :=B(H,H). The identity operator onHis denoted byIdH. IfX is a subset ofH, thenspanXstands for the linear span
of X and X stands for the closure ofX. We say thatT ∈ B(H)is a contraction if
kT xk ≤ kxkfor each x∈ H. By apower-bounded operator we mean T ∈ B(H)such that the sequence {kTnk}
n∈N is bounded. An operator T is said to be completely nonunitary ifT restricted to every reducing subspace of His nonunitary. As usual,
T∗stands for the adjoint ofT. We now recall some known classes of operators defined on a Hilbert spaceH. An operatorT ∈ B(H)is called hyponormal ifT∗T ≥T T∗, or
equivalently,kT∗xk ≤ kT xkfor eachx∈ H. An operator T is(p, k)-quasihyponormal
ifT∗k((T∗T)p−(T T∗)p)Tk≥0. Usually(p,0)-quasihyponormal operators are known as p-hyponormal operators. Another generalization of hyponormal operators are
c
k∗-paranormal operators. An operatorT ∈ B(H)isk∗-paranormal ifkT∗xkk≤ kTkxk for eachx∈ Hsuch thatkxk= 1. Moreover, by ak-paranormal operator we mean an operatorT ∈ B(H)which satisfieskT xkk ≤ kTkxkfor eachx∈ Hsuch thatkxk= 1. Fork= 2,k-paranormal and k∗-paranormal operators are called simplyparanormal and∗-paranormal operators, respectively.
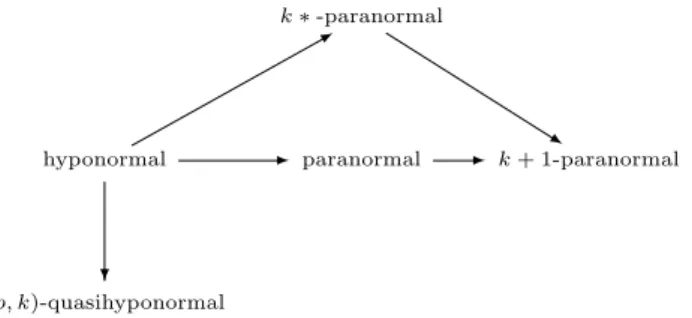
The inclusion relations between the above-mentioned classes of operators are shown in Figure 1 (cf. [7, 11]).
k∗-paranormal
hyponormal ✲ ✲
paranormal ✲ k+ 1-paranormal ✲
(p, k)-quasihyponormal
❄
Fig. 1. Inclusions between classes of operators
An operator T ∈ B(H) is said to be of class C0· if lim inf
n→∞ kT
nxk = 0 for each
x ∈ H. Note that a power-bounded operator T is of class C0· if and only if it is
strongly stable, i.e.Tn →0 in the strong operator topology (see [12]). Furthermore, we say thatT isof class C·0if its adjoint is of class C0·.
Definition 1.1 ([4]). An operator T ∈ B(H) is said to have the Putnam-Fuglede commutativity property (PF property for short) ifT∗X =XJ for anyX ∈ B(K,H)
and any isometry J∈ B(K)such thatT X =XJ∗.
2. INTRODUCTION
In [5] Duggal and Kubrusly have shown that a contraction T has the PF property if and only if T is the orthogonal sum T = U ⊕C of a unitary operator U and an operator C which is aC·0 contraction. In the subsequent section, using isometric
asymptotes (see [8]), we show that the above statement is also true for power-bounded operators. Moreover, we give the relation between operators with the PF property and
A-isometries.
In [11] we have shown thatk-paranormal,k∗-paranormal,(p, k)-quasihyponormal contractions and contractions of classQhave the PF property (see also [3, 4, 6]). Our main purpose is to answer the question:Which of the above mentioned operators (not necessarily contractions)have the PF property?
to the best of our knowledge, nothing was known about the PF property for noncon-tractivek∗-paranormal andk-paranormal operators.
In Section 3, we show thatk∗-paranormal operators have the PF property. Finally, in Section 4 we present an example of a paranormal (k-paranormal) operator without the PF property.
3. GENERAL REMARKS ON THE PF PROPERTY
In [5] Duggal and Kubrusly have shown the following result.
Proposition 3.1. If a nonunitary coisometry is a direct summand of a contraction
T, then T does not have the PF property. In particular, if a coisometry has the PF property, then it is a unitary operator.
Appealing to the above result we now show the following theorem.
Theorem 3.2. A power-bounded operatorT ∈ B(H)has the PF property if and only if it is a direct sum of a unitary operator and an operator of class C·0.
Proof. Forx, y∈ H, we set[x, y] :=glim{hT∗nx, T∗nyi}
n∈N, where glim denotes the Banach limit. In this way we obtain a new semi-inner product onH. Thus the factor spaceH/H0, whereH0stands for the linear manifoldH0:={x∈ H|[x, x] = 0}, is an
inner product space endowed with the inner product given by[x+H0, y+H0] = [x, y]
for x, y∈ H. LetK denote the resulting Hilbert space obtained by a completion of
H/H0. Denote byQthe canonical embeddingQ:H ∋x7→x+H0∈ K. Note that
kQT∗xk=kQxk, x∈ H.
Hence there is an isometryV :K → Ksuch thatQT∗=V Q, so from the PF property
we deduce that
QT∗=V Q⇐⇒T Q∗=Q∗V∗=⇒T∗Q∗=Q∗V ⇐⇒QT =V∗Q.
Therefore,R(Q∗)is an invariant subspace forT andT∗. This means thatR(Q∗) is
reducing forT.
Observe that, for allx, y∈ H, we have
[Qx, Qy] = [VnQx, QT∗ny] =hQ∗VnQx, T∗nyi=hT∗nQ∗Qx, T∗nyi (3.1)
and
glim{hT∗nQ∗Qx, T∗nyi}
n∈N= [QQ∗Qx, Qy]. (3.2) A combination of (3.1) and (3.2) yields [Qx, Qy] = [Q(Q∗Qx), Qy]. Since R(Q) is
dense in K, it follows that Q = QQ∗Q, so (Q∗Q)2 = Q∗Q. This means that P :=
Q∗Qis a projection. Additionally, by (3.1), we getQQ∗=Id
K. Therefore,R(Q∗) =
R(Q∗QQ∗)⊂ R(Q∗Q)⊂ R(Q∗). As a result,R(P) =R(Q∗). On the other hand, for
x∈ H, we get
and soN(P) =H0. HenceH=N(P)⊕ R(P) =H0⊕ R(Q∗). Takex∈ R(Q∗). Thus T∗x∈ R(Q∗), becauseR(Q∗)is reducing forT. Consequently,
kT∗xk=kP T∗xk=kQT∗xk=kQxk=kP xk=kxk.
This finally implies that T∗ is an isometry on R(Q∗), so by Proposition 3.1 it is a
unitary operator onR(Q∗).
It only remains to verify thatT∗ is strongly stable onH
0. To see this, fixx∈ H0.
Then lim inf n→∞ kT
∗nxk2 ≤ glim{kT∗nxk2}
n∈N = 0. Hence for each ε > 0 there exists
k∈Nsuch thatkTkxk< ε, so for allm > kwe have
kTmxk=kTm−kTkxk ≤ kTm−kkkTkxk ≤εsup n∈N
kTnk.
As a consequence, lim n→∞kT
∗nxk= 0.
The converse implication is true for all bounded operators (see the proof of [5, Theorem 1]).
It is plain that Theorem 3.2 does not hold for all bounded operators. To see this, it suffices to consider the operator2IdH having the PF property.
Proposition 3.3. If an operator T ∈ B(H) has the PF property, then T is a direct sum of a unitary operator and an operator G ∈ B(H0), which does not satisfy the
equation GX=XJ∗ for any nonzero X ∈ B(K,H
0)and any isometryJ ∈ B(K).
Proof. Suppose thatT X =XV∗for someX ∈ B(K,H)and some isometryV ∈ B(K).
Owing to the PF property we haveT∗X=XV. By this, for allx, y∈ H, we get
hXX∗x, yi=hX∗x, X∗yi=hV X∗x, V X∗yi=hV X∗x, X∗T∗yi= =hXV X∗x, T∗yi=hT∗XX∗x, T∗yi=hXX∗x, T T∗yi.
Hence T T∗ =IdonR(XX∗), butR(XX∗) =R(X)is reducing for T, soT| R(X) is
a coisometry.
Let T =T′⊕C with respect to H=R(X)⊕ N(X∗). It turns out that T′ has
the PF property. Indeed, if Y T′∗ =JY for some Y ∈ B(H,K′)and some isometry
J ∈ B(K′), then
(Y ⊕0)T∗= (Y ⊕0)(T′∗⊕C∗) = (J⊕Id)(Y ⊕0).
Hence, by the PF property ofT, we get
(Y ⊕0)(T′⊕C) = (J∗⊕Id)(Y ⊕0),
and soY T′ =J∗Y. This means thatT′ also has the PF property. As a consequence,
by Proposition 3.1, T′ =T|
R(X∗) is a unitary operator.
Next, letG∈ B(H0)be a completely nonunitary part ofT. By the above argument, Ghas the PF property. Hence if GsatisfiesGX =XJ∗ for someX ∈ B(K,H
0)and
Remark 3.4. In view of Proposition 3.3 a completely nonunitary operatorT ∈ B(H) has the PF property if and only if there does not existX ∈ B(K,H)and an isometry
J ∈ B(K)such thatT X=XJ∗.
IfT satisfies the PF property in a nontrivial way (that is, with a nonzeroX), then we have
k(XX∗)12xk=kX∗xk=kX∗T∗xk=k(XX∗) 1
2T∗xk, x∈ H.
Thus there exists an isometry V such that V(XX∗)1
2 = (XX∗)
1
2T∗. This means
that T∗ is an A-isometry for A = XX∗ (for more information about A-isometries
see [2, 13]). Hence the relation between the PF property and A-isometries can be formulated as follows.
Proposition 3.5. A completely nonunitary operator T has the PF property if and only if its adjoint is not an A-isometry for any positive operatorA.
4. THE PF PROPERTY FORk∗-PARANORMAL OPERATORS
In this section we show that ak∗-paranormal operator has PF property even if it is not a contraction.
Theorem 4.1. Each k∗-paranormal operator has the PF property.
Proof. Take k≥2. Let T ∈ B(H) be a(k−1)∗-paranormal operator. Suppose that there exist an operatorX∈ B(K,H)and an isometryV ∈ B(K)such that
T X =XV∗. (4.1)
Takex0∈ R(X). There existsx∈ K such thatx0=Xx. Let us define the sequence
{xn}n∈Z as follows:
xn:=
(
XVnx, n >0,
XV∗−nx, n <0.
By (4.1), it is immediate thatT xn+1=xn. Additionally, we have
kxnk ≤max{kXV|n|xk,kXV∗|n|xk} ≤ kXkkxk=:M, n∈Z.
Hence the sequence {kxnk}n∈Z is bounded by M. Each k∗-paranormal operator is (k+ 1)-paranormal (cf. [11, Proposition 4.8]), soT is ak-paranormal operator. Thus
kxnkk=kT xn+1kk ≤ kTkxn+1kkxn+1kk−1=kxn−k+1kkxn+1kk−1, n∈Z.
Using the mean inequality and puttingn+k−1instead ofnwe get
kxn+k−1k ≤
kxnk+ (k−1)kxn+kk
Next, multiplying both sides of this inequality bykand subtractingkxnk+kxn+1k+
kxn+2k+. . .+kxn+k−1kwe obtain
− kxnk − kxn+1k − kxn+2k+. . .− kxn+k−2k+ (k−1)kxn+k−1k ≤
≤ −kxn+1k − kxn+2k − kxn+3k+. . .− kxn+k−1k+ (k−1)kxn+kk.
Thus the sequence{An}n∈Z, where
An :=−kxnk − kxn+1k − kxn+2k+. . .− kxn+k−2k+ (k−1)kxn+k−1k, n∈Z,
is increasing. We now show that the sequence{An}n∈Z is constant equal to 0. Let us observe that for small enoughl and big enoughmwe get
m
X
n=l
An = m X
n=l
(−kxnk − kxn+1k+. . .− kxn+k−2k+ (k−1)kxn+k−1k)
=
=|(k−1)kxm+k−1k+ (k−2)kxm+k−2k+. . .+kxm+1k−
−(kxlk+ 2kxl+1k+ 3kxl+2k+. . .+ (k−1)kxl+k−2k)| ≤M k(k−1).
Thus
(m−l+ 1)Al= m
X
n=l
Al≤ m
X
n=l
An≤M k(k−1).
Hence
Al= lim m→∞
m−l+ 1
m Al≤mlim→∞
M k(k−1)
m = 0.
Similarly, we deduce that
(m−l+ 1)Am= m
X
n=l
Am≥ m
X
n=l
An ≥ −M k(k−1).
Therefore,
Am= lim l→−∞
m−l+ 1
−l Am≥l→−∞lim
−M k(k−1)
−l = 0.
Hence An= 0, thuskxnk+kxn+1k+. . .+kxn+k−2k= (k−1)kxn+k−1k. As before,
we get
kxn+k−1k=
kxnk+ (k−1)kxn+kk
k . (4.2)
On the other hand,
kxnk+ (k−1)kxn+kk
k ≥
k
q
kxnkkxn+kkk−1≥ kxn+k−1k,
so we have equality in the mean inequality. It follows thatkxnk=kxn+kk, so by (4.2) we obtainkxnk=kxn+1kfor eachn∈N. In particular,kT x0k=kx−1k=kx0k. Thus
Since T X = XV∗, it follows that T |
R(X) is a surjection. Thus it is a unitary
operator. We can expressT with respect toH=R(X)⊕ N(X∗)as
T =
T11 T21
0 T22
,
whereT11=T |R(X),T21∈ B(N(X∗),R(X))andT21∈ B(N(X∗)). Hence
T∗=
T∗
11 0 T∗
21 T22∗
.
Taking into account thatT is(k−1)∗-paranormal, we have
(1 +kT21∗xk2)k−1= (kxk2+kT21∗xk2)k−1=kT∗(x,0)k2(k−1)≤ kTk−1(x,0)k2=
=kTk−1
11 xk2=kxk2= 1
for eachx∈ R(X)such thatkxk= 1. As a result,T21= 0andT =T11⊕T22. Since
T X =XV∗, it follows that
XV =Id|R(X)XV =T11∗T11XV =T∗T XV =T∗XV∗V =T∗X.
This completes the proof.
As an immediate consequence of Theorem 4.1 we obtain the following corollary.
Corollary 4.2. Each ∗-paranormal operator has the PF property.
5. THE PF PROPERTY FOR PARANORMAL OPERATORS
An operator T is log-hyponormal iflog(T∗T)≥log(T T∗). Mecheri have shown that
log-hyponormal operators satisfy the Putnam-Fuglede theorem (see [10]). In particu-lar, this fact implies that all log-hyponormal operators have the PF property.
In [1] Andˆo has shown (see Theorem 2 therein) that each log-hyponormal operator which satisfies N(T) = N(T∗) is paranormal. Thus the log-hyponormal operators
are not far from being paranormal. Hence it can be surprising that there exists a paranormal operator without the PF property. In this section we give a suitable example of such an operator. To do this first we prove the following lemma.
Lemma 5.1. There are real bounded sequences {xn}n∈N+ and{yn}n∈N+ such that
(
xn=ynxn+1, n∈N+,
yn+1= (x2n+1+ 1)yn, n∈N+.
Proof. Let us define a sequence{yn}n∈N+ such that
(
y1= 1, y2= 2,
By the definition of{yn}n∈N+, we have
yn+2−yn+1=
yn+1−yn
yn
, n∈N+, (5.1)
so by induction we can deduce that the sequence{yn}n∈N+is positive and increasing. Henceyn≥2forn≥2. Moreover,y3−y2= 3−2 = 1, so again using (5.1) we can easily show thatyn+1−yn≤ 2n1−2 forn≥2. Thusyn=P
n
i=2(yi−yi−1) +y1≤4. It follows
that the positive sequence{yn}n∈N+ is bounded. Now, if we setxn+1 =
qy
n+1
yn −1 andx1= 1, it is easy to see that these two sequences satisfy the desired condition.
Example 5.2. Let H be a Hilbert space with an orthonormal basis {en}n∈Z ∪
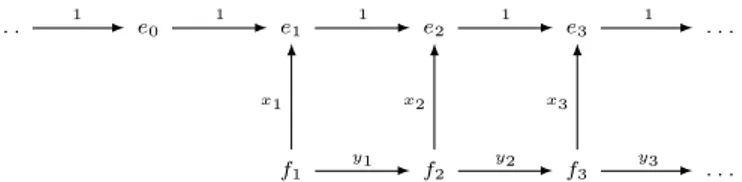
{fi}i∈N+. Let us define an operator S∈ B(H)by the formula
(
S(en) =en+1, n∈Z,
S(fk) =xkek+ykfk+1, k= 1,2, . . . ,
where{xn}n∈N+ and{yn}n∈N+ are as in Lemma 5.1.
Since the sequences {xn}n∈N+ and {yn}n∈N+ are bounded, the operator S is
bounded. We can express this operator with the help of the graph given in Figure 2.
. . . 1 ✲ e0
1 ✲
e1
1 ✲
e2
1 ✲
e3
1✲
. . .
f1
x1 ✻
y1✲
f2
x2 ✻
y2✲
f3
x3 ✻
y3✲
. . .
Fig. 2. The graph representation of the operatorS
An alternative definition of paranormal operators is as follows: An operator T ∈ B(H)is paranormal if and only if|T2|2−2λ|T|2+λ2Id
His nonnegative for allλ >0
(cf. [1]). This means thatT is paranormal if and only ifkT2hk2−2λkT hk2+λ2khk2≥0
for allλ >0 andh∈ H.
Using this definition we now show that S is paranormal. Let us fix an arbitrary
h = P
n∈Zαnen +
P
k∈N+βkfk and λ > 0. Hence h =
P
n∈Nhn +g, where g :=
P
k∈Z
−αkek and hn :=αnen+βn+1fn+1. First, observe thatkS
ThuskS2gk2−2λkSgk2+λ2kgk2= (λ−1)2kgk2. Using the relation between{x
n}n∈N+
and{yn}n∈N+ we can conduct the following calculations:
kS2hnk2−2λkShnk2+λ2khnk2= =kS2(α
nen+βn+1fn+1)k2−
−2λkS(αnen+βn+1fn+1)k2+λ2k(αnen+βn+1fn+1)k2=
=k(2xn+1βn+1+αn)en+2+yn+1yn+2βn+1fn+3k2−
−2λk(xn+1βn+1+αn)en+1+yn+1βn+1fn+2k2+
+λ2k(αnen+βn+1fn+1)k2=|2xn+1βn+1+αn|2+y2n+1yn2+2−
−2λ(|xn+1βn+1+αn|2+|yn+1βn+1|2) +λ2(|αn|2+|βn+1|2) =
=|(1−λ)αn+ 2xn+2yn+1βn+1|2+|βn+1|2(λ−(x2n+2yn2+1+y2n+1))2+
+|βn+1|2(y2n+1yn2+2−(x2n+2y2n+1+y2n+1)2).
The last part of this formula is equal to0. Hence
kS2h
nk2−2λkShnk2+λ2khnk2≥0.
Finally, let us observe that each of the sets {g} ∪ {hn}n∈N, {Sg} ∪ {Shn}n∈N and
{S2g} ∪ {S2h
n}n∈Nis orthogonal. Thus
kS2hk2−2λkShk2+λ2khk2=X n∈N
(kS2hnk2−2λkShnk2+λ2khnk2)+
+kS2gk2−2λkSgk2+λ2kgk2≥0.
This means thatS is paranormal.
It remains to show that the operator S does not have the PF property. In-deed, S satisfies the equality P S∗ = U P, where P is orthogonal projection on
E :=span{en|n∈Z} andU is a direct sum of a bilateral backward shift onE and the identity operator, but
P Sf1=x1e16= 0 =U P f1.
A part of Theorem 7.1.7 from [7] says that a paranormal operator isk-paranormal for eachk∈N. Owing to this result we see that the operatorS from Example 5.2 is
k-paranormal for each k= 2,3, . . .. On the other hand, due to Theorem 4.1,S is not
k∗-paranormal for anyk∈N+.
In [11] it was proved that eachk∗-paranormal operator is(k+ 1)-paranormal. We conclude the paper with the ensuing observation.
REFERENCES
[1] T. Andˆo, Operators with a norm condition, Acta Sci. Math. (Szeged) 33 (1972), 169–178.
[2] M.L. Arias, G. Corach, M.C. Gonzalez, Partial isometries in semi-Hilbertian spaces, Linear Algebra Appl.428(2008), 1460–1475.
[3] B.P. Duggal,On unitary parts of contractions, Indian J. Pure Appl. Math.25(1994), 1243–1227.
[4] B.P. Duggal, On characterising contractions with C10 pure part, Integral Equations
Operator Theory27(1997), 314–323.
[5] B.P. Duggal, C.S. Kubrusly,Contractions withC·0 direct summands, Adv. Math. Sci.
Appl.11(2001), 593–601.
[6] B.P. Duggal, C.S. Kubrusly, Paranormal contractions have property PF, Far East J. Math. Sci.14(2004), 237–249.
[7] V.I. Istrˇat¸escu,Introduction to Linear Operator Theory, Marcel Dekker Inc., New York, Basel, 1981.
[8] L. K´erchy,Isometric asymptotes of power bounded operators, Indiana Univ. Math. J. 38(1989), 173–188.
[9] I.H. Kim, The Fulglede-Putnam theorem for (p, k)-quasihyponormal operators, J. Inequal. Appl. Art. ID 47481 (2006), 7 pp.
[10] S. Mecheri, A generalization of Fuglede-Putnam theorem, J. Pure Math. 21 (2004), 31–38.
[11] P. Pagacz,On Wold-type decomposition, Linear Algebra Appl.436(2012), 3065–3071. [12] P. Pagacz,On the power-bounded operators of classesC0· andC1·, arXiv:1206.0492v1.
[13] L. Suciu, Maximum A-isometric part of an A-contraction and applications, Israel J. Math.174(2009), 419–443.
Patryk Pagacz
patryk.pagacz@im.uj.edu.pl
Uniwersytet Jagielloński Instytut Matematyki
ul. Łojasiewicza 6, PL-30348 Kraków, Poland Received: June 20, 2012.