Simulação termomecânica do processo de lingotamento contínuo utilizando o método de volumes finitos baseado em elementos

(1)

CENTRO DE TECNOLOGIA

DEPARTAMENTO DE ENGENHARIA METAL ÚRGICA E DE MATERIAIS PROGRAMA DE P ÓS-GRADUAÇ ÃO EM ENGENHARIA E CIÊNCIA DE

MATERIAIS

Paulo Vicente de Cassia Lima Pimenta

Simulac

¸˜

ao termomecˆ

anica do processo de

lingotamento cont´ınuo utilizando o m´

etodo de

volumes finitos baseado em elementos

(2)

Paulo Vicente de Cassia Lima Pimenta

Simulac

¸˜

ao termomecˆ

anica do processo de

lingotamento cont´ınuo utilizando o m´

etodo de

volumes finitos baseado em elementos

Disserta¸cão apresentada ao Programa de Pós-Gradua¸cão em Engenharia e Ciência de Materiais como parte dos requisitos para obten¸cão do t´ıtulo de Mestre em Engenharia e Ciência de Materi-ais. Área de concentra¸cão: Propriedades F´ısicas e Mecânicas dos Materiais.

Orientador: Prof. Dr. Francisco Marcondes Co-orientador: Prof. Dr. P´eter Zoltan Berke

(3)

Universidade Federal do Ceará

Biblioteca de Pós-Graduação em Engenharia - BPGE

P697s Pimenta, Paulo Vicente de Cassia Lima.

Simulação termomecânica do processo de lingotamento contínuo utilizando o método de volumes finitos baseado em elementos / Paulo Vicente de Cassia Lima Pimenta._–2014.

78 f. : il. color. , enc. ; 30 cm.

Dissertação (mestrado)–Universidade Federal do Ceará, Centro de Tecnologia, Departamento de Engenharia Metalúrgica e de Materiais, Programa de Pós-Graduação em Engenharia e Ciência de Materiais, Fortaleza, 2014.

Área de Concentração: Propriedades Físicas e Mecânicas dos Materiais. Orientação: Prof. Dr. Francisco Marcondes.

Coorientação: Prof. Dr. Péter Zoltan Berke.

1. Ciência dos materiais. 2. Acoplamentos. 3. Tensões. 4. Simulação. I. Título.

(4)

(5)

(6)

AGRADECIMENTOS

Agrade¸co a Deus.

Gostaria de agradecer tambémaos meus orientadores, Prof. Francisco Marcondes e o Prof. Péter Zoltan Berke, pelo suporte, pela dedica¸cão de tempo e paciência para comigo durante todo per´ıodo do curso de mestrado.

A minha m˜ae, Claudinete Lima Pimenta, pelo apoio e incentivo.

A minha tia Justina, que nos momentos mais dif´ıceis, me ajudou financeiramente.

A minha namorada, Ingred, pela dedica¸cão e paciência durantes os últimos 5 anos.

Aos meus colegas de trabalho do Laboratório de Dinâmica dos Fluidos Computacio-nal, que são eles: Bruno Ramon, Ivens Costa, Cláudio Oliveira, Alysson Gon¸calves, José Renê, Dênio Silva e Edilson Drumond, pela ajuda na constru¸cão do código e pela amizade.

(7)

RESUMO

A técnica de lingotamento cont´ınuo, nas últimas quatro décadas, é cada vez mais uti-lizada na produ¸cão de a¸co semiacabado. A transferência de calor é o principal mecanismo dominante e ocorre em todas as etapas do processo. A qualidade do a¸co, no lingotamento, está diretamente relacionada à forma que ocorrem as trocas de calor, pois as varia¸cões térmicas produzem carregamentos mecânicos, assim como as for¸cas de contato, as quais são geradas por intermédio dos rolos e da oscila¸cão do molde. Tais fatores podem causar defeitos, como fraturas ou trincas, no produto final, caso as tensões e deforma¸cões resul-tantes excedam valores cr´ıticos. O aprimoramento da técnica tem a finalidade de evitar o surgimento de defeitos e reduzir o tempo de produ¸cão. Para isso é fundamental uma boa compreensão dos fenômenos f´ısicos envolvidos ao longo do processo de solidifica¸cão. O foco deste trabalho é aplicar a abordagem do EbFVM (Element based Finite-Volume Method) no estudo dos efeitos das tensões lineares acopladas unidirecionalmente com a temperatura aplicado ao lingotamento cont´ınuo do a¸co 1013D (0,3% de carbono).

Nas simula¸cões, adotou-se algumas simplifica¸cões com o estado plano de tensões e isotropia do material. Descartando-se as for¸cas de corpo, o contato com os rolos, a pressão do a¸co l´ıquido nas paredes do lingote (pressão ferrostática) e o efeito convectivo. Contudo, apesar das simplifica¸cões adotadas, este trabalho traz informa¸cões quantitativas quanto a forma¸cão do acúmulo das tensões lineares, que apontam para regiões de poss´ıveis forma¸cões de trincas.

(8)

ABSTRACT

The continuous casting technique, in the last four decades, has been large used for to production of semi-finished steel. The heat transfer is major mechanism and it occurs in various steps during the continuous casting. The quality of steel is directly related to the way the heat transfer occur, because the thermal variations produce mechanical loads, as well as contact forces, which are generated through the rollers and shake of the mold. Such factors may cause defects such as fractures or cracks in the final product, if the resulting stresses and strains exceed critical values. The technique must be improved in order to reduce the appearance of defects and the production time. For this, a good understanding of physical phenomena involved during the solidification process is critical. The focus of this work is to apply the EbFVM (Element based Finite-Volume Method) approach to study the effects of linear tensions unidirectionally coupled with the temperature applied to continuous casting of the steel 1013D (0,3% of carbon).

In the simulations, we adopted some simplifications such as the Plane Strain and iso-tropic material. We also neglected the body forces, contact with the rollers, the liquid pressure on the walls of the steel ingot (ferrostatic pressure), and the convective effect. However, despite of the simplifications adopted, this work provides quantitative informa-tions on the linear tensions accumulation, that point out to areas of possible of cracks formations.

(9)

LISTA DE FIGURAS

1.1 Foto da m´aquina de lingotamento cont´ınuo . . . 1

1.2 Representa¸c˜ao esquem´atica do processo de lingotamento cont´ınuo . . . 3

2.1 Ilustra¸c˜ao da m´aquina de lingotamento real . . . 8

2.2 Figura ilustrativa da sec¸c˜ao do molde de cobre . . . 9

2.3 Diagrama de fases Fe-C . . . 9

2.4 Diagrama de fases Fe-C (a¸co 0,3%) . . . 10

2.5 Estado Plano de Tens˜ao em um dom´ınio cont´ınuo . . . 22

2.6 Estado Plano de Deforma¸c˜ao em um dom´ınio cont´ınuo . . . 23

2.7 Gr´aficos das propriedades mecˆanicas . . . 26

2.8 Representa¸cão das condi¸cões de contorno do problema mecânico . . . 27

3.1 Esquema de malha n˜ao estruturada utilizando a metodologia Cell vertex . 29 3.2 Esquema do elemento triangular . . . 30

3.3 Ilustra¸cão da área do elemento e da área que corresponde a fun¸cão de forma (em branco) . . . 31

3.4 Esquema do elemento triangular com as divisões dos subvolumes de controle 37 3.5 Fluxograma para o problema térmico (Variável desconhecida T) . . . 39

3.6 Fluxograma esquem´atico do problema termomecˆanico . . . 46

4.1 Campo de temperatura dentro e fora do molde . . . 48

4.2 Perfil da casca s´olida formada na sa´ıda do molde (z = 0,70m) . . . 49

4.3 Representa¸cão gráfica da forma¸cão percentual de sólido . . . 50

4.4 Ilustra¸cão do campo de temperatura no comprimento metalúrgico e na região de corte . . . 51

4.5 Representa¸cão das componentes do EPT na seçcão de corte (z = 12,0m) . 52 4.6 Representa¸cão do critério de von Mises na seçcão de corte (z = 12,0m) . . 53

4.7 Resultado do campo de tens˜oes dentro do molde (z = 0,43m) . . . 54

4.8 Campo de temperatura e o efeito acoplado das deforma¸cões térmicas e mecânicas . . . 55

(10)

LISTA DE TABELAS

A.1 Parâmetros da equa¸cão do coeficiente global de transferência de calor na

interface molde/metal . . . 66

A.2 Vaz˜ao dos sprays (ls−1_{) . . . 66}

A.3 Coeficientes de transferˆencia de calor nas regi˜oes dos sprays . . . 67

(11)

SUM ´

ARIO

1. INTRODUC¸ ˜AO . . . 1

1.1 O Problema Industrial . . . 1

1.2 Contribui¸c˜ao da Modelagem Num´erica . . . 4

1.3 Motiva¸c˜ao e Originalidade . . . 5

1.4 Panorama da Disserta¸c˜ao . . . 6

2. MODELO TERMOMEC ˆANICO ACOPLADO UNILATERALMENTE . . . 7

2.1 Preliminares . . . 7

2.2 A¸cos . . . 9

2.3 Problema T´ermico . . . 11

2.3.1 Condi¸c˜oes de Contorno do Problema T´ermico . . . 14

2.4 Tensão e Deforma¸cão Linear em um Sólido Isotrópico . . . 16

2.4.1 Estado Plano de Tens˜ao . . . 22

2.4.2 Estado Plano de Deforma¸c˜ao . . . 23

2.5 Modelo Termomecˆanico Aplicado ao Lingotamento Cont´ınuo . . . 24

2.5.1 Condi¸c˜oes de Contorno do Modelo Mecˆanico . . . 26

3. MODELO NUM´ERICO DO LINGOTAMENTO CONT´INUO . . . 28

3.2 Discretiza¸c˜ao da Equa¸c˜ao da Energia . . . 34

3.2.1 Condi¸c˜oes de Contorno . . . 37

3.3 EbFVM Aplicado ao Modelo Termomecˆanico . . . 38

3.3.1 Condi¸c˜oes de Contorno do Problema Termomecˆanico . . . 43

4. RESULTADOS . . . 47

4.2 Resultados T´ermicos . . . 48

4.3 Resultados da Simula¸c˜ao Termomecˆanica . . . 50

4.3.1 Resposta Mecˆanica a Partir do Comprimento Metal´urgico . . . 50

4.3.2 Resposta Mecˆanica Para o Lingotamento Cont´ınuo Completo . . . . 52

4.4 Limita¸c˜oes da Modelagem . . . 57

5. CONCLUS ˜AO . . . 59

6. TRABALHOS FUTUROS . . . 60

(12)

(13)

1. INTRODUC

¸ ˜

AO

1.1 O Problema Industrial

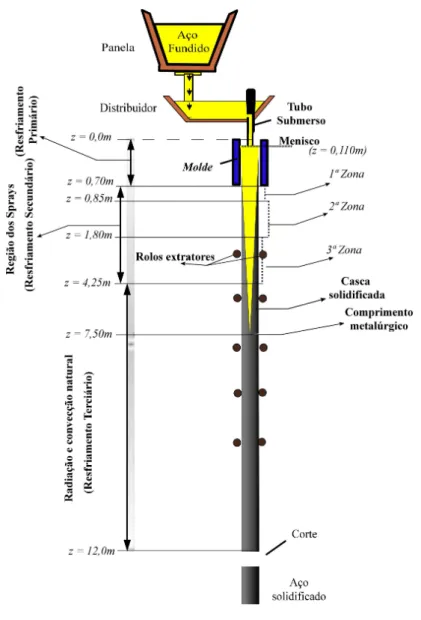
A técnica de lingotamento cont´ınuo, nas últimas quatro décadas, tem sido cada vez mais utilizada na produ¸cão de a¸co semiacabado. Na Fig. 1.1, é poss´ıvel observar uma das etapas da fabrica¸cão de tarugos e a máquina de lingotamento.

Figura 1.1: Foto da m´aquina de lingotamento cont´ınuo

(14)

Essa técnica recorre basicamente à transferência de calor durante as etapas de solidi-fica¸cão. O lingotamento come¸ca com a transferência do metal l´ıquido da panela para o distribuidor, no qual o a¸co é vazado através de um tubo de imersão e alimenta o molde de cobre. A região do molde é refrigerada à água (resfriamento primário) e também é responsável pela forma¸cão de uma casca sólida cuja espessura m´ınima deve estar entre 9−10mm [Anjos 2013] para suportar a pressão ferrostática e a for¸ca de corpo devido à a¸cão da gravidade na sa´ıda do molde. Subsequentemente, o lingote é submetido a outras regiões de resfriamento for¸cado, como é o caso da região dos sprays de ar-comprimido e água, composta pelas 1a_{, 2}a _{e 3}a _{zonas (veja Fig. 1.2), que correspondem a diferentes} vazões de água (resfriamento secundário). Por fim, ocorre o resfriamento por radia¸cão e conveçcão natural (resfriamento terciário) [Janik e Dyja 2004]. A Fig. 1.2 ilustra a máquina de lingotamento cont´ınuo com o molde e as regiões de resfriamento for¸cado e natural (radia¸cão e conveçcão natural).

A qualidade do a¸co no lingotamento está diretamente relacionada com o modo que ocorrem as trocas de calor e aos carregamentos mecânicos produzidos por for¸cas de con-tato, como os rolos. Observa-se que as altas varia¸cões térmicas durante o resfriamento produzem carregamentos térmicos, que podem causar defeitos (p.e. fraturas/trincas) no produto final, se as tensões e deforma¸cões resultantes excederem valores cr´ıticos.

O aprimoramento da técnica está em evitar o surgimento de defeitos e na redu¸cão do tempo de processamento. Para isso, é fundamental uma boa compreensão dos fenômenos f´ısicos envolvidos ao longo do processo de solidifica¸cão, como o efeito da temperatura sobre o comportamento elastoplástico do material, das tensões produzidas durante o contato com os rolos extratores, do tempo e a forma do resfriamento [Chen et al. 2009, Huespe

et al. 2000]. A compreensão desses fenômenos requer à utiliza¸cão de recursos qualitativos, como medidas experimentais e/ou análise numérica.

´

(15)

Figura 1.2: Representa¸c˜ao esquem´atica do processo de lingotamento cont´ınuo

envolvidos nas etapas de fabrica¸cão do a¸co. Como no trabalho de Das [1999], que obteve o campo de temperatura durante o processo de solidifica¸cão na região do molde; Bellet

(16)

1.2 Contribui¸c˜ao da Modelagem Num´erica

Todo processo eficiente de fabrica¸cão em larga escala dispõe de um projeto de en-genharia que basicamente está fundamentado em observa¸cões experimentais obtidas em laboratório e em informa¸cões obtidas por meio de análises computacionais (simula¸cão numérica).

As observa¸cões experimentais têm como principal vantagem o tratamento de problemas reais em ambiente controlado. Porém, o pesquisador não pode desacoplar os diferentes efeitos f´ısicos envolvidos sem comprometer a investiga¸cão. Outro aspecto relevante, é o custo de execu¸cão elevado.

Uma outra forma de análise dos fenômenos f´ısicos é a solu¸cão de modelos matemáticos através de métodos de solu¸cão anal´ıtica (solu¸cão exata). Em contrapartida, a utiliza¸cão desse recurso se limita a resolver uma pequena classe de problemas e que, em geral, estão muito distantes dos processos f´ısicos reais em decorrência do grande número de simplifica¸cões que são adotadas.

(17)

1.3 Motiva¸c˜ao e Originalidade

Neste trabalho será empregada a abordagem EbFVM (Element based Finite-Volume Method) na implementa¸cão dos problemas que serão analisados. Esse método numérico de solu¸cão de equa¸cões permite o emprego de malhas não estruturadas e, portanto, fle-xibiliza o tratamento de problemas com geometrias arbitrárias. Uma caracter´ıstica f´ısica importante do EbFVM é a conserva¸cão das propriedades em n´ıvel discreto [Maliska 2004]. O sucesso do método pode ser constatado pela grande variedade de trabalhos na área de mecânica dos fluidos, incluindo os multicomposicionais, como nas simula¸cões de re-servatório de petróleo [Cordazzo et al. 2006, Marcondes e Sepehrnoori 2007; 2010], de fluidos compress´ıveis e incompress´ıveis [Frink e Pirzadeh 1998].

O interesse de utilizar métodos cada vez mais robustos toma espa¸co na análise com-putacional moderna. Ferramentas numéricas que levam em considera¸cão o balan¸co de massa, energia e momento têm despertado a aten¸cão de pesquisadores para as vantagens do EbFVM no âmbito dos problemas estruturais [Bailey e Cross 1995, Limache e Idel-sohn 2007], fluido-estruturais [Slone et al. 2003, Wheel 1999] e em abordagens h´ıbridas (FVM-FEM) [Chandioet al. 2004].

Este trabalho se concentra na utiliza¸cão do EbFVM na solu¸cão numérica do mo-delo bidimensional térmico e mecânico acoplado unilateralmente aos efeitos da varia¸cão de temperatura, aplicado ao processo de lingotamento cont´ınuo do a¸co 0,3% carbono. Destaca-se que não foram encontrados relatos na literatura da aplica¸cão do EbFVM à problemas termomecânicos aplicado ao lingotamento cont´ınuo.

O tratamento do problema segue os seguintes passos:

• Dom´ınio do problema - Adota-se o dom´ınio bidimensional, ou seja, uma seçcão plana do lingote. Utiliza-se o referencial Lagrangiano afim de se observar as varia¸cões causadas pelas diferentes condi¸cões de contorno que pertencem a cada etapa do resfriamento.

(18)

calor devido a mudan¸ca de fase. Os coeficientes de transferência de calor nas faces do lingote foram obtidos numérico-experimentalmente1 _{em todas as etapas de} res-friamento do lingotamento cont´ınuo, iniciando-se no menisco e finalizando na região de corte;

• Estado de Tensão- Para o estudo das tensões lineares provocadas pelas varia¸cões térmicas, adota-se o estado plano de tensões (EPT) - O campo de tensões é analisado de duas formas: A primeira, com as propriedades mecânicas (E, ν, α) do material sem a dependência da temperatura, com o estado de referência na região do com-primento metalúrgico (veja - Fig. 1.2). A segunda, com as propriedades mecânicas do material variando com a temperatura e utilizando a temperatura solidus como estado de referência.

1.4 Panorama da Disserta¸c˜ao

O restante desta disserta¸cão está organizada da seguinte forma: O cap´ıtulo 2 aborda os modelos matemáticos térmico e mecânico que serão tratados, as considera¸cões adotadas e as condi¸cões de contorno. O cap´ıtulo 3 apresenta a metodologia EbFVM e mostra as equa¸cões aproximadas para os modelos térmico e mecânico acoplado. No cap´ıtulo 4, apresentam-se os resultados numéricos. No cap´ıtulo 5, observam-se as avalia¸cões dos resultados. No capitulo 6, apresentam-se sugestões para trabalhos futuros.

1

(19)

2. MODELO TERMOMEC ˆ

ANICO ACOPLADO

UNILATERALMENTE

Este cap´ıtulo aborda os modelos matemáticos que serão utilizados na simula¸cão. Mostra-se ainda as simplifica¸cões adotadas e as condi¸cões de contorno que serão em-pregadas.

2.1 Preliminares

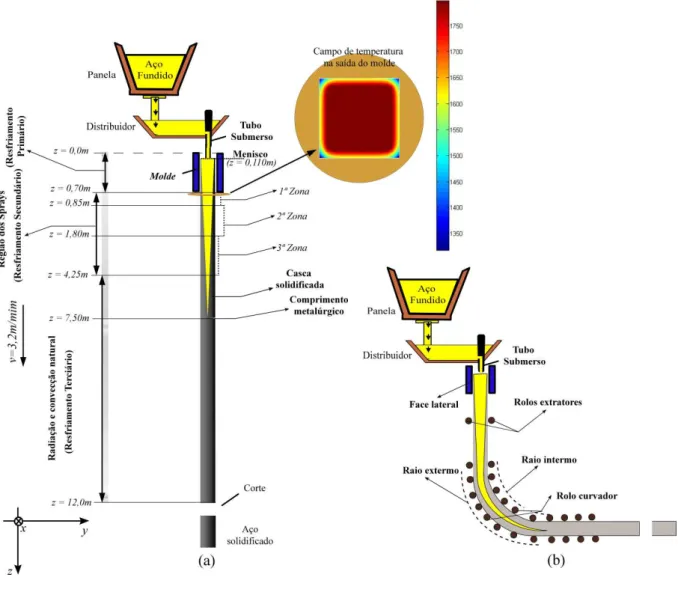
Durante as etapas de fabrica¸cão do a¸co no lingotamento cont´ınuo estão presentes vários ingredientes f´ısicos e um modelo f´ısico-matemático completo deve trazer aspectos, como as não linearidades térmicas e mecânicas assim como o acoplamento entre esses fenômenos, as for¸cas de contato produzidas pelos rolos, a friçcão no molde e rolos e o calor gerado, as formas de resfriamento, e as varia¸cões dos campos térmico e mecânico nas três dimensões espaciais (Fig. 2.1), deforma¸cões elásticas e plásticas. Contudo, o foco deste trabalho é obter uma primeira análise e para isso, algumas simplifica¸cões foram adotadas. O que se pretende analisar consiste na solu¸cão do problema bidimensional termomecânico com acoplamento unidirecional, assumindo-se que o material utilizado na simula¸cão apresente comportamento isotrópico e elástico linear.

Representa-se, de forma esquemática a máquina de lingotamento real (Fig. 2.1b) e a máquina considerada na simula¸cão (Fig. 2.1a). Por comodidade, as zonas de resfria-mento foram representadas apenas na Fig. 2.1a, porém essas mesmas zonas correspondem também à Fig. 2.1b.

(20)

Figura 2.1: Ilustra¸cão da Máquina de lingotamento real, à direita, e a utilizada na simula¸cão, à esquerda

(21)

Figura 2.2: Figura ilustrativa da sec¸c˜ao do molde de cobre

2.2 A¸cos

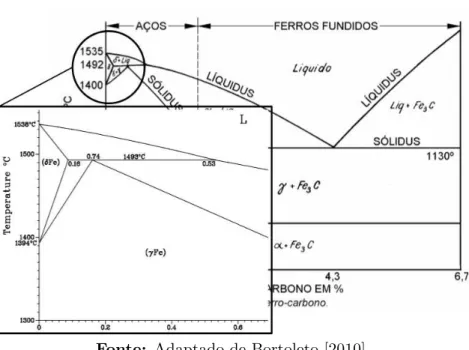
As ligas de ferro com até 2,1% de carbono são denominadas a¸cos. Observa-se que 2,11% é a separa¸cão teórica entre a¸cos e ferros fundidos. Para teores acima desse valor de referência, apresentam-se os ferros fundidos (Fig. 2.3). Os a¸cos, além do carbono, também podem conter outros elementos como Cr, Mn, Si, Mo,V, Nb, Ti e Ni, e são utilizados comumente na fabrica¸cão de ferramentas, pe¸cas industriais, estruturas de sustenta¸cão na constru¸cão civil e outras inúmeras aplica¸cões [Bortoleto 2010].

Figura 2.3: Diagrama de fases Fe-C

(22)

Ainda de acordo com a concentra¸cão de carbono, os a¸cos podem ser classificados como eutetóides, hipoeutetóides ou hipereutetóides, se, respectivamente, apresentarem porcentagem em massa de carbono iguais, inferiores ou superiores a 0,77%. Note-se, que o ponto eutetóide corresponde a menor temperatura de equil´ıbrio entre a ferrita, perlita e austenita, que no diagrama ferro-carbono (Fig. 2.3)1 _{equivale a 0,77%.}

Entretanto, este trabalho utiliza o a¸co 0,3% de carbono na simula¸cão e, para ilustrar as transforma¸cões de fases que ocorrem durante o resfriamento, evidencia-se, a partir da Fig. 2.3, a região na qual essas transforma¸cões acontecem (Fig. 2.4).

Figura 2.4: Diagrama de fases Fe-C(a¸co 0,3%)

Fonte: Adaptado de Bortoleto [2010]

Pelo diagrama da Fig. 2.4, fica claro que durante a solidifica¸c˜ao ocorrem diversas

1

Abcissa – Representa a escala horizontal, com a porcentagem de carbono; Ordenada – Representa as temperaturas;

A1– Indica o limite da existˆencia de austenita;

A3– Indica in´ıcio da passagem da estrutura CFC para CCC durante o resfriamento;

Acm– Indica o limite da quantidade de carbono dissolvido na austenita;

F e3C – ´E a f´ormula do carboneto de ferro, chamado cementita;

(23)

transforma¸c˜oes de fase e que essas dependem da composi¸c˜ao qu´ımica do a¸co. De acordo com o percentual de carbono, as ligas de a¸cos podem ser classificadas da seguinte maneira [Anjos 2013]:

1- A¸cos hipoperitéticos apresentam na sua composi¸cão teor de carbono menor ou igual 0,09% e se caracterizam pela forma¸cão, na fase sólida, de ferrita delta (δ−δFe);

2- A¸cos peritéticos apresentam concentra¸cão de carbono entre 0,09 e 0,53% e podem ser caracterizados pela rea¸cão da ferrita delta com a fase l´ıquida produzindo austenita (γ−γFe) a uma temperatura de 1493o_C;

3- A¸cos hiperperitéticos apresentam teor de carbono acima de 0,53%. Note-se que nesta concentra¸cão de carbono, não há a presen¸ca da fase ferrita delta.

Assim, para o a¸co 0,3% carbono (ragião dos a¸cos peritéticos), pode-se observar as transforma¸cões de fases que ocorrem no processo de solidifica¸cão e compreende a forma¸cão de a¸co l´ıquido, em seguida da fase l´ıquida mais a ferrita delta (L+δ), que produz a fase l´ıquida mais a austenita (L+γ) e por fim, a forma¸cão de austenita (γ).

2.3 Problema T´ermico

A rela¸cão fundamental utilizada na modelagem da solidifica¸cão é a equa¸cão bidimensi-onal da condu¸cão de calor transiente com gera¸cão de calor, expressa na forma conservativa por:

∂

∂t[ρ(T)c(T)T] = ∂ ∂x

¯¯

κ(T)∂T ∂x

+ ∂ ∂y

¯¯

κ(T)∂T ∂y

+ ˙q (2.1)

de modo que ρ´e a densidade do a¸co (kgm−3_), _c_{´e o calor espec´ıfico} _Jkg−1_K−1

, T é a temperatura (K), t é o tempo f´ısico (s), ¯¯κ é a condutividade térmica (W m−1_K−1_{) e ˙}_q _é

o termo de gera¸c˜ao oriundo do calor latente de mudan¸ca de fase (W m−3_).

(24)

(tensor de ordem zero) ¯¯ κ=    κ 0 0 κ    (2.2)

O termo de gera¸c˜ao de calor latente que surge devido a mudan¸ca de fase (l´ıquida -s´olida) pode ser escrito como:

˙

q =ρ(T)L∂fs

∂t (2.3)

sendoLo calor latente de fus˜ao Jkg−1

,fsa fra¸cão sólida formada. O termo de gera¸cão

ainda pode escrito, utilizando a regra da cadeia, na forma:

˙

q =ρ(T)L∂fs ∂T

∂T

∂t (2.4)

Substituindo a Eq.(2.4) na Eq.(2.1), obt´em-se

∂

∂t[ρ(T)c

′_(T₎_T_{] =} ∂

∂x

κ(T)∂T ∂x

+ ∂ ∂y

κ(T)∂T ∂y

(2.5)

uma vez que

c′_(T_{) =}_c_(T₎₋_L∂fs

∂T (2.6)

sendoc(T) expresso por

c(T) =

          

cs, se T 61770K (s´olido)

fscs+ (1−fs)cl

cl, se T >1792K (l´ıquido)

(2.7)

Nota-se que as vari´aveiscsecl representam o calor espec´ıfico das fases s´olida (cs = 800

Jkg−1_K−1_{) e l´ıquida (c}

l= 740 Jkg−1K−1), respectivamente.

(25)

expressa por uma rela¸c˜ao similar a do calor espec´ıfico e ´e representada por [Anjos 2013]:

κ(T) =

          

κs, se T 61770K (s´olido)

fsκs+ (1−fs)κl

κl, se T >1792K (l´ıquido)

(2.8)

sendo que as variáveisκseκlsão as condutividades térmicas para as fases sólida (κs = 33,6

W m−1_K−1_{) e l´ıquida (κ}

l = 34,7 W m−1K−1), respectivamente.

Da mesma forma, a densidade pode ser representada por

ρ(T) =

          

ρs, se T 61770K (s´olido)

fsρs+ (1−fs)ρl

ρl, se T >1792K (l´ıquido)

(2.9)

onde as vari´aveis ρs e ρl representam as massas espec´ıficas das fases s´olida (ρs = 7301

kgm−3_{) e l´ıquida (ρ}

l = 7011kgm−3), respectivamente.

A fra¸cão sólida (fs) depende dos constituintes da liga, bem como das intera¸cões

en-tre esses componentes durante a solidifica¸c˜ao. Na modelagem computacional, assume-se tamb´em que esse termo depende da temperatura na forma [Anjos 2013]

fs =

1 1−k0

Tliq−T

Tf −T

(2.10)

Derivando a Eq.(2.10) em rela¸c˜ao a temperatura, tem-se

∂fs

∂T =

1 1−k0

"

Tliq−T

(Tf −T)2

− 1 Tf −T

#

(2.11)

onde Tf é a temperatura do solvente (Tf = 1808 K), k0 é o coeficiente de parti¸cão do

soluto (k0 = 0,2) e Tliq ´e a temperaturaliquidus (Tliq = 1792 K).

´

(26)

consi-dera¸c˜ao. Mas substitui-se a condutividade t´ermica do l´ıquido por uma condutividade efetiva, dada por:

κef =Cκl (2.12)

assumindo a constante C = 7 [Anjos 2013].

2.3.1 Condi¸c˜oes de Contorno do Problema T´ermico

Como considerado anteriormente, na seçcão 2.1, existem diferen¸cas nos coeficientes de transferência de calor nos raios externo e interno do lingote. Admite-se que isso ocorra devido a curvatura da máquina de lingotamento, que promove diferentes trocas de calor. Porém, as faces laterais apresentam um padrão de simetria e, neste trabalho, considera-se não haver diferen¸cas nas trocas de calor nessas regiões. Com efeito, adota-se a analise dos efeitos térmicos e mecânicos em apenas metade do lingote, conforme ilustrado na Fig. 2.2. Os contornos que não estão sujeitos a condi¸cão de simetria, são tratados considerando o efeito convectivo:

Z

S

qdS =

Z

S

h(Tamb −T)dS (2.13)

Esta equa¸cão representa o fluxo l´ıquido de calor entrando através da área S, sendo h o coeficiente de pel´ıcula ou coeficiente convectivo de transferência de calor eTamb a

tempe-ratura ambiente.

Para a face lateral, raios externo e interno em cada zona de resfriamento do lingote, utiliza-se coeficientes de transferência de calor obtidos numérico-experimentalmente por Anjos [2013]. Esses coeficientes são organizados por regiões, como segue:

• Região de resfriamento primário - Molde- A equa¸cão do coeficiente global de transferência de calor na interface molde/metal é representado pela rela¸cão:

hg(z) =C+Ae−z(t)/B (2.14)

onde

(27)

sendo A, B e C constantes obtidas numérico-experimentalmente por Anjos [2013] e estão representadas na Tabela A.1 (Apêndice A), z(t) é a posi¸cão da seçcão plana ao longo do processo de lingotamento (m) (Fig. 2.1) em fun¸cão do tempo e v é a velocidade da seçcão (m/mim) ou velocidade do lingotamento, que este trabalho assume como sendo v = 3,2 m/mim.

• Região de resfriamento secundário- Os coeficientes de transferência de calor na região dos jatos, foram obtidos através de medi¸cões da temperatura superficial do lingote e da correla¸cão dessa com a vazão de água de acordo com expressão sugerida por Brimacombe et al. [1984]

h= 0,366Vn (2.16)

de modo que V é a vazão de água dos sprays (ls−1_{) e} _n_{é um n´}_{umero arbitrário. A}

Tabela A.2 apresenta as vaz˜oes de ´agua em cada zona de resfriamento for¸cado. Afim de arbitrar o valor de n, Anjos [2013] utilizou medidas de temperatura super-ficial do lingote e um simulador. Ao final do experimento, obteve o valor n = 0,56 de modo que a Eq.(2.16) pode ser expressa na forma:

h= 0,366V0,56 (2.17)

• Região de resfriamento por radia¸cão/conveçcão natural

Os valores do coeficiente de pel´ıcula podem ser encontrados na Tabela A.3.

Utilizando as vazões de água mostradas na Tabela A.2 e a Eq.(2.17), os coeficientes de transferência de calor podem calculados para cada zona de resfriamento secundário e esses valores podem ser encontrados na Tabela A.3.

(28)

coeficiente de pel´ıcula, por meio de um algoritmo. Caso o valor da temperatura superfi-cial simulada fosse diferente daquela medida via pirômetro, o valor do h (coeficiente de pel´ıcula) deveria ser ajustado. O valor dos coeficientes, h, baseado nesse procedimento é utilizado neste trabalho e podem ser observados no Apêndice (Apêndice A).

2.4 Tensão e Deforma¸cão Linear em um Sólido Isotrópico

Para o problema de mecânica do sólido que será tratado, considerou-se algumas sim-plifica¸cões, como isotropia, ausência de intera¸cões com as for¸cas de corpo e de contato, e também sem considerar as deforma¸cões plásticas do material. Assim, a partir da equa¸cão da conserva¸cão do momento linear [Voller 2009], pode-se escrever

∆σij,j = 0 (2.18)

onde ∆σij é a varia¸cão do tensor tensão de Cauchy a partir de um estado de referência

(os detalhes podem ser observados em Crisfield [1997]). A varia¸c˜ao do tensor por escrito em termos das componentes, como:

∆σij = 

    

∆σ11 ∆σ21 ∆σ31 ∆σ21 ∆σ22 ∆σ23 ∆σ31 ∆σ32 ∆σ33



    

(2.19)

De acordo com o princ´ıpio da conserva¸cão do momento linear e angular, uma vez que o corpo não está sujeito a nenhuma intera¸cão com for¸cas externas (equil´ıbrio de rota¸cão de transla¸cão), o tensor tensão é simétrico, ou seja,

∆σ[ij]= 0 (2.20)

e

(29)

podendo ser expresso em termos das vari´aveis independentes como:

∆σij = 

    

∆σ11 ∆σ21 ∆σ31 ∆σ22 ∆σ23

sim. ∆σ33



    

(2.22)

Observa-se que a nota¸c˜ao “sim.”denota as componentes sim´etricas da matriz.

Otensor tensão de Cauchy é aplicado na análise do estado de tensões de materiais su-jeitos a pequenas deforma¸cões (quando comparado as dimensões do corpo como um todo). Assim, considerando-se a rela¸cão conhecida como Lei de Hooke Generalizada escrita em termos do tensor tensão de Cauchy e do Tensor Deforma¸cão Infinitesimal, tem-se

∆σij =Cijkl∆εkl. (2.23)

sendo

∆εkl =

1

2(∆uk,l + ∆ul,k) (2.24)

onde uk é o vetor deslocamento (m). É importante observar também as condi¸cões de

simetria para o tensorεkl, isto ´e

∆εkl = ∆εlk (2.25)

O termo Cijkl é o tensor elástico clássico de 4a ordem e apresenta 81 componentes

independentes sem considerar nenhuma simplifica¸cão. Entretanto, esse número cai para 36 componentes independentes quando a condi¸cão de simetria é empregada (σij = σji),

levando-o a Cijkl = Cjikl = Cijlk = Cjilk. Ademais, a rela¸c˜ao exigida para um material

(30)

indepen-dentes se reduza para 21. Assim,                                σ11 σ22 σ33 σ12 σ23 σ31                                =                

C11 C12 C13 C14 C15 C16 C22 C23 C24 C25 C26 C33 C34 C35 C36 C44 C45 C46 C55 C56 sim. C66                                                ε11 ε22 ε33 2ε12 2ε23 2ε31                                (2.26)

O número de componentes também depende dos planos de simetria. Então, para uma material tridimensional, observa-se:

• Para 1 plano de simetria, o tensor Cijkl possui 13 componentes independentes;

• Para 2 planos de simetria, 9 componentes independentes (material ortotr´opico);

• Para 3 planos de simetria, 2 componentes independentes (material isotr´opico).

Conforme já mencionado, considerou-se o caso com 3 planos de simetria, isto é, um material isotrópico e as componentes são representadas por

λ=C12 (2.27)

µ= 1

2(C11−C12) (2.28)

(31)

o tensorCijkl em termos das constantes de Lam´e, observa-se

Cijkl =                

λ+ 2µ λ λ 0 0 0

λ+ 2µ λ 0 0 0

λ+ 2µ 0 0 0 µ 0 0 µ 0 sim. µ                 (2.29)

ou em nota¸c˜ao indicial,

Cijkl =λδijδkl+µ(δikδjl+δilδjk) (2.30)

sendo

δmn= 

 

 

0, m6=n 1, m=n Substituindo a Eq.(2.30) em (2.23), obt´em-se

∆σij = [λδijδkl+µ(δikδjl+δilδjk)]∆εkl (2.31)

resultando em

∆σij =λδij∆εkk+ 2µ∆εij (2.32)

Note-se que o ´ındice mudo kk representa os eixos do sistema de coordenadas (p.e. no sistema cartesianokk assumexx, yy e zz).

Usualmente as constantes de Lamé são escritas em termos do Modulo de Young E (N m−2_{) e do}_{Coeficiente de Poisson} _{ν. As constantes de Lamé em termos desses}

coefici-entes s˜ao dadas por

µ= E

2(1 +ν) (2.33)

λ= Eν

(32)

A matriz constitutiva do material, agora em termos do m´odulo de Young e do coefici-ente de Poisson, ´e escrita como

Cijkl =

E

(1 +ν)(1−2ν)

               

1−ν ν ν 0 0 0

1−ν ν 0 0 0

1−ν 0 0 0

(1−2ν)

2 0 0 (1−2ν)

2 0

sim. (1−2ν)

2                 (2.35)

A Eq.(2.35) ´e denominada lei constitutiva do material e se admite ter comportamento el´astico linear.

Se o corpo também estiver submetido a uma varia¸cão de temperatura, ∆T, deve-se incluir as deforma¸cões térmicas do material na Eq.(2.32). Assim, obtém-se

∆σij =

Eν

(1−2ν)(1 +ν)δij∆εkk+ E

(1 +ν)∆εij +β(T −Tref)δij (2.36)

onde Tref é a temperada de referência, e β é expresso por

β =− E

1−2ναi (2.37)

de modo queα é o coeficiente linear de expansão térmica (K−1_{). Note-se que}_T ₋_T

ref =

∆T, sendo ∆T a varia¸cão de temperatura (K) a partir de uma meidada local (T) em rela¸cão a temperatura de referência.

Para o tensor εij, tem-se

∆εij =

1

2(∆ui,j + ∆uj,i) (2.38)

E para o tensor εkk, ´e poss´ıvel escrever

(33)

A forma expressa na Eq.(2.36), apesar de simplificada, pode ser encontrada em diver-sas aplica¸cões, como na simula¸cão das tensões produzidas pelo efeito térmico durante a solidifica¸cão no lingotamento cont´ınuo [Das 1999, Huespeet al. 2000] e pode descrever o comportamento de muitos materiais.

Escrevendo a Eq.(2.18) na forma integral, isto é, integrando-se em um volume ar-bitrário, V, obtém-se

Z

V

∆σij,jdV = 0 (2.40)

E, pelo teorema da divergência, para a uma área arbitrária, S, pode-se escrever:

I

S

∆σijnjdS = 0 (2.41)

Em termos das componentes do tensor tens˜ao em fun¸c˜ao do campo de deslocamentos, reescreve-se a Eq.(2.41) como:

I

S

Eν

(1−2ν)(1 +ν)∆uk,kδij + E (1 +ν)

1

2(∆ui,j+ ∆uj,i)

njdS

−

I

S

E

1−2ναiδij(T −Tref)njdS = 0 (2.42)

´

(34)

2.4.1 Estado Plano de Tens˜ao

Um corpo r´ıgido ´e considerado em um Estado Plano de Tens˜ao quando se assume:

∆σ33 = ∆σ23 = ∆σ13= 0 (2.43)

De acordo com o esquema mostrado na Fig. 2.5 e adotando o sistema de coordenadas x1,x2 e x3, as tens˜oes normais ao plano s˜ao desprezadas devido espessura do dom´ınio.

Figura 2.5: Estado Plano de Tens˜ao em um dom´ınio cont´ınuo

Manipulando-se a Eq.(2.36), considerando a simplifica¸c˜ao dada acima, tem-se na forma matricial            ∆σ11 ∆σ22 ∆σ12            = E

1−ν2

     

1 ν 0

ν 1 0 0 0 1−ν

2                  ∆ε11 ∆ε22 2∆ε12           

− Eαi∆T 1−ν

           1 1 0            (2.44)

Pode-se também escrever a rela¸cão acima (Eq.(2.44)) em fun¸cão das componentes das deforma¸cões na forma matricial

           ∆ε11 ∆ε22 2∆ε12            = 1 E      

1 −ν 0

−ν 1 0 0 0 2(1 +ν)

                 ∆σ11 ∆σ22 ∆σ12           

(35)

Observa-se que no EPT, apesar da componente da tensão, ∆σ33 = 0, o mesmo não ocorre com a componente da deforma¸cão, ∆ε33. Considerando a Eq.(2.36) escrita em termos das deforma¸cões e aplicando algumas manipula¸cões algébricas se pode obter a equa¸cão para o cálculo de ∆ε33

∆ε33= 1

E[∆σ33−ν(∆σ11+ ∆σ22)] +α3∆T (2.46)

e assumindo ∆σ33= 0, obt´em-se

∆ε33=−ν

E(∆σ11+ ∆σ22) +α3∆T (2.47)

Assim, como ∆σ11 6= 0 e ∆σ22 6= 0, logo ∆ε336= 0.

2.4.2 Estado Plano de Deforma¸c˜ao

O Estado Plano de Deforma¸c˜ao apresenta

∆ε33 = ∆ε23 = ∆ε13 = 0 (2.48)

(36)

Ao contrário do EPT, uma das dimensão é assumidamente maior do que as demais, ou seja, considerando o sistema de coordenadasx1,x2 ex3, de acordo com a Fig. 2.6, e o plano x1Ox2, a deforma¸cão da dire¸cão x3 é descartada (∆ε33 ≈0) (mas as tensões nessa dire¸cão não são nulas).

Retomando a Eq.(2.36) e a simplifica¸c˜ao adotada na Eq.(2.48), obt´em-se

           ∆σ11 ∆σ22 ∆σ12            = E

(1 +ν)(1−2ν)

     

1−ν ν 0

ν 1−ν 0 0 0 1−2ν

2                  ∆ε11 ∆ε22 2∆ε12           

− Eαi∆T 1−2ν

           1 1 0            (2.49) Observa-se que no EPD a tensão σ33 é obtida por meio da manipula¸cão da Eq.(2.36), ou simplesmente tomando a Eq.(2.46) e aplicando na Eq.(2.48)

∆ε33= 1

E[∆σ33−ν(∆σ11+ ∆σ22)] +α3∆T = 0 (2.50)

resultando em,

∆σ33=ν(∆σ11+ ∆σ22)−α3∆T (2.51)

Para os objetivos deste trabalho, utiliza-se o Estado Plano de Tensão, pois todas as observa¸cões se concentram em uma seçcão do lingote, que pode ser visto como uma placa sujeita a varia¸cões não uniformes de temperatura nas fronteiras. Contudo, se pode transformar, com certa simplicidade, do Estado Plano de Tensão para o Estado Plano de Deforma¸cão ou vice-versa [Voller 2009].

2.5 Modelo Termomecˆanico Aplicado ao Lingotamento Cont´ınuo

(37)

Apesar disso, pode-se fazer uma avalia¸cão quantitativa dos locais de concentra¸cão das tensões lineares.

Assim, para as componentes da tens˜ao considerando o EPT no plano xOy, tem-se

∆σxx =

E

1−ν2 [∆εxx+ν∆εyy−(1 +ν)αx∆T] (2.52)

∆σyy =

E

1−ν2 [∆εyy+ν∆εxx−(1 +ν)αy∆T] (2.53)

∆σxy =

E

2 (1 +ν)∆εxy = ∆σyx (2.54)

ou ainda em termos do campo de deslocamentos

∆ui =      ∆u1 ∆u2      =      ∆u ∆v      , (2.55)

∆σxx =

E 1−ν2

∂∆u ∂x +ν

∂∆v

∂y −(1 +ν)αx∆T

(2.56)

∆σyy =

E 1−ν2

∂∆v ∂y +ν

∂∆u

∂x −(1 +ν)αy∆T

(2.57)

∆σxy =

E 2(1 +ν)

∂∆u ∂y + ∂∆v ∂x (2.58)

O problema foi tratado de duas maneiras, a primeira utilizando-se valores fixos de E (32378,0M P a),ν(0,33) eαxx =αyy =α(22,3×10−6K−1). E, a segunda, com os termos

(38)

Figura 2.7: Gr´aficos das propriedades mecˆanicas variando com a temperatura

Fonte: Adaptado de Huespeet al. _[2000].

2.5.1 Condi¸c˜oes de Contorno do Modelo Mecˆanico

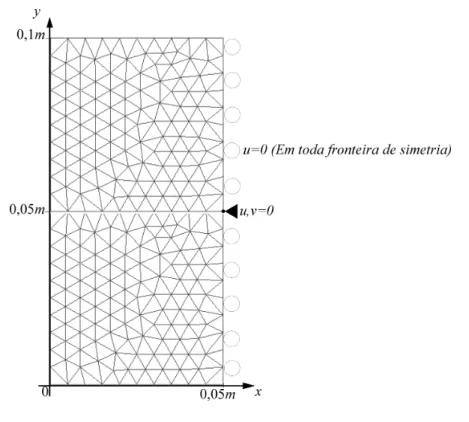
As condi¸cões de contorno para o problema mecânico serão abordadas na sequência: I - Simula¸cão Completa - Utiliza-se o dom´ınio de cálculo que foi representado na

Fig. 2.8. Quanto ao estado de referência das ten¸cões (σref = 0), adotou-se a região

do menisco (z = 0,110 m). Utiliza-se também parâmetros (E, ν, α) variáveis com a temperatura, como a finalidade de avaliar todas as poss´ıveis contribui¸cões para a forma¸cão de concentra¸cões das tensões lineares.

(39)

Figura 2.8: Representa¸cão das condi¸cões de contorno do problema mecânico

que descrevem o comportamento do a¸co durante o lingotamento são constantes e a temperatura de referência corresponde ao campo localizado no comprimento metalúrgico (Veja Fig. 2.1).

(40)

3. MODELO NUM´

ERICO DO LINGOTAMENTO

CONT´INUO

Este cap´ıtulo apresenta as equa¸cões aproximadas dos modelos térmico e mecânico acoplado. Utiliza-se, portanto, a equa¸cão da conserva¸cão da energia para a avalia¸cão do campo de temperatura e, para as tensões, a conserva¸cão do momento linear, adotando-se a forma simplificada proposta no cap´ıtulo anterior: o estado plano de tensões (EPT). Em ambos os modelos f´ısico-matemáticos, empregam-se a metodologia EbFVM (Element based Finite-Volume Method) em conjunto com elementos triangulares lineares.

3.1 Preliminares

Será utilizada a abordagem do método dos volumes finitos baseados em elementos -EbFVM. Nesse método, o dom´ınio de cálculo 2D é dividido em elementos triangulares e/ou quadrangulares (conforme pode ser visto na Fig. 3.1). Posteriormente, esses elementos são divididos em subelementos (ou subvolumes de controlesvc), de acordo com o número de vértices, e as equa¸cões de conserva¸cão são integradas para cada subelemento. Após o processo de integra¸cão, obtém-se a equa¸cão de conserva¸cão de cada volume de controle visitando-se todos os subelementos que compartilham o mesmo vértice, originando, dessa forma, uma formula¸cão baseada nos vértices da malha (cell vertex formulation). Essa ideia foi introduzida por Baliga e Patankar [1983] e Schneider e Zedan [1983] para elementos triangulares e quadrangulares, respectivamente. Neste trabalho, entretanto, somente os elementos triangulares (Fig. 3.2) serão utilizados.

´

E importante ressaltar que para essa técnica, que define o volume de controle em volta do vértice, encontram-se diversas denomina¸cões, tais como:

(41)

Figura 3.1: Esquema de malha n˜ao estruturada utilizando a metodologiaCell vertex

por Patankar [1980] e por Ferziger e Peri´c [2002];

• Element-based Finite Volume Method (EbFVM) - nomenclatura adotada por Ma-liska [2004], Marcondes e Sepehrnoori [2007; 2010];

• Vertex-based Finite Volume Method (VFVM) - termo adotado por Taylor et al.

[1999];

• Cell-vertex Finite Volume Method (CV-FV) - termo utilizado por Sloneet al. [2003].

Neste trabalho também será adotada a nomenclatura EbFVM, pois a mesma se refere a uma metodologia de volumes finitos que emprega elementos finitos e fun¸cões de forma, mas as equa¸cões aproximadas são obtidas obedecendo a conserva¸cão f´ısica da propriedade em cada elemento. No presente caso, conserva¸cão de energia e momento linear.

(42)

Figura 3.2: Esquema do elemento triangular com as divis˜oes dos subvolumes de controle (scv), os pontos nodais e (1, 2 e 3), nas faces de cada subvolume de controle, os pontos de integra¸c˜ao (ip)

considerandoφ como sendo uma propriedade que se quer avaliar em qualquer ponto den-tro do elemento, pode-se escreverφem termos da aproxima¸c˜ao (com interpola¸c˜ao linear):

φ≈ax+by+c, (3.1)

Contudo os coeficientes a, be cdevem satisfazer a rela¸c˜ao nodal

φi ≈aixi+biyi+ci, i= 1,2,3 (3.2)

A Eq.(3.1) poder se convenientemente definida em termos das fun¸c˜oes de forma Ni

com i= 1,2,3, tal que:

Ni(x, y) = 

 

 

0, Todos os pontos de lado oposto ao ponto nodal i

1, No ponto nodal

(3.3a)

3

X

i=1

Ni(x, y) = 1 em todos os pontos dentro do elemento (3.3b)

Sobre todo elemento, o campo cont´ınuo de uma propriedade arbitrária φ pode ser re-presentada como uma combina¸cão linear de valores nodais (i= 1,2,3), pela aproxima¸cão:

φ(x, y)≈ 3

X

i=1

(43)

sendo

N1 = Ap23/A123 (3.5)

N2 = Ap31/A123 (3.6)

N3 = Ap21/A123 (3.7)

onde A123 _{é área do elemento,} _p _{é um ponto arbitrário dentro do elemento,} _Ap23_{, A}p21 _e Ap31 _{são áreas, tais que}

Ap23+Ap31+Ap21 =A123 (3.8)

(essas áreas podem ser ilustradas pela região em branco apresentadas nos triângulos da Fig. 3.3). Observa-se que quando p assume valores que coincidem com o ponto nodal i (i= 1,2,3), implica em Ni = 1 e para valores dep do lado posto ao ponto nodali, a área

associada ´eNi = 0. Como pode se verificado pelas rela¸c˜oes

(44)

A123 = 1 2      

1 x1 y1 1 x2 y2 1 x3 y3

      (3.9) e

Ap23 = 1

2[(x2y3−x3y2)−xp(y3−y2) +yp(x3−x2)] (3.10) Ap31 = 1

2[(x3y1−x1y3)−xp(y1−y3) +yp(x1−x3)] (3.11) Ap12 = 1

2[(x1y2−x2y1)−xp(y2−y1) +yp(x2−x1)] (3.12)

Retomando a Eq.(3.4), a derivada de um propriedade φ, pode ser escrita em termos das fun¸c˜oes de forma como:

∂

∂xφ(x, y) ≈ 3

X

i=1 ∂

∂xNi(x, y)φi ∂

∂yφ(x, y) ≈ 3

X

i=1 ∂

∂yNi(x, y)φi (3.13)

Portanto, para as propriedades avaliadas nas faces, como, por exemplo, a difusivi-dade no subvolume de controle svc1, utilizando o ponto médio de cada face (ponto de integra¸cão), obtém-se

κip1 = 3

X

j=1

Niκi =

5 12κ1+

5 12κ2+

2

12κ3 (3.14)

κip2 = 3

X

j=1

Niκi =

5 12κ1+

2 12κ2+

5

12κ3 (3.15)

Note que i ´e o ´ındice do ponto nodal e Ni as fun¸c˜oes de forma definidas anteriormente.

Para as derivadas, expressa-se as componentes do operador ∇ (as duas componentes do operador - ∂

∂x, ∂

∂y) como

∂ ∂x =

3

X

i=1

(45)

∂ ∂y =

3

X

i=1

Niy (3.17)

N1x =

∂N1 ∂x =

(y2 −y3) 2Vele

N1y =

∂N1 ∂y =

(x3−x2) 2Vele

N2x =

∂N2 ∂x =

(y3 −y1)

2Vele (3.18)

N2y =

∂N2 ∂y =

(x1−x3) 2Vele

N3x =

∂N3 ∂x =

(y1 −y2) 2Vele

N3y =

∂N3 ∂y =

(x2−x1) 2Vele

sendo Vele _{o volume do elemento assumindo profundidade unit´aria e pode ser expresso}

como:

Vele = (x2y3 −x3y2) +x1(y2−y3) +y1(x3−x2)

2 (3.19)

A contribui¸c˜ao, para o volume, do subvolume de controle ´e

Vi =

1 3V

ele _(3.20)

Outra defini¸cão importante são os vetores unitários localizados nos pontos de inte-gra¸cão (ip), nas faces dos subvolumes de controle (scv). As componentes desses vetores unitários são expressas como:

~nxf1 = ∆yf1

Sf1 ~i

~nyf1 = ∆xf1

Sf1

(−~j) (3.21)

~nxf2 = ∆yf2

Sf2 ~i

~nyf2 = ∆xf2

(46)

em que

∆xf1 = x3 3 − x2 6 − x1 6 ∆yf1 =

y3 3 − y2 6 − y1 6 ∆xf2 =

−x2 3 + x3 6 + x1 6 ∆yf2 =

−y2 3 + y3 6 + y1 6

e as áreas das faces são dadas por (assumindo profundidade unitária):

Sf1 =

q

∆x2

f1 + ∆y 2

f1, Sf2 =

q

∆x2

f2 + ∆y 2

f2 (3.22)

3.2 Discretiza¸c˜ao da Equa¸c˜ao da Energia

Integrando-se a equa¸cão da energia, Eq.(2.5), apresentada no Cap´ıtulo (Cap. 2), no volume e no tempo, e aplicando o teorema de Gauss para o termo difusivo, obtém-se a rela¸cão na forma conservativa:

Z

t Z

V

∂

∂tρ(T)c

′_(T₎_{T dV dt} ₌

Z

t I

S

κ(T)∂T

∂xˆi+κ(T) ∂T ∂yˆj

·~ndSdt (3.23)

Para a discretiza¸cão da Eq.(3.23), considera-se primeiramente o termo condutivo e a integra¸cão no espa¸co. A tarefa é associar o dom´ınio de integra¸cão à área do volume de controle associado a um ponto nodal e avaliar a integral em cada face do subvolume de controle (nos pontos de integra¸cão - ip- Fig. 3.2).

I

S

κ(T)∂T

∂xˆi+κ(T) ∂T

∂yˆj

·~ndS =

Z

ip1

κ(T)∂T

∂xˆi+κ(T) ∂T

∂yˆj

·~ndS + Z ip2

κ(T)∂T

∂xˆi+κ(T) ∂T

∂yˆj

·~ndS (3.24)

(47)

a aproxima¸c˜ao, usando a regra do ponto m´edio,

I

S

κ(T)∂T

·~ndS ≈

κ(T)∂T

·~nS|ip1

+

κ(T)∂T

·~nS|ip1 (3.25)

e em termos das fun¸cões de forma, Eqs.(3.16) e (3.17), da rela¸cão proposta para os vetores unitários, Eq.(3.21), e Eq.(3.22), para as áreas das faces, têm-se

κ(T)∂T

∂xˆi+κ(T) ∂T

∂yˆj

·~nS|ip1 =κip1 3

X

i=1

NixTi∆yip1+κip1 3

X

i=1

NiyTi(−∆x)_ip₁ (3.26)

κ(T)∂T

∂xˆi+κ(T) ∂T

∂y

·~nS|ip2 =κip2 3

X

i=1

NixTi∆yip2+κip2 3

X

i=1

NiyTi(−∆x)_ip₂ (3.27)

ou agrupando os termos geom´etricos de cada face, observa-se

I

S

κ(T)∂T

∂xˆi+κ(T) ∂T

∂yˆj

·~ndS ≈ 3

X

i=1

(Gi1+Gi2)Ti =

3

X

i=1

FiTi (3.28)

Voltando a Eq.(3.23), trata-se agora o termo transiente que, para um ponto nodal i, pode ser expresso como

Z

t Z

V

∂

∂t[ρi(T)c

′

i(T)Ti]dV dt=N eti (3.29)

integrando no tempo e no volume, vem

N eti

∆t =

ρi(T)c′i(T)Ti|t+∆t−ρi(T)c′i(T)Ti|t

∆V (3.30)

(48)

difusivo, resta Z t I S

κ(T)∂T

·~ndSdt≈∆t

"

(1−θ) 3

X

i=1

FiTit+θ

3

X

i=1

FiTit+∆t #

(3.31)

o parˆametroθ (0≤θ ≤1) ´e usado como fator peso para aproximar o fluxo l´ıquido dentro do volume de controle, que representa o ponto nodal i, durante o intervalo de tempo [t, t+ ∆t], em termos da taxa que flui imediatamente ao entrar e ao sair do volume de controle ao longo do tempo.

Para os poss´ıveis valores de θ, as trˆes formas mais conhecidas s˜ao:

• Totalmente impl´ıcito θ= 1

N eti = ∆t

3

X

i=1

FiTit+∆t (3.32)

• Crank-Nicolson θ= 0,5

N eti =

∆t 2 " 1 2 3 X i=1

FiTit+∆t+

1 2

3

X

i=1 FiTit

#

(3.33)

• Expl´ıcito θ = 0

N eti = ∆t

3

X

i=1

FiTit (3.34)

A op¸cão que se faz neste trabalho é θ = 0, ou método Expl´ıcito. Então, para todos os pontos nodais i, de cada elemento k, percorrendo primeiramente os correspondentes subvolumes de controlej da malha (Fig. 3.4), a equa¸cão discretizada pode ser escrita na forma: nve X i=1 scv X j=1 ele X k=1

N etijk= ∆t nve X i=1 scv X j=1 ele X k=1

FijkTit (3.35)

(49)

Figura 3.4: Esquema do elemento triangular com as divis˜oes dos subvolumes de controle

3.2.1 Condi¸c˜oes de Contorno

Integrando-se a Eq.(2.5) no espa¸co e no tempo e substitu´ıdo o fluxo de calor pela condi¸c˜ao de contorno dada pela Eq.(2.13), obt´em-se

Z

t Z

V

∂

∂tρ(T)c

′_(T₎_{T dV dt} ₌

Z

t I

S

κ(T)∂T

∂xˆi+κ(T) ∂T

∂yˆj

·~ndSdt

+

Z

t Z

S

(50)

Logo, integrando-se nas faces que pertencem as fronteiras do dom´ınio,

Z

t Z

S

h(Tamb−T)dSdt≈ −BciTi∆t+BbiTamb∆t (3.37)

de modo que

Bci = hSi (3.38a)

Bbi = hTambSi (3.38b)

onde o coeficiente de pel´ıcula, h, ´e definido de acordo com as condi¸c˜oes de contorno ilustradas na Fig. 2.2 e podem ser listadas abaixo:

• Fronteira adiabática, h= 0 - É definida pela fronteira de simetria (Fig. 2.2), que, por essa razão, não apresenta fluxo de calor;

• Demais Fronteiras, h > 0 - Essas contornos representam a face lateral, raios externo e interno (Fig. 2.2). As equa¸c˜oes discretizadas, incluindo os termos de fronteira, podem ser representadas por:

[Bci∆t+ ∆Viρi(T)c

′

i(T)]Ti|t+∆t= "

∆Viρi(T)c′i(T) + ∆t

3

X

i=1 Fi

#t

T_it+Bbi∆t (3.39) Note-se que ∆Vi e a soma de todos os volumes que circundam o ponto nodali(vide

Fig. 3.4).

Na sequˆencia, apresenta-se de forma simplificada, o fluxograma do algoritmo do pro-blema t´ermico.

3.3 EbFVM Aplicado ao Modelo Termomecˆanico

(51)

Figura 3.5: Fluxograma para o problema t´ermico (Vari´avel desconhecida T)

no Cap´ıtulo (Cap. 2). Para a abordagem do EbFVM, reescreve-se essas componentes em fun¸c˜ao da varia¸c˜ao dos deslocamentos na forma integral

I

s

E 1−ν2

∂∆u ∂x +ν

∂∆v

∂y −(1 +ν)α∆T

ˆ_i₊ E 2 (1 +ν)

∂∆u ∂y +

∂∆v ∂x

ˆ_j_·_ndS_ˆ _{= 0} (3.40)

I

s

E 1−ν2

ν∂∆u ∂x +

∂∆v

∂y −(1 +ν)α∆T

ˆ_j₊ E 2 (1 +ν)

∂∆u ∂y +

∂∆v ∂x

ˆ_i

(52)

I

s

E 1−ν2

∂∆u ∂x +ν

∂∆v

∂y −(1 +ν)α∆T

ˆ_i₊ E 2 (1 +ν)

∂∆u ∂y + ∂∆v ∂x ˆ j

·ˆndS =Iipx1+Iipx2

onde

I_ipx₁ =

Z

ip1

E 1−ν2

∂∆u ∂x +ν

∂∆v

∂y −(1 +ν)α∆T

ˆ_i₊ E 2 (1 +ν)

∂∆u ∂y + ∂∆v ∂x ˆ j

·ndSˆ

I_ipx₂ =

Z

ip2

E 1−ν2

∂∆u ∂x +ν

∂∆v

∂y −(1 +ν)α∆T

ˆ_i₊ E 2 (1 +ν)

∂∆u ∂y + ∂∆v ∂x ˆ j

·ndSˆ

E para a Eq.(3.41),

I

s

E 1−ν2

ν∂∆u ∂x +

∂∆v

∂y −(1 +ν)α∆T

ˆ

j+ E 2 (1 +ν)

∂∆u ∂y + ∂∆v ∂x

ˆ_i_·ˆ_ndS ₌_Iy ip1+I

y ip2

onde

I_ipy₁ =

Z

ip1

E 1−ν2

ν∂∆u ∂x +

∂∆v

∂y −(1 +ν)α∆T

ˆ

j + E 2 (1 +ν)

∂∆u ∂y + ∂∆v ∂x ˆ_i

·ndSˆ

I_ipy₂ =

Z

ip2

E 1−ν2

ν∂∆u ∂x +

∂∆v

∂y −(1 +ν)α∆T

ˆ

j + E 2 (1 +ν)

∂∆u ∂y + ∂∆v ∂x ˆ_i

(53)

Assim, para cada ponto de integra¸c˜ao (Eq. 3.40),

I_ipx₁ ≈κxxip1

" ₃ X

j=1

Njx∆uj+νip1 3

X

j=1

Njy∆vj −(1 +νip1)αip1∆Tip1

#

∆yip1+

κ_xyip₁ 3

X

j=1

Njy∆uj +

3

X

j=1

Njx∆vj !

ip1

(−∆xip1)

I_ipx₂ ≈κxxip2

" ₃ X

j=1

Njx∆uj+νip2 3

X

j=1

#

∆yip2+

κ_xyip₂ 3

X

j=1

Njy∆uj +

3

X

j=1

Njx∆vj !

ip2

(−∆xip2)

Agora, para cada ponto de integra¸c˜ao da Eq.(3.41),

I_ipy₁ ≈κ_yyip₁

"

νip1 3

X

j=1

Njx∆uj+

3

X

j=1

#

(−∆xip1)

+κ_yxip₁ 3

X

j=1

Njy∆uj +

3

X

j=1

Njx∆vj !

ip1 ∆yip1

I_ipy₂ ≈κ_yyip₂

"

νip2 3

X

j=1

Njx∆uj+

3

X

j=1

#

(−∆xip2)

+κ_yxip₂ 3

X

j=1

Njy∆uj +

3

X

j=1

Njx∆vj !

ip2 ∆yip2

sendo

κxx =κyy =

E

1−ν2 (3.42)

κxy =κyx =

E

2 (1 +ν) (3.43)

Agrupando os termos geométricos para a discretiza¸cão da Eq.(3.40), obtém-se

I_ipx₁+I_ipx₂ ≈ 3

X

j=1

Gxx_j₁ +Gxx_j₂

∆uj+

3

X

j=1

Gxy_j₁ +Gxy_j₂

∆vj− Gthx1 +Gthx2

(54)

onde

Gxxj1 = κxxip1Njx∆yip1+κ_xyip₁Njy(−∆xip1)

Gxx_j₂ = κxxip2Njx∆yip2+κ_yxip₂Njy(−∆xip2)

Gxy_j₁ = κxxip1νip1Njy∆yip1+κ_xyip₁Njx(−∆xip1)

Gxy_j₂ = κxxip2νip1Njy∆yip2+κ_xyip₂Njx(−∆xip2) (3.45)

Gthx₁ = (1 +νip1)αip1∆Tip1∆yip1 Gthx₂ = (1 +νip2)αip2∆Tip2∆yip2

e para os termos da Eq.(3.41),

I_ipy₁+I_ipy₂ ≈ 3

X

j=1

Gyy_j₁ +Gyy_j₂

∆uj+

3

X

j=1

Gyx_j₁ +Gyx_j₂

∆vj−

Gthy₁ +Gthy₂ = 0 (3.46)

onde

Gyy_j₁ = κ_yyip₁Njy(−∆xip1) +κ_yxip₁Njx∆yip1

Gyy_j₂ = κ_yyip₂Njy(−∆xip2) +κ_yxip₂Njx∆yip2

Gyx_j₁ = κ_yyip₁νip1Njx(−∆xip1) +κ_yxip₁Njy∆yip1

Gyx_j₂ = κ_yyip₂νip2Njx(−∆xip2) +κ_yxip₂Njy∆yip2

(3.47) Gthy₁ = (1 +νip1)αip1∆Tip1(−∆xip1)

Gthy₂ = (1 +νip2)αip2∆Tip2(−∆xip2)

Após o processo de integra¸cão, obtém-se a equa¸cão de conserva¸cão de cada volume de controle visitando-se todos os subelementos que compartilham o mesmo vértice (nve). Assim, a forma discretizada da Eq.(3.40), pode ser expressa como:

nve X i=1 scv X j=1 ele X k=1

F_ijkxx∆uj+ nve X i=1 scv X j=1 ele X k=1

(55)

Do mesmo modo para a Eq.(3.41) nve X i=1 scv X j=1 ele X k=1

F_ijkyy∆vj + nve X i=1 scv X j=1 ele X k=1

F_ijkyx∆uj−Fyth ≈0 (3.49)

sendo

F_ijkxx = Gxx_j₁ +Gxx_j₂ F_ijkxy = Gxy_j₁ +Gxy_j₂ F_ijkyy = Gyy_j₁ +Gyy_j₂

F_ijkyx = Gyx_j₁ +Gyx_j₂ (3.50) F_xth = Gthx₁ +Gthx₂

F_yth = Gthy₁ +Gthy₂

Observa-se que o termoF corresponde a matriz de rigidez local, que ´e similar a express˜ao obtida pelo FEM (Finite Element Method) [Filippini 2011].

3.3.1 Condi¸c˜oes de Contorno do Problema Termomecˆanico

Para as condi¸c˜oes de contorno, evoca-se as Eqs.(3.48) e (3.49), acrescentando-se as constantesBbxx

j , Bb yy

j , Bcxxj e Bc yy j , nve X i=1 scv X j=1 ele X k=1

Bcxx_j +F_ijkxx

∆u_j+

F_ijkxy∆v_j−F_xth+Bbxx_j ≈0 (3.51)

Bcyy_j +F_ijkyy

∆v_j +

F_ijkyx∆u_j−F_yth+Bbyy_j ≈0 (3.52)

que representam as condi¸c˜oes de contorno para o problema mecˆanico.

Observando-se a regi˜ao de simetria, que est´a ilustrada na Fig. 2.8, para evitar mo-vimento de corpo r´ıgido, restringe-se os deslocamentos na horizontal representado pela componenteu, aplicando-se a Bcxx

(56)

Com esse valor, o deslocamento na dire¸cão horizontal (x), na fronteira de simetria, é aproximadamente nulo (u≈ 0). E para os deslocamento na dire¸cão vertical (y), toma-se apenas o ponto P(0,05; 0,05) e adota-se Bcyy_j = 106 _×_E

j(T), isto ´e, fixa-se a

compo-nente do campo de deslocamentovi em P(0,05; 0,05) e para os outros pontos do dom´ınio

Bcxx

j = 0 e Bc yy

j = 0. Como não há a presen¸ca de for¸cas de compressão ou tra¸cão

produ-zidas por agentes externos, as constantes Bbxx

j e Bb

yy

j recebem zero em todos os outros

elementos.

Na Fig. 3.6, encontra-se o fluxograma para o cálculo das variáveis desconhecidas ∆un+1 _{e ∆v}n+1_{. Um vez obtidos esses valores, efetuam-se as opera¸cões:}

un+1 _{= ∆u}n+1₊_un _(3.53)

e

vn+1 = ∆vn+1+vn (3.54)

Obtidos os campos de deslocamentosun+1 _e _vn+1_{, reescreve-se as Eqs.(2.56), (2.57) e} (2.58), na forma (detalhes em Voller [2009]):

∆σ_xxn+1_i = Ei (1−νi2)

     ele P i=1 Vele 3

∂∆un+1 i ∂x ele Vi

+νi ele P

i=1

Vele 3

∂∆vn+1 i ∂y ele Vi

−(1 +νi)αi∆Tin+1      (3.55)

∆σ_yyn+1_i = Ei (1−νi2)

     νi ele P i=1 Vele 3

∂∆un+1 i ∂x ele Vi + ele P i=1 Vele 3

∂∆vn+1 i ∂y ele Vi

−(1 +νi)αi∆Tin+1      (3.56) e

∆σ_xyn+1_i = ∆σ_yxn+1_i = Ei 2 (1 +νi)

     ele P i=1 Vele 3

∂∆un+1 i ∂y ele Vi + ele P i=1 Vele 3

(57)

Em seguida,

σ_xxn+1 =σ_xxn + ∆σn_xx+1, (3.58)

σ_yyn+1 =σ_yyn + ∆σn_yy+1 (3.59)

e

σxyn+1=σxyn + ∆σxyn+1 (3.60)

Note-se quen+ 1 indica a varia¸c˜ao atual e n, a varia¸c˜ao anterior.

Agora, é poss´ıvel calcular as componentes das tensões e deforma¸cões. Em seguida, para observar as regiões que acorrem acúmulo de tensões lineares, efetua-se o cálculo da tensão equivalente ou critério de von Mises, por meio da rela¸cão [Crisfield 1997]:

σvM = q

σ2

xx+σyy2 −σxxσyy+ 3σ2xy (3.61)

Com a Eq.(3.61), analisa-se as regiões de concentra¸cão do estado de tensões lineares e, assim, verificar se esses valores ultrapassam o limite de escoamento do material, σY

(58)

(59)

4. RESULTADOS

Neste cap´ıtulo são apresentados e discutidos os resultados das simula¸cões térmica e mecânica. Durante a simula¸cão, escolhe-se algumas seçcões que se julgou mais interessan-tes e essas são mostradas de acordo com a posi¸cão relativa à máquina de lingotamento z(t).

4.1 Preliminares

Aborda-se, neste texto, os resultados obtidos nas simula¸c˜oes para os seguintes casos:

I- Resultados térmicos - Apresentam-se os campos de temperatura de algumas seçcões e o gráfico da forma¸cão da casca sólida durante o resfriamento;

II- Simula¸cão iniciada no comprimento metalúrgico (região na qual toda seçcão do lingote é sólida)- Na simula¸cão iniciada no comprimento metalúrgico, foi observado o comportamento das tensões tanto com parâmetros constantes (E, ν, α) como dependentes da temperatura. Para o primeiro caso (propriedades mecânicas constantes), adotou-se os parâmetros f´ısicos mostrados na primeira linha da Ta-bela A.4, enquanto que para o segundo (propriedades mecânicas variáveis), utilizou-se o ajuste linear que foi mostrado na Fig. 2.7 e o conjunto de dados apreutilizou-sentado na Tabela A.4;

III- Simula¸cão iniciada no menisco - Na simula¸cão iniciada no menisco, as proprie-dades mecânicas variam com a temperatura, conforme o gráfico mostrado na Fig. 2.7 e os valores podem ser vistos na Tabela A.4.

(60)

4.2 Resultados T´ermicos

Com os coeficientes de transferência de calor obtidos por Anjos [2013], foi poss´ıvel implementar um algor´ıtimo e observar o perfil de temperatura durante todo processo de lingotamento. Representa-se na Fig. 4.1, os campos térmicos dentro, em z = 0,115 m, e fora do molde, em z = 2,0 m. Nota-se a diminui¸cão da região l´ıquida e a forma¸cão da casca sólida, que é definida pela região que representa as temperaturas T ≤ 1700 K (temperaturasolidos).

Figura 4.1: Campo de temperatura dentro e fora do molde

(61)

camada solidificada (e= 11mm- Fig. 4.2), que ´e um valor acima do m´ınimo, e portanto, considerado um bom resultado.

Figura 4.2: Perfil da casca s´olida formada na sa´ıda do molde (z= 0,70m)

Apresenta-se graficamente, na Fig. 4.3, a forma¸cão percentual da casca sólida em fun¸cão da distância (z) ao menisco, com velocidade de lingotamento de v = 3,2m/mim. Foram testadas malhas com diferentes números de elementos com o objetivo de verificar a dependência do resultado com o número de elementos e, como pode ser verificado no gráfico (Fig. 4.3), a malha mais grosseira (106 elementos) apresenta aproximadamente o mesmo resultado quando comparado a malha com 5.900 elementos. Contudo, para os resultados térmicos e mecânico acoplado utilizou-se a malha com 5.900 elementos.

(62)

consi-Figura 4.3: Representa¸cão gráfica da forma¸cão percentual de sólido

derável reaquecimento na superf´ıcie do lingote, que pode ser explicado pela redistribui¸cão da temperatura, devido a redu¸cão da retirada de calor na região de resfriamento terciário.

4.3 Resultados da Simula¸c˜ao Termomecˆanica

4.3.1 Resposta Mecˆanica a Partir do Comprimento Metal´urgico

As simula¸cões do problema mecânico acoplado cujos resultados são encontrados nesta seçcão, foram obtidos empregando-se parâmetros constantes (E, ν, α) e variáveis com a temperatura, utilizando-se as simplifica¸cões discutidas no Cap´ıtulo 2.

Na região denominada de comprimento metalúrgico, o a¸co está totalmente solidificado. Nos resultados mostrados nas Figs. 4.5 e 4.6, adota-se o comprimento metalúrgico como sendo a região de referência e isso significa que as tensões são nulas nessa seçcão do lingote. Assim, os resultados apresentados nas Figs. 4.5 e 4.6 são as contribui¸cões dos carregamentos térmicos na se¸cão de corte em rela¸cão ao comprimento metalúrgico, não observando as contribui¸cões das zonas mistas (sólido-l´ıquido).

(63)

Figura 4.4: Ilustra¸cão do campo de temperatura no comprimento metalúrgico e na região de corte

(σxy, σxx e σyy) s˜ao mostradas na Fig. 4.5. Observa-se, na Fig. 4.5a, os resultados com

(64)

Figura 4.5: Representa¸cão das componentes do EPT na seçcão de corte (z= 12,0m)

4.3.2 Resposta Mecˆanica Para o Lingotamento Cont´ınuo Completo

Os resultados da simula¸cão mecânica acoplada, com estado de referência no menisco (isto é, campo de tensões zero nessa região), sem o efeito da pressão ferrostática e com as propriedades mecânicas dependendo da temperatura são analisadas nesta seçcão.

A Fig. 4.7 apresenta os resultados do campo de deslocamentos e das componentes das tens˜oes σxx, σyy, σxy e σvM, nas Figs. 4.7a, b, c e d, respectivamente, na qual se observa