UNIVERSIDADE DE LISBOA ISCTE - INSTITUTO UNIVERSITÁRIO DE LISBOA
FACULDADE DE CIÊNCIAS ISCTE BUSINESS SCHOOL
DEPARTAMENTO DE MATEMÁTICA DEPARTAMENTO DE FINANÇAS
VFM/ULlogotipo.png VFM/ULlogotipo.pdf VFM/ULlogotipo.jpg VFM/ULlogotipo.mps VFM/ULlogotipo.tif quase …nal/1:pngquasef inal=
1:pdf quasef inal=1:jpgquasefinal=1:mpsquasef inal=1:tif
Expected Shortfall: Algumas abordagens
de implementação em séries …nanceiras
MESTRADO EM MATEMÁTICA FINANCEIRA
Vítor Manuel Ferreira Martins
Dissertação orientada por:
Professora Doutora Diana Elisabeta Aldea Mendes
UNIVERSIDADE DE LISBOA ISCTE - INSTITUTO UNIVERSITÁRIO DE LISBOA
FACULDADE DE CIÊNCIAS ISCTE BUSINESS SCHOOL
DEPARTAMENTO DE MATEMÁTICA DEPARTAMENTO DE FINANÇAS
VFM/ULlogotipo.png VFM/ULlogotipo.pdf VFM/ULlogotipo.jpg VFM/ULlogotipo.mps VFM/ULlogotipo.tif quase …nal/1:pngquasef inal=
1:pdf quasef inal=1:jpgquasefinal=1:mpsquasef inal=1:tif
Expected Shortfall: Algumas abordagens
de implementação em séries …nanceiras
MESTRADO EM MATEMÁTICA FINANCEIRA
Vítor Manuel Ferreira Martins
Dissertação orientada por:
Professora Doutora Diana Elisabeta Aldea Mendes
"O general que vence a batalha faz muitos cálculos antes de a travar. O general que perde a batalha faz poucos cálculos antecipadamente. Assim, muitos cálculos levam à vitória e poucos à derrota. Quem não …zer cálculo algum terá ainda menos possibilidades de vencer. É considerando este ponto que posso antever quem irá ganhar ou perder."
Sun Tzu
i
Resumo
Nos últimos anos, os mercados …nanceiros têm apresentado comportamentos que se têm traduzido em perdas avultadas em especial para as instituições …nanceiras. Nesse sentido, os orgãos reguladores têm fomentado a implementação de metodologias de prevenção e gestão de risco.
Ao nível das métricas mais populares para medir o risco encontram-se atualmente o value-at-risk (VaR), contudo tem-se mostrado que como medida de risco não é coerente. Alternativamente, tem vindo a ser proposto o Expected Shortfall (ES). Tanto o VaR como o ES conseguem atribuir um valor monetário ao risco, sendo assim possível avaliar e contabilizar os impactos efetivos nos investimentos efetuados.
Na linha da frente, a impulcionar esta mudança na utilização do VaR para o ES encontramos as diretivas europeias de solvência –mais direcionadas para o setor segurador –e os acordos de basileia emitidos pelo BCBS (Basel Committee on Banking Supervision) –mais direcionado para o sector bancário.
Nesta dissertação é apresentado e estudado como podem ser aplicadas, em séries …-nanceiras, algumas das metodologias de implementação do ES. Para isso foram aplicados quatro métodos distintos para prever a evolução dos retornos diários das cotações do EUR/GBP e EUR/CHF e um para prever diretamente as cotações. São eles a simulação histórica, simulação estocástica (de Monte Carlo), autorregressão (ARCH/GARCH), mé-dias móveis (EWMA) e teoria de caos (GenericPred) respetivamente. Com base nessas previsões dos retornos foi aplicado o ES para um nível de signi…cância de 1%, 2.5% e 5% tendo com isso sido possível medir o risco de mercado associado.
Por outro lado, como a metodologia do GenericPred (divulgada em 2014) apresentou evidências da sua rubustez na previsão de séries …nanceiras, foi utilizada para prever diretamente as cotações. Apesar de não ter revelado uma boa precisão para ambas as séries estudas conseguiu prever bastante bem os primeiros 50 dias para a série EUR/GBP.
Palavras-chave
Risco de Mercado, Séries Financeiras, Econometria, Modelos de Risco, Expected Short-fall, VaR, ARCH / GARCH, GenericPred, Teoria do Caos.
Classi…cação JEL
Abstract
In the last years, …nancial markets have shown some behaviours that resulted on huge losses, especially for …nancial institutions. In that context, regulators have encouraged the implementation of preventive and management risk methodologies.
On the top of most popular metrics to measure risk, we found nowadays value-at-risk (VaR), however it has been shown as a non-coherent risk measure. Alternatively, Expected Shortfall (ES) has been proposed. Both VaR and ES can give a monetary value to risk, becoming possible to evaluate and account the impacts on the investments.
On the front line, pushing forward this change from the use of the VaR to ES, we found the European solvency directives – related to insurance sector – and the Basel Accords, issued by the BCBS (Basel Committee on Banking Supervision) – related to banking sector.
In this dissertation it is shown and researched how can it be applied, on …nancial time series, some of the ES implementation methodologies. Because of that, it was used four distinct methods to forecast the daily returns of EUR/CHF, the daily returns of EUR/GBP and another one to forecast the directly the exchange rates. The methods are: historical simulation, stochastic simulation (Monte Carlo), autoregression (ARCH / GARCH), moving averages (EWMA), and chaos theory (GenericPred), respectively. Based on the forecasted returns, it was applied the ES using a 1%, 2.5% and 5% level of signi…cance, being with it possible to evaluate the associate market risk.
On the other hand, as the GenericPred methodology (published on 2014) came up with evidences of the robustness to the forecast of …nancial time series, it was used to directly predict the studied foreign exchange rates. Regardless of it has not revealed a well …tted forecast for both studied time series, it obtained a very good forecast for the …rst 50 days to EUR/GBP.
Key-words
Market Risk, Financial Series, Econometrics, Risk Models, Expected Shortfall, VaR, ARCH / GARCH, GenericPred, Chaos Theory.
JEL Classi…cation
iii
Agradecimentos
Quero agradecer aos professores que me acompanharam nesta árdua tarefa de aqui chegar. Em especial à minha orientadora pela amizade, pelo conhecimento cientí…co que partilhou e que mesmo num momento mais atribulado da sua vida se mostrou incansável para que este objectivo fosse concluído.
Agradeço também aos colegas, amigos e familiares que me apoiaram até aqui. A todos, muito obrigado.
Conteúdo
1 Introdução 1
1.1 Motivação e Objetivos . . . 2
1.2 Enquadramento Teórico . . . 3
1.2.1 Medidas de Risco . . . 3
1.2.2 Modelação e Previsão em Séries Financeiras . . . 7
2 Avaliação dos modelos 23 2.1 Backtest direto ao ES (Z2) . . . 25
2.1.1 Teste Z2 . . . 25
3 Resultados Empíricos 27 3.1 Identi…cação das séries . . . 27
3.1.1 Análise descritiva e testes de raiz unitária . . . 27
3.1.2 Aplicação dos modelos ARCH/GARCH . . . 31
3.2 Medição do risco . . . 36
3.2.1 Simulação Histórica e Simulação de Monte Carlo . . . 36
3.2.2 RiskMetrics e GARCH . . . 37
3.2.3 Reconstrução do atrator e GenericPred . . . 39 v
4 Conclusões e percursos para futuras investigações 45
Bibliogra…a 47
Anexos 49
A Teste de raíz unitária às séries dos retornos do EURCHF e EURGBP 49
B Modelo GARCH (1,2) t-student para os retornos do EURGBP 51
C Modelo GARCH (1,2) t-student com dummy para os retornos do
Lista de Figuras
3.1 Teste de raíz unitária à série EURCHF . . . 29
3.2 Teste de raíz unitária à série EURGBP . . . 29
3.3 Correlograma da série dos retornos do EURCHF . . . 32
3.4 Distribuição dos resíduos remanescentes do GARCH(1,2) - EUR/CHF . . . 33
3.5 Distríbuição dos resíduos remanescentes do GARCH(1,2) - EUR/GBP . . . 35
3.6 ES e VaR aplicado aos retornos do EURCHF . . . 37
3.7 ES e VaR aplicado aos retornos do EURGBP . . . 38
3.8 Atrator do EURGBP . . . 41
3.9 Atrator do EURCHF . . . 42
3.10 Previsão dos últimos 500 dias da cotação EURGBP . . . 42
3.11 Previsão dos últimos 500 dias da cotação EURCHF . . . 43
3.12 Comparação das previsões para o EURGBP . . . 43
3.13 Comparação das previsões para o EURCHF . . . 44
Lista de Tabelas
3.1 Grá…cos das séries EURCHF, EURGBP e respectivas distríbuições . . . 28
3.2 Grá…cos das séries dos retornos do EURCHF e EURGBP e respectivas distríbuições . . . 30
3.3 Seleção do modelo ARCH/GARCH para os retornos do EURCHF . . . 33
3.4 Seleção do modelo ARCH/GARCH para os retornos do EURGBP . . . 35
3.5 ES percentual por simulação histórica, Monte Carlo e distribuição normal . 36
3.6 ES percentual por RiskMetrics e GARCH . . . 38
3.7 ES por número de dias estimados . . . 39
3.8 Parâmetros para reconstrução do atrator . . . 40
Capítulo 1
Introdução
Nos últimos anos, com as quase consecutivas crises …nanceiras internacionais, investidores, supervisores, instituições …nanceiras e os Estados passaram a ter uma cada vez maior ne-cessidade de agirem ativamente face às incertezas de evolução de preços/cotações dos ativos …nanceiros. A redução do valor dos ativos e consequentemente as perdas potencialmente gravosas, em especial para as instituições …nanceiras que lidam diáriamente com este tipo de problemas, tem fomentado o estudo da gestão do risco.
Com o intuito de minimizar os impactos inesperados nessas instituições e até na econo-mia da região de onde se inserem, os supervisores e os bancos centrais têm vindo a exigir a adopção de medidas de gestão activa do risco1. É aqui que surge a necessidade de
identi…car o que é o risco …nanceiro, como medi-lo e acima de tudo como modelá-lo e prevê-lo.
1
Exemplo disto são:
- os Acordos de Basileia para o setor bancário: Basel I (1988), II (2004) e III (2010); e - as Directivas Europeias de Solvência para o setor segurador: Solvency I (1973) e II (2014).
1.1
Motivação e Objetivos
Havendo a necessidade de avaliar as prováveis perdas potenciais nos diversos ativos onde existe uma exposição, surge a necessidade de identi…car e testar algumas das possíveis alternativas para a modelação e previsão dos preços (ou seus retornos). Posteriormente aplicar a medida de risco para com isso avaliá-lo.
Tem surgido uma vasta discussão relativamente à forma de medir o risco. Inicialmente, falar em risco …nanceiro era automaticamente associado às medidas de dispersão como sejam a variância ou desvio-padrão. Hoje em dia, na prática, o value-at-risk (VaR) ainda é o mais utilizado. No entanto este não apresenta sensibilidade aos valores extremos e tem sido criticado por não ser uma medida de risco coerente. O expected shortfall (ES) tem surgido como a melhor alternativa tendo mesmo sido recomendável, em 2013, a sua adoção em detrimento do VaR pelo BCBS1 [5]. Por esse facto será essa a medida de risco utilizada neste trabalho.
A modelação e implementação da medição do risco é um passo fundamental para a monetarização do risco. Do ponto de vista da modelação, as séries …nanceiras são usualmente referidas como das mais complexas por mostrarem comportamentos não li-neares e portanto das mais difíceis de modelar. Por isso a adoção de modelos não lili-neares (estocásticos, econométricos, caóticos) apresentam melhores possibilidades de sucesso na implementação de previsão destas séries.
A identi…cação da distribuição da série tem vindo a assumir um papel crucial na sua modelação. A mais comumente estudada e aplicada é a distribuição gaussiana. No entanto, dada a sua leveza nas caudas tem-se constatado que a distribuição t-student apresenta uma
1
Introdução 3
melhor aderência a este tipo de séries.
Muito recentemente uma nova metodologia de previsão de séries temporais complexas foi desenvolvida tendo por base a teoria de caos e processos de optimização. Por esse motivo foi incluida neste estudo.
O principal propósito desta dissertação será mostrar como implementar e comparar os modelos estudados – simulação histórica, simulação estocástica (de Monte Carlo), autor-regressão (ARCH/GARCH), médias móveis (EWMA), teoria de caos (GenericPred) – , identi…cando por …m qual o mais adequado à estimação do ES sobre as séries dos retornos diários das cotações do EUR/CHF e EUR/GBP.
1.2
Enquadramento Teórico
1.2.1 Medidas de Risco
A de…nição de risco, em especial risco …nanceiro, não é consensual sendo associado à possibilidade de perder uma parte ou até a totalidade de um investimento ou sendo "o grau de incerteza dos retornos futuros"[24]. Como medida, já foi referido por Markowitz [20] como desvio padrão face ao valor esperado e semi-variancia [21]. Esses e outros exemplos de medidas de risco foram compiladas por exemplo em [25] e [26], das quais destaco o VaR, o TCE (Tail Conditional Expectation) e o ES. Contudo, algumas dessas medidas de risco são in‡uenciadas tanto pelos ganhos como pelas perdas, não se adequando perfeitamente à realidade.
De acordo com [9] as medidas de risco são avaliadas tendo como critérios: a coerência, a consistência e a facilidade de implementação. A última é a mais subjectiva já que pode depender dos recursos tecnológicos disponíveis nas organizações e da complexidade
da própria metodologia de implementação. A de…nição de medida de risco coerente foi apresentada pelo trabalho de [4], referindo quatro axiomas fundamentais que uma medida de risco deve respeitar, tal como se apresenta de seguida.
De…nição 1.2.1 (Medida de risco coerente): Sendo X, Y 2 R duas variáveis aleatórias, G a -álgebra gerada pelas funções reais que descrevem os riscos possíveis no estado do mundo , '(X) e '(Y ) são medidas de risco coerentes se:
Axioma 1.2.1 (Monotonia)
X; Y 2 G com X 6 Y =) ' (Y ) ' (X)
Axioma 1.2.2 (Translação invariante)
Para todo o X 2 G, 2 R, r > 0 =) ' (X + rf) = ' (X)
Axioma 1.2.3 (Homogeneidade positiva)
Para todo > 0 e todo o X 2 G, ' ( X) = ' (X)
Axioma 1.2.4 (Sub-aditividade)
Para todo X; Y 2 G, ' (X + Y ) ' (X) + ' (Y )
Pela monotonia podemos reconhecer de forma intuitiva que entre dois ativos, se o valor de um deles (X) for sempre inferior ao valor de outro (Y ), então o valor da perda será maior em X do que em Y resultando num maior risco de X face a Y . A translação invariante é interpretada como o investimento entre um ativo X e uma reserva monetária ( ) remunerada à taxa de juro sem risco (rf), sendo que o risco da estratégia resulta na
perda por desvalorização do ativo amortecida pela reserva …nanceira. A homogneidade positiva representa o facto do risco aumentar na mesma proporção ( ) do investimento
Introdução 5
realizado no ativo (X). A sub-aditividade é reconhecida pela vantagem de diversi…cação – o risco de um investimento diversi…cado tende a ser inferior a um investimento não diversi…cado.
O conceito de medida de risco consistente tem vindo a ser estudado por vários inves-tigadores tais como [14] e [9]. Destaca-se contudo este último, por ter apresentado uma abordagem baseada na dominância estocástica de primeira2 e segunda3 ordens e teoria da utilidade esperada que classi…ca genericamente uma medida de risco em três categorias.
De…nição 1.2.2 (Medida de risco consistente): Sendo X, Y 2 R duas variáveis aleatórias diz-se que a medida de risco '( ) é: (1) SD>Consistente se XSDY =) ' (X) 6 ' (Y );
(2) SD<Consistente se ' (X) 6 ' (Y ) =) XSDY ; (3) SD-Consistente se XSDY ()
' (X)6 ' (Y ), ou seja '( ) é simultaneamente SD>Consistente e SD<Consistente.
Em que XSDY : 8 > > > > > < > > > > > :
XF SDY : X tem 1a dominância estocástica (FSD) sobre Y
XSSDY : X tem 2a dominância estocástica (SSD) sobre Y
XLRY , XSSDY ^ E [X] = E [Y ] : X tem menor risco que Y
De notar que o facto de exitir FSD implica a existência de SSD.
Numa interpretação mais prática, uma medida de risco que seja classi…cada como: SD>Consistente poderá ser utilizada como ferramenta para a gestão da alocação de dife-rentes ativos num portfolio; SD<Consistente garante que independentemente do nível de con…ança escolhido e da curva de utilidade esperada de cada individuo todos concordarão quanto à ordenção dos ativos pelo seu risco associado; SD-Consistente permitirá ambas as situações anteriores.
2FSD: P [X6 ] = F
X( )6 FY( ) = P [Y 6 ], em que existe pelo menos um FX( ) < FY( )
3
SSD:R
1FX( )d R
Sublinha-se que apesar de SSD traduzir a preferência de investidores avessos ao risco por maiores rentabilidades, LR traduz a preferência exclusiva pelo menor risco quando a rentabilidade é idêntica, pelo que é o critério mais relevante em termos de medida de risco. Value at Risk –VaR
É inevitável falar-se em medidas de risco sem fazer referência áquela que nos últimos anos tem sido a mais utilizada – o VaR – com a metodologia RiskMetricsT M. O VaR cor-responde à perda potencial máxima para um período de tempo prede…nido, considerando um determinado nível de signi…cância (percentil).
Do ponto de vista matemático o VaR pode ser de…nido como:
V aRX( ) = inf fx 2 R j P (X x) > g = Q 1( ) (1.1)
em que Q 1( ) é a inversa da função de distribuição da variável aleatória X para um nível de signi…cância ( )4.
Contudo, esta medida de risco tem vindo a ser criticada pelo facto de não ser subaditiva para todas as distribuições dos retornos e portanto ser considerada uma medida de risco não coerente. A excepção será quando a distribuição dos retornos assumir uma distribuição elíptica, [26]. Atendendo à consistência, o VaR é classi…cado como LR>Consistente [9]. Expected Shorfall
Em alternativa ao VaR o ES tem vindo a ser sugerido por vários autores. Em [1] chegam mesmo a referi-lo como medida universal : por poder aplicar-se a qualquer instrumento; e completa: por permitir ter uma visão global dos riscos num portfolio. Por ter como
4
Ao nível de signi…cância ( ) corresponde um grau de con…ança (1 ) : Este último é por vezes
utilizado na identi…cação das medidas de risco. Exemplo: V ARX(5%) é também representado por
Introdução 7
principal vantagem ser uma medida subaditiva, é uma medida de risco coerente. Os autores de [9] vão mais longe e demonstram que o ES é também uma medida de risco LR-Consistente.
Uma vez que esta medida inside sobre informação da cauda esquerda da distribuição da variável aleatória até um determimado percentil, pode captar informação de eventos extremos ("black swans") e torna-se mais difícil de manipular.
Para uma distribuição genérica de retornos (X) e para um horizonte temporal pre-de…nido, Acerbi e Tasche de…nem o ES para um determinado nível de signi…cância ( ) como:
ESX( ) =
1
E X 1fX x( )g x ( ) (P [X x ( )] ) (1.2)
Considerando que a distribuição dos retornos é contínua, então P [X x ( )] = e portanto pode ser apresentada uma versão mais simples, também designada pela equação fundamental do ES:
ESX( ) =
1Z
0
QX1(p) dp (1.3)
em que QX1(p) = inf fx 2 R j Q(x) > pg. Esta fórmula é coincidente com a de…nição da TCE, [4].
1.2.2 Modelação e Previsão em Séries Financeiras
Diferentes abordagens têm vindo a ser tomadas na tentativa de modelar e prever o com-portamento de séries …nanceiras. Desde métodos não paramétricos, como a simulação histórica bem como métodos paramétricos, tais como os modelos de simulação estocástica de Monte Carlo, de médias móveis, autorregressão, caóticos. À partida não pode
a…rmar--se que um dos modelos representa melhor a realidade que os restantes. Deve averiguara…rmar--se de forma casuística a aderência à realidade de cada modelo para assim eleger o mais viável. Na análise e estudo das séries …nanceiras a variável que se pretende tomar é o retorno dos ativos. Usualmente consideram-se os retornos em tempo contínuo (rt) – variação
logaritmica. Isto é:
rt= ln
Pt
Pt 1
= pt pt 1 (1.4)
onde P corresponde ao preço do ativo nos momentos t e t 1; e p corresponde ao logaritmo neperiano de P em t e t 1.
Será sobre as séries com elementos rt que se irão aplicar os modelos de previsão e a
partir dessas previsões estimar o ES.
Do ponto de vista estatístico, estas séries apresentam comportamentos que indiciam a existência de dependência não linear, heterocedasticidade, distribuições com caudas pe-sadas. São por isso consideradas das mais desa…antes de estudar.
Por uma questão de simpli…cação e recorrendo ao teorema do limite central, é prática modelar estas séries tendo por base uma distribuição gaussiana. No entanto, a existência das caudas pesadas tem conduzido à utilização de outras distribuições como a t-student. Uma síntese dessas distribuições pode ser encontrada em [15].
Das mais variadas abordagens que poderiam ser escolhidas para apresentar a imple-mentação do ES, foram selecionados:
a simulação histórica (HS – Historic simulation), representante dos modelos não paramétricos e que se apresenta pela facilidade e rapidez de implementação;
es-Introdução 9
tocásticos e que têm como grande vantagem a facilidade de poder gerar números aleatórios simulando diferentes realidades (estados do mundo) e por ser amplamente utilizado na prática;
os modelos autorregressivos [generalizados] com heterocedasticidade condicionada (ARCH / GARCH – Autoregressive Conditional Heteroscedasticity / Generalized Autoregressive Conditional Heteroscedasticity), representantes dos modelos autor-regressivos e porque são mais sensíveis às grandes variações negativas do que às grandes variações positivas (de referir que são os retornos negativos que estamos mais interessados em captar), [18];
o modelo de médias móveis com ponderação exponencial (EWMA – Exponentially Weighted Moving Average), representante dos modelos de médias móveis, por ser o modelo criado pela RiskMetricsT M e bastante conhecido e estudado;
o GenericPred, modelo recente que tem por base a teoria de caos e mostrou muito bons resultados na previsão de séries temporais complexas, [13].
Simulação Histórica (HS)
A simulação histórica baseia-se no facto de que os eventos futuros são meramente repetições do passado. Por esta simples permissa, basta que se conheça a série dos valores históricos que se pretende analisar para aí aplicar/extrair diretamente a medida de risco pretendida. Apesar deste ser um método não paramétrico, a dimensão da janela temporal, i.e., o número de observações da série a ter em conta, assume especial relevância. Tomando em consideração [8], para a implementação do ES é recomendado um mínimo de 10 ob-servações, pelo que se considerarmos um nível de con…ança de 1% o tamanho mínimo da
janela temporal deverá ser de 1 000 observações.
Simulações de Monte-Carlo (MC)
Conhecida a distribuição estatística da váriavel que se pretende simular, o método de simu-lações de Monte-Carlo permite a geração de grande número de possíveis realidades (pos-síveis estados do mundo). Por isso tem assumido especial relevância na determinação do valor de produtos …nanceiros complexos tais como os produtos derivados. O alicerce deste método assenta na capacidade computacional de "pseudo"geração de números aleatórios de acordo com a distribuição teórica especí…cada.
Como exemplo de modelação estocástica do preço de um ativo tem-se o Movimento Browniano Geométrico, subejamente conhecido por estar na base do modelo Black-Scholes-Merton. Isto é,
Pt= P0 exp
2
2 t + W (t) (1.5)
onde P corresponde ao preço do ativo nos momentos t e 0, os parâmetros e são respetivamente a média e o desvio padrão e W (t) é um processo de Wiener. Quando considerado o retorno do ativo assim modelado pode concluir-se que o processo é descrito por uma distribuição normal com média 22 t e desvio padrão 2t [10],
rt = ln Pt P0 = 2 2 t + W (t) (1.6) rt N 2 2 t ; 2t . (1.7)
ou seja, poder-se-á simular o retorno de um ativo recorrendo às simulações estocásticas de MC e com base nos resultados aplicar-se a medida de risco.
Introdução 11
ARCH / GARCH
Os modelos ARCH (p) foram desenvolvidos por Engel (1982) tendo sido pioneiro ao tentar modelar séries em que a variância não é constante e se apresenta em forma de clusters – periodos de elevada volatilidade alternados por períodos de volatilidade reduzida. Esta nova abordagem veio possibilitar que as técnicas econométricas se foquem na modelação da variância a partir dos erros, ao invés de seguir uma abordagem mais tradicional onde se dá primazia às variáveis explicativas do valor esperado, negligenciando a informação desconhecida mas ainda contida nos erros.
No caso dos modelos ARCH (p), a variância condicional é modelada recorrendo a um processo autorregressivo a partir dos erros ("t), em que o desfasamento máximo da
informação a incorporar no processo é o parâmetro p.
Com o intuito de melhorar e dotar os modelos ARCH de maior ‡exibilidade e robustez, de acordo com [7], Bollerslev (1986) e Taylor (1986), propuseram de forma independente, a inclusão de uma nova parcela no processo: a dependência autorregressiva da própria variância condicional, com desfasamento máximo q. Passou assim a designar-se esta família de modelos por ARCH(p) / GARCH (p,q).
Do ponto de vista matemático [22], os modelos podem ser sintetizados em três equações: equação da média, que nos devolve o valor estimado da série dos retornos univariados (rt);
modela o valor dos erros ("t). rt = E [rt] + "t (1.8) 2 t = ! + p X i=1 i "2t i+ q X j=1 j 2t j (1.9) "t = t et ; et iid g (0; 1) (1.10)
Em que w > 0, i; j 0 e g (0; 1) é uma função de densidade de probabilidade com média zero e variância um [6].
Nos casos em que exista variância não condicional, ou seja em que exista convergência da variância condicional para a variância não condicional, esta pode ser obtida a partir destes modelos, sendo representada pela seguinte expressão.
2 = ! 1 p P i=1 i + q P j=1 j ! (1.11)
Não obstante, só existirá convergência se !; i; j 0 e
p P i=1 i + q P j=1 j < 1.
A implementação de um modelo desta família consiste em estimar os parâmetros !, i e j. Esta tarefa pode resultar num esforço hercúleo se forem considerados valores de p e q elevados.
EWMA
O EWMA surge da necessidade da RiskMetricsT M conseguir incorporar num modelo de previsão a heterocedasticidade observada nas séries …nanceiras.
Nos modelos de médias móveis tradicionais o efeito da volatilidade em forma de cluster não se faz sentir de forma imediata, uma vez que as variações incorporadas no modelo têm o mesmo peso. A inovação trazida pelo EWMA re‡ete-se na introdução de um
Introdução 13
factor/ponderador de decaímento exponencial (0 < < 1), que atribui maior peso à informação mais recente. Apesar de poder ser estimado o valor de é usual usar-se os valores de referência estimados pela RiskMetricsT M. Para previsões de um dia = 0:94 e para previsões de um mês = 0:97, [24].
De acordo com este modelo os retornos univariados (rt) são modelados recorrendo à
volatilidade condicional 2t :
rt = t et ; etiidN (0; 1) (1.12) 2
t = 2t 1+ (1 ) r2t 1 . (1.13)
Ao atentar neste modelo veri…ca-se que é um caso particular da família de modelos ARCH / GARCH: GARCH (1; 1), com E [rt] = 0, ! = 0, 1 = , 1 = (1 ) e
g (0; 1) = N (0; 1). GenericPred
Este método inovador recentemente divulgado [13], baseado em conceitos da teoria de caos e de processos de otimização, foi desenvolvido com o intuito de modelar séries temporais longas, complexas e que evidenciem comportamento caótico. Nos testes de aplicação apresentados foram usadas séries complexas, das quais se destaca a série dos preços de fecho diário do DJIA5 por se enquadrar no âmbito desta dissertação. Nesse exemplo conseguiram prever com bastante precisão a tendência da série, mesmo em situações de crise …nanceira. Dentro do período de teste, previram as tendências dos primeiros 500 dias, sendo que para os primeiros 300 conseguiram-no com elevada precisão.
Conceitos básicos da teoria de caos Antes de proceder à apresentação da
metodolo-5
gia seguida pelo GenericPred há que clari…car alguns pontos basilares à compreensão e fundamentação da utilização da teoria de caos na modelação da dinâmica não linear de séries temporais. Reitera-se que os conceitos por detrás deste ramo do conhecimento não se restringem aos aqui apresentados.
Complementando a ideia mais tradicional que a…rma que os preços/rentabilidades veri-…cados nos mercados são processos aleatórios, uma corrente mais recente tem vindo a de-fender que esses mesmos preços/rentabilidades podem esconder uma dinâmica complexa própria e que tendem a ser suscetíveis a pequenas alterações das condições iniciais. Isto é, apresentam um corportamento caótico, sendo descritos por um sistema dinâmico deter-minístico [23].
De…nição 1.2.3 (Sistema dinâmico): Um sistema dinâmico abstrato (S) é um terno (M; V; T ) onde M Rn é um espaço métrico compacto, designado espaço de fase, com dimensão d, V é uma aplicação contínua de M para M (V : T M ! M), designada por lei de evolução do tempo, e T é o conjunto do tempo.
De…nição 1.2.4 (Sistema dinâmico determinístico em tempo discreto): Se num sistema dinâmico (S) a lei de evolução do tempo (V ) for de…nida por um processo determinístico e se n 2 T Z, então esse sistema dinâmico é determinístico em tempo discreto e cada ponto pode ser obtido por:
Xn+1 = V (Xn) + n (1.14)
Em que é o nível de ruído e n os erros de medições.
Introdução 15
à n-ésima iterada de V ,em que Vn= V V V , isto é:
Xn= Vn(X0) + n (1.15)
De…nição 1.2.5 (Sistema dinâmico determinístico em tempo contínuo): Se num sistema dinâmico (S) a lei de evolução do tempo (V ) for de…nida por um processo determinístico e se t 2 T R, então esse sistema dinâmico é determinístico em tempo contínuo e em que cada ponto pode ser obtido por:
Xt= Vt(X0) + t (1.16)
Em que é o nível de ruído e t os erros de medições.
De…nição 1.2.6 (Sistema dinâmico invertível): No caso em que a lei de evolução (V ) e a sua função inversa (V 1) são continuas, V é um homeomor…smo e o sistema dinâmico diz-se invertível.
De…nição 1.2.7 (Sistema dinâmico regular): No caso em que a lei de evolução (V ) e a sua função inversa (V 1) são diferenciáveis V é um difeomor…smo e o sistema dinâmico
diz-se regular.
De…nição 1.2.8 (Atrator): Seja A o conjunto compacto e invariante (Vt(A) = A) de
pontos no estado de fase (M ). Diz-se que A é estável se para qualquer vizinhança U de A existir uma vizinhança W de A (U W ) tal que, para condições iniciais em W , qualquer solução do sistema permaneça em U . Se além disso T
t>0
Vt(W ) = A e existir uma orbita
densa então a …gura geométrica representada por A é um atrator, podendo ser um ponto …xo, um ciclo limite ou atrator estranho (fractal) [28].
Signi…ca isto que conhecendo-se o sistema dinâmico –e por conseguinte a forma como ele evolui ao longo do tempo –seremos capazes de identi…car em cada momento o estado do mundo. No entanto, numa série …nanceira o que desconhecemos é exatamente o mecanismo que o "gerou". Coloca-se por isso uma questão: se a série tiver um comportamento caótico, será que a partir desta é possivel determinar o sistema dinâmico que a possa ter gerado? A resposta provém do teorema (do mergulho ou da reconstrução) de Takens (embedding Theorem), [23], [17], [19]. De forma muito simplista, o teorema diz-nos que se tivermos perante um sistema dinâmico multivariado –a série temporal –e se escolhermos uma função (imersão) que nos permita medir esse sistema, então poderemos reproduzir a dinâmica do sistema original usando essa função.
Teorema 1.2.1 (Teorema do mergulho de Takens): Seja M um conjunto limitado. No espaço do produto cartesiano dos mapas C1em M (V : M ! M) e no espaço das funções
C1de M para R (f : M ! R) existe um subconjunto denso U (espaço de fase) tal que se (V; f ) 2 U então o mapa de reconstrução ( (V;f )(x)) é um mergulho, qualquer que seja
k > 2 dim (M ) = 2d. Para além disso, o mergulho é continuamente diferenciável, bem como a sua inversa. Isto é, o mergulho é um difeomor…smo.
(V;f )(x) = f (x) ; f VT1(x) ; f VT2(x) ; :::; f VTk 1>2d 1(x) (1.17)
No entanto, perante os valores de uma série temporal e ao sermos ignorantes em relação à dinâmica que a possa estar formar, podemos ser levados a crer, erradamente, que esteja a ser gerada por uma dinâmica estocástica.
É por isso necessário que a partir da série se consiga identi…car algum indício de caos. Urge de…nir alguns dos invariantes dinâmicos (ou medidas de não linearidade), como por
Introdução 17
exemplo os expoentes de Lyapunov, dimensão fractal e dimensão de correlação, [23], [3]. O expoente de Lyapunov, na sua versão mais simples, indica se o sistema apresenta dependência à sensibilidade a pequenas variações das condições iniciais. Isto é: se con-siderarmos que uma variação in…nitésimal no ponto xt, denominada por xt, depende da
variação in…nitésimal no ponto inicial x0, denominada por x0 e que o fator de
cresci-mento/divergência é uma taxa em regime contínuo , então essa taxa é o expoente de Lyapunov e revela o quão sensivel é o sistema a pequenas variações das condições iniciais. j xtj t e t j x0j ; > 0 (1.18)
De forma mais exata, para dimensão 1 e usando notação diferencial, pode ser apresen-tado pela equação abaixo. Para dimensões superiores os expoentes de Lyapunov podem ser estimados recorrendo à matriz jacobiana ou ao expoente maximal de Lyapunov.
(x0) = lim n !1 1 n ln dfn(x 0) dx (1.19)
A interpretação destes valores é essencial para a tipi…cação do sistema e por isso há que detalhar o conceito de estabilidade segundo Lyapunov. Os > 0 indicam a taxa de expansão, os < 0 indicam a taxa de contração/convergência e os = 0 indicam estabilidade. Consequentemente se a soma dos for positiva, temos um sistema caótico instável, se a soma dos for negativa temos um sistema dissipativo (que se contrai). No entanto, para que o sistema tenha um comportamento caótico determinístico é necessário que exista, pelo menos, um > 0. No caso de = +1, a série temporal é modelada por um sistema dinâmico estocástico; por outras palavras, a série é estocástica.
A dimensão fractal6 (D0) corresponde a uma medida que relaciona o volume e o
com-primento (") da grelha de partição do espaço ocupado pelo atractor. A metodologia para
6
o seu cálculo é denominda por box-counting e consiste na contagem das partições ocu-padas pelo atractor. De um ponto de vista mais vasto, o conceito de dimensão pode ser generalizado e ser assim de…nido pela dimensão generalizada:
Dq= lim "!0 1 q 1 lnPipqi ln (") (1.20)
em que q (q 2 Z0) especi…ca a que tipo de dimensão nos referimos, i numera cada caixa
da partição e pi corresponde à probabilidade do atractor ocupar a caixa i.
A dimensão de correlação (D2) encontra-se intrinsecamente relacionada com o teorema
de Takens, no sentido de que, recorde-se, k (número de graus de liberdade do mergulho) tem de obrigatóriamente ser superior ao dobro da dimensão do espaço métrico do sistema dinâmico (d). A dimensão de correlação é tida como uma aproximação à dimensão do mergulho (D2 k). Esta dimensão, atendendo ao algoritmo de Grassberg e Procaccia,
pode ser também obtida usando o integral de correlação (C2) e apresenta-se mais vantajosa
do ponto de vista de precisão e rapidez computacional [27], [11]:
D2 = lim "!0 (ln C2(")) ln (") (1.21) C2(") = 2 N (N 1) NX1 i=1 N X j=i+1 (" jxi xjj) (1.22)
onde representa a função de Heaviside. O valor de d será tal que:
d : int [dmin> D2] < d < int [dmax> 2 D2] (1.23)
Porque a escolha da dimensão é uma passo crucial, é usual aplicar-se técnicas alterna-tivas que auxiliem na escolha tal como o método dos vizinhos próximos falsos (VPF). Este consiste em avaliar se a trajetória de dois pontos (xi;j; i 6= j e i; j = 1; :::; N) se cruzam,
Introdução 19
dependendo da dimensão do mergulho (RD). Isto é, a dimensão do mergulho será a menor
em que a trajetória de dois pontos afastados no espaço de fase original nunca se cruzem no espaço de fase reconstruido. O critério para deteção dos VPF apresentado por Kennel et al em 1992, conforme [23], é: " R2D+1(i) R2D(i) R2D(i) #1 2 = kfi+D fj+Dk RD(i) > Rtol (1.24)
em que RD(i), corresponde à norma entre dois pontos7 e Rtol o valor de tolerância
(nor-malmente 10). Estando identi…cados os VPF, pode ser identi…cada a dimensão recorrendo a:
RD =
#V F P
N D + 1 (1.25)
D = arg D (RD) (1.26)
em que #V F P corresponde ao número de vizinhos próximos falsos.
Para além da dimensão do mergulho, a representação/reconstrução do atrator depen-derá também dos atrasos de tempo (T ). Para esta seleção a técnica usada será a identi…-cação do primeiro mínimo da função de informação mútua média (I (T ))8, sugerida por
[12].
I (T ) = X
f (n); f (n+T )
P (f (n) ; f (n + T )) log2 P (f (n) ; f (n + T ))
P (f (n)) P (f (n + T )) (1.27)
Onde P (f (n)) é a probabilidade de f (n) ; P (f (n + T )) a probabilidade de f (n + T ) e (f (n) ; f (n + T )) a probabilidade conjunta. 7 Rd(i) =hPdk=0(fi+k fj+k)2 i1 2 8
Descrição do modelo De acordo com [13], o método seguido pelo GenericPred assenta em duas regras basilares: (1) manter o valor da medida de não-linearidade o mais estável possível durante a previsão; (2) cada novo valor da série tem de ser escolhido de um conjunto de valores potenciais, gerados por uma distribuição de probabilidade.
Pretendem assim garantir, por um lado, que os valores estimados continuam dentro do atrator e por outro que a probabilidade condicionada de elementos sucessivos mantenha a mesma distribuição.
Passa-se agora a descrever este algoritmo. Considera-se a série temporal SN
SN = fx1; x2; :::xNg (1.28)
sobre a qual é calculada uma medida de não-linearidade V ( ). Como por exemplo o ex-poente de Lyapunov ou dimensão fractal, que caracterizam cada série com um valor único. Pode ser necessário um mapeamento, formando novas séries SNm= fyL; yL+1; :::; yNg, para
diferentes utilizações como:
yi = V (Si L+1;i) ; L i N onde Si L+1;i= fyi L+1; yi L+2; :::; yig (1.29)
caso contrário, Sm
N = SN, em que 0 < L < N é o tamanho da janela deslizante utilizada
para calcular o nível de caos local por V ( ). Portanto, quando o mapeamento é aplicado, as séries SNm correspondem à variação no tempo da medida de não-linearidade local na série original SN.
Como referência é utilizado o valor de V (SNm) para prever os próximos k valores da série:
Introdução 21
É estimado o desvio-padrão ( ) da distribuição N yi; 2 tendo por base a variação
de dois valores consecutivos (yi; yi+1) da série temporal SNm. Esta distribuição representa
a distribuição de probabilidade P (yij yi 1).
Para prever yN +ié gerado um conjunto de Nrand9 possibilidades, P os (yN +i), a partir
da distribuição N yjN +i 1; 2 : P os (yN +i) = n yN +ij ; 1 j Nrand o (1.31)
O valor de yN +i é escolhido selecionando o yjN +i em que a medida de não-linearidade
seja a mais próxima de V (Sm N):
jmin = arg min
j V S m N +i 1+ y j N +i V (S m N) ; (1.32) yN +i = yN +ijmin; (1.33) SN +i 1m + yN +ij = n y1; y2; :::; yN +i 1; yjN +i o (1.34)
O ponto fulcral é que o valor de referência (V (Sm
N)) seja sempre calculado sobre a série
temporal original.
9Apesar de uma maior quantidade de valores N
randgerados poder melhorar a qualidade de previsão, o
Capítulo 2
Avaliação dos modelos
Considerando o capítulo anterior, sobre o resultado obtido pelos modelos de previsão das séries dos retornos é aplicada a medida de risco ESX( ), podendo ser usada a distribuição
dos últimos 252 retornos ( ). Sublinha-se o caso em que = 2; 5% por ser o recomendado pelo BCBS [5]. É portanto de extrema relevância identi…car qual dos modelos representa um melhor grau de …abilidade na identi…cação do ES.
De forma genérica, a aplicação de qualquer modelo é validada ao confrontar o compor-tamento do modelo com a realidade, pelo que é usual recorrer-se à técnica de backtesting. Contudo, o teste aos modelos de ES por recurso a esta técnica tem vindo a ser contes-tada por alguns autores, referindo-se inclusive ser impossível fazê-lo. Não obstante, este "misticismo"foi esclarecido pelo trabalho de [16] e mais recentemente por [2].
Apesar de nesta dissertação não serem usados no estudo empírico os métodos para aplicação do backtesting ao ES resultante dos diferentes modelos de estimação, considerou-se relevante mostrar que essa possibilidade existe.
Segundo Acerbi e Szekely [2] o backtesting pode ser utilizado sobre o ES, pelo que chegam a sugerir três testes possíveis:
1. Teste ao ES após VaR (Z1);
2. Teste direto ao ES (Z2); e
3. Estimação do ES através de escalões alcançados (Z3).
Os dois primeiros testes (Z1 e Z2) podem ser utilizados para a concretização do
back-testing, sendo que o primeiro obriga a que seja efetuado conjuntamente com o backtest do VaR, ao passo que o segundo pode ser executado de forma isolada e exige menos recur-sos. O terceiro é encarado como um teste complementar para detetar falhas na correta especi…cação do parâmetro de cauda da distribuição.
Porque no âmbito deste trabalho nos focamos na estimação directa do ES, iremos dar mais relevância ao teste Z2.
Os pressupostos genéricos dos testes podem ser sintetizados no seguinte:
1. assume-se que em cada dia existe um Xn, n = 1; :::; N , que representa os retornos
distribuídos ao longo de uma distribuição real desconhecida F ;
2. assume-se que Xn possa ter sido estimado por um modelo que tenha subjacente a
distribuição Q condicional à informação passada utilizada para calcular o ESX( );
3. assume-se que variáveis aleatórias !X = fXng são independentes, mas não
identica-mente distribuidas;
4. não existe qualquer restrição à variância de F nem de Q ao longo do tempo;
5. as distribuições são contínuas e estritamente crescentes o que possibilita que
Avaliação dos Modelos 25
6. por defeito, a hipótese nula assume que a previsão é correta enquanto que a hipótese alternativa é de…nida para ser apenas na direção do risco subestimado;
7. denota-se por V aRFn( ) e ESnF( ) o valor da medida de risco quando X F .
2.1
Backtest direto ao ES (Z
2)
2.1.1 Teste Z2
O teste baseia-se na esperança não condicional e permite avaliar simultâneamente a fre-quência e a magnitude dos eventos ocorridos na "zona da cauda".
Conforme [2], à semelhança do referido no tópico Expected Shortfall, pode de…nir-se o ESn( ) como:
ESn( ) = E
Xn In
(2.2) In = (Xn+ V aRn( ) < 0) (para distribuições contínuas) (2.3)
In Bernoulli ( ) (2.4)
As hipóteses para o teste Z2 são:
H0 : Qn( ) = Fn( ) ; 8n (2.5)
H1 : ESnF( )> ESn( ) ; para todo o n e > para algum n (2.6)
: V aRFn( )> V aRn( ) , para todo o n (2.7)
A hipótese nula (H0) corresponde a uma coincidência perfeita entre a distribuição do
modelo a avaliar e a hipótese alternativa a uma subestimação do risco. O valor do teste é dado por:
Z2 !X = N X n=1 Xn In N ESn( ) + 1 (2.8)
sendo que EH0[Z2] = 0 e EH1[Z2] < 0.
O p-value do teste a uma realização Z (!x ) corresponderá a p = PZ(Z (!x )). Este será
conseguido recorrendo à simulação da distribuição QZ sobre H0. Os passos serão:
1. simular Xi
n Qn, 8n; 8i = 1; :::;
2. calcular Zi = Z !Xi
3. estimar p =Pi=1(Z
i<Z(!x))
Uma vez que In pode ser aproximada por uma Bernoulli, para efeitos de computação,
bastará guardar a zona da cauda de Qn( ).
Dado um nível de signi…cância prede…nido , aceita-se H0 se p > e não se aceita em
Capítulo 3
Resultados Empíricos
3.1
Identi…cação das séries
As séries utilizadas nesta dissertação correspondem às cotações diárias de fecho de dia das taxas de câmbio EUR/CHF (denotada por EURCHF) e EUR/GBP (denotada por EURGBP), registadas pela Bloomberg entre 1999-04-01 e 2015-09-01. Ter-se-á assim por base 4 347 observações para cada uma das taxas de câmbio. Sobre cada uma destas séries foram calculados os respetivos retornos diários (variação logarítmica).
3.1.1 Análise descritiva e testes de raiz unitária
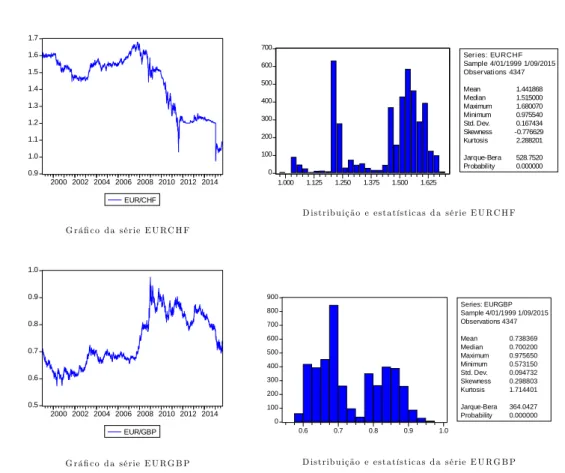
O primeira passo na análise das variáveis consideradas é a representação grá…ca das séries temporais por nível de detalhe. Pela observação dos grá…cos das séries, veri…ca-se que evidenciam um comportamento irregular, sem uma tendência monótona estabelecida. Do ponto de vista estatístico as séries aparentam ser não estacionarias. As distribuições das cotações não apresentam semelhanças com as distribuições teoricas, revelando até um grau médio de assimetria1 e um grau de achatamento (curtose) inferior à distribuição normal padrão (que é assumida ser igual a 3).
1
Numa distribuição simétrica, o nível de assimetria será zero.
0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 2000 2002 2004 2006 2008 2010 2012 2014 EUR/CHF G rá …c o d a s é rie E U R C H F 0 100 200 300 400 500 600 700 1.000 1.125 1.250 1.375 1.500 1.625
Seri es: EURCHF Sample 4/01/1999 1/09/2015 Observations 4347 Mean 1.441868 Median 1.515000 Maximum 1.680070 Minimum 0.975540 Std. Dev. 0.167434 Skewness -0.776629 Kurtosis 2.288201 Jarque-Bera 528.7520 Probability 0.000000
D is trib u iç ã o e e s ta tís tic a s d a s é rie E U R C H F
0.5 0.6 0.7 0.8 0.9 1.0 2000 2002 2004 2006 2008 2010 2012 2014 EUR/GBP G rá …c o d a s é rie E U R G B P 0 100 200 300 400 500 600 700 800 900 0.6 0.7 0.8 0.9 1.0 Series: EURGBP Sample 4/01/1999 1/09/2015 Observations 4347 Mean 0.738369 Median 0.700200 Maximum 0.975650 Minimum 0.573150 Std. Dev. 0.094732 Skewness 0.298803 Kurtosis 1.714401 Jarque-Bera 364.0427 Probability 0.000000
D is trib u iç ã o e e s ta tís tic a s d a s é rie E U R G B P
Tabela 3.1: Grá…cos das séries EURCHF, EURGBP e respectivas distríbuições
Neste contexto, a série EURCHF pode ser descrita como tendo uma média de 1.4418, desvio-padrão 0.1674, coe…ciente de assimetria -0.7766 e curtose 2.2882 ; a série EURGBP, apresenta média de 0.7383, desvio-padrão 0.0947, coe…ciente de assimetria 0.2988 e cur-tose 1.7144. Nota-se também que a série EURCHF tem assimetria moderada negativa, enquanto que a série EURGBP tem assimetria positiva.
Para comprovar a não estacionariedade destas séries que foi observada gra…camente, foi aplicado o teste de raiz unitária de ADF (Augmented Dickey-Fuller ) tendo sido obtido um p-value de 0.5573 e 0.2147, respetivamente2, o que con…rma a existência de uma raiz
2
Resultados Empíricos 29
unitária para cada uma das séries.
Figura 3.1: Teste de raíz unitária à série EURCHF
Figura 3.2: Teste de raíz unitária à série EURGBP
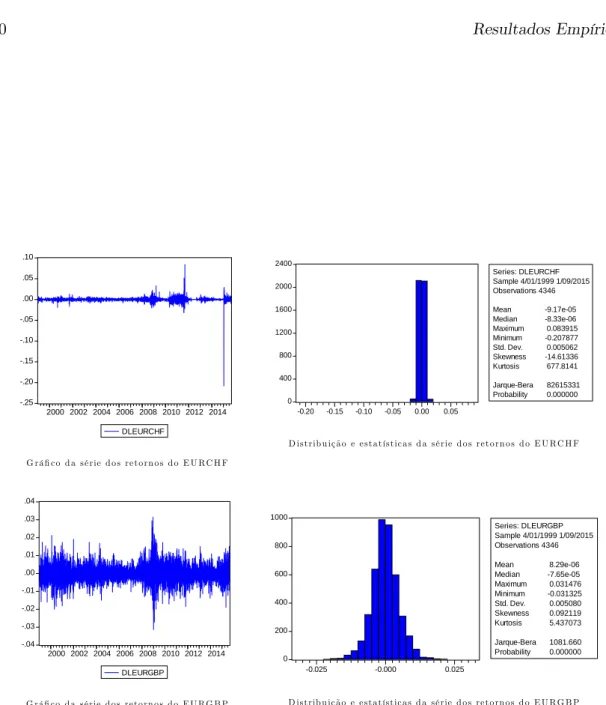
Se passarmos a considerar as séries dos retornos diários (diferença logaritmica) pode-mos constatar grá…camente que essas séries tendem já a ser estacionárias. Estas novas séries foram denotadas por DLEURCHF e DLEURGBP e correspondem aos retornos do EUR/CHF e retornos do EUR/GBP, respectivamente. Aplicádo o teste ADF con…rma-se que são estacionárias para os níveis de con…ança de 1%, 5% e 10% (ver Anexo I). Observa-se ainda a persistência de clusters de volatilidade nas duas séries, Observa-sendo estes fenómenos típicos nas séries …nanceiras.
modo, assumindo um nível de signi…cância de 5%, rejeita-se H0 se o p value <5% e não se rejeita nos
-.25 -.20 -.15 -.10 -.05 .00 .05 .10 2000 2002 2004 2006 2008 2010 2012 2014 DLEURCHF G rá …c o d a s é rie d o s re to rn o s d o E U R C H F 0 400 800 1200 1600 2000 2400 -0.20 -0.15 -0.10 -0.05 0.00 0.05 Series: DLEURCHF Sample 4/01/1999 1/09/2015 Observations 4346 Mean -9.17e-05 Median -8.33e-06 Maximum 0.083915 Minimum -0.207877 Std. Dev. 0.005062 Skewness -14.61336 Kurtosis 677.8141 Jarque-Bera 82615331 Probability 0.000000
D is trib u iç ã o e e s ta tís tic a s d a s é rie d o s re to rn o s d o E U R C H F
-.04 -.03 -.02 -.01 .00 .01 .02 .03 .04 2000 2002 2004 2006 2008 2010 2012 2014 DLEURGBP G rá …c o d a s é rie d o s re to rn o s d o E U R G B P 0 200 400 600 800 1000 -0.025 -0.000 0.025 Series: DLEURGBP Sample 4/01/1999 1/09/2015 Observations 4346 Mean 8.29e-06 Median -7.65e-05 Maximum 0.031476 Minimum -0.031325 Std. Dev. 0.005080 Skewness 0.092119 Kurtosis 5.437073 Jarque-Bera 1081.660 Probability 0.000000
D is trib u iç ã o e e s ta tís tic a s d a s é rie d o s re to rn o s d o E U R G B P
Tabela 3.2: Grá…cos das séries dos retornos do EURCHF e EURGBP e respectivas dis-tríbuições
Resultados Empíricos 31
Na primeira série há a destacar o valor correspondente a 2015.01.15, uma vez que nesse dia o Banco Nacional da Suiça surpreendeu o mercado ao comunicar que deixava de intervir no controlo do câmbio EUR/CHF - este é um caso típico de black swan ou outlier. De entre as outras características da estatistica descritiva destacamos que a série DLEURCHF tem desvio-padrão 0.005062, coe…ciente de assimetria -14.61336 e curtose 677.8141. Os últimos dois valores devem ser uma consequência do fenómeno de black swan. A série DLEURGBP tem desvio-padrão 0.005080, coe…ciente de assimetria muito próximo da normal padrão, 0.092119, e uma leptocurtose moderada situada em 5.437073. Para as duas séries, com base no p-value do teste de Jarque-Bera, rejeita-se a normal-idade das distribuições.
3.1.2 Aplicação dos modelos ARCH/GARCH
Retornos do EUR/CHF
Neste ponto tentaremos encontrar um modelo que melhor se ajuste aos dados das séries dos retornos. Como há evidências de clusters de volatilidade e heterocedasticidade, tentámos vários modelos da família ARCH/GARCH com o objectivo de encontrar aquele que possa dar a melhor previsão do risco de mercado. Para tal vamos estabelecer a equação da média e a equação da variância.
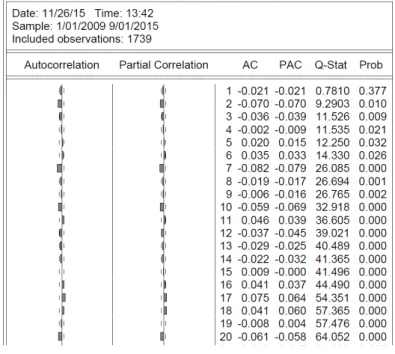
Efetuou-se o correlograma à série dos retornos, não tendo evidenciado qualquer padrão para médias móveis ou autoregressão pelo que se assume que a equação da média é dada pela constante, isto é:
DLEU RCHFt+1= a + "t
Aplicou-se teste para identi…car se a constante seria zero, tendo-se obtido um p value de 0.2324. Por ser superior a 5% implica que se aceita que a constante seja zero.
Figura 3.3: Correlograma da série dos retornos do EURCHF
Veri…camos a existência de efeitos ARCH nos resíduos da equação da média estabelecida com a aplicação do teste LM3, tendo obtido um p value de 0.0001 (inferior a 5%). Conclui-se que os resíduos são heterocedásticos (ou seja temos efeitos ARCH), …cando em aberto a possibilidade do modelo poder ser um ARMA. Nessa sequência, foram testadas algumas possibilidades tendo sido selecionado o modelo ARMA(1,1) com variável dummy para o dia 2015.01.15 e no qual se obteve o valor de -8.223734 para o AIC, p value de 0.0725 para o teste LM aos resíduos com desfasamento 2 e p value nulo para o teste à heterocedasticidade dos resíduos. Estes resultados apontam para que os modelos ARCH/GARCH possam ser considerados para a modelação destes retornos.
Efetuaram-se testes no sentido de selecionar o melhor modelo ARCH/GARCH, usando
3O teste de heterocedasticidade de LM (Lagrange Multipliers) tem como hipótese nula: variância é
Resultados Empíricos 33
como critério o AIC (Akaike information criterion). Dos modelos testados, o que apre-sentou melhor aderência para modelar os retornos do EUR/CHF foi o GARCH(1,2) com média descrita pelo processo ARMA(1,1) e com distribuição dos erros representada por uma t-student.
E [rt] 2t Distibuição de et AIC
ARMA(1,1) GARCH(1,0) Normal -8,685131
ARMA(1,1) GARCH(1,0) t-student -8,967998
ARMA(1,1) GARCH(1,1) Normal -9,059393
ARMA(1,1) GARCH(1,1) t-student -9,228627 ARMA(1,1) GARCH(2,1) t-student -9,229905 ARMA(1,1) GARCH(1,2) t-student -9,230851 ARMA(1,1) GARCH(2,2) t-student -9,230486 Tabela 3.3: Seleção do modelo ARCH/GARCH para os retornos do EURCHF
0 4 0 0 8 0 0 1 ,2 0 0 1 ,6 0 0 2 ,0 0 0 2 ,4 0 0 - 1 0 0 1 0 2 0 3 0 4 0
Series: Standardized Residuals Sample 6/01/1999 1/09/2015 Observations 4345 Mean -0.001765 Median -0.007445 Maximum 41.63835 Minimum -12. 85973 St d. Dev. 1.201439 Skewness 9.765287 Kurtosis 344. 1687 Jarque-Bera 21141593 Probability 0.000000
Figura 3.4: Distribuição dos resíduos remanescentes do GARCH(1,2) - EUR/CHF
Os testes aos resíduos remanescentes não evidenciaram a presença de heterocedasti-cidade (p value de 0.7821 no teste de LM) nem de correlação, de…nindo um processo de ruído branco não-gaussiano (teste de JB com valor de 21141593), o que implica que pode existir outra família de modelos (que não ARCH/GARCH) que melhor simulem estes
retornos.
Retornos do EUR/GBP
Tento agora em consideração a série dos retornos de EURGBP, procedemos a uma análise semelhante à efetuada no caso anterior.
Foi efetuado o correlograma à série dos retornos, não tendo evidenciado qualquer padrão para médias móveis ou autoregressão pelo que se assume que a equação da média é constante. Aplicou-se teste para identi…car se a constante seria zero, tendo-se obtido um p value de 0.9143. Por ser superior a 5% implica que se aceita ser zero a constante.
Procedeu-se à veri…cação da independência dos resíduos através da aplicação do teste de correlação de LM com parâmetro de desfasamento 1 tendo sido obtido um p value de 0.285769. Por ser superior a 5% evidencia que os resíduos são independentes. Esta informação é indicadora que um modelo ARMA pode estar a modelar a equação da média. Testou-se a heterocedasticidade dos resíduos, resultando num p value de zero (inferior a 1%, 5% 10%), o que signi…ca que a hipótese nula deste teste (os resíduos são homocedásti-cos) não é aceite. Os resíduos são portanto heterocedásticos. Esta informação é indicadora que os dados podem ser modelados por um ARCH/GARCH.
Após aplicação de vários modelos para a modelação da equação da média, revela-se como o mais adequado um ARMA(1,1).
Efetuaram-se testes no sentido de selecionar o melhor modelo ARCH/GARCH, usando como critério o AIC. Concluiu-se que dos modelos testados, o que apresentou melhor aderência para modelar os retornos diários do EUR/GBP é um GARCH(1,2), com média descrita por um processo ARMA(1,1) e com distribuição dos erros representados por uma t-student.
Resultados Empíricos 35 E [rt] 2t Distribuição de et AIC
ARMA(1,1) ARCH(1) Normal -7,781083
ARMA(1,1) ARCH(1) t-student -7,825342
ARMA(1,1) GARCH(0,1) Normal -7,725933
ARMA(1,1) GARCH(0,1) t-student -7,777414
ARMA(1,1) GARCH(1,1) Normal -7,910087
ARMA(1,1) GARCH(1,1) t-student -7,918193
ARMA(1,1) GARCH(1,2) t-student -7,919473
Tabela 3.4: Seleção do modelo ARCH/GARCH para os retornos do EURGBP
0 10 0 20 0 30 0 40 0 50 0 - 3 - 2 - 1 0 1 2 3 4
Series: Standardized Residuals Sample 6/01/1999 1/09/2015 Observations 4345 Mean 0.008936 Median -0.009805 Maximum 4.157315 Minimum -3.723207 Std. Dev. 1.000036 Skewness 0.081963 Kurtosis 3.529354 Jarque-Bera 55.59567 Probability 0.000000
Figura 3.5: Distríbuição dos resíduos remanescentes do GARCH(1,2) - EUR/GBP
Pela análise aos resíduos remanescentes, veri…ca-se que estes são ruído branco não-gaussiano (teste de normalidade dos resíduos de Jarque-Bera com p value 50.59567), são independentes e homocedásticos (teste de heterocedasticidade LM com p value de 0.5128). Signi…ca isto que pode existir outra família de modelos que melhor descrevam estes retornos.
3.2
Medição do risco
3.2.1 Simulação Histórica e Simulação de Monte Carlo
As simulações efetuadas nesta secção foram realizadas usando o programa Matlab. Os algoritmos são baseados nos programas disponibilizados por Blake LeBaron, da Brandeis University, EUA.
Para obtenção dos valores da medida de risco, neste caso o ES, vamos considerar os métodos de simulação histórica e de simulação estocástica (ou de Monte Carlo) descritos no capítulo anterior. Vamos usar toda a amostra e prever o risco para o dia a seguir. A previsão para n-dias seguintes obtém-se de forma análoga, repetindo.o processo n vezes.
A ideia base da simulação de Monte Carlo assenta em considerar uma certa distribuição – normal e t-student neste caso –, usar um gerador de números aleatórios (com 10.000 simulações) e posteriormente calcular o ES com métodos não-paramétricos; baseando-nos somente nas fórmulas matemáticas associadas às distribuições usadas.
Na tabela abaixo, representa-se a síntese da aplicação do ES para um dia, para os níveis de signi…cância de 1%, 2.5% e 5%, com recurso às técnicas de simulação histórica, simulação de Monte Carlo com distribuição normal, simulação a partir da fórmula análitica e simulação de Monte Carlo com distribuição t-student. Todos os valores do ES tabela foram multiplicados por 100; sendo apresentados em percentagem.
EURGBP EURCHF
1% 2.5% 5% 1% 2.5% 5%
Simul.histórica 1.6538 1.3495 1.1213 2.0767 1.3853 1.0070 Simul. MC normal 1.3521 1.1875 1.0472 1.3579 1.1936 1.0541 Fórmula analítica (Eq.1.7) 1.3531 1.1868 1.0470 1.3583 1.1925 1.1416 Simul. MC t-student 2.0568 1.4689 1.1325 2.0588 1.4834 1.0533
Resultados Empíricos 37
Observa-se que os resultados obtidos a partir da simulação de Monte Carlo com dis-tribuição normal assumem o menor valor de risco para cada uma das séries consideradas para qualquer nível de signi…cância. A exceção é para o EURCHF com nível de signi…cân-cia 2.5%. Para 5% as medidas de risco são muito homogéneas perante as várias técnicas consideradas.
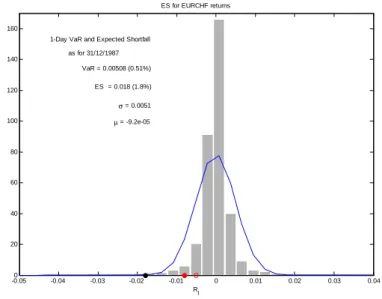
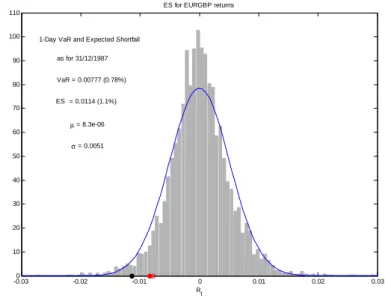
As próximas …guras ilustram a localização dos valores do VaR (a vermelho) e do ES (a preto) para cada uma das séries consideradas. Conforme se pode observar, o ES majoriza o VaR indo de encontro ao relatado pela teoria.
-0.050 -0.04 -0.03 -0.02 -0.01 0 0.01 0.02 0.03 0.04 20 40 60 80 100 120 140 160
1-Day VaR and Expected Shortfall as for 31/12/1987 VaR = 0.00508 (0.51%) ES = 0.018 (1.8%) µ = -9.2e-05 σ = 0.0051 Rt ES for EURCHF returns
Figura 3.6: ES e VaR aplicado aos retornos do EURCHF
3.2.2 RiskMetrics e GARCH
As simulações efetuadas nesta secção foram realizadas usando o programa Matlab. Os algoritmos são baseados nos programas disponibilizados no pacote de séries temporais.
-0.030 -0.02 -0.01 0 0.01 0.02 0.03 10 20 30 40 50 60 70 80 90 100 110
1-Day VaR and Expected Shortfall as for 31/12/1987 VaR = 0.00777 (0.78%) ES = 0.0114 (1.1%) µ = 8.3e-06 σ = 0.0051 Rt
ES for EURGBP returns
Figura 3.7: ES e VaR aplicado aos retornos do EURGBP
EURGBP EURCHF
1% 2.5% 5% 1% 2.5% 5%
RiskMetrics 1.7338 1.564 1.2650 1.1721 1.053 0.9720 GARCH t-student 1.9391 1.601 1.3861 1.9657 1.590 1.3994
Tabela 3.6: ES percentual por RiskMetrics e GARCH
2) com distribuição t student, encontra-se sintetizada na tabela 3.6 seguinte.
Mais uma vez considerámos os três níveis de signi…cância (1%, 2.5%, 5%) e a previsão do risco para um dia (out-of-sample). Observa-se que a medição de risco obtida pelo modelo GARCH com distribuição t-student é superior ao risco obtido pelo RiskMetrics e é bastante próxima dos resultados obtidos pela simulação de Monte Carlo com distribuição t-student. A simulação via RiskMetrics e a simulação histórica geram valores de risco bastante semelhantes. Nota-se que estes últimos dois métodos são dos mais utilizados
Resultados Empíricos 39
em termos práticos nas instituições …nanceiras, enquanto que os modelos GARCH e as simulações de Monte Carlo são ferramentas mais académicas.
De forma a avaliar e con…rmar que o risco por deter um ativo aumenta com o tempo, foi também calculado o ES2;5% sobre o modelo GARCH t-student, para os períodos de 5
e 10 dias. Essa comparação pode ser observada na tabela 3.7.
ES2:5% EURGBP EURCHF
N.o dias 1 5 10 1 5 10
GARCH t-student 1.60 3.89 5.27 1.59 3.77 5.38 Tabela 3.7: ES por número de dias estimados
Ao atentar sobre o valor da medida de risco, comprova-se que com o aumento do intervalo de tempo (número de dias) de previsão o valor da medida de risco também aumenta..
3.2.3 Reconstrução do atrator e GenericPred
Todas as simulações desta secção foram feitas usando o sofware Matlab. Os algoritmos são baseados nos programas disponibilizados nos pacotes Chaotic System Toolbox4 e TSTool5 diponíveis na internet.
No que segue, vamos utilizar ferramentas da teoria de caos para analisar de forma não-linear as séries temporais consideradas e para medição do risco usando o método GenericPred.
Como já foi visto no capítulo anterior para a reconstrução do atrator –que caracteriza a
4Elaborado por Alexandros Leontitsis, University of Ioannina, Greece
5
dinâmica gerada pela série temporal dada –é essencial determinar duas grandezas: o atraso de tempo (o primeiro mínimo da função informação mútua média); e a dimensão do espaço onde está mergulhado o atrator (pelo método dos vizinhos próximos falsos). Os valores destes parâmetros para cada uma das séries (EURCHF e EURGBP) são apresentados na tabela 3.8.
EURGBP EURCHF
Atraso de tempo 60 80
Dimensão de mergulho 4 5
Tabela 3.8: Parâmetros para reconstrução do atrator
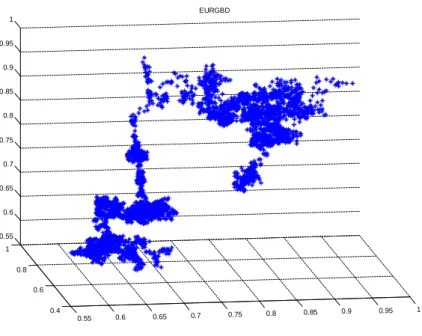
As próximas …guras mostram o mergulho dos pontos considerando o espaço de fases de dimensão 3. Nos dois casos observa-se uma certa dispersão na forma do atrator e a necessidade de passar para uma dimensão superior a 3 (4 e 5 conforme determinado) de forma a desdobrar todas as sobreposições ainda existentes.
Uma vez mostrada a provável proveniência deterministica (ou pelo menos de uma componente determinística) da série temporal escalar, segue-se a tarefa mais di…cil: a pre-visão dos estados futuros. Na prepre-visão foram consideradas todas as observações das séries temporais, …xando as primeiras 3847 para aprendizagem e deixando as últimas 500 para previsão. As …guras abaixo mostram uma previsão a médio prazo (500 observações futuras) para as séries EURGBP e EURCHF utilizando uma adaptação do método GenericPred.
Observa-se que a previsão é bastante boa para as primeiras 50 observações, afastando-se bastante para as restantes. De certa forma vai de encontro ao comportamento do expoente de Lyapunov maximal (que diverge em tempo).
Resultados Empíricos 41 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1 0.4 0.6 0.8 1 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1 EURGBD
Figura 3.8: Atrator do EURGBP
No caso da série EURCHF a série estimada tem menos qualidade (o padrão é mais incerto), pois o fenómeno de black swan pertence ao intervalo de previsão, subindo o grau de complexidade do processo.
Finalmente, na última …gura ilustra-se de forma comparativa a previsão da série tempo-ral EURGBP utilizando 3 métodos/modelos diferentes: GenericPred, GARCH e ARIMA. Uma visão mais detalhada da previsão, pode observar-se mais facilmente que o Gener-icPred ultrapassa a qualidade dos outros dois métodos considerados (baseados nos modelos GARCH e ARIMA), pelo menos ao curto prazo. A longo prazo o modelo ARIMA consegue a melhor previsão.
0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1 0.5 0.6 0.7 0.8 0.9 1 0.5 0.6 0.7 0.8 0.9 1 EURCHF
Figura 3.9: Atrator do EURCHF
2000 2500 3000 3500 4000 4500 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1 GenericPred EURGPB EURGBP GenericPred
Resultados Empíricos 43 2000 2500 3000 3500 4000 4500 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 GenericPred EURCHF EURCHF GenericPred
Figura 3.11: Previsão dos últimos 500 dias da cotação EURCHF
3000 3200 3400 3600 3800 4000 4200 0.7 0.75 0.8 0.85 0.9 Prediction EURGBP GenericPred GARCH ARIMA EURGBP
3880 3900 3920 3940 3960 3980 4000 4020 4040 0.78 0.79 0.8 0.81 0.82 0.83 0.84 0.85 0.86 0.87 Prediction EURGBP GenericPred GARCH ARIMA EURGBP
Capítulo 4
Conclusões e percursos para
futuras investigações
Desde cedo, as Finanças, têm procurado medir o nivel de risco envolvido nos diversos tipos de ativos/ investimentos. Começou por ser usada a volatilidade (variância), mas a necessidade de monetarizar o risco levou à utilização do VaR (Value-at-Risk). No entanto estas medidas não são consideradas medidas de risco coerentes [4]. Esta situação está a levar reguladores e instituições …nanceiras a direcionar os seu esforços para uma medida mais rigorosa –o Expected Shortfall (ES) –que além de ser uma medida coerente é também uma medida de risco consistente [9].
Apesar do conceito do ES ser relativamente simples, a verdade é que a sua estimação pode levar-nos para caminhos muito distintos. Por esse facto, abordou-se a sua esti-mação recorrendo à simulação histórica, simulação estocástica (de Monte Carlo), modelos ARCH/GARCH, EWMA e GenericPred (teoria de caos) [13].
Para testar a implementação do ES por essas vias, foram utilizadas as séries temporais das cotações diárias do EUR/CHF e EUR/GBP ou os seus retornos diários.Constatou-se que as séries das cotações são irregulares e não estacionárias e que as séries dos
tornos, apesar de serem estacionárias, não têm distribuição normal e evidenciam clusters de volatilidade (heterocedasticidade).
Estas características resultaram, coincidentemente, na seleção de um modelo GARCH(1,2) com os erros descritos pela distribuição t-student para ambas as séries dos retornos.
Na aplicação da metodologia adaptada do GenericPred, tentou modelar-se as cotações para EUR/CHF e EUR/GBP, sendo que para o primeiro caso, por essa série ter um outlier bastante signi…cativo (black swan), o resultado tem menos qualidade do que ambicionáva-mos. No segundo caso, a estimação é considerada bastante boa para os primeiros 50 dias previstos.
Em relação à aplicação do ES a 1%, 2.5% e 5%, comprovou-se que o valor deste é superior ao VaR, e que aumenta com o aumento do horizonte de estimação. A simulação via RiskMetrics e a simulação histórica geram valores de ES bastante semelhantes podendo ser considerados como os mais baixos. Os valores obtidos pelo GARCH t-student e MC t-student foram também na mesma ordem de grandeza sendo dos mais elevados.
Contudo surge agora uma dúvida: qual destes valores é o mais …ável. É neste âmbito que para percursos futuros poderá ser interessante tentar aplicar-se os teste de backtesting sugeridos por [2], ou até pensar-se em modelos de estimação do ES que não careçam da modelação prévia dos preços ou retornos.
Bibliogra…a
[1] Acerbi, C., and Tasche, D. Expected shortfall: A natural coherent alternative to value at risk. Economic Notes 31, 2 (2002), 379–388.
[2] Acerbi, C. . S. B. Backtesting expected shortfall. MSCI inc. (2014).
[3] Alves, A. M. Is the iberian electricity market chaotic? characterization and pre-diction with nonlinear methods. PhD thesis, ISCTE-IUL, Lisboa, 2013. Dissertação para obtenção do grau de Doutor em Métodos Quantitativos.
[4] Artzener, P., Delbaen, F., Eber, J., and Heath, D. Coherent measures of risk. Mathematical Finance 9, 3 (1999), 203–228.
[5] BCBS. Fundamental review of the trading book: A revised market risk framework. Tech. rep., BIS, 2013.
[6] Brockwell, P. J., and Davis, R. A. Introduction to time series and forecasting, 2 ed. Springer texts in statistics. Springer, 2002.
[7] Brooks, C. Introductory Econometrics for Finance, 2 ed. Cambridge University Press, 2008.
[8] Daníelsson, J. Financial Risk Forecasting - The Theory and Practice of Forecasting Market Risk with implementation in R and Matlab, 1 ed. Wiley Finance, 2011. [9] Daníelsson, J., Jorgensen, B. N., S., M., Vries, C. G., and Zigrand, J.
Consistent measures of risk, 2008.
[10] Ferreira, M., and Nunes, J. Opções …nanceiras - mestrado em …nanças, 2005. [11] Fontes, N. Sistemas dinâmicos, análise numérica de séries temporais e aplicações
às …nanças. Master’s thesis, ISEG, 2013. Dissertação de mestrado em Matemática Financeira.
[12] Fraser, A. M., and Swinney, H. L. Independent coordinates for strange attractor fromm mutual information. Physics Review A 33, 2 (1986), 1134–1140.