SIMPLIFICAÇÃO DE FRAÇÕES
ARITMÉTICAS E ALGÉBRICAS:
UM DIAGNÓSTICO COMPARATIVO DOS
PROCEDIMENTOS
Mestrado em Educação Matemática
SIMPLIFICAÇÃO DE FRAÇÕES ARITMÉTICAS E ALGÉBRICAS:
UM DIAGNÓSTICO COMPARATIVO DOS PROCEDIMENTOS
Texto apresentado à Banca Examinadora da Pontifícia Universidade Católica de São Paulo, como exigência parcial para a obtenção do título de Mestre em Educação Matemática, sob a orientação da Profa. Dra. Anna Franchi.
_________________________________
_________________________________
desta dissertação por processo eletrônico ou de fotocopiadora.
Vicente Notari, meu pai – “
in memorian
”.
A Deus e a todas as forças do Universo que me guiam.
À Professora Doutora Anna Franchi, pela orientação, compreensão,
paciência, amizade e empenho.
À Professora Doutora Sonia Barbosa Camargo Igliori, por tudo o que
fez por mim e que permitiu esse momento.
Ao Professor Doutor Vinício Macedo, por aceitar fazer parte da Banca
Examinadora.
A todos do Departamento CAVOC, das Faculdades Oswaldo Cruz,
especialmente, a meu amigo Arley.
Aos alunos que participaram do estudo.
Esta pesquisa tem como objetivo obter um diagnóstico sistemático dos principais erros e dificuldades manifestados por alunos do Ensino Fundamental e do Ensino Médio na simplificação de frações aritméticas e algébricas. Foram selecionadas, para a investigação, uma 8ª série do Ensino Fundamental e uma 1ª série do Ensino Médio de duas escolas públicas da Região Oeste, da cidade de São Paulo. Assumimos como referencial teórico os advindos de pesquisas em que a Álgebra, nesses níveis de ensino, deve buscar seus fundamentos nas leis da Aritmética. Entretanto, não o reduz a uma generalização dessas leis, uma vez que o sistema conceitual algébrico incorpora elementos e inter-relações com características próprias. Os dados foram obtidos por meio de estágio em uma classe de cada uma das séries mencionadas, de aplicação de uma prova e de entrevistas. As principais conclusões apontam para um elevado número de erros na simplificação de frações algébricas que revelam uma incompreensão das regras formais que regulamentam essas transformações. Entre esses, ocorre uma predominância de erros devidos a uma generalização de regras de uma situação para outra, sem uma análise das condições que validam essa generalização. Revelam no tratamento das expressões aritméticas um predomínio de procedimentos computacionais realizados automaticamente, sem uma reflexão sobre a natureza da tarefa proposta; indicam, ainda, uma ausência de integração entre os domínios conceituais aritméticos e algébricos.
This research has as objective to get a systematic diagnosis of the main errors and difficulties revealed for pupils of Basic Ensino and Average Ensino in the simplification of arithmetical and algebraic fractions. They had been selected, for the inquiry, one 8ª series of Basic Ensino and one 1ª series of Average Ensino of two public schools of the Region West, of the city of São Paulo. We assume as referencial theoretician the happened ones of research where Algebra, in these levels of education, must search its beddings in the laws of the Arithmetic. However, it does not reduce it to a generalization of these laws, a time that algebraic the conceptual system incorporates elements and Inter-relations with proper characteristics. The data had been gotten by means of period of training in a classroom of each one of the mentioned series, application of a test and interviews. The main conclusions point with respect to one high number of errors in the simplification of algebraic fractions that disclose a incompreensão of the formal rules that regulate these transformations. Between these, a predominance of errors due to a generalization of rules of a situation for another one occurs, without an analysis of the conditions that validate this generalization. They disclose in the treatment of the arithmetical expressions a predominance of automatically carried through computational procedures, without a reflection on the nature of the task proposal; they indicate, still, an absence of integration between the arithmetical and algebraic conceptual domínios.
APRESENTAÇÃO
Nesta pesquisa, procuramos investigar os procedimentos utilizados por alunos do Ensino Fundamental e do Ensino Médio na simplificação de frações aritméticas e algébricas, buscando, por um lado, verificar se estabelecem relações de equivalência entre a fração dada e a fração obtida pela simplificação; por outro lado, conhecer as manifestações dos sistemas conceituais aritméticos e algébricos no tratamento dessas expressões. O estudo desenvolveu-se em uma classe do Ensino Fundamental e em uma outra do Ensino Médio de Escola Pública, na cidade de São Paulo.
Nosso objetivo foi o de obter um diagnóstico sistemático dos principais erros e dificuldades manifestados por esses alunos na simplificação de frações aritméticas e algébricas, procurando compreendê-los.
Os fundamentos teóricos que nortearam esta pesquisa preconizam que a introdução da Álgebra no ensino básico é realizado pela via das regularidades que governam as leis numéricas. A Álgebra não se reduz à “generalização” da Aritmética, porque as regras formais de reescrita operam sobre as expressões algébricas e literais e, embora encontrem um fundamento no domínio aritmético, se inserem em um domínio conceitual próprio.
Privilegiamos as pesquisas de Booth (1988), Mason (1996), Kaput (1996) e os estudos apresentados por Lemoyne, Conne e Brun (1993), que consideram a hipótese de que os erros dos alunos em Álgebra estão diretamente relacionados aos hábitos escolares desenvolvidos ao longo dos estudos primários.
A escolha do tema deu-se em virtude da leitura e discussão de pesquisas relacionadas ao ensino de Álgebra, conforme aparecem citadas na fundamentação teórica deste estudo.
Encontramos um grande número de erros nas atividades de simplificação das frações algébricas, os quais revelam a incompreensão das regras formais que regulamentam as transformações necessárias nessa simplificação. Em atividades onde havia tratamento das expressões aritméticas, predominaram os procedimentos computacionais realizados automaticamente, sem a reflexão sobre a natureza da tarefa proposta, indicando ausência de integração entre os domínios conceituais aritméticos e algébricos.
Este trabalho está organizado em cinco capítulos, sendo que no Capítulo I, apresentamos Problemática e Justificativa.
No Capítulo II, descrevemos o Referencial Teórico utilizado, expondo o posicionamento de alguns dos pesquisadores que enfocam a Álgebra como “generalização das leis que regem as relações numéricas” e algumas das reflexões dadas por Lemoyne, Conne e Brun (1993) que apresentam erros de alunos em Álgebra, relacionados aos seus hábitos escolares durante os estudos primários.
No Capítulo III, Procedimentos Metodológicos, é apresentada a metodologia utilizada para a realização deste trabalho: o contato com as escolas, o período de estágio de campo, aelaboração e aplicação do instrumento piloto, de uma prova escrita, e entrevistas.
No Capítulo IV, Análise dos Resultados, está a categorização dos procedimentos e erros cometidos pelos alunos, como também as respectivas análises quantitativa e qualitativa.
CAPÍTULO I
PROBLEMÁTICA E JUSTIFICATIVA
“A Álgebra começa como a arte de manipular somas, produtos e potências de números. As regras para essas manipulações valem para todos os números, de modo que as manipulações podem ser levadas a efeito com letras que representem números. Revela-se, então, que as mesmas regras valem para diferentes espécies de números [...] e que as regras inclusive se aplicam às coisas [...] que de maneira nenhuma são números. Um sistema algébrico, como veremos, consiste em um conjunto de elementos de qualquer tipo sobre os quais operam funções como a adição e a multiplicação, contanto apenas que essas operações satisfaçam certas regras básicas” (1988; p.9).
No artigo de Usiskin (1998), apresentado em tradução, a Álgebra da escolamédia é relacionada com a compreensão das variáveis e das operações com essas variáveis em um determinado domínio. O autor considera o conceito de variável como multifacetário e afirma que “as finalidades da Álgebra são determinadas por, ou relacionam-se com,
concepções diferentes da Álgebra que correspondem à diferente importância relativa
dada aos diversos usos das variáveis” (1988; p.13).
Entre essas concepções, considera a que denomina de “Álgebra como Aritmética
generalizada”, em que as variáveis são pensadas como generalizadoras de modelos. Por
exemplo, generalização das propriedades formais das operações, formulação matemática de leis que descrevem as relações de dependência entre variáveis.
Kaput (1996) considera a Álgebra como generalização e formalização de regularidades e condições e, de modo especial, mas não exclusivamente, como raciocínio aritmético generalizado e raciocínio quantitativo generalizado. Conforme afirma, muitas atividades matemáticas têm como características intrínsecas a generalização e a formalização. Os contextos de situações e os sistemas matemáticos em que essas podem ocorrer, são ilimitados. As ações de generalização são traduzidas em expressões, em proposições algébricas, ou seja, em objetos simbólicos formais, sendo submetidas a raciocínios posteriores em que se busca a formalização. Um processo de formalização gradual deve preceder ao trabalho com formalismos. Esse autor considera também que o fracasso escolar no campo da Álgebra deve-se a formalização precoce da linguagem algébrica, assim, afirma: “têm sido demonstrados que os esforços para relacionar a experiência dos estudantes aos formalismos, depois de terem sido introduzidos, não têm obtido resultados satisfatórios” (Kaput; 1996, p.89).
O autor ainda sustenta que esse processo de generalização não se inicia nos primeiros anos do Ensino Fundamental nem se finaliza neles, aparecendo também nos níveis mais complexos do pensamento matemático como, por exemplo, na teoria dos números algébricos e na criação de modelos matemáticos avançados.
Em uma perspectiva mais abrangente, Mason (1996) acredita que a generalização é a essência do pensamento algébrico em um movimento de dupla via entre o particular e o geral, entre conjecturar e justificar. Nesse movimento, busca-se a produção de expressões aritméticas possíveis de serem generalizadas e, em que se trabalham implicitamente variáveis dependentes e independentes.
Embora essas abordagens diferenciem-se quanto à relevância dada a alguns aspectos específicos, apresentam em comum o fato de considerarem as leis da Aritmética como alicerce às leis da Álgebra e “(...) como instrumento para expressar generalidades e controlar o desconhecido” (Mason; 1996, p.8).
Esta pesquisa insere-se nessa direção, ou seja, no estudo de expressões algébricas pela via das regularidades que governam as leis numéricas. A Aritmética é tomada como fonte da Álgebra, porém, não se reduz à generalização da mesma.
reescrita operam sobre as expressões algébricas e literais. Determinadas regras derivam das propriedades das operações e podem encontrar um fundamento no domínio aritmético, mesmo se elas se separam para construir um domínio próprio, aquele da Álgebra. A aplicação de regras não tem necessariamente por objetivo efetuar um cálculo” (Lemoyne, Conne e Brun; 1993; p.338).
Este estudo investiga os procedimentos utilizados pelos alunos nos cálculos numéricos e literais efetuados na simplificação de frações, observando como as características específicas dos sistemas conceituais aritméticos e algébricos se manifestam no tratamento dessas expressões; se os alunos estabelecem relações de equivalência entre a fração dada e a fração obtida pela simplificação.
Nosso objetivo foi realizar um estudo diagnóstico sistemático dos principais erros e dificuldades manifestados por alunos e, simultaneamente, identificar os conhecimentos envolvidos em seus procedimentos corretos e incorretos de simplificação das frações propostas no instrumento diagnóstico.
A opção pela direção deste trabalho, referenciada acima, surgiu de nossa leitura e discussão de pesquisas relacionadas ao ensino da Álgebra nos níveis Fundamental e Médio, especialmente as desenvolvidas por Booth (1984, 1988), Lemoyne, Conne e Brun (1993), e pelo fato desse tema constar das propostas e da linha de pesquisa do subgrupo coordenadopela orientadora desta pesquisa.
As propostas e os resultados obtidos pelo SARESP – Sistema de Avaliação do Rendimento Escolar do Estado de São Paulo1, apontam para a pertinência e relevância de nosso estudo sobre as dificuldades e erros cometidos pelos alunos na aprendizagem inicial em Álgebra.
Analisando o material oferecido pelo SARESP, especialmente em sua edição de 1997, observamos um fraco desempenho em Álgebra, sendo que a médiados alunos da 8ª série do Ensino Fundamental correspondeu a 33,0%, moda e mediana a 30,0%, ou seja, muito próximas.
1 SARESP – Coordenado pela Secretaria da Educação do Estado de São Paulo, informações obtidas no site
Além disso, constatamos que os conteúdos da Matemática como de outras disciplinas requerem, na maioria das vezes, uma interpretação do aluno sobre a equivalência de frações aritméticas e algébricas. Na construção do gráfico da função real
dada por
c b ax x
f( )= + , a identificação de seus coeficientes angular e linear é
imprescindível, sendo a reescrita da lei dessa função o caminho mais apropriado; isto é,
rescrevê-la como c b x c a ) x (
f = + .
Também no estudo sobre aplicações matemáticas nas áreas da Economia e Administração, exige-se esse procedimento de reescrita de frações em casos como
2 50 3 + = q
Ct , em que Ct indica o custo total de uma dada empresa e q sua quantidade
produzida. Nesse caso, a reescrita dessa função econômica como Ct
2 350 q 2 3 +
= é que
possibilita ao aluno identificar nitidamente que seu custo fixo é de 175 reais; ou seja, 2 350
.
Nos dois exemplos, observamos que a não identificação da equivalência entre frações, utilizando-se sua reescrita, pode dificultar o reconhecimento dos alunos sobre os coeficientes das funções envolvidas; pode ainda levá-los a um procedimento incorreto de
simplificação, como
2 3 2 )
(x = x+
f em f(x)= x+3, conforme apontam pesquisas na área
que serão descritas no Capítulo seguinte.
Os erros na simplificação de frações algébricas, como os acima citados, não se manifestam, apenas em alunos do Ensino Fundamental e Médio, pois tambémobservamos e constatamos a existência dessas dificuldades e tipos de erros cometidos pelos próprios alunos do Ensino Superior.
Bertoni (1998) argumenta que “os erros revelam a diversidade profunda dos processos de aprendizagem dos alunos, sugerindo estratégias para atender as dificuldades específicas e melhorando a qualidade do ensino” (p.17).
Portanto, os subsídios para as propostas alternativas de ensino sobre as frações podem ser obtidos pela identificação, qualificação e compreensão dos erros cometidos pelos nossos alunos e suas justificativas nos procedimentos de simplificação dessas frações.
O diagnóstico sobre os erros na perspectiva acima descrita nos oferece as primeiras direções para a elaboração dos instrumentos de investigação.
Nosso estudo incide sobre uma população de alunos de escolas estaduais de 8ª série do Ensino Fundamental e 1ª série do Ensino Médio, contendo questões aritméticas e algébricas.
Pretendemos identificar osprocedimentos de simplificação utilizados pelos alunos na busca das frações equivalentes propostas na prova, a qualcontém questões aritméticas, em particular nos casos em que as frações apresentam numerador e denominador representados na forma fatorada. Quais os conhecimentos envolvidos e como se caracterizam.
Quanto aos aspectos algébricos, restringimo-nos a questões que envolvem
simplificação em frações do tipo
b x a.
,
x b ax+
e
x b ax.
, com b e x não nulos.
Pretendemos também verificar:
- como os alunos utilizam as propriedades aritméticas na simplificação de expressões algébricas, justificando seus procedimentos pela aplicação dessas propriedades; além disso, se eles relacionam essas propriedades às condições em que é possível aplicá-las;
- se os alunos manipulam expressões aritméticas e algébricas como inseridas em sistemas conceituais distintos e sem relação alguma;
- a ocorrência de erros que se situam na transição da Aritmética para a Álgebra, como os que se referem à aplicação indevida de uma determinada regra.
CAPÍTULO II
REFERENCIAL TEÓRICO
Neste Capítulo, apresentamos os fundamentos teóricos que nortearam o desenvol-vimento de nossa pesquisa.
Inicialmente, explicitamos o posicionamento dos pesquisadores que enfocam a Álgebra como “generalização das leis que regem as relações numéricas”, incluindo, eventualmente, referências a suas pesquisas.
Em um segundo momento, são apresentamos algumas das reflexões expostas por Lemoyne, Conne e Brun (1993) sobre as abordagens de análise dos erros. Fundamentados nessas reflexões, os autores formulam novas possibilidades de interpretação de erros.
Booth (1988) afirma que a compreensão incompleta das transformações permitidas sobre as expressões numéricas não coloca o aluno em boa posição para a aprendizagem sobre as manipulações algébricas.
“(...) a Álgebra não é isolada da Aritmética; na verdade é, em muitos aspectos, a Aritmética generalizada. E nisso está a fonte das dificuldades. Para compreender a generali-zação das relações e procedimentos aritméticos é preciso primeiro, que tais relações e procedi-mentos sejam apreendidos dentro do contexto aritmético. Se não forem reconhecidos ou se os alunos tiverem concepções erradas a respeito deles, seu desempenho em Álgebra poderá ser afetado. Nesse caso, as dificuldades que o aluno tem em Álgebra, não são tanto de Álgebra pro-priamente dita, mas, de problemas em Aritmética que não foram corrigidos” (Booth, 1988; p.32-33).
Macgregor (1996), em estudos realizados com alunos de escolas secundárias austra-lianas, com idades entre 11 e 16 anos, aponta que uma das causas das dificuldades dos alunos na aprendizagem da Álgebra reside nos conhecimentos deficientes da Aritmética, ou seja, não compreendem de modo suficiente as propriedades operatórias dos números.
no procedimento e não apenas na resposta; a compreensão das relações existentes entre as operações; o conhecimento das diversas interpretações do sinal de igual e o conhecimento das propriedades operatórias dos números. O primeiro aspecto indica que, os alunos preocupam-se muito mais em encontrar respostas diante de uma dada questão, em lugar de se interessarem pelos procedimentos que os conduzem a essa resposta. Especificamente à simplificação de frações algébricas, podemos pensar nesses procedimentos em termos de uma seqüência de operações selecionadas que levam uma fração a uma outra que lhe é equivalente.
O segundo aspecto que complementa o primeiro refere-se a conhecer as operações básicas, além da adição. Por exemplo, a diferença entre dois números, geralmente, é asso-ciada a uma operação de adição, isto é, se x – y = z, o valor de x é dado por y + z; a multi-plicação é interpretada como uma soma repetida, 3 vezes 5 é dado como 3 + 3 + 3 + 3 + 3, o que acarreta dificuldade para expressar 3 vezes x como 3x e na divisão, 8 dividido por 2 é igual a 4, pois 4 + 4 = 8. Essa interpretação pode prejudicar o entendimento de x sobre 2.
Quanto às interpretações do sinal de igual, os alunos utilizam-no para indicar um re-sultado, usando o verbo dar para denotar esse resultado. Por exemplo, na soma de 5 + 4 = 9, eles lêem 5 mais 4 DÁ 9, ou seja, entendem que esse sinal ( = ) vincula a pergunta a uma resposta. Em decorrência disso, algumas vezes, empregam de maneira informal a igualdade para unir as partes de um cálculo, como no caso de 5 + 4 = 9 x 6 = 54.
Consideramos que esse aspecto está estritamente ligado às concepções dos alunos sobre as operações em Aritmética. Booth (1988); Behr, Erlwanger e Nichols (1980); Ginsburg (1977); e Kieran (1981) consideram que, com freqüência , as operações em Aritmética indicam ações que se desenvolvem no tempo. Como conseqüência, o sinal de igualdade é tratado, geralmente, como indicativo do resultado dessas ações.
A ocorrência de erros em Álgebra, que consistem na simplificação de dois termos não semelhantes em um único termo, tem sido apontada nas pesquisas citadas como conseqüência da interpretação do sinal de igual somente como indicador de respostas.
Segundo Lemoyne, Conne e Brun (1993), Matz (1980) realiza um estudo investigativo, demonstrando que certas classes de erros são resultados de uma adaptação sistemática de conhecimentos anteriores, que se têm generalizado e extrapolado de forma inadequada. Assim, dois tipos principais de erros são definidos:
2º) os erros ligados às técnicas de extrapolação.
Matz (1980) compreende os primeiros erros como sendo uma conseqüência das relações entre os saberes aritméticos e algébricos, sob o ponto de vista de uma passagem da Aritmética à Álgebra. Considera que “(...) essa passagem efetua-se pela construção da noção do valor simbólico e pela extensão da relação de igualdade”.
Segundo o autor, os erros de concatenação enquadram-se nessa primeira categoria, considerando-os como sendo de natureza sintática. Argumenta que a escrita dos números em Aritmética ocorre pela concatenação dos algarismos, atribuindo a cada um desses algarismos um valor dependente de sua posição; além disso, na representação dos racionais, a justaposição de um número inteiro e uma fração implica adição, ou seja,
convenciona-se que 2 1
3+ deve ser escrito como 2 1
3 . Analisando as respostas freqüentes
dadas pelos alunos à questão “se x = 6, calcule 4x” são 46 ou 10, a primeira resposta faz referência aos conhecimentos sobre o valor de posição e a segunda, aos conhecimentos sobre a soma.
Além dos erros já discutidos, podemos citar outros que infligem as regras sintáticas do simbolismo algébrico. Referimo-nos às regras que regulam a ordem em que os cálculos devem ser efetuados em uma determinada expressão, o que implica o uso dos parênteses.
De acordo com Booth (1988), Kieran (1979) acredita que os alunos não usam parênteses porque, geralmente acham que a seqüência escrita de operações determina a ordem em que os cálculos devem ser efetuados; além de muitos considerarem que o valor de uma expressão permanece inalterado mesmo quando se muda a ordem dos cálculos.
[Keith, treze anos de idade, ao calcular 18 x 27 + 19, logo depois de ter calculado 27 + 19 x 18 da esquerda para a direita].
“Keith: Faço...27 mais 19, depois multiplico por 18. É a mesma coisa que o anterior, só que ao contrário.
E: Pois bem, suponha que eu resolvesse calcular e achasse que deveria multiplicar 18 por 27 e depois somar 19. Eu chegaria ao mesmo resultado?
K: Sim.
K: De qualquer uma! Depende do que passasse pela minha cabeça na hora!
E: Mas não importaria a maneira de fazer?
K: Não, a resposta seria a mesma.” (Booth, 1984; p.55)
Booth (1988) também acredita que a ordem dos cálculos depende do contexto a que a expressão escrita está relacionada.
“O que você pode escrever como área deste retângulo?
Neil: p vezes... a mais m. [Escreve p x a + m]
E: Muito bem, então, você escreveu p x a + m. E o que você faria realmente, o que você precisaria fazer primeiro?
N: Não estou entendendo.
E: Muito bem, por que você disse p vezes a mais m?
N: Porque estou multiplicando este lado [p] por aquele lado [a e m], e não dá para fazer aquele lado [a e m], e, assim, tenho de somar este [a] com aquele [m], para multiplicar os dois lados juntos.
E: Muito bem, então que parte você faria primeiro?
N: Eu somaria aqueles dois [a e m] e então multiplicaria por p.
E: E foi isso que você escreveu?
N: Foi .
E: Suponha que lhe diga que acho [ p x a + m] significa p vezes a. E depois mais m.
P
N: Ah, não, não pode ser isso. Se você fizer p vezes a só obterá uma parte dela [área]. Você teria de fazer a mais m para obter toda a base e então multiplicar por p. Você tem de somar a com m primeiro.” (Booth, 1984; p.22)
Por essas duas entrevistas, observamos que a necessidade do uso dos parênteses é ignorada. Conseqüentemente, as expressões algébricas que precisam do uso desses parênte-ses são escritas de modo incorreto, como exemplo, tem-se x . y + z, em lugar de x . (y + z), podendo acarretar outros erros na simplificação dessa expressão; por exemplo, x . y + z sendo reescrito como xy + z.
Retomando as proposições descritas por Matz (1980), passamos a analisar os erros da segunda categoria, ou seja, erros ligados às técnicas de extrapolação. Esses erros são considerados utilizações inapropriadas de regras corretas, porém, aplicadas a outros contextos distintos daqueles de sua validade. Observamos que uma forma de generalizar é ampliar o âmbito de aplicação de uma lei, estendendo-a para um campo em que não havia sido definida. Entretanto, essa extensão deve ser feita comprovando-se sua validade na nova situação. A preocupação parece estar ausente quando da ocorrência desses erros pelo aluno.
Matz (1980) afirma que os erros dessa segunda categoria tratam, essencialmente, da teorização psicológica sobre os processos de elaboração dos conhecimentos, fundamentada nos processos de assimilação e acomodação do modelo piagetiano de desenvolvimento dos conhecimentos: “(...) confrontado a uma nova situação, o aluno dispõe de dois modos de tratá-la: se ele conhece a regra a ser aplicada, ele pode se contentar em aplicá-la; se ele a ignora, pode, então, recorrer às técnicas de extrapolação” (apud, Lemoyne e outros, 1993; p.337).
Artigüe (1990) analisa erros dessa natureza relacionados a um processo presente no desenvolvimento histórico de numerosos domínios da Matemática, considerando-o como um produtor de obstáculos2. Os exemplos mais evidentes desse processo referem-se:
“(...) a extensão inadequada de regras operatórias de naturais para, por exemplo, os decimais. No que se refere às regras formais de manipulação de expressões algébricas
2 Artigüe (1990) considera, nesse artigo, os obstáculos citados como epistemológicos, baseando-se nas
essa generalização abusiva situa-se na origem de erros tenazes dos alunos como (a + b)2
= a2 + b2 ou raiz quadrada a+b = a + b ” (Artigüe, 1992; p.261).
Cauzinille, Mathiew e Resnick (1987), segundo Lemoyne e outros (1993), concluem na interpretação dos resultados de suas pesquisas, que os erros dos alunos em Álgebra ocorrem em razão de: “lacunas” nos conhecimentos (exemplo: cálculo dos relativos); às restrições na aplicação dos conhecimentos (exemplo: procedimento de reescrita de uma expressão com parênteses aplicado corretamente, só no que se trata de uma expressão numérica); e generalização das condições de aplicação dos conhecimentos (exemplo: comutatividade da subtração).
Para Lemoyne e outros (1993), as interpretações dos erros descritos por Cauzinille e outros (1987) não divergem essencialmente das propostas de Matz (1980).
A seguir, enfocamos os aspectos conceituais que se situam mais propriamente no sistema conceitual algébrico. Um deles refere-se ao conceito de variável , considerado por Booth (1988) como um dos aspectos mais importantes no estudo da Álgebra.
Segundo Booth (1988), uma das maiores diferenças entre Aritmética e Álgebra reside na utilização de letras como indicadoras de valores. As letras também aparecem em Aritmética, mas, de modo diferente. A letra m, por exemplo, pode ser utilizada em Aritmética para representar “metros”, mas não para representar o número de metros, como em Álgebra.
Booth (1988) afirma que os alunos têm uma forte tendência em considerar as letras como representação de valores específicos únicos, como em “x + 3 = 8”, e não números genéricos ou variáveis como um “x + y = y + x”. Na Aritmética, os símbolos que representam quantidades significam, sempre, valores únicos.
Os diferentes usos das letras podem acarretar uma “falta de referencial numérico”, por parte do aluno, na interpretação do significado das letras em Álgebra.
categorizou cada item em um dos seguintes seis níveis de interpretação de letras, de acordo com o nível mínimo requerido para um desempenho bem sucedido:
(a) Letra avaliada – A letra recebe um valor numérico desde o princípio;
(b) Letra não considerada – A letra é ignorada ou sua existência é reconhecida sem dar significado a ela;
(c) Letra considerada como um objeto concreto – A letra é vista como uma abreviação para um objeto concreto ou vista como um objeto concreto em si mesma;
(d) Letra considerada como uma incógnita específica – A letra é vista como um número específico, mas desconhecido;
(e) Letra considerada como um número generalizado – A letra é vista como representando ou, pelo menos, sendo capaz de assumir vários valores em lugar de apenas um;
(f) Letra considerada como variável – A letra é vista como representando um domínio de valores não específicos e uma relação sistemática é percebida entre dois conjuntos de valores.
Küchemann (1981) descobriu que, somente um pequeno número de estudantes, de 13 a 15 anos de idade, era capaz de considerar as letras como números generalizados, a despeito da experiência da classe em representar padrões numéricos como afirmações generalizadas, embora a interpretação dependesse, em parte, da natureza e complexidade da questão. Um número ainda menor foi capaz de interpretar letras como variáveis no sentido da classificação de Küchemann (1981). Um número maior de alunos conseguiu interpretar letras como incógnitas específicas ao invés de números generalizados. Todavia, a maioria dos estudantes (73,0% dos de 13 anos; 59,0% dos de 14; e 53,0% dos de 15) ou tratava as letras como objetos concretos ou as ignorava.
As considerações feitas até o momento incidem sobre os componentes sintáticos e semânticos da linguagem algébrica: convenções sintáticas, significado das operações e das relações de igualdade, das propriedades operatórias e de variável. Convém precisarmos um pouco mais esses componentes que, aliás, são característicos de qualquer linguagem.
O componente semântico realiza-se, conforme Franchi (1995), pela atribuição de significados a elementos, relações, procedimentos de uma situação ou pela própria construção do conhecimento do sistema conceitual da Matemática e de seu domínio de validade (...). Em outros termos, podemos afirmar, assim como Granell (1997), que no primeiro caso, o significado “referencial” permite associarmos os símbolos às situações reais (...) e, no segundo caso, o significado formal obedece às regras internas do próprio sistema.3
Granell (1997) considera que ensinar Matemática de uma forma significativa implica conhecermos os usos e as funções que o conhecimento matemático cumpre na sociedade e, em seguida, localizarmos a aprendizagem dos conceitos e procedimentos matemáticos no contexto de tais usos e funções.
Referindo-se a esses aspectos, Kaput (1996) assim se expressa:
“Quando falamos em formalismo (...), nos fixamos em símbolos e regras sintáticas para manipulá-los (modificar a sua forma). Não obstante, é possível atuar semanticamente sobre os formalismos: as ações guiam-se pelo significado que o indivíduo atribui aos símbolos” (p.91).
Por exemplo, uma base semântica para a resolução formal da equação –4x = 8, tomando-se como referência o sistema conceitual numérico, a solução precisaria ser necessariamente um número negativo, pois o resultado é um número positivo. Além disso, precisaria ser um determinado número que multiplicado por – 4, seja igual ao número 8. Para se encontrar a solução, uma maneira seria comparar os números -4 e 8, para se perceber que 8 é o dobro de 4, obtendo solução x = -2.4
Outra forma de resolução seria efetuar a mesma operação em ambos os termos da equação, o que significa dividir os dois termos por –4 para se chegar à unidade. Essas operações podem ser simplificadas pela transposição do –4 para o segundo membro, com a divisão, referindo-se à operação inversa da multiplicação.
Ao se referir à atividade algébrica, Drouhard (1995) afirma que essa atividade, mesmo limitada à fase do cálculo algébrico, não consiste em operações efetuadas
nicamente sobre as escritas. A todo momento, o indivíduo é solicitado a efetuar escolhas, por exemplo, que transformações deve efetuar e como justificá-las.
O autor coloca entre as respostas sintáticas as do tipo: “porque eu fatorei”, em que os argumentos são colocados sobre as transformações e não sobre as propriedades matemáticas.
Assim, uma perspectiva de ensino estritamente sintática enfatizaria as regras sem nenhuma preocupação com as justificativas matemáticas que autorizam a aplicação dessas regras. Por exemplo: na simplificação de frações, dividir numerador e denominador por um mesmo número; se multiplicar o numerador, multiplique também o denominador. Outras como: o que é igual pode cortar, em que não há nenhuma referência às condições das operações matemáticas em jogo nem mesmo às condições de aplicação.
Procedendo a análise dos diagnósticos dos erros em expressões algébricas no enfoque desenvolvido por Matz (1980), e exposto neste Capítulo, Lemoyne e outros (1993) apontam para o fato de que, à primeira vista, eles negligenciam a história escolar desses erros. Como é o caso das proposições que se referem à extensão dos conhecimentos sobre as propriedades das operações e as leis dos números.
Para efetuar uma análise desse tipo, seria exigido um estudo teórico mais aprofundado, bem como a implementação de procedimentos metodológicos pertinentes. Por isso, discutiremos apenas alguns aspectos relacionados a essa abordagem.
Um deles refere-se ao ensino na perspectiva acima descrita, em que se dissociam os aspectos sintáticos e semânticos da linguagem algébrica. Segundo Granell (1997), inúmeras pesquisas apontam que “boa parte dos erros que os alunos cometem, deve-se ao fato de terem aprendido a manipular símbolos de acordo com determinadas regras, sem se deterem no significado dos mesmos” (p.265).
Em uma perspectiva mais ampla, Lemoyne e outros (1993) afirmam que esse modo de operar sobre as expressões algébricas ou aritméticas sem se preocupar em justificá-las, provoca a constituição de uma relação do aluno5 com atividades de manipulação dessas expressões que influencia seu comportamento na resolução de tarefas escolares dessa natureza. Assim, alguns procedimentos são privilegiados em detrimento de outros, institucionalizando-se em função de determinadas práticas escolares.
CAPÍTULO III
PROCEDIMENTOS METODOLÓGICOS
Neste Capítulo, procuramos estudar os procedimentos e erros na simplificação de frações aritméticas e algébricas, de alunos da 8ª série do Ensino Fundamental e da 1ª série do Ensino Médio, de duas escolas estaduais da cidade de São Paulo. Um período de observação no lócus da pesquisa foi realizado, objetivando avaliar a pertinência do problema proposto. Inicialmente, fizemos um estudo piloto que consistiu na aplicação de um instrumento provisório para levantamento dos erros. Esse estudo nos permitiu a identificação das dificuldades manifestadas pelos alunos e a elaboração de um instrumento definitivo a seraplicado, seguido pelas entrevistas.
O ponto de partida para a nossa investigação sobre os erros foi a posição assumida e descrita na fundamentação teórica.
Procuramos, neste Capítulo, especificar cada uma das etapas já mencionadas acima, caracterizando a escola e, sinteticamente, todo o percurso realizado.
3.1 Procura da Escola
Fizemos um contato inicial com uma primeira escola A, da região central, onde aplicamos experimentalmente uma avaliação (instrumento piloto) em duas classes da 1ª série do Ensino Médio, totalizando 61 alunos. Ao mesmo tempo e nas mesmas condições, aplicamos a mesma avaliação em uma turma da 1ª série do Ensino Médio, na escola B em que lecionamos, com 31 alunos.
Para o desenvolvimento do trabalho, optamos por duas escolas públicas da Região Oeste, na cidade de São Paulo.
relação ao Ensino Fundamental e Médio.
O fato acima mencionado foi constatado, mediante a autorização da Direção de cada escola envolvida no trabalho, com consultas nos respectivos arquivos administrativo – documentos e matrículas atuais.
Além disso, encontramos um ambiente muito favorável para o desenvolvimento deste trabalho em ambas as escolas, tanto pelo grande número de alunos quanto pelo ambiente acolhedor de toda sua direção, funcionários e, sobretudo, do corpo docente.
3.2 Características da Escola
As escolas escolhidas são estaduais, na Região Oeste de São Paulo. A escola C atende alunos do Ensino Fundamental e Médio; e a escola D atende apenas alunos do Ensino Médio. As turmas de 8ª série da escola C funcionam no período matutino; as 1ªs séries do Ensino Médio da escola D, nos três períodos (matutino, vespertino e noturno). O estágio e a aplicação dos instrumentos diagnósticos foram realizados em escolas diferentes para garantirmos as mesmas características do público-alvo, pois numa mesma escola, deveríamos trabalhar com públicos de períodos diferentes.
3.3 Estágio de Campo
De acordo com Ludke e André (1986) “(...) a perspectiva dos participantes, isto é, a maneira como (...) encaram as questões que estão sendo focalizadas (...) os diferentes pontos de vista (...), o dinamismo interno das situações, geralmente, é inacessível ao observador externo” (p.12).
Confirmamos o proposto por Ludke e André (1986), pois constatamos que, mesmo que nosso objetivo fosse de modo prioritário a efetivação de análise das produções dos alunos, foi de extrema importância a realização de estágio para que o êxito de nossa investigação fosse obtido. A integração do pesquisador ao grupo, tornando-se parceiro e comprometido com as atividades propostas a esse grupo, é fundamental.
conhecermos melhor os alunos, anotarmos os conteúdos desenvolvidos em classe e conhecermos, também, o trabalho dos professores.
As descrições das observações das aulas, bem como das turmasescolhidas, são:
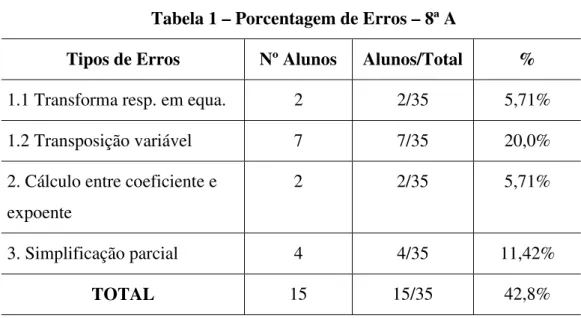
8ª SÉRIE C DO ENSINO FUNDAMENTAL (8ª C): Essa sala funcionava no período da manhã, com trinta e cinco alunos freqüentes. Foi caracterizada pela professora como uma turma que apresentava um bom desempenho, sem repetentes, e as idades desses alunos variavam entre treze e quatorze anos de idade.
Com relação ao material utilizado, a professora não seguia um livro didático específico, e apresentava questões relativas aos conteúdos matemáticos (resolução de equações de segundo grau nesse período) extraídas de diversas fontes. Não havia trabalhos ou atividades em equipe e os alunos sempre trabalhavam sozinhos na resolução das questões propostas. Aqueles com dificuldades pediam auxílio à professora, e a maioria deles conversava sobre os mais variados assuntos e, apenas alguns deles ajudavam os demais colegas. Depois de um certo tempo na mesma aula ou, na aula seguinte, as questões propostas eram corrigidas no quadro negro sem nenhum questionamento dos alunos com relação à resolução dessas questões, e a única preocupação da professora era fazer uma correção “rápida” para avançar em outros conteúdos. Em nenhum momento verificamos observações da professora com relação às condições de existência de uma equação de segundo grau, bem como suas relações com outros conteúdos.
Conteúdos desenvolvidos: observando o diário da professora e os cadernos dos alunos, desde o início do ano letivo de 2001 até o final do período de nosso estágio, pudemos verificar que os conteúdos desenvolvidos foram: produtos notáveis, resolução de equações de segundo grau e a construção do gráfico da função afim. A professora comentou que já havia trabalhado com esses mesmos alunos a simplificação de frações algébricas no ano letivo de2000.
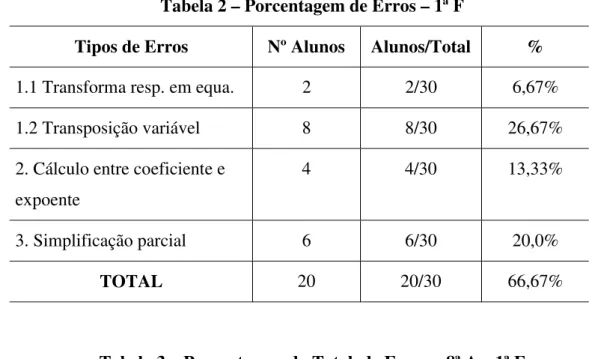
1ª SÉRIE F DO ENSINO MÉDIO (1ª F): Essa é uma turma do período da tarde que, segundo a professora, era mediana quanto ao seu desempenho, contando com trinta alunos freqüentes.
progressões aritméticas e algébricas) eram propostas aos alunos, pela professora, após a resolução de um modelo no quadro negro, e o comportamento dos alunos era o mesmo observado na turma anterior.
Em ambas as turmas, verificamos que o único objetivo dos professores era o de memorização de regras pelos alunos, através da resolução exaustiva de questões propostas em sala de aula, e nenhuma outra questão era proposta para que se enfatizasse as aplicações do conceito de progressões, por exemplo. Após conversas com essas duas professoras, com base em suas próprias falas, pudemos verificar a excessiva preocupação no cumprimento de um determinado “programa” e, verificamos, ainda, uma total despreocupação com a dimensão semântica da Álgebra. Em conversas com os alunos das duas escolas, observamos algumas reações de "espanto", expressas por eles, com relação aos procedimentos de simplificação de frações aritméticas e algébricas utilizados na correção e devolutiva da prova escrita.
Conteúdos desenvolvidos: os conteúdos trabalhados durante o período de estágio, desde o início do ano, foram: resolução de equações exponenciais, estudo e construção do gráfico da função exponencial e progressões (progressões aritméticas e algébricas). A professora comentou que seu trabalhar com esses alunos começou, somente, a partir de 2001, uma vez que essa escola atendia apenas o Ensino Médio.
Nesse período, estabelecemos uma ótima relação tanto com os alunos quanto com os professores das duas turmas envolvidas; esclarecemos dúvidas dos alunos no decorrer das aulas e até substituímos uma professora, ausente por um dia, na EscolaC.
Utilizamos o tempo restante, aproximadamente dez dias, para a aplicação da prova escrita e a realização das entrevistas.
3.4 Os Instrumentos
A aplicação desse instrumento piloto ocorreu na escola A, como já mencionado, com duas classes da 1ª série do Ensino Médio (61 alunos) e, paralelamente, na escola B com uma turma da mesma série (31 alunos).
Depois de corrigido, observamos que algumas das variáveis consideradas não se faziam pertinentes, principalmente por considerarmos nesse instrumento casos de frações que envolviam potências de grau maior que dois. Além disso, o instrumento mostrou-se muito extenso e repetitivo aos alunos.
Os resultados apresentados pelos alunos de ambas as escolas nos possibilitaram uma reelaboração do instrumento diagnóstico em relação às variáveis didáticas a serem consideradas. O lócus da investigação passou a ser a 8ª série A (Escola C) e a 1ª série F (Escola D). Assim, nessas turmas, aplicamos o instrumento diagnóstico definitivo (Anexo 2) e realizamos as entrevistas.
A fundamentação teórica nos serviu de base para a definição dos critérios de seleção das frações aplicadas aos alunos.
3.5 Instrumento Diagnóstico
Frações Arit m ét icas
Primeira Questão:
Ligue por meio de flechas cada fração da coluna 1 com as frações que lhe são correspondentes na coluna 2, se existir:
Coluna 1 Coluna 2
A) 4 . 5 . 7 5 . 3 . 7 6 11 28 21 B) 3 . 5 . 12 5 . 6 . 11 5 . 12 5 . 2 . 11 4 3 C) 15 . 4 5 . 32 36 66 8 3 4 . 5 5 . 3 3 . 5 . 2 5 . 11 Análise Preliminar:
As correspondências são:
4 . 5 . 7 5 . 3 . 7
(coluna 1) com as frações 28 21 , 4 3 e 4 . 5 5 . 3 (coluna 2); 3 . 5 . 12 5 . 6 . 11
15 . 4
5 . 32
não se corresponde com nenhuma fração da coluna 2.
Esperamos, com essas questões, verificar se os alunos reconhecem que, além do processo calculatório, existe, também, a possibilidade de se efetuar uma outra operação para se obter as possíveis correspondências, isto é, o “cancelamento de fatores comuns” ao numerador e denominador de uma dada fração.
Esperamos, ainda, verificar se os alunos identificam se essas correspondências indicam a equivalência entre frações.
Segunda Questão:
O resultado da simplificação da fração 12 . 4
8 . 6 . 3
é 3 e da 10 . 16
32 . 2 . 5
é 2; explique, em
cada um dos casos, duas maneiras distintas de se obter tal resultado.
Análise Preliminar:
Nessa questão, as duas maneiras distintas exigidas pelo enunciado podiam apenas ser obtidas pelo cancelamento de fatores comuns ao numerador e denominador da fração envolvida.
Nesse sentido, esperamos verificar quais os alunos que utilizamapenas esse tipo de cancelamento e, por outro lado, constatar se usam, essencialmente, o processo computacional como uma das maneiras exigidas. Além disso, esperamos encontrar alunos que percebam só esse processo computacional.
Terceira Questão:
Sabendo-se que 1.155 é resultado de 3 . 5 . 7 . 11, responda:
b) Élio dividiu 1.155 por três desses fatores e encontrou como quociente 5. Élio dividiu 1.155 por __________.
c) Silvio dividiu 1.155 por todos esses fatores e encontrou como quociente 1. Silvio dividiu 1.155 por _________.
Explique como você chegou a esses resultados. Mostre seus cálculos.
Análise Preliminar:
As respostas referentes a essa questão seriam:
a) 3 e 7;
b) 3, 7 e 11 e
c) 3, 5, 7 e 11
Nosso objetivo, nessa questão, foi verificar se os alunos conseguiam identificar a escrita de um número natural como produto de dois ou mais números. Ou seja, se identificam a escrita 1.155 com 3.5.7.11, respondendo a questão rapidamente; ou, no caso contrário, quais os procedimentos que eles utilizam, e quais as dificuldades encontradas.
Quarta Questão:
Tomando como base o modelo abaixo, preencha as lacunas e explique seus cálculos em cada item:
Modelo: 16 = 2 (3+5) = 2 . 3 + 2 . 5
a) 45 = _____(2 + 7) = _____ . _____ + _____ . _____
b) 72 = 9 . (_____ + _____) = 9 . 3 + 9 . _____
c) 28 = 7 . (1 + _____) = _____ . _____ + _____ . _____
Análise Preliminar:
Observamos que a resposta correta de cada item seria:
a) 45 = 5 (2 + 7) = 5 . 2 + 5 + 7
b) 72 = 9 . (3 + 5) = 9 . 3 + 9 . 5
c) 28 = 7 . (1 + 3) = 7 . 1 + 7 . 3
d) 27 = 9 . (5 – 2) = 9 . 5 – 9 . 2
Esperamos verificar:
- se alunos identificam que o sinal de igual serve também para indicar expressões equivalentes; nesse caso, duas escritas equivalentes de um mesmo número natural;
- se os alunos conseguem reconhecer que, nessa questão, implicitamente, trabalha-se com a propriedade da fatoração por evidência e;
- conseqüentemente, se a propriedade distributiva é reconhecida e se aplicam-na corretamente.
Quinta Questão:
A fração
6 24 48 36− +
é equivalente a 6 – 8 + 4.
Explique como essa equivalência pode ser obtida. Descreva todo o seu raciocínio, justificando-o.
Análise Preliminar:
A resposta a essa questão pode ser dada pela:
- comparação dos resultados obtidos em ambas as expressões propostas, efetuando
as operações de adição e subtração envolvidas, quais sejam:
6 24 48 36− +
= 6 12
= 2 e 6
- utilização da propriedade da fatoração pela evidência do termo em comum na
expressão
6 24 48 36− +
; nesse caso, 6 8 4
6 ) 4 8 6 ( 6 6 24 48
36− + = − + = − + , ou;
- pela reescrita da fração
6 24 48 36− +
em outras três frações de mesmo
denominador; isto é: 6 8 4
6 24 6 48 6 36 6 24 48 36 + − = + − = + − .
Nosso objetivo foi o de verificar se os procedimentos utilizados pelos alunos na resolução dessa questão seriam: o de fatoração por evidência do termo comum (nesse caso, o máximo divisor comum); a reescrita da fração do enunciado ou o cálculo de cada uma deles; e uma posterior comparação dos resultados obtidos.
Frações algébricas
Primeira Questão:
Simplifique as frações abaixo:
Análise Preliminar: a) 2x
b) y
8 7
c) 14
5
d)
yz x
3
Nessa questão, esperamos verificar:
- se “aceitam” simplificar frações que: ora apresentam somente a variável simplificável, no caso o item c), ora só apresentam os coeficientes simplificáveis, como é o caso da fração dada no item d).
Além disso, nesse último item, procuramos também verificar a “aceitação” dos alunos frente a uma resposta que consiste em uma fração de denominador algébrico.
Segunda Questão:
Simplifique, se possível, as frações abaixo:
a)
x xy
x 11
4 +
b) 3 2 4
a a ab+
c)
z z
xy 3
8 −
d)
y b x
Análise Preliminar:
Nesta questão, as respostas são:
a) 4 + 11y
b)
a b a a
b 4 3 4
3 + = +
c) 8 −3
z xy
d)
y b x
11 3 17 +
Nossos objetivos foram os de:
- verificar a utilização da propriedade da fatoração por evidência do termo comum, no caso da fração do item a);
- verificar a reescrita das frações propostas em outras de mesmo denominador para, dessa forma, efetuarem as possíveis simplificações pelo cancelamento de fatores comuns ou;
- desconsiderando-se as duas hipóteses anteriores, se esses alunos irão proceder cancelando, correta ou incorretamente, os fatores comuns ao numerador e denominador das
frações propostas, por exemplo: y
x xy x
11 4 11 4
+ = +
, cancelamento da variável “x” de
forma correta ou,
x xy
x 11
4 +
para 4 + 11xy , cancelamento da variável “x” de forma
incorreta.
Objetivamos, ainda, verificar como os alunos procedem frente a uma fração que
não admite simplificação, como é o caso de
y b x
11 3 17 +
Terceira Questão:
Simplifique as frações abaixo:
a) 5 2.8
a a ab
b)
x xy x.11 4
c)
d c a
19 17 . 13
d)
z z xy .3 6
Análise Preliminar: Respostas da questão:
a) 40ab
b) 44xy
c)
d ac
19 221
d) 18xy
Nosso objetivo foi o de verificar se os alunos simplificam as frações propostas, utilizando-se da computação entre os fatores ou, ainda, se efetuam o cancelamento de fatores comuns do numerador com o denominador.
3.6 Condições de aplicação
Para a aplicação do instrumento, foram necessárias duas aulas de 45 minutos em cada classe.
desenvolvimento de um trabalho que visava trazer contribuições para o ensino e, conseqüentemente, para eles próprios. Para tanto, comentamos que o trabalho teria de ser o mais “válido” possível e, que iríamos nos restringir apenas à leitura dos enunciados das questões, e que as dúvidas surgidas não poderiam ser explicadas ou esclarecidas. É importante registrar que, na leitura dos enunciados de cada questão, foram realizadas todas as necessárias instruções orais.
Na aplicação da prova escrita, as turmas foram divididas: uma metade respondia às questões aritméticas e a outra, às algébricas; ao término da resolução havia a troca. Com isso, procuramos controlar a influência da resolução pelo aluno das questões de Aritmética sobre as de Álgebra e vice-versa.
Embora consciente de que as resoluções das frações algébricas relacionam-se às suas condições de existência, não nos preocupamos em alertar os alunos nas instruções orais. A intenção foi a de abordar as questões tal como aparecem nos livros didáticos e são trabalhadas em sala de aula, informações extraídas pela observação durante o período correspondente ao estágio de campo.
3.7 Entrevistas
As entrevistas foram realizadas fora do horário de aula, na própria escola e, ao final do período, num total de doze. Todas as entrevistas foram gravadas em fitas cassete e encontram-se transcritas nos anexos.
A seleção dos alunos para as entrevistas baseou-se criteriosamente naqueles que apresentaram diversos tipos de erros nas simplificações das frações, tanto aritméticas como algébricas e, eventualmente, em alguns alunos que apresentaram bom desempenho, com acerto de quase todas as questões propostas.
Segundo Lüdke e André (1986):
CAPÍTULO IV
ANÁLISE DOS RESULTADOS
Neste Capítulo, serão apresentados os procedimentos utilizados pelos alunos no instrumento diagnóstico aplicado, organizados em categorias baseadas na fundamentação teórica.
No instrumento diagnóstico sobre Aritmética, nossa principal preocupação foi, como se indicou no Capítulo III, a de obtermos informações não apenas sobre o acerto ou o erro da resposta dada pelo aluno, mas também sobre os procedimentos utilizados na simplificação das frações aritméticas.
A análise desses procedimentos pode nos fornecer elementos indicativos de um determinado modo de relação do aluno com a atividade de simplificação dessas frações, influenciadas pelas suas concepções sobre os elementos constituintes da simbologia aritmética e pelas práticas escolares que legitimam determinado procedimento em detrimento de outros.
No instrumento diagnóstico sobre as expressões algébricas, nos preocupamos com a identificação e agrupamento dos erros em categorias, uma vez que as questões exigiam apenas a tarefa de simplificação.
André (1995) considera que uma pesquisa, que se utiliza basicamente de dados quantitativos, não deixa de ter uma dimensão qualitativa desde que na análise dos dados esteja presente seu referencial teórico. A autora também observa que, reportar aos dados dos depoimentos, entrevistas ou observações aos números não faz com que o estudo realizado deixe de ser qualitativo, afirmando que os números obtidos ajudam a explicitar essa dimensão. Ao se proceder a análise dos dados obtidos nessa pesquisa nas dimensões quantitativa e qualitativa, compartilhamos com as posições defendidas pela autora.
respeito de uma escola pública, no que se refere especificamente à habilidade dos alunos em simplificar frações aritméticas e algébricas.
Para a confecção das tabelas, computamos o número de erros ou procedimentos efetuados por aluno em cada categoria considerada.
As tabelas construídas, com base nos dados colhidos pela correção das provas aplicadas nos alunos, são:
4.1 Análise Quantitativa
I N STRUM EN TO ARI TM ÉTI CO
Primeira Questão:
Ligue por meio de flechas cada fração da coluna 1 com as frações que lhe são correspondentes na coluna 2, se existir:
Coluna 1 Coluna 2
A) 4 . 5 . 7 5 . 3 . 7 6 11 28 21 B) 3 . 5 . 12 5 . 6 . 11 5 . 12 5 . 2 . 11 4 3 C) 15 . 4 5 . 32 36 66 8 3 4 . 5 5 . 3 3 . 5 . 2 5 . 11
Procedimentos Utilizados na Primeira Questão
Procedimento 1 – Identificação de todas as frações equivalentes
Procedimento 2 – Identificação parcial das frações equivalentes
O aluno nº 18 da 1ª F apresenta 36 66
como única fração equivalente a . 5 . 12
5 . 6 . 11
na
referida questão.
O aluno nº 21 da 8ªA apresentou como correspondente a 4 . 5 . 7
5 . 3 . 7
somente a fração 4 3 .
Procedimento 3 – Não identifica equivalência alguma entre as frações:
O aluno nº 13 da 8ª A não ligou fração alguma da coluna 1 com as da coluna 2.
O aluno nº 36 da 1ª F também não apresentou correspondência alguma entre as frações dessas colunas.
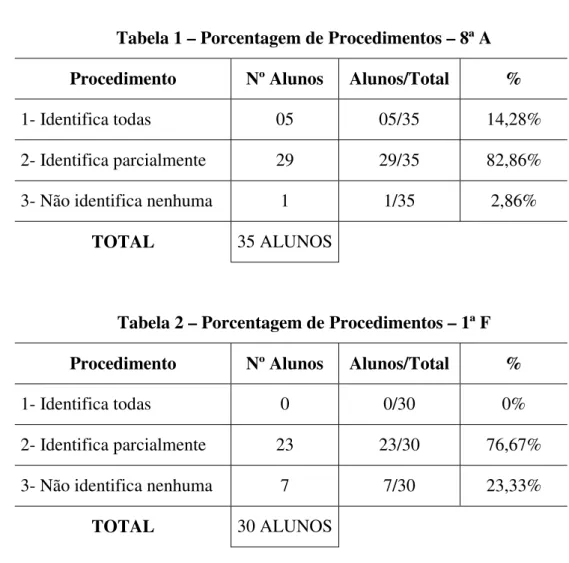
Tabela 1 – Porcentagem de Procedimentos – 8ª A Procedimento Nº Alunos Alunos/Total %
1- Identifica todas 05 05/35 14,28%
2- Identifica parcialmente 29 29/35 82,86%
3- Não identifica nenhuma 1 1/35 2,86%
TOTAL 35 ALUNOS
Tabela 2 – Porcentagem de Procedimentos – 1ª F Procedimento Nº Alunos Alunos/Total %
1- Identifica todas 0 0/30 0%
2- Identifica parcialmente 23 23/30 76,67%
3- Não identifica nenhuma 7 7/30 23,33%
Tabela 3 – Porcentagem do Total de Procedimentos – 8ª A e 1ª F Procedimento Nº Alunos Alunos/Total %
1- Identifica todas 5 5/65 7,69%
2- Identifica parcialmente 52 52/65 80%
3- Não identifica nenhuma 8 8/65 12,31%
TOTAL 65 ALUNOS
Observamos que:
Apenas 7,69% dessa população de alunos identificou todas as possíveis equivalências entre as frações propostas na questão; esses 7,69% incidem exclusivamente sobre a 8ª A;
A maior porcentagem de procedimentos utilizados pelos alunos corresponde à categoria de identificação parcial da equivalência entre essas frações, isto é, 80,0% do total de alunos;
Do total, 12,3% de alunos não identificaram nenhuma equivalência entre as frações das duas colunas;
O melhor desempenho, nessa questão, foi obtido pela 8ª A, considerando, sobretudo, que apenas 2,86% dessa turma não apresentou identificação de equivalência entre as frações dadas, enquanto que essa mesma porcentagem na 1ª F foi 23,33%, aproximadamente.
Procedimentos Utilizados na Segunda Questão Segunda Questão:
O resultado da simplificação da fração 12 . 4
8 . 6 . 3
é 3 e da 10 . 16
32 . 2 . 5
é 2; explique, em
cada um dos casos, duas maneiras distintas de se obter tal resultado.
Procedimento1 – Simplifica apenas pelo cálculo do quociente entre o
Os alunos nº 2 da 8ª A e nº 10 da 1ª F apresentaram como procedimento de
simplificação da fração 12 . 4 8 . 6 . 3
somente o correspondente ao quociente entre 48 144
, isto é,
3 1 3 3 9 6 18 12 36 24 72 48 144 = = = = = = .
Procedimento 2 – Simplifica dividindo numerador e denominador da
fração por fatores comuns.
Um exemplo é o procedimento apresentado pelo aluno 10 da 8ª A, que não determina o quociente entre o produto dos termos do numerador pelo denominador, ou seja, opera somente sobre os termos divisíveis dessa fração, então,
3 1 . 1 1 . 3 . 1 2 . 1 1 . 6 . 1 4 . 1 1 . 6 . 1 12 . 4 8 . 6 . 3 = = = = .
Procedimento 3 – Apresenta os dois procedimentos já citados, isto é,
simplifica pelo quociente do produto dos termos do numerador pelo produto dos termos do denominador e também simplifica pela divisibilidade dos termos
dessa fração.
Os alunos nº 12 e nº 16 da 8ª A apresentaram os dois procedimentos já citados.
Procedimento 4 – Não apresenta resolução.
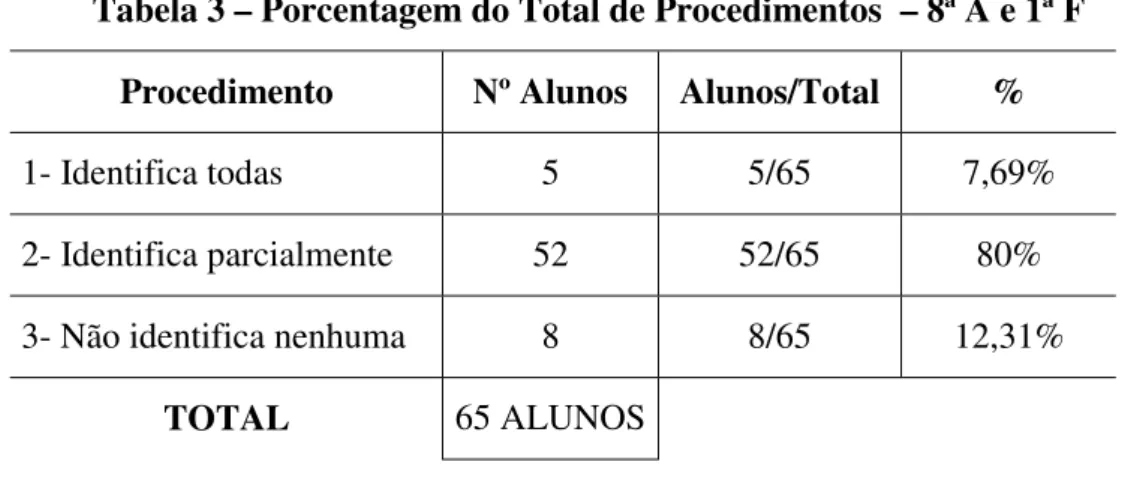
Tabela 4 – Porcentagem de Procedimentos – 8ª A Procedimento Nº Alunos Alunos/Total %
1- Simplifica quociente 17 17/35 48,57%
2- Simplifica pelos termos 2 2/35 5,71%
3- Quociente e termos 8 8/35 22,86%
4- Não apresenta resolução 8 8/35 22,86%
TOTAL 35 ALUNOS
Tabela 5 – Porcentagem de Procedimentos – 1ª F Procedimento Nº Alunos Alunos/Total %
1- Simplifica quociente 13 13/30 43,33%
2- Simplifica pelos termos 0 0/30 0,0%
3- Quociente e termos 6 6/30 20,0%
4- Não apresenta resolução 11 11/30 36,67%
TOTAL 30 ALUNOS
Tabela 6 – Porcentagem do Total de Procedimentos – 8ª A e 1ª F Procedimento Nº Alunos Alunos/Total %
1- Simplifica quociente 30 30/65 46,15%
2- Simplifica pelos termos 2 2/65 3,07%
3- Quociente e termos 14 14/65 21,54%
4- Não apresenta resolução 19 19/65 29,23%
Observamos que:
O procedimento privilegiado foi aquele em que os alunos calcularam o quociente entre os fatores do numerador pelos do denominador, sendo 46,15% do total dessa população.
A menor porcentagem referente aos procedimentos utilizados incidiu sobre o procedimento no qual os alunos simplificaram as frações pela divisibilidade apresentada pelos termos do numerador e denominador, correspondente a 3,07% do total, sendo que essa porcentagem na 1ª F correspondeu a 0,0%.
Dessa população selecionada para essa investigação, aproximadamente 30,0% de alunos não apresentaram procedimento algum.
Ainda, nesse caso, podemos dizer que os alunos da 8ª A apresentaram melhor desempenho que os da 1ª F.
Procedimentos utilizados na Terceira Questão Terceira Questão:
Sabendo-se que 1.155 é resultado de 3 . 5 . 7 . 11, responda:
a) João dividiu 1.155 por dois desses fatores e encontrou como quociente 55. João dividiu 1.155 por _________.
b) Élio dividiu 1.155 por três desses fatores e encontrou como quociente 5. Élio dividiu 1155 por __________.
c) Silvio dividiu 1.155 por todos esses fatores e encontrou como quociente 1. Silvio dividiu 1.155 por _________.
Explique como você chegou a esses resultados. Mostre seus cálculos.
Procedimento 1 – Escreve a fração correspondente à fração do enunciado,
na forma fatorada e a simplifica.
Procedimento 2 – Efetua diversas tentativas de divisão sobre o número
dado, nesse caso o número 1155, para determinar o divisor correspondente.
Os alunos nº 25 da 8ª A e nº 40 da 1ª F apresentaram esse procedimento, ou seja, efetuaram sucessivas divisões sobre o número 1.155 até encontrarem o quociente procurado.
Procedimento 3 – Não apresentaram resolução.
Os alunos que se enquadraram nesse procedimento foram os nºs 37 da 8ª A e 33 da 1ª F.
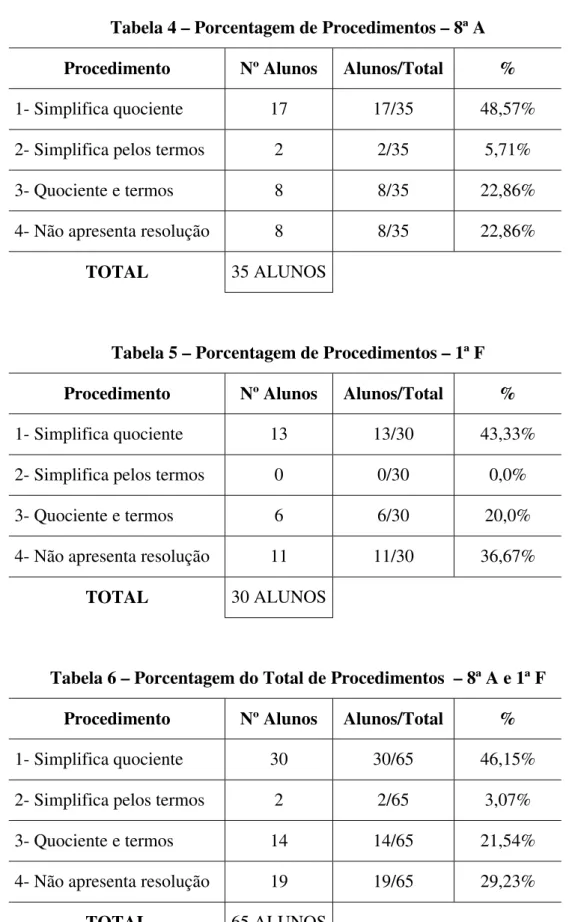
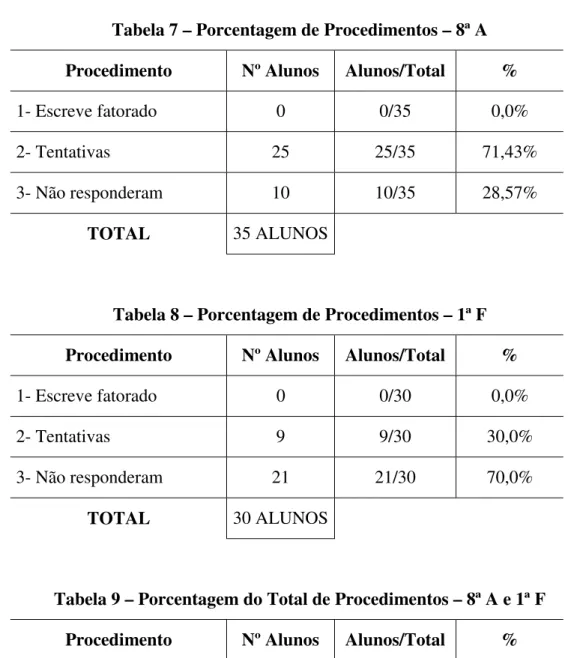
Tabela 7 – Porcentagem de Procedimentos – 8ª A Procedimento Nº Alunos Alunos/Total %
1- Escreve fatorado 0 0/35 0,0%
2- Tentativas 25 25/35 71,43%
3- Não responderam 10 10/35 28,57%
TOTAL 35 ALUNOS
Tabela 8 – Porcentagem de Procedimentos – 1ª F Procedimento Nº Alunos Alunos/Total %
1- Escreve fatorado 0 0/30 0,0%
2- Tentativas 9 9/30 30,0%
3- Não responderam 21 21/30 70,0%
TOTAL 30 ALUNOS
1- Escreve fatorado 0 0/65 0,0%
2- Tentativas 34 34/65 52,31%
3- Não responderam 31 31/65 47,69%
TOTAL 65 ALUNOS
Observamos que:
Nenhum aluno das duas turmas utilizou-se do procedimento de escrita da fração correspondente na forma fatorada e sua posterior simplificação.
52,31% de toda essa população utilizou-se do procedimento que envolveu tentativas de divisão do número dado para encontrar o divisor procurado.
47,69% do total de alunos investigados e 70,0% da turma da 1ª F não apresentaram resolução, o que indica uma porcentagem significativa.
A turma de alunos da 8ª A apresentou melhor desempenho que a da 1ª F, considerando-se que apenas 28,57% de alunos da 8ª A não apresentaram resolução e, em relação ao procedimento 2, a 1ª F apresentou 30,0%, enquanto a 8ª A, 71,43%.
Procedimentos utilizados na Quarta Questão Quarta Questão:
Tomando como base o modelo abaixo, preencha as lacunas e explique seus cálculos em cada item:
Modelo: 16 = 2 (3+5) = 2 . 3 + 2 . 5
a) 45 = _____(2 + 7) = _____ . _____ + _____ . _____
b) 72 = 9 . (_____ + _____) = 9 . 3 + 9 . _____
c) 28 = 7 . (1 + _____) = _____ . _____ + _____ . _____
d) 27 = 9 . (_____ - 2) = _____ . _____ - _____ . _____
O aluno nº 3 da 8ª A completou corretamente os espaços em branco de todos os itens dessa questão.
O aluno nº 7 da 1ª F também apresentou o mesmo procedimento.
Procedimento 2 – Não identificou a distributividade somente no caso que envolve a diferença entre os termos que estão entre parênteses.
Os alunos nº 38 da 8ª A e nº 6 da 1ª F somente erraram nesse item, isto é, não acertaram no item que apresentava distributividade na diferença.
Procedimento 3 – Não apresentou resolução.
Os alunos nº 29 da 8ª A e nº 32 da 1ª F não completaram os espaços de todos os itens.
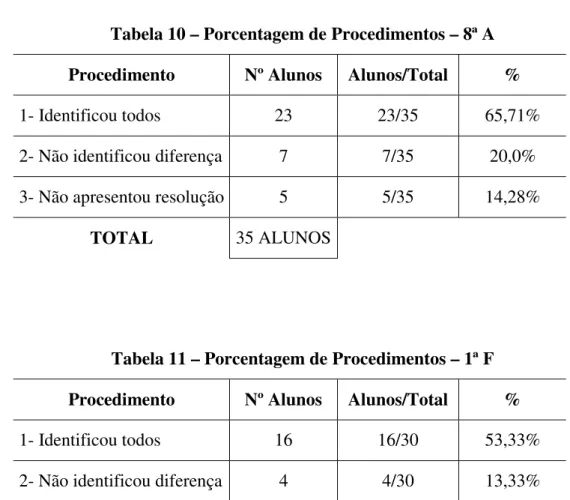
Tabela 10 – Porcentagem de Procedimentos – 8ª A Procedimento Nº Alunos Alunos/Total %
1- Identificou todos 23 23/35 65,71%
2- Não identificou diferença 7 7/35 20,0%
3- Não apresentou resolução 5 5/35 14,28%
TOTAL 35 ALUNOS
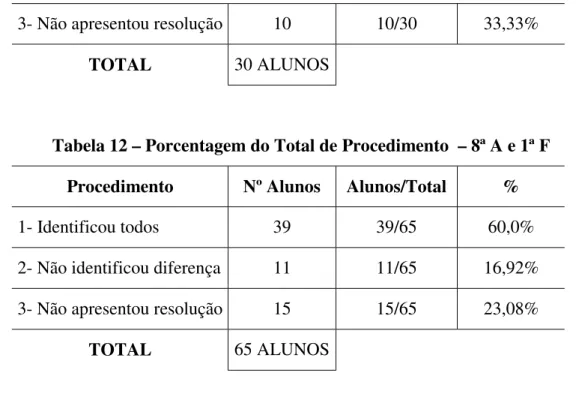
Tabela 11 – Porcentagem de Procedimentos – 1ª F Procedimento Nº Alunos Alunos/Total %
1- Identificou todos 16 16/30 53,33%
3- Não apresentou resolução 10 10/30 33,33%
TOTAL 30 ALUNOS
Tabela 12 – Porcentagem do Total de Procedimento – 8ª A e 1ª F Procedimento Nº Alunos Alunos/Total %
1- Identificou todos 39 39/65 60,0%
2- Não identificou diferença 11 11/65 16,92%
3- Não apresentou resolução 15 15/65 23,08%
TOTAL 65 ALUNOS
Observamos que:
Cerca de 60,0% dos alunos obtiveram acertos em todos os itens dessa questão, sendo que esses acertos foram mais acentuados na turma da 8ª A.
Cerca de 17,0% de alunos apresentaram erros, especificamente, no item d) dessa questão, que envolvia a distributividade em relação à diferença entre dois termos dentro dos parênteses.
Aproximadamente 23,08% dos alunos investigados não apresentaram proce-dimento algum nessa questão; o maior índice incidiu sobre a turma 1ª F, com 33,32%.
Observamos, novamente, que o melhor desempenho foi obtido pela 8ª A.
Procedimentos utilizados na Quinta Questão
Quinta Questão:
A fração
6 24 48 36− +
é equivalente a 6 – 8 + 4.
Procedimento 1 – Reescreve a fração dada indicando separadamente o quociente de cada termo do numerador pelo termo do denominador.
Os alunos nº 17 da 8ª A e nº 10 da 1ª F reescreveram
6 24 48 36− +
como
6 24 6 48 6
36− +
.
Procedimento 2 – Cálculo do quociente da soma dos termos do
numerador pelo termo do denominador e comparação dos resultados obtidos entre as expressões do primeiro e segundo termos do enunciado.
Os alunos nº 15 da 8ª A e nº 39 da 1ª F, assim, procederam:
6 24 48 36− +
=
2 6 12 6
48
60− = = e depois compararam com o resultado de 6 – 8 + 4.
Procedimento 3 – Não apresentaram resolução.
Os alunos nº 33 da 8ª A e nº 38 da 1ª F não apresentaram nenhum procedimento nessa questão.
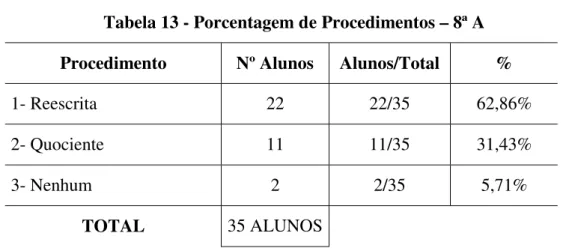
Tabela 13 - Porcentagem de Procedimentos – 8ª A Procedimento Nº Alunos Alunos/Total %
1- Reescrita 22 22/35 62,86%
2- Quociente 11 11/35 31,43%
3- Nenhum 2 2/35 5,71%
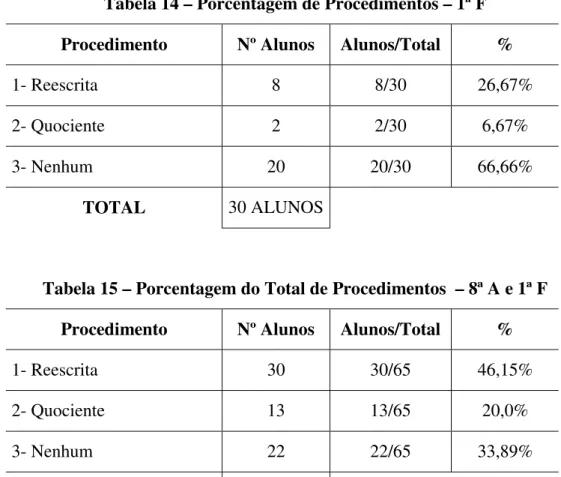
Tabela 14 – Porcentagem de Procedimentos – 1ª F Procedimento Nº Alunos Alunos/Total %
1- Reescrita 8 8/30 26,67%
2- Quociente 2 2/30 6,67%
3- Nenhum 20 20/30 66,66%
TOTAL 30 ALUNOS
Tabela 15 – Porcentagem do Total de Procedimentos – 8ª A e 1ª F Procedimento Nº Alunos Alunos/Total %
1- Reescrita 30 30/65 46,15%
2- Quociente 13 13/65 20,0%
3- Nenhum 22 22/65 33,89%
TOTAL 65 ALUNOS
Observamos que:
A maior porcentagem de procedimentos utilizados incidiu sobre aqueles que reescreveram a fração proposta na questão, ou seja, sobre o Procedimento 1, com 46,15%.
O procedimento correspondente ao cálculo do quociente da soma dos termos do numerador pelo termo do denominador apresentou a menor porcentagem, 20,0% do total de alunos.
Houve uma grande discrepância entre as turmas quanto a porcentagem de alunos que não apresentaram resolução, sendo apenas 5,71% na 8ª A e 66,66% na 1ª F.
Mais uma vez, a 8 ªA mostrou melhor desempenho que a turma da 1ª F.