DEPARTAMENTO DE F´ISICA
PROGRAMA DE P ´OS-GRADUAC¸ ˜AO EM F´ISICA
VICTOR NOCRATO MOURA
TEORIA DE GINZBURG-LANDAU COM PAR ˆAMETRO DE ORDEM
ESCONDIDO APLICADA AO ESTUDO DA SUPERCONDUTIVIDADE DE INTERFACE
TEORIA DE GINZBURG-LANDAU COM PAR ˆAMETRO DE ORDEM ESCONDIDO APLICADA AO ESTUDO DA SUPERCONDUTIVIDADE DE INTERFACE
Disserta¸c˜ao de Mestrado apresentada ao Pro-grama de P´os-Gradua¸c˜ao em F´ısica da Uni-versidade Federal do Cear´a, como requisito parcial para a obten¸c˜ao do T´ıtulo de Mes-tre em F´ısica. ´Area de Concentra¸c˜ao: F´ısica da Mat´eria Condensada.
Orientador: Prof. Dr. Andrey Chaves.
Universidade Federal do Ceará (UFC)
Universidade da Integração lntemacional da Lusofouia Afro-Braileira Dr. João Milton Pereira Júnior
Universidade Federal do Ceará (UFC)
GTNTLAB)
TEORIA DE GINZBURG-LANDAU COM PARÂMETRO DE ORDEM ESCONDIDO
APLICADA AO ESTUDO DA SUPERCONDUTIVIDADE DE INTERFACE
Dissertação
de
Mestrado
apresentada ao Programade
Pós-Graduaçãoerl
Física daUniversidade Federal do Ceará, como requisito
parcial paÍa a obtenção do TítLrlo de Mestre ent Física. Area de Concentração: Física da Matéria Condensada.
Aprovada
em
21 I 0212017Gerada automaticamente pelo módulo Catalog, mediante os dados fornecidos pelo(a) autor(a)
M889t Moura, Victor Nocrato.
Teoria de Ginzburg-Landau com parâmetro de ordem escondido aplicado ao estudo da supercondutividade de interface / Victor Nocrato Moura. – 2017.
92 f. : il. color.
Dissertação (mestrado) – Universidade Federal do Ceará, Centro de Ciências, Programa de Pós-Graduação em Física, Fortaleza, 2017.
Orientação: Prof. Dr. Andrey Chaves.
Aos meus pais, Jo˜ao Carlos e Suzete dos Santos, pelo carinho e apoio incondi-cional. Aos meus irm˜aos Mariana e Tiago.
Ao Prof. Dr. Andrey Chaves pela orienta¸c˜ao, disponibilidade e acredidar no trabalho desenvolvido.
A todos os amigos do Departamento de F´ısica da UFC, em especial a Wagner Sena, Daniel Linhares, Pedro Henrique, Laura Barth, Duarte Jos´e, Gabriel Oliveira, Luan Vieira, Ravenna Rodrigues e Icaro Rodrigues.
Aos todos os professores do Departamento de F´ısica que contribuiram para minha forma¸c˜ao.
Nos ´ultimos anos foram reportados diversos experimentos em que a supercondutividade de interface foi observada em heteroestruturas de diferentes materiais, inclusive em n˜ao-supercondutores a priori. A origem dessa supercondutividade ainda n˜ao foi elucidada e n˜ao existe uma teoria bem estabelecida para explicar esse fenˆomeno. Em 2015 foi pro-posto um modelo com base na teoria de Ginzburg-Landau que explicaria o fenˆomeno de supercondutividade de interface assumindo um sistema com dois parˆametros de ordem. Foi proposto que o parˆametro de ordem que caracteriza o materialbulk com uma camada defeituosa, ou dopada, permite a forma¸c˜ao de um segundo parˆametro que compete com o primeiro e prevalece sobre ele nas proximidades da interface. A supercondutividade na interface ´e ent˜ao explicada pelo crescimento deste segundo parˆametro de ordem apenas nesta regi˜ao, permancecendo ainda “escondido”dentro do bulk. O modelo foi aplicado para um sistema unidimensional com uma interface, apresentando um resultado surpre-endente: a supercondutividade escondida aparece em temperaturas cr´ıticas quantizadas, podendo ent˜ao existir v´arios autoestados do sistema, com diferentes temperaturas cr´ıticas. Nessa disserta¸c˜ao utilizamos esse modelo e investigamos os desdobramentos da super-condutividade escondida e suas temperaturas quantizadas. Percebemos que as interfaces assemelham-se com po¸cos quˆanticos unidimensionais, com a temperatura cr´ıtica fazendo o an´alogo ao da energia no caso quˆantico. Seguindo essa ideia utilizamos m´etodos num´ericos para resolver as equa¸c˜oes de Ginzburg-Landau para um sistema com um n´umero arbitr´ario de interface paralelas. Nossos resultados mostram que neste caso, as temperaturas cr´ıticas, al´em de quantizadas, s˜ao degeneradas quando as interfaces est˜ao muito separadas, mas tem essa degenerescˆencia quebrada quando aproximamos as interfaces, como ocorre em uma rede de po¸cos quadrados. Propusemos ent˜ao um modelo tipo tight-binding para estimar temperaturas cr´ıticas em interfaces paralelas e verificamos a validade dessa apro-xima¸c˜ao atrav´es da solu¸c˜ao num´erica do problema completo. Analisamos tamb´em os estados de v´ortices para um defeito bidimensional quadrado, verificando a possibilidade de se criar ou destruir v´ortices na regi˜ao de supercondutividade escondida atrav´es de um campo magn´etico externo.
In recent years, several experiments have been reported in which interface super-conductivity was observed in heterostructures of different materials, inclunding non-superconductors. The origin of this superconductivity has not yet been elucidated and there is no well-established theory to explain this phenomenon. In 2015 a model based on the Ginzburg-Landau theory was proposed that would explain the interface superconduc-tivity phenomenon assuming a system with two order parameters. It has been proposed that the order parameter characterizing the bulk material with a defective or doped layer permits the formation of a second parameter which competes with the former and pre-vails over it in the vicinity of the interface. The superconductivity at the interface is then explained by the growth of this second order parameter only in this region, remaining still “hidden”inside the bulk. The model was applied to a one-dimensional system with an interface, which presented a surprising result: the “hidden”superconductivity appers in quantized critical temperatures, this allowing the existence of several eigenstates of the system, with different critical temperatures. In this dissertation, we use this model and investigate the unfolding of hidden superconductivity and its quantized temperatu-res. We observe that the interfaces resemble one-dimensional quantum wells, with the critical temperature playing the role of the energy in the quantum case. Following this idea we use numerical methods to solve the Ginzburg-Landau equations for a system with an arbitrary number of parallel interfaces. Our results show that in this case, the critical temperatures are quantized and degenerate when the interfaces are very separated, but it has its degeneracy broken when we approach the interfaces, as it happens in a lattice of square wells. We then proposed a tight-binding model to estimate critical temperatures on parallel interfaces and verified the validity of this approximation through the nume-rical solution of the complete problem. We also analyze the vortex states for a square two-dimensional defect, verifying the possibility of creating or destroying vortices in the region of “ hidden”superconductivity through an external magnetic field.
Figura 1 – Evolu¸c˜ao da temperatura cr´ıtica de supercondutores . . . 12
Figura 2 – Experimento de H. K. Onnes . . . 13
Figura 3 – Efeito Meissner-Ochsenfeld . . . 14
Figura 4 – Representa¸c˜ao do gap na teoria BCS . . . 17
Figura 5 – Compara¸c˜ao entre supercondutores tipo-I e tipo-II . . . 18
Figura 6 – Supercondutividade de YBCO . . . 19
Figura 7 – Gr´afico de supercondutividade em ´oxidos . . . 20
Figura 8 – Solenoide . . . 23
Figura 9 – Diagrama de fase para supercondutores tipo-I e tipo-II . . . 25
Figura 10 –Energia livre . . . 28
Figura 11 –Parˆametro de ordem em fun¸c˜ao da temperatura . . . 29
Figura 12 –Comprimento de coerˆencia . . . 32
Figura 13 –Campo magn´etico na interface de um supercondutor . . . 34
Figura 14 –Anel supercondutor . . . 36
Figura 15 –M´ınimos de energia em fun¸c˜ao do quantum de fluxo . . . 38
Figura 16 –Rede de v´ortices de Abrikosov . . . 43
Figura 17 –Primeira observa¸c˜ao da rede de Abrikosov . . . 43
Figura 18 –Esquema de um sistema que apresenta supercondutividade de interface . 46 Figura 19 –Solu¸c˜oes da equa¸c˜ao hipergeom´etrica para sistema com interface unidi-mensional . . . 49
Figura 20 –Discretiza¸c˜ao do espa¸co . . . 52
Figura 21 –Degenerescˆencia da energia em fun¸c˜ao de um parˆametro dehopping . . . 54
Figura 22 –Rede discreta bidimensional . . . 55
Figura 23 –Parˆametro de ordemW normalizado . . . 60
Figura 24 –Parˆametros de ordem ∆n normalizados . . . 61
Figura 25 –Parˆametros de ordem W e ∆n normalizados . . . 63
Figura 26 –Energia em fun¸c˜ao da distˆancia para duas interfaces . . . 64
Figura 27 –Hopping em fun¸c˜ao da distˆancia . . . 65
Figura 28 –Parˆametro de ordemW normalizado para trˆes interfaces . . . 67
Figura 29 –Estado fundamental do parˆametro de ordem ∆n normalizado para trˆes interfaces . . . 68
interfaces . . . 71
Figura 33 –Autovalores em fun¸c˜ao da distˆancia para quatro interfaces . . . 72
Figura 34 –Diagrama de fases para um sistema com defeito ocupando 20% . . . 75
Figura 35 –Diagrama de fases para um sistema com defeito ocupando 15% . . . 76
Figura 36 –Estado de v´ortices para 20% . . . 78
Figura 37 –Estado de v´ortices para 20% . . . 79
Figura 38 –Metaestados do parˆametro de ordem ∆ para 20% . . . 80
ABNT Associa¸c˜ao Brasileira de Normas T´ecnicas
CNPq Conselho Nacional de Desenvolvimento Cient´ıfico e Tecnol´ogico BCS Bardeen-Cooper-Schrieffer
1 INTRODUC¸ ˜AO . . . 12
1.1 Supercondutividade: Hist´oria . . . 13
1.2 Supercondutividade de interface e novas descobertas . . . 20
2 TEORIA GINZBURG-LANDAU . . . 22
2.1 Energia de condensa¸c˜ao . . . 23
2.2 Teoria de Ginzburg-Landau no bulk . . . . 26
2.3 Teoria de GL em sistemas n˜ao-homogˆeneos e em campo magn´etico 29 2.4 Equa¸c˜oes de Ginzburg-Landau . . . 30
2.4.1 Primeira equa¸c˜ao de GL . . . 30
2.4.2 Segunda equa¸c˜ao de GL . . . 31
2.5 Superf´ıcies em supercondutores e comprimentos caracter´ısticos 32 2.6 Estado de v´ortices . . . 35
2.6.1 Quantiza¸c˜ao do fluxo . . . 36
2.6.2 Rede de Abrikosov . . . 38
3 PAR ˆAMETRO ESCONDIDO COMO FONTE DA SUPER-CONDUTIVIDADE ESCONDIDA . . . 44
3.1 Introdu¸c˜ao . . . 44
3.2 Energia livre e equa¸c˜oes de GL . . . 44
3.3 Interface . . . 45
4 MODELAGEM E M´ETODOS NUM´ERICOS . . . 51
4.1 Caso unidimensional . . . 51
4.2 Caso bidimensional . . . 54
5 DEGENERESCˆENCIA DAS TEMPERATURAS CR´ıTICAS QUANTIZADAS . . . 59
5.1 M´ultiplas interfaces . . . 62
6 ESTADOS DE V ´ORTICES . . . 74
7 CONCLUS ˜AO E PERSPECTIVAS . . . 83
APˆENDICE A -- EQUAC¸ ˜AO DE GINZBURG-LANDAU ADI-MENSIONAL . . . 85
1 INTRODUC¸ ˜AO
A supercondutividade vem sendo estudada h´a mais de 100 anos, desde que foi descoberta por Heike Kamerlingh Onnes em 1911 [1]. Muitos experimentos foram realizados e teorias desenvolvidas durante este tempo.
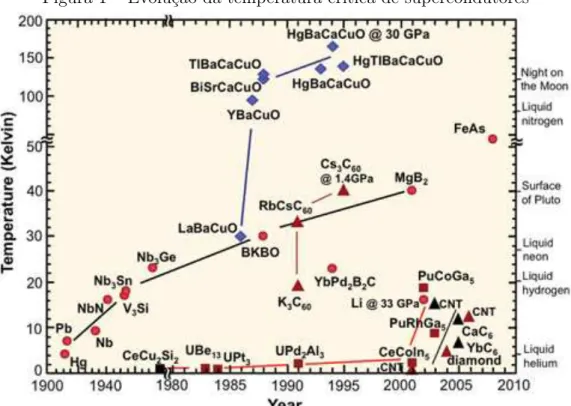
Figura 1 – Evolu¸c˜ao da temperatura cr´ıtica de supercondutores
Fonte: Fig. retirado de [2]. Temperaturas cr´ıticas de diversos materiais e o ano de sua des-coberta. O recorde atual pertence ao HgBaCaCuO com 150K, a uma press˜ao de 30GPa. A maior temperatura cr´ıtica a press˜ao atmosf´erica ´e do HgTIBaCaCuO com temperatura pr´oxima a 140K.
1.1 Supercondutividade: Hist´oria
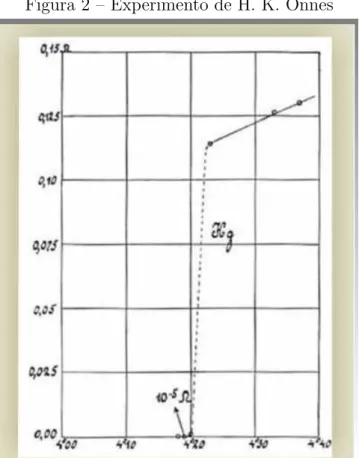
A supercondutividade foi descoberta em 1911 por Heike K. Onnes [1] em Lei-den, Holanda, trˆes anos ap´os ele conseguir liquefazer o h´elio. Em seu trabalho, H. K. Onnes resfriou diferentes metais at´e temperaturas de 1.8 K. Usando merc´urio como teste, Onnes diminuiu a temperatura abaixo da temperatura de liquefa¸c˜ao do h´elio e gradativa-mente a aumentava. Ele ent˜ao registrou em seu caderno de anota¸c˜oes: “A 4 K, nenhum aumento apreci´avel na resistˆencia”. A resistˆencia detectada foi de 10−5 Ω, menor valor que seu maquin´ario conseguia detectar.
Figura 2 – Experimento de H. K. Onnes
Fonte: Figura retirada de [1]. Resistˆencia (Ω) como fun¸c˜ao da temperatura (Kelvin) do merc´urio. O experimento mostra a transi¸c˜ao para supercondutor a 4.2K.
Heike K. Onnes, ap´os a descoberta da supercondutividade, concentrou-se na pergunta: Qu˜ao pequena ´e a resistˆencia residual no estado supercondutor? Ele ent˜ao pro-jetou um experimento que media o tempo de decaimento de uma corrente magneticamente induzida em um anel supercondutor. As correntes persistentes, como foram chamadas, n˜ao apresentaram qualquer sinal de decaimento, sendo essa observa¸c˜ao a prova que a super-condutividade era um novo fenˆomeno [1]. Experimentos atuais j´a observaram correntes, uma vez ajustadas, flu´ırem sem qualquer decaimento por um ano e as menores estimativas mostram que elas possuem um tempo de decaimento de 105 anos [10]. Assim, a perfeita condutividade ´e a primeira e mais tradicional caracter´ıstica de um supercondutor.
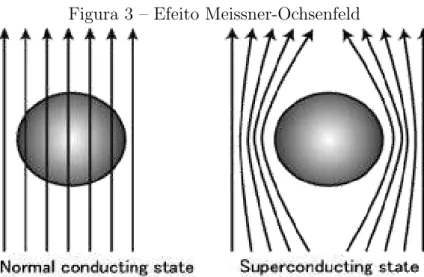
A segunda caracter´ıstica de um supercondutor ´e o perfeito diamagnetismo descoberto em 1933 por W. Meissner e R. Ochsenfeld [11]. O campo magn´etico n˜ao entra em um supercondutor massivo (j´a que o campo penetra a uma distˆancia finita, aproximadamente 500˚A), o que pode ser explicado pela condutividade perfeita. O mais interessante, por´em, ´e que o campo ´e expelido quando o material ´e resfriado abaixo da temperatura cr´ıtica. Esse efeito n˜ao pode ser explicado somente pela condutividade perfeita, que tende a confinar o campo no interior da amostra.
Figura 3 – Efeito Meissner-Ochsenfeld
Fonte: Figura retirada de [12]. Diagrama esquem´atico da exclus˜ao do campo magn´etico em um supercondutor massivo.
A existˆencia de um efeito Meissner revers´ıvel implica que a supercondutivi-dade pode ser destru´ıda por um campo magn´etico cr´ıticoHc. A dependˆencia do campo magn´etico cr´ıticoHc(T) com a temperatura foi empiricamente encontrada e ´e bem apro-ximada por uma lei parab´olica [10]:
Hc(T)≈Hc(0)
"
1−
T Tc
2#
. (1.1)
em alguns destes sistemas, onde h´a cria¸c˜ao de v´ortices de Abrikosov [13].
A descri¸c˜ao das duas propriedades b´asicas foi bem desenvolvida em 1935 por F. e H. London [14], que propuseram mudar a lei de Ohm por uma “equa¸c˜ao de acelera¸c˜ao”da forma:
Λ ˙Js=E, (1.2)
onde Λ ´e um parˆametro fenomenol´ogico com valor: Λ = m
ne2. (1.3)
A equa¸c˜ao 1.2 descreve a condutividade perfeita, j´a que qualquer campo el´etrico acelera os el´etrons supercondutores ao inv´es de apenas sustentar a velocidade contra a resistˆencia do material, como ´e descrito na lei de Ohm para um condutor normal. Por de-fini¸c˜ao, o parˆametro Λ deve ser positivo. Como consequˆencia, correntes estacionarias s˜ao poss´ıveis quando o campo el´etrico ´e zero. Utilizando a “equa¸c˜ao da acelera¸c˜ao”´e poss´ıvel encontrar a equa¸c˜ao que descreve o efeito Meissner. Aplicar o rotacional na eq. 1.2 e utilizar as equa¸c˜oes de Maxwell nos leva a:
∇2H= H
λ2; (1.4)
λ2 = Λc2
4π . (1.5)
A solu¸c˜ao da eq. 1.4 mostra que o campo magn´etico decai exponencialmente no interior do supercondutor com comprimento de penetra¸c˜aoλ, o que ´e visto como consequˆencia, o efeito Meissner.
Na d´ecada de 1950 ocorreram importantes contribui¸c˜oes para a supercondu-tividade, sendo duas as mais importantes; a teoria fenomenol´ogica de Ginzburg-Landau (GL) e a teoria microsc´opica de Bardeen-Cooper-Schrieffer (BCS).
Seguindo a linha fenomenol´ogica, Ginzburg e Landau publicaram sua teoria em 1950 [15], e nela introduziram uma pseudo-fun¸c˜ao de onda complexa Ψ como um parˆametro de ordem na teoria geral de transi¸c˜oes de fase de segunda ordem de Landau. Em seu discurso de aceita¸c˜ao do Prˆemio Nobel de F´ısica, Ginzburg explica a necessidade de generalizar a teoria dos irm˜aos London. O trabalho de Ginzburg desenvolvido em 1944 [15] mostra que a teoria de London n˜ao ´e aplic´avel para campos magn´eticos intensos, pr´oximo ao campo magn´etico cr´ıticoHc.
Como usaremos essa teoria como base para essa disserta¸c˜ao a discutiremos em maiores detalhes nos cap´ıtulos subsequentes.
em 1953. Em seu artigo, publicado naProceedings of the Royal Society Aem 1953, Pippard introduz o comprimento de coerˆencia enquanto prop˜oe uma generaliza¸c˜ao da equa¸c˜ao de London (1.2). Pippard argumentou que a fun¸c˜ao de onda supercondutora deveria possuir uma dimens˜ao caracter´ısticaξ0 que poderia ser estimado pelo argumento de princ´ıpio de incerteza: Somente el´etrons com energia a∼kTc de distˆancia da energia de Fermi podem ter um papel apreci´avel em um fenˆomeno que ocorre em Tc e esses el´etrons possuem momento na ordem ∆p≈kTc/vF, onde vF ´e a velocidade de Fermi. Assim:
∆x≥¯h/∆p≈¯hvF/kTc,
definindo o comprimento caracter´ıstico: ξ0 =a
¯ hvF kTc
(1.6) onde a´e uma constante a ser determinada [10].
Pippard descobriu que poderia reproduzir os dados experimentais do estanho e do alum´ınio com um ´unico valor de a = 0.15 na eq. 1.6. A teoria de BCS confirma os resultados de Pippard com a constantea= 0.18.
As pesquisas experimentais foram direcionadas para estabelecer que em super-condutores existia um gap de energia da ordem de kTc entre o estado fundamental e as quasi-part´ıculas excitadas do sistema. Esse conceito foi sugerido inicialmente em 1946 por Daunt e Mendelssohn [17] em seu artigoAn Experiment on the Mechanism of Super-conductivity, no qual sugerem que o supercondutor pode ser caracterizado por um gap no espectro de energia. Por´em, a primeira evidˆencia experimental ocorreu em 1954, onde Corak et al. [18, 19] realizaram medidas precisas do calor espec´ıfico de supercondutores. Suas medi¸c˜oes mostraram que bem abaixo da temperatura critica Tc o calor especifico eletrˆonico possui uma forte dependˆencia exponencial do tipo:
Ces ≈γTcae −bTc
T , (1.7)
onde o calor especifico eletrˆonico do estado normal ´e Cen = γT e a e b s˜ao constantes num´ericas.
Em 1957, R. E. Glover e M. Tinkham publicaram seus resultados de medidas de transmiss˜ao em supercondutores finos [20]. Utilizando frequˆencias na faixa de far infrared e micro-ondas em amostras de chumbo e cobre, eles mostram que para T = 0 existia umgap de aproximadamente 3kTc entre o estado fundamental e as quasi-part´ıculas excitadas, a fig. 4 ilustra o essegap.
London e Ginzburg-Landau, generaliza¸c˜oes, eletrodinˆamica n˜ao-localizada de Pippard e resultados experimentais que mostram existir umgap para as part´ıculas. Por´em, n˜ao che-gamos a descrever microscopicamente um supercondutor, o que realmente est´a por tr´as da supercondutividade. Isso ocorre no mesmo ano das publica¸c˜oes de R. E. Glover e M. Tinkham. No artigo Theory of Superconductivity [21], Bardeen, Cooper e Schrieffer de-mostram que, mesmo uma intera¸c˜ao muito fraca entre el´etrons, causada por uma intera¸c˜ao de segunda ordem el´etron-phonon, causam a forma¸c˜ao de pares ligados de el´etrons com momentos e spins iguais e contr´arios, que s˜ao chamados de pares de Cooper. De forma simplista, os pares deCooper s˜ao os portadores de cargas supercondutoras previstas nas teorias fenomenol´ogicas.
Figura 4 – Representa¸c˜ao do gap na teoria BCS
Fonte: Figura retirada de [22]. Gapde energia 2∆ da teoria BCS visualizado na densidade de estados como fun¸c˜ao da energia. O gap sempre est´a em torno da energia de Fermi e diferentemente de um isolante ou semicondutor, sempre existe a possibilidade de condu¸c˜ao.
A teoria microsc´opica permitiu prever diversos resultados para os supercon-dutores, sendo um dos principais a existˆencia de uma energia m´ınima, que abaixo da temperatura cr´ıtica Tc a densidade de estados dos el´etrons adquire um pequeno gap se-parando os estados ocupados e n˜ao ocupados.
g(ǫ) = 2∆ = 3.528kTc (1.8)
Confirmando os valores encontrados por Glover e Tinkam. Ap´os a teoria BCS (Bardeen, Cooper, Schrieffer) diversos trabalhos experimentais para o valor dogap 2∆ foram reali-zados; dentre os mais importante foram os com espectrˆometro de tunelamento eletrˆonico, que mostram diretamente que o gap aparece devido a um acoplamento el´etron-phonon.
sendo este diretamente relacionado `a fun¸c˜ao de onda dos pares de Cooper e proporcional ao parˆametro degap ∆.
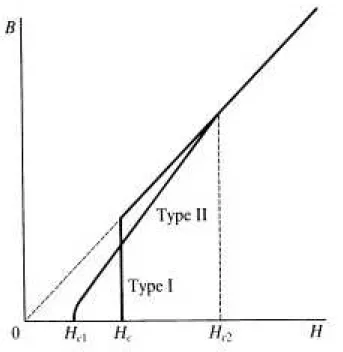
Devido `a grande popularidade e importˆancia da teoria BCS, outro trabalho de igual importˆancia foi quase deixado de lado em 1957. O artigo: The magnetic properties of superconducting alloys de A. A. Abrikosov investiga o que aconteceria na teoria de Ginzburg-Landau se o comprimento de coerˆencia ξ fosse pequeno, isto ´e, seξ < λ. Para materiais em que isso ocorre, a quebra de supercondutividade pelo campo magn´etico ´e uma transi¸c˜ao suave, com fluxo magn´etico entrando no supercondutor a partir de um campo cr´ıtico Hc1 e at´e um campo cr´ıtico mais alto Hc2, como pode ser visto na fig. 5. Devido ao comportamento ser t˜ao diferente dos supercondutores cl´assicos, Abrikosov os chamou de supercondutores tipo-II.
Figura 5 – Compara¸c˜ao entre supercondutores tipo-I e tipo-II
Fonte: Figura retirada de [10]. Compara¸c˜ao entre o comportamento da penetra¸c˜ao do campo magn´etico em supercondutores do tipo-I e do tipo-II. Perceba que para o tipo-II a supercondutividade possui dois campos cr´ıticos, o primeiro,Hc1, onde existe um estado misto e o segundo,Hc2, onde a supercondutividade ´e destru´ıda.
Uma consequˆencia da penetra¸c˜ao parcial do campo magn´etico ´e que o custo de energia para manter o diamagnetismo ´e menor, assim o campo cr´ıtico Hc2 pode ser muito maior que o campo cr´ıtico Hc1. Essa propriedade permite que sejam produzidos supercondutores de altos campos magn´eticos para eletro´ım˜as.
experimentais para fins acadˆemicos, sem qualquer utilidade pr´atica, o que era um grande potencial desperdi¸cado. A principal limita¸c˜ao era a temperatura, sempre pr´oxima a do h´elio l´ıquido, que tornava impratic´avel seu uso fora de um laborat´orio bem equipado, at´e que em 1986 foram descobertos os supercondutores de altas temperaturas.
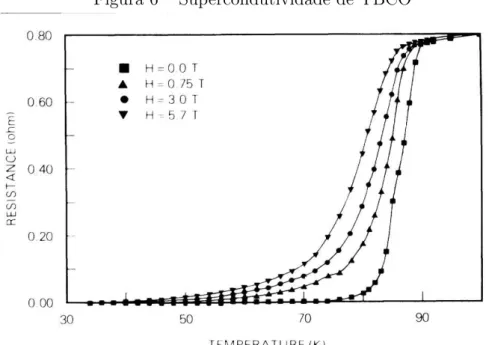
G. Bednorz e K. A. M¨uller em seu artigo, Possible High Tc Superconductivity in the Ba-La-Cu-O System [24], deixaram a comunidade cient´ıfica perplexa, pois encon-traram supercondutividade em um material cerˆamico, que usualmente ´e isolante, e com temperatura cr´ıtica de 30K, a maior at´e ent˜ao. Tal descoberta impulsionou pesquisas experimentais em ´oxidos de cobre visando encontrar compostos com temperatura critica alta suficiente para ser usado na pr´atica. A ideia era bater a barreira de 77 K, tempera-tura de ebuli¸c˜ao do nitrogˆenio l´ıquido, temperatempera-tura que ´e bem mais f´acil de atingir que os 4.2 K do h´elio. A barreira foi superada no ano seguinte `a descoberta de G. Bednorz e K. A. M¨uller. Chu Ching-wu e Mang-Kang Wu, das universidades de Houston e Alabama respectivamente, e suas equipes publicaram o artigo que culminaria no que foi chamado de “Woodstock”da f´ısica, onde mais de 2000 f´ısicos reuniram-se em Nova Iorque para 51 apresenta¸c˜oes sobre supercondutores de alta temperatura [25]. A descoberta da fase su-percondutora no material YBa2Cu3O7 a uma temperatura de 93 K e um campo cr´ıtico m´aximo estimado em 180T [26] foi um marco na f´ısica e na supercondutividade, pois tornaram-se poss´ıvel aplica¸c˜oes tecnol´ogicas para esse fenˆomeno. A figura 6 mostra re-sistividade em fun¸c˜ao da temperatura de uma amostra de YBCO. Sem campo magn´etico externo, o ponto de transi¸c˜ao para o estado supercondutor se da a 90 K
Figura 6 – Supercondutividade de YBCO
1.2 Supercondutividade de interface e novas descobertas
Desde a descoberta de supercondutores de altas temperaturas, as aplica¸c˜oes pr´aticas para a supercondutividade cresceram. A necessidade de resfriar o metal a tem-peraturas pr´oximas do nitrogˆenio l´ıquido tornou poss´ıvel a cria¸c˜ao de cabos supercon-dutores utilizados na Alemanha [27, 28] e geradores nos Estados Unidos [29], por exem-plo. A capacidade de gerar altos campos magn´eticos tamb´em possui aplicabilidade, como em m´aquinas de ressonˆancia magn´etica. Com propriedades t˜ao interessantes para usos pr´aticos, o estudo de supercondutores visa descobrir materiais que ultrapassem as li-mita¸c˜oes de temperatura. Um novo e interessante fenˆomeno foi descoberto h´a alguns anos. A temperatura cr´ıtica em heteroestruturas (supercondutores em bi-camadas) ´e maior que em filmes puros do material, que inclusive podendo ser isolante.
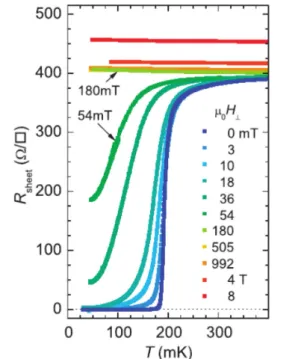
Em um trabalho pioneiro de 2004, A. Ohtomo e H. Y. Hwang [30] demostraram que um sistema de el´etrons com alta mobilidade pode ser induzido na interface entre dois isolantes LaAlO3 e SrTiO3. Essa descoberta impulsionou novas pesquisas em ´oxidos, que culminou na descoberta de N. Reyrenet al.[31] em 2007, onde mostroou-se que um g´as de el´etrons condensa em um estado supercondutor (ver fig. 7) confinado na interface entre os materiais. Curiosamente, a ideia de um supercondutor bidimensional j´a havia sido proposta por Ginzburg em 1964 [3].
Figura 7 – Gr´afico de supercondutividade em ´oxidos
Fonte: Figura retirada de [31]. Resistˆencia da amostra em fun¸c˜ao da temperaturaT com campo magn´etico aplicado perpendicularmente `a interface.
´oxidos complexos tornou-se um dos sistemas mais interessantes a serem estudados, devido a suas propriedades n˜ao usuais e a possibilidade de se obter supercondutividade de alta temperatura confinada em interfaces nanom´etricas. Esta ´ultima qualidade tem alto valor cient´ıfico, como ressalta A. Gozar et al. [7], para potenciais aplica¸c˜oes e para estudo de fenˆomenos quˆanticos em dimens˜oes reduzidas, e ´e extremamente dif´ıcil de encontrar em metais convencionais, devido `a grande quantidade de portadores de carga, que restringem os efeitos da interface em regi˜oes muito menores que seus comprimento de coerˆencia. Em contrapartida, em ´oxidos de cobre, a densidade dos portadores de carga ´e pequena, a temperatura cr´ıticaTc ´e alta e o comprimento de coerˆencia ´e da ordem da interface, o que faz esses ´oxidos serem mais f´aceis de se estudar, por´em com o custo de que a interface deve ser atomicamente perfeita. Em 2009, S. Smadiciet al. [32] mostraram em seu artigo que uma super-rede de La2Cu04−La1.64Sr0.36CuO4 dopado possui uma fase supercondutora, com Tc = 38 K, apesar dos materiais serem n˜ao-supercondutores. Os resultados obtidos sugerem que a supercondutividade est´a ligada com a dopagem das camadas dos materiais constituintes da hetroestrutura. Em 2012, um grupo experimental chinˆes [9] observou supercondutividade em heteroestruturas com uma temperatura cr´ıtica de Tc = 77 K.
2 TEORIA GINZBURG-LANDAU
Antes de especificarmos o problema discutido nesta disserta¸c˜ao faz-se ne-cess´ario introduzir a teoria Ginzburg-Landau (GL) para supercondutividade. A teoria desenvolvida em 1950 por V. L. Ginzburg com colabora¸c˜ao de L. D. Landau [3] foi pro-posta com base no modelo de Landau para descrever transi¸c˜oes de fase de segunda ordem onde um parˆametro de ordem era utilizado para descrever o sistema macroscopicamente. Sendo uma teoria fenomenol´ogica, foi considerada um dos maiores fa¸canhas da intui¸c˜ao f´ısica [10], propondo que o estado supercondutor poderia ser descrito por uma pseudo-fun¸c˜ao de onda ψ(~r), que seria um parˆametro de ordem complexo no modelo de Landau para transi¸c˜oes de fase. A teoria foi desenvolvida aplicando o m´etodo variacional pra uma certa densidade de energia livre que ´e fun¸c˜ao de|ψ|2 e|∇ψ|2, levando a um par de equa¸c˜oes diferenciais acopladas paraψ(~r) e para o potencial vetor A(~r).~
Um outro modelo fenomenol´ogico para a supercondutividade j´a havia sido proposto em 1935 pelos irm˜aos London [14], o qual conseguia explicar os fenˆomenos des-cobertos at´e aquele momento em supercondutores, por´em o pr´oprio Ginzburg explica a necessidade de outra teoria em seuNobel Lecture: On superconductivity and superfluidity (what I have and have not managed to do) as well as on the “physical minimum” at the
beginning of the XXI century [15]. A teoria de London n˜ao conseguia lidar com a situa¸c˜ao em que os portadores de cargansvariam no espa¸co e com a resposta n˜ao linear dos campos que s˜ao fortes o suficiente para mudar ns. Apesar do sucesso em explicar fenˆomenos em supercondutores, pouca aten¸c˜ao foi dada `a teoria de GL por cientistas ocidentais devido a sua fundamenta¸c˜ao fenomenol´ogica. A situa¸c˜ao mudou em 1959 quando Gor’kov [23] mostrou que a teoria de GL ´e um caso limite da teoria microsc´opica BCS. Foi mostrado que a teoria de GL ´e valida para temperaturas suficientemente pr´oximas da temperatura criticaTc e quando as derivadas espaciais deψ e ˜A n˜ao variam rapidamente.
2.1 Energia de condensa¸c˜ao
Vamos come¸car com um problema simples que mostrar´a importantes propri-edades termodinˆamicas dos supercondutores. Considere um longo cilindro envolto por
Figura 8 – Solenoide
Esquema de um solenoide.
um solenoide que passa uma corrente I, como na fig. 8. O campo magn´etico dentro do cilindro ´e:
~ H= N
LI~ez. (2.1)
O solenoide possui NL an´eis por metro e~ez ´e o vetor unit´ario ao longo do eixo do cilindro. O trabalho total d′W quando aumenta infinitesimalmente a corrente de I para I +dI
pode ser calculado:
d′W = −N ǫIdt, = NdΨ
dt Idt, = N IdΨ, = N AIdB, = N V ~H·d ~B,
= µ0V(H~ ·d ~M +H~ ·d ~H), (2.2) onde V = AL ´e o volume, ǫ = −dΨ
dt ´e a for¸ca eletromotriz induzida no solenoide pela mudan¸ca no fluxo magn´etico Ψ e utilizando a identidade B~ = µ0(H~ +M~), onde M~ ´e a magnetiza¸c˜ao do cilindro.
Este problema simples nos mostra que podemos dividir o trabalho em duas partes distintas, sendo a primeira, o trabalho realizado no sistema para modificar a mag-netiza¸c˜ao por unidade de volume:
e a segunda, o trabalho de autoindutˆancia do solenoide por unidade de volume:
d′wauto=µ0H~ ·d ~H. (2.4) O trabalho de autoindutˆancia ´e a mudan¸ca de energia eletromagn´etica no v´acuo se n˜ao houvesse a magnetiza¸c˜ao M~, isto ´e, se n˜ao existisse o cilindro. Vamos definir que o trabalho feito sobre o cilindro n˜ao inclua a mudan¸ca da energia eletromagn´etica, assim o trabalho sobre o cilindro ´e apenas o trabalho da equa¸c˜ao 2.3.
Com o trabalho calculado podemos usar a primeira lei da termodinˆamica para encontrar a energia interna:
dU =T dS+µ0V ~H·d ~M . (2.5) Comparando com a energia interna de um g´as ´e f´acil de ver que o trabalho faz o papel do trabalho mecˆanico−P dV e da mesma forma que podemos retirar informa¸c˜oes sobre a temperatura e press˜ao no g´as, podemos encontrar o campoH~ e a temperatura T utilizando a equa¸c˜ao 2.5.
T = ∂U
∂S, (2.6)
~ H = 1
µ0V ∂U
∂ ~M. (2.7)
Apesar de termos calculado a temperatura T e o campo magn´etico H, a en-~ tropia S e a magnetiza¸c˜ao M~ n˜ao s˜ao as vari´aveis mais convenientes para se trabalhar em um laborat´orio. Experimentalmente ´e mais f´acil controlar a temperatura e o campo magn´etico, dessa forma podemos fazer transforma¸c˜oes de Legendre na energia interna, eq. 2.5, e definir os an´alogos magn´eticos da energia livre de Helmholtz F e Gibbs G.
F(T, ~M) =U −T S, (2.8)
G(T, ~H) = U −T S−µ0V ~H·M .~ (2.9) A energia livre de Gibbs ´e a mais pratica a ser usada j´a que depende das vari´aveis controladas em experimentos. Podemos escrever agora
dG=−SdT −µ0V ~M ·d ~H. (2.10)
Em termos deG podemos calcular a entropia e a magnetiza¸c˜ao: S =−∂G
~
M =− 1 µ0V
∂G
∂ ~H (2.12)
Al´em da praticidade, com a energia livre de Gibbs podemos reconstruir a energia livre de HelmholtzF =G+µ0V ~M·H~ e a energia interna U =F +T S.
Quando estudamos gases podemos utilizar um diagrama de fases de suas vari´aveis termodinˆamicas, normalmente P e V, para analisar suas transi¸c˜oes de fase. Podemos fazer o mesmo para supercondutores, utilizado as vari´aveis adequadas ´e poss´ıvel criar diagramas de fase que demostram como o supercondutor se comporta com a mudan¸ca de um par de parˆametros. A energia livre G ou F, temperatura T, campo aplicado H e magnetiza¸c˜ao podem ser utilizados para esse fim. As figuras 9a e 9b s˜ao exemplos de di-agramas de fases que utilizam o campo aplicadoH e a temperatura T como parˆametros. Os diagramas que utilizam a energia livre e o campo ser˜ao utilizados para analisar os estados de v´ortices em supercondutores mais adiante nesta disserta¸c˜ao.
Figura 9 – Diagrama de fase para supercondutores tipo-I e tipo-II
(a) (b)
Fonte: Figuras adaptadas de [33]. Esquema do diagrama de fases para supercondutores do tipo-I (a) e tipo-II (b). Obtemos a energia de condensa¸c˜ao integrando no caminho indicado pela seta.
Podemos utilizar energia livre de GibbsGpara calcular a diferen¸ca de energia livre entre o estado supercondutor e o normal. Para fazer isso integramos a equa¸c˜ao 2.10 sobre uma linha vertical como na fig. 9a. Ao longo dessa linhadT = 0 e n˜ao precisaremos nos preocupar com a entropia, ficando apenas a parte do trabalho sobre a magnetiza¸c˜ao:
Gs(T, Hc)−Gs(T,0) =−µ0V
Z Hc
0 ~
M d ~H. (2.13)
magnetiza¸c˜ao M~ cancela o campo magn´etico H:~ ~
M =−H.~ (2.14)
Substituindo na integral 2.13 e integrando temos:
Gs(T, Hc)−Gs(T,0) =µ0V H2
c
2 . (2.15)
O estado normal possui magnetiza¸c˜ao aproximadamente zero, podemos desconsiderar qualquer tipo de paramagnetismo ou diamagnetismo normal em qualquer metal, com isso a integral da energia livre de Gibbs ´e zero:
Gn(T, Hc)−Gn(T,0) = 0. (2.16) No ponto de campo criticoHc os estados normal e supercondutor est˜ao em equil´ıbrio, ou seja:
Gs(T, Hc) =Gn(T, Hc). (2.17) Subtraindo as equa¸c˜oes 2.15 e 2.16 temos que:
Gs(T, Hc)−Gs(T,0)−Gn(T, Hc) +Gn(T,0) = −µ0V H2
c
2 , (2.18) Gs(T,0)−Gn(T,0) = −µ0V
H2
c
2 . (2.19) O estado supercondutor possui uma energia de Gibbs menor que o estado normal em campo zero, sendo assim um estado est´avel. O mesmo pode ser feito com a energia livre de Helmholtz, usando F =G−µ0V ~H·H~ o resultado ´e o mesmo:
Fs(T,0)−Fn(T,0) =−µ0V H2
c
2 . (2.20)
A quantidade µ0Hc2/2 ´e a energia de condensa¸c˜ao, que mede o ganho de energia livre por unidade de volume do estado supercondutor em compara¸c˜ao com o estado normal na mesma temperatura. Hc ´e o campo critico termodinˆamico de um supercondutor, que para um supercondutor de tipo I ocorre uma transi¸c˜ao de fase enquanto que em supercondutor do tipo II as transi¸c˜oes ocorrem emHc1 eHc2 eHc apenas mede a energia de condensa¸c˜ao.
2.2 Teoria de Ginzburg-Landau no bulk
de fase de segunda ordem envolvem uma mudan¸ca na simetria do sistema: em um sistema ferromagn´etico os momentos de spin s˜ao alinhados espontaneamente quando abaixo da temperatura de Curie. Em um supercondutor, a supercondutividade aparece espontane-amente, j´a que ´e um estado mais est´avel, abaixo de uma temperatura cr´ıtica. Landau percebeu que essas transi¸c˜oes poderiam ser caracterizadas por um parˆametro de ordem que ´e zero acima da temperatura critica e diferente de zero abaixo da temperatura, no caso do ferromagn´etico, a magnetiza¸c˜ao faz o papel do parˆametro de ordem.
Para supercondutores, Ginzburg postulou que um parˆametro de ordem com-plexo ψ caracteriza o estado supercondutor e que |ψ|2 ´e a densidade de part´ıculas super-condutoras. O verdadeiro significado de |ψ|2 s´o ficou claro quando Gor‘kov [23] mostrou que a teoria de GL ´e um caso particular da teoria do BCS. Fisicamente, |ψ|2 pode ser interpretado como a fun¸c˜ao de onda do centro de massa dos pares de Copper. A n˜ao interpreta¸c˜ao completa do parˆametro de ordem foi uma grande frustra¸c˜ao para Ginzburg e para Landau, como pode ser evidenciado em seunobel lectures [15]. No texto, ele revela que esse assunto foi bastante discutido com Landau. Ginzburg chegou `a conclus˜ao que a carga das part´ıculas supercondutoras deveria ser duas ou trˆes vezes a do el´etrone, por´em Landau argumentou que a carga das part´ıculas seria uma quantidade efetiva, assim como a massa efetiva em semicondutores, e que dependeria das coordenadas. Sem conseguir refutar o argumento de Landau, a quest˜ao ficou sem resposta at´e a teoria BCS.
A teoria de GL sup˜oe que a energia livre de um supercondutor deve depen-der suavemente do parˆametro ψ e como ψ ´e complexo e a energia livre real, esta s´o pode depender do |ψ|. Podemos expandir densidade de energia f em serie de Taylor nas proximidades deTc:
fs(T)−fn(T) =α(T)|ψ|2+ 1
2β(T)|ψ|
4, (2.21)
onde fs e fn s˜ao as densidades de energia do estado supercondutor e do estado normal, respectivamente. As vari´aveis α e β s˜ao parˆametros fenomenol´ogicos que dependem da temperatura de forma suave. Devemos assumir que β(T) ´e sempre positivo para que a energia possua um m´ınimo. O parametro α n˜ao tem nenhuma restri¸c˜ao, podendo ser tanto negativo como positivo, assim temos duas possibilidades, como esquematizado na figura 10:
Figura 10 – Energia livre
Fonte: Figura retirada de [22]. Diferen¸ca entre a energia livre do estado supercondutor e do estado normal por unidade de volume em fun¸c˜ao do parˆametro de ordem. ParaT < Tc a energia livre tem m´ınimos em ψ0, enquanto para T > Tc o unimo m´ınimo ´e em ψ = 0.
da energia muda para fs −fn = −|α(T)|2/2β(T) e podemos identificar a temperatura onde α(T) zera como temperatura critica Tc.
Na proximidade da temperatura critica Tc, assumimos que os coeficientes α e β dependem suavemente da temperatura. Podemos expandir-los em serie de Taylor e utilizar apenas o primeiro termo de cada expans˜ao:
α(T)≈α0(T −Tc) +. . . , (2.22)
β(T)≈β+. . . . (2.23)
A constante β n˜ao depende mais da temperatura e o parˆametro α(T) agora segue a premissa de Ginzburg e Landau. Em termos dessas constantes, as solu¸c˜oes para o m´ınimo de energia em |ψ| tomam a forma:
|ψ|=
α0
β
12
(T −Tc)
1
2 se T < Tc,
0 se T > Tc.
(2.24)
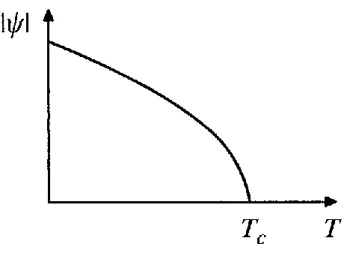
´
E f´acil de observar a mudan¸ca abrupta na fun¸c˜ao |ψ| quando reduzimos a temperatura, a figura 11 demostra a curva do parˆametro de ordem. A curva ´e similar a encontrada em outras transi¸c˜oes de fase de segunda ordem na teoria geral de Landau, por isso dizemos que a supercondutividade ´e uma transi¸c˜ao de segunda ordem na temperatura.
Figura 11 – Parˆametro de ordem em fun¸c˜ao da temperatura
Fonte: Figura retirada de [22]. Dependˆencia do parˆametro de ordem com a temperatura.
condensa¸c˜ao que encontramos na se¸c˜ao passada:
fs(T)−fn(T) = − α2
0(T −Tc)2
2β =−µ0 H2
c
2 . (2.25)
Encontramos assim o campo critico termodinˆamico em termos nos parˆametros fenome-nol´ogicos nas proximidades de Tc:
Hc = α0 (µ0β)1/2
(Tc−T). (2.26)
2.3 Teoria de GL em sistemas n˜ao-homogˆeneos e em campo magn´etico A teoria completa de GL permite que o parˆametro de ordem dependa da posi¸c˜ao, ψ(~r), e que o campo magn´etico seja inclu´ıdo. A n˜ao-homogeneidade de ψ entra na forma de uma dependˆencia da energia livre com o gradiente de ψ(~r) e os efeitos do campo magn´etico s˜ao inclu´ıdos como se ψ fosse uma fun¸c˜ao de onda de uma part´ıcula carregada, ou seja, fazendo a mudan¸ca usual na mecˆanica quˆantica:
¯ h
i∇ → ¯ h
i∇ −q
∗A,~ (2.27)
ondeA~ ´e o potencial vetor eq= 2e. Com essas mudan¸cas, a energia livre toma sua forma completa:
Fs(T) = Fn(T) +
Z " ¯h2
2m∗ ¯ h
i∇ −2e ~A
ψ 2!
+α|ψ|2+β 2|ψ|
4
#
d3r+
+
Z
1 2µ0
B2(~r)d3r.
A primeira integral ´e feita no supercondutor, a segunda feita em todo o espa¸co. ´E f´acil ver que se n˜ao houver campo magn´etico eψ(~r) for uma constante voltamos `a se¸c˜ao anterior. A nova constante m∗ determina a energia associada com o gradiente de ψ(~r), possui
dimens˜ao de massa e tem o papel de massa efetiva de sistemas quˆanticos.
Incluindo a dependˆencia no espa¸co e o campo magn´etico podemos resolver diferentes casos e encontrar os principais efeitos de supercondutores, o efeito Meiss-ner, equa¸c˜oes de London e v´ortices de Abrikosov. A seguir deduziremos as equa¸c˜oes de Ginzburg-Landau e as utilizaremos para resolver alguns casos particulares.
2.4 Equa¸c˜oes de Ginzburg-Landau
As equa¸c˜oes de GL s˜ao encontradas utilizando o principio variacional, onde minimizamos o funcional F = Fs−Fn em rela¸c˜ao ao parˆametro de ordem ψ (primeira
equa¸c˜ao) e ao potencial vetor A~ (segunda equa¸c˜ao). 2.4.1 Primeira equa¸c˜ao de GL
Utilizando a equa¸c˜ao de Euler-Lagrange em rela¸c˜ao a ψ† [34], temos:
∂F
∂ψ† − ∇
∂F
∂(∇ψ†)
= 0. (2.29)
Substituindo|ψ|4 = (ψ†ψ)2, temos que: ∂|ψ|4
∂ψ† = 2|ψ|
2ψ†, (2.30)
e assim podemos reescrever o termo do gradiente da equa¸c˜ao 2.28 como:
−i¯h∇ −2e ~Aψ
2
=−i¯h∇ −2e ~Aψ ·i¯h∇ −2e ~Aψ†,
−i¯h∇ −2e ~Aψ
2
onde ϕ=−i¯h∇ −2e ~Aψ e a partir da equa¸c˜ao 2.29:
αψ+β|ψ|2ψ + 1 2m∗
h
ϕ−2e ~Ai− 1
2m∗(i¯h∇ϕ) = 0
αψ+β|ψ|2ψ+ 1 2m∗
h
−i¯h∇ −2e ~A·−2e ~A−i¯h∇−i¯h∇ −2e ~Aiψ = 0 αψ+β|ψ|2ψ+ 1
2m∗
h
i¯h2e∇A~+ (2e)2A~2+ (i¯h)2∇2 +i¯h2e∇A~iψ = 0 αψ+β|ψ|2ψ+ 1
2m∗
h
−h¯2∇2+ 4i¯he∇A~+ (2e)2A~2iψ = 0
αψ+β|ψ|2ψ− h¯ 2
2m∗
"
∇2−4ie
¯ h∇A~+
2e ¯ h 2 ~ A2 #
ψ = 0
α+β|ψ|2
ψ− ¯h 2 2m∗ ∇ − 2ie ¯ h ~ A 2
ψ = 0. (2.32)
A primeira equa¸c˜ao de GL ´e semelhante `a equa¸c˜ao de Schr¨odinger, por´em com um termo de segunda ordem, o que a torna uma equa¸c˜ao n˜ao-linear. Devido a esse termo, o princ´ıpio da superposi¸c˜ao n˜ao pode ser aplicado.
2.4.2 Segunda equa¸c˜ao de GL
A equa¸c˜ao de Euler-Lagrange em rela¸c˜ao ao potencial vetor [34] ´e: ∂F
∂ ~A − ∇ ×
"
∂F
∂(∇ ×A)~
#
= 0. (2.33)
Novamente, reescrevemos o termo do gradiente como:
−i¯h∇ − e
∗
cA~
ψ 2 =
−i¯h∇ − e
∗
c A~
ψ·
i¯h∇ − e
∗
cA~
ψ†, (2.34)
e o campo magn´etico:
~
B =∇ ×A.~ (2.35)
Derivando os termos da equa¸c˜ao 2.33, encontramos a segunda equa¸c˜ao de GL:
2i¯he 2m∗c ψ
†
∇ψ−ψ∇ψ†
+ 1 m∗2e
2ψ†Aψ~
+∇ × ∇ ×A~ = 0, (2.36)
e utilizando a equa¸c˜ao de Maxwell:
∇ ×H~ =J~s, (2.37)
temos:
~ Js=−
i¯h2e 2m∗ ψ
†
∇ψ−ψ∇ψ†
−4e
2
m∗|ψ|
2A.~ (2.38)
se comportam no supercondutor, ondeJ~s ´e a densidade de corrente supercondutora.
2.5 Superf´ıcies em supercondutores e comprimentos caracter´ısticos
As equa¸c˜oes 2.32 e 2.38 s˜ao utilizadas para resolver problemas de supercon-dutores em diferentes situa¸c˜oes, sendo na maioria delas ´e necess´ario o uso de m´etodos num´ericos, pois a equa¸c˜ao 2.32 ´e n˜ao-linear. No entanto, existem duas situa¸c˜oes em que ´e poss´ıvel resolver as equa¸c˜oes, o que ´e de fundamental importˆancia para o melhor enten-dimento de como se comporta o parˆametro de ordem ψ e o campo magn´etico H, como~ discutiremos a seguir.
Primeiro, vamos considerar um modelo simples de interface entre um metal e um supercondutor na ausˆencia de um campo magn´etico. Suponha que a interface esteja contida no plano yz e separa a regi˜ao met´alica, x < 0, da supercondutora, x > 0, como ilustrado no fig. 12. Na regi˜ao met´alica, o parˆametro de ordem deve ser zero. Na regi˜ao
Figura 12 – Comprimento de coerˆencia
Fonte: Figura retirada de [22]. Esquema demostrando o comprimento de coerˆencia. O parˆametro de ordem pr´oximo a superf´ıcie recupera o valor ψ0 ap´os o comprimento carac-ter´ısticoξ.
supercondutora, ´e valida a equa¸c˜ao 2.32, sem a parte do potencial vetor. Assumindo que ψ ´e continuo, ficamos com o problema de resolver a equa¸c˜ao diferencial:
α+β|ψ|2
ψ− ¯h 2
2m∗
d2ψ
dx2 = 0, (2.39)
substitui¸c˜ao:
f =
s
β
|α|ψ, (2.40)
usamos|α|pois para que haja supercondutividade ´e necess´ario queα =−|α|, assim temos a equa¸c˜ao diferencial:
¯ h2 2m∗|α|f
′′+f
−f3 = 0, (2.41)
cuja a solu¸c˜ao ´e [10]
ψ(x) =ψ0tanh
x
√
2ξ(T)
, (2.42)
onde ψ0 ´e o valor do parˆametro de ordem no interior do supercondutor e o parˆametro ξ(T), que possui dimens˜ao de comprimento, ´e definido como:
ξ(T) =
s
¯ h2
2m∗|α(T)|. (2.43)
Essa quantidade ´e chamada de comprimento de coerˆencia de Ginzburg-Landau e mede a distˆancia da interface que o parˆametro de ordem volta a ter o valor m´aximo igual ao do interior do supercondutor, como ser observado na fig. 12 .
O comprimento de coerˆencia de GL aparece em quase todos os casos em que o supercondutor ´e n˜ao-homogˆeneo, incluindo superf´ıcies, interfaces, defeitos e v´ortices. Usa-remos a solu¸c˜ao 2.42 mais a frente, no capitulo 3, quando formos especificar os problemas a serem estudados nessa disserta¸c˜ao.
Podemos usar a dependˆencia de α com a temperatura para mostrar que ξ(T) diverge quandoT =Tc. Comoα(T) = α0(T −Tc), temos
ξ(T) = p ξ(0)
1−T /Tc
. (2.44)
EmT = 0 o comprimento de GL concorda com o comprimento de coerˆencia de Pippard para supercondutores que falamos na introdu¸c˜ao.
O segundo problema que podemos resolver ´e o caso da interface de um super-condutor homogˆeneo, ou seja |ψ|2 =|α|/β, em um campo magn´etico. Como no primeiro caso, vamos considerar a mesma interface, no planoyz com o campo magn´etico na dire¸c˜ao z. A figura 13 ilustra essa situa¸c˜ao.
A densidade de corrente pode ser calculada usando a equa¸c˜ao 2.38, ~
Js =− 4e2 m∗|ψ|
Figura 13 – Campo magn´etico na interface de um supercondutor
Fonte: Figura retirada de [35]. Esquema do comportamento do campo magn´etico na in-terface supercondutor-metal. O campo penetra o comprimento caracter´ıstico λ antes de desaparecer no interior do supercondutor.
Aplicando o rotacional na equa¸c˜ao acima, obtemos
∇ ×J~s =−
4e2 m∗|ψ|
2
∇ ×A.~ (2.46)
Usando as rela¸c˜oes ∇ ×J~s =∇ × ∇ ×H,~ ∇ ×A~ =H, ficamos com a equa¸c˜ao~
∇ × ∇ ×H~ =−4e
2
m∗|ψ|
2H~ (2.47)
e usando a identidade vetorial∇×∇×H~ =∇(∇·H)~ −∇2H, temos a equa¸c˜ao diferencial:~
∇2H~ = 4e
2
m∗
|α|
β H.~ (2.48)
A solu¸c˜ao para essa equa¸c˜ao ´e
H =H0e− z
λ(T), (2.49)
onde definimos
λ(T) =
s
m∗β
4e2|α(T)|. (2.50) O parˆametro λ ´e chamado de comprimento de penetra¸c˜ao de London e ´e a distˆancia que o campo magn´etico penetra o supercondutor antes de desaparecer. Assim como o comprimento de coerˆencia,λpossui dependˆencia com a temperatura e diverge emT =Tc. Com esses dois comprimentos caracter´ısticos podemos caracterizar os super-condutores. A tabela 1 mostra alguns valores de λ(0) e ξ(0) para diferentes supercondu-tores.
Ginzburg e Landau introduziram um parˆametro adimensional que n˜ao depende da temperatura,
κ= λ(T)
ξ(T). (2.51)
supercon-Tabela 1 – Comprimento de penetra¸c˜ao λ(0) e comprimento de coerˆencia ξ(0) para temperatura zero.
λ(0) (nm) ξ(0) (nm) κ
Al 1150 45 0,03
Sn 180 42 0,23
Pb 87 39 0,48
Nb 39 52 1,3
Nb3Ge 3 90 30
YNi2B2C 8,1 103 12,7
K3C60 2,8 240 95
YBa2Cu3O7−δ 1,65 156 95
Dados retirados de [22]
dutores em dois tipos: Tipo-I (κ < 1/√2) e Tipo-II (κ > 1/√2). Em supercondutores do tipo-I, a supercondutividade ´e destru´ıda quando se atinge o campo critico, como pode ser visto na fig. 9a. Esse tipo foi o primeiro a ser estudado e a maioria dos metais puros comportam-se dessa forma quando s˜ao resfriados at´e entrarem na fase supercondutora. Os do tipo-II foram descobertos quando A. Abrikosov [13] estudou o que aconteceria se ξ(T) < λ(T), ou seja quando κ fosse grande. Em seu artigo foi demostrado que, para esse tipo de supercondutor, ocorria uma transi¸c˜ao de fase de segunda ordem em rela¸c˜ao ao campo magn´etico. No lugar da destrui¸c˜ao abrupta da supercondutividade, Abrikosov mostrou que existe um crescimento continuo do fluxo magn´etico dentro do supercondutor a partir de um campo cr´ıtico Hc1 at´e um segundo campo cr´ıtico Hc2, onde a supercon-dutividade ´e destru´ıda. A fig. 9b mostra esse comportamento. Dedicaremos a pr´oxima se¸c˜ao para o estudo do trabalho de Abrikosov e de como o fluxo magn´etico penetra o supercondutor, al´em de iremos mostrar o porquˆe da divis˜ao dos tipo de supercondutores ocorrer quandoκ = 1/√2.
2.6 Estado de v´ortices
complexo, ´e a rede de fluxos de Abrikosov. Em 1957, A.A. Abisksov [13] publicou seu trabalho em que solucionava as equa¸c˜oes de GL para um supercondutor tipo- II em um campo magn´etico. O resultado ´e impressionante, al´em de encontrar uma solu¸c˜ao exata para as equa¸c˜oes pr´oximo ao campo criticoHc2, tamb´em previu que pouco abaixo deHc2 o parˆametro de ordem forma uma rede peri´odica de v´ortices, onde cada v´ortice carrega um quantum de fluxo magn´etico. Esse resultado explica porque supercondutores do tipo-II deixam entrar campo magn´etico sem perder a supercondutividade e explica o porque de κ = 1/√2 como a divis˜ao entre tipo-I e tipo-II. O resultando de Abrikosov rendeu o premio Nobel de f´ısica em 2003.
Figura 14 – Anel supercondutor
Fonte: Figura retirada de [22]. Esquema de um anel supercondutor em um campo magn´etico.
2.6.1 Quantiza¸c˜ao do fluxo
Vamos aplicar a teoria de GL ao primeiro problema. A melhor forma de descrever o anel supercondutor ´e em coordenadas cil´ındricas; com isso temos uma condi¸c˜ao de contorno que deve sempre ser obedecida: o parˆametro de ordem ψ(r, φ, z) deve ser peri´odico emφ. Assumindo que o anel ´e uniforme, a solu¸c˜ao n˜ao depende dez our, dessa forma uma poss´ıvel solu¸c˜ao para o parˆametro de ordem tem a forma:
ψ(φ) = ψ0einφ, (2.52)
onde n ´e inteiro e ψ0 uma constante. O fluxo magn´etico passando pelo fio ´e dado pela integral
Φ =
Z
~
B·d~S =
Z
(∇ ×A)~ ·d~S =
I
~
A·d~r= 2πrAφ, (2.53) onde o potencial vetor pode ser escrito como
Aφ= Φ
A energia livre de Helmholtz pode ser escrita usando os resultados 2.52, 2.54 e o gradiente em coordenadas cil´ındricas
Fs(T) = Fn(T) +
Z
d3r ¯h 2 2m∗
∇+ 2ei
¯ h A~
ψ 2
+α|ψ|2+β 2|ψ|
4
!
+EB
ou
Fs(T) = Fs0+V ¯ h2 2m∗ in R − 2eiΦ 2π¯hR 2
|ψ|2
!
+EB, (2.55)
onde V ´e o volume do anel, F0
s = Fn(T) +
R
d3rα|ψ|2+β
2|ψ|
4 ´e a energia livre do anel na ausˆencia de fluxo magn´etico e EB = 2µ10
R
B2d3r ´e a energia do campo magn´etico no v´acuo e ´e proporcional ao quadrado do fluxo que atravessa o anel
Eb ∝Φ2. (2.56)
O segundo termo depende do fluxo e do valor de n. Vamos manipul´a-lo de forma que o termo do fluxo seja isolado
V ¯h 2 2m∗ in R − 2eiΦ 2π¯hR 2
|ψ|2 = V¯h 2
2m∗R2 (Φ−nΦ0) 2
|ψ|2, (2.57)
onde Φ0 = h/2e. A energia livre pode ser escrita em fun¸c˜ao do fluxo, isso nos da uma ideia de o que significa Φ0:
Fs(T) =Fs0+const.(Φ−nΦ0)2|ψ|2+const.Φ2. (2.58)
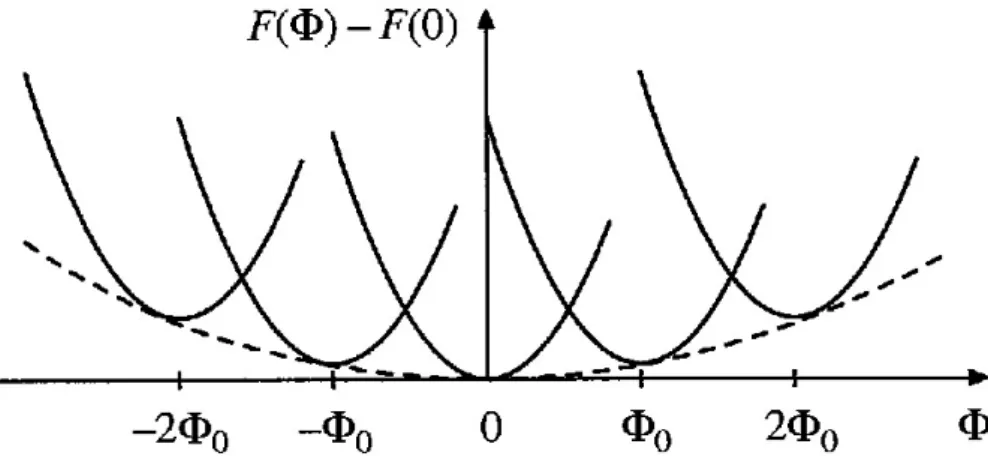
Perceba que a energia livre ser´a m´ınima quando o fluxo atravessando o supercondutor ´e m´ultiplo de Φ0, ou seja, o fluxo que penetra no supercondutor ´e quantizado pelo quantum de fluxo Φ0 = h/2e = 2,07×10−15Wb. ´E interessante notar que como temos v´arios valores de n temos diferentes m´ınimos para a energia livre. Quando resfriamos o anel abaixo da temperatura Tc o sistema ir´a para um dos metaestados, como mostra a fig. 15, dependendo do campo aplicado. Preso em um dos m´ınimos, o campo magn´etico induzir´a uma corrente no anel supercondutor para que o fluxo permane¸ca constante. Se desligarmos o campo magn´etico, o anel ainda estar´a em um dos m´ınimos e a corrente induzida continuar´a existindo para que o fluxo continue continuo, por esse motivo essas correntes s˜ao chamadas de correntes persistentes.
Outro ponto interessante desse problema ´e que o quantum de fluxo Φ0 ´e obser-vado em unidades deh/2e e n˜ao deh/e, indicando que a carga relevante ´e 2e, implicando assim na existˆencia dos pares de Cooper.
Figura 15 – M´ınimos de energia em fun¸c˜ao do quantum de fluxo
Fonte: Figura retirada de [22]. M´ınimos de energia em fun¸c˜ao do quantum de fluxo. Quando resfriamos um supercondutor em um campo magn´etico, o supercondutor fica preso em um dos m´ınimos de energia dependendo do campo aplicado.
uma rede peri´odica de forma a minimizar a energia livre.
2.6.2 Rede de Abrikosov
A grande peculiaridade dos supercondutores tipo-II ´e a entrada de campo magn´etico sem destruir a supercondutividade, sendo esta uma transi¸c˜ao de fase de se-gunda ordem no campo. O fluxo magn´etico aumenta continuamente de um campo cr´ıtico Hc1 at´e um campo cr´ıtico Hc2, onde finalmente a supercondutividade ´e destru´ıda. A. A. Abrikosov desenvolveu uma teoria que explica esse comportamento, demostrando a existˆencia dos dois tipos de supercondutores [13] e existˆencia de uma rede peri´odica de v´ortices magn´eticos.
A ideia ´e que para supercondutores do tipo-II, o parˆametro de ordem ψ e a magnetiza¸c˜ao M s˜ao pequenos nas proximidades de Hc2. ´E f´acil de observar esse fato, j´a que pr´oximo a Hc2 o supercondutor est´a quase mudando para o estado normal e a uma grande quantidade de campo o atravessa. Com essa premissa podemos assumir que
~
B =µ0H,~ (2.59)
onde H~ ´e o campo magn´etico externo, e que B~ ´e uniforme ~
B = (0,0, B). (2.60)
Podemos utilizar o calibre de Landau para escrever o potencial vetor ~
de forma que quando substitu´ımosA~na primeira equa¸c˜ao de GL, eq. 2.32, ficamos apenas com
− ¯h
2
2m∗
∇+2eBi
¯ h xˆy
·
∇+ 2eBi
¯ h xˆy
ψ+α(T)ψ +β|ψ|2ψ = 0, (2.62)
onde ˆy ´e o vetor unit´ario na dire¸c˜ao y. A equa¸c˜ao 2.62 ´e complicada de ser resolvida analiticamente devido ao termo n˜ao linearβ|ψ|2ψ. Por´em, podemos descartar esse termo com o argumento queψ ´e pequeno. Ficamos com a equa¸c˜ao de GL linearizada
−2mh¯∗
∇2+ 4eBi
¯ h x ∂ ∂y − (2eB)2 ¯ h2 x
2
ψ+α(T)ψ = 0 (2.63)
Introduzindoωc = 2meB∗ e lembrando queα´e negativo no regime supercondutor, a equa¸c˜ao acima pode ser escrita de forma de uma equa¸c˜ao de autovalor
−2mh¯∗∇2−¯hωcix ∂ ∂y +
m∗ω2
c 2 x
2
ψ =|α|ψ. (2.64)
A equa¸c˜ao tem a forma de uma equa¸c˜ao de Schr¨odinger para uma part´ıcula carregada em um campo magn´etico [37]. A solu¸c˜ao a equa¸c˜ao tem a forma
ψ(~r) = ei(kyy+kzz)f(x), (2.65)
onde ´e necess´ario encontrar a fun¸c˜ao desconhecidaf(x). Vamos ent˜ao substituir a solu¸c˜ao na equa¸c˜ao 2.64, obtemos
− ¯h
2
2m∗
d2f dx2 +
¯
hωckyx+ m∗ω2
c 2 x
2
f = |α| −h¯ 2(k2
y+kz2) 2m∗
!
f. (2.66)
Podemos completar o quadrado do termo entre parenteses do lado direito
¯
hωckyx+ m∗ω2
c 2 x
2
= m
∗ω2
c 2 x
2(x
−x0)2− m∗ω2
c 2 x
2
0, (2.67) onde x0 = ¯hky/m∗ωc, e rearranjar os termos
− ¯h
2
2m∗
d2f dx2 +
m∗ωc2
2 (x−x0) 2f =
|α| −h¯ 2
k2z 2m∗
f. (2.68)
A equa¸c˜ao 2.68 nada mais ´e que a equa¸c˜ao de Schr¨odinger para o oscilador harmˆonico deslocado da origem de x0, ondef faz papel de um autoestado,
logo o termo entre parenteses do lado esquerdo ´e a energia do oscilador:
n+ 1 2
¯
hωc =|α| − ¯ h2k2
z
2m∗, (2.70)
isolando|α|,
|α(T)|=
n+1 2
¯ hωc+
¯ h2k2
z
2m∗. (2.71)
Vamos analisar situa¸c˜oes poss´ıveis para a equa¸c˜ao 2.71. Primeiro vamos explicitar a dependencia deα com a temperatura,
α0(Tc −T) =
n+ 1 2
¯ hωc +
¯ h2k2
z
2m∗. (2.72)
Agora imagine que tenhamos um supercondutor em um campo magn´etico externo H e gradualmente diminu´ımos a temperatura. Na temperatura cr´ıtica Tc(0), onde essa ´e a temperatura cr´ıtica no campo zero, ser´a imposs´ıvel solucionar a equa¸c˜ao 2.72, pois o lado direito deveria ser zero, enquanto a energia m´ınima de um oscilador, no estado fundamental, com n = 0 e kz = 0 ´e ¯hωc/2. A ´unica solu¸c˜ao aceit´avel para esse caso ´e quando estamos a uma temperatura T muito abaixo de Tc, assim estaremos no estado fundamental
¯ hωc
2 =α0(Tc−T), T(H) = Tc(0)−
2e¯hµ0 2α0m∗
H. (2.73)
A temperatura que precisamos atingir para que haja a transi¸c˜ao de fase vai diminuindo com o aumento do campo.
Outra situa¸c˜ao poss´ıvel ´e mantermos a temperatura fixa, abaixo deTc e irmos diminuindo o campo aplicado H de um valor acima at´e abaixo de Hc2. Dessa forma, o campo depende da temperatura e, no estado fundamental, temos a mesma express˜ao que o caso anterior,
1 2h¯
2eB
m∗ =α0(Tc−T)
Bc2 = 2m∗α
0(Tc −T) ¯
h2
¯ h 2π Hc2 =
1 2πµ0
Φ0
ξ(T)2, (2.74)
existir simultaneamente no supercondutor.
Quando encontramos o campo cr´ıtico termodinˆamico, equa¸c˜ao 2.26, vimos que ele est´a relacionado com a diferen¸ca de energia livre entre o estado normal e o estado supercondutor, equa¸c˜ao 2.25. Na se¸c˜ao anterior encontramos um outro campo cr´ıticoHc2 que tamb´em est´a relacionado com a transi¸c˜ao entre a fase supercondutora e a normal — temos um problema de ambiguidade. Vamos comparar as equa¸c˜oes para termos uma ideia do que est´a ocorrendo.
Hc = α0 (µ0β)1/2
(Tc−T), (2.75)
Hc =
Φ0 2πµ0
√
2ξλ, (2.76)
ou
Hc = Hc2
√
2κ, (2.77)
de forma que
Hc2 =
√
2κHc. (2.78)
Podemos deduzir que para κ > 1/√2, Hc2 > Hc e teremos que o parˆametro de ordem decresce de forma continua at´e zero emHc2, sendo esse o ponto em que temos a diferen¸ca entre o estado supercondutor e o normal. O ponto Hc representa a transi¸c˜ao entre o es-tado Meissner puro, sem v´ortices, para o eses-tado misto com rede de v´ortices de Abrikosov. Esses supercondutores ´e que s˜ao classificados como tipo-II. Para oκ <1/√2,Hc2 < Hc e a transi¸c˜ao de fase ´e de primeira ordem emHc, onde o parˆametro de ordem muda abrup-tamente. Esses supercondutores s˜ao classificados de tipo-I. Resolvemos a ambiguidade separando os supercondutores em dois grupos distintos.
A equa¸c˜ao de GL linearizada 2.63 permitiu encontrarmos o valor deHc2 e com isso classificarmos os supercondutores, por´em ainda n˜ao temos nenhuma informa¸c˜ao sobre o parˆametro de ordem abaixo desse ponto cr´ıtico. Para isso precisamos voltar a equa¸c˜ao n˜ao linear 2.62 e tentar resolvˆe-la. Abrikosov resolveu a equa¸c˜ao usando um palpite genial que o levou `a solu¸c˜ao. Ele percebeu que na solu¸c˜ao da equa¸c˜ao linearizada 2.63, apenas o estado fundamental do oscilador, n = 0 e kz = 0, tem importˆancia, por´em ainda exstem infinitos estados degenerados, que correspondem aos diferentes valores de ky. A solu¸c˜ao para o estado fundamental de um oscilador ´e uma fun¸c˜ao gaussiana [37]
ψ(~r) =Ceikyye−(x−x0)2/ξ(T)2, (2.79)
teste de forma a restringir o valor de ky ky =
2π ly
n, (2.80)
onde n ´e inteiro, podendo ser positivo ou negativo, e ly o per´ıodo . O termo que desloca o oscilador da origemx0 toma o valor de
x0 =− 2π¯h mωcly
n =−Φ0 Bly
n. (2.81)
A solu¸c˜ao peri´odica de Abrikosov tem a forma
ψ(~r) =
∞
X
n=−∞
Cnei(2πny/ly)e−(x+nΦ0/Bly)
2/ξ(T)2
. (2.82)
O parˆametro Cn pode ser interpretado como um parˆametro variacional que deve ser es-colhido de forma a minimizar a energia livre do sistema.
A solu¸c˜ao ´e peri´odica em y, mas n˜ao em x, Abrikosov for¸cou a solu¸c˜ao ser peri´odica emx fazendo com que os coeficientesCn fossem peri´odicos para um parˆametro ν
Cn+ν =Cn, (2.83)
e o per´ıodolx ´e dado por
lx =ν Φ0 Bly
. (2.84)
Agora a solu¸c˜ao ´e peri´odica em y e x, resta escolher o valor de ν em que a energia livre seja m´ınima.
O estudo de Abrikosov foi feito utilizandoν = 1, isso cria uma rede quadrada. Estudos posteriores mostraram que a rede triangular, com ν = 2, tem uma energia livre um pouco menor que a rede quadrada [38]. Qualquer que seja a configura¸c˜ao, o parˆametro de ordem ψ(~r) vai a zero em um ponto para cada c´elula unit´aria e um quantum de fluxo Φ0 penetra no supercondutor. A solu¸c˜ao final ´e, ent˜ao, uma rede peri´odica de v´ortices, como ilustrada na figura 16.
Figura 16 – Rede de v´ortices de Abrikosov
Fonte: Figura retirada de [22]. Amplitude do parˆametro de ordem|ψ|2 para a menor energia da rede triangular. Cada c´elula unit´aria cont´em um quantum de fluxo Φ0.
Figura 17 – Primeira observa¸c˜ao da rede de Abrikosov
(a) (b)
3 PAR ˆAMETRO ESCONDIDO COMO FONTE DA SUPERCONDUTIVIDADE ESCONDIDA
O cap´ıtulo anterior foi dedicado `a teoria b´asica de GL: mostramos sua for¸ca em resolver problemas de supercondutores e demostramos suas principais caracter´ısticas. Agora, vamos utilizar essa teoria para o problema especificamente de supercondutividade de interface.
Na Introdu¸c˜ao, mostramos diversos experimentos desde 2007 onde a interface entre materiais em heteroestruturas tem um papel na supercondutividade. Seguiremos os passos de A. Moor, A. F. Volkov e K. B. Efetov [36] para tentar explicar os fenˆomenos apresentados anteriormente.
3.1 Introdu¸c˜ao
Apesar de origem da supercondutividade em interfaces de heteroestruturas permanecer obscura, tem-se evidˆencia de que ela ocorre na interface entre os materiais e de que a dopagem nesses pontos tem influˆencia no aparecimento dessa supercondutividade. Em 2015 A. Moor et al. [36] propuseram um mecanismo geral para supercondutividade de interface usando sistemas com dois parˆametros de ordem. Eles assumiram que os parˆametros que caracterizam o material permitem a forma¸c˜ao de uma onda de densidade de carga ou densidade de spin que prevalece no bulk, mas que compete com o segundo parˆametro de ordem , o qual representa uma supercondutividade “escondida”. A dopagem ou defeitos existentes na interface suprimem o primeiro parˆametro de ordem fazendo com que a supercondutividade escondida apare¸ca.
A teoria foi baseada na teoria de GL e foi demostrado que uma supercon-dutividade local aparece na interface e que pode ser descrita pelo parˆametro de ordem ∆(x). Resolvendo as equa¸c˜oes de GL acopladas para os dois parˆametros de ordem foram encontradas temperaturas cr´ıticas quantizadasTc∆para a supercondutividade escondida.
3.2 Energia livre e equa¸c˜oes de GL
Come¸camos com a express˜ao para energia livre F para um sistema com dois
parˆametros de ordem, ∆ e W. A express˜ao ´e igual a equa¸c˜ao 2.28 para cada parˆametro e adicionado de um termo de acoplamento, em uma dimens˜ao e sem campo magn´etico temos:
F =
Z
dx
ξs2(∆′)2+αs∆2+ βs
2 ∆
4+γ∆2W2+ξ2
w(W′)2+αwW2+ βw
2 W 4
, (3.1)
onde ∆′eW′s˜ao as derivadas espaciais e os coeficientesxi
s,w,αs,w eβs,ws˜ao os parˆametros do material. O coeficiente αs possui dependˆencia com a temperatura igual ao deduzido no Cap´ıtulo 2, αs =−(1−T /Ts). J´a a αw possui uma express˜ao mais complicada e os autores propuseram que a dopagem e defeitos do material est´a ligada com a temperatura cr´ıticaTdw da onda de densidade, de forma que αw ´e proporcional a αs e `a dopagem, ou seja,
αw =c1αs−c2µ2 (3.2) A temperatura Tdw pode ser ajustada de forma a coincidir com a temperatura cr´ıtica do supercondutor Ts. A vari´avel γ ´e um coeficiente de acoplamento entre os parˆametros de ordem.
As equa¸c˜oes de GL para cada parˆametro s˜ao encontradas da mesma forma que no cap´ıtulo 2. Ficamos com duas equa¸c˜oes, uma para cada parˆametro. Por consistˆencia com o artigo original utilizaremos o αw,s → −αw,s.
−ξs2∆′′+ ∆
−αs+βs∆2 +γW2
= 0, (3.3)
−ξwW′′+W
−αw+βwW2+γ∆2
= 0. (3.4)
3.3 Interface
O caso de heteroestruturas resume-se a resolver o par de equa¸c˜oes de GL acopladas com as condi¸c˜oes de que longe da interface o parˆametro W±∞ =
p
αw/βw e ∆±∞ = 0. A interface est´a ligada `a dopagemµou defeitos do material e que o coeficiente
αw ´e o com a principal dependˆencia desses fatores [36, 44]. A modelagem do compor-tamento de W na interface pode ser feita utilizando o coeficiente αw com dependˆencia espacial,
αw(x) =
−α0, |x|< L,
αw, |x|> L,
onde L ´e o comprimento da interface em que W ´e suprimido. No caso de |x| > L a equa¸c˜ao 3.4 tem solu¸c˜ao trivial do caso homogˆeneo W =pαw/βw, como em 2.24. Para que seja poss´ıvel descrever o comportamento de ∆ tamb´em foi considerado queαs possui dependˆencia espacial.
αs(x) =
−αs0, |x|> L,
αs, |x|< L,
(3.6)
Figura 18 – Esquema de um sistema que apresenta supercondutividade de interface
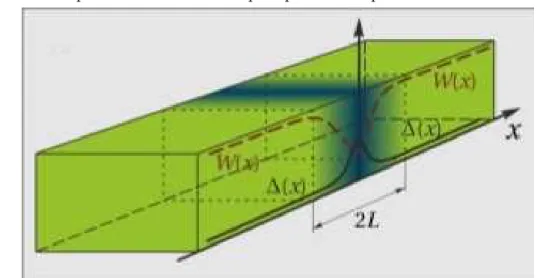
Fonte: Figura retirada de [36]. Esquema do sistema a ser estudado. Parˆametro de ordemW ´e suprimido pr´oximo a interface 2L entre os materiais. A supress˜ao de W leva ao aparecimento da supercondutividade ∆ `a principio encoberta por W.
Assumindo que ∆ seja muito pequeno comparado a W e que a equa¸c˜ao 3.4 possa ser aproximada por
−ξw2W′′+W
−αw(x) +βwW2
= 0, (3.7)
a solu¸c˜ao da equa¸c˜ao 3.7 ´e conhecida, restringida para o caso de uma regi˜ao de supress˜ao estreita
W(x) = W∞tanh[κw(|x|+x0)] (3.8) onde x0 obedece
sinh(2x0κ) = 4ξ2
wκw α0L ≡
r, (3.9)
com κw =ξw−1
p
αw/2.
Foram considerados dois casos separados, o de forte supress˜ao (r ≪1) e o de fraca supress˜ao (r ≫ 1). Explicitaremos o caso de forte supress˜ao, pois ser´a com esse resultado que desenvolveremos os resultados desta disserta¸c˜ao.