Deflexão solar do gráviton-energia gravitacional em uma teoria não-simétrica da ...

Universidade de São Paulo Instituto de Física de São Carlos

Deflexão Solar do Gráviton

-Energia Gravitacional em uma

Teoria Não-Simétrica da

Gravitação.

Lucas Chibebe Céleri

Dissertação apresentada ao Instituto de Física de São Carlos, da Universidade de São Paulo, para a obtenção do título de Mestre _{em Ciências :} Física Básica_.

Orientador: Prof. Dr. Silvestre Ragusa

Deflexão Solar do Gráviton - Energia Gravitacional em uma Teoria Não-Simétrica da Gravitação. Lucas Chibebe Céleri - São Carlos, 2003. 62 p.

Dissertação (Mestrado) - Instituto de Física de São Carlos, 2003.

Orientador: Prof. Dr. Silvestre Ragusa.

...

Dianzi a me non fuor cose create Se non etterne, e io etterna duro Lasciate ogne speranza, voi ch’intrate 1

1_{Antes de mim não foi criado mais/ Nada senão eterno, e eterna eu duro./ Deixai toda}

Agradecimentos

Conteúdo

1 Deflexão Solar do Gráviton 11

1.1 Introdução . . . 12 1.2 Cálculo Semi-Clássico da Seção de Choque

Diferencial de Espalhamento de um Gráviton

pelo Sol . . . 17 1.3 Cálculo do Ângulo de Deflexão Solar

do Gráviton . . . 22

2 Energia Gravitacional em uma Teoria Não-Simétrica da

Gravi-tação 24

2.1 Introdução . . . 25 2.2 Análise da Energia . . . 31 2.3 Cálculo das Constantes de Expansão

da Métrica . . . 36

3 Conclusões e Perspectivas 41

3.1 Deflexão Solar do Gráviton . . . 42 3.2 Energia Gravitacional em uma Teoria Não-Simétrica da Gravitação 43

A Espalhamento de Rutherford: Tratamento Quântico 45

C Soma Sobre as Polarizações do Gráviton 50

D Cálculo de T_Bµν 53

E Cálculo do Determinante da Métrica 55

F Cálculo da Função R(r) 57

Resumo

Neste trabalho são estudados dois problemas, como resumidos abaixo

Parte I - Deflexão Solar do Gráviton

Neste trabalho calculamos o ângulo de deflexão do gráviton pelo Sol através de sua seção de choque diferencial de espalhamento. A expressão para a seção de choque é obtida através de uma teoria semi-clássica. O resultado obtido para o ângulo de desvio do gráviton, para pequenos ângulos, é o mesmo atribuído à luz, na sua geodésica nula.

O conteúdo deste trabalho deu origem ao artigo:

Parte II - Energia Gravitacional em uma Teoria Não-Simétrica da

Gravitação

A ausência de modos radiativos de energia negativa numa proposta teoria da gravitação baseada em uma métrica não-simétrica é reanalizada. Isto porque a contribuição de uma parte da lagrangeana deixou de ser considerada. Mostramos aqui que tal contribuição para a energia é nula. O caráter de positividade da energia na teoria fica então firmemente estabelecido.

O conteúdo deste trabalho deu origem ao trabalho:

Abstract

Neste trabalho são estudados dois problemas, como resumidos abaixo

Parte I - Deflexão Solar do Gráviton

Neste trabalho calculamos o ângulo de deflexão do gráviton pelo Sol através de sua seção de choque diferencial de espalhamento. A expressão para a seção de choque é obtida através de uma teoria semi-clássica. O resultado obtido para o ângulo de desvio do gráviton, para pequenos ângulos, é o mesmo atribuído à luz, na sua geodésica nula.

O conteúdo deste trabalho deu origem ao artigo:

Parte II - Energia Gravitacional em uma Teoria Não-Simétrica da

Gravitação

A ausência de modos radiativos de energia negativa numa proposta teoria da gravitação baseada em uma métrica não-simétrica é reanalizada. Isto porque a contribuição de uma parte da lagrangeana deixou de ser considerada. Mostramos aqui que tal contribuição para a energia é nula. O caráter de positividade da energia na teoria fica então firmemente estabelecido.

O conteúdo deste trabalho deu origem ao trabalho:

Capítulo 1

1.1 Introdução

Quando estudamos a deflexão da luz pelo campo gravitacional do Sol na Teoria da Relatividade Geral (RG), a trajetória do raio de luz é descrito pela geodésica nula. Nada é dito a respeito do caráter tensorial da radiação. Portanto, a única propriedade usada é que a radiação se propaga com velocidadec. Podemos então suspeitar de que todos os tipos de ondas não massivas, que viajam então com velocidadec, devam ser defletidos pelo mesmo ângulo. Neste trabalho verificamos isto para o caso do gráviton.

A maneira de se trazer a tona o caráter tensorial da onda é calculando-se o ângulo de desvio através da seção de choque diferencial de espalhamento. Este cálculo foi feito para o caso do fóton, no contexto da Teoria Quântica de Campos, por Boccalett et al. [1], dando o mesmo resultado da RG. Mais recentemente [2] o cálculo para o caso do bóson escalar não massivo levou ao mesmo resultado.

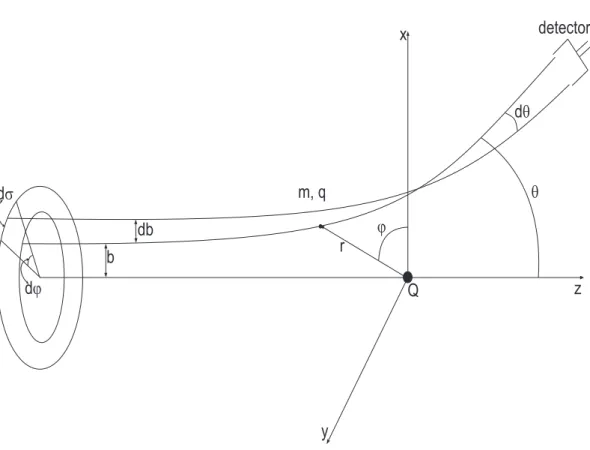
Neste trabalho calculamos o ângulo de deflexão do gráviton e mostramos que o resultado é também igual ao obtido através da geodésica nula. Afim de ilustrar o procedimento de obtenção do desvio do gráviton à partir da seção de choque vamos considerar como exemplo o caso do espalhamento de Rutherford. A Fig. 1.1 ilustra o espalhamento da partícula α, de carga q e massa m com velocidade inicial v0 ao ser desviada por um núcleo com carga Q.

Na descrição clássica, partindo da lei de Newton e da força coulombiana obtém-se a relação entre o parâmetro de impacto b e o ângulo de deflexão θ,

b= qQ mv2

0

cotg

µ

θ 2

¶

b db

dj

ds

j

q

dq

detector

z Q

m, q

x

y r

Figura 1.1: Espalhamento de Rutherford

As partículas que chegam ao detector com ângulo sólido dΩ são aquelas que

passam pela área transversal elementar dσ chamada seção de choque. Da Fig.

1.1 temosdΩ =₋senθdθdφ e dσ =bdφdb. Portanto, a distribuição angular é

dσ dΩ =−

bdϕdb

senθdθdϕ =− bdb

senθdθ. (1.2)

O sinal negativo está de acordo com o fato de que uma diminuição do parâmetro

de impacto corresponde a um aumento no ângulo de desvio. Usando a Eq (1.1)

em (1.2) obtemos o conhecido resultado

dσ dΩ =

·

qQ

2mv2 0

¸2

1

sen4¡_θ

2

¢. (1.3)

Notemos agora que, inversamente, conhecendo-se a expressão para a seção

espalhamento. Esta situação é a que poderia ocorrer quando o problema do espalhamento de Rutherford é tratado quanticamente (este cálculo é apresentado no Apêndice A), pois neste caso a Eq. (1.3) é obtida diretamente. Vejamos como isto pode ser feito pois esta é a situação na qual estaremos envolvidos ao querermos a expressão do parâmetro de impacto quando de posse da seção de choque de espalhamento do gráviton pelo Sol. Tendo a Eq. (1.3) e usando a Eq. (1.2) obtemos

−_senθdθbdb =

·

qQ 2mv2

0

¸2

1 sen4¡_θ

2

¢. (1.4)

Logo, usando a relação senθ= 2sen(θ/2)cos(θ/2) resulta

bdb=₋

·

qQ 2mv2

0

¸2 _2cos¡θ

2

¢

dθ sen3¡_θ

2

¢ . (1.5)

Integrando o lado esquerdo desta equação nos limites entre 0 eb e os correspon-dentes valoresπ e θ do ângulo obtemos

b2 ₌

µ

qQ mv2

0

¶2 _cos2¡θ

2

¢

sen2¡_θ

2

¢. (1.6)

Portanto, vem para b o resultado escrito na Eq. (1.1).

Antes de entrar no nosso problema vejamos algum detalhe dos casos da de-flexão solar da luz e do bóson escalar não-massivo. Para a luz a expressão para a seção de choque diferencial de espalhamento pelo Sol obtida através da Teoria Quântica de Campos é [1]

dσ dΩ =

µ GM c2 ¶2 cotg4 µ θ 2 ¶ . (1.7)

o método descrito anteriormente para calcular a relação entre o parâmetro de impacto e o ângulo de desvio. Das Eqs. (1.2) e (1.7) obtemos

− bdb senθdθ = µ GM c2 ¶2 cotg4 µ θ 2 ¶ . (1.8) Integrando obtemos

b2 = 4

µ

GM c2

¶2"

1 sen2¡_θ

2

¢ −sen

2

µ

θ 2

¶

+ 4ln

· sen µ θ 2 ¶¸# . (1.9) Dividindo por b2 _{e chamando f(θ) a expressão dentro do colchetes resulta}

1 = 4

µ

GM bc2

¶2

f(θ). (1.10)

Para deflexão rasante ao Sol com raio R, temos b = R. Neste caso o fator que multiplica f(θ) é da ordem de 10−12 _{e menor ainda se b > R. Concluímos então}

que a função f(θ)tem que ser da ordem de 1012 ou maior. Dada à sua estrutura vemos que isto só é possível se θ for próximo de zero. Neste caso f(θ) se reduz a 4/θ4_{. Obtemos então}

R2 = 4

µ

GM c2

¶2µ

4 θ2

¶

. (1.11)

Logo, para um vôo rasante ao Sol

θ = 4GM

c2_R , (1.12)

dσ dΩ =

M2G2 c4_sen4¡_θ

2

¢. (1.13)

Usando a Eq. (1.2) e integrando obtemos

b2 =₋2M

2_G2

c4

"

−2cos2¡_θ

2

¢

sen2¡_θ

2

¢ #

. (1.14)

Usando o mesmo raciocínio chega-se ao mesmo resultado escrito na Eq. (1.12). Em 1967 DeWitt [3] calculou, via Teoria Quântica de Campos, a seção de choque para o espalhamento de um gráviton por um bóson escalar massivo. No limite não-relativístico em que se despreza o recuo do bóson o resultado obtido foi

dσ dΩ =

G2_M2

c4_sen4¡_θ

2 ¢ · sen8 µ θ 2 ¶

+cos8

µ

θ 2

¶¸

. (1.15)

1.2 Cálculo Semi-Clássico da Seção de Choque

Diferencial de Espalhamento de um Gráviton

pelo Sol

A densidade de lagrangeana de interação entre o campo gravitacional do Sol e o gráviton é

L =₋1

2h

(s)

µνTµν. (1.16)

Nesta expressão h(µνs) = g(µνs)−ηµν é o desvio do espaço chato do campo externo do Sol com métrica g(µνs). Tµν é o tensor de energia-momentum do gráviton. Sua expressão é [4]

Tµν =hαβ µ, hαβ,ν− 1 2η

µν_hαβ

,ρhαβ,ρ. (1.17) Usaremos agora o fato de que a combinaçãoh(_µνs) =h(µνs)−(1/2)ηµνh(s), comh(s) = ηµν_h(s)

µν, só tem como componente não nulah

(s)

00 =−4GM/rc2. Isto mostramos no

Apêndice B. É interessante então colocarmosL em termos de h(_µνs). Disto resulta

L=₋1

2h

(s)

µνh µ

αβ, hαβ,ν. (1.18)

Na gauge hoµ=hαα = 0, somente hij é não nulo. Logo

L=₋1

2h

(s)

00hij,0hij,0. (1.19) O gráviton é descrito semiclassicamente pela onda plana

hij =

r

¯ h

2ωVεij(ˆk)

³

com coeficiente fixado de tal modo que a energia associada à onda é, seguindo Einstein, igual a ¯hω (tratamento semiclássico). Em detalhe, partimos da onda plana

hij = 2H0εijcos(~k·~r−ωt+iα)

=Hεijei(~k·~r−ωt)+H∗εije−i(~k·~r−ωt),

(1.21)

com H =H0eiα, frequência ω, vetor de onda~k e polarização εij (εijεij = 1). A energia da onda dentro da caixa de normalização com volume V =L3 _{é, da Eq.}

(1.17)

E =

Z

T00dV =

Z

hij,0h_ij,0dV . (1.22) Daqui resulta

E =

Z

4H₀2ω2cos2(~k_·~r₋ωt+iα)dV

= 4H₀2ω2

Z L/2

−L/2

Z L/2

−L/2

Z L/2

−L/2

cos2(~k_·~r₋ωt+iα)dV .

(1.23)

Usando ki =ni2π/L, comni =±1,±2,· · ·, proveniente da condição de contorno periódica, o valor da integral é V /2. Logo, E = 2H02ω2V. Com E = ¯hω resulta

H0 =

p

¯

h/2ωV =_|H_|. O valor da integral também decorre se tomarmos o valor médio temporal de seu integrando.

A solução geral é, indicando a polarização λ da onda,

hij =

X λ X ~k r ¯ h 2ωVε

(λ)

ij (ˆk)

³

A amplitude de probabilidade de transição do estado inicial (ε(_ijλ), ~k) para o estado final (ε(_ijλ′), ~k′_)é

S = i ¯ h

Z

LdV dt

= 2i ¯ h

Z

h00h′ijhijωω′dV dt.

(1.25)

Nesta expressão hij descreve o gráviton incidente com frequênciaω eh′ij descreve o gráviton espalhado com frequência ω′_{. Seguindo o tratamento semiclássico a}

parte come−iωt_{descreve destruição (absorção) e a parte come}iωt _{descreve criação} (emissão). Logo devemos ter para o gráviton incidente

hij =

r

¯ h 2ωV ε

(λ)

ij (ˆk)ei(~k·~r−ωt) (1.26) e

h′_ij =

r

¯ h 2ω′_V ε

(λ′₎

ij (ˆk′)e−i(~k ′_·~r−ω′_t)

(1.27) para o gráviton espalhado. Substituindo (1.26) e (1.27) na Eq. (1.25) obtemos

S= i V

Z

h00

√

ωω′_ε(λ′)

ij ε

(λ)

ij ei( ~k−~k′_)·~r

e−i(ω−ω′)tdV dt. (1.28) Chamando ~q=~k₋~k′ _{e introduzindo a transformada de Fourier de h}(s)

00(r)

h(₀₀s)(q) =

Z

h(₀₀s)(r)ei~q·~rdV , (1.29) resulta

S= iπ V

√

ωω′_ε(λ′)

ij ε

(λ)

ij h

(s)

A probabilidade de transição por unidade de tempo com o gráviton final no ângulo sólido dΩé

dw=

Z |S_|2

T dη, (1.31)

com dη = (V k′₂

dk′_dΩ)/(2π)3 _{sendo o número de estados correspondentes. Logo}

dw= ω

4

16π2_c3_V (εijε

′

ij)2|h

(E)

00 (~q)|2dΩ. (1.32)

A seção de choque diferencial édσ =dw/J, ondeJ =c/V é a corrente incidente. Portanto, a distribuição angular para raios não polarizados é

dσ dΩ =

ω4

16π2_c4|h (E) 00 (~q)|2

1 2

X

λλ′

(εijεmn)(ε′ijε′mn). (1.33) Como h(₀₀s)(r) =₋4GM/rc2_{, a Eq. (1.29) nos dá}

h(₀₀s)(q) = ₋ 4πGM c2_k2_sen2¡_θ

2

¢. (1.34)

A soma sobre as polarizações do gráviton incidente é [5]

X

λ

ε(_ijλ)ε(_mnλ) = 1

2(δimδjn+δinδjm−δijδmn−δimˆkjˆkn−δjnkˆikˆm

−δinˆkjkˆm−δjmkˆikˆn+δijkˆmkˆn+δmnˆkikˆj + ˆkiˆkjkˆmkˆn).

(1.35)

No Apêndice C é mostrado como obter esta expressão. Lembrando que _kˆ_ikˆ_{i = 1} e ˆ_kiˆ_k′

i =cosθ, resulta 1 2

X

λλ′

(εijεmn)(ε′ijε′mn) =cos8

µ

θ 2

¶

+sen8

µ

θ 2

¶

. (1.36)

dσ dΩ =

G2M2 c4_sen4¡_θ

2

¢ µ

cos8

µ

θ 2

¶

+sen8

µ

θ 2

¶¶

, (1.37)

1.3 Cálculo do Ângulo de Deflexão Solar

do Gráviton

Das Eqs. (1.2) e (1.15) obtemos

bdb=₋ G

2_M2

c4_sen4¡_θ

2 ¢ µ cos8 µ θ 2 ¶

+sen8

µ

θ 2

¶¶

senθdθ. (1.38)

Integrando esta relação para b entre os valores de 0 e b e com os valores corre-spondentes de θ entreπ eθ obtemos

b2 =

µ

2GM c2

¶2

[ 1

sen2¡_θ

2

¢ + 4ln µ sen µ θ 2 ¶¶

−6sen2

µ

θ 2

¶

+ 2sen4

µ

θ 2

¶

− 2₃sen6

µ

θ 2

¶

+ 11 3 ].

(1.39)

Seguindo o mesmo raciocínio apresentado na introdução, escrevemos o termo entre colchetes como f(θ) e dividimos a Eq. (1.39) por b2_{. Logo}

1 =

µ

2GM bc2

¶2

f(θ). (1.40)

Como assinalado anteriormente, o fator que multiplica f(θ)é da ordem de 10−12

(para b = R) ou menor. Portanto f(θ) tem que ser da ordem de 1012 _{ou maior}

(seb > R). Analisando sua estrutura vemos que isto só pode ocorrer para o caso em que o ângulo θ é próximo de zero. Neste caso f(θ) se reduz a 4/θ2 _{e a Eq.}

(1.39) torna-se

R2 =

µ

4GM c2_θ

¶2

. (1.41)

θ = 4GM

c2_R . (1.42)

Capítulo 2

Energia Gravitacional em uma

2.1 Introdução

Alguns anos atrás uma teoria extendida da gravitação baseada em uma métrica não-simétrica foi elaborada por Ragusa [6] (referido como I daqui para diante). Trata-se de gravitação pura, sem associação da parte anti-simétrica da métrica com o tensor do campo eletromagnético. Num segundo trabalho [7] (referido como II daqui para diante) foi obtida a solução das equações de campo para uma fonte pontual, junto com as implicações para o movimento de partículas e luz. Mostrou-se que a teoria é consistente com os quatro testes solares clássicos da Relatividade Geral (RG).

A teoria foi desenvolvida para tentar resolver o problema do aparecimento de modos radiativos de energia negativa (fantasmas) que, como apontado por Damour et al. (DDM) [8], estava presente em teorias anteriores. Antes de discu-tirmos em detalhes este problema vamos apresentar a estrutura da teoria proposta em I afim de definirmos precisamente que parte da energia será analisada neste trabalho. A teoria baseia-se numa métrica gαβ não simétrica como utilizada por Einstein ao elaborar sua teoria unificada, mas sem a identificação da parte anti-simétrica com o eletromagnetismo. A geometria do espaço é exatamente a mesma. O espaço é não-riemaniano tendo tanto gαβ como a conexão Γσαβ não simétricos em relação aos índicesαeβ. É importante o fato de que a parte anti-simétrica da conexãoΓσ

[αβ]= (1/2)(Γσαβ−Γσβα)é um tensor de terceira ordem1. Por contração resulta um tensor de primeira ordem,Γα = Γσ

[ασ]. Temos então em mãos tensores

1_{É fácil ver da Eq. (2.37) que}

Γλ

[αβ](x) =

∂xλ

∂xη

∂xρ

∂xα

∂xσ

∂xβΓ η

de ordem ímpar envolvendo a conexão, não presentes na RG. Como na RG, a lagrangeana é escrita sob a forma

L=gαβ(Qαβ + 1

2Λgαβ). (2.1)

Aqui Λ é a constante cosmológica. Usamos a notação A = √₋gA, sendo g o determinante do tensor métricogµν. A pergunta é qual é a expressão do tensor de segunda ordemQαβ contendo somente derivadas primeiras e produtos quadráticos da conexão, como é o caso do tensor de Ricci na RG em relação aos símbolos de Christoffel. Santaló [9], estudando matematicamente a estrutura do espaço não riemaniano de Einstein mostrou que existem oito destes possíveis tensores. Uma combinação conveniente adotada em I envolve a parte simétrica P(αβ) e a parte

anti-simétrica P[αβ] do tensor usado por Einstein [10]

Pαβ = Γλαβ,λ− 1 2

¡

Γλ_αλ,β + Γλ_λα,β¢

+ Γλ_αβΓρ_(λρ)−Γλ_αρΓρ_λβ. (2.2) O conjunto completo é

P(αβ) , P[αβ] , Γλ[αρ]Γ

ρ

[λβ] , ΓαΓβ , Γ(α;β)

Γ(α;β) , Γλ[αβ]Γλ , Γλ(αλ),β−Γλ(βλ),α.

(2.3)

presente temos o tensor de primeira ordemΓµ, o que permite a entrada da corrente como fonte do campo.

Em vez de Jµ _{é utilizado em I a corrente S}µ _{= F n}µ_{, onde n}µ _{é a densidade} de corrente numérica e o fatorF mede seu acoplamento com a geometria. Temos nµ_=nuµ_{, onde né a densidade numérica de partículas. Esta quantidade é usada} já na RG para a descrição do interior de estrelas associada às partículas estáveis próton, neutron e elétron. A lagrangeana de interação da matéria com o campo é [6]

L_M =₋8π√₋gTαβgαβ + 4π√−gSαΓα, (2.4) com a condição de não se fazer a variação de √−g.

As ondas gravitacionais provem agora de ambas as fontes, sendo a devida a Sµ _{relacionada diretamente com a parte anti-simétrica da métrica, g}

[αβ]. DDM

mostraram que em teorias anteriores as ondas devidas a Sµ_{tem energia negativa.} Com o intuito de tê-las com energia positiva a teoria em I foi construída de tal modo que g[αβ] obedecesse equações do tipo de Maxwell no vácuo. Desse

modo foi possível produzir as respectivas ondas com energia positiva como o são as eletromagnéticas na teoria de Maxwell. Escrevendo o tensor Qαβ em (2.1) como uma combinação linear dos oito tensores em (2.3) e fazendo as variações da lagrangeana do campo no vácuo com relação a gαβ _eΓσ

(√₋gg[αβ]),β = 0 (2.5) e que

Λg[αβ] =∂αΓβ −∂βΓα, (2.6) isto é, que g[αβ] deriva de uma função tipo potencial. Como consequência g[αβ]

obedece a equação do rotacional

g[αβ],µ+g[βµ],α+g[µα],β = 0. (2.7)

As outras duas equações de campo são

Uαβ + Λg(αβ)= 0, (2.8)

onde Uαβ é a parte do tensor P(αβ) que contém somente a parte simétrica da

conexão.

Uαβ = Γλ(αβ),λ−Γλ(αλ),β+ Γ ρ

(αβ)Γ

λ

(ρλ)−Γ

ρ

(αλ)Γ

λ

(ρβ). (2.9)

A outra equação é

g(αβ)_,γ+g(αµ)Γβ_(µγ)+g(βµ)Γα

(µγ)−g(αβ)Γ

µ

(µγ) = 0 (2.10)

que nos dá a relação entre Γσ

(αβ) e a métrica. Tal relação é

Γα_(µν) = 1 2g

(αλ)_(s

γν,µ+sµγ,ν−sµν,γ) + 1 4 µ lns g ¶ ,γ ¡

g(αγ)sµν−δναδµγ−δγνδµα

¢

.

Nesta equaçãosαβ simétrico e com determinantes, é o inverso deg(αβ),g(αβ)sαγ = δβ

γ. É de se notar que o sistema de equações é compatível com o número de incógnitas. De fato, com a Eq. (2.11) o tensor Uαβ fica conhecido em termos do tensor métrico. Com isso as Eqs. (2.5), (2.7) e (2.8) constituem um conjunto completo de 12 equações diferenciais para os doze componentes independentes da métrica (existem 16, mas quatro podem ser removidos pelo fato de que existem quatro transformações de coordenadas arbitrárias). Temos nas Eq. (2.5), (2.7) e (2.8) 4 + 4 + 10 = 18equações. Entretanto, existem em primeiro lugar os quatro vínculos impostos pelas quatro identidades do tipo Bianchi. Em segundo lugar temos as outras duas identidades

g[αβ]_,α,β = 0 (2.12)

e

εαβγµg[αβ],γ,µ = 0. (2.13) Com estas seis identidades o número de equações diferenciais é reduzido de18para 12, que é igual ao número de elementos independentes da métrica. A densidade de lagrangeana livre que resulta da teoria é

L=gαβ

µ

Uαβ + 1

2Λgαβ+ Γ[α,β]

¶

. (2.14)

É fácil verificar que as equações de campo obtidas, (2.5), (2.7) e (2.8), podem ser reobtidas desta expressão final para a lagrangeana fazendo a variação em relação a gαβ_{, a Γ}σ

(αβ) e a Γα. As equações de campo completas com as fontes são

Uαβ + Λg(αβ) = 8π

µ

T(αβ)−

1 2g(αβ)g

µν_T µν

¶

Λg[αβ]+ Γ[α,β]= 8π

µ

T[αβ]−

1 2g[αβ]g

µν_T µν

¶

, (2.16)

g[αβ]_,β = 4πSα (2.17)

e a Eq. (2.10).

2.2 Análise da Energia

Em I foi afirmado que as ondas gravitacionais devidas a Sµ _{tem energia positiva} definida. Entretanto, na análise desta radiação só a parte da lagrangeana (2.14) envolvendo a parte anti-simétrica g[αβ] _{de g}αβ _{= g}(αβ) _+g[αβ] _{foi considerada.}

Ficou então em aberto a questão de qual a contribuição vinda da outra parte, envolvendo a parcela simétrica g(αβ)_{. Neste trabalho completamos este cálculo}

mostrando que a contribuição dessa última parte é nula. Isso garante que a teoria está realmente livre de fantasmas.

Para estabelecermos um contado com I reescreveremos a Eq. (2.14) sob a forma

L=g(αβ)

µ

Uαβ+ 1 2Λg(αβ)

¶

+g[αβ]

µ

1

2Λg[αβ]+ Γ[α,β]

¶

. (2.18) Só a contribuição da segunda parcela foi considerada em I, levando a uma energia positiva. A primeira parcela é a que será analisada aqui.

Seguindo DDM, a idéia por trás do cálculo, que foi seguido em I, consiste em expandir a densidade lagrangeana em torno de um espaço de fundo riemaniano da RG com métrica Gαβ. Escrevemos então gαβ = Gαβ +gαβ e expandimos gαβ = g(αβ) +g[αβ] em potências da parte anti-simétrica de ordem mais baixa

Bαβ =g(1)αβ, que atua como uma perturbação. Mantendo a expansão até segunda ordem, temos

a métrica Gαβ, Bαρ = GρβBαβ. O que desejamos é calcular a contribuição do campo Bαβ para o fluxo de energia na zona de radiação. Este fluxo é dado por uma integral cujo elemento de integração contém um fator r2_{. Como o campo}

de radiação tem dependência r−1_{, os termos que irão contribuir serão aqueles}

quadráticos em Bαβ, o que justifica pararmos a expansão em segunda ordem. Com tal expansão a densidade de lagrangeana fica separada em dois termos

L=√₋GGαβ

µ

Rαβ+ 1 2ΛGαβ

¶

+LB, (2.20)

sendo o primeiro termo a lagrangeana correspondente ao campo de fundo rie-maniano com o tensor de Ricci Rαβ. G é o determinante da métrica de fundo, Gαβ. LB é a contribuição do campoBαβ, que se comporta então como a parte de lagrangeana de “matéria” no campo de fundo.

Nesta formulação o tensor energia-momentum devido ao campoBαβ é definido pela variação da ação correspondente a B, de acordo com [11] δI=R

δLBd4x= 8πR

T_BαβδGαβd4x, isto é

T_Bαβ = 1 8π√₋G

δLB δGαβ

. (2.21)

Como dito anteriormente, só a contribuição da segunda parcela de (2.18) foi analisada em I levando ao seguinte resultado para a contribuição para o tensor energia-momentum

T_Bµν =₋ 1 8πΛ

µ

1 4GµνB

αβ_B

αβ −BµβBνβ

¶

, (2.22)

Vamos agora calcular a contribuição vinda do primeiro termo da Eq. (2.18). Como mostraremos em seguida esta contribuição é nula. Feita a expansão, o primeiro termo de (2.18) terá a forma

L1 =

√

−G(R+ 2Λ) +L1B, (2.23)

onde L1B é a contribuição de Bαβ. Para determinarmos sua forma explícita precisamos conhecer as expansões de g, gαβ _{e de s}

αβ em termos dos parâmetros a e b. O determinante da métrica é

g = 1 24ε

αβγδ_εµνσρ_g

αµgβνgγσgδρ. (2.24) Da expressão para a expansão da métrica, Eq. (2.19), e definindo B2 _=Bµν_B

µν temos, como mostrado detalhadamente no Apêndice E

√

−g =√₋G

·

1 + 1 2

µ

1

2−a+ 4b

¶

B2

¸

. (2.25)

O inverso do tensor métrico é dado por

gαβ =Gαβ+Bαβ + (1₋a)BαρB_ρβ₋bGαβBρσBρσ. (2.26)

O inverso da parte simétrica da Eq. (2.26) é

sαβ =Gαβ −(1−a)Bρ(αBβ)ρ+bGαβB

2_{. (2.27)}

De posse destas expressões podemos escrever a expansão de Γσ

(αβ), dada na Eq.

(2.11). Tal expansão é

O primeiro termo desta expansão é o símbolo de Christoffel do campo de fundo Gαβ e o segundo termo é a contribuição do campo Bαβ. Tal contribuição é da ordem O(B2_{) e maior, pois s}

αβ = Gαβ +O(B2). Substituindo esta equação na expressão para o tensor Uαβ, na Eq. (2.9), resulta

Uαβ =Rαβ +Uαβ, (2.29)

com

Uαβ = Γ λ

(αβ)|λ−Γ λ

(αλ)|β + Γ λ

(αβ)Γ

ρ

(λρ)−Γ

λ

(αρ)Γ

ρ

(λβ). (2.30)

As barras verticais nos dois primeiros termos indicam derivadas covariantes em relação ao símbolo de Christoffel. Sabendo de tudo isso é fácil escrever a expressão para L1B em termos de a e b. Notemos que como cada Γ é da ordem O(B2) o termo √−GGαβ_U

αβ, que provém da expansão do primeiro termo do lado direito da Eq. (2.18) não pode dar contribuição nessa ordem. Isto porque os produtos quadráticos dos Γ em (2.30) são de quarta ordem e os dois primeiros termos darão contribuições que podem ser escritas como derivadas ordinárias totais, 2

não contribuindo então para a lagrangeana. Até a desejada segunda ordem, a expressão final para L1B é

2

Estes termos vão aparecer na lagrangeana sob a forma √−GGαβ_Γλ

(αβ)|λ. Como a derivada

covariante deGαβ _{em relação aos símbolos de Christoffel é nula, podemos escrever}

√

−GGαβ_Γλ

(αβ)|λ=

√

−G³Gαβ_Γλ

(αβ)

´

|λ=

√ −G

·_³

Gαβ_Γλ

(αβ)

´

,λ+G αβ_Γρ

(αβ)Σλρλ

¸

. (2.31)

Usando a relaçãoΣλ ρλ=

√ −G,ρ/

√

−Gobtemos√−GGαβ_Γλ

(αβ)|λ=

³√

−GGαβ_Γλ

(αβ)

´

L(2)_1B =√₋G

µ·

1

4(1−2a+ 4b)G

αβ_B2_{+ (1}

−a)BαµB_µβ

¸

Rαβ+ Λ(4b−a)B2

¶

2.3 Cálculo das Constantes de Expansão

da Métrica

Para a determinação dos dois parâmetros na Eq. (2.19) faremos uso da solução das equações de campo encontradas em II para uma massa pontual. A solução para gαβ correspondendo ao elemento de linha estático e esfericamente simétrico, dado em sua forma padrão por

ds2 =γdt2₋αdr2₋r2(dθ2+senθdφ2), (2.33) é

γ =

µ

1 + F

2

r4

¶1/2Ã

1₋ 2M r

·

1 + F

2

r4

¸−1/4!

(2.34) e

1 α =

µ

1 + F

2

r4

¶Ã

1₋ 2M r

·

1 + F

2

r4

¸−1/4!

, (2.35)

onde M é a massa da partícula. Os últimos componentes não nulos da métrica são

g[r0]=−g[0r]=

F

r2_{(1 +F}2_/r2₎3/4. (2.36)

Construiremos agora as coordenadas harmônicasXα _{a partir das coordenadas} padrão xµ_{= (t, r, θ, φ)seguindo os mesmos passos encontrados na RG [12]. Este} sistema de coordenadas é usado em problemas de radiação, no qual estamos en-volvidos. A condição harmônica é definida pela relação g(αβ)(X)Γλ

(αβ)(X) = 0,

Γλ_αβ(x) = ∂x λ ∂Xη µ ∂Xρ ∂xα ∂Xσ ∂xβ Γ

η

ρσ(X) +

∂2Xη ∂xα_∂xβ

¶

. (2.37)

Contraindo a Eq. (2.37) com g(αβ)_{(x) obtemos}

g(αβ)(x)Γλ_(αβ)(x) = ∂x λ ∂Xη µ ∂Xρ ∂xα ∂Xσ ∂xβ g

(αβ)_(x)Γη

ρσ(X) +g(αβ)(x) ∂2_Xη ∂xα_∂xβ

¶

. (2.38)

Utilizando agora a condição harmônica e também o fato de que

gαβ(X) = ∂X ρ ∂xα

∂Xσ ∂xβ g

αβ_{(x), (2.39)}

obtemos a condição harmônica escrita no sistema de coordenadas xµ

g(µν)

µ

∂2_Xη ∂xµ_∂xν −Γ

λ

(µν)

∂Xη ∂xλ

¶

= 0. (2.40)

Definimos agora as novas coordenadas Xµ _como

X1 _{=R(r)senθcosφ, (2.41)}

X2 _{=R(r)senθsenφ (2.42)}

e

X3 =R(r)cosθ. (2.43)

constantes. Com isso e tomando termos até ordem F2_/r4 _{obtemos as seguintes}

expansões para os elementos da métrica dados pelas Eq. (2.34) e (2.35).

γ = 1 + F

2

2r4 (2.44)

e

1

α = 1 + F2

r4 . (2.45)

As componentes necessárias da conexão são dadas em II. Substituindo estas re-lações na Eq. (2.40) obtemos a equação diferencial de segunda ordem que deve ser satisfeita pela função R(r). No Apêndice F mostramos que esta equação é

R′′+

µ

2 r −

5F2

r5

¶

R′₋ 2R r2 +

4RF2

r6 = 0. (2.46)

A solução dessa equação é do tipoR =r+y(r)F2_{, resultando paray(r)a equação}

y′′+2 ry

′

− _r22y−

1

r5 = 0. (2.47)

É fácil ver que a solução desta equação é proporcional a r−3_{. O resultado é}

y= 1

4r3, (2.48)

Logo, a solução da Eq. (2.46) é

R =r+ F

2

4r3. (2.49)

ds2 =

µ

1 + F

2

2r4

¶

dt2₋

·µ

1₋ F

2

2r4

¶

δij + F2

r4

XiXi R2

¸

dXidXj. (2.50)

Daqui vemos que

g00= 1 +

F2

2r4 (2.51)

e

gij =

µ

−1 + F

2

2r4

¶

δij − F2

r4

XiXi

R2 . (2.52)

Da Eq. (2.19) obtemos, em ordem mais baixa

g00= 1 + (a−2b)B0iB0i (2.53) e

gij =−(1−2bB0kB0k)δij −aB0iB0j. (2.54) Comparando a Eq. (2.53) com a Eq. (2.51) vemos que a₋2b= 1/2 e B0iB0i = F2_/r4_{. Notemos que esta segunda relação está de acordo com o termo de primeira}

ordem em (2.36) g(1)_[r0] =F/r2 ₌ √_B

0iB0i, o módulo deB0i. Da Eq. (2.54) e da Eq. (2.52) vemos que 2b = 1/2 e a = 1. O resultado final para os parâmetros é então

a= 1 (2.55)

e

b = 1

4. (2.56)

Capítulo 3

3.1 Deflexão Solar do Gráviton

Neste trabalho calculamos o ângulo de desvio do gráviton pelo Sol através do cálculo da seção de choque diferencial, que foi obtida anteriormente via Teoria Quântica de Campos [3]. Mostramos como tal seção de choque pode ser obtida através de um tratamento semiclássico. Como a grandeza GM/c2_{R é pequena}

para o Sol, da ordem de 10−6_{, o ângulo de desvio é pequeno, como o é na RG. O}

resultado obtido é o mesmo que aquele atribuído a luz na sua geodésica nula. O cálculo foi motivado pelo fato de que resultados idênticos foram obtidos também através da seção de choque tanto para a luz [1] como para o bóson escalar não-massivo [2]. A deflexão da trajetória atribuída a luz na geodésica nula só utiliza o fato de que sua velocidade é c, nada sendo dito a respeito do caráter tensorial da onda. Pode-se então suspeitar de que tal resultado deve ser o mesmo para qualquer campo não-massivo. Isto foi mostrado ser correto fazendo o cálculo da deflexão através da seção de choque onde aparece então o caráter tensorial da onda. Com o valor obtido também para o gráviton pode-se conjecturar que o resultado é válido para qualquer outro campo não-massivo.

3.2 Energia Gravitacional em uma Teoria

Não-Simétrica da Gravitação

Em I foi desenvolvida uma nova teoria não-simétrica da gravitação que se prop-unha a resolver o problema do aparecimento de modos radiativos de energia negativa. Tal problema estava presente em teorias anteriores, como mostrado por DDM. As ondas gravitacionais nesta nova teoria são geradas por duas fontes, a corrente Sα _{e o tensor energia-momentum T}µν_{. DDM mostraram que em} teo-rias anteriores as ondas devidas a Sα _{tem energia negativa. Em I foi feita a} análise da energia dessas ondas e foi afirmado que a teoria é livre de modos radia-tivos de energia negativa. Entretanto somente a parte da lagrangeana contendo a parcela anti-simétrica g[αβ] _{de g}αβ _{= g}(αβ) _+g[αβ] _{foi levada em consideração,}

deixando em aberto a parte contendo g(αβ)_{. O resultado da análise feita em I é}

Apêndice A

Espalhamento de Rutherford:

Tratamento Quântico

Da regra de ouro de Fermi segue que a probabilidade por unidade de tempo na transição da partícula com momento inicial~p0 =m~v0 para o grupo dednestados

com momento entre ~p e ~p+d~p induzida pelo potencial V é

w= 2π ¯

h |< ~p|V(r)|~p0 >|

2

µ

dn dE

¶

E=E0

. (A.1)

Dividindo pela corrente incidente J =v0/V, sendoV o volume de normalização,

obtemos a seção de choque dσ. Como dn = (V p2_dp)/(2π¯h)3 _{e dE/dp = p/m}

resulta

dσ = m

2

(2π¯h2)2

¯ ¯ ¯ ¯ Z

V(r)ei(~k0−~k)·~r dV ¯ ¯ ¯ ¯ 2

dΩ. (A.2)

Calculando a transformada de Fourier de V =qQ/r obtemos

Z

V(r)ei(~k0−~k)·~r

dV = πqQ

k2_sen2¡_θ

2

¢. (A.3)

dσ dΩ =

µ

qQm 2k2_¯h2

¶2

1 sen4¡_θ

2

¢. (A.4)

Apêndice B

Cálculo de

h

_µν

Com a expansão gµν =ηµν +hµν os símbolos de Christoffel até primeira ordem em hµν ficam

Σ(1)_αβλ = 1 2η

λρ_(h

ρν,µ+hρν,µ−hµν,ρ). (B.1) O tensor de Ricci em primeira ordem fica

R_µν(1) = Σ(1)_µν,λλ ₋Σ(1)_νλ,µλ

=₋1 2h ρ µν,ρ + 1 2h ρ ρµ,ν − 1 2h,µν +

1 2h

ρ ρν,µ ,

(B.2)

com h=ηµν_h

µν. A expansão para o escalar de Ricci é

R(1) =h_ρσ,ρσ₋h_,ρρ. (B.3) De posse destas expressões podemos escrever as equações de Einstein em primeira ordem (linearizadas) Rµν(1)−(1/2)ηµνR(1) = (8πG/c4)Tµν(0). O resultado é

−1₂h_µν,ρ ρ₋1 2h,µν+

1 2

¡

h_ρµ,νρ+h_ρν,µρ¢

−1₂ηµν

¡

h_ρσ,ρσ₋h_,ρρ¢

= 8πG c4 T

(0)

Como a teoria é livre por uma transformação geral de coordenadas podemos escolher um sistema de coordenadas que simplifique estas equações. Um sistema conveniente é o sistema harmônico de coordenadas, definido por gαβ_Σλ

αβ = 0. Esta relação em primeira ordem no campo hαβ fica

hλ µ_µ, = 1 2h

λ

, . (B.5)

Com esta relação a Eq. (B.4) toma a forma

−1₂ µ

hµν − 1 2ηµνh

¶ ρ

,ρ

= 8πG c4 T

(0)

µν. (B.6)

Chamando

hµν =hµν− 1

2ηµνh (B.7)

temos

h_,ρρ=₋16πG c4 T

(0)

µν . (B.8)

No caso estático as componentes do tensor energia-momentumTµν(0) sãoT₀₀(0) = ρc2_{, T}(0)

0i = 0 e T

(0)

ij = 0. Com isto, e lembrando que o campo hµν não depende do tempo, as componentes da Eq. (B.8) tornam-se

∇2h00 =−

16πG

c2 ρ, (B.9)

∇2h0i = 0 (B.10)

e

Como as duas últimas equações devem valer para todo o espaço, devemos ter h0i = 0 e hij = 0. Para uma massa pontual M temos ρ=M δ(~r), e resulta

h00 =

4M G

c2_r (B.12)

Apêndice C

Soma Sobre as Polarizações do

Gráviton

A forma mais geral de εijεmn é

X

λ

ε(_ijλ)ε(_mnλ) =aδijδmn+b(δimδjn+δinδjm) +c(δimkjkn+δjnkikm

+δinkjkm+δjmkikn) +d(δijkmkn+δmnkikj) +ekikjkmkn.

(C.1)

Sendo a, b, c, d e e constantes a serem determinadas. Os termos agrupados sob os mesmos coeficientes vêm do fato de que o tensor deve respeitar a simetria entre os índices (i, j), (m, n) e também dos pares (jm, in). Este tensor satisfaz as condições εijki = 0 (transversalidade), εii = 0 (traço nulo) e εijεij = 1 (nor-malização). Contraindo (C.1) com ki e utilizando a condição de transversalidade temos

δmnkj(a+d) +δjnkm(b+c) +δmjkn(b+c) +kjkmkn(2c+e+d) = 0 (C.2)

a+d= 0

b+c= 0

2c+e+d= 0.

(C.3)

Disto resulta

e =a+ 2b. (C.4)

Usando agora a condição de traço nulo na Eq. (C.1), temos

δmn(3a+ 2b+d) +kmkn(4c+ 3d+e) = 0. (C.5) Usando (C.4), chegamos a

a =c

a =₋b

a =₋e.

(C.6)

Da condição de normalização vem

3a+ 12b+ 8c+ 2d+e= 2. (C.7) Logo

a =₋1

2. (C.8)

X

λ

ε(_ijλ)ε(_mnλ) = 1

2(δimδjn+δinδjm−δijδmn−δimkjkn−δjnkikm−δinkjkm

−δjmkikn+δijkmkn+δmnkikj +kikjkmkn).

Apêndice D

Cálculo de

T

_B

µν

Vamos aqui reproduzir o cálculo apresentado em I para a contribuição do campo Bαβ vinda da parte lagrangeana que contém a parte anti-simétrica de gαβ. Da Eq. (2.18) temos

L2B =g[αβ]

µ

1

2Λg[αβ]+ Γ[α,β]

¶

. (D.1)

Em segunda ordem esta equação se torna

L(2)_2B =√₋GBαβ

µ

1

2ΛBαβ + Γ

(1) [α,β]

¶

. (D.2)

Da Eq. (2.6) vemos que Γ(1)_[α,β] =₋ΛBαβ. Disto resulta

L(2)_2B =₋Λ 2

√

−GBαβBαβ

=₋Λ 2

√

−GGαρGσβBρσBαβ.

(D.3)

Das relações δ√₋G = (1/2)√₋GGαβδGαβ e δGµν = −Gµ(αGβ)νδGαβ resulta para a variação da lagrangeana

δL(2)_2B =√₋GΛ

µ

BµρBν_ρ− 1 4GµνB

2

¶

Apêndice E

Cálculo do Determinante da

Métrica

O determinante da métrica é

g = 1 24ε

αβγδ_εµνση_g

αµgβνgγσgδη. (E.1) Reescrevendo a Eq. (2.19) sob a formagαµ=Gαµ+gαµ;gαµ =Bαµ+aBαρBρµ+ bGαµB2 tem-se, até a segunda ordem considerada

g =G+ 1 24ε

αβγδ_εµνρσ£

4GαµGβνGγρgδσ+ 6GαµGβνgγρgδσ

¤

. (E.2) Notemos que o termo Bδσ contido em gδσ não dará contribuição porque é anti-simétrico. Usando as relações εµνρσ_G

αµGβν = −Gεαβτ ωGτ ρGωσ e também a re-lação εαβγδ_ε

αβτ ω =−2(δτγδωδ −δτδδωγ) obtemos

g =G

µ

1 +

·

1

2 −a+ 4b

¸

B2

¶

. (E.3)

√

−g =√₋G

µ

1 + 1 2

·

1

2−a+ 4b

¸

B2

¶

Apêndice F

Cálculo da Função

R

(

r

)

A condição harmônica no sistema de coordenadas xµ _{= (t,−r,−θ,−φ) fica (Eq.} (2.40))

✷Xi ≡g(µν)

µ

∂2_X

i ∂xµ_∂xν −Γ

λ

(µν)

∂Xi ∂xλ

¶

= 0. (F.1)

Como somente a parte simétrica do tensor gαβ _{aparece nesta equação, os únicos} termos não nulos serão aqueles da diagonal, portanto

✷Xi =−g00Γ100Xi,1+g11Xi,11−g11Γ111Xi,1−g33Γ133Xi,1−g22Γ122Xi,1

+g22Xi,22−g33Γ332 Xi,2+g33Xi,33.

(F.2)

As componentes necessárias de gαβ _{e da conexão, com ω =g}

r0, são [7]

g00= α

αγ₋ω2; g 11 ₌

−_αγ γ

−ω2;

g22=₋1

r2; g 33₌

− 1

r2_sen2_θ

e

Γ1₀₀ = γ

′

2γ +

γF2

αr(r4_+F2₎;

Γ1₁₁ = α

′

2α +

F2

r(r4_+F2₎;

Γ1₂₂ =₋r α; Γ1₃₃ =₋−rsen

2_θ

α ;

Γ2₃₃ =₋senθcosθ.

(F.4)

Aqui usamos a notação γ′ _{= γ}

,r. Destas expressões e também das Eq. (2.41) -(2.43) obtemos, definindo A=r4_+F2 _{por simplicidade}

✷Xi =−g00

·

γ′

2α + γF2

αrA

¸

R′Xi R +g

11_R′′Xi R −

·

α′

2α + γF2

rA

¸

g11R′Xi R

− 2XiR

′

rαR +

2Xi r2 .

(F.5)

Fatorando o termo g11_X

i/R e lembrando queg00/g11=−α/γ, obtemos

✷Xi = g11_X

i R

·µ

γ′

2γ − α′

2α − 2 rαg11

¶

R′+R′′+ 2R r2_g11

¸

. (F.6)

Usando a condição harmônica, ✷Xi = 0 obtemos a equação diferencial para a função R(r)

µ

γ′

2γ − α′

2α − 2 rαg11

¶

R′+R′′+ 2R

r2_g11 = 0, (F.7)

Até a desejada ordem F2_/r4 _{resultam as seguintes relações}

γ′

2γ =− F2

r5, (F.8)

α′

2α =− 2F2

2

rαg11 =−

2 r

µ

1₋ F

2

r4

¶

(F.10) e

2

r2_g11 =−

2 r2

µ

1₋ 2F

2

r4

¶

. (F.11)

Com estas expressões, a Eq. (F.7) torna-se

R′′₊

µ

2 r −

5F2

r5

¶

R′₋ 2R r2 +

4RF2

r6 = 0. (F.12)

Apêndice G

Transformação de Coordenadas do

Elemento de Linha

Partimos do elemento de linha no sistema padrão de coordenadas.

ds2 =γdt2₋αdr2₋r2(dθ2+senθdφ2)

=γdt2₋αdr2₋r2dΩ.

(G.1)

Da definição das coordenadas harmônicas vemos que R2 _=X2

1 +X22 +X32.

Por-tanto, temos dR= (X~ _·d ~X)/R, sendoX~ _·d ~X =X1dX1+X2dX2+X3dX3. Como

dR = (dR/dr)dr=R′_{dr obtemos}

dr2 = (X~ ·d ~X)

2

(RR′₎2 . (G.2)

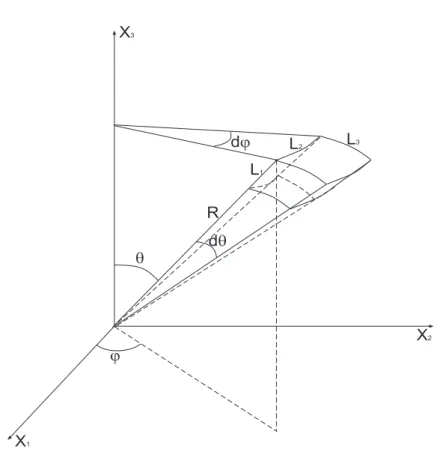
Passemos agora para a transformação do elemento dΩ. Vemos que os lados do paralelepípedo mostrado na Fig. G.1 são dados por L1 =dR, L2 =Rsenθdφ

e L3 =Rdθ. Como sua hipotenusa é dXidXi =L21+L22+L23 obtemos

X3 X1 X2 q dq dj L1 L3 L2 R j

Figura G.1: Transformação do elemento de linha

Substituindo as Eqs. (G.2) e (G.2) na Eq. (G.1) obtemos

ds2 =γdt2₋ α

(RR′₎2(X~ ·d ~X) 2

− r

2

R2

µ

dXidXi− 1

(R′₎2(X~ ·d ~X) 2

¶

(G.4)

Substituindo agora a expressão para R dada na Eq. (2.49), juntamente com as

expressões paraγ e α dadas em (2.44) e (2.45), obtemos

ds2 =

µ

1 + F

2

2r4

¶

dt2 ₋

·µ

1₋ F

2

2r4

¶

δij+

F2

r4

XiXi

R2

¸

dXidXj, (G.5)

[1] Bocaletti, D. de Sabbata, V. Gualdi, C. e Fortini, P. Nuevo Cimento, 48 A, 58 (1967).

[2] Accioly, A. e Ragusa, S., Class. Quantum Grav., 19, 5429 (2002).

[3] DeWitt, B. S., Phys. Rev., 162, 1239 (1967).

[4] Landau, L e Lifshitz, E. Teoria do Campo, (1980). Editora Mir. p. 450.

[5] Landau, L e Lifshitz, E. Teoria do Campo, (1980). Editora Mir. p. 461.

[6] Ragusa, S., Physical Review D, 56, 2864-873 (1997).

[7] Ragusa, S., Gen. Relat. Grav., p.275 (1998).

[8] Damour, T., Deser, S., McMarthy, J.. Phys. Rev. D, 45, R3289 (1993).

[9] Santaló, L. A. Perspectives in Geometry and Relativity, (1963). Editado por B. Hoffmann (Indiana University Press, Bloomington).

[10] Einstein, A., Ann. Math. 46, 578 (1945); Einstein, A. and Straus, E. G., ibid. 47, 731 (1946)

[11] Landau, L e Lifshitz, E. Teoria do Campo, (1980). Editora Mir. p. 110.

[12] Weinberg, S. Gravitation and Cosmology: Principles and Aplications of the General Therory of Relativity, (1972). John Wiley & Sons, Inc.